Elastic Spatial Query Processing in OpenStack Cloud Computing Environment for Time-Constraint Data Analysis
Abstract
:1. Introduction
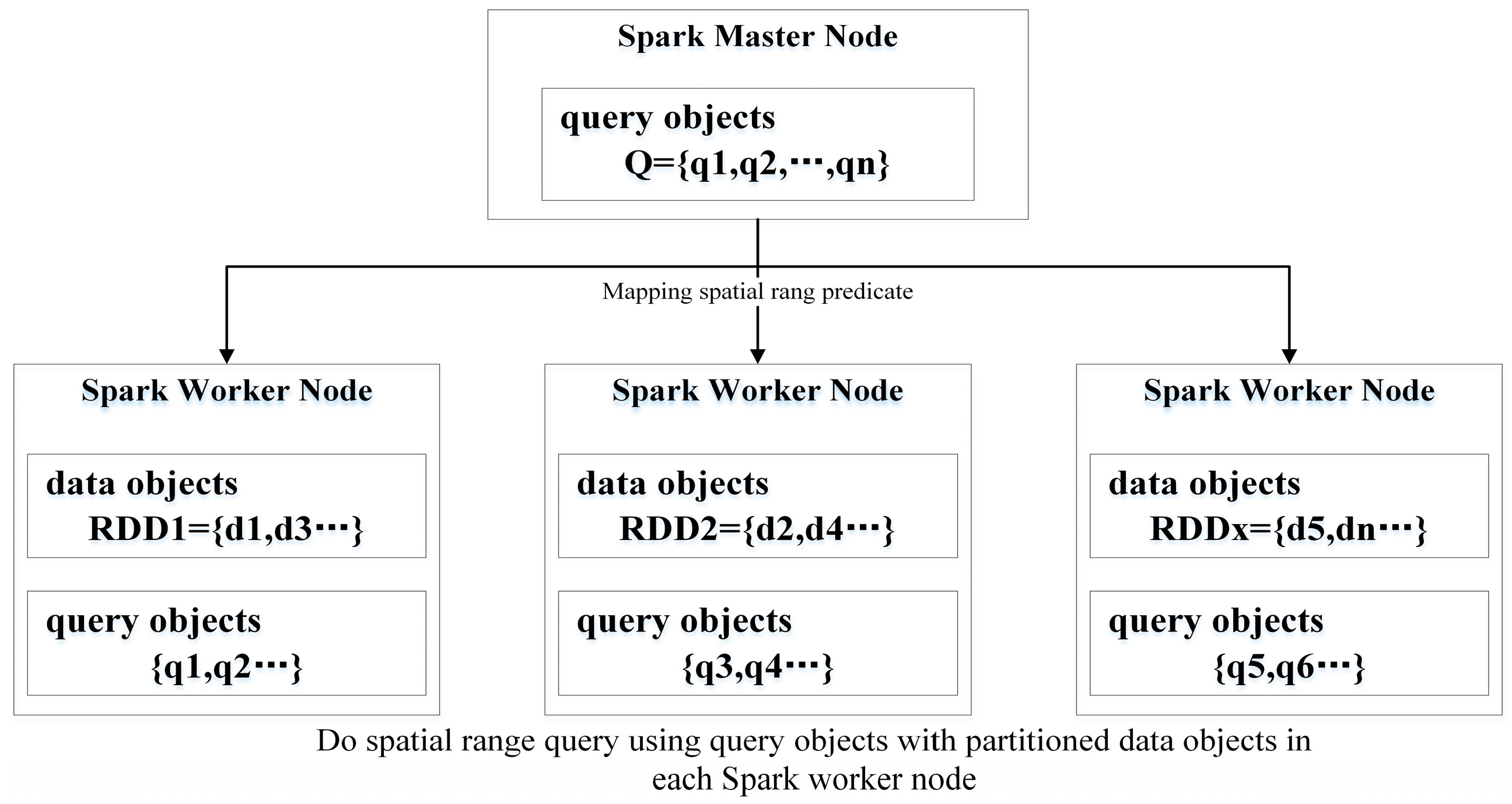
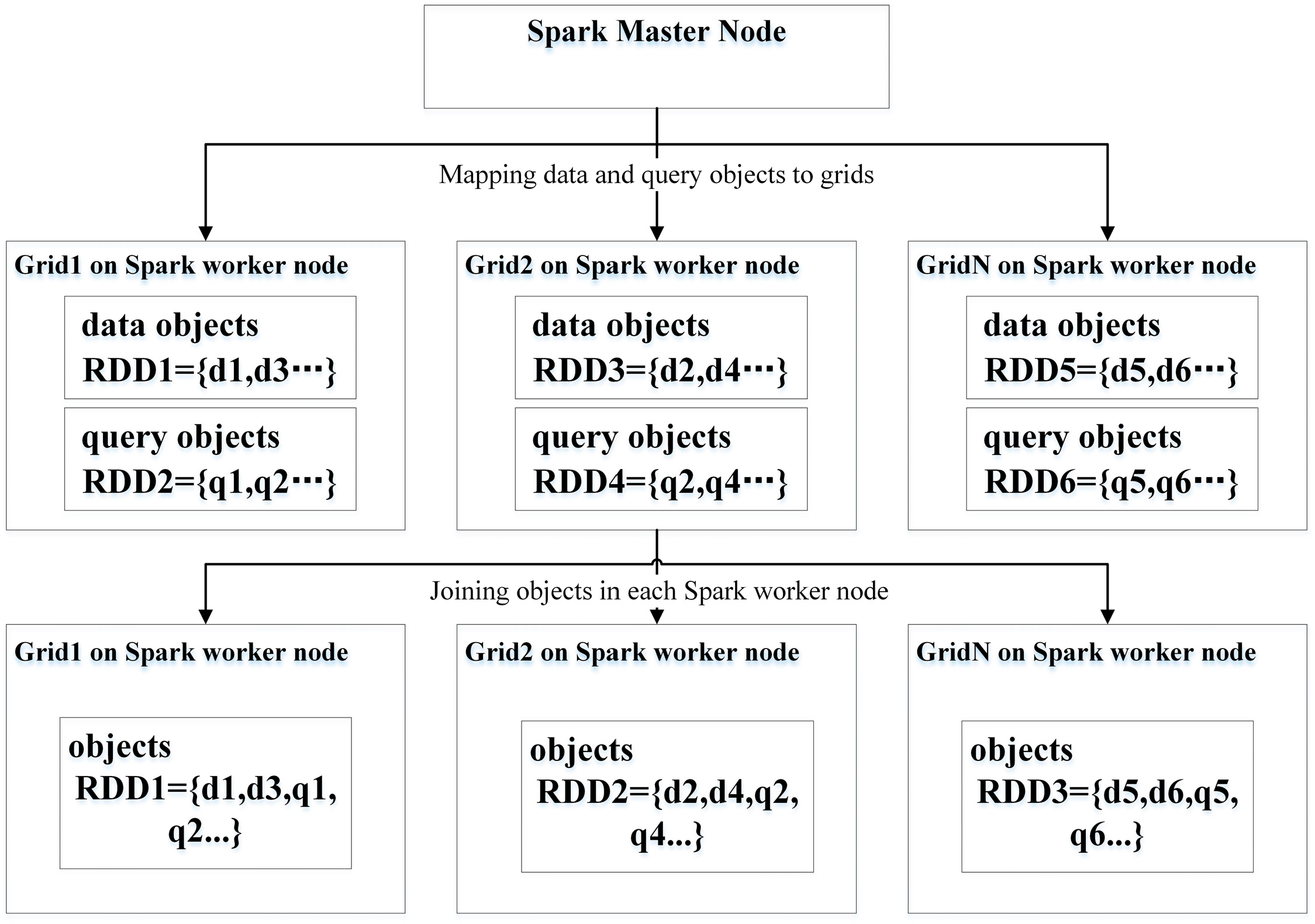
2. Parallel SQPAs Using Spark CM
2.1. PSQPAs Using Spark CM
2.2. Identifying Factors Impacting the Efficiency of Spark-Based PSQPAs
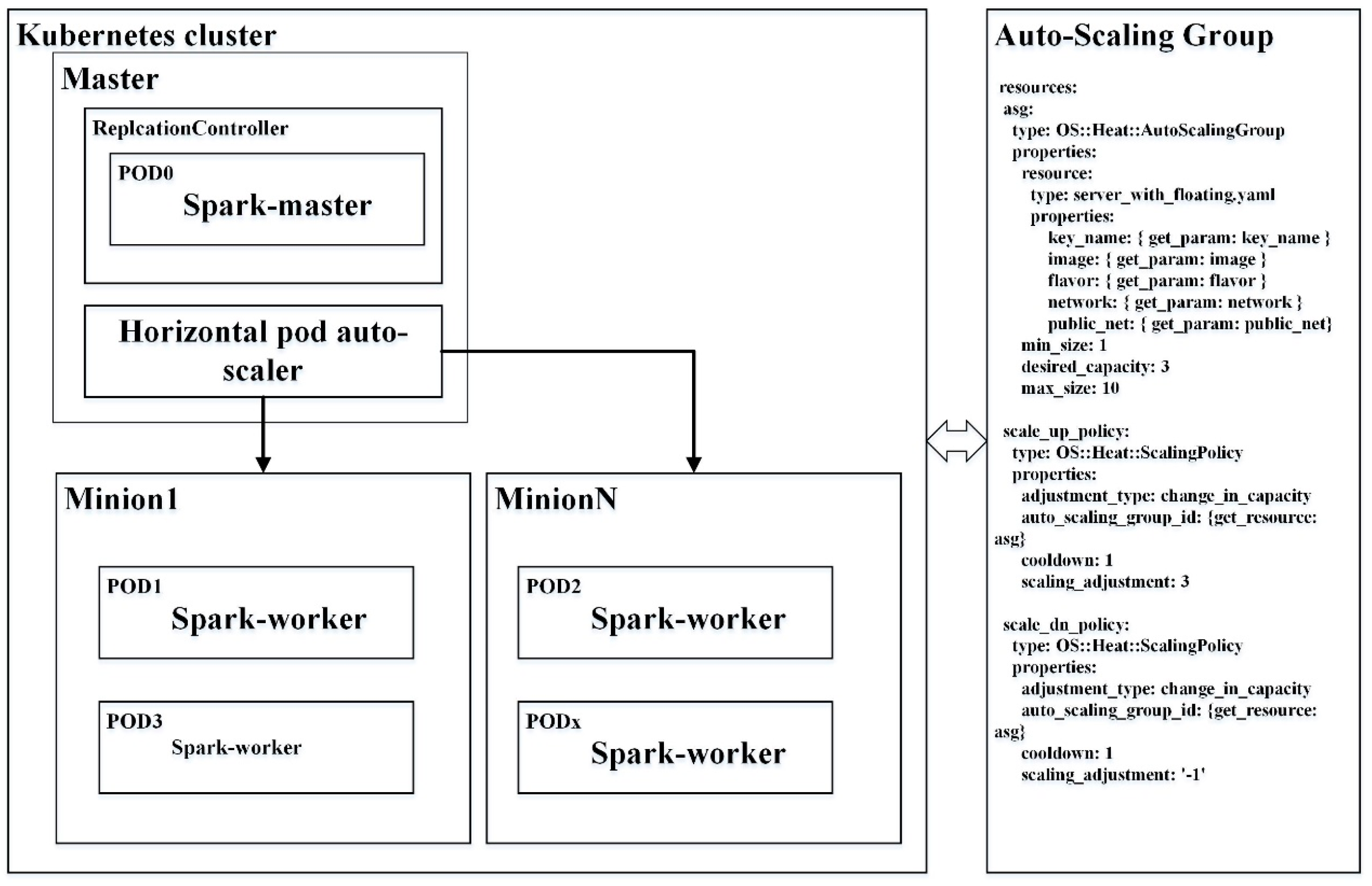
3. Horizontal Auto-Scaling Containers for Elastic Spatial Query Processing
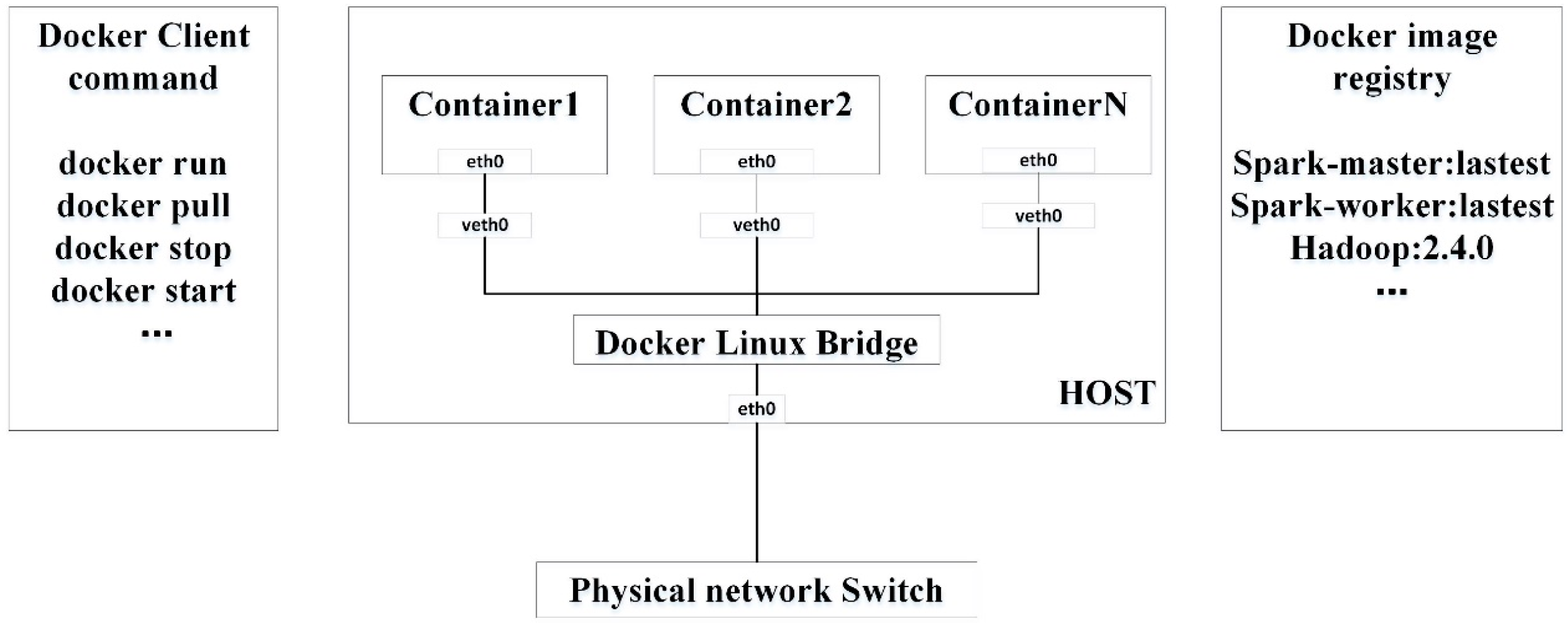
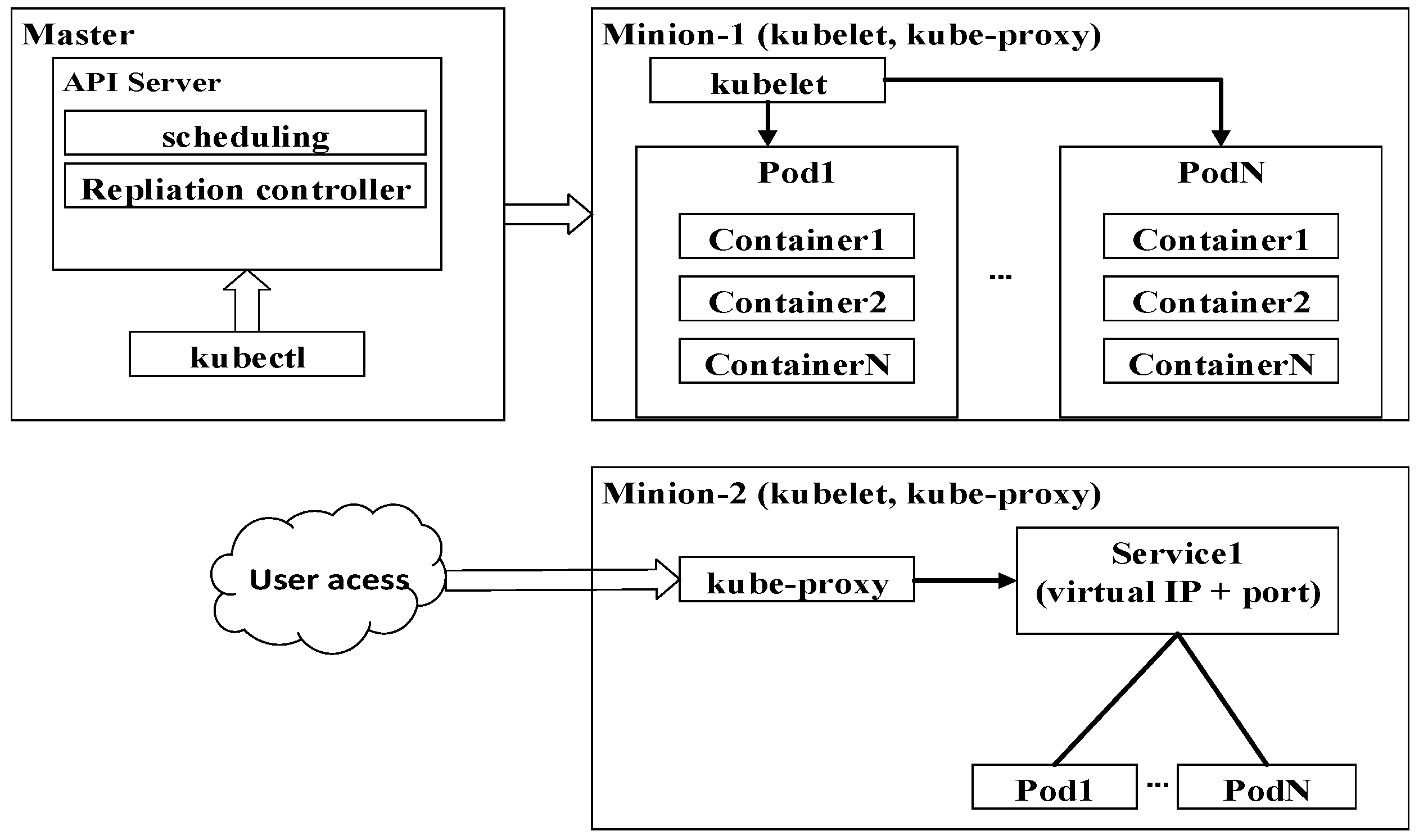
3.1. Docker with Kubernetes Orchestration for Clustering Containers
3.2. Horizontal Auto-Scaling Containers for Elastic Spatial Query Processing
4. Experiments and Results
4.1. Spatial Datasets for A Spatial Query Processing Case
4.2. Cloud Computing Environemt
4.3. Result
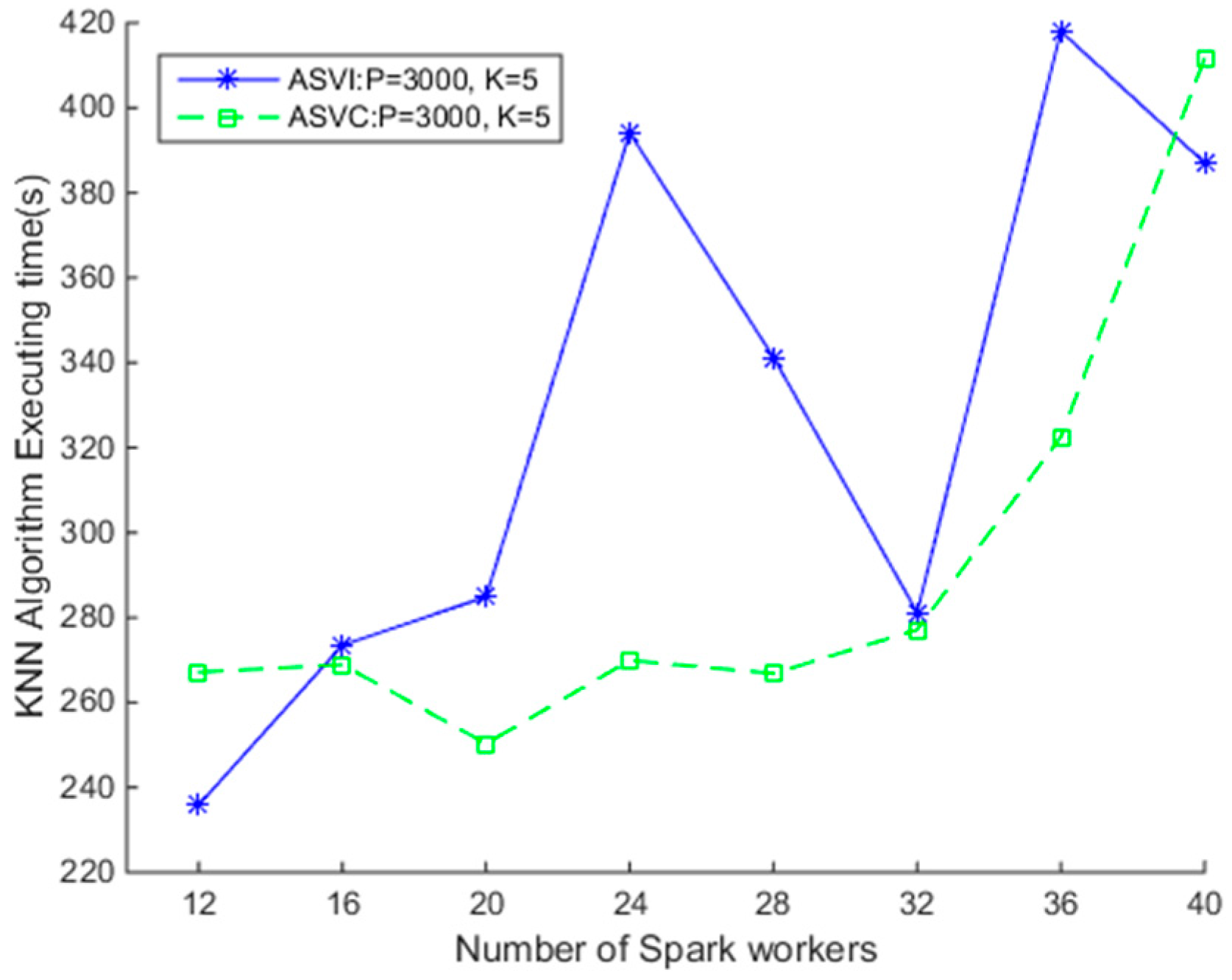
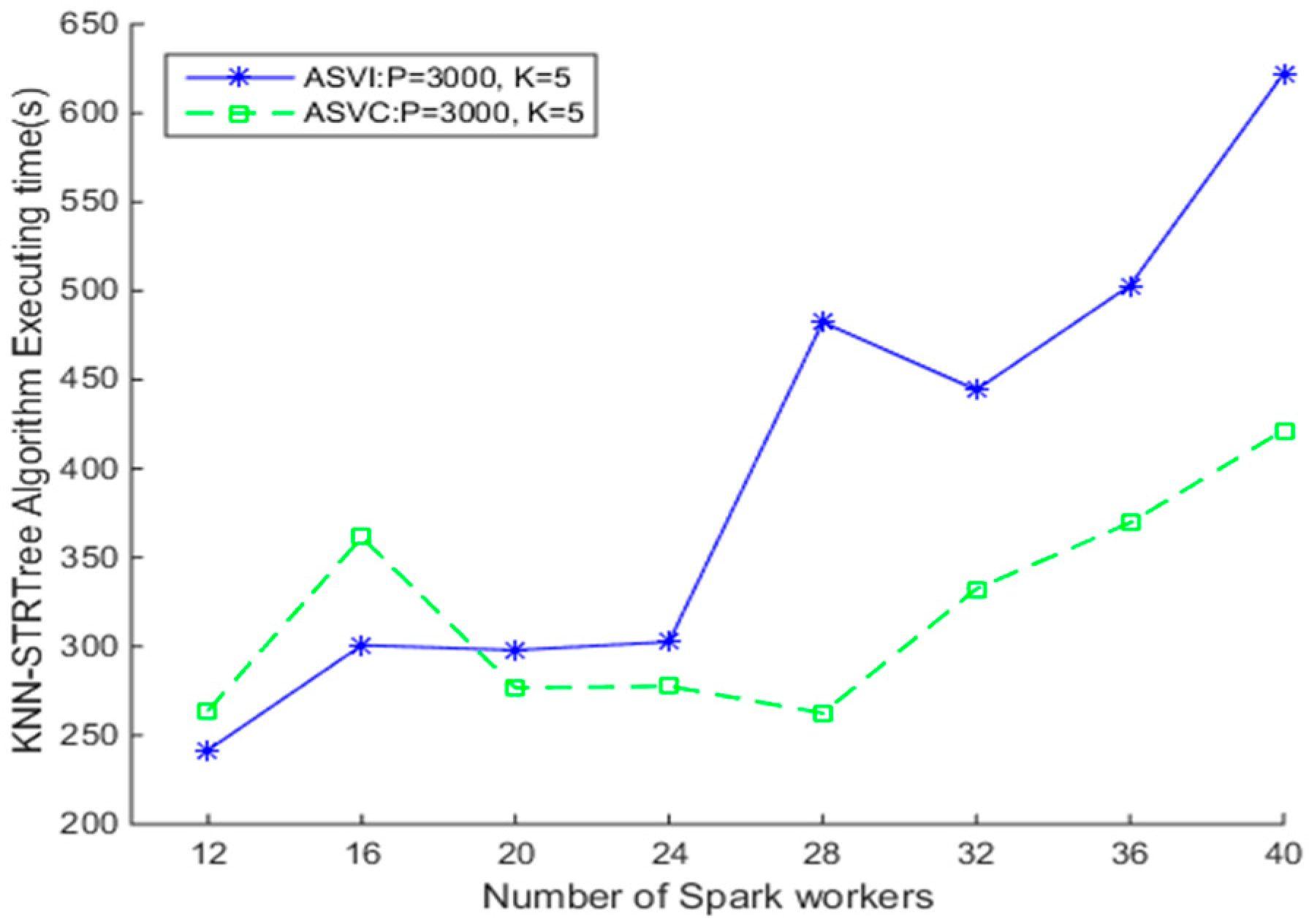
4.3.1. Comparison of SNNQAs using ASVI and ASVC
4.3.2. SNNQAs Using ASVC
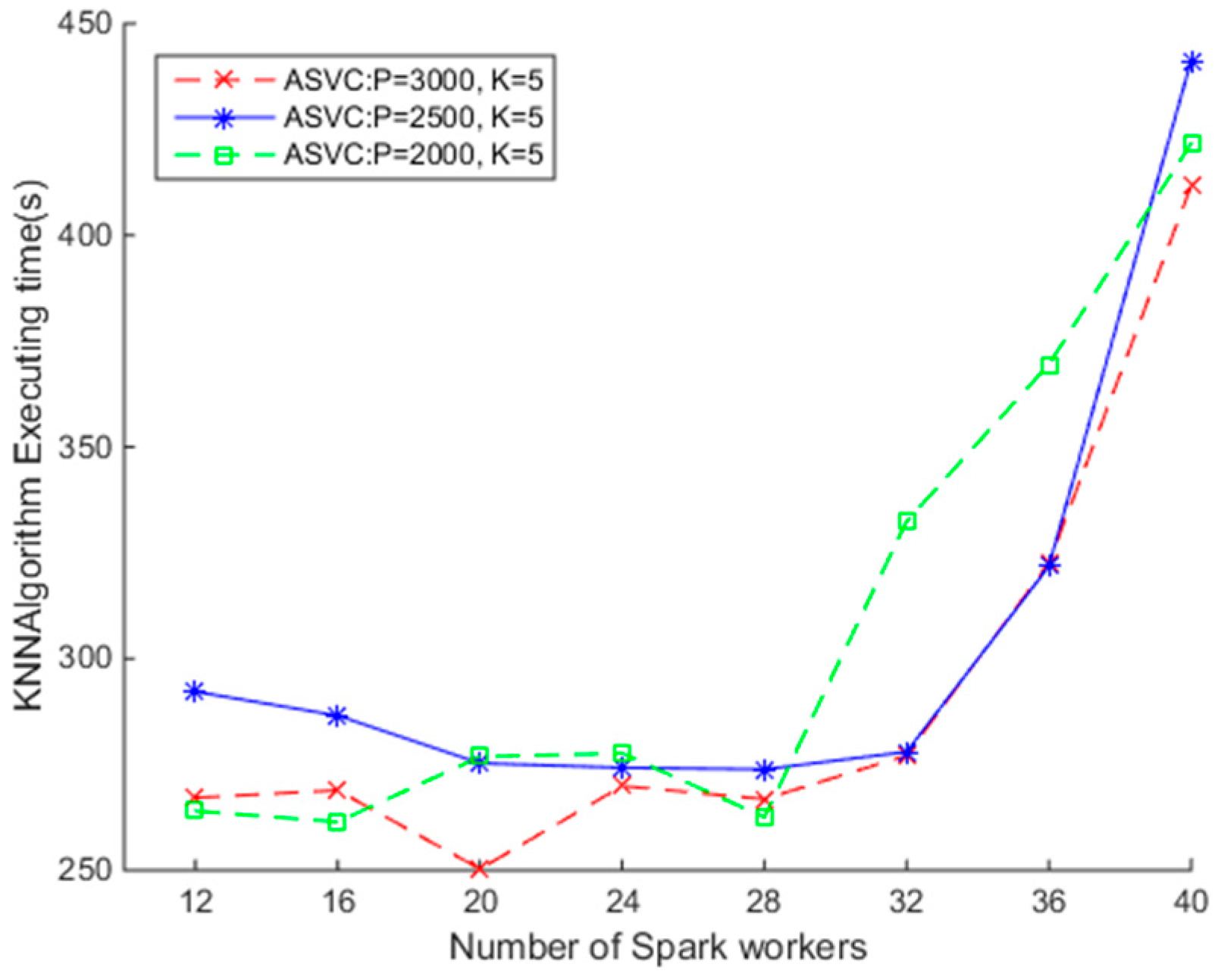
4.3.3. SNNQAs Using Different ASVC Strategies
4.3.4. SNNQAs Using ASVC in an Auto-Scaling Group
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lee, J.G.; Kang, M. Geospatial big data: Challenges and opportunities. Big Data Res. 2015, 2, 74–81. [Google Scholar] [CrossRef]
- Yang, C.; Huang, Q.; Li, Z.; Liu, K.; Hu, F. Big data and cloud computing: Innovation opportunities and challenges. Int. J. Digit. Earth 2017, 10, 13–53. [Google Scholar] [CrossRef]
- Li, S.; Dragicevic, S.; Castro, F.A.; Sester, M.; Winter, S.; Coltekin, A.; Pettit, C.; Jiang, B.; Haworth, J.; Stein, A. Geospatial big data handling theory and methods: A review and research challenges. ISPRS J. Photogramm. Remote Sens. 2016, 115, 119–133. [Google Scholar] [CrossRef]
- Li, Z.; Yang, C.; Liu, K.; Hu, F.; Jin, B. Automatic scaling hadoop in the cloud for efficient process of big geospatial data. ISPRS Int. J. Geo-Inf. 2016, 5, 173. [Google Scholar] [CrossRef]
- Yang, C.; Goodchild, M.; Huang, Q.; Nebert, D.; Raskin, R.; Xu, Y.; Bambacus, M.; Fay, D. Spatial cloud computing: How can the geospatial sciences use and help shape cloud computing? Int. J. Digit. Earth 2011, 4, 305–329. [Google Scholar] [CrossRef]
- Aji, A.; Wang, F. High performance spatial query processing for large scale scientific data. In Proceedings of the SIGMOD/PODS 2012 PhD Symposium, Scottsdale, AZ, USA, May 2012; ACM: New York, NY, USA, 2012; pp. 9–14. [Google Scholar]
- Orenstein, J.A. Spatial query processing in an object-oriented database system. In ACM SIGMOD Record; ACM: New York, NY, USA, 1986; Volume 15, pp. 326–336. [Google Scholar]
- You, S.; Zhang, J.; Gruenwald, L. Large-scale spatial join query processing in cloud. In Proceedings of the 2015 31st IEEE International Conference on Data Engineering Workshops (ICDEW), Seoul, Korea, 13–17 April 2015; pp. 34–41.
- Zhong, Y.; Han, J.; Zhang, T.; Li, Z.; Fang, J.; Chen, G. Towards parallel spatial query processing for big spatial data. In Proceedings of the 2012 IEEE 26th International Parallel and Distributed Processing Symposium Workshops & PhD Forum (IPDPSW), Shanghai, China, 21–25 May 2012; pp. 2085–2094.
- Huang, W.; Meng, L.; Zhang, D.; Zhang, W. In-memory parallel processing of massive remotely sensed data using an apache spark on hadoop yarn model. IEEE J.Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 3–19. [Google Scholar] [CrossRef]
- Zaharia, M.; Chowdhury, M.; Das, T.; Dave, A.; Ma, J.; McCauley, M.; Franklin, M.J.; Shenker, S.; Stoica, I. Resilient distributed datasets: A fault-tolerant abstraction for in-memory cluster computing. In Proceedings of the 9th USENIX Conference on Networked Systems Design and Implementation, San Jose, CA, USA, April 2012; USENIX Association: Berkeley, CA, USA, 2012; p. 2. [Google Scholar]
- Zaharia, M.; Xin, R.S.; Wendell, P.; Das, T.; Armbrust, M.; Dave, A.; Meng, X.; Rosen, J.; Venkataraman, S.; Franklin, M.J. Apache spark: A unified engine for big data processing. Commun. ACM 2016, 59, 56–65. [Google Scholar] [CrossRef]
- Yu, J.; Wu, J.; Sarwat, M. Geospark: A cluster computing framework for processing large-scale spatial data. In Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems; ACM: New York, NY, USA, 2015; p. 70. [Google Scholar]
- Tang, M.; Yu, Y.; Malluhi, Q.M.; Ouzzani, M.; Aref, W.G. Locationspark: A distributed in-memory data management system for big spatial data. Proc. VLDB Endow. 2016, 9, 1565–1568. [Google Scholar] [CrossRef]
- Ray, S.; Simion, B.; Brown, A.D.; Johnson, R. Skew-resistant parallel in-memory spatial join. In Proceedings of the 26th International Conference on Scientific and Statistical Database Management; ACM: New York, NY, USA, 2014; p. 6. [Google Scholar]
- Herbst, N.R.; Kounev, S.; Reussner, R. Elasticity in cloud computing: What it is, and what it is not. In Proceedings of the 10th International Conference on Autonomic Computing (ICAC 13), San jose, CA, USA, 26–28 June 2013; pp. 23–27.
- Galante, G.; De Bona, L.C.E.; Mury, A.R.; Schulze, B.; da Rosa Righi, R. An analysis of public clouds elasticity in the execution of scientific applications: A survey. J. Grid Comput. 2016, 14, 193–216. [Google Scholar] [CrossRef]
- Leitner, P.; Cito, J. Patterns in the chaos—a study of performance variation and predictability in public iaas clouds. ACM Trans. Internet Tech. (TOIT) 2016, 16, 15. [Google Scholar] [CrossRef]
- Lorido-Botran, T.; Miguel-Alonso, J.; Lozano, J.A. A review of auto-scaling techniques for elastic applications in cloud environments. J. Grid Comput. 2014, 12, 559–592. [Google Scholar] [CrossRef]
- Kang, S.; Lee, K. Auto-scaling of geo-based image processing in an openstack cloud computing environment. Remote Sens. 2016, 8, 662. [Google Scholar] [CrossRef]
- Soltesz, S.; Pötzl, H.; Fiuczynski, M.E.; Bavier, A.; Peterson, L. Container-based operating system virtualization: A scalable, high-performance alternative to hypervisors. In ACM SIGOPS Operating Systems Review; ACM: New York, NY, USA, 2007; pp. 275–287. [Google Scholar]
- Felter, W.; Ferreira, A.; Rajamony, R.; Rubio, J. An updated performance comparison of virtual machines and linux containers. In Proceedings of the 2015 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), Philadelphia, PA, USA, 29–31 March 2015; pp. 171–172.
- Brinkhoff, T.; Kriegel, H.-P.; Seeger, B. Efficient Processing of Spatial Joins Using R-trees; ACM: New York, NY, USA, 1993; Volume 22. [Google Scholar]
- Akdogan, A.; Demiryurek, U.; Banaei-Kashani, F.; Shahabi, C. Voronoi-based geospatial query processing with mapreduce. In Proceedings of the 2010 IEEE Second International Conference on Cloud Computing Technology and Science (CloudCom), Indianapolis, IN, USA, 30 November–3 December 2010 ; pp. 9–16.
- Brinkhoff, T.; Kriegel, H.-P.; Schneider, R.; Seeger, B. Multi-step Processing of Spatial Joins; ACM: New York, NY, USA, 1994; Volume 23. [Google Scholar]
- Lee, K.; Ganti, R.K.; Srivatsa, M.; Liu, L. Efficient spatial query processing for big data. In Proceedings of the 22nd ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems; ACM: New York, NY, USA, 2014; pp. 469–472. [Google Scholar]
- Chen, H.-L.; Chang, Y.-I. Neighbor-finding based on space-filling curves. Inf. Syst. 2005, 30, 205–226. [Google Scholar] [CrossRef]
- Gupta, H.; Chawda, B.; Negi, S.; Faruquie, T.A.; Subramaniam, L.V.; Mohania, M. Processing multi-way spatial joins on map-reduce. In Proceedings of the 16th International Conference on Extending Database Technology; ACM: New York, NY, USA, 2013; pp. 113–124. [Google Scholar]
- Mouat, A. Using Docker: Developing and Deploying Software with Containers; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2015. [Google Scholar]
- Peinl, R.; Holzschuher, F.; Pfitzer, F. Docker cluster management for the cloud-survey results and own solution. J. Grid Comput. 2016, 14, 265–282. [Google Scholar] [CrossRef]
- Burns, B.; Grant, B.; Oppenheimer, D.; Brewer, E.; Wilkes, J. Borg, omega, and kubernetes. Commun. ACM 2016, 59, 50–57. [Google Scholar] [CrossRef]
- Jansen, C.; Witt, M.; Krefting, D. Employing docker swarm on openstack for biomedical analysis. In Proceedings of the International Conference on Computational Science and Its Applications; Springer: Berlin, Germany, 2016; pp. 303–318. [Google Scholar]
- Jackson, K.; Bunch, C.; Sigler, E. Openstack Cloud Computing Cookbook; Packt Publishing Ltd.: Birmingham, UK, 2015. [Google Scholar]
- Liu, Y.; Kang, C.; Gao, S.; Xiao, Y.; Tian, Y. Understanding intra-urban trip patterns from taxi trajectory data. J. Geogr. Syst. 2012, 14, 463–483. [Google Scholar] [CrossRef]
- Liu, X.; Gong, L.; Gong, Y.; Liu, Y. Revealing travel patterns and city structure with taxi trip data. J. Transp. Geogr. 2015, 43, 78–90. [Google Scholar] [CrossRef]

| Node | Cloud Actors | Specification | Services |
|---|---|---|---|
| 192.168.203.135 | Controller | 4 cores, 4 GB memory and 500 GB disks | Nova-cert, Nova-consoleauth, Nova-scheduler, Nova-conductor, Cinder-scheduler, Neutron-metadata-agent, Neutron-linuxbridge-agent, Neutron-l3-agent, Neutron-dhcp-agent, Heat-engine |
| 192.168.203.16 | Compute | 24 cores, 92 GB memory and 160 GB disks | Nova-compute, Neutron-linuxbridge-agent |
| 192.168.200.97 | Compute | 24 cores, 48 GB memory and 500 GB disks | Nova-compute, Neutron-linuxbridge-agent |
| 192.168.200.109 | Compute | 24 cores, 48 GB memory and 500 GB disks | Nova-compute, Neutron-linuxbridge-agent |
| 192.168.200.111 | Compute | 24 cores, 48 GB memory and 500 GB disks | Nova-compute, Neutron-linuxbridge-agent |
| 192.168.203.16 | Block Storage | 8 cores, 32 GB memory and 3 TB disks | Cinder-volume |
| Virtual Cluster | Specification | Images and Software |
|---|---|---|
| Ubuntu_cluster | 1 instance with 4 VCPUs and 8 GB RAM, and 4 instances each with 2V-CPus and 4 GB RAM | Ubuntu 14.04.5 trusty image with Spark 1.5.2, Java(TM) SE Runtime Environment (build 1.7.0_45-b18), Scala 2.10.4 |
| CoreOS_cluster | 1 instance with 4 VCPUs and 8 GB RAM, and 4 instances each with 2V-CPus and 4 GB RAM | CoreOS 1185.3.0 image with Kubernetes 1.3.4, Heapster 1.1.0 and Docker 1.11.2 |
| Software | Version |
|---|---|
| Docker | 1.11.2 |
| CoreOS | 1185.3.0 |
| Spark | 1.5.2 |
| Scala | 2.10.4 |
| JDK | 1.7.0_45-b18 |
| Heapster | 1.1.0 |
| Kubernetes | 1.3.4 |
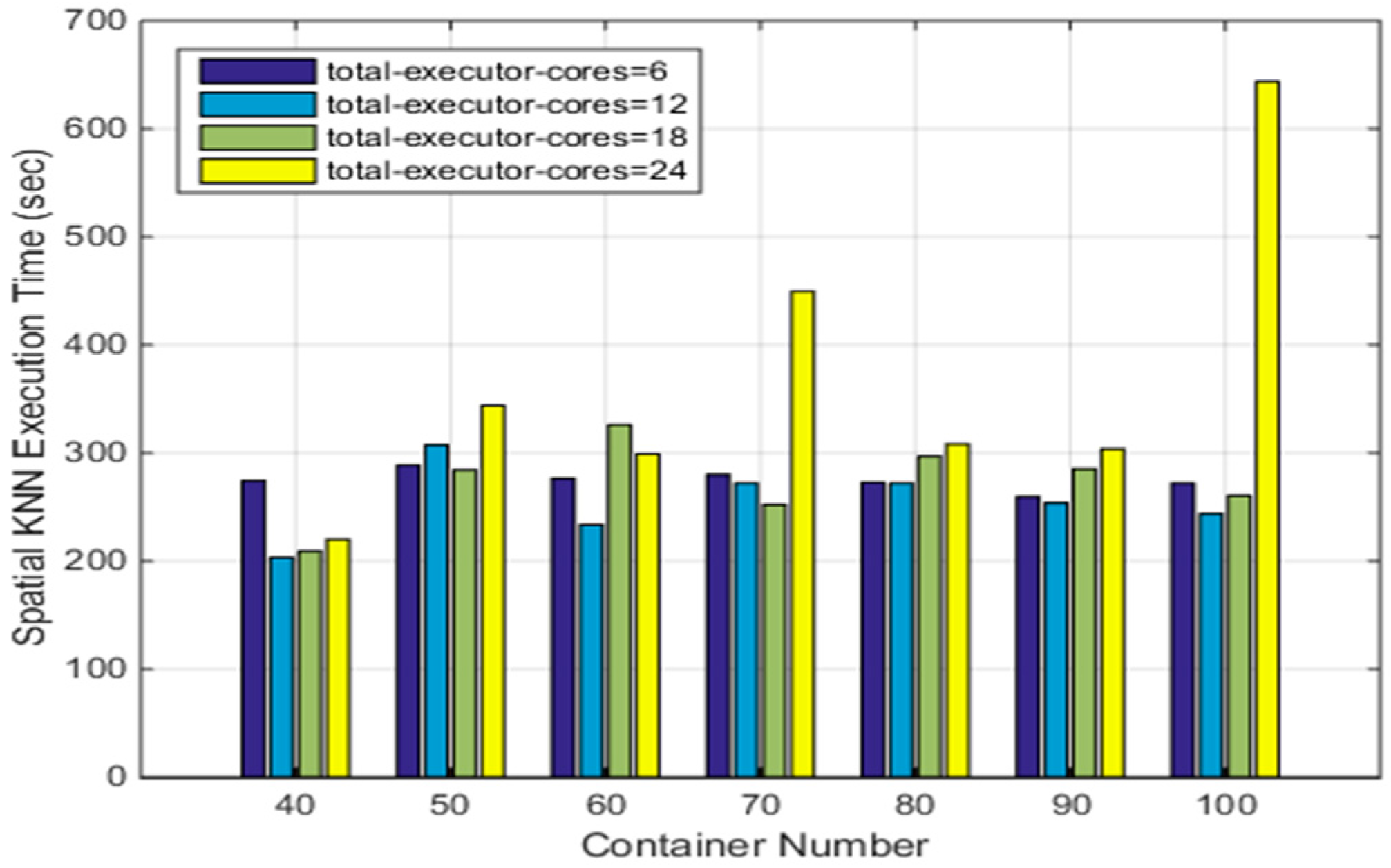
| Container Number | Execution Time |
|---|---|
| 32 | 271.89 s |
| 36 | 285.16 s |
| 40 | 274.20 s |
| 50 | 288.50 s |
| 60 | 276.39 s |
| 70 | 279.95 s |
| 80 | 272.63 s |
| 90 | 259.53 s |
| 100 | 271.92 s |
| Total Executor Cores | MinReplicas | MaxReplica | TargetPercentage | Execution Time |
|---|---|---|---|---|
| 6 | 1 | 40 | 50% | 303.49 s |
| 6 | 10 | 40 | 50% | 247.68 s |
| 6 | 20 | 40 | 50% | 253.91 s |
| 6 | 30 | 40 | 50% | 242.62 s |
| 6 | 1 | 40 | 80% | 272.56 s |
| 6 | 10 | 40 | 80% | 249.89 s |
| 6 | 20 | 40 | 80% | 252.53 s |
| 6 | 30 | 40 | 80% | 262.80 s |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Zhang, W.; Zhang, D.; Meng, L. Elastic Spatial Query Processing in OpenStack Cloud Computing Environment for Time-Constraint Data Analysis. ISPRS Int. J. Geo-Inf. 2017, 6, 84. https://doi.org/10.3390/ijgi6030084
Huang W, Zhang W, Zhang D, Meng L. Elastic Spatial Query Processing in OpenStack Cloud Computing Environment for Time-Constraint Data Analysis. ISPRS International Journal of Geo-Information. 2017; 6(3):84. https://doi.org/10.3390/ijgi6030084
Chicago/Turabian StyleHuang, Wei, Wen Zhang, Dongying Zhang, and Lingkui Meng. 2017. "Elastic Spatial Query Processing in OpenStack Cloud Computing Environment for Time-Constraint Data Analysis" ISPRS International Journal of Geo-Information 6, no. 3: 84. https://doi.org/10.3390/ijgi6030084
APA StyleHuang, W., Zhang, W., Zhang, D., & Meng, L. (2017). Elastic Spatial Query Processing in OpenStack Cloud Computing Environment for Time-Constraint Data Analysis. ISPRS International Journal of Geo-Information, 6(3), 84. https://doi.org/10.3390/ijgi6030084







