A Formal Framework for Integrated Environment Modeling Systems
Abstract
:1. Introduction
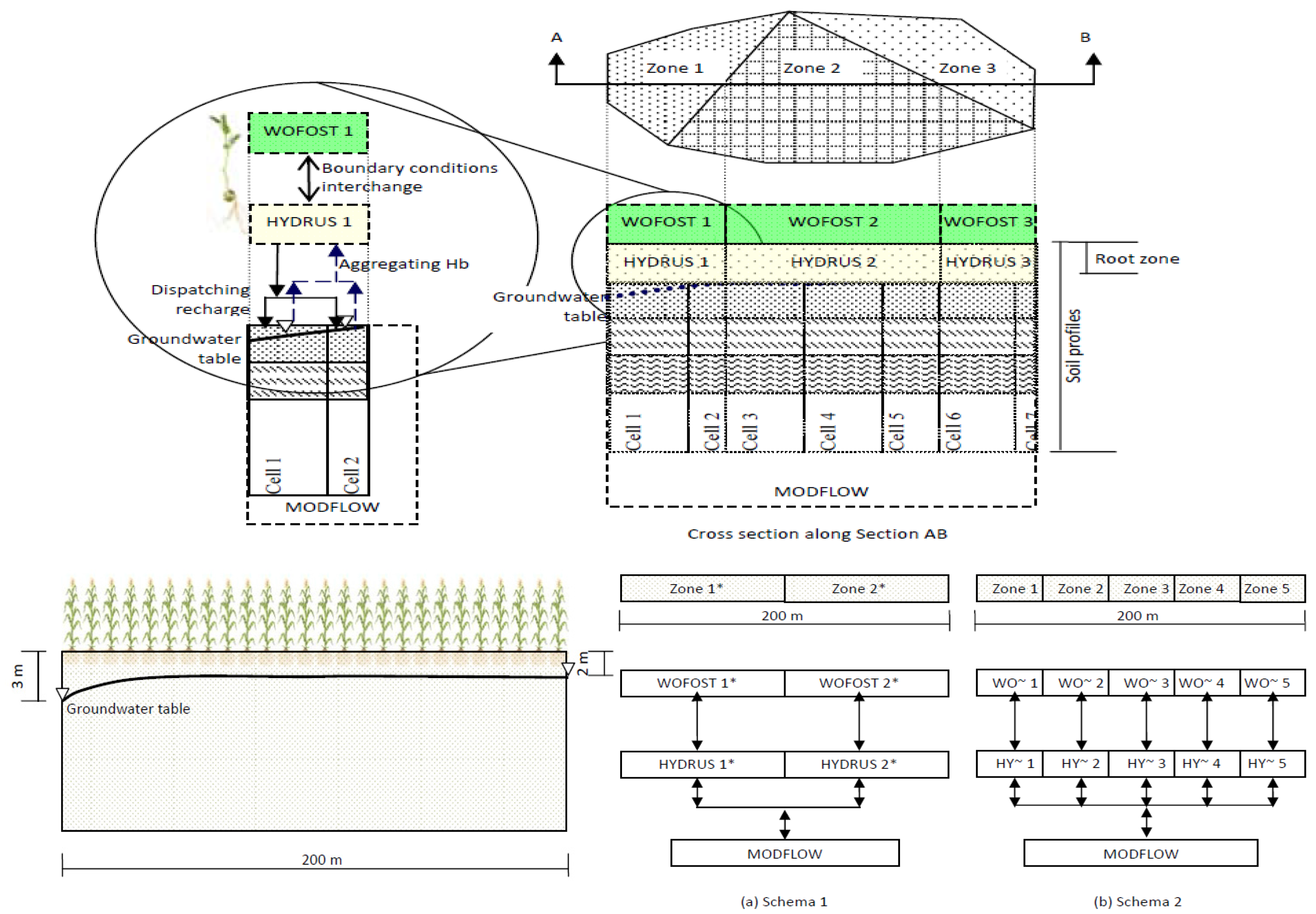
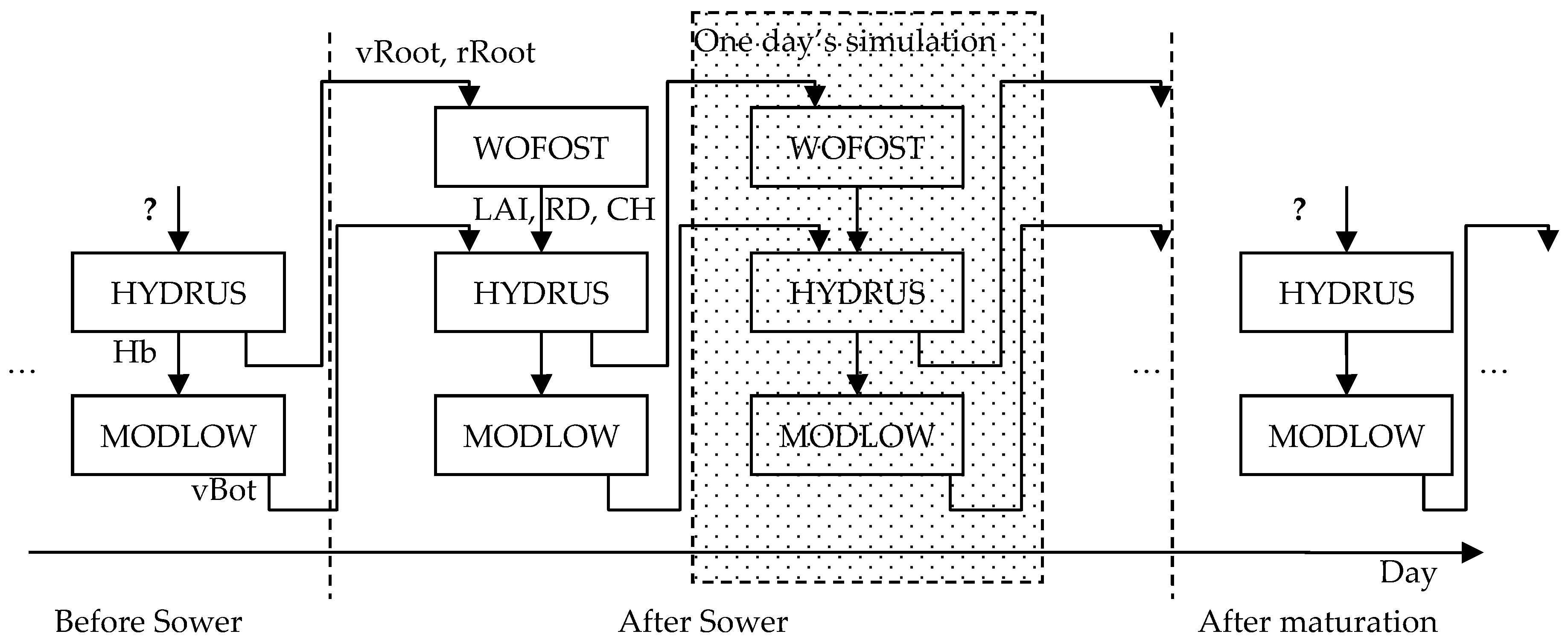
2. A Use Case as an Example of IEM
3. Unified View of the Model
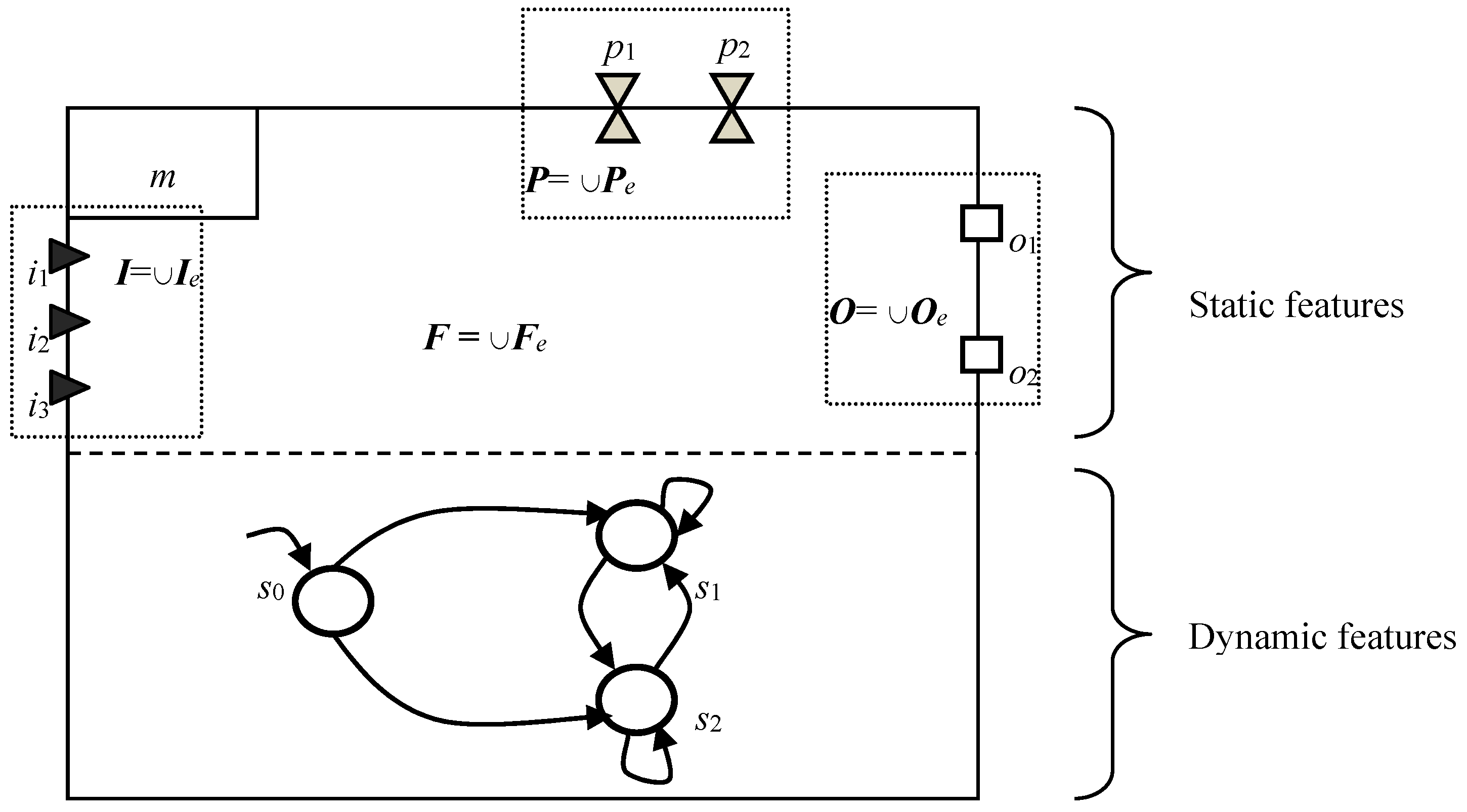
3.1. Formal Definition of the Model
3.2. Algebra for Integrating Models
4. Formal Operational Semantics of Integrated Modeling
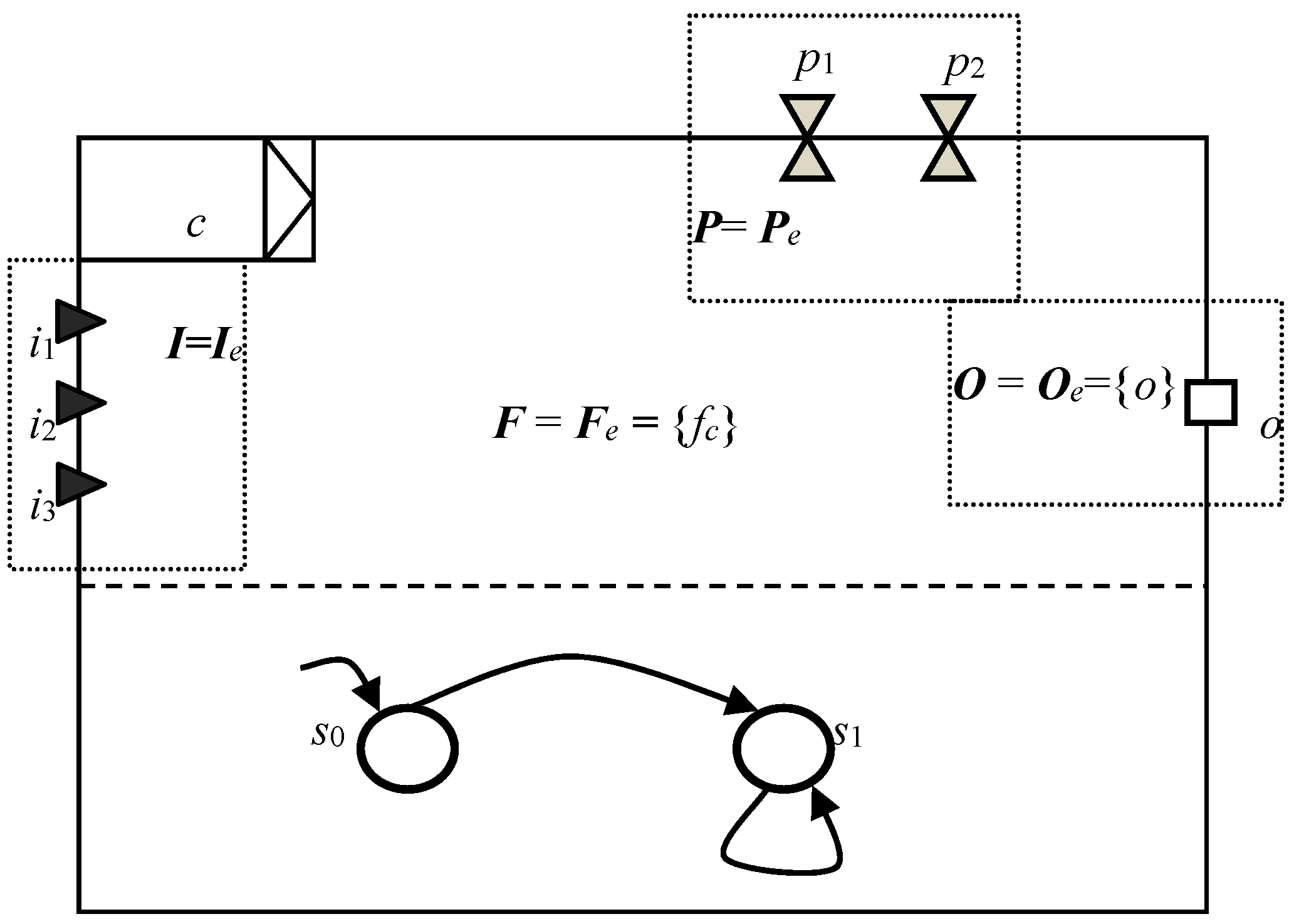
4.1. Connector
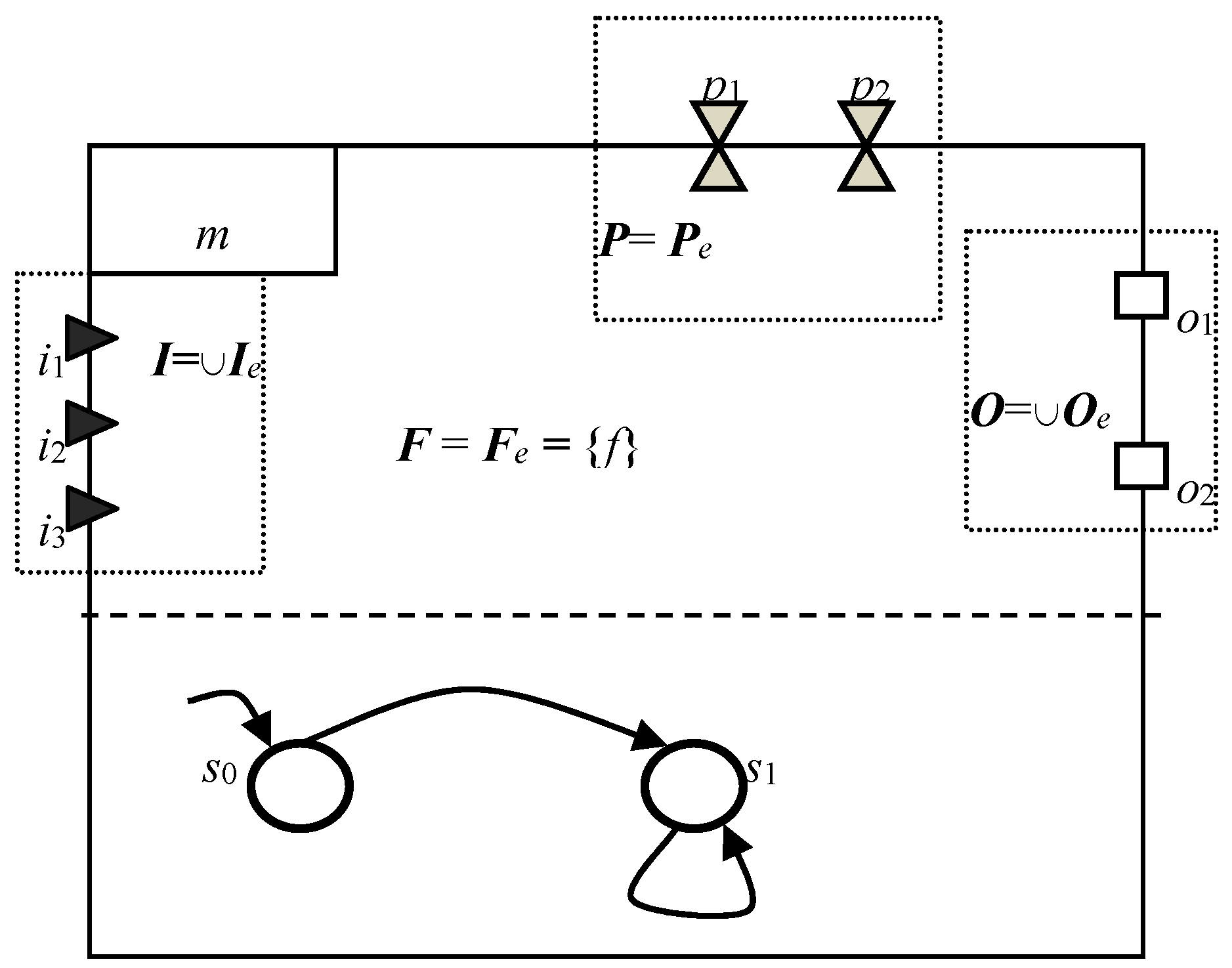
4.2. Semantics for the Algebraic Operator
4.2.1. Empty Model
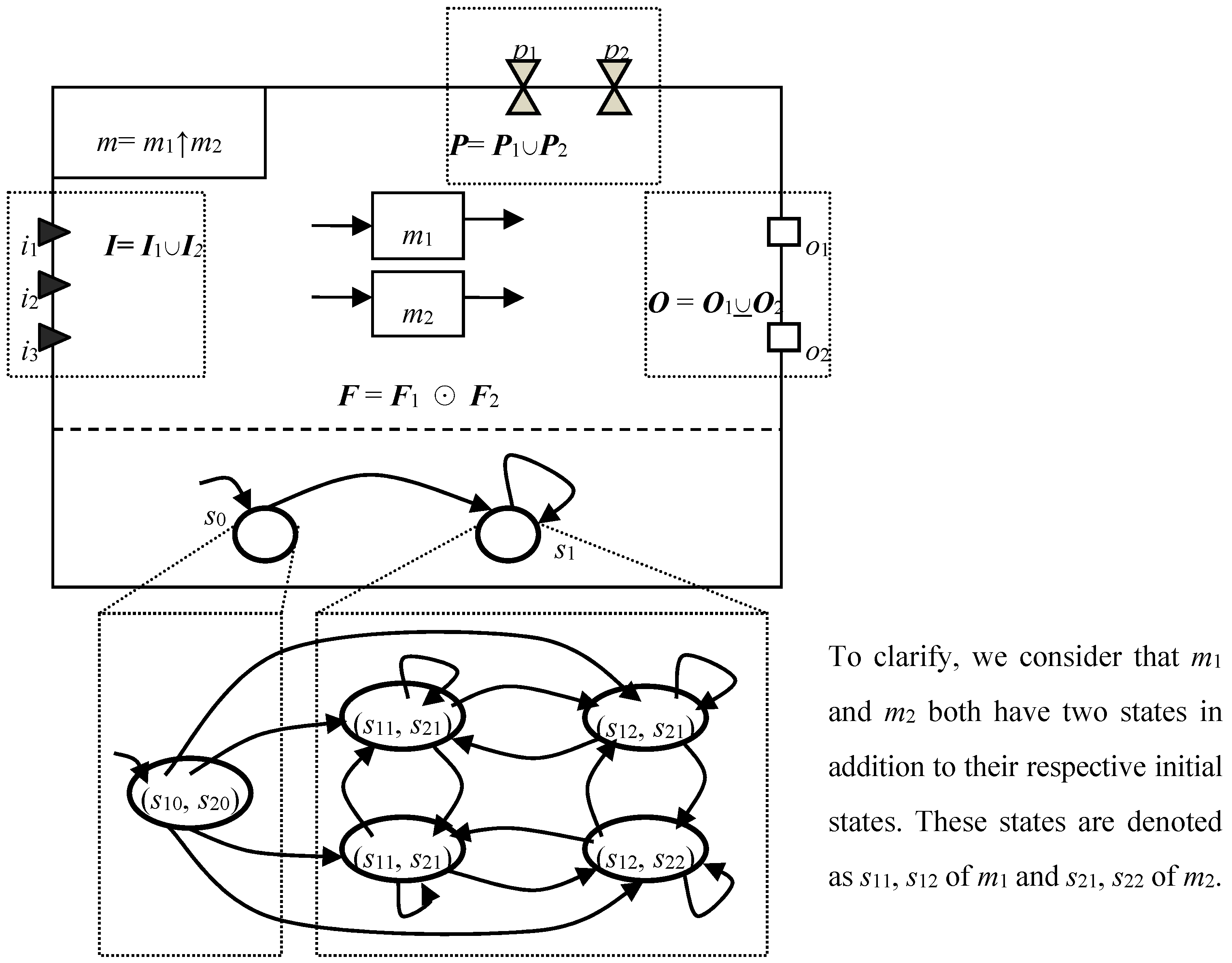
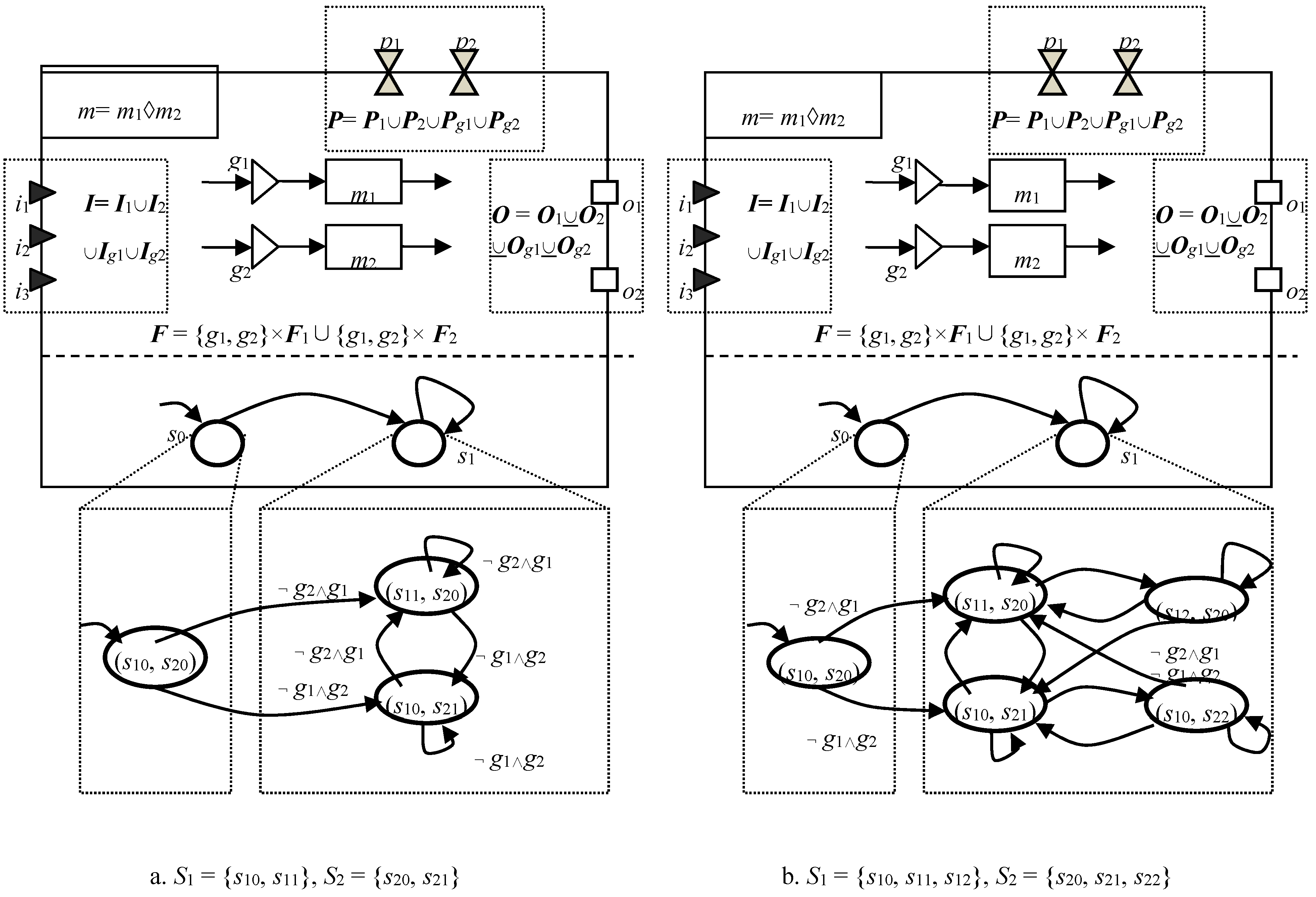
4.2.2. Parallel
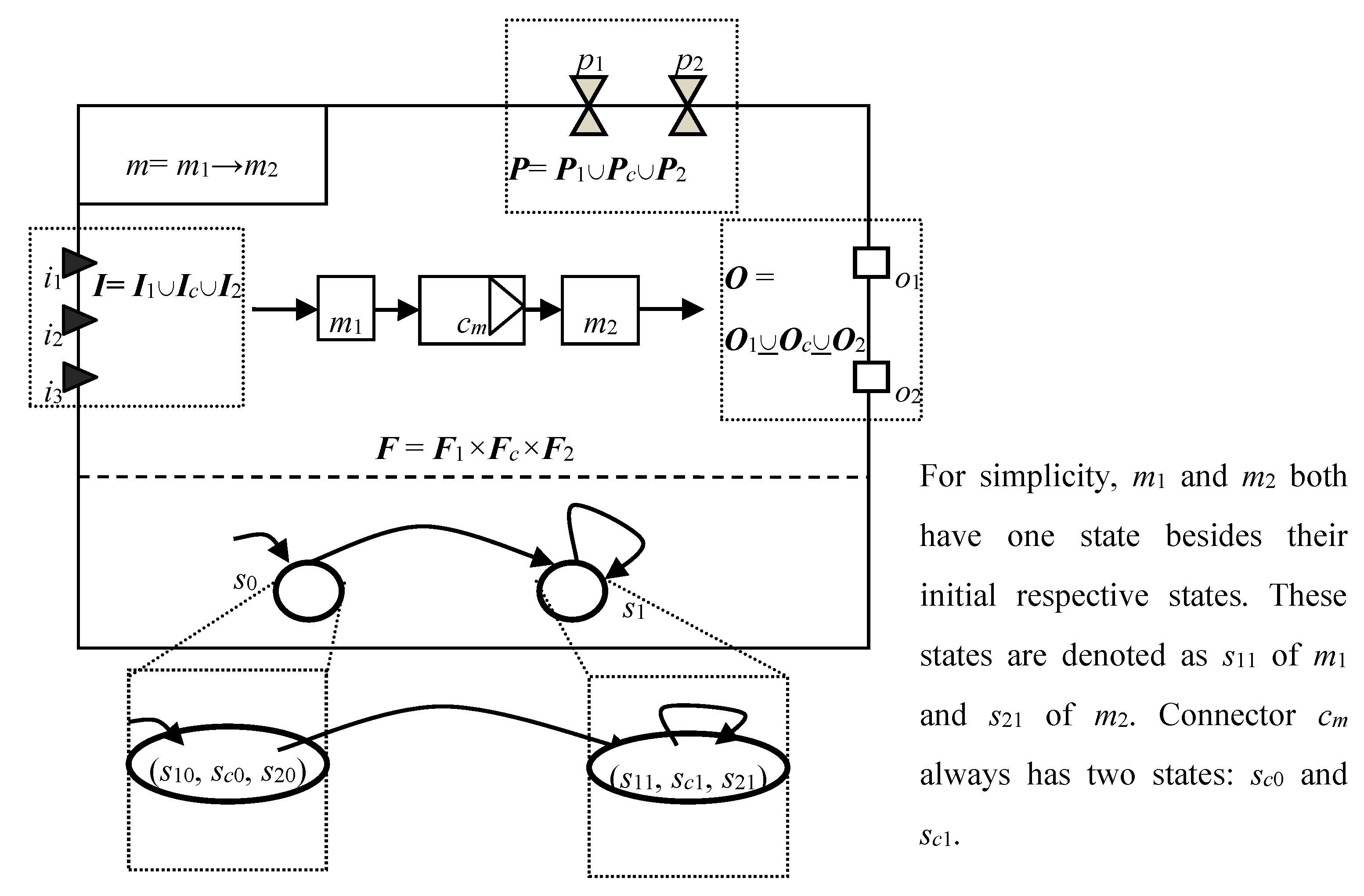
4.2.3. Sequence
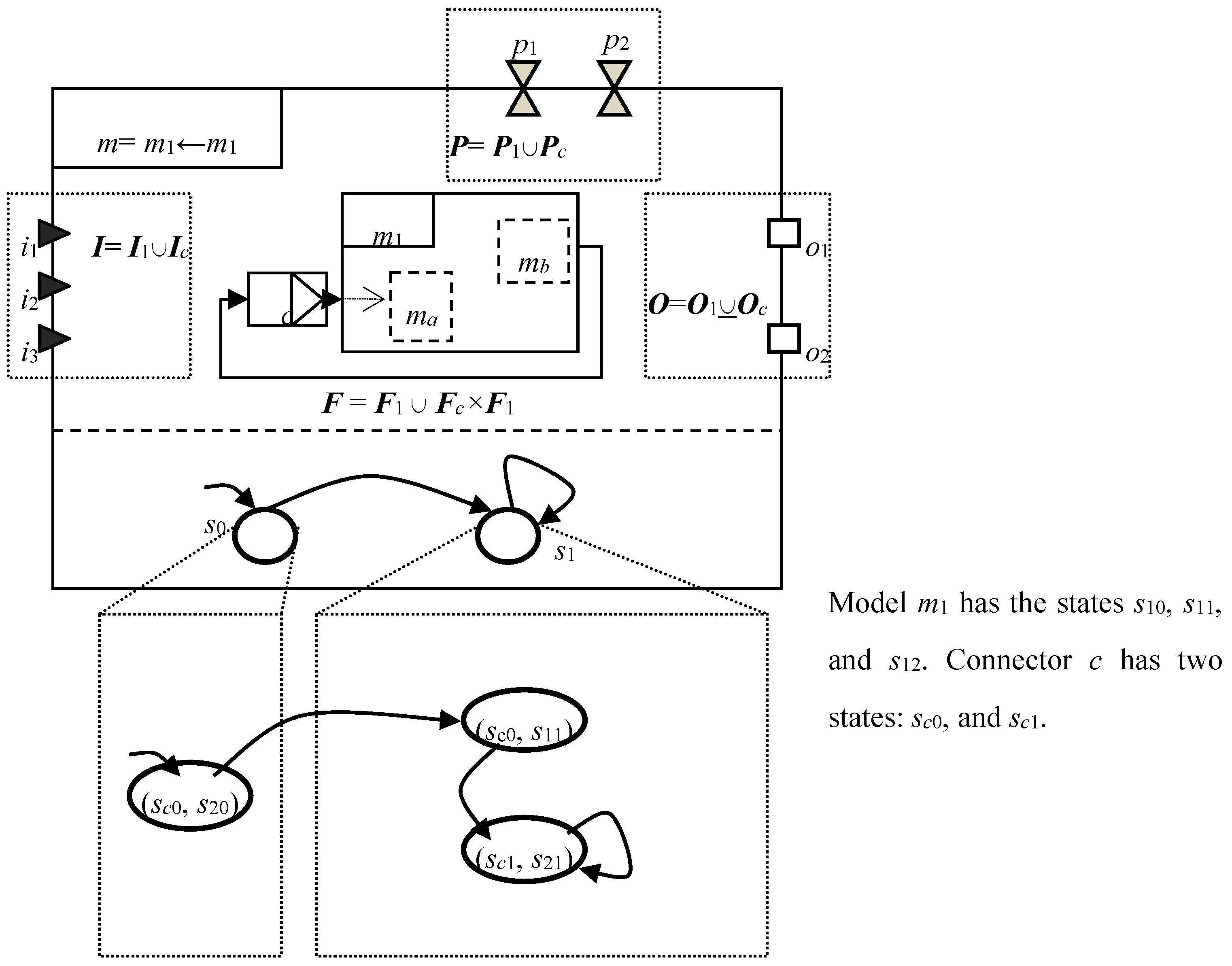
4.2.4. Feedback
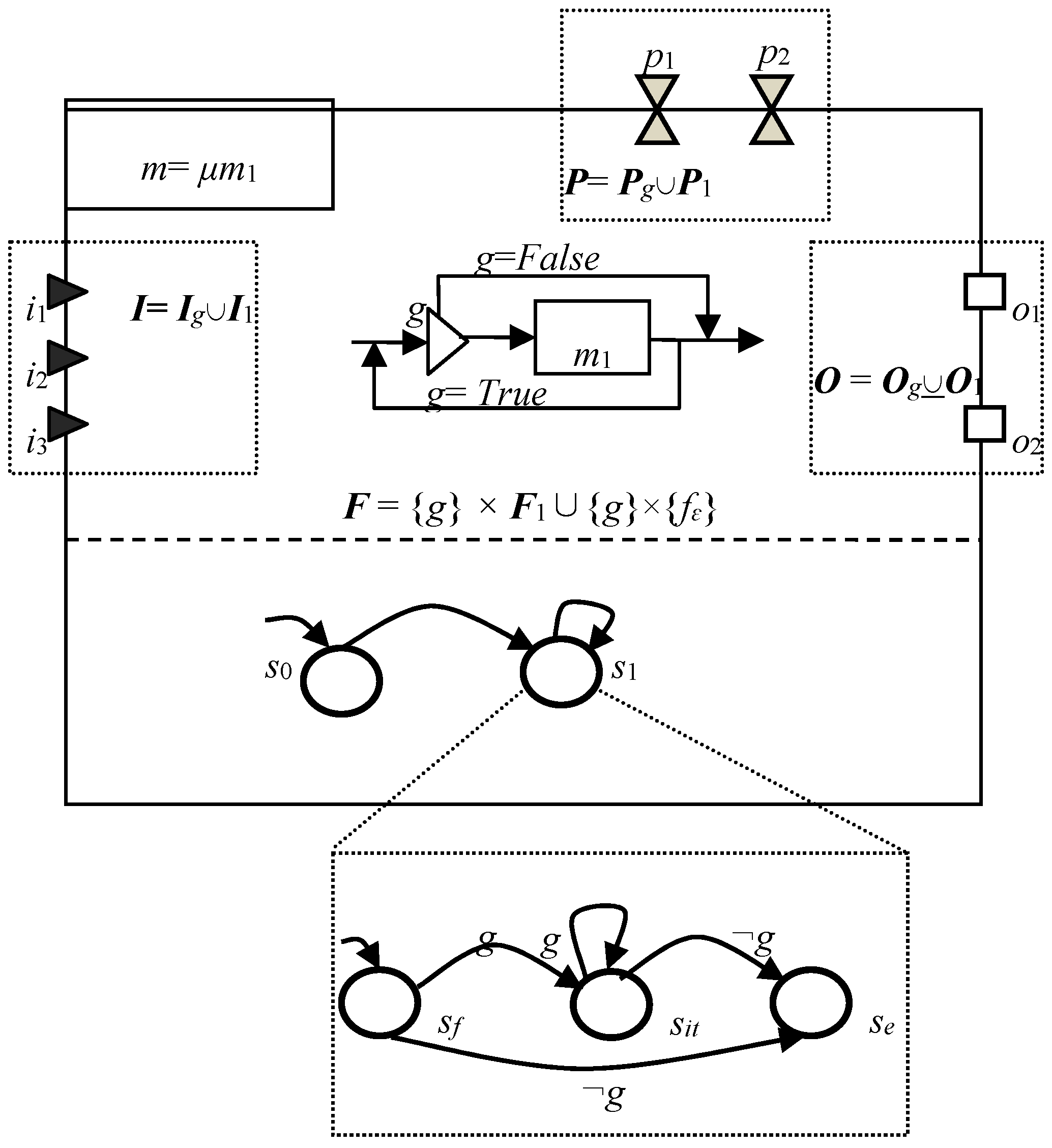
4.2.5. Select
4.2.6. Iterate
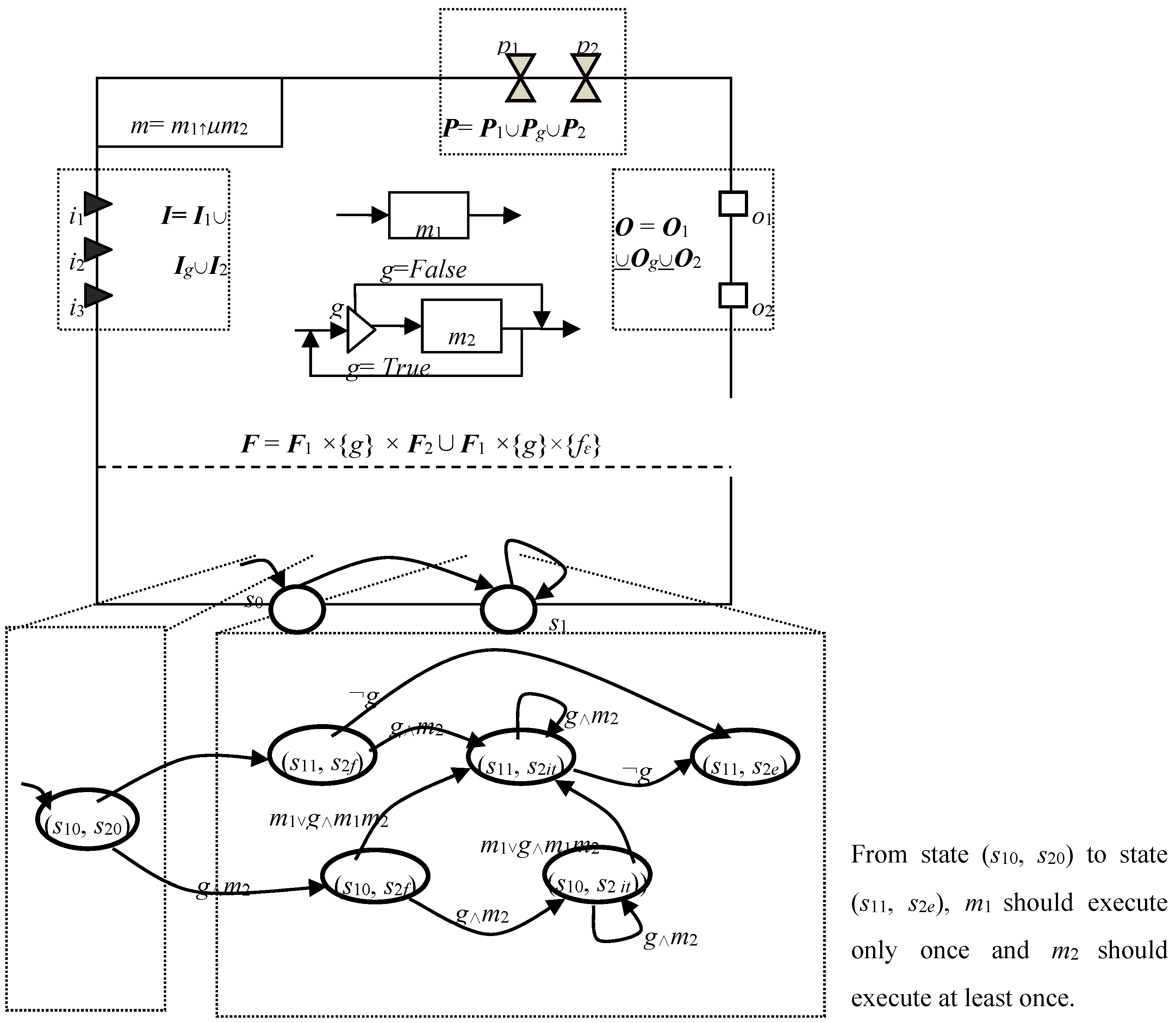
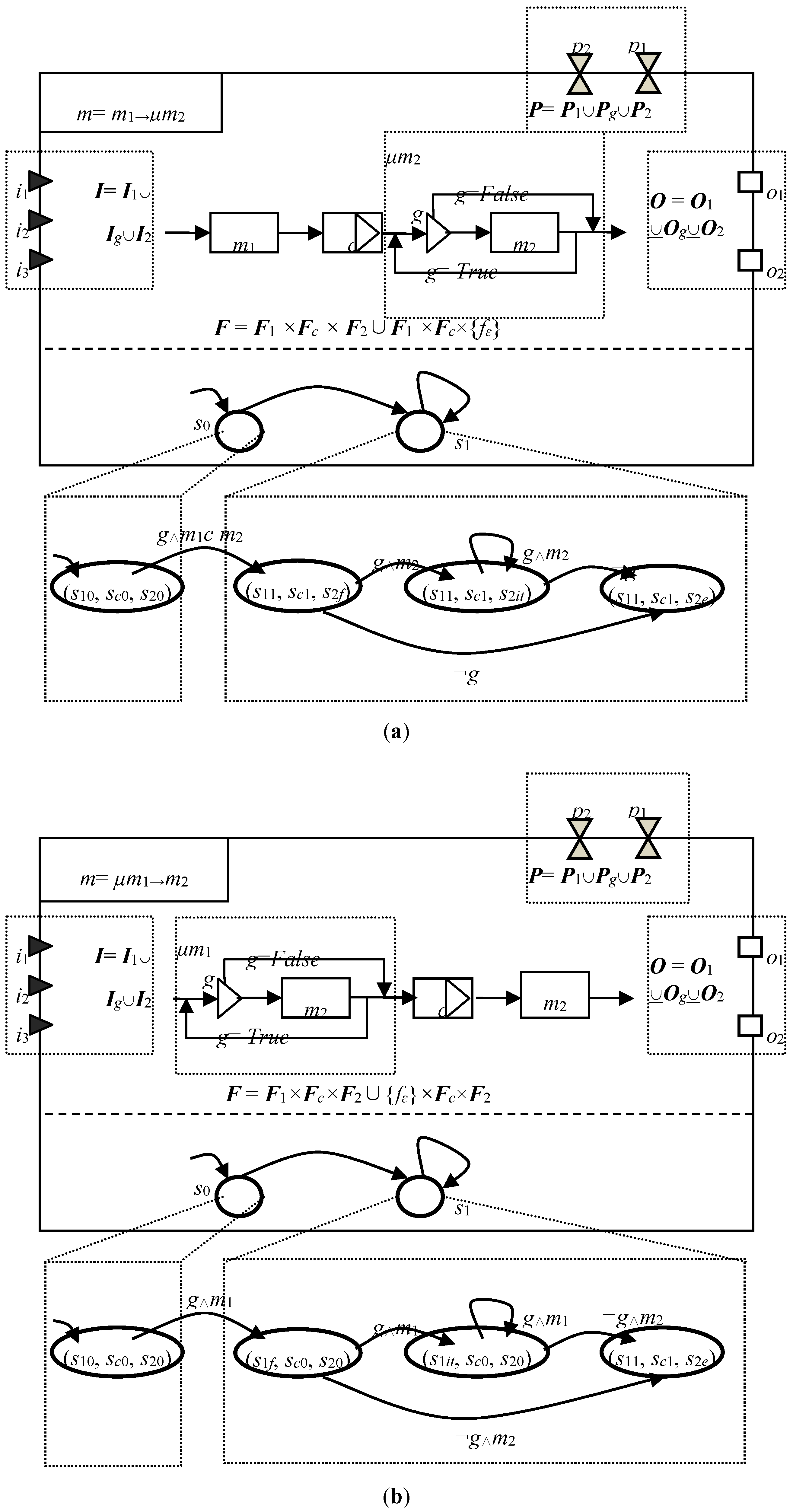
4.2.7. Combine Iterate with Other Operators
5. Complex Integrated Model
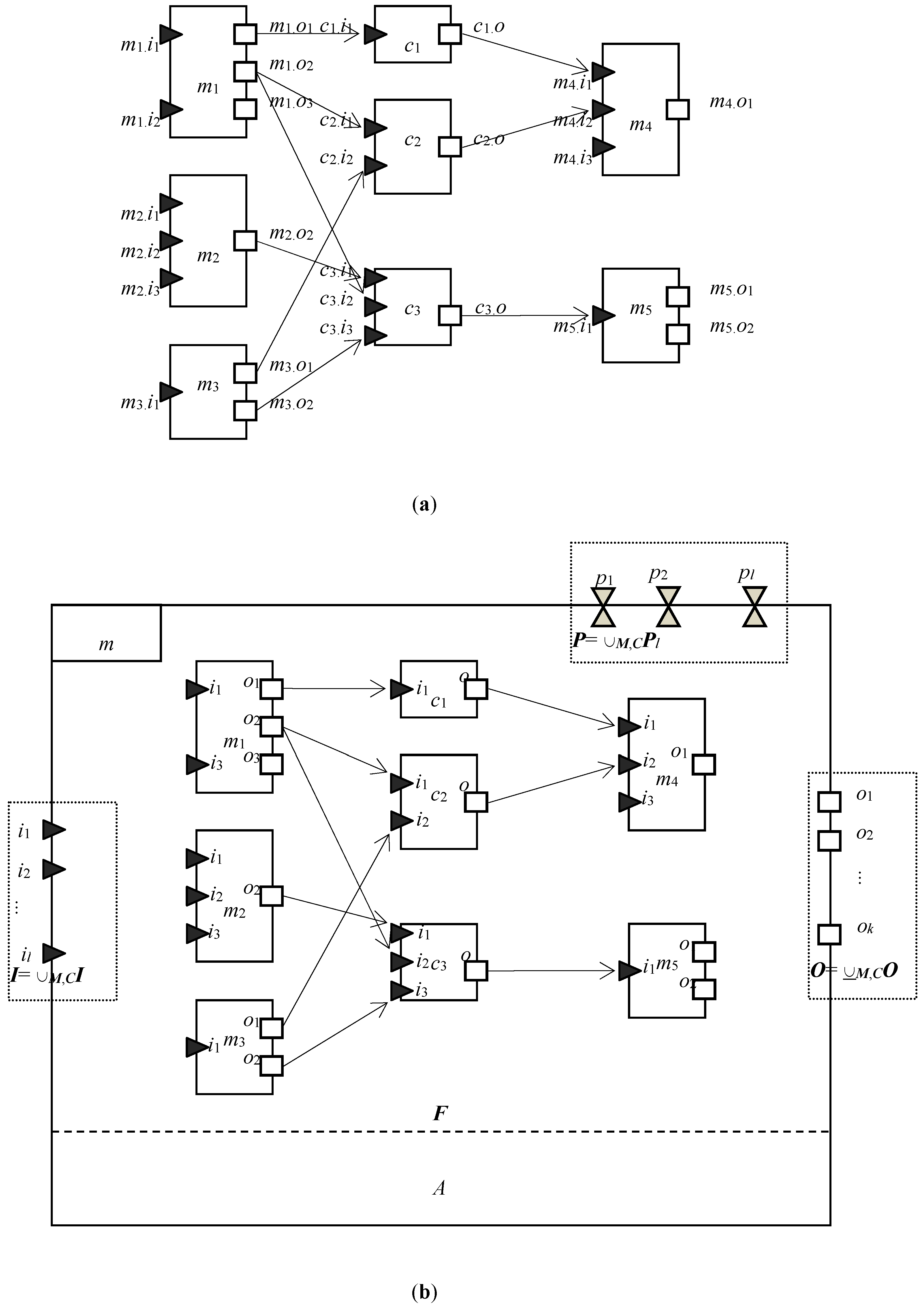
5.1. Model Graph
5.2. Formal Semantics of Model Graph
5.3. Construct Complex Integrated Model
6. Results
7. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Some Code Snippet with irDSL for the Integrated Model in Figure 1.
References
- Bailey, G.W.; Mulkey, L.A.; Swank, R.R. Environmental implications of conservation tillage: A system approach. In A System Approach to Conservation Tillage; D’Itri, F.M., Ed.; Lewis Publishers Inc.: Chelsea, MI, USA, 1985; pp. 239–265. [Google Scholar]
- Cohen, Y. Pollutants in a Multimedia Environmental; Plenum Press: New York, NY, USA, 1986. [Google Scholar]
- Mackay, D. Multimedia Environmental Models: The Fugacity Approach; Lewis Publishers: Michigan, MI, USA, 1991. [Google Scholar]
- Walters, C.J. Adaptive Management of Renewable Resources; Macmillan Publishing Co.: New York, NY, USA, 1986. [Google Scholar]
- Voinov, A.; Shugart, H. ‘Integronsters’, integral and integrated modelling. Environ. Model. Softw. 2013, 39, 149–158. [Google Scholar] [CrossRef]
- Laniak, G.F.; Olchin, G.; Goodall, J.; Voinov, A.; Hill, M.; Glynn, P.; Whelan, G.; Geller, G.; Quinn, N.; Blind, M.; et al. Integrated environmental modelling: a vision and roadmap for future. Environ. Model. Softw. 2013, 39, 3–23. [Google Scholar] [CrossRef]
- Leavesley, G.H.; Markstrom, S.L.; Brewer, M.S.; Viger, R.J. The Modular Modelling System (MMS)—The physical process modelling component of a database-centered decision support system for water and power management. Water Air Soil Pollut. 1996, 90, 303–311. [Google Scholar] [CrossRef]
- OpenMI. The OpenMI Open Midel Interface Project. 2016. Available online: https://publicwiki.deltares.nl/display /OPENMI/Version+2.0 (accessed on 24 December 2016).
- David, O.; Markstrom, S.L.; Rojas, K.W.; Ahuja, L.R.; Schneider, W. The object modelling system. In Agricultural System Models in Field Research and Technology Transfer; Ahuja, L.R., Ma, L., Howell, T.A., Eds.; Lewis Publishers: Boca Raton, FL, USA, 2002; pp. 317–344. [Google Scholar]
- David, O.; Ascough, J.C., II; Lloyd, W.; Green, T.R.; Rojas, K.W.; Leavesley, G.H.; Ahuja, L.R. A software engineering perspective on environmental modelling framework design: The object modelling system. Environ. Model. Softw. 2013, 39, 201–213. [Google Scholar] [CrossRef]
- Hill, C.; DeLuca, C.; Balaji, V.; Suarez, M.; da Silva, A. The architecture of the earth system modelling framework. Comput. Sci. Eng. 2004, 6, 18–28. [Google Scholar] [CrossRef]
- Thurman, D.A.; Cowell, A.J.; Taira, R.Y.; Frodge, J. Designing a collaborative problem solving environment for integrated water resource modelling. In Brownfields: Multimedia Modelling and Assessment; Whelan, G., Ed.; WIT Press: Southampton, UK, 2004. [Google Scholar]
- Aquaveo. Water Modelling Solutions; Aquaveo: Provo, UT, USA, 2012; Available online: http://www.aquaveo.com/ (accessed on 8 December 2013).
- Peckham, S.D. Evaluation of model coupling frameworks for use by the Community Surface Dynamics Modelling System (CSDMS). In Proceedings of the MODFLOW and MORE, Golden, CO, USA, 18 May 2008.
- van Ittersum, M.K.; Ewert, F.; Heckelei, T.; Wery, J.; Olsson, J.A.; Andersen, E.; Bezlepkina, I.; Brouwer, F.; Donatelli, M.; Flichman, G.; et al. Integrated assessment of agricultural systems e a component-based framework for the European Union (SEAMLESS). Agric. Syst. 2008, 96, 150–165. [Google Scholar] [CrossRef]
- Parker, D.; Manson, S.; Janssen, M.; Hoffmann, M.; Deadman, P. Multi-agent systems for the simulation of land-use and land-cover change: A review. Ann. Assoc. Am. Geogr. 2003, 93, 314–337. [Google Scholar] [CrossRef]
- Zhao, J.; Cai, X.; Wang, Z. Comparing administered and market-based water allocation systems through a consistent agent-based modelling framework. J. Environ. Manag. 2013, 123, 120–130. [Google Scholar] [CrossRef] [PubMed]
- Zhao, G.; Bryan, B.A.; King, D.; Luo, Z.; Wang, E.; Bende-Michlc, U.; Song, X.; Yu, Q. Largescale, high-resolution agricultural systems modelling using a hybrid approach combining grid computing and parallel processing. Environ. Model. Softw. 2013, 41, 231–238. [Google Scholar] [CrossRef]
- Yalew, S.; van Griensven, A.; Ray, N.; Kokoszkiewicz, L.; Betrie, G.D. Distributed computation of large scale SWAT models on the Grid. Environ. Model. Softw. 2013, 41, 223–230. [Google Scholar] [CrossRef]
- Granell, C.; Díaz, L.; Gould, M. Service-oriented applications for environmental models: Reusable geospatial services. Environ. Model. Softw. 2010, 25, 182–198. [Google Scholar] [CrossRef]
- Goodall, J.L.; Robinson, B.F.; Castronova, A.M. Modelling water resource systems using a service-oriented computing paradigm. Environ. Model. Softw. 2011, 26, 573–582. [Google Scholar] [CrossRef]
- Bastin, L.; Cornford, D.; Jones, R.; Heuvelink, G.B.M.; Pebesma, E.; Stasch, C.; Nativi, S.; Mazzetti, P.; Williams, M. Managing uncertainty in integrated environmental modelling: The UncertWeb framework. Environ. Model. Softw. 2013, 39, 116–134. [Google Scholar] [CrossRef]
- Wing, J.M. A specifier’s introduction to formal methods. Computer 1990, 23, 8–24. [Google Scholar] [CrossRef]
- Argent, R.M. An overview of model integration for environmental applications-components, frameworks and semantics. Environ. Model. Softw. 2004, 19, 219–234. [Google Scholar] [CrossRef]
- Argent, R.M.; Voinov, A.; Maxwell, T.; Cuddy, S.M.; Rahman, J.M.; Seaton, S.; Vertessy, R.A.; Braddock, R.D. Comparing modelling frameworks: A workshop approach. Environ. Model. Softw. 2006, 21, 895–910. [Google Scholar] [CrossRef]
- Voinov, A.; Cerco, C. Model integration and the role of data. Environ. Model. Softw. 2006, 25, 965–969. [Google Scholar] [CrossRef]
- Rizzoli, A.E.; Donatelli, M.; Athanasiadis, I.N.; Villa, F.; Huber, D. Semantic links in integrated modelling frameworks. Math. Comput. Simul. 2007, 78, 412–423. [Google Scholar] [CrossRef]
- Schmitz, O.; Karssebnerg, D.; de Jong, K.; de Kok, J.-L. Constructing integrated models: A scheduler to execute coupled components. In Proceedings of the AGILE 2011, the 14th AGILE International Conference on Geographic Information Science, Advancing Geoinformation Science for a Changing World, Utrecht, The Netherlands, 18 April 2011.
- Kragt, M.E.; Robson, B.J.; Macleod, C.J.A. Modellers roles in Structuring integrative research projects. Environ. Model. Softw. 2013, 39, 322–330. [Google Scholar] [CrossRef]
- Lloyd, W.; David, O.; Ascough, J.C., II; Rojas, K.W.; Carlson, J.R.; Leavesley, G.H.; Krause, P.; Green, T.R.; Ahuja, L.R. Environmental modelling framework invasiveness: Analysis and implications. Environ. Model. Softw. 2011, 26, 1240–1250. [Google Scholar] [CrossRef]
- Peña-Haro, S.; Zhou, J.; Zhang, G.; Chen, C.; Stauffer, F.; Kinzelbach, W. A multi-approach framework to couple independent models for simulating the interaction between crop growth and unsaturated-saturated flow processes. In Proceedings of the International Environmental Modelling and Software Society (iEMSs) 2012 International Congress on Environmental Modelling and Software: Managing Resources of a Limited Planet: Pathways and Visions under Uncertainty, Sixth Biennial Meeting (iEMSs 2012), Leipzig, Germany, 1 July 2012; pp. 1224–1231.
- Zhang, G.; Zhou, J.; Zhou, Q.; Cheng, G.; Li, X. Integrated Eco-hydrological modelling by a combination of coupled-model and algorithm using OMS3. In Proceedings of the International Environmental Modelling and Software Society (iEMSs) 2012 International Congress on Environmental Modelling and Software: Managing Resources of a Limited Planet: Pathways and Visions under Uncertainty, Sixth Biennial Meeting (iEMSs 2012), Leipzig, Germany, 1 July 2012; pp. 1201–1207.
- Hamadi, R.; Benatallah, B. A Petri net-based model for web service composition. In Proceedings of the ADC '03 14th Australasian database conference of CRPIT, Adelaide, Australia, 1 February 2003; Volume 17.
- Dumez, C.; Bakhouya, M.; Gaber, J.; Wack, M.; Lorenz, P. Model-driven approach supporting formal verification for web service composition protocols. J. Netw. Comput. Appl. 2013, 36, 1102–1115. [Google Scholar] [CrossRef]
- Lomazova, I. Nested Petri nets—A formalism for specification and verification of multi-agent distributed systems. Fundam. Inf. 2000, 43, 195–214. [Google Scholar]
- Alur, R.; Yannakakis, M. Model checking of hierarchical state machines. In Proceedings of the Sixth ACM FSE, Orlando, FL, USA, 1 November 1998.
- Girault, A.; Lee, B.; Lee, E.A. Hierarchical finite state machines with multiple concurrency models. IEEE Trans. Comput.-Aided Design Integr. Circuits Syst. 1999, 18, 742–760. [Google Scholar] [CrossRef]
- Lee, E.A.; Tripakis, S. Modal models in Ptolemy. In Proceedings of the 3rd International Workshop on Equation-Based Object-Oriented Modelling Languages and Tools (EOOLT), Oslo, Norway, 3 October 2010; Volume 47, pp. 11–21.
- OMS3. The OMS3 Doc Website. 2011. Available online: http://nrrc.ars.usda.gov/ModelFrameworks/ObjectModeling System/Documentation.aspx (accessed on 20 September 2016). [Google Scholar]
- ESMF. The ESMF User Doc. 2014. Available online: http://www.earthsystemmodeling.org/esmf_releases/ public/last/ESMF_usrdoc/ESMF_usrdoc.html (accessed on 20 January 2017).
- Dustdar, S.; Zdun, U. Model-driven and pattern-based integration of process-driven SOA Models. Int. J. Bus. Process Integr. Manag. 2006, 2, 109–119. [Google Scholar]

| Our Framework | OMS3 | OpenMI | ESMF | ||
|---|---|---|---|---|---|
| Technological Basis | / | Object-Oriented | Component-Based | ||
| / | DSL + POJO + Annotation | Interface-Based | Mediator Pattern | ||
| Dataflow | yes | yes | yes | yes | |
| sequence | yes | yes | yes | yes | |
| Formalism | feedback | yes | yes | yes | yes |
| select | yes | no | extra codes | extra codes | |
| iterate | yes | no | extra codes | extra codes | |
| Integration reusable | easy | difficult | difficult | difficult | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Li, Y.; Chen, C.; Zhou, R.; Chen, D.; Zhou, Q. A Formal Framework for Integrated Environment Modeling Systems. ISPRS Int. J. Geo-Inf. 2017, 6, 47. https://doi.org/10.3390/ijgi6020047
Zhang G, Li Y, Chen C, Zhou R, Chen D, Zhou Q. A Formal Framework for Integrated Environment Modeling Systems. ISPRS International Journal of Geo-Information. 2017; 6(2):47. https://doi.org/10.3390/ijgi6020047
Chicago/Turabian StyleZhang, Gaofeng, Yan Li, Chong Chen, Rui Zhou, Dan Chen, and Qingguo Zhou. 2017. "A Formal Framework for Integrated Environment Modeling Systems" ISPRS International Journal of Geo-Information 6, no. 2: 47. https://doi.org/10.3390/ijgi6020047
APA StyleZhang, G., Li, Y., Chen, C., Zhou, R., Chen, D., & Zhou, Q. (2017). A Formal Framework for Integrated Environment Modeling Systems. ISPRS International Journal of Geo-Information, 6(2), 47. https://doi.org/10.3390/ijgi6020047






