1. Introduction
The spatial relations between spatial entities are as important as the entities themselves [
1]. A spatial relation specifies how an object is located in space in relation to some reference object. Topological relations, distance relations and orientation relations are commonly used types of spatial relations. Topological properties are the most fundamental in spatial language and spatial cognition when compared to Euclidean, metric and vector spaces [
2,
3,
4]. Topological relations remain constant when the coordinate space is deformed, such as by twisting or stretching. Consequently, the topological relations of spatial objects are commonly used in GIS. Simple queries, such as “Which universities are located in this city?” or “Are these two land parcels disjoint?” are widely addressed, while more complex queries, such as “How many times does the river cross this state’s boundary?” and “What are the dimension of these intersections?” require further analysis.
Previous studies have investigated the formalization of topological relations, such as interval- based temporal logic [
5,
6], point-set topology [
1,
7,
8,
9] and region connection calculus (RCC) [
10,
11,
12,
13,
14,
15]. In the scope of this paper, point-set topology, which is the study of the general abstract nature of continuity or the connectedness of spaces, has been used to discuss the formalization of topological relations.
Over the past three decades, research to formalize topological relations based on point-set topology has been conducted, and the four-intersection model (4IM) [
7], the nine-intersection model (9IM) [
8], the Voronoi-based nine-intersection model [
1], the intersection and difference model [
16], an extended model expressed as 4 × 4 matrices [
17], the 9
+-intersection model [
18], the uncertain intersection and difference model [
19] and the double straight line four-intersection models [
20] have been proposed. All of the above models consider the content invariant (i.e., the emptiness or non-emptiness) of the intersections. The 4IM and 9IM were compared on spatial relations, and the result was that 9IM with the content invariant provides more details than does the 4IM [
9]. A complete classification of spatial relations was demonstrated using the Voronoi-based nine-intersection model [
21]. Topological relations for spatial scene [
22,
23] and compound spatial objects [
24] were also presented. We can conclude that the 4IM and 9IM, as well as extended models based on these have been widely studied.
In addition to the content invariant, other topological invariants have been used to further describe topological relations details. Many refinements of the empty/non-empty intersections have been proposed. For instance, the dimension of intersections [
25], the number of separations in intersections [
26], four invariants, including the dimension of the components, their types, their relationships with respect to the exterior neighborhood and the sequence of the components [
27], three invariants, including intersection sequence, intersection type and collinearity sense for lines [
28] and a set of hierarchically topological invariants, including content, separation number, dimension, element type and sequence [
16], has been proposed. These methods are refinements of the existing 4IM and 9IM and can represent more topological relation details whenever necessary.
In recent years, topological relationships from metric refinements have been discussed in the GIS literature, such as splitting ratios and closeness measures [
29], splitting, closeness and approximate alongness for line-region relations [
30] and three content measures to characterize spatial configurations [
31]. Moreover, the 9IM has been extended by capturing the metric details for line-line relations through splitting ratios and closeness measures [
32], and a comprehensive set of eleven metric refinements [
33], a distance based interpretation for mereotopology [
34] and expansion closeness and contraction closeness [
35] have been investigated over the past few years. Metric refinements are the refinement of the intersection model and can provide additional information for topological relations. Metric refinements represent ranges of values that together claim a topological relation.
The scope of this paper includes the definition of a formalism (model) to describe the topological relations of spatial objects embedded in the plane. To describe the details of topological relations, a comprehensive model for topological spatial relations is proposed, and two topological invariants are considered: (1) the dimension of the intersections and (2) the number of separations.
The remainder of this paper presents the proposed comprehensive model for topological spatial relations used to specify the dimension and the number of separations.
Section 2 introduces the model.
Section 3 describes six groups of topological relations described by the 27IM.
Section 4 discusses the refinement and interoperability of the 27IM, and
Section 5 provides conclusions and discusses future work.
2. Methods
2.1. Spatial Data Model
To describe the geometry of spatial objects, many spatial data models, such as the simplicial complex [
36], the three-dimensional formal data structure [
37], the tetrahedron network [
38,
39], the cell complex [
40,
41], the geometry object model [
42], the simplified spatial model [
43], the multi-level model [
44], the combinatorial data model [
45], the common information model [
46] and the geometric algebra model [
47,
48], have been proposed. Generally, these models maintain four geometric abstractions of a real object: point, line, surface and body. The differences between these models lie in their spatial object’s components and their mode of organization. The geometric object model defined by the OpenGIS Simple Features Specification has been widely accepted for two-dimensional spatial objects. In this paper, the definition of spatial objects in two-dimensional space refers to the OpenGIS Simple Features Specification.
Point set theory provides a framework for modeling the intersection of two spatial objects. Every spatial object is characterized by the following spatial attributes: an interior, a boundary and an exterior. The definitions of interior, boundary and exterior are given below [
49].
Definition 1: Let A be a subset of a topological space X. The interior of A is the union of all open sets contained in A. The closure of A is the intersection of all closed sets containing A.
Definition 2: Let A be a subset of a topological space X. The boundary of A is the set of the closure of A minus the interior of A.
Definition 3 Let A be a subset of a topological space X. The exterior of A is the set of X minus the closure of A.
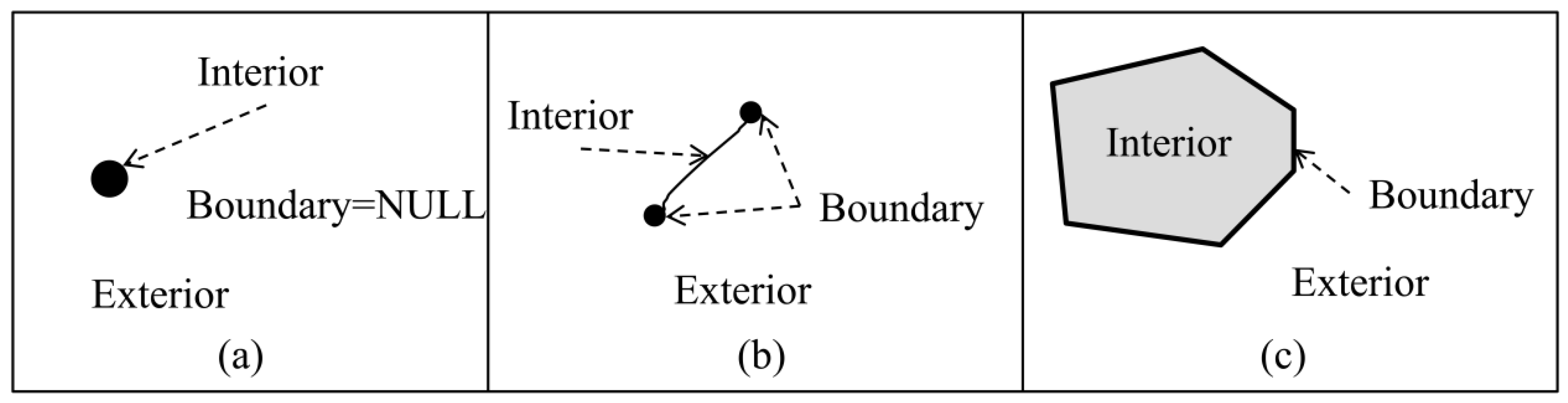
Based on the OpenGIS Simple Features Specification and algebraic topology, definitions and their interior, boundary and exterior of point, line and region are given as follows (
Figure 1).
A point is a 0-dimensional geometry and represents a single location in coordinate space (
Figure 1a). The interior of a point is a point; the boundary of a point is an empty set; and the exterior of a point includes everything that is not the point.
A line is a one-dimensional geometric object usually stored as a sequence of points with linear interpolation between the points (
Figure 1b). A line never passes through the same point twice. The interior of a line is a line without its endpoints; the boundary of a line is its two endpoints; and the exterior of a line is a set of points that does not contain the line.
A region is a closed 2-dimensional geometric object defined by one exterior boundary (
Figure 1c). The interior of the region is the set of points inside the boundary; the boundary of a region is the lines forming the boundary, and the exterior of a region is a set of points that do not include the region.
According to the dimensions of spatial objects, there are six groups of topological relations: point/point, point/line, point/region, line/line, line/region and region/region relations, which will be described.
2.2. Different Topological Invariants for Topological Relations
Topological relations between two spatial objects,
A and
B, are based on the intersection of
A’s interior, boundary and exterior with
B’s interior, boundary and exterior. The nine intersections between
A and
B can be described by a topological relation using a 3 × 3 matrix. The content, the dimension and the number of separation invariants are used to describe topological relations. Taking the spatial objects in
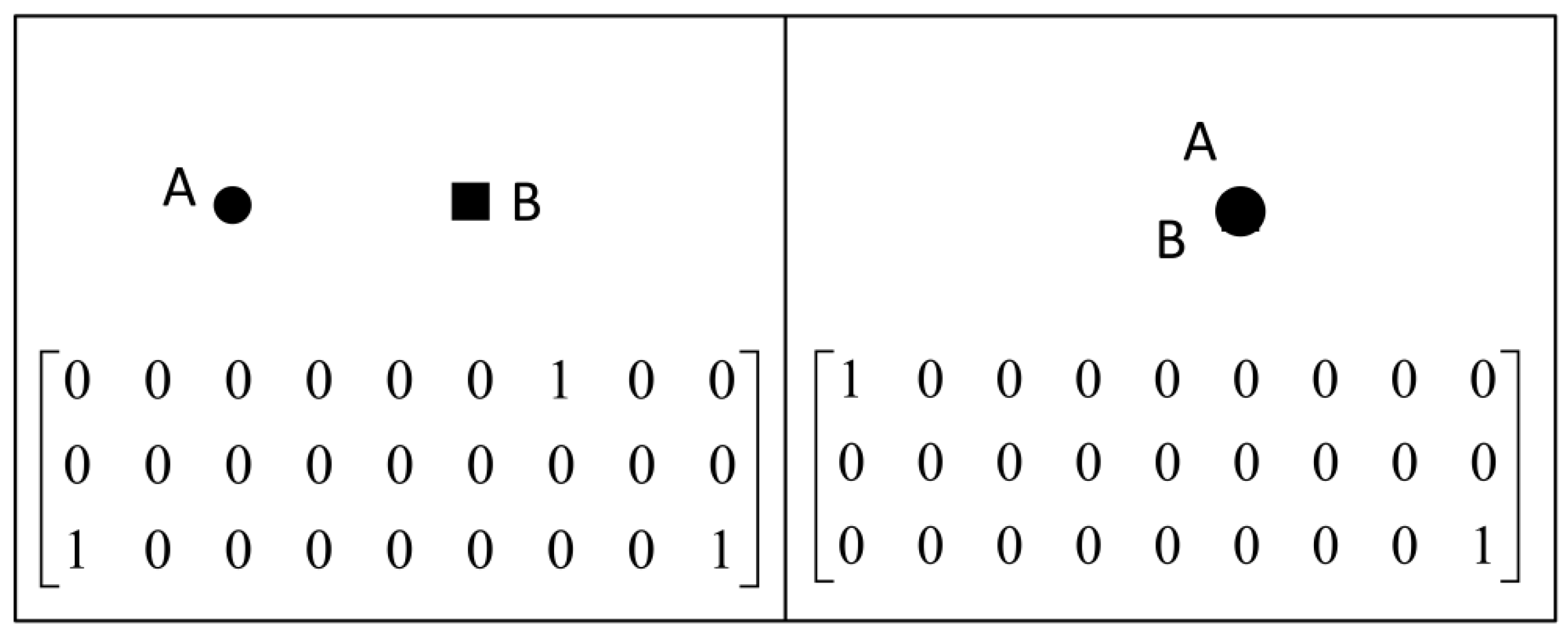
Figure 2 as examples, their topological relations can be described by following topological relation models.
A 3 × 3 matrix with empty and non-empty values is represented by Equation (1).
A’s interior,
A’s boundary,
A’s exterior,
B’s interior,
B’s boundary and
B’s exterior are denoted by
,
,
,
,
and
, respectively. By considering the empty and non-empty values, 512 (512 = 2
9) binary topological relations can be distinguished in theory. However, not all 512 binary topological relations can be implemented. The 9IM can distinguish 33 relations between two simple lines, 19 relations between a simple line and a region and 8 relations between two simple regions [
8]. The value of the intersection in Equation (1) can be drawn from {0, 1}, where a 0 means that the intersection is null and a 1 represents that the intersection is not null,
Based on the 9IM, the topological relations between A and B are described below. The formalisms of the topological relations in
Figure 2a–c expressed by the 9IM are all the same. In other words, all of the topological relations in
Figure 2a–c can be described as follows:
A dimensionally-extended nine-intersection matrix (DE-9IM) is represented by Equation (3). The dimension invariant is used to distinguish the dimension of the intersection and is not higher than the lowest dimension of the two spatial objects. Therefore, the largest value of the dimension of the intersection is 2 between simple points, lines and regions. The dimension of the intersection is −1 if the intersection is empty. The dimension of a non-empty intersection is taken to be the maximum of the dimensions of the intersection. For example, if the intersections contain both points and lines, the dimension of the intersection is set to 1. Considering the dimensions of intersections, 262,144 (262,144 = 4
9) topological relations can be distinguished in theory. However, not all 262,144 topological relations can be implemented, and some topological relations have no practical significance.
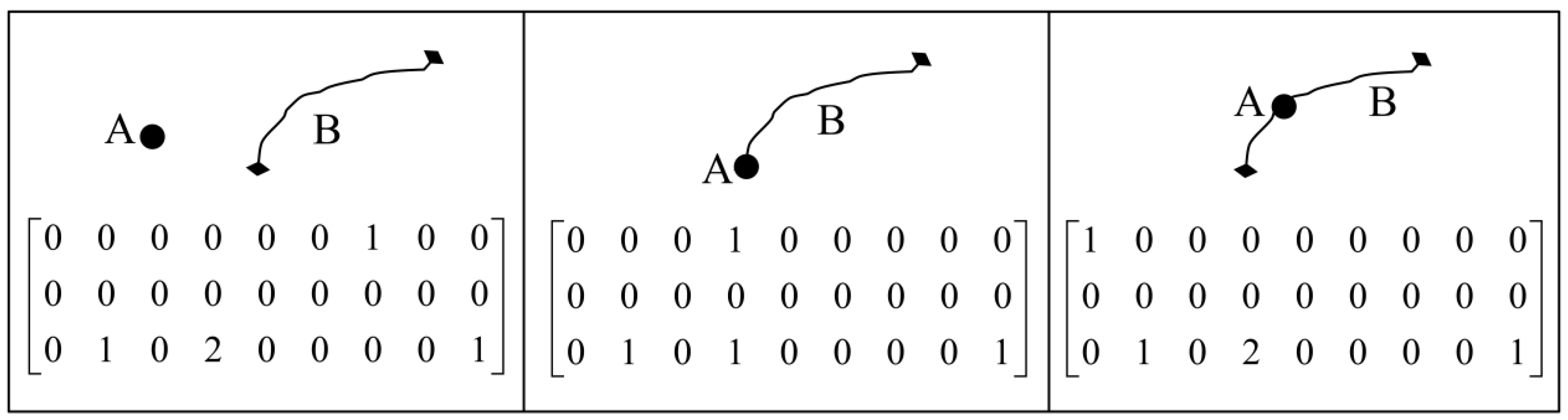
Based on the DE-9IM, the topological relations between
A and
B are described below. The formalisms of topological relations in
Figure 2a,c expressed by the DE-9IM are the same (Equation (4)), whereas the formalism of topological relations in
Figure 2b (Equation (5)) is different from that of
Figure 2a,c. Compared with the 9IM, the DE-9IM can not only distinguish whether two sets intersect, but also the dimensions of the intersections:
Short for a 3 × 3 matrix that shows the number of separations, the separation number extended nine-intersection matrix (SNE-9IM) is represented by Equation (6). The number of separations is used to express the number of connected components. The measure for the separation is the topological invariant of the Euler–Poincare characteristic [
26], but the value may be negative. The number of separations is defined as a positive number in this study. Because the number of separations can be any integer greater or equal to 0, in theory, the SNE-9IM can distinguish innumerable topological relations:
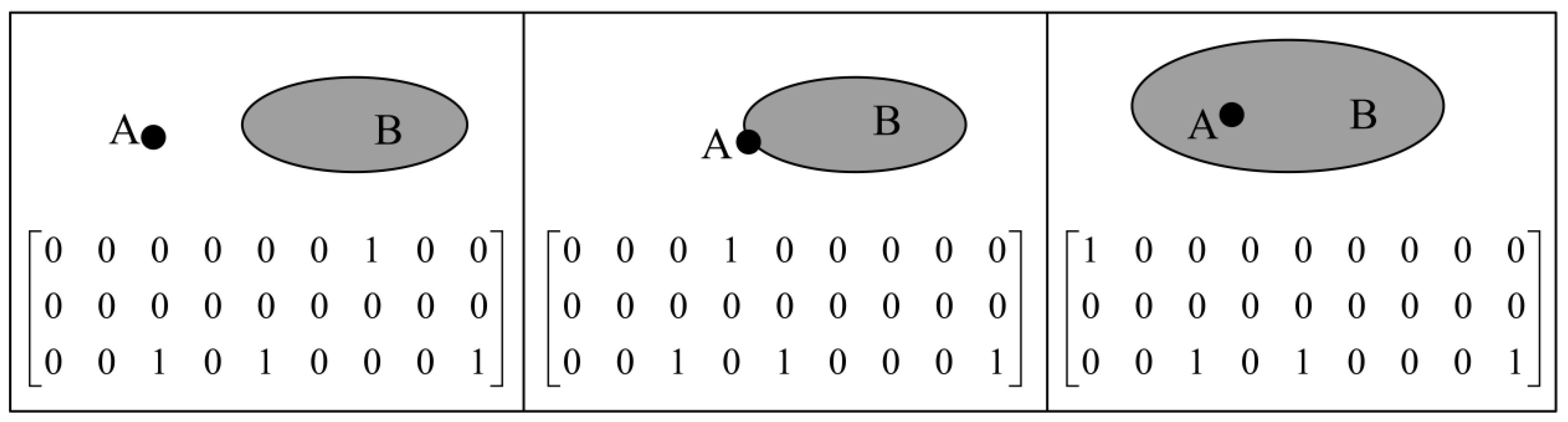
Based on the SNE-9IM, the topological relations between
A and
B are described below. The formalisms of the topological relations in
Figure 2a,b expressed by the SNE-9IM are identical (Equation (7)), whereas the formalism of the topological relations in
Figure 2c (Equation (8)) is different from that of
Figure 2a,b. Compared with the 9IM, the SNE-9IM can not only distinguish whether two sets intersect, but also the number of separations.
2.3. A Comprehensive Model for Topological Relations
Both the dimensions and the number of separations are taken into account in the proposed comprehensive model. This comprehensive model represents the topological spatial relations between two spatial objects,
A and
B, based on a consideration of the number of separations of the interiors, boundaries and exteriors of
A and
B in each dimension. The framework for this comprehensive model is the ordered set of the 27 intersections, called the 27-intersection model (27IM), which is concisely represented as a 9 × 3 matrix (Equation (9)).
Every member in Equation (9) contains three intersections, for example, represents the intersection of , and . Here, , and separately represent the number of the separations in 0 dimensions, 1 dimension and 2 dimensions. Equation (9) can also be represented as a twenty-seven-tuple, i.e., , , , , , , , , , , , , , , , , , , , , , , , , , and . The value of the above intersections records the number of separations in each dimension.
The 27IM is a general framework for representing the relations between two spatial objects in two-dimensional space. However, it cannot represent all of the possible intersections; therefore, some propositions are proposed to exclude the relations that cannot be represented.
Proposition 1: The dimension of two sets is no greater than the smallest dimension of the sets (Equation (10)). In Equation (10), and are two sets, and ,
and are separately the dimension of the ,
and the intersection of and .
Proof: If one set is and the other set is , the intersection is not only a subset of , but also a subset of . Therefore, the dimension of the intersection is no greater than the dimension of or .
Proposition 2: The value of the dimension of the intersection is constrained by the types of two spatial objects.
Condition 1: If the intersection is not null, the only possible value for a line’s interior and a region’s interior is drawn from {1}. In Equation (11), and are separately the interior of the line and the interior of the region, and is the dimension of the intersection of and .
Proof: If the interior of a line intersects with a region’s interior, the dimension of the intersection can only be drawn from {0, 1} according to Proposition 1. If a point belongs to both the interior of a line and a region, the neighborhood of must be in the interior of the region. Moreover, a subset of the line’s interior must be in the neighborhood of . The dimension of the subset of line’s interior is 1.
Condition 2: If the intersection is not null, the only possible value for one region’s interior and other region’s interior is drawn from {2}. In Equation (12), and are the interior of two regions, and is the dimension of the intersection of and .
Proof: If the interior of a region intersects with another region’s interior, the dimension of the intersection is drawn from {0, 1, 2} according to Proposition 1. If a point belongs to the interior of two regions, the neighborhood of must be in the interior of both regions. Therefore, the intersection of two regions can only be a region when the intersection is not null.
Proposition 3: The dimension of the intersection between two exteriors is drawn from {2}.
Proof: or is the set of all points in the embedding space not contained in or . Because , and are subsets of , or are two-dimensional, and and must have intersections. The dimension of the intersection is drawn from {0, 1, 2} according to Proposition 1. If a point belongs to the exterior of and , the neighborhood of must be in the exterior of or ; therefore, the dimension of two regions’ intersection can only be two-dimensional.
Proposition 4: The dimension of the intersection between the boundary of a point and other sets is null.
Proof: Because the boundary of a point is an empty set, the intersection between the boundary of a point and another set must be an empty set; therefore, the dimension of the intersection is null.
Based on the above propositions,
Table 1 lists the possible tuples for the six groups of topological relations: point/point, point/line, point/region, line/line, line/region and region/region. If the tuples can be implemented, the corresponding cell in
Table 1 contains a checkmark (“√”); otherwise, the cell contains a “×”.
3. Results
Three types of spatial objects, including point, line and region, are defined; therefore, six groups of topological relations are summarized. These six groups of topological relations are point/point, point/line, point/region, line/line, line/region and region/region relations, and they are described by the 27IM in this study.
First, point/point topological relations are described. Because the boundary of a point is empty, one point may be disjoint or equal to another point. Therefore, two topological relations can be realized between two points.
Figure 3 shows the formalism of the 27IM and the corresponding geometric interpretations of the two relations between two points.
Second, point/line topological relations are described. Because the dimension of a point is lower than that of a line, the relation between a point and a line may be disjoint, meet or within. Therefore, there are three topological relations between a point and a line.
Figure 4 shows the formalism of the 27IM and the corresponding geometric interpretations of the three relations between a point and a line.
Third, point/region topological relations are described. Similar to point/line topological relations, there are three topological relations between a point and a region.
Figure 5 shows the formalism of the 27IM and the corresponding geometric interpretations of the three relations between a point and a region.
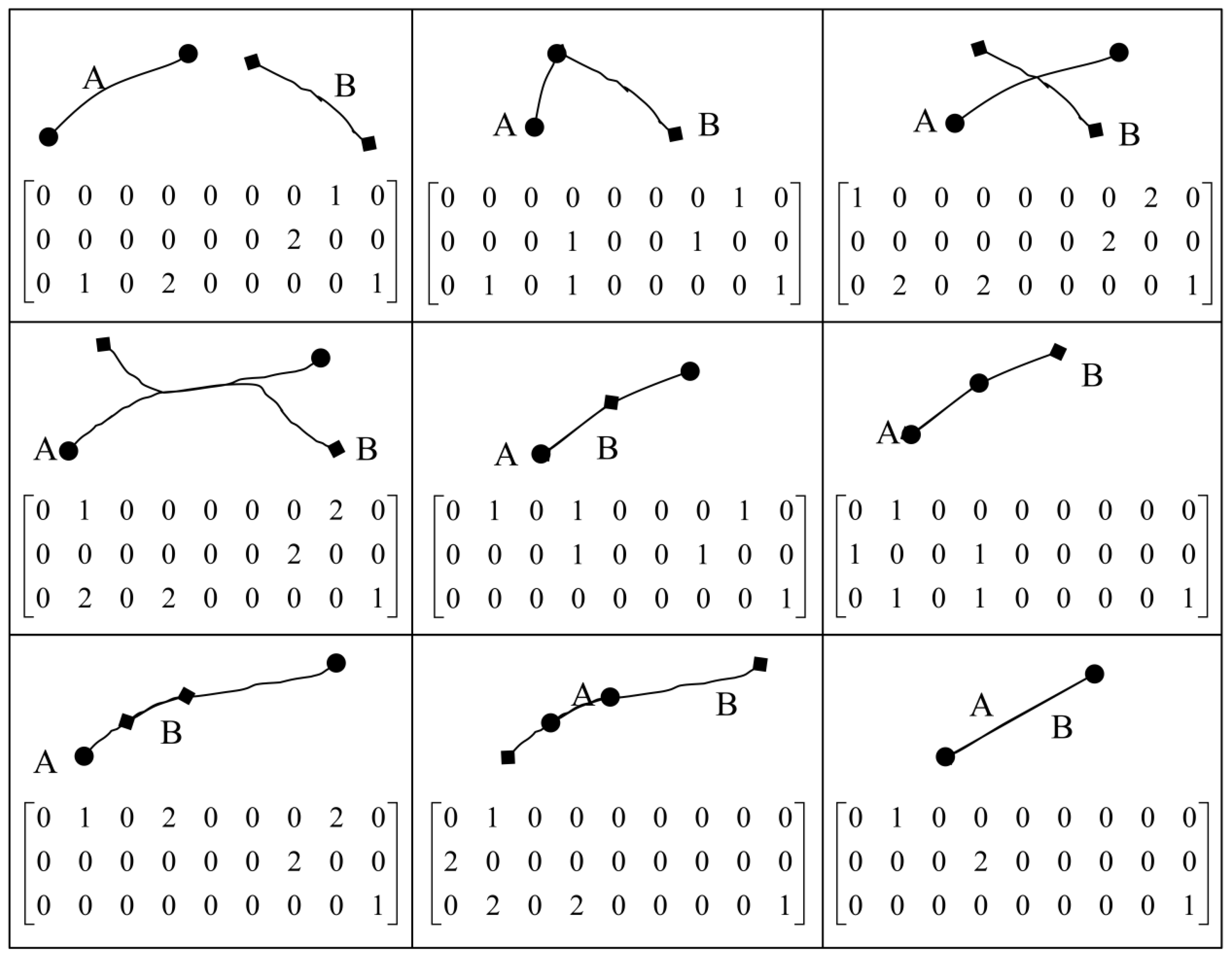
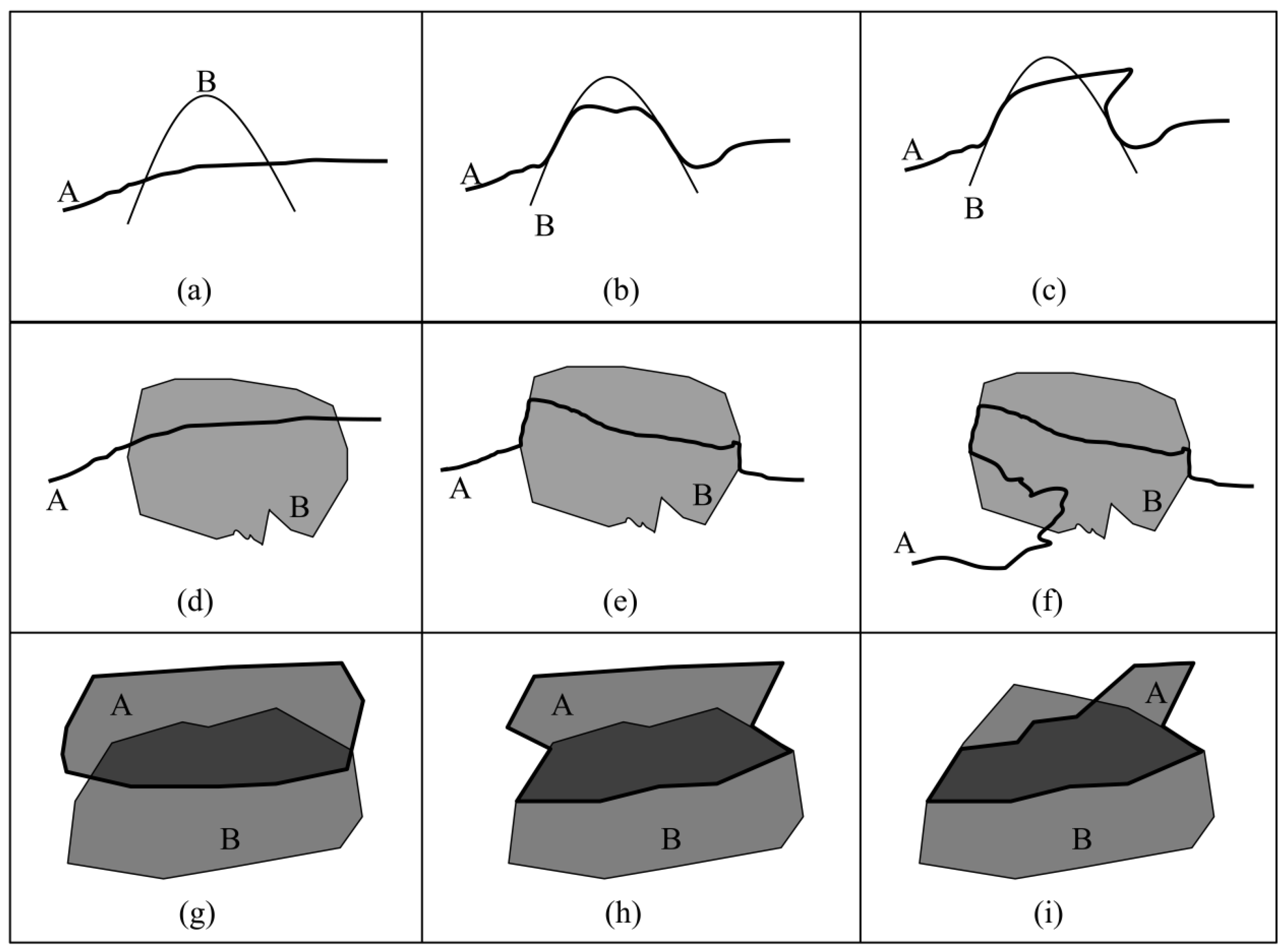
Fourth, line/line topological relations are described. Considering the dimension and the number of separations (for example, the number of intersections between the interior of two lines may be infinite), there are countless theoretical topological relations between two lines; therefore, it is impossible to express all of the possible topological relations. Instead,
Figure 6 shows the formalism of the 27IM and the corresponding geometric interpretations of nine typical relations between two lines.
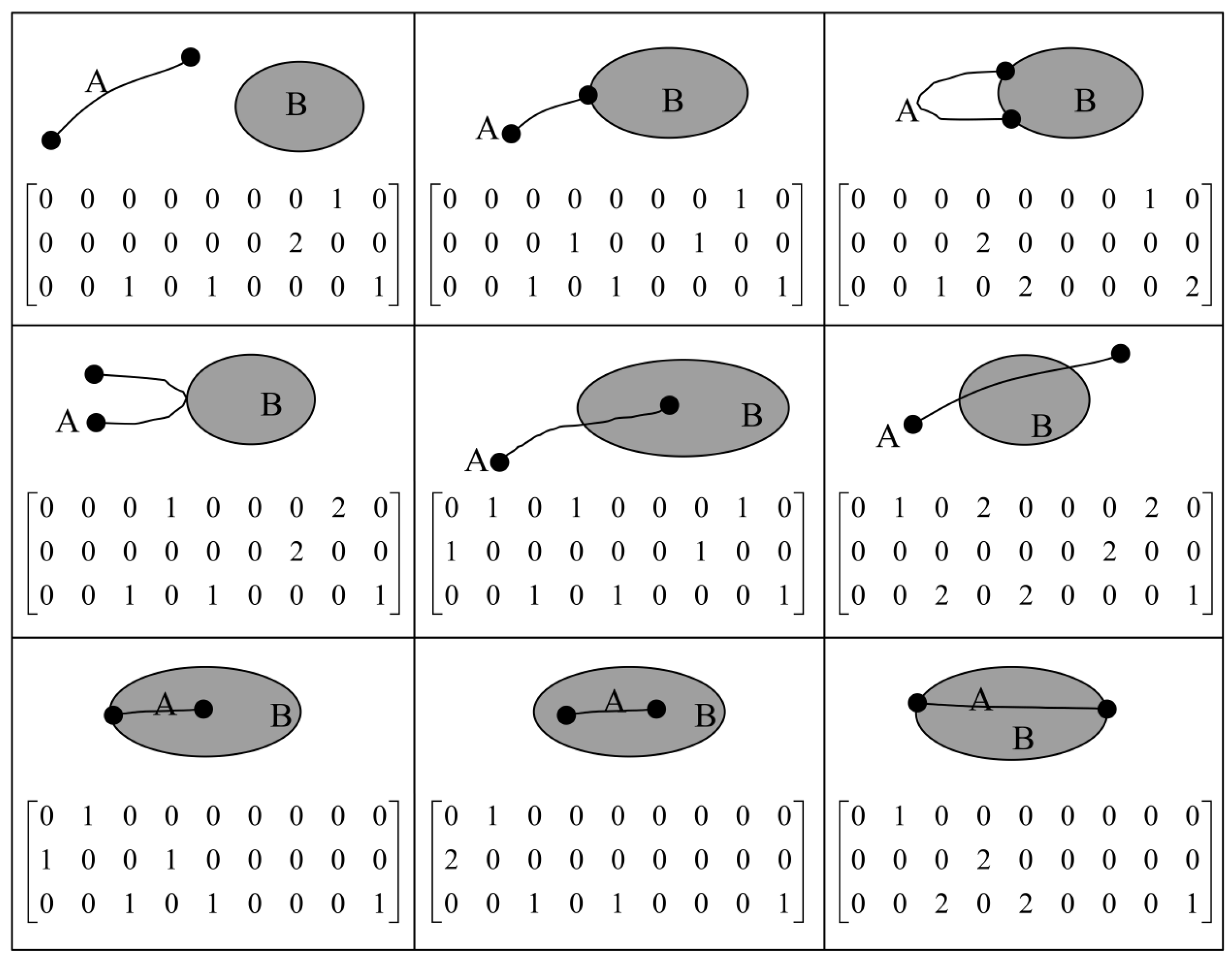
Fifth, line/region topological relations are described. Considering dimensions and the number of separations (for example, the number of intersections between the interior of a line and the boundary of a region, the number of intersections between the interior of a line and the interior of a region and the number of intersections between the interior of a line and the exterior of a region may be infinite), there are countless topological relations between a line and a region; therefore, it is impossible to express all of the possible topological relations. Instead,
Figure 7 shows the formalism of the 27IM and the corresponding geometric interpretations of nine typical relations between a line and a region.
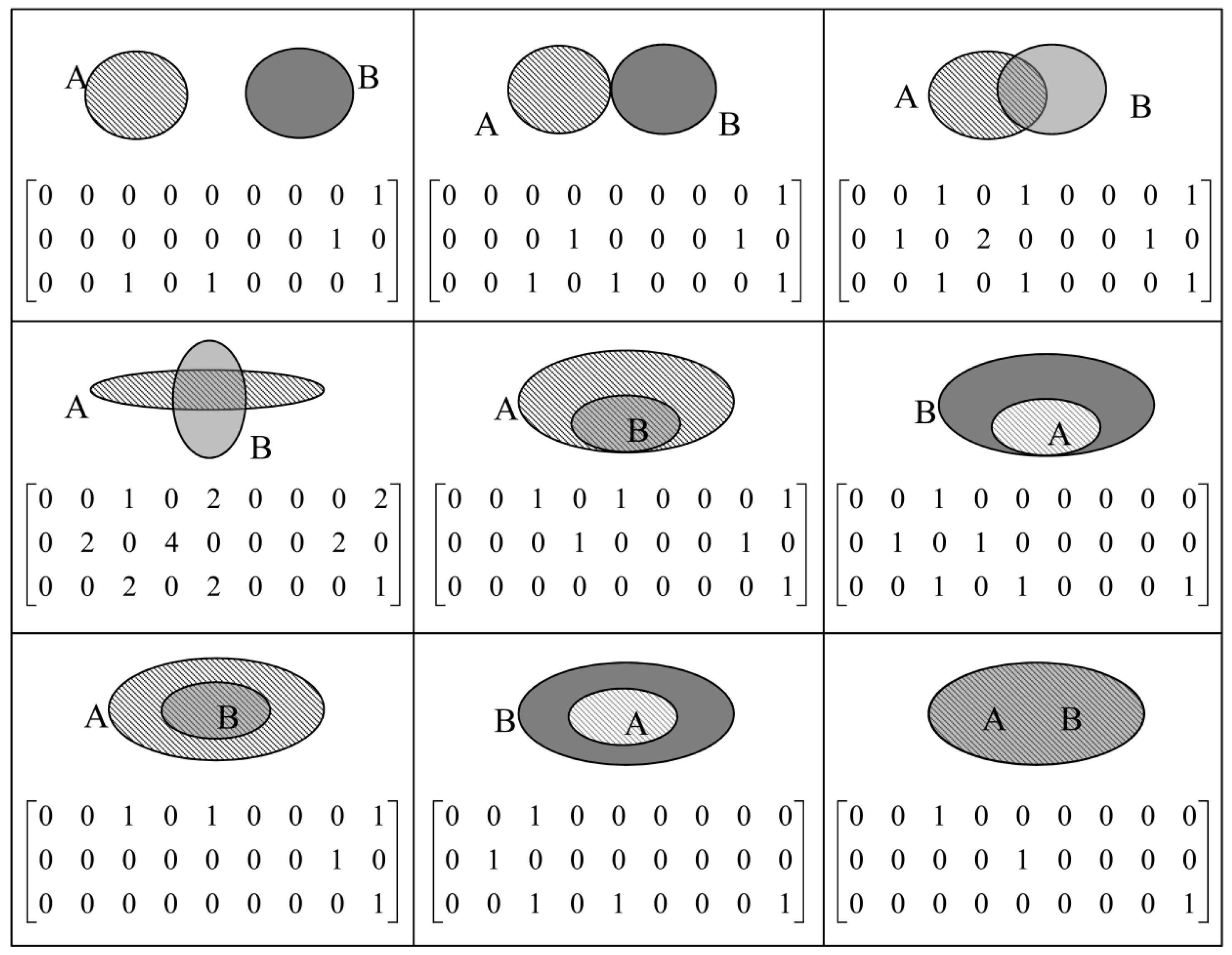
Sixth, region/region topological relations are described. Considering dimensions and the number of separations (for instance, the number of intersections between the interior of two regions and the number of intersections between the boundaries of two regions may be infinite), there are countless topological relations between two regions; therefore, it is impossible to express all of the possible topological relations. Instead,
Figure 8 shows the formalism of the 27IM and the corresponding geometric interpretations of nine typical relations between two regions.
5. Conclusions
The major novel contribution of this paper lies in its proposal of a comprehensive model for topological relations called the 27IM, which considers both the dimension and the number of separations. The 27IM describes six groups of topological relations: point/point, point/line, point/region, line/line, line/region and region/region relations. The first advantage of the 27IM is that the topological relations are preserved under topological transformations. The second advantage of the 27IM is that it distinguishes further topological relations compared with the 9IM, DE-9IM and SNE-9IM. The third advantage of the 27IM is that the interoperability of the 27IM with the 9IM, DE-9IM and SNE-9IM is good.
Although the 27IM is a detailed model, it is more complex than the 9IM, DE-9IM and SNE-9IM, which each requiring only a nine-tuple, while the 27IM requiring a 27-tuple. It is inevitable that many invalid spatial topological relations appear in the 27IM. To exclude impossible spatial topological relations, the 23 conditions proposed by Egenhofer and Herring (1991) can be revised for the 27IM. It is impossible to contain all of the details for the 27IM. Some other topological invariants (i.e., the sequence of boundary-boundary intersection or the types of boundary-boundary intersections) are not considered. The 27IM can be extended to represent more topological relation details whenever necessary. This study addresses only simple objects; complex objects, such as multi-point, multi-line and multi-region objects, are not considered. As is common knowledge, complex objects can be considered as combinations of simple objects. Therefore, the 27IM can also describe the topological relations between complex objects. The numbers of possible topological relations involved in line/line, line/region and region/region relations are countless; consequently, only some typical relations and their corresponding geometric interpretations are included. Only two-dimensional spatial objects are discussed; three-dimensional spatial objects are not included. Although the 27IM cannot be directly used for three-dimensional spatial objects, the 27IM can be extended to the 36-intersection model (36IM) for three-dimensional spatial object. The 36IM would be a 12 × 3 matrix, which represents the number of the separations in zero dimensions, one dimension, two dimensions and three dimensions.
Finally, the 27IM could distinguish further topological relations based on the recognition of the dimension and the number of separations. Other topological invariants as refinements of the empty/non-empty specifications will be included in the future. The topological relations of three-dimensional objects and complex objects will also be discussed.