Evaluating Influential Nodes in Social Networks by Local Centrality with a Coefficient
Abstract
:1. Introduction
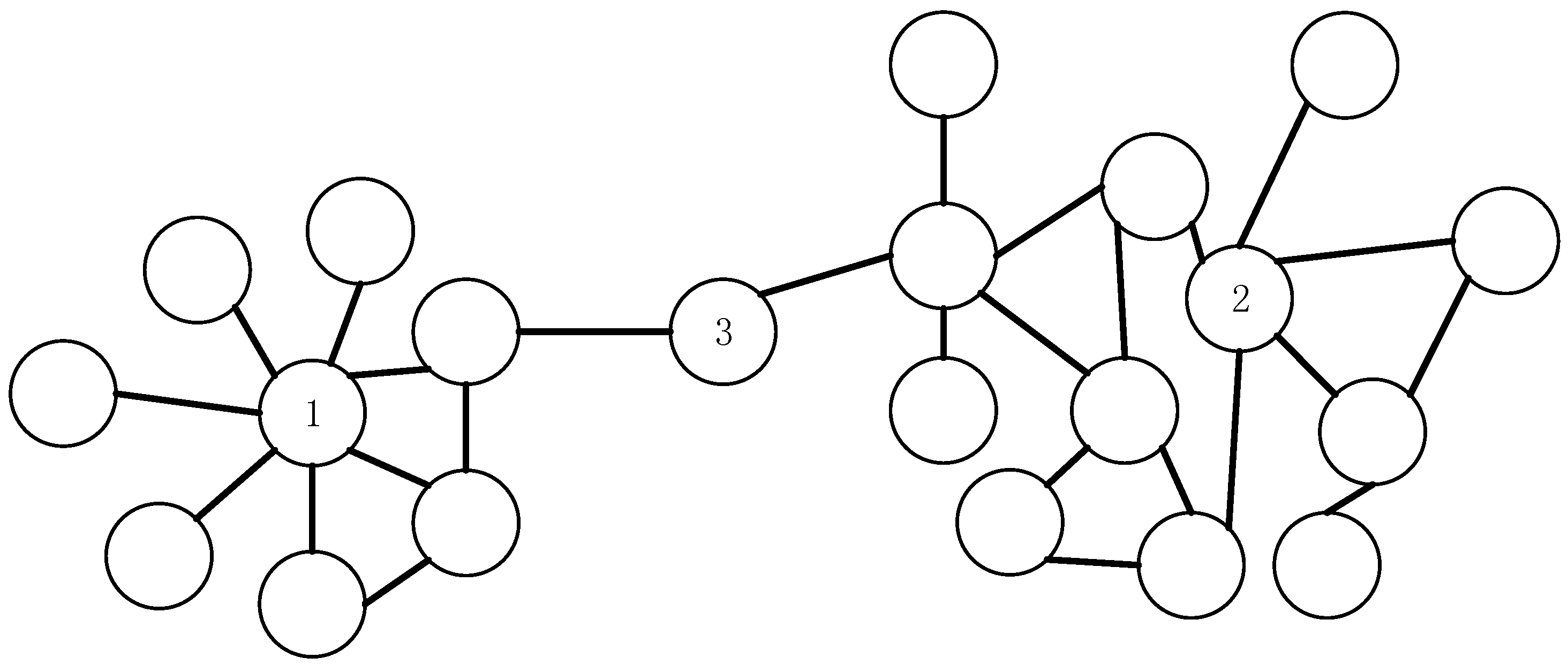
2. Local Centrality with a Coefficient to Measure Node Influence
3. Experimental Results
3.1. The Datasets Used in the Experiments
3.2. Evaluation Methodologies
3.3. Experimental Results and Analysis
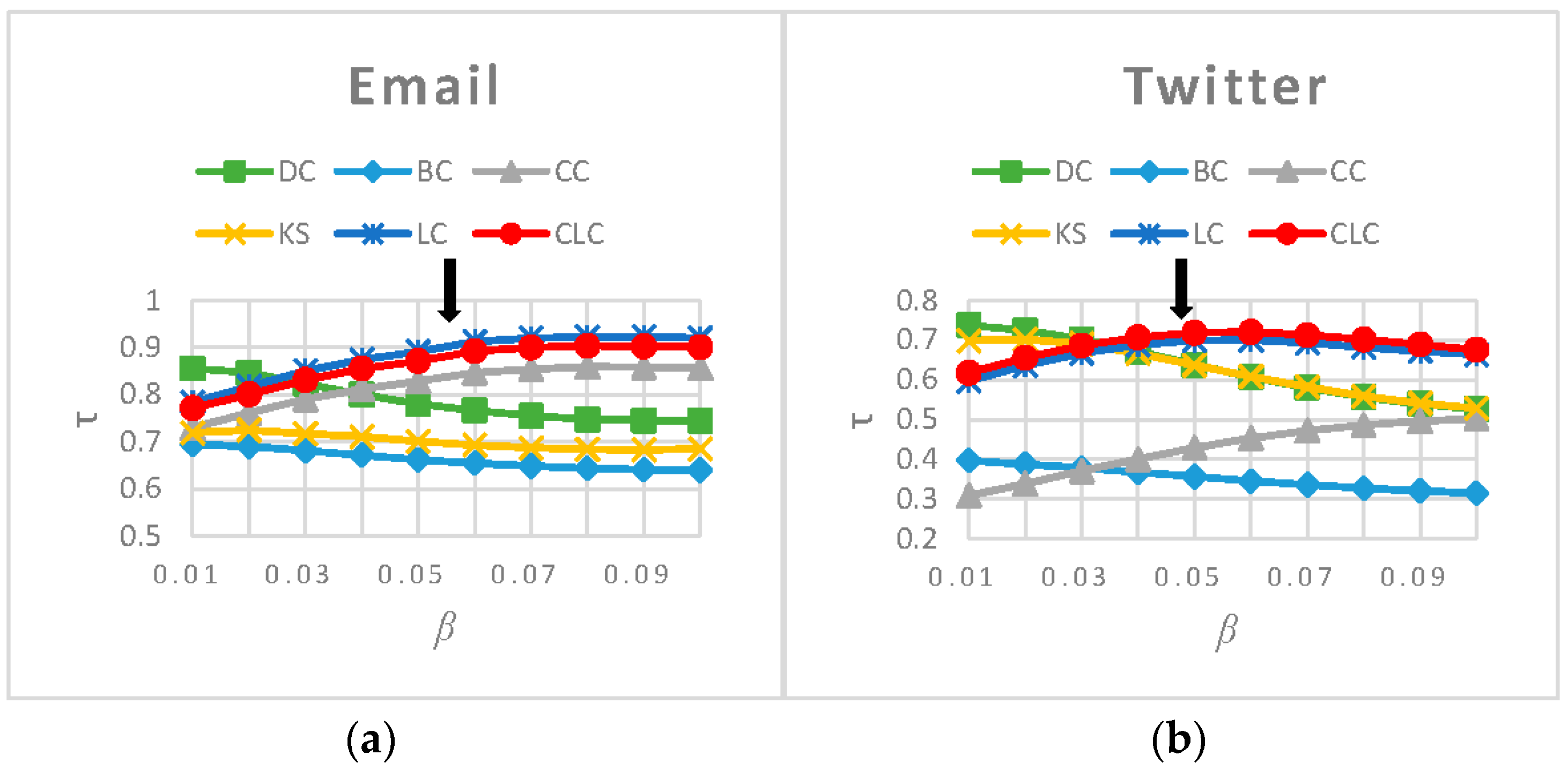
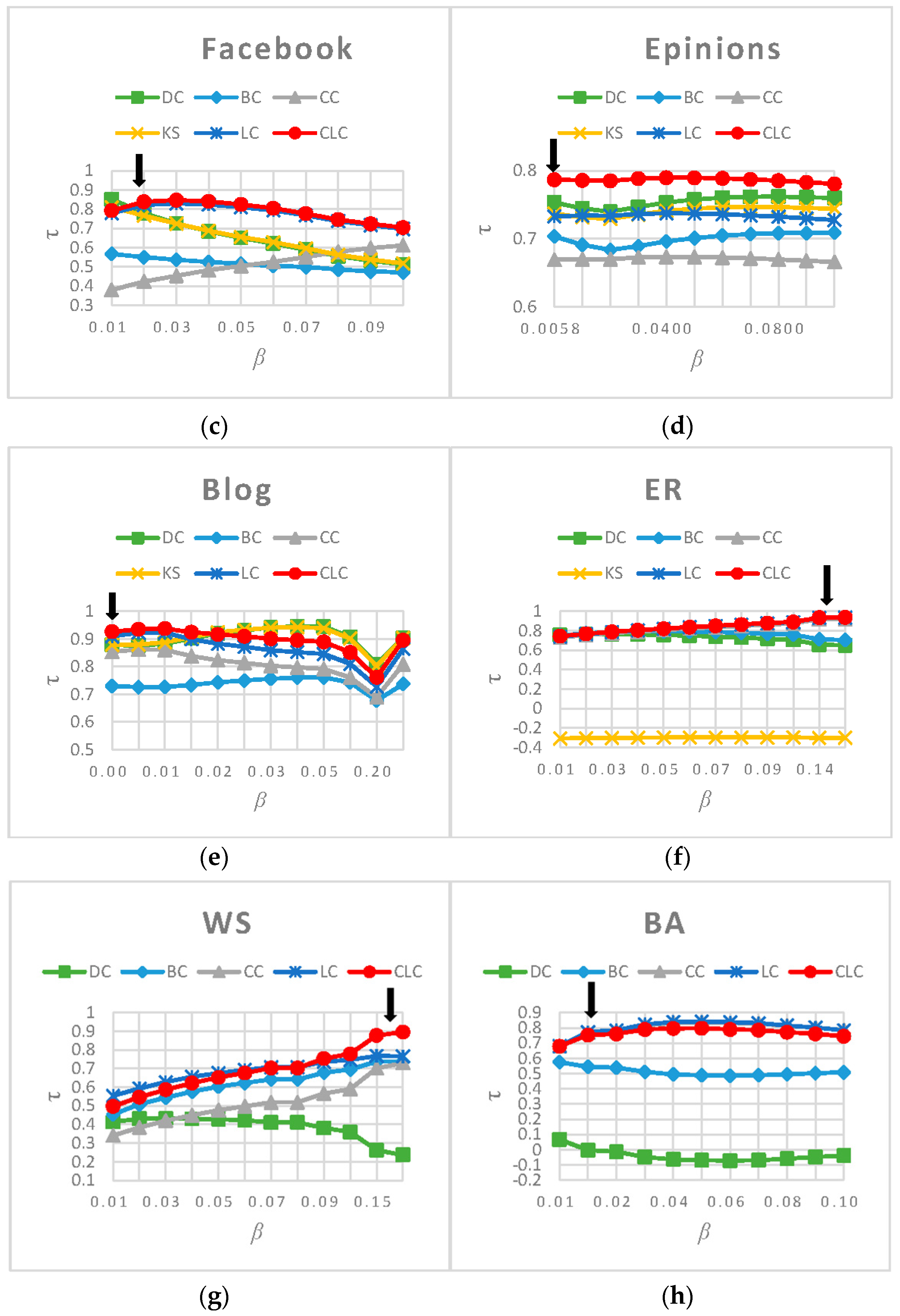
3.3.1. Rank Influence of Nodes
3.3.2. Rank the Most Influential Nodes
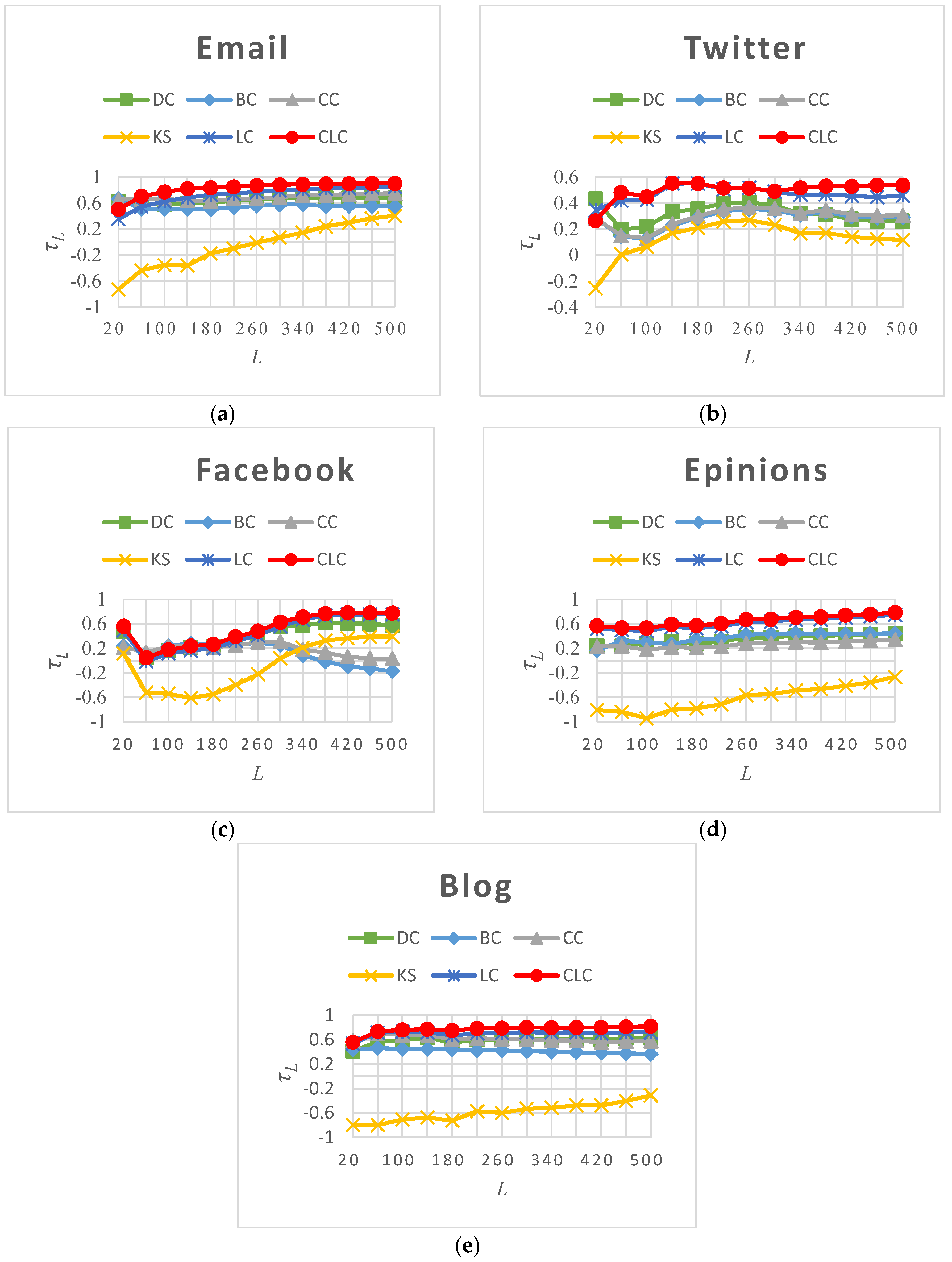
3.3.3. Capability of Distinguishing Nodes’ Spreading Ability
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mislove, A.E. Online Social Networks: Measurement, Analysis, and Applications to Distributed Information Systems. Ph.D. Thesis, Rice University, Houston, TX, USA, 2009. [Google Scholar]
- Albert, R.; Jeong, H.; Barabasi, A.L. Error and attack tolerance of complex networks. Nature 2000, 406, 542. [Google Scholar] [CrossRef] [PubMed]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Krackhardt, D. Assessing the political landscape: Structure, cognition, and power in organizations. Adm. Sci. Q. 1990, 35, 342–369. [Google Scholar] [CrossRef]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Eugene Stanley, H.; Makse, H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888–893. [Google Scholar] [CrossRef]
- Ren, X.; Lü, L.; Ren, X. Review of ranking nodes in complex networks. Chin. J. 2014, 59, 1175–1188. [Google Scholar] [CrossRef]
- Chen, D.; Lü, L.; Shang, M.S.; Zhang, Y.C.; Zhou, T. Identifying influential nodes in complex networks. Phys. A Stat. Mech. Appl. 2012, 391, 1777–1787. [Google Scholar] [CrossRef]
- Wang, X.F.; Li, X.; Chen, G.R. The importance and similarity of nodes. In Network Science: An Introduction; Liu, Y., Ed.; Higher Education Press: Beijing, China, 2012; pp. 157–185. [Google Scholar]
- Liu, Y.; Tang, M.; Zhou, T.; Do, Y. Core-like groups result in invalidation of identifying super-spreader by k-shell decomposition. Sci. Rep. 2015, 5, 9602–9609. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Tang, M.; Zhou, T.; Do, Y. Improving the accuracy of the k-shell method by removing redundant links: From a perspective of spreading dynamics. Sci. Rep. 2015, 5, 13172–13182. [Google Scholar] [CrossRef] [PubMed]
- Ugander, J.; Backstrom, L.; Marlow, C.; Kleinberg, J. Structural diversity in social contagion. Proc. Natl. Acad. Sci. USA 2012, 109, 5962–5966. [Google Scholar] [CrossRef] [PubMed]
- Su, X.P.; Song, Y.R. Leveraging neighborhood “structural holes” to identifying key spreaders in social networks. Acta Phys. Sin. Chin. Ed. 2015, 64, 20101. [Google Scholar]
- Eguíluz, V.M.; Klemm, K. Epidemic threshold in structured scale-free networks. Phys. Rev. Lett. 2002, 89, 108701–108704. [Google Scholar] [CrossRef] [PubMed]
- Petermann, T.; de Los Rios, P. Role of clustering and gridlike ordering in epidemic spreading. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2004, 69, 279–307. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Yan, G.; Wang, B.H. Maximal planar networks with large clustering coefficient and power-law degree distribution. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 71, 046141. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of small-world networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Guimera, R.; Danon, L.; Diaz-Guilera, A.; Giralt, F.; Arenas, A. Self-similar community structure in a network of human interactions. Phys. Rev. E 2003, 68, 065103. [Google Scholar] [CrossRef] [PubMed]
- Mcauley, J.J.; Leskovec, J. Learning to discover social circles in ego networks. Adv. Neural Inf. Process. Syst. 2012, 25, 539–547. [Google Scholar]
- Traud, A.L.; Mucha, P.J.; Porter, M.A. Social structure of Facebook networks. Phys. A Stat. Mech. Appl. 2011, 391, 4165–4180. [Google Scholar] [CrossRef]
- Richardson, M.; Agrawal, R.; Domingos, P. Trust Management for the Semantic Web. Lect. Notes Comput. Sci. 2003, 2870, 351–368. [Google Scholar]
- Gregory, S. Finding overlapping communities using disjoint community detection algorithms. Complex Netw. 2009, 207, 47–61. [Google Scholar]
- Castellano, C.; Pastor-Satorras, R. Thresholds for epidemic spreading in networks. Phys. Rev. Lett. 2010, 105, 3305. [Google Scholar] [CrossRef] [PubMed]
- Dorogovtsev, S.N.; Goltsev, A.V.; Mendes, J.F.F. Critical phenomena in complex networks. Rev. Mod. Phys. 2007, 80, 1275–1335. [Google Scholar] [CrossRef]
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, M.; Zhou, T.; Do, Y. Identify influential spreaders in complex networks, the role of neighborhood. Phys. A Stat. Mech. Appl. 2016, 452, 289–298. [Google Scholar] [CrossRef]
- Gao, S.; Ma, J.; Chen, Z.; Wang, G.; Xing, C.M. Ranking the spreading ability of nodes in complex networks based on local structure. Phys. A Stat. Mech. Appl. 2014, 403, 130–147. [Google Scholar] [CrossRef]
- Song, C.; Havlin, S.; Makse, H.A. Self-similarity of complex networks. Nature 2005, 433, 392–395. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Havlin, S.; Makse, H.A. Origins of fractality in the growth of complex networks. Nat. Phys. 2006, 2, 275–281. [Google Scholar] [CrossRef]
| Network | DC | BC | CC | KS | LC | CLC |
|---|---|---|---|---|---|---|
| 0.0001 | 0.3551 | 0.5616 | 0.5621 | 0.2350 | 0.2372 | |
| 0.0003 | 24.5725 | 37.7616 | 37.7718 | 14.4024 | 14.6907 | |
| 0.0003 | 17.0798 | 33.6466 | 33.6534 | 11.6703 | 11.8865 | |
| Epinions | 0.0003 | 26.6689 | 40.6052 | 40.6201 | 16.3923 | 16.6214 |
| Blog | 0.0006 | 56.4583 | 85.3895 | 85.4497 | 30.0134 | 30.4575 |
| Network | n | m | C | |||
|---|---|---|---|---|---|---|
| 1133 | 5451 | 9.62 | 71 | 0.22020 | 0.05350 | |
| 5000 | 135,610 | 27.12 | 733 | 0.26070 | 0.04740 | |
| 4039 | 88,234 | 43.69 | 1045 | 0.51917 | 0.01938 | |
| Epinions | 5000 | 180,493 | 36.10 | 1344 | 0.15240 | 0.00580 |
| Blog | 10,312 | 333,983 | 64.78 | 3992 | 0.09139 | 0.00181 |
| ER | 2000 | 6000 | 6 | 18 | 0.00023 | 0.14220 |
| WS | 2000 | 6000 | 6 | 11 | 0.30014 | 0.16067 |
| BA | 2000 | 11,988 | 5.99 | 414 | 0.01124 | 0.01828 |
| Network | Epinions | Blog | ER | WS | BA | |||
|---|---|---|---|---|---|---|---|---|
| β | 0.01 | 0.01 | 0.01 | 0.0058 | 0.00181 | 0.01 | 0.01 | 0.01 |
| 0.02 | 0.02 | 0.02 | 0.01 | 0.003 | 0.02 | 0.02 | 0.0183 | |
| 0.03 | 0.03 | 0.03 | 0.02 | 0.005 | 0.03 | 0.03 | 0.02 | |
| 0.04 | 0.04 | 0.04 | 0.03 | 0.01 | 0.04 | 0.04 | 03 | |
| 0.05 | 0.05 | 0.05 | 0.04 | 0.015 | 0.05 | 0.05 | 0.04 | |
| 0.0535 | 0.06 | 0.06 | 0.05 | 0.02 | 0.06 | 0.06 | 0.05 | |
| 0.06 | 0.07 | 0.07 | 0.06 | 0.03 | 0.07 | 0.07 | 0.06 | |
| 0.07 | 0.08 | 0.08 | 0.07 | 0.04 | 0.08 | 0.08 | 0.07 | |
| 0.08 | 0.09 | 0.09 | 0.08 | 0.05 | 0.09 | 0.09 | 0.08 | |
| 0.09 | 0.1 | 0.1 | 0.09 | 0.1 | 0.1 | 0.1 | 0.09 | |
| 0.1 | 0.1 | 0.2 | 0.1422 | 0.15 | 0.1 | |||
| 0.15 | 0.1607 |
| Network | /Rank | /Rank | /Rank | /Rank | /Rank | /Rank |
|---|---|---|---|---|---|---|
| 0.786259/4 | 0.662523/6 | 0.819400/3 | 0.700200/5 | 0.881227/1 | 0.862679/2 | |
| 0.637459/3 | 0.356691/6 | 0.417217/5 | 0.628729/4 | 0.665546/2 | 0.684402/1 | |
| 0.650335/3 | 0.512972/5 | 0.510590/6 | 0.648818/4 | 0.778076/2 | 0.790055/1 | |
| Epinions | 0.754799/2 | 0.700373/5 | 0.670692/6 | 0.740910/3 | 0.734021/4 | 0.786574/1 |
| Blog | 0.903491/2 | 0.736955/6 | 0.808483/5 | 0.903646/1 | 0.864197/4 | 0.895490/3 |
| ER | 0.729468/5 | 0.767019/4 | 0.829537/3 | −0.300700/6 | 0.841899/2 | 0.843974/1 |
| WS | 0.384922/5 | 0.620022/3 | 0.516354/4 | / | 0.686010/2 | 0.691206/1 |
| BA | −0.037630/5 | 0.512135/4 | 0.76890/2 | / | 0.801210/1 | 0.766298/3 |
| Network | ||||||
|---|---|---|---|---|---|---|
| 0.6440 | 0.5502 | 0.6870 | −0.0482 | 0.7229 | 0.8241 | |
| 0.3190 | 0.2781 | 0.2899 | 0.1292 | 0.4688 | 0.4975 | |
| 0.4171 | 0.1247 | 0.1818 | −0.0770 | 0.4564 | 0.5080 | |
| Epinions | 0.3468 | 0.3730 | 0.2653 | −0.6165 | 0.6108 | 0.6499 |
| Blog | 0.5892 | 0.4174 | 0.6130 | −0.5851 | 0.6998 | 0.7674 |
| Network | ||||||
|---|---|---|---|---|---|---|
| 0.043248 | 0.819064 | 0.741395 | 0.010591 | 0.963813 | 0.969991 | |
| 0.071800 | 0.908400 | 0.747600 | 0.02700 | 0.988400 | 0.989800 | |
| 0.056202 | 0.866304 | 0.300569 | 0.023768 | 0.954444 | 0.95593 | |
| Epinions | 0.089400 | 0.897200 | 0.606200 | 0.018400 | 0.942400 | 0.943500 |
| Blog | 0.055857 | 0.925524 | 0.584756 | 0.011055 | 0.980023 | 0.980100 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Liu, F.; Wang, J.; Li, T. Evaluating Influential Nodes in Social Networks by Local Centrality with a Coefficient. ISPRS Int. J. Geo-Inf. 2017, 6, 35. https://doi.org/10.3390/ijgi6020035
Zhao X, Liu F, Wang J, Li T. Evaluating Influential Nodes in Social Networks by Local Centrality with a Coefficient. ISPRS International Journal of Geo-Information. 2017; 6(2):35. https://doi.org/10.3390/ijgi6020035
Chicago/Turabian StyleZhao, Xiaohui, Fang’ai Liu, Jinlong Wang, and Tianlai Li. 2017. "Evaluating Influential Nodes in Social Networks by Local Centrality with a Coefficient" ISPRS International Journal of Geo-Information 6, no. 2: 35. https://doi.org/10.3390/ijgi6020035
APA StyleZhao, X., Liu, F., Wang, J., & Li, T. (2017). Evaluating Influential Nodes in Social Networks by Local Centrality with a Coefficient. ISPRS International Journal of Geo-Information, 6(2), 35. https://doi.org/10.3390/ijgi6020035






