Development of a Change Detection Method with Low-Performance Point Cloud Data for Updating Three-Dimensional Road Maps
Abstract
:1. Introduction
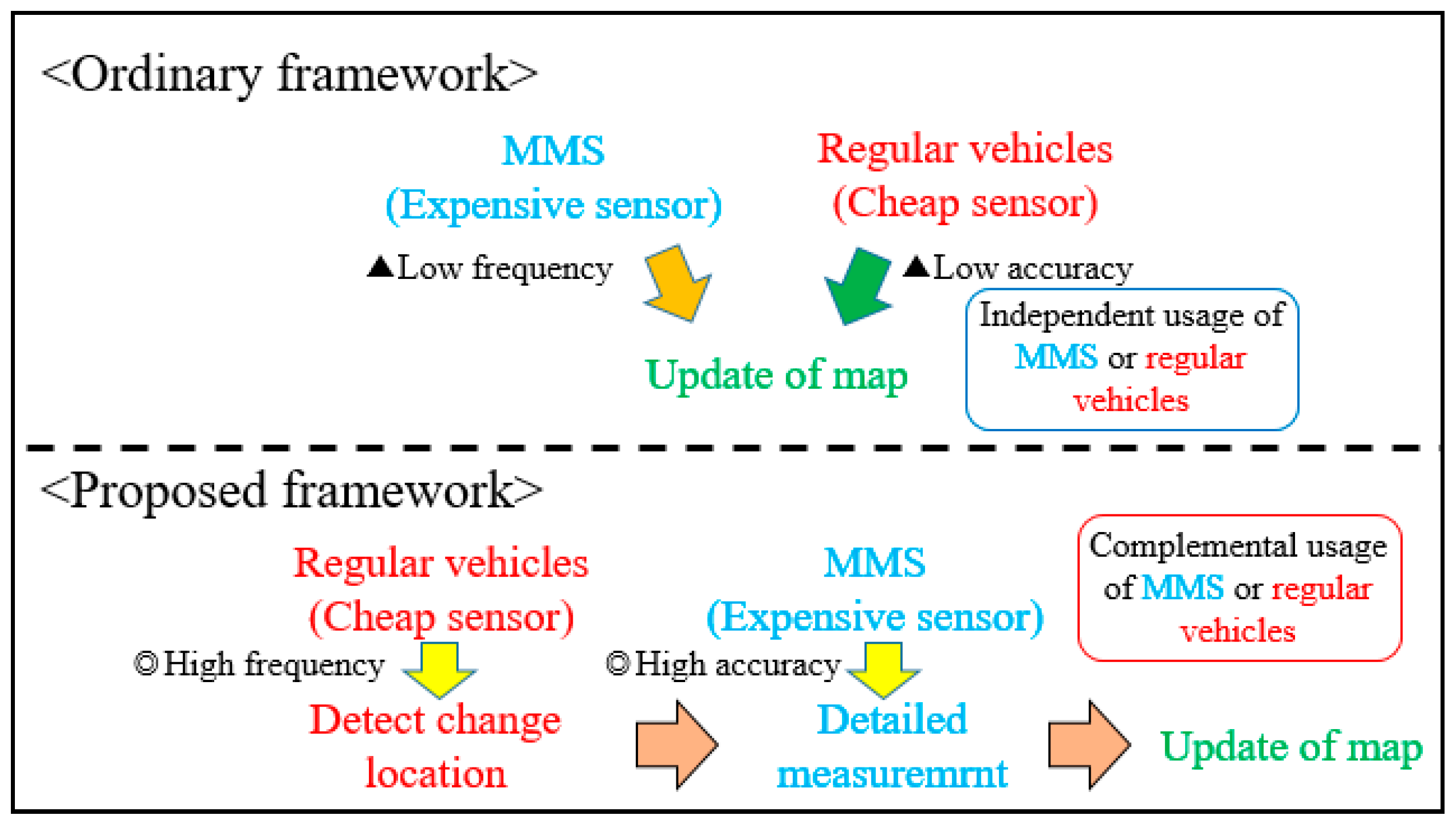
1.1. Research Background
1.2. Related Work
- Distinguishing real changes from occlusions and tentative changes,
- Detecting changes in point cloud data with varying accuracies and point densities,
- Integrating registration and the above change detection, and visualizing the result.
2. Method
2.1. Overview of the Proposed Method
2.2. Registration
2.3. Estimation of Occupancy Rate
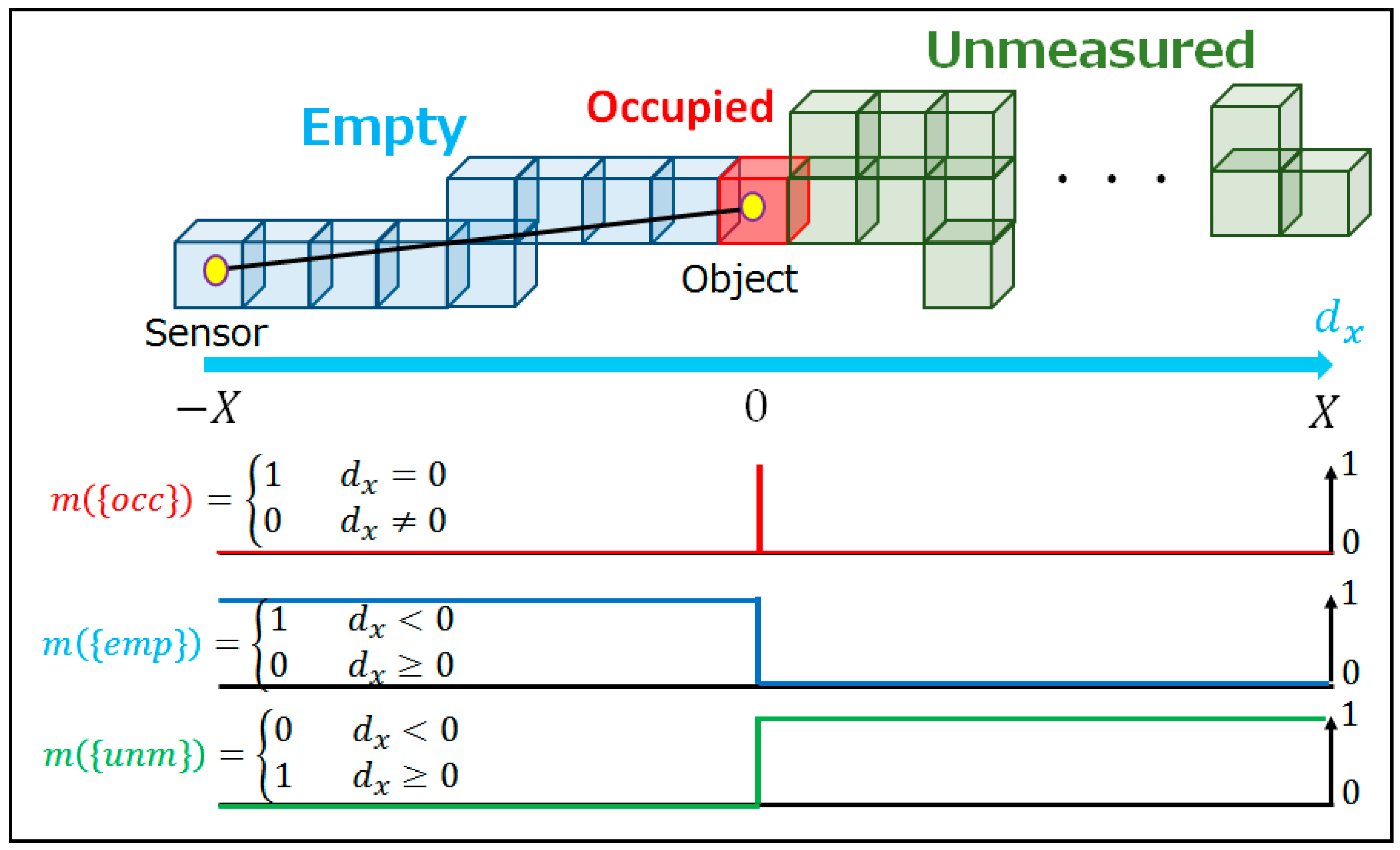
2.3.1. Occupancy Status at Voxels
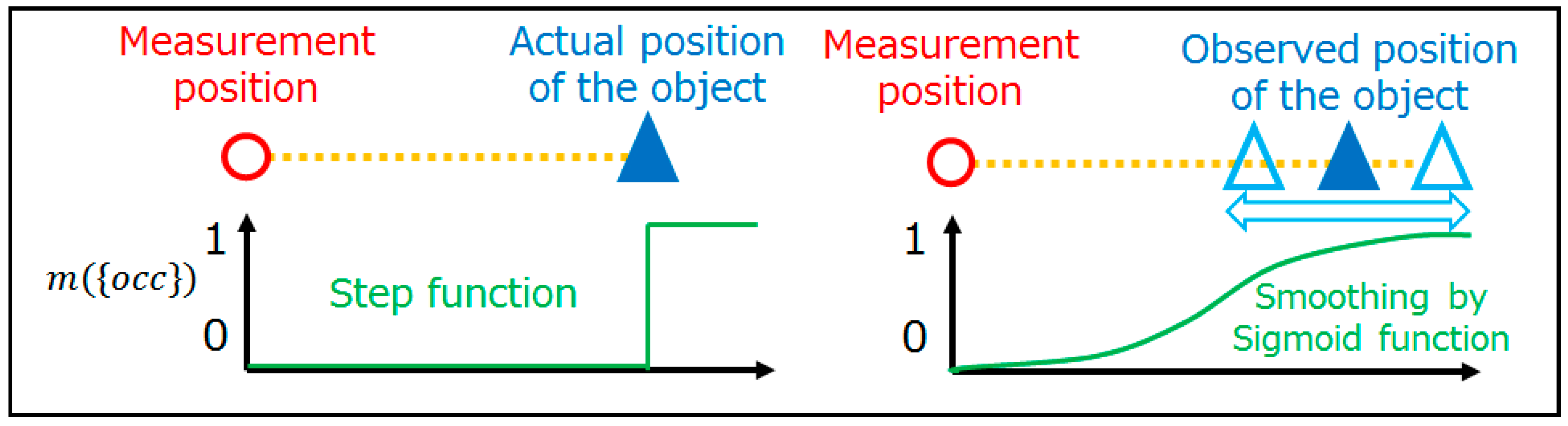
2.3.2. Sensor Model
2.3.3. Occupancy Rate Calculation
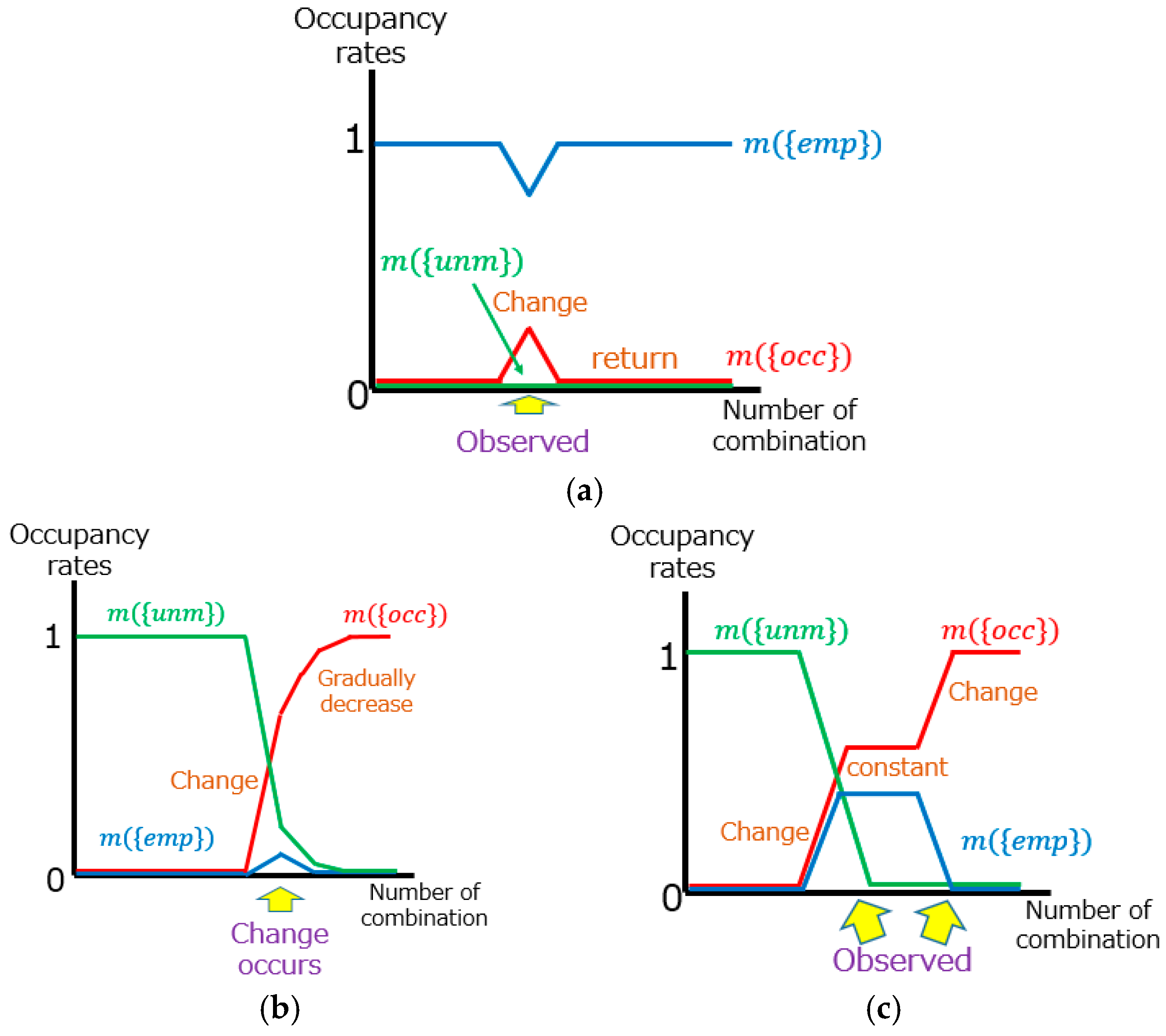
2.4. Change Detection by Transition of Occupancy Rate
3. Results
3.1. Data
3.1.1. Specification of Data
3.1.2. Road Environment Change and Tentative Change
3.2. Experimental Results
3.2.1. Parameters Setting
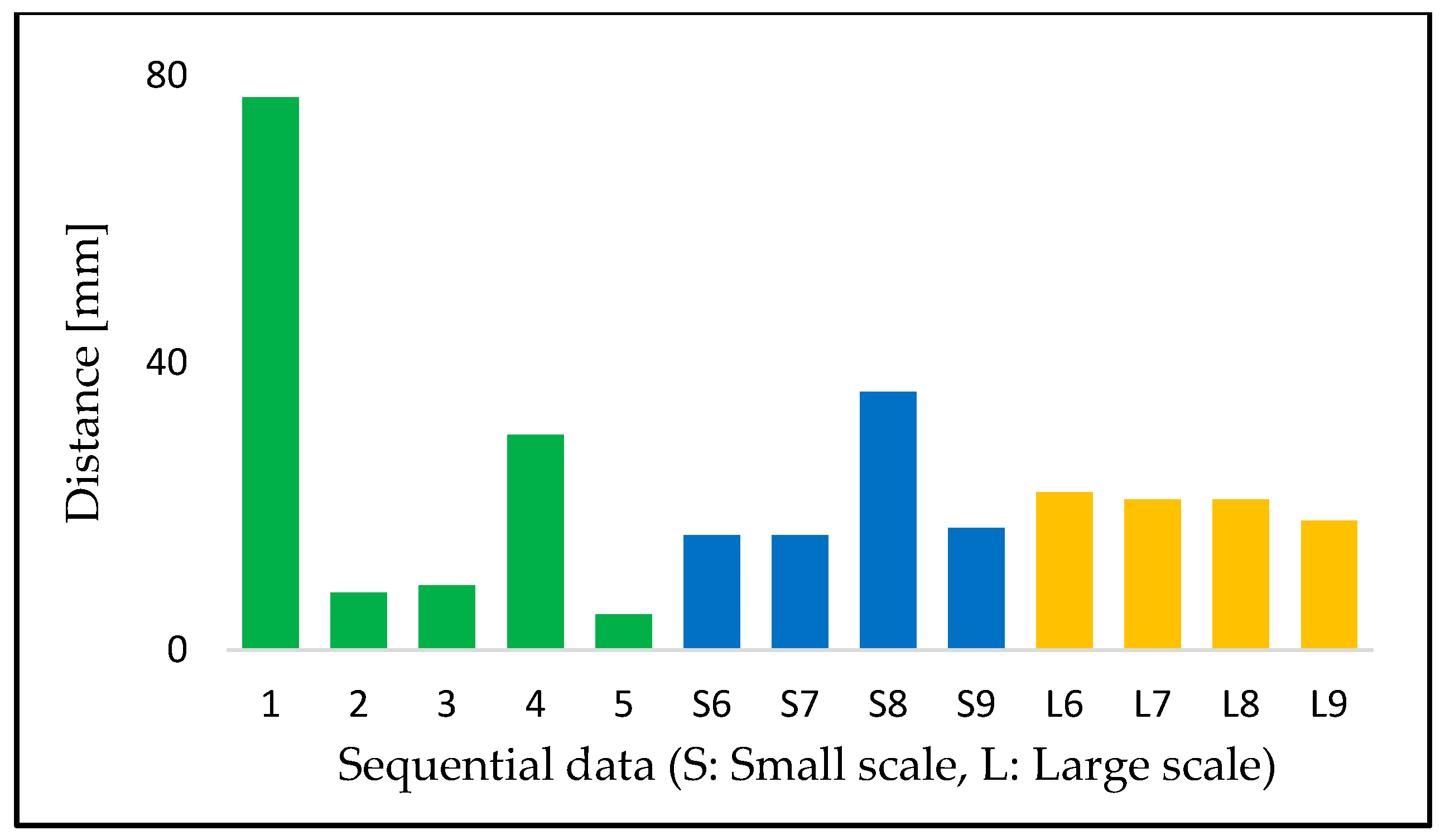
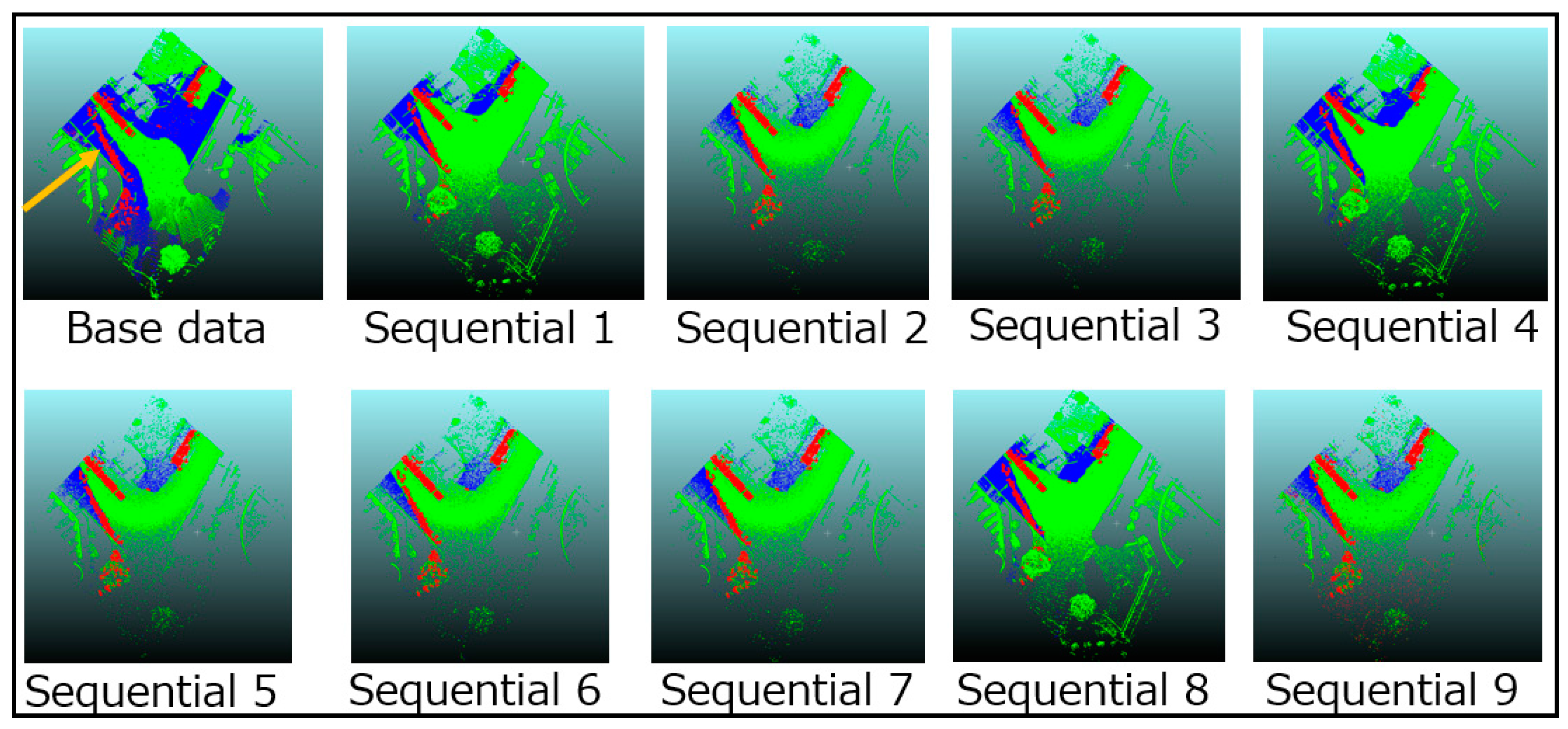
3.2.2. Registration
3.2.3. Tentative Changes and Differences of Measurement Areas
3.2.4. Road Environmental Change
4. Discussion
4.1. Registration
4.2. Change Detection
4.2.1. Different Measurement Areas and Tentative Changes
4.2.2. Large-Scale Change Scenarios and Correcting Processes
4.2.3. Small-Scale Change Scenario
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shimada, H.; Yamaguchi, A.; Takada, H.; Sato, K. Implementation and Evaluation of Local Dynamic Map in Safety Driving Systems. J. Transp. Technol. 2015, 5, 102–112. [Google Scholar] [CrossRef]
- Moravec, H.; Elfes, A. High resolution maps from wide angle sonar. In Proceedings of the IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; Volume 2, pp. 116–121. [Google Scholar]
- Dempster, A.P. Upper and Lower Probabilities Induced by a Multivalued Mapping. Ann. Math. Stat. 1967, 38, 325–339. [Google Scholar] [CrossRef]
- Shafer, G. A Mathematical Theory of Evidence; Princeton University Press: Princeton, NJ, USA, 1976; ISBN 978-0-691-10042-5. [Google Scholar]
- Scovanner, P.; Ali, S.; Shah, M. A 3-dimensional sift descriptor and its application to action recognition. In Proceedings of the 15th ACM International Conference on Multimedia, Augsburg, Germany, 25–29 September 2007; ACM: New York, NY, USA, 2007; pp. 357–360. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Sipiran, I.; Bustos, B. Harris 3D: A robust extension of the Harris operator for interest point detection on 3D meshes. Vis. Comput. 2011, 27, 963–976. [Google Scholar] [CrossRef]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J.; Kwok, N.M. A Comprehensive Performance Evaluation of 3D Local Feature Descriptors. Int. J. Comput. Vis. 2016, 116, 66–89. [Google Scholar] [CrossRef]
- Hashimoto, M. 3D Features for point cloud data processing. Presented at the DIA2015 Workshop, Hiroshima, Japan, 5–6 March 2015; Intelligent Sensing Laboratory, Chukyo University: Nagoya, Japan, 2015. Available online: http://isl.sist.chukyo-u.ac.jp/Archives/archives-e.html (accessed on 19 October 2017).
- Johnson, A.E.; Hebert, M. Using spin images for efficient object recognition in cluttered 3D scenes. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 433–449. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Marton, Z.C.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast Point Feature Histograms (FPFH) for 3D registration. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Tombari, F.; Salti, S.; Di Stefano, L. Unique signatures of histograms for local surface description. In Proceedings of the European Conference on Computer Vision, Crete, Greece, 5–11 September 2010; Springer: Berlin, Germany, 2010; pp. 356–369. [Google Scholar]
- Drost, B.; Ulrich, M.; Navab, N.; Ilic, S. Model globally, match locally: Efficient and robust 3D object recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 998–1005. [Google Scholar]
- Tombari, F.; Salti, S.; Stefano, L.D. A combined texture-shape descriptor for enhanced 3D feature matching. In Proceedings of the 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 809–812. [Google Scholar]
- Point Cloud Library (PCL). Available online: http://pointclouds.org/ (accessed on 19 October 2017).
- Hänsch, R.; Weber, T.; Hellwich, O. Comparison of 3D interest point detectors and descriptors for point cloud fusion. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 57–64. [Google Scholar] [CrossRef]
- Kim, H.; Hilton, A. Evaluation of 3D Feature Descriptors for Multi-modal Data Registration. In Proceedings of the International Conference on 3D Vision—3DV, Seattle, WA, USA, 29 June–1 July 2013; pp. 119–126. [Google Scholar]
- Salvi, J.; Matabosch, C.; Fofi, D.; Forest, J. A review of recent range image registration methods with accuracy evaluation. Image Vis. Comput. 2007, 25, 578–596. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Chen, Y.; Medioni, G. Object modeling by registration of multiple range images. In Proceedings of the IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; Volume 3, pp. 2724–2729. [Google Scholar]
- Turk, G.; Levoy, M. Zippered Polygon Meshes from Range Images. In Proceedings of the 21st Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ’94, Orlando, FL USA, 24–29 July 1994; ACM: New York, NY, USA, 1994; pp. 311–318. [Google Scholar]
- Masuda, T.; Sakaue, K.; Yokoya, N. Registration and Integration of Multiple Range Images for 3-D Model Construction. In Proceedings of the 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996; Volume 1, pp. 879–883. [Google Scholar]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings of the Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar]
- Qin, R.; Gruen, A. 3D change detection at street level using mobile laser scanning point clouds and terrestrial images. ISPRS J. Photogramm. Remote Sens. 2014, 90, 23–35. [Google Scholar] [CrossRef]
- Girardeau-Montaut, D.; Roux, M.; Marc, R.; Thibault, G. Change detection on points cloud data acquired with a ground laser scanner. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Enschede, The Netherlands, 12–14 September 2005; p. W19. [Google Scholar]
- Hebel, M.; Arens, M.; Stilla, U. Change detection in urban areas by direct comparison of multi-view and multi-temporal ALS data. In Photogrammetric Image Analysis; Stilla, U., Rottensteiner, F., Mayer, H., Jutzi, B., Butenuth, M., Eds.; Springer: Berlin, Germany, 2011; pp. 185–196. [Google Scholar]
- Hebel, M.; Arens, M.; Stilla, U. Change detection in urban areas by object-based analysis and on-the-fly comparison of multi-view ALS data. ISPRS J. Photogramm. Remote Sens. 2013, 86, 52–64. [Google Scholar] [CrossRef]
- Xiao, W.; Vallet, B.; Paparoditis, N. Change Detection in 3D Point Clouds Acquired by a Mobile Mapping System. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, II-5/W2, 331–336. [Google Scholar] [CrossRef]
- Xiao, W.; Vallet, B.; Brédif, M.; Paparoditis, N. Street environment change detection from mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2015, 107, 38–49. [Google Scholar] [CrossRef]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics; MIT Press: Cambridge, MA, USA, 2005; ISBN 978-0-262-20162-9. [Google Scholar]
- Hackett, J.K.; Shah, M. Multi-sensor fusion: A perspective. In Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati, OH, USA, 13–18 May 1990; Volume 2, pp. 1324–1330. [Google Scholar]
- Puente, E.A.; Moreno, L.; Salichs, M.A.; Gachet, D. Analysis of data fusion methods in certainty grids application to collision danger monitoring. In Proceedings of the International Conference on Industrial Electronics, Control and Instrumentation (IECON ’91), Kobe, Japan, 28 October–1 November 1991; Volume 2, pp. 1133–1137. [Google Scholar]
- Kulchandani, J.S.; Dangarwala, K.J. Moving object detection: Review of recent research trends. In Proceedings of the International Conference on Pervasive Computing (ICPC), Pune, India, 8–10 January 2015; pp. 1–5. [Google Scholar]
- Deymier, C.; Chateau, T. IPCC algorithm: Moving object detection in 3D-Lidar and camera data. In Proceedings of the IEEE Intelligent Vehicles Symposium (IV), Gold Coast, Australia, 23–26 June 2013; pp. 817–822. [Google Scholar]
- Yan, J.; Chen, D.; Myeong, H.; Shiratori, T.; Ma, Y. Automatic Extraction of Moving Objects from Image and LIDAR Sequences. In Proceedings of the 2nd International Conference on 3D Vision, Tokyo, Japan, 8–11 December 2014; Volume 1, pp. 673–680. [Google Scholar]
- Bresenham, J.E. Algorithm for computer control of a digital plotter. IBM Syst. J. 1965, 4, 25–30. [Google Scholar] [CrossRef]
- CloudCompare—Open Source Project. Available online: http://www.danielgm.net/cc/ (accessed on 19 October 2017).







| Type of Data | Application | Advantage | Disadvantage |
|---|---|---|---|
| Base data | Map building | High accuracy | High cost |
| High density | Less frequent | ||
| Sequential data | Change detection | Low cost | Low accuracy |
| More frequent | Low density |
| Data | Positioning Error (X,Y,Z) (Meter) | Angle Error (Roll, Pitch, Yaw) (Degree) | Point Density (MMS = 1) | Measurement Range | Ratio in All Data |
|---|---|---|---|---|---|
| (A) | (5,5,5) | (0.1, 0.05, 0.05) | Wide | Low (33%) | |
| (B) | (10,10,10) | (0.1, 0.1, 0.1) | Narrow | High (67%) |
| Scenario | Number in Figure 8 | Object | Change | Scenario | Number in Figure 8 | Object | Change |
|---|---|---|---|---|---|---|---|
| Large | 1 | Roadway | Removal | Small | 4 | Signboard | Removal |
| Large | 2 | Roadway | Expansion | Small | 5 | Lamppost | Removal |
| Large | 3 | Roadway | Removal | Small | 6 | Flasher | Removal |
| Large | 4 | Median strip | Removal | Small | 7 | Lamppost | Expansion |
| Small | 1 | Signboard | Removal | Small | 8 | Rubber pole | Moving |
| Small | 2 | Traffic signal | Moving | Small | 9 | Traffic enforcement camera | Removal |
| Small | 3 | Traffic enforcement camera | Moving | Small | 10 | Short pole | Removal |
| Sequential # | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Performance | (A) | (B) | (B) | (A) | (B) | (B) | (B) | (A) | (B) |
| Recorded change | T | T | T | T | T | T·RE | T·RE | T·RE | T·RE |
| Object | Change | Sequential Data Number | Total | ||
|---|---|---|---|---|---|
| 6 | 7 | 8 | |||
| Pedestrian | Addition | - | 3/4 (75) | - | 3/4 (75) |
| Removal | - | 3/3 (100) | 2/2 (100) | 5/5 (100) | |
| Vehicle | Addition | - | 2/2 (100) | - | 2/2 (100) |
| Removal | 4/4 (100) | - | 2/2 (100) | 6/6 (100) | |
| Shadow | Apparance | 1/2 (50) | 1/1 (100) | 1/1 (100) | 3/4 (75) |
| disappearance | - | 3/3 (100) | - | 3/3 (100) | |
| Road Environment (Before Change) | State in Base Data | Road Environment (After Change) | Pattern | Number of Changes |
|---|---|---|---|---|
| occupied | occupied | empty | (a) | 8 |
| unmeasured | (b) | 1 | ||
| empty | empty | occupied | (c) | 3 |
| unmeasured | occupied | (d) | 1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fuse, T.; Yokozawa, N. Development of a Change Detection Method with Low-Performance Point Cloud Data for Updating Three-Dimensional Road Maps. ISPRS Int. J. Geo-Inf. 2017, 6, 398. https://doi.org/10.3390/ijgi6120398
Fuse T, Yokozawa N. Development of a Change Detection Method with Low-Performance Point Cloud Data for Updating Three-Dimensional Road Maps. ISPRS International Journal of Geo-Information. 2017; 6(12):398. https://doi.org/10.3390/ijgi6120398
Chicago/Turabian StyleFuse, Takashi, and Naoto Yokozawa. 2017. "Development of a Change Detection Method with Low-Performance Point Cloud Data for Updating Three-Dimensional Road Maps" ISPRS International Journal of Geo-Information 6, no. 12: 398. https://doi.org/10.3390/ijgi6120398
APA StyleFuse, T., & Yokozawa, N. (2017). Development of a Change Detection Method with Low-Performance Point Cloud Data for Updating Three-Dimensional Road Maps. ISPRS International Journal of Geo-Information, 6(12), 398. https://doi.org/10.3390/ijgi6120398




