Transdisciplinary Foundations of Geospatial Data Science
Abstract
:1. Introduction
1.1. Motivation
1.2. Transdisciplinary Foundations: Mathematics, Statistics and Computer Science
1.3. Geospatial Techniques
1.4. Scope and Outline
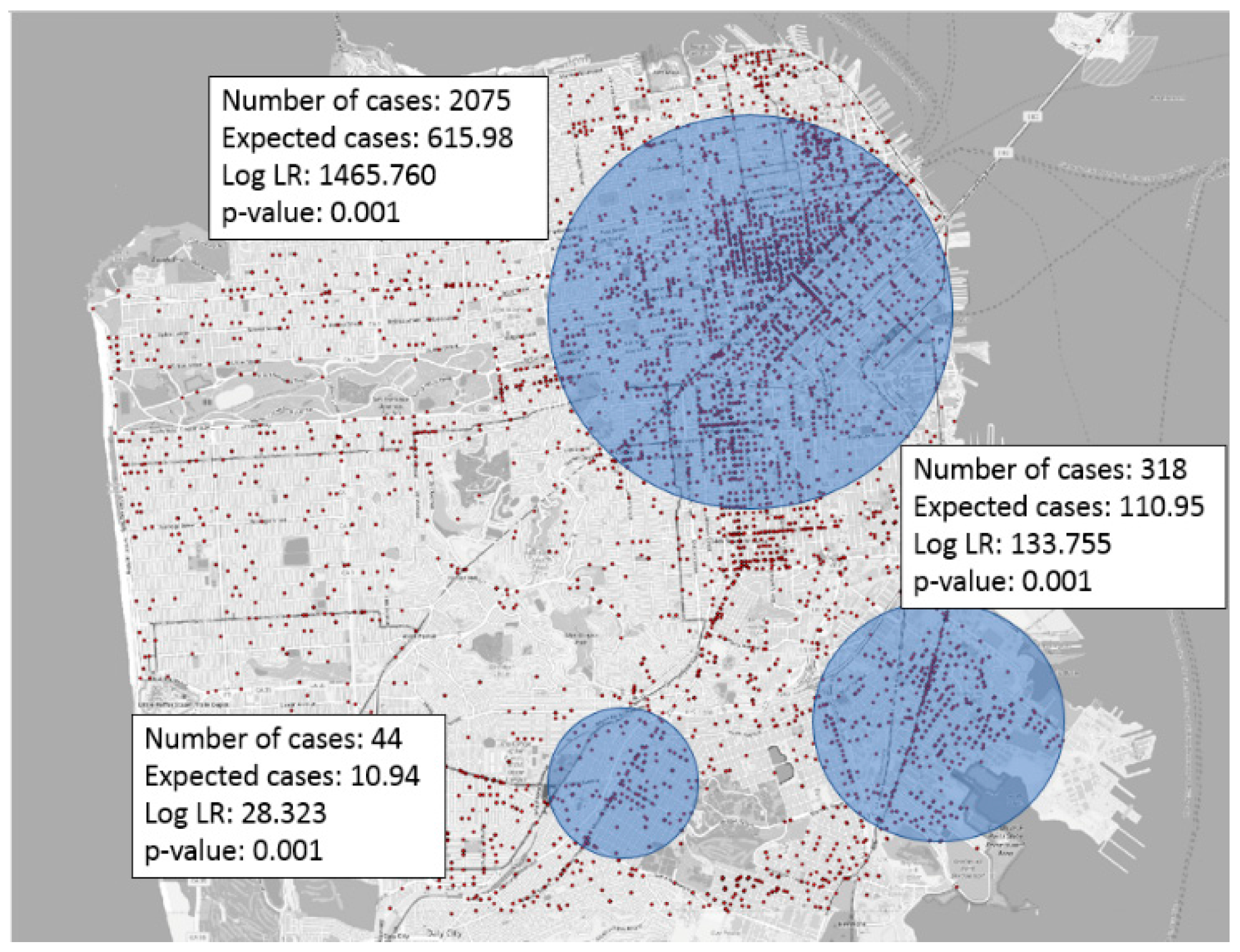
2. Foundations of Hotspot Detection
2.1. Mathematical Foundation of Hotspot Detection
2.2. Statistical Foundation of Hotspot Detection
2.3. Computer Science Foundation of Hotspot Detection
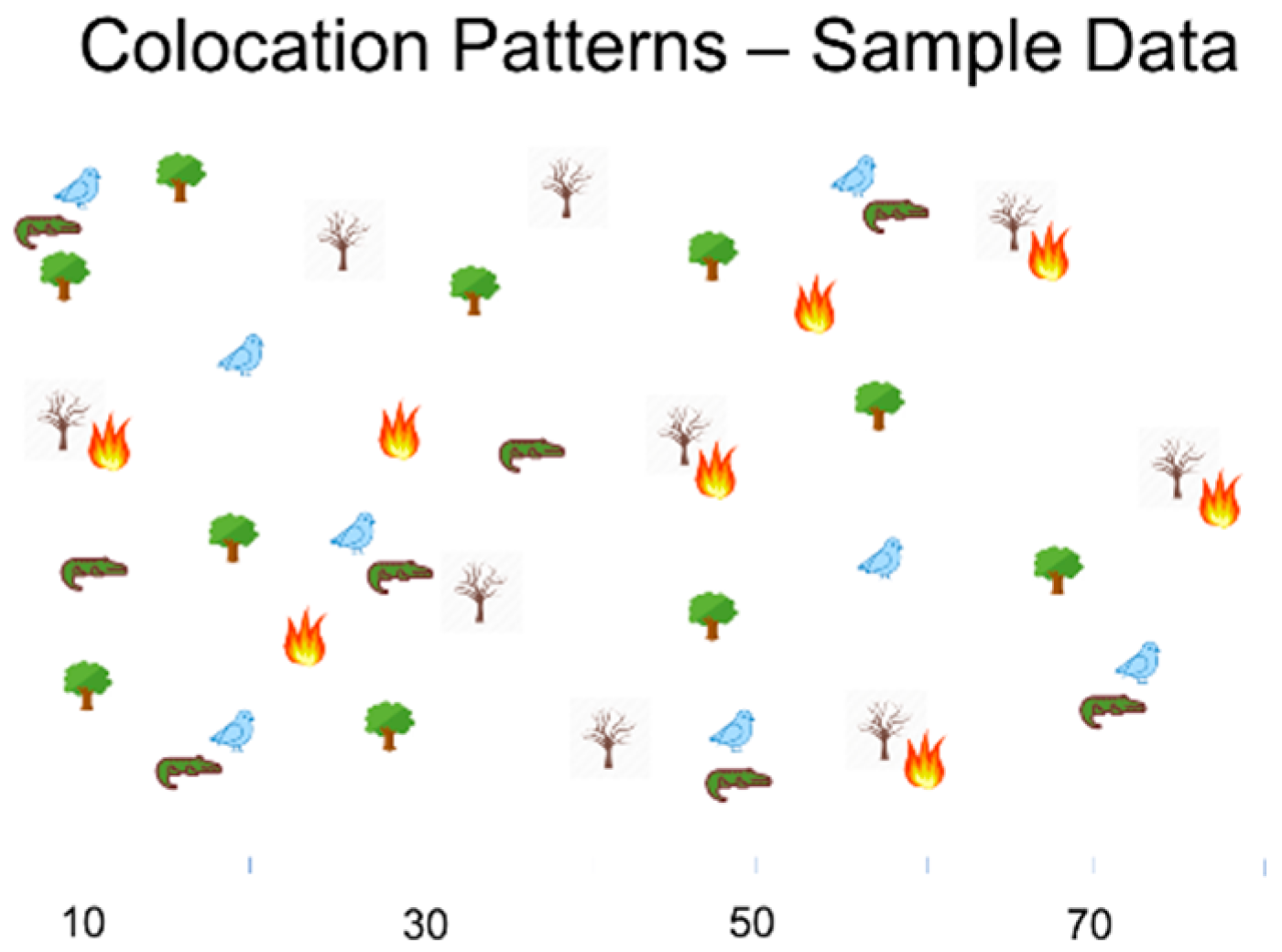
3. Foundations of Colocation Detection
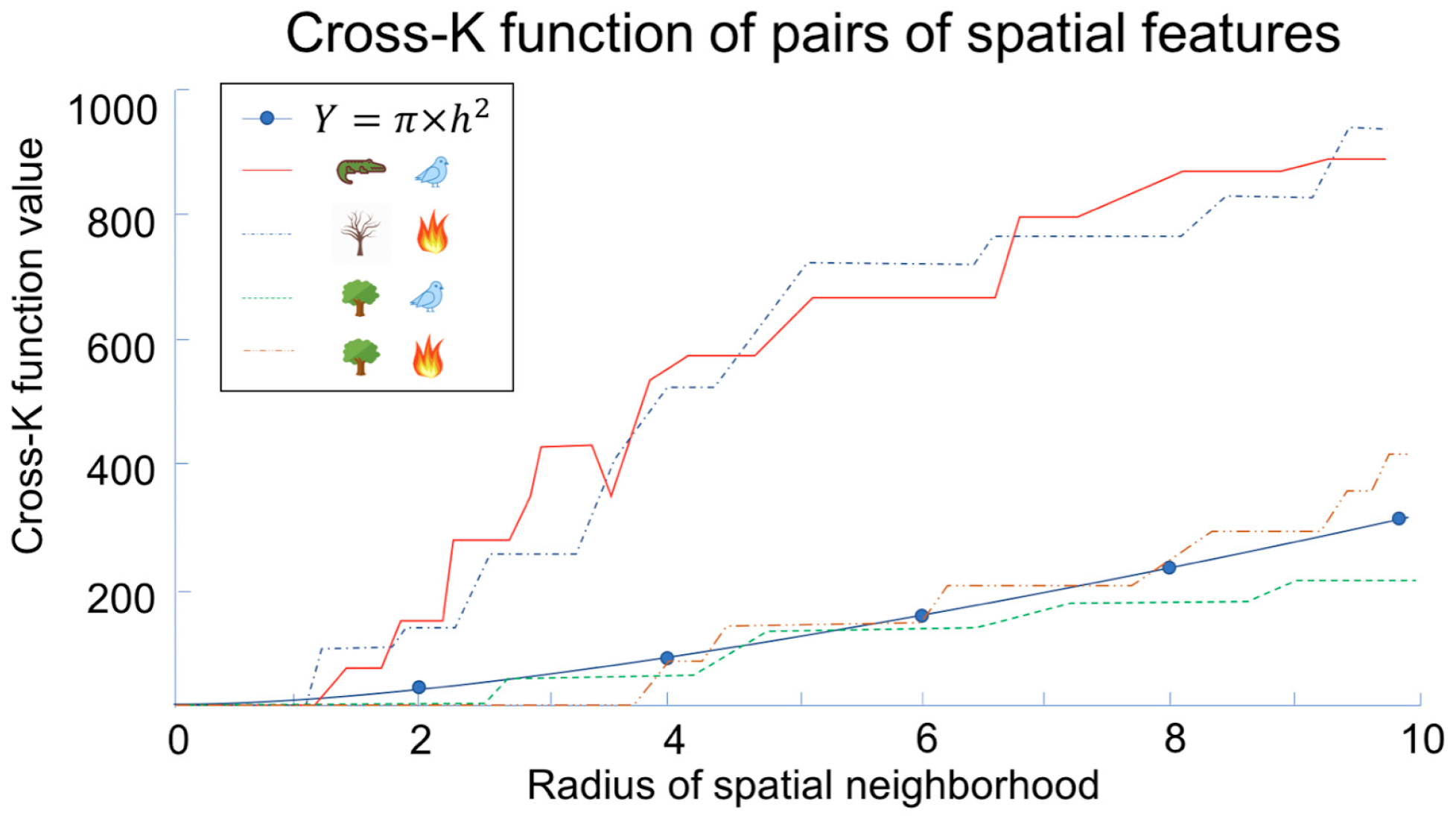
3.1. Mathematical Foundation of Colocation Detection
3.2. Statistical Foundation of Colocation Detection
3.3. Computer Science Foundation of Colocation Detection
4. Foundations of Spatial Prediction
4.1. Mathematical Foundation of Spatial Prediction
4.2. Statistical Foundation of Spatial Prediction
4.3. Computer Science Foundation of Spatial Prediction
5. Foundations of Spatial Outlier Detection
5.1. Mathematical Foundation of Spatial Outlier Detection
5.2. Statistical Foundation of Spatial Outlier Detection
5.3. Computer Science Foundation of Spatial Outlier Detection
6. Foundations of Teleconnection Discovery
6.1. Mathematical Foundation of Teleconnection Discovery
6.2. Statistical Foundation of Teleconnection Discovery
6.3. Computer Science Foundation of Teleconnection
7. Discussion
7.1. Gaps and Opportunities
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Transdisciplinary Foundations: Mathematics, Statistics and Computer Science
A.1. Mathematics
A.2. Statistics
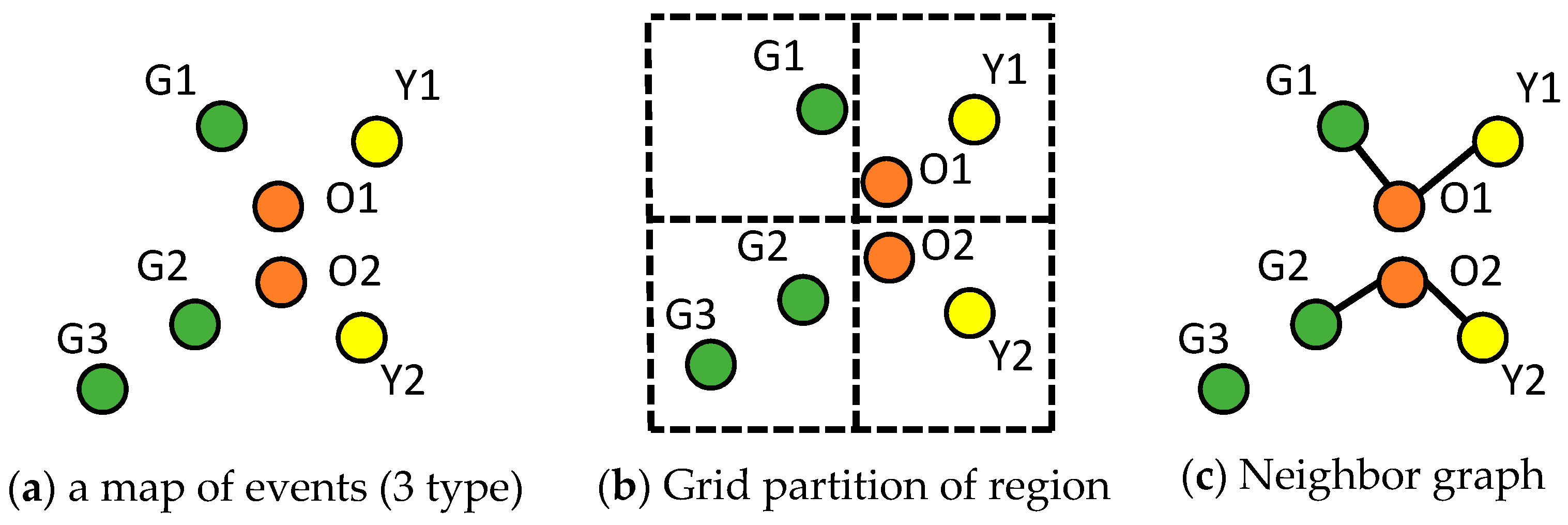
| Event Pairs | Pearson’s Correlation Coefficient | Participation Index |
|---|---|---|
| (Green, Orange) | −0.90 | 0.67 |
| (Yellow, Orange) | 1 | 1 |
A.3. Computer Science
References
- Castelvecchi, D. Can we open the black box of AI? Nature 2016, 538, 20–23. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.M.; Edwards, D.L. Tipping Points, Butterflies, and Black Swans: A Vision for Spatio-temporal Data Mining Analysis. In Advances in Spatial and Temporal Databases (SSTD-11); Springer: Berlin/Heidelberg, Germany, 2011; pp. 454–457. [Google Scholar]
- Institue for Mathematics and Its Applications. Transdisciplinary Foundations of Data Science [Online]. Available online: https://www.ima.umn.edu/2016-2017/SW9.14-16.16 (accessed on 4 November 2017).
- Kaiser, M.S.; Cressie, N.; Lee, J. Spatial mixture models based on exponential family conditional distributions. Stat. Sin. 2002, 12, 449–474. [Google Scholar]
- Wasserman, L. Rise of the Machines. Available online: http://www.stat.cmu.edu/~larry/Wasserman.pdf (accessed on 18 September 2017).
- Jiang, Z.; Shekhar, S.; Zhou, X.; Knight, J.; Corcoran, J. Focal-Test-Based Spatial Decision Tree Learning. IEEE Trans. Knowl. Data Eng. 2015, 27, 1547–1559. [Google Scholar] [CrossRef]
- Baker, M. Statisticians issue warning over misuse of p values. Nature 2016, 531, 151. [Google Scholar] [CrossRef] [PubMed]
- American Statistical Association. Releases Statement on Statistical Significance and p-Values. Available online: http://www.amstat.org/asa/files/pdfs/P-ValueStatement.pdf (accessed on 18 September 2017).
- Eftelioglu, E.; Ali, R.; Tang, X.; Xie, Y.; Li, Y.; Shekhar, S. Spatial Data Science: An Interdisciplinary Approach. In Geospatial Data Science: Techniques and Applications, 1st ed.; Karimi, H.A., Karimi, B., Eds.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 1138626449. [Google Scholar]
- Blaschke, T.; Merschdorf, H. Geographic Information Science as a Multidisciplinary and Multiparadigmatic Field. Cartogr. Geogr. Inf. Sci. 2014, 41, 196–213. [Google Scholar] [CrossRef]
- Dragiæeviæ, S.; Balram, S. Collaborative Geographic Information Systems and Science: A Transdisciplinary Evolution; IGI Global: Hershey, PA, USA, 2006. [Google Scholar]
- Gunasekera, R. Use of GIS for environmental impact assessment: An interdisciplinary approach. Interdiscip. Sci. Rev. 2004, 29, 37–48. [Google Scholar] [CrossRef]
- Wang, T. Interdisciplinary urban GIS for smart cities: Advancements and opportunities. Geo-Spat. Inf. Sci. 2013, 16, 25–34. [Google Scholar]
- Cromley, E.K.; McLafferty, S. GIS and Public Health; The Guilford Press: New York, NY, USA, 2012. [Google Scholar]
- Xie, Y.; Runck, B.C.; Shekhar, S.; Kne, L.; Mulla, D.; Jordan, N.; Wiringa, P. Collaborative Geodesign and Spatial Optimization for Fragmentation-Free Land Allocation. ISPRS Int. J. Geo-Inf. 2017, 6, 226. [Google Scholar] [CrossRef]
- Kulldorff, M.; Nagarwalla, N. Spatial disease clusters: Detection and inference. Stat. Med. 1995, 14, 799–810. [Google Scholar] [CrossRef] [PubMed]
- Openshaw, S.; Craft, A.W.; Charlton, M.; Birch, J.M. Investigation of leukaemia clusters by use of a Geographical Analysis Machine. Lancet 1988, 1, 272–273. [Google Scholar] [CrossRef]
- Eftelioglu, E.; Shekhar, S.; Oliver, D.; Zhou, X.; Evans, M.R.; Xie, Y.; Kang, J.M.; Laubscher, R.; Farah, C. Ring-Shaped Hotspot Detection: A Summary of Results. In Proceedings of the IEEE International Conference on Data Mining (ICDM), Shenzhen, China, 14–17 December 2014; pp. 815–820. [Google Scholar]
- Eftelioglu, E.; Shekhar, S.; Kang, J.M.; Farah, C.C. Ring-Shaped Hotspot Detection. IEEE Trans. Knowl. Data Eng. 2016, 28, 3367–3381. [Google Scholar] [CrossRef]
- Kulldorff, M. A spatial scan statistic. Commun. Stat. Theory Methods 1997, 26, 1481–1496. [Google Scholar] [CrossRef]
- Kulldorff, M. SaTScan User Guide. Available online: https://www.satscan.org/cgi-bin/satscan/register.pl/SaTScan_Users_Guide.pdf?todo=process_userguide_download (accessed on 18 September 2017).
- Kulldorff, M. Spatial scan statistics: Models, calculations, and applications. In Scan Statistics and Applications; Springer: Berlin, Germany, 1999; pp. 303–322. [Google Scholar]
- Neill, D.B.; Moore, A.W. Rapid Detection of Significant Spatial Clusters. In Proceedings of the ACM SIGKDD (KDD ’04), Seattle, WA, USA, 22–25 August 2004. [Google Scholar]
- Tang, X.; Eftelioglu, E.; Oliver, D.; Shekhar, S. Significant Linear Hotspot Discovery. IEEE Trans. Big Data 2017, 3, 140–153. [Google Scholar] [CrossRef]
- Eftelioglu, E.; Li, Y.; Tang, X.; Shekhar, S.; Kang, J.M.; Farah, C. Mining Network Hotspots with Holes: A Summary of Results. In Proceedings of the International Conference on Geographic Information Science, Montreal, QC, Canada, 27–30 September 2016; pp. 51–67. [Google Scholar]
- Tan, P.; Steinbach, M.; Kumar, V. Introduction to Data Mining, 1st ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 2005. [Google Scholar]
- Han, J.; Kammber, M.; Pei, J. Data Mining—Concepts and Techniques; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD ’96), Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Neill, D.B.; Moore, A.W.; Sabhnani, M.; Daniel, K. Detection of Emerging Space-Time Clusters. In Proceedings of the Eleventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’05), Chicago, IL, USA, 21–24 August 2005; pp. 218–227. [Google Scholar]
- Neill, D.B.; Moore, A.W.; Cooper, G.F. A Bayesian Spatial Scan Statistic. In Proceedings of the Neural Information Processing Systems Conference (NIPS), Vancouver, BC, Canada, 6–9 December 2005; pp. 1003–1010. [Google Scholar]
- Pang, L.X.; Chawla, S.; Scholz, B.; Wilcox, G. A Scalable Approach for LRT Computation in GPGPU Environments. In Proceedings of the 15th Asia-Pacific Web Conference (APWeb 2013), Sydney, Australia, 4–6 April 2013; pp. 595–608. [Google Scholar]
- Yoo, J.S.; Bow, M. Mining spatial colocation patterns: A different framework. Data Min. Knowl. Discov. 2012, 24, 159–194. [Google Scholar] [CrossRef]
- Huang, Y.; Shekhar, S.; Xiong, H. Discovering colocation patterns from spatial data sets: A general approach. IEEE Trans. Knowl. Data Eng. 2004, 16, 1472–1485. [Google Scholar] [CrossRef]
- Barua, S.; Sander, J. Mining Statistically Significant Co-location and Segregation Patterns. IEEE Trans. Knowl. Data Eng. 2014, 26, 1185–1199. [Google Scholar] [CrossRef]
- Yoo, J.S.; Shekhar, S. A joinless approach for mining spatial colocation patterns. IEEE Trans. Knowl. Data Eng. 2006, 18, 1323–1337. [Google Scholar]
- Hipp, J.; Güntzer, U.; Nakhaeizadeh, G. Algorithms for association rule mining—A general survey and comparison. ACM SIGKDD Explor. Newsl. 2000, 2, 58–64. [Google Scholar] [CrossRef]
- Xiong, H.; Shekhar, S.; Huang, Y.; Kumar, V.; Ma, X.; Yoc, J. A Framework for Discovering Co-location Patterns in Data Sets with Extended Spatial Objects. In Proceedings of the SIAM International Conference on Data Mining, Lake Buena Vista, FL, USA, 4–6 April 2004; pp. 78–89. [Google Scholar]
- Wang, S.; Huang, Y.; Wang, X.S. Regional Co-locations of Arbitrary Shapes. In Advances in Spatial and Temporal Databases, Proceedings of the 13th International Symposium, SSTD 2013, Munich, Germany, 21–23 August 2013; Springer: Berlin, Germany, 2013; pp. 19–37. [Google Scholar]
- Deng, M.; Cai, J.; Liu, Q.; He, Z.; Tang, J. Multi-level method for discovery of regional co-location patterns. Int. J. Geogr. Inf. Sci. 2017, 31, 1846–1870. [Google Scholar] [CrossRef]
- Eick, C.F.; Parmar, R.; Ding, W.; Stepinski, T.F.; Nicot, J.-P. Finding regional co-location patterns for sets of continuous variables in spatial datasets. In Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (GIS ’08), Irvine, CA, USA, 5–7 November 2008. [Google Scholar]
- Dixon, P.M. Ripley’s K Function. In Encyclopedia of Environmetrics; John Wiley & Sons, Ltd: Chichester, UK, 2002; pp. 1796–1803. [Google Scholar]
- Shekhar, S.; Huang, Y. Discovering Spatial Co-location Patterns: A Summary of Results. In Advances in Spatial and Temporal Databases, Proceedings of the 7th International Symposium, SSTD 2001, Redondo Beach, CA, USA, 12–15 July 2001; Springer: Berlin, Germany, 2001; pp. 236–256. [Google Scholar]
- Agrawal, R.; Srikant, R. Fast algorithms for mining association rules. In Proceedings of the 20th International Conference on Very Large Data Bases (VLDB), Santiago de Chile, Chile, 12–15 September 1994; pp. 487–499. [Google Scholar]
- Yoo, J.S.; Boulware, D.; Kimmey, D. A Parallel Spatial Co-location Mining Algorithm Based on MapReduce. In Proceedings of the 2014 IEEE International Congress on Big Data, Anchorage, AK, USA, 27 June–2 July 2014; pp. 25–31. [Google Scholar]
- Qian, F.; He, Q.; He, J. Mining spatial co-location patterns with dynamic neighborhood constraint. In Machine Learning and Knowledge Discovery in Databases, Proceedings of the European Conference (ECML PKDD 2009), Bled, Slovenia, 7–11 September 2009; Springer: Berlin, Germany, 2009; pp. 238–253. [Google Scholar]
- Shekhar, S.; Schrater, P.R.; Vatsavai, R.R.; Wu, W.; Chawla, S. Spatial contextual classification and prediction models for mining geospatial data. IEEE Trans. Multimed. 2002, 4, 174–188. [Google Scholar] [CrossRef]
- Shekhar, S.; Jiang, Z.; Ali, R.Y.; Eftelioglu, E.; Tang, X.; Gunturi, V.; Zhou, X. Spatiotemporal Data Mining: A Computational Perspective. ISPRS Int. J. Geo-Inf. 2015, 4, 2306–2338. [Google Scholar] [CrossRef]
- Fauvel, M.; Chanussot, J.; Benediktsson, J.A. A spatial–spectral kernel-based approach for the classification of remote-sensing images. Pattern Recognit. 2012, 45, 381–392. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically Weighted Regression. J. R. Stat. Soc. Ser. D 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Celik, M.; Kazar, B.M.; Shekhar, S.; Boley, D.; Lilja, D.J. Spatial dependency modeling using spatial auto-regression. In Proceedings of the ICA Workshop on Geospatial Analysis and Modeling, Vienna, Austria, 8 July 2006; pp. 186–197. [Google Scholar]
- Kazar, B.M.; Shekhar, S.; Lilja, D.J.; Boley, D. A Parallel Formulation of the Spatial Auto-Regression Model for Mining Large Geo-Spatial Datasets. In Proceedings of the 2004 SIAM International Conference on Data Mining, Workshop on High Performance and Distributed Mining (HPDM 2004), Lake Buena Vista, FL, USA, 22–24 April 2004. [Google Scholar]
- Wall, M.M. A close look at the spatial structure implied by the CAR and SAR models. J. Stat. Plan. Inference 2004, 121, 311–324. [Google Scholar] [CrossRef]
- Griffith, D.A. A linear regression solution to the spatial autocorrelation problem. J. Geogr. Syst. 2000, 2, 141–156. [Google Scholar] [CrossRef]
- Gagliasso, D.; Hummel, S.; Temesgen, H. A Comparison of Selected Parametric and Non-Parametric Imputation Methods for Estimating Forest Biomass and Basal Area. Open J. For. 2014, 4, 42–48. [Google Scholar] [CrossRef]
- Celik, M.; Kazar, B.M.; Shashi, S.; Boley, D.; Lilja, D.J. A Parameter Estimation Method for the Spatial Autoregression Model. 2007. Available online: http://www-users.cs.umn.edu/~boley/publications/papers/NASA06.pdf (accessed on 18 September 2017).
- Pace, R.K.; LeSage, J.P. Closed-form maximum likelihood estimates for spatial problems. Geogr. Anal. 2000, 32, 154–172. [Google Scholar] [CrossRef]
- Li, B. Implementing spatial statistics on parallel computers. In Practical Handbook of Spatial Statistics; CRC Press: Boca Raton, FL, USA, 1996; pp. 107–148. [Google Scholar]
- Kazar, B.M.; Shekhar, S.; Lilja, D.J.; Vatsavai, R.R.; Pace, R.K. Comparing exact and approximate spatial auto-regression model solutions for spatial data analysis. In Proceedings of the International Conference on Geographic Information Science, Adelphi, MD, USA, 20–23 October 2004; pp. 140–161. [Google Scholar]
- Martin, R.J. Approximations to the determinant term in Gaussian maximum likelihood estimation of some spatial models. Commun. Stat. Methods 1992, 22, 189–205. [Google Scholar] [CrossRef]
- Pace, R.K.; LeSage, J.P. Chebyshev approximation of log-determinants of spatial weight matrices. Comput. Stat. Data Anal. 2004, 45, 179–196. [Google Scholar] [CrossRef]
- Kazar, B.M.; Celik, M. Spatial AutoRegression (SAR) Model; Springer: Boston, MA, USA, 2012. [Google Scholar]
- Shekhar, S.; Lu, C.T.; Zhang, P. A unified approach to detecting spatial outliers. Geoinformatica 2003, 7, 139–166. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Outlier analysis. In Data mining; Springer: Berlin, Germany, 2015; pp. 237–263. [Google Scholar]
- Haslett, J.; Bradley, R.; Craig, P.; Unwin, A.; Wills, G. Dynamic graphics for exploring spatial data with application to locating global and local anomalies. Am. Stat. 1991, 45, 234–242. [Google Scholar]
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Anselin, L. Exploratory spatial data analysis and geographic information systems. New Tools Spat. Anal. 1994, 17, 45–54. [Google Scholar]
- Liu, X.; Chen, F.; Lu, C.-T. On detecting spatial categorical outliers. Geoinformatica 2014, 18, 501–536. [Google Scholar] [CrossRef]
- Chen, D.; Lu, C.-T.; Kou, Y.; Chen, F. On detecting spatial outliers. Geoinformatica 2008, 12, 455–475. [Google Scholar] [CrossRef]
- Kang, J.M.; Shekhar, S.; Wennen, C.; Novak, P. Discovering flow anomalies: A SWEET approach. In Proceedings of the 8th IEEE International Conference on Data Mining (ICDM), Pisa, Italy, 15–19 December 2008; pp. 851–856. [Google Scholar]
- Mazimpaka, J.D.; Timpf, S. Trajectory data mining: A review of methods and applications. J. Spat. Inf. Sci. 2016, 2016, 61–99. [Google Scholar] [CrossRef]
- Zheng, Y. Trajectory Data Mining. ACM Trans. Intell. Syst. Technol. 2015, 6, 1–41. [Google Scholar] [CrossRef]
- Kuang, W.; An, S.; Jiang, H. Detecting Traffic Anomalies in Urban Areas Using Taxi GPS Data. Math. Probl. Eng. 2015, 2015, 809582. [Google Scholar] [CrossRef]
- Lee, J.-G.; Han, J.; Li, X. Trajectory Outlier Detection: A Partition-and-Detect Framework. In Proceedings of the 24th IEEE International Conference on Data Engineering (ICDE), Cancun, Mexico, 7–12 April 2008; pp. 140–149. [Google Scholar]
- Liu, L.; Qiao, S.; Zhang, Y.; Hu, J. An efficient outlying trajectories mining approach based on relative distance. Int. J. Geogr. Inf. Sci. 2012, 26, 1789–1810. [Google Scholar] [CrossRef]
- Yuan, G.; Xia, S.; Zhang, L.; Zhou, Y.; Ji, C. Trajectory Outlier Detection Algorithm Based on Structural Features. J. Comput. Inf. Syst. 2011, 7, 4137–4144. [Google Scholar]
- Kawale, J.; Steinbach, M.; Kumar, V. Discovering dynamic dipoles in climate data. In Proceedings of the 2011 SIAM International Conference on Data Mining, Mesa, AZ, USA, 28–30 April 2011; pp. 107–118. [Google Scholar]
- Zhang, P.; Huang, Y.; Shekhar, S.; Kumar, V. Correlation analysis of spatial time series datasets: A filter-and-refine approach. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Seoul, Korea, 30 April–2 May 2003; pp. 532–544. [Google Scholar]
- Zhang, P.; Huang, Y.; Shekhar, S.; Kumar, V. Exploiting spatial autocorrelation to efficiently process correlation-based similarity queries. In Advances in Spatial and Temporal Database, Proceedings of the 8th International Symposium, SSTD 2003, Santorini Island, Greece, 24–27 July 2003; Springer: Berlin, Germany; pp. 449–468.
- Kawale, J.; Chatterjee, S.; Ormsby, D.; Steinhaeuser, K.; Liess, S.; Kumar, V. Testing the significance of spatio-temporal teleconnection patterns. In Proceedings of the ACM SIGKDD (KDD ’12), Beijing, China, 12–16 August 2012; pp. 642–650. [Google Scholar]
- Mohan, P.; Shekhar, S.; Shine, J.A.; Rogers, J.P. Cascading Spatio-Temporal Pattern Discovery. IEEE Trans. Knowl. Data Eng. 2012, 24, 1977–1992. [Google Scholar] [CrossRef]
- Zhou, X.; Shekhar, S.; Mohan, P.; Liess, S.; Snyder, P.K. Discovering Interesting Sub-paths in Spatiotemporal Datasets: A Summary of Results. In Proceedings of the 19th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (ACM SIGSPATIAL 2011), Chicago, IL, USA, 1–4 November 2011; pp. 44–53. [Google Scholar]
- Ali, R.Y.; Gunturi, V.M.V.; Kotz, A.J.; Shekhar, S.; Northrop, W.F. Discovering Non-compliant Window Co-Occurrence Patterns: A Summary of Results. In Advances in Spatial and Temporal Databases, Proceedings of the 14th International Symposium, SSTD 2015, Hong Kong, China, 26–28 August 2015; Springer: Berlin, Germany, 2015; pp. 391–410. [Google Scholar]
- Bland, J.M.; Altman, D.G. Multiple significance tests: The Bonferroni method. BMJ 1995, 310, 170. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. Statistical Power Analysis. Curr. Dir. Psychol. Sci. 1992, 1, 98–101. [Google Scholar] [CrossRef]
- Cressie, N.A.C.; Wikle, C.K. Statistics for Spatio-Temporal Data; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Prasad, S.K.; Aghajarian, D.; McDermott, M.; Shah, D.; Mokbel, M.; Puri, S.; Rey, S.J.; Shekhar, S.; Xe, Y.; Vatsavai, R.R.; et al. Parallel Processing over Spatial-Temporal Datasets from Geo, Bio, Climate and Social Science Communities: A Research Roadmap. In Proceedings of the 2017 IEEE International Congress on Big Data (BigData Congress), Honolulu, HI, USA, 25–30 June 2017; pp. 232–250. [Google Scholar]
- Yu, H.; Shaw, S. Exploring potential human activities in physical and virtual spaces: A spatio-temporal GIS approach. Int. J. Geogr. Inf. Sci. 2008, 22, 409–430. [Google Scholar] [CrossRef]
- Gebbert, S.; Pebesma, E. TGRASS: A temporal GIS for field based environmental modeling. Environ. Model. Softw. 2014, 53, 1–12. [Google Scholar] [CrossRef]
- Evans, M.R.; Yang, K.S.; Kang, J.M.; Shekhar, S. A Lagrangian approach for storage of spatio-temporal network datasets: A summary of results. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 3–5 November 2010; pp. 212–221. [Google Scholar]
- Köhler, E.; Langkau, K.; Skutella, M. Time-expanded graphs for flow-dependent transit times. In Proceedings of the 10th Annual European Symposium on Algorithms, ESA ’02, Rome, Italy, 17–21 September 2002; pp. 49–56. [Google Scholar]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical Development, Applications, and Future Research Directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Van der Knijff, J.M.; Younis, J.; de Roo, A.P.J. LISFLOOD: A GIS-based distributed model for river basin scale water balance and flood simulation. Int. J. Geogr. Inf. Sci. 2010, 24, 189–212. [Google Scholar] [CrossRef]
- Kucuksari, S.; Khaleghi, A.M.; Hamidi, M.; Zhang, Y.; Szidarovszky, F.; Bayraksan, G.; Son, Y.J. An Integrated GIS, optimization and simulation framework for optimal PV size and location in campus area environments. Appl. Energy 2014, 113, 1601–1613. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R.; van Liew, M. Approximating SWAT Model Using Artificial Neural Network and Support Vector Machine. JAWRA J. Am. Water Resour. Assoc. 2009, 45, 460–474. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, K.; Shekhar, S.; Dalzell, B.; Mulla, D. Spatially Constrained Geodesign Optimization (GOP) for Improving Agricultural Watershed Sustainability. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence (AAAI-17), Workshop on AI and OR for Social Good, San Francisco, CA, USA, 4–9 February 2017; pp. 57–63. [Google Scholar]
- Xie, Y.; Shekhar, S. FF-SA: Fragmentation-Free Spatial Allocation. In Advances in Spatial and Temporal Databases, Proceedings of the 15th International Symposium, SSTD 2017, Arlington, VA, USA, 21–23 August 2017; Springer: Berlin, Germany; pp. 319–338.
- Li, X.; Han, J.; Lee, J.-G.; Gonzalez, H. Traffic Density-Based Discovery of Hot Routes in Road Networks. In Proceedings of the 10th International Conference on Advances in Spatial and Temporal Databases, Boston, MA, USA, 16–18 July 2007; pp. 441–459. [Google Scholar]
- Yang, K.; Hirsh, S.A.; Oliver, D.; Shekhar, S. Capacity-Constrained Network-Voronoi Diagram. IEEE Trans. Knowl. Data Eng. 2015, 27, 2919–2932. [Google Scholar] [CrossRef]
- Fagan, W.F.; Fortin, M.-J.; Soykan, C. Integrating edge detection and dynamic modeling in quantitative analyses of ecological boundaries. AIBS Bull. 2003, 53, 730–738. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Cressie, N.A.C. 01 Statistics for Spatial Data. In Statistics for Spatial Data; Wiley: Hoboken, NJ, USA, 1993; pp. 1–26. [Google Scholar]
- Millennium Problems|Clay Mathematics Institute. Available online: http://www.claymath.org/millennium-problems (accessed on 18 September 2017).
- Ausiello, G. Complexity and Approximation: Combinatorial Optimization Problems and Their Approximability Properties; Springer: Berlin, Germany, 1999. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Wang, S. CyberGIS and Spatial Data Science. GeoJournal 2016, 81, 965–968. [Google Scholar] [CrossRef]

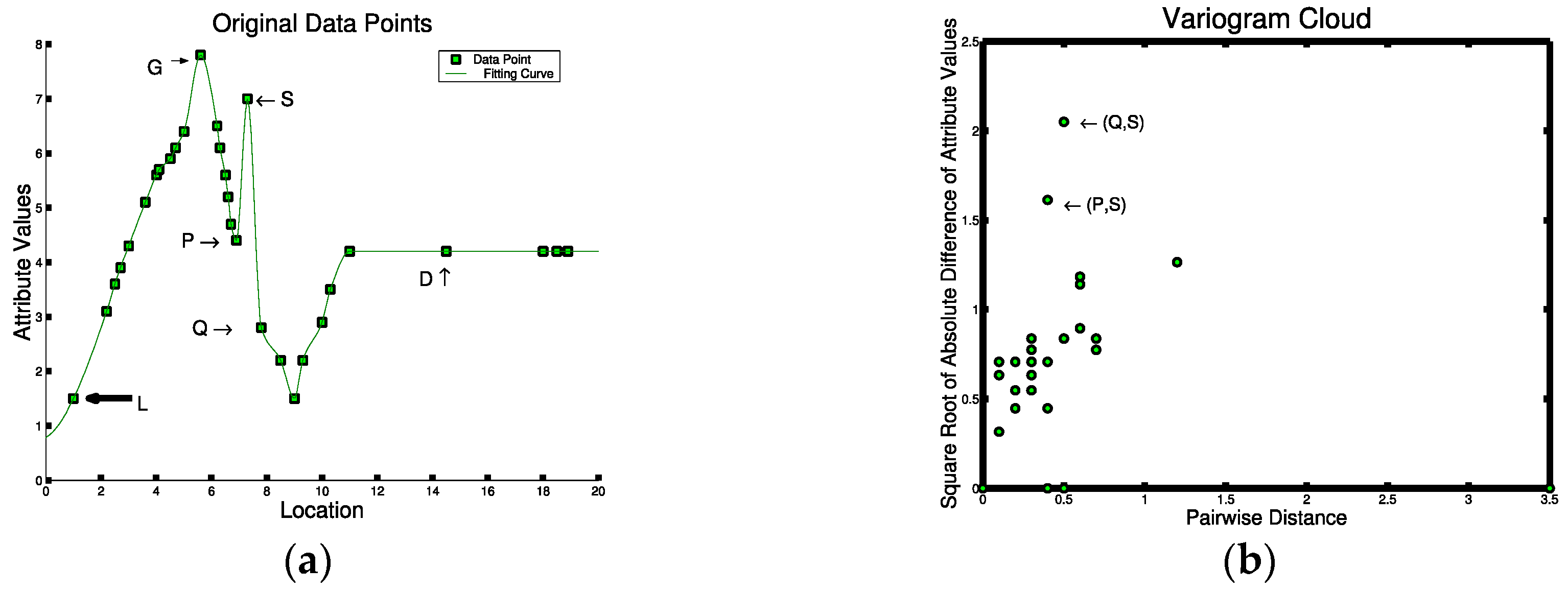
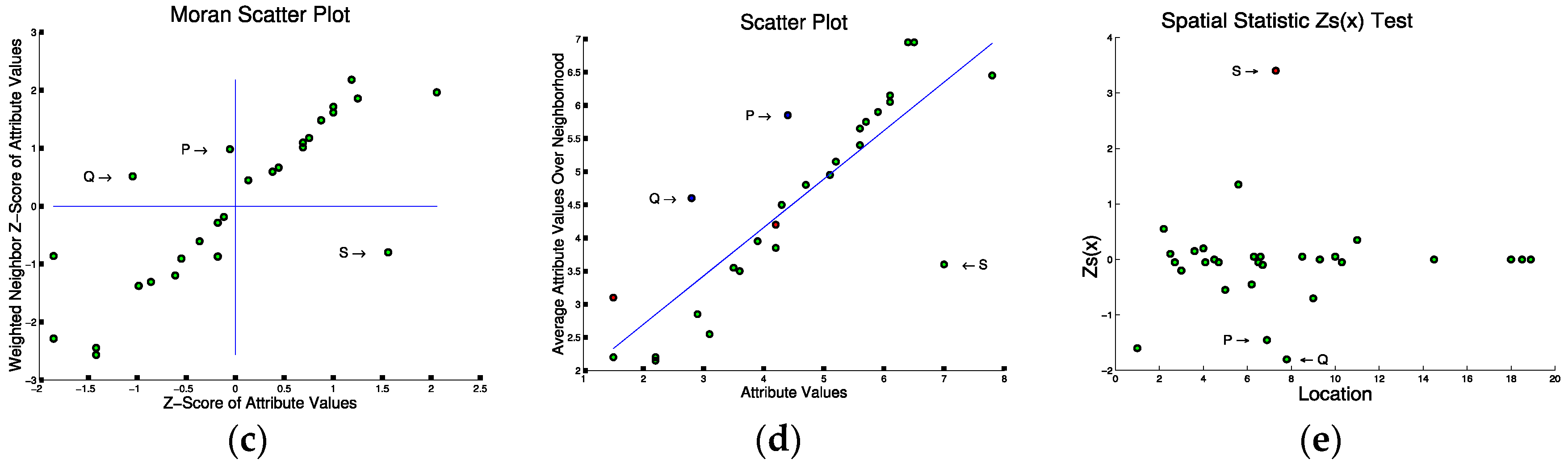
| Challenge | Approach |
|---|---|
| Spatial and temporal autocorrelation. | Spatio-temporal dependencies are captured by using a time series decomposition that requires each end of the dipole to share the same global component and using an auto-regressive term to capture time dependencies. |
| Seasonality and trends. | The time-series decomposition captures the seasonality and trends by extracting the underlying governing time series against local noise variations. |
| Generating random samples under the null hypothesis. | A “wild bootstrap” approach generates samples by multiplying random noise to the residuals |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Eftelioglu, E.; Ali, R.Y.; Tang, X.; Li, Y.; Doshi, R.; Shekhar, S. Transdisciplinary Foundations of Geospatial Data Science. ISPRS Int. J. Geo-Inf. 2017, 6, 395. https://doi.org/10.3390/ijgi6120395
Xie Y, Eftelioglu E, Ali RY, Tang X, Li Y, Doshi R, Shekhar S. Transdisciplinary Foundations of Geospatial Data Science. ISPRS International Journal of Geo-Information. 2017; 6(12):395. https://doi.org/10.3390/ijgi6120395
Chicago/Turabian StyleXie, Yiqun, Emre Eftelioglu, Reem Y. Ali, Xun Tang, Yan Li, Ruhi Doshi, and Shashi Shekhar. 2017. "Transdisciplinary Foundations of Geospatial Data Science" ISPRS International Journal of Geo-Information 6, no. 12: 395. https://doi.org/10.3390/ijgi6120395
APA StyleXie, Y., Eftelioglu, E., Ali, R. Y., Tang, X., Li, Y., Doshi, R., & Shekhar, S. (2017). Transdisciplinary Foundations of Geospatial Data Science. ISPRS International Journal of Geo-Information, 6(12), 395. https://doi.org/10.3390/ijgi6120395




