Abstract
Invasive alien species are among the most important, least controlled, and least reversible of human impacts on the world’s ecosystems, with negative consequences affecting biodiversity and socioeconomic systems. Species distribution models have become a fundamental tool in assessing the potential spread of invasive species in face of their native counterparts. In this study we compared two different modeling techniques: (i) fixed effects models accounting for the effect of ecogeographical variables (EGVs); and (ii) mixed effects models including also a Gaussian random field (GRF) to model spatial correlation (Matérn covariance function). To estimate the potential distribution of Pittosporum undulatum and Morella faya (respectively, invasive and native trees), we used geo-referenced data of their distribution in Pico and São Miguel islands (Azores) and topographic, climatic and land use EGVs. Fixed effects models run with maximum likelihood or the INLA (Integrated Nested Laplace Approximation) approach provided very similar results, even when reducing the size of the presences data set. The addition of the GRF increased model adjustment (lower Deviance Information Criterion), particularly for the less abundant tree, M. faya. However, the random field parameters were clearly affected by sample size and species distribution pattern. A high degree of spatial autocorrelation was found and should be taken into account when modeling species distribution.
1. Introduction
Invasive species are among the most important, least controlled, and least reversible of human impacts on the world’s ecosystems, with negative consequences, affecting their sustainability, biodiversity, biogeochemistry and social/economic systems [1,2,3,4]. This invasive presence is known to influence the structure and function of invaded ecological communities and is recognized as a major component of global environmental change, constraining sustainable management and/or conservation goals [1,5,6,7]. Moreover, biological invasions represent 40% of the economic losses in agricultural, grassland and forest ecosystems [8,9,10].
A main challenge in ecology is identifying and classifying determinants of invasiveness that provide suitable species habitats, such as, environmental variables and biotic interactions [11,12,13].
Oceanic islands have long been considered to be particularly vulnerable to biotic invasions, and much research has focused on invasive plants [14]. The vulnerability can be explained for two main reasons. Firstly, these islands are isolated and vary broadly in size, geology and ecology [14,15,16,17]. The second explanation is linked to the socioeconomic variables. The high level of islands invasions depends on several driven traits, such as, human demography, agriculture, forestry, trade, industry and tourism [18,19].
In the Azores Islands, the land use changes were extensive following human colonization in the 15th century when native vegetation became gradually extinct or highly modified [20]. The increase in pastureland and spread of invasive plants can produce dramatic changes in the ecosystems, causing serious problems not only for biodiversity, but also in forestry farming and hydrologic cycles [21,22,23,24]. Azorean native vegetation is threatened by several aggressive invaders (e.g., Pittosporum undulatum) which compete with indigenous species (e.g., Morella faya).
A variety of predictive models is currently in use to support management decisions and test key hypotheses regarding the patterns of spread of invasive plants [25,26,27,28]. Species distribution models (SDMs) have become a fundamental tool in ecology and biodiversity, and have broad applications in assessing the relationships between species occurrence, the environment and the impact of ecological change [29,30,31,32].
The strength of a SDM, in a certain way, is determined by the correlation of species distribution (presence or presence–absence) at multiple locations with relevant environmental covariates to estimate habitat preferences or predict distributions [32]. Linear regression is known to be one of the most widely used techniques to investigate how environmental variables influence species distribution patterns and occurrence, mainly due to its easy use and straightforward interpretation [33]. However, ecological data are often complex, unbalanced and contain missing values [34,35]. Therefore, conventional modeling techniques might originate non-significant predictions, leaving high amounts of unexplained variation [33,36,37] leading to under fit models, having insufficient suppleness to describe observed occurrence–environment relationships, and originating a misinterpretation of the factors shaping species distributions [38].
There are numerous methods for developing SDMs, which allowed improving the capability to predict complex systems, namely through their performance to detect and represent nonlinear and highly interactive relationships [39]. These techniques can provide new insights regarding the drivers of complex patterns, eventually increasing modeling accuracy [35,38,40,41,42].
Several statistical techniques have been applied to invasive plant distribution including logistic regression, generalized linear/additive models, tree-based models, fuzzy envelope models, genetic algorithms and maximum entropy [43,44,45,46,47]. These models differ in the underlying assumptions and algorithms, and must be chosen according with the type of the relationships between the environment, the occurrence, and species distribution, also considering the particular situation and goal [48,49,50].
One of the most pressing challenges in improving SDM performance is to consider spatial and temporal correlations and how this could affect spatial inference [51]. With the increasing availability of geocoded scientific data, hierarchical spatial models (e.g., Bayesian implementation) have received attention from ecologists [52,53].
Recently, the use of Gaussian random fields has acquired an important role, since it is ideally suited for fitting complex models to many of the rich spatial data sets [54,55]. The Integrated Nested Laplace Approximation (INLA; [56]) is designed for latent Gaussian models, a very wide and flexible class of models, including generalized linear mixed models (spatial and spatio-temporal models), and can be used in a wide variety of applications [54,57,58]. INLA makes use of deterministic nested Laplace approximations, as an algorithm tailored to the class of latent Gaussian models (LGMs) [51,56,59]. In fitting these models, INLA calculates accurate, deterministic approximations to posterior marginal distributions in place of long Markov Chain Monte Carlo (MCMC) simulations, gaining in time [52].
Moreover, INLA can integrate the Stochastic Partial Differential Equation (SPDE) approach proposed by Lindgren et al. [60] for the implementation of spatial and spatio-temporal models for point-reference data [55]. INLA handles Bayesian Markov random field models [56,61] with the additional advantage of integrating modeling approaches (such as Generalized Linear Models, GLM, and Generalized Additive Models, GAM) and uncertainty analyses into a more general hierarchical framework. As INLA is valid for generalized Gaussian Markov Random Field (GMRF) models, it can be used in situations where a latent Gaussian model (i.e., a linear regression type model) represents the basic process of interest and is observed via one of several possible sampling or measurement distributions (e.g., Gaussian, binomial, Poisson; [62]). In these conditions, the hierarchical model can be reparametrized, since the latent Gaussian process and regression coefficients from a GMRF and the remaining model parameters (termed “hyperparameters”) are scarce. For these specifications, the INLA procedure can be used to find approximate marginal posterior distributions with considerably less computational effort than stochastic methods [56,62]. All required computations are performed by a program called “inla” written in the language “C” which is bundled within a “R” library (R Development Core Team [63]) improving usability as a standard tool ([56,64]; www.r-inla.org).
A binomial Generalized Linear Model uses presence–absence records to model the distribution of the species based on a relationship (i.e., link function) between the mean of the response variable and the linear combination of the explanatory variables [65,66]. In INLA this can be complemented with SPDE. This consists in representing a continuous spatial process (e.g., Gaussian Field; GF) with the Matérn covariance function, as a discretely indexed spatial random process (e.g., GMRF; [52,60]).
Comparative studies of different applications of SDMs to forest species in the Azores are scarce and only a few studies evaluate which modeling method produce the most accurate spatial predictions [23,24,67,68,69].
The present study focuses on testing a methodology for producing more robust distribution models by selecting the main topographical and environmental characteristics in the study area, in order to predict the potential distribution of invasive and native shrubs in a woodland environment. We compared the application of two different modeling techniques: (i) a fixed effects model calculated both using maximum likelihood methods and INLA; and (ii) a mixed effects model including the spatial structure of the data as a random element.
The main goal of this research was to investigate if the addition of a GMRF, which accounts for spatial autocorrelation, will improve the modeling performance of SDMs. We started the modeling process following a maximum likelihood approach with a fixed effects model, we compared this approach with similar calculations in a Bayesian context (INLA), and finally we used the SPDE approach available in INLA to add the effect of a random field. Our hypothesis was that the use of mixed GLMs, including as stochastic element the GMRF, would show a better performance in terms of predictions, than the fixed effects GLMs. To test this hypothesis we used distribution data from invasive (Pittosporum undulatum) and native tree species (Morella faya) collected in two Azores islands, Pico and São Miguel, which are very distinct in terms of land use and geomorphology.
2. Materials and Methods
2.1. Study Area
The Azores is an archipelago in the Atlantic Ocean composed of nine volcanic islands. The islands are dispersed along a general WNW–ESE trend crossing the Mid-Atlantic Ridge in the area where Eurasian, African and North American lithospheric plates meet [70]. The islands are located in the North Atlantic Ocean about west of Portugal mainland, between latitudes 36°55′43′′ North and 39°43′23′′ North and longitudes 24°46′15′′ West and 31°16′24′′ West; with a land surface of 2333 km2 and about 780 km of coastline [71,72]. The climate is temperate oceanic with a mean annual temperature of 17 °C at sea level; Relative humidity is high and rainfall ranges from 1500 to more than 3000 mm/m2 per year, increasing with altitude and from east to west [73,74]. Maximum altitude of the islands ranges from 402 m to 2351 m, with several islands reaching more than 1000 m [75].
All the Azorean islands were uninhabited by humans until the late 15th century, although recent paleoecological studies suggest an earlier settlement [76]. Since then, the vegetation cover of the islands suffered pronounced changes with the onset of human settlements [77]. Clearing of native forests, that was intense shortly after colonization, land use changes, and the introduction of invasive plants caused major vegetation changes [78,79,80].
Pico Island is the youngest island of the Azores archipelago, with a land surface of 449 km2 and less than 300,000 years, originated by subaerial volcanic activity and is located between the coordinates 38°30′ North and 28°20′ West [81,82]. It is noted for its eponymous volcano, Ponta do Pico, which is the highest mountain in Portugal with 2351 m [83].
São Miguel Island is the largest (747 km2) and the most populous of the Azores, located at 37°50′ North and 25°30′ West [84]. The island is characterized by a large variety of volcanic structures, including three active trachytic composite volcanoes with caldera (i.e., Sete Cidades, Fogo and Furnas; [85]). The highest elevation of the island (Pico da Vara, 1103 m) is localized between Povoação and Nordeste.
2.2. Study Species
We selected Pittosporum undulatum Ventenat (Pittosporaceae), the most common invasive tree, and Morella faya (Aiton) Wilbur (Myricaceae) one of the most common native trees [67].
Sweet pittosporum [86] is a long lived evergreen tree native to forests in southeastern Australia that grows up to 15 m [87,88,89]. It is invasive outside its native range in Australia, in the Portuguese mainland, in the Azores, North America, Southern Africa and in many oceanic islands [88,89,90,91,92]. For more information see the reviews by Hortal et al. [67] and Lourenço et al. [92].
Morella faya is an evergreen shrub or small tree, found on all the Azores islands, and considered as a frequent member of the coastal and middle altitude natural forests [79,93,94,95,96]. Nevertheless, it can also be found at up to 600 m of altitude and even as high as 1000 m in Pico Island whereas in the Canary Islands and Madeira it is found up to 1300 m [94,95]. It was originally introduced to the Hawaiian Islands in the late 1800s and was used in forestry plantations in the late 1920s becoming invasive [97,98]. For more information see Silva and Tavares [99] and Elias et al. [96], and references therein.
2.3. Species Distribution Data
2.3.1. Presence Data
Data were taken from the Forest Inventory of the Azores Government ([100], (see [92], for further details). The data, provided in vectorial format (shapefile), were converted to raster (RST) and comma-separated values (CSV) formats for further analysis. All biological data was geocoded to a grid of 100 × 100 m in order to match the EGVs used. We used the training set (100%) and then proceeded to a random and progressive reduction in three steps (Table 1). A completely random selection of samples was conducted in software QGIS Valmiera 2.2, using an appropriate vector function.

Table 1.
Number of species records used in modeling, per island and species. PU: Pittosporum undulatum; MF: Morella faya.
2.3.2. Pseudo-Absences
As absences were not available in the original data set, pseudo-absences were generated by a random selection. This method involves taking pseudo-absence points from the background data, randomly, across the whole study area. We used 10,000 pseudo-absences/absences, as recommended in previous research [101,102,103,104], and followed the general guidelines provided in the literature [105,106,107,108,109].
2.4. Ecogeographical Variables
In this study all data layers (ecogeographical variables) were stored in a geographical information system (GIS) and used to describe 100 × 100 m cells covering the entire study area (Table 2).

Table 2.
List of the 27 ecogeographical variables (EGVs) used to model indigenous and non-indigenous woody species.
2.4.1. Topographical Variables
Topographical variables were derived based on a digital elevation model (DEM) available in “Clima Insular à Escala Local” (CIELO) model ([22,23,69,73,74,110]; see http://www.climaat.angra.uac.pt). The variables used were digital elevation model, aspect, slope, curvature, flow accumulation, summer hill shade and winter hill shade. Curvature is the second derivative of the surface, which highlights the local geomorphology, specifically the flatness, convexity and concavity of the surface. Flow accumulation is a simulation of the superficial flow by considering that all raster cells flow into each downslope cell in the DEM. Hill shade is a simulation of the lighting conditions on the surface dictated by the topography and the position of the Sun (the Summer and Winter solstices were considered). For further details see Costa et al. [22,23] and Dutra Silva et al. [69].
2.4.2. Climatic Variables
Climatic variables were derived from CIELO model developed by Azevedo [110]. This model simulates the climatic variables in an island reproducing the thermodynamic transformations experienced by an air mass crossing the orography, and simulates the evolution of the air parcel’s properties starting from the sea level [73]. The model consists of two main sub-models. One, relative to the advective component simulation, assumes the Foehn effect to reproduce the dynamic and thermodynamic processes. The second concerns the radiative component and energy balance as affected by the orographic clouds and by topography. The climatic variables selected, were air temperature, precipitation, relative humidity with maximum and minimum extremes, seasonal variation, annual and monthly averages and a summary obtained by Principal Component Analysis (PCA) (see [23,24,69]).
2.4.3. Land Use Variables
Land use variables included one variable expressing the distance to six types of land use (forest; natural vegetation; pastureland; agriculture; barren/bare areas; and urban/industrial areas) [23,24,69]).
2.5. Modeling Approach
Based on R, a language and environment for statistical computing, we used the glm() function and the INLA package [56] to fit GLMs following three approaches: (i) a binomial fixed effects GLM with a maximum likelihood calculation; (ii) a binomial fixed effects GLM with calculations in a Bayesian context (INLA); and (iii) a binomial mixed effects GLM including a random spatial effect.
The modeling procedures followed a sequential approach:
- (i)
- We started by an intensive evaluation of fixed effects models using both glm() function and INLA, by testing 400 models including different combinations of EGVs.
- (ii)
- After this preliminary evaluation, we tested the bests models including topographic, climatic and land use data, and compared results obtained using glm() and INLA.
- (iii)
- The best models were further selected and we used INLA to derive mixed effects models, including spatial correlation as the random element.
The response variable is binary, representing the presence (1) or absence (0) of the species in each location sampled, representing the occurrence. Consequently, the conditional distribution of the data is:
assuming that observations are conditionally independent given , which is the probability of occurrence at location .
Therefore, the fixed effects model would be:
where represents the vector of the regression coefficients, is the matrix of covariates and the logit transformation is defined as .
And the mixed effects model would be:
where represents the spatially structured random effect.
The spatially structured random effect was modelled by using the SPDE approach that models GRFs relatively fast, including datasets with complex spatial structure [60,111]. This is often the case of forest data, since the target species often show clustered spatial patterns with regions without any values [112].
is assumed to be Gaussian with a given covariance matrix , depending on the distance between locations and with hyperparameters and representing, respectively the variance and the range of spatial effect [60]:
When using the SPDE approach the correlation function is not modeled directly. The Markov property makes the covariance matrix (Q) sparse, enabling the use of efficient and faster numerical algorithms and the use of the Matérn covariance function [60,112].
Under this perspective, Equation (4) can be stated as follows:
The Gaussian field, depends on two different parameters, and , which determine the range of the effect and the total variance, respectively. The aim is to estimate the parameters and specify the prior distributions for each parameter involved in the model (. We used the default priors and hyperparameters currently implemented in R-INLA. In particular, for the parameters involved in the fixed effects, we used the Gaussian distribution to specify the parameter portion of the model and the regression coefficients. The precision parameter for the random effects was given a LogGamma ) prior. To model the spatial correlation, we assumed a spatial Matérn covariance using the SPDE approach, with parameters and , where and are assigned a joint normal prior distribution [60,64,113].
2.6. Model Selection
Best candidate models were selected based on Akaike Information Criterion (AIC; [114,115,116,117,118]). AIC forms the basis of information-theoretic approaches to modeling and can be associated with identifying variables for inclusion or exclusion in models. These decisions are based on the principle of parsimony and the AIC is actually equivalent to twice the log-likelihood of the model fitted plus two times the number of parameters estimates in its information.
To assess the robustness and predictive ability of the models, the method proposed by Boyce et al. [119] and improved by Hirzel et al. [120] was used. The validation criteria considered was based on the analysis of continuous Boyce indexes and curve shape: (i) the standard deviation around the curves should be narrow; (ii) the curves should be linear and ascending; and (iii) the O (Observed)/E (Expected) ratio should be high [23,120]. Ideally, a good habitat suitability (HS) model produces a monotonically increasing curve and its goodness of fit is measured by the Spearman rank correlation coefficient [23,120].
Model accuracy was evaluated in terms of the Area Under the Curve (AUC) [42,121,122,123,124]. AUC values were calculated based on a 10-k fold cross validation [125] of the respective data set. This means that AUC calculations were repeated 10 times for each model, using 75% of the data for training and 25% for testing. A good model is defined by a curve that maximizes sensitivity for low values of the false positive fraction [126]. The significance of the curve is quantified by AUC and the values range from 0.5 to 1. Values close to 0.5 indicate a fit no better than expected by random, while a value of 1 indicates a perfect model [127,128].
In the case of the implementation of the INLA/SPDE approach [56], marginal posterior distributions were summarized by 95% Bayesian Credible Intervals (BCI; the 0.025 and 0.975 quantiles of the posterior distribution), while Deviance Information Criterion (DIC; [129]) and Watanable-Akaike Information Criterion (WAIC; [130]) were used for model comparison. DIC is a hierarchical modeling generalization of the AIC and the Bayesian Information Criterion (BIC). It is a criterion for comparing complex hierarchical models introduced by Spiegelhalter et al. [129] and defined as
where is the posterior mean of deviance of the model and is the effective number of parameters in the model (see [129]). Details on how to compute the quantities in Equation (6) using the INLA approach are described in Rue et al. [56]. DIC has gained popularity in part through its implementation in the graphical modeling package BUGS [129] but it is known to have some problems, arising in part from not being fully Bayesian in that it is based on a point estimate. According to Vehtari et al. [131] for DIC, there is a similar variance-based computation of the number of parameters that is notoriously unreliable, but the WAIC version is more stable because it computes the variance separately for each data point and then sums; the summing yields stability. WAIC is a more fully Bayesian approach for estimating the out-of-sample expectation based on the log pointwise posterior predictive density [130,131]. It is based on the series expansion of leave-one-out cross-validation (LOO), and asymptotically they are equal [130]. Another factor that measured the quality of the models was the mean Brier Score [132]. We used the mean Brier Score and “leave-one-out” cross validation to assess the predictive power of each model, based on the Conditional Predictive Ordinate statistic (CPO; [133,134]). The Brier Score is an appropriate score function that measures the accuracy of probabilistic predictions. As indicated by Roos and Held [135], we computed the mean logarithm CPO (LCPO). CPO is a predictive measure that can be used to validate and to compare models; and as a device to detect possible outliers or surprising observations [135]. Lower values for DIC, WAIC and LCPO represent the best compromise between fit and parsimony.
2.7. Calculation of the Posterior Distribution and of the Random Field
Once the inference has been carried out, the next step is to predict the occurrence of the target species. The SPDE module allows the construction of a Delaunay triangulation around the sampled points in the region of interest [136]. As opposed to a regular grid, triangulation is a partition of the region into triangles, satisfying constraints on their size and shape in order to ensure smooth transitions between large and small triangles [112,137]. Firstly, observations are treated as initial vertices for the triangulation and extra vertices are added heuristically to minimize the number of triangles needed to cover the region subject to the triangulation constraints [137]. These extra vertices are used as prediction locations.
The function inla.mesh.2d() creates the Constrained Refined Delaunay Triangulation (CRDT), called mesh, on which the Gaussian Random Field is to be built. This is straightforward in R-INLA, but still requires some tuning of the cutoff and max.edge parameters. Several values were tested following the guidelines of the INLA authors [56,57,60]. We opted for a value of cutoff = 100 and max.edge = c(500, 1000). The cutoff parameter was used to avoid building many small triangles around clustered input locations while max.edge parameter specified the maximum allowed triangle edge lengths in the inner domain and in the outer extension [60] (it should be noted that our geographical information system was set up in a UTM projection, therefore in meters). These parameters allowed obtaining a regular and even covering of the studied area, and a clear transition to the “no data” region outside of the study area (i.e., the ocean).
After the prediction is performed in the selected location, there are additional functions that linearly interpolate the results within each triangle into a finer regular grid. As a result of the process, we obtain a predictive posterior distribution of P. undulatum and M. faya occurrence for the study area. The prediction in INLA was performed with model calculation, considering the prediction locations as points where the response was missing [137].
3. Results
3.1. Preliminary Selection of Models
A preliminary screening/analysis was performed to investigate which variables would be more suitable for modeling the presence–absence of both species by testing 400 models with different combinations of EGVs, including topographic, climatic and land use data. According to the AIC, the continuous Boyce Index and to the AUC, the models with best fit were obtained by using the EGV sets described in Table 3.

Table 3.
Sets of EGV (1–5) that produced models with highest fit in Pico and São Miguel islands using fixed effects GLMs.
3.2. Fixed Effects Models
Table 4 includes results for different scenarios (EGV sets) and different locations. Consistent results were found among all EGV sets both for P. undulatum and M. faya. In particular, we found no systematic difference in the statistical performance of glm() and INLA.

Table 4.
Results of fixed and mixed effects models regarding different combinations of variables for P. undulatum and M. faya in Pico and São Miguel islands. BI: Boyce Index; sd: standard deviation; BS: Brier Score.
Regarding P. undulatum in Pico Island, the two information criteria gave identical results regardless of the EGV set. Small differences in AUC and Boyce Index were observed between the five EGV sets. The AUC values generally increased with the addition of environmental variables (EGV set 1 to 5). For M. faya, the values of AIC and DIC were similar. The models fitted the data well, with the mean AUC of 0.883 and a high value for Boyce Index (Table 4). This suggested that the models for Pico Island were robust and could accurately predict the occurrence of both species within the range of predictor variables used.
Concerning São Miguel Island scenarios for P. undulatum, we found a considerable agreement between methods glm() and INLA. However, AUC scores and Boyce Index were generally lower, compared to the results for Pico Island. The mean of AUC varied from 0.796 (EGV set 1) to 0.877 (EGV set 5). We detected clear differences between models at the Boyce Index (ranged between −0.480 to 0.991). With regard to the results for M. faya in São Miguel Island, the values of AIC and DIC were similar. The same variation in the Boyce Index was also found.
Based on our results, in general, the EGV set 5 was the best predictive model for both species and islands with the minimum values of AIC and DIC, and highest values for AUC and the Boyce Index.
3.3. Mixed Effects Models
Table 4 shows the most relevant models regarding different combinations of variables (EGV set 5) for P. undulatum and M. faya. Models including a spatial random field performed better (lower DIC) than the respective fixed effects models.
Regarding M. faya in São Miguel Island, the model with a spatial effect did not allowed the calculation of the DIC. A possible explanation is the difference in the orographic conditions of the study area, as well as the peculiar distribution of M. faya. The type distribution of M. faya in São Miguel seems to be highly dependent on land use. In the past this species was very abundant in São Miguel Island. Due to forest clearing, it remained only in refuges, such as volcanic crater ridges. With a distribution that could be largely dependent on land use, model adjustment could be affected in a relevant manner. However, we were able to calculate WAIC (Table 4).
The values of the mean Brier Score ranged between 0.002 and 0.120, which represent a good degree of adjustment (Table 4, Table 5 and Table 6). As can be seen in Table 5 and Table 6 the values of DIC and LCPO have decreased according to the sample size. All methods (fixed and mixed effects models) provided the same trend when using sampling reduction, as expected. All model choice criteria were in agreement, indicating a reasonable predictive quality. In particular, model comparison indicated that sample size plays a determining role in P. undulatum and M. faya distribution modeling, namely when a spatial random effect is also included.

Table 5.
Results of sampling reduction on fixed and mixed effects models regarding EGV set 5 for P. undulatum and M. faya in Pico Island. BI: Boyce Index; sd: standard deviation; BS: Brier Score; PU: P. undulatum; MF: M. faya; P: Pico. Variables with non-significant values were excluded from the model (code: D) (Supplementary Materials).

Table 6.
Results of sampling reduction for fixed and mixed effects models regarding EGV set 5 for P. undulatum and M. faya in São Miguel Island. BI: Boyce Index; sd: standard deviation; BS: Brier Score; PU: P. undulatum; MF: M. faya; SM: São Miguel. Variables with non-significant values were excluded from the model (code: D) (Supplementary Materials).
3.3.1. Pico Island
There was a positive effect of slope, annual relative humidity range, and annual precipitation range, and a negative effect of annual mean precipitation and distance to forest in the probability of P. undulatum occurrence (Table 7).

Table 7.
Numerical summary of the posterior distributions of the parameters for the best mixed effects model for the two species studied and islands. This summary contains the mean, the standard deviation (sd), and 95% credibility interval. SM: São Miguel.
There was a positive effect of slope, and a negative effect of elevation, annual temperature range, annual mean precipitation, distance to forest and distance to agricultural areas in the probability of M. faya occurrence (Table 7).
3.3.2. São Miguel Island
There was a positive effect of slope, flow accumulation, and winter hill shade, and a negative effect of annual mean temperature, annual mean temperature range, annual mean relative humidity, annual mean precipitation, distance to forest and distance to natural vegetation in the probability of P. undulatum occurrence (Table 7).
There was a negative effect of summer hill shade, annual mean temperature range, annual relative humidity range, annual mean precipitation range, distance to forest and distance to barren areas in the probability of M. faya occurrence (Table 7).
3.4. Prediction of the Random Field
Table 8 shows the hyperparameters for the best models selected where is the hyperparameter related with , the spatial scale parameter, and is the hyperparameter that controls the variance of the random field.

Table 8.
Random field hyperparameters for the best model selected (EGV set 5).
The parameters of the random field are log () = and log () = , where is the local variance parameter. We calculated the posterior marginal distribution of log () and also of 1/ which corresponds to the range parameter, expressed in meters. Posterior marginal distributions of the nominal variance of the random field and of the practical range were also obtained. Results for all species and islands are shown in Table 9. The variance of the random field decreased with the sample reduction and elimination of EGVs with non-significant effect. For both islands, the variance of the random field was relatively higher for M. faya than for P. undulatum.

Table 9.
Numerical summary of the posterior distributions of the best mixed effects models and their reduction for the two species studied in Pico and São Miguel islands. This summary contains the DIC, the posterior marginal distribution of log () and 1/, the posterior marginal distribution of nominal variance of random field) and posterior marginal distribution of the practical range (meters). PU: P. undulatum; MF: M. faya; P: Pico; SM: São Miguel. Variables with non-significant values were excluded from the model (code: D) (Supplementary Materials).
3.4.1. Pico Island
For P. undulatum the random field (Figure 1) showed high values in the coastal zone of the island where most presences were located, and low values in the central area of the island. With regard to M. faya (Figure 2), high values appear in western part of Pico Island, where presences were more common. A reduction in the the number of presences apparently leads to an increase in the values of the practical range. Also, the structure of the spatial random field starts to collapse from 500 to 50 presences for P. undulatum and between 300 and 30 presences for M. faya.
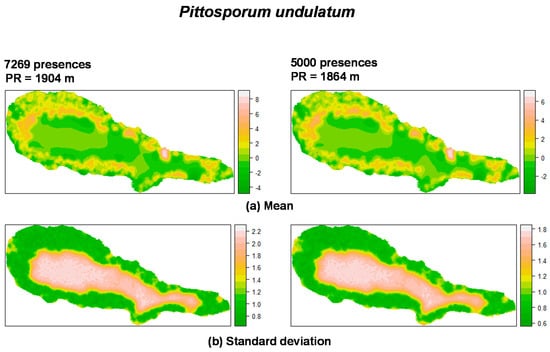
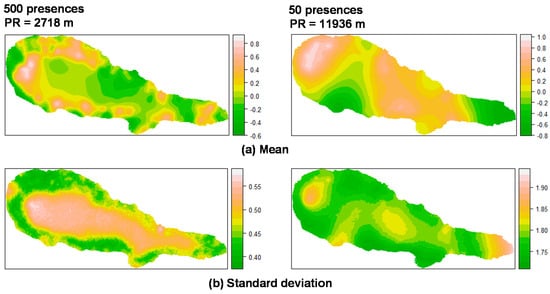
Figure 1.
Summary of the spatial random effect (Gaussian random field) for the best mixed effects models and their reduction for P. undulatum in Pico Island. Mean (a); Standard deviation (b). PR: Practical range.
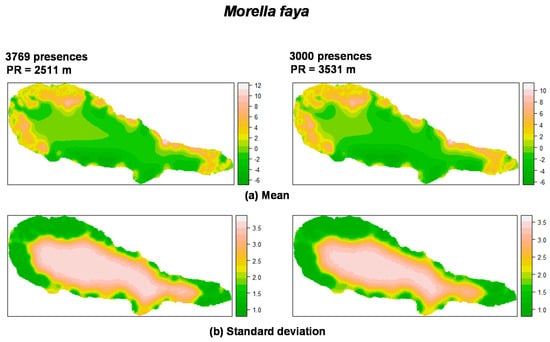
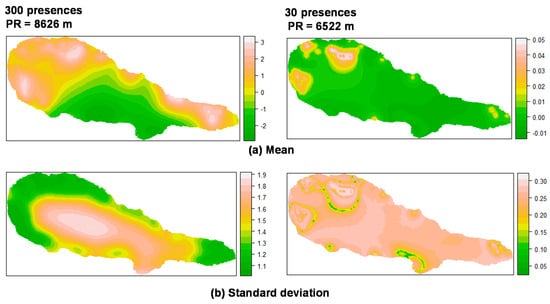
Figure 2.
Summary of the spatial random effect (Gaussian random field) for the best mixed effects models and their reduction for M. faya in Pico Island. Mean (a); Standard deviation (b). PR: Practical range.
3.4.2. São Miguel Island
The mean and standard deviation of the spatial random field are shown in Figure 3 and Figure 4. Regarding P. undulatum, results indicate a strong effect with high values in specific zones of the island: southeastern, northeastern and caldera ridge located on the western portion of the island (Figure 3).
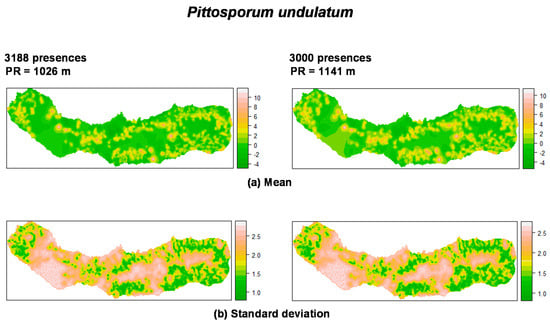
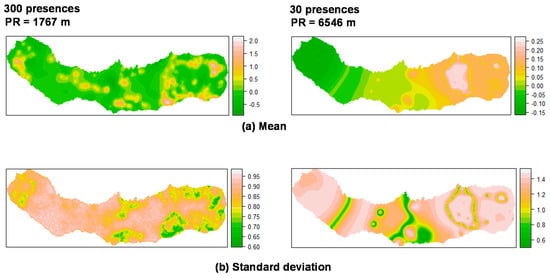
Figure 3.
Summary of the spatial random effect (Gaussian random field) for the best mixed effects models and their reduction for P. undulatum in São Miguel Island. Mean (a); Standard deviation (b). PR: Practical range.
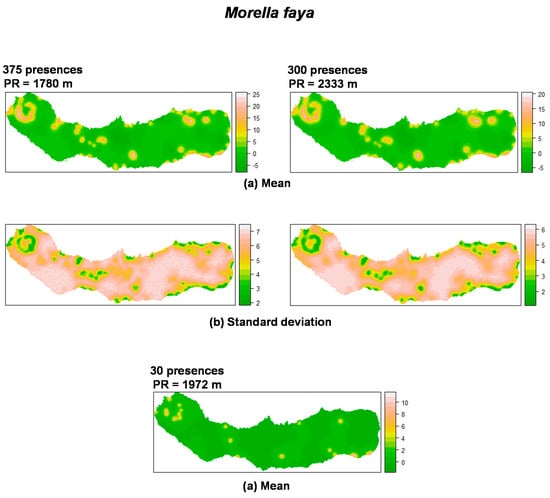

Figure 4.
Summary of the spatial random effect (Gaussian random field) for the best mixed effects models and their reduction for M. faya in São Miguel Island. Mean (a); Standard deviation (b). PR: Practical range.
As can be seen in Figure 4, M. faya presents a peculiar spatial structure derived from the low number of presences. The random field shows high values in the caldera ridge located on the western portion of the island. The trend resulting from the reduction of sample size is again observed, affecting the spatial scale parameter. Also, the structure of the spatial random field starts to collapse from 300 to 30 presences for P. undulatum and from 300 to 30 presences for M. faya. Standard deviation patterns for the spatial random field are driven by the amount of information. The variation on standard deviation is due to the density of presences over the study area.
3.5. Prediction of the Response Grid
We predicted the response jointly with the estimation process by computation of the posterior distributions, also called posterior mean of linear predictor. We see at the Figure 5, Figure 6, Figure 7 and Figure 8 a clear pattern on the average probability of occurrence. The posterior mean of the linear predictor confirms that orographic conditions play a key role in the distribution of P. undulatum and M. faya.
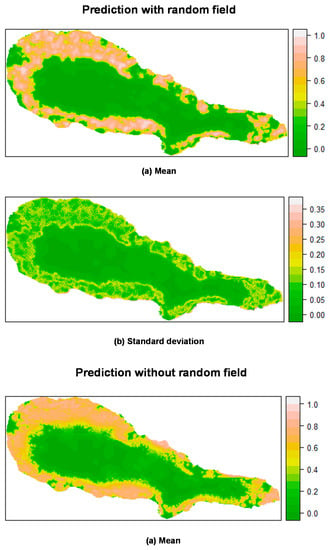
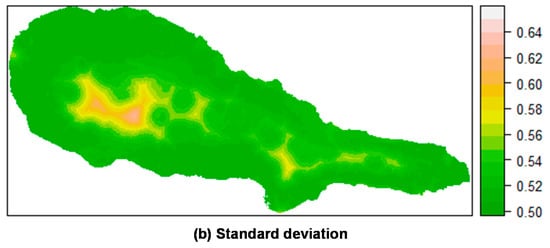
Figure 5.
Prediction of P. undulatum occurrence in Pico Island by posterior mean (a) and standard deviation (b) of the linear predictor. Top: Mixed effects model including a random field; Bottom: Fixed effects model (without a random field). All models calculated using INLA.
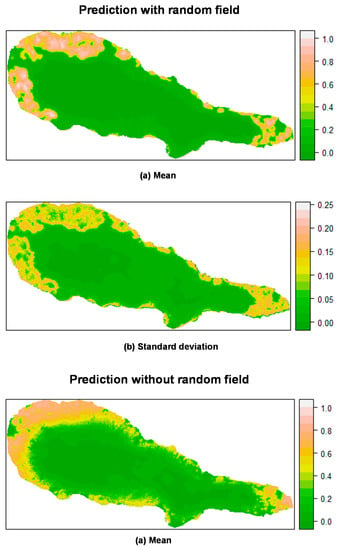
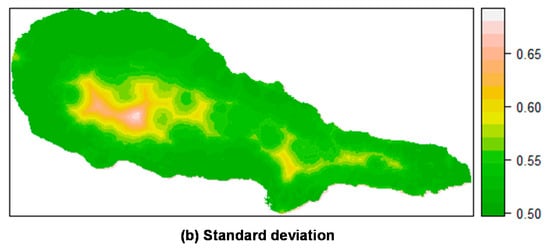
Figure 6.
Prediction of M. faya occurrence in Pico Island by posterior mean (a) and standard deviation (b) of the linear predictor. Top: Mixed effects model including a random field; Bottom: Fixed effects model (without a random field). All models calculated using INLA.
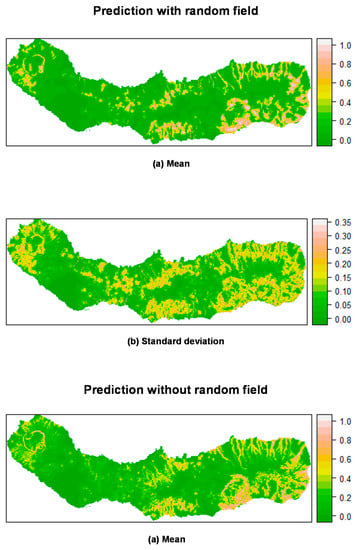
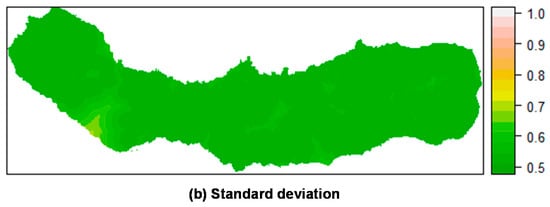
Figure 7.
Prediction of P. undulatum occurrence in São Miguel Island by posterior mean (a) and standard deviation (b) of the linear predictor. Top: Mixed effects model including a random field; Bottom: Fixed effects model (without a random field). All models calculated using INLA.
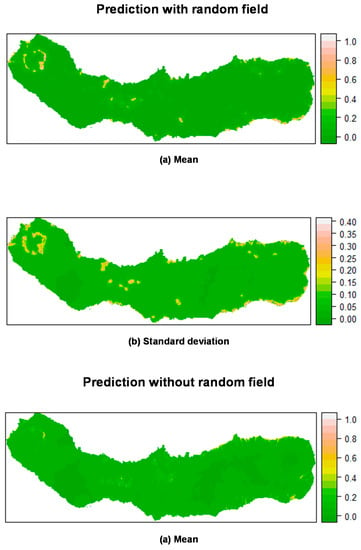
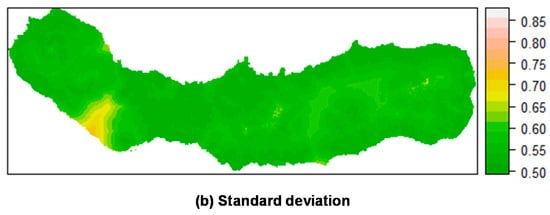
Figure 8.
Prediction of M. faya occurrence in São Miguel Island by posterior mean (a) and standard deviation (b) of the linear predictor. Top: Mixed effects model including a random field; Bottom: Fixed effects model (without a random field). All models calculated using INLA.
3.5.1. Pico Island
For P. undulatum, the probability of occurrence in Pico Island was greatest at the lowest elevation belt (Figure 5). Along, and somewhat above the coastal zone, mean values of the linear predictor showed high values, where the concentration of presences was higher and, as we move inland, the mean probability of occurrence decreased sharply. The predictions including the random field seem to be more sharp and precise, with a lower variation than the predictions obtained with the fixed effects model. Similar results were found for M. faya (Figure 6). Clearly, the predictive resolution of the mixed effects models seems to be higher when compared with that of fixed effects models. This is in agreement with the model comparison presented above, and where mixed effects models showed better adjustment than fixed effects models.
3.5.2. São Miguel Island
Figure 7 shows the mean posterior probability of ocurrence for P. undulatum. Areas with high probability of occurrence include southeast, northeast and the caldera ridges located on the western and eastern portions of the island, as well as several areas along the water lines. Again, the predictions including the random field seemed to be more sharp and precise, with a lower variation than the predictions produced without the random field. M. faya (Figure 8) showed a high probability of occurrence in the caldera ridge located on the western portion of the island, as well as along the coast in the eastern part of the island (see Section 3.4.2). Again, the predictions seem to be much sharper when including the random field, as compared with the results of the fixed effects model.
4. Discussion
Species distibutions models are an important tool in ecology and can be applied to different research purposes. It is extremely important to understand the relationship between species and their habitats. Understanding the spatial distribution and identifying environmental variables that drive species abundance are key factors to produce a set of rules that predict the suitability of a site for the species, and to be able to implement management strategies.
In this study, we presented a retrospective analysis of the distribution of both invasive and native woody plants species to develop and compare statistical models. Our goal is to assess spatial transferability of the EGVs of woody plants, using different approaches. We compared two different modeling techniques: (i) fixed effects models accounting for the effect EGVs, calculated both using a maximum likelihood or a Bayesian approach; and (ii) mixed effects models including also a GRF to model spatial correlation (Matérn covariance function). Azorean forests include some widespread invaders. To evaluate the different modeling approaches, we used geo-referenced data for P.undulatum and M. faya (respectively, invasive and native trees), decribing their distribution in Pico and São Miguel islands, as well as topographic, climatic and land use EGVs.
From an inspection of our GLMs, we could find evidence that EGV set 5 showed the best fit. Model selection is important, as under-fitting a model may not capture the true nature of variability in the outcome variable, while an over-fitted model loses generality [138]. Our aim was then to select the model that best balanced these drawbacks [138,139]. Therefore, model adjustment was checked using different parameters (e.g., AIC, Boyce Index, AUC), to avoid a selection based on a unique potentially biased criterion. A model is only as good as the data which have generated it, and model selection will depend on the set of candidate models specified before the analyses are conducted [140,141,142]. We should point to the fact that, in general, the different criteria pointed out in the same direction.
It should also be noted that EGV set 5 included data of three different categories (i.e., topographic, climatic, land use), showing the importance of considering explanatory variables that can potentially provide complementary information [23,47,49,102,105,143]. Moreover, this also shows that land use data, while directly associated with the human action on the landscape, can have a decisive effect on the distribution patterns of native and invasive species [23,24,67,144,145,146]. Also, modeling projects based on climate variables only might not always be effective [145,147].
Fixed effects models run with maximum likelihood or a Bayesian approach (INLA) provided very similar results, even after reducing the size of the presence data set. In fact, maximum likelihood methods and Bayesian methods based on non-informative priors originate the same results [56,60,148,149].
Generally, consistent subset selection and optimized prediction performance cannot be achieved at the same time [150,151]. However, our results suggested the selection of the same combination of EGVs when using different sample sizes. Meanwhile, in some cases the effect of particular EGVs became non-significant for very small samples. This should be taken into account when dealing with species represented by a relatively low number of presences [24,69].
It should also be noted that our fixed effects models originated predictions that are globally similar to those previously obtained using other modeling approaches such as maximum entropy and ecological niche factor analysis (e.g., [23,24,67,69]).
Another approach was the use of mixed effects models including also a GRF to model spatial correlation (Matérn covariance function). Several remarks regarding mixed effects models can be drawn from our study. First, the results that were obtained with the addition of the random field were more sharp and precise than model outcomes originated with fixed effects only, since the spatial structure accounted for a considerable amount of the global deviance. The addition of the random field increased model adjustment (lower DIC, WAIC), particularly for the less abundant tree, M. faya. This was evident, not only through the analysis of the different parameters used to evaluate model fit and to estimate the variation on the probability of species occurrence, but also when comparing the graphical output obtained for the two approaches.
Regarding M. faya in São Miguel Island, the model with spatial effect did not allowed the calculation of the DIC. A possible explanation is the difference in the orographic conditions of the study area, as well as the peculiar distribution of M. faya. The type distribution of M. faya in São Miguel seems to be highly dependent on land use. In the past this species was very abundant in São Miguel Island but due to forest clearing, it remained only in refuges, such as volcanic crater ridges [23,67]. With a distribution that could be largely dependent on land use, model adjustment could be affected in a relevant manner. However, we are able to calculate WAIC. According to Vehtari et al. [131] for DIC, there is a similar variance-based computation of the number of parameters that could be unreliable, while the WAIC version is more stable because it computes the variance separately for each data point and then sums up the partial results, yielding computational stability.
It was clear that the size of the data set affected the estimation of the spatial structure, showing that a sharp reduction in sample size might lead to the collapse or dissipation of the underlying spatial structure. This could have a considerable importance when modeling species that are not at equilibrium with the environment, such as invasive species, that might still extend their range, or native species that underwent a sharp reduction of a previously wider distribution range [23]. This was evident in the differences obtained between islands, and between species. In fact, the GRF values were consistently different for M. faya, most likely due to its somewhat restricted present distribution, since it might have declined from a previously common native species to a relict species that was replaced due to land use changes and the expansion by P. undulatum [23,96]. Also, both species showed a more irregular distribution in São Miguel Island which clearly affected the GRF parameters. It was apparent from our results that both species were mostly limited by elevation on Pico Island, while land use might have been more important in São Miguel Island, where both species occurred in particular refuges such as the ridges of volcanic craters or along water stream margins, since most of the forest was cleared outside those areas and replaced by pastureland.
Undoubtedly, a high degree of spatial autocorrelation is present and should be taken into account when modeling Azorean forest species. This confirms previous comparative results obtained for a wide range of Gaussian latent models [56]. Furthermore, while the average value of the GRF provides insights about the spatial structure of the data, its variance discriminates between areas of data accumulation or data deficiency [60,112]. Moreover, the processing time for fitting hierarchical spatial models is considered to be faster than MCMC simulations [57,113,134,152] and the use of INLA with R interface greatly facilitates implementation of Bayesian hierarchical spatial models. However, according to our experience, the approach including a random field is very demanding in terms of computation time, particularly when calculating the posterior probabilities on a grid.
Nevertheless, our results clearly show that the inclusion of a GRF in a mixed model approach provides new insights into the role of spatial correlation on forest species distribution patterns. A random field is a stochastic process, taking values in a Euclidean space, and defined over a parameter space with at least one dimension [64]. Since multivariate Gaussian distributions are determined by means and covariances, it is immediate that GRFs are determined by their mean and covariance functions, defined by hyperparameters [64,153]. The random field allows analyzing the heterogeneity of species distribution across the landscape and it is an important first step to obtain a spatial analysis of ecological data, by identifying the distribution and magnitude of species density. In fact, the variation on the mean of the random field expresses the variation remaining after the consideration of the effects of the covariates (i.e., EGVs) on the models. On the other hand, the variation on the standard deviation of the random field is due to changes in species density over the target region. Moreover, taking spatial dependence into account can lead to better inference, superior predictions, and more accurate estimates of the variability of model parameters, and a potential advantage of GMRF models for binary data is that they can aggregate pieces of binary information from neighboring regions to better estimate spatial dependence [154].
These methods have now been applied in ecology [55,62,112,137,155,156,157], climate research [158] and health sciences [159,160,161] and have very promising application in invasion and forest sciences. Moreover, the use of this approach in constructing species distribution maps might help the design of integrated management programs. Probability maps can be easily obtained from the posterior distribution and results are more intuitive and interpretable (i.e., the probability is explicit) for non-statisticians than p values [111,162].
The framework developed here can be expanded to support Azorean forestry management, and could be replicated in other island systems and forest regions, not only in projects addressing the ecology of particular forest species, but also when handling research questions related with the prediction of plant invader success and expansion (e.g., monitoring and risk assessment; [89,163,164]), the detection of areas potentially suited for restoration projects (e.g., potential distribution of rare species; [165]), modeling based on remote sense data [166,167], and modeling of the potential effect of climate change [168].
Supplementary Materials
The following are available online at www.mdpi.com/2073-4425/8/12/391/s1. Table S1: Variables with significance (+) and non-significance (−) regarding EGV set 5 for P. undulatum and M. faya in Pico Island. PU: P. undulatum; MF: M. faya; P: Pico; D: Deleting variables; Table S2: Variables with significance (+) and non-significance (−) regarding EGV set 5 for P. undulatum and M. faya in São Miguel Island. PU: P. undulatum; MF: M. faya; SM: São Miguel; D: Deleting variables; and an R Script with an example of the modeling calculations.
Author Contributions
Lara Dutra Silva and Luís Silva conceived and designed the modeling questions, performed the modeling exercises and analyzed the data; Eduardo Brito de Azevedo contributed with EGV information and Rui Bento Elias revised the paper and discussion.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Vitousek, P.M.; D’Antonio, C.M.; Loope, L.L.; Rejmánek, M.; Westbrooks, R. Introduced species: A significant component of human-caused global change. N. Z. J. Ecol. 1997, 21, 1–16. [Google Scholar]
- Cox, G.W. Alien Species in North America and Hawaii; Island Press: Washington, DC, USA, 1999; p. 387. [Google Scholar]
- Miller, D.A.; Nichols, J.D.; McClintock, B.T.; Campbell Grant, E.H.; Bailey, L.L.; Weir, L.A. Improving occupancy estimation when two types of observation error occur: Non detection and species misidentification. Ecology 2011, 92, 1422–1428. [Google Scholar] [CrossRef] [PubMed]
- Lockwood, J.L.; Hoopes, M.F.; Marchetti, M.P. Invasion Ecology; John Wiley & Sons: Hoboken, NJ, USA, 2013; p. 466. [Google Scholar]
- Mack, R.N.; Simberloff, D.; Mark Lonsdale, W.; Evans, H.; Clout, M.; Bazzaz, F.A. Biotic invasions: Causes, epidemiology, global consequences, and control. Ecol. Appl. 2000, 10, 689–710. [Google Scholar] [CrossRef]
- Ricciardi, A. Are modern biological invasions an unprecedented form of global change? Conserv. Biol. 2007, 21, 329–336. [Google Scholar] [CrossRef] [PubMed]
- Roura-Pascual, N.; Brotons, L.; Peterson, A.; Thuiller, W. Consensual predictions of potential distributional areas for invasive species: A case study of Argentine ants in the Iberian Peninsula. Biol. Invasions 2009, 11, 1017–1031. [Google Scholar] [CrossRef]
- Pimentel, D.; McNair, S.; Janecka, J.; Wightman, J.; Simmonds, C.; O’Connell, C.; Wong, E.; Russel, L.; Zern, J.; Aquino, T.; et al. Economic and environmental threats of alien plant, animal, and microbe invasions. Agric. Ecosyst. Environ. 2001, 84, 1–20. [Google Scholar] [CrossRef]
- Hulme, P.E. Weed risk assessment: A way forward or a waste of time? J. Appl. Ecol. 2012, 49, 10–19. [Google Scholar] [CrossRef]
- Chen, L.; Peng, S.; Yang, B. Predicting alien herb invasion with machine learning models: Biogeographical and life-history traits both matter. Biol. Invasions 2015, 17, 2187–2198. [Google Scholar] [CrossRef]
- Leibold, M.A.; Holyoak, M.; Mouquet, N.; Amarasekare, P.; Chase, J.M.; Hoopes, M.F.; Holt, R.D.; Shurin, J.B.; Law, R.; Tilman, D.; et al. The metacommunity concept: A framework for multi-scale community ecology. Ecol. Lett. 2004, 7, 601–613. [Google Scholar] [CrossRef]
- Van Kleunen, M.; Dawson, M.; Schaepfer, D.; Jeschke, J.M.; Fischer, M. Are invaders different? A conceptual framework of comparative approaches for assessing determinants of invasiveness. Ecol. Lett. 2010, 13, 947–958. [Google Scholar] [CrossRef] [PubMed]
- Mainali, K.P.; Warren, D.L.; Dhileepan, K.; McConnachie, A.; Strathie, L.; Hassan, G.; Karki, D.; Shrestha, B.B.; Parmesan, C. Projecting future expansion of invasive species: Comparing and improving methodologies for species distribution modeling. Glob. Chang. Biol. 2015, 21, 4464–4480. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, R.G.; Claridge, E.M.; Roderick, G.K. Biodiversity dynamics in isolated island communities: Interaction between natural and human-mediated processes. Mol. Ecol. 2008, 17, 15–57. [Google Scholar] [CrossRef] [PubMed]
- Kueffer, C.; Daehler, C.C.; Torres-Santana, C.W.; Lavergne, C.; Meyer, J.Y.; Otto, R.; Silva, L. A global comparison of plant invasions on oceanic islands. Perspect. Plant Ecol. Evol. Syst. 2010, 12, 145–161. [Google Scholar] [CrossRef]
- Denslow, J.S.; Space, J.; Thomas, P.A. Invasive exotic plants in the tropical Pacific Islands. Biotropica 2009, 41, 162–170. [Google Scholar] [CrossRef]
- Kaiser-Bunbury, C.N.; Valentin, T.; Mougal, J.; Matatiken, D.; Ghazoul, J. The tolerance of island plant—Pollinator networks to alien plants. J. Ecol. 2011, 99, 202–213. [Google Scholar] [CrossRef]
- Preston, C.D.; Pearman, D.A.; Hall, A.R. Archaeophytes in Britain. Bot. J. Linn. Soc. 2004, 145, 257–294. [Google Scholar] [CrossRef]
- Guézou, A.; Trueman, M.; Buddenhagen, C.E.; Chamorro, S.; Guerrero, A.M.; Pozo, P.; Atkinson, R. An extensive alien plant inventory from the inhabited areas of Galápagos. PLoS ONE 2010, 5, e10276. [Google Scholar] [CrossRef] [PubMed]
- Borges, P.A.; Lobo, J.M.; Azevedo, E.B.; Gaspar, C.S.; Melo, C.; Nunes, L.V. Invasibility and species richness of island endemic arthropods: A general model of endemic vs. exotic species. J. Biogeogr. 2006, 33, 169–187. [Google Scholar] [CrossRef]
- Silva, L.; Smith, C.W. A quantitative approach to the study of non-indigenous plants: An example from the Azores Archipelago. Biodivers. Conserv. 2006, 15, 1661–1679. [Google Scholar] [CrossRef]
- Silva, L.; Ojeda-Land, E.; Rodríguez-Luengo, J.L. Invasive Terrestrial Flora and Fauna of Macaronesia: Top 100 in Azores, Madeira and Canaries; ARENA - Agência Regional da Energia e Ambiente da Região Autónoma dos Açores: Ponta Delgada, Portugal, 2008; p. 546. [Google Scholar]
- Costa, H.; Aranda, S.; Lourenço, P.; Medeiros, V.; Azevedo, E.B.; Silva, L. Predicting successful replacement of forest invaders by native species using species distribution models: The case of Pittosporum undulatum and Morella faya in the Azores. For. Ecol. Manag. 2012, 279, 90–96. [Google Scholar] [CrossRef]
- Costa, H.; Medeiros, V.; Azevedo, E.B.; Silva, L. Evaluating ecological-niche factor analysis as a modeling tool for environmental weed management in island systems. Weed Res. 2013, 53, 221–230. [Google Scholar] [CrossRef]
- Guisan, A.; Zimmermann, N.E. Predictive habitat distribution models in ecology. Ecol. Model. 2000, 135, 147–186. [Google Scholar] [CrossRef]
- Andrew, M.E.; Ustin, S.L. The effects of temporally variable dispersal and landscape structure on invasive species spread. Ecol. Appl. 2010, 20, 593–608. [Google Scholar] [CrossRef] [PubMed]
- Petty, A.M.; Setterfield, S.A.; Ferdinands, K.B.; Barrow, P. Inferring habitat suitability and spread patterns from large-scale distributions of an exotic invasive pasture grass in north Australia. J. Appl. Ecol. 2012, 49, 742–752. [Google Scholar] [CrossRef]
- Fukuda, S.; De Baets, B.; Waegeman, W.; Verwaeren, J.; Mouton, A.M. Habitat prediction and knowledge extraction for spawning European grayling (Thymallus thymallus L.) using a broad range of species distribution models. Environ. Model. Softw. 2013, 47, 1–6. [Google Scholar] [CrossRef]
- Newbold, T. Applications and limitations of museum data for conservation and ecology, with particular attention to species distribution models. Prog. Phys. Geogr. 2010, 34, 3–22. [Google Scholar] [CrossRef]
- Franklin, J. Species distribution models in conservation biogeography: Developments and challenges. Divers. Distrib. 2013, 19, 1217–1223. [Google Scholar] [CrossRef]
- Guisan, A.; Tingley, R.; Baumgartner, J.B.; Naujokaitis-Lewis, I.; Sutcliffe, P.R.; Tulloch, A.I.T.; Regan, T.J.; Brotons, L.; McDonald-Madden, E.; Mantyka-Pringle, C.; et al. Predicting species distributions for conservation decisions. Ecol. Lett. 2013, 16, 1424–1435. [Google Scholar] [CrossRef] [PubMed]
- Guillera-Arroita, G.; Lahoz-Monfort, J.J.; Elith, J.; Gordon, A.; Kujala, H.; Lentini, P.E.; McCarthy, M.A.; Tingley, R.; Wintle, B.A. Is my species distribution model fit for purpose? Matching data and models to applications. Glob. Ecol. Biogeogr. 2015, 24, 276–292. [Google Scholar] [CrossRef]
- Aertsen, W.; Kint, V.; Van Orshoven, J.; Özkan, K.; Muys, B. Comparison and ranking of different modelling techniques for prediction of site index in Mediterranean mountain forests. Ecol. Model. 2010, 221, 1119–1130. [Google Scholar] [CrossRef]
- Potts, J.M.; Elith, J. Comparing species abundance models. Ecol. Model. 2006, 199, 153–163. [Google Scholar] [CrossRef]
- Merow, C.; Silander, J.A. A comparison of Maxlike and Maxent for modelling species distributions. Methods Ecol. Evol. 2014, 5, 215–225. [Google Scholar] [CrossRef]
- Austin, M.P. The potential contribution of vegetation ecology to biodiversity research. Ecography 1999, 22, 465–484. [Google Scholar] [CrossRef]
- De’ath, G.; Fabricious, K.E. Classification and regression trees: A powerful yet simple technique for the analysis of complex ecological data. Ecology 2000, 81, 3178–3192. [Google Scholar] [CrossRef]
- Merow, C.; Latimer, A.; Wilson, A.M.; McMahon, S.M.; Rebelo, A.G.; Silander, J.A., Jr. On using integral projection models to build demographically driven species distribution models. Ecography 2014, 37, 1167–1183. [Google Scholar] [CrossRef]
- Austin, M.P. Species distribution models and ecological theory: A critical assessment and some possible new approaches. Ecol. Model. 2007, 200, 1–19. [Google Scholar] [CrossRef]
- Guisan, A.; Thuiller, W. Predicting species distribution: Offering more than simple habitat models. Ecol. Lett. 2005, 8, 993–1009. [Google Scholar] [CrossRef]
- Knudby, A.; Brenning, A.; LeDrew, E. New approaches to modelling fish habitat relationships. Ecol. Model. 2010, 221, 503–511. [Google Scholar] [CrossRef]
- Rivera, Ó.R.; López-Quílez, A. Development and Comparison of Species Distribution Models for Forest Inventories. ISPRS Int. J. Geo-Inf. 2017, 6, 176. [Google Scholar] [CrossRef]
- Underwood, E.C.; Klinger, R.; Moore, P.E. Predicting patterns of non-native plant invasions in Yosemite National Park, California, USA. Divers. Distrib. 2004, 10, 447–459. [Google Scholar] [CrossRef]
- Hoffman, J.D.; Narumalani, S.; Mishra, D.R.; Merani, P.; Wilson, R.G. Predicting potential occurrence and spread of invasive plant species along the North Platte River, NebraskaI. Invasive Plant Sci. Manag. 2008, 1, 359–367. [Google Scholar] [CrossRef]
- Smolik, M.G.; Dullinger, S.; Essl, F.; Kleinbauer, I.; Leitner, M.; Peterseil, J.; Stadler, L.M.; Vogl, G. Integrating species distribution models and interacting particle systems to predict the spread of an invasive alien plant. J. Biogeogr. 2010, 37, 411–422. [Google Scholar] [CrossRef]
- Lemke, D.; Brown, J.A. Habitat modeling of alien plant species at varying levels of occupancy. Forests 2012, 3, 799–817. [Google Scholar] [CrossRef]
- Gallien, L.; Mazel, F.; Lavergne, S.; Renaud, J.; Douzet, R.; Thuiller, W. Contrasting the effects of environment, dispersal and biotic interactions to explain the distribution of invasive plants in alpine communities. Biol. Invasions 2015, 17, 1407–1423. [Google Scholar] [CrossRef] [PubMed]
- Segurado, P.; Araújo, M.B. An evaluation of methods for modelling species distribution. J. Biogeogr. 2004, 31, 1555–1568. [Google Scholar] [CrossRef]
- Elith, J.; Graham, C.H.; Anderson, R.P.; Dudík, M.; Ferrier, S.; Guisan, A.; Hijmans, R.J.; Huettmann, F.; Leathwick, J.R.; Lehmann, A.; et al. Novel methods improve prediction of species’ distributions from occurrence data. Ecography 2006, 29, 129–151. [Google Scholar] [CrossRef]
- Meynard, C.N.; Kaplan, D.M. The effect of a gradual response to the environment on species distribution modeling performance. Ecography 2012, 35, 499–509. [Google Scholar] [CrossRef]
- Eidsvik, J.; Finley, A.O.; Banerjee, S.; Rue, H. Approximate Bayesian inference for large spatial datasets using predictive process models. Comput. Stat. Data Anal. 2012, 56, 1362–1380. [Google Scholar] [CrossRef]
- Beguin, J.; Martino, S.; Rue, H.; Cumming, S.G. Hierarchical analysis of spatially autocorrelated ecological data using integrated nested Laplace approximation. Methods Ecol. Evol. 2012, 3, 921–929. [Google Scholar] [CrossRef]
- Martins, T.G.; Simpson, D.; Lindgren, F.; Rue, H. Bayesian computing with INLA: New features. Comput. Stat. Data Anal. 2013, 67, 68–83. [Google Scholar] [CrossRef]
- Blangiardo, M.; Cameletti, M.; Baio, G.; Rue, H. Spatial and spatio-temporal models with R-INLA. Spat. Spatiotemporal Epidemiol. 2013, 7, 39–55. [Google Scholar] [CrossRef] [PubMed]
- Illian, J.B.; Martino, S.; Sørbye, S.H.; Gallego-Fernández, J.B.; Zunzunegui, M.; Esquivias, M.P.; Travis, J.M. Fitting complex ecological point process models with integrated nested Laplace approximation. Methods Ecol. Evol. 2013, 4, 305–315. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B Stat. Methodol. 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Martino, S.; Akerkar, R.; Rue, H. Approximate Bayesian inference for survival models. Scand. Stat. Theory Appl. 2011, 38, 514–528. [Google Scholar] [CrossRef]
- Riebler, A.; Held, L.; Rue, H. Estimation and extrapolation of time trends in registry data-borrowing strength from related populations. Ann. Appl. Stat. 2012, 304–333. [Google Scholar] [CrossRef]
- Tierney, L.; Kadane, J.B. Accurate approximations for posterior moments and marginal densities. J. Am. Stat. Assoc. 1986, 81, 82–86. [Google Scholar] [CrossRef]
- Lindgren, F.; Rue, H.; Lindström, J. An explicit link between Gaussian fields and Gaussian Markov random fields: The stochastic partial differential equation approach. J. R. Stat. Soc. Ser. B Stat. Methodol. 2011, 73, 423–498. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S. Approximate Bayesian inference for hierarchical Gaussian Markov random field models. J. Stat. Plan. Inference 2007, 137, 3177–3192. [Google Scholar] [CrossRef]
- Haas, S.E.; Hooten, M.B.; Rizzo, D.M.; Meentemeyer, R.K. Forest species diversity reduces disease risk in a generalist plant pathogen invasion. Ecol. Lett. 2011, 14, 1108–1116. [Google Scholar] [CrossRef] [PubMed]
- R Development Core Team R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna. 2016. Available online: http://www.R-project.org (accessed on 19 September 2016).
- Rue, H.; Held, L. Gaussian Markov Random Fields: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2005; pp. 1–280. [Google Scholar]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; CRC Press: Boca Raton, FL, USA, 1990; Volume 43, pp. 1–352. [Google Scholar]
- Guisan, A.; Edwards, T.C.; Hastie, T. Generalized linear and generalized additive models in studies of species distributions: Setting the scene. Ecol. Model. 2002, 157, 89–100. [Google Scholar] [CrossRef]
- Hortal, J.; Borges, P.A.V.; Jimenéz-Valverde, A.; Azevedo, E.B.; Silva, L. Assessing the areas under risk of invasion within islands through potential distribution modelling: The case of Pittosporum undulatum in São Miguel, Azores. J. Nat. Conserv. 2010, 18, 247–257. [Google Scholar] [CrossRef]
- Costa, H.; Ponte, N.B.; Azevedo, E.B.; Gil, A. Fuzzy set theory for predicting the potential distribution and cost-effective monitoring of invasive species. Ecol. Model. 2015, 316, 122–132. [Google Scholar] [CrossRef]
- Dutra Silva, L.; Costa, H.; Brito de Azevedo, E.; Medeiros, V.; Alves, M.; Bento Elias, R.; Silva, L. Modelling native and invasive woody species: A comparison of ENFA and MaxEnt applied to the Azorean forest. In Modeling, Dynamics, Optimization and Bioeconomics II; Pinto, A.A., Zilberman, D., Eds.; Springer Proceedings in Mathematics and Statistics 195; Springer: Berlin, Germany, 2017. [Google Scholar]
- Gaspar, J.L.; Queiroz, G.; Ferreira, T.; Medeiros, A.R.; Goulart, C.; Medeiros, J. Earthquakes and volcanic eruptions in the Azores region: Geodynamic implications from major historical events and instrumental seismicity. Geol. Soc. Lond. Mem. 2015, 44, 33–49. [Google Scholar] [CrossRef]
- Serviço Regional de Estatística dos Açores (SREA). Açores em Números 2013; Região Autónoma dos Açores, Vice-Presidência do Governo, Emprego e Competitividade Empresarial, Serviço Regional de Estatística dos Açores: Angra do Heroísmo, Portugal, 2015; pp. 1–68.
- Cruz, J.V.; França, Z. Hydrogeochemistry of thermal and mineral water springs of the Azores archipelago (Portugal). J. Volcanol. Geotherm. Res. 2006, 151, 382–398. [Google Scholar] [CrossRef]
- Azevedo, E.B.; Pereira, L.S.; Itier, B. Modelling the local climate in island environments: Water balance applications. Agric. Water Manag. 1999, 40, 393–403. [Google Scholar] [CrossRef]
- Azevedo, E.B. Projecto CLIMAAT—Clima e Meteorologia dos Arquipélagos Atlânticos. PIC Interreg IIIB Mac2, 3/A3. 2003. [Google Scholar]
- Silva, L.; Smith, C.W. A characterization of the non-indigenous flora of the Azores Archipelago. Biol. Invasions 2004, 6, 193–204. [Google Scholar] [CrossRef]
- Raposeiro, P.M.; Rubio, M.J.; González, A.; Hernández, A.; Sánchez-López, G.; Vázquez-Loureiro, D.; Rull, V.; Bao, R.; Costa, A.C.; Gonçalves, V.; et al. Impact of the historical introduction of exotic fishes on the chironomid community of Lake Azul (Azores Islands). Palaeogeography 2017, 466, 77–88. [Google Scholar] [CrossRef]
- Monteiro, L.R.; Ramos, J.A.; Furness, R.W. Past and present status and conservation of the seabirds breeding in the Azores archipelago. Biol. Conserv. 1996, 78, 319–328. [Google Scholar] [CrossRef]
- Frutuoso, G. Saudades da Terra, 2nd ed.; 1978 to 1983; Rodrigues, J.B.O., Ed.; Instituto Cultural de Ponta Delgada: Ponta Delgada, Portugal, 1561; Volume 6, p. 920. [Google Scholar]
- Sjögren, E. Recent changes in the vascular flora and vegetation of the Azores Islands. Memórias da Sociedade Broteriana 1973, 22, 1–113. [Google Scholar]
- Marcelino, J.A.; Silva, L.; Garcia, P.V.; Weber, E.; Soares, A.O. Using species spectra to evaluate plant community conservation value along a gradient of anthropogenic disturbance. Environ. Monit. Assess. 2013, 185, 6221–6233. [Google Scholar] [CrossRef] [PubMed]
- Cruz, J.V.; Silva, M.O. Groundwater salinization in Pico Island (Azores, Portugal): Origin and mechanisms. Environ. Geol. 2000, 39, 1181–1189. [Google Scholar] [CrossRef]
- França, Z.; Cruz, J.V.; Nunes, J.C.; Forjaz, V.H. Geologia dos Açores: Uma Perspectiva Actual. Açoreana 2005, 10, 11–140. [Google Scholar]
- Nunes, J.C. A Actividade Vulcânica na Ilha do Pico do Plistocénio Superior ao Holocénio: Mecanismo Eruptivo e Hazard Vulcânico; Tese de Doutoramento no Ramo de Geologia, Especialidade de Vulcanologia, Universidade dos Açores: Ponta Delgada, Portugal, 1999; p. 357. [Google Scholar]
- Moore, R.B. Volcanic geology and eruption frequency, São Miguel, Azores. Bull. Volcanol. 1990, 52, 602–614. [Google Scholar] [CrossRef]
- Marques, R.; Zêzere, J.; Trigo, R.; Gaspar, J.; Trigo, I. Rainfall patterns and critical values associated with landslides in Povoação County (São Miguel Island, Azores): Relationships with the North Atlantic Oscillation. Hydrol. Process 2008, 22, 478. [Google Scholar] [CrossRef]
- García Gallo, A.; Rodríguez Delgado, O.; Ojeda Land, E.; Silva, L. Pittosporum undulatum Vent. In Invasive Terrestrial Flora and Fauna of Macaronesia. TOP 100 in Azores, Madeira and Canaries; Silva, L., Ojeda Land, E., Rodríguez Luengo, J.L., Eds.; ARENA- Agência Regional da Energia e Ambiente da Região Autónoma dos Açores: Ponta Delgada, Portugal, 2008; pp. 225–228. [Google Scholar]
- Bellingham, P.J.; Tanner, E.V.; Healey, J.R. Hurricane disturbance accelerates invasion by the alien tree Pittosporum undulatum in Jamaican montane rain forests. J. Veg. Sci. 2005, 16, 675–684. [Google Scholar] [CrossRef]
- Ferreira, N.J.; Meireles de Sousa, I.G.; Luís, T.C.; Currais, A.J.M.; Figueiredo, A.C.; Costa, M.M.; Lima, A.S.B.; Santos, P.A.G.; Barroso, J.G.; Pedro, L.G.; et al. Pittosporum undulatum Vent. grown in Portugal: Secretory structures, seasonal variation and enantiomeric composition of its essential oil. Flavour Fragr. J. 2007, 22, 1–9. [Google Scholar] [CrossRef]
- Cronk, Q.C.B.; Fuller, J.L. Plant Invaders: The Threat to Natural Ecosystems; Chapman and Hall: New York, NY, USA, 2014; p. 256. [Google Scholar]
- Gleadow, R.M.; Ashton, D.H. Invasion by Pittosporum undulatum of the forests of central Victoria. I. Invasion patterns and plant morphology. Aust. J. Bot. 1981, 29, 705–720. [Google Scholar] [CrossRef]
- Healey, J.R.; Goodland, T.; Hall, J.B. The Impact on Forest Biodiversity of an Invasive Tree Species and the Development of Methods for its Control Report to the British Overseas Development Administration. Final Report of ODA Forestry Research Project; School of Agricultural and Forest Science, University of Wales: Cardiff, UK, 1993. [Google Scholar]
- Lourenço, P.; Medeiros, V.; Gil, A.; Silva, L. Distribution, habitat and biomass of Pittosporum undulatum, the most important woody plant invader in the Azores Archipelago. For. Ecol. Manag. 2011, 262, 178–187. [Google Scholar] [CrossRef]
- Dröuet, H. Catalogue de la Flore des îles Açores; Baillière and Fils: Paris, France, 1866; p. 153. [Google Scholar]
- Silva, L.; Tavares, J. Phytophagous Insects Associated with Endemic, Macaronesian, and Exotic Plants in the Azores; Editorial, Comité, Ed.; Avances en Entomologia Ibérica; Museo Nacional de Ciencias Naturales (CSIC) y Universidad Autónoma de Madrid: Madrid, Spain, 1995; pp. 179–187. [Google Scholar]
- Wagner, W.L.; Herbst, D.R.; Sohmer, S.H. Manual of the Flowering Plants of Hawai’I; Bishop Museum Press: Honolulu, HI, USA, 1999; Volumes 1–2. [Google Scholar]
- Elias, R.B.; Gil, A.; Silva, L.; Fernández-Palacios, J.M.; Azevedo, E.B.; Reis, F. Natural zonal vegetation of the Azores Islands: Characterization and potential distribution. Phytocoenologia 2016, 46, 107–123. [Google Scholar] [CrossRef]
- Whiteaker, L.D.; Gardner, D.E. The Distribution of Myrica faya Ait. In the State of Hawaii. 1985. Available online: http://hdl.handle.net/10125/3312 (accessed on 27 November 2017).
- Asner, G.P.; Loarie, S.R.; Heyder, U. Combined effects of climate and land-use change on the future of humid tropical forests. Conserv. Lett. 2010, 3, 395–403. [Google Scholar] [CrossRef]
- Silva, L.; Tavares, J. Factors affecting Myrica faya Aiton demography in the Azores. Açoreana 1997, 8, 359–374. [Google Scholar]
- Direcção Regional dos Recursos Florestais (DRRF). Avaliação da Biomassa Disponível em Povoamentos Florestais na Região Autónoma dos Açores (Evaluation of Available Biomass in Forestry Stands in the Azores Autonomic Region); Inventário Florestal da Região Autónoma dos Açores; Direcção Regional dos Recursos Florestais: Secretaria Regional da Agricultura e Florestas da Região Autónoma dos Açores, Ponta Delgada, Portugal, 2007; p. 8. [Google Scholar]
- Wintle, B.A.; Elith, J.; Potts, J.M. Fauna habitat modelling and mapping: A review and case study in the Lower Hunter Central Coast region of NSW. Austral Ecol. 2005, 30, 719–738. [Google Scholar] [CrossRef]
- Phillips, S.J.; Dudík, M. Modeling of species distributions with Maxent: New extensions and a comprehensive evaluation. Ecography 2008, 31, 161–175. [Google Scholar] [CrossRef]
- Barbet-Massin, M.; Jiguet, F.; Albert, C.H.; Thuiller, W. Selecting pseudo-absences for species distribution models: How, where and how many? Methods Ecol. Evol. 2012, 3, 327–338. [Google Scholar] [CrossRef]
- Wintle, B.A.; Walshe, T.V.; Parris, K.M.; McCarthy, M.A. Designing occupancy surveys and interpreting non-detection when observations are imperfect. Divers. Distrib. 2012, 18, 417–424. [Google Scholar] [CrossRef]
- Ferrier, S.; Watson, G. An Evaluation of the Effectiveness of Environmental Surrogates and Modelling Techniques in Predicting the Distribution of Biological Diversity; Environment Australia: Canberra, Australia, 1997.
- Stockwell, D.R.; Peterson, A.T. Effects of sample size on accuracy of species distribution models. Ecol. Model. 2002, 148, 1–13. [Google Scholar] [CrossRef]
- Lobo, J.M.; Jiménez-Valverde, A.; Real, R. AUC: A misleading measure of the performance of predictive distribution models. Glob. Ecol. Biogeogr. 2008, 17, 145–151. [Google Scholar] [CrossRef]
- Lobo, J.M.; Jiménez-Valverde, A.; Hortal, J. The uncertain nature of absences and their importance in species distribution modelling. Ecography 2010, 33, 103–114. [Google Scholar] [CrossRef]
- Senay, S.D.; Worner, S.P.; Ikeda, T. Novel three-step pseudo-absence selection technique for improved species distribution modelling. PLoS ONE 2013, 8, e71218. [Google Scholar] [CrossRef] [PubMed]
- Azevedo, E.B. Modelação ao do Clima Insular à Escala Local. Modelo CIELO aplicado à ilha Terceira. Tese de Doutoramento no Ramo de Ciências Agrárias, Universidade dos Açores: Angra do Heroísmo, Portugal, 1996; p. 247. [Google Scholar]
- Cosandey-Godin, A.; Krainski, E.T.; Worm, B.; Flemming, J.M. Applying Bayesian spatiotemporal models to fisheries bycatch in the Canadian Arctic. Can. J. Fish. Aquat. Sci. 2015, 72, 1–12. [Google Scholar] [CrossRef]
- Pennino, M.G.; Muñoz, F.; Conesa, D.; López-Quίlez, A.; Bellido, J.M. Modeling sensitive elasmobranch habitats. J. Sea Res. 2013, 83, 209–218. [Google Scholar] [CrossRef]
- Lindgren, F.; Rue, H. Bayesian spatial modelling with R-INLA. J. Stat. Softw. 2015, 63, 63. [Google Scholar] [CrossRef]
- Akaike, H. Maximum likelihood identification of Gaussian autoregressive moving average models. Biometrika 1973, 60, 255–265. [Google Scholar] [CrossRef]
- Rushton, S.P.; Ormerod, S.J.; Kerby, G. New paradigms for modelling species distributions? J. Appl. Ecol. 2004, 41, 193–200. [Google Scholar] [CrossRef]
- Randin, C.F.; Dirnböck, T.; Dullinger, S.; Zimmermann, N.E.; Zappa, M.; Guisan, A. Are niche-based species distribution models transferable in space? J. Biogeogr. 2006, 33, 1689–1703. [Google Scholar] [CrossRef]
- Symonds, M.R.; Moussalli, A. A brief guide to model selection, multimodel inference and model averaging in behavioural ecology using Akaike’s information criterion. Behav. Ecol. Sociobiol. 2011, 65, 13–21. [Google Scholar] [CrossRef]
- Nakagawa, S.; Schielzeth, H. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evol. 2013, 4, 133–142. [Google Scholar] [CrossRef]
- Boyce, M.S.; Vernier, P.R.; Nielsen, S.E.; Schmiegelow, F.K.A. Evaluating resource selection functions. Ecol. Model. 2002, 157, 281–300. [Google Scholar] [CrossRef]
- Hirzel, A.H.; Le Lay, G.; Helfer, V.; Randin, C.; Guisan, A. Evaluating the ability of habitat suitability models to predict species presences. Ecol. Model. 2006, 199, 142–152. [Google Scholar] [CrossRef]
- Fielding, A.H.; Bell, J.F. A review of methods for the assessment of prediction errors in conservation presence/absence models. Environ. Conserv. 1997, 24, 38–49. [Google Scholar] [CrossRef]
- Fawcett, T. ROC graphs: Notes and practical considerations for researchers. Mach. Learn. 2004, 31, 1–38. [Google Scholar]
- Peterson, A.T.; Papeş, M.; Eaton, M. Transferability and model evaluation in ecological niche modelling: A comparison of GARP and Maxent. Ecography 2007, 30, 550–560. [Google Scholar] [CrossRef]
- Mas, J.F.; Soares Filho, B.; Pontius, R.G.; Farfán Gutiérrez, M.; Rodrigues, H. A suite of tools for ROC analysis of spatial models. ISPRS Int. J. Geo-Inf. 2013, 2, 869–887. [Google Scholar] [CrossRef]
- Van Houwelingen, J.C.; Le Cessie, S. Predictive value of statistical models. Stat. Med. 1990, 9, 1303–1325. [Google Scholar] [CrossRef] [PubMed]
- Hernandez, P.A.; Graham, C.H.; Master, L.L.; Albert, D.L. The effect of sample size and species characteristics on performance of different species distribution modeling methods. Ecography 2006, 29, 773–785. [Google Scholar] [CrossRef]
- Wisz, M.S.; Hijmans, R.J.; Li, J.; Peterson, A.T.; Graham, C.H.; Guisan, A. Effects of sample size on the performance of species distribution models. Divers. Distrib. 2008, 14, 763–773. [Google Scholar] [CrossRef]
- Baldwin, R.A. Use of maximum entropy modeling in wildlife research. Entropy 2009, 11, 854–866. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; van der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B Stat. Methodol. 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Watanabe, S. Equations of states in singular statistical estimation. Neural Netw. 2010, 23, 20–34. [Google Scholar] [CrossRef] [PubMed]
- Vehtari, A.; Gelman, A.; Gabry, J. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Stat. Comput. 2017, 27, 1413–1432. [Google Scholar] [CrossRef]
- Schmid, C.H.; Griffith, J.L. Multivariate classification rules: Calibration and discrimination. Encycl. Biostat. 2005. [Google Scholar] [CrossRef]
- Geisser, S. Predictive Inference: An Introduction; CRC Press: Boca Raton, FL, USA, 1993; Volume 55, p. 240. [Google Scholar]
- Held, L.; Schrödle, B.; Rue, H. Posterior and cross-validatory predictive checks: A comparison of MCMC and INLA. Stat. Model. Regres. Struct. 2010, 91–110. [Google Scholar] [CrossRef]
- Roos, M.; Held, L. Sensitivity analysis in Bayesian generalized linear mixed models for binary data. Bayesian Anal. 2011, 6, 259–278. [Google Scholar] [CrossRef]
- Hjelle, Ø.; Dæhlen, M. Algorithms for Delaunay Triangulation. In Triangulations and Applications; Hjelle, Ø., Dæhlen, M., Eds.; Springer: Berlin, Germany, 2006; pp. 73–93. [Google Scholar]
- Munõz, F.; Pennino, M.G.; Conesa, D.; López-Quílez, A.; Bellido, J.M. Estimation and prediction of the spatial occurrence of fish species using Bayesian latent Gaussian models. Stoch. Environ. Res. Risk Assess. 2013, 27, 1171–1180. [Google Scholar] [CrossRef]
- Snipes, M.; Taylor, D.C. Model selection and Akaike Information Criteria: An example from wine ratings and prices. Wine Econ. Policy 2014, 3, 3–9. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel Inference Understanding AIC and BIC in model selection. Sociol. Methods. Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Anderson, D.R.; Burnham, K.P.; White, G.C. AIC model selection in overdispersed capture-recapture data. Ecology 1994, 75, 1780–1793. [Google Scholar] [CrossRef]
- Agresti, A. An Introduction to Categorical Data Analysis; Wiley: New York, NY, USA, 1996; Volume 135, p. 394. [Google Scholar]
- Mazerolle, M.J. Improving data analysis in herpetology: Using Akaike’s Information Criterion (AIC) to assess the strength of biological hypotheses. Amphibia-Reptilia 2006, 27, 169–180. [Google Scholar] [CrossRef]
- Bailey, J.J.; Boyd, D.S.; Hjort, J.; Lavers, C.P.; Field, R. Modelling native and alien vascular plant species richness: At which scales is geodiversity most relevant? Glob. Ecol. Biogeogr. 2017. [Google Scholar] [CrossRef]
- Thuiller, W.; Richardson, D.M.; Rouget, M.; Procheş, Ş.; Wilson, J.R. Interactions between environment, species traits, and human uses describe patterns of plant invasions. Ecology 2006, 87, 1755–1769. [Google Scholar] [CrossRef]
- Bradley, B.A.; Blumenthal, D.M.; Wilcove, D.S.; Ziska, L.H. Predicting plant invasions in an era of global change. Trends Ecol. Evol. 2010, 25, 310–318. [Google Scholar] [CrossRef] [PubMed]
- Hejda, M.; Chytrý, M.; Pergl, J.; Pyšek, P. Native-range habitats of invasive plants: Are they similar to invaded-range habitats and do they differ according to the geographical direction of invasion? Divers. Distrib. 2015, 21, 312–321. [Google Scholar] [CrossRef]
- Araújo, M.B.; Luoto, M. The importance of biotic interactions for modelling species distributions under climate change. Glob. Ecol. Biogeogr. 2007, 16, 743–753. [Google Scholar] [CrossRef]
- McCarthy, M.A. Bayesian Methods for Ecology; Cambridge University Press: Cambridge, UK, 2007; p. 296. [Google Scholar]
- Kéry, M.; Schaub, M. Bayesian Population Analysis Using WinBUGS: A Hierarchical Perspective; Academic Press: Cambridge, MA, USA, 2012; p. 555. [Google Scholar]
- MacNally, R. Regression and model building in conservation biology, biogeography and ecology: The distinction between and reconciliation of ‘predictive’ and ‘explanatory’ models. Biol. Conserv. 2000, 9, 655–671. [Google Scholar] [CrossRef]
- MacNally, R. Multiple regression and inference in ecology and conservation biology: Further comments on identifying important predictor variables. Biol. Conserv. 2002, 11, 1397–1401. [Google Scholar] [CrossRef]
- Martino, S.; Rue, H. Case studies in Bayesian computation using INLA. In Complex Data Modeling and Computationally Intensive Statistical Methods; Mantovan, P., Secchi, P., Eds.; Springer: Milan, Italy, 2010; pp. 99–114. [Google Scholar]
- Rue, H.; Riebler, A.; Sørbye, S.H.; Illian, J.B.; Simpson, D.P.; Lindgren, F.K. Bayesian computing with INLA: A review. Annu. Rev. Stat. Appl. 2017, 4, 395–421. [Google Scholar] [CrossRef]
- Haran, M. Gaussian random field models for spatial data. In Handbook of Markov Chain Monte Carlo; Brooks, S., Gelman, A., Jones, G., Meng, X.-L., Eds.; CRC Press: Boca Raton, FL, USA, 2011; pp. 449–478. [Google Scholar]
- Johnson, D.S.; London, J.M.; Kuhn, C.E. Bayesian inference for animal space use and other movement metrics. J. Agric. Biol. Environ. Stat. 2011, 16, 357–370. [Google Scholar] [CrossRef]
- Leach, K.; Montgomery, W.I.; Reid, N. Modelling the influence of biotic factors on species distribution patterns. Ecol. Lett. 2016, 337, 96–106. [Google Scholar] [CrossRef]
- Norman, A.J.; Stronen, A.V.; Fuglstad, G.A.; Ruiz-Gonzalez, A.; Kindberg, J.; Street, N.R.; Spong, G. Landscape relatedness: Detecting contemporary fine-scale spatial structure in wild populations. Landsc. Ecol. 2017, 32, 181–194. [Google Scholar] [CrossRef]
- Cameletti, M.; Lindgren, F.; Simpson, D.; Rue, H. Spatio-temporal modeling of particulate matter concentration through the SPDE approach. AStA Adv. Stat. Anal. 2013, 97, 109–131. [Google Scholar] [CrossRef]
- Bessell, P.R.; Matthews, L.; Smith-Palmer, A.; Rotariu, O.; Strachan, N.J.; Forbes, K.J.; Cowden, J.M.; Reid, S.W.; Innocent, G.T. Geographic determinants of reported human Campylobacter infections in Scotland. BMC Public Health 2010, 10, 423. [Google Scholar] [CrossRef] [PubMed]
- Musenge, E.; Vounatsou, P.; Collinson, M.; Tollman, S.; Kahn, K. The contribution of spatial analysis to understanding HIV/TB mortality in children: A structural equation modelling approach. Glob. Health Action 2013, 6, 38–48. [Google Scholar] [CrossRef] [PubMed]
- Morrison, K.T.; Shaddick, G.; Henderson, S.B.; Buckeridge, D.L. A latent process model for forecasting multiple time series in environmental public health surveillance. Stat. Med. 2016, 35, 3085–3100. [Google Scholar] [CrossRef] [PubMed]
- Wade, P.R. Bayesian methods in conservation biology. Conserv. Biol. 2000, 14, 1308–1316. [Google Scholar] [CrossRef]
- Daehler, C.C.; Denslow, J.S.; Ansari, S.; Kuo, H.C. A risk-assessment system for screening out invasive pest plants from Hawaii and other Pacific islands. Conserv. Biol. 2004, 18, 360–368. [Google Scholar] [CrossRef]
- Sitzia, T.; Campagnaro, T.; Kowarik, I.; Trentanovi, G. Using forest management to control invasive alien species: Helping implement the new European regulation on invasive alien species. Biol. Invasions 2016, 18, 1–7. [Google Scholar] [CrossRef]
- Silva, L.; Dias, E.F.; Sardos, J.; Azevedo, E.B.; Schaefer, H.; Moura, M. Towards a more holistic research approach to plant conservation: The case of rare plants on oceanic islands. AoB Plants 2015, 7, plv066. [Google Scholar] [CrossRef] [PubMed]
- Gil, A.; Yu, Q.; Lobo, A.; Lourenço, P.; Silva, L.; Calado, H. Assessing the effectiveness of high resolution satellite imagery for vegetation mapping in small islands protected areas. J. Coast. Res. 2011, 64, 1663–1667. [Google Scholar]
- Gil, A.; Lobo, A.; Abadi, M.; Silva, L.; Calado, H. Mapping invasive woody plants in Azores Protected Areas by using very high-resolution multispectral imagery. Eur. J. Remote Sens. 2013, 46, 289–304. [Google Scholar] [CrossRef]
- Ferreira, M.T.; Cardoso, P.; Borges, P.A.; Gabriel, R.; de Azevedo, E.B.; Reis, F.; Araújo, M.B.; Elias, R.B. Effects of climate change on the distribution of indigenous species in oceanic islands (Azores). Clim. Chang. 2016, 138, 603–615. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).