Abstract
The Delaunay triangulation is the standard choice for building triangulated irregular networks (TINs) to represent terrain surfaces. However, the Delaunay triangulation is based only on the 2D coordinates of the data points, ignoring their elevation. This can affect the quality of the approximating surface. In fact, it has long been recognized that sometimes it may be beneficial to use other, non-Delaunay, criteria that take elevation into account to build TINs. Data-dependent triangulations were introduced decades ago to address this exact issue. However, data-dependent trianguations are rarely used in practice, mostly because the optimization of data-dependent criteria often results in triangulations with many slivers (i.e., thin and elongated triangles), which can cause several types of problems. More recently, in the field of computational geometry, higher order Delaunay triangulations (HODTs) were introduced, trying to tackle both issues at the same time—data-dependent criteria and good triangle shape—by combining data-dependent criteria with a relaxation of the Delaunay criterion. In this paper, we present the first extensive experimental study on the practical use of HODTs, as a tool to build data-dependent TINs. We present experiments with two USGS 30m digital elevation models that show that the use of HODTs can give significant improvements over the Delaunay triangulation for the criteria previously identified as most important for data-dependent triangulations, often with only a minor increase in running times. The triangulations produced have measure values comparable to those obtained with pure data-dependent approaches, without compromising the shape of the triangles, and can be computed much faster.
1. Introduction
Triangulated irregular networks (TINs) provide one of the basic ways to represent surfaces in GIS. A TIN is constructed from a set of sample points, by triangulating the points in 2D. The resulting triangulation gives a continuous interpolating surface that is piecewise linear, in which each face is a triangle. The elevations of the vertices of the triangles are known, since they correspond to sample points, while the elevation for any other point can be computed by linear (or higher degree) interpolation based on the triangle containing it. It is well-known that a set of two dimensional points can be triangulated in many different ways. For surface modeling, the choice of the triangulation can make a big difference: different triangulations can result in entirely different interpolating surfaces. However, in practice, the question of what triangulation to use rarely arises while constructing TINs with GIS: most GIS will simply use the Delaunay triangulation.
The Delaunay triangulation (DT) is defined using the so-called Delaunay criterion: a triangle is Delaunay if the circle defined by its three vertices does not contain any sample point. A triangulation is Delaunay if all its triangles are Delaunay. In general, unless there are four or more points lying on exactly the same circle, the DT is uniquely defined by the point set. There are many good reasons for the DT to be the standard choice for TINs. The main one is that the DT is considered to have well-shaped triangles: triangles that are close to equilateral. This is because, among all possible triangulations of the same set of points, the DT maximizes the minimum angle of all triangles, avoiding slivers (long and skinny triangles) as much as possible. Slivers are a major concern in triangulations for terrain modeling, since they usually result in high interpolation error, can create visual artifacts, and operations with them are prone to roundoff errors, among other problems. Another important advantage of the DT is that it can be computed efficiently, and with relatively simple algorithms.
However, the DT in 2D suffers from one major limitation: it only considers the 2D coordinates of the sample points, i.e., it ignores all elevation data. This means, for instance, that two sets of sample points with the same 2D distribution will end up with exactly the same triangulation, no matter how different the original surfaces were. This can result in an interpolating surface that does not adapt to the real topography, producing a poor approximation.
Realizing that an accurate surface approximation should take into account all data available, Dyn et al. [1] introduced the concept of data-dependent triangulations, defined as triangulations that are optimal with respect to criteria that involve all three coordinates of the data. For example, for surfaces that are rather smooth, Dyn et al. [1] concluded that the criterion of minimizing the angle between the normal vectors of adjacent triangles gives better results than the DT. Later studies [1,2,3,4,5] about data-dependent triangulations arrived at similar conclusions, and proposed other data-dependent criteria to improve over the DT. Despite this, in most GIS software today, the DT is still the only choice to triangulate points. The main reason for this is that, even though data-dependent criteria can improve some aspects of the approximation, they often produce too many slivers [4,6]. Thus, the advantages obtained by data-dependent criteria are outweighed by the negative effects of ill-shaped triangles. It follows that an ideal triangulation method should be able to combine both approaches: aim at optimizing relevant data-dependent criteria, while at the same time trying to avoid slivers [4,6].
The problem of combining good triangle shape with data-dependent criteria was also studied in the field of computational geometry. Gudmundsson et al. [7] proposed higher order Delaunay triangulations (HODTs): a generalization of the Delaunay triangulation that offers well-shaped triangles, but, at the same time, flexibility to optimize extra criteria. HODTs are defined by allowing up to k points inside the circles defined by the triangles, for k a parameter called the order of the triangulation (see Figure 1). Formally, a triangle in a point set S is order-k Delaunay if the circle defined by u, v and w contains at most k points of S. A triangulation of S is order-k Delaunay if every triangle of the triangulation is order-k.
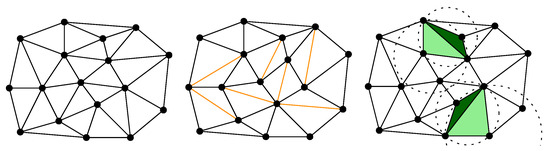
Figure 1.
Three higher order Delaunay triangulations of the same set of points, with three different orders: (left), (center), and (right). Order-1 edges shown in orange, order-1 triangles shown in light green, order-2 triangles shown in dark green.
For , any set of points (in which no four points are cocircular) has only one higher order Delaunay triangulation, equal to the DT. As k is increased, more points inside the circles imply a potential reduction of the triangle shape quality, but also an increase in the number of triangulations that are considered. This last aspect is what makes the optimization of extra criteria possible: for each order , there is potentially a whole family of different triangulations with well-shaped triangles, among which one can choose the one that is best according to some other, data-dependent, criterion.
Some theoretical studies about HODTs have studied the number of HODTs that one can expect, as a function of the number of points n and the order k. However, most of that work has focused mainly on determining, which criteria can be optimized efficiently (i.e., in polynomial time) and which of them are intractable (i.e., NP-hard), either for general values of k, or for the simpler case of . Positive results in this direction can have important practical implications if they come with easy-to-implement methods to optimize the criteria. As already mentioned, for points drawn uniformly at random, the expected number of different triangulations is exponential already for , roughly larger than [8]. This is encouraging from a practical point of view because it implies that there should be many triangulations to choose from to optimize data-dependent criteria. However, having a large number of triangulations available does not guarantee that some of them will be significantly better than the DT with respect to data-dependent criteria. Also of theoretical interest, there has been some preliminary studies about how to enumerate all order-k triangulations, although results so far are limited to very small orders [9].
The more practical aspects of HODTs have not been studied much. The few papers that have studied and implemented optimization algorithms for some concrete criteria for real terrains [10,11,12] have focused on very specific criteria. Namely, the minimization of pits, avoiding interrupted valley lines, and slope fidelity. In all cases, heuristics were presented, and a few experiments with real terrains were shown. However, one important conclusion that can be drawn from these studies is that even though the exact optimization of these criteria is algorithmically difficult, local optimization heuristics can give important improvements for very low orders of k. For instance, experiments for orders with real terrain data by [12] found that, for minimizing the total number of pits, the reductions obtained can be of 15–20% for , and of up to 50% for .
Being a generalization of the DT, in terms of optimizing a data-dependent criterion, the use of HODTs will always give better, or at least not worse, triangulations than the DT—always from a data-dependent point of view. This can be explained by the fact that, by definition, the set of order-k Delaunay triangulations includes all those of order less than k (thus including the Delaunay triangulation, which is a 0-OD triangulation). To this point, it is important to note that this does not imply that there will be always a k-OD triangulation with order greater than zero that is better than the DT but, since there are more options, there may be the possibility of this happening. Therefore, the key question with HODTs could be stated as whether HODTs are worth the effort. Firstly, optimization software for HODTs is not readily available, thus using HODTs instead of the DT implies, at least, a certain implementation overhead. Secondly, optimizing over all HODTs of a certain order, even , will necessarily imply a longer running time than simply computing the DT.
Hence, several important practical questions arise: (i) How much improvement does it give over the Delaunay triangulation? (ii) Do higher order Delaunay triangulations actually preserve the good shape of the triangles, as expected in theory? (iii) How complicated is it to implement some type of optimization over HODTs? In this paper, we try to answer these questions.
There is very little previous work devoted to the more practical aspects of HODTs. Only a few papers have studied the optimization of concrete data-dependent criteria for real terrains [10,11,12]. They focused on very specific criteria related to the minimization of pits, avoiding broken valley lines, and slope fidelity. Ad hoc heuristics were presented for each of them, and a few experiments with real terrains are shown. The results suggest that simple heuristics for optimizing those criteria for low orders (1.8) can give a significant improvement over the Delaunay triangulation.
Contributions. We present an extensive study on the practical use of HODTs, as a way to build data-dependent triangulations. Our main goal is to evaluate whether the improvements in the data-dependent criteria that can be obtained by using HODTs, compared to the Delaunay triangulation, are significant enough as to justify implementing a more complex triangulation algorithm. Our secondary goal is to describe some of the implementation aspects of HODTs, never considered until now.
We selected three data-dependent criteria that have been claimed in the literature to give the most important improvements over the DT (angle between normals, jump normals derivatives, refined angle between normals). We implemented and tested two variants of an optimization algorithm based on the well-known Lawson’s Optimization method (LOP) [13]. This method was chosen due its simplicity and generality: it is easy to implement, and can be used to optimize any criterion. In addition, we also implemented and tested the exact algorithm by Van Kreveld et al. [14] for first order Delaunay triangulations. In fact, we implemented two variants of this method as well: the algorithm as proposed in [14], and a simple variant that improves the shape of the resulting triangulation even further, by prioritizing Delaunay triangles. This is the first time that the algorithm by Van Kreveld et al. [14] is implemented and evaluated experimentally.
We present experiments with real terrains for each criterion, measuring the improvements obtained by optimizing over HODTs. Data used was obtained from the two USGS terrains used in [4], the most extensive previous study on data-dependent triangulations on real terrains. Our experiments cover different values of Delaunay order k, different optimization algorithms, and evaluate the value obtained for each criterion, together with several other parameters of interest. The decision to use natural terrains, as opposed to synthetic terrains, as done in early related work [1,3,15], is motivated by the fact that it has been questioned whether synthetic terrains are suitable to evaluate data-dependent triangulations [4,6]. Thus, it becomes particularly interesting to evaluate whether improvements observed for synthetic terrains for data-dependent triangulations also show up with real terrains using HODTs.
Our experiments shed some new light on the efficacy of three data-dependent criteria that, despite having been proposed a long time ago, had only been tested on real terrains a few times. Our results also show that a simple optimization heuristic for HODTs, similar to LOP, can give substantial improvements over the data-dependent criteria studied, already for very low orders (thus with triangles close to Delaunay). Therefore, we conclude that HODTs can be considered a practical tool to implement data-dependent triangulations, and that the benefits obtained are worth the extra overhead of implementing them, if improving on the data-dependent criterion is important.
2. Related Work
In this section, we review the relevant related work in more detail. We first review some of the most important data-dependent criteria proposed for surface interpolation, and later discuss the existing experimental studies on them.
2.1. Main Data-Dependent Criteria
Many criteria consist of a cost function associated with each edge e of the triangulation. Very often, is a function of the neighborhood of the edge (for instance, that is the case for the three measures studied in this paper). The neighborhood of an edge in a triangulation is composed of the two triangles sharing e (except for convex hull edges, which only belong to one) and the four vertices involved (see Figure 2). The value of for the whole triangulation is defined as the minimum of the values over all edges in the triangulation. Each of the data-dependent criteria below varies on how exactly the value of an edge is defined. The criteria that have been shown to yield better results in the literature on data-dependent triangulations are mostly those related to minimizing elevation changes between adjacent triangles [1,2,3,4,5,6]. For that reason, many of the criteria discussed below are related to smoothness. They are designed to prefer triangulations with coplanar triangles (smooth surfaces), and they attain their minimum when the triangles of the quadrilateral are coplanar, and increase as they become less coplanar. The difference between them is the way to measure to what extent two triangles are coplanar. It is worth noting that the use of criteria that favor certain surface characteristics, for instance, smoothness or roughness, may result in a specific error biases, such as being prone to surfaces that are under- or over-fitted. The list that follows is not exhaustive, but contains the criteria most relevant for this work.
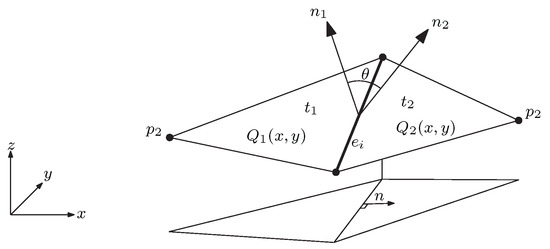
Figure 2.
The geometric information of the of that is often used to define the cost functions. The edge is the diagonal of the convex quadrilateral defined by two triangles and . and are the planes defined by and , with normal vectors and . The vector n is a 2D unit vector orthogonal to the projection of in the plane . Based on a figure from [16].
Angle Between Normals (ABN) [1]. is given by the angle between the normal vectors of the two planes spanned by the triangles adjacent to an edge e. This function measures the local smoothness of e in , thus minimizing should lead to a surface exhibiting little changes when passing through the edges of the triangulation. One could also maximize or any of the other measures in this section, if the goal was to produce a rugged surface. However, minimization is the setting for which best results have been reported.
Jump Normals Derivatives (JND) [1]. is given by the difference of the derivatives of the two planes around e measured in a direction orthogonal to e’s projection (see vector n in Figure 2).
With the same goal of producing smooth surfaces, Dyn et al. [1] also proposed criteria Deviations from Linear Polynomials (DLP) and Distances From Planes (DFP), which measure the distance between the plane associated with a triangle and the other point of the quadrilateral.
Refined Angle Between Normals (WABN) [5]. A variation of ABN that takes into account the length of the edge e, given by . Its goal is to penalize longer edges, in order to reduce the number of slivers.
Most data-dependent criteria proposed are functions of an edge, or equivalently, a pair of adjacent triangles. However, this does not need to be the case. The following is an example of a data-dependent criterion based on the triangles incident to a vertex.
Piecewise Linear analog of Curvature (PLC) [3]. It is a generalization of ABN to vertices instead of edges, given by the sum of the angles between normals of neighboring triangles around a given vertex u.
Finally, we present a global data-dependent criterion that is not based on the the local neighborhood of edges.
Error-based criteria (ERR). Given that often the goal of using a data-dependent criterion is reducing the approximation error between the TIN and the original surface, it is reasonable to try to use the error itself to guide the triangulation process. Error-based criteria have been considered several times [1,4], essentially by defining the measure of the current triangulation as the total error between the current triangulation and a set of fixed ground truth points.
2.2. Comparisons of Data-Dependent Criteria
Despite the relatively large number of data-dependent criteria proposed, there have been few studies comparing them to each other. The seminal paper by Dyn et al. [1] supported the proposed data-dependent criteria with a set of experiments for sets of 100 data points distributed uniformly at random in a unit square, and a second set with 33 data points with uneven distribution. The elevations used came from nine different mathematical functions that intended to produce surfaces that resembled terrains. Data-dependent criteria were optimized with Lawson’s Optimization method (LOP, explained in Section 3.2), and compared against the Delaunay triangulation, using the approximation error as comparison measure. Their results showed that, while some of the functions (i.e., terrains) did not benefit significantly from data-dependent triangulations, some of them showed important improvements, especially in the case of surfaces with a clear preferred direction. The data-dependent criteria yielding the best results were those aiming at smoothness, with ABN and JND being best most of the times. The success of data-dependent triangulations for surfaces with a preferred direction was also confirmed by Rippa [15]. He concluded that the interpolation functions (i.e., the triangulation) must be related to the (elevation) data, and that triangles should be long in directions where the magnitude of the second directional derivative of the surface is small, and thin in directions where this magnitude is large. A later study by Brown [3], based also on mathematically-generated surfaces, confirmed that ABN and PLC yielded significantly better results than Delaunay for surfaces with a preferred direction. Years later, Weisz et al. [5], when proposing WABN, repeated part of the experiments in [1], comparing WABN with ABN and Delaunay, and concluded that, in all but one case, the data-dependent criteria produced better approximations.
None of the previously mentioned studies used real terrain data. In the context of terrain approximation algorithms, Garland and Heckbert [6] evaluated several data-dependent criteria on one real terrain, from which they concluded that “it seems that the surfaces for which data-dependent triangulation excels are statistically uncommon among natural terrains”. Furthermore, they conjectured that, on natural terrains, data-dependent triangulation should give results that are only marginally better than the Delaunay triangulation. One of the problems identified was that data-dependent criteria could result in the creation of very thin slivers.
The most complete study up to date was the one carried out in [4]. Since the structure of our experiments follows closely that of those of Wang et al., a more detailed description is in order. Wang et al. [4] presented a comparison of several triangulation methods, including Delaunay and data-dependent criteria, using two USGS digital elevation models and LOP as optimization algorithm. However, the setting was slightly different to ours, since Wang et al. mostly considered methods that integrate the point selection (i.e., choosing which points from the original raster DEM will be triangulated) with the triangulation itself.
In this paper, we assume that the points to be triangulated are given, hence we are interested only in the triangulation phase. Thus, results obtained by Wang et al. (in the same way of our results) cannot be directly extrapolated to methods that only triangulate, but it is still worth discussing some of their findings.
The triangulation criteria considered by Wang et al. that are most relevant in our context are: (i) Delaunay after point selection, (ii) Delaunay combined with point selection, (iii) minimizing ABN starting from the result of (ii), (iv) maximizing ABN starting from the result of (ii), (v) min ERR, (vi) hybrid. The hybrid method was proposed by Wang et al., motivated by observing that “the major drawback of the data-dependent triangulation is that it contains too many slivers”. The method intended to combine the DT with data-dependent triangulations by alternating the data-dependent optimization criterion from (v) with the Delaunay criterion, depending on the aspect ratio of the triangles.
The experiments in [4] tested each method for two terrains (and three different sample sizes). The accuracy of the approximation was measured using a ground truth set of 900 points taken from the DEM. Wang et al. also studied the steepness and aspect ratio of the triangles produced. The main conclusion from the experiments was that method (ii), which combines the point selection with the Delaunay criterion, outperforms all others, followed closely by method (iii), min ABN. However, Wang et al. point out that, since the input to min ABN is the output from (ii), the ABN criterion is actually making the surface approximation worse. However, the error increase is relatively small. This is in clear contrast to (iv), which also starts from the output of (ii), but ranks as one of the worst methods. The standard Delaunay method, (i), ranks 3rd or 4th in all experiments, but at a much larger distance from the second best method. Finally, method (v) that directly aimed at minimizing the approximation error, produced very poor results, mostly due to the presence of many slivers and steep triangles. The authors concluded that pure data-dependent triangulations do not perform well on terrain surfaces, mainly due to the sliver problem. Their hybrid method produced better result than pure data-dependent criteria, but worse than (ii).
In summary, previous work on real terrains suggests that the appearance of slivers outweighs the possible positive results that can be obtained by data-dependent triangulations. For this reason, it seems particularly interesting to determine whether HODTs can provide a practical way to control slivers, while, at the same time, leaving enough room to optimize data-dependent criteria.
3. Methodology
In this section, we describe in more detail the data, experimental setup, and optimization methods used.
3.1. Data
In contrast to most previous experimental work with data-dependent triangulations, which used elevation data generated by mathematical functions, we use real terrain data. Our experiments are based on the two USGS 30 m DEMs considered by Wang et al. [4] (see Figure 3). The decision to reuse these terrains was twofold. Firstly, it facilitates the comparison with the work of Wang et al. [4], which albeit different in spirit, is the closest previous work to this research. Secondly, the two terrains are also very appropriate in our setting because they present two rather contrasting topographies: one rather rough, and the other one rather flat:

Figure 3.
Terrains used in the experiments. (a) Kinzel Springs, Tennessee: 35.75 N, 35.625 S, −83.875 W, −83.75 E; (b) Moorehead SE, Iowa: 41.875 N, 41.75 S, −95.875 W, −95.75 E.
- Kinzel Springs, Tennessee (KS): this area has a very rough topography. It has been strongly influenced by tectonic movement and fluvial processes with rivers cutting deeply into valleys. Mountains mostly extend from the southwest corner to the northeast corner. Vertical relief of about 850 m. The DEM has dimensions 390 × 473.
- Moorehead South East (SE), Iowa (MH): this area is flatter and smoother than the previous one because it is a region that was shaped by erosion caused by melting glaciers. Vertical relief of about 100 m. The DEM has dimensions 361 × 474.In a preliminary version of this work [17], we also considered two additional terrains with topographic characteristics in-between those of KS and MH, but the differences in the results obtained did not justify the inclusion in this paper.
- Point selection method. For each DEM, we generated two sets of sample points to be the input to the triangulation algorithms. It is well known that the choice of the sample points has a strong influence on the TIN approximation quality. We used the VIP (very important point) method as implemented in ArcGIS 10 raster to multipoint tool. VIP is a well-known method to generate sample points from a raster terrain that intends to sample the most relevant topographic features (mainly local peaks and pits). In addition, following [4], we generated for each terrain a set of 900 random points to be used as ground truth set, in order to evaluate the approximation error of the generated TINs.
- Compensation of boundary effect. The Delaunay triangles that are close to the boundary of the point sample are often long and skinny. The reason why these slivers can also be Delaunay is that their Delaunay circles face the exterior face of the triangulation, thus are empty of sample points. However, this creates a possible problem for HODT optimization because removing such triangles by flips while keeping the Delaunay order low is sometimes not possible, since all the flips necessary produce high-order intermediate triangles. In a preliminary round of experiments, we noticed that often the maximum values of the criteria were achieved in such boundary slivers. This forced the optimization to end very quickly and with poor results. Since this is due to an artifact caused by the terrain boundary, for the purposes of order computation, data-dependent, and quality measures, we ignored a buffer around the terrain boundary containing 5% of the sample points.
Other Aspects Measured
In addition to the value of the specific criterion (ABN, JND, WABN) measured at each run, we also analyzed the following aspects: running time, total number of flips done, approximation error, and aspect ratio.
The approximation error of each TIN was defined based on the ground truth points as the root mean square error (RMSE) between the TIN and the original DEM, as in [4]. More precisely, it is defined as , where are the coordinates of the i ground truth point, is the elevation of the TIN at coordinate , and m is the number of ground truth points. Following [4], in our tests we also computed the error using the mean absolute error (MAE), and metrics, but given that no significant differences were observed, we only report on the RMSE values here.
The average aspect ratio of the resulting TIN triangles was computed as a way to measure the amount of slivers in a triangulation, similarly to [4]. The aspect ratio of a triangle △ was defined as , where is the length of the longest edge e of △ and is its height (the perpendicular distance from e to the opposite vertex).
3.2. Implementation Considerations
The implementation was done in C++ with the help of the Computational Geometry Algorithms Library (http://www.cgal.org). CGAL is an open-source library that provides efficient and robust geometric algorithms for dozens of application areas. In our case, we made use of CGAL’s implementation of Delaunay triangulations, which was extended to be able to handle HODTs. The extensions needed to allow for higher order triangulations and to implement LOP for data-dependent criteria were straightforward.
Next, we described the optimization methods used.
Lawson’s optimization method. Data-dependent triangulations require optimizing a criterion over the space of all possible triangulations of a point set. Since finding global optima is in general an intractable problem, in practice, local optimization is used. The most widely used method to (locally) optimize triangulations is Lawson’s optimization procedure (LOP) [13]. The main advantage of LOP is its simplicity: it only requires a few lines of code, assuming the triangulations are stored in a data structure providing basic topological information. The method works by identifying edges whose flip (i.e., removing the edge and inserting the other diagonal of the quadrilateral formed) improves the triangulation, and flipping them, until no such edge remains. Next, we present the method more formally. Let e be an edge of a triangulation of a point set . We denote the cost of e (i.e., according to some data-dependent criterion) in by , and the cost of by . For all criteria considered in this paper, . If e is an interior edge of , it is the diagonal of a quadrilateral formed by the two triangles that share e. If such a quadrilateral is convex, then e can be exchanged by the other diagonal of the quadrilateral. This operation is called a flip, and we say that e is flippable. Let be the triangulation obtained after flipping e in .
An edge e of is called locally optimal if: (i) e is not flippable, or (ii) e is flippable and flipping e does not improve the triangulation, i.e., . Analogously, a triangulation is locally optimal if all its edges are locally optimal. The successive application of the edge-flip method to a triangulation converges, in a finite number of steps, to a locally optimal triangulation. See Algorithm 1.
Note that the result of LOP is a locally optimal triangulation, which can be arbitrarily far from a global optimum. There have been only a few attempts to produce data-dependent triangulations using other optimization methods, which usually try to get closer to a global optimum. Most of them used simulated annealing (e.g., [18,19]) in the context of image reconstruction, but other meta-heuristics like genetic algorithms have been used as well (see, e.g., [20]).
| Algorithm 1: Lawson’s optimization method (LOP) |
 |
Order-k Delaunay LOP (k-OD LOP). The modifications needed for LOP to handle HODTs are simple. Following the terminology in Algorithm 1, we can define a locally k-OD optimal triangulation as follows. We say that an edge e of is locally k-OD optimal if: (i) e is not flippable, or (ii) e is flippable and flipping e does not improve the triangulation, i.e., , or produces a triangle with order larger than k. Analogously, we say that the triangulation is locally k-OD optimal if all of its edges are locally k-OD optimal. See Algorithm 2.
In practice, only two modifications are important. The first one is making sure that when an edge is considered to be flipped, the two new triangles that would be produced have order k. This extra check results in a time overhead over the standard LOP. In our implementation, the priority was ease of code, thus the order of a triangle was computed by simply checking each point for containment in the corresponding circle. Note, however, that the linear-time overhead incurred can be substantially reduced if more advanced techniques [7] are used.
| Algorithm 2: Lawson’s optimization method for HODTs (k-OD LOP) |
 |
The second modification is how to choose the starting triangulation . A first natural option is to always start from the Delaunay triangulations, which is order-k for any k. In our experiments, since we test many consecutive values for k, we also considered a second alternative: starting from the result of the previous iteration. This gives rise to two variants of the k-OD LOP method:
- Standard k-OD LOP (LOP-0): is the Delaunay triangulation.
- Incremental k-OD LOP (LOP-INC): is the result of the previous run for maximum order (or the largest available maximum order if k = inf).
Exact algorithm for . This work also includes an implementation of the exact algorithm presented in [14] for first order Delaunay Triangulations. The method works for MinMax criteria that are functions of pairs of adjacent triangles (such as the three measures studied in this paper). The algorithm is based on identifying all Delaunay edges that must be present in all order-1 Delaunay triangulations. These form a subdivision of the convex hull of the set of points into triangles and quadrilaterals, such that any order-1 Delaunay triangulation can be produced by choosing one of the two diagonals for each quadrilateral. In [14], it was shown that exact solutions for measures like ABN, JND, and WABN (that are local to pairs of adjacent triangles) can be found by solving a series of instances of the boolean satisfiability problem (2-SAT), which can be solved in time proportional to the number of quadrilaterals. In our implementation, we used the http://minisat.se/ to solve the 2-SAT instances.
As previously mentioned, we present two implementations of the exact algorithm:
- Exact algorithm from [14] (1-exact-KLS): Implementation of the exact algorithm for first order Delaunay Triangulations as presented in [14].
- Exact algorithm prioritizing DT edges (1-exact-DT): Implementation of the exact algorithm for first order Delaunay Triangulations from [14] modified to prioritize Delaunay edges. In particular, the algorithm proceeds as in 1-exact-KLS until obtaining the final solution given by the last 2-SAT instance solved. After that, we find all flipped edges with respect to the Delaunay triangulation and revert all the flips that do not worsen the max value of the optimal triangulation. In this way, all flips that are not necessary to optimize the value are avoided, keeping as many Delaunay edges as possible.
3.3. Research Design
The implemented algorithms were tested over two point samples of each terrain, with 1% and 3% of the original data points. The full set of variants considered is the following:
- Point set size n. For each DEM, we produced two sample points using ArcGIS 10 raster to multipoint tool, containing 1% and 3% of the original data points, respectively (with roughly 1700 and 5100 points, resp.; these sizes are comparable to two of the ones used in [4]).
- Maximum order k. A total of 23 different values for the maximum order k were tested, in three groups. (i) Fixed k: the order the triangulation is at most a fixed value k, for . The optimization method consisted on two variants of k-OD LOP (presented in Section 3.2). (ii) : the order of the triangulation is not constrained. The optimization method is LOP. That is, a flip is performed every time the measure improves, until the triangulation does not change anymore. This comes down to the pure data-dependent triangulation method originally proposed by Dyn et al. [1]. (iii) , exact algorithm: implementation of two variants of the exact algorithm in [14], described in Section 3.2.
- Criteria analysis and selection. Based on the study of previous literature on different criteria (see Section 2.1), we selected three data-dependent criteria to be tested: ABN, JND, and WABN. The first two are the most mentioned data-dependent criteria in the context of terrain interpolation (e.g., see [1,2,3,4,5,6]), while WABN is a simple variation of ABN that addresses explicitly the presence of slivers, thus it seemed appropriate to include it in this comparison.
In summary, the experiments tested two terrains, each with two sets of points, for 23 different values of maximum order k (including the two variants of the exact algorithm), three data-dependent criteria , and the two variants of the LOP method. In total, this generated different TINs.
4. Results
The amount of data generated makes it hard to present all results in tabular form. Nevertheless, as a sample, we present in Table 1 the results obtained for ABN and the larger terrain sizes. It will be more convenient to analyze the results through the graphs presented in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. In the following, we discuss briefly the results obtained for the different aspects evaluated. In general, we do not observe a clear difference in behavior between the smaller and larger terrain sizes (i.e., 1% and 3%).

Table 1.
Minimization of maximum ABN value for Kinzel Springs and Moorehead SE, over 3% sample point set using LOP—0, 1-exact—KLS and 1-exact-DT.
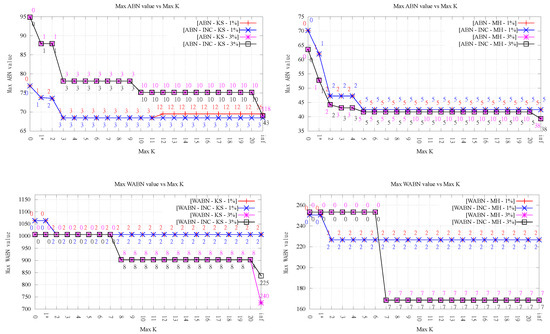
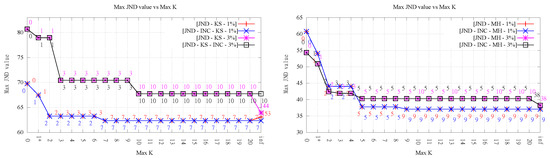
Figure 4.
Minimization of maximum value for Kinzel Springs (left) and Moorehead SE (right) as the maximum order k increases. In each column, from top to bottom: ABN, WABN and JND. Numbers indicate the final order. * Maximum value for 1-exact-KLS, 1-exact-DT, LOP-0 and LOP-INC coincide. Therefore, and w.l.o.g., such value is referred as .
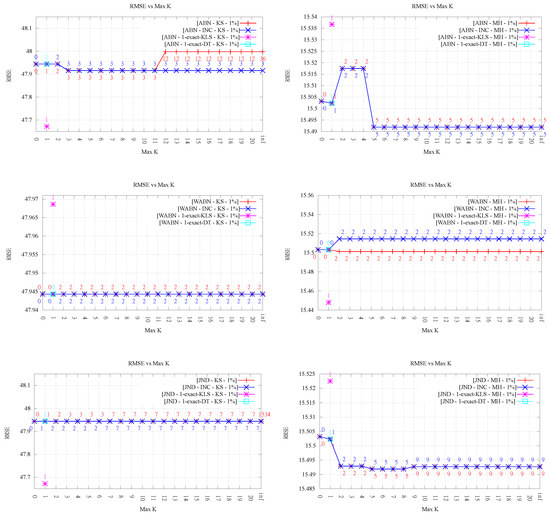
Figure 5.
RMSE evaluation for Kinzel Springs (left) and Moorehead SE (right) over 1% sample point set as the maximum order k increases. In each column, from top to bottom: ABN, WABN and JND. Numbers indicate the final order.

Figure 6.
RMSE evaluation for Kinzel Springs (left) and Moorehead SE (right) over 3% sample point set as the maximum order k increases. In each column, from top to bottom: ABN, WABN and JND. Numbers indicate the final order.
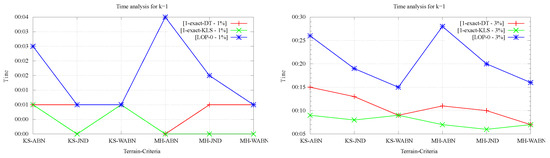
Figure 7.
Running times of 1-exact-DT, 1-exact-KLS and LOP-0 for Kinzel Springs and Moorehead SE for 1% (left) and 3% (right) sample sets with , for ABN, JND and WABN.
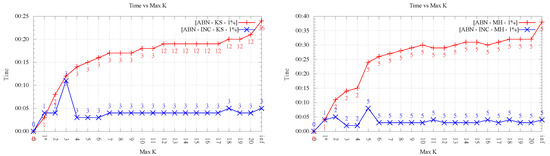
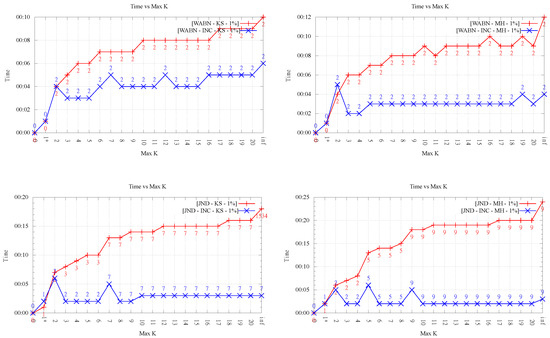
Figure 8.
Running times for Kinzel Springs (left) and Moorehead SE (right) for 1% sample set size as the maximum order k increases, for ABN, WABN and JND. * Analysis for the exact algorithms is presented in Section 4.4; thus, results for those algorithms are not exhibited here.
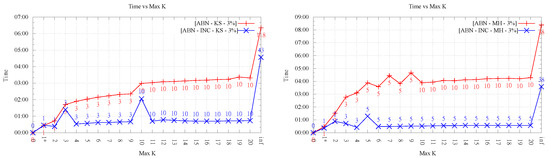
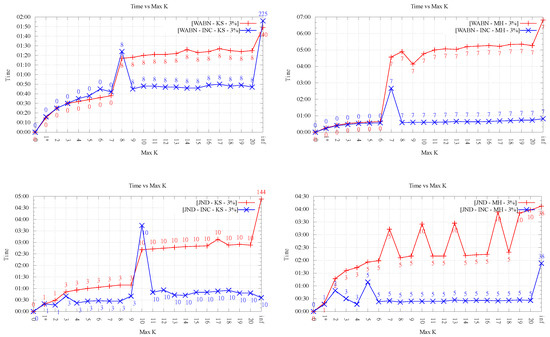
Figure 9.
Running times for Kinzel Springs (left) and Moorehead SE (right) for 3% sample set size as the maximum order k increases, for ABN, WABN and JND. * Analysis for the exact algorithms is presented in Section 4.4; thus, results for those algorithms are not exhibited here.
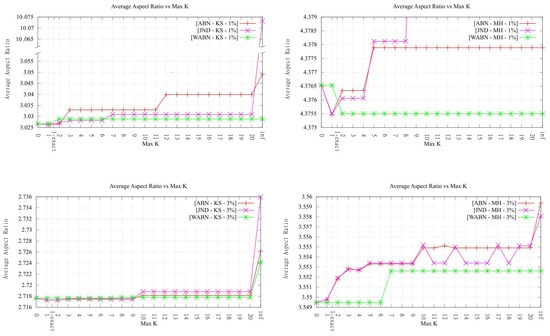
Figure 10.
Average aspect ratio comparison between all criteria for Kinzel Springs (left) and Moorehead SE (right) as the maximum order k increases (excluding exact algorithms). In each column, from top to bottom: 1% and 3%.
4.1. Maximum Value
Figure 4 presents the maximum value obtained for each measure, for the different orders k, both terrain sizes, both LOP variants, and both exact implementations.
It can be observed that, in general, increasing the maximum order allows for improving all three measures significantly. For both LOP variants, the reductions obtained with respect to the Delaunay triangulation for orders were between 5.35% and 39.50%, with an average of 12.12% for Kinzel Springs and 30.27% for Moorehead SE.
Another important observation from Figure 4 is that, in the majority of cases, significant improvements were obtained for very low orders. Even more, in many cases, the result obtained for low orders is as good as the one for infinite order, and, when this is not the case, often the difference was small.
For the LOP-0 implementation, it can be observed that, in most cases, increasing the maximum order k results in a measure value as good or better than for the previous order. However, we observed in two settings (KS-ABN and KS-JND) that the max value became slightly worse after increasing k. Since this may appear counterintuitive, it is worth explaining the phenomenon. This is basically due to the fact that executions of LOP-0 for consecutive values of k are totally independent. That is, they always start from the Delaunay triangulation. This means that the flip decisions taken during the execution for order k need not be a subset nor related to those taken for , explaining that the end result can be worse than the previous one. In fact, for the same reason it can also occur that the final order of the resulting HODTs for order k is lower than that for order (always respecting the maximum order). This behavior is in contrast to that of LOP-INC where, by construction, the value decreases monotonically with k. However, it must be noted that this fact does not necessarily imply that LOP-INC performs always better than LOP-0 in terms of minimization of the maximum value (see, for instance, the case of WABN for Kinzel Springs over 3% sample with in Figure 4). What may happen for LOP-INC with respect to LOP-0 is that a flip used to produce the starting triangulation for order k prohibits a better flip in the construction of the k-ODT, resulting in a maximum value higher than the one obtained by performing such restricted flip. Thus, the resulting k-ODT will always have a measure value less or equal than the one in -ODT but not necessarily better than the one measured in the k-ODT obtained by LOP-0.
4.2. Quality of Approximation
Despite the clear improvement in the measure values shown in the previous section, the trend in the quality of approximation of the TINs, as measured by the RMSE based on the ground truth points, is less clear. This is rather relevant because this is arguably the most important metric motivating the use of data-dependent triangulations.
Analyzing the results for LOP-0 (a total of 12 evaluations, shown in Figure 5 and Figure 6), for low orders (), and ignoring the particular case of k = 1-exact (discussed in Section 4.4), we can see that the RMSE stays roughly constant or decreases in nine cases (four and five, respectively), while it worsens in the other three cases. In all cases, the variation is rather small, something understandable given that the changes in the triangulations for affect relatively few triangles, and thus have a limited impact on the overall RMSE. The fact that in some cases the RMSE gets worse is interesting, given that, in early work on data-dependent triangulations, it was argued that one of the reasons to optimize angle-related measures like ABN was to improve the approximation quality. It is also interesting to note that the results do not vary much for ; on the contrary, they are slightly worse (RMSE stays equal, decreases or increases in three, four, and five cases, respectively).
Overall, we can conclude that the approximation error in most cases does not get worse or even improves slightly, but not always, and that constraining the order of the triangulations has a positive effect, in comparison with the pure data-dependent approach (i.e., the case ).
The conclusions with respect to the overall behavior of RMSE for LOP-INC are the same as that for LOP-0. The differences in the final RMSE values observed between both algorithms are inherent to the fact that both methods are heuristic. It is important to note that even though the final order of the triangulation may be the same, this does not necessarily imply that the flips performed are the same (in other words, they do not produce necessarily the same triangulations). For that reason, there are cases where we observe different RMSE values for the same value of k. In some cases, the error is better for LOP-INC (for instance, in KS-ABN 3%), while, in some other runs, LOP-0 produced smaller error (for instance, in MH-ABN 1%).
4.3. Presence of Slivers in HODTs
To evaluate if the increase in order resulted in an important increase in the presence of slivers, we measured the average aspect ratio of the triangles in each final triangulation, as previously done in [4]. From the results, it can be observed that, except for the exact algorithm from [14] (1-exact-KLS) analyzed in Section 4.4, the values remain more or less low (i.e., similar to the ones measured in the original Delaunay triangulation) and lower for lower k order (maximum and final) values. This indicates that HODTs do not change significantly the shape of the triangles, with respect to the Delaunay triangulation. Most tests for (except for one, Kinzel Springs JND) also resulted in only a mild increase in aspect ratios. This behavior, which is likely to be rather terrain-dependent, is probably explained in this case by the fact that the average aspect ratio is hard to change significantly by only a few flips.
4.4. Comparison between Heuristic and Exact Algorithm for k = 1
Regarding the performance of the exact algorithm for from [14], there are two aspects worth mentioning.
Firstly, the maximum values obtained by both variants of the exact algorithm for were in all cases equal to the ones obtained by k-OD LOP (see Figure 4). In other words, for , our modified LOP procedures obtained the optimal value in all cases. This is particularly interesting given that all but one case already presented improvements for .
Secondly, it can be observed that, for the 1-exact-DT, the average aspect ratio remains equals to the one measured in the heuristic. This is explained by the fact that by prioritizing Delaunay edges (only performing a flip when it actually improves the target value) only a few changes are done to the original DT in order to obtain the best 1-ODT. In Table 2, it can be observed the differences between the amount of flips performed by 1-exact implementation from [14] (1-exact-KLS) and the variant (1-exact-DT). Note that the number of flips performed by 1-exact-KLS lead to a higher average aspect ratio than the one observed for 1-exact-DT.

Table 2.
Number of flips performed for Kinzel Springs and Moorehead SE, over 1% and 3% sample point sets 1-exact-KLS and 1-exact-DT.
Thus, the average aspect ratios were significantly worse for the exact algorithm from [14] (1-exact-KLS), and something similar holds for the RMSE metric in several cases (see Figure 5 and Figure 6). As we mentioned before, this is due to the fact that the exact algorithm 1-exact-KLS makes no attempt to preserve the original Delaunay edges, since its only concern is minimizing the maximum value. On the contrary, in k-OD LOP, the starting triangulation is Delaunay, thus most edges in the final triangulation are Delaunay as well. This results in better overall triangular shape, even though the worst triangles are the same. On the other hand, the variant 1-exact-DT, did not affect the maximum measure value and exhibited low average aspect ratios (see Table 2). It is worth noting that, in every case, the 1-ODT obtained by 1-exact-DT is the same that the one obtained by the heuristic for .
On the positive side, as shown in Figure 7, the running times of the exact algorithms were in every case lower than that of 1-OD LOP being that difference more significant for the larger data sets. It’s worth noting that, by construction, running time measurements for LOP-INC and LOP-0 for coincide thus, only the data for LOP-0 is presented in Figure 7. Regarding the comparison of running times between both 1-exact variants, it can be observed that for 1-exact-DT time measurements are always worse or equal than those observed for 1-exact-KLS. This is explained by the overhead that exists in the 1-exact-DT implementation when verifying whether or not it is worth doing the flip suggested by the result of the 2-SAT solver.
4.5. Running Time for
In this section, we analyze the running time as the order k increases. As mentioned before, our implementation was not optimized, thus it is not the actual time values but the overall behavior that is interesting to observe.
Figure 8 and Figure 9 show an important growing trend of runtime as a function of k. Even though the growing trend is very clear, the absence of monotonicity in the plot of LOP-0 is explained, again, by the fact that different orders behave independently and can result in very different flips. It is clear from these experiments that, as k increases, the search space of order-k Delaunay triangulations increases considerably, involving higher running times.
Likewise, it is interesting to note that in all cases, order-k (for ) optimization was faster than . This shows that restricting the order gives always faster methods in comparison with the unconstrained LOP method (for both variants), as proposed in the original data-dependent literature.
It can also be observed a clear difference in behavior between the two LOP variants; while, for LOP-0, a growing trend of time is seen as order k increases, LOP-INC exhibits generally much lower values except for some peaks where the flips changing the final order of triangulation are performed. Thus, as expected, the running times registered by the executions of LOP-INC are considerably lower for LOP-0. Indeed, LOP-INC was faster in almost every run, with speed-ups of a factor between 2 and 9 for . This is explained by the fact that, for LOP-INC, the starting point of the k-ODT construction is the -ODT, resulting in less flips per execution and consequently less running time.
4.6. Comparison between ABN, WABN and JND
Although it is not the aim of this paper to determine which data-dependent measure is most suitable, a couple of remarks about them are in order. (In the following analysis, we only refer to the results obtained with of k-OD LOP-0.) Perhaps the most interesting aspect to evaluate, as a way to compare the quality of the approximations obtained by each criterion, is the behavior between ABN, WABN and JND with respect to the error metrics. Here, we observe that in every case the behavior of WABN was different, presenting in general higher RMSE values. Regarding JND and ABN, their behavior was similar for Kinzel Springs and different for Moorehead SE. Another aspect one can observe is the average aspect ratio of the resulting triangles. In this respect, when comparing ABN and WABN, Figure 10 shows that in the majority of cases WABN produced a lower average aspect ratio than ABN, as expected.
This behaviour was observed in both variants of the LOP method.
5. Conclusions
This work studied the practical use of higher order Delaunay triangulations as a tool to implement data-dependent triangulations. We consider that the results obtained answer, to a large extent, the questions posed at the introduction, suggesting that HODTs are indeed suitable for data-dependent triangulations.
The most important question was whether HODTs allowed for obtaining a significant improvement in the value of data-dependent criteria. In our experiments, it was shown that, even for low orders, improvements can be significant, even when restricted to very small orders like . In addition, restricting to such small orders has the advantage that the running time overhead, in comparison with using the Delaunay triangulation, is kept under control. In relation to the standard LOP (i.e., )—the most standard way to implement data-dependent triangulations—our experiments suggest that LOP does not give any important benefit over k-OD LOP for low orders. On the contrary, LOP takes longer to run (at least 50% longer for the 1% data set and 35% longer for the 3% data set, in comparison with k-OD LOP for ), and may produce more slivers and higher approximation error.
The average aspect ratio does not seem to get significantly worse for the orders tested. In fact, for very small orders (e.g., ), there is no discernible difference. This is in contrast with the case , for which, as expected, the average aspect ratio got worse in most cases (although the difference in the average was, in general, rather small).
The implementation of the exact method for revealed several interesting aspects. Especially noteworthy is the fact that k-OD LOP always matched the optimal solution. This is encouraging, and shows that even though the theory can suggest that optimizing over may be intractable, in practice simple methods like k-OD LOP may give very acceptable solutions. On the other hand, 1-exact-KLS and 1-exact-DT ran in the majority of cases faster, although for practical use it seems better to use 1-exact-DT, which gives priority to Delaunay edges, due to the notably better RMSE values obtained.
Of the two variants of LOP implemented, LOP-INC showed in general advantages over LOP-0:
- a lower final order of triangulations,
- fewer flips,
- monotonically decreasing values,
- and—probably the most important difference—considerably faster.
Thus, from a practical point of view, it seems that, for an exploratory use of HODTs where many values of k want to be tested, LOP-INC is highly preferable.
Regarding the practicality of implementing HODTs, the k-OD LOP method resulted almost as simple as LOP-0, requiring only minimal additions to be able to compute the order of a triangle. The exact algorithm implementation was a bit more complex and required the use of an external library for SAT solving, but still can be considered a practical method, especially given its speed and that for almost all tests resulted in improvements.
Finally, in [1,2,3,4,5,6], it was argued that the improvement of methods based on minimization of curvature often gave improvements in the RMSE. However, in our experiments, this is not entirely clear. The RMSE results obtained for the three data-dependent measures show only a mild improvement in approximation error. Our experiments achieve significant improvements in the maximum ABN, but not always accompanied by improvements in the RMSE. Even though it was never the goal of this work to question the different data-dependent criteria, it does raise the question of whether these data-dependent criteria can improve significantly the approximation error for real terrains, or whether other criteria should be explored further. In any case, it seems that HODTs will be a useful tool to optimize data-dependent criteria in general.
We consider that the main pending issues for future work are: (1) exploring further whether some data-dependent measures, in combination with HODTs, can significantly improve the approximation error in relation to that of the Delaunay triangulation, and (2) making HODTs widely available to users (at least from a practical standpoint). In relation to (1), it is worth noting that the experiments presented in this paper are based on two real terrains, but as such they have the limitation of not covering many other types of terrains for which results may be different. It is therefore another interesting line of future research to extend these experiments to a wider family of terrains, preferably natural, that provide a more comprehensive sample of relevant terrain topographies. At this point, the use of synthetic terrains is also a valid option, as long as the selection and their design is justified in terms of geographic criteria (as opposed to the synthetic terrains used in previous work mentioned in Section 2). As for (2), this work showed that a general optimization module based on local optimization is relatively easy to program; a good next step would be to make it available off-the-shelf in some of the major GIS, with the option of customizing the optimization criteria. Then, the users could decide by themselves whether HODTs and data-dependent triangulations can offer a better alternative to Delaunay.
Acknowledgments
The authors would like to thank the reviewers for their detailed, thoughtful, and constructive comments. The authors also thank Matias Reparaz for his help and support with an earlier version of this work. R.I.S. was partially supported by projects MTM2015-63791-R (MINECO/FEDER) and Gen. Cat. DGR2014SGR46, and by MINECO through the Ramón y Cajal program.
Author Contributions
Both authors conceived and designed the study. Natalia Rodríguez implemented the software, ran the experiments, analyzed the results, and wrote the corresponding sections of the article. Rodrigo Silveira wrote the introduction and related work sections, supervised the study and reviewed the manuscript. Both authors read and approved the final version.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dyn, N.; Levin, D.; Rippa, S. Data dependent triangulations for piecewise linear interpolation. IMA J. Numer. Anal. 1990, 10, 137–154. [Google Scholar] [CrossRef]
- Alboul, L.; Kloosterman, G.; Traas, C.; van Damme, R. Best data-dependent triangulations. J. Comput. Appl. Math. 2000, 119, 1–12. [Google Scholar] [CrossRef]
- Brown, J. Vertex based data dependent triangulations. Comput. Aided Geom. Des. 1991, 8, 239–251. [Google Scholar] [CrossRef]
- Wang, K.; Lo, C.P.; Brook, G.A.; Arabnia, H.R. Comparison of existing triangulation methods for regularly and irregularly spaced height fields. Int. J. Geogr. Inf. Sci. 2001, 15, 743–762. [Google Scholar] [CrossRef]
- Weisz, J.; Bodnar, R. A refined angle between normals criterion for scattered data interpolation. Comput. Math. Appl. 2001, 41, 531–534. [Google Scholar] [CrossRef]
- Garland, M.; Heckbert, P.S. Fast Polygonal Approximation of Terrains and Height Fields; Technical Report CMU-CS-95-181; Carnegie Mellon University: Pittsburgh, PA, USA, 1995. [Google Scholar]
- Gudmundsson, J.; Hammar, M.; van Kreveld, M. Higher Order Delaunay Triangulations. Comput. Geom. Theory Appl. 2002, 4, 85–98. [Google Scholar] [CrossRef]
- Mitsche, D.; Saumell, M.; Silveira, R.I. On the number of higher order Delaunay triangulations. Theor. Comput. Sci. 2011, 412, 3589–3597. [Google Scholar] [CrossRef]
- Abe, Y.; Okamoto, Y. On Algorithmic Enumeration of Higher-Order Delaunay Triangulations. In Proceedings of the 11th Japan-Korea Joint Workshop on Algorithms and Computation, Seoul, Korea, 19–20 July 2008. [Google Scholar]
- Biniaz, A.; Dastghaibyfard, G. Drainage reality in terrains with higher-order Delaunay triangulations. In Advances in 3D Geoinformation Systems; van Oosterom, P., Zlatanova, S., Penninga, F., Fendel, E.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 199–211. [Google Scholar]
- Biniaz, A.; Dastghaibyfard, G. Slope Fidelity in Terrains with Higher-Order Delaunay Triangulations. In Proceedings of the 16th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision, Plzen, Czech Republic, 4–7 February 2008; pp. 17–23. [Google Scholar]
- De Kok, T.; van Kreveld, M.; Löffler, M. Generating Realistic Terrains with Higher-Order Delaunay Triangulations. Algorithms 2005, 3669, 85–98. [Google Scholar]
- Lawson, C.L. Mathematical Software III; Software for C1 surface interpolation; Academic Press: New York, NY, USA, 1977; pp. 161–194. [Google Scholar]
- Van Kreveld, M.; Löffler, M.; Silveira, R.I. Optimization for first order Delaunay triangulations. Comput. Geom. 2010, 43, 377–394. [Google Scholar] [CrossRef]
- Rippa, S. Long and thin triangles can be good for linear interpolation. SIAM J. Numer. Anal. 1992, 29, 257–270. [Google Scholar] [CrossRef]
- Hjelle, O.; Daehlen, M. Triangulations and Applications; Springer-Verlag Inc.: Secaucus, NJ, USA, 2006. [Google Scholar]
- Reparaz, M.; Rodriguez, N. Higher Order Delaunay Triangulations in Practice. Master’s Thesis, Universidad de Buenos Aires, Buenos Aires, Argentina, 2014. [Google Scholar]
- Schumaker, L.L. Computing optimal triangulations using simulated annealing. Comput. Aided Geom. Des. 1993, 10, 329–345. [Google Scholar] [CrossRef]
- Kreylos, O.; Hamann, B. On Simulated Annealing and the Construction of Linear Spline Approximations for Scattered Data. IEEE Trans. Vis. Comput. Graph. 2001, 7, 17–31. [Google Scholar] [CrossRef]
- Kolingerová, I.; Ferko, A. Multicriteria-optimized triangulations. Vis. Comput. 2001, 17, 380–395. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).