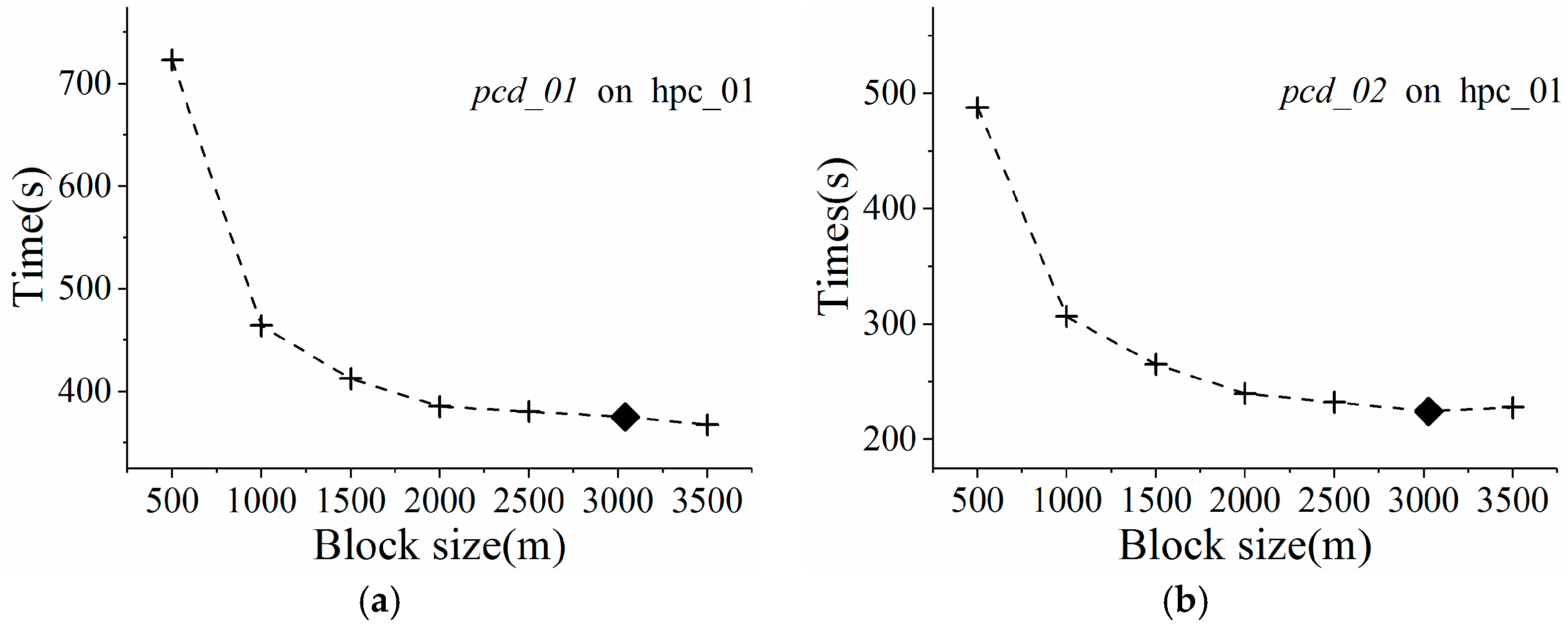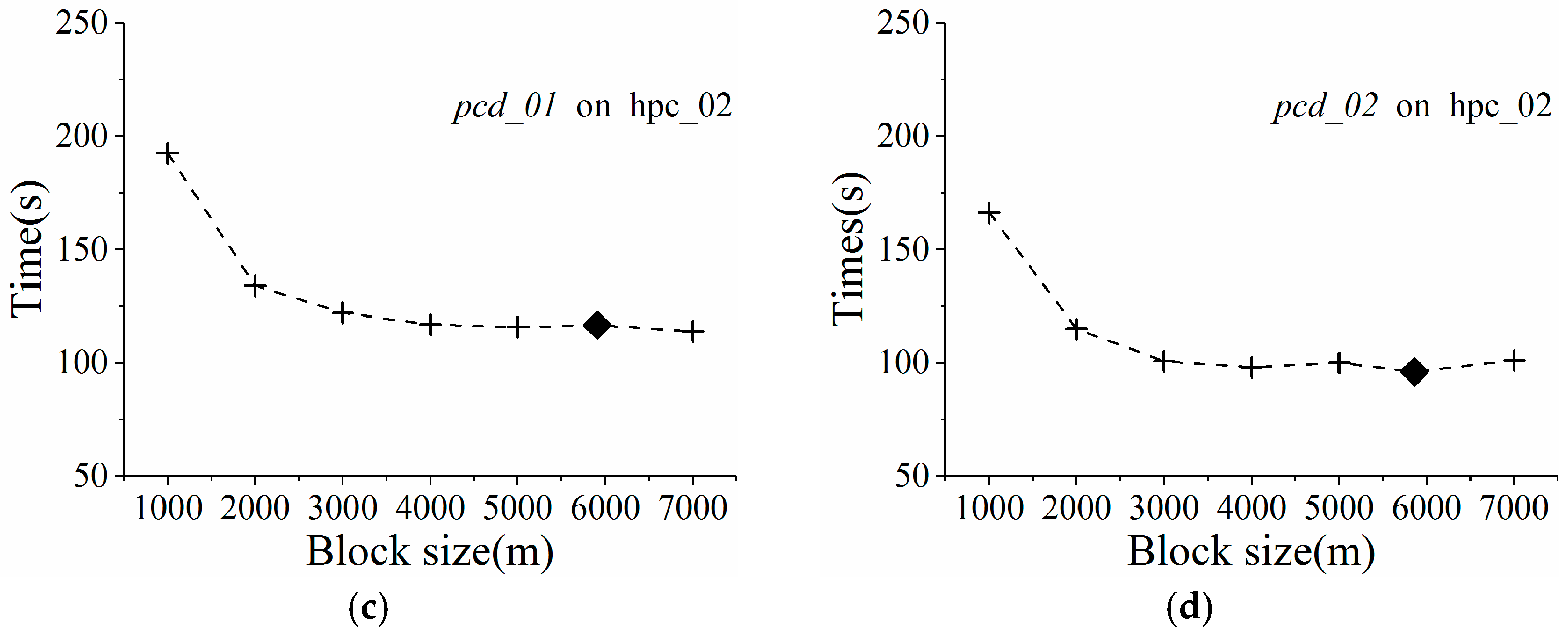1. Introduction
Spatial interpolation (SI) is a well-studied spatial analysis functionality in GIS for deriving a smoothed surface from a limited but usually large number of scattered sample points. SI analysis can help researchers understand implicit spatial trends of geographical phenomena, such as elevation, rainfall, or chemical concentrations. A variety of SI methods have been developed [
1], including Inverse Distance Weighting (IDW), Natural Neighbor, and Spline and Kriging. These interpolation methods, however, are usually computationally expensive and time-consuming. Furthermore, given the rapid and ongoing development of spatial data acquisition technologies, an explosive increase in data volume has dramatically aggravated the performance issues confronting SI algorithms. For example, the point density of airborne LiDAR data can reach up to 100 pts/m
2, and thus easily generates billions of points [
2]. Faced with these massive point clouds, traditional sequential SI methods cannot perform efficiently.
To address these challenges, numerous acceleration methods have been put forward to take advantage of available parallel resources. In the last decades, most parallel SI algorithms were implemented in super computing systems, e.g., MasPar [
3], Cray T3D [
4], CM5 [
5], and parallel clusters [
6]. While being highly efficient, these methods were implemented on high-end hardware, and thus were unaffordable and inaccessible to normal users. With the emergence and development of multicore CPUs, many researchers began to accelerate SI algorithms on these cost-effective and accessible platforms. For example, Cheng et al. parallelized universal Kriging interpolation based on OpenMP [
7]; Guan et al. [
8] accelerated the IDW algorithm by leveraging the power of multicores. In recent years, the rapid rise of general-purpose GPUs (GPGPU) has attracted considerable attention for their superior computing power, high memory bandwidth, and low power consumption. As a result, more and more SI algorithms, such as ordinary Kriging [
9], universal Kriging [
10], and Natural Neighbor interpolation [
11] have been further accelerated on many-core GPU platforms.
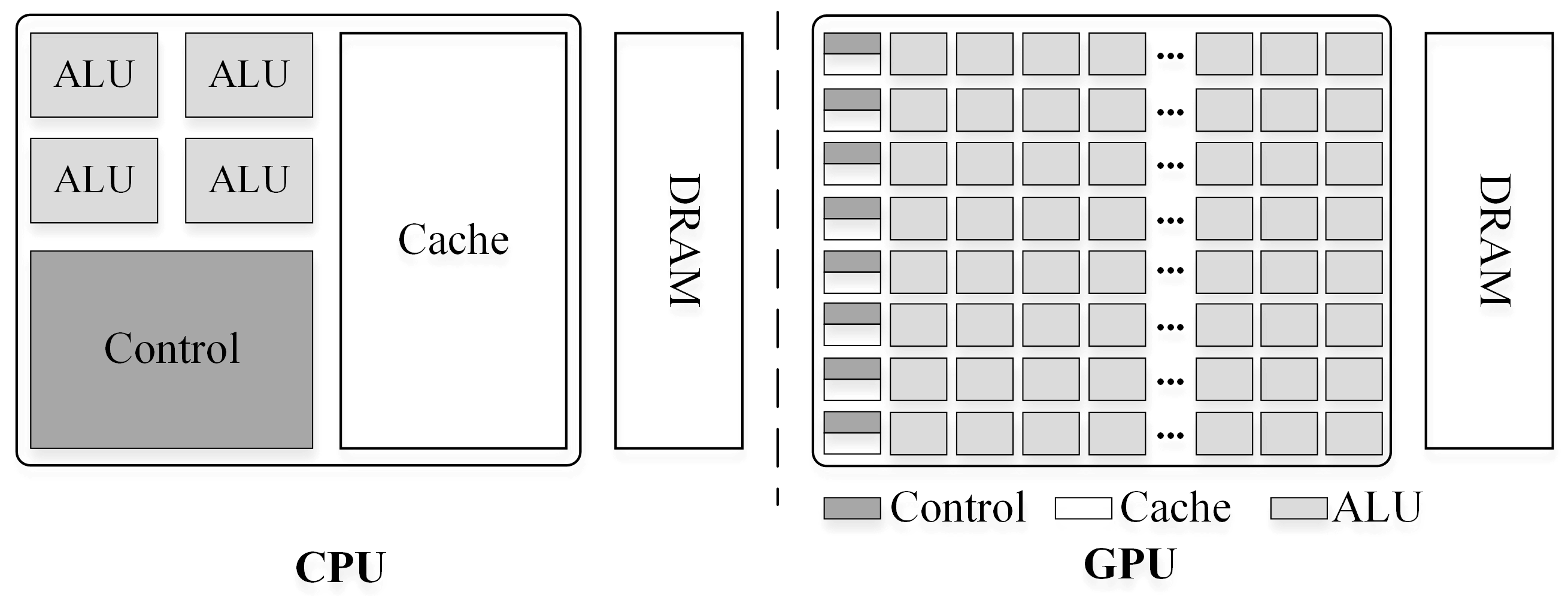
Modern commodity computers including laptops, desktops, and high performance workstations, are usually equipped with both multicore CPUs and many-core GPUs. These heterogeneous computing systems are ubiquitous, but current CPU-only and GPU-only algorithms exploit just one type of parallel processor, thus resulting in a waste of computing resources. To the best of our knowledge, few studies have explored the acceleration of SI algorithms simultaneously leveraging both types of Processing Units (PUs).
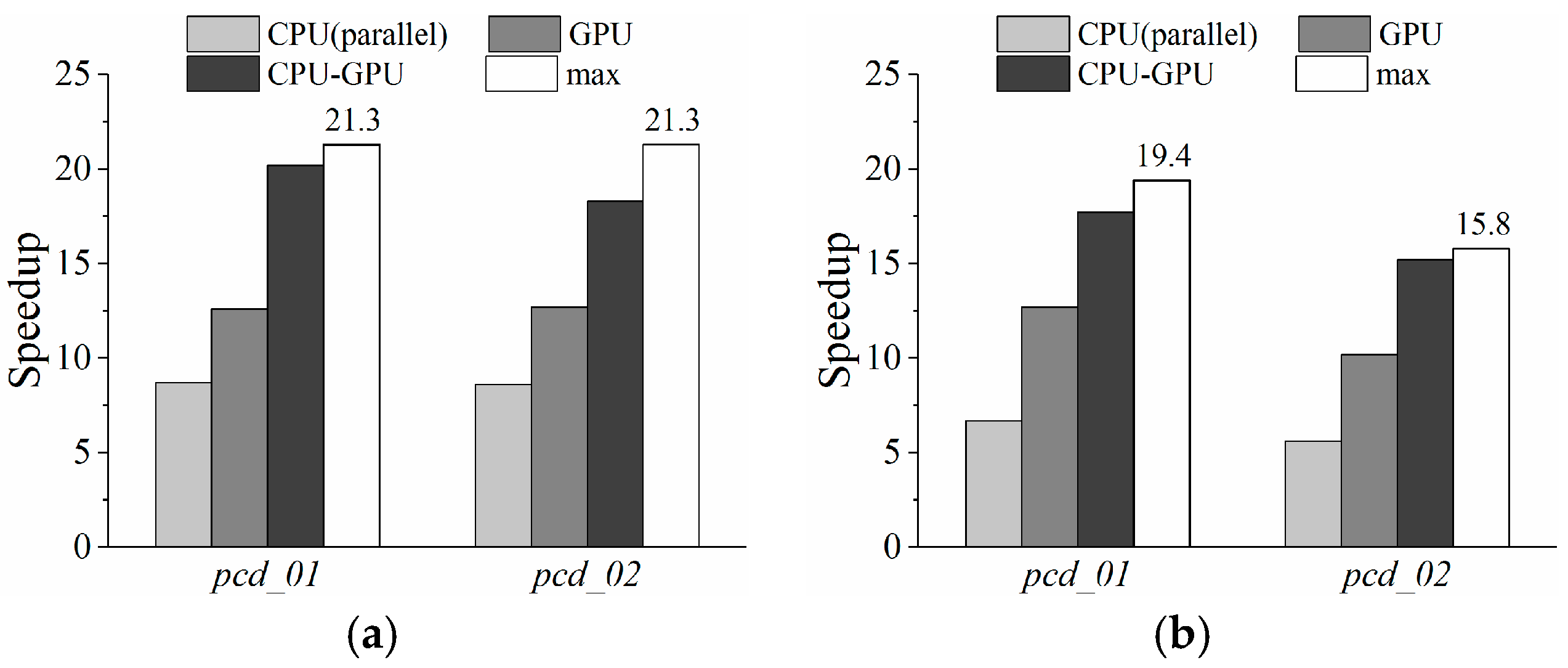
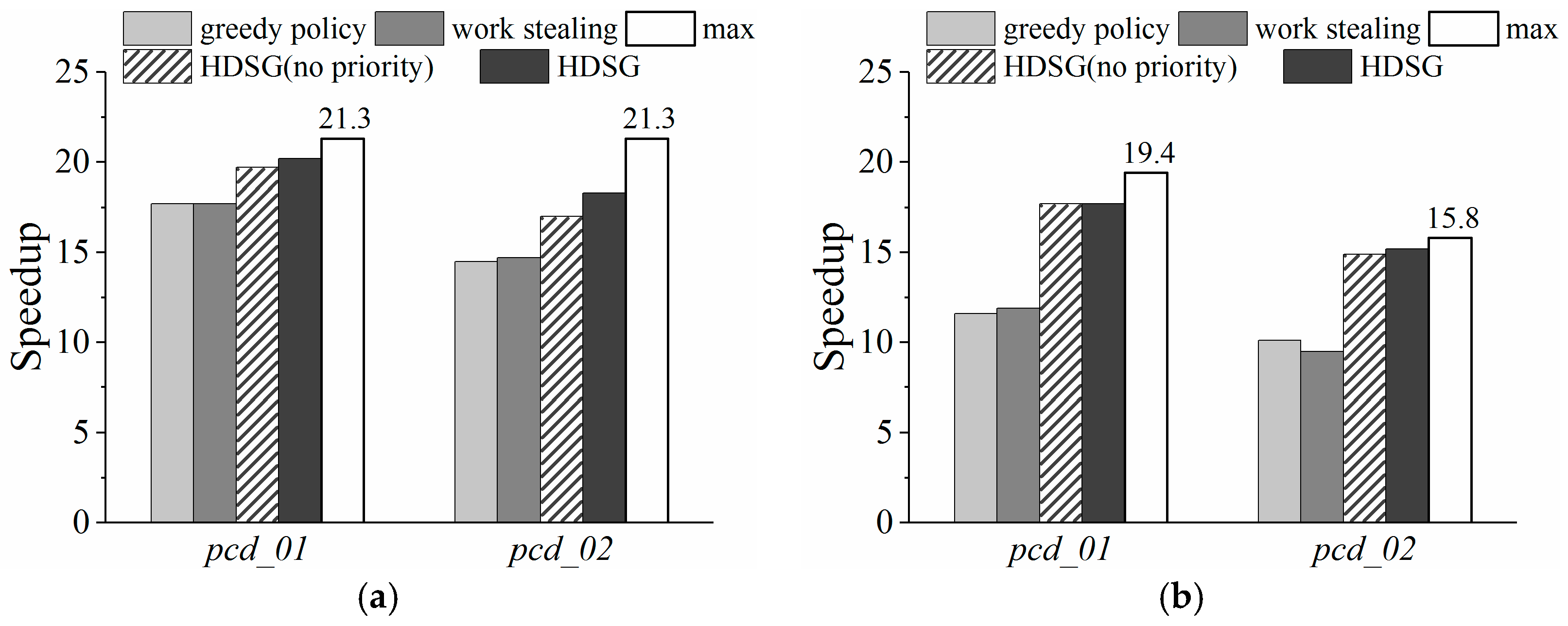
In this paper, we address the gap and propose a hybrid parallel algorithm that parallelizes the Thin Plate Spline (TPS) algorithm to speed up spatial interpolation from massive LiDAR point clouds. On heterogeneous platforms, the hardware architecture, programming models, and computing power of multicore CPUs and many-core GPUs are dramatically different. The integration challenges therefore include unavailable uniform programming models, inefficient CPU-GPU collaboration, and task scheduling. Our research focuses on addressing the last two challenges. A parallel interpolation framework based on a hybrid-programming model was designed to leverage the computing power of both CPU and GPU. Based on this framework, a fast online training method for computing capability estimation is proposed for rapidly finding the optimal task decomposition granularity to keep each PU running at maximum speed. Workload balance is realized with a Heterogeneous Dynamic Scheduler based on the Greedy policy (HDSG), which supports data subdivision. This HDSG policy also helps to improve GPU utilization by task priority declaration. Experimental results demonstrate that both PUs are fully exploited under the optimal granularity, and the hybrid parallel TPS algorithm obtains significant performance improvement. For example, the highest speedup achieved on one of the experimental point clouds was about 20.2. In contrast, the corresponding speedups of the CPU-only and GPU-only algorithms were about 8.7 and 12.6, respectively. Using our HDSG policy, the interpolation time was reduced by about 12% in comparison with other common scheduling strategies (i.e., greedy policy, work stealing).
The rest of this paper is organized as follows:
Section 2 reviews the background of the CPU/GPU hardware architecture, programming models, and heterogeneous computing.
Section 3 introduces TPS interpolation algorithm and the transformation to local TPS.
Section 4 explains the details of the proposed hybrid parallel interpolation framework, including fast online training, streaming spatial decomposition, and the HDSG scheduling strategy.
Section 5 presents a performance evaluation and discussion. Finally,
Section 6 draws conclusions and outlines directions for future research.
4. Framework of the Hybrid Parallel Interpolation
4.1. Introduction of the Interpolation Framework
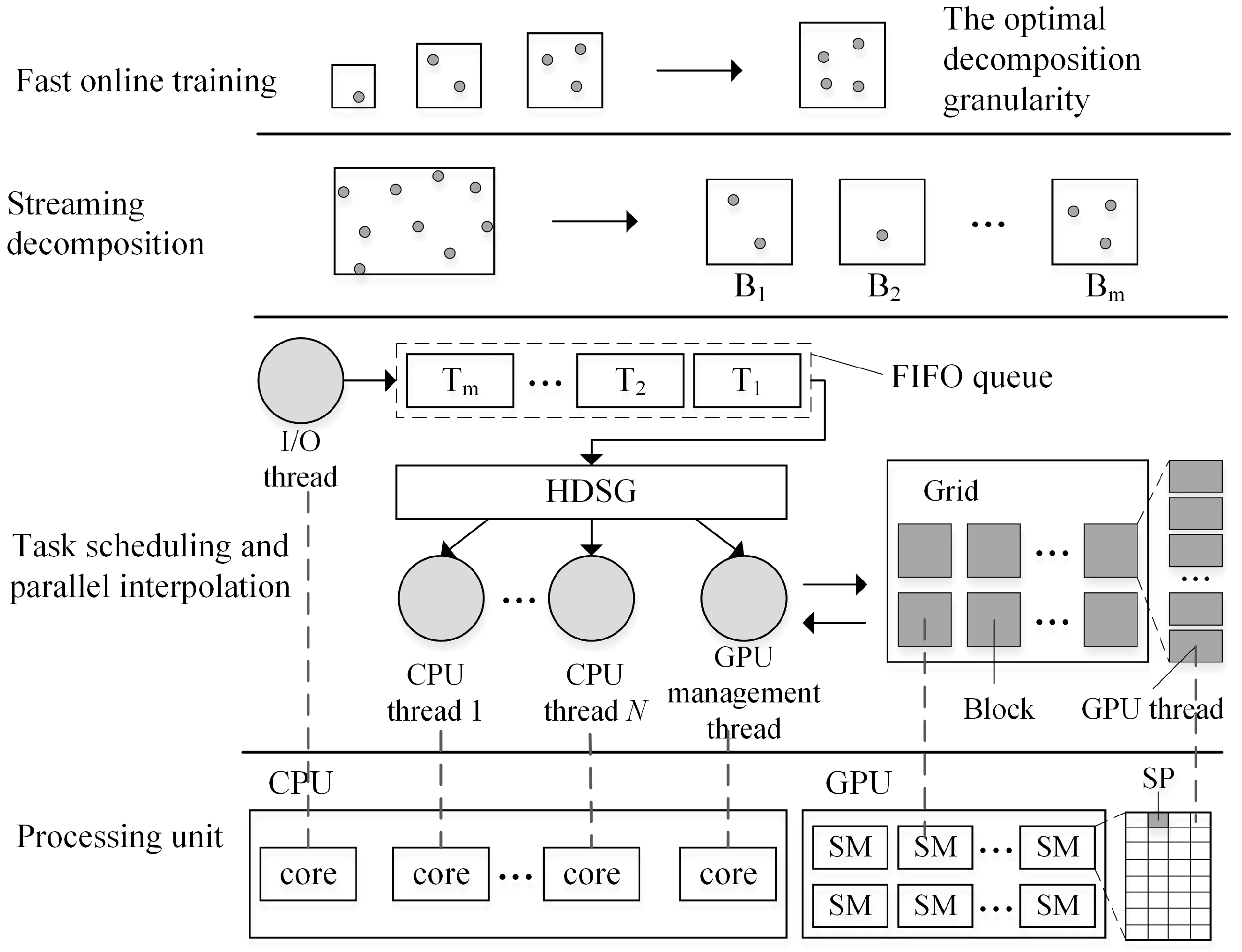
As shown in
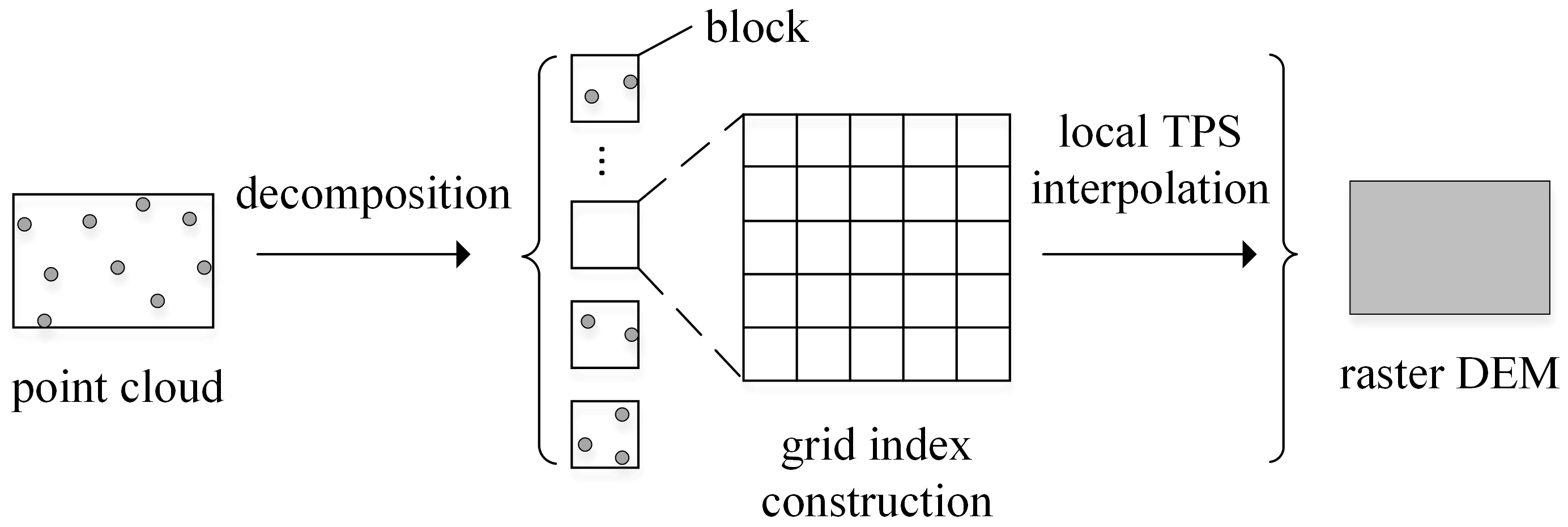
Figure 3, a parallel framework based on a hybrid-programming model (Pthreads + Intel TBB + CUDA) was designed to accelerate TPS interpolation from massive LiDAR point clouds. This parallel interpolation framework contains four stages: fast online training, streaming decomposition, task scheduling, and parallel interpolation. The first stage quickly finds the optimal decomposition granularity so that each PU is able to run at maximum speed. Based on the derived granularity, raw point clouds are then decomposed into a stream of discrete blocks with a streaming decomposition method. In the third stage, a dynamic scheduler called HDSG is proposed to assign blocks and computation to each PU so that parallel TPS interpolation can be executed in the fourth stage.
Once a block is ready, it is delivered to a First-In-First-Out (FIFO) task queue. This task queue is shared by CPU threads and supports concurrent accesses. Two operations are supported on this queue: task submission (push), and request for a task to execute (pop). In implementation, more than one task queue is generated and used for data storage and task scheduling.
In this framework, N + 2 CPU threads are generated. One I/O thread is responsible for data reading and decomposition, and another thread is dedicated to GPU management, including device initialization, data transfer, and kernel launching. The other N CPU threads are assigned to do TPS interpolation in parallel. The multicore CPU can process N blocks simultaneously, while the GPU handles only one block at a time. Since interpolation of each point is independent in local TPS, it is executed in a GPU thread as the smallest work unit. By launching a massive number of GPU threads simultaneously, the parallel computing power of the GPU can be fully exploited.
4.2. Fast Online Training
In a heterogeneous CPU-GPU system, as the computing capability of the CPU and GPU are much different, block size becomes a key factor to achieve a balanced workload and efficient resource utilization. GPU performance is much more sensitive to block size than a CPU given the massive-threaded parallelism of a GPU. If the block size is too small, thread initialization and data transfer between the CPU and GPU will take most of the time, thus leading to GPU underutilization. On the other hand, larger blocks can achieve better GPU performance, but may result in a severe workload imbalance between the CPU and GPU.
To find the optimal decomposition granularity, a series of experiments were conducted to model the quantitative relationship between block size and GPU processing speed. Sample data consisting of four point clouds at different point densities were chosen for the decomposition experiments implemented on an NVIDIA Fermi C2050 GPU. According to empirical research, only about 10–30 neighboring points are required to interpolate each point [
28]. In these experiments, the number of neighboring points requested for local interpolation was set to 15, and the radius of neighbor search and interpolation resolution were set to 15 m and one meter, respectively.
In
Figure 4, block sizes are represented by the number of pixels (i.e., interpolation points), while GPU processing speed is measured in pixels per second. Based on the distribution of scatter points in
Figure 4, we infer that GPU processing speed over block size obeys a logarithmic curve. When the block size is very small, the GPU is underutilized due to lack of enough GPU threads. The interpolation speed increases rapidly with block size, finally evolving towards stability as the block size exceeds the number of CUDA cores inside the GPU. This trend illustrates that the massive-threaded parallelism within the GPU was gradually exploited. For validation,
R square was used to measure the confidence of fit curves.
Figure 4 shows that the
R square values for different LiDAR point clouds were very high, ranging from 0.9256 to 0.9709. A higher value for
R square indicates a better fit. Therefore, the curve fit results validate the assumption that GPU processing speed over block size indeed obeys a logarithmic curve.
Hence, the optimal block size
(in pixels) can be predicted with a logarithmic equation
where
u and
v denote the number of pixels in a block and GPU processing speed, respectively. In order to reach convergence quickly, least squares estimation is used in online training to fit the logarithmic curve with as few samples as possible (e.g., four block sizes). As long as the parameters
a,
b are calculated, the slope of the fitted logarithmic curve is used to measure whether the GPU processing speed reaches stability. When the slope decreases to a reasonable threshold, which is empirically set as 0.01, the GPU processing speed will be treated as stable. Thus, the optimal block size
is obtained and the optimal decomposition granularity
d (in meters) can be calculated according to
where
r denotes the raster resolution for spatial interpolation. The online training method is fast and timesaving because the logarithmic curve fitting is rapid and the calculation of
d is simple.
4.3. Streaming Decomposition
After calculating the optimal decomposition granularity d, the input point clouds are split into discrete blocks so that all of the blocks can be dispatched to different PUs for parallel interpolation. Based on d and the overlap width w, a regular square block decomposition strategy is adopted. The overlap width w is used to guarantee the same nearest neighbor search results on the edge of each block and preserve the smoothness and continuity of the derived raster surface. Therefore, the overlap width w should be no smaller than the neighbor search radius. Since the data volume of LiDAR point clouds can be tens or even hundreds of times of the memory capacity, a streaming decomposition method is implemented to continuously generate discrete blocks.
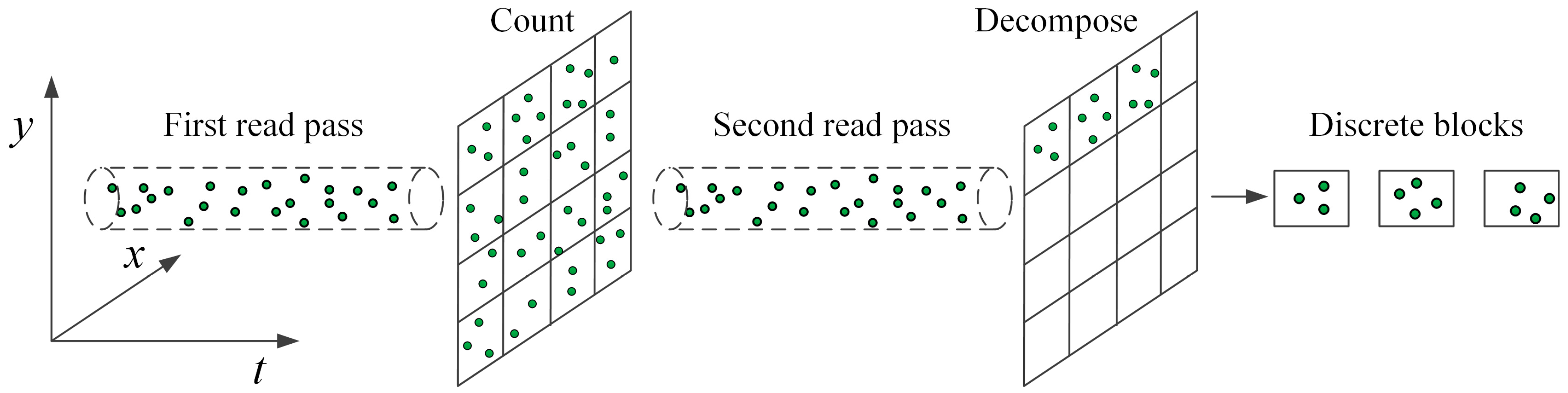
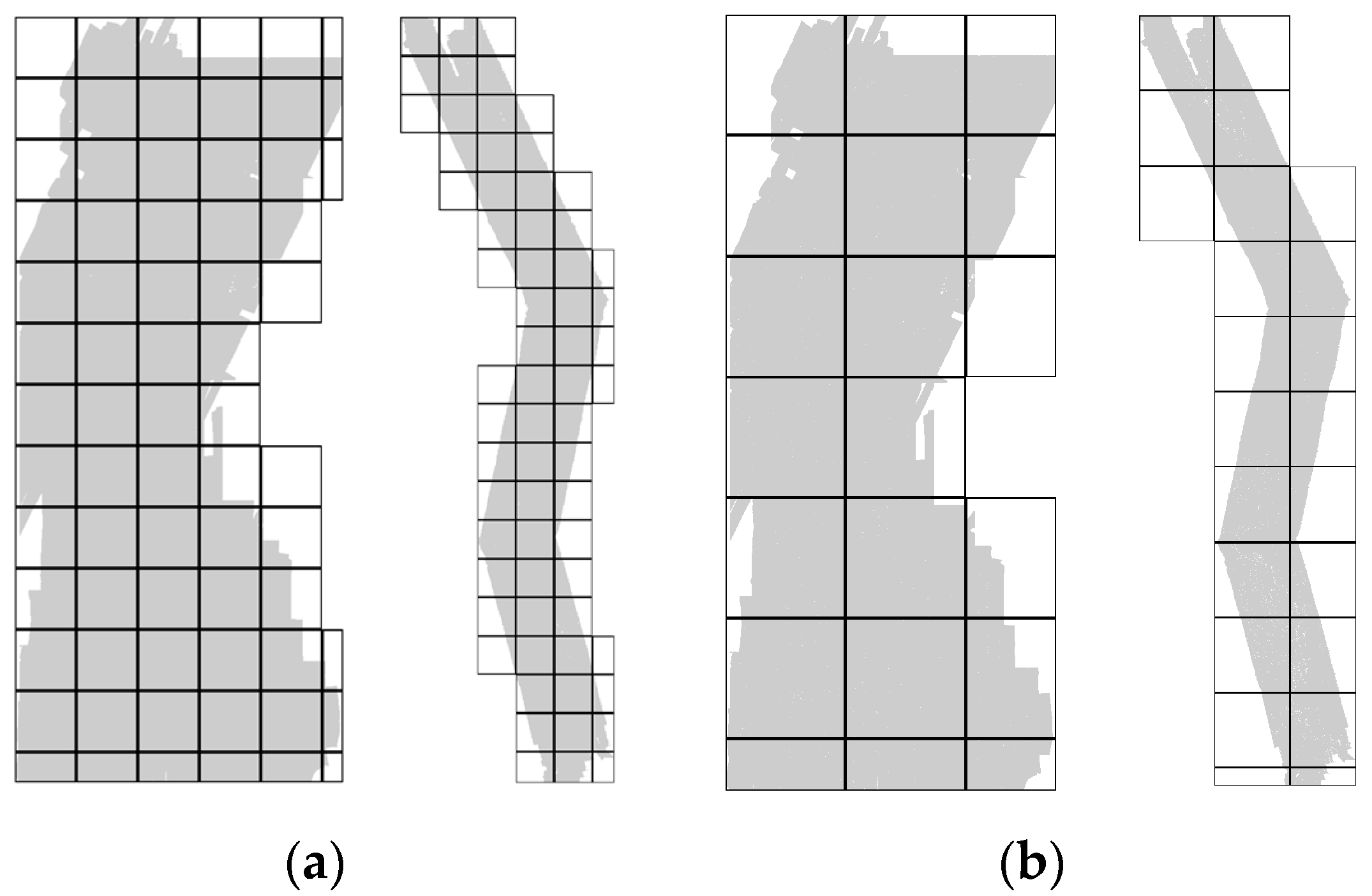
Shown in
Figure 5, the streaming decomposition method reads LiDAR points twice. The decomposition grid frame is established from the obtained block width
d and the boundary rectangle of input data. A first read pass is applied over all of the input points to count the number of points within each block. These counts are later used to identify whether blocks are full in the second read pass and therefore ready to pipe into FIFO task queues. Due to the streaming decomposition, at any given time only a small fraction of the raw point clouds resides in the main memory, while the remainder still resides on the hard drive.
4.4. HDSG Scheduling Strategy
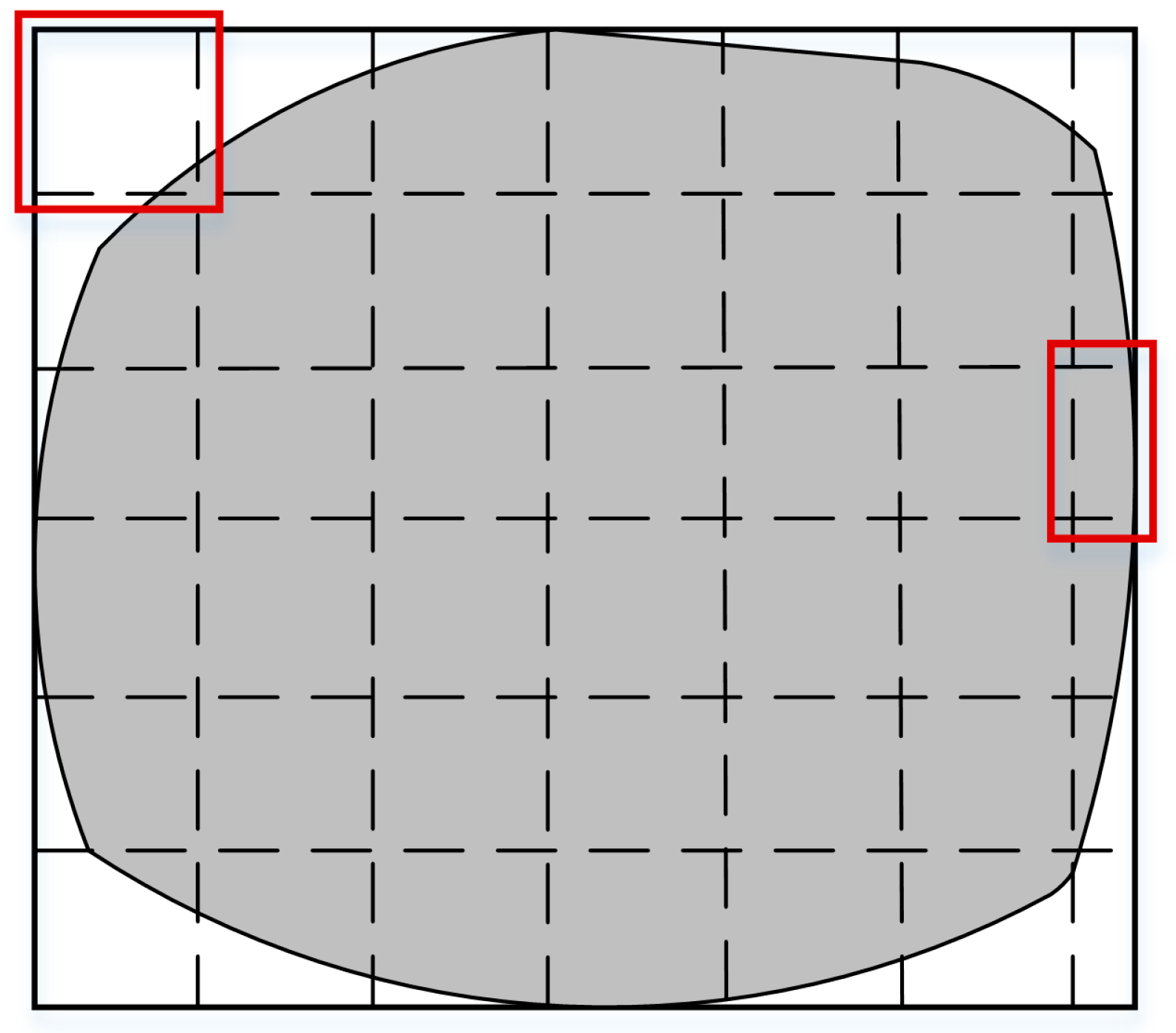
Due to the irregular shape of input point clouds (illustrated in
Figure 6), square block decomposition generates many edge blocks that are much smaller and contain fewer points than the other blocks. These blocks, if allocated to GPU, will cause resource underutilization. At the same time, fixed block size partitioning is prone to load imbalance due to the huge performance gap between the CPU and GPU. For example, when interpolation ends, the GPU is very likely to be idle and waits for slow CPU cores to finish the remaining tasks.
For fixed block size partitioning, the two best available dynamic scheduling strategies are the greedy policy and work stealing. In the greedy policy, idle workers (i.e., computation resources) actively request tasks from a central queue to process. Work stealing creates per-worker queues instead of a central queue. If a worker becomes idle, it steals a task from the worker with the heaviest load. These two scheduling strategies are easy to implement, but they cannot address the differences in CPU/GPU computing capabilities. Thus, HDSG, a heterogeneous dynamic scheduler based on the greedy policy, is proposed with two extensions—task priority declaration and block resizing.
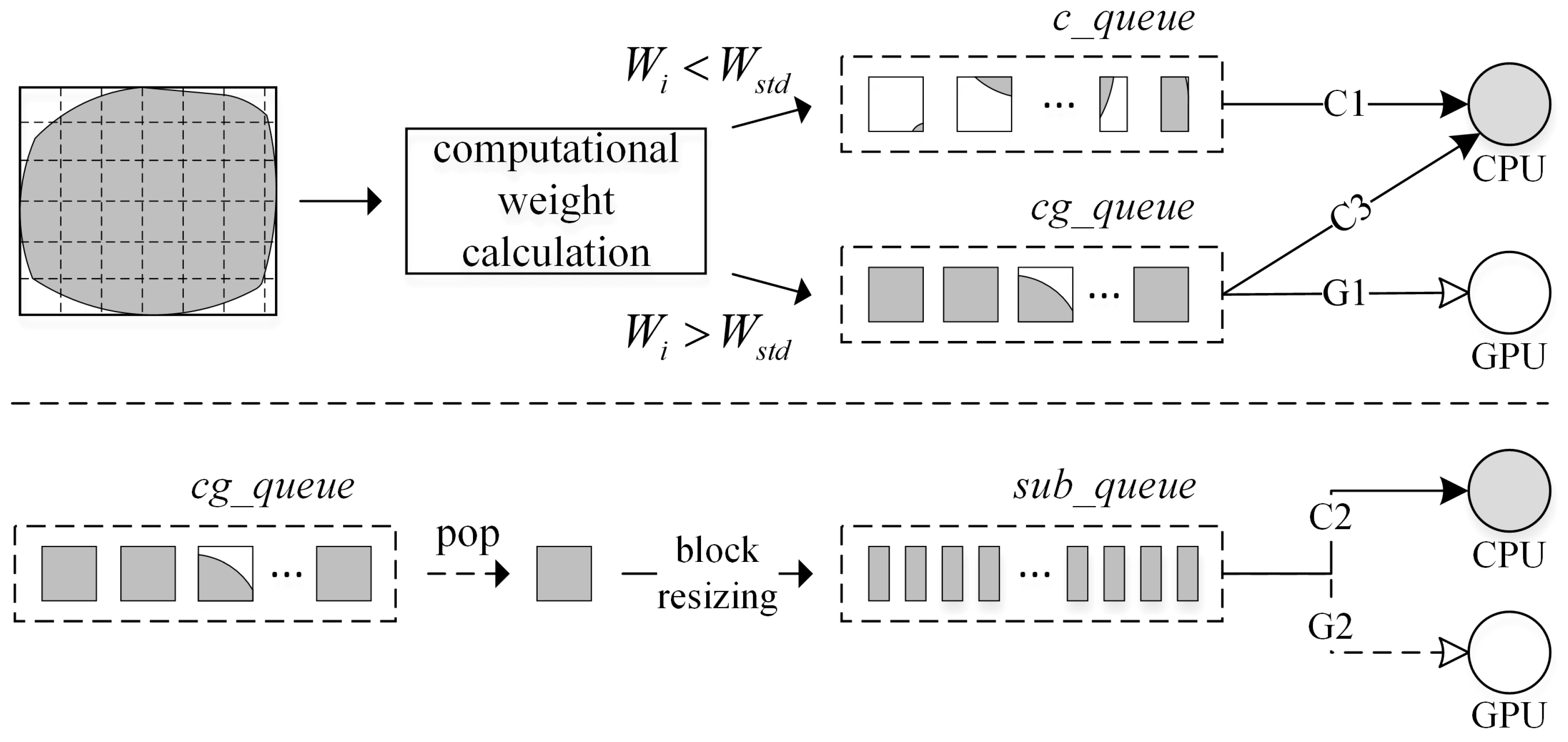
As shown in
Figure 7, the generated blocks are divided into two groups based on the computational weight, which represents the computation burden of each block. The computational weight of each block is expressed as
where
are the average point density and the block size (in pixels) of the
ith block, respectively;
denotes the optimal block size
;
represents the global average point density; and,
is a threshold set empirically as 0.1. Blocks with larger computational weight (
) are pushed into a task queue called
cg_queue, and the rest of the blocks that may lead to GPU underutilization will be delivered into
c_queue and processed only by the CPU. Each task queue will be given at least one priority level, represented by a string (e.g., “C1”). Taking the
cg_queue as an example, it has two priority levels—“G1” and “C3”, meaning that both the GPU and CPU have access to the
cg_queue; and processing blocks in the
cg_queue is the highest priority for the GPU but only the third highest priority for the CPU.
Since the CPU is less sensitive to block sizes, block resizing is adopted for the CPU to ensure better load balancing. Blocks in the cg_queue can be popped and further divided into a collection of sub-blocks. These sub-blocks are stored in another task queue called sub_queue, which is shared by the CPU and GPU. Block resizing can be implemented at any time during the interpolation, and as long as the sub_queue is not empty, the CPU will request blocks from the sub_queue instead of the cg_queue. GPU may turn to the sub_queue for blocks near the end of interpolation if the cg_queue becomes empty. Block resizing is realized based on the average interpolation speed of GPU (VGPU) and CPU (VCPU), which is tracked and updated throughout the execution. A block in the cg_queue is divided into a collection of stripes horizontally/vertically on the condition that the number of stripes is equal to VGPU/VCPU. Notably, the size of sub_queue is set to a small value (e.g., N) so as not to generate too many sub-blocks, which would reduce GPU utilization near the end of completion.
6. Conclusions and Future Work
Nowadays, CPU-GPU computing platforms are available everywhere, from commercial personal computers to dedicated powerful workstations. The emergent challenge for researchers is how to design and implement efficient parallel algorithms to harvest all of the available heterogeneous parallel resources. In this paper, a TPS interpolation for massive point clouds was explored to address this challenge in the integration of multicore CPUs and many-core GPUs.
A simple yet powerful SI framework was designed to leverage the power of both the CPU and GPU. Using a logarithmic function model, optimum decomposition granularity can be rapidly calculated to maximize the GPU utilization. Our HDSG scheduling strategy keeps the heterogeneous system fully loaded and alleviates workload imbalance by priority declaration and block resizing. Experiments on high-end workstations demonstrate the efficient exploitation of heterogeneous parallel resources.
In the future, this hybrid parallel SI framework will integrate more local spatial interpolation algorithms, such as IDW and Kriging, to make it more feasible for practical use. When faced with even larger volumes of point clouds, this framework can be extended to accommodate heterogeneous CPU-GPU clusters for further improvement in overall performance.