Quantifying Tourist Behavior Patterns by Travel Motifs and Geo-Tagged Photos from Flickr
Abstract
:1. Introduction
2. Methods
2.1. Tourist Trajectory
2.1.1. Constructing Travel Trajectory
2.1.2. Differentiating Natives and Tourists
2.1.3. Segmenting Individual Travel Journey
- Criterion I: It is intuitive that a tourist seldom takes no photos in consecutive days during a trip. If this situation happens, it is highly possible that the tourist pays another visit to the target city. In this sense, we segment tourists’ travel trajectories into distinct journeys if the time interval between two consecutive semantic photos exceeds a predefined days. Mathematically, if , we break the travel path into different parts.
- Criterion II: Journeys are abandoned if the total duration of staying at the tourism destination is less than minutes. Mathematically, if , we drop this journey from further analysis.
2.2. Travel Motif
2.2.1. Topological Travel Motif
2.2.2. Temporal Travel Motif
- If the given topological motif contains less than K distinct locations (i.e., ), its corresponding temporal travel sequence is:
- If the given topological motif contains exactly K distinct locations (i.e., ), its corresponding temporal travel sequence is:
- If the given topological motif contains more than K distinct locations (i.e., ), its corresponding temporal travel sequence is:which means that the staying time of the K-th location is replaced by the average of staying times from the K-th location to the last location.
2.2.3. Semantic Travel Motif
- Regarding the first factor, landmarks are classified into L distinct categories, where landmarks in each category are semantically homogenous on the basis of common sense [31]. In this way, a semantic topological travel motif can be transformed into an L-type semantic-category sequence. For instance, “The Museum of Modern Art → Bryant Park → Times Square” is represented as “Cultural → Business → Natural”. In this sense, a semantic travel sequence is formally defined as:where denotes the semantic category of the i-th location.
- With regard to the alignment of different semantic types of landmarks, the semantic travel motif is generated by the relative value of each category of attractions. Here, we define the value as the average of subscripts of categories that are identical to the target category in a semantic travel sequence and denote it by the operator as:
2.3. Motif-Based Clustering
3. Data and Results
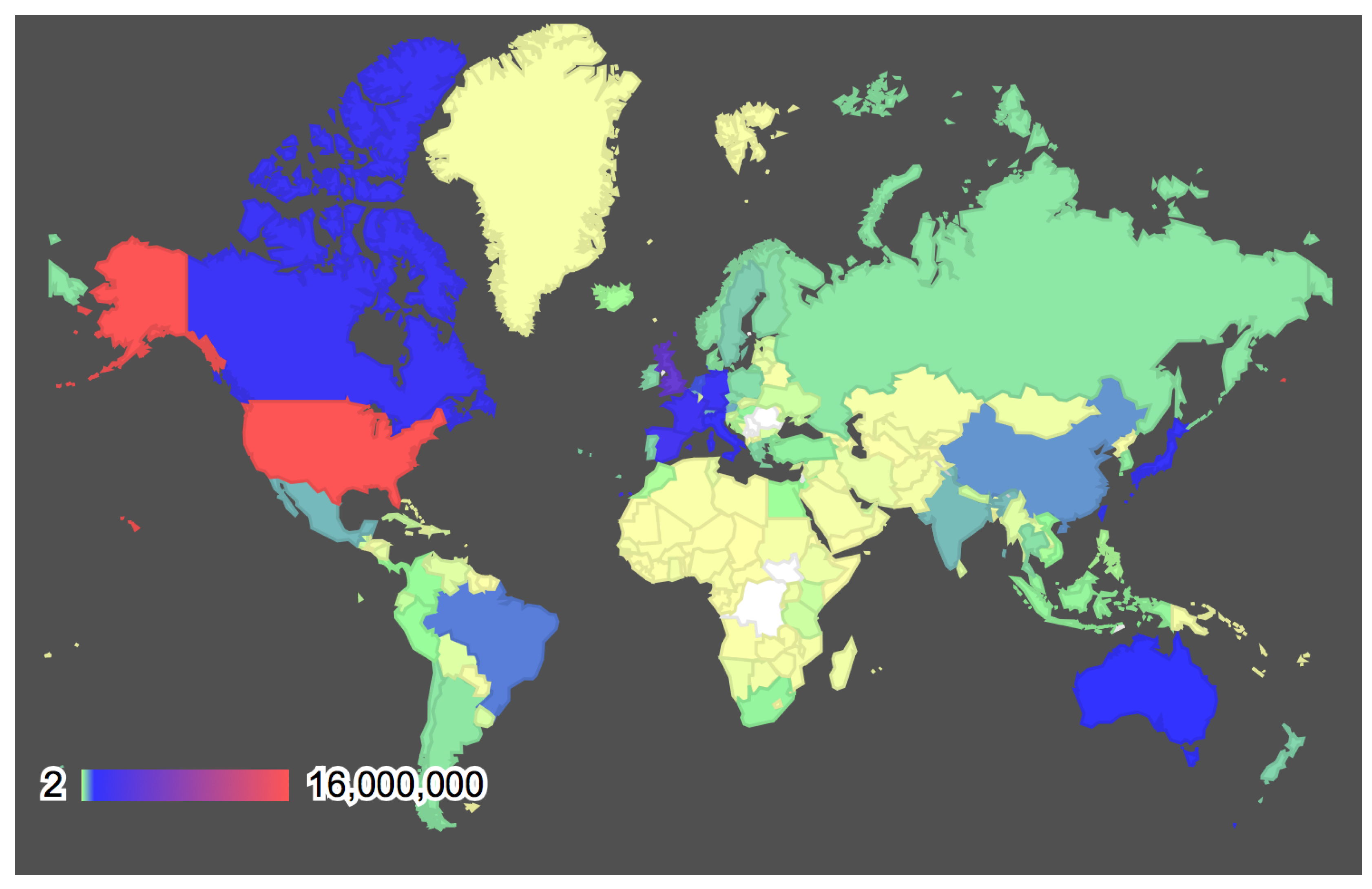
3.1. Yahoo Flickr Creative Commons 100M Dataset
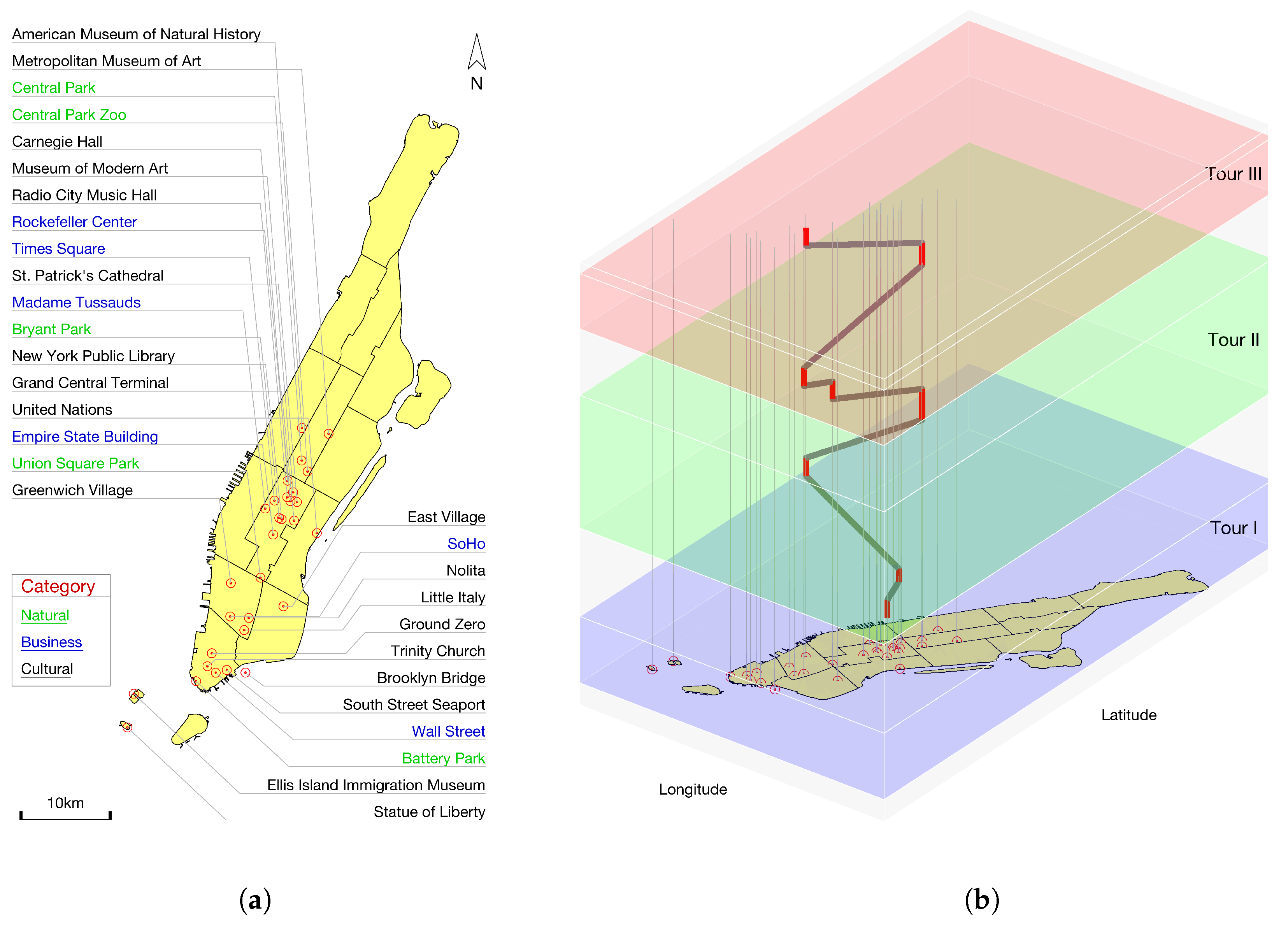
3.2. Typical Travel Motifs in Manhattan
3.2.1. Characteristics of Topological Travel Motifs
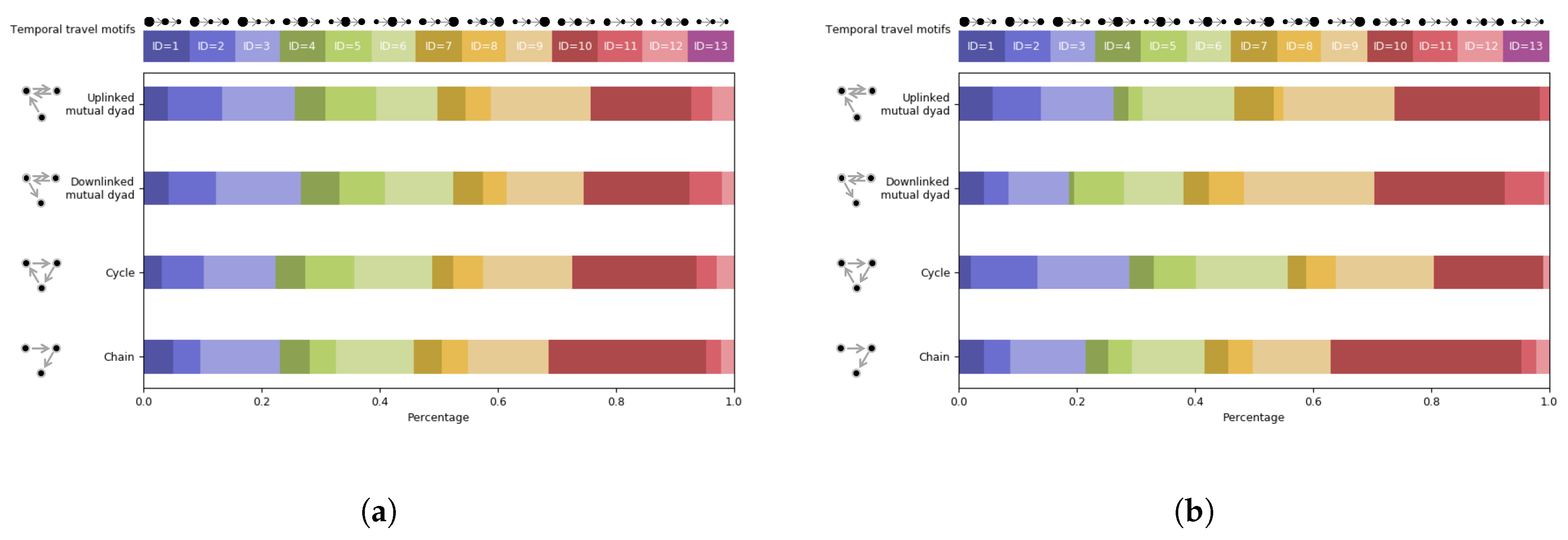
3.2.2. Characteristics of Temporal Travel Motifs
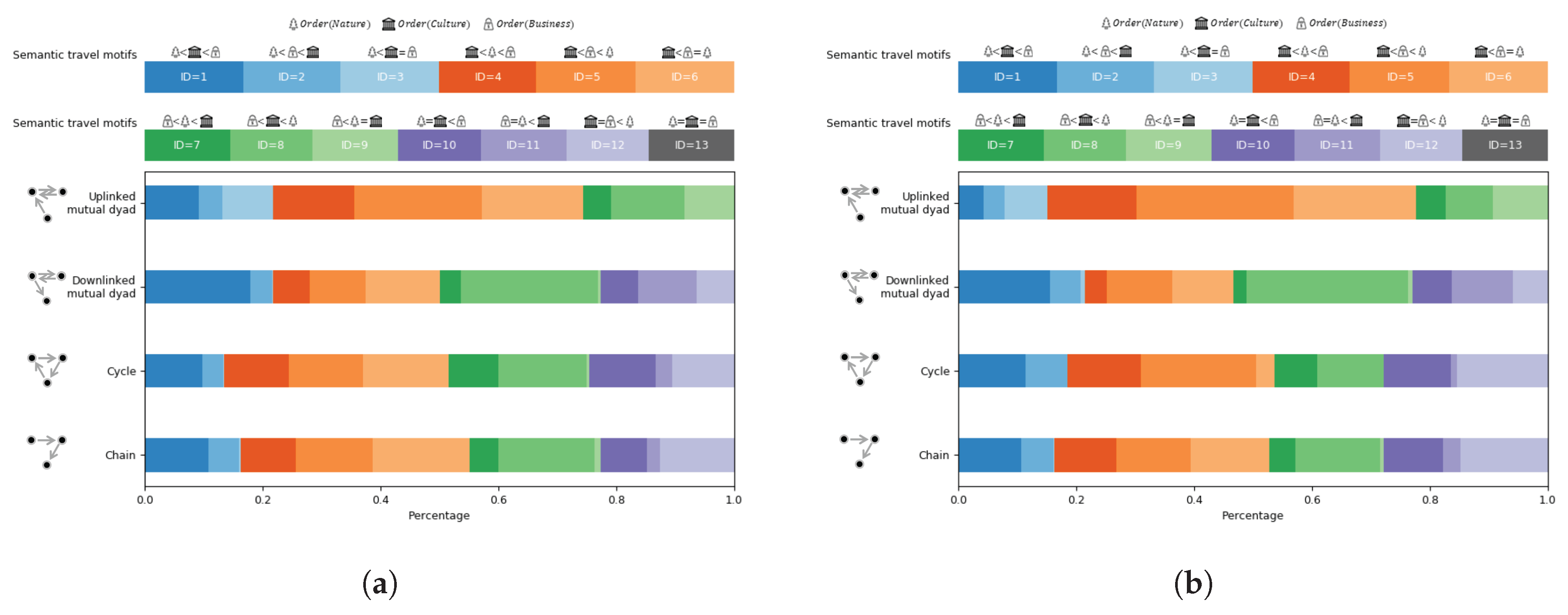
3.2.3. Characteristics of Semantic Travel Motifs
 ”, “
”, “  ”, “
”, “  ”, “
”, “ 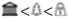 ”, “
”, “ 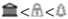 ”, “
”, “ 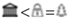 ”, “
”, “ 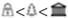 ”, “
”, “  ”, “
”, “ 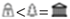 ”, “
”, “  ”, “
”, “ 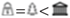 ”, “
”, “ 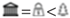 ”, “
”, “  ”} , where “
”} , where “  ” represents “natural” landmark, “
” represents “natural” landmark, “ 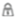 ” represents “business” landmark, and “
” represents “business” landmark, and “  ” represents “cultural” landmark.
” represents “cultural” landmark.3.3. Tourists’ Distinct Travel Patterns
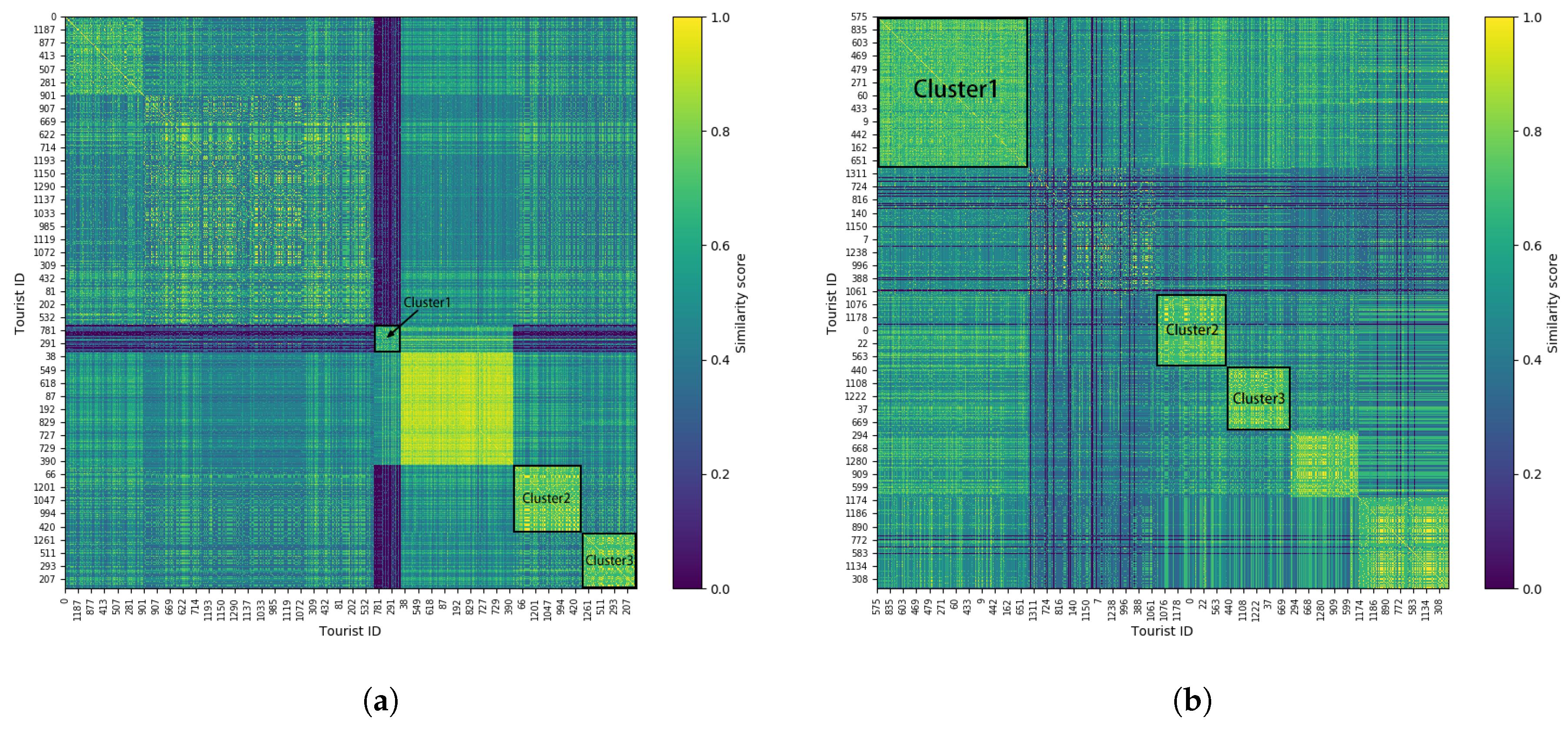
- Cluster 1 denotes tourists who relate to uncommon topological travel motifs, i.e., “cycle”, “downlinked mutual dyad”, “central linked dyad” and “uplinked dyad”. Take Tourist 781 and 291 as examples. Tourist 781 traveled to “Empire State Building → Ground Zero → Brooklyn Bridge → Empire State Building” in a “circle” pattern. Tourist 291 has two trips to New York. The first trip “Time Square → Greenwich Village → Time Square” pertains to the “mutual dyad” topological pattern, and the second trip “Grand Central Terminal → Time Square” is a “chain”. The same characteristic of their trips is that “mutual dyad” exists in both of them.
- Unlike Cluster 1, Cluster 2 represents tourists following the common “chain” topological travel motif. Furthermore, this group of tourists is more interested in “business” than “cultural” and has the least interest in “natural” attractions. For instance, Tourists 66 and 1201 visited “business → business → cultural → cultural” and “business → cultural”, respectively. They both take “Empire State Building” (a “business” attraction) as the first choice and “cultural” attractions as later targets. Besides, they did not travel to “natural” attractions.
- Tourists in Cluster 3 follow the “chain” topological pattern like those in Cluster 2, but they have a preference for “cultural” rather than “business”. For example, Tourists 1261 and 207 traveled to “Greenwich Village → Rockefeller Center” and “Time Square → Rockefeller Center → Central Park → Central Park Zoo”, respectively. They both firstly visited a “cultural” attraction followed by a “business” place (i.e., “Rockefeller Center”).
- Cluster 1 contains tourists who like to stay in the first and second place for a similar duration. Taking Tourists 835 and 469 as examples, following “chain” topological travel motifs with three and eight places respectively, they both spent little time in the first and second places and more time in their remaining visitations.
- Cluster 2 represents tourists who prefer to visit “natural” attractions firstly. Taking Tourists 563 and 0 as examples, Tourist 563 visited “Central Park → Brooklyn Bridge → Rockefeller Center”, and Tourist 0 visited “Central Park → Ground Zero → Greenwich Village → Empire State Building”. They both take the “natural” attraction “Central Park” as the first target.
- Cluster 3 stands for a group of tourists who are more interested in both “cultural” and “natural” than “business”. For example, Tourist 37 follows a semantic travel motif “cultural → cultural → natural → natural → cultural → natural → cultural”, without “business” attractions visited. Tourist 868 followed the semantic travel motif “natural → cultural → business → natural”, traveling to a “business” attraction after “cultural” and “natural” attractions.
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zheng, Y.; Zhou, X. Computing with Spatial Trajectories, 1st ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Zheng, Y.; Zhang, L.; Xie, X.; Ma, W.Y. Mining Interesting Locations and Travel Sequences from GPS Trajectories. In Proceedings of the 18th International Conference on World Wide Web (WWW ’09), Madrid, Spain, 20–24 April 2009; ACM: New York, NY, USA, 2009; pp. 791–800. [Google Scholar]
- Zheng, Y.; Zhang, L.; Ma, Z.; Xie, X.; Ma, W.Y. Recommending Friends and Locations Based on Individual Location History. ACM Trans. Web 2011, 5, 1–44. [Google Scholar] [CrossRef]
- Lew, A.A.; McKercher, B. Trip Destinations, Gateways and Itineraries: The Example of Hong Kong. Tour. Manag. 2002, 23, 609–621. [Google Scholar] [CrossRef]
- Mckercher, B.; Lau, G. Movement Patterns of Tourists within a Destination. Tour. Geogr. 2008, 10, 355–374. [Google Scholar] [CrossRef]
- Wood, S.A.; Guerry, A.D.; Silver, J.M.; Lacayo, M. Using Social Media to Quantify Nature-Based Tourism and Recreation. Sci. Rep. 2013, 3, srep02976. [Google Scholar] [CrossRef] [PubMed]
- Kavitha, S.; Jobi, V.; Rajeswari, S. Tourism Recommendation Using Social Media Profiles. In Artificial Intelligence and Evolutionary Computations in Engineering Systems; Springer: Singapore, 2017; pp. 243–253. [Google Scholar]
- Liu, Y.; Sui, Z.; Kang, C.; Gao, Y. Uncovering Patterns of Inter-Urban Trip and Spatial Interaction from Social Media Check-In Data. PLoS ONE 2014, 9, e86026. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Medel, M. Characterizing International Travel Behavior from Geotagged Photos: A Case Study of Flickr. PLoS ONE 2016, 11, e0154885. [Google Scholar] [CrossRef] [PubMed]
- Popescu, A.; Grefenstette, G.; Moëllic, P.A. Mining tourist information from user-supplied collections. In Proceedings of the 18th ACM Conference on Information and Knowledge Management, Hong Kong, China, 2–6 November 2009; ACM: New York, NY, USA, 2009; pp. 1713–1716. [Google Scholar]
- Kennedy, L.; Naaman, M.; Ahern, S.; Nair, R.; Rattenbury, T. How Flickr Helps Us Make Sense of the World: Context and Content in Community-Contributed Media Collections. In Proceedings of the 15th ACM international conference on Multimedia, Augsburg, Germany, 23–28 September 2007; ACM: New York, NY, USA, 2007; pp. 631–640. [Google Scholar]
- Zeng, Z.; Zhang, R.; Liu, X.; Guo, X.; Sun, H. Generating Tourism Path from Trajectories and Geo-Photos. Proceedings of the 13th International Conference on Web Information Systems Engineering, Paphos, Cyprus, 28–30 November 2012; Wang, X.S., Cruz, I., Delis, A., Huang, G., Eds.; Springer: Berlin/Heidelberg, German, 2012; pp. 199–212. [Google Scholar]
- Paldino, S.; Bojic, I.; Sobolevsky, S.; Ratti, C.; González, M.C. Urban Magnetism through the Lens of Geo-Tagged Photography. EPJ Data Sci. 2015, 4, 5. [Google Scholar] [CrossRef]
- Arase, Y.; Xie, X.; Hara, T.; Nishio, S. Mining People’s Trips from Large Scale Geo-Tagged Photos; ACM Multimedia: Mountain View, CA, USA, 2010; pp. 133–142. [Google Scholar]
- Lu, X.; Wang, C.; Yang, J.M.; Pang, Y.; Zhang, L. Photo2trip: Generating Travel Routes from Geo-Tagged Photos for Trip Planning. In Proceedings of the 18th ACM International Conference on Multimedia, Firenze, Italy, 25–29 October 2010; ACM: New York, NY, USA, 2010; pp. 143–152. [Google Scholar]
- Zheng, Y.T.; Zha, Z.J.; Chua, T.S. Mining Travel Patterns from Geotagged Photos. ACM Trans. Intell. Syst. Technol. 2012, 3, 1–18. [Google Scholar] [CrossRef]
- Sun, Y.; Fan, H.; Bakillah, M.; Zipf, A. Road-Based Travel Recommendation Using Geo-Tagged Images. Comput. Environ. Urban Syst. 2015, 53, 110–122. [Google Scholar] [CrossRef]
- Vu, H.Q.; Li, G.; Law, R.; Ye, B.H. Exploring the Travel Behaviors of Inbound Tourists to Hong Kong Using Geotagged Photos. Tour. Manag. 2015, 46, 222–232. [Google Scholar] [CrossRef]
- Becker, M.; Singer, P.; Lemmerich, F.; Hotho, A.; Helic, D.; Strohmaier, M. Photowalking the City: Comparing Hypotheses About Urban Photo Trails on Flickr; SocInfo: Oxford, UK, 2015; pp. 227–244. [Google Scholar]
- Clements, M.; Serdyukov, P.; De Vries, A.P.; Reinders, M.J. Using Flickr Geotags to Predict User Travel Behaviour. In Proceedings of the 33rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Geneva, Switzerland, 19–23 July 2010; ACM: New York, NY, USA, 2010; pp. 851–852. [Google Scholar]
- Majid, A.; Chen, L.; Chen, G.; Mirza, H.T.; Hussain, I.; Woodward, J. A Context-Aware Personalized Travel Recommendation System Based on Geotagged Social Media Data Mining. Int. J. Geogr. Inf. Sci. 2013, 27, 662–684. [Google Scholar] [CrossRef]
- Barchiesi, D.; Preis, T.; Bishop, S.; Moat, H.S. Modelling Human Mobility Patterns Using Photographic Data Shared Online. R. Soc. Open Sci. 2015, 2, 150046. [Google Scholar] [CrossRef] [PubMed]
- Beiró, M.G.; Panisson, A.; Tizzoni, M.; Cattuto, C. Predicting Human Mobility Through the Assimilation of Social Media Traces into Mobility Models. EPJ Data Sci. 2016, 5, 30. [Google Scholar] [CrossRef]
- Milo, R.; Shen-Orr, S.; Itzkovitz, S.; Kashtan, N.; Chklovskii, D.; Alon, U. Network Motifs: Simple Building Blocks of Complex Networks. Science 2002, 298, 824–827. [Google Scholar] [CrossRef] [PubMed]
- Jackson, M.O. Social and Economic Networks; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Kovanen, L.; Karsai, M.; Kaski, K.; Kertész, J.; Saramäki, J. Temporal Motifs in Time-Dependent Networks. J. Stat. Mech. Theory Exp. 2011, 2011, P11005. [Google Scholar] [CrossRef]
- Schneider, C.M.; Belik, V.; Couronné, T.; Smoreda, Z.; González, M.C. Unravelling Daily Human Mobility Motifs. J. R. Soc. Interface 2013, 10, 20130246. [Google Scholar] [CrossRef] [PubMed]
- Kurashima, T.; Iwata, T.; Irie, G.; Fujimura, K. Travel Route Recommendation Using Geotags in Photo Sharing Sites. In Proceedings of the 19th ACM International Conference on Information and Knowledge Management, Toronto, ON, Canada, 26–30 October 2010; ACM: New York, NY, USA, 2010; pp. 579–588. [Google Scholar]
- Kurashima, T.; Iwata, T.; Irie, G.; Fujimura, K. Travel Route Recommendation Using Geotagged Photos. Knowl. Inf. Syst. 2013, 37, 37–60. [Google Scholar] [CrossRef]
- Shao, H.; Zhang, Y.; Li, W. Extraction and Analysis of City’s Tourism Districts Based on Social Media Data. Comput. Environ. Urban Syst. 2017, 65, 66–78. [Google Scholar] [CrossRef]
- Shi, Y.; Serdyukov, P.; Hanjalic, A.; Larson, M. Personalized Landmark Recommendation Based on Geotags from Photo Sharing Sites. In Proceedings of the 5th International AAAI Conference on Weblogs and Social Media, Barcelona, Spain, 17–21 July 2011; Volume 11, pp. 622–625. [Google Scholar]
- Thomee, B.; Shamma, D.A.; Friedland, G.; Elizalde, B.; Ni, K.; Poland, D.; Borth, D.; Li, L.J. YFCC100M: The New Data in Multimedia Research. Commun. ACM 2016, 59, 64–73. [Google Scholar] [CrossRef]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data Clustering: A Review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Wu, L.; Liu, Y.; Kang, C. Quantifying Tourist Behavior Patterns by Travel Motifs and Geo-Tagged Photos from Flickr. ISPRS Int. J. Geo-Inf. 2017, 6, 345. https://doi.org/10.3390/ijgi6110345
Yang L, Wu L, Liu Y, Kang C. Quantifying Tourist Behavior Patterns by Travel Motifs and Geo-Tagged Photos from Flickr. ISPRS International Journal of Geo-Information. 2017; 6(11):345. https://doi.org/10.3390/ijgi6110345
Chicago/Turabian StyleYang, Liu, Lun Wu, Yu Liu, and Chaogui Kang. 2017. "Quantifying Tourist Behavior Patterns by Travel Motifs and Geo-Tagged Photos from Flickr" ISPRS International Journal of Geo-Information 6, no. 11: 345. https://doi.org/10.3390/ijgi6110345
APA StyleYang, L., Wu, L., Liu, Y., & Kang, C. (2017). Quantifying Tourist Behavior Patterns by Travel Motifs and Geo-Tagged Photos from Flickr. ISPRS International Journal of Geo-Information, 6(11), 345. https://doi.org/10.3390/ijgi6110345




