1. Introduction
With the rise of the mobile Internet and a wide range of location services, people have more demands for the use of space [
1]. Because of the complexity of the indoor spatial structure and the diversity of user needs, the traditional spatial information application is difficult to migrate directly to a room. Indoor space information on indoor positioning, indoor path planning, emergency evacuation, indoor and outdoor integrated navigation, and other types of application support is insufficient [
2]. Therefore, it is of great significance to expand the new theory of indoor spatial data and establish a highly efficient and available indoor spatial data model and database management system for realizing diversified indoor space applications [
3].
At present, various indoor spatial data models have been proposed for different indoor space applications. They include the geometric model, grid model, topology model, and semantic model. The geometric model describes the spatial structure and components of the interior by means of geometric elements with precise coordinates, such as points, lines, faces, and bodies. For example, Coleman et al. compared the key elements of the indoor location service with the areas that are currently in the spatial data infrastructure. They linked the spatial data model framework based on the multidimensional criteria in the framework of the outdoor spatial data model [
4]. Gao et al. proposed seven research hypotheses based on the theory of the technical acceptance model (TAM) and used the survey data of the indoor location service to test the model and these hypotheses, five of which were validated [
5]. Kim et al. established an interior spatial data model that includes the CityGML application domain extension model and the IndoorGML topology model [
6]. Kim et al. integrates both IndoorGML and CityGML LoD4 standards, and automatically deduced indoor GML data and external references from objects in the IndoorGML instance to CityGML data [
7]. Ryoo et al. examined the strengths and weaknesses of the OGC CityGML and OGC IndoorGML standards and how they can be applied to the interior spatial data model [
8]. However, the geometric model cannot directly meet the complex application of indoor space. For example, Lin et al. generally used the geometric model as a data source for other spatial data models in the study of location-oriented interior space models [
9]. The grid model uses regular (square grid [
10], triangular grid [
11]) or irregular (Voronoi diagram [
12]) grids to divide the interior space to achieve seamless coverage of the interior space. However, the large number of grids increases the complexity of the model, and affects the efficiency of interior space query and analysis. The topology model stipulates the formation of topological networks by establishing nodes and connections for different forms of abstraction (for example, the room is abstracted as a point, and the corridor is abstracted as a line) of interior space. For example, Rabiee et al. proposed a tree-like structure based on data segmentation [
13]. Goetz and Zipf [
14] and Lee [
15] used the grid structure in the interior model to construct the building internal path model. The topological model preserves the topological relationship of the interior space, which is very efficient in the application of indoor path planning, but ignores the geometric location information within the space. The semantic model describes the identity, attributes, functions, and relationships of different types of spatial objects by distinguishing the different types of indoor spatial objects. Different applications will produce different classification bases, resulting in different semantic models; thus, the general lack of versatility. For example, Brumitt and Shafer built a topological world model based on semantic space [
16]. Bhatt et al. proposed a spatial design based on spatial semantic reasoning [
17]. Yang and Worboys constructed four ontologies to study indoor and outdoor seamless navigation [
18]. These semantic models have their own adaptation of the scene. It can be seen that the interior space geometry model, the grid model, the topology model, and the semantic model are different, but it is difficult to achieve both availability and efficiency.
In order to compensate for the limitations of the single form model, scholars have proposed various hybrid models to improve the model’s balance. For example, Stevens et al. conducted path analysis by establishing three-dimensional lattice topological relations for two-dimensional planar data [
19]. Li proposed an interior model based on concept lattice that shows the connection of indoor space through the connection diagram between location and exit [
20]. Becker et al. divided the interior space into a number of different levels of information, and established a multi-level model, in which the topological layer expresses the topological relations between the interior elements [
21]. According to the analysis of the characteristics of real estate data, Wen et al. used the ‘path’ and ‘node’ as the key elements to express the spatial relationship and the topological structure of the building and apply it to the construction of emergency evacuation buildings [
22]. Yang and Worboys proposed a formal model based on combinatorial graphs to enhance the geometric and semantic information, and automatically calculate the indoor space navigation map [
23]. Based on the standard CityGML LOD2, which can generate a large number of 3D city models automatically, Boeters et al. defined a new detail level LOD2+, and studied the method of generating indoor geometry based on the existing LOD2 outer set shape [
24]. Tashakkori et al. [
25] studied the IFC (Industry Foundation Classes) -based indoor emergency space model (IESM). This model combines the 3D interior architectural semantic information needed by the rescuers at the time of an indoor disaster with the indoor and outdoor geographic information to improve situational awareness of the interaction between the rescuers and the indoor and outdoor components, so as to realize the emergency response and management [
25]. Teo and Cho proposed a BIM (Building Information Modeling)-based multipurpose geometric network model (MGNM). The model can automatically generate and connect from the BIM indoor and outdoor network, and achieves pedestrian path planning. Compared with the traditional indoor network model, the model gives significantly lower actual error [
26]. These hybrid models are difficult to build and need to reorganize the data to build two sets of models. They are not fully integrated hybrid models, so there is a problem with data update and maintenance. Further, the above hybrid model has its adaptation of the scene, different scales of the scene do not have the same effect.
In addition, many interesting approaches associated with interior space models have been presented. For example, Walton and Worboys proposed a dynamic indoor model based on Millner’s dual graph theory [
27], which has a significant advantage in dealing with the impact of events on the indoor environment [
28]. Doore et al. used descriptive spatial prepositions based on linguistics, machine learning, and cluster analysis to create a rich and detailed VE scene to help people understand the indoor environment [
29]. Afyouni et al. created an interior space model with indoor path continuous search function for moving objects that can be extended to multi-user service [
30]. Kor and Bennett focused on a hybrid model between direction reasoning and qualitative topological reasoning [
31]. Dube and Egenhofer create the surrounds relation from a network of partitions which could be used in interior spatial models [
32]. These services are based on a variety of simple and efficient interior space models.
In this paper, we propose a hybrid model of interior space based on topology and grid (hereinafter referred to as the hybrid model) for the shortcomings of low efficiency and low spatial position geometric information in indoor spatial lattice models. This paper discusses the problem of spatial partitioning, gridding, and model connection in the establishment of hybrid models. Finally, the results of experiments in which the efficiency of the two shortest path query algorithms in the hybrid model and the traditional indoor spatial grid model were compared are presented.
2. Methodology
Car routing solutions are omnipresent and solutions for pedestrians also exist. Furthermore, public or commercial buildings are getting bigger and the complexity of their internal structure has increased. Consequently, the need for indoor routing solutions has emerged [
14]. Traditional spatial information applications are mostly for outdoor network services. Their road network is established when the vehicle is traveling on a larger scale. The optimal path choice on the road network is to judge the direction of travel of the vehicle at each node and intersection. In contrast, an interior space hybrid model based on topology and grid is proposed for the service of pedestrians on a smaller scale. Pedestrians walk arbitrarily in the interior space, they do not walk in accordance with the established route to walk. Assuming that the ground is the same size as the grid, pedestrian movement will highlight cross-grid attributes.
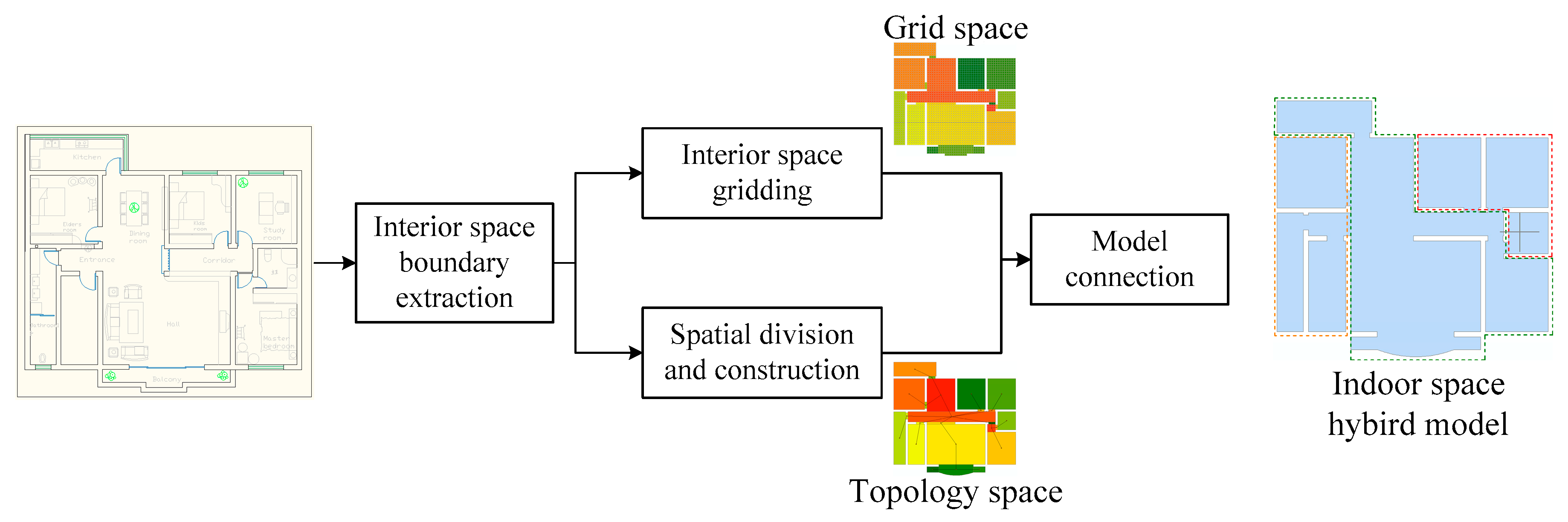
The grid-based interior spatial data model highlights the shortcomings of the grid model arbitrarily, increases the path search algorithm in an unnecessary direction of grid traversal, and extends the pathfinder time. The indoor hybrid model, which combines the indoor space topology information, significantly reduces the number of traversal paths of the path search algorithm, so as to obtain accurate indoor pathfinding results quickly. The indoor space hybrid model separates the interior space from the grid subspaces. It is also divided into different topological subspaces and establishes an association between the lattice space and the topological subspace. The spatial position information is preserved and the topological connectivity information is also taken into account. The proposed indoor space hybrid model is described in
Figure 1.
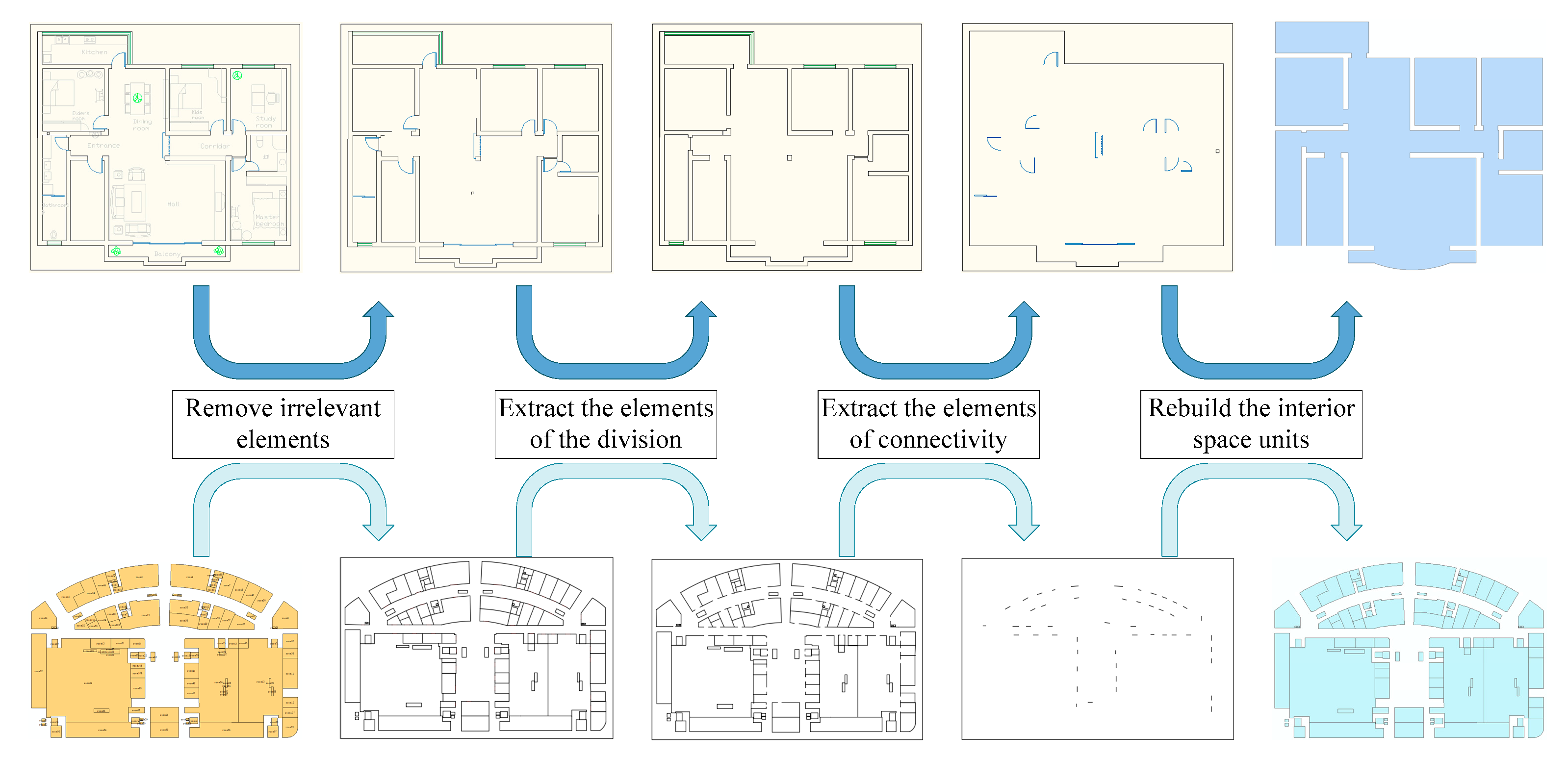
As shown in
Figure 1, the proposed indoor space hybrid modeling approach includes four steps: Firstly, the indoor space boundary is extracted from the boundary of the wall and the fixed obstacle according to the original plan of the building. Next, the interior space is divided into subspaces. Then, the meso space is meshed by the interior space boundary. Finally, through the model connection, the connection between subspace and topological subspace is established.
In order to facilitate the discussion, it is assumed that the indoor space studied in this paper is the architectural plane, without considering the three-dimensional space and the internal movable obstacle. Thus, the following definitions are given:
Interior space refers to the bounded space set formed by the walls of the building and the fixed obstruction, and is denoted IS.
Grid subspace refers to the spatial elements represented by the grid cells after meshing the interior space, and is denoted Sgi, i = . The collection is represented by Sg.
Topological subspace refers to the independent space divided by the actual partition, it has a specific function and has topological relationships with each other, and is denoted Stj, j = . The collection is represented by St.
In addition, the interior space, the grid subspace, and the topological subspace satisfy the following properties:
{}, .
For all , , there is . Among them and}.
Property 1 shows that the grid subspace is the basic unit of the interior space; the topological subspace is a subset of the interior space.
Property 2 states that no two topological subspaces in the interior space contain the same mesh subspace.
2.1. Interior Space Boundary Extraction
Indoor space is a closed area composed of walls, columns, doors, and windows. According to its use of different functional properties, it can be divided into rooms, walkways, staircases, and so on. In this study, indoor plan drawed in AutoCAD was used as the initial data source. On this basis, ArcGIS was used to process the indoor plan, the subspace boundary extracted, and the interior top subspace and its boundary line obtained.
Step 1: Clean up the CAD room data, remove spatial divisions not related to the indoor display and other related graphic elements manually;
Step 2: Extract division elements and connectivity elements of the interior space by the format conversion algorithm, and divide them into different layers;
Step 3: Establish the topological connected relationship of interior elements in ArcMap by the toolbox;
Step 4: Reconstitute and combine interior elements.
2.2. Interior Space Division
Topological subspace is a subset of interior space with specific functions, such as rooms, walkways, living rooms, and balconies. Partitioning the interior space can assist in the establishment of topological networks and provides a record of the spatial connectivity information. It is also important for guiding indoor path analysis and query. However, the structure of the interior space is often more complex and different classification criteria will lead to different topological subspace structures. However, in general, there are regular rules among different classification criteria.
For example,
Figure 2a is a room in the interior space. By dividing the topological subspace of the interior space, it is possible to obtain the four division results of
Figure 2b–e, where different topological subspaces are represented by different color separations. The topological subspaces of
Figure 2b,e are divided into convex polygons, which can ensure that there is no obstruction at any two points in the topological subspace, which is beneficial for path analysis.
Figure 2d divides three topological subspaces, increasing the number of topological network nodes and the depth of topological subspace connections, which affects efficiency.
Figure 2b–e are equivalent from the point of view of complexity of the topology network. However, considering that the acute and narrow spaces do not conform to the architectural space design principles,
Figure 2e is the optimal division result to satisfy the principle of the shortest dividing line.
Therefore, in order to ensure the feasibility of the topological subspace division method and the rationality of the division result, this paper summarizes the five principles and priorities of the spatial subdivision of indoor space and gives the basis for the corresponding principles to be followed by analyzing the actual case of interior space division and forming a model application and architectural design point of view, as shown in
Table 1. When the internal space cannot meet the six principles at the same time, priority should be given to the higher priority classification criteria.
The first criteria is the most important. Splitting a concave polygon into a convex polygon is a necessary step to refine the rough topological subspace. This facilitates grid-based pathfinding within the refined topological subspace. Technically, there are methods to achieve the step:
(1) Connect the concave point(s) to the convex point(s) until all internal angles are less than 180 degrees;
(2) Extend the edge adjacent edge(s) of the concave to achieve the division.
The example data produces the four division results shown in
Figure 2 through Step 1. Thus, the lower five priority criteria are used to filter the results.
2.3. Interior Space Gridding and Gradating
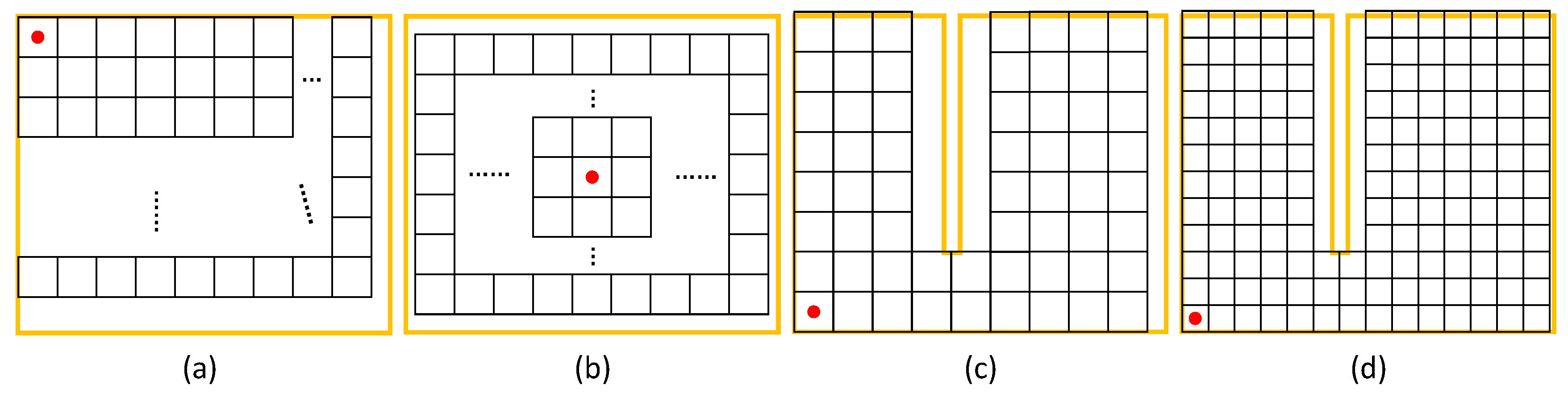
The grid subspace is the basic element of the interior space. The interior space is gridded into a basic object with coordinates and index information, such that the interior space has the function of a locatable query. Interior space gridding mainly involves the grid method and the grid size selection—two questions. There are two main types of spatial gridding methods: (1) Select the appropriate grid size according to the size of the topological subspace, grid it based on a certain reference point, and make the grid fill the topology subspace. (2) Determine the size of the global grid, from a benchmark, begin to display a large enough network, and with the indoor space boundary overlay analysis, delete the space and the wall and fixed obstacles occupied by the grid.
Figure 3a,b show the topological subspace gridding results based on method 1. The reference points are the upper left corner and the center point, respectively. It can be seen that although this method is practical and flexible, and different grid sizes can be selected according to the characteristics of the topological subspace, it is easy to leave a gap in the topology subspace boundary, resulting in an edge between the topological subspaces.
Figure 3c,d show the results of the indoor spatial division based on method 2 and the reference point in the lower left corner of the different grid sizes. The advantage of this method is that the processing is convenient, but the results are the effect of grid size. Compared with
Figure 3c,d, the smaller the grid size, the more accurate the wall is expressed.
Different interior space applications determine the size of the grid size selection. In the indoor positioning navigation application, because the application of the object is human, generally choose the average size of the human body as the grid size, and the average size is 40 cm × 40 cm [
34]. In the application of indoor emergency evacuation, consider the rapid movement of people, the general use of the average step size as a grid size, approximately 70 cm × 70 cm [
35,
36]. For smaller indoor applications, such as indoor gas diffusion simulation, a smaller mesh size is required [
37,
38]. In order to minimize the number of grids, we guarantee that the topological subspace occupied by the gate is at least one grid width. Therefore, the grid size is the thickness of the wall where the gate is located.
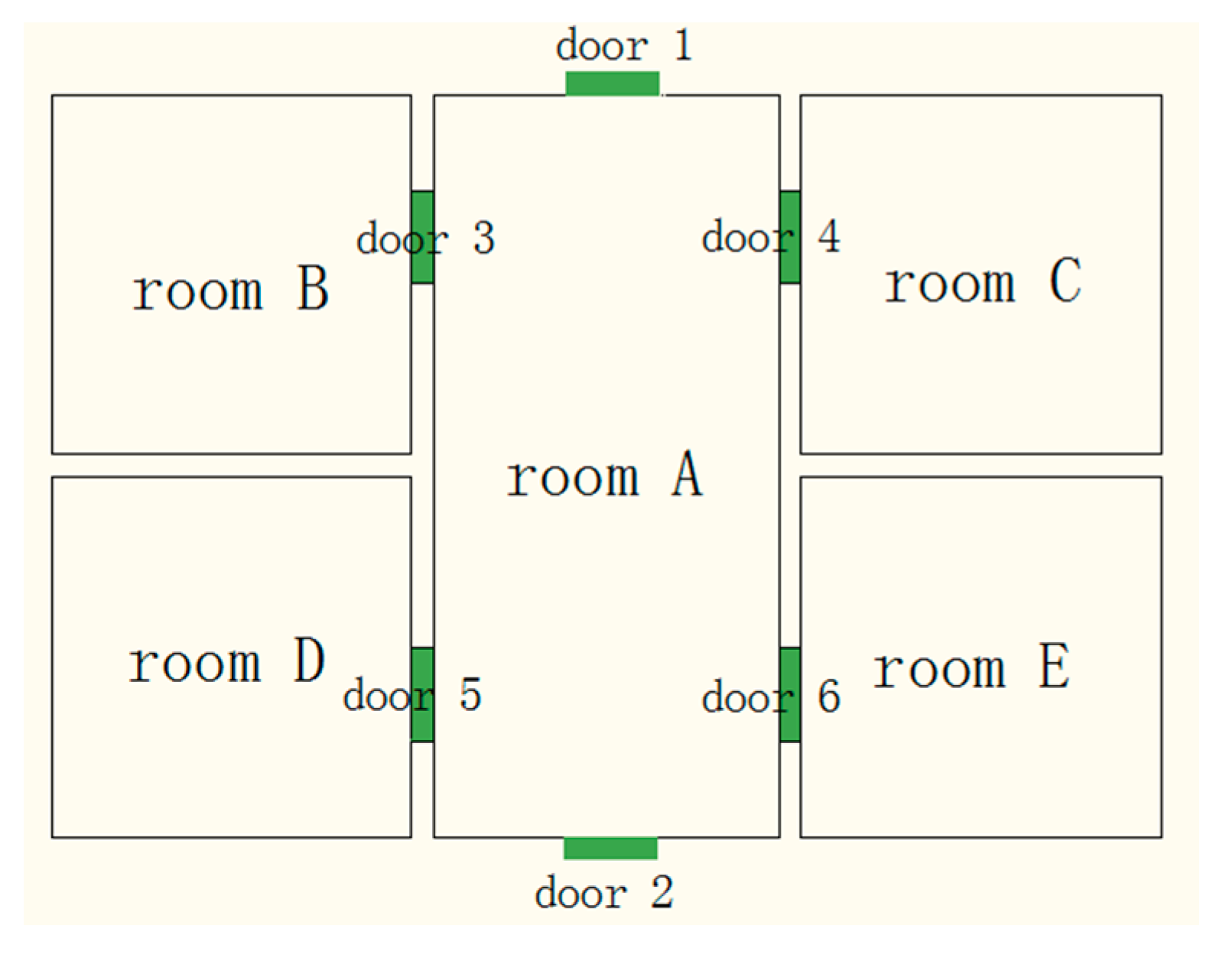
The interior space has a hierarchical nature, which is manifested in the space openings; that is, the level of the door elements. As shown in
Figure 4, the interior space is constituted by gates 1 and 2 and the door space at the first level. At the second level, the top room is composed of room doors 3–6 and its door rooms, corridor entrances, and corridor.
The interior space can be decomposed into the second level, which has a relatively simple space structure. This paper uses the connection relationship of the subspace and the door elements to represent the specific structure of the indoor space, as shown in
Table 2 and
Table 3.
In the interior space, high-level space is composed of a number of low-level subspaces, these subspaces with common features or locations can be divided into classes. As shown in
Figure 5, the example indoor space can be simply divided into left, middle, and right areas. Similarly, residential can also be divided into public areas and living areas. Large shopping malls can also be based on the layout of the shop layout and indoor trails on the overall space. The complex interior space is divided into several different features that simplify the search of the indoor topology path. Through several parts of the connection elements, the search can quickly be conducted from the starting point to the end of the topology path. There is no need for unnecessary searching.
2.4. Model Connection
Model connection establishes the adjacency relation between the topological subspace and the grid subspace and the process of the subordinate space between the grid subspace and the topological subspace by using the abstraction of the nodes and edges in graph theory. This is also a key step in establishing the interior space hybrid model. A graph G can be described as a collection of edges for all nodes and join nodes: . For each node, to assign an index value, the edge can be determined by the index value of the two nodes to which it is connected. The adjacency relation between the topological subspace and the grid subspace is similar to that of the adjacency subspace, which is abstracted by the adjacent topological/grid subspace as a node, and the adjacency relation is abstracted as an edge. Adjacency relation of the topological subspace depends on the result of spatial partitioning, while the adjacency relation of the grid subspace is based on eight neighborhood relations. Further, the relationship between the establishment of the grid subspace and the topological subspace is achieved by superposition analysis. Add a “Belongto” attribute to the grid subspace, and set the corresponding attribute value where the grid subspace center node falls within the topological subspace to the index value of the corresponding topological subspace.
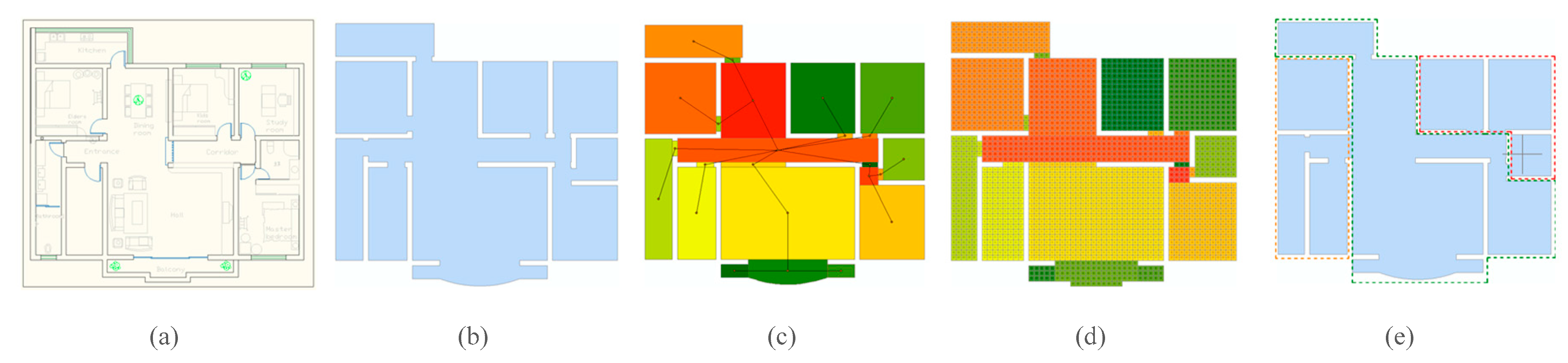
Figure 6a is a simple interior space plan.
Figure 6b is the topological subspace obtained by spatial partitioning and the topological subspace connectivity graphs based on adjacency relations.
Figure 6c is a grid subspace and a grid subspace join graph based on eight neighborhood relations. Because grid subspaces S
g1, S
g2, and S
g3 are in the topological subspaces S
t1, S
t3, and S
t5 respectively. The corresponding “Belongto” attribute values are assigned to S
g1, S
g2, and S
g3 respectively. In
Figure 6, we use different colors to represent different grids with different “Belongto” attribute valuesTherefore, the interior space hybrid model
can be regarded as the combination of the topological subspace linkage graph
and the grid subspace connectivity graph
, which is
, meet
,
makes
. The structure of “Index” and “Belongto” are shown in
Table 4 and
Table 5.
3. Experimental Analysis
The proposed interior space hybrid model establishes the connectivity information of the topological subspace in the upper layer of the grid subspace. This makes it more efficient in the internal path query and analysis application than the traditional grid model. The interior spatial data model, which is built only by the grid, uses the overall optimization strategy algorithm in indoor pathfinding, which traverses most of the rasters in the region and slows the operation. If the topology information is added on the basis of the grid subspace, the global optimization in the path is transformed into several local optimizations, and the secondary grid is optimized on the basis of the optimal topology path. This can reduce the number of traversals of the grid, thereby improving the efficiency of pathfinding.
3.1. Experimental Method
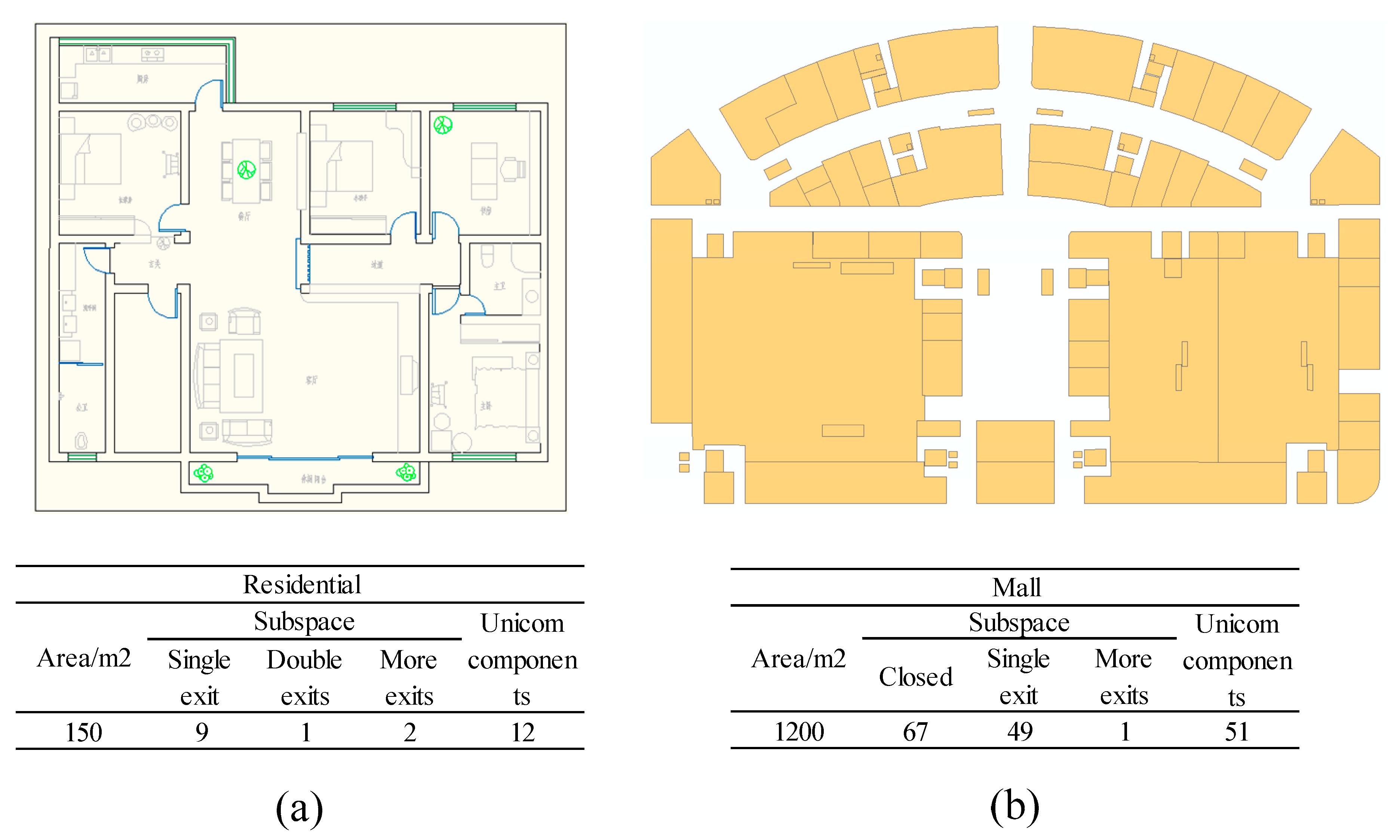
In order to verify the efficiency of the indoor space hybrid model in practical application, the indoor plane CAD drawing of an apartment and a shopping mall were chosen as the raw data. Spatial space boundary extraction, topological subspace division, grid subspace extraction, and model connection were carried out to establish the hybrid model of residential indoor space.
The traditional A* algorithm is a heuristic shortest path algorithm that generally uses the current point and the end of the Euclidean distance or explicit distance of the estimated value as a heuristic function [
39]. However, the interior space is partitioned by walls and fixed obstacles, and the distance between two points does not necessarily represent the actual distance between two indoor spaces. Thus, the effect of the traditional heuristic function is not ideal and it is relatively easy for the candidate point to enter a ‘dead end’, thus forming an invalid traversal.
We therefore optimized the candidate traversal conditions of the A* algorithm by using the indoor space hybrid model. When the shortest path between the grids in different topological subspaces is obtained, verification is carried out as to whether the topological subspace of the traversed grid and the topological subspace of the target grid have a path that has not passed through the topological subspace. If there is no such path, the grid points belonging to the topological subspace do not have to traverse the subspace (the pseudo-code of the algorithm is shown in
Table 6.
Code execution: First, take the grid in the open list as the current grid, and traverse its eight neighborhoods to get the lowest-cost grid. When the value of “Belongto” of the lowest-cost grid matches the “Index” of the line contained in the topology path, change the lowest-cost grid to the open list as the current grid, and put the previous point into the closed list. Repeat the process until the target grid obtained, the Closed list will contain the grid path and give the total costs.
3.2. Experimental Dataset
As shown in
Figure 7, these are our experimental data. In Experiment I, a set of two-bedroom indoor residential floor plans was selected as the original data. In Experiment II, the first-floor plan of a mall was selected as the raw data.
3.3. Hybrid Space Model of the Experimental Dataset
As shown in
Figure 8, two datasets were processed separately according to the hybrid model construction method described above. First, the extra elements were removed. Then, the elements and connectivity elements were extracted. Finally, the topological subspace was obtained.
3.4. Efficiency Assessment of the Proposed Hybrid Space Model
Figure 9 shows the raw data of the apartment and the intermediate process of the hybrid model establishment.
In this study, typical interior home activities, including entrance rest, balcony viewing, caring for children, work and study, kitchen cooking, leisure and entertainment—a total of six paths—were chosen. Based on these six paths, the query results of the shortest path analysis were compared with the A* algorithm and the optimization algorithm in this paper, as shown in
Figure 10. In each roadmap, the left side is the result of the optimization algorithm based on the hybrid model. The right side is the A* algorithm based on the grid model. The red line represents the shortest path tree of the traversed points in the path query process.
As can be seen in
Figure 10, the optimization algorithm avoids traversal of the grid points in the unconnected topological subspace, due to the use of the connectivity information between the topological subspace of the grid subspace, which greatly reduces the number of traversal grid points. Furthermore, the number of grid subspace traversals and the algorithmic time consumption of the shortest path query of the two algorithms under different routes were statistically counted. The results are shown in
Table 7 (Test environment: Windows 10, Intel Core i7-4700MQ, 8 GB RAM).
The data were analyzed and the line and scatter plot shown in
Figure 11 obtained.
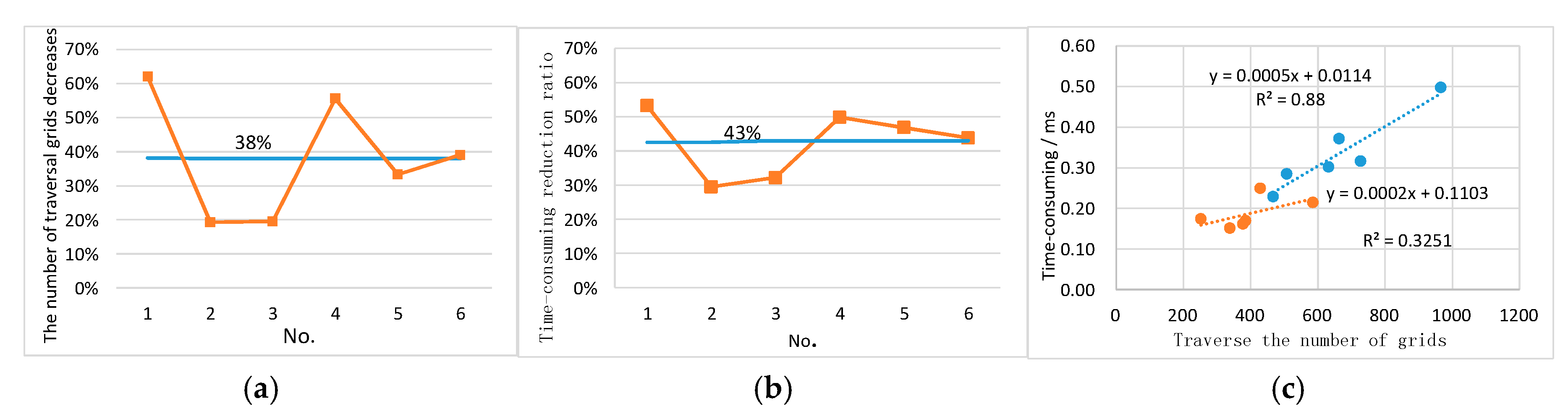
Figure 11a,b show that the A* optimization algorithm based on the hybrid model has a significant efficiency advantage over the A* algorithm based on the grid model in the typical indoor activity scenario. Among them, orange lines indicate the effficiency increase of each path, blue lines indicate average efficiency increase. The number of grids traversed and the algorithmic time consumption were reduced by an average of 38% and 43%, respectively.
Figure 11c shows the linear correlation between the number of grids traversed by the different algorithms and the time consumption. It can be seen from the blue line that the number of grids traversed and the time consumption of the traditional A* algorithm based on the grid model have a significant positive correlation (determination coefficient = 0.88). This shows that the time taken by the algorithm increases with the number of grids. In contrast, there is no obvious correlation between the number of grids traversed and the time consumption of the optimization algorithm which can be seen from the orange line (coefficient = 0.32). With the increase in the number of grids, the time consumed is not obvious.
It can be seen that the hybrid model of interior space based on grid and topology has a significant effect on the efficiency of path query, which also confirms the relative superiority of the hybrid model.
3.5. Experiment II
In order to verify the efficiency of the indoor space hybrid model in more complex indoor environment applications, we used a shopping mall as the experimental object. The interior space boundary extraction, topological subspace partitioning, grid subspace extraction, and model connection of the mall were established. Further, the hybrid model of residential indoor space was established, and the A* shortest path algorithm was used to compare the experiment.
The mall’s range of activities is a 51 m × 82 m rectangle. In the indoor activities of the mall, the pace of the customer is relatively slow. In this experiment, the average step length was chosen as 40 cm × 40 cm for the grid size; the whole rectangle was divided into 128 × 205 grids. This study chose four typical mall indoor activities: the most recent path (two adjacent stores), the farthest path (two stores at both stores), the most complex path (from the corner of the mall to the corner of the supermarket), the most urgent path (from the restaurant to the bank owing to lack of cash). The first three scenes are space-based activities, corresponding to the shortest, longest and most complex in space. The fourth scene is based on the time activity, corresponding to the actual situation in the emergency situation. Based on these four activities, the query results of the shortest path analysis were compared with the optimization algorithm of A* and this algorithm, as shown in
Figure 12. The left subimages are results of the optimized algorithm in the hybrid model. The central subimages are results of the A* algorithm in the grid model. The right subimages are the results of lines smoothed. The red line represents the shortest path tree of the traversed points in the path query process.
The complex mall in Experiment II is different from the simple apartment in Experiment I. If the shortest path is zigzag and “glued to” the wall, this will not correspond to the user’s path in practice. Therefore, after obtaining the shortest path, the path is smoothed and translated to show a form consistent with human cognition. The smooth paths are showed in the right subimages in
Figure 12.
It can be seen from the
Figure 12 that the optimization algorithm avoids traversal of the grid points in the unconnected topological subspace, which greatly reduces the number of grid points traversed by the connectivity information between the topological subspaces of the grid subspace. Furthermore, the number of traversals of the grid subspace and the algorithmic time consumption of the shortest path query of the two algorithms under different routes were counted. The results are shown in
Table 8.
The data were analyzed and line and scatter plots drawn, as shown in
Figure 13.
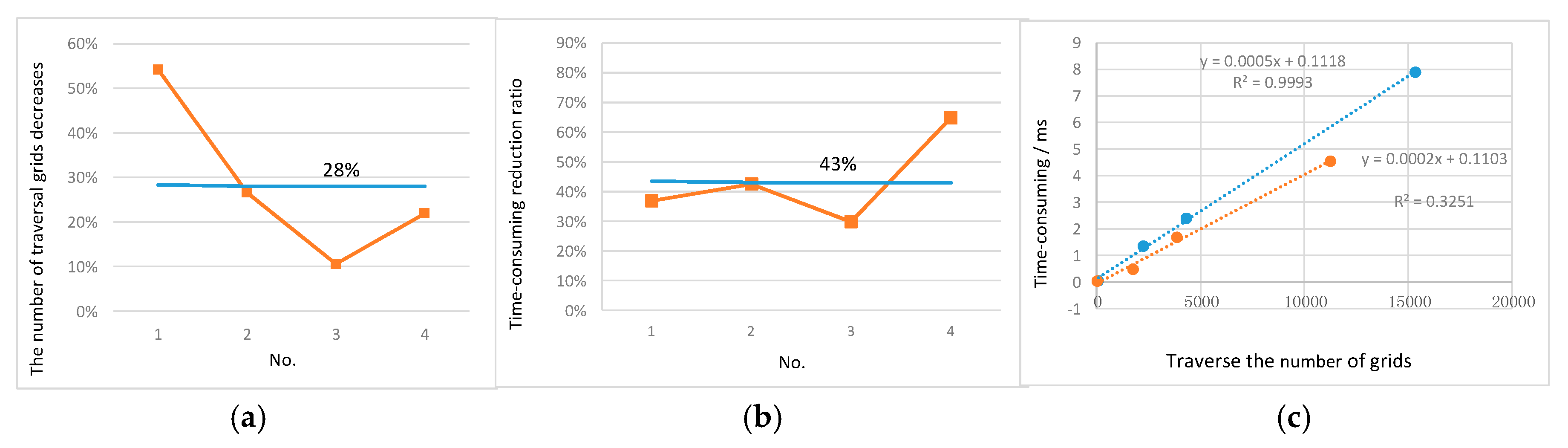
Figure 13a,b show that the optimized A* algorithm based on the hybrid model has a significant efficiency advantage over the A* algorithm based on the grid model in the typical indoor activities. Among them, orange lines indicate the effficiency increase of each path, blue lines indicate average efficiency increase. The number of grids traversed and the algorithmic time consumption were reduced by an average of 28% and 43%, respectively.
Figure 13c shows the linear correlation between the number of traversed grids of different algorithms and the time consumption. It can be seen from the blue line that the traversed grid number and time consumption of the traditional A* algorithm based on the grid model show a significant positive correlation (coefficient = 0.993). It shows that the time taken by the algorithm increases with the number of grids. In contrast, the correlation between the number of traversed grids and the time consumption of the algorithm is not obvious which can be seen from the orange line (coefficient = 0.325). With the increase in the number of grids, the time consumed is not obvious.
Compared with Experiment I, the total number of grids in Experiment II increased and the topological relation is more complicated. The time consumed by the algorithm of indoor path finding has also increased. In Experiment II, the optimization algorithm is not obvious compared with the efficiency of A* algorithm in Experiment I, this confirms the relative superiority of the hybrid model.
4. Conclusions
This paper proposed a hybrid model of interior space based on grid and topology. The problem of spatial partition, grid, and model connection in the process of establishing the model was discussed. The advantages of the hybrid model over the traditional grid model for analysis of indoor paths were demonstrated experimentally.
In this paper, we considered the extraction of spatial boundaries, subspace zoning, topological relations of subspace, scale size of meshes, and comparison between the topological model and the indoor model based on the hybrid model. The number of grids traversed and the time consumed by the path search algorithm were also considered. The cross-section of the room was not considered. Cross-layer finding is actually a special case of step-by-step path; as long as the topological relationship between the floors is established, the overall optimal topology path can be found and the grid used for local optimal routing.
In this study, two experiments were carried out. In Experiment I, a single-layer residence was selected as the experimental object, and two different algorithms were used to query the indoor model and compared. In Experiment II, the first-floor space of a shopping mall was selected as the experimental object, and the indoor space was partitioned. The experiment was carried out according to the steps of Experiment I to verify the operation of the indoor space mixed model and A* optimization algorithm in a large indoor space.
The experiments show that the hybrid model takes into account the spatial geometric position information of the grid model and the spatial connectivity information of the topological model. The average efficiency in the shortest path analysis application for typical home activities and typical shopping mall indoor activities increased by 43%. We foresee that the advantages of the hybrid model will become more apparent as the application area is expanded and the spatial structure becomes more complicated.
Although the method and the priority of indoor spatial classification are refined, there are still different results satisfying the priority criterion for the same indoor space. At the same time, for the indoor space grid of the benchmark and size selection there is a certain degree of flexibility. Therefore, further study can explore the effect of different spatial and gridding results on the application efficiency of the indoor space hybrid model. In addition, in order to improve the automation degree of the indoor space hybrid model establishment process, the indoor space topological subspace automatic partitioning method is also worthy of study.