1. Introduction
As GPS-enabled portable devices become easily available [
1], trajectory data with continuously recorded spatiotemporal footprints receive unprecedented attention from studies examining the moving patterns of subjects and their interaction with environment [
2]. However, a typical raw GPS trajectory dataset is limited for direct analysis as its sheer size often presents challenges for data storage, transfer, and analysis. A wide array of literature has discussed these challenges for handling GPS trajectory data [
1,
3,
4,
5,
6,
7]. Being able to effectively simplify GPS trajectory data is essential for understanding subjects’ movement, activity patterns, and environment interaction.
The fact that GPS trajectories normally present themselves as linear features, simplification of these trajectories is inherently connected to line generalization and simplification. A number of classical algorithms were developed with a focus on preserving geometrical properties. Bellman algorithm ensures that the segments connecting a specific number of points along a curve in post-simplification are closest to the original curve in geometry [
8]. Douglas–Peucker (DP) algorithm is a well-known classical method that preserves location, orientation, and shape of a line through a recursive and refinement approach of preserving a vertex that is furthest away from a line segment of interest [
9]. Various other algorithms aimed at preserving geometric properties of a line while effectively reducing dataset size. Examples include fractal-based line generalization [
10,
11], a re-evaluated DP algorithm through visualization [
12], Li–Openshaw algorithm [
13], decision tree based road network generalization [
14], progressive line simplification algorithm [
15], and oblique-dividing-curve based simplifying algorithm [
16]. Gudmundsson et al. developed an extended Douglas–Peucker algorithm that can effectively preserve geometry of self-intersecting polylines [
17].
Recent development in trajectory simplification methods moved beyond simple geometry preservation. Some algorithms incorporate rules that consider movement patterns or specific range of point data for trajectory simplification. For example, Potamias et al. developed STTrace algorithm that utilizes a heuristic prediction by giving more weight to the points immediately precedent or subsequent a point when deciding if a point should be preserved [
18]. Muckell et al. put forward Spatial QUalIty Simplification Heuristic Method that seeks to reduce computation time for trajectory simplification by assessing and selecting critical points at local scale—a predefined segment of trajectory [
19]. Other recently developed algorithms emphasize quality of simplification through effective error control. Chen et al. [
20] presented a fast polygonal approximation algorithm under the so-called integral square synchronous distance error criterion; it uses geometry distance as a constraint to enhance the algorithm. Birnbaum et al. [
21] proposed a trajectory simplification algorithm by considering multiple records of the same trajectory and identifying the shared geometries among them. SQUISH-E by Muckell et al. [
1] and Trajic by Nibali et al. [
22] are both trajectory simplification algorithms that achieve both good compression ratio and small error margin. Still other trajectory simplification algorithms made progress in improving algorithm efficiency. For example, to account for travel speed variation along a trajectory, uniform sampling algorithm takes every
ith point in trajectory coordinates [
23]. Meratinia and Rolf [
24] proposed a top-down speed–based algorithm and a top-down time-ratio algorithm to significantly reduce the running time of line simplification. However, GPS trajectory data contain information that is more than a sequence of point locations; there are movement patterns and other inherent features [
25]. Information on movement speed, direction, acceleration, etc. is stored in these data; transportation mode and some activities may be derived from trajectory data. Therefore, an effective GPS trajectory simplification should preserve not only the geometry and movement properties but also the related spatial-temporal activity patterns that can be derived or inferred from a trajectory dataset.
GPS trajectory data contain critical locations for a subject’s activities, such as point locations along a trajectory that indicates particular activities or routine [
26] (e.g., breakfast taco pick-up place along morning commuting route) or change of travel mode or transportation situation (e.g., a significant speed change that may indicate a change from walking to commuting train riding). These locations are activity nodes along a subject’s spatial-temporal trajectories and should not be treated as ordinary location points and be dropped by an automatic algorithm that is designed to preserve geometry of a line. Contextual information for understanding spatial-temporal behavior and patterns must be preserved during trajectory simplification. Schmid et al. [
27] proposed that trajectory data simplification should consider semantic information, e.g., street name, bus, tram and train line of transportation networks. Chen et al. [
28] developed a trajectory simplification method for location-based social networking services. This method differs from DP algorithm in two aspects. First, it considers both local optimization and global optimization. Second, it takes into accounts both shape skeleton and semantic meanings of a trajectory.
This paper contributes to GPS trajectory simplification by developing an Enhanced Douglas–Peucker (EDP) algorithm that considers both geometry properties of linear features and movement and contextual information of a trajectory. A set of Enhanced Spatial-Temporal Constraints (ESTC) is incorporated into our algorithm. The ESTC-EDP algorithm takes a holistic approach to preserve the essential characteristics that define a trajectory. Given the importance of speed and change of speed for describing a trajectory and for deriving information about a subject’s spatial-temporal behavior, preserving speed properties along a trajectory, or a trajectory’s speed profile, must be achieved for GPS trajectory simplification. The ESTC-EDP algorithm is evaluated by examining speed–information loss after trajectory simplification. For a particular empirical trajectory, a set of ESTC with particular parameters should be designed and implemented to minimize both geometric error and speed profile distortion.
The rest of this paper is structured as follows.
Section 2 discusses traditional PD algorithm and the ESTC-EDP algorithm, focusing on the spatial-temporal constraints adopted by the new algorithm.
Section 3 focuses on accuracy assessment of trajectory simplification. In addition to traditional positional accuracy, speed profile preservation was introduced.
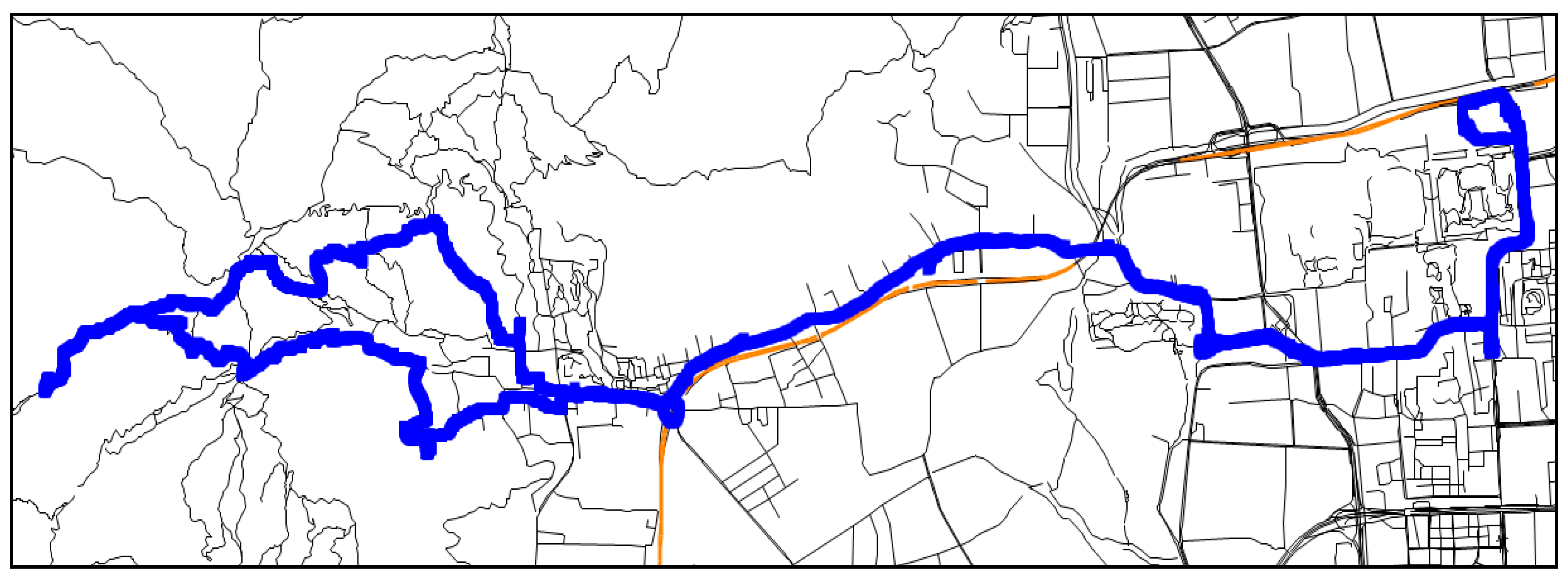
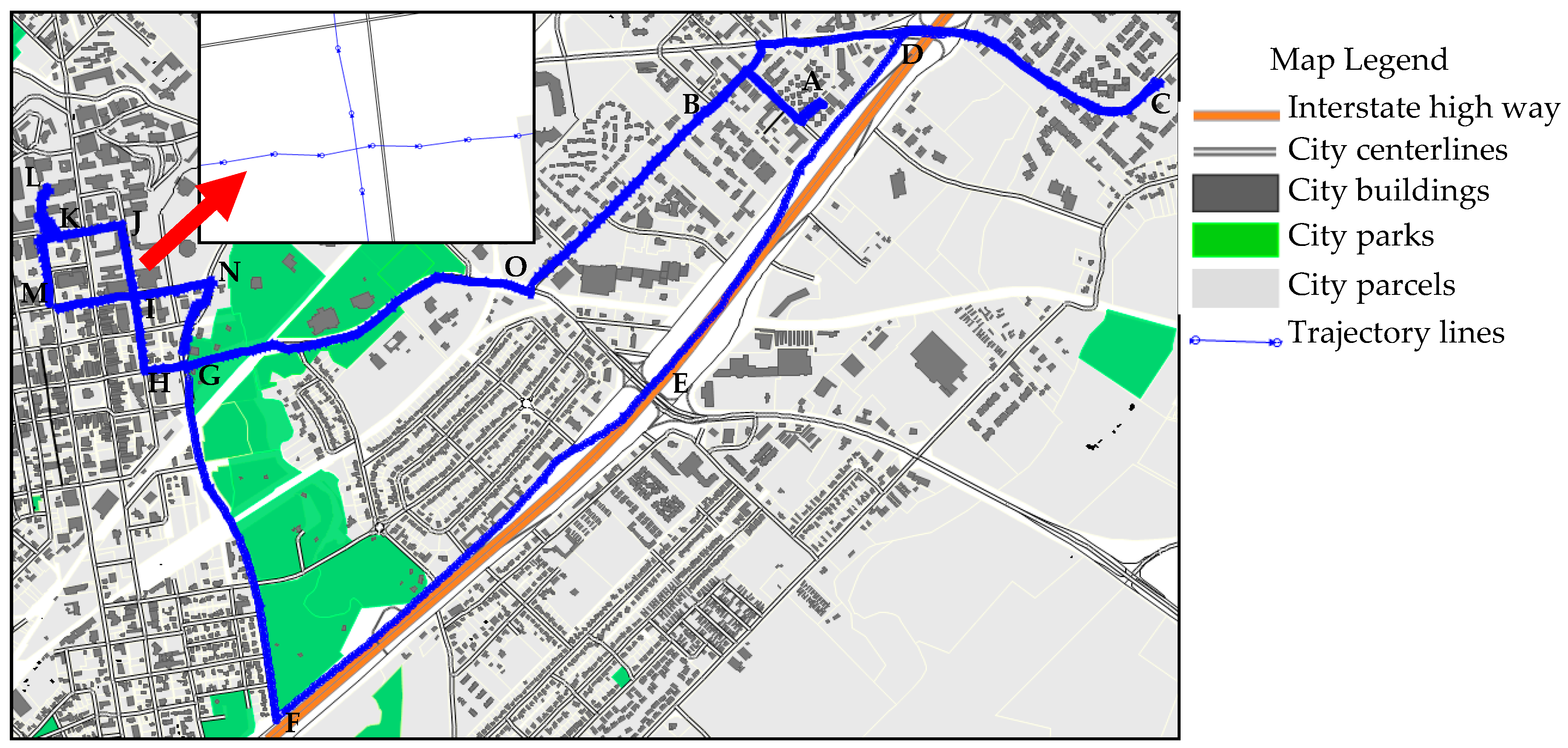
Section 4 applies both DP and ESTC-EDP to two sets of GPS trajectory data. The experimental trajectory data include a pedestrian GPS trajectory and a GPS trajectory of mixed transportation modes. The results from these two algorithms are evaluated and compared.
Section 5 includes conclusions and discussion as well as directions for future work.
2. Enhancing Traditional DP with Spatial-Temporal Constraints
One of the most well-known techniques for line generalization is Douglas–Peucker (DP) algorithm [
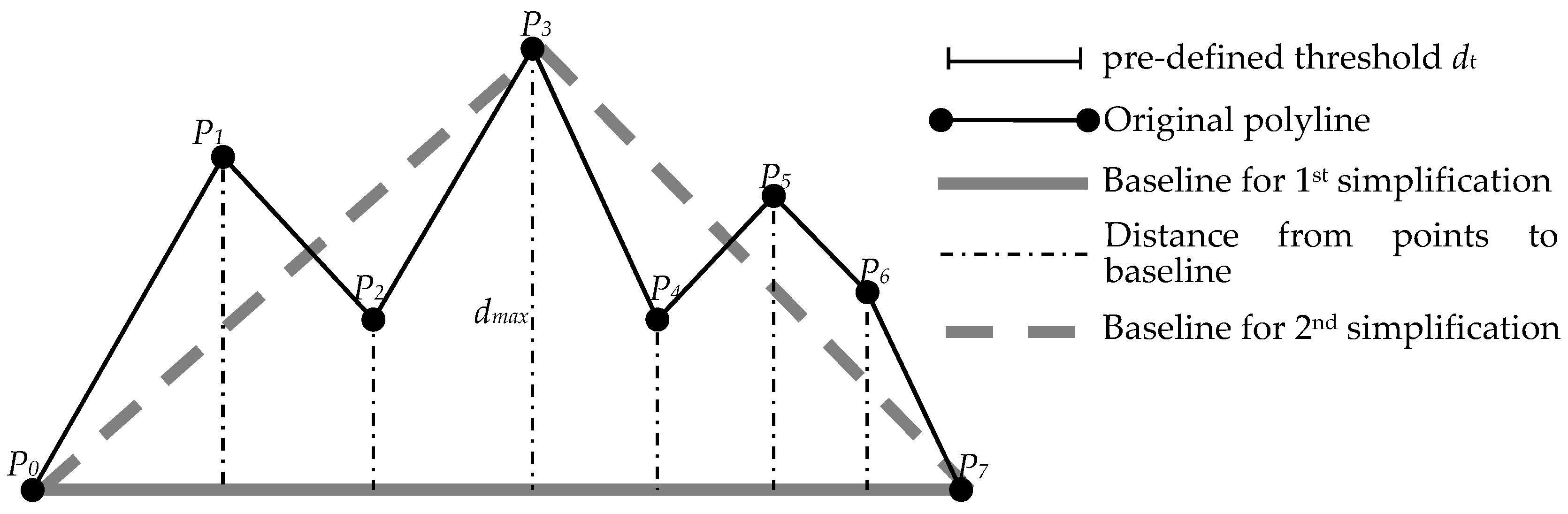
9]. DP algorithm employs a constructive refinement strategy. Vertices are sequentially inserted between the points defining the two ends of a polyline or line segment in accordance with a pre-defined distance threshold. The process repeats until the threshold is met. Algorithms such as this are often called global algorithm since they process an entire line at once.
Applied to the polyline in
Figure 1, DP algorithm preserves the end points P
0 and P
7 and connect them by a straight line. Then point P
3 is identified as the furthest vertex from line P
0P
7; its distance from line P
0P
7,
dmax, is compared with a pre-defined threshold,
dt. Since
dmax >
dt, P
3 is preserved for line generalization, and it is connected to both P
0 with P
7 to form a new polyline P
0P
3P
7. This process is repeated for line segments P
0P
3 and P
3P
7. The process will stop until the furthest point along the original polyline is within threshold distance
dt to its closest line segment. DP algorithm follows a recursive process.
GPS trajectory contains more characteristics than traditional geographic line features. Information on time, elevation, speed, etc. is important for describing a subject’s spatial-temporal behavior along a trajectory. Among these, speed information is most important because speed is a direct reflection of moving types such as passing versus staying, walking versus bus-riding, traveling by subway versus ground transportation and so on [
29]. Traditional line generalization such as DP algorithm treat all points as equivalent, leading to preserving only the points important for geometry; some location points along a trajectory that contain critical speed or elevation information but are not essential for geometry may be deleted during a DP simplification. However, these location points are
critical points for a trajectory and must be preserved to support correct depiction of the spatial-temporal movement and the related behavior along a trajectory.
Therefore, an effective simplification algorithm for GPS trajectory data must accomplish two goals: (1) to preserve the geometry of a linear feature, which was the focus of traditional line simplification algorithms; and (2) to preserve the additional characteristics of GPS trajectory that are essential for describing spatial-temporal movement, for example speed dynamics through travel time, elevation, and spatial relationship. To achieve these goals, the traditional line generalization algorithms may be augmented by a set of enhanced spatial-temporal constraints (ESTC) that are tailored to preserve the critical context information of a trajectory. How much enhancement a set of such spatial-temporal constraints need to consider is determined by what type of information from the trajectory must be preserved during trajectory simplification. In general, an effective set of ESTC for a GPS trajectory should consider the following aspects.
2.1. Speed Constraint
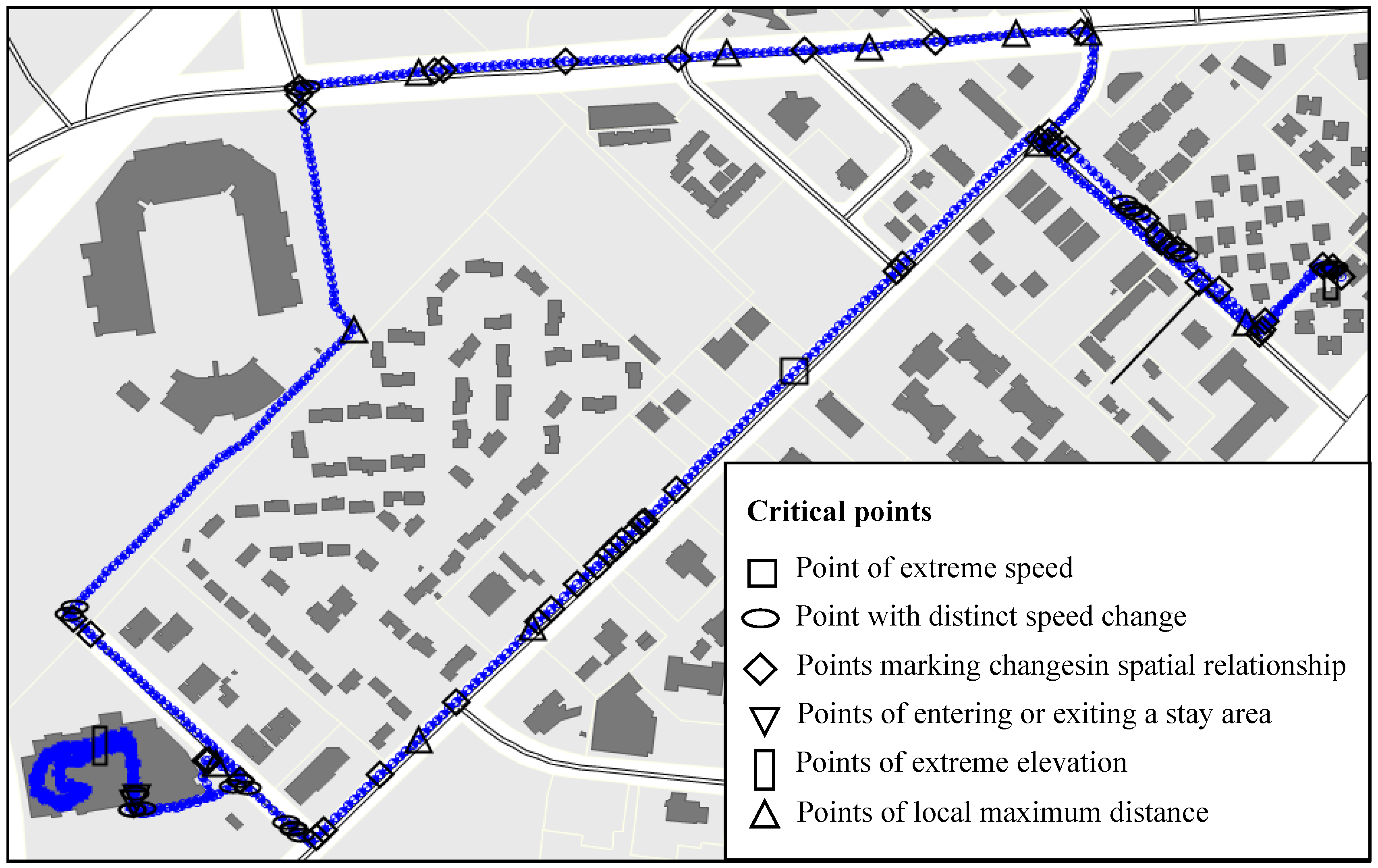
Speed is one of the most important aspects for GPS trajectory. Trajectory points with similar speed normally represent a same type of movement along trajectory, while points with distinct speed change may indicate a sudden change in moving condition. The following two kinds of points should be preserved during trajectory simplification.
Points of extreme speed: This constraint requires that the points with extreme speed at a local level be preserved during trajectory simplification regardless of their geometry significance for a trajectory. If the points with locally maximal or minimal speed are deleted, the implied travel information may be lost or modified.
Points with distinct speed change: This constraint requires that a point showing a distinct speed change from its precedent or subsequent point be preserved during trajectory simplification regardless of its geometry significance for a trajectory. Sudden speed change may very likely indicate a change in transportation, for example from walking to biking, or driving. Keep these points will allow for accurate interpretation of transportation mode and mode change.
2.2. Time Constraint
GPS trajectory points can be classified into two types based on motion: staying points and passing points. Correctly identifying these two types of points are important for understanding the spatial-temporal movement of a subject. Most researches identify staying points using clustering methods based on predefined spatial and temporal thresholds [
26,
30]. However, this approach may incorrectly include passing points into a cluster of staying points. For example, all points within the circle in
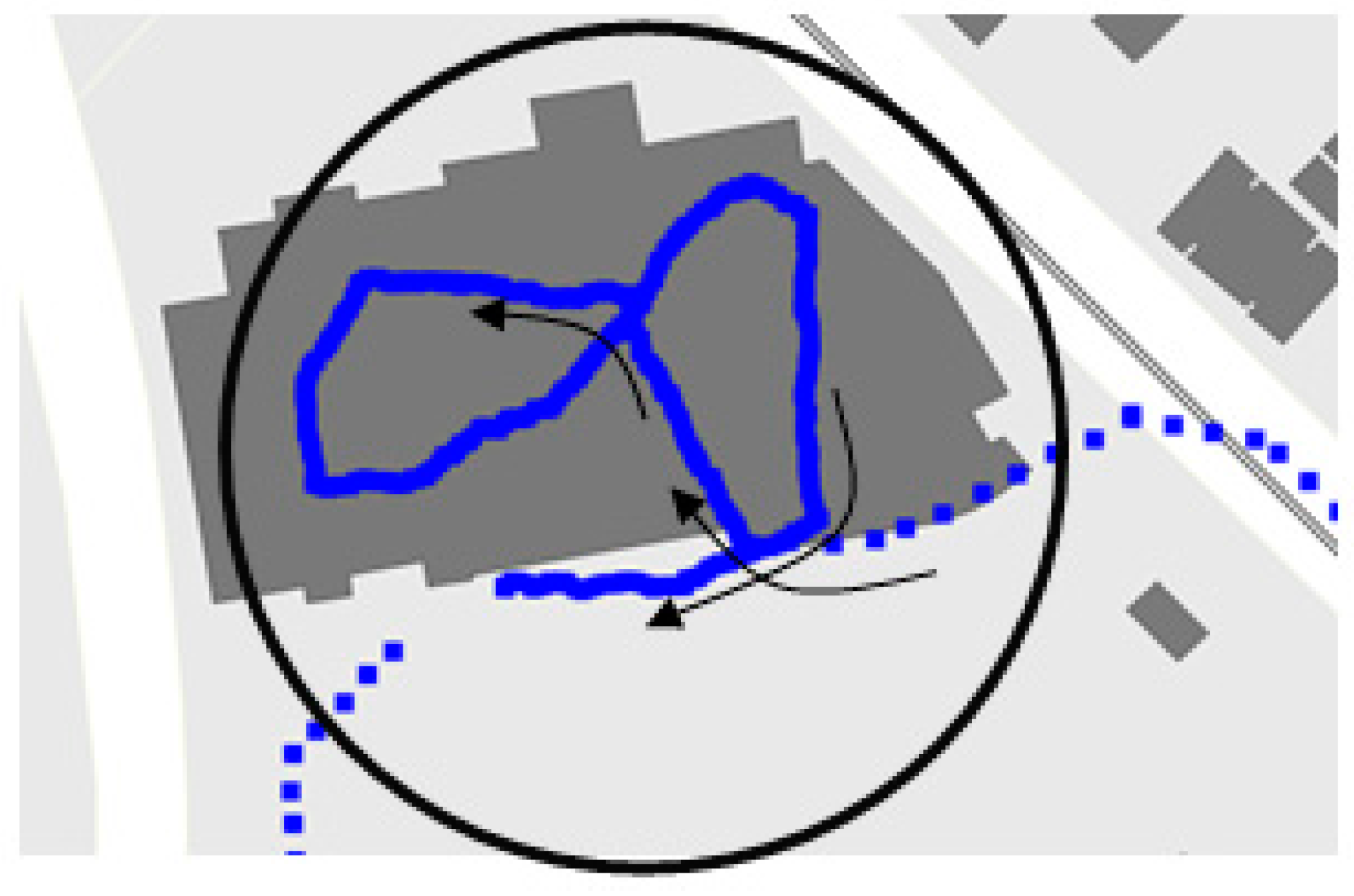
Figure 2 satisfy the thresholds of 200 m in distance and 10 min in time for defining a cluster of staying points at one place; the passing points outside the building (red colored polygon) while within the circle would be recognized as staying points by mistake (
Figure 2). However, if we know the beginning and ending time of staying activity, we can use the information during trajectory simplification to minimize false-identification of passing points as staying points.
Points defining staying time: The constraint requires that for a group of staying points, the starting and ending points of the staying time be preserved and that the time information be used to separate passing points from staying ones. Time stamp for entering and exiting a building or other area of interesting can be identified using other information, including time stamp for points where spatial relationship changes between a trajectory and certain land features (see the discussion of the next constraint). The total staying time at a place can be calculated. This way, passing points can be separated from staying points.
2.3. Constraint of Spatial Relationship
The spatial relationships between GPS trajectory and geography features (including roads and off-road places such as buildings or open markets) are important for understanding human activities. Thus, the GPS points that mark changes of such spatial relationships should be preserved during trajectory simplification.
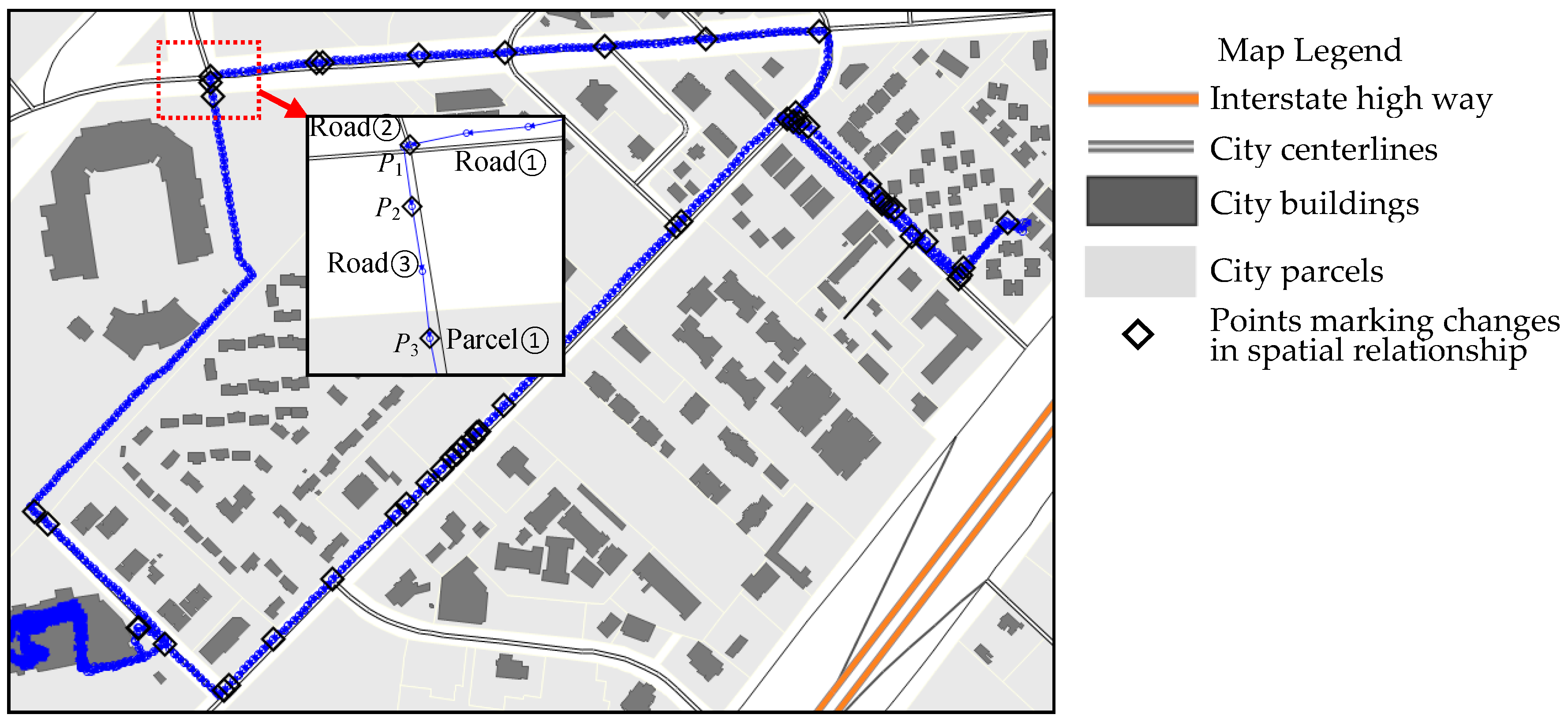
Points marking changes in spatial relationship: This constraint requires that the points that mark topological changes between a GPS trajectory and geographical features be preserved. Keeping these points where the topological relationship between a trajectory line and geographical features changes are critical for describing not only the geometry of trajectory but also the related spatial-temporal activities of a subject. These points may indicate transition along a journey from one road onto another or from moving to staying activities (e.g., location points P
1, P
2, and P
3, as illustrated in
Figure 3). For transition between moving and staying activities, pending on algorithms used, spatial-relationship constraint may be observed together with time constraint, for the points marking topology change may also mark the starting or ending points for a staying activity.
| The relationships of P1, P2 and P3 to other features. |
| Characteristic Points | Relationships to Others |
| P1 | road ①, road ② |
| P2 | road ③ |
| P3 | road ③, parcel ① |
2.4. Elevation Constraint
Another piece of information from GPS data is elevation, with which we can determine whether the GPS trajectory for moving object underground, on the ground, or flying in the air. Combining elevation with speed information will allow us to better understand the context of spatial-temporal activities as well as moving or transportation mode. Thus, points with distinct value of elevation should be preserved.
Points of extreme elevation: This constraint requires that the GPS points of local highest or lowest elevation values be preserved during GPS trajectory simplification. These points are likely good indicators of actual activities places and travel mode.
2.5. Additional Geometry Constraint
Although traditional DP algorithm considers geometry properties, points with important geometric characteristics may get deleted occasionally. Therefore, additional constraints are necessary to help better preserve geometry properties. For example,
partial maximum distance (PMD) method is used for map generalization to preserve a point that is furthest away from its related road segment; geometry shape of a trajectory at a local segment is better preserved this way. Note that PMD is different from DP’s recursive selection of critical points (
Figure 1) as PMD seeks to preserve points that are furthest from real-world road segments not from line segments in a graphic representation of a trajectory.
Points of local maximum distance: This constraint requires that a GPS point that is furthest away from its related road segment be preserved.
It is important to note that these ESTCs as discussed above are not meant to exclusively cover all important aspects of GPS trajectory data. By no means any set of ESTCs can include all possible scenarios. Furthermore, a particular GPS trajectory simplification must implement the constraints by considering particular environment context and traveling situation. The parameters for constraints must be defined to reflect the peculiarity of a trajectory. For example, for a ground transportation, an extremely large speed such as 200 miles per hour is more likely a data error than an extreme speed to preserve under “speed constraint”. Similarly, elevation constraint may not apply when simplifying a trajectory that known to occur on a relative flat landscape.
Furthermore, note that GPS data cleaning, such as that described in Schuessler and Axhausen [
31], should be performed on raw data before conducting trajectory simplification. For the GPS empirical datasets used in this paper, Lagrange fitting algorithm was applied to correct apparent errors in data before ESTC-EDP was used. Cleaning raw GPS trajectory data will reduce the chances for incorrectly keeping spurious locations as critical points during trajectory simplification.
3. Evaluating the Effectiveness of Trajectory Simplification
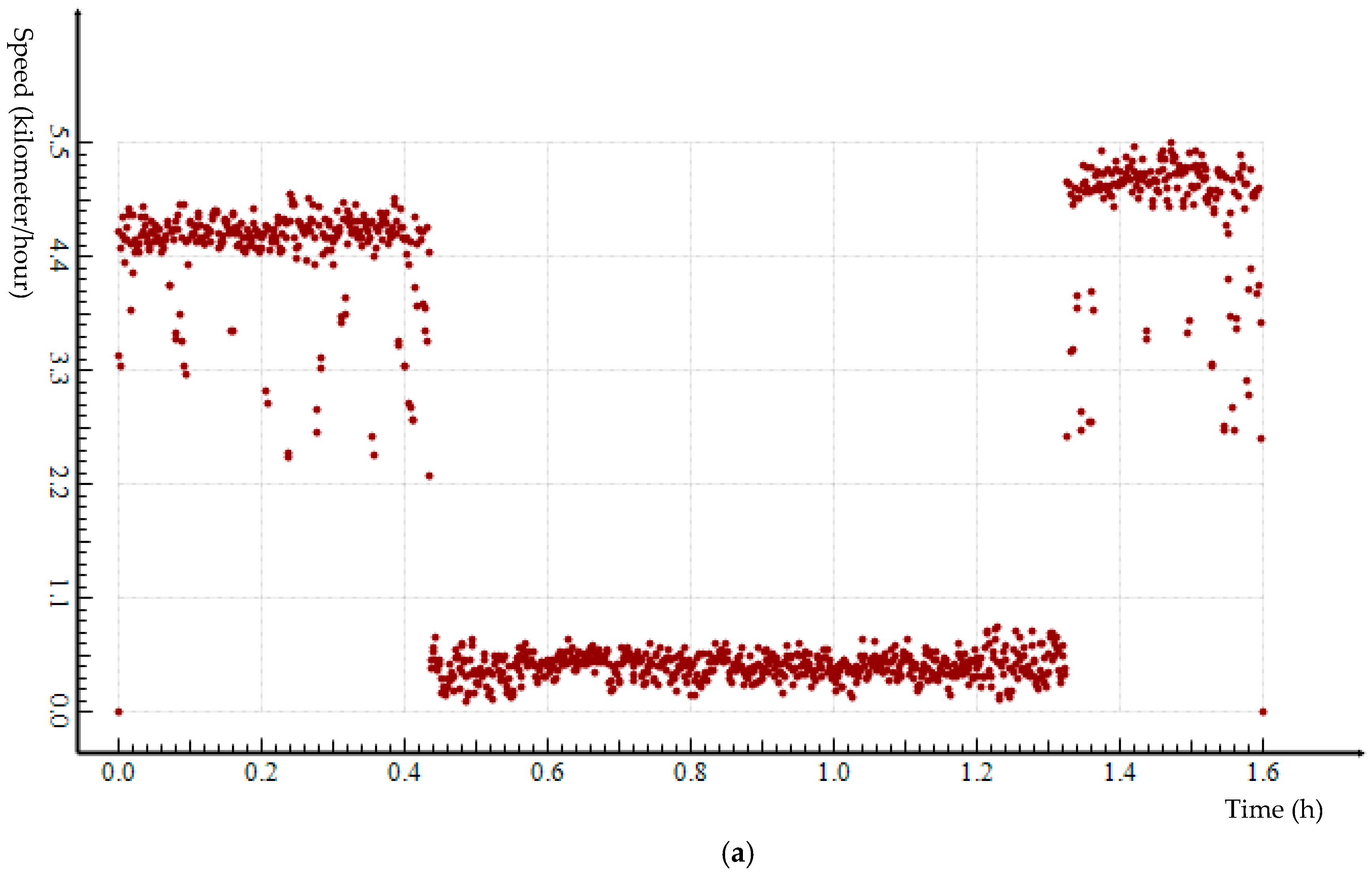
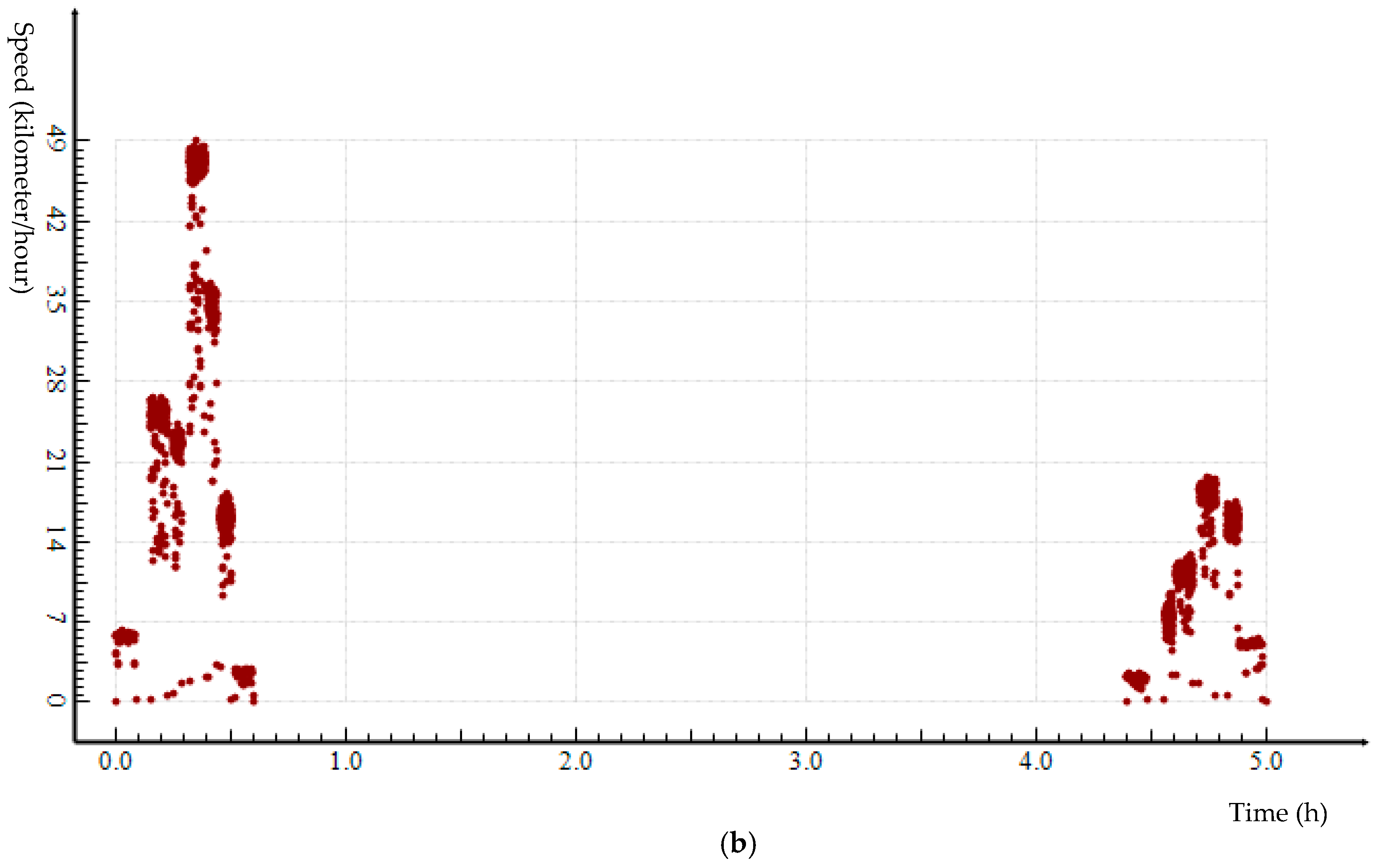
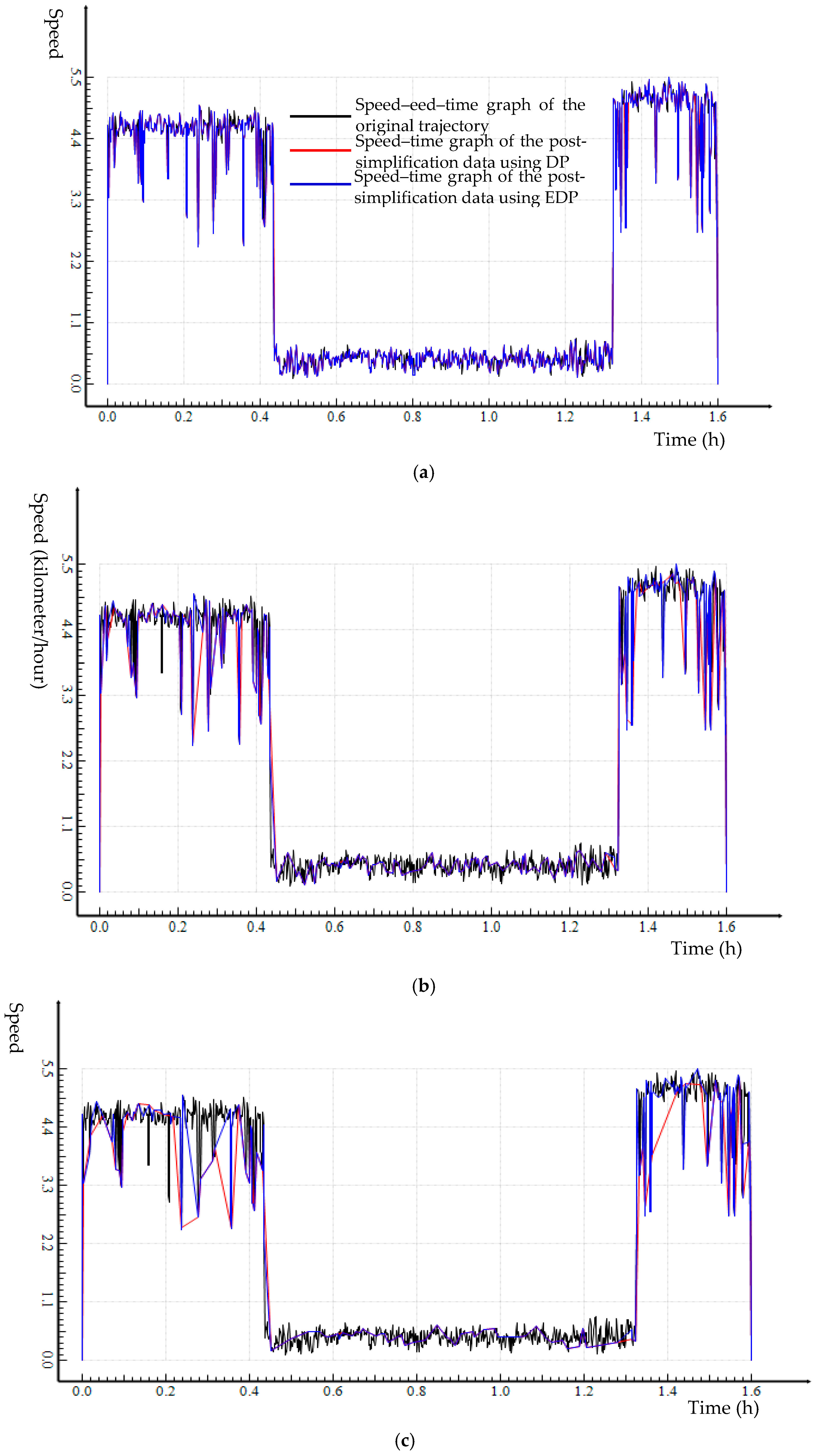
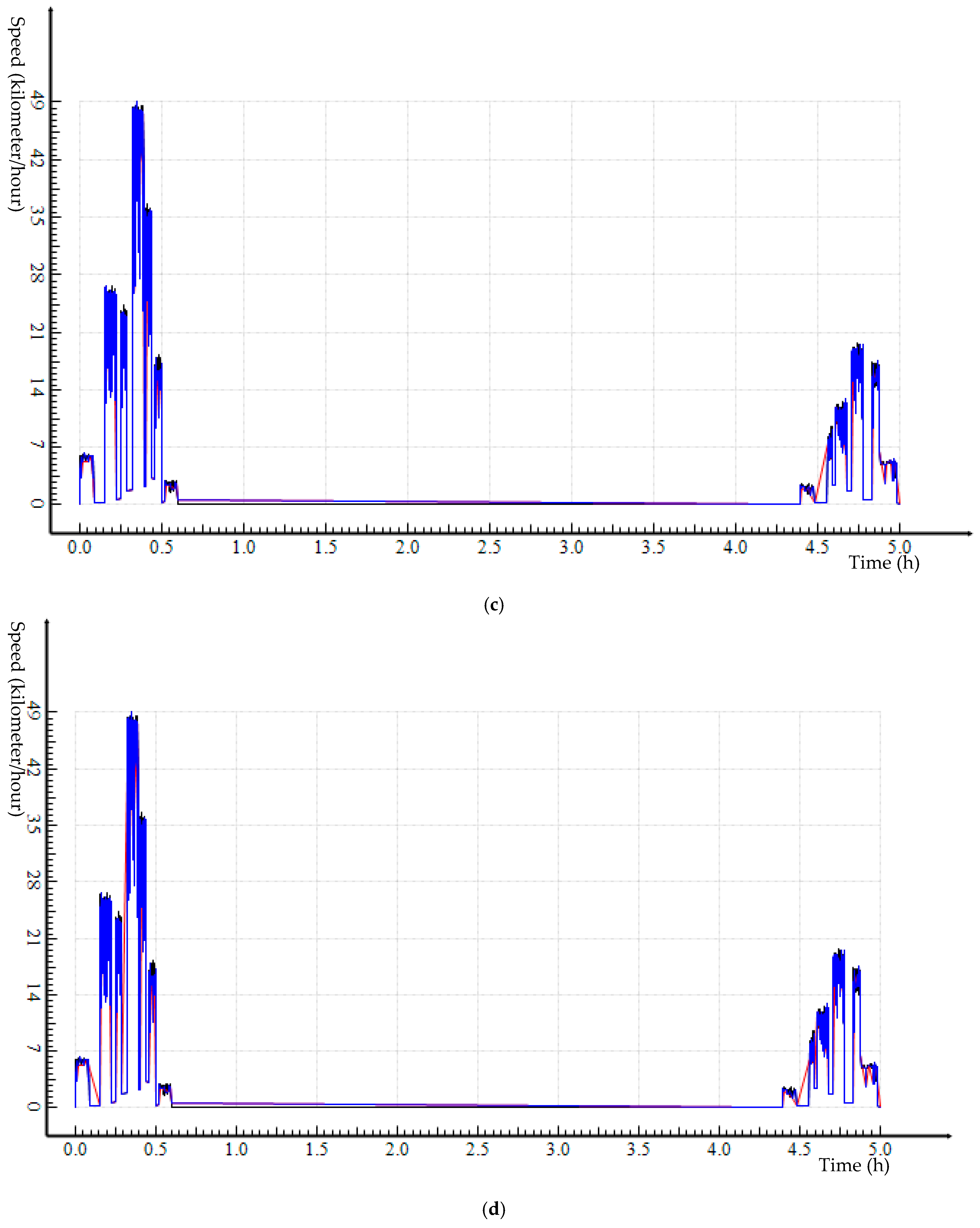
In addition to geometry properties, how the locations are connected through time (i.e., speed) is essential for describing a trajectory. Moreover, the change of speed through time describes the dynamics of moving status throughout a trajectory. Hence, together with geometry, speed and the change of speed throughout a trajectory uniquely define a trajectory. We use the term, speed–time profile, to refer to speed and changes of speed throughout a trajectory. An effective GPS trajectory simplification preserves the geometry of a trajectory so that location, orientation, and shape are kept as close to the original data as possible; it also preserves the speed–time profile of a trajectory so that there is minimum difference between pre- and post-simplified trajectory data.
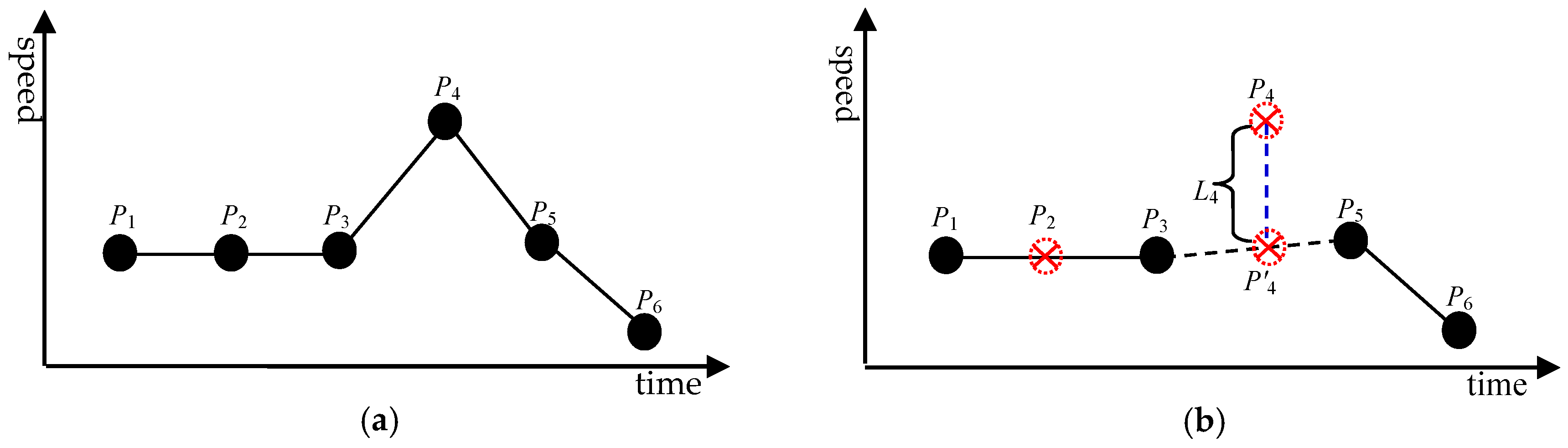
A
speed–time graph of a trajectory uses y-axis to show speed and x-axis time to describe speed and its variation through time. A speed–time graph presents a holistic picture about how fast/slow a subject travel at any time during a trajectory (
Figure 4a). A trajectory simplification process would drop some points from the original GPS dataset, but the speed–time profile as revealed by a speed–time graph should reveal minimum change for post-simplification data compared to pre-simplification data.
Using the speed–time graph in
Figure 4a as an example, the speeds at points
P1,
P2 and
P3 are equivalent. If point
P2 is deleted through a trajectory simplification, there will be no speed information loss as the speed at point
P2 can be accurately interpolated based on speed data for
P1 and
P3. However, the situation is different for points
P3,
P4 and
P5. If point
P4 is deleted, the original trajectory segment of
P3–
P4–
P5 will be recorded as
P3–
P5 (
Figure 4b). In this case, it will be quite a challenge to interpolate accurately the speed at point
P4 based on speed information for
P3 and
P5. If
P'4 is generated through interpolation, the gap between
P4 and
P'4 indicates an error, and it measures the magnitude of speed information loss, referred to as
speed loss in this paper.
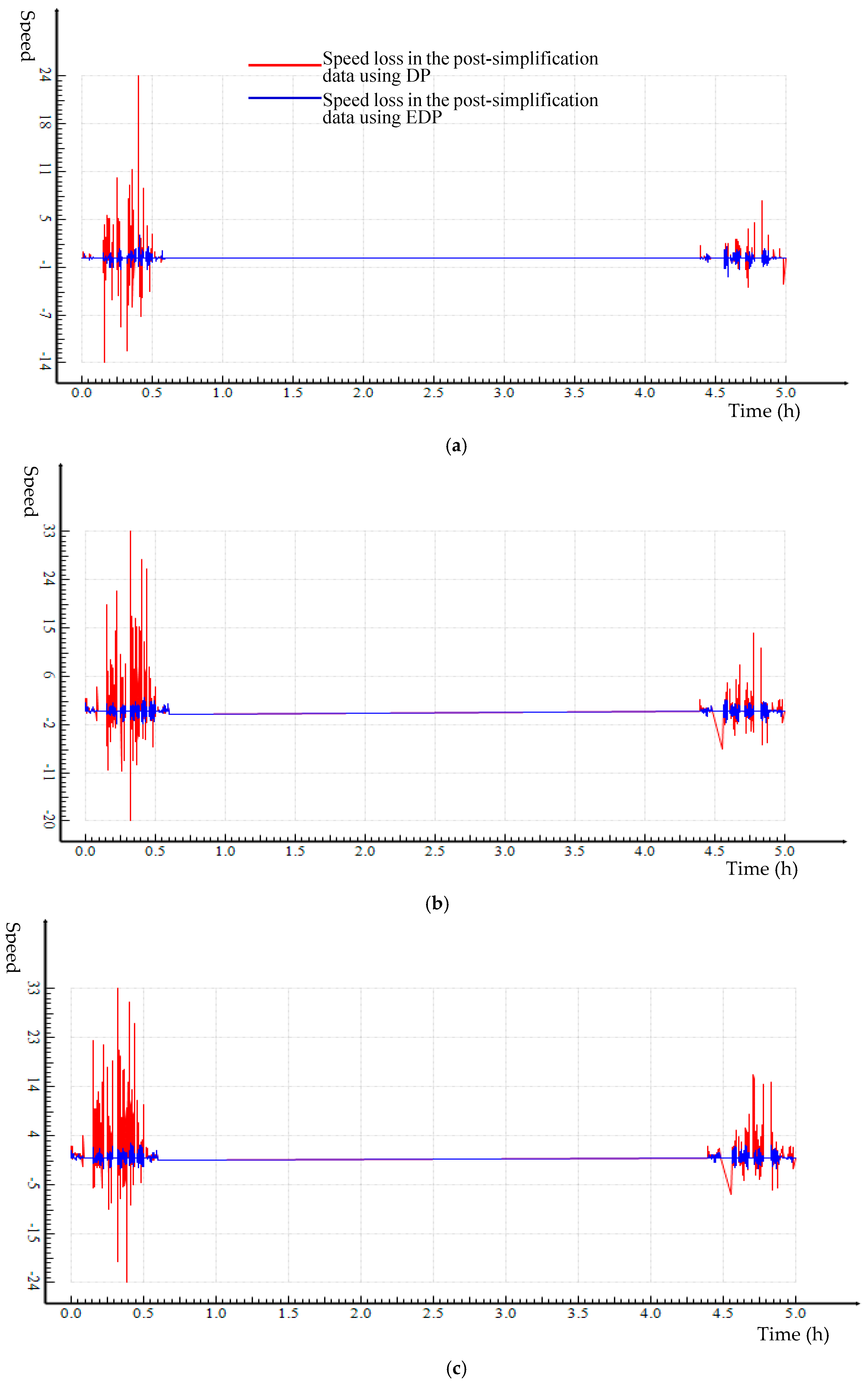
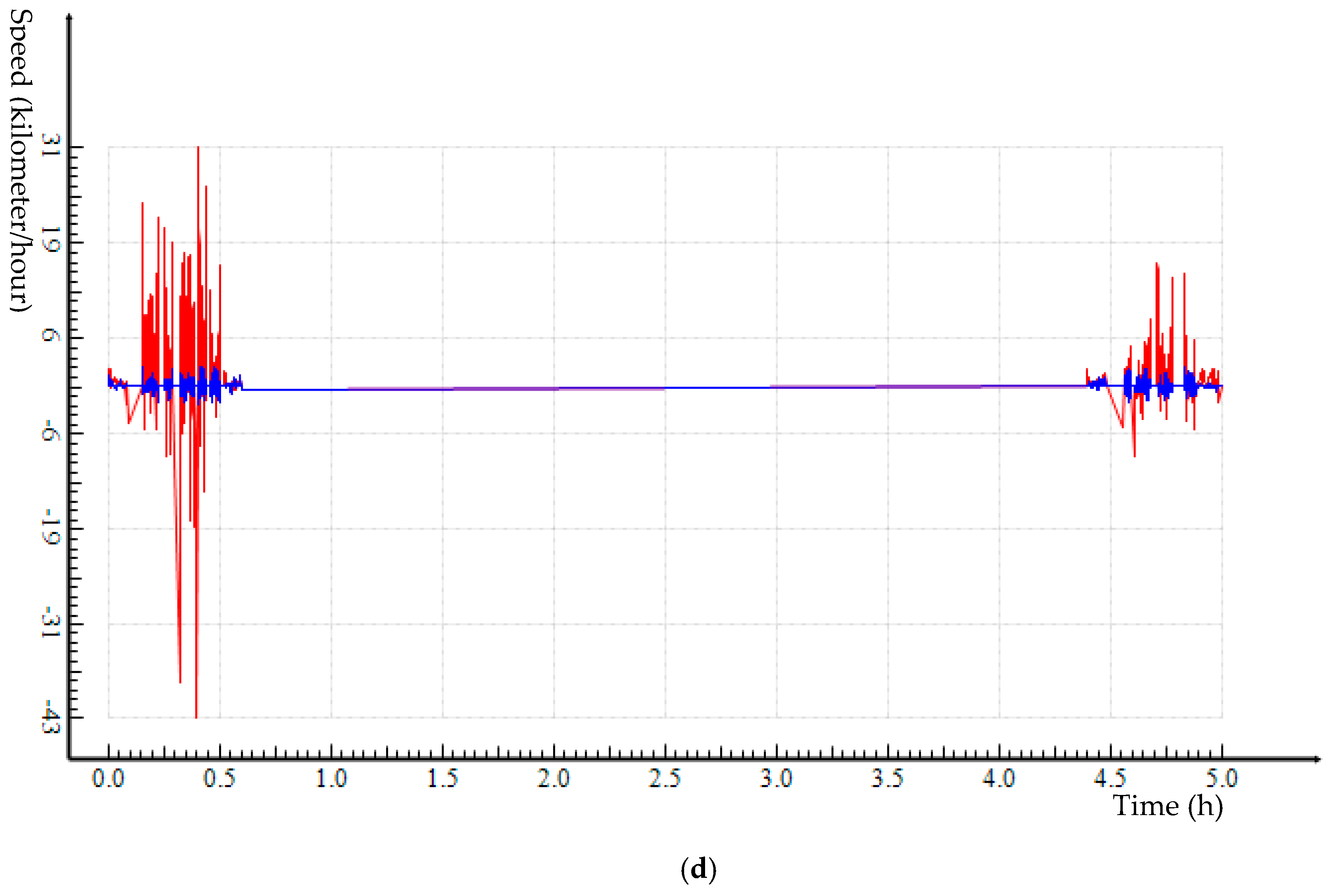
When simplifying a complete trajectory, we can calculate speed loss for every point that was dropped. Dividing the total speed loss for all removed points by the total number of points removed will generate average speed loss. Relative average speed loss is the percentage of average speed loss from trajectory simplification to average speed of a trajectory. These indicators can be used to assess the effectiveness of a trajectory simplification algorithm.
5. Conclusions and Discussion
To effectively simplify a very large GPS trajectory dataset, traditional line generalization algorithms can be enhanced by a set of spatial-temporal constraints so that both geometrical and non-geometrical characteristics that are essential for defining and describing spatial-temporal movement and the related travel behavior can be preserved. Considering that variations exist regarding trajectory environment, moving modes, subjects’ behavior, etc., this paper discusses enhanced spatial-temporal constraints (ESTC) from five aspects: speed constraint, time constrain, constraint of spatial relationship, elevation constraint, and additional geometry constraint. The implementation of these constraints for a trajectory must reflect the peculiarity of spatial-temporal and individual activity context.
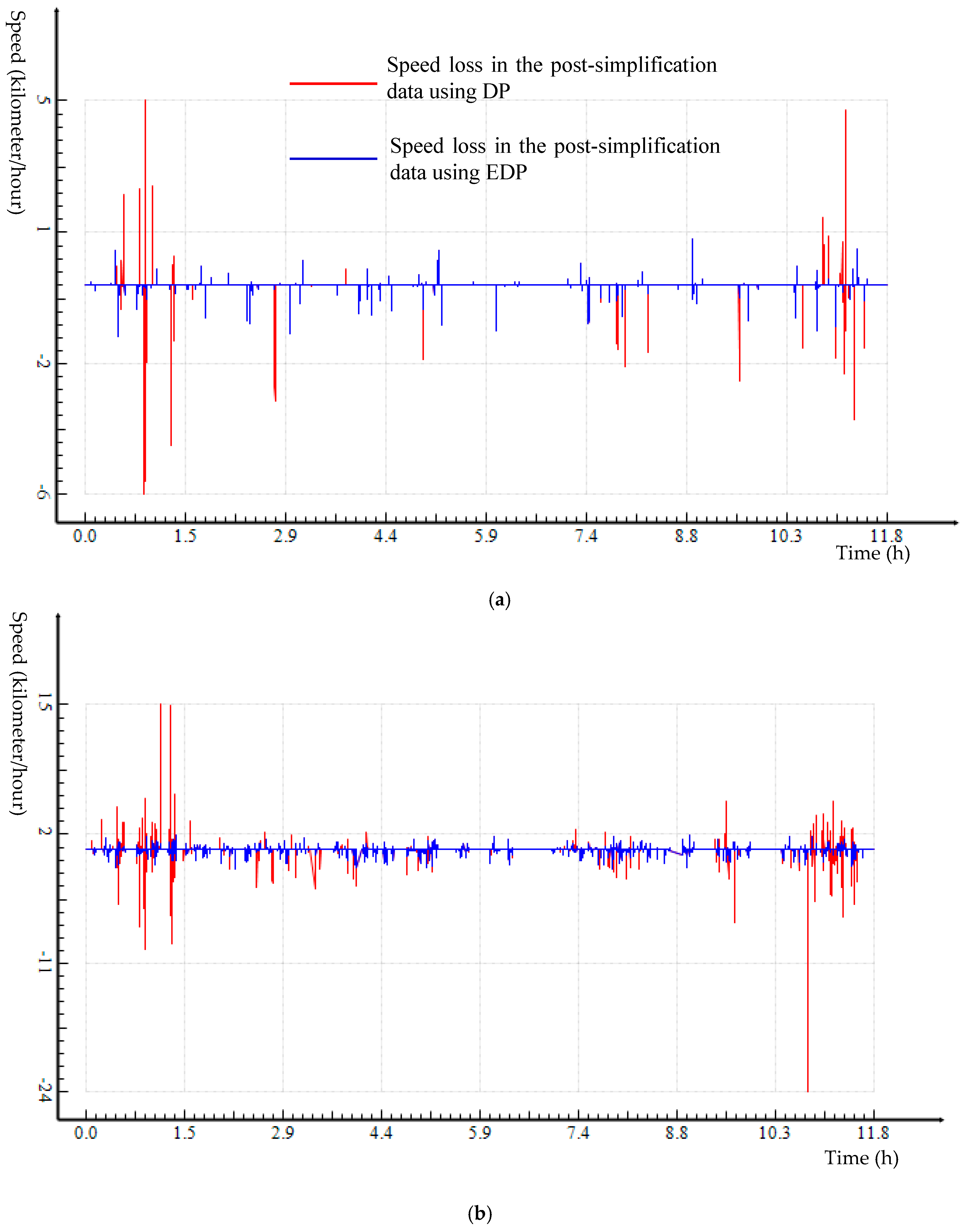
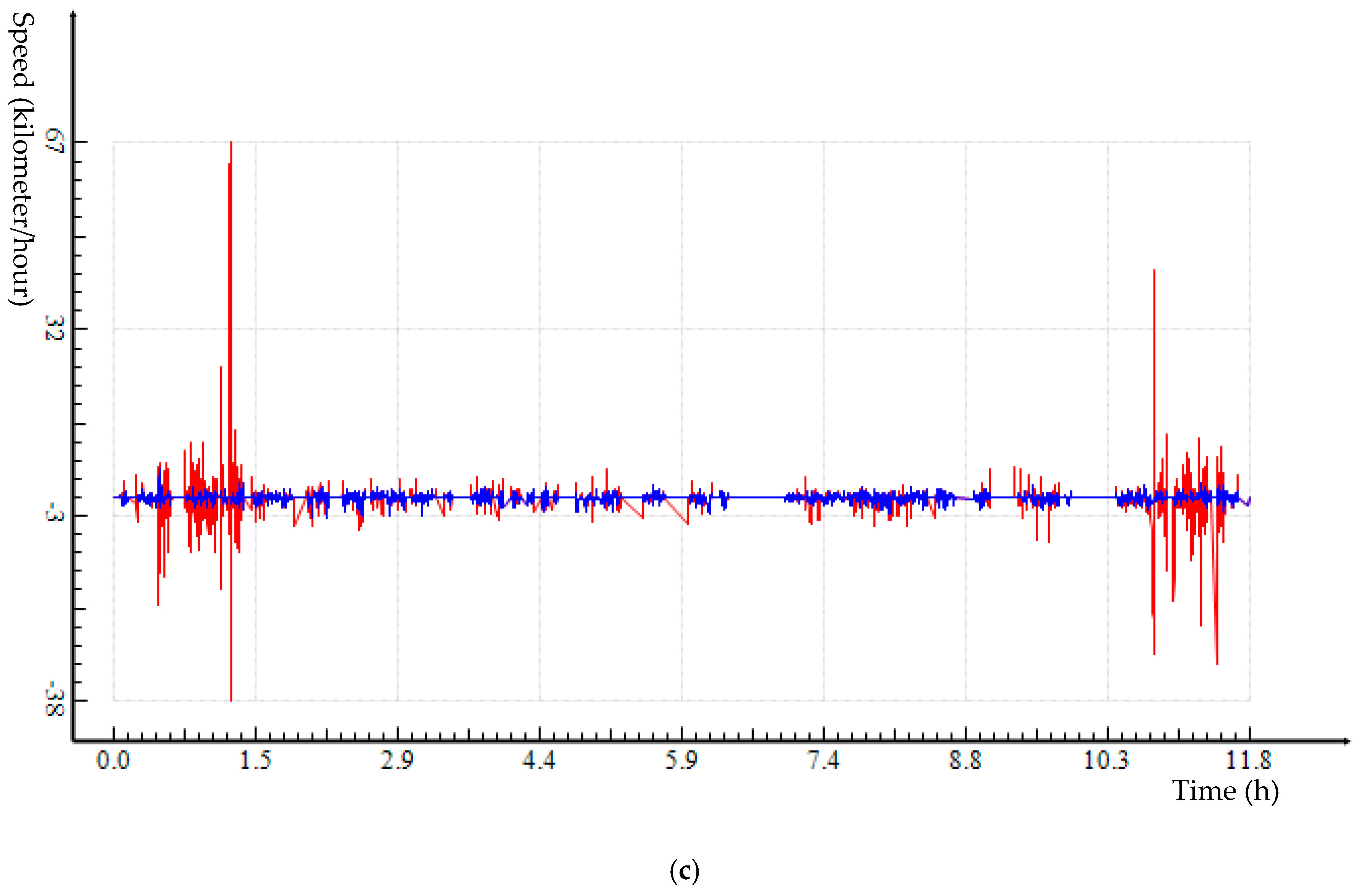
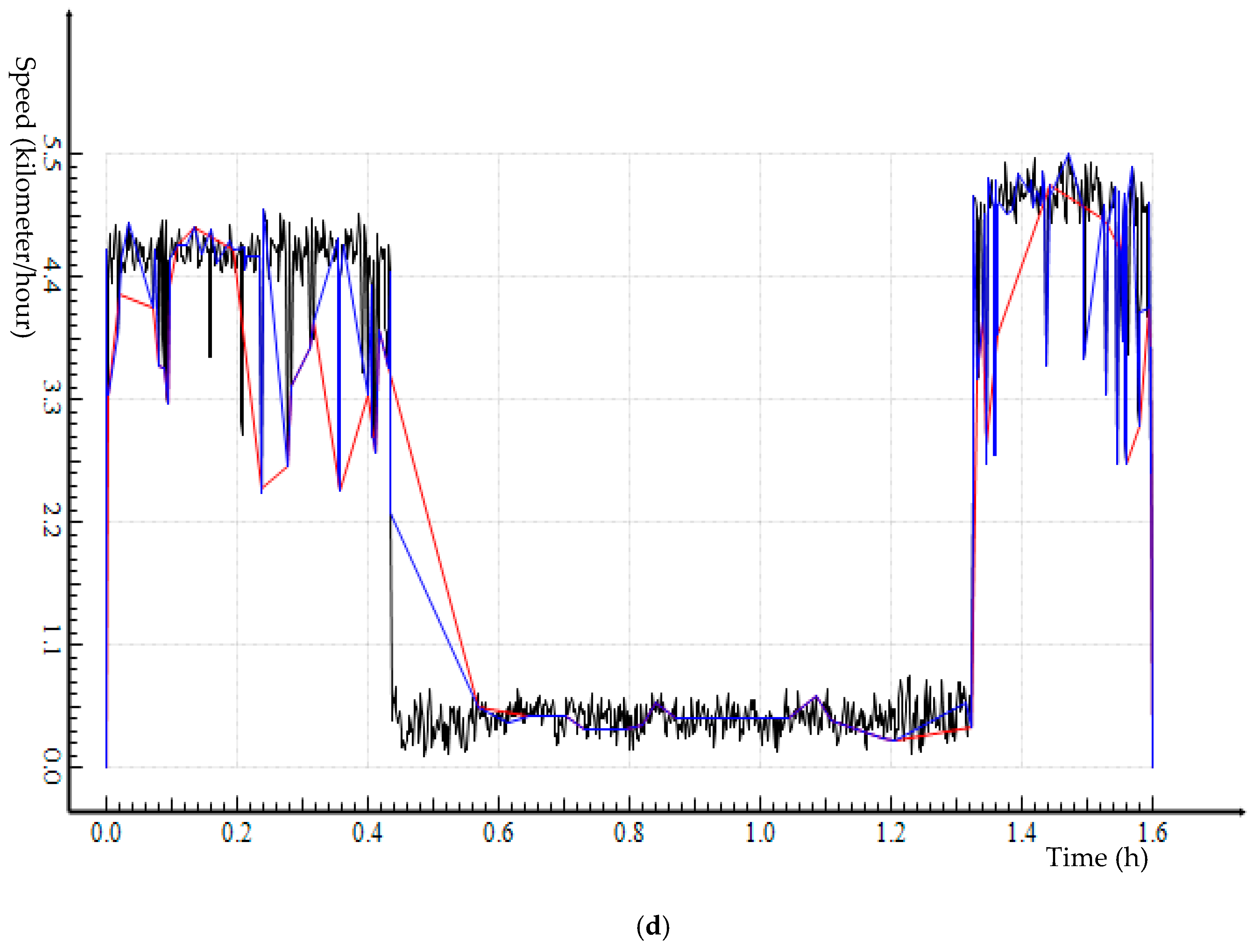
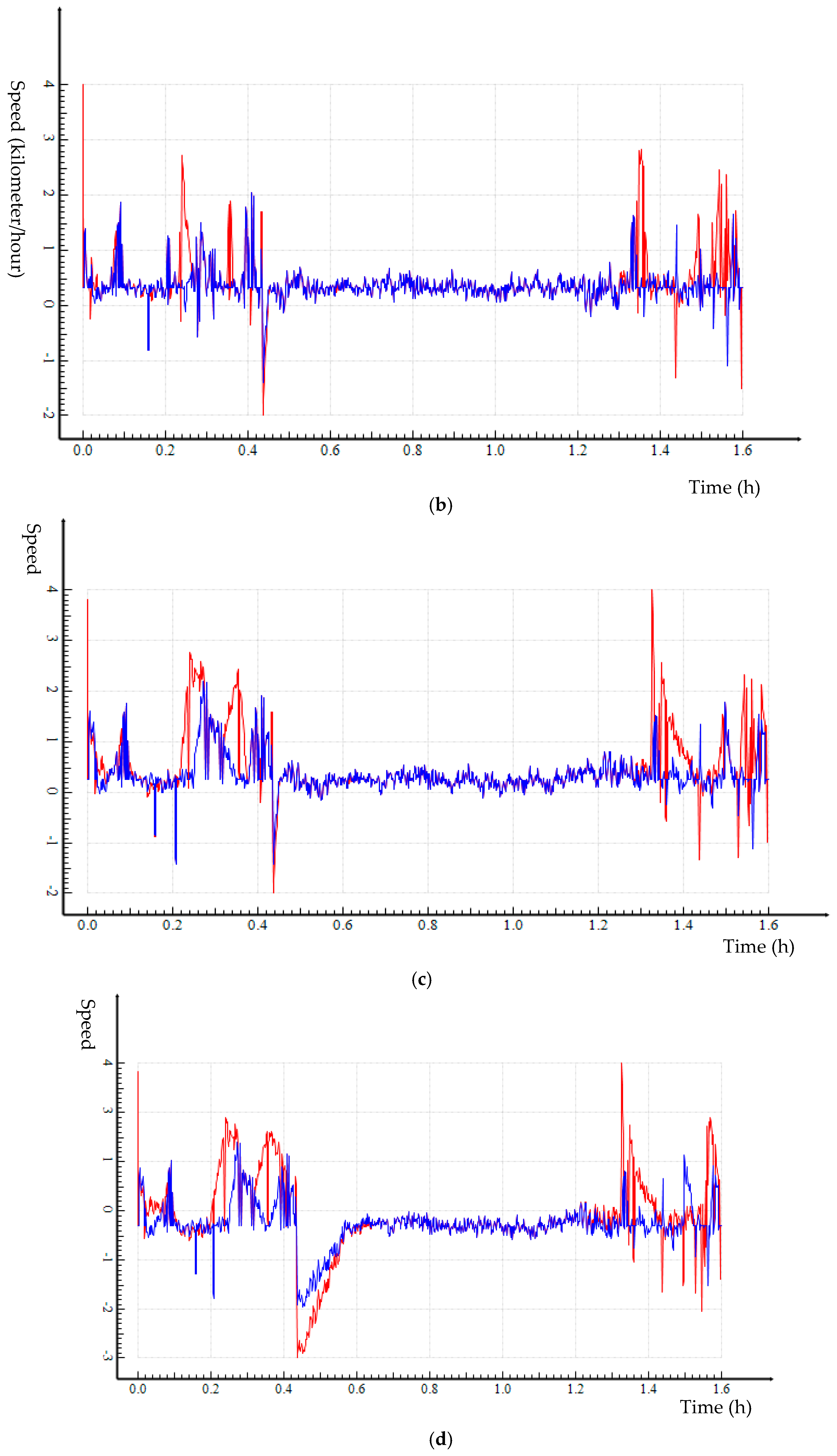
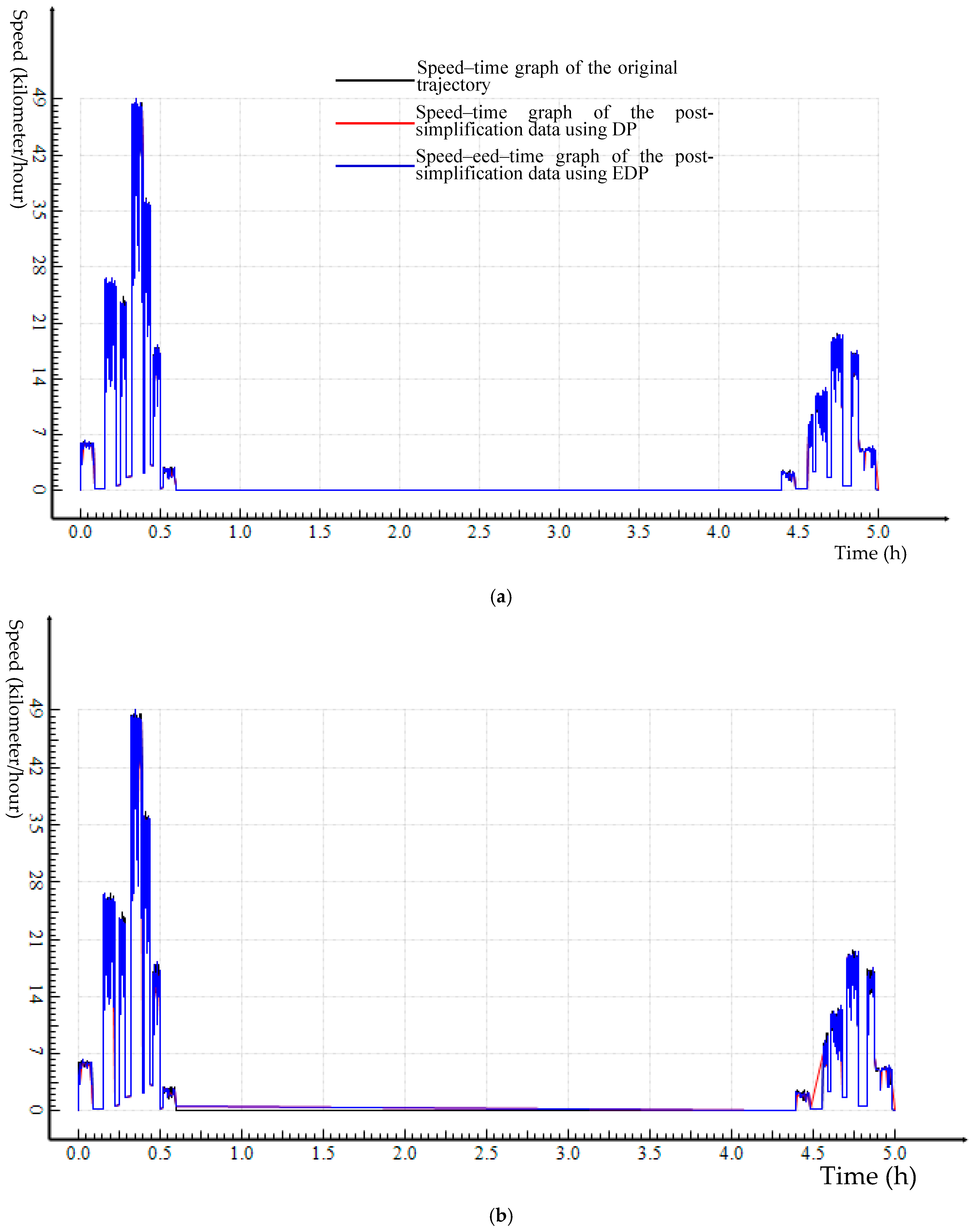
Both Douglas–Peuker (DP) and Enhanced DP (EDP) algorithms were applied to two empirical trajectory datasets that were collected by the researchers. A range of distance thresholds was used for trajectory simplification. It is clear that, compared to DP, EDP trajectory simplification performs consistently better across the distance thresholds for both trajectory datasets. EDP preserves all critical points through implementing the various ESTCs (
Table 1 and
Table 3); keeps the speed profile of trajectory closer to the original data (
Figure 9 and
Figure 11); and controls speed loss better (
Table 2 and
Table 3, and
Figure 10 and
Figure 12).
We noticed that literature has started seeing attempts seeking to preserve speed during trajectory simplification. For example Ying and Su [
33] proposed an approach for trajectory simplification with velocity preservation. However, their method only ensures that the velocity difference between a simplified trajectory and the original data is below a threshold. They failed to consider other aspects that are important for a trajectory, which can be preserved by our ESTC-EDP method through the five spatial-temporal constraints as explained in
Section 2. A simplified trajectory following [
32] may fail to catch the movement of a trajectory that enters and/or exists a market or a public park if there is no big speed change in the process; similarly, it may mistakenly delete the elevation peak point along a trajectory. Our ESTC-EDP method enforces the preservation of these critical points along a trajectory.
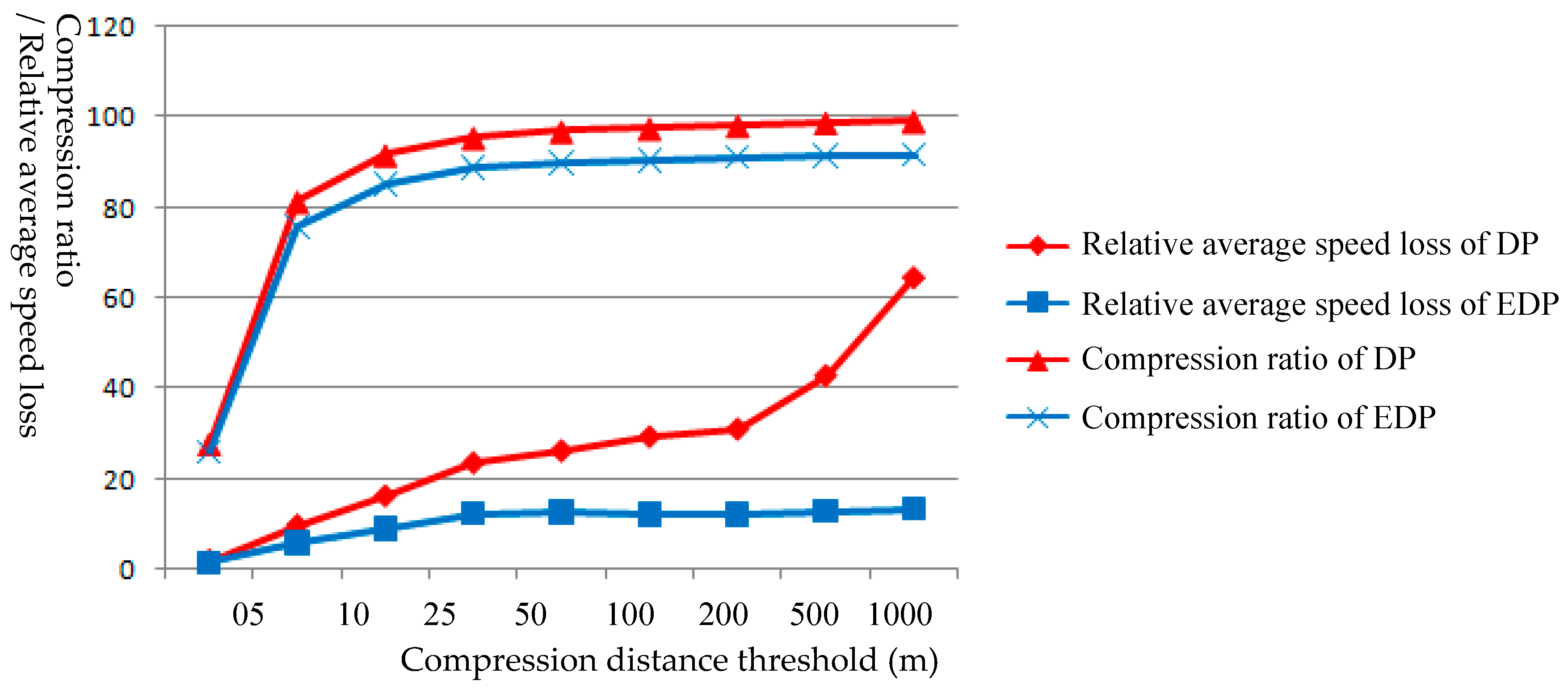
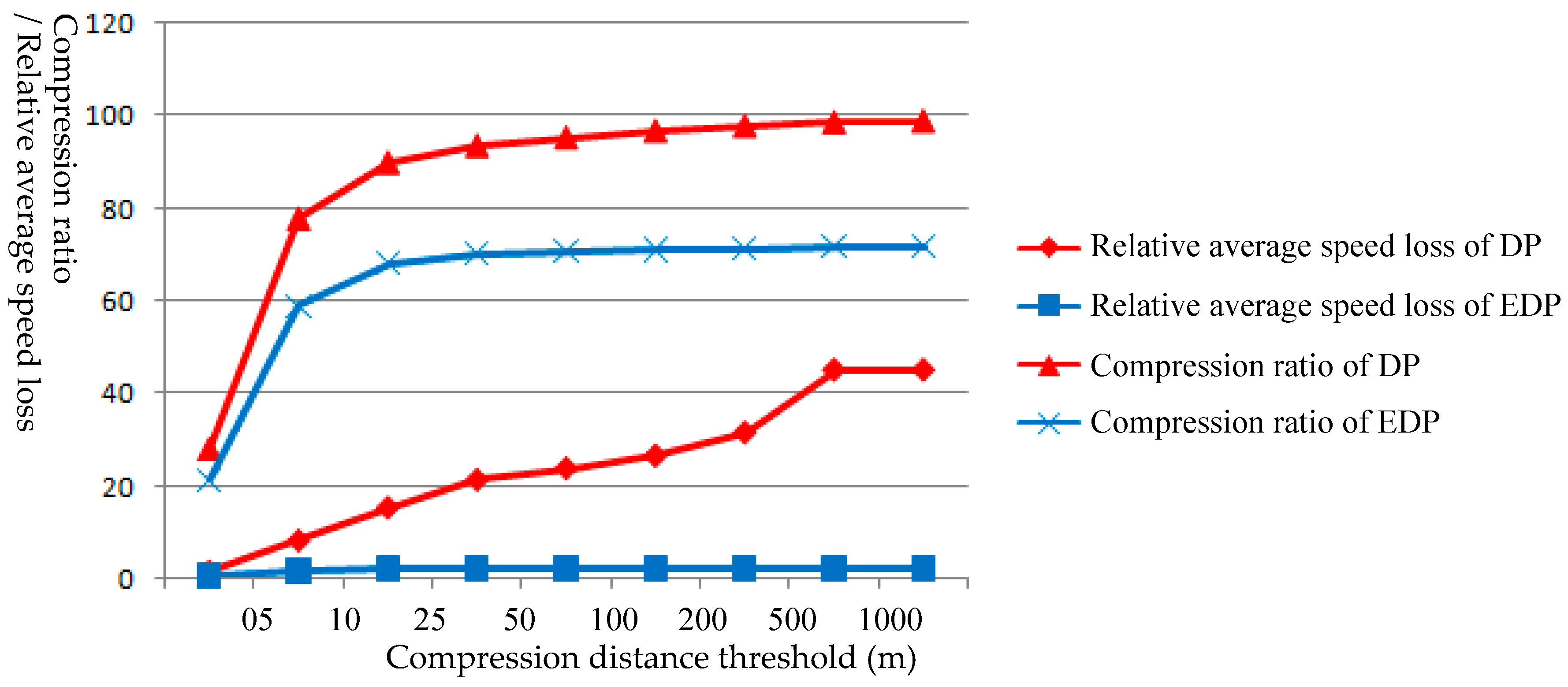
To further the discussion on comparing the effectiveness of DP and EDP,
Figure 13 and
Figure 14 are created to show the change of trajectory data
compression ratio and
relative average speed loss when the distance threshold for simplification increases. For illustration purpose, we have reported in the two graphs very large distance thresholds for the purpose of showing trend; these thresholds are not likely to be used in real cases. We can see that, despite that
compression ratio has a converging trend for both DP and EDP algorithms,
relative average speed loss of DP and EDP algorithms show different patterns. The relative average speed loss for DP simplification continues to increase as distance threshold increases, while that for EDP simplification starts to stay stable at a relatively small value.
It can also be observed in
Figure 13 and
Figure 14 that when DP and EDP methods are applied to both trajectory datasets, the compression ratio of both approaches converge to a level after a certain distance threshold, around 25-m for the empirical datasets in the experiments. This threshold may vary across different landscapes as well as GPS data qualities. It is an important parameter to know for deciding on trajectory simplification parameters. Note that the compression ratio from DP algorithm is expected to be larger than that from EDP algorithm, as EDP uses ESTCs to enforce the preservation of critical points in addition to the geometrically essential points along a trajectory. However, the compression ratios from DP and EDP are more similar for Trajectory 1 than those for Trajectory 2. This may indicate that EDP simplification for Trajectory 1 produced results more similar to that from DP, and EDP algorithm is more effective for simplification of Trajectory 2 dataset. This could be due to the fact that travel mode for Trajectory 1 is relative simple with mostly walking and staying while Trajectory 2 contains a lot of bus moving-and-stop and traffic speed variation. It is also important to notice that, with more critical points preserved for Trajectory 2 by EDP, the average speed loss is noticeably smaller for Trajectory 2 simplification than for Trajectory 1. This suggests that EDP simplification have greatly improved the trajectory simplification of Dataset 2, for which critical points are better preserved and average speed loss better controlled.
We recognize that more experiments are needed to test for the effectiveness of the proposed ESTC-EDP simplification method. The two trajectories used for case studies in this paper were collected by the authors in very similar environment settings (i.e., the same city). To further illustrate the effectiveness of ESTC-EDP, we applied it on a secondary trajectory dataset that were collected in a different place. The analyses and results are reported in
Appendix A. Similar to the findings reported above, ESTC-EDP is proven to be more effective for trajectory simplification.
Like any other studies, this reported trajectory simplification approach and the empirical analyses are not without limitations. First, the empirical trajectory datasets used here are limited to built environment and are all intra-city movements. Future studies should further investigate how the effectiveness of EDP may be related to the different aspects of trajectories, including topography, land use patterns, traffic variation, transportation modes and mixture of modes, and frequency of staying-moving transition. With ESTC to be designed to reflect the environment for and the spatial-temporal movement variations of a trajectory, EDP is effective in considering the peculiarity of more complexed settings and trajectories. Second, systematic design should be applied to collect trajectory datasets to enable further comparison of EDP and DP simplification at selected context settings. Speed–time graph and relative average speed loss can be used as measures for the effectiveness of a trajectory simplification.