Road2Vec: Measuring Traffic Interactions in Urban Road System from Massive Travel Routes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Word-Embedding Techniques and the Word2Vec Model
2.1.1. Word-Embedding Techniques
2.1.2. Word2Vec Model
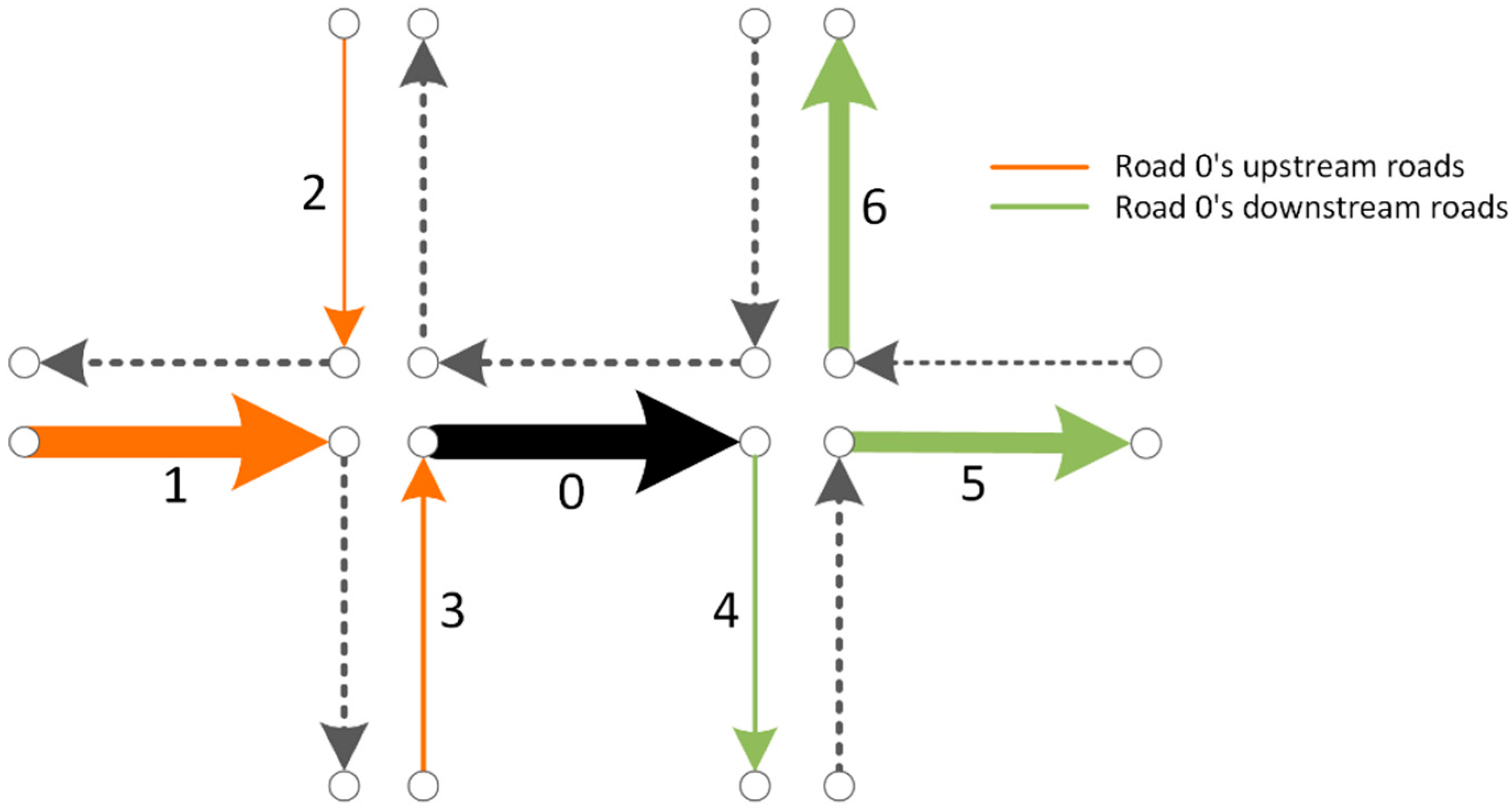
2.2. Measurement of Traffic Interaction among Roads
2.2.1. Analogous Relationships among Routes and Documents
2.2.2. Training Road Segment Vectors
- documents are lists of textual documents, and each document is a list of words in a serial order;
- dimension is the dimension of the word vectors, and reasonable values are in the tens to hundreds; and
- window is the most important parameter that determines how many words will be used as each word’s contexts. For instance, a window equaling to 5 indicates that the five words ahead and five words behind will be used as the contexts for the center word in the training.
2.2.3. Calculating Similarities among Road Segment Vectors
3. Results
3.1. Data
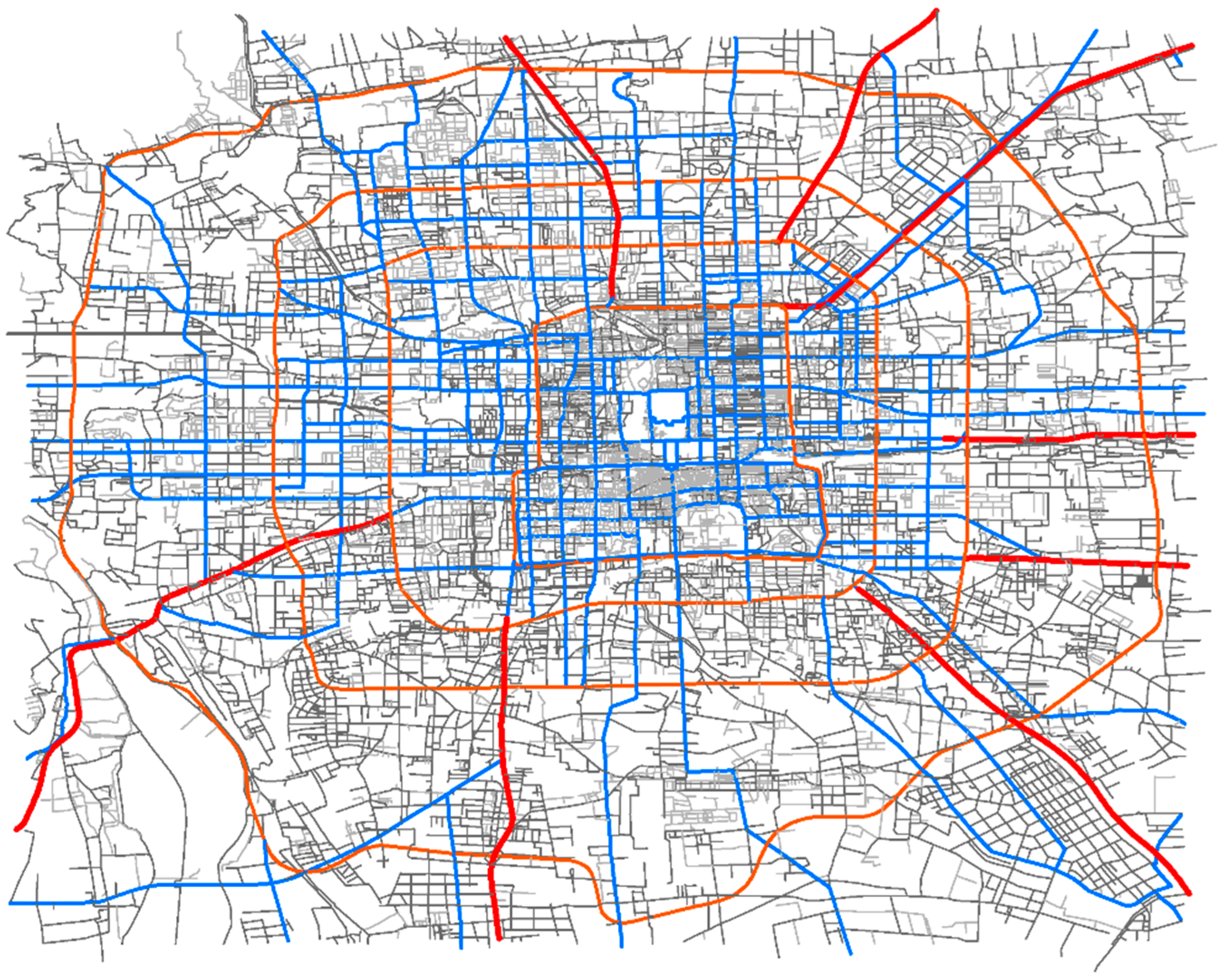
3.1.1. Road Network
3.1.2. Floating Car Data
- 1.
- Travel routesWe map all the GPS points between passengers’ pick-up and drop-off locations (i.e., travel trajectories) to the road network using a map matching algorithm called ST-CRF, which can process low-frequency (i.e., sparse) FCD [25]. After mapping each GPS point to a road segment, we proceed as follows:
- (1)
- if more than one consecutive GPS points are mapped onto the same road segment, then the road segment is only counted once in the travel route;
- (2)
- if two consecutive GPS points are mapped onto different road segments that are not topologically adjacent in a road network, then we use the shortest path between the two road segments to form the travel route.
- 2.
- Traffic statesThe speed on each road segment in each time interval on each day is extracted from the FCD by calculating the average speeds of the passing cars during the current time interval. If there is no car passing through during the current time interval, then, we use a valid value from another day in the same time interval as an alternative. Because we set the period of each time interval as 5 min, there are 288 total time intervals in a day. For each road segment, the speed data on different days are reconstructed into five long time series according to the period, that is, workday morning rush hours, workday evening rush hours, workday non-rush hours, weekends, and holidays. Each of the five long time series is formatted as follows:where represents the total days in the workday/weekend/holiday, while represents the number of intervals in the workday morning rush hours, workday evening rush hours, workday non-rush hours, weekend, or holiday on each corresponding day.
3.2. Results
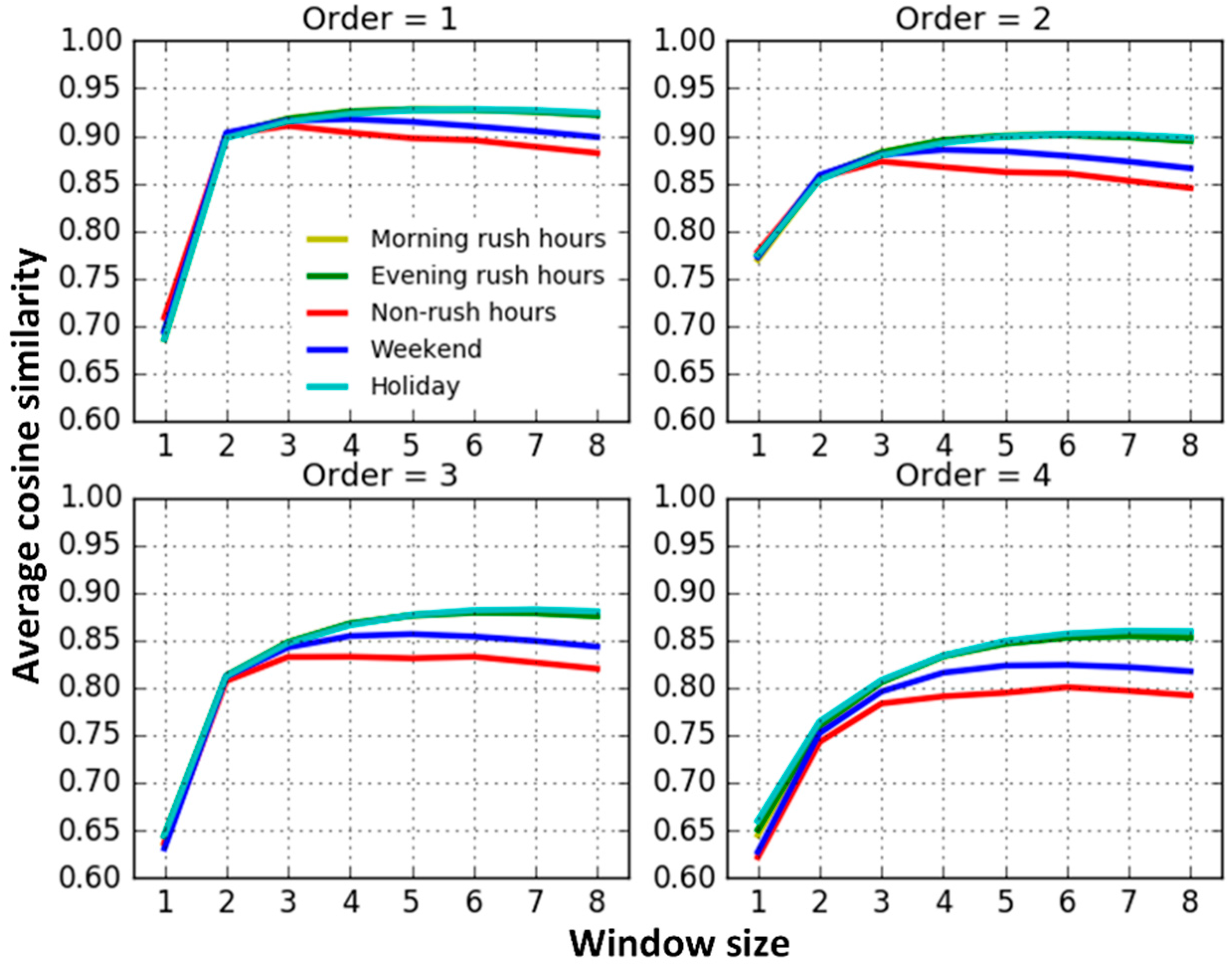
- (1)
- When the window size equals 1, the traffic interactions among roads are very weak and apparently different from the results trained from models with larger window sizes. This may result from the insufficient contextual information attempting to capture road interaction relationships. The results trained from models with the window sizes from two to eight slightly increase at first, and then remain steady.
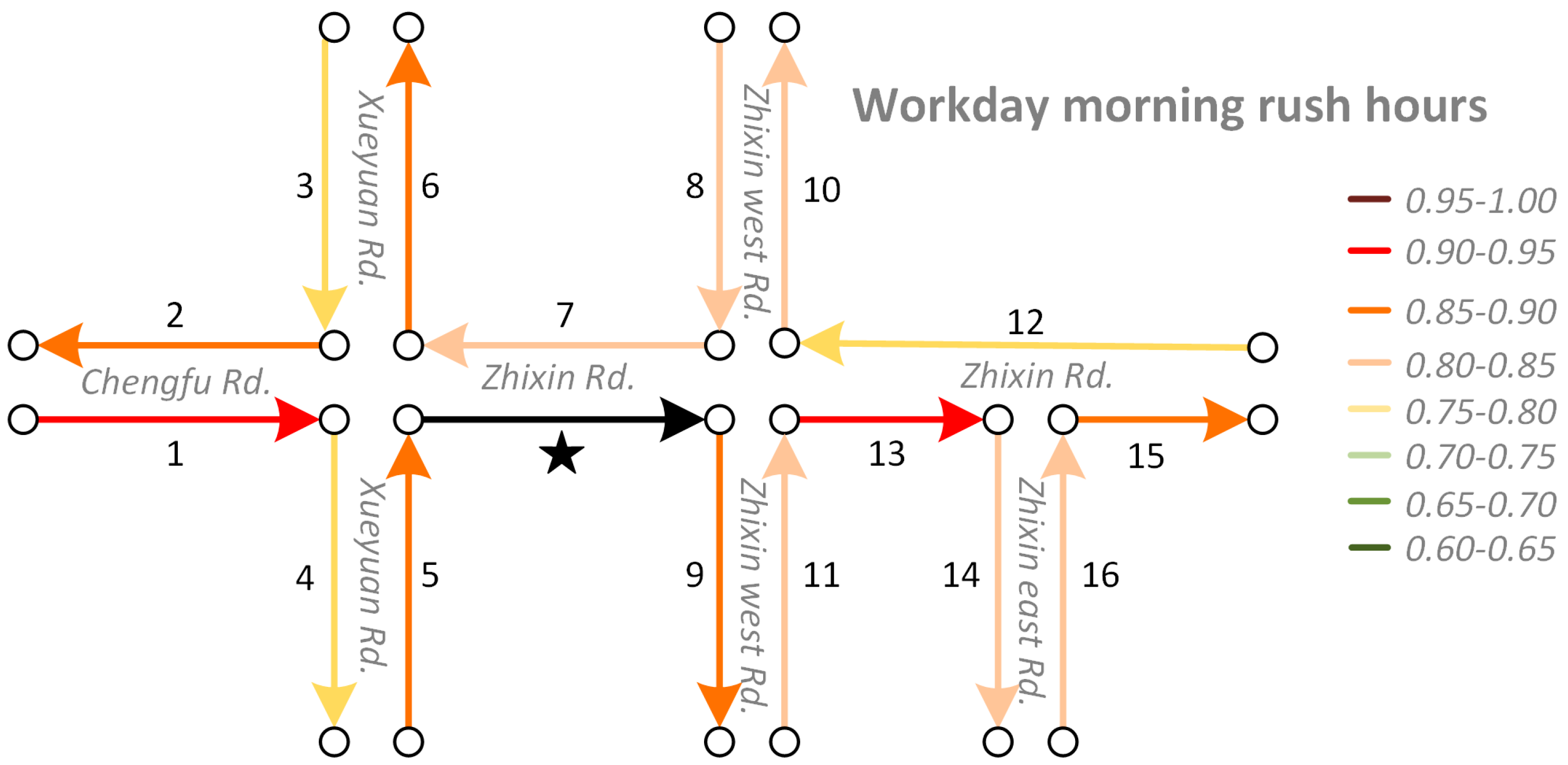
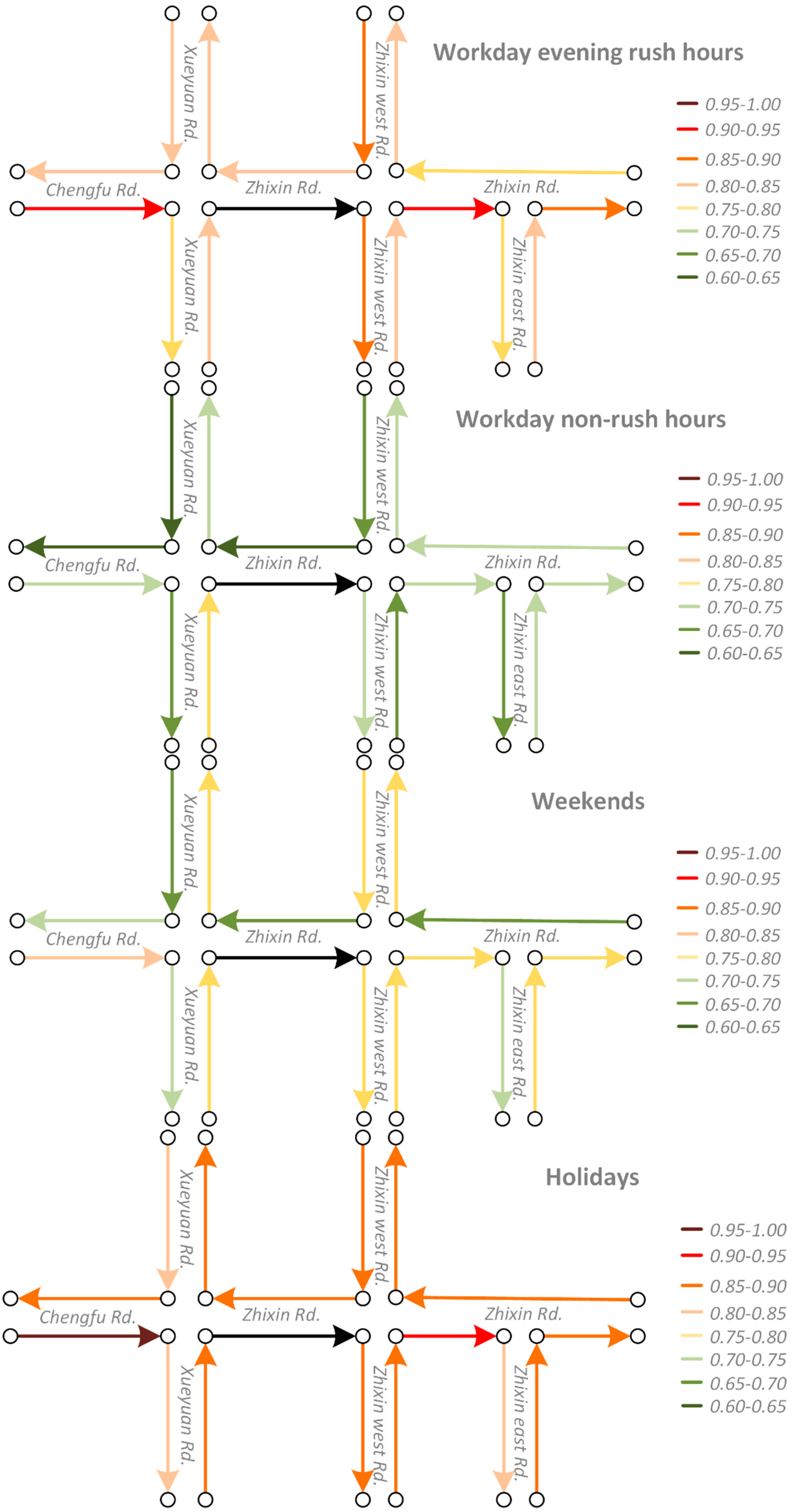
- (2)
- The average similarity on workday morning rush hours, workday evening rush hours and holidays are relatively similar and they are higher than on weekends and workday non-rush hours. When traffic volumes on the road system are larger, such as during workday peak hours and holidays, road traffic interactions are also stronger. Conversely, when the traffic volumes are relatively small, such as workday non-rush hours and weekends, road interactions are also relatively weaker. The findings match well with the default transportation patterns and this indicates that we correctly capture the temporal heterogeneity of road traffic interaction.
- (3)
- Excluding the results trained from models with window sizes equal to 1, the average similarity between neighboring roads decreases progressively along with an increase in the topological order. That is, on average, topologically-closer road segments have stronger traffic interactions, indicating that our Road2Vec approach also captures the influence of topological distance.
3.3. Results Evaluation
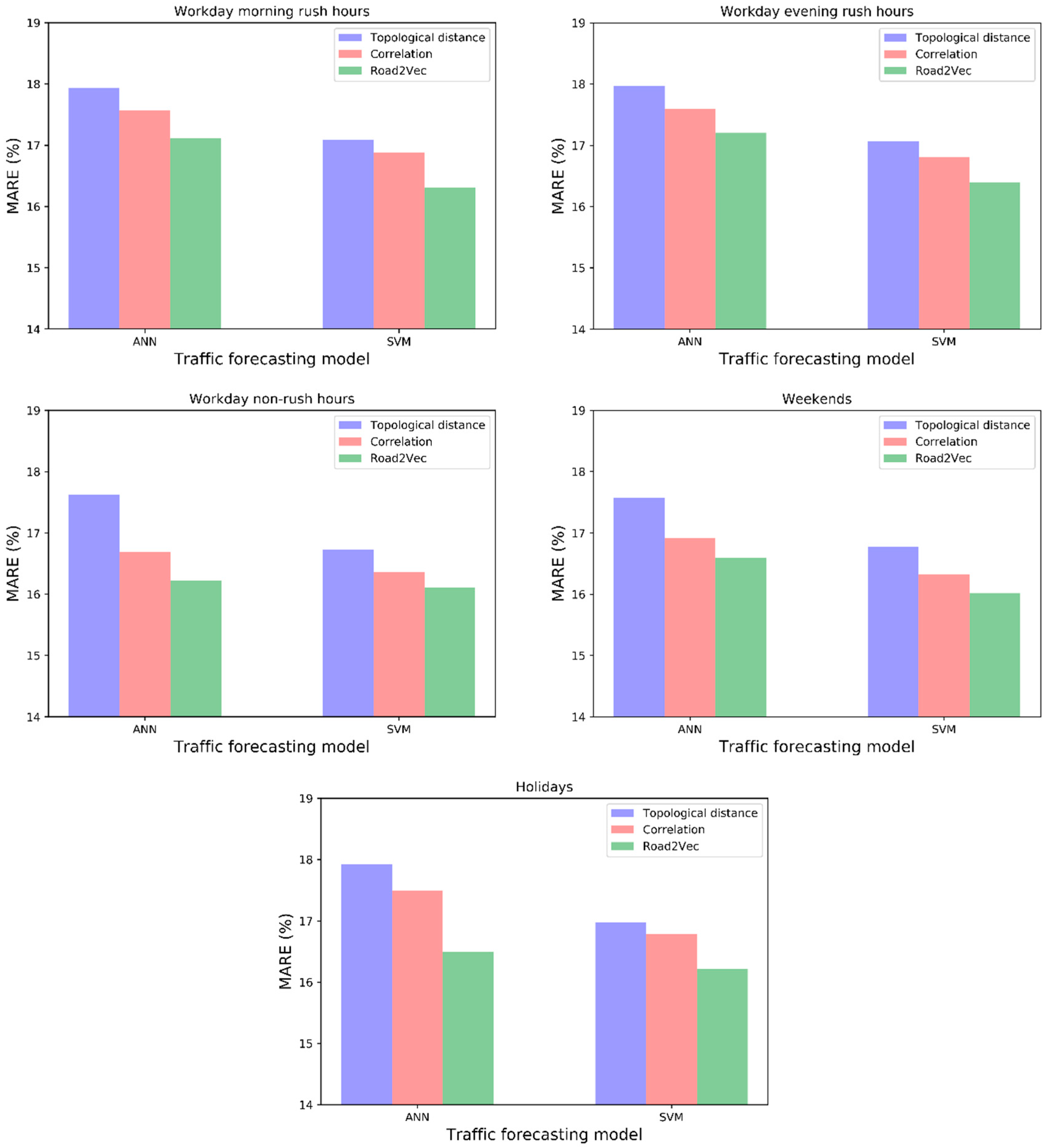
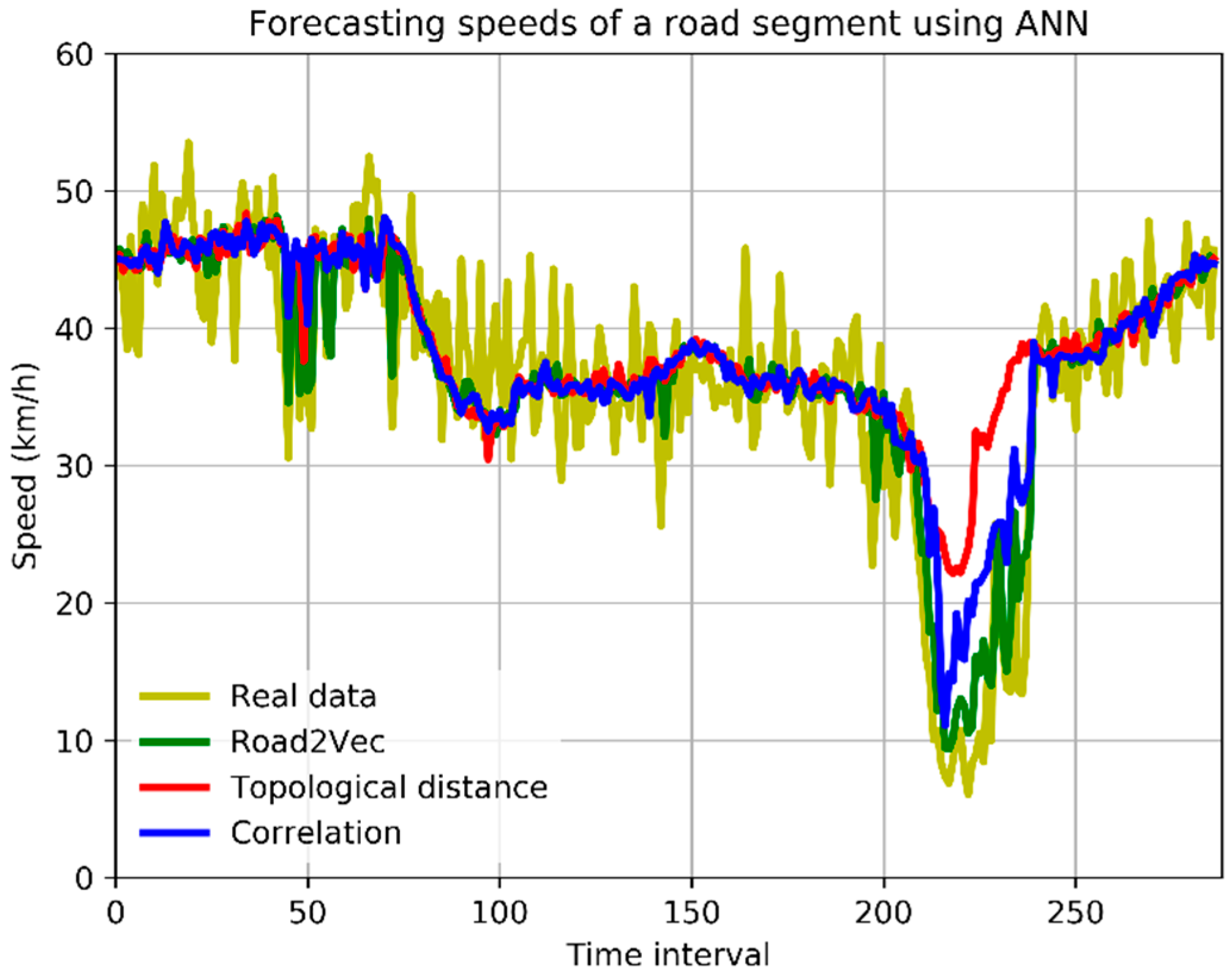
- (1)
- The forecasting models with spatio-temporal inputs selected by the Road2Vec-based method and the correlation-based method behave better than the topological-distance-based method. This is because the topological-distance-based method neglects the spatio-temporal heterogeneity of traffic influence on urban road systems.
- (2)
- The forecasting models with spatio-temporal inputs selected by the Road2Vec-based method behave better than the correlation-based method during all five periods, which proved that our proposed Road2Vec approach can effectively measure the traffic interactions among urban roads. This is because the Road2Vec can derive the implicit and complicated relationships from the moving trajectories of massive vehicles, whereas a correlation-based method cannot capture the non-linear relationships existing in the urban road system well.
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yue, Y.; Yeh, A.G.O. Spatiotemporal Traffic-Flow Dependency and Short-Term Traffic Forecasting. Environ. Plan. B Plan. Des. 2008, 35, 762–771. [Google Scholar] [CrossRef]
- Ma, X.; Dai, Z.; He, Z.; Ma, J.; Wang, Y.; Wang, Y. Learning Traffic as Images: A Deep Convolutional Neural Network for Large-Scale Transportation Network Speed Prediction. Sensors 2017, 17, 818. [Google Scholar] [CrossRef] [PubMed]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.Y. Traffic Flow Prediction with Big Data: A Deep Learning Approach. IEEE Trans. Intell. Transp. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
- Yang, S.; Shi, S.; Hu, X.; Wang, M. Spatiotemporal Context Awareness for Urban Traffic Modeling and Prediction: Sparse Representation Based Variable Selection. PLoS ONE 2015, 10, e0141223. [Google Scholar] [CrossRef] [PubMed]
- Cai, P.; Wang, Y.; Lu, G.; Chen, P.; Ding, C.; Sun, J. A spatiotemporal correlative k-nearest neighbor model for short-term traffic multistep forecasting. Transp. Res. Part. C Emerg. Technol. 2016, 62, 21–34. [Google Scholar] [CrossRef]
- Cheng, T.; Haworth, J.; Wang, J. Spatio-temporal autocorrelation of road network data. J. Geogr. Syst. 2012, 14, 389–413. [Google Scholar] [CrossRef]
- Kamarianakis, Y.; Prastacos, P. Space-time modeling of traffic flow. Comput. Geosci. 2005, 31, 119–133. [Google Scholar] [CrossRef]
- Min, X.; Hu, J.; Zhang, Z. Urban traffic network modeling and short-term traffic flow forecasting based on GSTARIMA model. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; pp. 1535–1540. [Google Scholar]
- Ishak, S.; Kotha, P.; Alecsandru, C. Optimization of Dynamic Neural Network Performance for Short-Term Traffic Prediction. Transp. Res. Record: J. Transp. Res. Board 2003, 1836, 45–56. [Google Scholar] [CrossRef]
- Min, W.; Wynter, L. Real-time road traffic prediction with spatio-temporal correlations. Transp. Res. Part. C Emerg. Technol. 2011, 19, 606–616. [Google Scholar] [CrossRef]
- Ding, Q.Y.; Wang, X.F.; Zhang, X.Y.; Sun, Z.Q. Forecasting Traffic Volume with Space-Time ARIMA Model. Adv. Mater. Res. 2011, 156–157, 979–983. [Google Scholar] [CrossRef]
- Chan, K.Y.; Khadem, S.; Dillon, T.S.; Palade, V.; Singh, J.; Chang, E. Selection of Significant On-Road Sensor Data for Short-Term Traffic Flow Forecasting Using the Taguchi Method. IEEE Trans. Ind. Inform. 2012, 8, 255–266. [Google Scholar] [CrossRef]
- Yang, S. On feature selection for traffic congestion prediction. Transp. Res. Part. C Emerg. Technol. 2013, 26, 160–169. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Karlaftis, M.G.; Golias, J.C. Short-term traffic forecasting: Where we are and where we’re going. Transp. Res. Part C: Emerg. Technol. 2014, 43, 3–19. [Google Scholar] [CrossRef]
- Fusco, G.; Colombaroni, C.; Comelli, L.; Isaenko, N. Short-term traffic predictions on large urban traffic networks: Applications of network-based machine learning models and dynamic traffic assignment models. In Proceedings of the 2015 International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Budapest, Hungary, 3–5 June 2015; pp. 93–101. [Google Scholar]
- Csikós, A.; Viharos, Z.J.; Kis, K.B.; Tettamanti, T.; Varga, I. Traffic speed prediction method for urban networks-an ANN approach. In Proceedings of the 2015 International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Budapest, Hungary, 3–5 June 2015; pp. 102–108. [Google Scholar]
- Jiang, B. Street hierarchies: a minority of streets account for a majority of traffic flow. Int. J. Geogr. Inf. Sci. 2009, 23, 1033–1048. [Google Scholar] [CrossRef]
- Gao, S.; Wang, Y.; Gao, Y.; Liu, Y. Understanding Urban Traffic-Flow Characteristics: A Rethinking of Betweenness Centrality. Environ. Plan. B-Plan. Des. 2013, 40, 135–153. [Google Scholar] [CrossRef]
- Liu, X.; Lu, F.; Zhang, H.; Qiu, P. Intersection delay estimation from floating car data via principal curves: A case study on Beijing’s road network. Front. Earth Sci. 2013, 7, 206–216. [Google Scholar] [CrossRef]
- Bengio, Y.; Ducharme, R.; Vincent, P.; Jauvin, C. A Neural Probabilistic Language Model. J. Mach. Learn. Res. 2003, 3, 1137–1155. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. In Proceedings of the Workshop at International Conference on Learning Representations, Scottsdale, AZ, USA, 2–4 May 2013; pp. 1–12. [Google Scholar]
- Deerwester, S.; Dumais, S.T.; Furnas, G.W.; Landauer, T.K.; Harshman, R. Indexing by Latent Semantic Analysis. J. Am. Soc. Inf. Sci. 1990, 41, 391–407. [Google Scholar] [CrossRef]
- Pennington, J.; Socher, R.; Manning, C.D. Glove: Global vectors for word representation. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Liu, X.; Liu, K.; Li, M.; Lu, F. A ST-CRF Map-Matching Method for Low-Frequency Floating Car Data. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1241–1254. [Google Scholar] [CrossRef]
- Petty, K.F.; Bickel, P.; Ostland, M.; Rice, J.; Schoenberg, F.; Jiang, J.; Ritov, Y. Accurate estimation of travel times from single-loop detectors. Transp. Res. Part A Policy Pract. 1998, 32, 1–17. [Google Scholar] [CrossRef]
- Vythoulkas, P. Alternative approaches to short term traffic forecasting for use in driver information systems. Transp. Traffic Theory 1993, 12, 485–506. [Google Scholar]
- Basu, D.; Maitra, B. Modeling stream speed in heterogeneous traffic environment using ANN-lessons learnt. Transport 2006, 21, 269–273. [Google Scholar]
- Vanajakshi, L.; Rilett, L.R. A comparison of the performance of artificial neural networks and support vector machines for the prediction of traffic speed. In Proceedings of the IEEE Intelligent Vehicles Symposium, Parma, Italy, 14–17 June 2004; pp. 194–199. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, K.; Gao, S.; Qiu, P.; Liu, X.; Yan, B.; Lu, F. Road2Vec: Measuring Traffic Interactions in Urban Road System from Massive Travel Routes. ISPRS Int. J. Geo-Inf. 2017, 6, 321. https://doi.org/10.3390/ijgi6110321
Liu K, Gao S, Qiu P, Liu X, Yan B, Lu F. Road2Vec: Measuring Traffic Interactions in Urban Road System from Massive Travel Routes. ISPRS International Journal of Geo-Information. 2017; 6(11):321. https://doi.org/10.3390/ijgi6110321
Chicago/Turabian StyleLiu, Kang, Song Gao, Peiyuan Qiu, Xiliang Liu, Bo Yan, and Feng Lu. 2017. "Road2Vec: Measuring Traffic Interactions in Urban Road System from Massive Travel Routes" ISPRS International Journal of Geo-Information 6, no. 11: 321. https://doi.org/10.3390/ijgi6110321
APA StyleLiu, K., Gao, S., Qiu, P., Liu, X., Yan, B., & Lu, F. (2017). Road2Vec: Measuring Traffic Interactions in Urban Road System from Massive Travel Routes. ISPRS International Journal of Geo-Information, 6(11), 321. https://doi.org/10.3390/ijgi6110321





