A New Approach for Interpreting the Morisita Index of Aggregation through Quadrat Size

Abstract

Spatial point pattern analysis is commonly used in ecology to examine the spatial distribution of individual organisms or events, which may shed light on the operation of underlying ecological processes driving the development of a spatial pattern. Commonly used quadrat-based methods of measuring spatial clustering or dispersion tend to be strongly influenced by the choice of quadrat size and population density. Using valley oak (Quercus lobata) stands at multiple sites, we show that values of the Morisita Index are sensitive to the choice of quadrat size, and that the comparative interpretation of the index for multiple sites or populations is problematic due to differences in scale and clustering intensity from site to site, which may call for different quadrat sizes for each site. We present a new method for analyzing the Morisita Index to estimate the appropriate quadrat size for a given site and to aid interpretation of the clustering index across multiple sites with local differences. By plotting the maximum clustering intensity (Imr) found across a range of quadrat sizes, we were able to describe how a spatial pattern changes when quadrat size varies and to identify scales of clustering and quadrat sizes for analysis of spatial patterns under different local conditions. Computing and plotting the instantaneous rate of change (first derivative of rMax), we were able to evaluate clustering across multiple sites on a standardized scale. The magnitude of the rMax first derivative is a useful tool to quantify the degree of crowding, dispersion, or random spatial distribution as a function of quadrat size.

1. Introduction

Spatial point pattern analysis is an approach commonly used in ecology to examine the spatial distribution—clustered, dispersed, or random—of individual organisms within a given area or in relation to other organisms, which can shed light on underlying ecological processes, e.g., resource competition or population dynamics [1,2,3,4]. However, scale is an intrinsic variable taken into account when spatial patterns of individuals are evaluated. Ecological processes can often be studied at multiple scales, and variables can occur at different spatial scales of variation in different places, making it difficult to find the “correct” scale. Given the importance of the chosen scale of analysis, ecological point-pattern analysis must be studied as the variation of organisms through different scales at the same time, where its effect may or may not to be consistent through different spatial frames of analysis [5,6]. In fact, Levin [6] states that spatial variability and window size are dominated by the distance between points. The larger the scale of analysis, the more unpredictable the spatial pattern and thus there is no single, “correct” scale to study any population. If pattern depends on the scales of observation, it is possible to measure clustering or dispersion as a function of scale or distance. One common method performing this task is Ripley’s K, which computes spatial dependence through distances to illustrate the statistically significant degree of clustering or dispersion [7,8].

Common methods of spatial point pattern analysis include quadrat-based counting methods, distance-based methods, density analysis, and spatial autocorrelation of point attribute data (i.e., analysis of both point location and potentially related variables, such as individual size, age, sex, etc.) [2,3,4,9,10]. The various point pattern analysis techniques have strengths and weaknesses, and each may be more or less appropriate for particular questions one may have about spatial patterns and ecology. Our purpose is not to review the pros and cons of the many existing spatial analysis techniques, rather to focus on a related group of quadrat methods and to develop a new approach that addresses the limitations of the Morisita Index of aggregation for ecological interpretations.

The spatial patterns of organisms in the landscape are both the result of ecological processes, and a functional part of the landscape that gives rise to future spatial patterns [11]. Changes in the spatial distribution of organisms can have implications for all parts of an ecosystem, biotic and abiotic. Patterns of forest cover, composition, and structure affect the occurrence, abundances, and ecological dynamics of associated plant and animal species, natural disturbance, and bio-geochemical processes of the landscape [5,11,12]. Clustering, dispersion, or spatially random patterns of individuals may be evidence of either an endogenous biological or ecological process (e.g., clustering of saplings around parent trees) or a response to environmental variation or environmental change (e.g., spatial variability of soil moisture or nutrients) [13,14]. Spatial patterns can then feed back to affect ecological dynamics, further reinforcing or altering patterns dependent on local interactions; pollen exchange among individuals in a population, the abundance and distance to habitat or food sources are examples of processes that can be altered by changing patterns in one variable, that then will affect ecological processes and future spatial patterns [11,12]. Measuring these spatial patterns in ways that can clearly link them to ecological processes of interest remains an ongoing area of research in ecology.

The Morisita Index of aggregation (I${}_M$) has been shown to provide a method for an ecological, rather than a strictly statistical or relative, interpretation of point patterns [15,16,17,18]. It is instructive to determine whether a distribution of individuals is grouped together more or less closely than expected for a spatially random distribution of individuals, however, it may be more ecologically useful to determine not just whether a distribution is clustered, but also whether the degree of clustering, or crowding, as defined by a specified number of individuals, is above or below a hypothetical threshold level. Many different observed distributions of individuals may be Poisson or non-Poisson distributed and can have the same mean–variance ratios. Further, many observed distributions will be non-random, but this not randomness should be the expectation, and the test criterion for ecological significance should be a hypothesized level of non-randomness under specific conditions (number of individuals in a given area above or below a threshold value of non-randomness, a given size of quadrats, the species being studied, etc.). However, most indices have a high dependence on quadrat size and mean density [19], both variables that should be taken into account when asking about the spatial patterns of a population and its degree of departure from complete spatial randomness. The choice of quadrat size is dependent on the expertise and judgment of the researcher and the “optimal” quadrat size may be different at different sites, which can make comparing results across sites or among other studies difficult. Further, index values are dependent on the choice of quadrat size, also complicating interpretation [5,6]. I${}_M$ and modifications of the Index have been applied to examine spatial patterns and processes of seed dispersal, seed bank, and tree establishment [20,21,22,23], to compare spatial patterns of recruitment and adult trees [24,25] and to compare and rank (aggregated to uniform) the spatial distributions of species within a forest [15]. Hurlbert [18] argues that I${}_M$ provides an unambiguous interpretation of whether a point pattern is clustered, dispersed, or random, and extends I${}_M$ to measure how the probability of clustering changes as the definition of clustering is changed by the researcher.

This paper explores the properties of I${}_M$—a quadrat-based method—to build upon its usefulness for an ecological interpretation of clustering and to develop a method that allows a clear quantitative comparison of the index’s values across multiple sites that have different point distributions. Our method provides objective measures for choosing a quadrat size at different sites and quantifies differences among sites even when different quadrat sizes are used from site to site.

We first apply a standard Morisita approach to stem locations of valley oak trees (Quercus lobata) to show that the index is useful to explore how index values change with quadrat size, and to demonstrate the first step in Morisita analysis, upon which subsequent steps are built. Second, we implement Hurlbert’s multi-point Morisita index [18], I${}_{Mr}$, to illustrate that this index is precise in measuring differences in the degree (number of m individuals when the index value peaks) and intensity (index value for a given number of r individuals) of crowding, however, comparison among two or more sites turns out to be problematic because the index scale is not interpretable across sites except in a relative sense, and different quadrat sizes may be more appropriate at some sites, which would change the results or require the researcher to compare values on different scales. To address this problem of comparison, we first extend I${}_{Mr}$ results to examine how the degree of maximum crowding intensity changes as a function of quadrat size. Finally, we plot the first derivative of I${}_{Mr}$, d${}_M$, as a function of quadrat size to help researchers make a more direct comparison of how the intensity of crowding varies among sites that may differ in spatial scale and require different size quadrats for analysis.

2. Materials and Methods

2.1. Study area

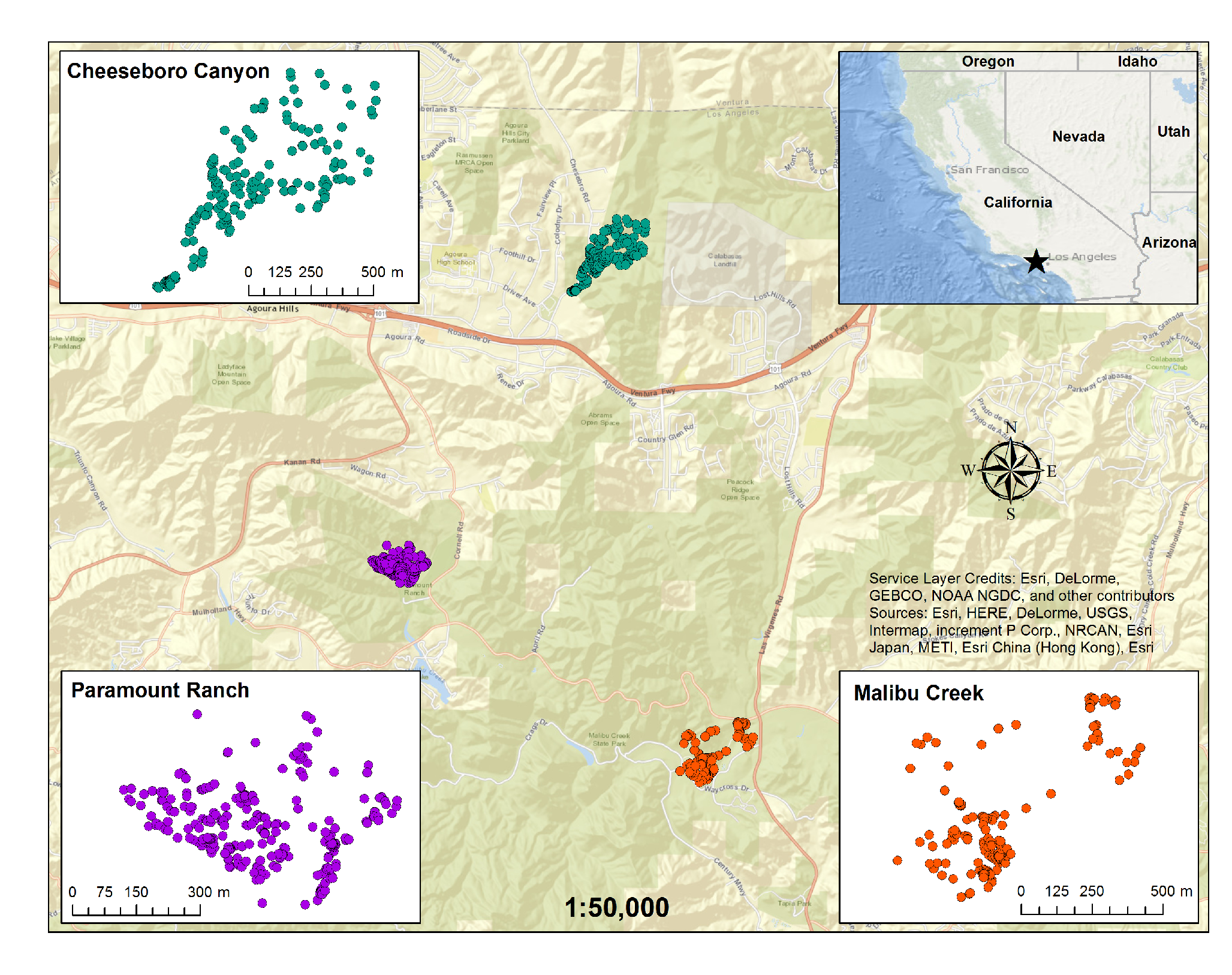
To demonstrate our application and development of the Morisita approach, we used valley oak populations from three sites in the Santa Monica Mountains in southern California (Figure 1). The three sites, Cheeseboro Canyon (CHE), Paramount Ranch (PAR), and Malibu Creek State Park (MAC), are part of the Santa Monica Mountains National Recreation Area and are managed by the US National Park Service (CHE and PAR) and California Department of Parks and Recreation (MAC). The sites’ histories and their valley oak communities have been described and analyzed by Thomas [26], McLaughlin and Zavaleta [27], Hayes [28], Hayes and Donnelly [29], Hayes and Donnell [30].

Valley oak is a deciduous oak endemic to California that has been, and is expected to continue, experiencing changes in spatial distribution at local and regional scales in response to land use and climate change [27,28,29,31,32,33]. Valley oak has received much attention due to conservation concerns as impacts associated with climate change, habitat loss, and poor regeneration have become increasingly apparent [26,32,33,34,35,36,37,38,39,40,41]. Valley oak distribution and numbers have greatly declined as stands have been cleared for residential, commercial, and agricultural development [36]. The possibility of regeneration failure of valley oak populations has been a concern in the literature for decades as researchers have noted low recruitment of seedlings and saplings while older trees die without replacement. Regeneration failure and valley oak population dynamics continue to be investigated. As an ecological foundation species, valley oak distribution and population dynamics have ecological and biological implications for other plant and animal species, as well as physical processes in the landscape [42]. The relationships among spatial and structural patterns of valley oak stands, and the population and community ecology of other plant species, birds, mammals, and invertebrates as well as the spread of disturbance and disease, have been well studied [36,43,44,45,46,47].

At each site, a grid of 100 × 100 m was mapped across the property and an outer boundary was established at each site based on the park boundaries and topographic and cultural features (e.g., roads, fences), so that only potential valley oak habitat was included. Each study site included a spectrum of topographic variability from hill tops to riparian corridors. Each 100 × 100 m cell within the study area boundary was censused for all valley oak stems greater or equal to 1 cm diameter at breast height (dbh). The dbh of each stem was measured and all were mapped with 30 cm accuracy using a Trimble GeoXH GPS [48]. The CHE and MAC stands have bimodal size-class distributions with distinct cohorts of large (older) trees and small saplings, with few intermediate sized trees. CHE has the largest individuals and the largest median diameter at breast height (dbh) of 56.7 cm with an interquartile range (IQR) of 82.5 cm, indicating high variability in dbh as compared to the other sites. Median dbh and IQR at MAC (10.2 cm, 22.8 cm) and PAR (9.2 cm, 44.7 cm), were much smaller and less variable. Regeneration at the sites is variable with sapling: adult ratios of 1.13 at PAR, 0.99 at MAC, and 0.53 at CHE [28].

2.2. Morisita Index

Our first step was to apply $I_M$ in its original implementation as explained by Morisita [19] and Hurlbert [18]. $I_M$ provides a measure of how many times more (or less) likely it is that two randomly selected individuals in a given distribution were found within the same quadrat compared to that of a random distribution [19]. If the individuals were randomly distributed (from a Poisson distribution), $I_M$ values were close to 1, greater than 1 if clustered, and less than 1 if dispersed [49]. Golay et al. [16] pointed out that the index can approach 0 for dispersed patterns at small scales.

$$I_M=Q\frac{{\sum }_{k=1}^Q{n}_k(n_k-1)}{N(N-1)}$$

(1)

where, Q is the total of quadrats, $n_k$ is the number of individuals in the $kth$ quadrat, and N is the total number of individuals.

This index is advantageous as a crowding measure because it is independent of sample density except possibly for very low sample sizes. This means it can be used without corrections for effects of sample size [50,51,52].

Since the index is sensitive to quadrat size, it is recommended that a range of quadrat sizes are examined to understand how quadrat size might affect interpretation of the index in particular cases. To determine initial bounds of quadrat sizes, we calculated the minimum, maximum, and mean nearest-neighbor distance between individuals to the specified number of nearest neighbor (N is the input parameter for a set of features as implemented in ArcGIS for Desktop software) [53] (

Table 1. Distance band in meters from neighbor count for the three populations.

Population	Minimum	Average	Maximum
Cheeseboro	0.2928	16.022	70.4373
Malibu	0.1064	13.4648	102.4362
Paramount	0.1118	8.2808	115.1634

). To calculate the distances, we used two neighbors to determine the mean nearest neighbor distance for all pairs of stems at each of the three sites.

Given a general idea about the range of separation between stems from Table 1, we calculated the mean of the minimum and maximum distance for the three populations, which ranged between 0.17 and 96.01, for our initial analysis of quadrat-size on $I_M$. We then divided the range (roughly) into four parts to examine a discrete set of quadrat sizes: 25, 50, 75, and 100 m.

2.3. $I_{Mr}$ Index

We examined thresholds of crowding in the stem data by examining how the probability of aggregation changed as the definition of aggregation changed, from two stems/quadrat to N stems/quadrat, increasing by one for each iteration, at a given quadrat size. Hurlbert [18] stated a generalized version of the Morisita index, termed the multipoint-Morisita index $I_{Mr}$. This $I_{Mr}$ index measures the degree to which the probability of finding all r individuals in the same quadrat is greater or less than it would be in a random distribution. As explained by Hurlbert [18], the statistical origin of the Morisita index is interpretable as a biological or ecological measure of aggregation accounting for the number of individuals contributing to the measure of aggregation. Notice that the original formulation of $I_M$ is equivalent to r = 2.

$$I_{Mr}=\frac{Q^{r-1}(N-r)!}{N!}\sum _{k=r}^w\frac{q_k·k!}{(k-r)!}$$

(2)

where, N is the total number of individuals, r is the number of individuals randomly selected, Q is the total of quadrats, w is the largest number of individuals observed in any quadrat, k is the number of individuals per quadrat, and $q_k$ is the number of quadrats containing k individuals.

Unlike $I_M$, $I_{Mr}$ allows examination of how the probability of reaching a hypothetical threshold level of crowding, rMax, (rather than only two stems) changes with increasing values of r as the threshold is approached and exceeded. This approach captures more information about the site-specific structure of clustering by evaluating the index as a function of the r parameter. That is, we can observe whether the probability of clustering tends to increase or decrease as more r stems are added to a quadrat. The value of r at which $I_{Mr}$ is maximum, rMax, (if it exists) represents the number of individuals for which the likelihood of co-occurrence in the same quadrat is most divergent from a randomly distributed population. Therefore, rMax can indicate a potential ecological threshold for stem crowding when the probability of finding more than rMax stems continues to decrease as r increases. Different rMax values for different sites could indicate various levels of crowding, and competition among individuals, or varying spatial scales of other controlling variables, i.e., soil moisture, micro-climate conditions, etc. The rMax data can help identify further hypotheses to explain why particular thresholds are or are not reached or exceeded in particular cases.

2.4. rMax Analysis

As with the Morisita index, we chose a fixed quadrat size to calculate $I_{Mr}$, however, the question was more complicated for the multi-r formulation. Note that for the $I_M$, we examined a range of quadrat sizes, and for an individual site or population we can examined how $I_{Mr}$ changed with quadrat size, but to compare $I_{Mr}$ among multiple sites we must use the same quadrat size for each site since Hurlbert’s plot [18] represents r as the independent variable and $I_{Mr}$ as the dependent variable. It would seem logical to use a common quadrat size for all sites to be compared, however, the size chosen may not be the best for all sites if the sites differ, for example, in overall density, have very different scales of clumping or spacing, or the study areas have irregular shapes and boundaries.

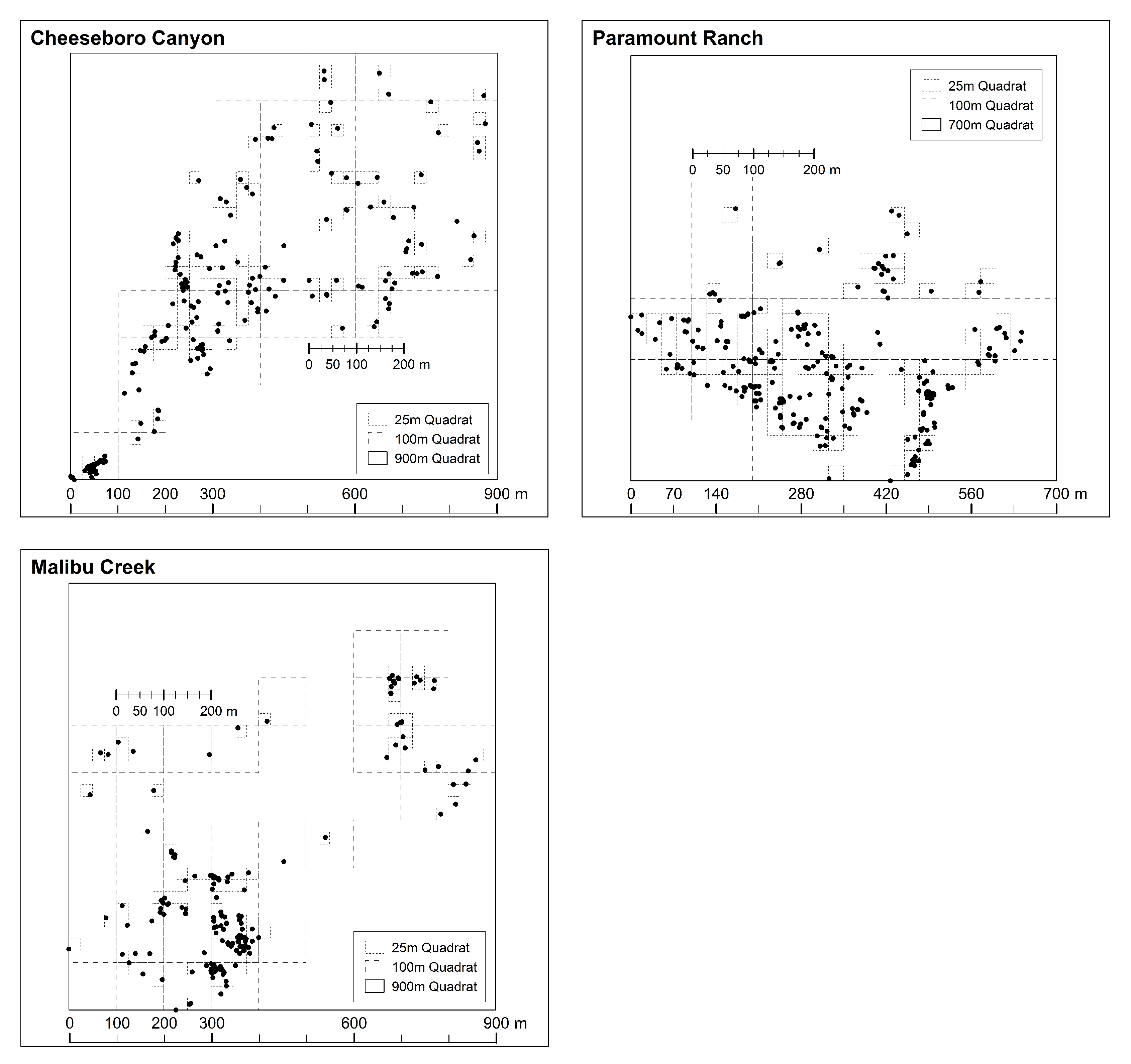
To help identify an appropriate quadrat size based on local conditions, we examined how the values of rMax (number of stems at $I_{Mr}$ peaks) changed if different quadrat sizes were chosen. For this analysis, we used the whole range of quadrat sizes in 1 m increments from 1 m to the minimum quadrat size necessary to completely contain all N stems at the site. The range of quadrat sizes examined for Cheeseboro was 1–875 m, Paramount was 1–643 m, and for Malibu was 1–859 m. To simplify the representation, we rounded the final largest quadrat size up to the nearest hundred. Note that our use of very large quadrats, up to bounding the entire study site (Figure 2), is for the purpose of exploring the clustering index behavior, and for a variety of reasons we would not use such large quadrat sizes in a field study of spatial ecology.

When the plotted curve of rMax and quadrat size for a site peaks, a crowding threshold of r stems is revealed along with the quadrat size used to identify that threshold. If we were to do our spatial analysis using a smaller or larger quadrat size, one could only conclude that the stems were spatially clustered, but remain ignorant of whether they were experiencing crowding or were near an ecological threshold. If rMax increased as quadrat size increased, this would indicate that the quadrat size with the greatest number of stems per quadrat, while being maximally different from a random distribution, had not yet been found and that ecological crowding or competition is not present at the site scale. Decreasing rMax as quadrat size increases would suggest that using a larger quadrat size would underestimate the degree of crowding found at the site and that crowding occurs at smaller spatial scales. By applying this approach to a group of study sites we make an evidence-based choice of (1) the optimal quadrat size for each site and (2) a definition of aggregation or crowding for each site to allow for a more appropriate comparison of spatial analysis results among sites.

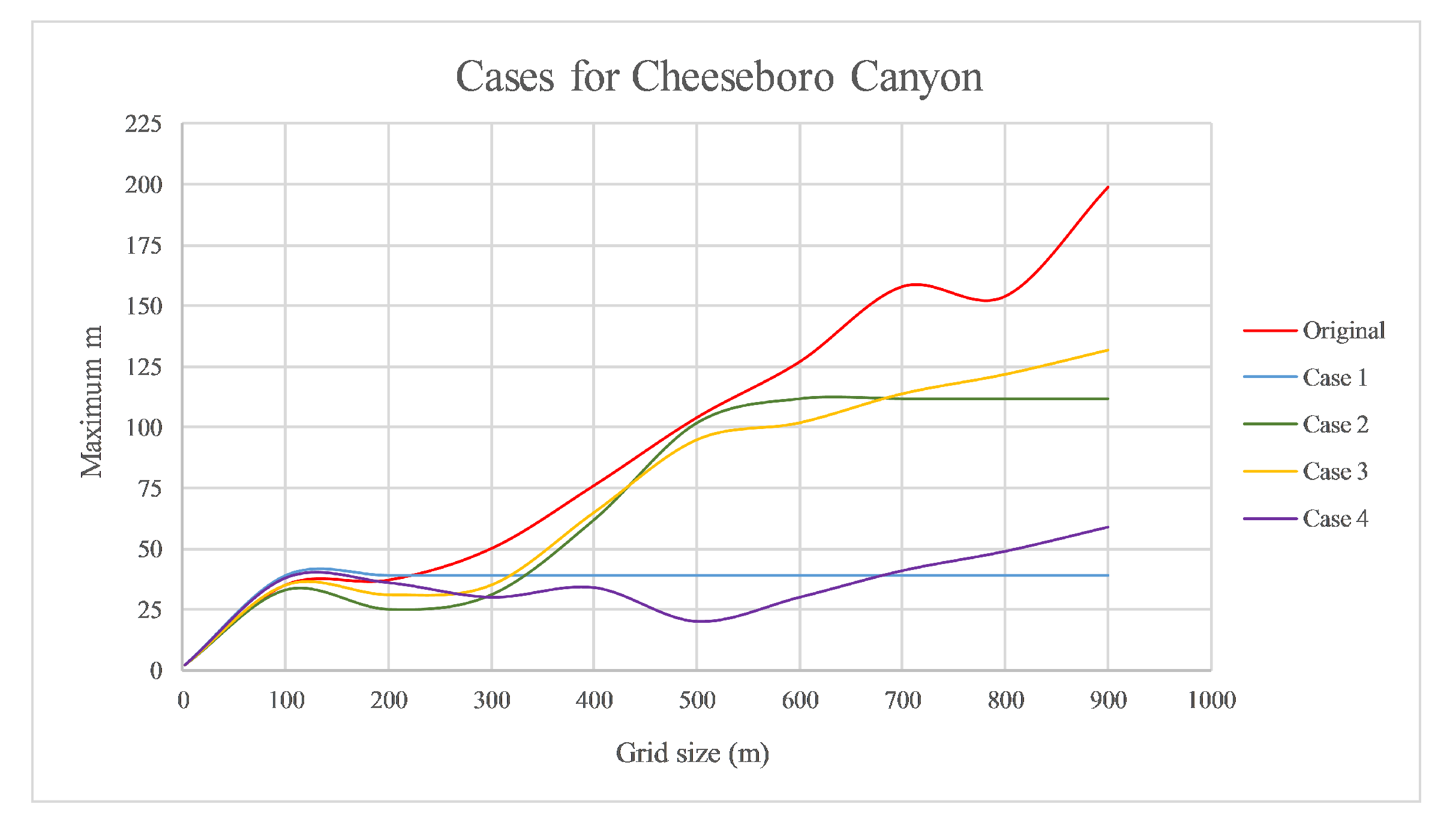
Before applying the rMax approach to the data from the three study sites we first explored the data from CHE and partitioned it into four hypothetical cases to illustrate how the mMax curves behave under different conditions. Based on familiarity with the site, we identified three clumps of different sizes and density, which we used to create four cases of hypothetical spatial pattern (Figure 3). Each clump is pruned in order to highlight changes across the study site. By closely examining the mMax curves from these somewhat contrived data, one can more easily see the diagnostic aspects of the approach when interpreting the plotted curves and relating them to the four hypothetical cases.

Using the hypothetical cases from CHE, we calculated the $I_{Mr}$ values for each case across the full range of quadrat sizes for CHE described above the plotted the curves of rMax and quadrat size for each case.

2.5. $d_m$ Analysis

To make a comparison of ecological crowding of stems across all study sites, we derived a standardized measure of aggregation so that, once a quadrat size and clustering definition are identified, we could make a direct comparison—with the caveat that $I_{Mr}$ values themselves are not directly interpretable from site to site. To accomplish this, we defined a new descriptor based on the $I_M$ index. Using the discrete values of $I_{Mr}$, we calculated a numerical derivative to get actual values of similarity among the populations. Instantaneous rate of change was selected because it is simple to compute and provides scale flexibility depending on the interval of measurement. The values are calculated and plotted for 100 m quadrat-size intervals to quantify the degree of aggregation.

3. Results

3.1. $I_M$ (r = 2)

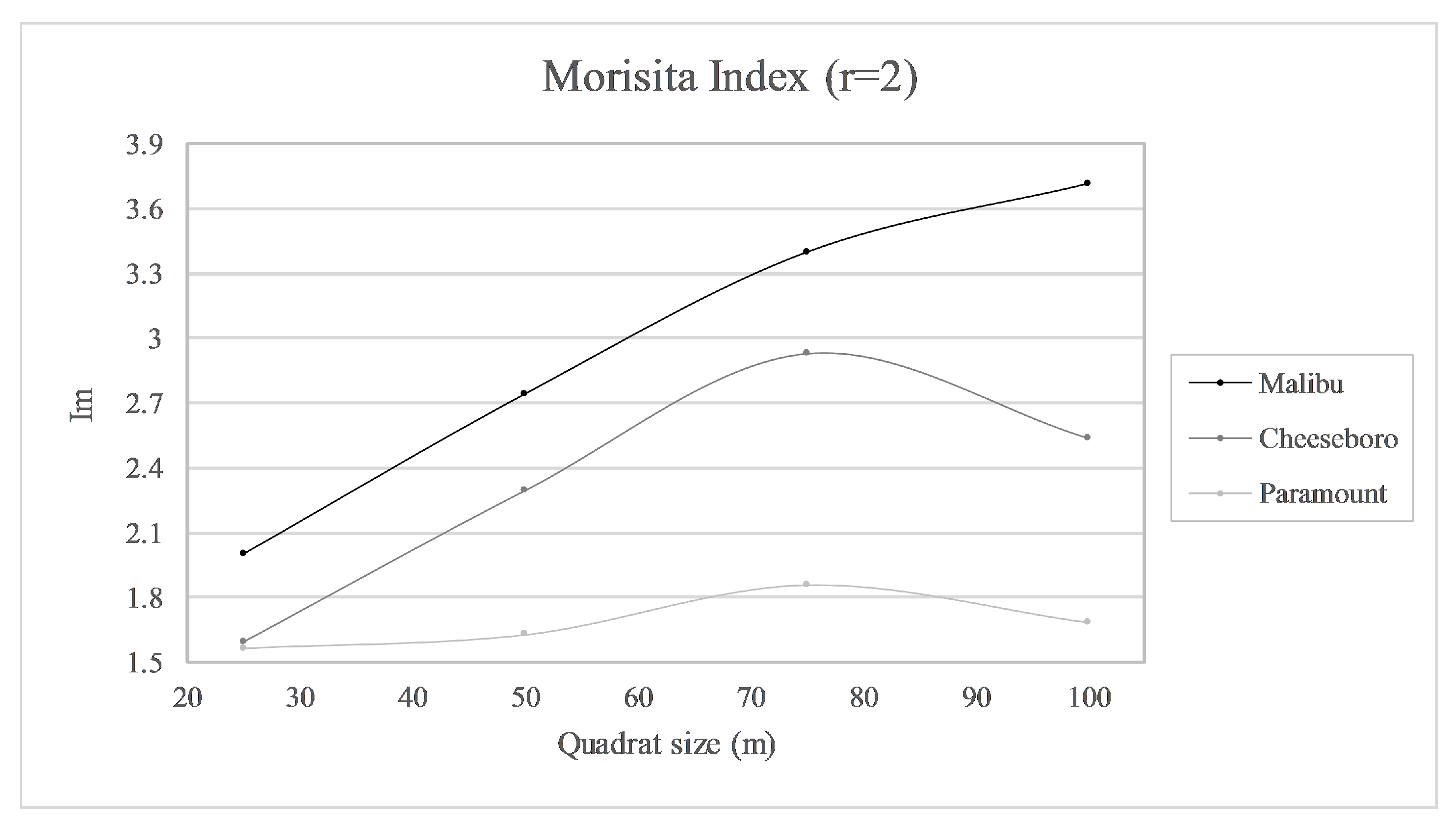
Morisita Index (r = 2 stems) results indicated a clustered distribution of stems at all three sites on the 25 m, 50 m, 75 m, and 100 m quadrats (Figure 4). Clustering was greatest (most positive deviation from random expectation) for MAC, least for PAR, and intermediate for CHE except on the 25 m quadrat grid, which had similar clustering results for PAR and CHE. As quadrat size increased, the clustering index increased steadily and at similar rates for CHE and MAC, while rising only slightly for PAR. Clustering peaked for CHE and was dubious for PAR in the 75 m grid, but increased to its highest level for MAC on the 100 m grid, though the rate of increase slowed between 75 m and 100 m.

3.2. $I_{Mr}$

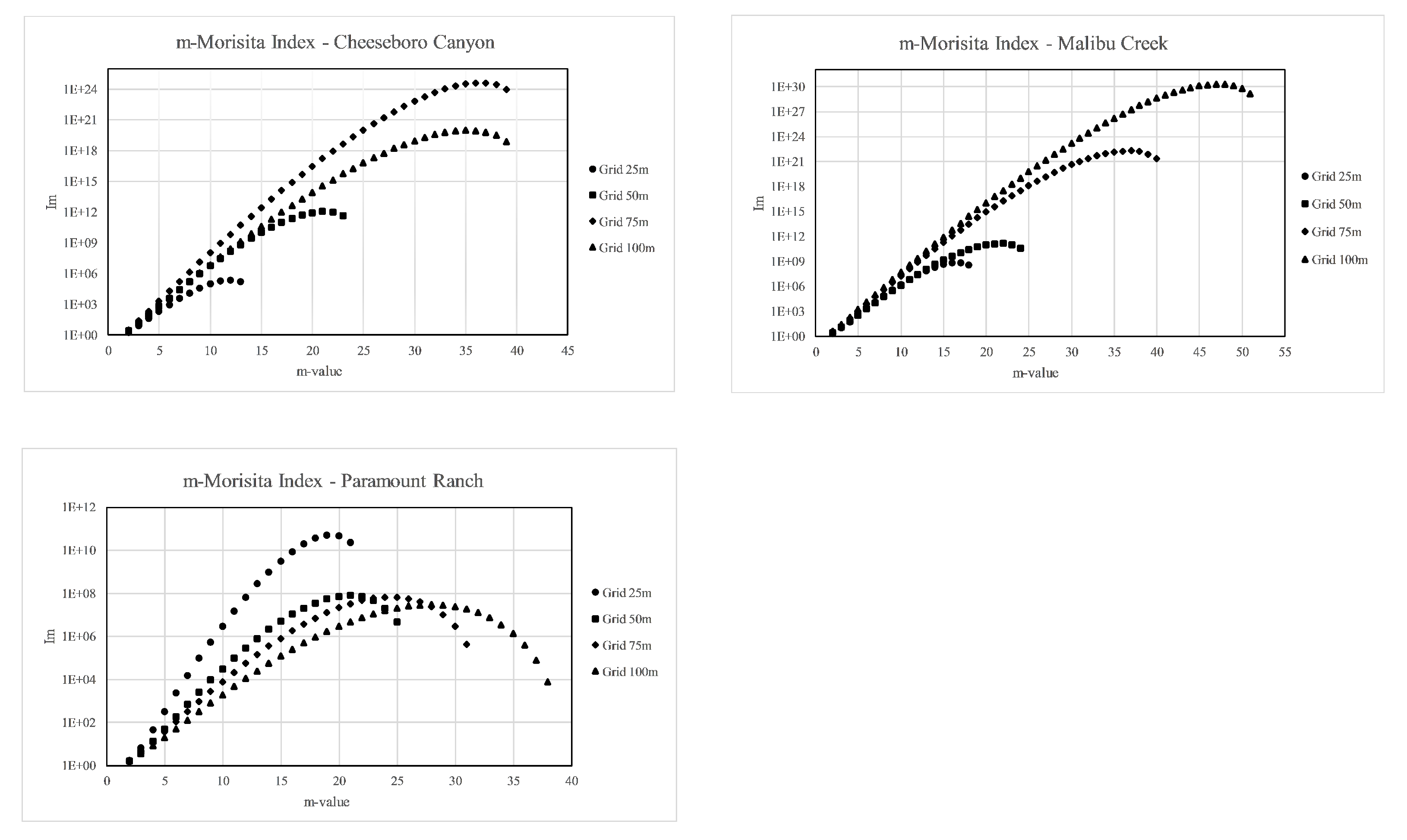
$I_{Mr}$ results showed a clustered pattern ($I_{Mr}>1$) for all three sites and revealed that maximum deviation from random (greatest values of $I_{Mr}$) occurred for different numbers of stems (r) at each site and for each quadrat size examined (Figure 5). $I_{Mr}$ reached a maximum value (rMax) for r = 36 stems on the 75 m quadrats at CHE, for r = 19 stems on the 25 m quadrats at PAR, and for r = 47 stems on the 100 m quadrats at MAC. The departure from randomness or the clustering value, $I_{Mr}$, also increased as rMax increased, even in larger area quadrats, except for the 25 m quadrats at PAR, where rMax of 19 was more intensely clustered than larger quadrats with more stems. Examining the $I_{Mr}$ graphs for points of comparison among the three sites, we observed that there appeared to be a common clustering or crowding threshold of approximately 20 stems when the 50 m quadrats were used and that clustering of more than 20 stems at this scale became less likely. Nevertheless, interpreting this value of 20 stems as a crowding threshold for valley oak in general is problematic because the stems at PAR are much more intensely crowded (higher $I_{Mr}$) than at CHE or MAC, possibly indicating a difference in site-level spatial distribution rather than a meaningful comparison of crowding intensity. Further, each of the values themselves were very large and difficult to interpret from site-to-site. A comparison of crowding levels among the three populations based on this index was problematic because interpretation of the values themselves is not clear except in a relative sense.

3.3. rMax analysis

Analysis of rMax values using hypothetical cases of spatial patterns at CHE allowed us to choose an appropriate quadrat size to compare clustering and crowding among sites. Plots of the rMax curves for the hypothetical CHE cases (Figure 6) indicated that the number of peaks in the rMax curves across the range of quadrat sizes correspond to the number of clumps found in the population. The rMax value or number of stems (r) for peak $I_M$, on a range of quadrat sizes from 1 m to 875 mm for CHE indicated that rMax increased as quadrat size increased for all cases, up to about the 100 m quadrat size, then leveled off or fell again (Figure 6). Between 100 m and approximately 300 m, the curves remained flat (case 1) or decreased then began to rise again. The flat curve for case 1 indicated that there was no change in clustering beyond 100 m quadrats since all stems were accounted for and increasing quadrat size does not change the value. For cases 2 and 3 however, curves rose and peaked at around 500 m, which indicated the presence of another cluster of stems at the 500 m quadrat scale. The flat slope of case 2 beyond the size of the second cluster indicated no change in values as quadrat size increased. Case 3 also showed two downward concavities and a third mild concavity. Comparing the case 3 curve with its point pattern (Figure 5), the upper right clump was shown to not be precisely a cluster but rather a dispersed or uniform spatial distribution, which dampened the curve. Note that in case 4, there was no cluster at the 500 m scale but rather a large gap in the distribution which was reflected in the lack of increase in the case 4 curve; these large spatial gaps or holes in the data resulted in the curves having an unexpected behavior. Due to this, we need to use another metric to better detect those scenarios. The valuable part of this index is the study of the r-value when $I_{Mr}$ reaches a maximum value or values at different quadrat sizes showing higher or lower degrees of clumping for different quadrat sizes.

The slope of the curve is related to the intensity of aggregation or density of the spatial distribution relative to the scale of measurement. In case 3 (see Figure 6), we distinguished three clumps through the positive slope of the tangent line and also the degree of aggregation by the steepness of the slope. The degree of aggregation decreased from left to right across the graph, hence the first clump had the greatest slope value, then the second clump with a smaller slope, and finally the last one was not clearly a clump and the slope tended to zero. Regarding case 4, from 100 to 500 m (where there was an absence of stems), the slope was less than or equal to zero. The hypothetical cases allowed us to see where the slope was positive the population is aggregated or clustered, and slopes close to zero were random, while negative slopes indicated a uniform or dispersed pattern. While the validity of these mathematical relations can be demonstrated using advanced calculus, it is not the goal of this paper.

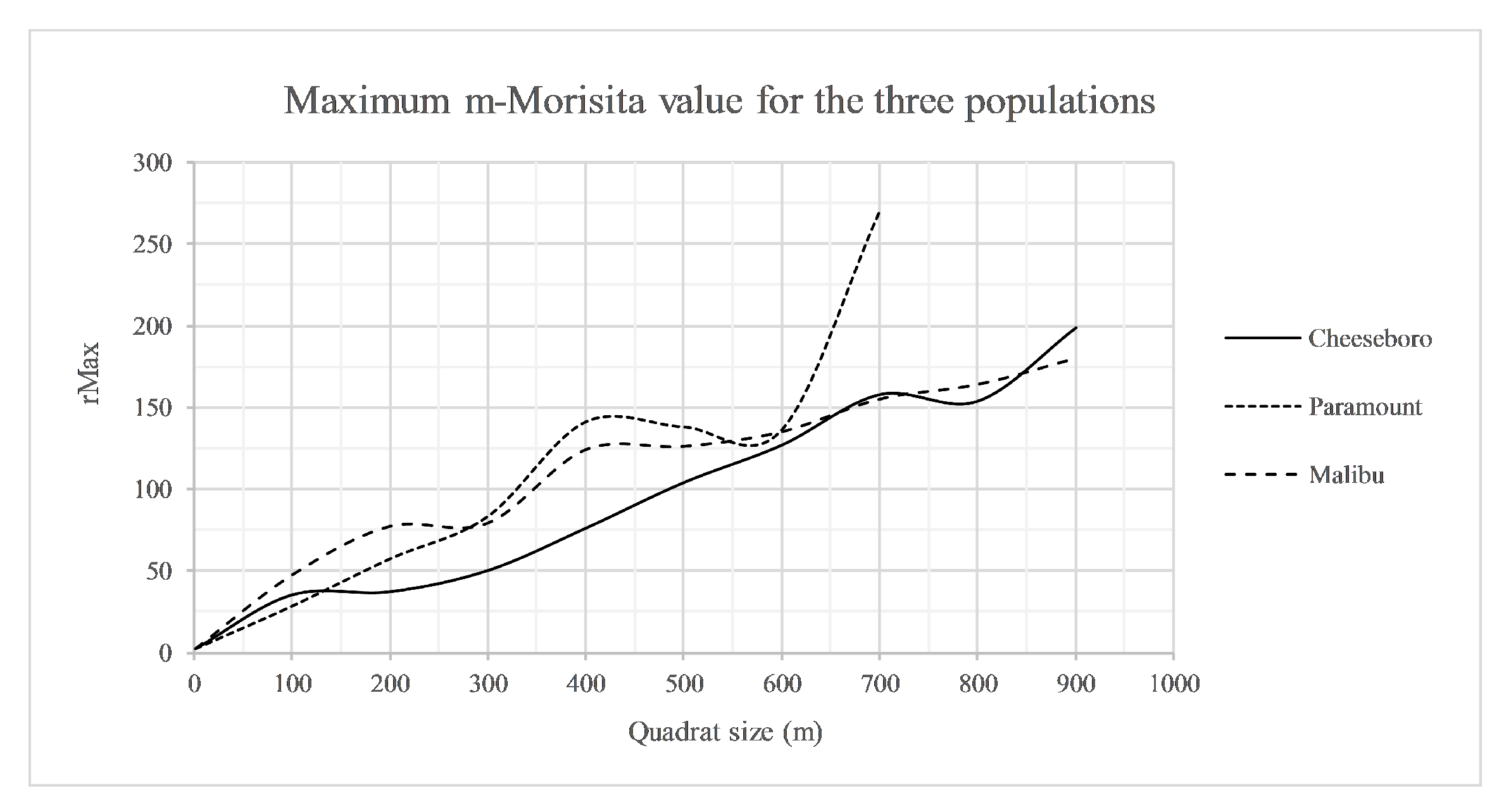
3.4. $d_M$ Analysis

We applied our interpretation of the rMax analysis from CHE to all three sites and identified patterns of clustering occurring at different scales across the sites (Figure 7). CHE exhibited clustering from 0 to 100 m and from 200 to 700 m but with less intensity at the larger quadrat sizes. At PAR, clustering was present at all quadrat sizes, from 0 to 400 m, and was more intense from 300 to 400 m. Finally, at MAC there was clustering from 0 to 200 m and from 300 to 400 m.

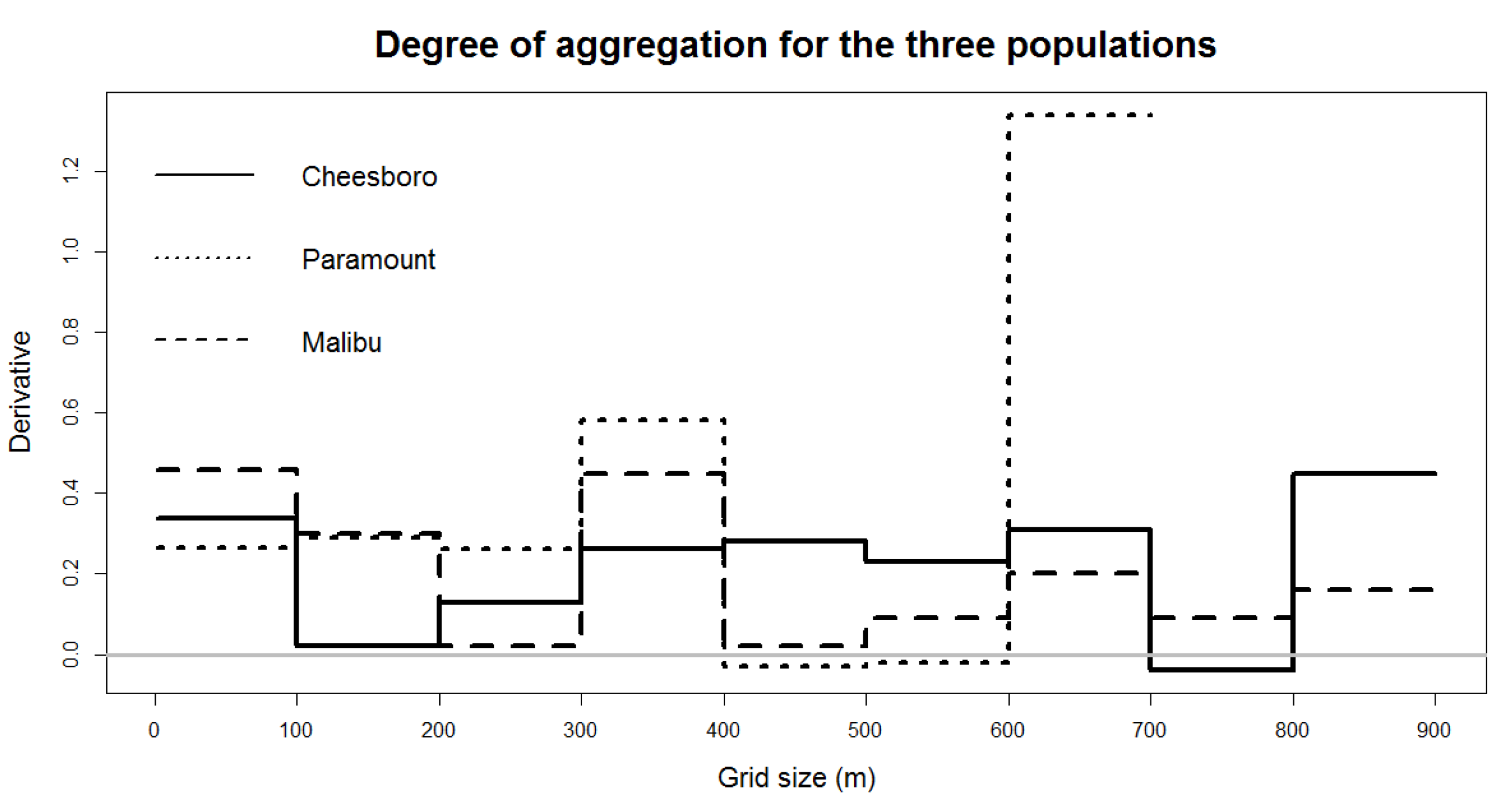
Computing the r-value when the first derivative of $I_{Mr}$ was equal to zero provided a relative measure of difference in aggregation between different populations. Interpretation of the $d_M$ curves (Figure 8) is similar to that of the rMax curves (Figure 7) above, however, the $d_M$ curves provide the advantage of having an index for all sites and quadrat sizes on a single scale. The horizontal gray line (y = 0) denotes a random distribution, and positive or negative deviations from zero indicate clustered or dispersed distributions, respectively. Clustering was apparent for all sites at the 100 m quadrat scale and corresponded to the relative degree of clustering indicated by the other implementations of the Morisita approach above. Degree of aggregation as measured by the $d_M$ index indicated that all three sites had clustered distributions at scales up to 100 m. MAC was most strongly clustered, followed by CHE, and finally by PAR, which exhibited clustering but with the least intensity at the 100 m scale of analysis.

While this result was similar to the results for the $I_M$ approach (m = 2) for several quadrat sizes, note, using $I_M$ analysis indicated the highest intenisty of clustering at PAR on the 50 m grid.

As quadrat size increased, the intensity of clustering changed, and the relative intensity among sites also changed. Examining the $d_M$ for larger quadrat sizes revealed that the intensity of clustering changed, increasing or decreasing for each site. At the 200 m scale, the $d_M$ for CHE was nearly zero, indicating an approximately random, non-clustered distribution, but it remained high for MAC and PAR. At the 300 m scale, the $d_M$ for MAC dropped to near zero but rose again for CHE while the value for PAR remained steady. Such changes illustrate how the choice of quadrat size, in combination with the particular arrangement of stems and habitat distribution, at the sites influenced both measures of spatial pattern and the relative degree of clustering among sites.

The relatively steady value of $d_M$ for PAR up to 300 m was due to the relatively stable pattern of clustering across the site—there was clustering of stems but without clear isolated clumps. With quadrat sizes larger than 300 m at PAR, the grid began to include “empty” (unsampled) open space outside the study area boundary and the $d_M$ values were drastically altered. Similarly, the initially high value for MAC was due to strong clustering and clumps found at the 100 m scale but, expanding to 200 m, quadrats diluted the strength of the clustering measure as more open space was included along with stems in the larger quadrats. At 300 m the clustering pattern was diluted, and again larger quadrats at this site became confounding due to including large empty areas that were not sampled. Finally, clustering was strong for CHE at the 100 m scale, but it quickly dropped off, and this was due to the presence of relatively small areas of clumping at the site, with more open space between clumps rather than a more evenly distributed dense pattern across the site as at MAC and PAR. Only when the quadrat size increased above 200 and 300 m were the small, somewhat isolated clumps at CHE again grouped into quadrats, increasing the $d_M$ value.

4. Discussion

The Morisita index of aggregation and the $I_{Mr}$ index provide ecologically interpretable measures of clustering or dispersion in spatial point pattern data. While many measures of spatial point patterns do not clearly distinguish among diverse distributions (which may or may not be clustered), Morisita’s original implementation and Hurlbert’s [18]$I_{Mr}$ approach provide well defined definitions of clustering and a measure of departure from randomness. We recognize that the Morisita Index of aggregation has experienced a lack of attention, perhaps because of its difficulties in interpretation and similar techniques such as Ripley’s K function appear to be easier to interpret. Golay et al. [16] stated a robust and interesting methodology to deal with the notion of scale and the Morisita Index, nevertheless we propose a simpler method based on the same index to classify any population in random or non-random spatial distribution. If local clusters are found, we can use the derivative plot (Figure 8) to quantify the degree of clustering compared to either the population itself as a whole or clusters in different populations.

While the $I_{Mr}$ index helps researchers closely examine different definitions or thresholds of clustering, a remaining limitation is that it is difficult or perhaps not possible to assess differences in spatial aggregation among multiple sites due to (1) the requirement to use the same quadrat size at different sites when that size may not be best for all sites and (2) the scale of the index values is not clearly interpretable. The theory stated by Morisita [19] and further studies [18,54,55] do not specify how to define the range of the quadrat size or how to choose a quadrat size for $I_{Mr}$. Golay et al. [16] tackled the scale problem by linking $I_{Mr}$ index and the multifractality concept through quadrat-based methods, i.e., Rényi’s generalized dimensions and the lacunarity index [16,17,56]. It appears that we are approaching the problem of scale by measuring the degree of crowding for different quadrat sizes. Consequently, an “appropriate” quadrat size for each site must be chosen by the researcher. Our approach to use the rMax values from the $I_{Mr}$ analysis to identify the scale of clustering provides a method to identify whether different sized quadrats may be appropriate at different sites and provides a guide for choosing what those quadrat sizes might be. Differences in $I_{Mr}$ values do not have a clear interpretation other than “higher” or “lower”, and analyzing differences in the index generated with different quadrat sizes is even more confounding. For example, Hayes and Donnell [30] applied $I_M$ and $I_{Mr}$ to valley oak stem locations at the same sites examined in the present paper, and they found clear evidence of clustering at all three sites, for multiple quadrat sizes. Their results, however, demonstrate the difficulty of comparing the index values across sites since only relative statements about differences in the degree and intensity of crowding could be made and only when the sites are analyzed using the same quadrat size.

It is also important to highlight the exploratory value of using the two nearest neighbor distance bands (Table 1), which are useful to choose initial quadrat sizes. Beginning with the maximum nearest-neighbor distance, we are able to change the level of detail by using a smaller or larger quadrat size depending on the data or assumptions of the researcher. Smaller sampling sizes would also lead to finer resolution in the derivative plot.

The results produced in our analysis here illustrate the nuanced interpretations possible with the rMax approach. Examining the curves of rMax for the three sites (see Figure 7), we were able to identify a pattern of clustering at distances <100 m at CHE, dispersion at slightly larger distances (100–200 m), and a return to a clustering pattern at distances >200 m. The rMax curve for PAR revealed that the spatial distribution there was clustered consistently using quadrats between 0 and 400 m, and that an inflection point of increased clustering occurs at 300 m, a scale at which a large amount of unsampled area is included and most stems are grouped into few quadrats. The rMax curve for MAC shows a similar pattern to that of PAR, though its slope becomes negative and indicates dispersion at scales >200 m, up to the 300 m scale, after which clustering is again indicated. This detailed examination of how rMax changes with quadrat size in the context of individual sites provides more information for choosing a quadrat size to analyze ecological crowding. Examining the rMax curves for the three sites, and considering the size of each study area, the distance between points at each site, and arrangement of open unsampled space at the sites, we choose to use 100 m quadrats for an analysis of ecological crowding of valley oak in this landscape. The 100 m quadrats capture the clustering that all of the measures indicate, yet are not so large that they would incorrectly indicate dispersion or underestimate clustering at CHE while indicating higher clustering at PAR and MAC as a 200 m quadrat grid would indicate. Further, since the rMax curves are based on maximum $I_{Mr}$ values and the r number of stems for that maximum value, using the $I_{Mr}$ curves to choose our quadrat size assures that the definition of clustering is based on an empirical limit of r stems being clustered using the quadrat size chosen. While Hayes and Donnell [30] examined $I_{Mr}$ values at the three sites using multiple quadrat sizes for analysis, interpretation was constrained by the necessity of having results from each quadrat size on different scales, and the clearest interpretation of differences among sites was possible only when the same quadrat size was used for all three sites. Applying our final measure of clustering, $d_M$ (see Figure 8), we showed a new approach to solve the problem of scale in terms of a single quadrat size. In the case of our valley oak populations, the trees are clustering at all three sites, however, there are differences in the intensity of the clustering with trees at MAC being the most intensely crowded, followed by CHE, and finally PAR, which has a clustered distribution but with the least intensity of clustering among the sites (Figure 8).

5. Conclusions

The approach suggested here captures relevant and interpretable information on the dispersion patterns in a population. The use of the derivative of $I_{Mr}$ allows us to quantify and interpret the degree of clustered, random, or dispersed distribution in any population. Plotting the derivative as a function of quadrat size deals with the relative scale in the data, offering a new approach to analyze ecological crowding over a range of scales. An advantage of this approach is the ability to directly compare the degree of crowding for different population sizes, densities, and local conditions, in the same analysis space, or across multiple sites.

Although our approach using $d_M$ offers some advantages for comparing spatial clustering and intensity of crowding among sites, some challenges exist. As quadrats increase in size the researcher has less control over shaping the study area boundary and more space outside the study boundary, or dominated by other species, may be incorporated in the analysis, giving a misleading result. Another challenge and possible opportunity is that square quadrats are typically used, but could be rectangular, which would allow more flexibility and potential to avoid the inclusion of unsampled space in our quadrats. This alternative opens multiple options, such as analyzing spatial aggregation if uniform anisotropy is detected in the data. As spatial patterns will be commonly determined by competition for resources such as water and nutrient availability along topographic and culturally influenced boundaries, more work examining how to summarize spatial point patterns that takes these variables into account will be helpful for better understanding pattern-process relationships.