Spatiotemporal Modeling of Urban Growth Predictions Based on Driving Force Factors in Five Saudi Arabian Cities
Abstract
:1. Introduction
2. Materials and Methods
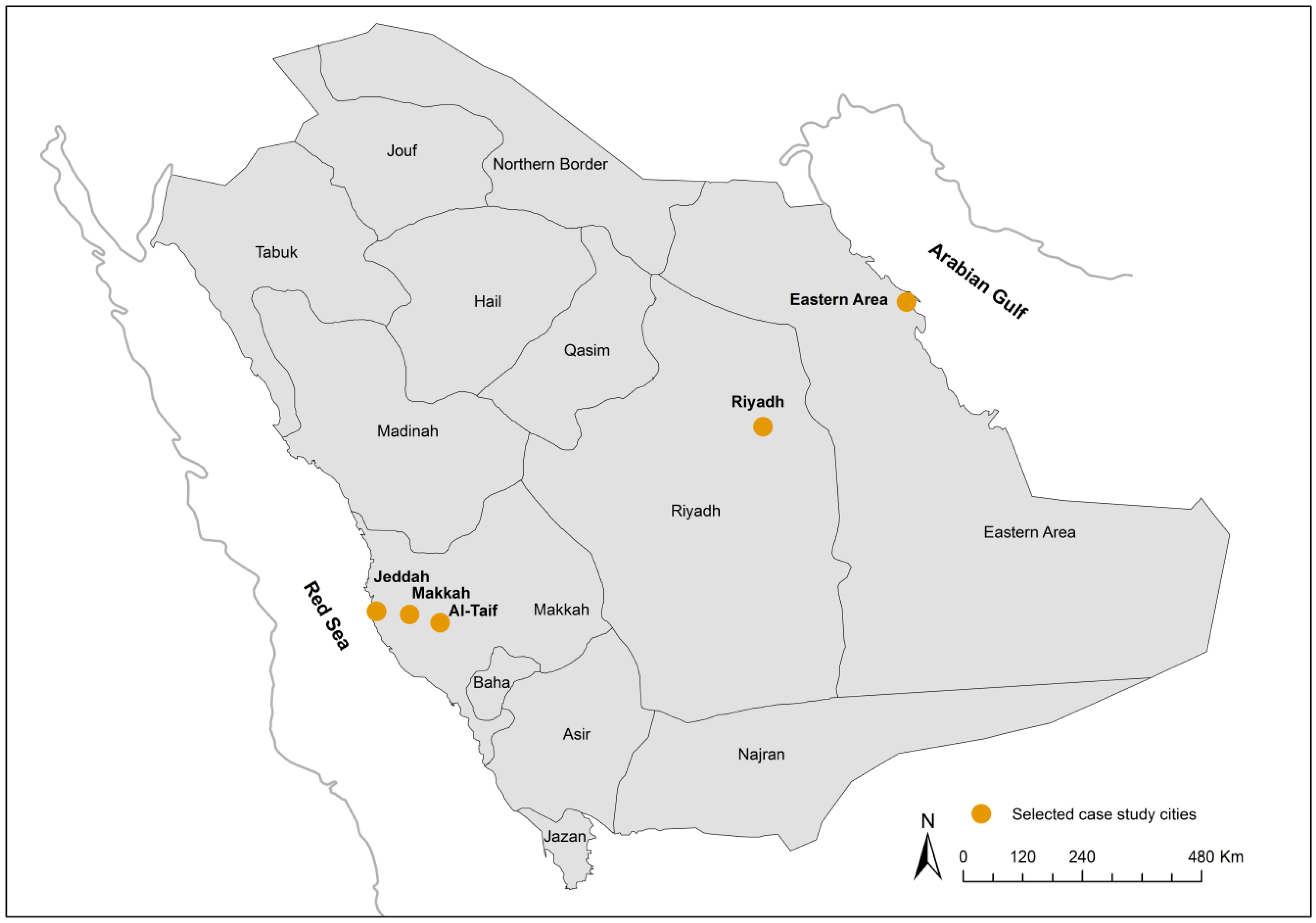
2.1. Study Area
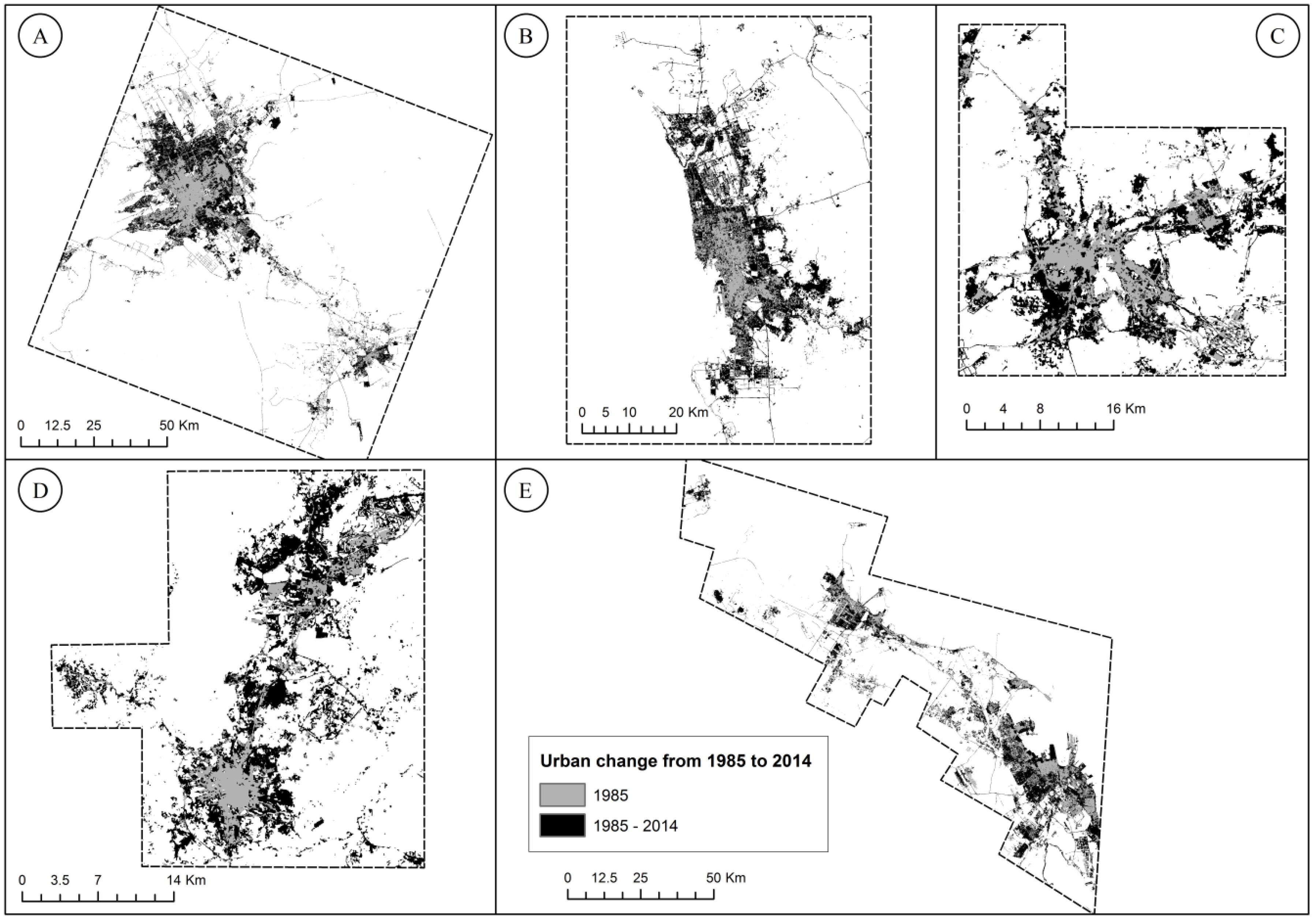
2.2. Quantifying the Spatial Distribution of Urban Expansion from 1985 to 2014
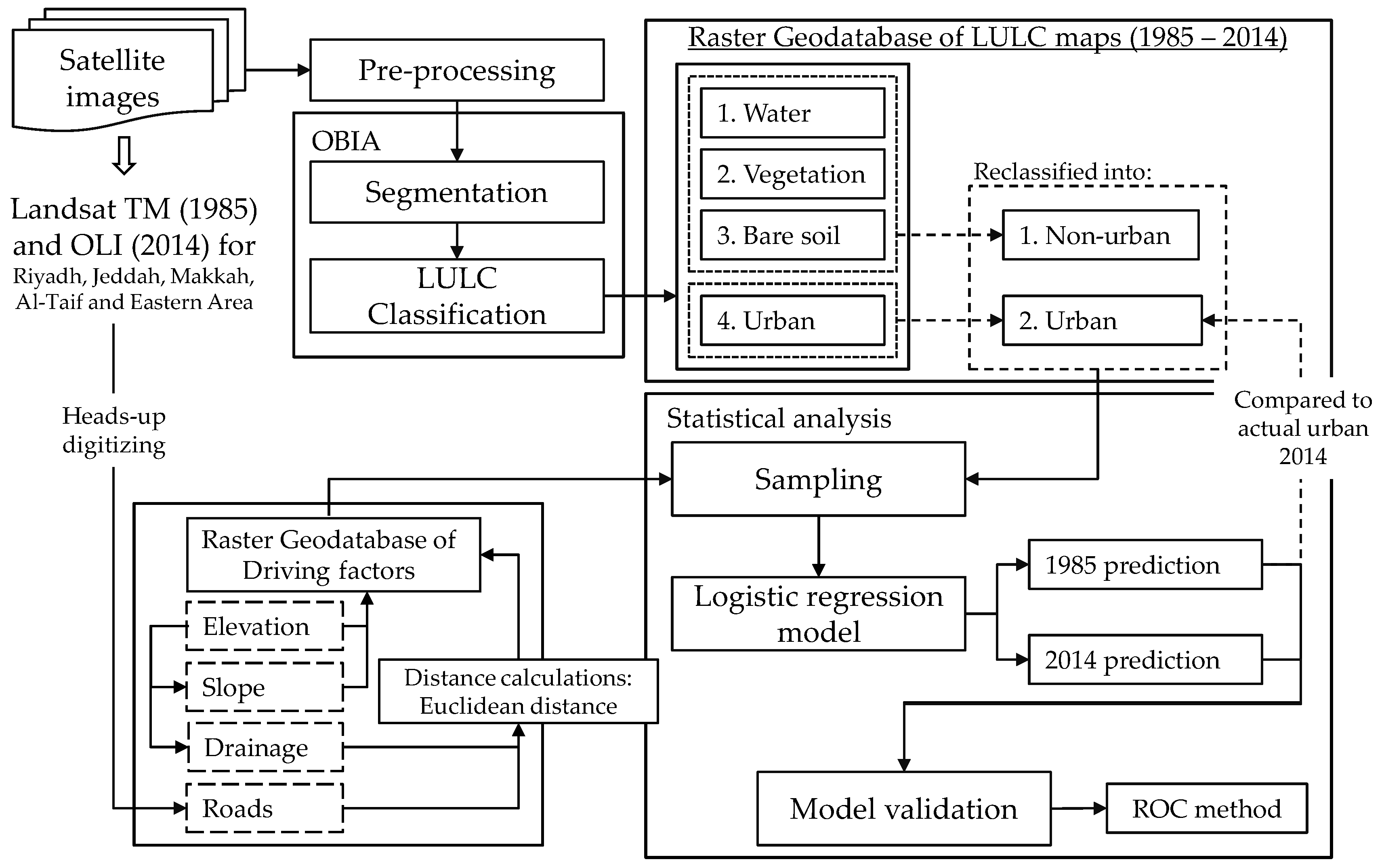
2.2.1. Data and Pre-Processing
2.2.2. Image Classification and Accuracy Assessment
2.3. Potential Driving Factors of Urban Expansion
2.4. Statistical Analysis
2.4.1. Urban and Non-Urban Data Sampling
2.4.2. Logistic Regression
2.4.3. Prediction of Spatial Patterns of Urban Distribution
2.4.4. Model Validation
3. Results
3.1. Spatial Statistical Modeling of Urban Expansion
3.2. Urban Probability among the Five Cities (1985)
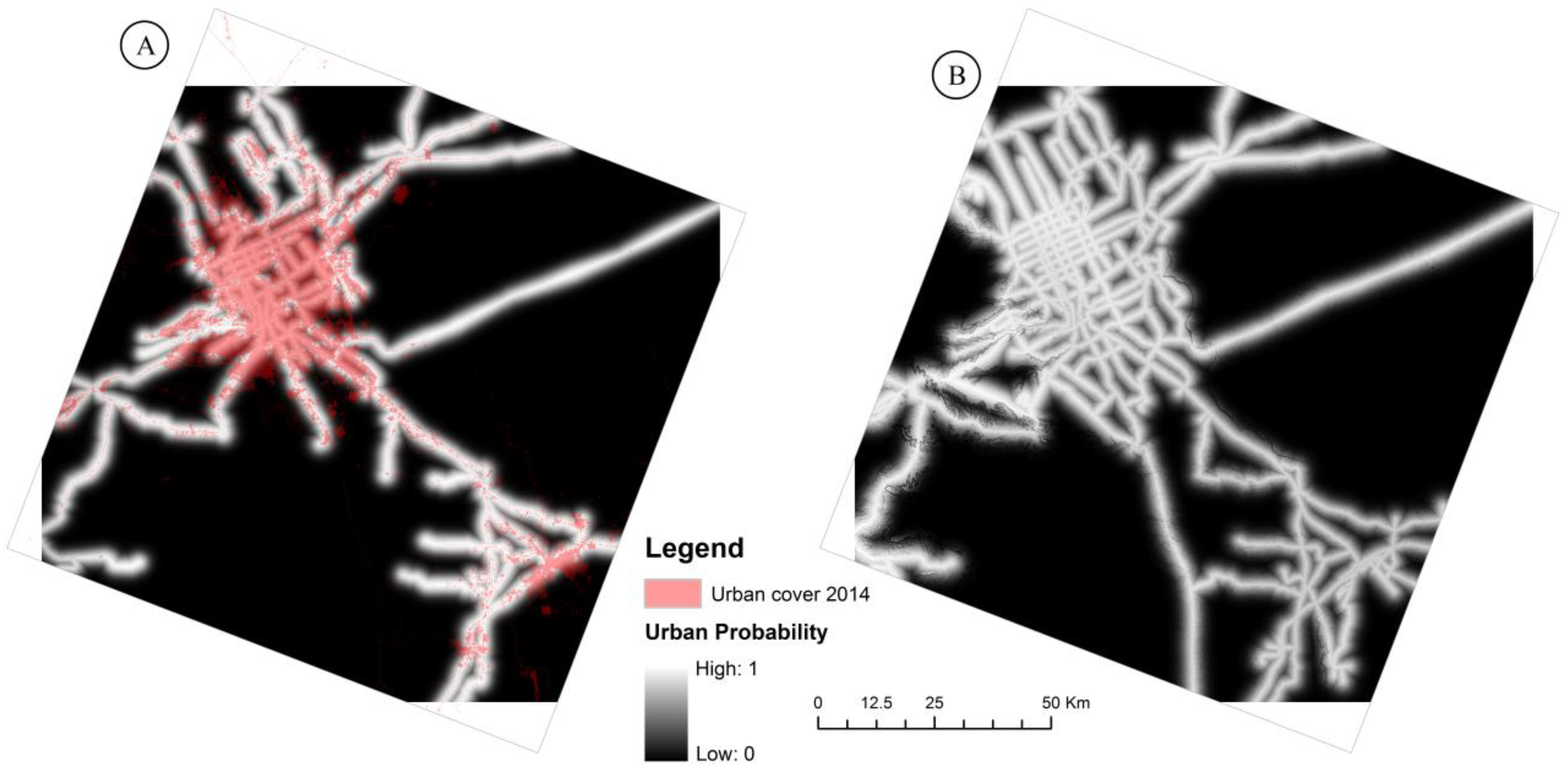
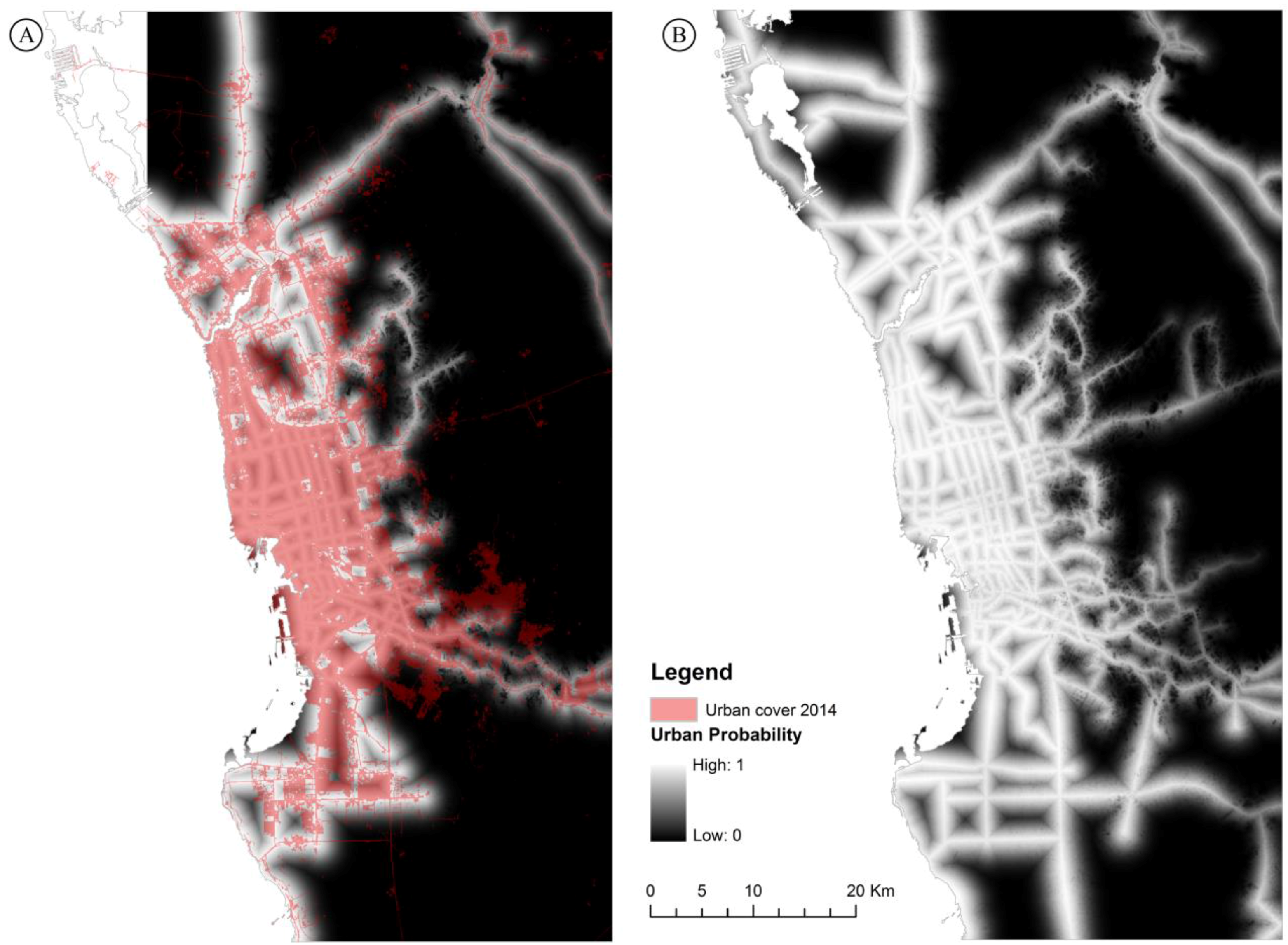
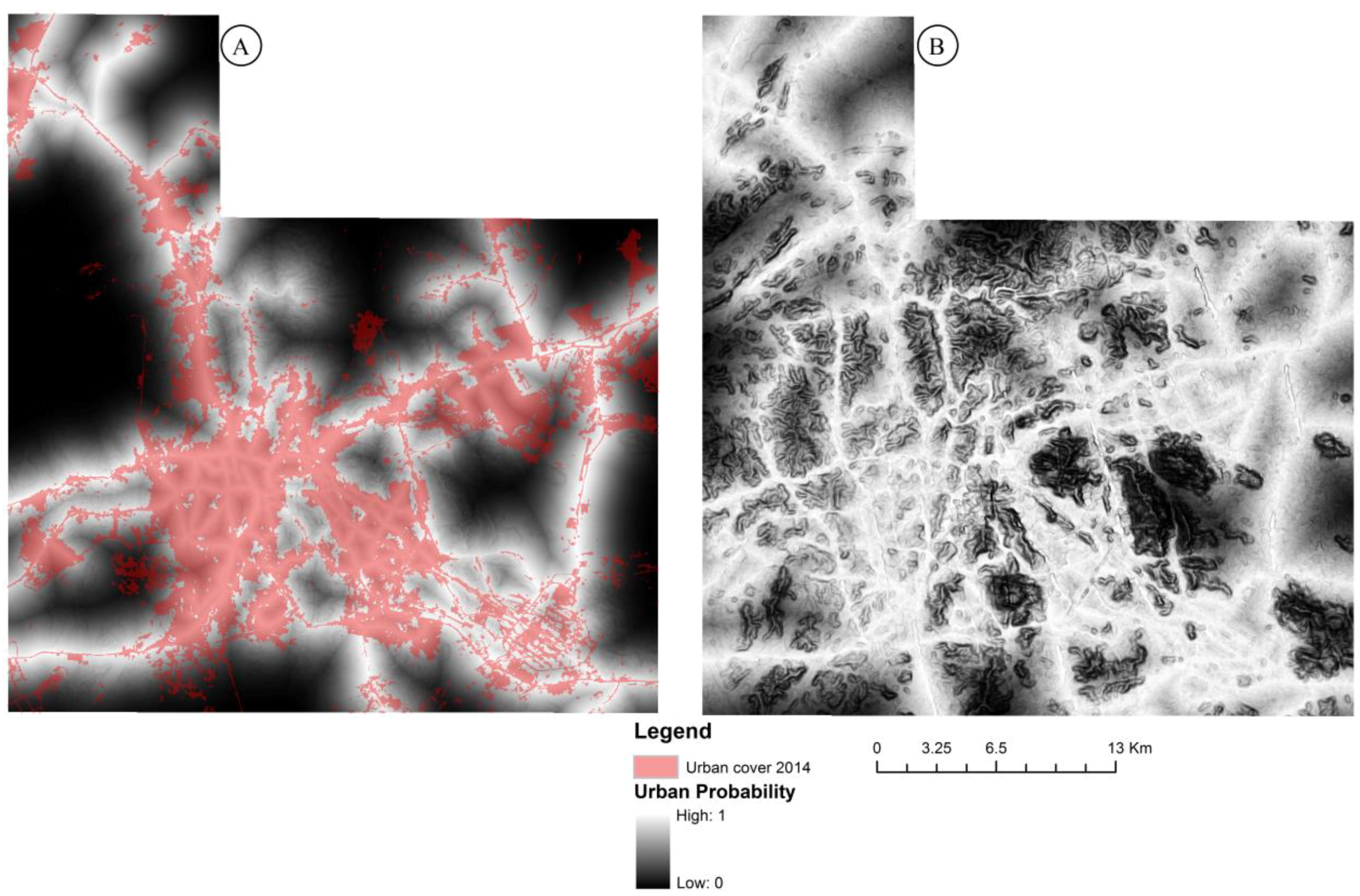
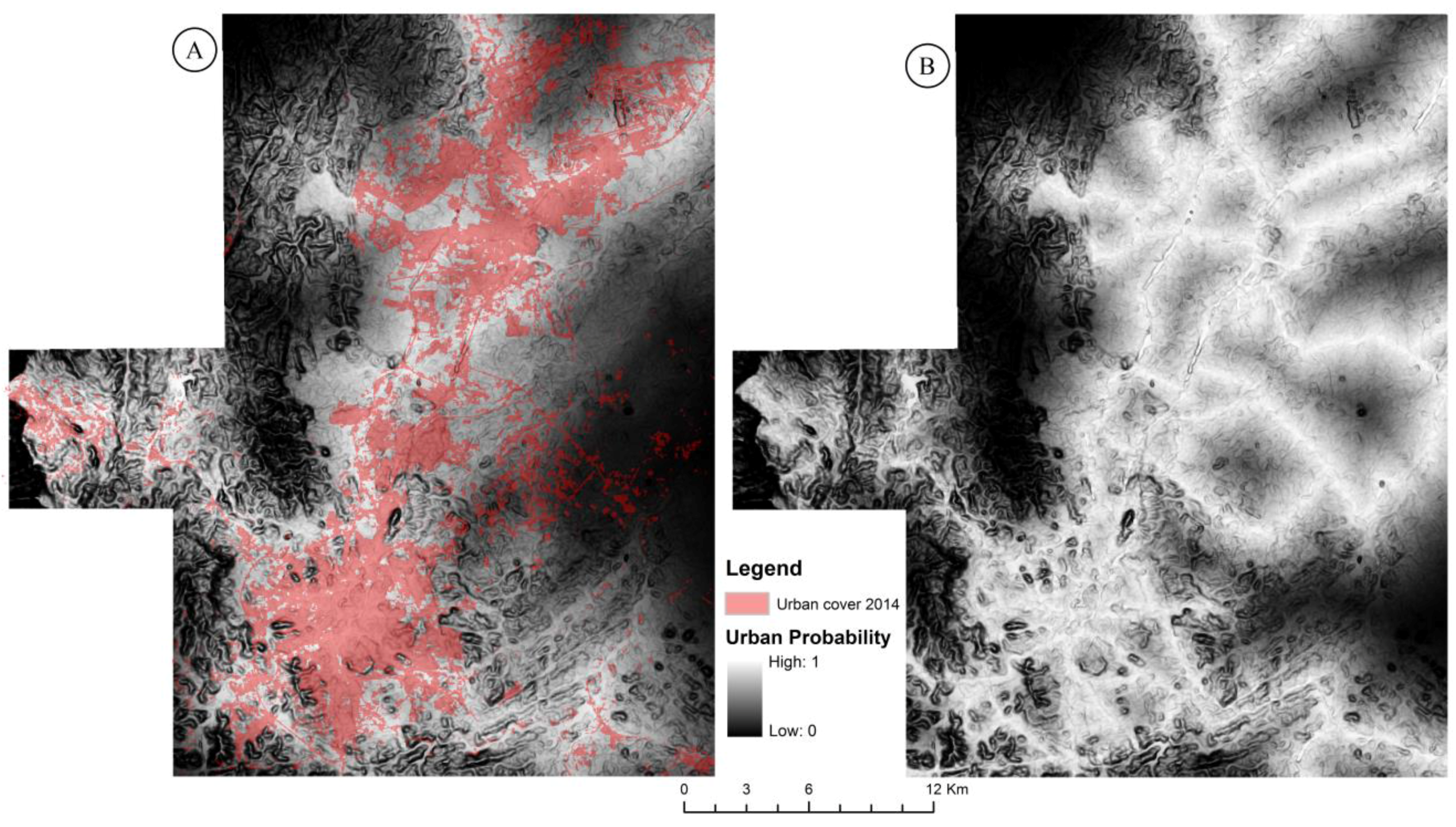
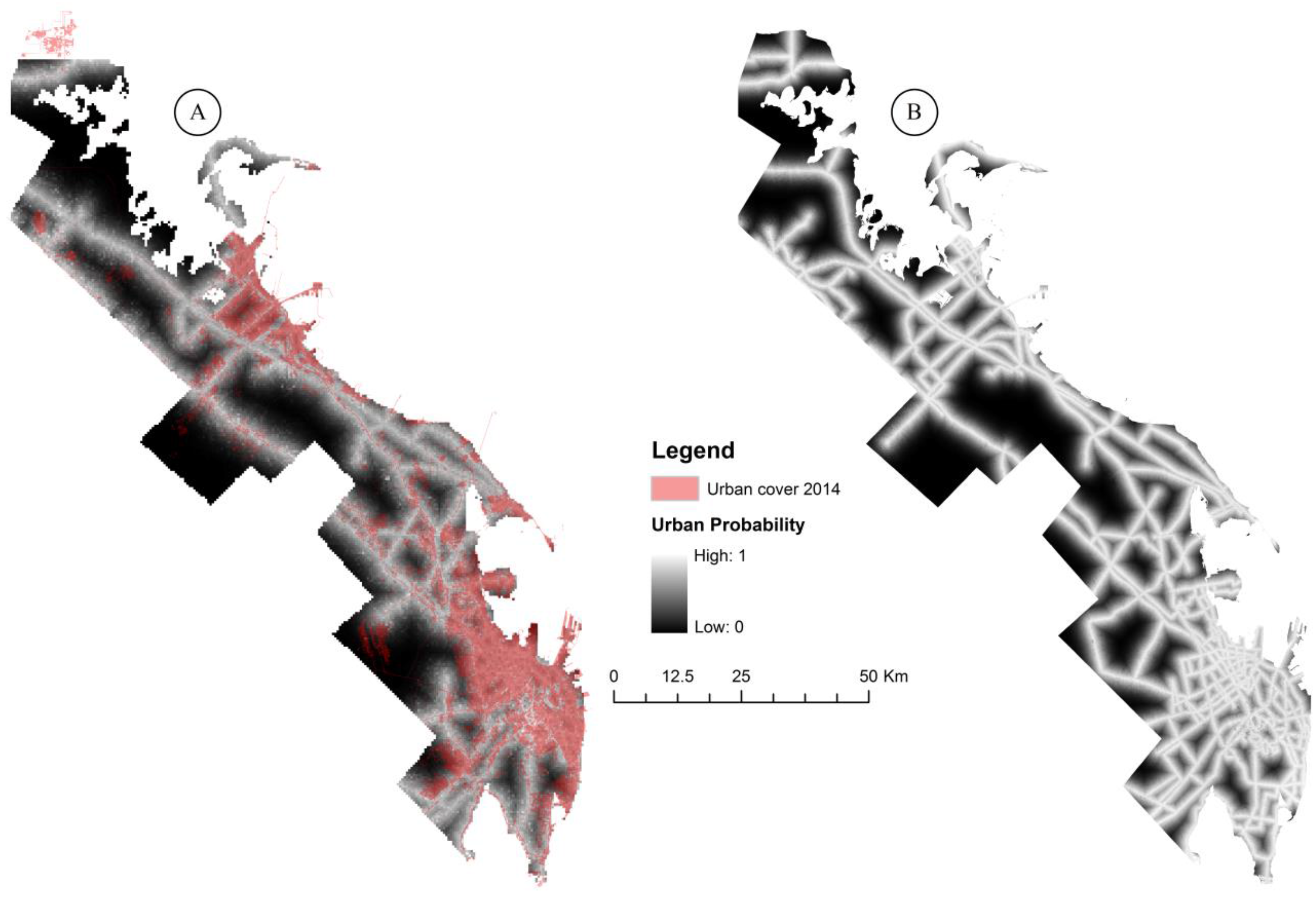
3.3. Urban Probability among the Five Cities (2014)
3.4. Model Validation Using the Relative Operating Characteristics (ROC) Method
3.5. The Importance of Predictor Variables
4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Masek, J.G.; Lindsay, F.E.; Goward, S.N. Dynamics of urban growth in the washington dc metropolitan area, 1973–1996, from landsat observations. Int. J. Remote Sens. 2000, 21, 3473–3486. [Google Scholar]
- Xu, H. Extraction of urban build-up land features from landsat imagery using a thematicoriented index combination technique. Photogramm. Eng. Remote. Sens. 2007, 73, 1381–1391. [Google Scholar] [CrossRef]
- Weng, Q. What is special about global urban remote sensing? In Global Urban. Monitoring and Assessment through Earth Observation; CRC Press: Boca Raton, FL, USA, 2014; pp. 1–12. [Google Scholar]
- Seto, K. Global urban issues. In Global Mapping of Human Settlement; CRC Press: Boca Raton, FL, USA, 2009; pp. 3–9. [Google Scholar]
- Rahman, A.; Aggarwal, S.P.; Netzband, M.; Fazal, S. Monitoring urban sprawl using remote sensing and gis techniques of a fast growing urban centre, india. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 56–64. [Google Scholar] [CrossRef]
- Cohen, B. Urban growth in developing countries: A review of current trends and a caution regarding existing forecasts. World Dev. 2004, 32, 23–51. [Google Scholar] [CrossRef]
- Grimmond, S.U.E. Urbanization and global environmental change: Local effects of urban warming. Geogr. J. 2007, 173, 83–88. [Google Scholar] [CrossRef]
- Hoymann, J.; Goetzke, R. Simulation and evaluation of urban growth for germany including climate change mitigation and adaptation measures. ISPRS Int. J. Geo-Inf. 2016, 5. [Google Scholar] [CrossRef]
- Al-Ahmadi, K.; See, L.; Heppenstall, A.; Hogg, J. Calibration of a fuzzy cellular automata model of urban dynamics in saudi arabia. Ecol. Complex. 2009, 6, 80–101. [Google Scholar] [CrossRef]
- Alqurashi, A.; Kumar, L. Land use and land cover change detection in the saudi arabian desert cities of makkah and al-taif using satellite data. Adv. Remote Sens. 2014, 3, 106–119. [Google Scholar] [CrossRef]
- Aljoufie, M. Toward integrated land use and transport planning in fast-growing cities: The case of jeddah, saudi arabia. Habitat Int. 2014, 41, 205–215. [Google Scholar] [CrossRef]
- Kamusoko, C.; Gamba, J. Simulating urban growth using a random forest-cellular automata (rf-ca) model. ISPRS Int. J. Geo-Inf. 2015, 4. [Google Scholar] [CrossRef]
- Batisani, N.; Yarnal, B. Urban expansion in centre county, pennsylvania: Spatial dynamics and landscape transformations. Appl. Geogr. 2009, 29, 235–249. [Google Scholar] [CrossRef]
- Cheng, J.; Masser, I. Urban growth pattern modeling: A case study of wuhan city, pr china. Landsc. Urban Plan. 2003, 62, 199–217. [Google Scholar] [CrossRef]
- Dubovyk, O.; Sliuzas, R.; Flacke, J. Spatio-temporal modelling of informal settlement development in sancaktepe district, istanbul, turkey. ISPRS J. Photogramm. Remote Sens. 2011, 66, 235–246. [Google Scholar] [CrossRef]
- Hu, Z.; Lo, C.P. Modeling urban growth in atlanta using logistic regression. Comput. Environ. Urban Syst. 2007, 31, 667–688. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z. Forty years of urban expansion in beijing: What is the relative importance of physical, socioeconomic, and neighborhood factors? Appl. Geogr. 2013, 38, 1–10. [Google Scholar] [CrossRef]
- Liu, H.; Zhou, Q. Developing urban growth predictions from spatial indicators based on multi-temporal images. Comput. Environ. Urban Syst. 2005, 29, 580–594. [Google Scholar] [CrossRef]
- Zeng, C.; Zhang, M.; Cui, J.; He, S. Monitoring and modeling urban expansion—A spatially explicit and multi-scale perspective. Cities 2015, 43, 92–103. [Google Scholar] [CrossRef]
- Arsanjani, J.J.; Helbich, M.; Mousivand, A.J. A morphological approach to predicting urban expansion. Trans. GIS 2014, 18, 219–233. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Helbich, M. Spatiotemporal variability of urban growth factors: A global and local perspective on the megacity of mumbai. Int. J. Appl. Earth Obs. Geoinform. 2015, 35, Part B. 187–198. [Google Scholar] [CrossRef]
- Ahmed, B.; Ahmed, R. Modeling urban land cover growth dynamics using multi‑temporal satellite images: A case study of dhaka, bangladesh. ISPRS Int. J. Geo-Inf. 2012, 1. [Google Scholar] [CrossRef]
- Maniquiz, M.C.; Lee, S.; Kim, L.-H. Multiple linear regression models of urban runoff pollutant load and event mean concentration considering rainfall variables. J. Environ. Sci. 2010, 22, 946–952. [Google Scholar] [CrossRef]
- Crespo, R.; Grêt-Regamey, A. Spatially explicit inverse modeling for urban planning. Appl. Geogr. 2012, 34, 47–56. [Google Scholar] [CrossRef]
- Wu, K.-y.; Zhang, H. Land use dynamics, built-up land expansion patterns, and driving forces analysis of the fast-growing hangzhou metropolitan area, eastern china (1978–2008). Appl. Geogr. 2012, 34, 137–145. [Google Scholar] [CrossRef]
- Reilly, M.K.; O’Mara, M.P.; Seto, K.C. From bangalore to the bay area: Comparing transportation and activity accessibility as drivers of urban growth. Landsc. Urban Plan. 2009, 92, 24–33. [Google Scholar] [CrossRef]
- Tsutsumida, N.; Saizen, I.; Matsuoka, M.; Ishii, R. Addressing urban expansion using feature-oriented spatial data in a peripheral area of ulaanbaatar, mongolia. Habitat Int. 2015, 47, 196–204. [Google Scholar] [CrossRef]
- Taubenböck, H.; Esch, T.; Felbier, A.; Wiesner, M.; Roth, A.; Dech, S. Monitoring urbanization in mega cities from space. Remote Sens. Environ. 2012, 117, 162–176. [Google Scholar] [CrossRef]
- Meyer, M.D.; Miller, E.J. Urban Transportation Planning: A Decision-Oriented Approach; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Crk, T.; Uriarte, M.; Corsi, F.; Flynn, D. Forest recovery in a tropical landscape: What is the relative importance of biophysical, socioeconomic, and landscape variables? Landsc. Ecol. 2009, 24, 629–642. [Google Scholar] [CrossRef]
- Luo, J.; Wei, Y.H.D. Modeling spatial variations of urban growth patterns in Chinese cities: The case of Nanjing. Landsc. Urban Plan. 2009, 91, 51–64. [Google Scholar] [CrossRef]
- Kleinbaum, D.G.; Klein, M. Logistic Regression: A Self-Learning Text, 3rd ed.; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- McCullagh, P.; Nelder, J.A.; McCullagh, P. Generalized Linear Models; Chapman and Hall London: Boca Raton, FL, USA, 1989. [Google Scholar]
- Liao, J.; Tang, L.; Shao, G.; Su, X.; Chen, D.; Xu, T. Incorporation of extended neighborhood mechanisms and its impact on urban land-use cellular automata simulations. Environ. Model. Softw. 2016, 75, 163–175. [Google Scholar] [CrossRef]
- Rienow, A.; Goetzke, R. Supporting sleuth—Enhancing a cellular automaton with support vector machines for urban growth modeling. Computers, Environ. Urban Syst. 2015, 49, 66–81. [Google Scholar] [CrossRef]
- Pontius, R.G. Quantification error versus location error in comparison of categorical maps. Photogramm. Eng. Remote Sens. 2000, 66, 1011–1016. [Google Scholar]
- Mas, J.-F.; Soares Filho, B.; Pontius, R.G.; Farfán Gutiérrez, M.; Rodrigues, H. A suite of tools for roc analysis of spatial models. ISPRS Int. J. Geo-Inf. 2013, 2, 869–887. [Google Scholar] [CrossRef]
- Pontius, R., Jr.; Parmentier, B. Recommendations for using the relative operating characteristic (roc). Landsc. Ecol. 2014, 29, 367–382. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Schneider, L.C. Land-cover change model validation by an roc method for the ipswich watershed, massachusetts, USA. Agric. Ecosyst. Environ. 2001, 85, 239–248. [Google Scholar] [CrossRef]
- Dincer, I.; Hussain, M.M.; Al-Zaharnah, I. Energy and exergy utilization in transportation sector of Saudi Arabia. Appl. Therm. Eng. 2004, 24, 525–538. [Google Scholar] [CrossRef]
- Müller, K.; Steinmeier, C.; Küchler, M. Urban growth along motorways in switzerland. Landsc. Urban Plan. 2010, 98, 3–12. [Google Scholar] [CrossRef]
- Assaf, S.A.; Bubshaitr, A.A.; Al-Muwasheer, F. Factors affecting affordable housing cost in Saudi Arabia. Int. J. Hous. Mark. Anal. 2010, 3, 290–307. [Google Scholar] [CrossRef]
- Ye, Y.; Zhang, H.; Liu, K.; Wu, Q. Research on the influence of site factors on the expansion of construction land in the pearl river delta, china: By using gis and remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 366–373. [Google Scholar] [CrossRef]
- Aspinall, R. Modelling land use change with generalized linear models—A multi-model analysis of change between 1860 and 2000 in gallatin valley, montana. J. Environ. Manag. 2004, 72, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Triantakonstantis, D.; Mountrakis, G. Urban growth prediction: A review of computational models and human perceptions. J. Geogr. Inf. Syst. 2012, 4, 555–587. [Google Scholar] [CrossRef]
- Dendoncker, N.; Rounsevell, M.; Bogaert, P. Spatial analysis and modelling of land use distributions in belgium. Comput. Environ. Urban Syst. 2007, 31, 188–205. [Google Scholar] [CrossRef]
- Vincent, P. Saudi Arabia: An Environmental Overview; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Lee, J.; Heaney, J. Estimation of urban imperviousness and its impacts on storm water systems. J. Water Resour. Plan. Manag. 2003, 129, 419–426. [Google Scholar] [CrossRef]
- Al Saud, M. Assessment of flood hazard of jeddah area 2009, Saudi Arabia. J. Water Resour. Prot. 2010, 2, 839–847. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Long, Y.; Gu, Y.; Han, H. Spatiotemporal heterogeneity of urban planning implementation effectiveness: Evidence from five urban master plans of Beijing. Landsc. Urban Plan. 2012, 108, 103–111. [Google Scholar] [CrossRef]

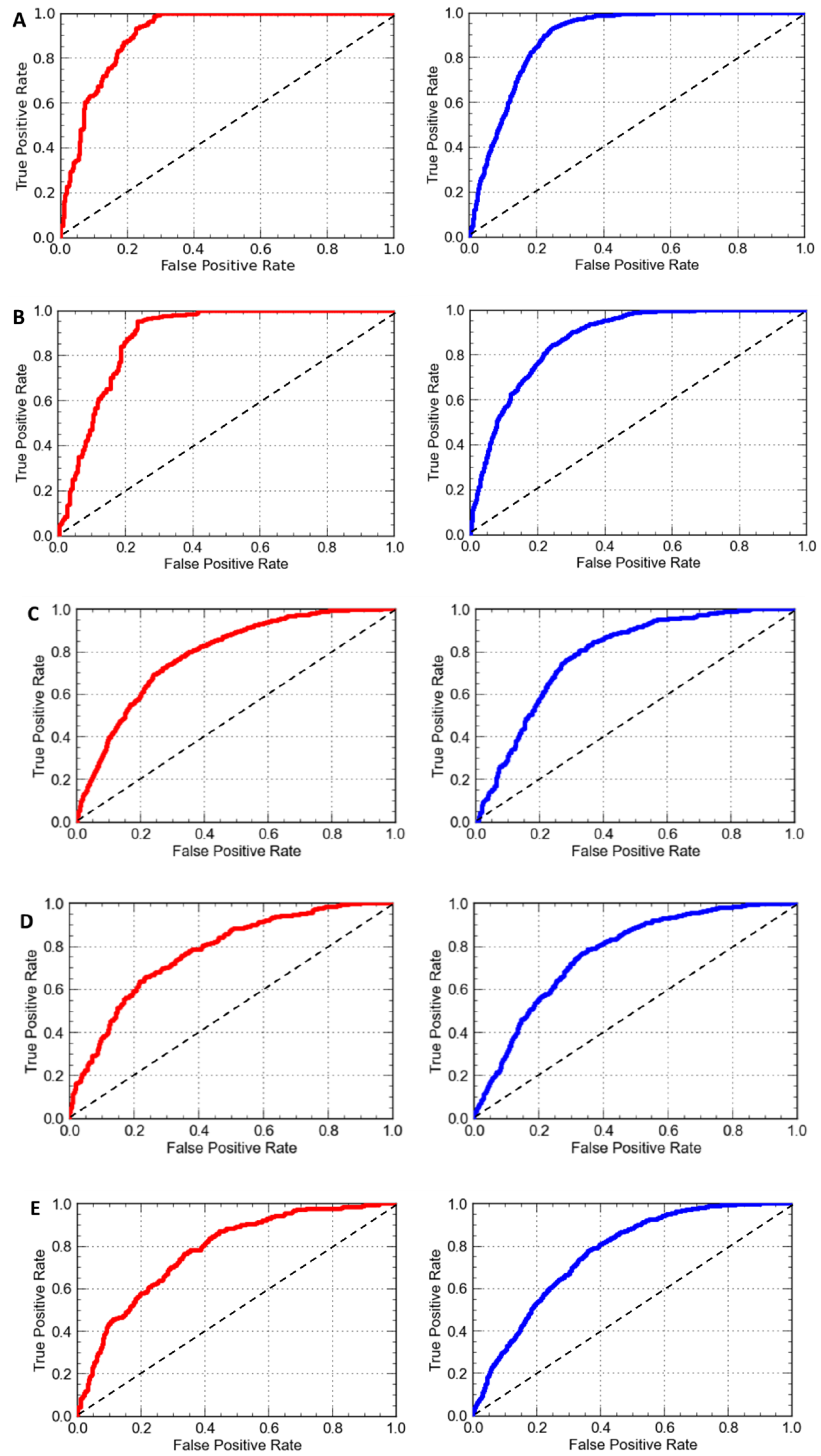
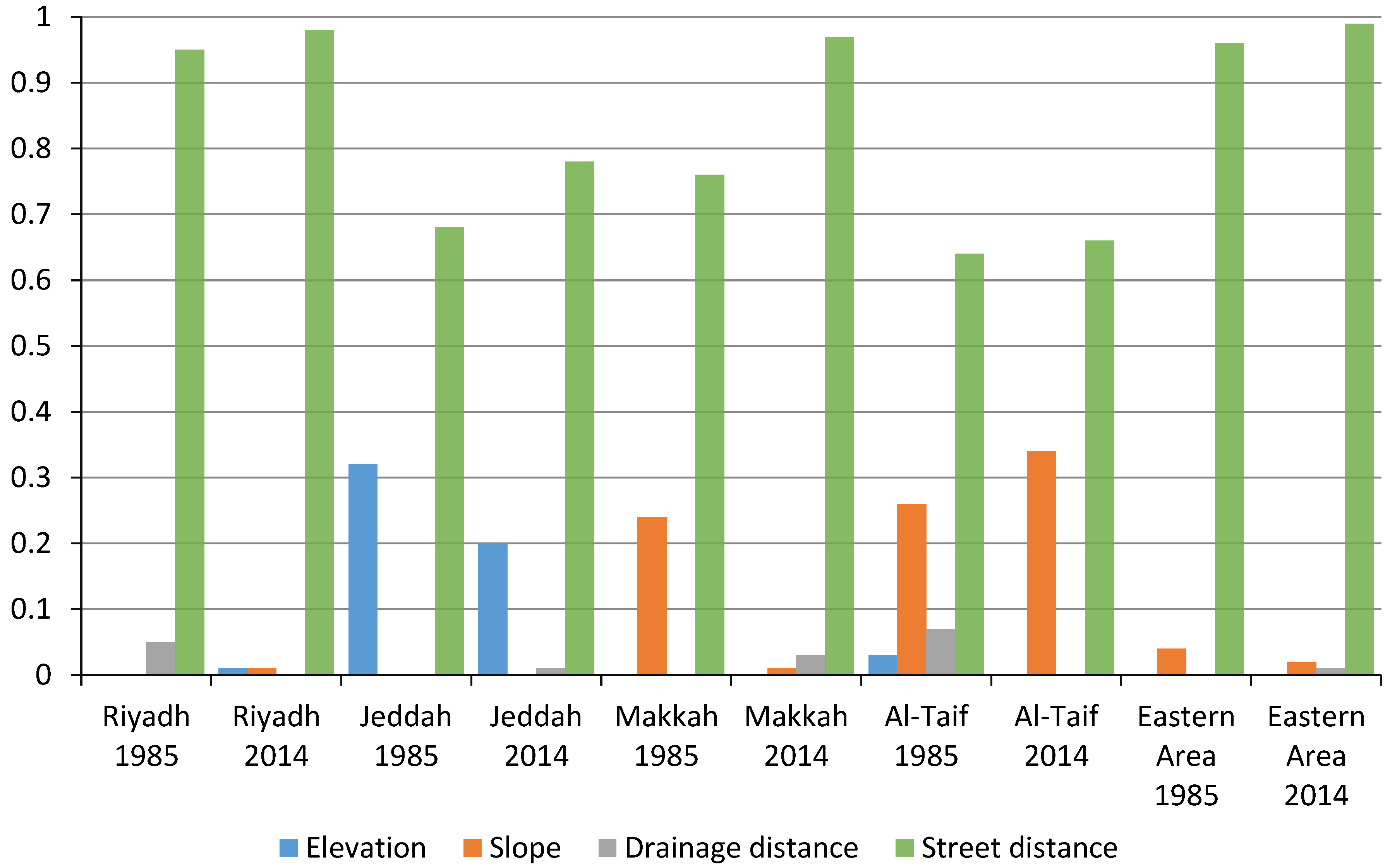
| No | Path | Row | Sensor | Date | Cloud Cover (%) | Covered Area |
|---|---|---|---|---|---|---|
| 1 | 164 | 41 | TM | 4-April-1985 | 1 | Eastern Area |
| 2 | OLI | 2-August-2014 | 0 | |||
| 3 | 164 | 42 | TM | 4-April-1985 | 0 | |
| 4 | OLI | 2-August-14 | 0 | |||
| 5 | 165 | 43 | TM | 13-January-1985 | 0 | Riyadh |
| 6 | OLI | 20-January-2014 | 0 | |||
| 7 | 166 | 43 | TM | 14-August-1985 | 0 | |
| 8 | OLI | 16-August-2014 | 0 | |||
| 9 | 169 | 45 | TM | 30-March-1985 | 8 | Makah and Al-Taif |
| 10 | OLI | 4-May-2014 | 3 | |||
| 11 | 170 | 45 | TM | 9-June-1985 | 0 | Jeddah |
| 12 | OLI | 9-June-2014 | 0 |
| Variables | 1985 | 2014 | ||||||
|---|---|---|---|---|---|---|---|---|
| β | S.E. | p (>|z|) | Exp (β) | β | S.E. | p (>|z|) | Exp (β) | |
| Intercept | 2.8603 ** | 1.0386 | 0.0059 | 17.4671 | 0.1164 | 0.3842 | 0.7619 | 1.1235 |
| Elevation | −0.0003 | 0.0018 | 0.8490 | 0.9997 | 0.0032 *** | 0.0007 | 0.0000 | 1.0031 |
| Slope | −0.0006 | 0.0221 | 0.9786 | 0.9994 | −0.0332 *** | 0.0087 | 0.0001 | 0.9674 |
| Drainages distance | −0.0001. | 0.0000 | 0.0884 | 0.9999 | 0.0000. | 0.0000 | 0.0965 | 1.0000 |
| Street distance | −0.0014 *** | 0.0001 | 0.0000 | 0.9986 | −0.0012 *** | 0.0001 | 0.0000 | 0.9988 |
| PCP | 85.1911 | 83.8340 | ||||||
| Neg. R2 | 0.68 | 0.61 | ||||||
| 2 Log Likelihood | 424.5 | 1966.0 | ||||||
| Variables | 1985 | 2014 | ||||||
|---|---|---|---|---|---|---|---|---|
| β | S.E. | p (>|z|) | Exp (β) | β | S.E. | p (>|z|) | Exp (β) | |
| Intercept | 2.2401 *** | 0.2535 | 0.0000 | 9.3946 | 2.472966 | 0.116307 | 2.5E−100 | 11.85756 |
| Elevation | −0.0212 *** | 0.0041 | 0.0000 | 0.9790 | −0.0153 *** | 0.001489 | 1.22E−24 | 0.984854 |
| Slope | 0.0149 | 0.0226 | 0.5111 | 1.0150 | −0.0108 *** | 0.009136 | 0.236826 | 0.989251 |
| Drainages distance | 0.0000 | 0.0001 | 0.8634 | 1.0000 | −0.0001 | 3E−05. | 0.000207 | 0.999889 |
| Street distance | −0.0016 *** | 0.0002 | 0.0000 | 0.9984 | −0.0015 *** | 8.65E−05 | 5.01E−71 | 0.99846 |
| PCP | 85.2140 | 79.69256 | ||||||
| Neg. R2 | 0.63 | 0.54 | ||||||
| 2 Log Likelihood | 385.5 | 2150.3 | ||||||
| Variables | 1985 | 2014 | ||||||
|---|---|---|---|---|---|---|---|---|
| β | S.E. | p (>|z|) | Exp (β) | β | S.E. | p (>|z|) | Exp (β) | |
| Intercept | 1.3834 *** | 0.1939 | 0.0000 | 3.9885 | 1.5837 *** | 0.2710 | 0.0000 | 4.8727 |
| Elevation | 0.0001 | 0.0006 | 0.8692 | 1.0001 | −0.0002 | 0.0009 | 0.8366 | 0.9998 |
| Slope | −0.0044 | 0.0043 | 0.3007 | 0.9956 | −0.0523 *** | 0.0074 | 0.0000 | 0.9491 |
| Drainages distance | −0.0002 *** | 0.0000 | 0.0001 | 0.9998 | 0.0000 | 0.0001 | 0.6946 | 1.0000 |
| Street distance | −0.0012 *** | 0.0001 | 0.0000 | 0.9988 | −0.0010 *** | 0.0001 | 0.0000 | 0.9990 |
| PCP | 71.6411 | 73.6136 | ||||||
| Neg. R2 | 0.32 | 0.34 | ||||||
| 2 Log Likelihood | 2459.8 | 1216.6 | ||||||
| Variables | 1985 | 2014 | ||||||
|---|---|---|---|---|---|---|---|---|
| β | S.E. | p (>|z|) | Exp (β) | β | S.E. | p (>|z|) | Exp (β) | |
| Intercept | −1.0969 | 1.0557 | 0.2988 | 0.3339 | 2.6620 *** | 0.7302 | 0.0003 | 14.3245 |
| Elevation | 0.0017 * | 0.0007 | 0.0108 | 1.0017 | −0.0008. | 0.0005 | 0.0836 | 0.9992 |
| Slope | −0.0830 *** | 0.0135 | 0.0000 | 0.9204 | −0.0781 *** | 0.0101 | 0.0000 | 0.9249 |
| Drainages distance | −0.0004 *** | 0.0001 | 0.0001 | 0.9996 | 0.0000 | 0.0001 | 0.9934 | 1.0000 |
| Street distance | −0.0004 *** | 0.0000 | 0.0000 | 0.9996 | −0.0008 *** | 0.0001 | 0.0000 | 0.9992 |
| PCP | 70.0730 | 70.8333 | ||||||
| Neg. R2 | 0.29 | 0.29 | ||||||
| 2 Log Likelihood | 935.4 | 2024.3 | ||||||
| Variables | 1985 | 2014 | ||||||
|---|---|---|---|---|---|---|---|---|
| β | S.E. | p (>|z|) | Exp (β) | β | S.E. | p (>|z|) | Exp (β) | |
| Intercept | 0.5358 ** | 0.2035 | 0.0085 | 1.7088 | 1.1041 *** | 0.1270 | 0.0000 | 3.0166 |
| Elevation | 0.0033 | 0.0090 | 0.7147 | 1.0033 | 0.0008 | 0.0052 | 0.8803 | 1.0008 |
| Slope | 0.0564. | 0.0301 | 0.0612 | 1.0580 | −0.0400 * | 0.0174 | 0.0216 | 0.9608 |
| Drainages distance | 0.0000 | 0.0000 | 0.5990 | 1.0000 | 0.0000 | 0.0000 | 0.2482 | 1.0000 |
| Street distance | −0.0007 *** | 0.0001 | 0.0000 | 0.9993 | −0.0011 *** | 0.0001 | 0.0000 | 0.9989 |
| PCP | 71.0983 | 70.1521 | ||||||
| Neg. R2 | 0.28 | 0.31 | ||||||
| 2 Log Likelihood | 798.9 | 2367.2 | ||||||
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqurashi, A.F.; Kumar, L.; Al-Ghamdi, K.A. Spatiotemporal Modeling of Urban Growth Predictions Based on Driving Force Factors in Five Saudi Arabian Cities. ISPRS Int. J. Geo-Inf. 2016, 5, 139. https://doi.org/10.3390/ijgi5080139
Alqurashi AF, Kumar L, Al-Ghamdi KA. Spatiotemporal Modeling of Urban Growth Predictions Based on Driving Force Factors in Five Saudi Arabian Cities. ISPRS International Journal of Geo-Information. 2016; 5(8):139. https://doi.org/10.3390/ijgi5080139
Chicago/Turabian StyleAlqurashi, Abdullah F., Lalit Kumar, and Khalid A. Al-Ghamdi. 2016. "Spatiotemporal Modeling of Urban Growth Predictions Based on Driving Force Factors in Five Saudi Arabian Cities" ISPRS International Journal of Geo-Information 5, no. 8: 139. https://doi.org/10.3390/ijgi5080139
APA StyleAlqurashi, A. F., Kumar, L., & Al-Ghamdi, K. A. (2016). Spatiotemporal Modeling of Urban Growth Predictions Based on Driving Force Factors in Five Saudi Arabian Cities. ISPRS International Journal of Geo-Information, 5(8), 139. https://doi.org/10.3390/ijgi5080139






