1. Introduction
Spatial Interpolation (SI) is a process employed to estimate the values of properties at unknown points within an area covered by existing observed points [
1]. In many situations, SI is performed to provide contours so data can be displayed graphically, to calculate property values for the surface at a given point or to analyze and predict a trend surface. In Digital Earth (DE) research, SI has always been a powerful tool for modeling and simulation [
2,
3]. Technological developments have greatly enriched the methods that are available for acquiring and accessing data, and in many large-scale engineering applications, huge amounts of data need to be processed using interpolation algorithms. Indeed, SI is particularly important for prediction and representation in many fields, including geographical information systems and remote sensing [
4,
5,
6], geology [
7], mining [
8], hydrogeology [
9], soil research [
10], geophysics [
11], oceanography [
12], meteorology [
13], ecology and environmental studies [
14,
15].
Several different types of classification methods are used by SI procedures, e.g., point-area, global-local and exact-approximate interpolation [
16]. Many techniques exist for both global and local interpolation. Trend surface analysis and Fourier series are examples of global techniques, whereas proximal, kriging and B-splines are local techniques. In particular, the kriging SI algorithm is a typical local interpolation algorithm. The universal kriging interpolation algorithm is a type of linear and unbiased optimal kriging SI algorithm, which is used widely in many scientific and engineering applications. However, in many applications, severe performance bottlenecks occur when using the serial universal kriging algorithm because the computational cost increases exponentially with the input data size [
17,
18].
In order to accelerate the process and obtain better performance, researchers have developed different methods in the past decades to implement parallel SI algorithms that target high performance computing systems, e.g., MasPar [
19], Cray T3D [
20], parallel clusters [
21], multi-core platforms [
22] and grid computing environments [
23]. In particular, there have been several studies of parallel kriging interpolation algorithm design. For example, Kerry
et al. [
24] used a dedicated high performance computer to implement a parallel kriging algorithm that greatly reduces the CPU time. However, this method is quite expensive, and it demands a high standard hardware configuration to accelerate processing. Pedelty
et al. [
25] implemented a parallel kriging algorithm using the message passing interface parallel programming model on a commodity cluster, where their implementation achieved satisfactory performance and good efficiency. However, the requirement for real-time processing and the rapid growth in the data size demands many more computing nodes, which inevitably increases both the hardware and maintenance costs, as well as requiring high energy consumption [
26]. Some studies have also developed parallel kriging algorithms using multi-core parallelism methods. For example, Strzelczyk
et al. [
27] designed a parallel kriging algorithm based on multiple cores, but there were efficiency issues when multi-core parallelism was applied to specialized scientific applications, e.g., big data processing, because of the slow system memory access.
Recently, due to the rapid increase in the computing capacity of accelerators, such as Graphics Processor Units (GPUs) and Intel Xeon Phi (Intel Many Integrated Core architecture (MIC)), the use of accelerators for big data processing has become a hot research topic in various fields. Many studies of GPUs have been conducted in the geo-sciences field [
28,
29,
30,
31]. In particular, there have been some studies of universal kriging algorithms; for example, Cheng
et al. implemented a parallel universal kriging algorithm using the NVIDIA Compute Unified Device Architecture (CUDA) on a GPU platform [
32]. However, there have been few studies on the Intel MIC platform because MIC is a relatively new accelerator technology. Previous studies based on MIC focused mainly on comparisons with GPU or programming aspects of the platform instead of the design or implementation of a parallel SI algorithm or applications. For instance, Heinecke
et al. [
33] compared the architecture and performance of a General Purpose GPU (GPGPU) with an Intel MIC and demonstrated the benefits of MIC. Wang
et al. [
34] described measures to avoid bottlenecks in the memory capacity, network bandwidth,
etc., and enhanced the parallel programming thread extensibility on the MIC platform. However, their implementations were not portable across different platforms because different computing platforms,
i.e., GPU and MIC, require different programming models and tools.
A heterogeneous computing system is a computing system that can integrate the GPU and Intel Xeon Phi acceleration components into conventional computing systems to implement computing tasks together with the CPU. Heterogeneous computing integrates each heterogeneous platform in an asynchronous manner by utilizing separate resources for computing or task scheduling, thereby maximizing the overall efficiency of a computing system by assigning tasks based on considerations of the capacities of each computing device [
35].
Heterogeneous computing is playing increasingly important roles in big data processing, and we envision the rapid adoption of heterogeneous computing for large-scale spatial data interpolation processing using improved algorithms. This approach can potentially achieve high performance on coprocessor computing platforms with speedups of more than 10×, as well as effectively avoiding the aforementioned problems that are encountered on a traditional CPU-only cluster. It is also desirable to have an optimized cross-platform implementation of a parallel universal kriging algorithm that runs on different heterogeneous platforms. To the best of our knowledge, few studies have addressed the application of heterogeneous computing in the geo-sciences field.
In this study, we present the design and implementation of a parallel universal kriging algorithm, as well as demonstrating its performance and cross-platform features. The remainder of this paper is organized as follows. In
Section 2, we give a brief introduction to the universal kriging algorithm, heterogeneous computing and the OpenCL development model.
Section 3 focuses on the implementation of the serial kriging algorithm, hotspot analysis and the corresponding parallelization techniques. In
Section 4, we describe the design and implementation of the parallel universal kriging algorithm.
Section 5 presents the experimental results and analysis. Finally, we give our conclusions in
Section 6.
3. Serial Universal Kriging Algorithm
3.1. Implementation of the Serial Universal Kriging Algorithm
The primary task involved in the implementation of the serial algorithm is selecting an appropriate space variation function model, as well as code development for this variation function model. In this study, we calculate the estimated value for each point using the neighboring points searching approach.
3.1.1. Selecting the Variation Function Model
The variation function model can be divided into three categories in geo-statistics: (1) the model with sill [
40], which includes a spherical model, an index model and a Gaussian model; (2) the model without sill [
2], which includes a power function and a linear model; and (3) the cavity effect model [
41]. We use the spherical model, which is employed frequently in geo-statistics, as our serial universal kriging algorithm’s variogram function. The spherical model can be expressed by Equation (8):
where
is the nugget effect,
c is the partial sill of the semi-variogram model and
a is the range of influence.
3.1.2. Implementation of the Serial Algorithm
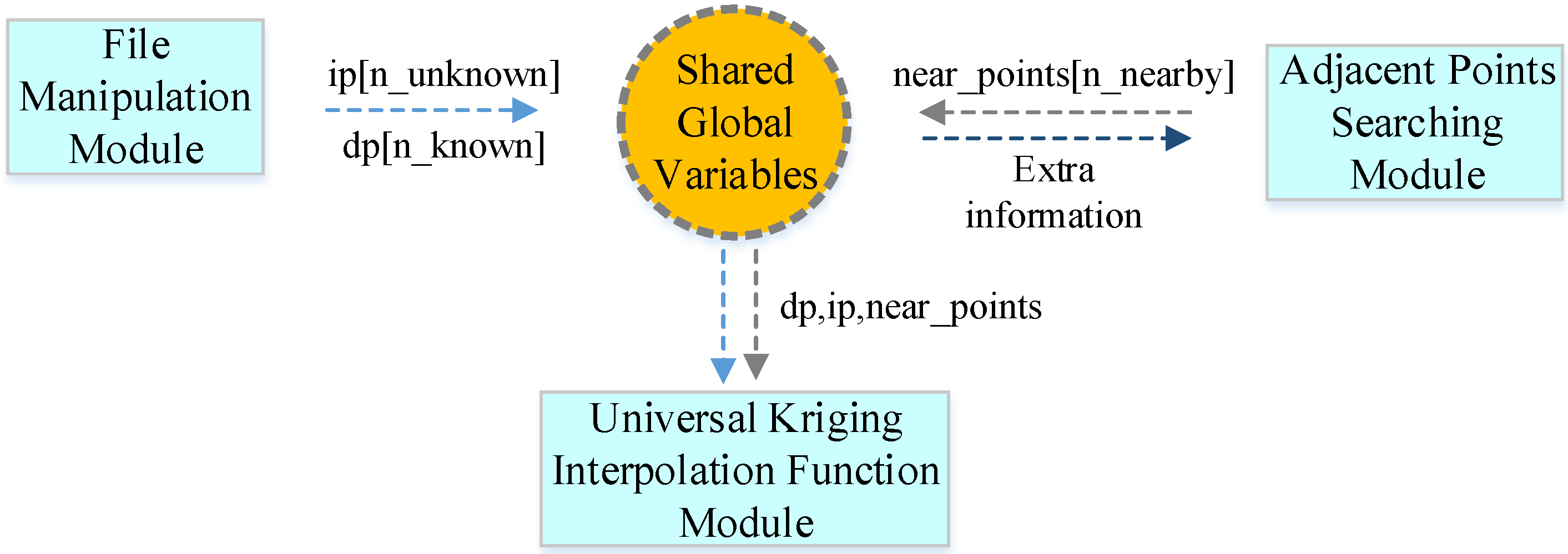
Following the principle of the universal kriging algorithm, using the selected variation function, the serial algorithm can be implemented based mainly on three components: (1) the File Manipulation Module (FMM); (2) the Adjacent Points Searching Module (APSM); and (3) the Universal Kriging Interpolation Function Module (UKIFM). FMM is responsible for reading the input shape file to obtain the three-dimensional coordinates for the known points and other information. When the interpolation results are ready, this module also writes the data as the output. These functions are implemented using an open-source spatial data format conversion library, GDAL (Geospatial Data Abstraction Library) [
16]. APSM focuses mainly on calculating the plane coordinates
of the unknown points according to the coordinate range of the known points and using a fixed step. The
n neighbor points of every unknown point are searched where the searching procedure employs the k-nearest neighborhood algorithm [
42], which searches
k neighbors of the search point. The UKIFM module is the numerical kernel used for interpolation (see
Figure 1).
All of the modules use some shared global variables to complete data interaction and data processing. First, the serial algorithm needs two global arrays, i.e., double dp[n_known] and ip[n_unknown] in FMM, where the former is for the known points and the latter is for the points where interpolation takes place. Thus, the array dp[n_known] is initialized to store the data extracted from the input shape file, and the array ip[n_unknown] is filled with the plane coordinates’ information, i.e., , for each unknown point by searching the appropriate points with a fixed step length on a global scale for the whole input image. Second, during the search process, an extra array called double near_points[n_nearby] is introduced to store the n_nearby adjacent points found for each unknown point. Third, UKIFM uses the plane coordinates of the unknown points and the coordinates of their corresponding adjacent points to calculate the estimated values, which are output together with the coordinates, i.e., for these unknown points.
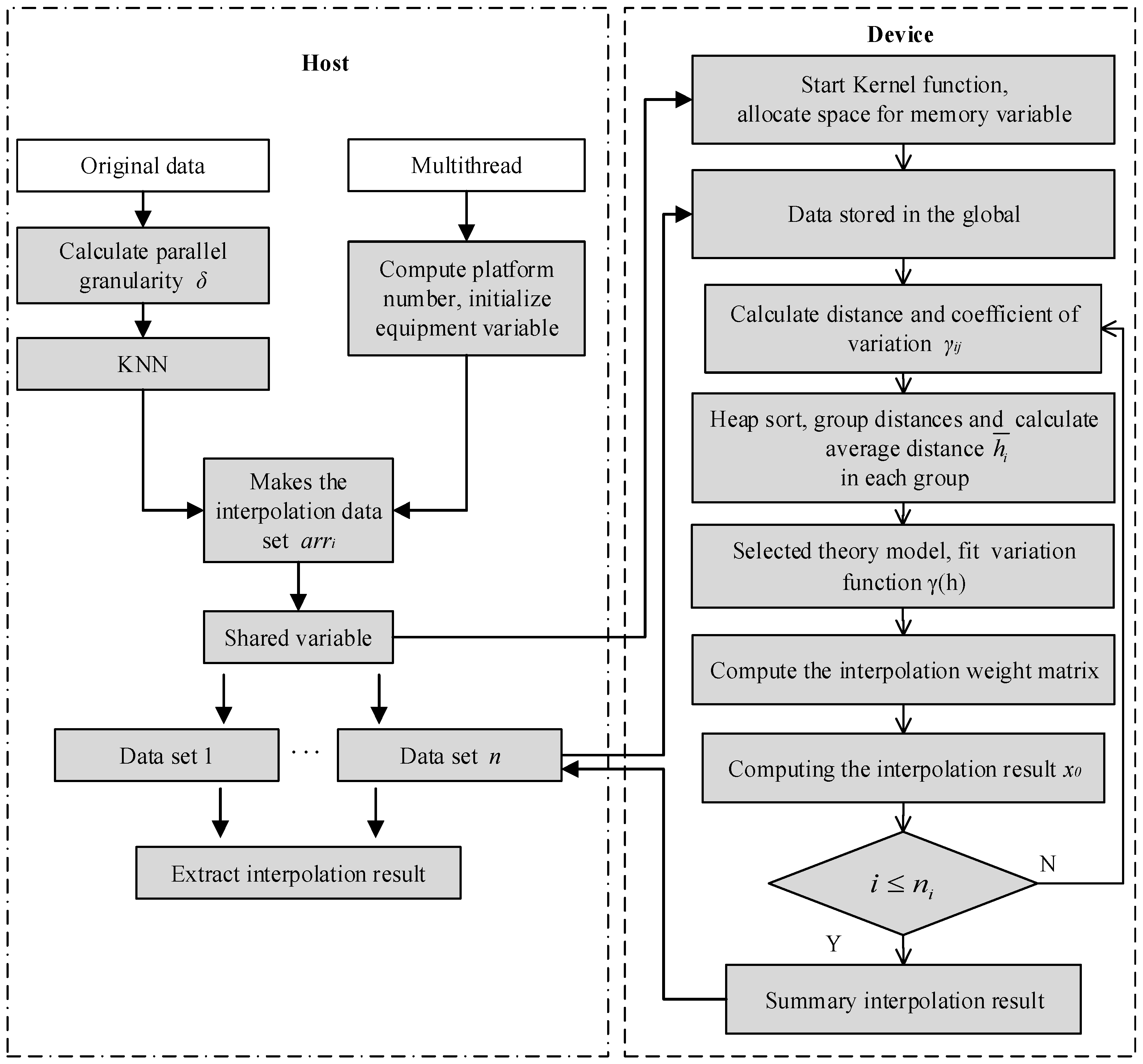
Specifically, the serial algorithm can be expressed in detail by the following four steps.
Step (1): Read the data information, i.e., , the three-dimensional coordinates of the known points from source files.
Step (2): Calculate the plane coordinates of the unknown points according to the coordinate range of the known points. Based on the known points, select the points that need to be interpolated with a specified space interval and then calculate their corresponding plane coordinates .
Step (3): Establish a k-d tree using the three-dimensional coordinates’ information for the known points and then search the neighboring points (among the known points) for each unknown point according to the algorithm.
Step (4): Transfer the coordinates’ information for the unknown points and the three-dimensional coordinates of their neighboring points to the UKIFM to calculate the estimated values of the unknown points.
In particular, Step (2) and Step (3) are used to provide the known points and the plane coordinates’ information for the points that need to be inserted, while Step (4) is the main calculation component of the serial universal kriging algorithm. In fact, the implementation of Step (4) is complex, and it can be further divided into seven sub-steps (Sub-steps a–g) (
Figure 2), as follows.
Sub-step a: Calculate the distance between a point that needs to be interpolated and its adjacent points (known points, where the sum is n), i.e., .
Sub-step b: Sort the distance values obtained into ascending order.
Sub-step c: Divide the sorted values into k groups.
Sub-step d: Calculate the average distance in each group according to their values. The estimated parameters of the variation function are then calculated using Equation (8). According to the selected theoretical mode of the variation function, function fitting is conducted to determine the variation function and the regression coefficient.
Sub-step e: Place the distance values of the sampling points and the point into the variation function to construct the coefficient matrix.
Sub-step f: Solve the inverse matrix of the coefficient matrix in Sub-step (e).
Sub-step g: Calculate the estimated value of the unknown point until all of the points have been processed.
3.2. Hotspot Analysis and the Corresponding Parallelism Approach
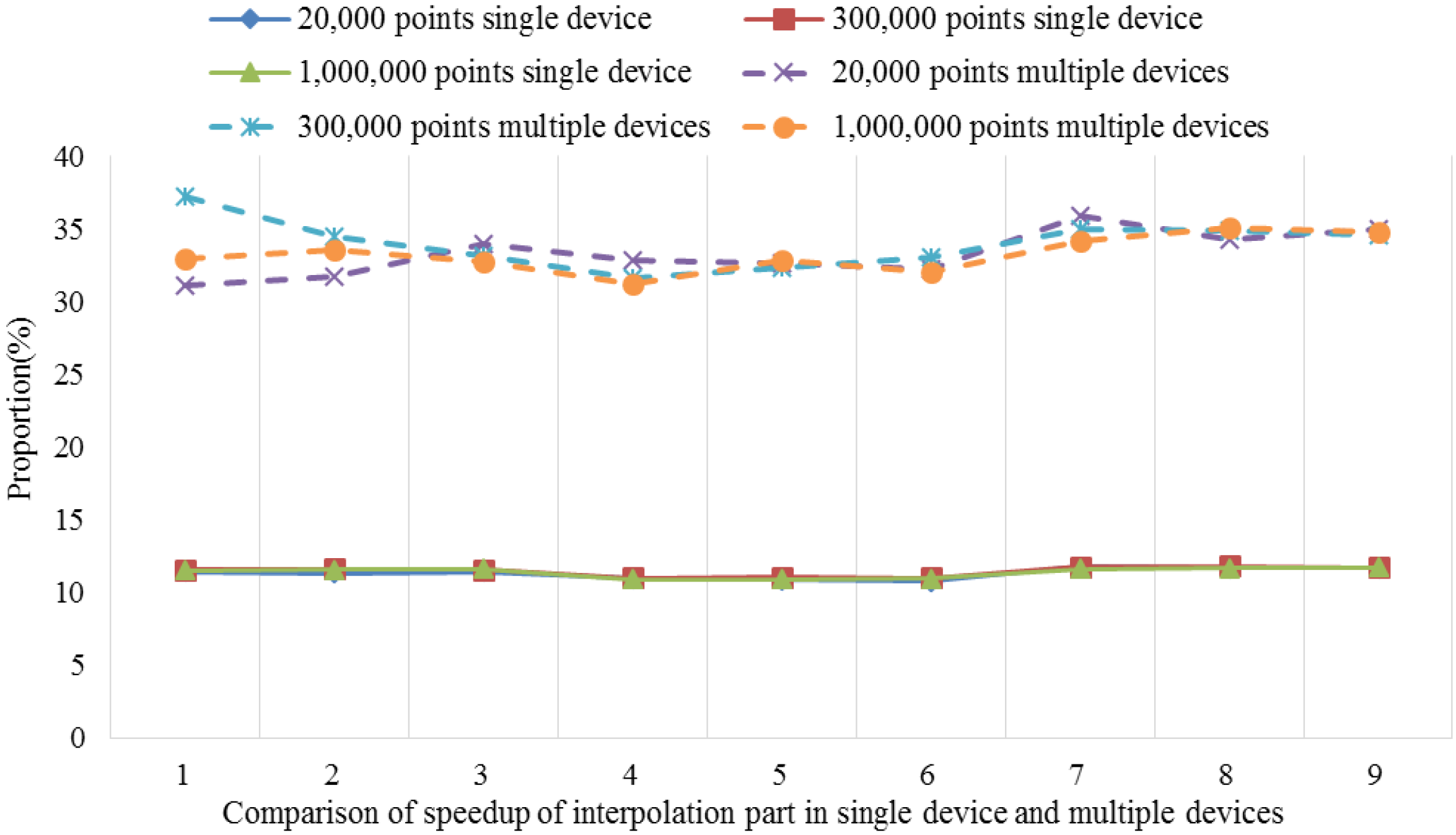
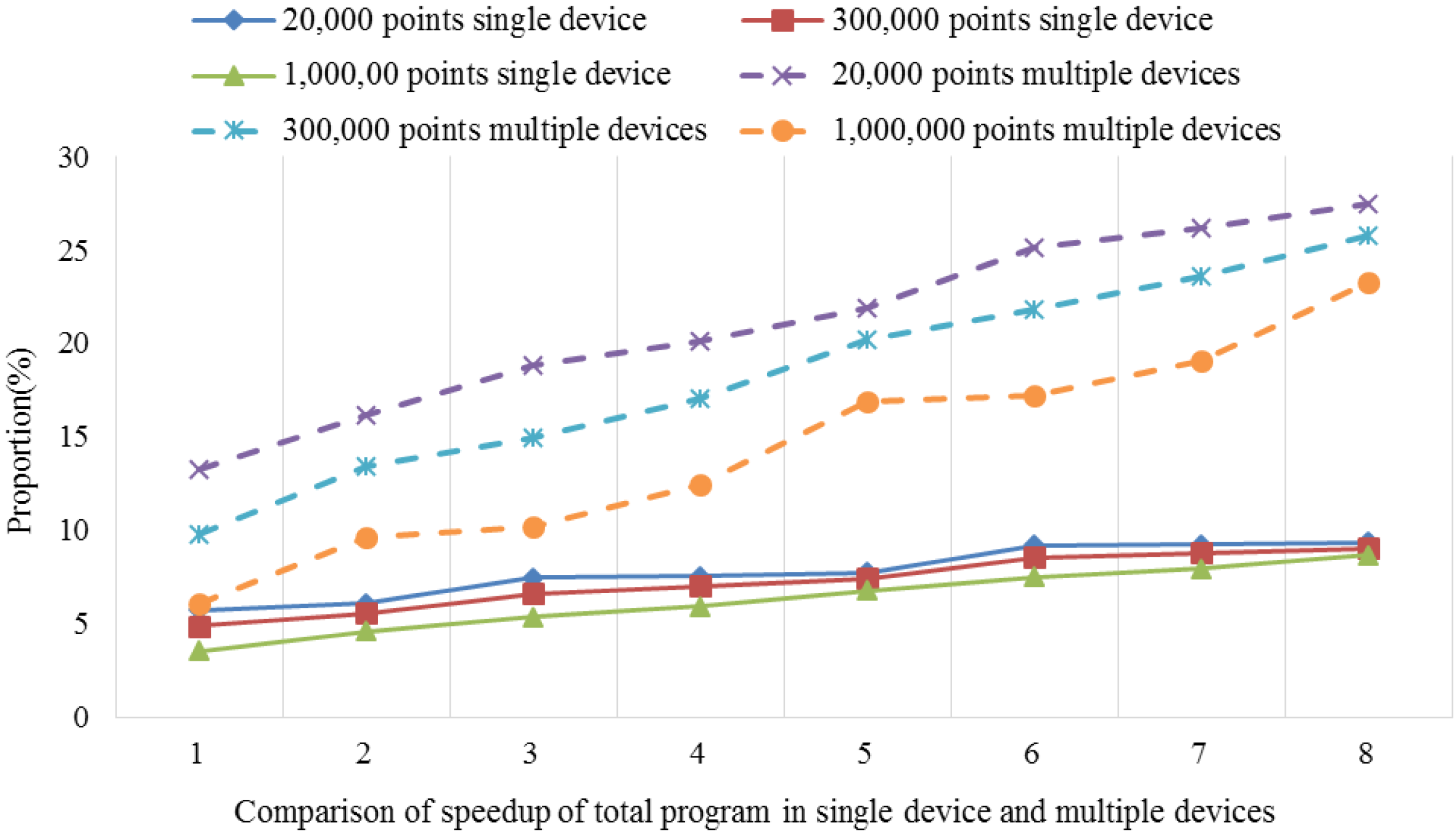
After performing the time consumption analysis using the serial universal kriging algorithm, we found that Step 4, i.e., the kriging interpolation function module, required 85.2%–97.6% of the total elapsed time for different dataset sizes, e.g., small, medium and large datasets. The time consumption percentage was closely related to the number of interpolation points involved and the searches of the adjacent points. Thus, as the number increased, the time consumption percentage tended to increase. For example, the number of search points was set to six in our test, but when this number was 12, which is that used by most real-world applications, the time consumption proportion increased to 90.0%–95.6% with the same dataset groups. Clearly, Step 4 is the hotspot in the serial algorithm.
Therefore, in order to fully accelerate the serial universal kriging algorithm to obtain good performance, the hotspot, i.e., Step 4, requires full consideration. In this step, the calculations of the unknown points are independent of each other, which facilitates the parallelization procedure. Thus, the present study focused mainly on the implementation of parallelism for this step. It should be noted that some specific application issues, such as the estimation of the variogram and the parameters’ settings, are not considered in the parallel implementation. Thus, the parameters used in the proposed parallel algorithm are identified by serial interpolation.
4. Parallel Universal Kriging Algorithm Design and Implementation with OpenCL
4.1. Design and Framework of the Parallel Algorithm
According to the analysis given above, it is clear that Step 4 should be parallelized. However, during the design and implementation of the corresponding efficient parallel algorithm, aspects such as the data structure, data transmission between the host and devices, task partition granularity and load balancing for multiple types of cooperating equipment also require full consideration [
43]. Some of these issues are independent of others, whereas there are specific dependencies on others.
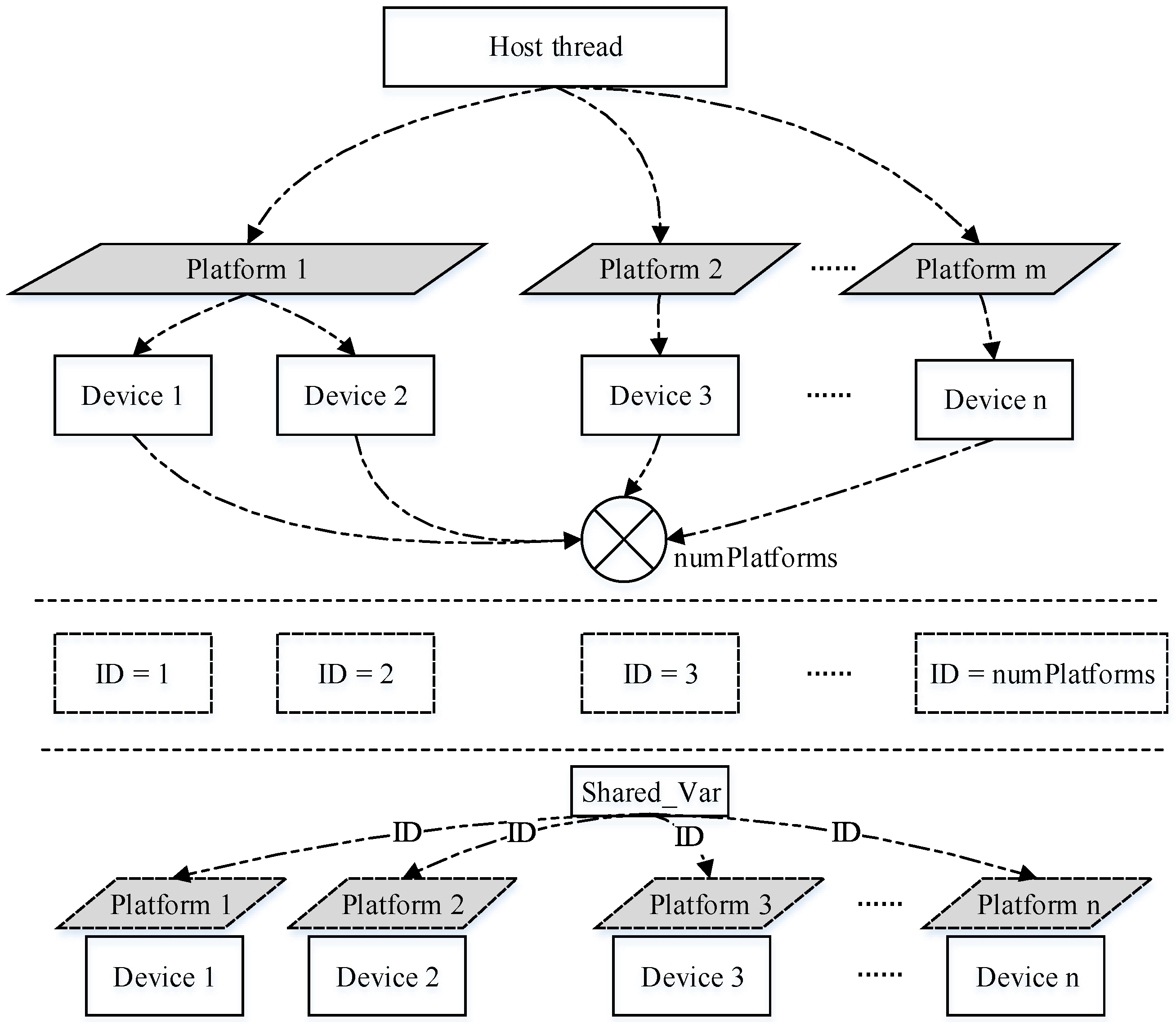
To fully consider aspects, such as different platforms, the number of equipped accelerated processors and system memory limitations, we propose the overall framework for the parallel algorithm shown in
Figure 3.
According to
Figure 3, the framework can be divided into two parts: the host and the device end. Obviously, the main calculation is accomplished in the device. The host only performs control tasks, such as data distribution and collecting results. The host and the device are related by some shared variables.
To develop a parallel algorithm with OpenCL, it is very important to design and implement modules that are highly compliant with the OpenCL framework. When designing the parallel universal kriging algorithm for high performance computing equipment, the main focus is on how to make Step 4, the hotspot, fully fused with the parallel framework in OpenCL. This problem depends mainly on the specific combination, design and implementation of four different programming models: (1) the platform model; (2) the execution model; (3) the memory model; and (4) the programming model. These programming models complement each other, and they are integrated into the overall framework. Thus, other models may be involved when designing and implementing a specific model. According to this rule, in the following, we describe the four models and the proposed framework in detail.
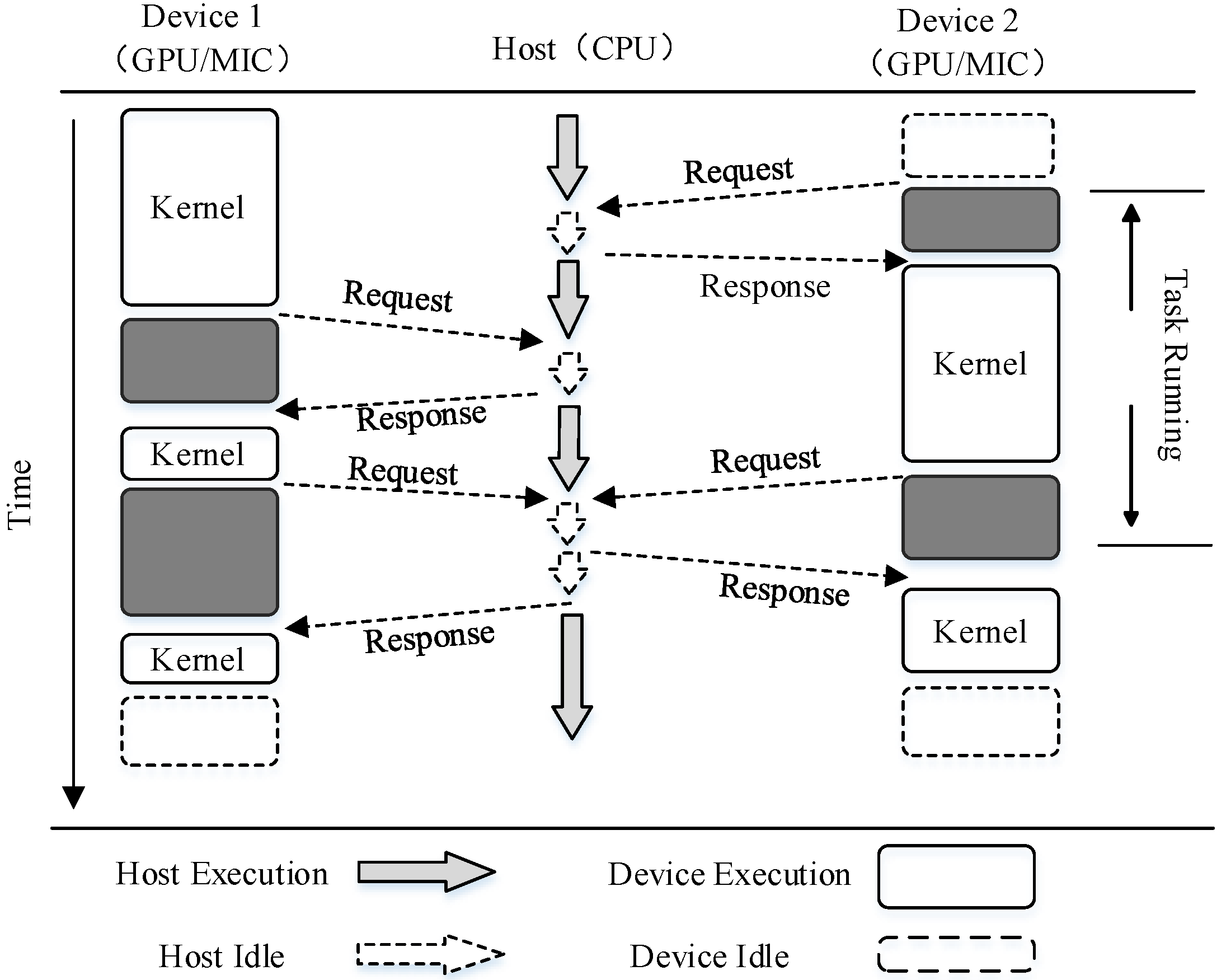
4.2. Platform Model Implementation
The OpenCL platform model defines a manifestation when using a heterogeneous platform [
44]. This blocks the underlying implementation of the equipment, which can only be used by developers in the form of a device, so an additional collaboration pattern between the host and multiple devices needs to be designed. First, the function for creating threads will create suitable threads according to the number of devices. Then, the subsequent steps involve creating platforms, selecting the equipment and creating buffers. Thus, the devices can complete all of the computing tasks cooperatively, and the corresponding implementation is shown in
Figure 4.
In
Figure 4, the main thread shares information with its child threads. The information includes the task assignment information, platform information pointing to the current equipment and variable information for the insertion time shared by threads. The main thread first obtains the number of available platforms and the devices on each platform, before calculating the total number of all available devices. Next, an equipotent number of threads is created, and some shared variables that transform information with child threads are constructed. Thus, the device ID number stored in the variables shared by each piece of equipment is initialized. Subsequently, the child threads perform operations to recreate the platforms, and they can obtain the corresponding device information given by the main threads.
In the following experiments, we employed two heterogeneous computing platforms: a GPU platform equipped with two GPU cards and an Intel Xeon Phi platform equipped with three MIC cards. In general, a similar procedure was followed to implement the platforms. In the GPU computing platforms, the two GPU cards were treated as OpenCL devices. First, the main process was created in the host end, where its responsibility was to manage the OpenCL platforms and OpenCL devices. Next, two sub-processes were created after the main process found these two OpenCL devices, which mainly operated after the OpenCL device’s initialization. The initialization process mainly comprised context creation, buffer creation, command queue creation, program creation and setting the kernel parameters. Finally, the parallel algorithm sent the kernel and the corresponding data to the appropriate devices, as described above.
4.3. Execution Model Implementation
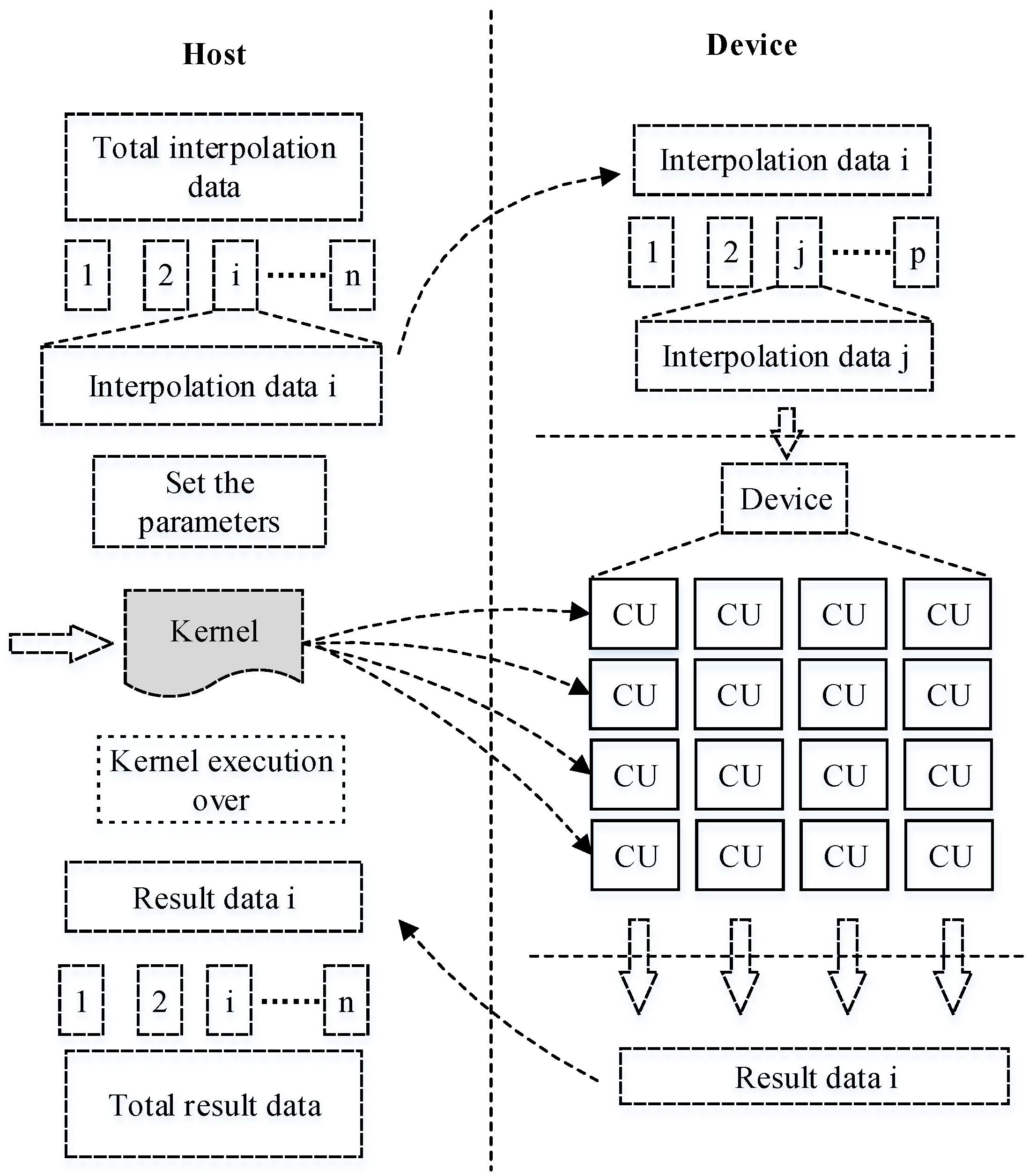
The OpenCL execution model defines the method for executing the kernel function that runs on equipment supporting OpenCL. The OpenCL application comprises two parts: the host machine program and one or more kernels. However, the OpenCL execution model does not define the details of the host machine program. Thus, when there are multiple devices, meticulous work is still required by the developer to divide the workload and to design the tasks collaboratively. In this study, the kernel function was transformed from the part of the serial universal kriging function that needs to be parallelized. When using the data decomposition parallelism method, the host device distributes the kernel function programs to every device (in this case, Computing Units (CUs)). These kernel programs were executed by their corresponding threads; in fact, these threads were created by the host (see
Figure 5). It should be noted that the calculations for every unknown point are independent of each other, so there was no need to consider the communication among the kernels or threads.
As shown in
Figure 5, the calculation can be completed at one time for a small dataset. The process includes operations, such as data filling, computing and retrieving results. Given that fairly large datasets need to be calculated, it is useful to employ a loop operation to perform the task due to memory limitations. In this case, the data are first divided into
n groups according to the memory capacity and the number of CUs (shown on the left in
Figure 5). Each group, e.g., group
i, is transformed into the devices during an iteration and then decomposed into
p portions, which are suitable for calculation by one CU. In this manner, these operations can be repeated many times during one iteration to process large amounts of data. In addition, the host must formulate the distribution of data over multiple devices to ensure the orderly processing of data.
4.4. Memory Model Implementation
The memory model represents how OpenCL divides the memory among the host and the devices for data interactions, where we use the memory object to complete data transmission. In this study, the problem of memory implementation has two aspects: (1) memory mode implementation on the host; and (2) memory mode implementation on computing devices; which are described separately in the following.
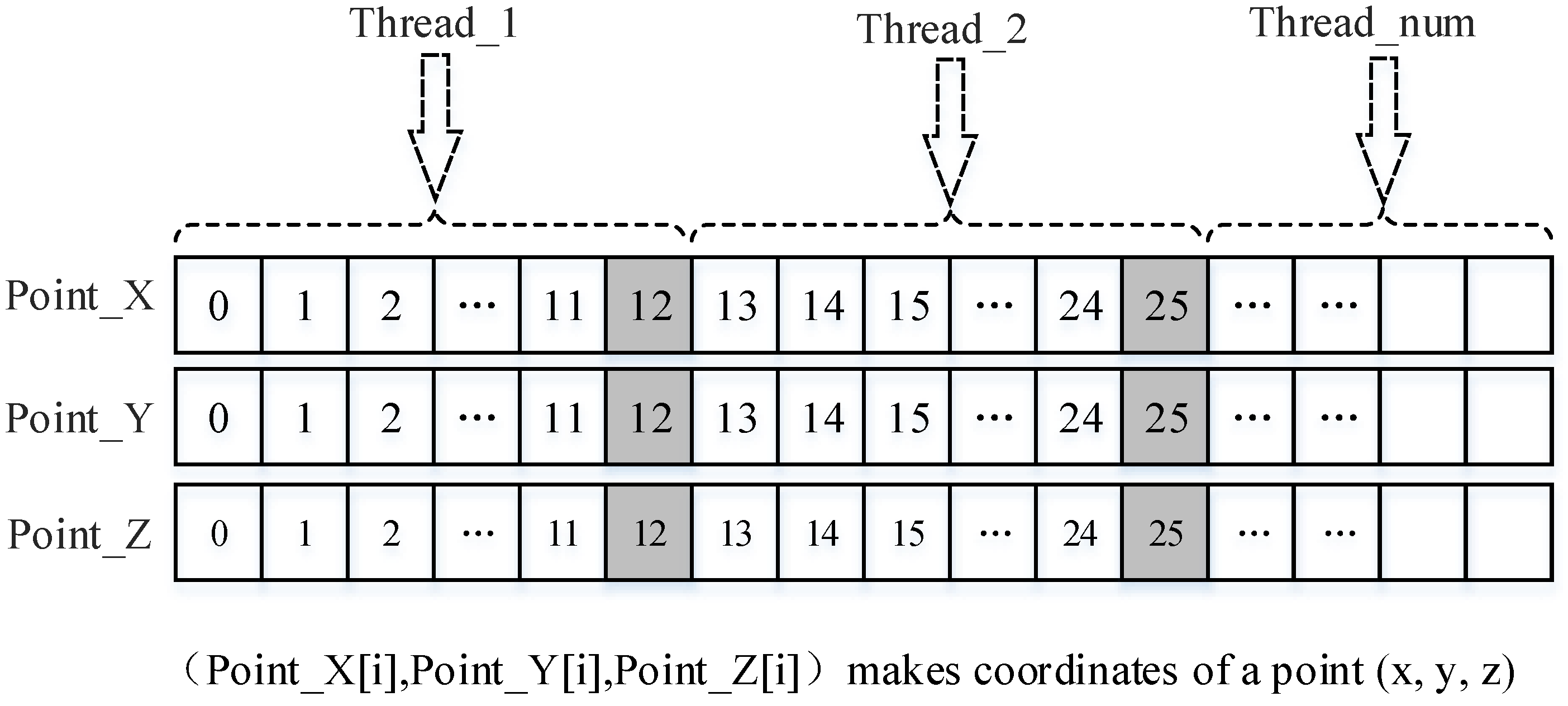
Memory mode implementation on the host: In the host, the three-dimensional coordinate information for the interpolation data points is read into the system memory first. The array size is determined by the number of points
n_points, which is pre-read from the Shapefile formatted file. Next, the number of units that need to be interpolated is created according to the number of parallel threads and the size of memory that can be used by the operating system. The size of the interpolation units is
search_n+1, where
search_n units are stored with the data information of the
search_n neighboring points for the last point that needs to be interpolated. The organization of the data structure for the interpolation unit in each thread is shown in
Figure 6.
To avoid wasting time on frequent memory allocation and deallocation, as well as the problem of memory shortages in the computing devices, the memory should be controlled to a certain degree while interpolating. In this study, the maximum limit is
, which is determined by controlling the memory percentage or giving a specific size. The optimization code is described as follows.
Finally, buffers are constructed by the corresponding threads in each device. Thus, operations such as transferring the interpolation data unit to the buffer and sending back the results can be processed continuously. The transmission of data between the master and equipment is completed over several time iterations.
- 2.
Memory mode implementation on computing devices: the data units that need to be processed can be shared in the form of a global memory between the kernel function and the kernel calling function. The function located on computing devices defines some variables in the form of a private memory to complete data processing in the devices.
Large amounts of data are involved in massive data processing application, where a large number of threads run on the computing devices, so the shared memory and private memory become valuable because these resources are usually limited on hardware. Therefore, we employ a method that directly reads and writes the global variable several times, rather than loading all of the interpolation data from the global variable into the devices each time. This optimization method will affect the processing speed to some extent, but it increases the number of threads that can be run on the devices at the same time, thereby improving the overall performance.
4.5. Programming Model Implementation
The programming model determines the operational strategy that allows the algorithm to be parallelized and to run on OpenCL devices. There are two different programming models in OpenCL: tasks in parallel and data in parallel [
39]. It is important to apply the most suitable mode for this algorithm.
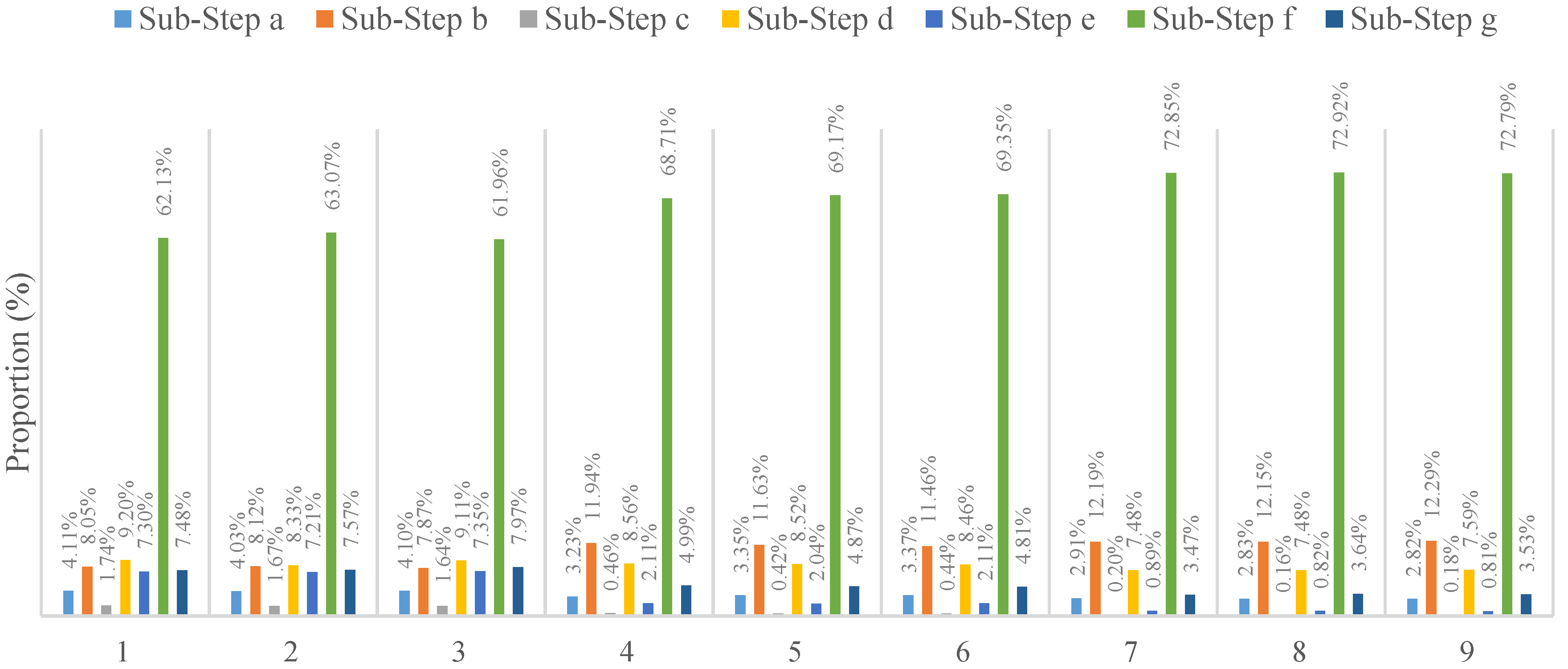
Based on
Section 3.1.2, when implementing the parallel universal kriging algorithm, the key step is to parallelize Step 4, which is implemented by the universal kriging function. This function also has seven sub-steps (a–g), which represent operations such as sorting, grouping and calculating the matrix inversion. According to the analyses of the time consumed by every sub-step using a professional performance analyzer, the results for different dataset sizes with various setting parameters are illustrated in
Figure 7.
Figure 7 shows that the matrix inversion calculation procedure accounts for 61.9%–72.9% of the runtime for the serial algorithm, which is the highest proportion among all of the sub-steps, and it contains no other steps, such as data reading or searching for adjacent points. However, if we regard this step as the hotspot, the acceleration effect will be very limited. In addition, there are dependencies among other steps, so the task level parallelization mode is not suitable for this algorithm. By contrast, the data that need to be processed can be executed in parallel using the designed structure, where each work-item does not require interactions with other data and there are no data dependencies. Thus, this is the most suitable level for data parallelization. We use this form of data parallelization to implement universal kriging algorithm parallelization (as shown in
Figure 3).
4.6. Load Balancing Strategy for Multiple Devices
The task partition granularity and the load-balancing problem must be addressed when there are multiple computing devices. The main thread needs to distribute the overall task to multiple devices for processing, before collecting and combining the computing results to obtain the final SI results. Based on our experimental verification, the parallel algorithm uses a strategy that divides the specific memory according to the average number of equipment, where it considers the maximum number of points that the memory can allow for insertion as the parallelism granularity. In addition, we use the lock mechanism to implement the dynamic load-balancing strategy to compute the task distribution schedule. The detailed implementation of the load-balancing scheduling strategy is illustrated in
Figure 8.