Next Article in Journal / Special Issue
Motorways in Metropolitan Areas: The Northwestern Growth of Florence and the Urban Use of Motorway A1
Previous Article in Journal
Understanding Public Opinions from Geosocial Media
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJGI
Volume 5
Issue 6
10.3390/ijgi5060076
ijgi-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Comprehensive View on Urban Spatial Structure: Urban Density Patterns of German City Regions

by
Angelika Krehl
1,*,
Stefan Siedentop
1,
Hannes Taubenböck
2 and
Michael Wurm
2
1
Research Institute for Regional and Urban Development (ILS), Brüderweg 22-24, 44135 Dortmund, Germany
2
German Aerospace Center (DLR), German Remote Sensing Data Center (DFD), Oberpfaffenhofen, 82234 Weßling, Germany
*
Author to whom correspondence should be addressed.
ISPRS Int. J. Geo-Inf. 2016, 5(6), 76; https://doi.org/10.3390/ijgi5060076
Submission received: 27 February 2016 / Revised: 18 April 2016 / Accepted: 9 May 2016 / Published: 25 May 2016
(This article belongs to the Special Issue Recent Trends in Spatial Analysis and Modelling of Built-Environment Characteristics)
Browse Figures
Versions Notes

Abstract

:
Urban density must be considered a key concept in the description of a city’s urban spatial structure. Countless studies have provided evidence of a close relationship between built density and activity densities, on the one hand, and urban environmental conditions or social practices, on the other hand. However, despite the concept’s common use in urban research, urban density is a rather fuzzy and highly complex concept that is accompanied by a confusing variety of indicators and measurement approaches. To date, an internationally-accepted standard for the implementation of density indicators that permits a robust comparison of different countries, regions or cities is widely missing. This paper discusses the analytical opportunities that recent remote sensing data offer in regard to an objective and transparent measurement of built density patterns of city regions. It furthermore clarifies the interrelations between built and activity densities. We apply our approach to four German city regions to demonstrate the analytical capacity of spatially-refined density indicators for the purposes of comparative urban research at a regional scale. In so doing, we contribute to a more encompassing and robust understanding of the urban density concept when analyzing regional morphology.

1. Introduction

In urban research and planning, the spatial densification of human activities and their physical manifestation as built density are key factors in describing the form and structure of the built environment [1,2,3,4,5]. The density of built structures is a precondition for the spatial proximity of individuals and actors—residents, employees, inventors, entrepreneurs or creative people—and proximity in turn has a complex influence on urban behavioral patterns and processes of economic and social interaction.
In recent years, great progress has been made in better understanding the relationships between the built structures of urban areas and the variegated socioeconomic processes. Research into this topic has taken place within a wide variety of scientific disciplines. Numerous empirical studies in the fields of urban planning and transportation have been able to demonstrate close relationships between built density and corresponding activity densities (such as population or job densities), on the one hand, and individual mobility behavior, on the other hand [6,7,8,9,10]. With an increase in the built density of a city, the number of trips that are made on foot, by bicycle or public transportation increases, as the average trip distance decreases and the quality of transit services increases, everything else being equal [2,7,11,12]. Furthermore, the greater degree of physical activity in denser urban neighborhoods in comparison to suburban areas with lower densities has positive effects on the health of a population [13,14,15]. The positive relationship between built density and energy consumption that has already been demonstrated for mobility also applies to the construction sector. Here, studies have shown that the demand of energy for heating and cooling purposes in large-volume buildings is lower than in smaller buildings owing to a more favorable surface-to-volume ratio [16,17].
Economic sciences have also addressed the impact of the size and density of urban areas in recent years. Studies in this field emphasize the topic’s relevance for the prosperity and innovation capacity of economic systems [2,18,19,20,21,22,23]. Empirical studies have been able to show that higher densities facilitate the exchange of ideas and knowledge between individuals and firms. Density creates positive returns to scale, and it is exactly this reason why knowledge-intensive business services, which are especially dependent on spatial proximity and knowledge spillovers, can particularly be found in urban centers [24,25,26,27]. However, these returns to scale are not just applicable to spatial proximity and the corresponding advantages in labor market economics: it can also be stated that specific costs for the provision of infrastructure services decrease when demand density increases, since high capital expenditures, particularly those related to technical infrastructure, can be allocated to a greater number of users (see [28] (p. 6 et seqq.) with further references [29,30]).
Meanwhile, high densities also carry disadvantages, as they might be accompanied by high rent and property prices, transportation system congestion [27,31,32], low air quality and a discomforting urban microclimate [33,34]. For instance, the vulnerability of dense urban areas regarding summer heat waves and the health risks related to this are significantly higher than in suburban or rural settlement areas [35]. Historically, high densities were also critically examined from a military perspective and for reasons of social hygiene. The often extreme population densities that were evident during times of industrialization (and that are still present today in the metropolises of the Global South) are considered to be partially responsible for the emergence and spread of epidemics and other diseases [36,37].
Against this backdrop, it must be surprising that, despite the remarkable significance attributed to the density of a city or city region as an explanation for environmental conditions, social practices and economic relationships, few empirical studies of urban and regional density patterns exist [38,39,40,41]. Compared to other measures of the built form of cities—for instance, the “concentration” and “mixture” of urban functions or the “compactness” of the physical settlement area—built density appears at first glance to be a simple, objective, easily understood and manageable measure. Upon closer inspection, however, it is clear that a simple empirical approach alone fails to fully embrace the concept [36]. In this regard, Churchman pointed out at the end of the 1990s that no internationally-recognized measure of built density existed to date and that indicators of built density for various countries, regions and cities are generally not comparable (or only comparable to a limited extent) if they come from different sources [3] (p. 390). This assessment is still true today.
The empirical study of the density of a city or city region is fraught with challenges that are, on the one hand, conceptual, but can, on the other hand, also be explained by restrictions to the availability of basic data (see Section 2 for a more detailed discussion). In this way, the validity and interpretability of density indicators often suffer from a lack or an unclear definition of a spatial relationship ([8], p. 3). Frequently, it is also not clear whether density should be interpreted as a gross or net value, since it is not obvious which types of area (plot area, public spaces or the total settlement areas) have been considered in the density calculation. Rather practical problems emerge in the analysis of density values, as the necessary data are not always available [16]. This especially concerns the assessment of built densities at the level of built-up properties, blocks or neighborhoods. However, population or job densities can also not always be determined with the desired spatial resolution, since the availability of demographic and employment data at the sub-municipal level is often limited; see also [24].
In this context, the extensive and increasingly affordable availability of remote sensing data, with which not only land use, but also the height of built structures can be modeled, offers entirely new opportunities. Large-scale volume calculations can be made, from which density measures, such as the floor area ratio, can be derived. Further benefits ensue as a result of: (i) the objectivity of the density calculation, since building heights and volumes can be reliably determined; (ii) the high spatial resolution of the data and the possibility to aggregate them at will into spatial reference systems (such as ring zones or grid cells) that are independent of local administrative units; (iii) the extensive availability at comparatively moderate costs; and (iv) the ability to easily link data with demographic and socioeconomic data at the sub-municipal level.
Consequently, in recent years, an increasing number of studies have used remote sensing data or respective derivate products to approach the concept of urban density. Most of these studies have addressed two-dimensional settlement densities as proxies for the analysis of the spatial configuration of built structures [42,43,44,45]. The latest developments, however, allow for morphologic density analyses using 3D city models, while overcoming the restriction of limited area coverage [46,47].
This article addresses the analytical opportunities of new geodata in determining the multifaceted density patterns of urban areas. These issues are pursued by elaborating three main objectives:
  • To present a novel method for a region-wide detection of built densities.
  • To demonstrate the practical feasibility of our approach based on four German city regions. In doing so, we illustrate the analytical capacity of fine-grained spatial density data for the characterization of urban spatial structure.
  • To shed light on the interrelations between built and activity densities.
With the methodological approach introduced here, it is, for the first time, possible to conduct a region-wide, detailed analysis of the urban spatial structure that also considers built densities. Previous studies in this field only illustrate urban morphology in a two-dimensional space using socioeconomic and land use data, whereas our approach achieves a higher level of analytic depth. In this way, the relationship between socioeconomic processes and built physical structures can also be examined more closely. Thus, this paper supports a more encompassing and robust understanding of the urban density concept and its variegated applications in urban research and planning practice.
The remainder is organized as follows: After a short discussion of the scientific background of the topic (Section 2), we introduce our methodological approach to generating high-resolution density data. We then address in detail the analysis of fine-grained geospatial basic data using Earth observation methods (Section 3). The aim of this is to create a comprehensive image of the morphology of a city region. In Section 4 and Section 5, we illustrate and discuss this using the examples of four case study regions (Frankfurt/Main, Cologne, Munich and Stuttgart). This article concludes with a short summary regarding potential explanatory factors of urban density patterns (such as topography, urbanization history or economic structures) and future applications of spatially-differentiated density data (Section 6).

2. Conceptualization of Built Density

The discussion surrounding the “appropriate” density of a city is perhaps as old as the discipline of urban planning itself, and it can certainly be seen as one of the most controversial issues within this field. “Density” is a distinct interdisciplinary concept [48], whose significance has always been prone to change over time. It is indisputable that the perception and valuation of density is largely subject to cultural and social values (e.g., [5] (p. 6), [36] (p. 2)). An objective benchmark that can classify built or use-related densities into “high” and “low” or “good” and “bad” labels does not exist.
Dealing with the concept of density is, however, not only challenging from a normative urban planning perspective: the objective measurement of urban density is also subject to various restrictions. It is indisputable that density represents a measure of the relation of objects (which can include, among others, residents, buildings, dwellings or jobs) and a reference area upon which these objects are located. Density is expressed by using a fraction in which the number of objects is the numerator and the size of the reference area is the denominator. A general distinction can be made between built densities and use or activity densities: built densities are related to the ratio of built structures (such as the number of buildings, floor space or the number of dwelling units) to a reference area, while activity densities express the intensity of human use on built-up areas. The former are of a rather static nature, since built structures, at least in a larger spatial context, only change very slowly. In contrast, activity densities are subject to constant change, as they are underpinned by dynamic, often discontinuous, demographic and socioeconomic processes. Table 1 provides an overview of the urban density indicators that are frequently found in research and planning practice.
Beyond this general understanding, however, the measurement of built densities poses a couple of empirical problems that are positively correlated with the spatial level of the respective observation. Especially the property, block or neighborhood levels frequently lack precise and up-to-date density values. The reason for this is that data at the property or block level are usually not covered by official statistical surveys (such as censuses). Studies based on one’s own data collection (e.g., using site visits) or private geodatabases are of limited use owing either to their complexity or to the lack of transparency in the data. Until now, density studies have mostly been carried out in the form of individual municipal analyses or collections of case studies [41,49] whose results are often only comparable in a limited way with other municipalities or territorial units. These challenges potentiate themselves when attempting to conduct international comparative density analyses.
The modeling of urban density surfaces and structures therefore suffers in particular from a low degree of spatial granularity. This not only has negative effects on planning practice (e.g., in the modeling of noise pollution or climate vulnerability), but also interferes with urban and spatial research. The significance of built density as a factor in explaining the spatial variance of particular phenomena, such as modal split or infrastructure costs, places high demands on the quality of available data. In many studies, however, simple activity density measures (such as gross population density) must be applied, since more precise structural density indicators are unavailable. Such restrictions greatly limit the performance of descriptive and explanatory research.
Built density can be determined in a number of ways as Table 1 demonstrated. Frequently, corresponding indicators address the relationship between a building’s floor space or volume to the plot area. Here, a standard indicator is the floor area ratio (FAR; also referred to as the floor area density or floor-space index) [3,5,46]. It is commonly defined as the amount of floor space of building divided by that building’s plot area. Still, determining the floor area ratio is a complex task, since official surveys of building metrics (e.g., floor number, volume or height data) are typically not available. While many studies do provide ranges for built density figures at the level of selected building and development types (e.g., the FAR; cf. [41]), the results of such studies are often not comparable, since various definitions of density are applied or the approaches to data collection differ.
This directs our focus to a second, rather conceptual, problem: the use of density indicators often suffers from an imprecise definition of the reference area [41]. In this regard, it is not always clear whether the entire surface area of a territorial unit or only the area that is being occupied by a certain use (e.g., residential) has been considered in the calculation. In such cases, it often remains unclear whether figures are to be interpreted as gross or net densities. In net density calculations, the number of countable objects is related to the relevant useable area (e.g., the number of residents to residentially-used plots). Other land uses, such as roads and sidewalks or public green spaces, are not taken into consideration. Net density calculations provide information about the “reality” of densification in a much more appropriate way, since they are less dependent on a spatial definition of the study area. The so-called “modifiable areal unit problem” [50], when the aggregated measurement results of spatial phenomena vary with the size of the basic study area, can be alleviated by applying net density values. However, most density studies that can be found in the literature offer gross density values.
The remainder of this article presents methods for determining and describing the density characteristics of cities and city regions at a high spatial resolution and using new kinds of data from remote sensing, as well as population and employment statistics.

3. Measuring Built Density

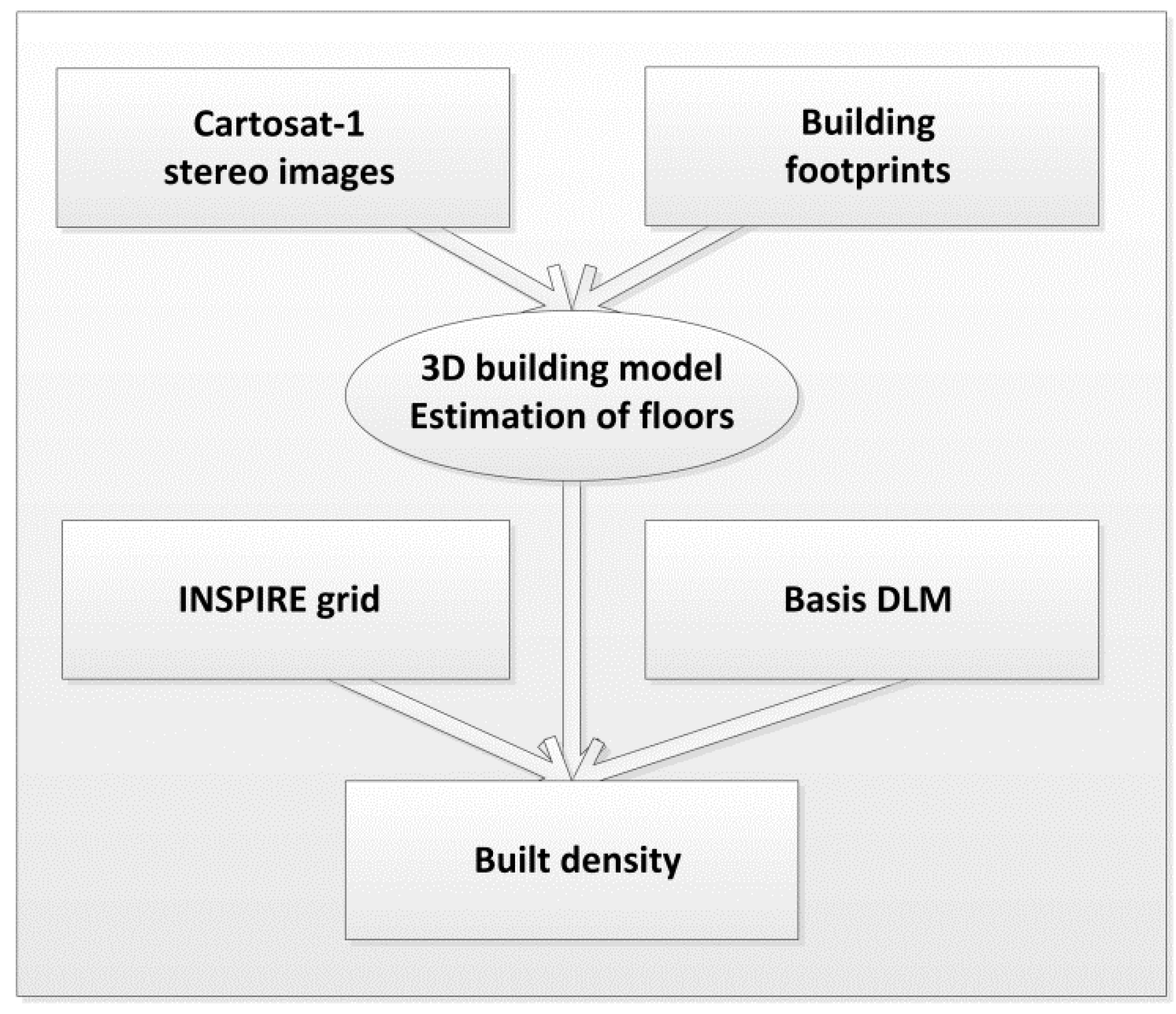
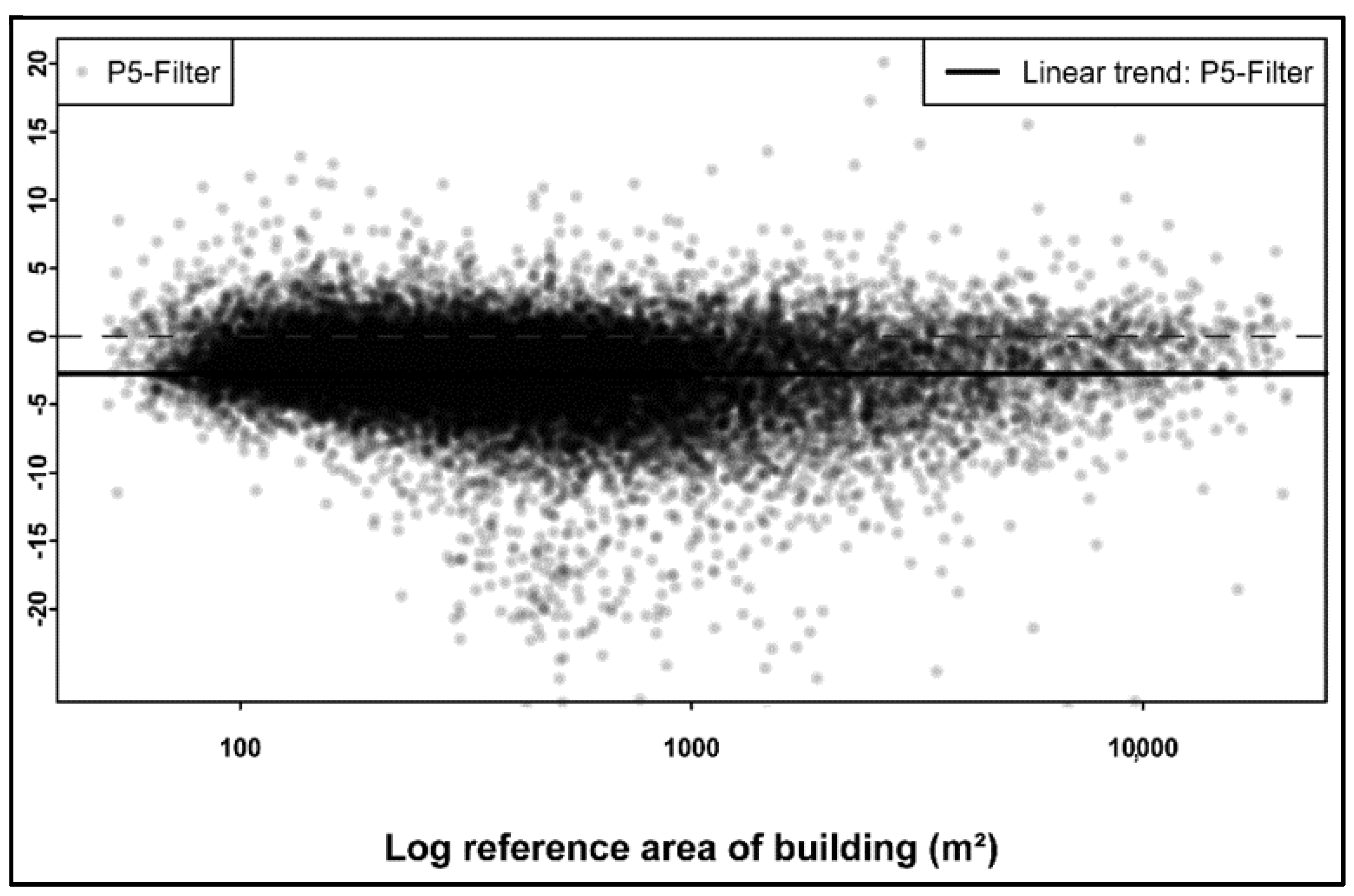
3.1. Remote Sensing-Based Measurement of Built-Up Volume and the Number of Floors

Recent developments in Earth observation allow satellite-based remote sensing technology to derive large-area information on urban features with a well-balanced trade-off between cost-effectiveness and accuracy. Today, a broad range of imaging sensors and methods for the determination of geometrically high-resolution measurements of the urban spatial structure exists. Three-dimensional (3D) data, which include information about height, are decisive in the extraction of information on the physical urban morphology. Height can be determined either by using stereoscopic aerial images or airborne laser scanning and, more recently, by satellite-based stereo images. The main difference between aerial and space-borne data acquisition is that airborne imaging is, on the one hand, less flexible in terms of spatial coverage and can be rather cost-intensive for large areas, but its geometric resolution, on the other hand, can be as fine as a few centimeters. Greater flexibility is provided by new satellite-based stereoscopic measurements, such as QuickBird, WorldView-2 or Pléiades, which are also capable of deriving geometrically very high-resolution stereo models. However, the same disadvantage of spatial limitation in the context of large-area acquisitions also applies to these data. For the desired height information in our analysis, both of these data sources were ruled out beforehand because we aim at comparing four different city regions with a total area of about 14,000 km2, which is larger than the entire Los Angeles metropolitan area.
To overcome the restrictions in terms of imaged area and degree of detail, in the current analysis, we used stereo images acquired by the Indian Remote Sensing Satellite (IRS), which employs the Cartosat-1 stereo sensor on board. This sensor (IRS-P5) has the advantage that images are almost constantly acquired all over the world, as it was specifically designed for large-scale and large-area stereo mapping and the generation of digital surface models (DSM). The acquired stereo images cover a swath of 27 km and at a pixel spacing of 2.5 m, which can be exploited to generate DSMs with 5-m spacing [51,52]. Since the launch of Cartosat-1 in May 2005, large parts of the Earth have been mapped, including a coverage of Europe. In light of these characteristics, Cartosat-1 meets both the spatial and the geometric requirements for an area-wide and cost-effective derivation of height information from various large urban regions. The geometric accuracy of Cartosat-1 height measurements in the context of urban analysis at the spatial level of individual buildings has been analyzed in a few studies and demonstrated to be between a 3- and a 3.5-m standard deviation [47,53]. For an overview of the steps performed in modelling built density, please refer to Figure 1. This figure summarizes the steps performed in building modelling using Cartosat-1 stereo images and building footprints for the generation of 3D building models and ancillary data, such as INSPIRE (Infrastructure for Spatial Information in the European Community) grid geometries and land use data from the Basis DLM, to derive the desired built density.
In the process of modeling built-up volume for the four city regions, 3D building models were generated using Cartosat-1 DSMs. These were derived by applying an adapted semi-global matching procedure (see [54]) from a total of 129 Cartosat-1 stereo pairs over all four city regions at a pixel spacing of 5 m with a mean error of less than 0.5 m. The DSM was normalized (nDSM) using a reference digital terrain model. Then, the building models were generated by combining nDSM heights with building footprints, which were extracted from digital topographic maps at a scale of 1:25,000. By doing this, we obtained a mapping of individual building footprints that were merged with height data from Cartosat-1 in the subsequent step (see Figure 2 and Figure 3). A detailed description of the method for DSM generation and building modeling is described in [47].
In a further step, the large-area 3D building models at the Level of Detail 1 (LoD1) were generated using a combination of the building footprints and height values from the nDSM. LoD1 means that each building is represented by a single building height. A perspective view of the 3D building models of the historic centers of the four city regions is depicted in Figure 3.
In a thorough performance evaluation analysis of official cadastral reference data, the generated 3D building models were checked for their accuracy and geometric detail [47]. The results of the study report that, due to generalization procedures in the production process of the map, individual building footprints may be larger than the reference buildings. This effect especially accounts for smaller buildings with footprints of less than 300 m2 whose areal deviation is comparatively much larger than that of larger buildings. An overall agreement of a kappa value of 0.71 could be observed in the study. Cohen’s kappa coefficient κ is a measure used for the evaluation of accuracy. The kappa statistic incorporates the off-diagonal elements of the error matrix; in other words, omission and commission errors are included. The value of κ shows the randomness of the results, meaning κ = 0 denotes complete statistical randomness, while κ = 1 indicates perfect positive statistical connectivity [56].
Regarding the accuracy of building height, the study reports the following outcomes: first, an overall agreement between the modeled building heights and the reference data shows a standard deviation of 3.67 m and a mean absolute error of 3.21 m at the spatial level of individual buildings. In a structured analysis, no significant correlation between the building footprint area and the accuracy of the building height could be observed, apart from buildings with very small areas (less than 300 m2; see Figure 4).
A second experiment reveals correlations between accuracy and building height. This means that the deviations between the modeled heights and the reference data can be observed alongside increasing building heights. The metric error tends to be smaller for low-rise buildings (around a 2-m standard deviation for buildings with a height of less than 6 m) and rises with increasing building heights: up to a 5-m standard deviation for buildings with a height of 20 m. Thus, the observed error in the building model is also higher for taller buildings. This effect can be explained by the acquisition geometries of the stereo images and can be overcome either by using more stereo images that provide better stereo angles or by applying linear correction models. The latter can be used to correct the models, since the correlation of height errors is a linear function of a building’s height. The same effect applies for the derived built-up volume, which is calculated at the spatial level of buildings. In the present analysis, these effects are of minor importance, since all buildings are affected in the same way. Thus, from a relative perspective, the building heights and therefore also the built-up volume can be compared between the four city regions. However, attention has to be paid when the derived volumes and floor area ratios are compared to “real-world” reference values, since experiments have demonstrated that volumes and floor area ratios tend to be slightly underestimated. It is observed that a general underestimation of 3–4 m applies for the derived building models.
To quantify the quality of the derived built-up volume on the spatial level of grid cells, a third evaluation exercise has been performed. Comparisons with the reference building model are in line with the observations from the prior accuracy assessments on the building level: since the estimated building heights are lower than the reference building heights, built-up volume on the grid cell level deviates relatively by approximately 10% with higher deviations for lower built-up volumes.
Our 3D building models permit the measurement of built-up volume at the level of individual buildings. While built-up volume can be seen as an easily understandable measure, its dimensions are difficult to compare. Thus, in urban planning and the analysis of the urban spatial structure, the FAR is a well-established and widely-accepted measure of urban density (see Section 2). However, the calculation of the FAR requires information on or an estimation of the number of floors [38,57,58]. Therefore, the number of floors is modeled based on building height. In this way, we use empirically-estimated quantitative relationships between the building height and the number of floors applied in prior studies to establish a function of floors and height [47,59]. The accuracy of the relationship between the building height and the number of floors has proven to be accurate for 60% of buildings at an error of zero floors. If an error of one floor is acceptable (due to varying definitions of floors regarding roofs), the exact number of floors can even be derived for 90% of all buildings [46,59]. Based on the 3D building model, built-up volume and floor area are separately calculated for each individual building as the product of the building’s footprint, height and number of floors.

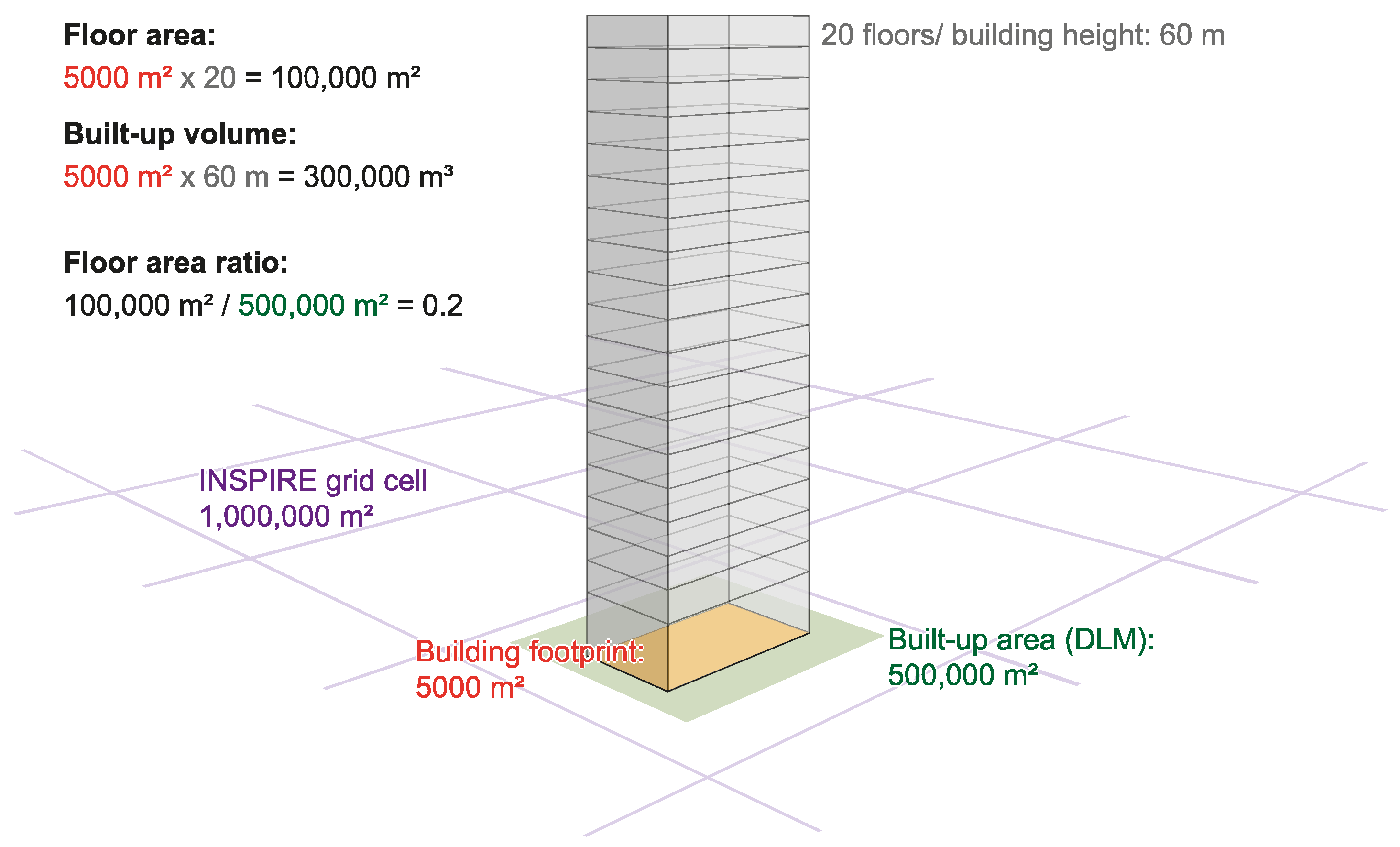
3.2. Derivation of Urban Density per Grid Cell: Built-Up Volume and FAR

The aforementioned 3D building model including the estimated number of floors represents the number of elements per spatial unit in the density calculation. The spatial unit can be chosen from manifold options, such as plots or urban blocks, which are widely used in research studies and practical urban development applications. However, these units can be too small in terms of data availability for the integration of ancillary socioeconomic data, such as population sizes or the number of employees (see Section 2), and therefore implicate shortcomings in the spatial transferability of the proposed approach. Thus, we calculate the FAR at the spatial level of regular cells of the INSPIRE grid [60], which is a standardized dataset containing grid cells covering the countries of the European Union (EU27). Thus, for the derivation of urban densities, we related built-up volume and floor area from the derived building block models to the 1 × 1-km grid cells as a reference plane.
The derived urban density value (the FAR) represents a net density, implying that the reference area, that is, each grid cell, is reduced to its built-up area (in contrast to gross density, where the entire grid area represents the reference area). In this way, vegetation areas and land used for transportation are excluded from the 1-km2 grid cells, resulting in varying reference areas for the calculation of the FAR. Thus, only “areas dominated by buildings” per grid cell are used for the calculation of the FAR. These areas are integrated from the German digital landscape model (DLM), which is provided by the Federal Agency for Cartography and Geodesy [61]. In this way, the built-up volume per INSPIRE grid cell results from the cumulative building volumes in all “areas dominated by buildings” within the particular INSPIRE grid cell. The FAR is calculated as the sum of the total floor area divided by the total built-up area as outlined by the DLM within an INSPIRE grid cell. For buildings that are crossed by the border of one or more grid cells, only the volume of the respective part of the building is taken into account. A graphical depiction of the calculation of built-up volume and FAR is presented in Figure 5 below.

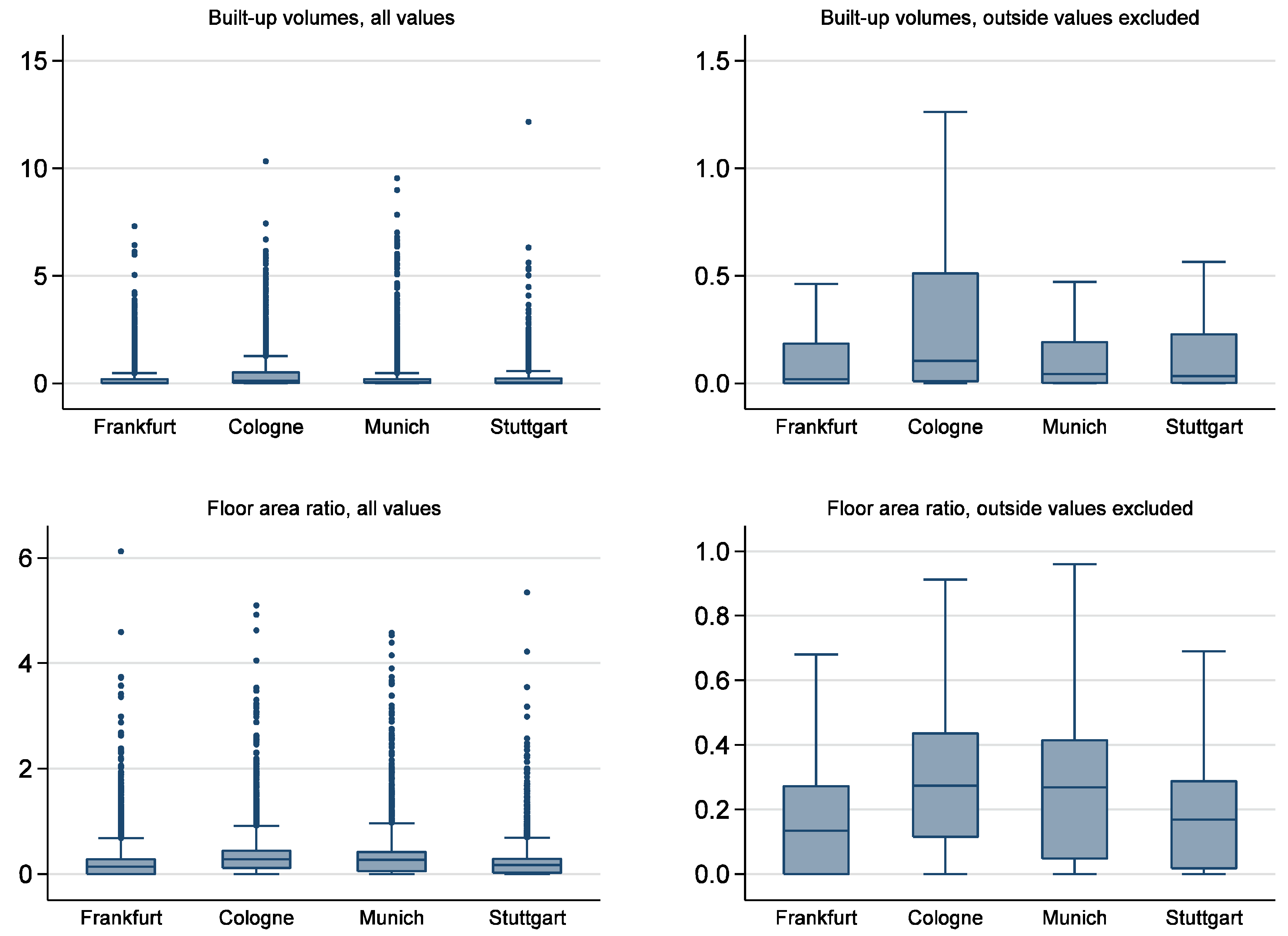
4. Patterns of Built Densities and Their Relation to Activity Densities

As already mentioned in the Introduction (Section 1), the methodological approach introduced here permits a region-wide, detailed analysis of urban spatial structure that also considers built densities. We thus achieve a higher level of analytic depth than previous studies and examine the relationship between socioeconomic processes and built physical structures more closely. The following discussion provides a more detailed picture of this relationship using a comparison of four German city regions. At the same time, it highlights both the complex concept of urban density and the prospects of still providing inter-regionally comparative measure of the same.
Table 2 provides an overview of the central parameters of urban spatial structure in these regions. All regions can be classified as highly urbanized, as evidenced by the above-average population density (the average value in Germany is just under 230 residents per km2). We estimate the total regional built stock to have values of around 660 million m3 (Stuttgart region) and 1160 million m3 (Cologne region) built-up volume and 216 million m2 (Stuttgart region) and 374 million m2 (Cologne region) of floor area. The values for both of the other urban regions, Munich and Frankfurt, score between these figures.
These global values already display surprisingly clear differences in built density, which cannot be explained by regional population and employment figures alone. This becomes apparent when considering the average FAR, which was calculated by dividing the total floor area by the total built-up area of the regions (see Section 3.2). While values of around 0.6 were obtained for the rather monocentrically characterized regions of Munich and Cologne, the average built density in Frankfurt and Stuttgart is significantly lower, scoring values of just over 0.4.
The complexity of the relationships between socioeconomic characteristics and the built environment also becomes apparent when considering the intensity of the use of the urbanized area. This relationship is addressed here by relating the number of residents and jobs to a certain floor area (→ floor area per resident and job) and built-up volume (→ built-up volume per resident and job) (Table 2). The larger the floor area or built-up volume per resident and job, the lower is the intensity of use. While it can generally be assumed that density increases alongside the size of a region, density is apparently also influenced by regionally- and locally-effective factors, such as topography, economic structure, prosperity level or urban and regional planning. We discuss these relationships in greater detail in the following paragraphs.
Our results show that the regions of Cologne and Munich have the highest built densities among all regions included (considering the average FAR values), while the intensity of use in the regions of Frankfurt and Stuttgart is noticeably higher. This finding can possibly be explained by the different land use efficiency of certain economic sectors. Furthermore, varying levels of infrastructural provision in regional centers, such as trade fairs and event and congress centers, could also account for this finding. Such services mostly encompass large-volume building complexes.
An analysis of our data at the spatial level of grid cells furthermore indicates that the density distribution has an upwards bias in all regions owing to extremely high values in a few spatial units. The following box plots illustrate this issue, considering the fact that the vast majority of grid cells have very low FAR and built-up volume values. When regarding standardized values, it becomes apparent that the median value is in part distinctly lower than the mean value. This also hints at the upwardly-biased distribution owing to outliers. The median built-up volume in all regions is lower than 0.1 million m3, while the FAR is under 0.3. In contrast, central locations display values that sometimes reach over 5 million m3 per km2 of reference area or FAR values of over 4.0.
These box plot results indicate that extreme disparities exist in all study regions. Comparing the left and right columns in Figure 6 supports this finding. Omitting the outliers, that is all grid cells with built-up volume (upper row) or FAR (lower row) values greater than 1.5-times the inter-quartile range, shows that the remaining grid cells are built at a much lower density and land use intensity. However, nothing is revealed regarding the outliers’ spatial location. Therefore, characterizing the regions as monocentric or polycentric is not feasible using this kind of information alone.
Figure 6 also suggests that the data are log-normally distributed. However, log-transforming the data is not helpful here, as it considerably narrows the data’s range. The logs also cause differences between consecutive values to diminish as the values grow larger. Thus, disparities are not as prominent in logs as they are in levels. On the one hand, this “leveling-out” is what is intended when doing such a transformation. On the other hand, this transformation eliminates much of the variability in the data that we actually need to characterize the density patterns: for that, we use the levels instead of the logs.
Having these results in mind, Figure 7 provides further insight into this by illustrating the built-up volumes and the average FAR of the four study regions at the spatial level of grid cells (1 km2). Clearly recognizable are the different basic settlement patterns in the regions. For instance, the axial structure of the Stuttgart region stands in clear contrast to the monocentric Munich region. The latter is characterized by a strongly densified core, while in bands of density, the Stuttgart region can be observed stretching from the inner city along the regional rail corridors into the hinterland. By way of contrast, the Frankfurt region is characterized by a rather polycentric and dispersed land use pattern, evident in the concentration of high built-up volume in the inner cities of the four core cities (Frankfurt, Darmstadt, Mainz and Wiesbaden). Upon closer observation, however, it becomes apparent that extremely high built-up volume of over 5 million m3 per km2 can only be encountered in the inner city of Frankfurt. The other three core cities of this polycentric region display consistently lower built-up volumes.
These analyses are supported by Krehl [24], who calculated global and local indicators of spatial association for selected variables of activity and built density. It can be shown that the global Moran’s I values are positive and statistically significant below the 5% significance level, indicating positive spatial autocorrelation, i.e., a spatially-concentrated urban pattern, in all study regions. The corresponding local Moran’s I values support the polycentric notion of the Frankfurt and Stuttgart region, respectively.
It also becomes apparent that all regions are characterized by a significant core-periphery gradient in built density. Even the core cities’ fringes (not to be confused with the regions’ periphery) are characterized by rather low-density urban areas, whose FARs are mostly below a value of 0.5. Here, predominantly low-density commercial uses and residential areas with detached single-family homes can be observed. However, the spatial extent of the dense core areas of the regions varies markedly. In Munich and Cologne, a larger, more compact urban core is visible, while the dense inner cities of Frankfurt and especially Stuttgart give way to lower-density construction within a few kilometers (see also Figure 8 or [64] for further insights into this). Thus, the diverse density structures within each of the four city regions considered here can also be explained by the varying spatial extent of the compact regional core (see also [24]).
Figure 8 stresses this using an east-west cross-section through each region. It illustrates the built-up volumes (left scale) and the average FAR (right scale) of those grid cells that are located on the same latitude as the grid cell of each regional center. These figures are related to the distance from the center in both eastern and western direction (recorded on the x-axis). Similar results have been obtained by Siedentop et al. [65] (p. 185) for a similar dataset. These authors considered the average floor area ratio in rings of 0–2, 2–5 and 5–10 km around the central business district. While these average rings shed light on a rather “smoothed” urban density surface, the analyses in Figure 8 (below) shed light on the density surface of a selected cross-section within each region. These patterns certainly cannot be generalized to the entire urban spatial structure. Sensitivity analyses, however, have shown that they provide a robust picture. Additionally, the qualitative findings of Siedentop et al. [65] and the analyses presented here are complementary to each other.
In the rather monocentric regions of Munich and Cologne, the highly densified area along the east-west plane extends across approximately ten kilometers, while this area only reaches across seven to eight kilometers in the Frankfurt region and only two to three kilometers in the Stuttgart region. Accordingly, the defined regional core is indeed relevant in the polycentric regions and displays comparable built-up volume and floor area ratios, but its spatial extent is markedly smaller than in monocentric regions. While the monocentric regions display a spatially-expansive core, (sub)urban settlement patterns are already apparent within a radial distance of about five to ten kilometers from the center in both rather polycentric regions. These (sub)urban settlement patterns include both peripheral urban settlement areas and, somewhat further away, the historic inner cities of mid-sized regional centers (see also Figure 7).
Finally, our comprehensive dataset also permits an analysis of the relationship between urban morphology and the distribution of socioeconomic activity. To briefly exploit this and also gain deeper insight into the relation between the two map series in Figure 7, we calculated Spearman’s rank correlation coefficients between the FAR, built-up volume and the number of employees and residents per grid cell. These variables are complemented by two further variables: the average floor space per building and the number of buildings per grid cell. Our a priori expectation is that the five variables should be highly and positively correlated on a region-wide average. This expectation is supported by the results displayed in Table 3. All rank correlations are statistically significant below the 0.1% significance level and are also positive.
The correlations between the FAR and the buildings’ average floor space score higher values (0.55–0.69) than the correlations between the FAR and the number of buildings (0.30–0.41). This finding implies that high floor area ratios are not necessarily the result of many (individual) buildings within a grid cell. Very high correlations can be observed if the number of residents and employees and the absolute density values, such as the built-up volume or the number of buildings, are considered. The correlations between the FAR and the employee-resident value, however, are much smaller. Figure 9 visualizes these relationships using scatterplot matrices. It provides evidence of positive relationships among the built density indicators and positive, but less clear-cut relationships between the built and the activity densities.
Thus, if there is a great deal of built-up volume in a grid cell, socioeconomic activity in this grid cell tends to be high. Floor area ratios and the socioeconomic activity’s correlations are positive, but much smaller. Explanations for this could be that people work and live in buildings, but that this fact is not necessarily associated with a linear/proportional amount of land or floor area demand (one may think of examples such as individual preferences for certain types of housing or the production needs of manufacturing firms compared to those of knowledge-intensive business services). However, going into greater detail on this topic is beyond the scope of this paper.

5. Discussion

The empirical findings introduced in the previous section reveal regionally-specific morphological structures. We have shown that urban density cannot be solely considered either by built or by activity densities. Rather, these have to undergo a joint consideration in order to better understand urban spatial structure. As all analyses are descriptive, detecting significant causalities is beyond this paper’s scope.
To briefly contextualize our results, we draft some strands of explanations. We assume that the identified patterns can be partially explained by topographical situations and transportation infrastructure. The Stuttgart region is a fairly good example of this. Previous studies regarding the density patterns of built-up volume and employees have shown an axial system that follows regional development axes, such as highways and rivers. Similar patterns can also be observed in the Cologne region along the river Rhine [24].
Additionally, historical path dependencies of economic and settlement history or regional and urban planning practices might also have contributed to these patterns. Thus, varying levels of built density could be the result of industrialization or urbanization processes that started at different times. Waves of urbanization towards the end of the 19th century produced higher built densities than later phases of urban growth characterized by residential and commercial suburbanization.
By the same token, the economic structure and its development could also explain the regional differences in density. The respective composition of the manufacturing and service industries manifests itself in a specific land use efficiency (i.e., as used area per employed person), which in turn influences the built density situation. Looking at the Frankfurt or Stuttgart region provides evidence of this relation: whereas the correlation between the sum of employees and residents, on the one hand, and built-up volume, on the other hand, is fairly high (Table 3: 0.83 for Frankfurt and 0.86 for Stuttgart), the density maps of employees, employees in service sectors and built-up volumes clearly indicate that this global value is distorted by local peculiarities. The reasons for this are the concentration of employees in service sectors in the regions core city centers, who work in offices, and the concentration of employees, in the manufacturing sectors, in rather suburban areas, such as Russelsheim, where the automotive sector is strong. Similar patterns can be identified for the Stuttgart region, where the manufacturing sector is concentrated along the river Neckar and in the municipalities of Böblingen/Sindelfingen (see [24,64] for details).
Complementary data also show that suburban settlements from the 1950s to the 1970s, whose establishment was facilitated by mass motorization and low land prices, have apparently undergone very little subsequent densification [68]. For this reason, the transition from a compact regional core to a more scattered suburban environment still characterizes the settlement structure of the regions to this day. In this way, low built densities and therefore also low population-job densities are quite often evident, even in inner-city locations or in close proximity to stations along rail-based transportation corridors. The densification of such areas, which has been vigorously supported by urban planners (see the discussion in [69,70,71]), is subject to the provisions of planning law designed to protect existing structures and is also very rarely consistently sought after for reasons of low social acceptance.
A final factor can be seen in urban planning regulations. Urban density in Germany is regulated by municipal land use and development planning. The essential legal provisions for this (Baunutzungsverordnung, the Federal Land Use Ordinance) set a maximum limit for floor area ratio at 1.2 for residential uses and 3.0 for certain commercial uses. While higher densities may be allowed in particular exceptional cases, German planning law tends to restrict rather than support strong densification. Additionally, regional and local planning cultures and practices vary greatly. For instance, high-rise development is not permitted in the City of Munich, whereas this has long been a common practice in Frankfurt. The radial structure of density in the Stuttgart region appears not only to be an expression of topographical conditions, but also of the regulations made by regional planning.
The approach introduced here and the data generated in this manner offer improved analytical opportunities for the future understanding of the complex relationships between economic and social, as well as built structures and changes in urban regions. In this context, our analyses also show that there is not one perfect measurement of density. Rather, the complexity and diversity of the urban spatial structure reveals itself when considering multiple, conceptually different density figures, such as the FAR, the built-up volume or the density of socioeconomic use. Correlations between the individual variables are certainly sometimes high (see Table 3 or also [24]), but this does not apply in all cases. Future research endeavors will certainly contribute to both a better understanding of the causational factors of these relationships and a better estimation of their implications for humans and their environment.

6. Conclusions and Outlook

The present discussion shows that it is possible to generate region-wide built density models using remote sensing data. In this way, a significant gap in the ongoing observation of processes of urban and regional development can be narrowed.
To date, available mapping products, such as the European Urban Atlas, provide data regarding density for two dimensions to a limited extent. Analyses of urban morphology and form, however, are related to the built-up volume and, thus, to the third dimension. In this context, our approach described and applied above presents a framework for the generation of spatial built densities for very large areas at low costs compared to other DSM acquisition technologies by the multi-source combination of digital surface models and building footprints. The integration of building footprints allows for the derivation of 3D building models with high accuracies for such large areas as the four city regions presented in our study. Current and future Earth observation missions, such as TanDEM-X or Cartosat, with their large area data acquisition to global coverage, will add to this capability for 3D monitoring. Thus, remote sensing will be able to systematically monitor the built environment of cities over time. In this way, the consistency of the data may permit international comparative urban studies.
The availability of fine-grained density data offers new possibilities, both from a practical planning perspective and from a scientific view. Applications can be found, for example, in urban climatology and ecology and especially in exposure studies. Precisely, vulnerability evaluation methods and models could be refined. Examples are the application of built-up volume as triggers of local heat island phenomena or their influence on local wind systems [72]. Noise transmission calculations can also be methodologically refined by taking into account the exact geographic location and height of buildings. Another issue is that the planning of urban revitalization could also profit from building and density data in that strategies of planned shrinkage and demolition of vacant buildings, among others, can be investigated regarding their effects on infrastructure [73,74]. The same applies to the evaluation of densification projects with their positive and negative impacts (e.g., the improvement of infrastructural efficiency, reduction of open space). In this way, the potential for densifications around subway or commuter rail stations, for example, can also be determined.
Fina et al. [46] furthermore point out that the expansion of conventional spatial monitoring systems offers chances for a multidimensional observation of urban and regional development, since density indicators can be integrated and combined with other statistics and metrics. The resulting improved availability of sub-municipal data also allows for an interregional comparative analysis of the conditions and developments in urban areas that has not yet been possible in Germany.

Acknowledgments

The authors would like to thank the German Research Foundation (DFG) for financing the research project “Polyzentralität deutscher Stadtregionen” (The polycentricity of German metropolitan areas) with the grant number: TA 800/1-1 & SI 932/4-1.

Author Contributions

Angelika Krehl and Stefan Siedentop mainly contributed to Section 1, Section 2 and Section 4, Section 5 and Section 6. Hannes Taubenböck and Michael Wurm mainly contributed to Section 3.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
FARfloor area ratio
IRSIndian Remote Sensing Satellite
DSMdigital surface models
BKGBundesamt für Kartographie und Geodäsie (Federal Agency for Cartography and Geodesy)
INSPIREInfrastructure for Spatial Information in the European Community
DLMdigital basis landscape model
nDSMnormalized DSM
DTK25-VDigitale Topographische Karte 1:25 000, Vorläufige Ausgabe (georeferenced digital topographic maps)
LoD1Level of Detail 1
WZ 2008Klassifikation der Wirtschaftszweige 2008 (Classification of Economic Activities, 2008 edition)
FDZForschungsdatenzentrum (Research Data Centre)
BABundesagentur für Arbeit (Federal Employment Agency)
IABInstitut für Arbeitsmarkt- und Berufsforschung (Institute for Employment Research)

References

  1. Ewing, R.; Hamidi, S. Compactness versus sprawl: A review of recent evidence from the United States. J. Plan. Lit. 2015, 30, 413–432. [Google Scholar] [CrossRef]
  2. OECD. Compact City Policies: A Comparative Assessment; OECD: Paris, France, 2012. [Google Scholar]
  3. Churchman, A. Disentangling the concept of density. J. Plan. Lit. 1999, 13, 389–411. [Google Scholar] [CrossRef]
  4. Roberts, B.H. Changes in urban density: Its implications on the sustainable development of Australian cities. In Proceedings of the State of Australian Cities National Conference, Adelaide, Australia, 28–30 November 2007.
  5. Acioly, C.; Davidson, F. Density in urban development. Build. Issues 1996, 8, 3–25. [Google Scholar]
  6. Ewing, R.; Cervero, R. Travel and the built environment. J. Am. Plan. Assoc. 2010, 76, 265–294. [Google Scholar] [CrossRef]
  7. Ewing, R.; Rong, F. The impact of urban form on U.S. residential energy use. Hous. Policy Debate 2008, 19, 1–30. [Google Scholar] [CrossRef]
  8. Forsyth, A. Measuring density: Working definitions for residential density and building intensity. Desi. Brief 2003, 8, 1–8. [Google Scholar]
  9. Forsyth, A.; Oakes, J.M.; Schmitz, K.H.; Hearst, M. Does residential density increase walking and other physical activity? Urban Stud. 2007, 44, 679–697. [Google Scholar] [CrossRef]
  10. Newman, P.W.G.; Kenworthy, J.R. Gasoline consumption and cities. J. Am. Plan. Assoc. 1989, 55, 24–37. [Google Scholar] [CrossRef]
  11. OECD. Cities and Climate Change, 1st ed.; OECD: Paris, France, 2010. [Google Scholar]
  12. Brownstone, D.; Golob, T.F. The impact of residential density on vehicle usage and energy consumption. J. Urban Econ. 2009, 65, 91–98. [Google Scholar] [CrossRef]
  13. Ewing, R.; Meakins, G.; Hamidi, S.; Nelson, A.C. Relationship between urban sprawl and physical activity, obesity, and morbidity—Update and refinement. Health Place 2014, 26, 118–126. [Google Scholar] [CrossRef] [PubMed]
  14. Hinde, S.; Dixon, J. Changing the obesogenic environment: Insights from a cultural economy of car reliance. Transp. Res. Part D: Transp. Environ. 2005, 10, 31–53. [Google Scholar] [CrossRef]
  15. Kelly-Schwartz, A.C.; Stockard, J.; Doyle, S.; Schlossberg, M. Is sprawl unhealthy? A multilevel analysis of the relationship of metropolitan sprawl to the health of individuals. J. Plan. Educ. Res. 2004, 24, 184–196. [Google Scholar] [CrossRef]
  16. Schläpfer, M.; Lee, J.; Bettencourt, L.M.A. Urban Skylines: Building Heights and Shapes As Measures of City Size. Available online: http://arxiv.org/pdf/1512.00946 (accessed on 11 May 2016).
  17. Rode, P.; Keim, C.; Robazza, G.; Viejo, P.; Schofield, J. Cities and energy: Urban morphology and residential heat-energy demand. Environ. Plan. B Plan. Des. 2014, 41, 138–162. [Google Scholar] [CrossRef] [Green Version]
  18. Angel, S.; Blei, A.M. The productivity of American cities: How densification, relocation, and greater mobility sustain the productive advantage of larger U.S. metropolitan labor markets. Cities 2016, 51, 36–51. [Google Scholar] [CrossRef]
  19. UN Habitat. Urban Patterns for a Green Economy; United Nations Human Settlements Programme: Nairobi, Kenya, 2012. [Google Scholar]
  20. Bettencourt, L.M.A.; West, G.B. A unified theory of urban living. Nature 2010, 467, 912–913. [Google Scholar] [CrossRef] [PubMed]
  21. Bettencourt, L.M.A.; Lobo, J.; Helbing, D.; Kühnert, C.; West, G.B. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301–7306. [Google Scholar] [CrossRef] [PubMed]
  22. Ciccone, A.; Hall, R.E. Productivity and the density of economic activity. Am. Econ. Rev. 1996, 86, 54–70. [Google Scholar]
  23. Harris, T.F.; Ioannides, Y.M. Productivity and Metropolitan Density; Department of Economics, Tufts University: Medford, MA, USA, 2000. [Google Scholar]
  24. Krehl, A. Urban spatial structure: An interaction between employment and built-up volumes. Reg. Stud. Reg. Sci. 2015, 2, 289–307. [Google Scholar] [CrossRef]
  25. Muñiz, I.; Garcia-López, M.-À. The polycentric knowledge economy in Barcelona. Urban Geogr. 2010, 31, 774–799. [Google Scholar] [CrossRef]
  26. Guillain, R.; Le Gallo, J.; Boiteux-Orain, C. Changes in spatial and sectoral patterns of employment in Ile-de-France, 1978–1997. Urban Stud. 2006, 43, 2075–2098. [Google Scholar] [CrossRef]
  27. Duranton, G.; Puga, D. From sectoral to functional urban specialisation. J. Urban Econ. 2005, 57, 343–370. [Google Scholar] [CrossRef]
  28. Siedentop, S.; Schiller, G.; Gutsche, J.-M.; Koziol, M.; Walther, J. Siedlungsentwicklung und Infrastrukturfolgekosten. Bilanzierung und Strategieentwicklung; Bundesamt für Bauwesen und Raumordnung: Bonn, Germany, 2006. [Google Scholar]
  29. Burchell, R.W.; Mukherji, S. Conventional development versus managed growth: The costs of sprawl. Am. J. Public Health 2003, 93, 1534–1540. [Google Scholar] [CrossRef] [PubMed]
  30. Doubek, C.; Zanetti, G. Siedlungsstruktur und Öffentliche Haushalte: Gutachten des Österreichischen Instituts für Raumplanung (ÖIR); Österreichisches Institut für Raumplanung: Wien, Austria, 1999. [Google Scholar]
  31. Melo, P.C.; Graham, D.J.; Levinson, D.; Aarabi, S. Agglomeration, accessibility and productivity: Evidence for large metropolitan areas in the US. Urban Stud. 2016. [Google Scholar] [CrossRef]
  32. Ahlfeldt, G.M. If Alonso was right: Modeling accessibility and explaining the residential land gradient. J. Reg. Sci. 2011, 51, 318–338. [Google Scholar] [CrossRef]
  33. Kropp, J.; Holsten, A.; Lissner, T.; Roithmeier, O.; Hattermann, F.; Huang, S.; Rock, J.; Wechsung, F.; Lüttger, A.; Pompe, S.; et al. Klimawandel in Nordrhein-Westfalen—Regionale Abschätzung der Anfälligkeit ausgewählter Sektoren; Potsdam Institut für Klimafolgenforschung: Potsdam, Germany, 2009. [Google Scholar]
  34. Watkins, R.; Palmer, J.; Kolokotroni, M. Increased temperature and intensification of the urban heat island: Implications for human comfort and urban design. Built Environ. 2007, 33, 85–96. [Google Scholar] [CrossRef]
  35. Koppe, C.; Kovats, S.; Jendritzky, G.; Menne, B.; Breuer, D.J. Heat Waves: Risks and Responses; Regional Office for Europe, World Health Organization: Copenhagen, Denmark, 2004. [Google Scholar]
  36. McFarlane, C. The geographies of urban density: Topology, politics and the city. Prog. Hum. Geogr. 2015. [Google Scholar] [CrossRef] [Green Version]
  37. Patel, R.B.; Burke, T.F. Urbanization—An emerging humanitarian disaster. New Engl. J. Med. 2009, 361, 741–743. [Google Scholar] [CrossRef] [PubMed]
  38. Barr, J.; Cohen, J.P. The floor area ratio gradient: New York City, 1890–2009. Reg. Sci. Urban Econ. 2014, 48, 110–119. [Google Scholar] [CrossRef]
  39. Susaki, J.; Kajimoto, M.; Kishimoto, M. Urban density mapping of global megacities from polarimetric SAR images. Remote Sens. Environ. 2014, 155, 334–348. [Google Scholar] [CrossRef] [Green Version]
  40. Jahn, A.; Hecht, R.; Meinel, G. 3D-Gebäudemodelle: Grundlage siedlungsstruktureller Analysen am Beispiel Sachsens. In Flächennutzungsmonitoring VII: Boden, Flächenmanagement, Analysen und Szenarien; Meinel, G., Schumacher, U., Behnisch, M., Krüger, T., Eds.; Rhombos-Verlag: Berlin, Germany, 2015; pp. 233–243. [Google Scholar]
  41. Landcom. Residential Density Guide; Landcom: Parramatta, Australia, 2011. [Google Scholar]
  42. Angel, S. Making Room for a Planet of Cities; Lincoln Institute of Land Policy: Cambridge, MA, USA, 2011. [Google Scholar]
  43. Siedentop, S.; Fina, S. Who sprawls most? Exploring the patterns of urban growth across 26 European countries. Environ. Plan. A 2012, 44, 2765–2784. [Google Scholar] [CrossRef]
  44. Taubenböck, H.; Wiesner, M. The spatial network of megaregions—Types of connectivity between cities based on settlement patterns derived from EO-data. Comput. Environ. Urban 2015, 54, 165–180. [Google Scholar] [CrossRef]
  45. Guérois, M.; Pumain, D. Built-up encroachment and the urban field: A comparison of forty European cities. Environ. Plan. A 2008, 40, 2186–2203. [Google Scholar] [CrossRef]
  46. Fina, S.; Krehl, A.; Siedentop, S.; Taubenböck, H.; Wurm, M. Dichter dran! Neue Möglichkeiten der Vernetzung von Geobasis-, Statistik- und Erdbeobachtungsdaten zur räumlichen Analyse und Visualisierung von Stadtstrukturen mit Dichteoberflächen und-profilen. Raumforsch. Raumordn. 2014, 72, 179–194. [Google Scholar] [CrossRef]
  47. Wurm, M.; d’Angelo, P.; Reinartz, P.; Taubenböck, H. Investigating the applicability of Cartosat-1 DEMs and topographic maps to localize large-area urban mass concentration. IEEE J. Sel. Top Appl. 2014, 7, 4138–4152. [Google Scholar] [CrossRef]
  48. Roskamm, N. Dichte: Eine Transdisziplinäre Dekonstruktion; Diskurse zu Stadt und Raum, 1st ed.; Transcript: Bielefeld, Germany, 2011. [Google Scholar]
  49. Landeshauptstadt Stuttgart. Stadträumliche Dichte. Flächenbilanz von Wohngebieten in Stuttgart; Landeshauptstadt Stuttgart: Stuttgart, Germany, 2005. [Google Scholar]
  50. Openshaw, S. The Modifiable Areal Unit Problem; Geo Books: Norwich, UK, 1983. [Google Scholar]
  51. NRSA. Cartosat-1 Data User’s Handbook. 2006. Available online: http://www.euromap.de/download/P5_data_user_handbook.pdf (accessed on 14 February 2016).
  52. d’Angelo, P.; Lehner, M.; Krauss, T.; Hoja, D.; Reinartz, P. Towards automated DEM generation from high resolution stereo satellite images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, XXXVII, 1137–1143. [Google Scholar]
  53. Tian, J.; Reinartz, P.; d’Angelo, P.; Ehlers, M. Region-based automatic building and forest change detection on Cartosat-1 stereo imagery. ISPRS J. Photogramm. 2013, 79, 226–239. [Google Scholar] [CrossRef]
  54. Hirschmuller, H. Stereo processing by semiglobal matching and mutual information. IEEE T Pattern. Anal. 2008, 30, 328–341. [Google Scholar] [CrossRef] [PubMed]
  55. GeoBasis-DE. Digital Topographic Map 1:25,000, Preliminary Edition. DTK25-V. Available online: http://www.geodatenzentrum.de/docpdf/dtk25-v_eng.pdf (accessed on 17 May 2016).
  56. Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
  57. Wurm, M.; Taubenböck, H.; Goebel, J.; Wagner, G.G. At the edge of the city center: discrimination of the physical city center by subjective perception and satellite data. In Proceedings of the 2015 Joint Urban Remote Sensing Event (JURSE), Lausanne, Switzerland, 30 March–1 April 2015.
  58. Taubenböck, H.; Wurm, M. disP Service: Wo beginnt die Stadt? Urbane Fernerkundung für stadtgeographische Forschung. disP-Plan. Rev. 2015, 51, 78–89. [Google Scholar] [CrossRef]
  59. Wurm, M.; Taubenböck, H.; Schardt, M.; Esch, T.; Dech, S. Object-based image information fusion using multisensor Earth observation data over urban areas. Int. J. Image Data Fusion 2011, 2, 121–147. [Google Scholar] [CrossRef]
  60. European Forum for Geography and Statistics. GRID_ETRS89_LAEA_1K. Available online: http://www.efgs.info/data/european-datasets/eurogrid (accessed on 29 January 2016).
  61. BKG. The Digital Basic Landscape Model (AAA). Available online: http://www.geodatenzentrum.de/docpdf/basis-dlm-aaa_eng.pdf (accessed on 14 February 2016).
  62. Statistik der Bundesagentur für Arbeit. Sozialversicherungspflichtig Beschäftigte nach Wohn- und Arbeitsort mit Pendlerdaten. Available online: https://Statistik.Arbeitsagentur.De/Statistikdaten/Detail/201012/Iiia6/Sozbe-Gemwoao/Gemwoao-D-0-Xls.Xls (accessed on 20 May 2016).
  63. Statistische Ämter des Bundes und der Länder. Bevölkerungsstand: Bevölkerung nach Geschlecht-Stichtag 31.12.-regionale Tiefe: Gemeinden, Samt-/Verbandsgemeinden. Table 173-01-5. Available online: https://www.regionalstatistik.de/genesis/online;jsessionid=C447F1580D6891A6425855D54364F85F?sequenz=tabelleErgebnis&selectionname=173-01-5 (accessed on 20 May 2016).
  64. Krehl, A. Polyzentralität in deutschen Stadtregionen—Eine integrierte Bestandsaufnahme. In Globale Urbanisierung—Perspektive aus dem All; Taubenböck, H., Wurm, M., Esch, T., Dech, S., Eds.; SpringerSpektrum: Berlin, Germany; Heidelberg, Germany, 2015; pp. 159–170. [Google Scholar]
  65. Siedentop, S.; Krehl, A.; Taubenböck, H.; Wurm, M. Die bauliche Dichte der Stadtregion—Erzeugung kleinräumiger Dichtedaten mit fernerkundlichen Mitteln. In Flächennutzungsmonitoring VI.: Innenentwicklung—Prognose—Datenschutz; Meinel, G., Schumacher, U., Behnisch, M., Eds.; Rhombos: Berlin, Germany, 2014; pp. 179–188. [Google Scholar]
  66. Scholz, T.; Rauscher, C.; Reiher, J.; Bachteler, T. Geocoding of German Administrative Data: The Case of the Institute for Employment Research; Bundesagentur für Arbeit: Nürnberg, Germany, 2012. [Google Scholar]
  67. Eurostat. GEOSTAT 2011 Grid Dataset. Available online: http://ec.europa.eu/eurostat/web/gisco/geodata/reference-data/population-distribution-demography (accessed on 4 February 2016).
  68. Filion, P. Suburban inertia: The Entrenchment of dispersed suburbanism. Int. J. Urban Reg. 2015, 39, 633–640. [Google Scholar] [CrossRef]
  69. Jessen, J.; Roost, F. Refitting Suburbia: Erneuerung der Stadt des 20. Jahrhunderts in Deutschland und den USA; Jovis: Berlin, Germany, 2015. [Google Scholar]
  70. Grant, J.L.; Nelson, A.C.; Forsyth, A.; Thompson-Fawcett’s, M.; Blais, P.; Filion, P. The future of the suburbs. Suburbs in transition/The resettlement of America’s suburbs/Suburbs in global context: The challenges of continued growth and retrofitting/Suburban urbanity: Re-envisioning indigenous settlement practices/Toward a new suburban America: Will we catch the wave?/Optimistic and pessimistic perspectives on the evolution of the North American suburb/Response. Plan. Theory Pract. 2013, 14, 391–415. [Google Scholar]
  71. Dunham-Jones, E.; Williamson, J. Retrofitting Suburbia. Urban Design Solutions for Redesigning Suburbs; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
  72. Harlan, S.L.; Brazel, A.J.; Prashad, L.; Stefanov, W.L.; Larsen, L. Neighborhood microclimates and vulnerability to heat stress. Soc. Sci. Med. 2006, 63, 2847–2863. [Google Scholar] [CrossRef] [PubMed]
  73. Moss, T. “Cold spots” of urban infrastructure: “Shrinking” processes in Eastern Germany and the modern infrastructural ideal. Int. J. Urban Reg. 2008, 32, 436–451. [Google Scholar] [CrossRef]
  74. Schiller, G.; Siedentop, S. Infrastrukturfolgekosten der siedlungsentwicklung unter schrumpfungsbedingungen. disP-Plan. Rev. 2005, 41, 83–93. [Google Scholar] [CrossRef]
Ijgi 05 00076 g001 1024
Figure 1. Flowchart of the steps performed for modeling the built densities.
Figure 1. Flowchart of the steps performed for modeling the built densities.
Ijgi 05 00076 g001
Ijgi 05 00076 g002 1024
Figure 2. Spatial data input for the generation of the 3D building models using the example of the center of the Munich city region; left: normalized digital surface model; right: extracted building footprint objects from the topographic map DTK25-V. Topographic map: © GeoBasis-DE/BKG (2010), cf. [55].
Figure 2. Spatial data input for the generation of the 3D building models using the example of the center of the Munich city region; left: normalized digital surface model; right: extracted building footprint objects from the topographic map DTK25-V. Topographic map: © GeoBasis-DE/BKG (2010), cf. [55].
Ijgi 05 00076 g002
Ijgi 05 00076 g003 1024
Figure 3. Perspective view of 3D building models derived from space-borne Cartosat-1 height measurements and building footprints from digital topographic maps (top left: Cologne; top right: Frankfurt; bottom left: Stuttgart; bottom right: Munich). Topographic map: © GeoBasis-DE/BKG (2010), cf. [55].
Figure 3. Perspective view of 3D building models derived from space-borne Cartosat-1 height measurements and building footprints from digital topographic maps (top left: Cologne; top right: Frankfurt; bottom left: Stuttgart; bottom right: Munich). Topographic map: © GeoBasis-DE/BKG (2010), cf. [55].
Ijgi 05 00076 g003
Ijgi 05 00076 g004 1024
Figure 4. Correlation between building area and the deviation of building height against the reference data.
Figure 4. Correlation between building area and the deviation of building height against the reference data.
Ijgi 05 00076 g004
Ijgi 05 00076 g005 1024
Figure 5. Calculation of built-up volume and FAR per INSPIRE grid cell.
Figure 5. Calculation of built-up volume and FAR per INSPIRE grid cell.
Ijgi 05 00076 g005
Ijgi 05 00076 g006 1024
Figure 6. Box plots of built-up volumes (million m3) and floor area ratios.
Figure 6. Box plots of built-up volumes (million m3) and floor area ratios.
Ijgi 05 00076 g006
Ijgi 05 00076 g007 1024
Figure 7. Patterns of built densities represented by built-up volume (left) and mean floor area ratio (right) for 1-km2 grid cells.
Figure 7. Patterns of built densities represented by built-up volume (left) and mean floor area ratio (right) for 1-km2 grid cells.
Ijgi 05 00076 g007
Ijgi 05 00076 g008 1024
Figure 8. Selected density profiles of the case study regions; built-up volume and floor area ratio values for the grid cells located along the respective core city’s latitude, the latter indicated by the town hall’s geographic location.
Figure 8. Selected density profiles of the case study regions; built-up volume and floor area ratio values for the grid cells located along the respective core city’s latitude, the latter indicated by the town hall’s geographic location.
Ijgi 05 00076 g008
Ijgi 05 00076 g009 1024
Figure 9. Scatterplot matrices showing the relationship between built and activity densities (both measured in levels). Employment data are taken from georeferenced Integrated Employment Biographies (georeferenced IEB) as of 30 June 2009, which are provided by the Research Data Centre (FDZ) of the Federal Employment Agency (BA) at the Institute for Employment Research (IAB) (for details and documentation, see [66]).
Figure 9. Scatterplot matrices showing the relationship between built and activity densities (both measured in levels). Employment data are taken from georeferenced Integrated Employment Biographies (georeferenced IEB) as of 30 June 2009, which are provided by the Research Data Centre (FDZ) of the Federal Employment Agency (BA) at the Institute for Employment Research (IAB) (for details and documentation, see [66]).
Ijgi 05 00076 g009
Table
Table 1. Urban density indicators and their meanings.
Table 1. Urban density indicators and their meanings.
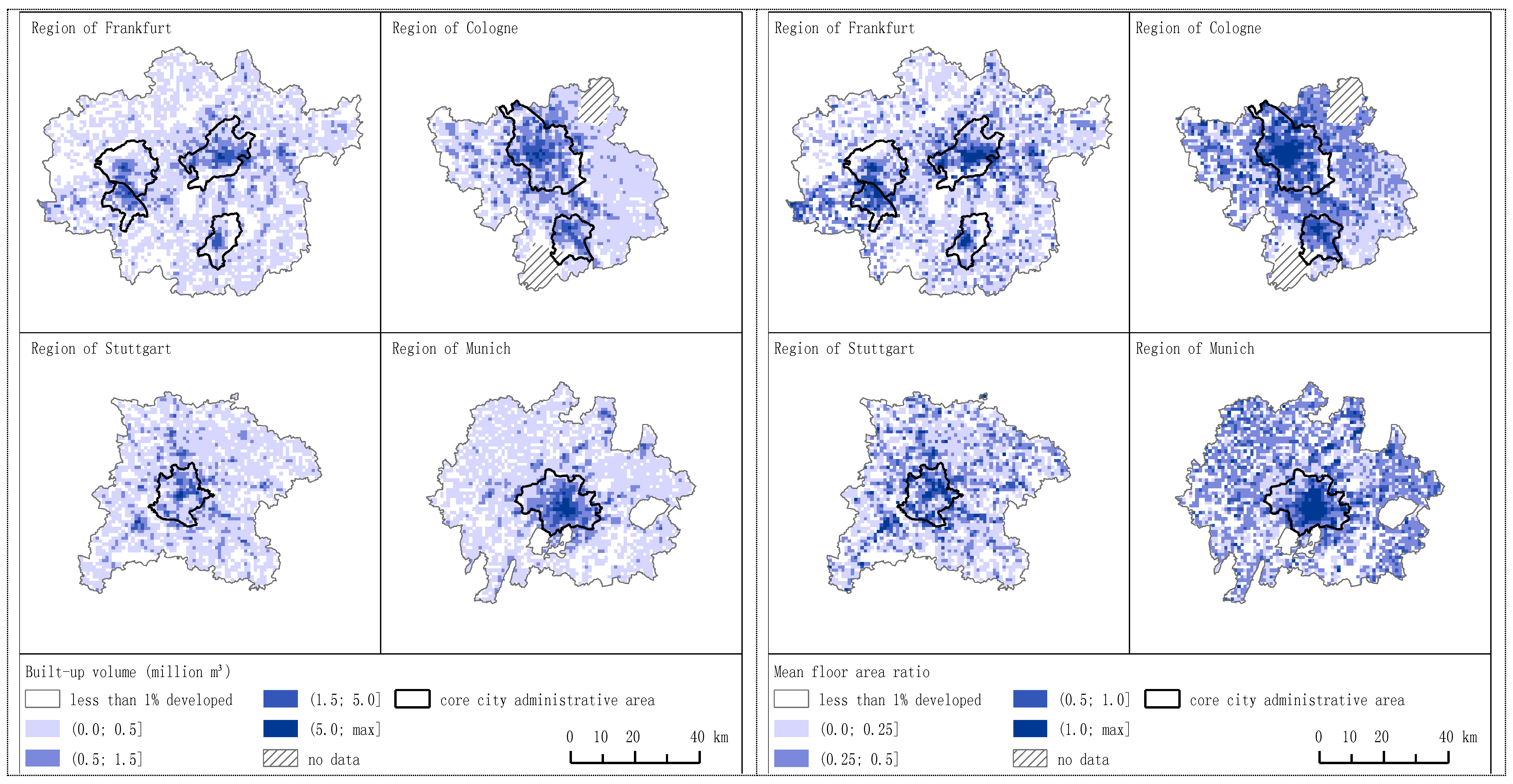
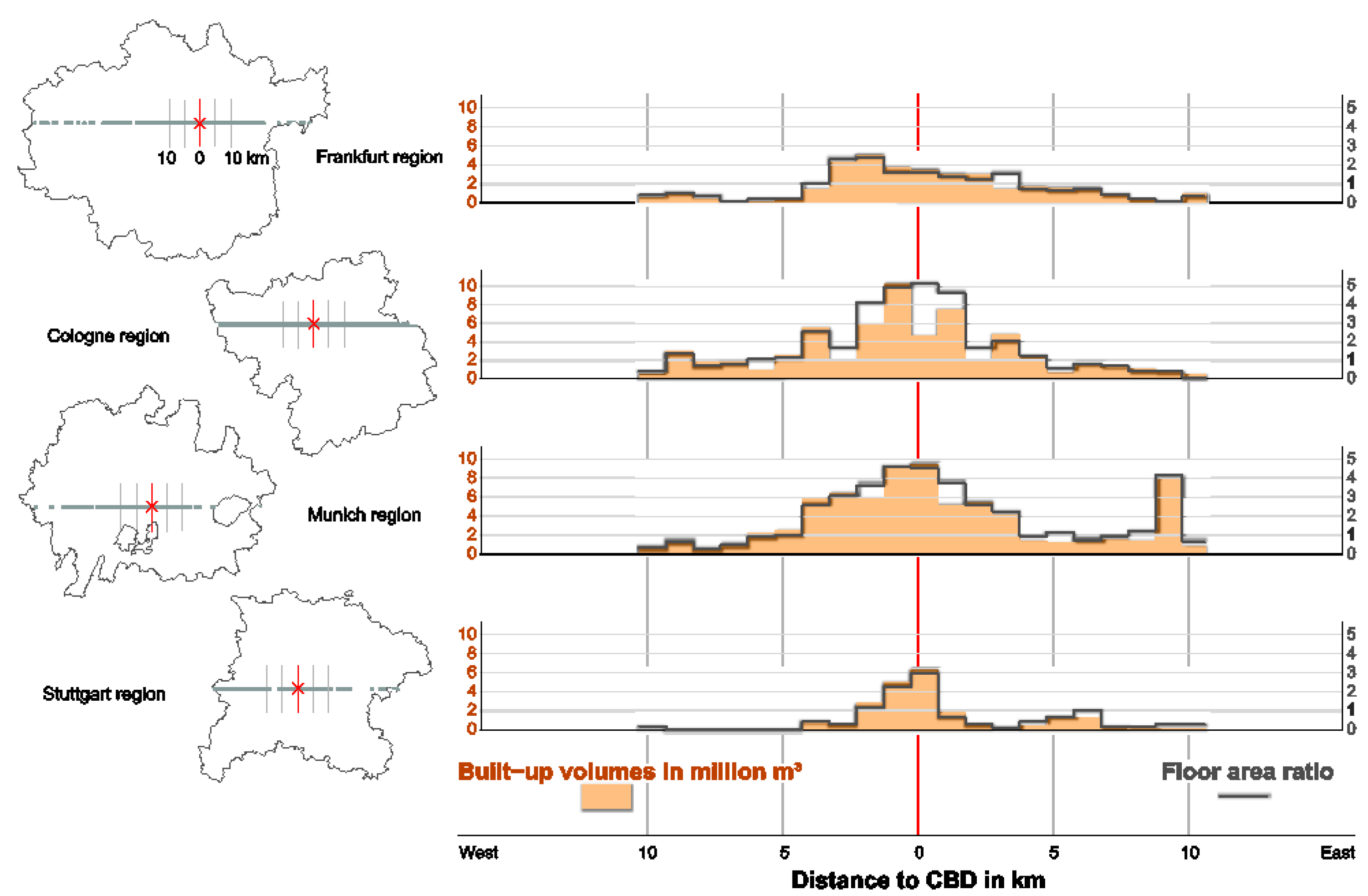
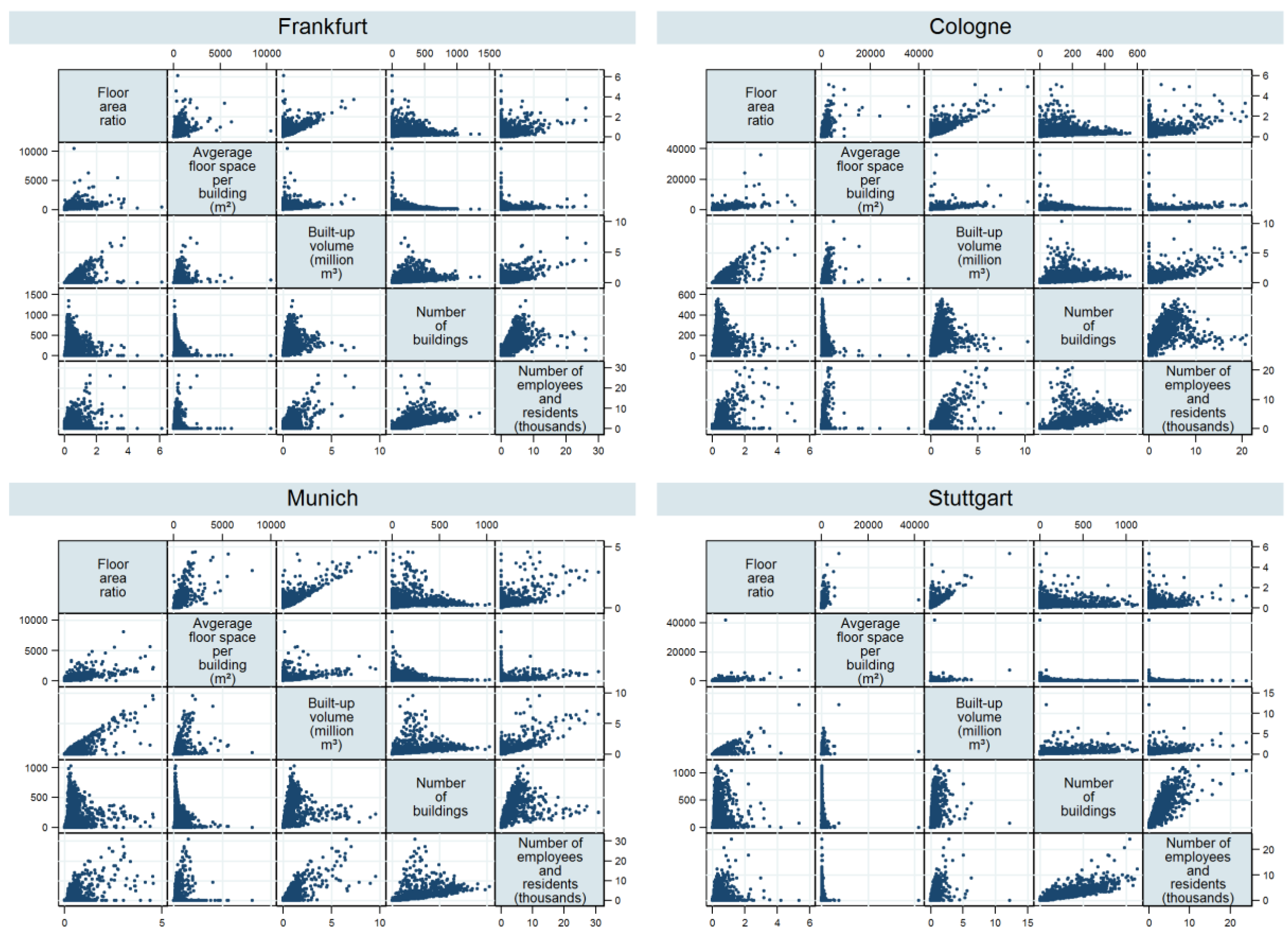
IndicatorScaleMeaning/MeasurementIncluded Land Resources
Metropolitan densityRegionPeople, jobs or dwelling units per land area unitAdministrative area
Urban (residential) densityCity, city districtPeople, jobs or dwelling units per land area unitUrbanized area
Gross residential densityNeighborhood, urban blockPeople or dwelling units per land area unitResidential area (including streets, pavements, local community services and public open spaces)
Net residential densityNeighborhood, urban blockPeople or dwelling units per land area unitResidential area (not including streets, local community services public open spaces)
Site densityPlot, propertyDwelling units per land area unit; floor area per land area unitSingle plot, property
Occupation densityDwelling unitPeople per dwelling unitSingle dwelling unit
(Source: own compilation based on information and definitions provided in [3,41])
Table
Table 2. Overview of spatial indicators.
Table 2. Overview of spatial indicators.
IndicatorCity Region
CologneFrankfurtMunichStuttgart
Area (km2)2812484332772842
Population (million residents)2.813.572.432.40
Employment (million jobs)0.991.461.090.96
Built-up area (km2)623807535505
Built-up volume (million m3)11591029942659
Floor area (km2)374335328216
Population density (people per km2)1000736742845
Mean floor area ratio (FAR)0.600.410.610.43
Floor area per resident and job (m2)99679364
Built-up volume per resident and job (m3)305205268197
Employment data are taken from the Federal Employment Agency, “Beschäftigungsstatistik, Sozialversicherungspflichtig Beschäftigte nach Wohn- und Arbeitsort mit Pendlerdaten, Nürnberg, Stichtag 30. Juni 2010” [62]; population data are data on the spatial level of municipalities as of 31 December 2010, taken from “Statistische Ämter des Bundes und der Länder”, version as of 2013; and called “Bevölkerungsstand: Bevölkerung nach Geschlecht, Stichtag 31.12. regionale Tiefe: Gemeinden, Samt-/Verbandsgemeinden” [63] Both employees and residents have been summarized into the regional delineations used in this study.
Table
Table 3. Spearman’s rank correlation coefficients for several density measures.
Table 3. Spearman’s rank correlation coefficients for several density measures.
City Region
CologneFrankfurtMunichStuttgart
Floor area ratio (FAR)
Average floor space per building0.690.610.620.55
Built-up volume0.700.660.530.66
Number of buildings0.410.390.300.38
Number of residents and employees0.430.380.330.38
Number of residents and employees
Floor area ratio (FAR)0.430.380.330.38
Average floor space per building0.27//−0.06
Built-up volume0.820.830.880.86
Number of buildings0.900.920.950.95
Employment data are taken from georeferenced Integrated Employment Biographies (georeferenced IEB) as of 30 June 2009, which are provided by the Research Data Centre (FDZ) of the Federal Employment Agency (BA) at the Institute for Employment Research (IAB) (for details and documentation, see [66]); population data as of 2011, provided by Eurostat [67].

Share and Cite

MDPI and ACS Style

Krehl, A.; Siedentop, S.; Taubenböck, H.; Wurm, M. A Comprehensive View on Urban Spatial Structure: Urban Density Patterns of German City Regions. ISPRS Int. J. Geo-Inf. 2016, 5, 76. https://doi.org/10.3390/ijgi5060076

AMA Style

Krehl A, Siedentop S, Taubenböck H, Wurm M. A Comprehensive View on Urban Spatial Structure: Urban Density Patterns of German City Regions. ISPRS International Journal of Geo-Information. 2016; 5(6):76. https://doi.org/10.3390/ijgi5060076

Chicago/Turabian Style

Krehl, Angelika, Stefan Siedentop, Hannes Taubenböck, and Michael Wurm. 2016. "A Comprehensive View on Urban Spatial Structure: Urban Density Patterns of German City Regions" ISPRS International Journal of Geo-Information 5, no. 6: 76. https://doi.org/10.3390/ijgi5060076

APA Style

Krehl, A., Siedentop, S., Taubenböck, H., & Wurm, M. (2016). A Comprehensive View on Urban Spatial Structure: Urban Density Patterns of German City Regions. ISPRS International Journal of Geo-Information, 5(6), 76. https://doi.org/10.3390/ijgi5060076

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop