1. Introduction
Due to an increasing demand for land use in urban areas, the future direction of urban development involves extending the current land use to higher spaces and the underground. With increasingly complex three-dimensional (3D) structures, the traditional two-dimensional (2D) cadastre is becoming more limited for handling complex 3D cadastral objects in urban areas. A 3D cadastre is needed to address these limitations. Several countries and regions have begun to register and manage complex 3D cadastral objects via urban cadastral management [
1,
2,
3,
4,
5,
6]. Relative theories and technologies, including organization, storage and query of 3D spatial units, have recently gained attention.
A 3D cadastral data model focuses on methods to organize, store and represent spatial representations for 3D cadastral objects in a cadastral database. Because land ownership boundaries and rights should be accurately defined in a cadastral registration, a large percentage of cadastral data models represent the structures of 3D spatial units by describing topological relations among composed elements [
7,
8,
9]. The majority of existing data representation models of traditional 3D cadastres are topological-based [
7]. Several topological-based 3D cadastral data models, which are based on Euclidean Geometry (EG), have been developed for 3D cadastral management [
7,
8,
9,
10,
11,
12,
13]. Because EG space lacks a unified form in dimensional expansion, the extension from a classical 2D cadastre to a 3D cadastre that is based on EG is not direct or simple. Representations of 3D spatial units are more complicated than representations of 2D spatial units in EG space [
14], which is one of the main obstacles in 3D cadastre implementation. EG-based cadastral data models organize, store and represent geometry according to their topological relations, which are contained in 3D cadastral objects in a cadastral database. The topological structures and relations are logged and maintained during the entire procedure of data storage, relationship representation, operation, division of rights, and validation [
13]. Universally accepted 3D cadastral data models have not been constructed for efficient complex spatial representations. How to store and represent spatial representations efficiently for 3D cadastral objects in a database remains a challenge in 3D cadastre development [
15].
One of the main issues caused by the division of multidimensionality in EG space is the separation between the representation of geometry and the representation of algebra. Geometric elements with higher dimensions in EG space cannot be expressed directly and algebraically by their geometric components, which have lower dimensions. A separation exists between the expression of geometry and the expression of algebra [
16], which produces the diversity of distinct expressions and computational structures in objects of different dimensions. EG-based 3D data models focus on the description of topological relations among different dimensional construction elements of 3D objects [
7]. These methods for spatial representations are not intuitive. They cannot handle a complex hierarchical structure, especially the dimensional hierarchical structure in a 3D cadastre as an entity. Topological relations among different dimensions, such as points, boundary lines, boundary faces and spatial units, are commonly employed to indirectly realize the spatial representations of 3D objects [
17,
18,
19,
20]. For instance, lines and surfaces are expressed by the descriptions of construction points and lines, respectively, whereas a 3D spatial unit is represented by recording of relative surfaces. The principle of EG-based data models is a 3D extension of the topological relations among points, lines and planes in 2D space. In these data models, the geometries only comprise symbols that are logged or described in the database instead of the real computational primitives that are represented algebraically. The topological relations in EG-based data models resemble the connection structures between these symbolized geometries [
21,
22,
23]. Due to the complexity of 3D objects and the limitations of EG in complex 3D object representation, EG-based data models cannot realize the integration of geometry and topology as an entity. Although several studies have attempted to integrate geometry and topology [
24,
25,
26], none have achieved this goal due to the limitation of EG. New mathematical theories are needed to integrate geometric and algebraic representations as an entity.
In this paper, conformal geometric algebra (CGA) is introduced as the theoretical foundation of 3D cadastral spatial representations to solve problems in cadastral development from a 2D structure to a 3D structure. As a branch of Clifford algebra [
27,
28], CGA can integrate the geometric and algebraic representations of spatial objects. CGA can also solve geometric problems directly in an algebraic way [
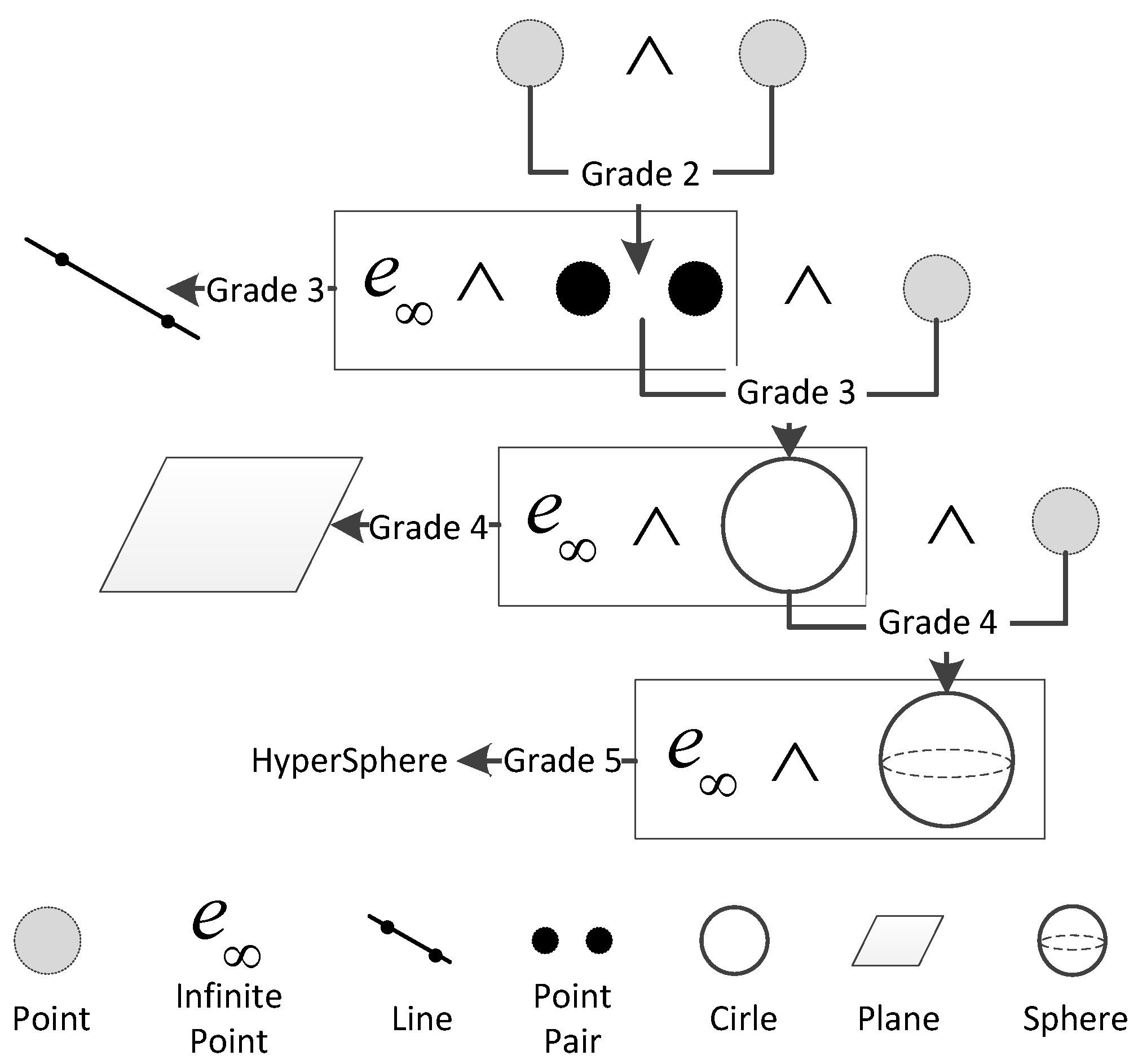
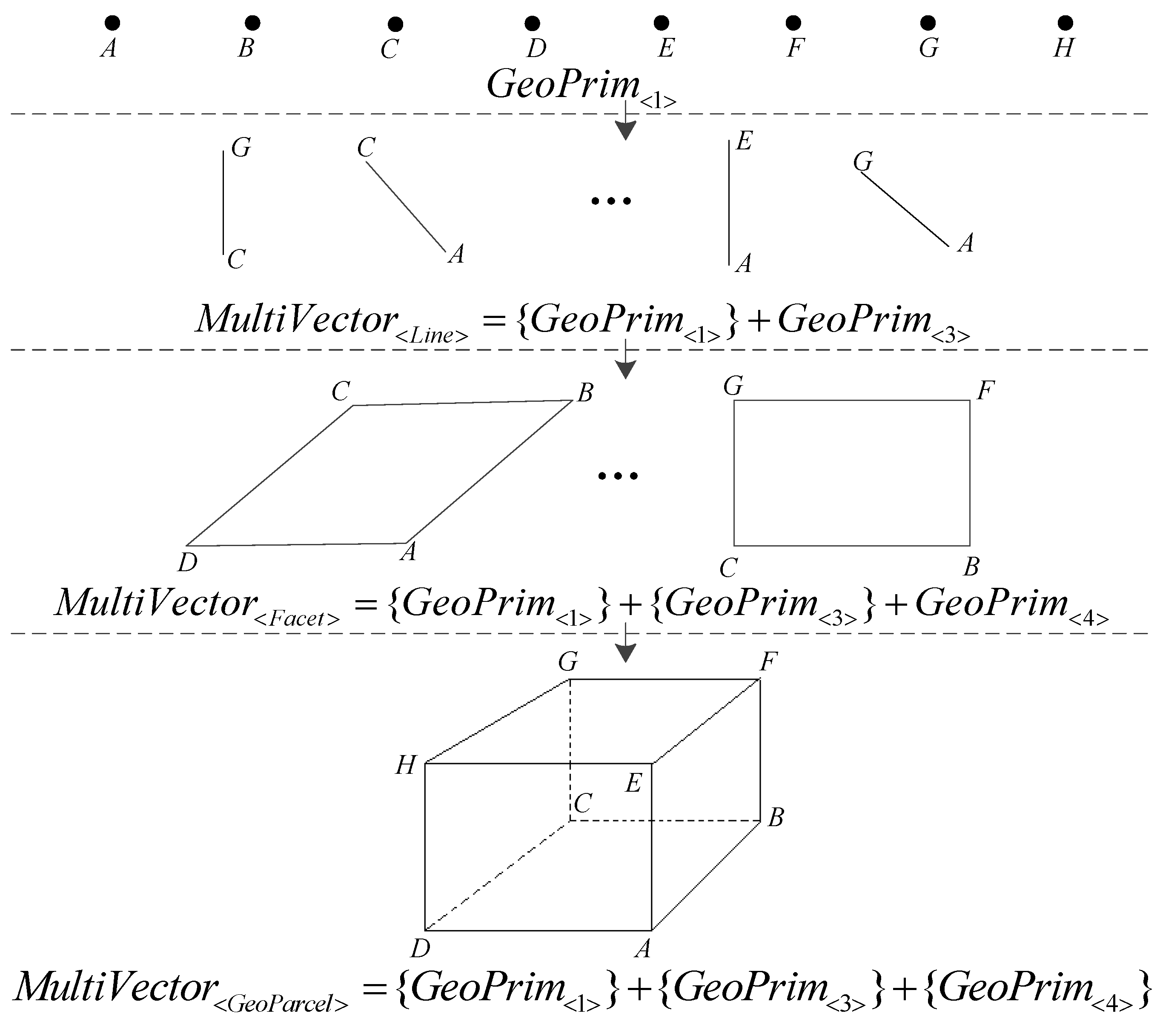
29]. Compared with EG, different dimensional elements in CGA can be expressed in a unified form by outer products consistent with the Grassmann structure, as shown in
Figure 1, which indicates that the geometric structure of spatial units is consistent with the Grassmann dimensional structure. Several achievements that introduce CGA into geographic information systems (GISs) research are as follows: a multi-dimensional integrated GIS model [
23,
30], a spatial analysis computation [
31,
32,
33], and an expression of topological relations and operations integration [
34,
35]. Yuan et al (2014) suggest that CGA has the potential to become the fundamental theory and technology for constructing a multidimensional unified GIS [
35]. Therefore, it has high potential to serve as a solid foundation for 3D cadastral data modeling.
This paper is organized as follows: In
Section 2, we review the fundamental idea of constructing a 3D cadastral data model with CGA. The construction and development of the 3D cadastral data model are presented in
Section 3. Both the theoretical and the technological implementations of the data model are discussed. In
Section 4, we test the CGA-based 3D cadastral data model using real-world case studies. The characteristics, improvements and future directions of the 3D cadastral data model are discussed in
Section 5. We state our conclusions in
Section 6.
2. Basic Idea
The unification of geometric and topological representations is one of the objectives in cadastral data modeling. The key to integrating geometry and topology is the integrated representation of the geometric structure and the dimensional structure of geometric elements of different dimensions. This representation is not possible in EG because traditional Euclidean space lacks consistency in the representation of geometries of different dimensions [
14]. To achieve synchronization between geometry and topology at different dimensions, a distinct and unified mathematical representation and data organization structure are necessary.
CGA is one of the most powerful geometric algebra (GA) systems. Compared with other geometric systems, such as Euclidean geometry and projective geometry, CGA has the unique advantages of simple and intuitive structure, distinct geometric meaning and unified characteristics with regard to the expression of the geometry [
35,
36,
37,
38]. Because dimensional and topological structures in CGA are consistent with the Grassmann dimensional structure, different dimensional elements can be expressed directly via outer products with conformal points. The structure of the Grassmann hierarchy is similar to the topological structures of different dimensional objects [
39], which enables the construction of a unified representation for different dimensional geometries in CGA [
40]. The unified representation of the geometric construction is purely algebraic, which indicates that geometric objects can be expressed as an algebraic entity [
41]. With the expression of the structure of the geometric objects in CGA, the topological relations are implicitly contained in their algebraic expression [
42]. In this manner, the unified representation of geometries and topological relations can be achieved.
Fundamental primitives (e.g., points, point pairs, lines, circles, planes and spheres) in CGA can be represented consistently using the outer product with the integration of geometries and topological relations. However, the representation of arbitrary geometries may not fit a hierarchal Grassmann structure. To ensure compatibility with an existing GIS data model, a 3D cadastral data model with a complex-simplex structure is formed. For example, complex geometries should be composed of elementary geometries. In this combination, topological structures should also be encoded and represented in the expression of geometric structures. Although CGA includes six primitives, only points, lines and planes are employed in the spatial representations to fit the characteristics of accurate cadastral boundary representation. Because the elemental geometric objects in CGA have different dimensions, a unified representation structure that represents different dimensional objects is preferable.
The multivector structure, which is the fundamental algebraic structure in CGA, combines different dimensional objects. In a multivector structure, different dimensional geometric elements that comprise the complete object are represented as blade subspaces of the CGA according to the grades (
i.e., dimensions) of the objects. The structures of the objects are coded in the weight, amplitude and orientation of the components of the multivectors [
33]. In this manner, the representation of geometries in a multivector structure can be expressed algebraically. With well-defined data structures (e.g., the hierarchal structure according to the dimensions [
35]), consistent topological relations can be maintained even if complex geometries are represented. For example, we can represent complex 3D cadastral spatial units according to the combination of points, lines and planes. In a multivector structure, the topological relations among these different dimensional elements can be formulated using the coefficients of the blades in the multivectors, and the geometric construction relations can be completely investigated using the structures of the multidimensional organization structures. The multivector structure provides a unified and ideal structure for storing different dimensional objects by integrating geometric and topological structures in an algebraic manner.
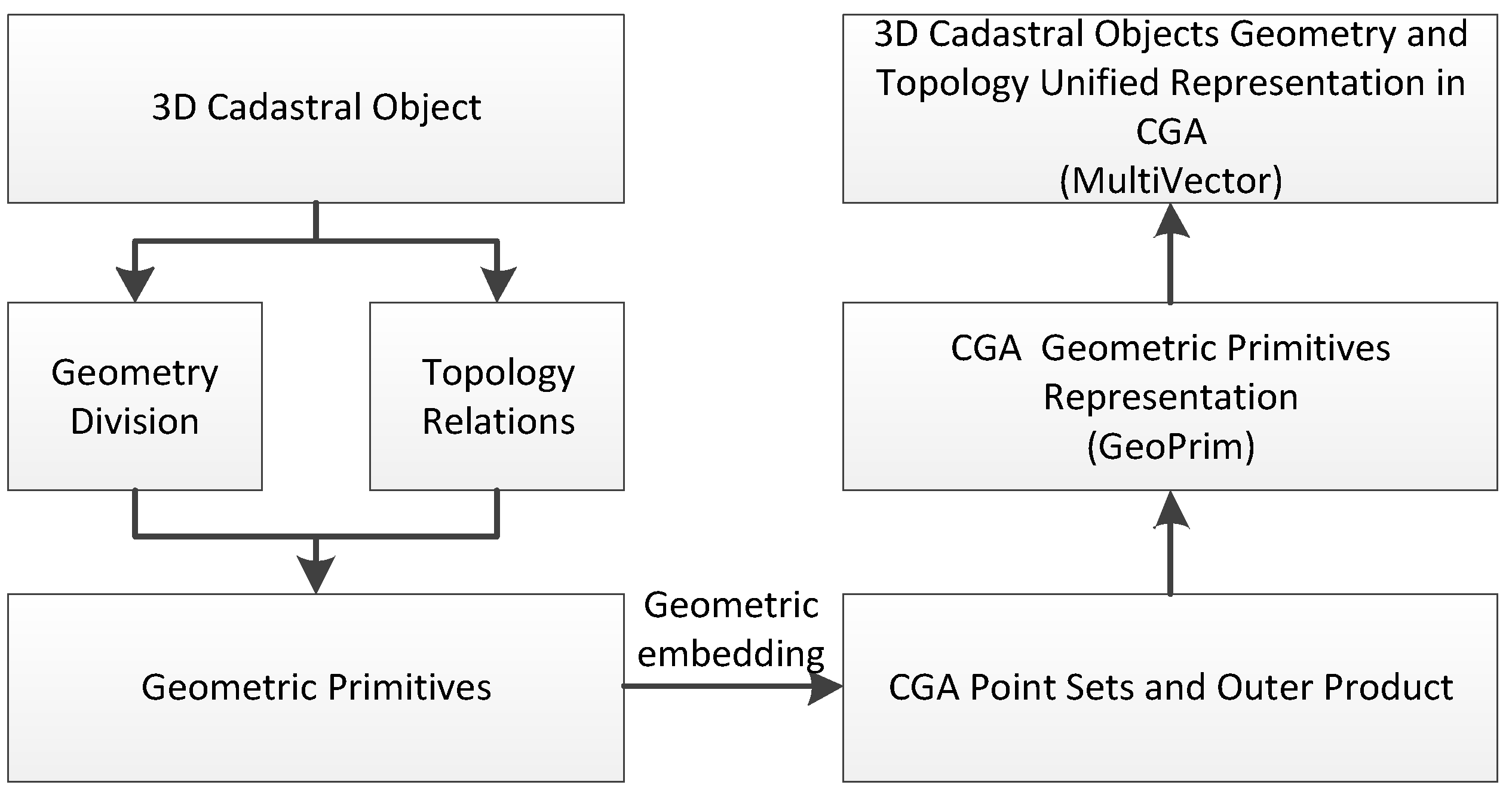
We developed a multidimensional-unified 3D cadastral data model using CGA. The premise of the construction of the data model is illustrated in
Figure 2. In the first phase, 3D cadastral objects are decomposed into geometric and topological components from which we can obtain simplex elements that are composed of complex objects. Conformal points can be obtained from original Euclidean point sets via expression in CGA in the second phase. These simplex elements, which are employed to construct 3D cadastral spatial units, can be consistently represented by conformal point sets using the outer product operation in CGA in the third phase. Complex 3D cadastral spatial units are expressed via the multivector structure, in which different dimensional construction simplexes are integrated to realize a unified expression for geometric information and topological relations.
3. Methods
3.1. Geometrically and Topologically Unified Representation in CGA
Using nonlinear spherical projection, the Euclidean space is embedded in a high-dimensional space, which is subject to a homogeneous projection transformation to obtain the conformal model of Euclidean geometry [
33,
43], where
are the five vectors that support the space
and the
coordinates of the Euclidean space are the coefficients of the
vectors, respectively. In this paper,
denotes the basic coordinate origin, whose coefficient is normally kept constant in CGA, and
is the infinity point, whose coefficients can be calculated by Euclidean coordinates. The outer product of two arbitrary vectors in CGA is defined as follows:
Definition 1: If
a and
b are two vectors in the conformal space
, the outer product is defined as
where both
ab and
ba are the geometric products of vectors
a and
b [
41], which produce scalars and bivectors. This definition indicates that the dimensions of geometric objects can be encoded based on the outer product operation.
The geometric objects of different dimensions in the conformal space are constructed by the outer product, which can realize the uniform expression form for the different dimensional geometric objects. By introducing the two additional dimensions of the origin and the infinity point, the geometric object dimensional structure completely corresponds to the Grassmann structure in the conformal space [
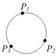
30]. The expression ability of geometric entities in CGA has been significantly expanded. These features enable the geometric objects of different dimensions in CGA to be directly constructed via the outer product of conformal point sets, which is shown in
Table 1. For example, the outer product of two conformal points, which comprises a one-dimensional (1D) subspace in CGA, can directly express 2D subspace point pairs. Conformal lines, which comprise a 3D subspace, can be represented by a 2D subspace outer product with the infinity point
, whereas a plane is expressed by the outer product of three conformal points and the infinity point
.
Table 1 lists the basic geometric objects, which are expressed by the outer product of the conformal points in CGA. As shown in the table, different dimensional geometric objects follow a uniform manner of expression in CGA. The line and circle and the plane and sphere in CGA achieve a unified expression form and geometric meaning, respectively [
34,
44].
A multivector is a basic mathematical element that can simultaneously integrate multiple dimensional objects in CGA. The multidimensional unified expression of a common geometric object by a multivector in conformal space is defined as follows:
Definition 2: If
are points in conformal space
, then the multivector A, which is composed of points, lines and planes in
, is expressed as
where n is the number of points and {} represents the sets of geometric elements with the same dimensions. The multivector definition indicates that the geometric elements in different dimensions are connected by addition.
According to Definition 2, the integration and unification of different geometric dimensions can be realized via the multivector structure in CGA. Simplex objects, such as points, lines and surfaces, can be integrated within a multivector to express complex 3D geometric objects. Elements of different dimensions are independent in the multivector structure. With the multivector structure, multidimensional fusion expression for 3D complex geometric objects can be realized and topological relations among different dimensional construction elements are distinctly expressed by the topological hierarchy that is constructed from multidimensional components.
3.2. 3D Cadastral Object Data Model Based on CGA
This section introduces a detailed description of the expression method of 3D cadastral objects in CGA. First, the relationship between the main research contents and the land administration domain model (LADM) [
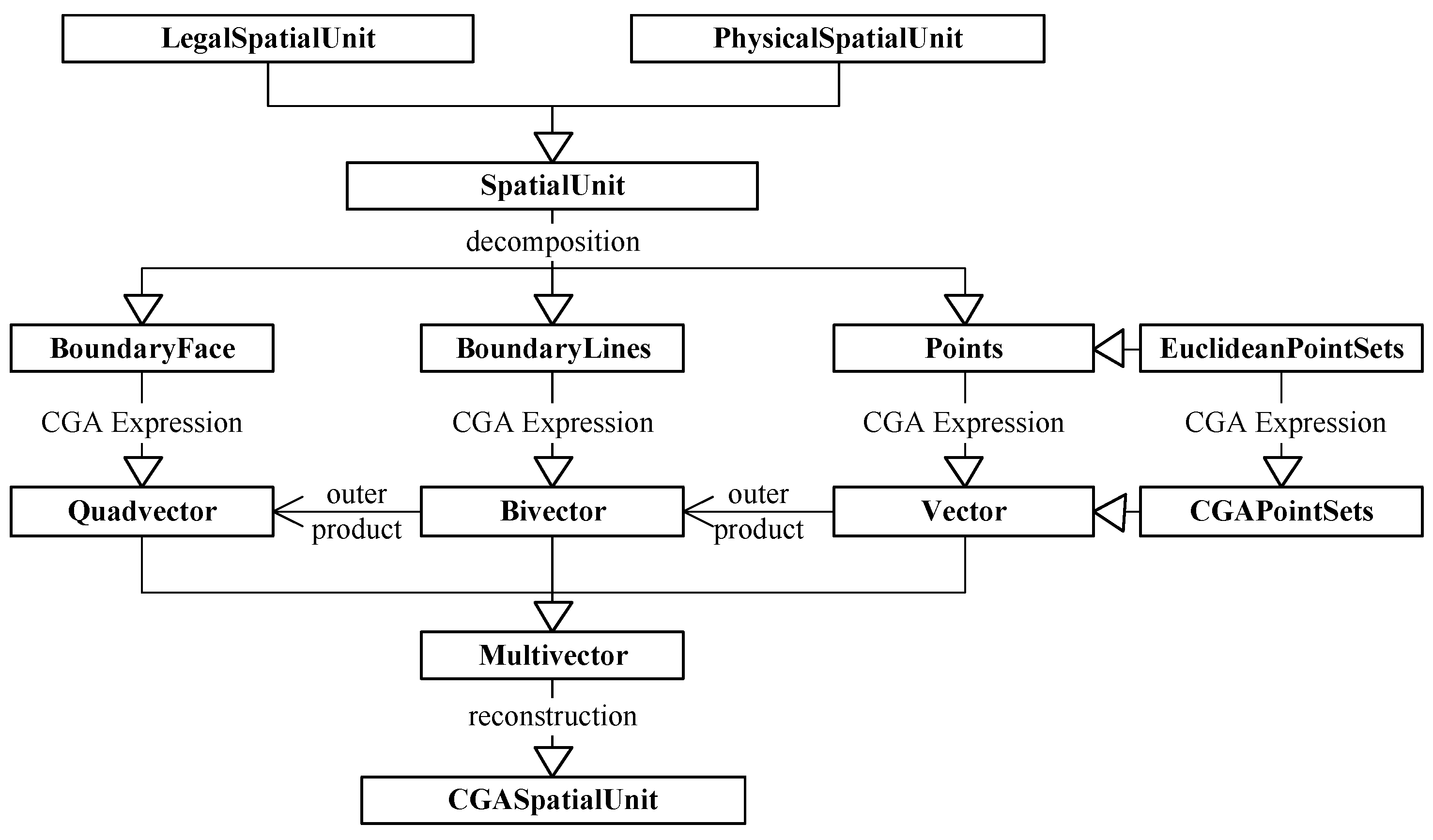
45] is discussed. Second, the concept and scope of a 3D cadastral spatial unit are defined as semantics. Third, a method to realize a unified multidimensional expression of geometry and topology for 3D cadastral objects, which is based on CGA, is introduced. We obtained a 3D cadastral spatial unit from the abstraction of both the legal and physical levels of the 3D cadastral objects. The 3D cadastral spatial unit is decomposed to obtain a series of geometric simplexes, which can be represented by different dimensional blades in CGA. To achieve the multidimensional expression for the complex 3D cadastral spatial unit, the multivector, which is a spatial mathematical structure in CGA, is employed. The 3D cadastral data model, which is based on CGA, is shown in
Figure 3. Last, the structure of 3D cadastral spatial unit data storage organization in CGA is designed.
3.2.1. Initial Conditions
The Land Administration Domain Model (LADM), which includes a 3D cadastre, is a conceptual model for cadastral management [
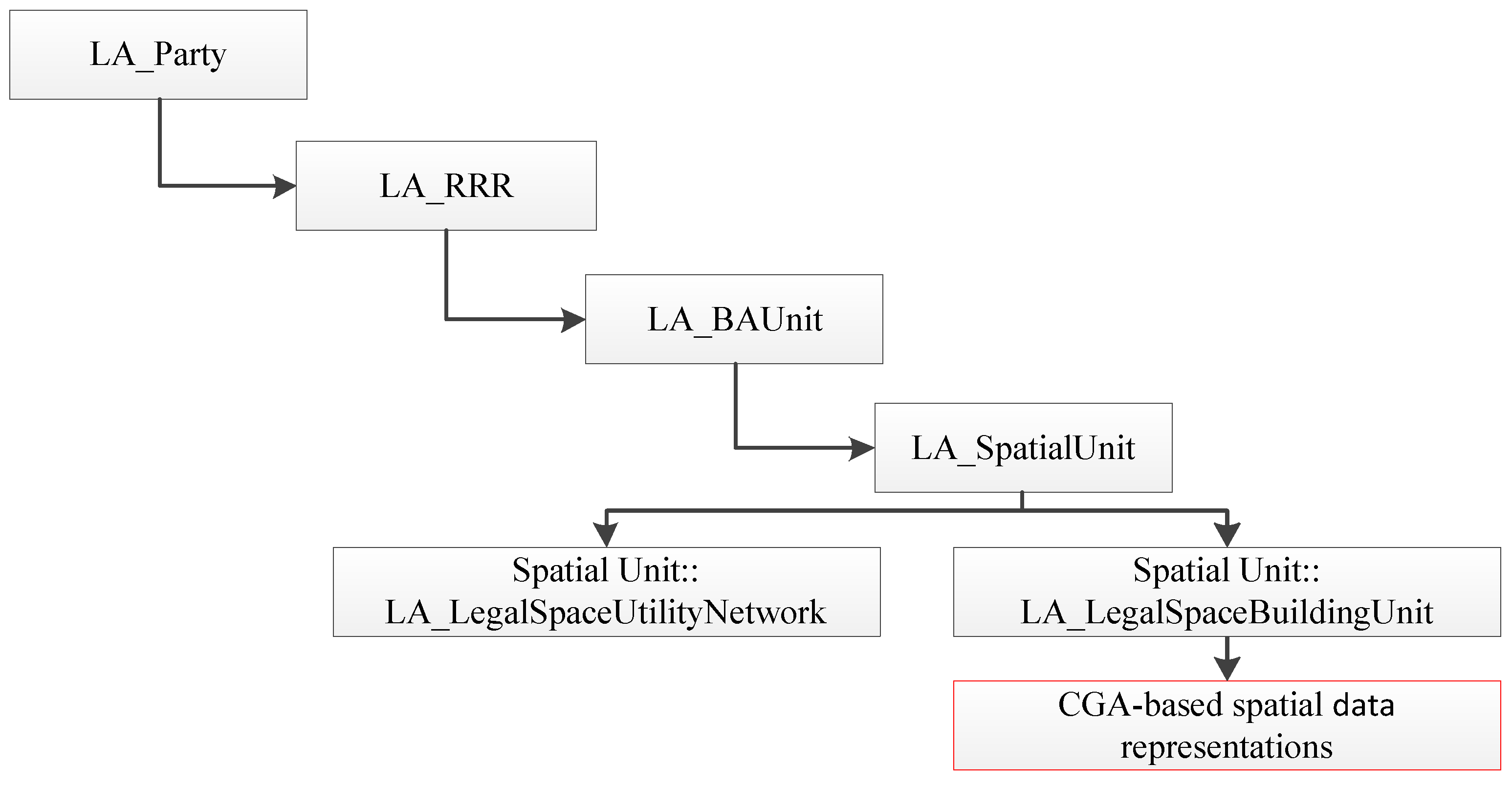
46]. The LADM has obtained the certification of the International Organization for Standardization (ISO). The LADM contains four parts, as shown in
Figure 4: a party (LA_Party); rights, restrictions, responsibilities (LA_RRR); a basic administrative unit (LA_BAUnit); and a spatial unit (LA_SpatialUnit). The main research contents of this paper belongs to the spatial unit in the LADM. It is primarily based on CGA theory to investigate data organization and the relationship between geometry and topology, which is integrated in the expression for 3D spatial units. The construction of a 3D cadastral data model that is based on CGA is an extension of the spatial units in the LADM. The relationship between the CGA-based data model and the LADM is depicted in
Figure 4.
Prior to building a 3D cadastral data model, a description of the concept of a basic unit in a 3D cadastre—the 3D cadastral spatial unit—is needed. A 3D cadastral spatial unit is a combined object that is abstracted from a legal object and a 3D physical object in the real world. It is the smallest unit in 3D cadastral management. From a legal perspective, a 3D cadastral spatial unit is a closed 3D space with legally binding and distinct 3D boundaries. The difference among ownership rights is the main criterion for distinguishing the boundary of a cadastral spatial unit. The internal consistency of ownership rights is the premise of 3D cadastral management. From the point of view of real physical objects, 3D cadastral spatial units comprise the abstract expression of a realistic 3D cadastral management object according to the needs of cadastral management. 3D spatial units of physical objects can be an independent building that is located on, below, or above ground. It can also be a semi-enclosed building (e.g., a sports stadium) that needs to be abstracted to obtain the 3D ownership boundary according to relative cadastral laws. 3D spatial units may simultaneously contain many buildings with identical ownership, such as a factory spatial unit that contains multiple workshops or a villa that contains houses, courtyards and an underground garage.
3.2.2. 3D Cadastral Object Reconstruction in CGA
The premise of a 3D cadastral data model is the abstract expression of 3D cadastral entities in the real world. The geometric decomposition of complex 3D cadastral objects is needed to organize and store these objects in a cadastral database. The representation of a current 3D cadastral data model and cadastral requirements for distinct boundary ownership are both considered in 3D cadastral object decomposition. In this paper, 3D cadastral objects can be decomposed into four geometric objects as follows: points, lines, surfaces, and spatial units. By further decomposition of these geometric objects, we obtain three types of basic geometric primitives: nodes, boundary lines, and boundary faces.
The complex 3D cadastral objects are represented by these different dimensional basic primitives, which should be expressed in CGA to realize a consistent representation form. Different dimensional basic geometric simplexes in CGA can be directly constructed by the outer product of conformal point sets, which is illustrated in
Table 1. However, these simplexes in
Table 1 do not have boundary constraints, which are very important in cadastral registration and management. Boundary limitations for these basic simplexes, which are expressed by conformal point sets, are needed to accurately describe the boundaries of 3D cadastral objects. The coordinates of these point sets can be employed to limit the boundaries of corresponding geometric objects, which is defined as follows:
Definition 3: If
is a basic geometric primitive of the k-dimensional subspace in
and
denotes the conformal point sets that compose
, then the geometric representation of
by the outer product can be defined as follows:
where n is the number of points that compose
.
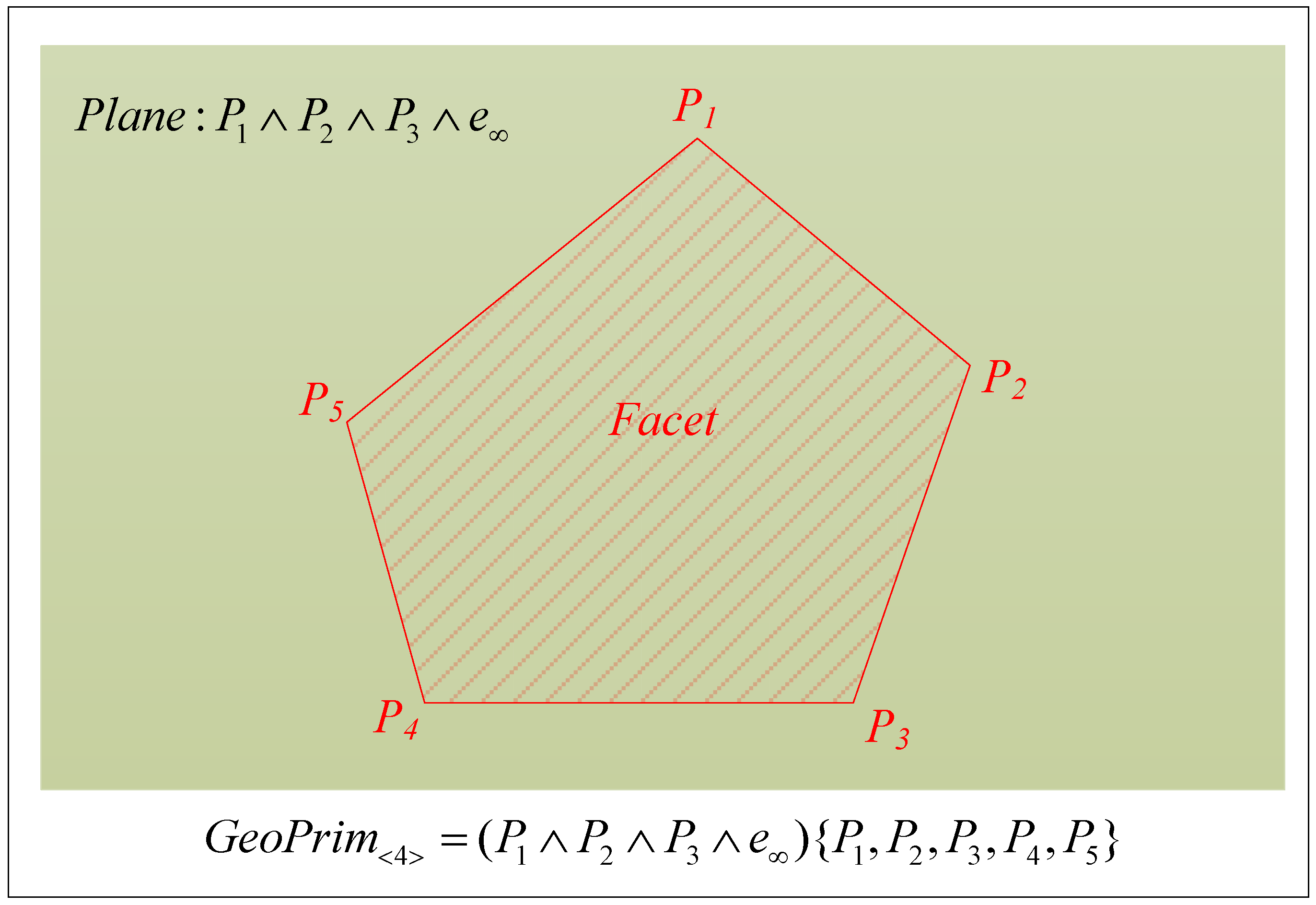
Consider a primitive facet that is composed of five points, as shown in
Figure 5. The plane that contains the facet in
can be represented by
, whereas the boundary of the facet is restricted by the five composing points.
Figure 5 and the definition of
indicate that the basic geometric simplexes are directly represented by the outer product of conformal point sets. The geometric ranges of these simplexes are restricted by the sequence of point sets that compose the corresponding boundary simplexes. In this manner, we realize the accurate and united representation for different dimensional simplexes in CGA. Complex geometric objects in CGA can be expressed by integrating different dimensional simplexes. To realize the expression of complex 3D cadastral objects as an entity, the mathematical structure of a multivector in CGA is employed to realize the unified expression of multidimensional simplexes, which is defined as follows:
Definition 4: If
is an arbitrary 3D cadastral spatial unit in CGA
, the geometry and topology of this 3D cadastral object can be expressed by the following algebraic formula in CGA
where
are simplex sets that compose
.
It should be noted that , and are not used in cadastral spatial representations. As represents scalars, it is useless in cadastral spatial representations. The characteristics of cannot accurately express a cadastral boundary because it can be represented by either an arc or a segment. In cadastral management, is not used to express any cadastral unit directly. Instead, lower-dimensional elements are used to define the cadastral boundary accurately.
According to the definition of the algebraic representation formula for a 3D cadastral spatial unit, the 3D cadastral spatial unit is a multidimensional unified structure. All components of the 3D cadastral spatial unit, such as points, boundary lines and boundary faces, are integrated in the multivector structure. The geometric information about the 3D cadastral object is represented by integrating all the different dimensional components that compose it. The topological structure of the 3D cadastral object is expressed by the dimensional construction structure contained in the multivector structure. This manner of multidimensional fusion expression of geometric objects with different dimensions realizes the integrated multidimensional expression for the geometry and topology of a 3D cadastral spatial unit.
The construction process of a 3D cadastral data model that is based on CGA reflects a distinct topological hierarchy relationship among different dimensional geometry objects. A cuboid is selected to represent a 3D cadastral spatial unit, which is illustrated in
Figure 6. The construction process of the multidimensional unified expression for the 3D cadastral object is described. The 3D cadastral object, which is represented by the multivector structure, is a complex structure that is composed of points, boundary lines and boundary facets. All components that are contained in the multivector are independent. Topological relations among different dimensional components are obtained in the process of different dimensional, geometric and simplex constructions by the outer product. The 3D cadastral spatial unit is at the top of the hierarchical structure.
3.3. 3D Cadastral Data Organization Based on CGA in A Database
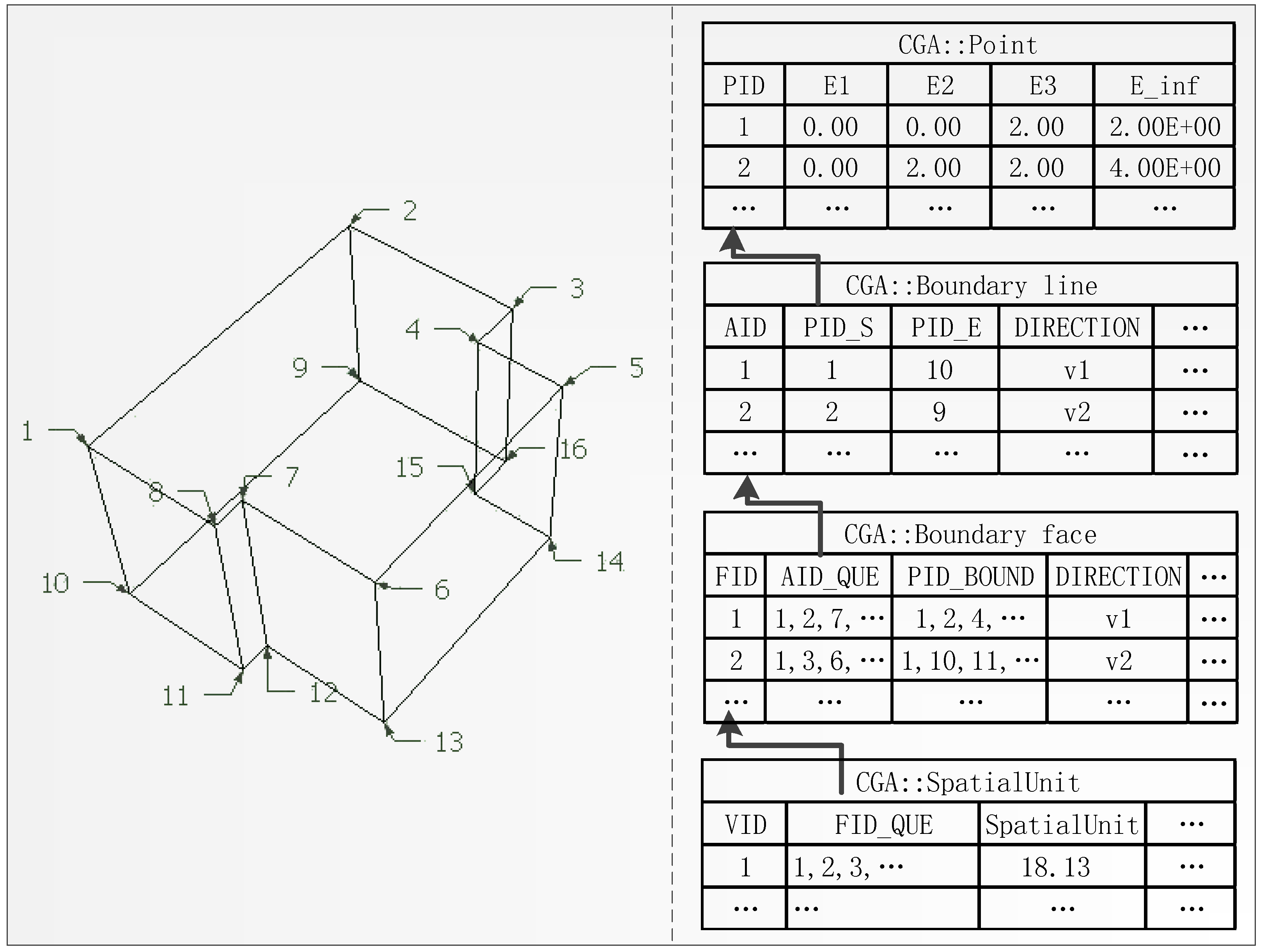
The 3D cadastral data structure based on CGA is organized in a cadastral database, as shown in
Figure 7. The data storage contains four types of data, including points, boundary lines, boundary faces and spatial units. The conformal point sets that compose the left 3D cadastral spatial unit in
Figure 7 can be obtained from Euclidean point sets by embedding in CGA. Because the conformal space contains five basis vectors, the coordinates x, y and z of the original point become coefficients of the basis vector
, respectively. Because normally the coefficient of
is the constant 1, it is not stored in the point table and the coefficient of
can be computed with the Euclidean coordinates x, y and z [
41]. Because different dimensional geometric objects can be constructed from conformal point sets by the outer product, only the original coordinates are stored in the point table. The boundary line and the boundary face tables store point IDs, which are employed in connection with the point table. Relative point IDs are stored in both the boundary line and boundary face tables in a specified order to define the range of corresponding objects. To ensure compatibility with the existing method in which lines form facets, the boundary line IDs that compose boundary faces are also stored in the corresponding boundary face table. Direction information about boundary lines and boundary faces are stored in each table in the form of a vector. The 3D cadastral spatial unit is organized by storing the constituent boundary face IDs.
The characteristics of the 3D cadastral data organization and correlation method are similar to the characteristics of the multivector structure, which is not only a mathematical structure but also a data storage structure. Based on the design of point, boundary line, boundary face and spatial unit data storage structures, conformal points and lines are stored in the boundary face table. Boundary faces, which are employed to construct the 3D cadastral spatial unit, can be represented by outer products with conformal point sets, as shown in definition 3, or represented by the boundary line ID that belongs to the boundary face. Similar to the multivector structure that integrates different dimensional objects, the boundary face table also contains all primitives that are employed to compose the table. These characteristics are also listed in the spatial unit table, which stores boundary face IDs to realize multidimensional object storage. In this manner of data organization, the complex 3D cadastral spatial unit can be easily expressed and stored in the multivector structure. The topological relations among different dimensional constructed objects can be clearly described in the hierarchical data storage and the multivector structure, whereas the geometric information can be represented within the multivector by the outer product. The geometry and topology of 3D cadastral objects can be expressed in a multidimensional unified form that is integrated in the multivector structure.
4. Case Studies
Cadastral data for an urban residential community in Xuzhou, Jiangsu province, are selected as the experimental data in our case study. The experimental data includes 17,618 points, 28,487 boundary lines, 9,462 boundary faces and 1,484 buildings. These building models are imported into the software system CAUSTA [
32]. The data model is implemented as a plug of the system CAUSTA. To ensure compatibility with GA-based operations, the experimental data are reorganized in CaVector data formats for the storage structure. The storage structure is subsequently assembled according to the multivector structure. With these transformations and organizations, we can manage the 3D cadastral spatial units in CAUSTA. The demonstrations are performed in the hardware environment of a Lenovo E420 notebook with a 2.4-GHz Intel Core i5-2430M CPU and 4 GB of RAM. The software environment is a Windows 7 operating system with Visual Studio 2008.
Conventional 3D cadastral data models, which are based on a simplified spatial model (SSM) [
18] and an object-oriented 3D GIS model (OO3D) [
46], have been selected to make a comparison with the performance of a CGA-based cadastral data model. The results for memory requirements and response time in 3D visualization for the SSM, OO3D and CGA-based data models are listed in
Table 2. The comparison results indicate that the CGA-based data model performs more efficiently than the SSM data model concerning response time and memory occupancy. Although data storage in the CGA-based data model occupies less memory than the OO3D data model, it has a slightly longer response time than the OO3D data model.
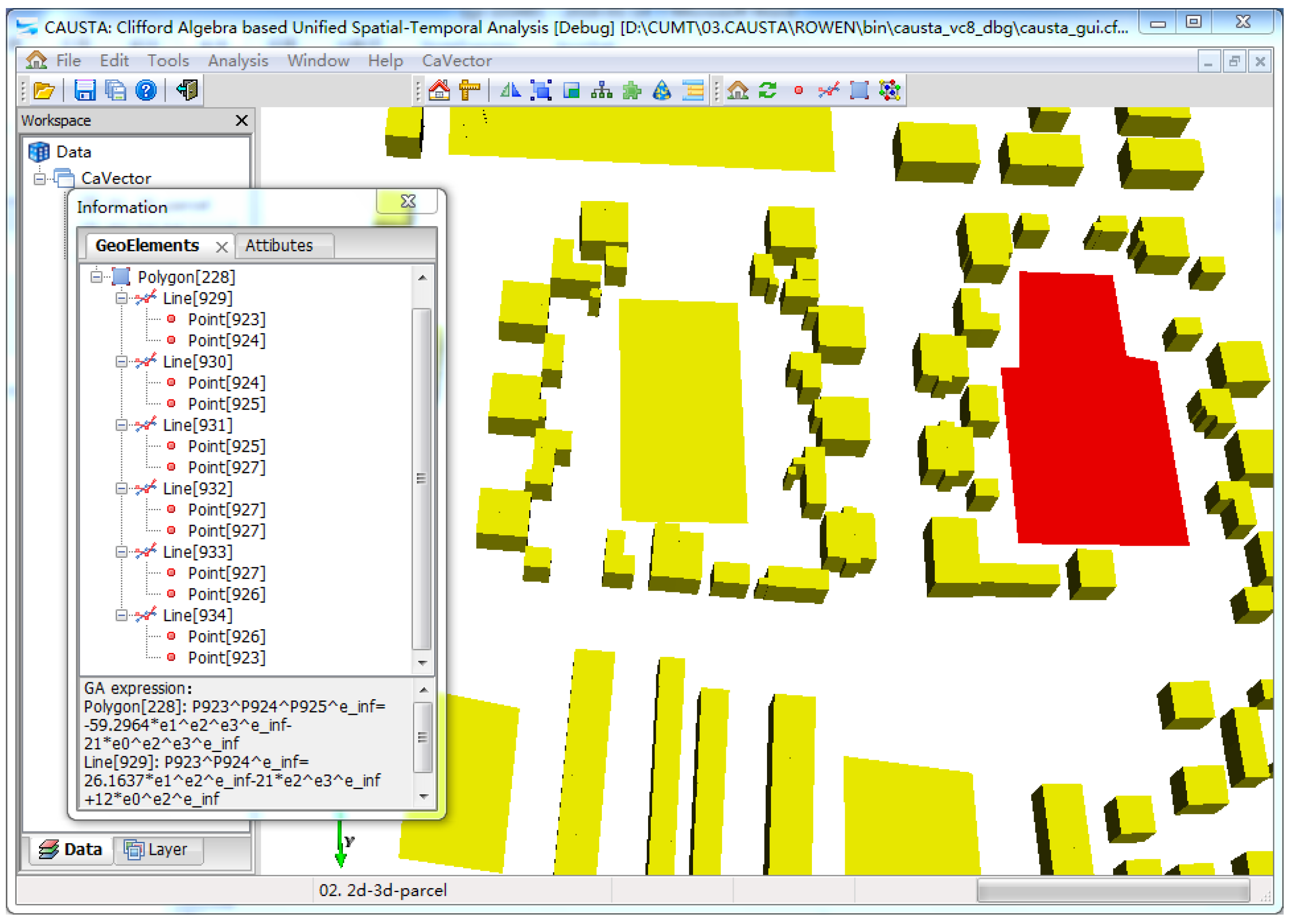
The geometric and algebraic representation of 3D spatial units in the CGA-based 3D cadastral data model are displayed in
Figure 8. The representation and organization of the spatial units differ from the representation in Euclidean space. In the CGA representation, the dimensional structures of objects are represented according to the hierarchical Grassmann structure.
Figure 8 shows the algebraic equations for each spatial unit, which are constructed by the outer product. Different dimensional geometry objects, such as the lines and planes shown in
Figure 8, can be uniformly expressed with the outer product in CGA. In Euclidean space, representations of geometry objects are primarily based on coordinates, which causes problems such as complicated expression structure, non-uniform expression form in different dimensions, and unclear geometry meaning [
47]. Geometric objects are expressed in CGA, and the outer product differs from the traditional methods, which are based on Euclidean geometry. Geometric objects that are represented by the outer product not only support uniform expression among different dimensions but also propose a simpler construction structure and clearer geometric meanings for the geometric object expression of different dimensions. These advantages can be applied to represent complex 3D geometric objects, as shown in
Figure 9.
With the unified expression form for geometric objects of different dimensions, geometric information and topological relations of complex cadastral objects can be represented within the multivector structure in CGA. One of the 3D cadastral objects was selected to demonstrate how to represent complex cadastral objects with the multivector structure, as illustrated in
Figure 9. Compared with the separate expression of different dimensional geometric objects in Euclidean space, all dimensional elements that comprise the 3D cadastral objects are multidimensional and integrated in the multivector structure. Geometric information about cadastral objects is expressed by an algebraic formula with hybrid dimensional components, and topological relations among different dimensional components can be represented in the distinct dimensional hierarchy. The geometric information and topological relationships of a cadastral object can be expressed in the multidimensional multivector structure in a unified manner, which distinguishes our method from existing approaches based on Euclidean geometry. The multidimensional unified method for the geometry and topology provide a flexible and convincing method for topological relations analysis and geo-object updating [
30,
34].
Compared with existing 3D cadastral data models that are based on Euclidean geometry, the data model that is based on CGA realizes a geometrically and topologically multidimensional unified expression for 3D cadastral objects. A 3D cadastral data model that is based on CGA provides a compact and geometrically distinct method for representing cadastral objects in a cadastral database. Multidimensional construction elements are integrated in a multivector structure to express 3D cadastral objects, which enables the spatial unit to be handled as an entity in topological and spatial analysis [
31,
32,
34]. With the advantage of the outer product in the representation of dimensional objects, cadastral objects can be directly and simply expressed. All dimensional components of 3D cadastral objects can be expressed within a multivector structure. In addition, a multivector structure can be employed to express cadastral objects and provides a hierarchical data storage form, which is helpful in organizing 3D cadastral data in a database.
5. Discussion
In this paper, we introduce the theory of CGA to 3D cadastral data modeling to solve problems with spatial representations that are encountered in the extension from a 2D cadastre to a 3D cadastre. With the advantages of CGA in geometric representation, expression forms for both 2D and 3D spatial units have been united in an algebraic manner. The geometric information and topological relations of spatial units have also been integrated into the algebraic expressions. In CGA, different dimensional objects are uniformly represented using outer products, which enables a direct and intuitive extension of spatial representations from 2D structures to 3D structures. The multivector structure is subsequently employed to algebraically integrate the multidimensional geometric components for complex 3D spatial units as entities. The geometries and topological relations of spatial units are represented in a unified manner in the form of algebraic expressions. With the development of a CGA-based 3D cadastral data model, the representations of spatial units in the 3D cadastral database not only have distinct geometric meanings but also combine the representations of the geometries and the topological relations. The CGA-based 3D cadastral data model also unifies the representation of multidimensional objects in the same representation form. Therefore, direct, compact and unified representations of objects are feasible.
In this paper, we primarily focus on a unified expression form between 2D spatial units and 3D spatial units and the integration of geometry and topology for spatial units. However, cadastral registration and transaction data may update daily, which indicates that the time component of cadastral data should be considered in 3D cadastre development. A method for the construction of a spatio-temporal cadastral data model will be a future research topic. The integrated updating of both the geometries and the topological relations remains complex. Although the computation ability of CGA is very powerful, we did not discuss the spatial analysis and updating of 3D cadastral objects using GA operators or algorithms. For example, the division and combination of the spatial units in the 3D cadastre can be achieved with the intersection product in CGA [
31] because the geometric construction in CGA is coordinate-free,
i.e., the geometries can be adaptively modified according to the relative construction structures that are related to the dimensional structures and the topological relations. The complete utilization of these advantages in CGA to develop an integrated data updating method that updates both the geometries and topological relations in the integrated framework is also an important objective of future studies. The topological relations computations are potentially more complete than the classical 9IM model for 3D triangles using the CGA model [
35]. Because the 3D cadastral model is the foundation of the data representation, the construction of the analysis using the CGA operators is simple and direct. This topic is another potential direction for CGA-based 3D cadastre development.