Typification for Façade Structures Based on User Perception

1. Introduction

Generalization of building objects has been a topic in recent years because (1) the efficient rendering of building objects requires representation of buildings at different levels of detail (LoDs); and (2) for the visualization of buildings on small display devices such as mobile phones, PDAs, etc., abstractive buildings models have to be generated.

Since Staufenbiel [1] proposed a rule-based approach for the simplification of 2D building ground plan, a number of algorithms have been made available for generalization of building models. The early works focused on developing techniques for generalizing building ground plans in 2D [2,3,4,5]. Using these techniques, the amount of detail in the ground plan can be reduced by removing line segments with some criteria, i.e., minimum length of a façade. For instance, Sester [6] proposed a two-step procedure: (1) removing the minimal forms guides by rules; and (2) adjusting the form of the simplified building to the original form using least-squares adjustment. In this second step, certain characteristics of the buildings can be preserved or even emphasized, e.g., rectangularity and parallelism or size. Other approaches apply methods of pattern recognition to replace the original ground plan with a standard shape [7].

In the recent years, a number of algorithms have been proposed specifically for the generalization of 3D building models. Lal and Meng [8] defined some rules and constraints for 3D generalization. However, the generalization is restricted on one operation, namely, aggregation. Kada [9] extended Sester’s approach [6]. He developed rules to remove structures that were too small in the 3D polyhedron at first then adjust the simplified building to its original shape.

On the basis of the polyhedron segmentation proposed by Ribelles et al. [10], Thiemann and his colleagues suggested decomposing a building into basic 3D primitives and eliminating those with small volumes [11,12]. Kada [13,14] proposed a structurally similar approach. He defined parts of simplified buildings as intersections of half-planes based on which cell decomposition and primitive instancing are applied. More related research can be found in [15,16].

The above mentioned studies focus mainly on simplification of buildings by removing smaller wall elements. The features on building façades are seldom concerned, but they also need generalization e.g., windows need to be enlarged so that they are legible in a reduced display space. However, enlargement may cause feature overlaps. Typification may be used to circumvent this problem. On the other hand, with the further shrinkage of display space, buildings have to be generalized in groups. For this case, the operation of typification is preferred when buildings are distributed regularly [15].

The operator of typification is defined as a process of replacing a large number of objects with a smaller number of uniformly shaped objects while preserving the appropriate characteristics of the pattern. Regarding the approach for typification, in [17], every four polygons neighboring each other were replaced by a new polygon created by connecting the center points of the four polygons. Regnauld’s typification algorithm [4] was based on the minimum spanning tree in graph theory. In [18] the procedure of typification was divided into two steps: positioning and representation, while the positioning step determines the number and the positions of the buildings based on Delaunay triangulation, in the representation step the size and orientation for the replacement will be calculated. Besides, most previous works like [19,20,21,22] determined the density of objects using Tröpfer’s radical law [23]. Furthermore, this kind of operation was used in many literatures for generalization and various results were presented in [5,11,14,24]. However, it is not discussed why their results are reasonable. Meanwhile, there exists a similar problem in the field of computer science. For layout management of Graphical User Interface (GUIs) in graphics, typification is used to rearrange buttons (or icons) with the changing size of GUIs for different devices or scales. A number of algorithms are currently available for this issue; for instance, Luyten et al. [25] described a method to combine abstract User Interface (UI) descriptions and constraint-based layout management system for different devices. Unfortunately, there is no investigation of finding a reasonable result of typfication either.

In our work a user survey has been conducted to find out what kind of representation after typification is best associated to the original dataset with respect to the human visual perception. In order to verify the results of the user survey, Attributed Relational Graphs (ARGs) are generated from the original dataset and the candidate representation after typification. Then the Nested Structure of Earth Mover’s Distance (NEMD) [26] between these ARGs is calculated. The NEMD values denote the similarities between the typified façades and the original façades and can be regarded as a quantitative measure to guide the automatic approach of typification.

The rest of the paper is structured as follows: the user survey for typification is presented in Section 2 at first. In Section 3, the ARG and NEMD algorithms are described in order to verify the results of the user survey. The automatic approach of typification based on the results of our user survey is elicited in Section 4 with the experimental results shown in Section 5. Finally, the conclusion and work to be done in the future are given in Section 6.

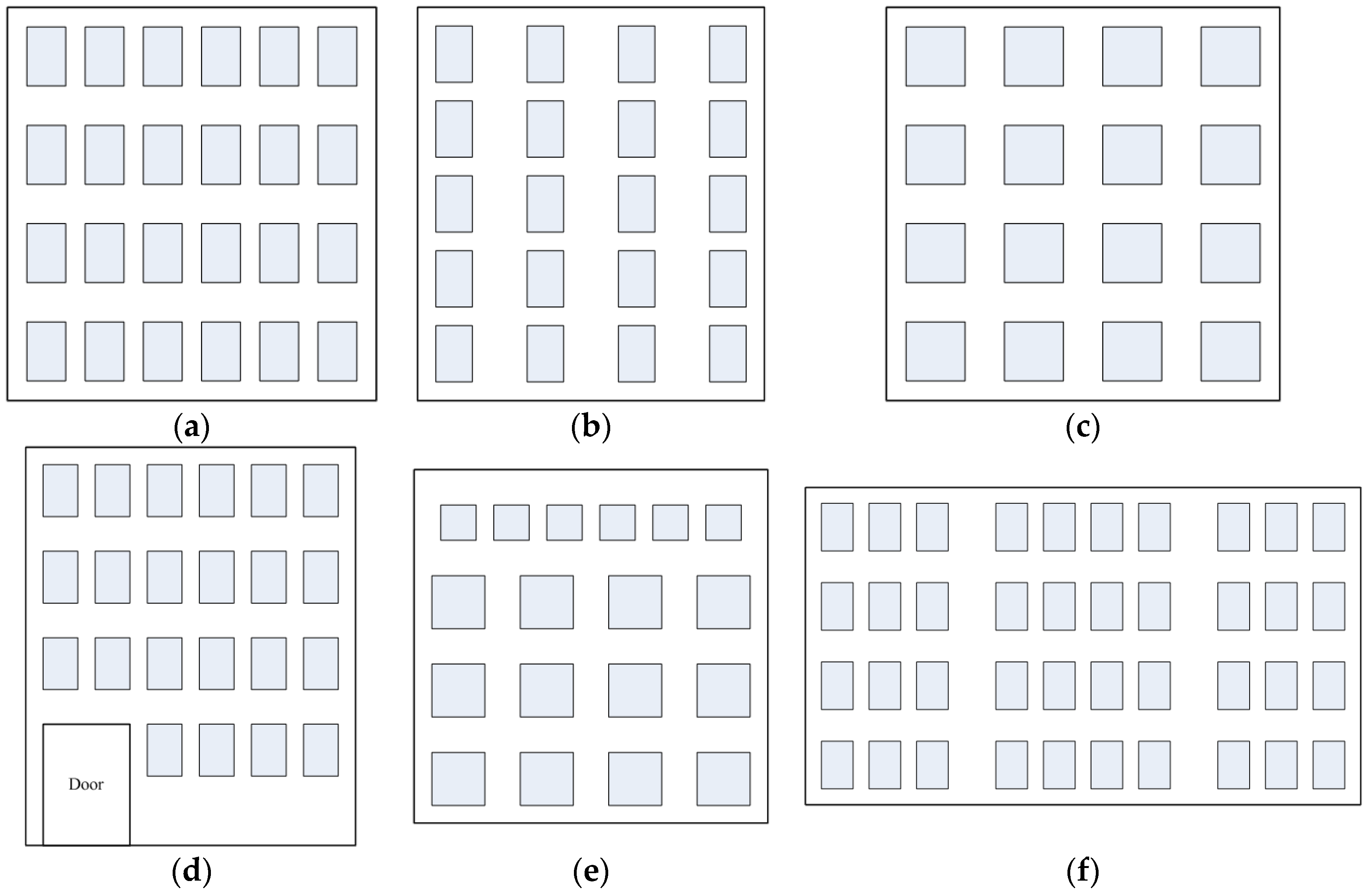
2. A User Survey for Typification

2.1. Constraints of Typification

The user survey is focused on the analysis of building façades with windows, since windows are the most common structures on façades. Moreover, windows on a façade are in most cases uniform in shape and size, and distributed regularly. In the user survey, the different constraints are identified which contribute to the preservation of the similarity between the typified façade and the original one:

• keeping the area covered by windows,
• keeping the ratio between the height and the width of the windows,
• keeping the distances between windows,
• keeping the distances between windows and the outline of the façade,
• keeping windows distributed in the tendency direction.

By combining the above constraints, we developed different options for typification which lay down a base for the user test with the aim of identifying the most reasonable typification. Figure 1 shows an example façade with regularly distributed windows, and different options of typification are demonstrated in Figure 2.

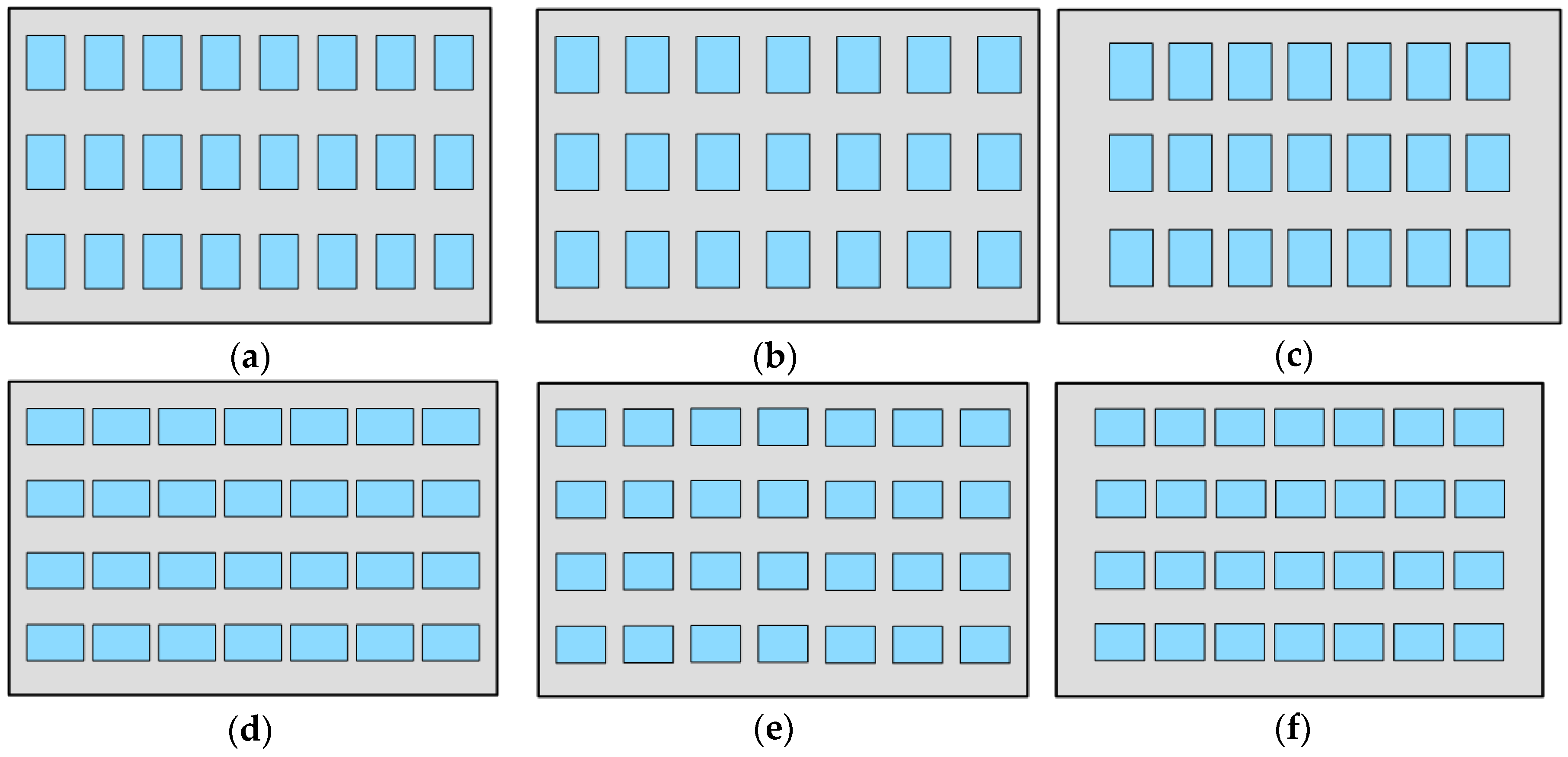
2.2. User Survey and the Results

The six options are applied to three different façades (Figure 3) including the one (b) presented in Figure 1. These façades have different tendency directions or they have no directions which tend to stay in the foreground. Façade (a) has no tendency direction. The distances between windows in horizontal and vertical direction are almost equal. Façade (b) has a tendency in the horizontal direction because the distances between windows in horizontal direction are smaller than that in vertical direction. Façade (c) has its tendency in the vertical direction. The distances between windows in the vertical direction are smaller than that in the horizontal direction.

All three façades have regular distribution of a gridiron pattern. We extracted them to a vector-based representation and typified them to six candidates corresponding to the six options in Section 2.1. We also designed several visualizations with appropriate questions for the participants to conduct the user test. These visualizations are visually coded and the participants are unaware of which constraints are used during the typification. An example of a question is: please rank the images in the order in which they will resemble the original image. For every question two or three options are compared with each other. The participants have to rank the façades in the order (from best to worst); in other words they should say which kind of typification is best associated to the original extracted façade and which is their second and third choice.

The user survey was carried out during a lecture on the 12 November 2008 at the Technische Universität München. The subjects consist of 9 female and 12 male undergraduate students majoring in geodesy. Their ages ranged from 19 to 26 years. Each subject was given 15 s to look at the extracted windows and their typification options. Then they have to make their decision.

The results of the user survey are summarized and averaged for the three façades (

Table 1. Average values for the six options.

Options	1	2	3	4	5	6
Values	8.72	6.45	6.14	6.67	7.54	5.50

). These values indicate at which degree the six options (Figure 2) can be associated to the original façade.

Table 1 reflects the similarities of the six options to the original façade. We assume that the more similar the option is to the original façade, the more significant the constraints (compare Figure 2) deployed for the corresponding option are. The significance degrees of the constraints (Section 2.1) for the typification are calculated. They are weighted and normalized by 10 to make the results more comparable.

Table 2. Results of the user test for typification in decreasing order of significance.

	Value	Constraint
more significant less significant	10.0	Keeping ratio of height and width of the windows
	7.0	Keeping the distances between windows and the outline of the façade, and keeping the distances among windows at the same time
	5.3	Keeping the distances between windows and the outline of the façade
	4.7	Keeping the distances between windows
	4.6	Typification in tendency direction
	3.9	Keeping the area covered by windows

shows the declining significance values of the options. This may underpin the assumption that keeping the shape of the façade elements (shape conformal) is the most significant. The second significant constraint is to keep the distances among windows, and keep the distances between windows and the outline of façade at the same time. This finding will be used in similarity quantization with ARG and NEMD in the subsequent section.

3. Verification of the User Survey Using ARG and NEMD Algorithm

To quantify the visual similarity between façades, pattern recognition methods are employed. Attributed Relational Graph (ARG) has been widely used to represent objects or structures to be recognized in computer vision and pattern recognition [27]. In this paper, ARG is used to represent windows of the façade. Therefore the visual similarity evaluation between the typified façade and the original one can be quantified by matching their ARGs. Lots of algorithms are proposed for ARG matching such as the graduated assignment graph matching (GAGM) [28], and least squares graph matching (LSGM) [29]. The Nested Earth Mover’s Distance (NEMD) algorithm is chosen since it shows a better performance in ARG matching according to the results in [26].

An ARG G is defined as G = {V,R} in which V = {v_i|1 ≤ I ≤ n} and R = {r_ij|1 ≤ I ≤ n, 1 ≤ j ≤ n}. V is the set of n nodes and each v_i represents a window in the façade. R is an $n\times n$ matrix and each r_ij is the relationship between the window v_i and v_j. In this application the node contains attributes about the window such as width and height and the relationship between nodes will represent the spatial and topological relations between the windows on the façade.

The ARG matching can be implemented as a two-step procedure, constructing a distance matrix and establishing the correspondence based on the distance matrix. More specifically, NEMD consists of inner EMD (Earth Mover’s Distance) and outer EMD. The inner EMD reflects the difference between corresponding nodes from two ARGs. The outer EMD is composed of inner EMD distances of all node pairs, and we can establish the correspondence between nodes in the two ARGs and get the distance of the two ARGs by selecting and adding the minimum element in each column or row of outer EMD. The details about NEMD calculation is given in [26,30].

A simplified example of NEMD calculation of 2 ARGs shown in Figure 4 is given by Kim et al. 2004. The difference between the example in Figure 4 and the method proposed for generalization evaluation is the definition of distance between nodes and relationships. In order to simplify the calculation, the node feature only contains one figure and the distance between the nodes is the difference value of their figures. It is the same for the relationships in Figure 4. For quality assessment, we just replace the distance functions Δnode and Δrelation in Equation (1) with the functions defined in Section 3.2.

$${\Delta }_{inner}(j,j\prime )=(1-\alpha )\times {\Delta }_{\mathrm{node}}(v_j,{v^{\prime }}_{j^{\prime }})+\alpha \times {\Delta }_{\mathrm{relation}}(r_{ij},{r^{\prime }}_{i^{\prime }{j}^{\prime }})$$

(1)

In Figure 4, G’ is the sub-graph of G with nodes 1, 2, 3 in G’ corresponding to nodes 4, 2, 1 in G. The distance between nodes and distance between the relationships are the differences of their values given in Figure 4.

First, the inner EMD between every pair of nodes in G and G’ is calculated from inner matrix D_inner, in which every element is generated from Equation (1). For example, the D_inner of node v₁ in G and v’₁ in G’ (v_i and v’_i’) is given in Equation (3), in which the 1st row and 2nd column of inner matrix D_inner, Δ_inner(1, 2) can be calculated with Equation (2).

$${\Delta }_{inner}(1,2)=(1-\alpha )\times {\Delta }_{\mathrm{node}}(v_1,{v^{\prime }}_2)+\alpha \times {\Delta }_{\mathrm{relation}}(r_{11},{r^{\prime }}_{12})$$

(2)

In which, I = 1, I’ = 1, j = 1, j’ = 2, Δ_node(v₁, v’₂) = |0.8 − 0.3| = 0.5, Δ_relation(r₁₁,r’₁₂) = |0 − 0.2| = 0.2, α = 0.5. Therefore, Δ_inner(1, 2) = 0.35. Similarly, we can calculate all Δ_inner(j, j’) and compose the D_inner for the node pair v₁ and v’₁ as shown in Equation (3). Based on that, the inner EMD of node v₁ in G and v’₁ in G’ is 0.1 + 0.3 + 0.35 = 0.75 (the minimum sum of minimum value in each column or row).

The D_outer of G and G’ is also given in Equation (3), in which the first element is 0.75 according to previous calculation. The EMD between G and G’ is 0 based on the D_outer, because G’ is the sub graph of G. But in our application, not only partial but also overall difference between ARGs should be considered. Therefore, the difference between two ARGs is the maximum sum of the minimum value in each column or row of the D_outer, e.g., 0.05 for G and G’ in Figure 4.

$$D_{inner}(v_1,{v^{\prime }}_1)=\left[\begin{array}{ccc}0.35& 0.35& 0.35\\ 0.5& 0.3& 0.3\\ 0.7& 0.5& 0.1\\ 0.35& 0.35& 0.35\end{array}\right],D_{outer}=\left[\begin{array}{ccc}0.75& 0.65& 0\\ 0.25& 0& 0.75\\ 0.65& 0.55& 0.05\\ 0& 0.25& 0.95\end{array}\right]$$

(3)

This rest of the section focuses on creating the ARG of façade and constructing the distance matrix of nodes and relations.

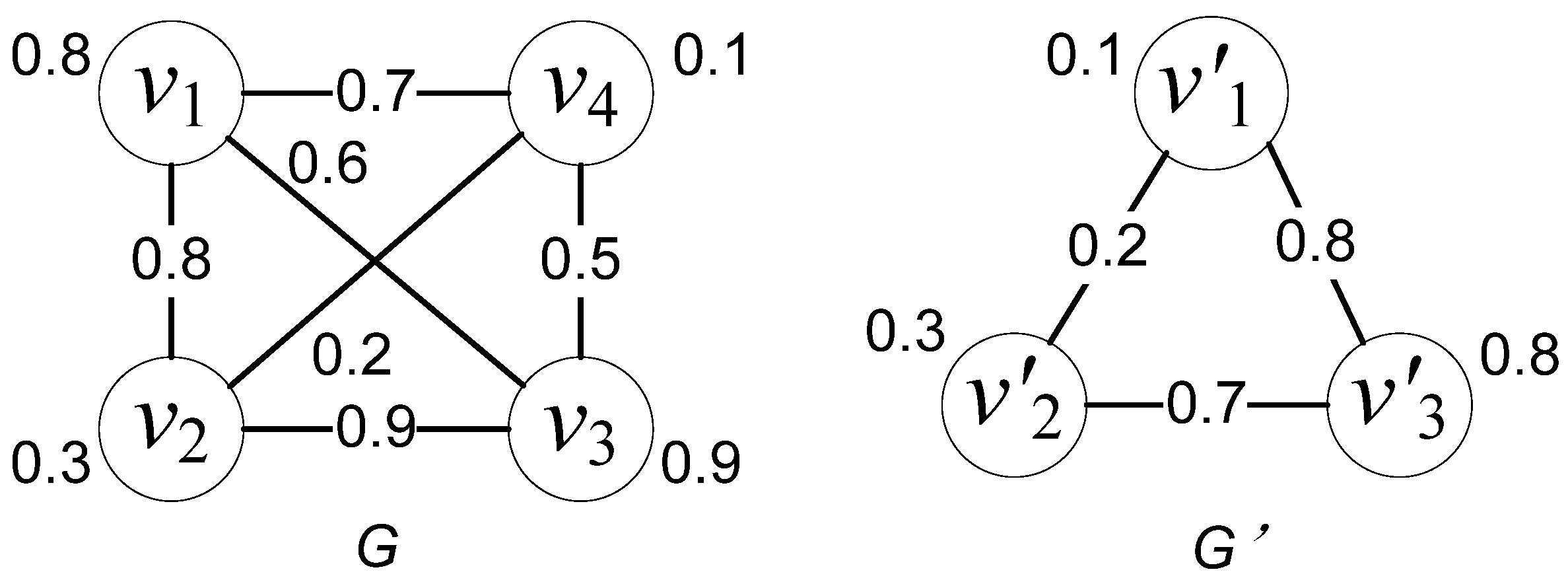
3.1. ARG Generation

Since windows are all rectangles in our test façade data, the width and height of the window are saved as attributes of the node. v_i = (w_i, h_i) in which is v_i represent the i-th window in the façade; w_i and h_i are the width and height of the window. The relationship between two windows is set to the ratio of the distance between two polygons of the windows and their area sum. However, absolute distance alone is not sufficient to reflect the visual relationship between two windows on the façade since two large windows would look more similar to each other than two smaller ones even if they have same distance.

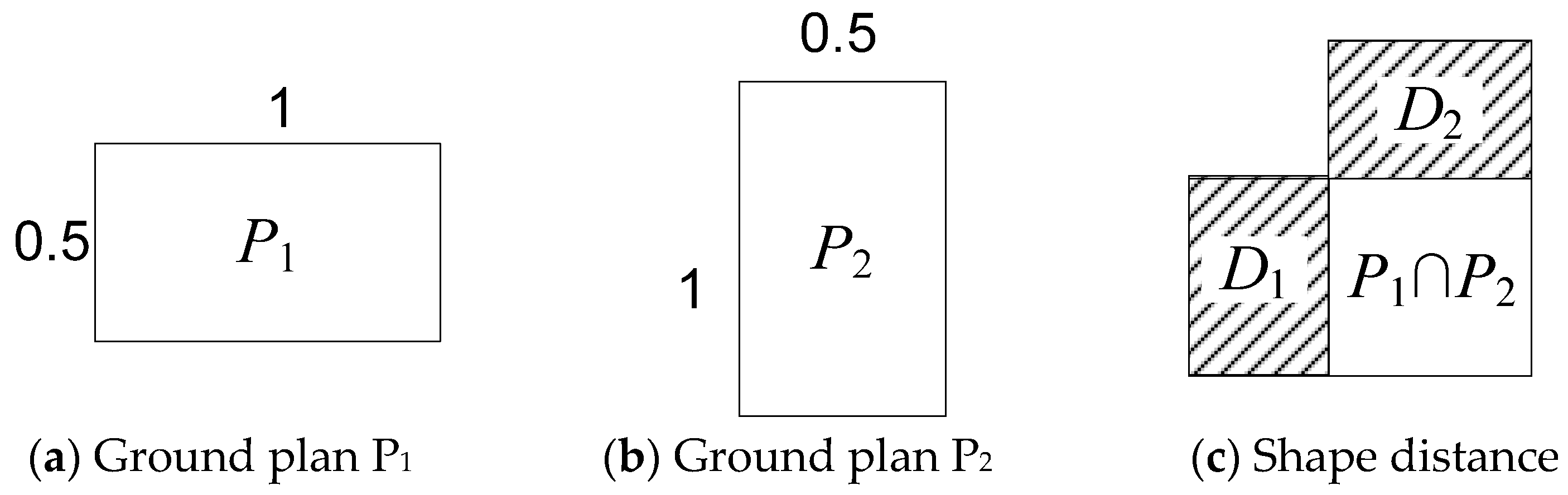
3.2. Distance Definition

Three types of distance are required by NEMD, and they are (1) distance between nodes; (2) distance between relationships; and (3) distance combining the previous two types. Node distance represents the difference between the shapes of each window pair; relationship distance represents the spatial distribution and topological difference of the window group; the combined distance is the weighted sum of node distance and relationship distance. All these distance values are normalized from 0 to 1in which 0 represent exactly the same and 1 represent completely different.

Node distance Δ_node is composed by two parts: shape distance Δ_shape and area distance Δ_area. Assuming v_i and v_j are two nodes, Δ_node can be calculated as follows:

$$v_i=(w_i,h_i),v_j=(w_j,h_j)$$

(4)

$$m{x}_i=\max \{w_i,h_i\},m{x}_j=\max \{w_j,h_j\}$$

(5)

$$w_{min}=\min \{\frac{w_i}{m{x}_i},\frac{w_j}{m{x}_j}\},h_{min}=\min \{\frac{h_i}{m{x}_i},\frac{h_j}{m{x}_j}\}$$

(6)

$${\Delta }_{shape}=\left|\frac{w_i}{m{x}_i}-\frac{w_j}{m{x}_j}\right|·h_{min}+\left|\frac{h_i}{m{x}_i}-\frac{h_j}{m{x}_j}\right|·w_{min}$$

(7)

$$are{a}_i=\frac{w_i·h_i}{W_i.H_i},are{a}_j=\frac{w_j·h_j}{W_j.H_j}$$

(8)

$${\Delta }_{area}=\frac{\left|are{a}_i-are{a}_j\right|}{\max \{are{a}_i,are{a}_j\}}$$

(9)

$${\Delta }_{node}=\alpha ·{\Delta }_{shape}+(1-\alpha )·{\Delta }_{area}$$

(10)

As shown in Figure 5, Δ_shape equals the sum area of D₁ and D₂ (the shaded part in Figure 5c). Since rectangle P₁ and P₂ are normalized to the rectangle with 1 as their longest edge, Δ_shape is a value between 0 (means exactly the same) and 1 (completely different). In Equation (8), $W_i$ and $H_i$ are the total width and length of the façade which contains $v_i$, so are $W_i$ and $H_i$. Δ_area is the normalized area difference. α is a number between 0 and 1 which gives the weight of the shape and area distance in final node distance.

Relationship distance ${\Delta }_{relationship}$ is the normalized difference between two relative distances. Assume $r_{ij}=(v_i,v_j)$ is the relationship between two polygons $v_i$ and $v_j$, so is $r_{pq}=(v_p,v_q)$. Then the relationship distance between $r_{ij}$ and $r_{pq}$ can be calculated as follows:

$$a_{ij}=area(v_i)+area(v_j),a_{pq}=area(v_p)+area(v_q)$$

(11)

$${\Delta }_{relationship}=\left|\frac{{\Delta }_{ij}}{a_{ij}}-\frac{{\Delta }_{pq}}{a_{pq}}\right|/\max \{\frac{{\Delta }_{ij}}{a_{ij}},\frac{{\Delta }_{pq}}{a_{pq}}\}$$

(12)

In Equation (11), $area(v_i)$ is the area of the polygon. Δ_ij and Δ_pq indicate respectively the node distance between $v_i$ and $v_j$ and the node distance between v_p and v_q. The combined distance is the same as Equation (1), ${\Delta }_{inner}=\alpha ·{\Delta }_{node}+(1-\alpha )·{\Delta }_{relationship}$, where α is a number between 0 and 1 and gives the weight of the node and relationship distance. In our implementation, α is set to 0.5 in Equation (10) because the importance of shape and area are considered to be the same. For the combined distance in Equation (1), α is set to 10/17 according to the value in Table 2, in which the importance value is 10 for the windows and 7 for the relationship between windows. Therefore, the weight for node is set to 10/(10 + 7) and weight for relationship is set to 7/(10 + 7). If there is not apredefined weight, the default weights for the NEMD calculation are identical in the process, e.g., α = 0.5 in Equation (10). Otherwise, the weights are generated to reflect the rational, e.g., α = 10/17 in Equation (1).

3.3. Similarity Values

The NEMD values between the original façade and the typified ones are calculated based on the distance definitions in Section 3.2. We will verify the NEMD values by the user survey results.

Table 3. NEMD and results of the user survey.

Options	1	2	3	4	5	6
NEMD	43.5	47.8	56.5	55.2	47.5	50.1
User survey	8.72	6.45	6.14	6.67	7.54	5.50

demonstrates the NEMD values calculated for six options of typification of the test ground plans in comparison to the results of the user survey.

The NEMD values in Table 3 denote the dissimilarities of the six options to the original distribution, while the values of the user survey present similarities. In order to make these two sets of values comparable, the NEMD values are linearly transformed and the values of the user survey are transformed into dissimilarities. Assume that an NEMD value is a and a user survey value is b. Let a’ = a/5 − 7.5 and b’ = 10 − b. This linear transformation is used to map the NEMD and user survey value into the same range and to illustrate their correlation. a’ and b’ of all six options are given in Figure 6, from which it is shown that the proposed NEMD method can correctly reflect the user’s visual perception of similarity in our case. In Figure 6, the lower NEMD indicates a better association between the original and typified façade, while the user survey value (b) is converted into (10-b) that means the higher user survey (b) suggests the better association.

4. The Automatic Approach of Typification

As indicated in the user survey the most significant constraint for the typification of façade is the preservation of the shape of its elements, i.e., windows in our case (shape conformal). On this basis an automatic approach is developed.

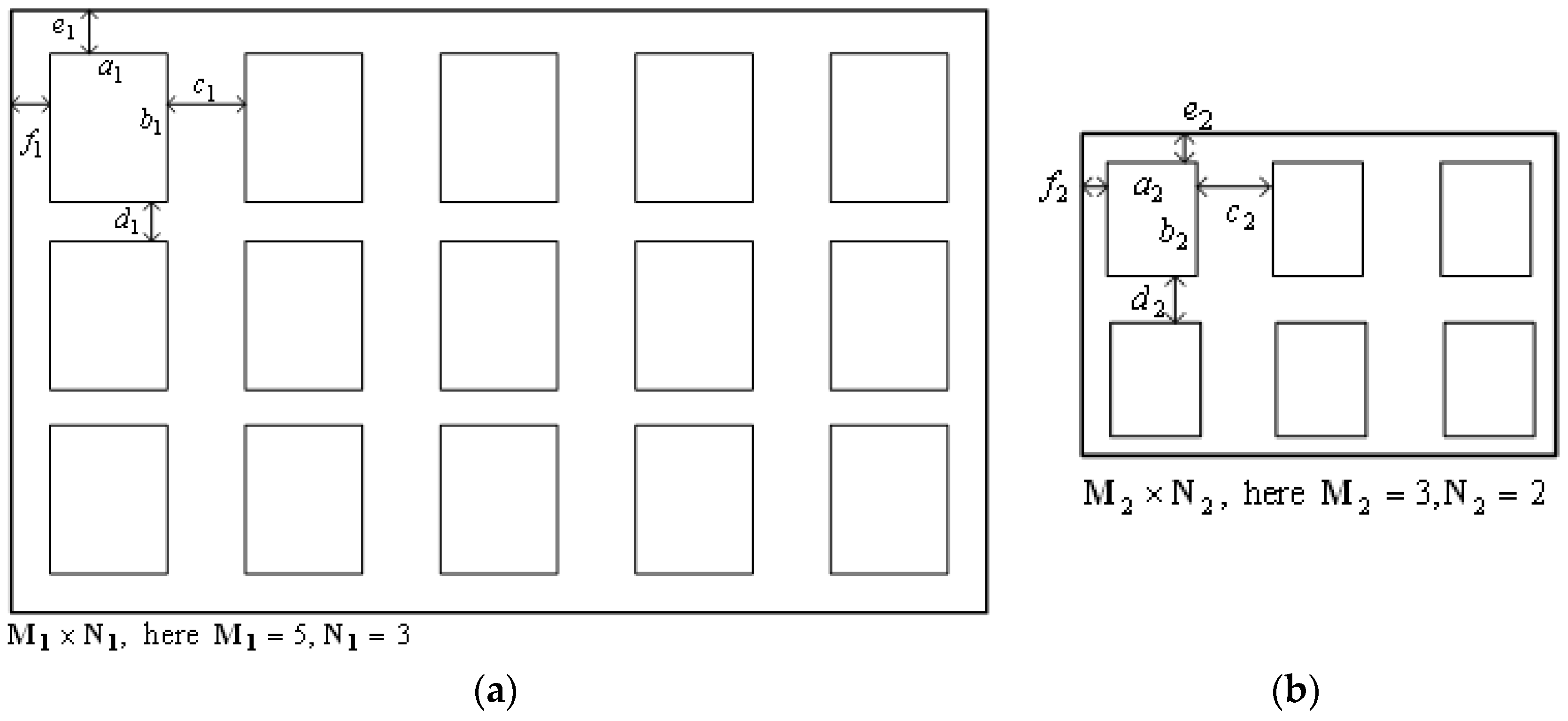
4.1. Typical Distribution of Windows on a Façade

Although windows reveal a vast diversity in structure and distribution, most of them show regularities. Figure 7 illustrates a set of window distributions on façades. Figure 7a has a tendency in the horizontal direction; in other words, the distances among windows in horizontal direction are smaller than those in vertical direction. Conversely, Figure 7b has a tendency in the vertical direction. Furthermore, the distribution would be regarded as having no tendency, if the distances among windows are the same in both directions (Figure 7c). However, sometimes the regularity might be locally broken due to different architecture styles (Figure 7d–f). In such cases, some pre-processing like new partitioning can be employed before the automatic process of typification. In this paper, the windows on façade are vector data, and the segmentation of window group is implemented by testing the size of window and the distance between the windows. For a façade in raster format, e.g., texture images, windows reconstruction methods are proposed by Ripperda and Brenner [31] and Becker [32].

4.2. The Process of Typification

In advance of typifying windows on a façade, the overall pattern is segmented into a number of subpatterns that contain regularly distributed windows. If the windows are distributed irregularly on a façade (i.e., Figure 7d–f), they will at first be partitioned into several segments with regular distributions and the automatic process is conducted for each segment separately. Figure 8a illustrates the parameterization of windows’ distribution before the process of typification: $a_1,b_1$ stand for the sides of windows in the horizontal and vertical direction respectively; $c_1,d_1$ stand for the distances among windows in horizontal and vertical direction respectively; $e_1,f_1$ stand for the distances between the block of windows and outline of façade in horizontal and vertical direction respectively. Besides, the number of windows in horizontal direction is equal to $M_1$, and the number of windows in vertical direction is equal to $N_1$. Then the lengths of façade in the horizontal and vertical directions $L_{h1}$ and $L_{v1}$ can be calculated as follows:

$$L_{h1}=2f_1+M_1·a_1+(M_1-1)·c_1$$

(13)

$$L_{v1}=2e_1+N_1·b_1+(N_1-1)·d_1$$

(14)

The process of typification is trigged when the distances among windows in either horizontal or vertical direction are smaller than a minimum value $\epsilon$. We assume that the outcome of typification is represented in Figure 8b. Then there are some relationships between these two distributions:

$$L_{h2}=(m_i/m_f)·L_{h1}$$

(15)

$$L_{v2}=(m_i/m_f)·L_{v1}$$

(16)

where $L_{h2}$ and $L_{v2}$ stand for the lengths of façade in horizontal and vertical direction after typification, while $m_i$ and $m_f$ stand for the original and the target scale. Similar to the original distribution, the lengths of façade after typification can be expressed as:

$$L_{h2}=2f_2+M_2·a_2+(M_2-1)·c_2$$

(17)

$$L_{v2}=2e_2+N_2·b_2+(N_2-1)·d_2$$

(18)

According to our user survey, the relationships between the parameters of the original distribution and those after typification can be established as follows:

$$a_1/b_1=a_2/b_2$$

(19)

$$e_2=\tau ·e_1·(m_i/m_f)$$

(20)

$$f_2=\tau ·f_1·(m_i/m_f)$$

(21)

$$\min \left\{c_2,d_2\right\}={\kappa }_1·\epsilon$$

(22)

$$\frac{\max \left\{c_2,d_2\right\}}{\max \left\{c_1,d_1\right\}}={\kappa }_2·\frac{\min \left\{c_2,d_2\right\}}{\min \left\{c_1,d_1\right\}}$$

(23)

$$\left(M_2·N_2\right)·\left(a_2·b_2\right)=\gamma ·\left(\left(M_1·N_1\right)·\left(a_1·b_1\right)\right)·(m_i/m_f)$$

(24)

As “shape conformal” is identified as the most significant constraint for the typification, the ratio of height and width of the windows must be preserved. In a declining order of significance, $\tau$, ${\kappa }_1$, ${\kappa }_2$, $\gamma$ respectively stand for the relative stiffness of satisfying the constraints “keeping the distances between windows and the outline of the façade”, “windows have to be merged in the tendency direction”, “keeping the distances between windows” and “area conformal” constraint.

Now there are eight equations (Equations (17)–(24)), 12 unknowns to be solved, namely, $M_2$, $N_2$, $a_2$, $b_2$, $c_2$, $d_2$, $e_2$, $f_2$; and $\tau ,{\kappa }_1,{\kappa }_2,\gamma$. That means that this equation system is underdetermined. In our practical implementation, Equation (24) was not considered during the calculation, since (1) “area conformal” is the least significant constraint for the typification and (2) the availability of this equation has no influence on the unknowns except the factor $\gamma$. The remaining equation system can be solved recursively by setting initial value for the significance constraint in line with the results of user survey:

(1)

The initial step: let the constraint significances equal one. Then the sides of window can be set initially according to the change of distances among windows: $a_2=a_1·\frac{\min \left\{c_2,d_2\right\}}{\min \left\{c_1,d_1\right\}}$, and $b_2=b_1·\frac{\min \left\{c_2,d_2\right\}}{\min \left\{c_1,d_1\right\}}$.

(2)

Put the initial values into Equations (17) and (18), and the number of windows in row and column can be then calculated by:

$$M_2=(c_2+L_{h2}-2f_2)/(a_2+c_2)$$

(25)

$$N_2=(d_2+L_{v2}-2e_2)/(a_2+d_2)$$

(26)

(3)

$M_2$ and $N_2$ are rounded to the nearest integer. The differences between the calculated values $M_2$, $N_2$ and their nearest integer can be utilized to judge whether the process should terminate or not. In our work $\left|round(M_2)-M_2\right|<0.25$ and $\left|round(N_2)-N_2\right|<0.25$ were set as the thresholds below which the process will be terminated.

(4)

If the threshold is not yet reached, ${\kappa }_1$ will be increased by 0.01, i.e., ${\kappa }_1={\kappa }_1+0.01$. Then the new $M_2$ and $N_2$ will be calculated. If the threshold is reached, the process will terminate; otherwise it will go on to the subsequent step.

(5)

${\kappa }_2$ will be increased by 0.01, i.e., ${\kappa }_2={\kappa }_2+0.01$. Then the new $M_2$ and $N_2$ will be calculated. If the threshold is reached, the process will terminate, otherwise it will go on to the subsequent step.

(6)

$\tau$ will be increased by 0.01, i.e., $\tau =\tau +0.01$. Then the new $M_2$ and $N_2$ will be calculated. If the threshold is reached, the process will terminate, otherwise it will go back to step 4.

When the iteration terminates, $M_2=round(M_2)$ and $N_2=round(N_2)$. The new distances among windows $c_2$ and $d_2$ can be calculated by:

$$c_2=\frac{L_{h2}-2f_2-M_2·a_2}{M_2-1}$$

(27)

$$d_2=\frac{L_{v2}-2e_2-N_2·b_2}{N_2-1}$$

(28)

With these calculated parameters, the positions of the new windows can be determined. Thus the result of the typification is obtained.

As mentioned at the beginning of this subsection, the designed algorithm is tailored for the façades on which the windows are distributed regularly in more than one row and column. However, sometimes there is only one row (or column) of windows on a façade, or there is one row (or column) of windows in addition to a matrix distribution of windows i.e., Figure 7e. Here, the windows in one column (or one row) will be treated as a special case in the process of automatic typification by ignoring the calculations for the columns (or rows).

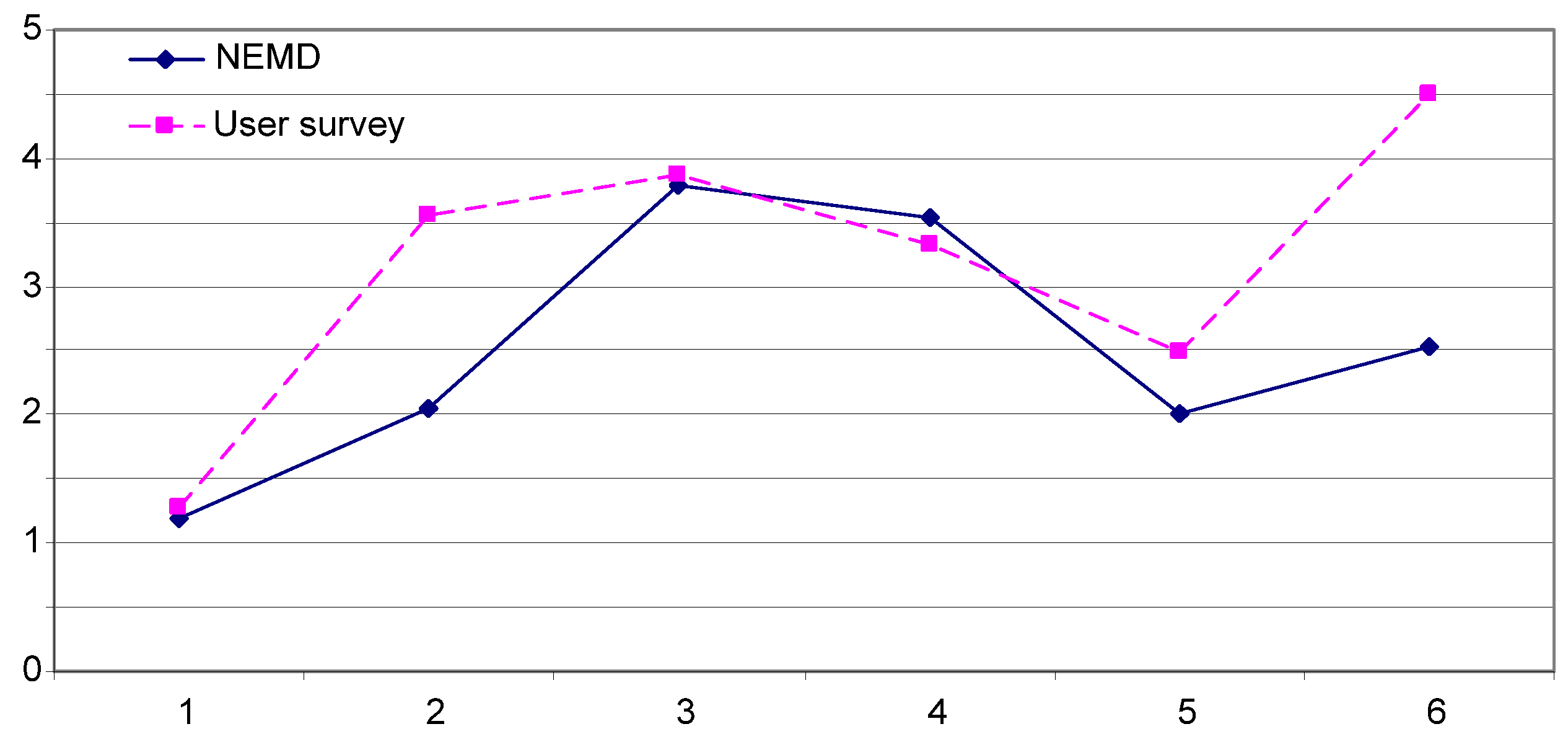
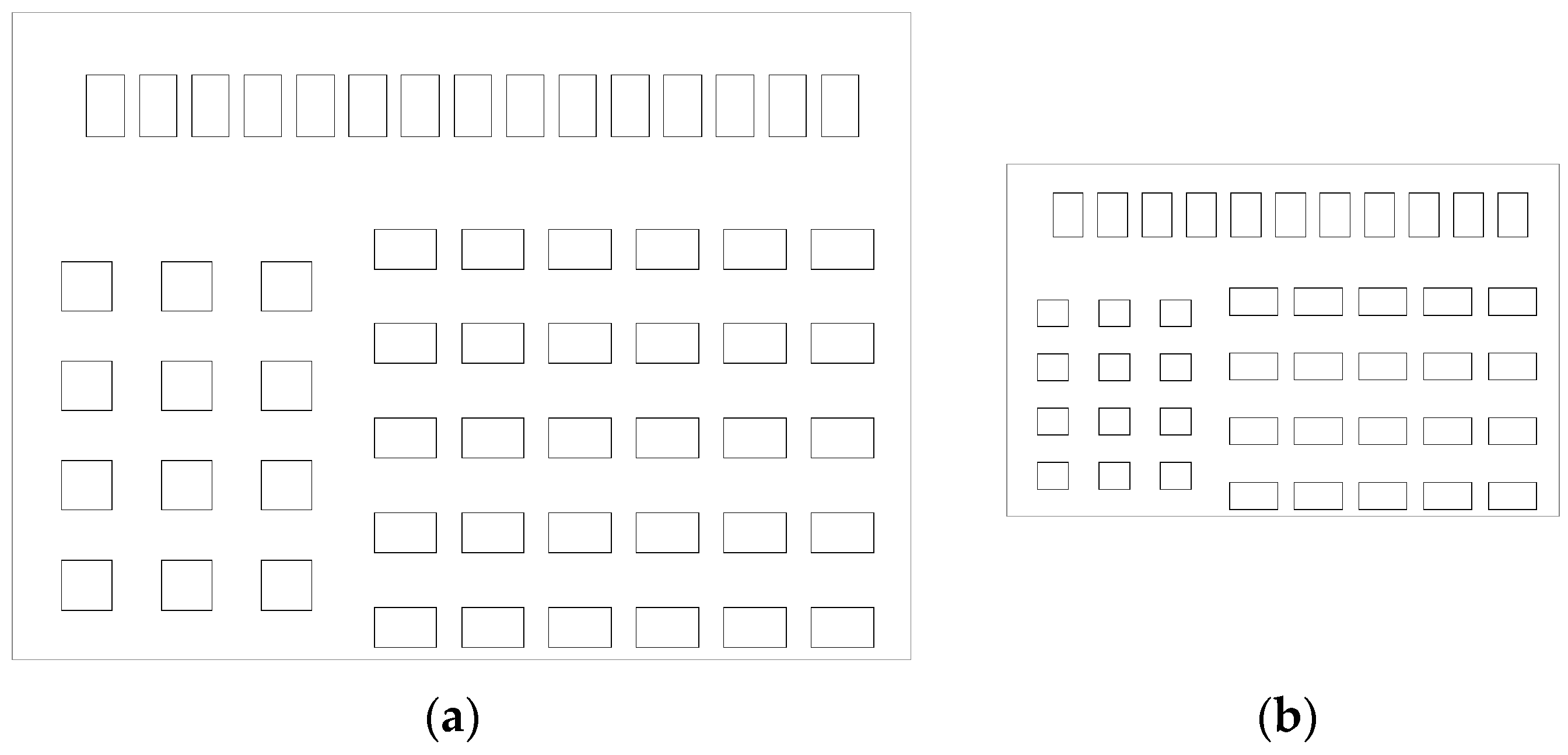
5. Experiments and Evaluation

The algorithm for automatic typification has been implemented using Matlab (version Matlab 7.4) on a number of façades. A selection of examples is presented in this section. Figure 9 shows the result of typification for a façade in which all the windows are distributed regularly in rows and columns. Figure 9b denotes the new distribution of windows after typification for a scale reduction by two times.

In order to evaluate the proposed approach, two alternative results for the typification of Figure 9a are generated manually (Figure 9c,d). Then the similarities 9b, 9c and 9d to the original distribution (Figure 9a) are calculated using the algorithm presented in Section 3.2. The NEMD values of Figure 9b, 9c and 9d to 9a are 42.41, 75.82, and 76.83 respectively. It clearly denotes that the result of our approach is better than other typification solutions.

Another type of quite common façade with windows might be when the windows are distributed evenly in one direction, but not in the other, although they are well aligned. An example is shown in Figure 10a. In this case the whole façade had to be partitioned into several segments at first by comparing the sizes of windows and the distances among windows. Then the process of typification is carried out for each segment. At the same time the process should consider the results of typification of neighboring segments. In other words, the windows after the typification should reflect the original distribution character. In our implementation, we first calculate the distribution of windows for the segment in which there are more windows than in other segments (in case of Figure 10a, the middle segment is typified at first). Then the number of windows in the column is determined for all the other segments. That means that the parameter $N_2$ is treated as known during the process of typification for other segments. Figure 10b presents the result of typification for the original distribution of Figure 10a with consideration of context between segments.

Figure 11a shows a façade with well-aligned but irregularly distributed windows. Similar to the façade in Figure 10, the windows had to be partitioned into three segments and typified segment after segment (Figure 11b).

6. Conclusions and Further Works

This paper presented a user survey to find out which kind of representation after typification is visually best associated with the original dataset. The results of the user test revealed that “the ratio between height and width of the windows” and “the distribution pattern of window elements” are the most important clues for preserving the graphic characteristics of façades.

In order to verify the results of the user survey, ARG and NEMD algorithms are introduced to quantify the similarity between the original façade and the typified ones. The similarity values coincide very well with the results of our user survey.

Based on the user test, which reveals different significance values of constraints, an automatic approach for typification is developed which can iteratively satisfy the given constraints. The algorithm has been implemented and tested on a number of façades. Experiments show that the results of typification can effectively reflect the distribution character of the original façades.

The main contribution of this work is that the approach can, for the first time, quantitatively typify regular distributed polygonal objects on building facades. Because the method of the proposed typification fully considers the factors and their weights for the consistency of visual impression while reducing the number of façade objects and repositioning them, the results generated by the proposed approach can preserve the graphic characteristics of the façade as much as possible. This can be applied to simplify façade objects in the process of 3D generalization. In a broad sense, the method proposed in this paper can be used for the typification of polygonal objects (i.e., building footprints or urban blocks) on a 2D map in case the objects form patterns which fulfill the condition of the typification.

However, our approach is only used to typify façades with rectangular windows. For windows with complicated structures, more parameters have to be introduced. In the near future, a contextual typification will be investigated, which means that the typification for windows on a façade should consider the distributions of windows on its neighboring façades. Moreover, the developed approach will be tested on extensive ground plans of densely distributed buildings. The algorithm for automatic typification has been implemented using Matlab (version Matlab 7.4) on a number of façades. A selection of examples is presented in this section. Figure 9 shows the result of typification for a façade in which all the windows are distributed regularly in rows and columns. Figure 9b denotes the new distribution of windows after typification for a scale reduction by two times.