An Adaptive Density-Based Time Series Clustering Algorithm: A Case Study on Rainfall Patterns
Abstract
:1. Introduction
2. Methods for Time Series Clustering
2.1. Measurement of Similarity between Objects
2.2. A New Adaptive Strategy for Time Series Clustering
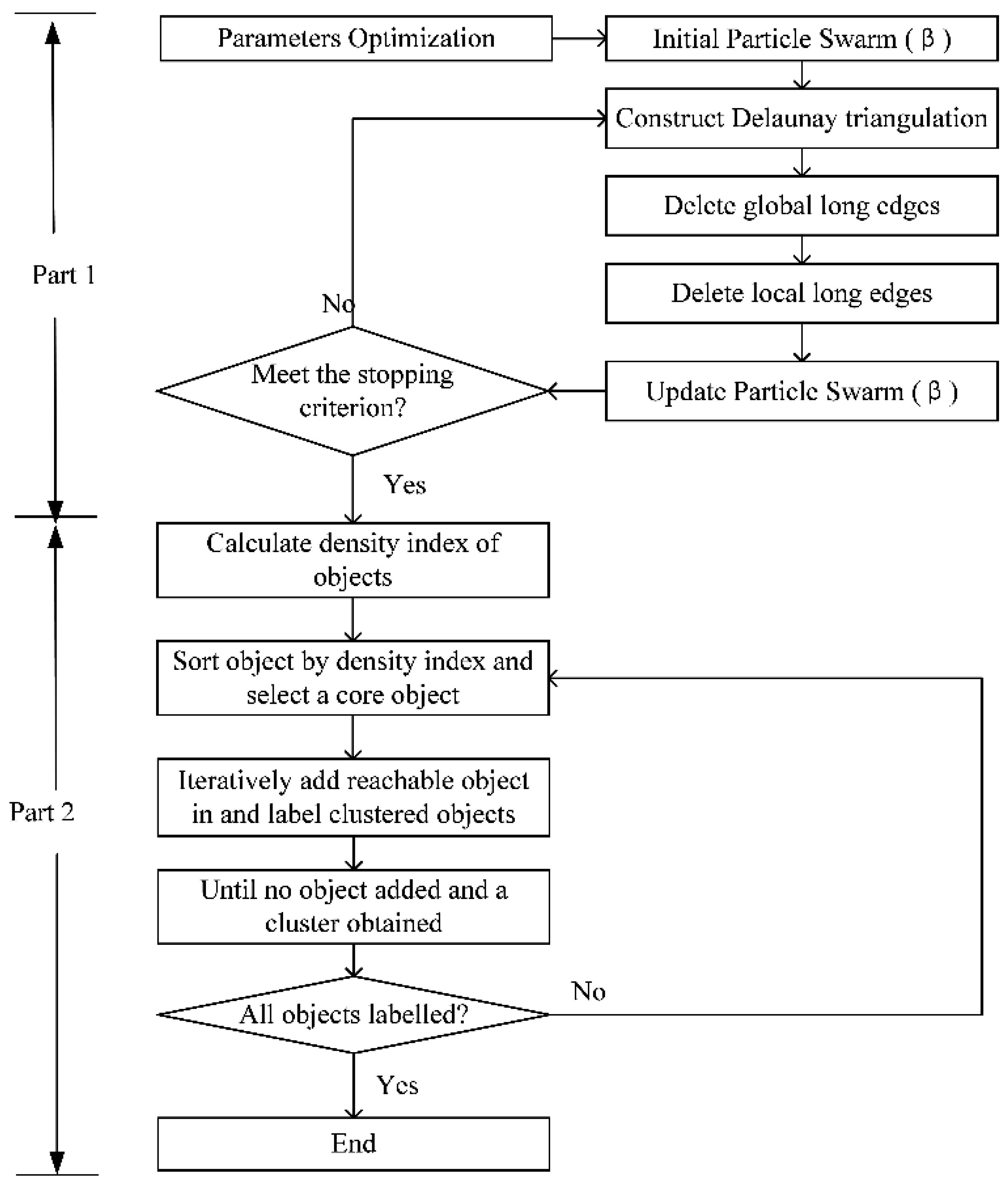
3. The DTSC Algorithm
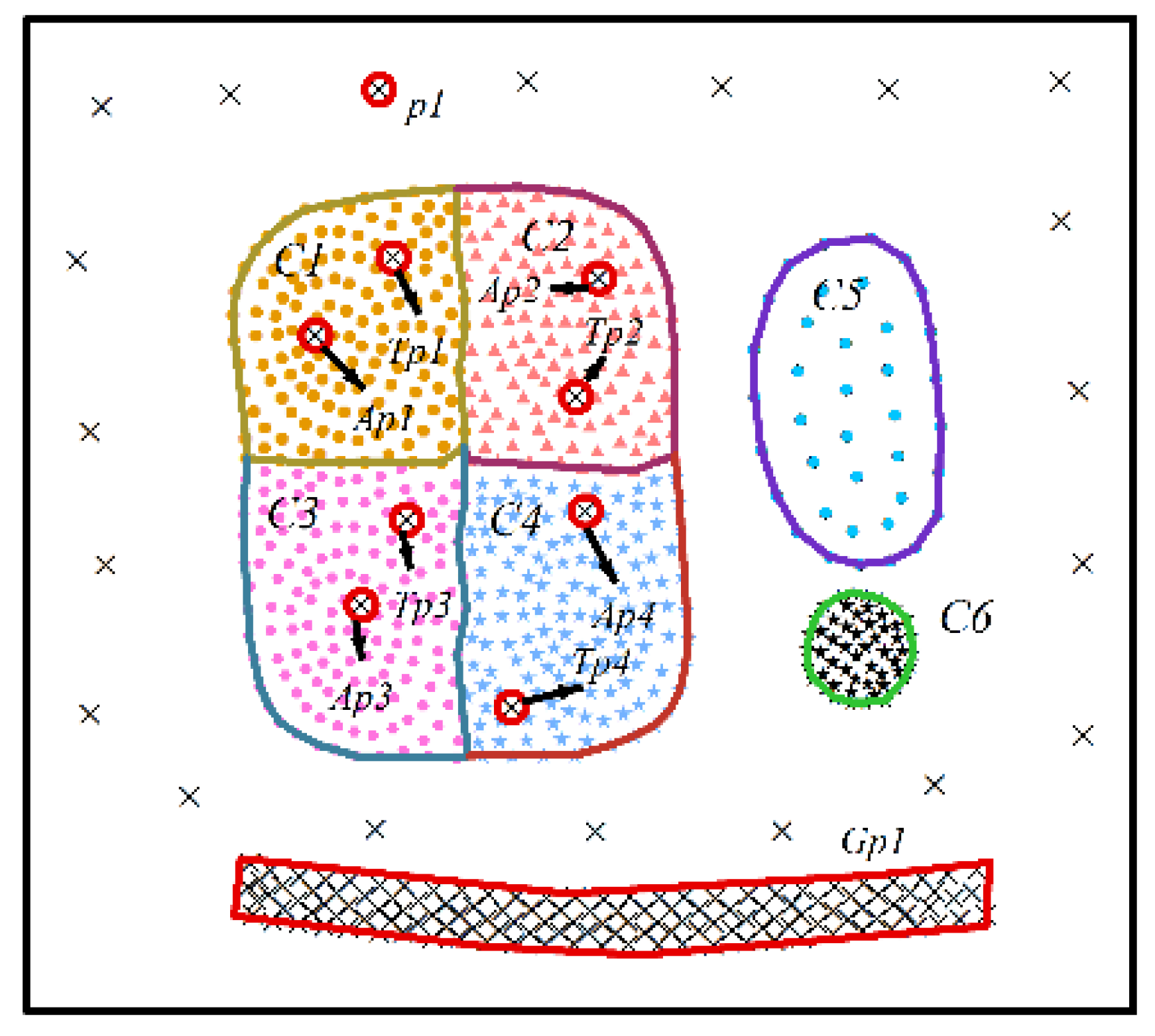
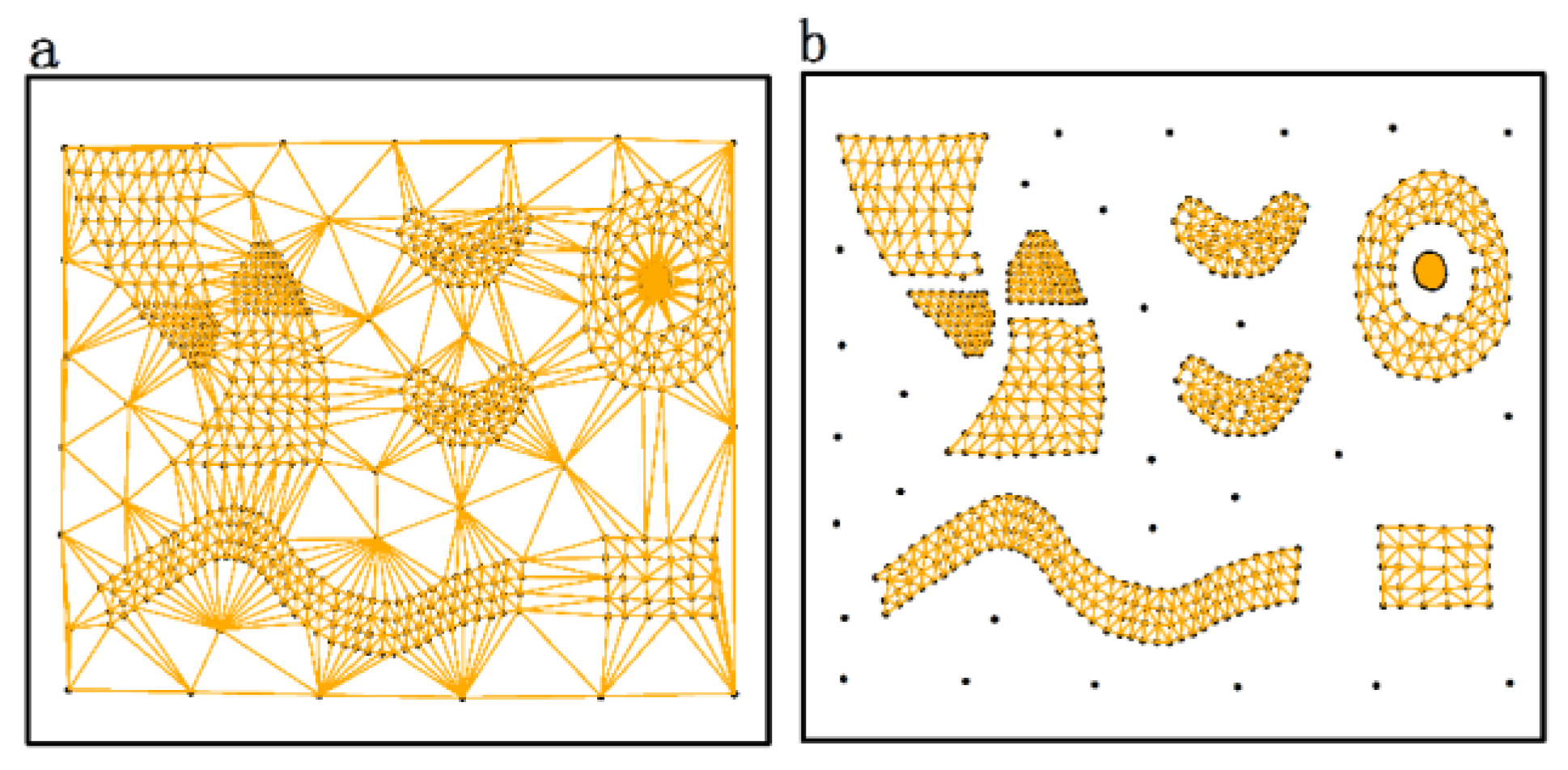
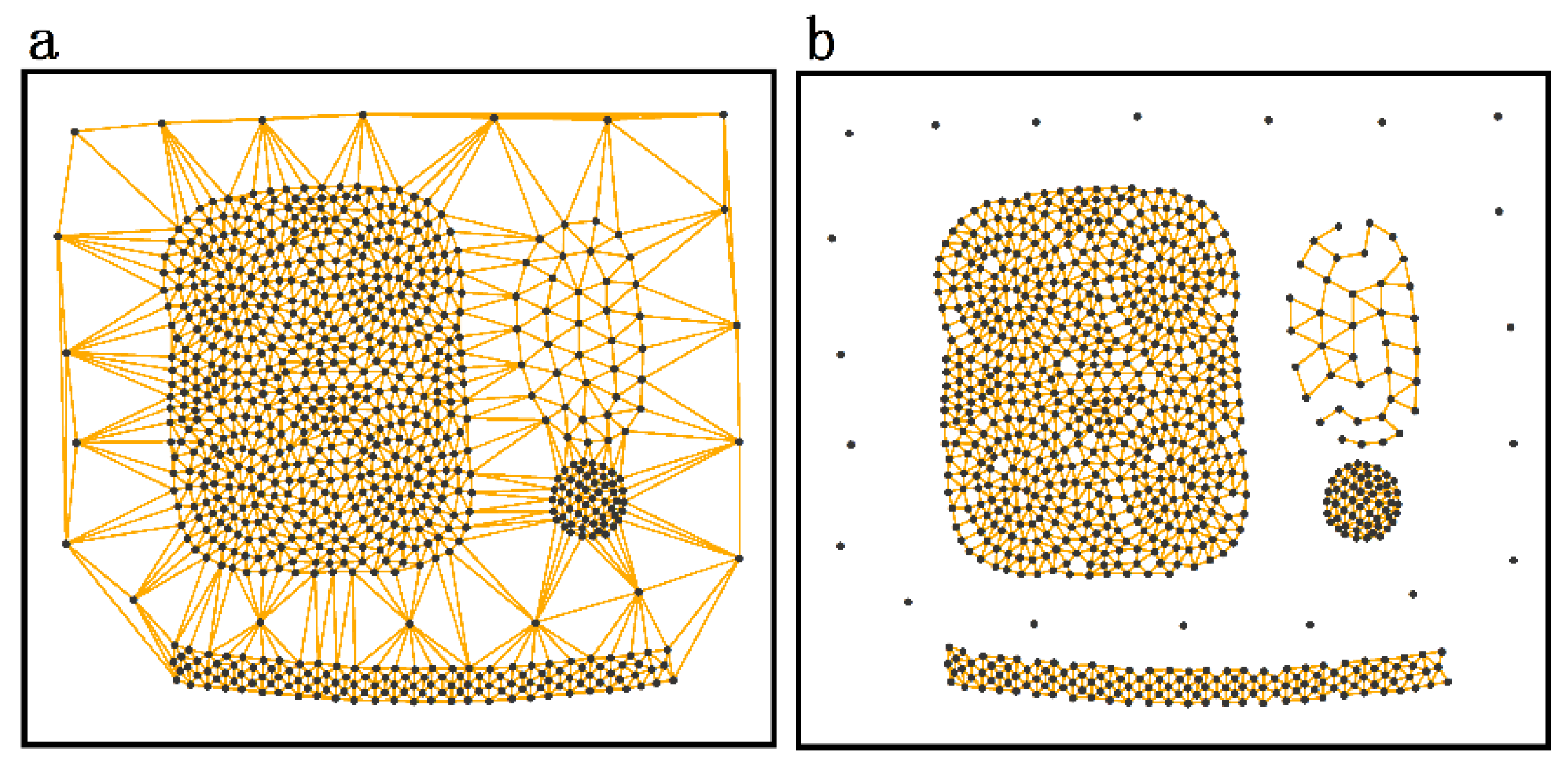
3.1. Construction of Spatial Proximity Relationships
3.2. Clustering Objects with Similar Time Series Attributes
- (1)
- Spatial neighbors: Objects connected by edges in the modified Delaunay triangulation.
- (2)
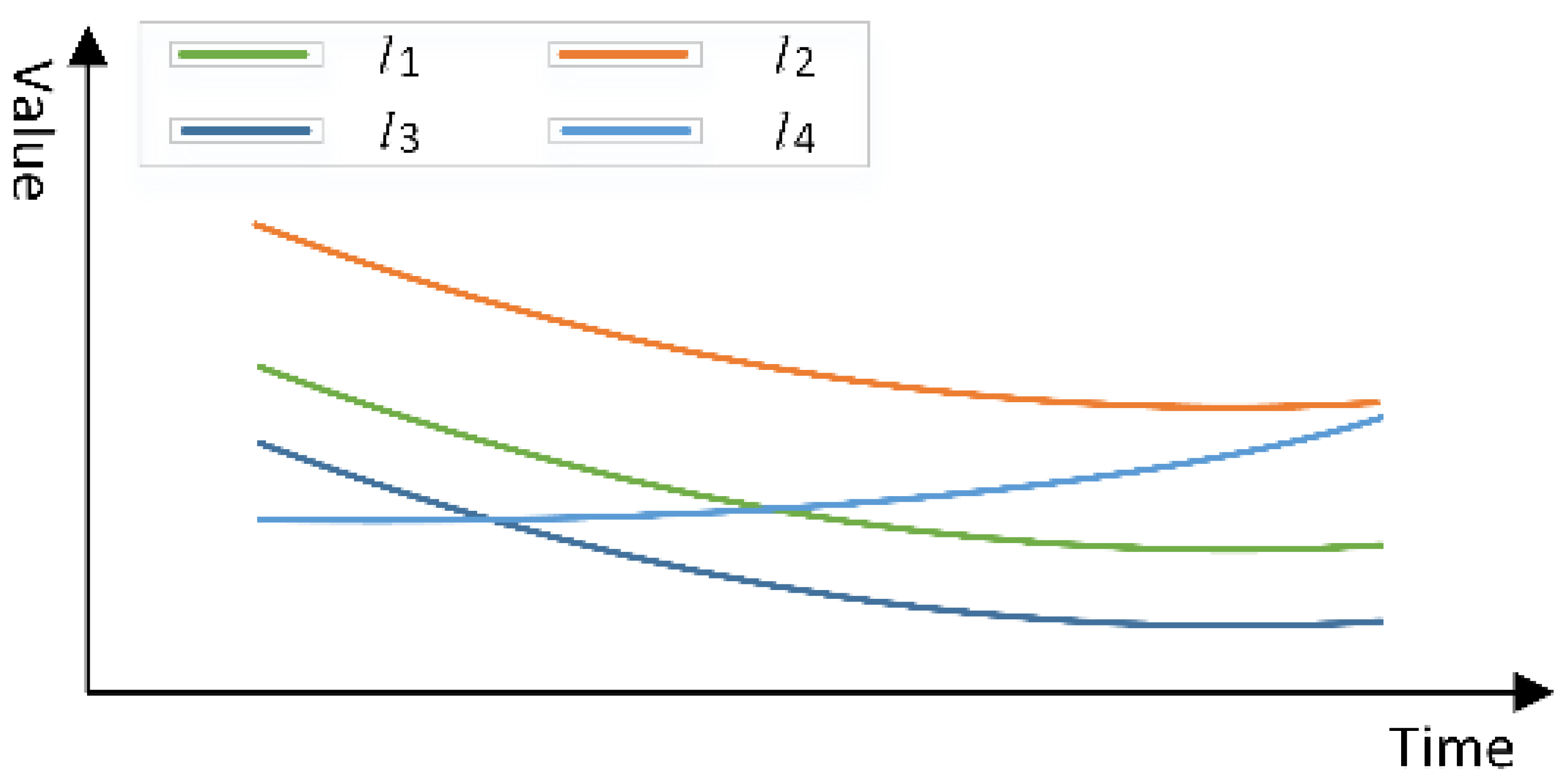
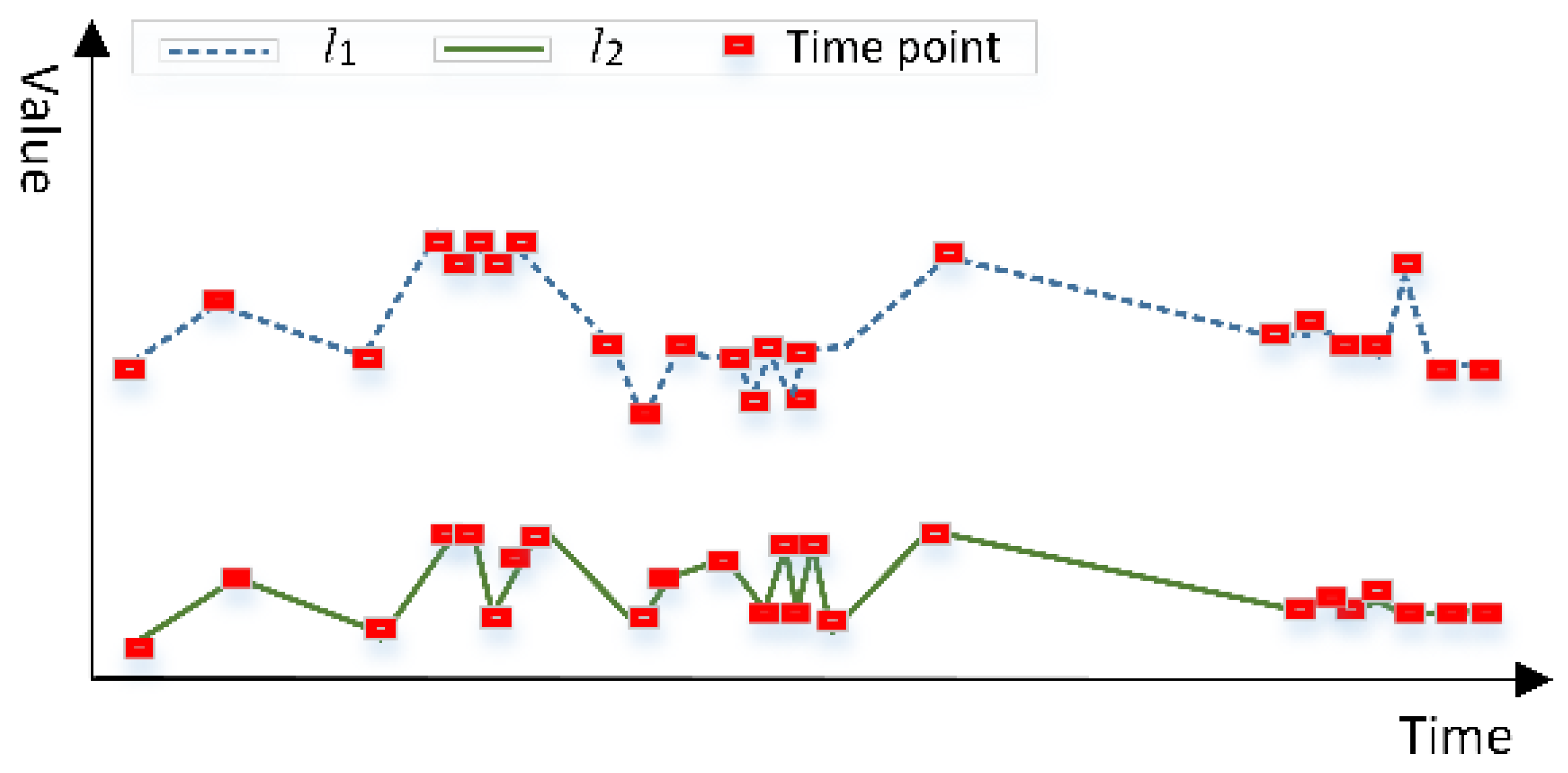
- Attribute directly reachable: Objects with similar time series attribute values and attribute trends are considered as attribute directly reachable. The object and are attribute directly reachable, if
- (i)
- and ; and
- (ii)
- (3)
- Attribute reachable: Attribute reachable measures the similarity between an object and its neighboring objects. For a set of objects S, its neighboring object is considered attribute reachable from S if the attribute distance between and the mean value of S is less than TS.
- (4)
- Density indicator: Density indicator represents the density of objects with similar attributes in the spatial domain. For an object , the density indicator is calculated with the following equation:where is the number of objects that are attribute directly reachable from . is the number of neighbors of .
3.3. Accuracy Evaluation of Clustering Results
4. Results
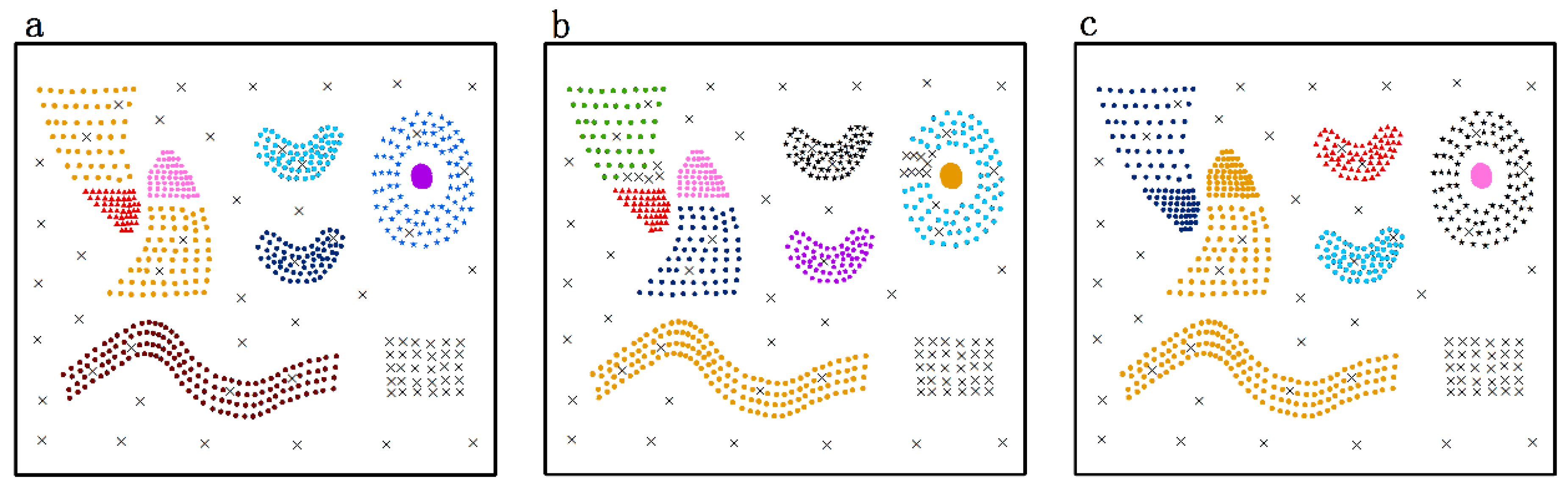
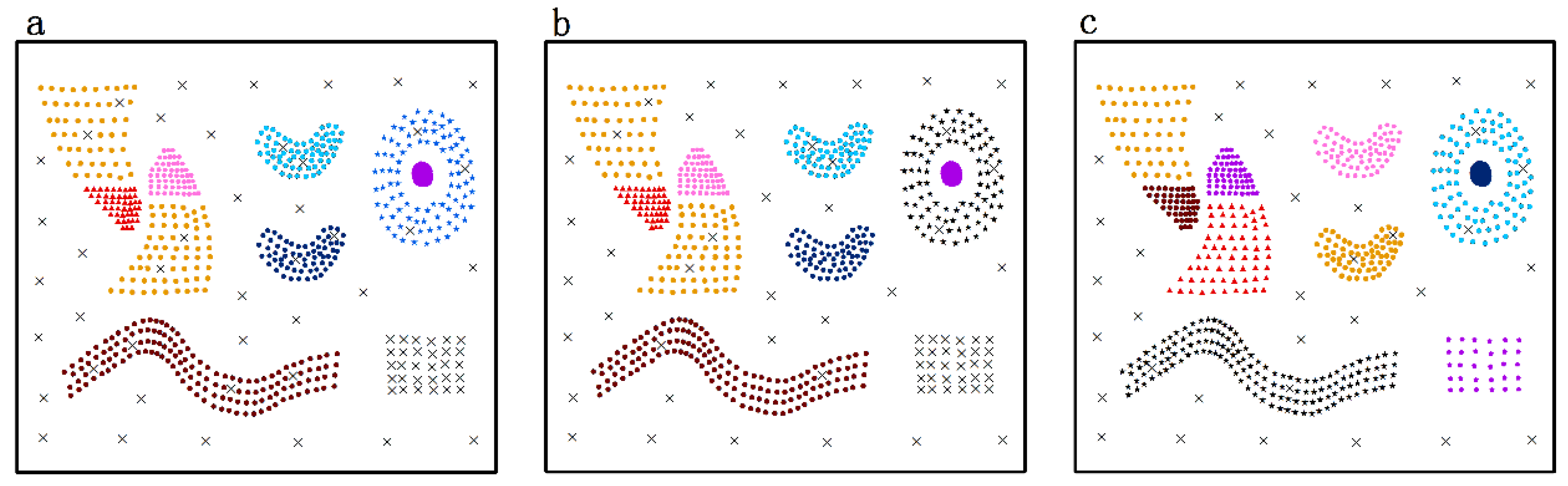
4.1. Validation of DTSC Algorithm on Simulated Datasets
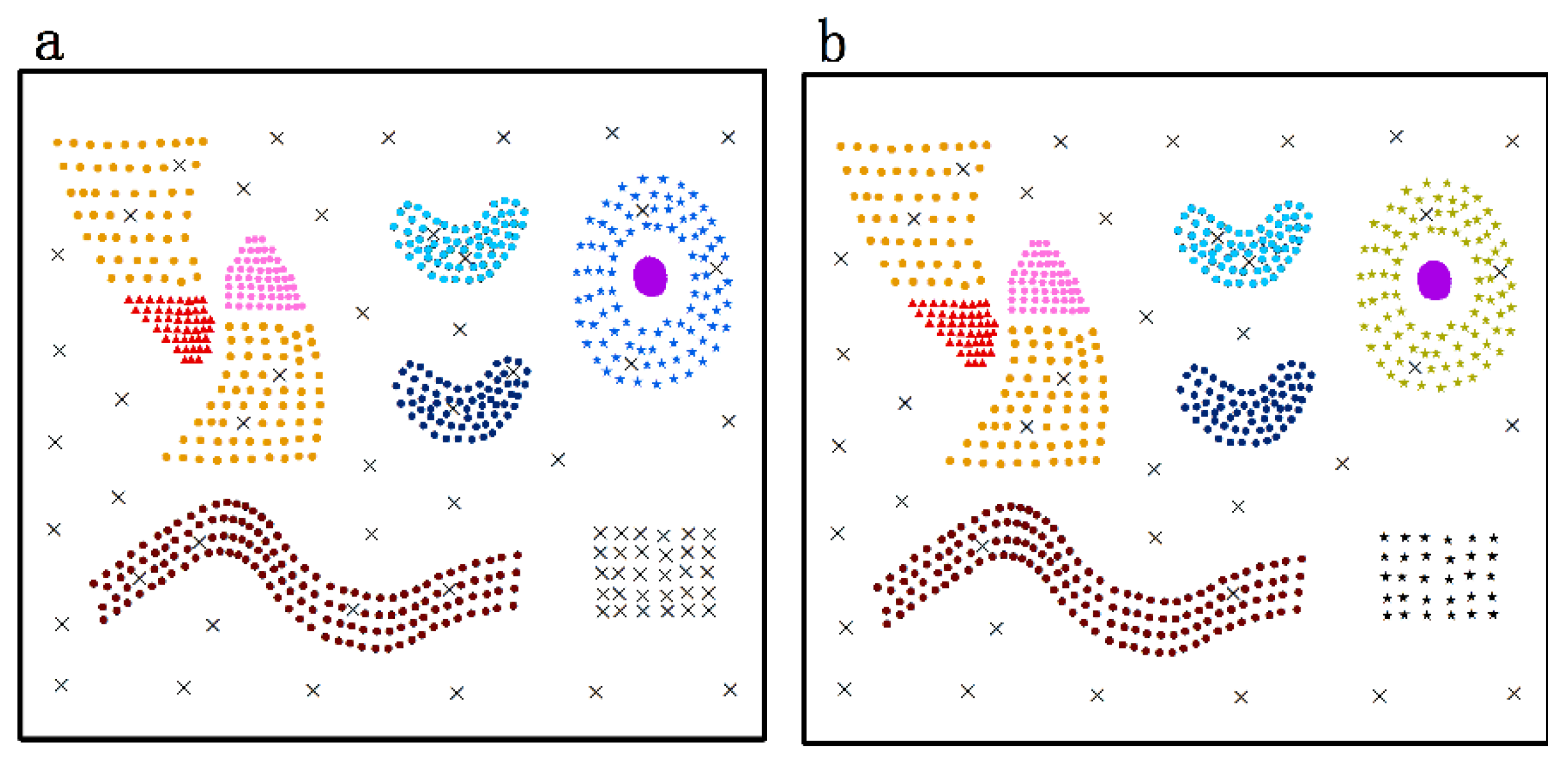
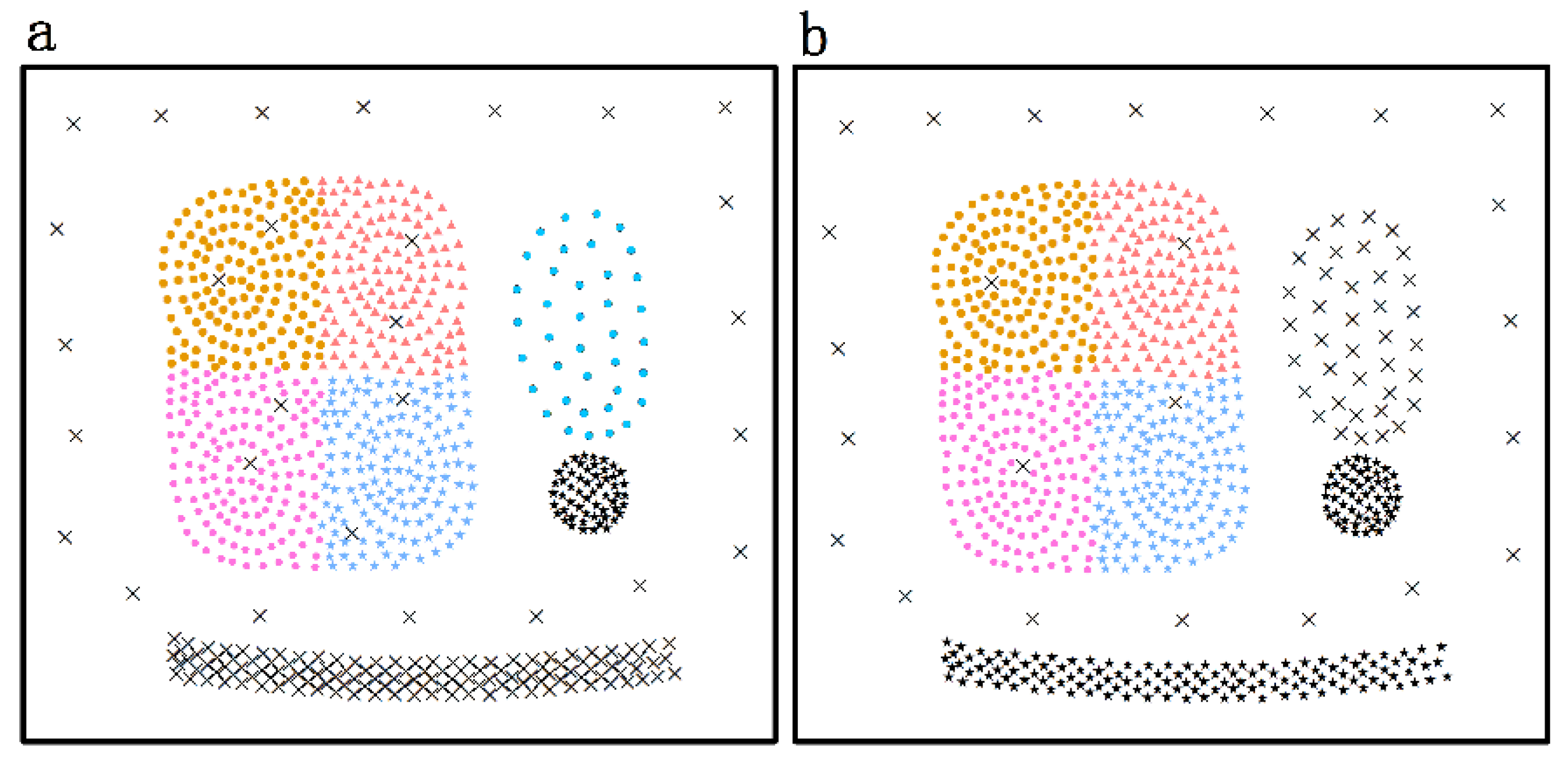
4.1.1. Validation of DTSC Algorithm Based on Simulated Dataset
- (1)
- and contain 759 and 806 objects, respectively,
- (2)
- The time dimensionality is 20 and the neighboring time intervals are equal,
- (3)
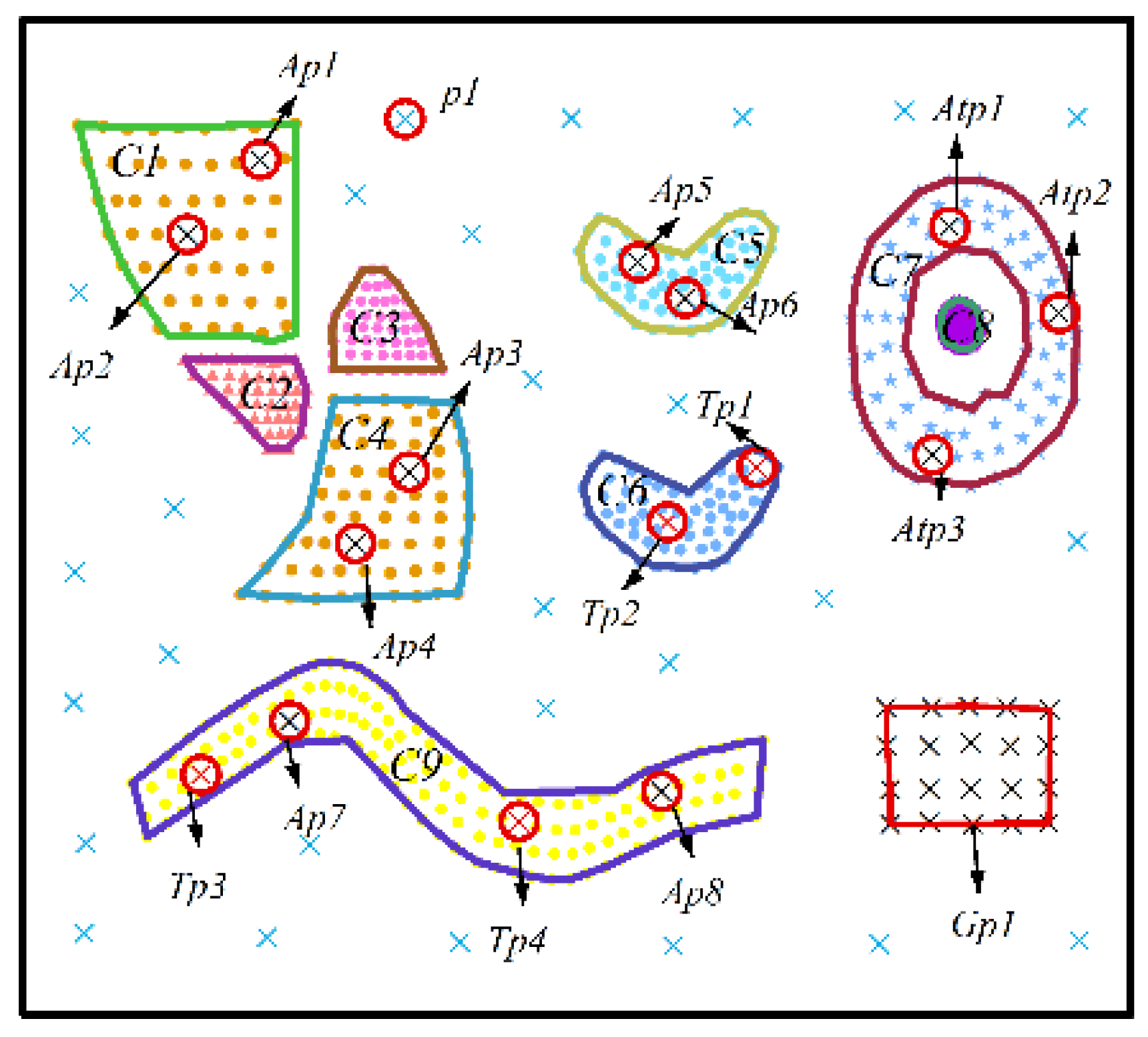
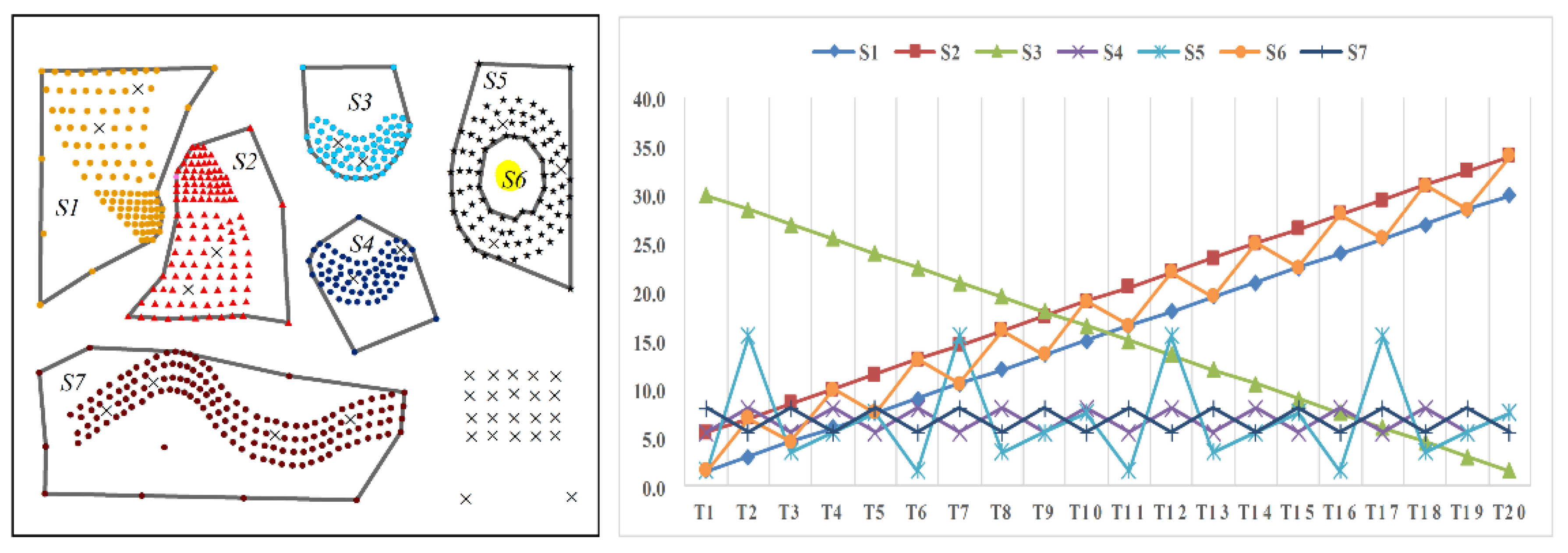
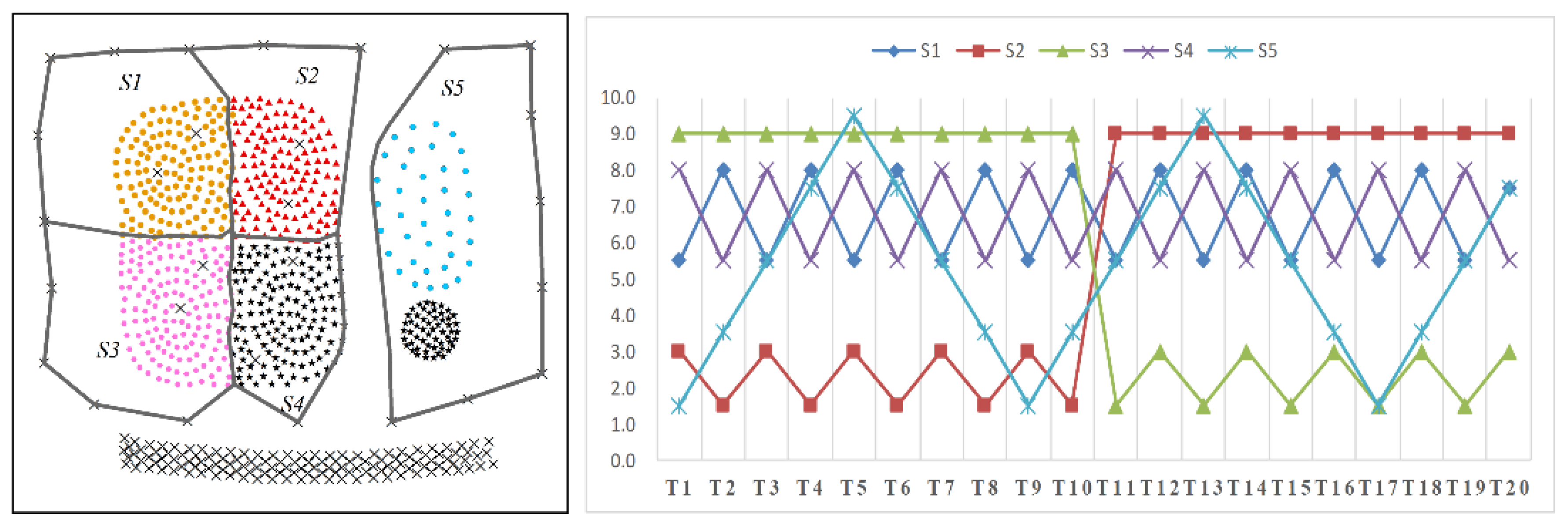
- Nine predefined clusters labeled as to in (in Figure 4) and five predefined clusters labeled as to in (in Figure 6) exist. These clusters possess arbitrary geometrical shapes and different densities. The non-spatial attributes of the cluster at every time point are randomly distributed under one range, and the mean value of attributes in every cluster are shown in Figure 5 and Figure 7,
- (4)
- To maintain consistency with the real applications, noises are set in the simulated datasets and are classified into five types. Type 1 comprises the spatial noises that have a meaning similar to that of spatial outliers whose spatial attribute values are significantly different from those of other objects in their spatial neighborhood; these are labeled as (such as ). The non-spatial attributes of spatial noises are similar to the nearest clusters in dataset . Types 2 and 3 are the non-spatial attribute noises and non-spatial attribute trend noises, respectively, which are labeled as (such as to ) and (such as to ), respectively. The attributes of these types of noises are significantly different from those of their neighboring objects. Type 4 comprises noises whose attribute values and attribute trends are both significantly different from those of neighboring objects; these noises are labeled as (such as to ). Type 5 comprises gradually changing noises, whose attribute values change in a descending or ascending fashion along the spatial position although their attribute trends are similar. For example, the temperature decreases as the altitude increases, and the temperature trend is similar at different altitudes with seasonal variations. These gradually changing noises are labeled as (such as ).
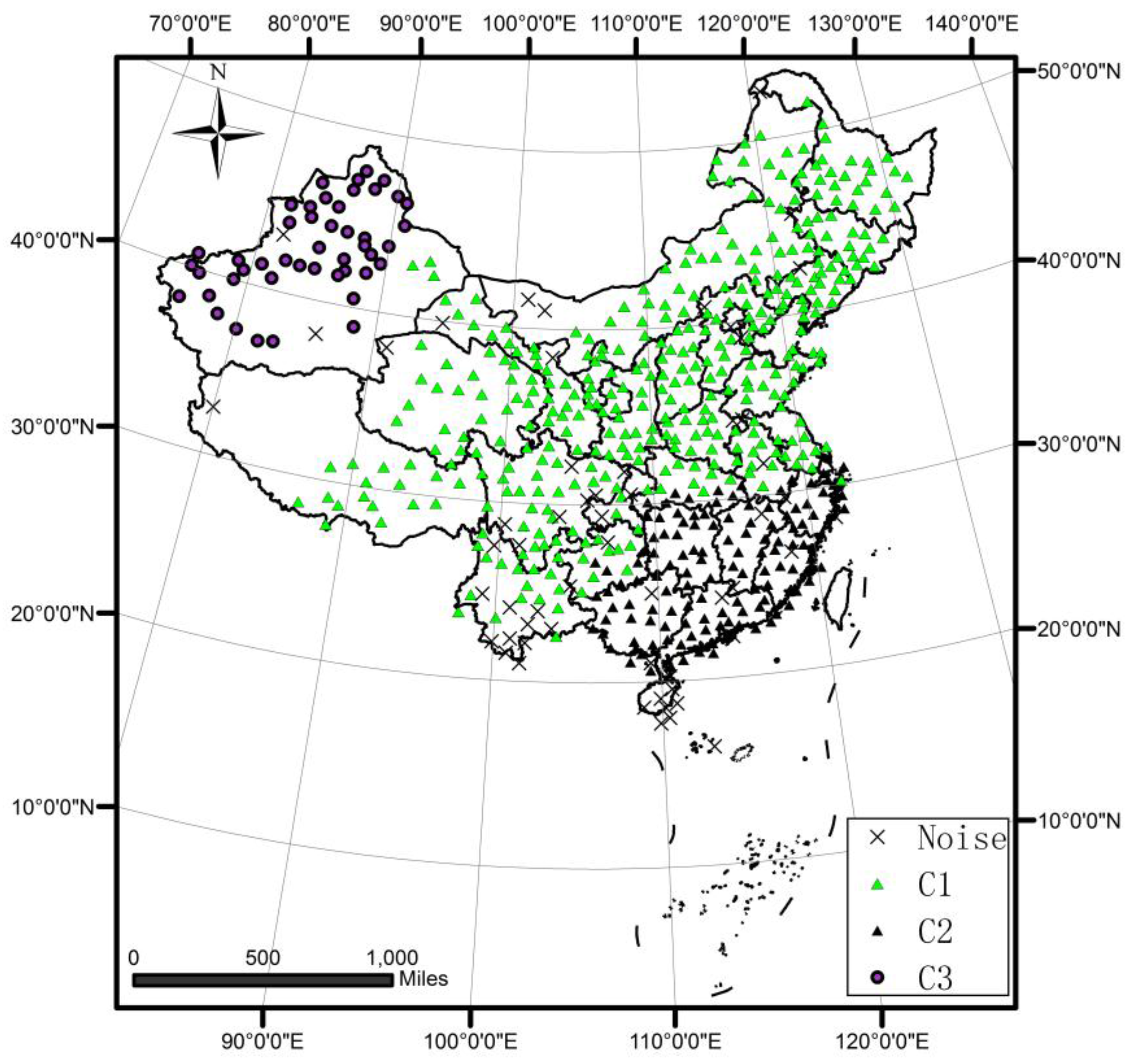
4.1.2. Comparison between DTSC and Typical Algorithms
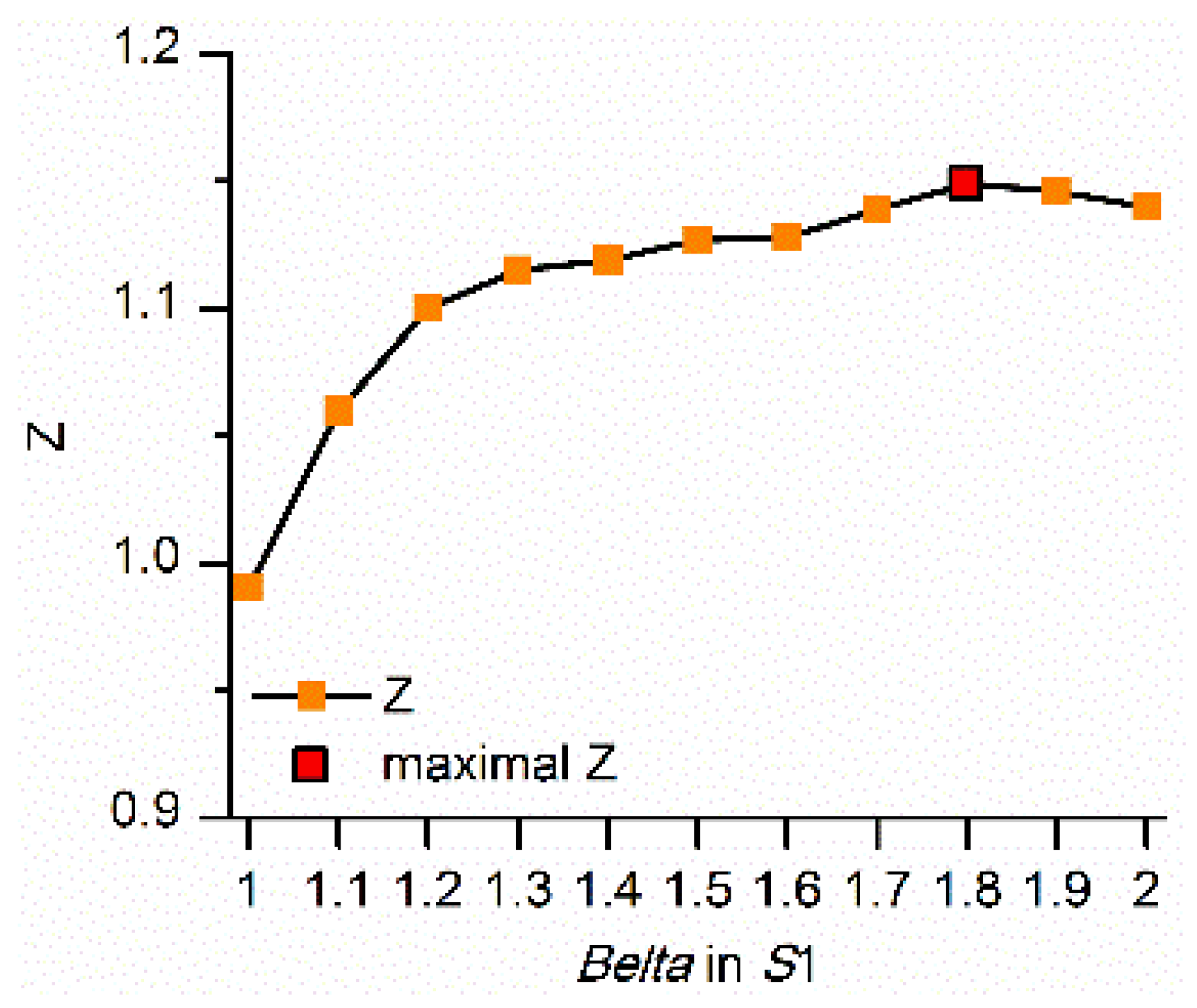
4.1.3. Comparison of the DTSC Algorithm with Optimal and Non-Optimal Parameters in the Spatial Domain
4.1.4. Comparison of the DTSC Algorithm with Proposed Similarity Measurements and Typical Similarity Measurements in the Non-Spatial Domain
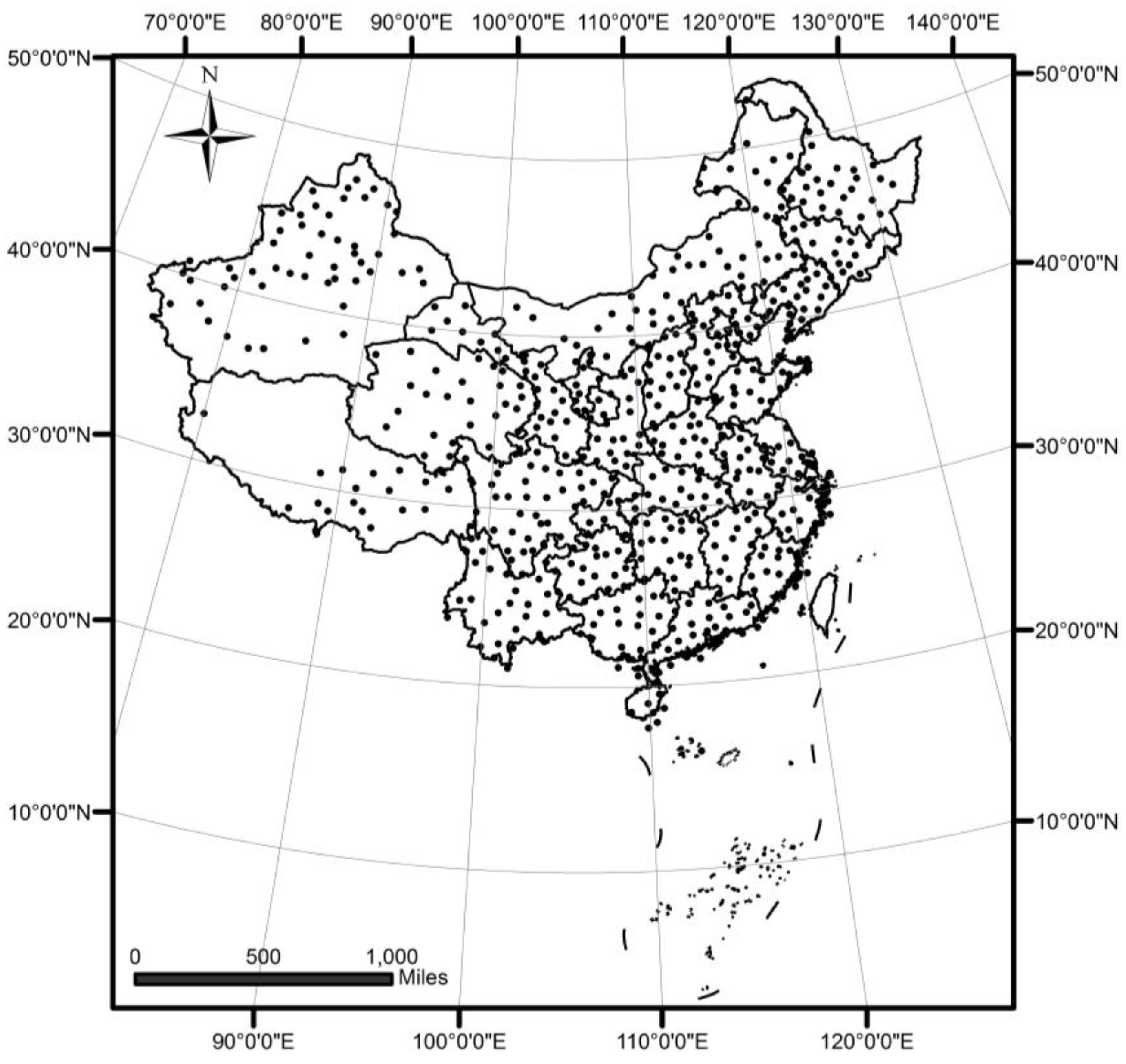
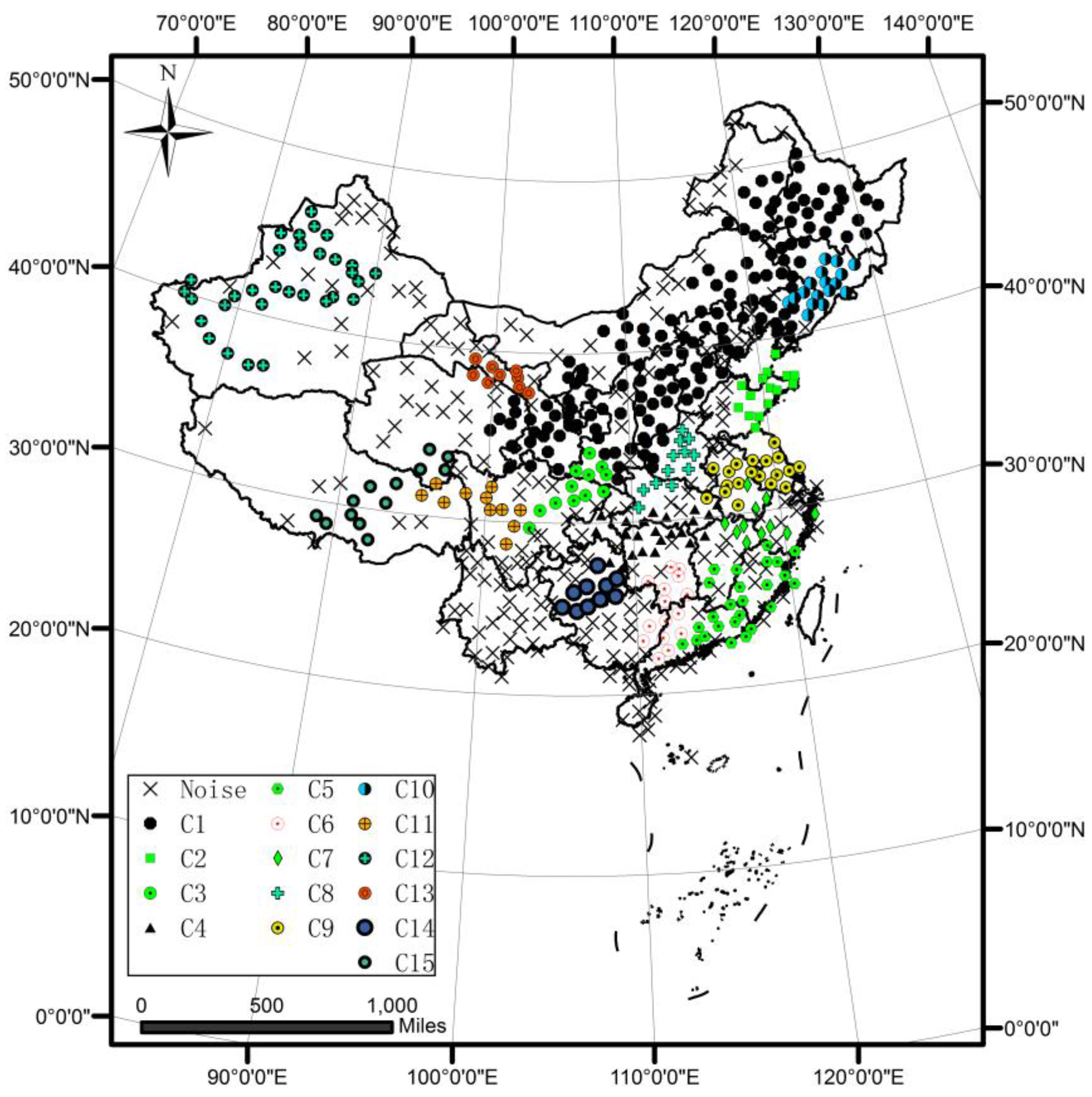
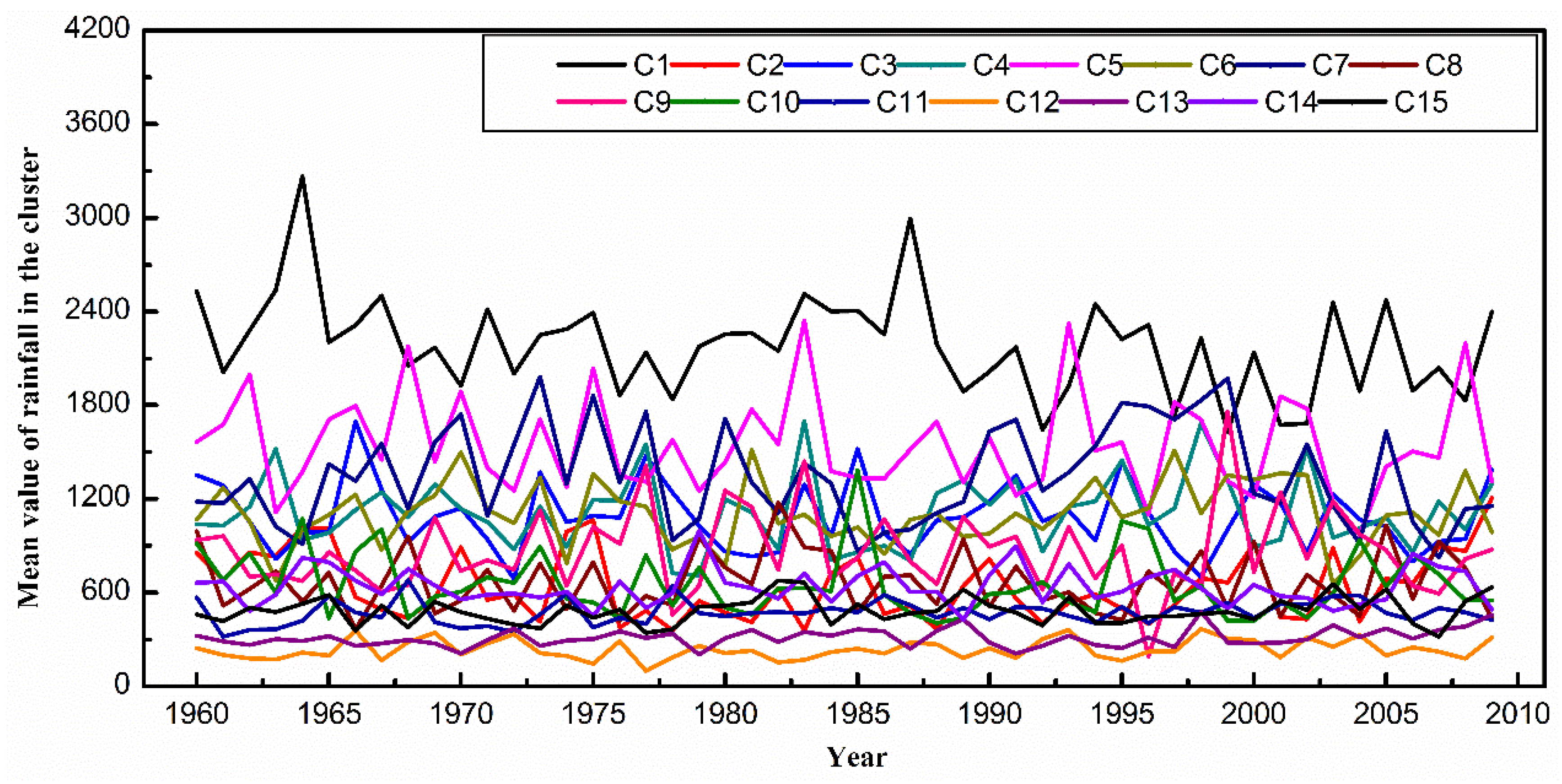
4.2. A Case Study of DTSC on Rainfall Data
5. Discussion and Further Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Guyet, T.; Nicolas, H. Long term analysis of time series of satellite images. Pattern Recognit. Lett. 2016, 70, 17–23. [Google Scholar] [CrossRef]
- Bidari, P.S.; Manshaei, R.; Lohrasebi, T.; Feizi, A.; Malboobi, M.A.; Alirezaie, J. Time series gene expression data clustering and pattern extraction in arabidopsis thaliana phosphatase-encoding genes. In Proceedings of the 8th IEEE International Conference on BioInformatics and BioEngineering, Athens, Greece, 8–10 October 2008; pp. 1–6.
- Kaur, G.; Dhar, J.; Guha, R.K. Minimal variability owa operator combining anfis and fuzzy c-means for forecasting bse index. Math. Comput. Simul. 2016, 122, 69–80. [Google Scholar] [CrossRef]
- Yin, J.; Zhou, D.; Xie, Q.Q. A clustering algorithm for time series data. In Proceedings of the 7th International Conference on Parallel and Distributed Computing, Applications and Technologies, Taipei, Taiwan, 4–7 December 2006; pp. 119–122.
- Uijlings, J.R.R.; Duta, I.C.; Rostamzadeh, N.; Sebe, N. Realtime video classification using dense HOF/HOG. In Proceedings of the ICMR 2014: International Conference on Multimedia Retrieval, Glasgow, UK, 1–4 April 2014; pp. 145–152.
- Chandrakala, S.; Sekhar, C.C. A density based method for multivariate time series clustering in kernel feature space. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hongkong, China, 1–8 June 2008.
- Yeang, C.; Jaakkola, T. Time series analysis of gene expression and location data. Int. J. Artif. Intell. Tools 2003, 14, 305–312. [Google Scholar] [CrossRef]
- Xu, T.; Shang, X.; Yang, M.; Wang, M. Bicluster algorithm on discrete time-series gene expression data. Appl. Res. Comput. 2013, 30, 3552–3557. [Google Scholar]
- Yan, L.; Kong, Z.; Wu, Y.; Zhang, B. Biclustering nonl inearly correlated time series gene expression data. J. Comput. Res. Dev. 2008, 45, 1865–1873. [Google Scholar]
- Liu, Q.; Deng, M.; Shi, Y.; Wang, J. A density-based spatial clustering algorithm considering both spatial proximity and attribute similarity. Comput. Geosci. 2012, 46, 296–309. [Google Scholar] [CrossRef]
- Ramirez-Lopez, L.; Schmidt, K.; Behrens, T.; van Wesemael, B.; Demattê, J.A.M.; Scholten, T. Sampling optimal calibration sets in soil infrared spectroscopy. Geoderma 2014, 226–227, 140–150. [Google Scholar] [CrossRef]
- Chan, C.-W. Modified particle swarm optimization algorithm for multi-objective optimization design of hybrid journal bearings. J. Tribol. 2014, 137. [Google Scholar] [CrossRef]
- Liu, Q.; Deng, M.; Shi, Y. Adaptive spatial clustering in the presence of obstacles and facilitators. Comput. Geosci. 2013, 56, 104–118. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Liu, D.; Liu, L. An adaptive dual clustering algorithm based on hierarchical structure: A case study of settlements zoning. Trans. GIS 2016, in press. [Google Scholar]
- Liu, Q.; Deng, M.; Peng, D.; Wang, J. Validity assessment of spatial clustering methods based on gravitational theory. Geomat. Inf. Sci. Wuhan Univ. 2011, 36, 982–986. [Google Scholar]
- Guo, W.Z.; Chen, J.Y.; Chen, G.L.; Zheng, H.F. Trust dynamic task allocation algorithm with nash equilibrium for heterogeneous wireless sensor network. Secur. Commun. Netw. 2015, 8, 1865–1877. [Google Scholar] [CrossRef]
- Grubesic, T.H.; Wei, R.; Murray, A.T. Spatial clustering overview and comparison: Accuracy, sensitivity, and computational expense. Ann. Assoc. Am. Geogr. 2014, 104, 1134–1156. [Google Scholar] [CrossRef]
- Sanderson, M.; Christopher, D. Manning, Prabhakar Raghavan, Hinrich Schütze, Introduction to Information Retrieval; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Meng, F.; Li, X.; Pei, J. A feature point matching based on spatial order constraints bilateral-neighbor vote. IEEE Trans. Image Process. 2015, 24, 4160–4171. [Google Scholar] [CrossRef] [PubMed]
- Nosovskiy, G.V.; Liu, D.; Sourina, O. Automatic clustering and boundary detection algorithm based on adaptive influence function. Pattern Recognit. 2008, 41, 2757–2776. [Google Scholar] [CrossRef]
- Hou, G.; Wang, J.; Guo, Q.; Yan, X. A study on the cumulative distributions of rainfall rate R_1 (0.01) over China. J. Beijing Inst. Technol. 2002, 22, 262–264. [Google Scholar]
- Keogh, E.; Chakrabarti, K.; Pazzani, M.; Mehrotra, S. Dimensionality reduction for fast similarity search in large time series databases. Knowl. Inf. Syst. 2002, 3, 263–286. [Google Scholar] [CrossRef]
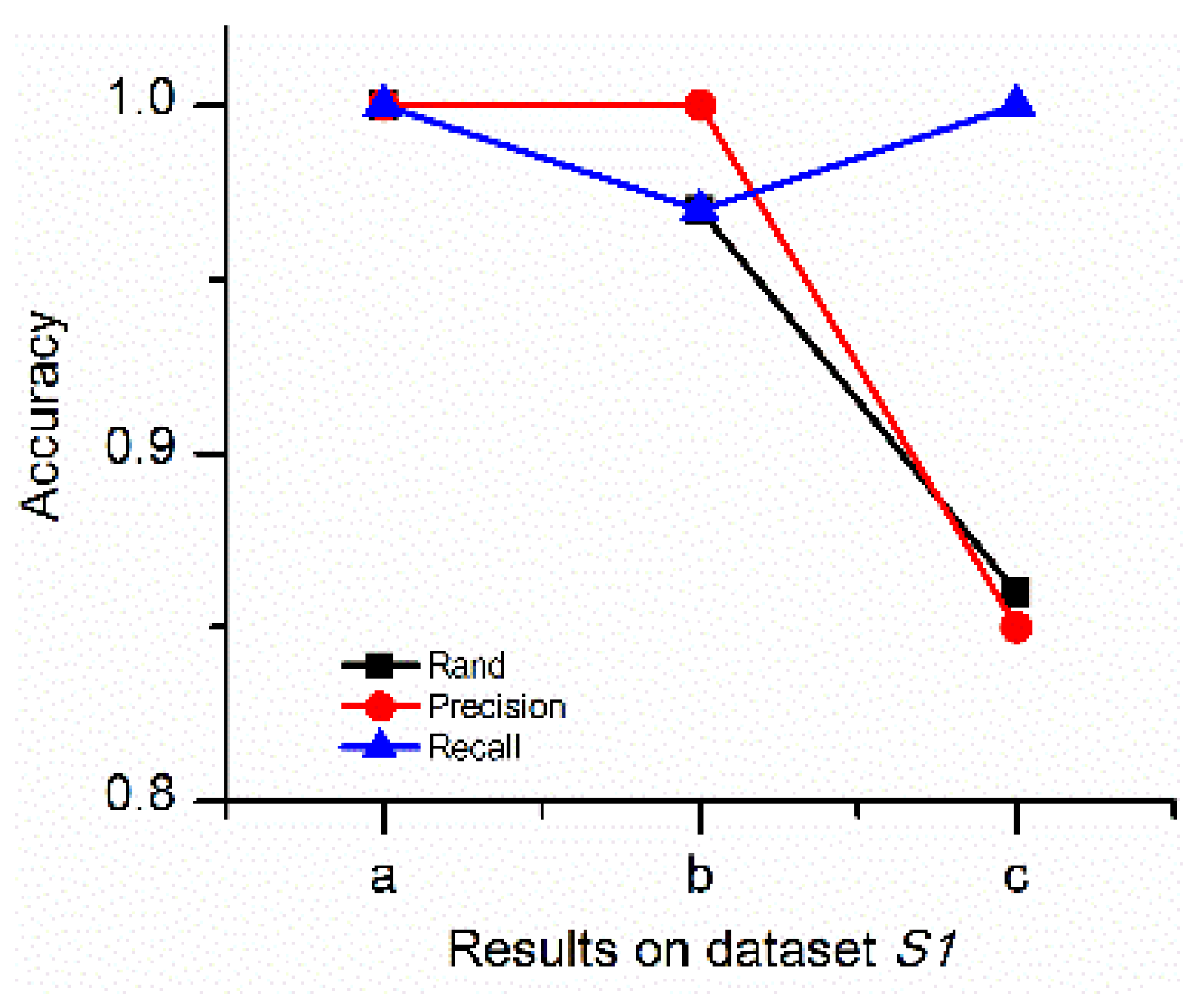

| Clustering Results | Simulated Dataset | Accuracy Values | Computation Cost | |||
|---|---|---|---|---|---|---|
| Rand | Precision | Recall | Time (s) | |||
| Results of DTSC | √ | 1 | 1 | 1 | 5 | |
| Results of density-based time series clustering algorithm | √ | 0.95 | 0.95 | 1 | 4 | |
| Results of DTSC | √ | 1 | 1 | 1 | 4 | |
| Results of density-based time series clustering algorithm | √ | 0.65 | 0.55 | 0.44 | 3 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Liu, Y.; Chen, Y.; Liu, Y. An Adaptive Density-Based Time Series Clustering Algorithm: A Case Study on Rainfall Patterns. ISPRS Int. J. Geo-Inf. 2016, 5, 205. https://doi.org/10.3390/ijgi5110205
Wang X, Liu Y, Chen Y, Liu Y. An Adaptive Density-Based Time Series Clustering Algorithm: A Case Study on Rainfall Patterns. ISPRS International Journal of Geo-Information. 2016; 5(11):205. https://doi.org/10.3390/ijgi5110205
Chicago/Turabian StyleWang, Xiaomi, Yaolin Liu, Yiyun Chen, and Yi Liu. 2016. "An Adaptive Density-Based Time Series Clustering Algorithm: A Case Study on Rainfall Patterns" ISPRS International Journal of Geo-Information 5, no. 11: 205. https://doi.org/10.3390/ijgi5110205
APA StyleWang, X., Liu, Y., Chen, Y., & Liu, Y. (2016). An Adaptive Density-Based Time Series Clustering Algorithm: A Case Study on Rainfall Patterns. ISPRS International Journal of Geo-Information, 5(11), 205. https://doi.org/10.3390/ijgi5110205








