1. Introduction
In this paper we propose a semi-automatic mobile modelling system for creating building plans. Specifically, we tackle the problem of constructing as-built plans of residential homes. In this scenario, accurate and aesthetically pleasing building plans are extremely desirable. Homeowners require precise metric modelling of domestic spaces for house renovations or new furniture arrangements. Similarly, estate agents need high quality interior measurements, often with quality requirements defined by a regulatory body.
While advances in laser scanning (e.g., Mura
et al. [
1] and Oesau
et al. [
2]), low-cost depth cameras (e.g., Henry
et al. [
3] and Khoshelham and Elberink [
4]) and imagery-based photogrammetric methods (e.g., Colburn
et al. [
5] and Cabral and Furukawa [
6]) are making indoor 3D reconstruction more accessible, such methods often require expensive equipment, trained operators and further detailed and skilled modelling steps to generate useful information from large point cloud datasets. For these reasons, and given the prevalence of smartphones, our experiments and system design focus on using imprecise measurements of interior spaces estimated from mobile phone orientation sensors. In particular, we use the accelerometer, magnetometer and gyroscope sensors.
The mapping of building interiors to generate accurate floor plans is a time-consuming and error prone task. Discrepancies in room dimensions, wall thicknesses, imprecise and inaccurate measurement tools inevitably lead to gaps and conflicts in the plan drafts. When the measurements are assembled to form a complete plan, the geometry representing walls and rooms may be found to under- or overshoot the exterior boundary. To resolve these deficiencies, manual adjustments to the plan often need to be carried out by hand in order to generate an aesthetic and coherent representation of a building. When utilising a measurement device that generates particularly noisy and imprecise representations, many adjustments to the input data may be required to create a satisfactory result.
Approach: In this work we use a simple interactive mobile tool for users to measure the internal surfaces of the building. The user navigates through a floor of a building, measuring each interior space or room as an individual 2D shape. These individual representations are assembled within a precise building outline in plan view on the mobile device. Then using the building outline and interior topology, automatic adjustments to room measurements are carried out. Using constrained modelling we simultaneously improve positional accuracy and resolve discrepancies in the building plan geometry. The building plans may then be used to generate extruded 2.5D building models.
Our contributions include:
demonstration of an end-to-end system for semi-automatic generation of semantic building models from imprecise interior measurements made with an interactive smartphone application;
a constrained optimisation model that exploits knowledge of building construction and exterior data to scale and refine interior measurements using stochastic optimisation;
quantitative evaluation of improvements in positional accuracy from use of the optimisation model;
a comparison of the proposed method with simple registration and scaling of imprecise plan measurements.
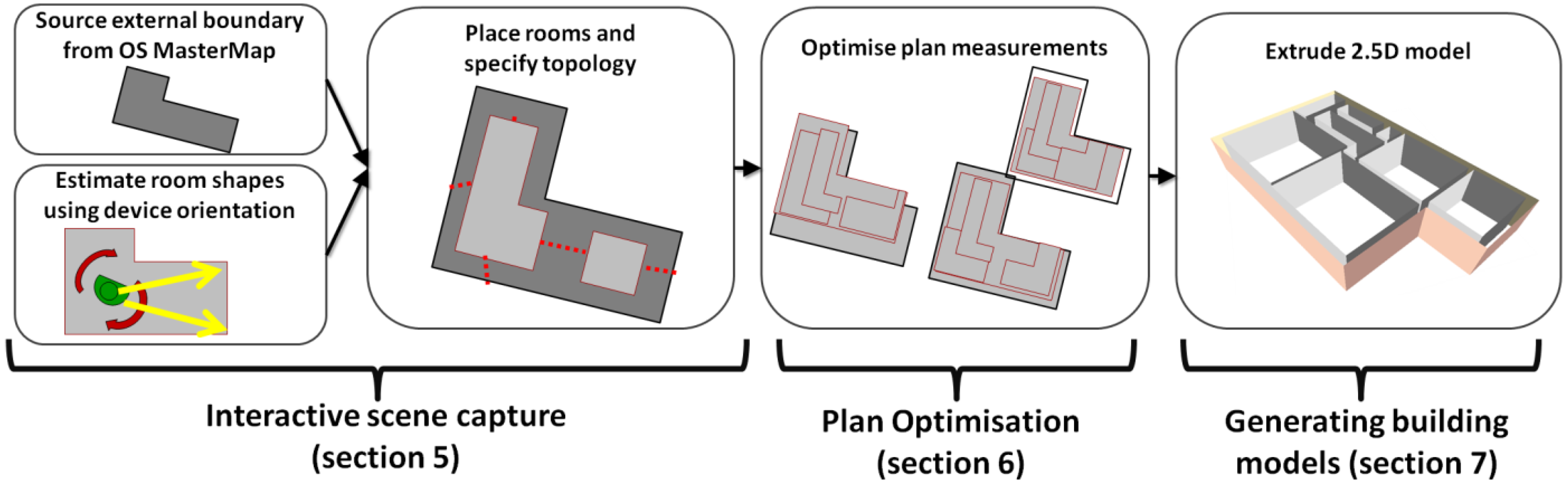
4. System Overview
Our system enables semi-automatic construction of metric scale semantic building models that fulfil the Manhattan-world assumption. The Manhattan-world view asserts that the planar geometry of the interior space comprises three dominant orientations. The system uses a simple orientation-based smartphone application to measure room dimensions. After user specification of room topology (door and wall adjacencies), internal measurements are automatically improved by fusing the interior data with a building outline sourced from a topographic map database. Finally, semantic building models are constructed with appropriate wall adjacencies and room connectivity information.
Figure 1 provides an overview of the system processes.
Figure 1.
System overview and associated paper sections.
Figure 1.
System overview and associated paper sections.
5. Interactive Scene Capture
5.1. Interior Measurements
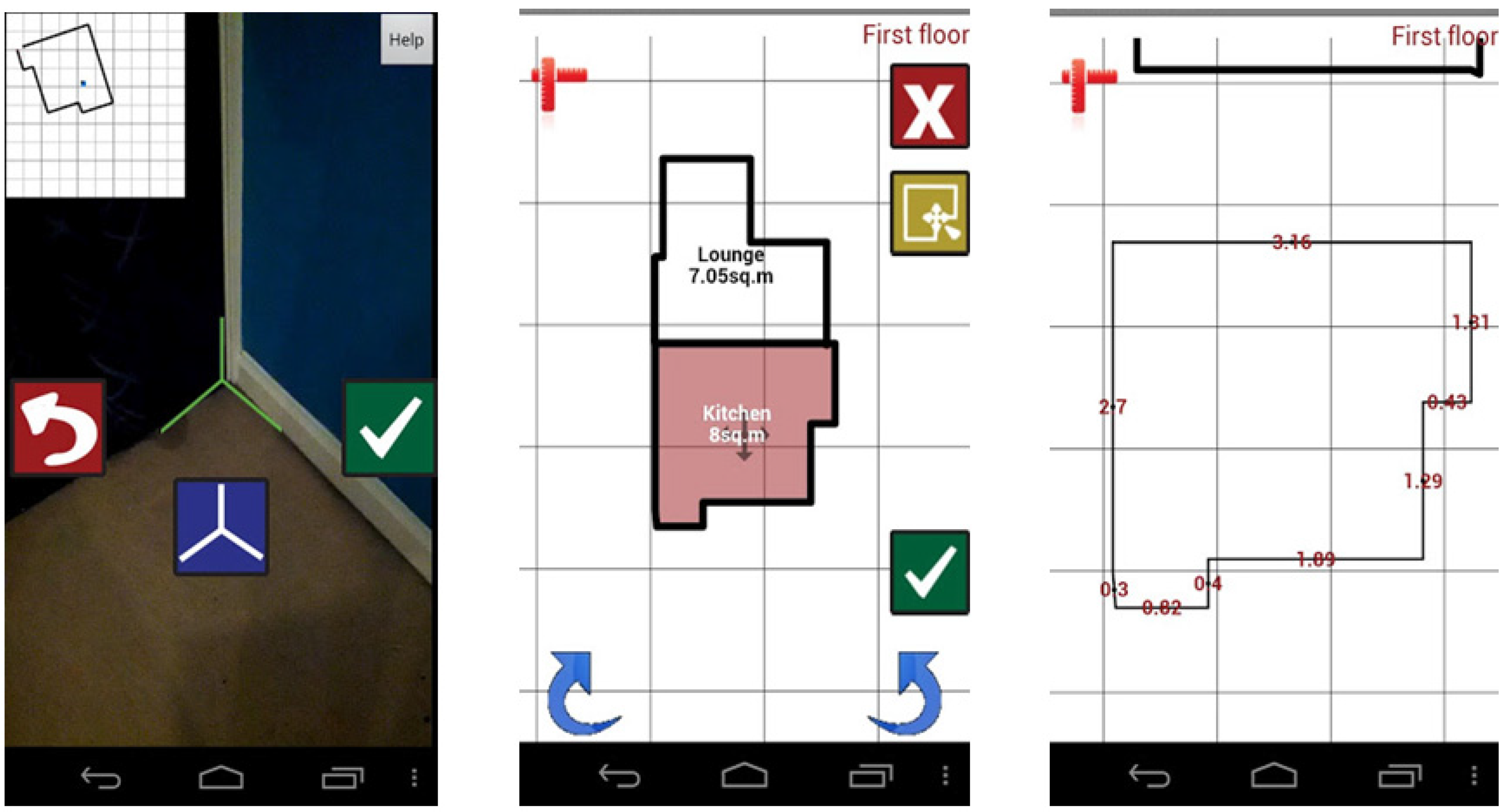
For interactive capture of building measurements, we use a smartphone-based room measuring tool (further details, see Rosser
et al. [
28]). In brief, the tool utilises the orientation sensors embedded within the device and a camera preview to capture room shape and height data. Users fulfil an interaction similar to capturing a panoramic photograph—a process considered to be familiar to many smartphone operators. Users rotate on the spot in the centre of the room and capture wall corner points at floor level (see
Figure 2 left). Points are added in order, with a 2D polyline constructed and displayed to the user in real-time. As users are relied upon to denote corner points which may be occluded in some indoor scenes, this display enables gross blunders in measurements to be detected during the capture process. For each point denoted, the device orientation (azimuth, pitch and roll) is estimated using the accelerometer, magnetometer and gyroscope sensors. The relative locations of corner points are calculated by assuming a pre-specified device height and trigonometry to estimate range. Collectively these points represent the internal boundary of a room.
Figure 2.
Mobile application screens. Room capture (left), room layout (centre), room measurement detail (right).
Figure 2.
Mobile application screens. Room capture (left), room layout (centre), room measurement detail (right).
This simple modelling approach assumes a particular device height which scales the room geometry. However, an accurate value is not necessary as during plan optimisation (see
Section 6) the measurements are resolved to fit within the building footprint, resulting in an appropriate scaling. To help with the measurement collection we assume the room geometry comprises parallel and orthogonal walls and solve for the rectilinear shape defined by the corner points using least-squares.
The constrained least-squares approach by Gander and von Matt [
29] is adopted, with a system of linear equations (in this case representing wall surfaces) constructed and solved during scene capture. The rectilinear constraint asserts that all lines must be either parallel or orthogonal to each other and this is exploited within the least-squares approach. The approach assumes that room points are added in sequence and together form a polyline. As a new line is added during the room capture process, the angle between itself and the previous line is evaluated and the line is labelled as parallel or orthogonal. The lines form measurement observations within the least-squares system which is solved using QR decomposition and Singular Value Decomposition. To ensure lines are labelled correctly as orthogonal or parallel, the application displays feedback to the user of the constructed room shape during scene capture. Once points of all room corners are added by the user—a process that takes approximately 20 seconds per room—the final best fit rectilinear room shape may be computed.
5.2. Initial Plan Layout and Topology Generation
Complete plans of building floors may be generated using the above technique and a sequence of simple user interactions. Each room is measured independently and manually placed in a plan view (see
Figure 2 centre). Individual wall measurements may also be visualised (see
Figure 2 right). During layout, any extraneous features that may be evident in the building outline taken from the topographic map data can be edited out. Any interior spaces that can’t easily be measured, such as cupboards built into walls, may be flagged as padding areas between rooms. Lastly, users specify adjacency relations between paired walls and doors. These maybe defined by tapping or clicking points on each room shape.
While a number of these steps could be achieved automatically and/or can be skipped, the inclusion of these low complexity interactions that can be performed on the capture device provides the opportunity to the user to trade off additional interaction for increased plan accuracy.
5.3. External Boundary
An external boundary representing the building outline provides an enclosed space within which interior measurements are positioned and adjusted. The boundary is assumed to be a polygon captured to a high accuracy and representing the exterior footprint (outline) of the building. In our experiments we test building footprints generated both from ground-survey and large-scale topographic mapping sourced from a national mapping agency. Our rationale is that topographic mapping provides a high-level of accuracy and a widely available source of scale and geographic coordinate reference data. For example, Ordnance Survey MasterMap data is defined to have a nominal accuracy of 1 m (99% confidence interval) in urban areas [
30].
5.4. Representation
Interior plans are modelled as a set of rectilinear polygons representing internal measurable dimensions of rooms. We distinguish between different types of topological structure with the model: Rooms connected by doorways and shared walls. Each door opening is modelled as two individual points positioned along each boundary (wall) of the corresponding rooms. Adjacent walls (polygon edges) are also modelled in a pairwise fashion, but are labelled differently to support different cost terms during optimisation (see
Section 6.4.2).
6. Plan Optimisation
Various factors contribute to errors in the interior dimensions produced using the interactive capture tool. Noise in the sensor data creates errors in the corner point estimation. Users may incorrectly mark corners in the camera preview by accident or as a result of scene obstructions. Furthermore, while room dimensions are calculated based on a user specified device height the scale of the model cannot be assumed to be correct. These errors result in room measurements that are incompatible between different rooms or with building footprint data, requiring further optimisation.
The core of our system makes automatic adjustments of imprecise room models to find the best fit of measurements within the constraints of the building outline. A set of interior and exterior measurements and specified adjacency data structures between rooms and exterior features form the inputs to the optimisation. The result of the adjustment process is a set of room measurements with improved accuracy and a plausible integration with topographic map data allowing generation of georeferenced 2.5D semantic building models.
6.1. Simulated Annealing
The optimisation problem is complex as the shape and position of each room in the plan must be adjusted across a continuous distribution of possible values. However, modifications to individual room geometry can also generate conflicts with other parts of the plan. A global approach is required that enforces soft constraints on the geometry (such as wall dimensions, room area and position) and hard constraints (such as room shape and topology). This limits the usefulness of local search techniques (such as gradient-descent) which are prone to getting trapped in local minima.
To address this problem a stochastic optimisation method is adopted, specifically simulated annealing, to search for a good approximation to the global optimum [
31]. Simulated annealing accepts moves that decrease a cost function but avoids becoming trapped in local minima by also accepting poor state adjustments at a certain level of probability. The probability with which poor moves are accepted decreases according to a cooling schedule. A cooling schedule that is too quick will result in insufficient exploration of the search space and is likely to return a local minimum solution. However, a rate that is too slow is inefficient and may take too long to converge to be of practical use.
The Metropolis criterion is used to determine the probability of transitioning to a configuration using a Boltzmann-like objective function
where
is a building plan,
C is the cost function defined in
Section 6.4 and
is a constant. At each iteration, an adjustment produces a new configuration
which is accepted with probability.
6.2. Proposal Moves
To carry out cost evaluations within the simulated annealing optimisation process, the system must generate proposal moves. Proposal moves form a neighbourhood of candidate solutions around the current state of the system. It is of critical importance to generate a good range of alternative proposals if the optimisation is to fully explore the solution space and converge to a satisfactory solution. In particular, a candidate solution should be reachable from any other through the application of a sequence of proposal moves [
32].
Four proposal adjustments have been designed and implemented. A large number of proposal moves creates a large neighbourhood space. In general, small neighbourhoods are preferable [
32]. During each iteration of the algorithm, a proposal move is chosen for evaluation according to a uniform probability. In this work four moves have been defined. The first, room displacement, modifies a room’s entire geometry. The remaining three moves modify specific aspects of an individual room’s geometry. Hard constraints (discussed in
Section 6.3) prevent generation of plans with infeasible topology and maintain basic initial room shapes. See
Figure 3 for illustrations of each proposal move.
Figure 3.
Proposal moves. Room displacement (left), corner adjustment (centre left), wall adjustment (centre right), shared wall adjustment (right).
Figure 3.
Proposal moves. Room displacement (left), corner adjustment (centre left), wall adjustment (centre right), shared wall adjustment (right).
6.2.1. Room Displacement
A single room is permitted to move independently within the free space defined by the exterior building shell and other room elements. The move comprises a 2D translation. The magnitude and direction is determined from a normal distribution. Thus for room object i, its position defined as coordinates , maybe updated as where and x and y are variables relating to x and y coordinates. An effective value for was determined experimentally as 0.05 m.
6.2.2. Corner Adjustment
A pair of joined orthogonal walls of an individual room maybe translated normal to each of their respective directions. The corner vertex of the room is selected at random with each wall then translated by an equal amount. Using an equal amount allows rooms to enlarge and contract while maintaining a similar, but not identical, shape. This means an additional proposal move for scaling the room is not required. The magnitude of each wall translation is determined from a normal distribution where was determined experimentally as 0.05 m.
6.2.3. Wall Adjustment
The shape of a single room is adjusted by moving an individual wall. The wall is randomly chosen and translated orthogonal to its direction. The magnitude of the translation is determined from a normal distribution where was determined experimentally as 0.05 m.
6.2.4. Shared Wall Adjustment
Shared wall adjustment randomly chooses a pair of adjacent (parallel) walls and slides both features by the same distance. The magnitude of the translation is determined from a normal distribution where was determined experimentally as 0.05 m.
6.3. Hard Constraints
We define hard constraints to help limit the neighbourhood space and prevent generation of infeasible building plans. Proposed plans are tested for hard constraints before evaluation in the cost function and are rejected if found to contravene the following:
Shape constraints. Initial plans comprise rectilinear definitions of room shape. In cases where rooms are not rectangular (such as L-shapes), proposal moves modifying wall or corner positions should not generate inverted or reflected shapes.
Topological constraints. The topological structure of the plan that defines adjacent rooms, shared walls and doorways is assumed to be correct, and is preserved to ensure adjustments generate consistent building plans. Rooms in any configuration x must be inside the area defined by the exterior shell of the building. In effect, this ensures appropriate conflation of an exterior model with imprecise interior measurements. Similarly, rooms should not overlap each other.
6.4. Cost Function
The cost function
C(x) defines constraints appropriate to the layout of building interiors and provides the function for evaluating the quality of a given plan. The aim of the optimisation process is to minimise this cost function thus improving measurement quality. The choice of constraints is based on prior knowledge of likely building structure and preservation of essential information captured with the measuring device. The cost function is defined as
where
x is the building plan and
,
,
and
are weighting coefficients that define the relative importance of each corresponding cost term. In this work all weights were set to 1. The cost terms, wall thickness
Cwt, wall adjacency
Caw, door adjacency
Cad, room shape
Crs and room area
Cra, are defined individually below.
6.4.1. Wall Thickness
Walls are not infinitely thin and their thickness may vary substantially between different buildings and even within the same building. While many residential houses are of brick construction, the presence or absence of an external cavity wall varies wall thickness. For example, in the U.K many buildings built before the 1920s are formed from solid brick walls (maybe only 210 mm thick) whereas more recent constructions tend to have cavity walls [
33]. Interior wall partitions may also vary depending on load-bearing characteristics. To account for this variation we model both interior-exterior and interior-interior adjacencies and use an objective function to evaluate wall thickness. Let
denote all walls in the plan. The wall thickness cost for adjacent walls is
where
k = number of contiguous walls, where
D is the distance operator,
and
are a pair of walls,
= 1 if
and
are adjacent and 0 otherwise,
l and
u are lower and upper thickness bounds and
t is a thickness function. The objective function
t is defined as
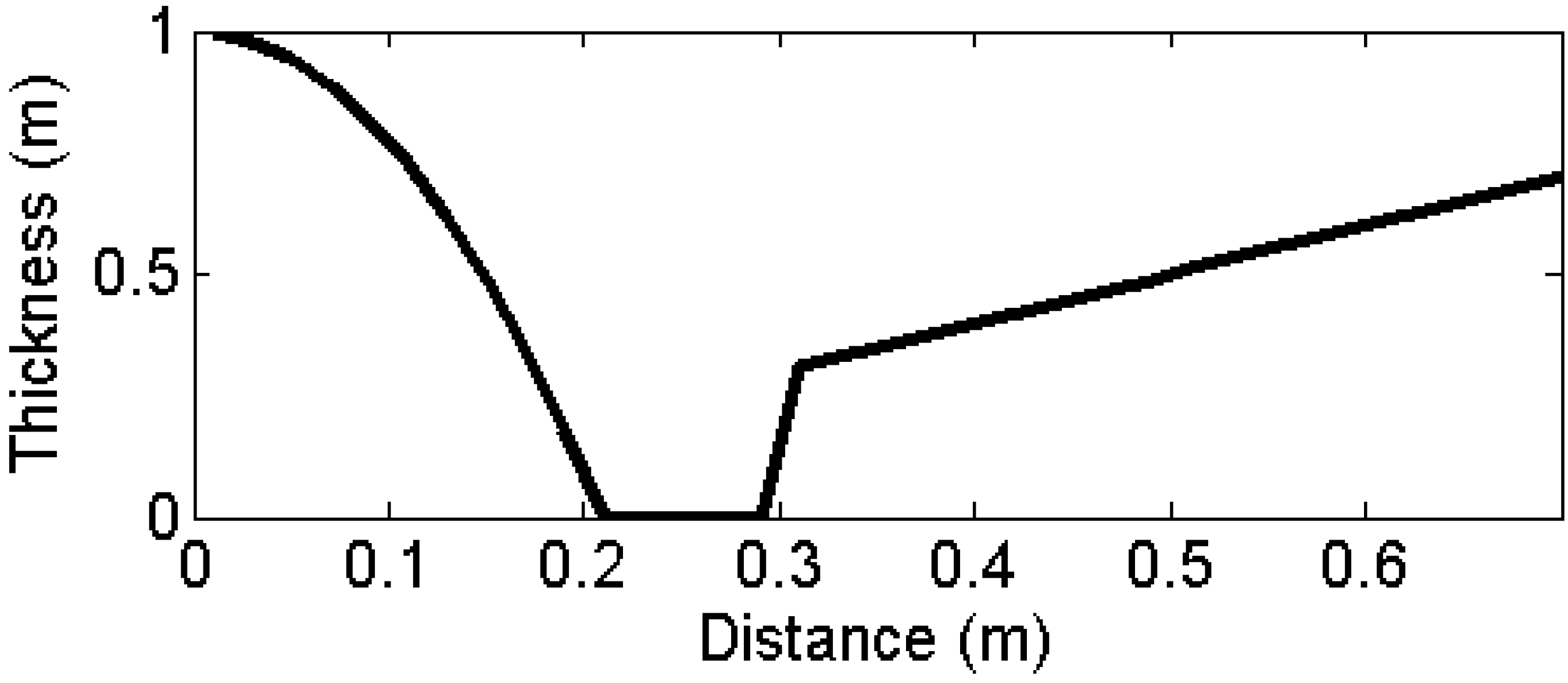
Function
t, illustrated in
Figure 4, drops to zero when distance
d is within the recommended range as defined by
l and
u. Values for
l and
u for interior-exterior walls were set as 0.21 m and 0.30 m to support single brick thickness and thicker cavity walls. Values for
l and
u for interior-interior walls were set at 0.15 m and 0.2 m respectively based on single brick and typical internal partition thicknesses [
34].
Figure 4.
Example function t(d,0.21,0.30).
Figure 4.
Example function t(d,0.21,0.30).
6.4.2. Plan Topology
The topological structure of a building, as defined by wall adjacencies and connecting doorways, must be maintained to ensure a likely building plan is generated. To achieve this we utilise the pairwise relationships between objects. For a pair of adjacent walls
f and
g, we take the maximum distance where the thickness is outside of the recommended upper limit
u, as defined in
Section 6.4.1.
where
= 1 if
f and
g are paired walls and 0 otherwise,
w is the set of walls and with
and
D is the distance operator. Intuitively, the term prevents rooms drifting apart excessively and prevents exploration of unlikely plan configurations during optimisation.
We also define a term to encourage additional cohesion between room models connected by a doorway.
where
= 1 if
a and
b are paired door points and 0 otherwise.
6.4.3. Room Shape
The input plan provides initial rectilinear polygonal room shapes. The room shape cost controls the similarity between initial shapes and those generated during the optimisation process. We use the edge proportionality to maintain room shape similarity. Intuitively, this term maintains the relative lengths of each section of wall that make up the room shape. The room shape cost is
where
is an edge in the initial room shape, and
e is the corresponding edge in the adjusted shape,
is an initial room shape,
R is the corresponding adjusted shape,
P is the perimeter operator
, m is the number of shape edges,
n is the number of rooms and ||.|| computes the Euclidean length of the edge.
6.4.4. Room Area
As with room shape, room area proportion is maintained to control similarities between initial plans and proposed adjustments. The room area cost is defined as
where
A is the area operator,
is an initial room shape,
is the corresponding adjusted shape and
n is the number of rooms.
7. Generating Building Models
Given a set of interior measurements and corresponding building footprint data we undertake post-processing prior to generating building models. We adopt the CityGML semantic data model which has been designed for defining and exchanging 3D urban information [
26]. It is defined so as to be applicable to the wide range of possible uses of 3D building models, contains accuracy recommendations and integrates with existing geospatial data referenced using global coordinate reference frames. Generation of semantic models with appropriately defined building components completes our approach as an end to end modelling system. The focus is on CityGML version 2 which is defined according to a UML conceptual schema for geographic information (ISO TS 19103) [
27].
Interior Geometry Post-Processing
External and internal walls may be extruded automatically and assigned with appropriate CityGML properties. Specifically, defining the external walls as a single polygon, the polygon may extruded to a pre-determined height, setting the extruded edges as WallSurface elements and setting the resulting MultiSurface as a LoD1 solid. Interior walls can be formed similarly with extruded edges set as InteriorWallSurface elements. The resulting LoD4 solid is set as a room and as part of the overall building element.
Doorways may also be added to the representations. In this work, doorway positions are modelled as single points on the walls, rather than a 2D or 3D geometry. However, instances of the semantic element Doorway, a sub-class of Opening maybe added to each room.
8. Results
To evaluate the proposed system, we present results for six building plans, denoted as plans A–F. Plans A and B model the same building interior but, to help evaluate our constrained optimisation model, for plan A alone we use external building footprint data based on ground-survey measurements taken using a Leica DISTO laser range finder. Plans B-F use external building footprints based on the Ordnance Survey’s MasterMap topographic mapping product. The interior dimension estimates were captured with a Samsung Galaxy Nexus mobile device and forms in the input data to the subsequent optimisation.
To provide ground-truth data for evaluation, measured surveys of each room were completed using a laser range finder. To enable accuracy comparisons, ground-truth survey data was represented in the same way as adjusted data i.e., ground-truth measurements, input measurements and output measurements contain an equal number of data points (corner coordinates). Positions of doorways are not included as part of the accuracy assessment as doorway positions are not estimated in the initial data collection. We also assess the area measurements.
Our constrained optimisation model is compared against a simple registration and enlargement of the input plan completed using stochastic gradient-descent, from here on referred to as gradient-descent for brevity. The method attempts to fit the initial plan, captured using the mobile tool, within building outline through iterative global enlargement and displacement and without modification of the individual imprecise measurements. To prevent production of implausible building plans, the minimum distance must be more than 0.21 m from the outline—the same common minimum external wall thickness used in our proposed model, see
Section 6.4.1.
For each plan an initial temperature for the simulated annealing process was found where between 40% and 60% of proposed moves that increase the cost were accepted [35]. In all cases the temperature T was cooled with a geometric schedule and stopped at a temperature of 0.3, after approximately 16,000 iterations.
8.1. Plan Adjustment Results
Our first experiment, plan A, investigates adjustments using an exterior building footprint based on ground-survey.
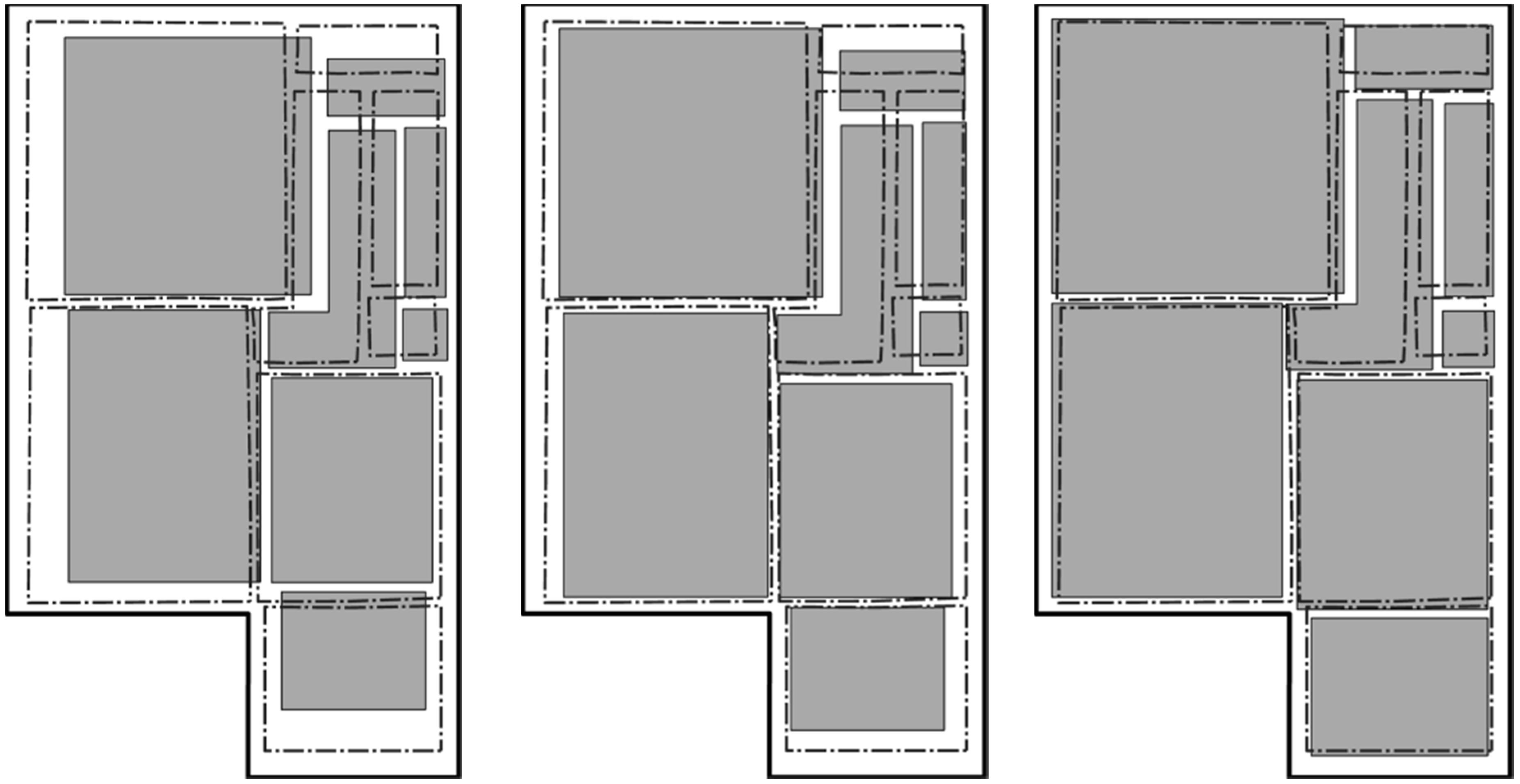
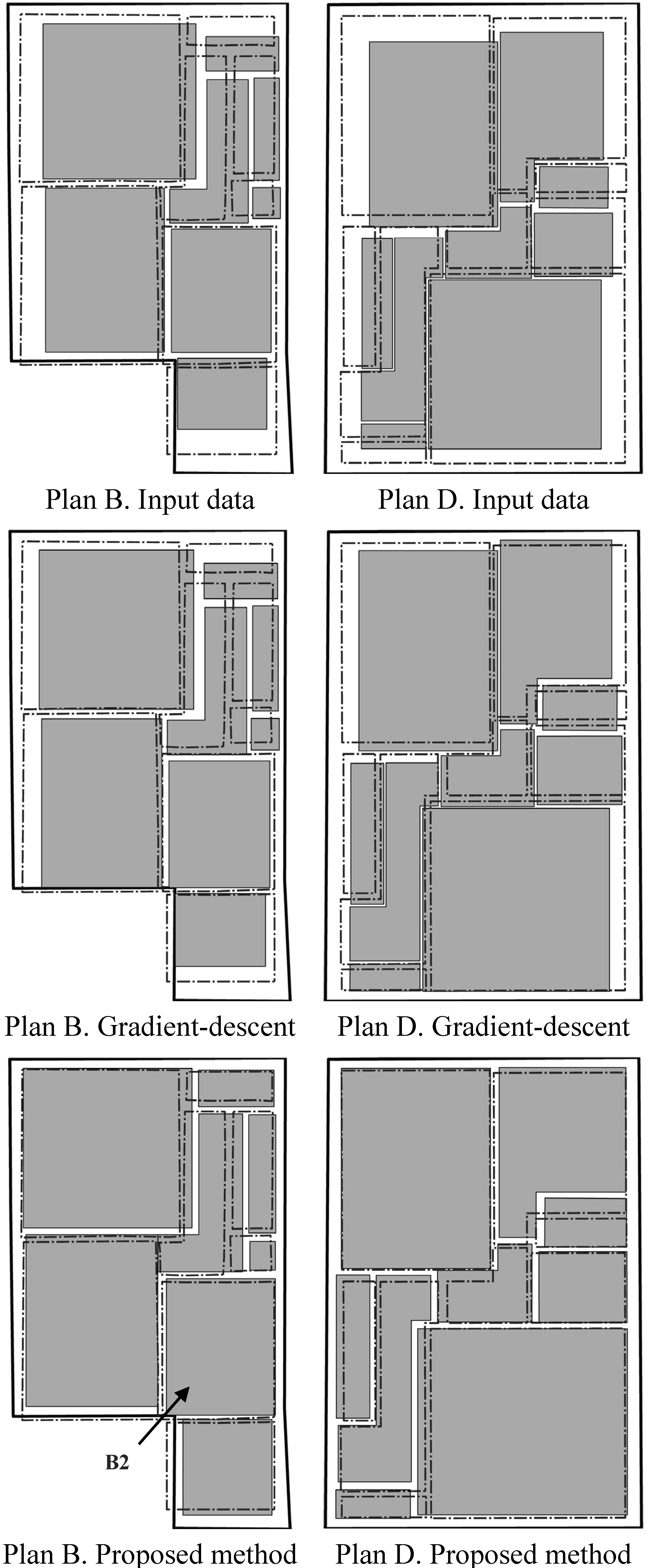
Figure 5 shows input data for plan A with adjustment results of the gradient-descent method and our proposed approach. Visually, the proposed approach shows an improved match to the ground-truth data compared with the simpler method. Appropriate inter-room and external wall thicknesses are maintained.
The rest of our experiments details tests on plans constrained by topographic map data.
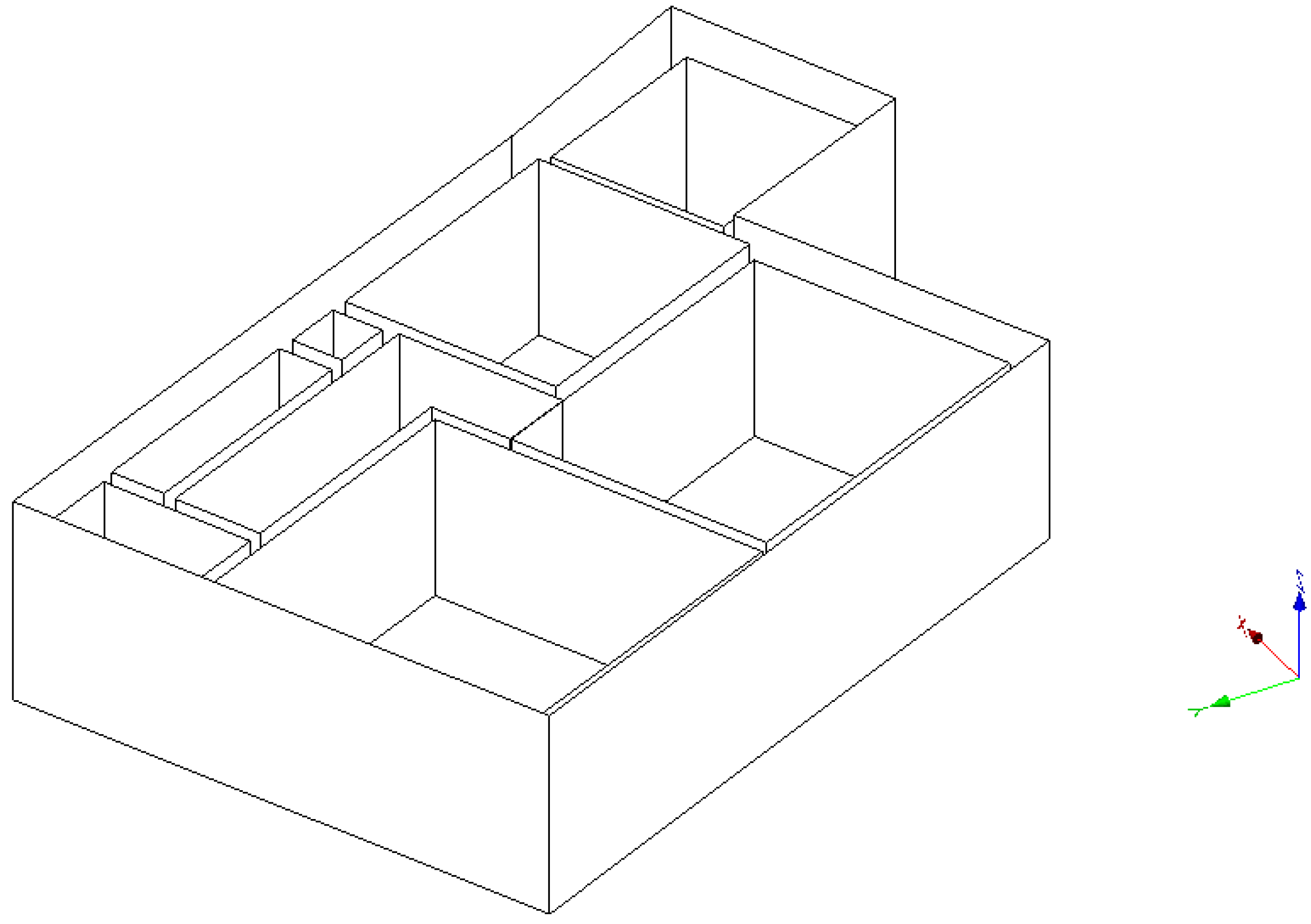
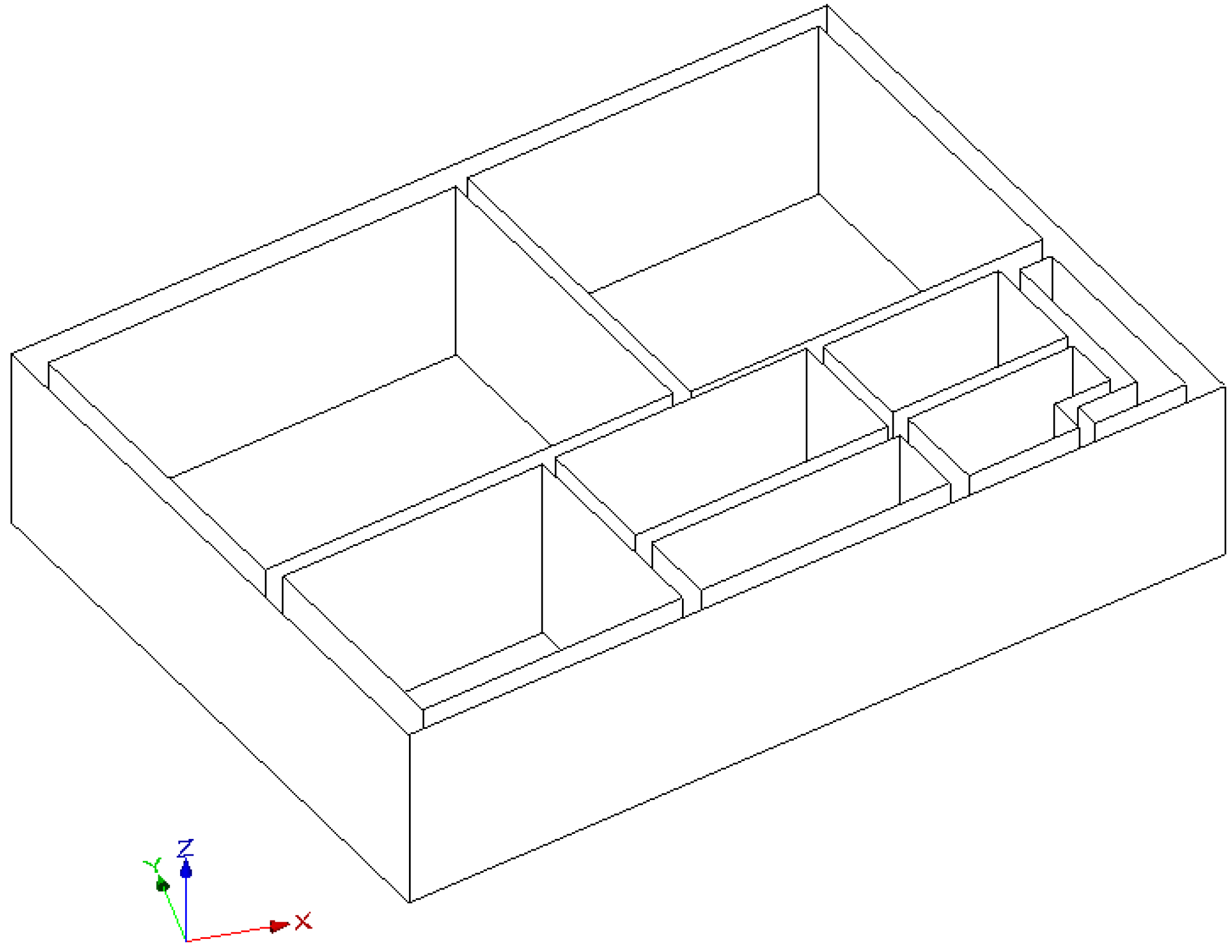
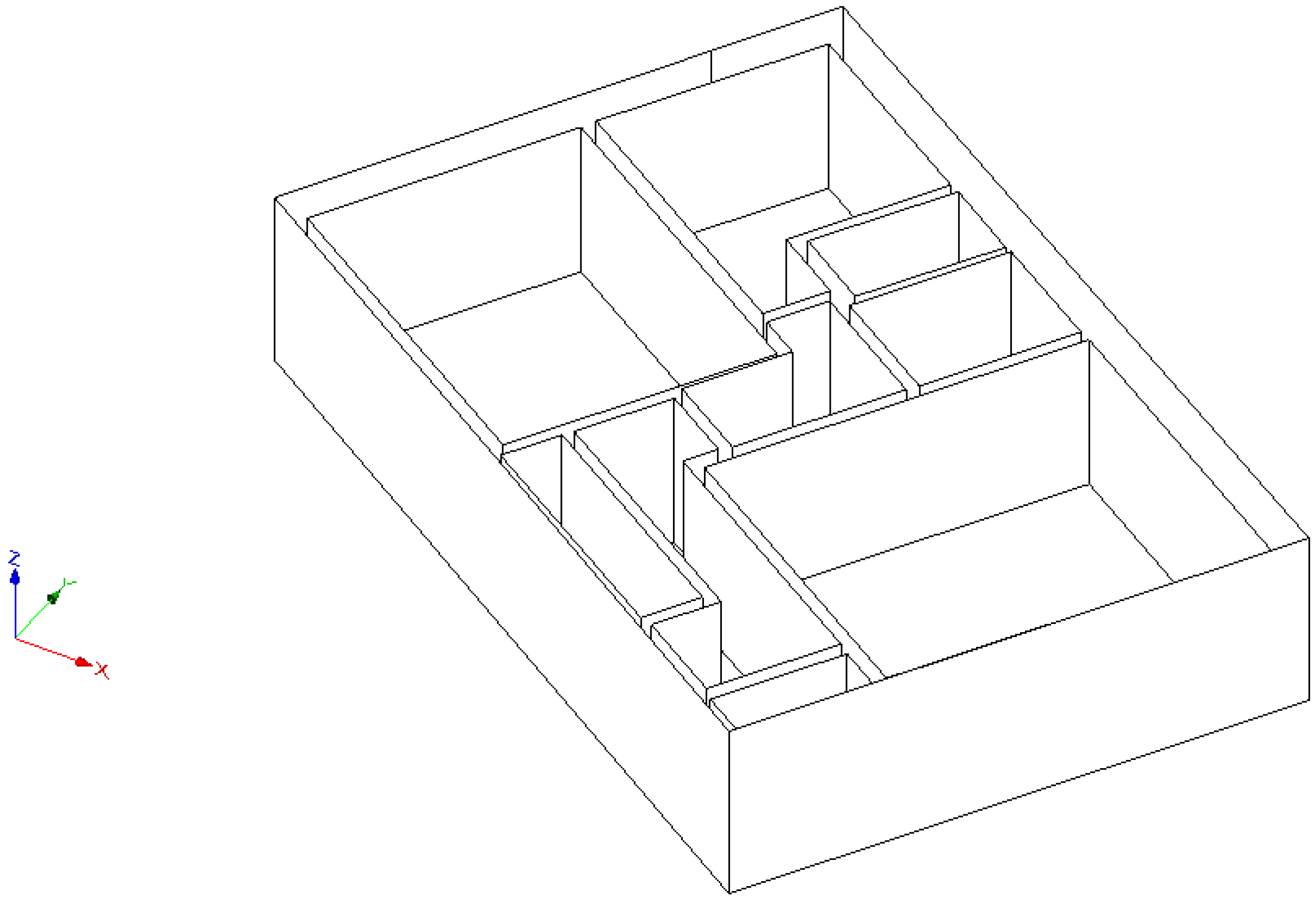
Figure 6 shows the input data and results generated using the gradient-descent based registration method and using the proposed simulated annealing-based method for plans B and D. The proposed method appears to resolve most anomalous measurements in the input data. Fewer large discrepancies between the ground-truth and the room measurements using the proposed method appear in comparison to gradient-descent registration. Notice that for plan B, the ground-truth measurements extend beyond the building footprint due to slight underestimation of dimensions in the topographic mapping. We assume the boundary as correct, making adjustments inside it, thus the proposed method is limited in the improvement it may make. However, the final result is still qualitatively better than gradient-descent. Plans C, E and F results are included in
Appendix A (
Figure A1). Extruded 2.5D models of plans B, C and D are shown in
Figure 7,
Figure 8 and
Figure 9, visualised using FZKViewer [
36].
Figure 5.
Input plan (left), gradient-descent (centre) and proposed method results for plan A (right). Plan measurements (solid grey), ground-truth (dashed lines).
Figure 5.
Input plan (left), gradient-descent (centre) and proposed method results for plan A (right). Plan measurements (solid grey), ground-truth (dashed lines).
Figure 6.
Input plans, gradient-descent and proposed method estimation results for plans B (
left) and D (
right). Plan measurements (solid grey), ground-truth (dashed lines). See
Section 8.3 regarding B2 annotation.
Figure 6.
Input plans, gradient-descent and proposed method estimation results for plans B (
left) and D (
right). Plan measurements (solid grey), ground-truth (dashed lines). See
Section 8.3 regarding B2 annotation.
Figure 7.
Plan B, extruded models viewed as CityGML.
Figure 7.
Plan B, extruded models viewed as CityGML.
Figure 8.
Plan C, extruded models viewed as CityGML.
Figure 8.
Plan C, extruded models viewed as CityGML.
Figure 9.
Plan D, extruded models viewed as CityGML.
Figure 9.
Plan D, extruded models viewed as CityGML.
8.2. Accuracy Assessment
We considered a range of accuracy assessments, choosing plan root mean squared error (RMSE), individual room RMSE and area measures as most appropriate to the production of accurate semantic building models. Plan RMSE is defined as
where
d is the distance between corresponding pairs of room corner points in the adjusted and ground-truth data and
n is the total number of pairs across the whole plan. Individual room RMSE is computed in a similar fashion—evaluating corresponding corner points on a per-room basis.
Table 1 compares RMSE across all plans from the gradient-descent and the proposed methods. For the full set of results by room, see
Appendix B (
Table B1). Overall, the proposed method was found to improve input data accuracy by 46%, lowering the mean RMSE from 0.45 m to 0.24 m. The gradient-descent method improved accuracy by 28%, achieving 0.33 m. On average the proposed method was found to give a 25% improvement on RMSE over the gradient-descent approach, in real terms a mean positional accuracy advantage of 0.09 m.
While the mean performance over an entire building is an important measure of accuracy, it is often the case that plans are used in practice on a room by room basis. As such, the overall utility of building plans are often limited by the individual room accuracy. As an additional indicator of accuracy we therefore report the worst case room RMSE for each building. This is shown in
Table 1. On average, worst case room accuracy was 0.32 m with the proposed method compared to 0.44 m using the gradient-descent approach. It is notable that for plan B, the gradient-descent approach worst case positional accuracy is 0.60 m, with the proposed method improving this to 0.33 m.
Table 1.
RMSE (m) by plan vs. ground truth.
Table 1.
RMSE (m) by plan vs. ground truth.
| Plan | Plan Accuracy RMSE | Max Room RMSE |
|---|
| Input | Gradient Desc. | Proposed Method | Input | Grad. Desc | Proposed Method |
|---|
| A | 0.47 | 0.34 | 0.23 | 0.61 | 0.48 | 0.32 |
| B | 0.44 | 0.27 | 0.60 | 0.33 |
| C | 0.49 | 0.28 | 0.18 | 0.64 | 0.40 | 0.25 |
| D | 0.43 | 0.27 | 0.25 | 0.65 | 0.35 | 0.36 |
| E | 0.48 | 0.36 | 0.30 | 0.55 | 0.44 | 0.38 |
| F | 0.39 | 0.29 | 0.23 | 0.57 | 0.36 | 0.27 |
In addition to absolute geometric position, accurate measures of room area are important for indoor survey applications and provide an indication of relative accuracy. Area values, percentage improvement on input data, and absolute area accuracy are presented in
Table 2. On average the input data area was improved by 89% using the proposed method while gradient-descent provided a 47% improvement. The proposed method showed a mean absolute area accuracy of 98%, compared to 89% using gradient-descent.
Table 2.
Area results.
| Plan | Total Area (m2) | Improvement On Input Data (%) | Absolute Area Accuracy (%) |
|---|
| Input | Grad. Desc. | Proposed Method | Ground Truth | Grad. Desc. | Proposed Method | Grad. Desc. | Proposed Method |
|---|
| A | 38.56 | 42.03 | 48.02 | 47.32 | 40 | 92 | 89 | 99 |
| B | 40.62 | 45.92 | 24 | 84 | 86 | 97 |
| C | 34.88 | 41.71 | 46.93 | 45.81 | 62 | 90 | 91 | 98 |
| D | 48.92 | 57.28 | 62.29 | 61.54 | 66 | 94 | 93 | 99 |
| E | 38.86 | 42.40 | 47.52 | 46.87 | 44 | 92 | 90 | 99 |
| F | 32.27 | 36.64 | 40.04 | 41.91 | 45 | 81 | 87 | 96 |
It is important to note that the accuracy of the gradient-descent method is highly sensitive to the initial placement of the rooms in the exterior boundary (in this case from MasterMap data). While for this evaluation careful placement was undertaken so as to not significantly disadvantage the gradient-descent in the evaluation, in general this stage would be achieved using a simple graphical user interface and prone to arbitrary amounts of error. Therefore it is important to note that in real use environments the gradient-descent method may in fact result in worse performance than reported here since, unlike the proposed method, there are no adjustments to individual room positions during optimisation. Thus the quality of the resulting plan is dependent on accurate initial relative placement of each room geometry.
Together the RMSE and area results show a marked improvement on building plan quality through the application of the constraint-based optimisation presented in this work. With the proposed method’s tolerance to imprecise initial room placement within the exterior measurements, the approach results in a positional accuracy demonstrably closer to the CityGML recommended requirement of 0.2 m.
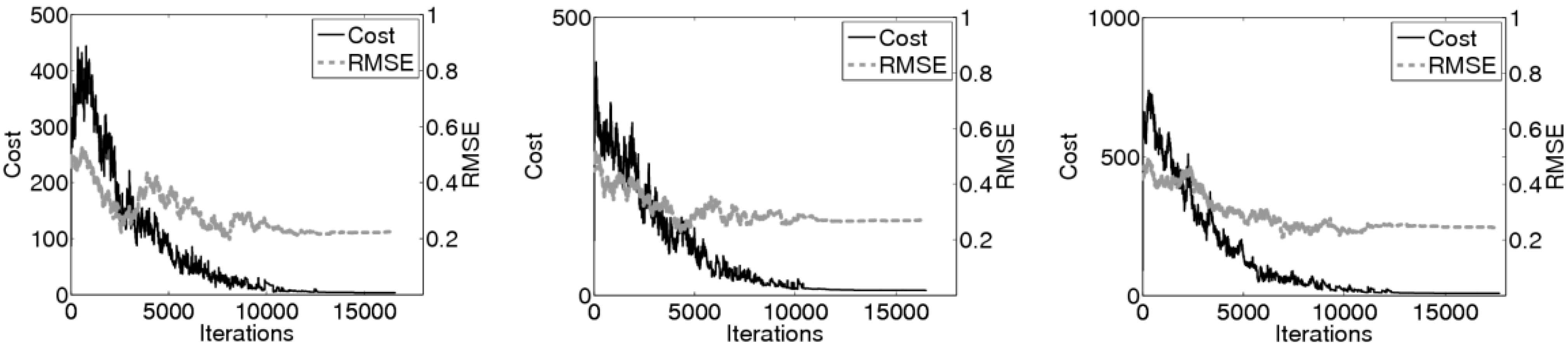
8.3. Solution Stability
As a stochastic optimisation, simulated annealing produces slightly different solutions for each trial run. To be useful, the optimisation model should consistently converge close to the optimal arrangement. To assess the stability of the optimisation, 50 trials each were completed on plans A, B and D. The annealing parameters matched those used in the main experiments.
Table 3 shows mean and standard deviation results for cost and RMSE. Recall that plan A and plan B comprise the same interior measurements but use different external boundary data. The high standard deviation in cost for plan B is due to the underestimated external boundary. Specifically, the concave shape of the boundary results in two cost minima, where the room B2 may be deformed either horizontally or vertically to fit within the L-shaped plan (see
Figure 5, plan A
versus Figure 6, plan B—for plan B the less optimal minimum has been chosen.
Figure 10 shows example optimisation runs and RMSE improvement for plans A, B and D. At the start of the optimisation process the RMSE is seen to be high when room models are incorrectly scaled and positioned. As the cost decreases, the accepted moves result in a more accurate plan until convergence.
Table 3.
Stability results.
Table 3.
Stability results.
| Plan | Cost | Cost | (m) RMSE | (m) RMSE |
|---|
| A | 4.41 | 0.46 | 0.24 | 0.02 |
| B | 10.92 | 3.19 | 0.30 | 0.04 |
| D | 8.2 | 0.89 | 0.25 | 0.03 |
Figure 10.
Example optimisation runs for plans A (left), B (centre) and D (right) showing cost and RMSE vs. iteration number.
Figure 10.
Example optimisation runs for plans A (left), B (centre) and D (right) showing cost and RMSE vs. iteration number.
8.4. Discussion of Modelling Limitations
Several limitations in this research should be highlighted. One notable drawback of the process concerns the handling of geometric modelling of doorways. At LoD4 the CityGML specification recommends explicit representation of “elements and openings” [
27]. In this work, these opening spaces are not geometrically modelled, with the position of a doorway represented as a single vertex located along each adjacent wall edge. Therefore, further investigation is required to include such measurements to fully satisfy the CityGML LoD4 recommendations. A simple automatic creation of geometric models of doorways would be possible if a vertical rectangular shape for the opening is assumed and included in the extrusion of the room shape. Going further, doorway dimensions may also be measured and included within the plan optimisation, providing both additional positional information and the possibility of a hard constraint to constrain the search space to areas where doorways can fit.
The method proposed here is limited to building layouts where the external boundary represents the building with both a high level of detail and positional accuracy. Even with large scale topographic mapping, such as OS MasterMap, generalisation of the shape means this data will not always be an accurate reflection of the building boundary. A small example of this is apparent in plan B (lower right wall) which can be seen to deviate from the true rectilinear shape (as seen in plan A). In some situations, such issues may be rectified with simple user interface controls to modify footprints (e.g., an unneeded protrusion in the footprint can be “slid” back or removed to make two sections of wall collinear). While this does involve additional user interaction in many cases it will be minimal.
The MasterMap product was chosen in these experiments due to its wide availability and positional accuracy. The accuracy is stated to be 1m, yet this limits the level of improvement attainable for a system aiming for 0.20 m. Where available, use of higher accuracy representations such as cadastral boundaries would be desirable. It is important to note that the method is not restricted to using 2D topographic mapping. With National Mapping Agencies becoming increasingly interested in 3D data products, it is conceivable that suitable input models of the building exterior with high levels of detail may become more widely available. For example, with further advances in automated reconstruction of urban areas, CityGML LoD3 models may become more widespread. These models would provide more precise definition of a building’s 3D shape, such as overhanging areas, balconies and the changes in floor shape and area found across different storeys.
9. Conclusions and Future Work
This paper presents a method for constructing as-built plans of residential building interiors using mobile phone sensor data. The core contribution is an approach for improving imprecise measurements of interiors through imposing soft and hard constraints on the building geometry. The method uses stochastic optimisation to iteratively improve noisy data by fusing indoor measurements with high accuracy building footprints sourced from external survey or topographic map data. We demonstrated quality improvements arising from using our method and compared these to a simple naïve registration and fitting method.
As future work, additional sources of data and aspects of buildings might be modelled to provide extra adjustment improvements. Incorporation of vertical dimensions and multi-level plan adjustments would extend the system to better support the 3D aspects of buildings. Currently, the system focuses on 2D optimisation of geometry, with height values added after the adjustment for extrusion purposes. However, buildings often have structural walls that span multiple floors, and therefore further consideration of the 3D processing is possible. For example, common walls might be used within an optimisation computed across many floors simultaneously.
Another important extension would be to allow interactive resolving of interior measurements in real time. This could be achieved directly on the device using the GPU or using a high performance remote service. Imprecise measurements that aren’t fixed in the adjustment process could then be identified and re-measured on the spot.