Characterization of Black Spot Zones for Vulnerable Road Users in São Paulo (Brazil) and Rome (Italy)
Abstract
:1. Introduction
2. Background
2.1. Traffic Accident Research
2.2. VRU Traffic Accidents
2.3. Spatial Analysis of VRU Accidents
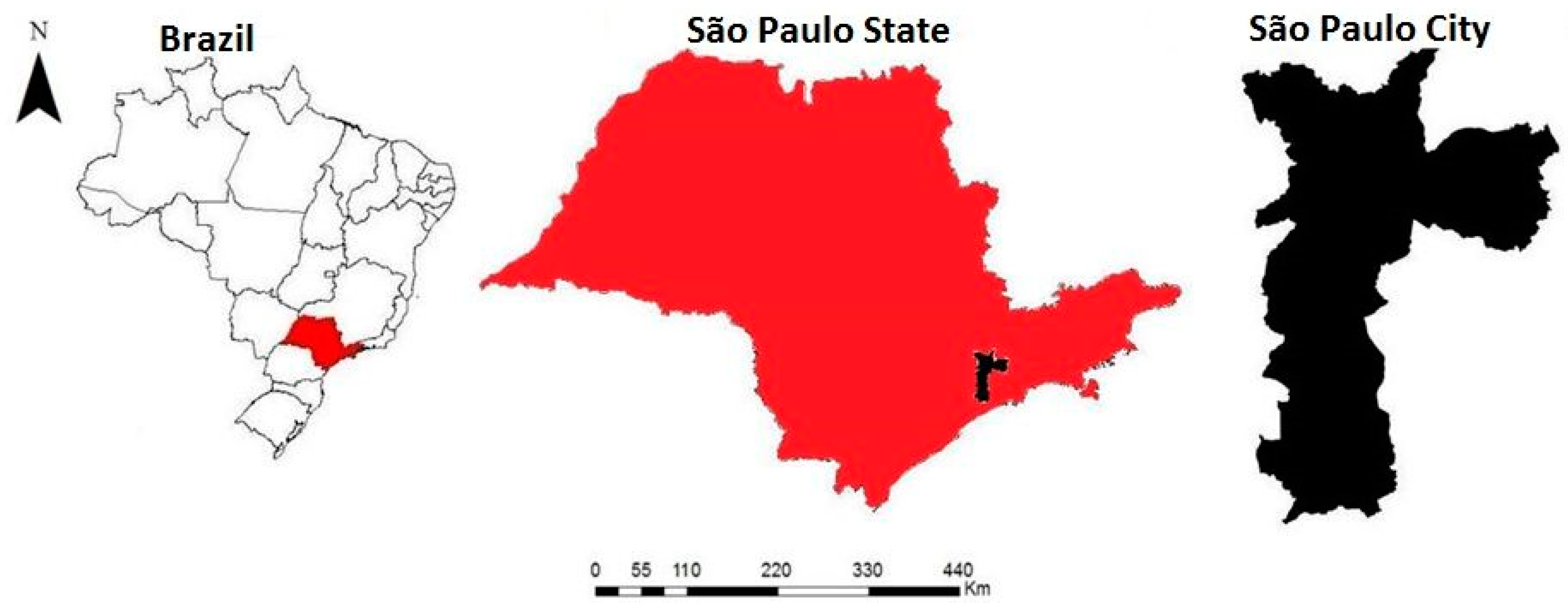
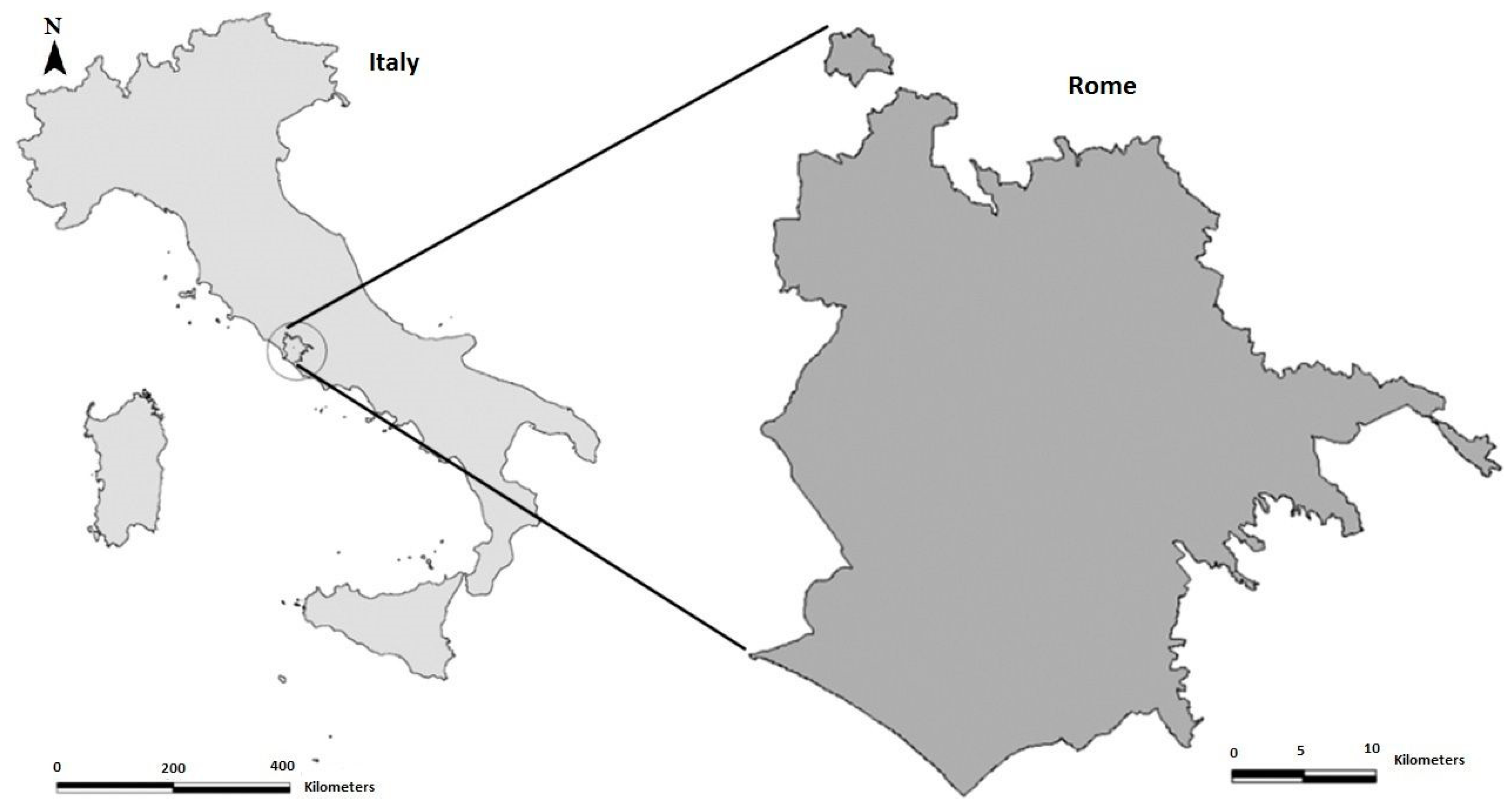
3. Study Areas
4. Description of Data and Methods
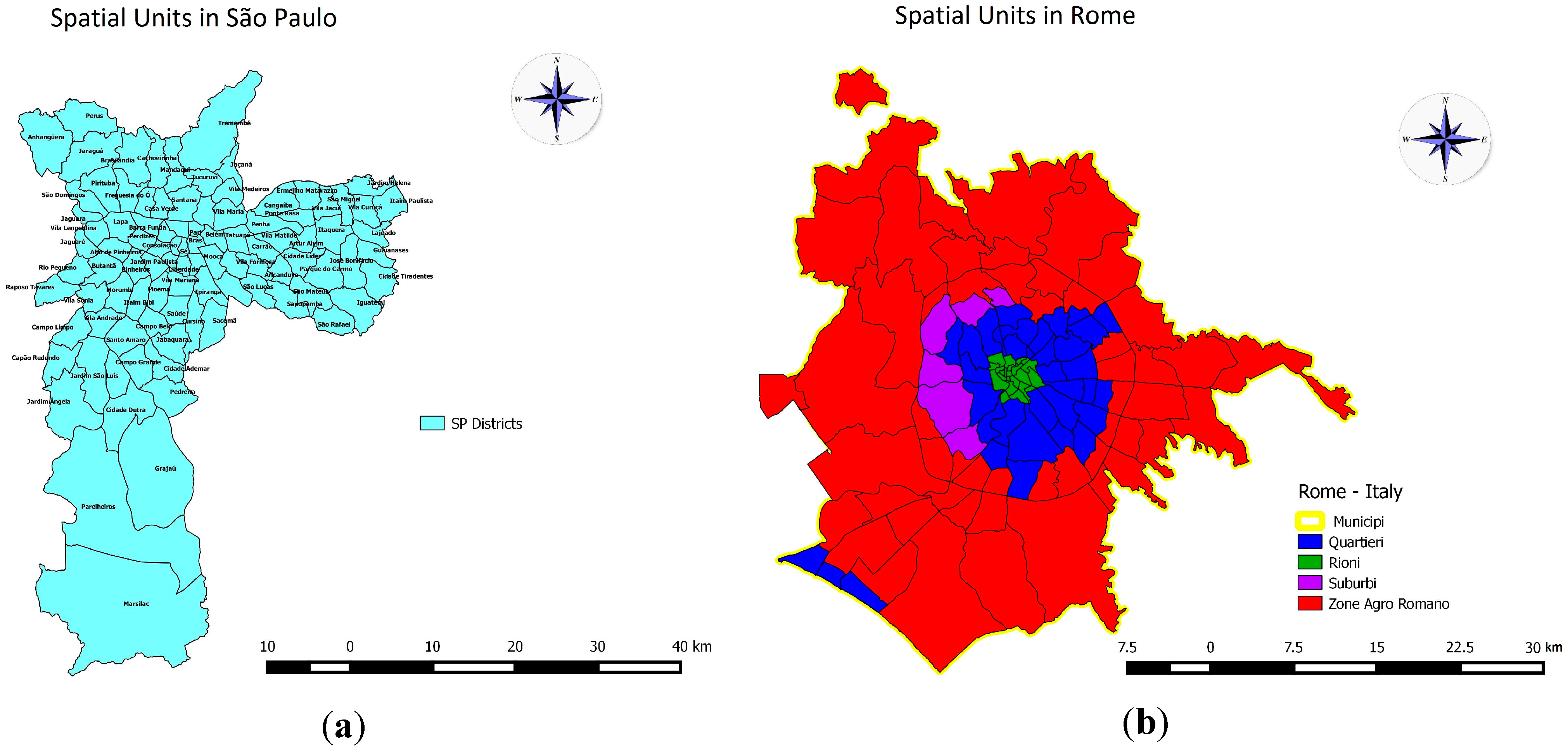
4.1. São Paulo
4.2. Rome
4.3. Methodology
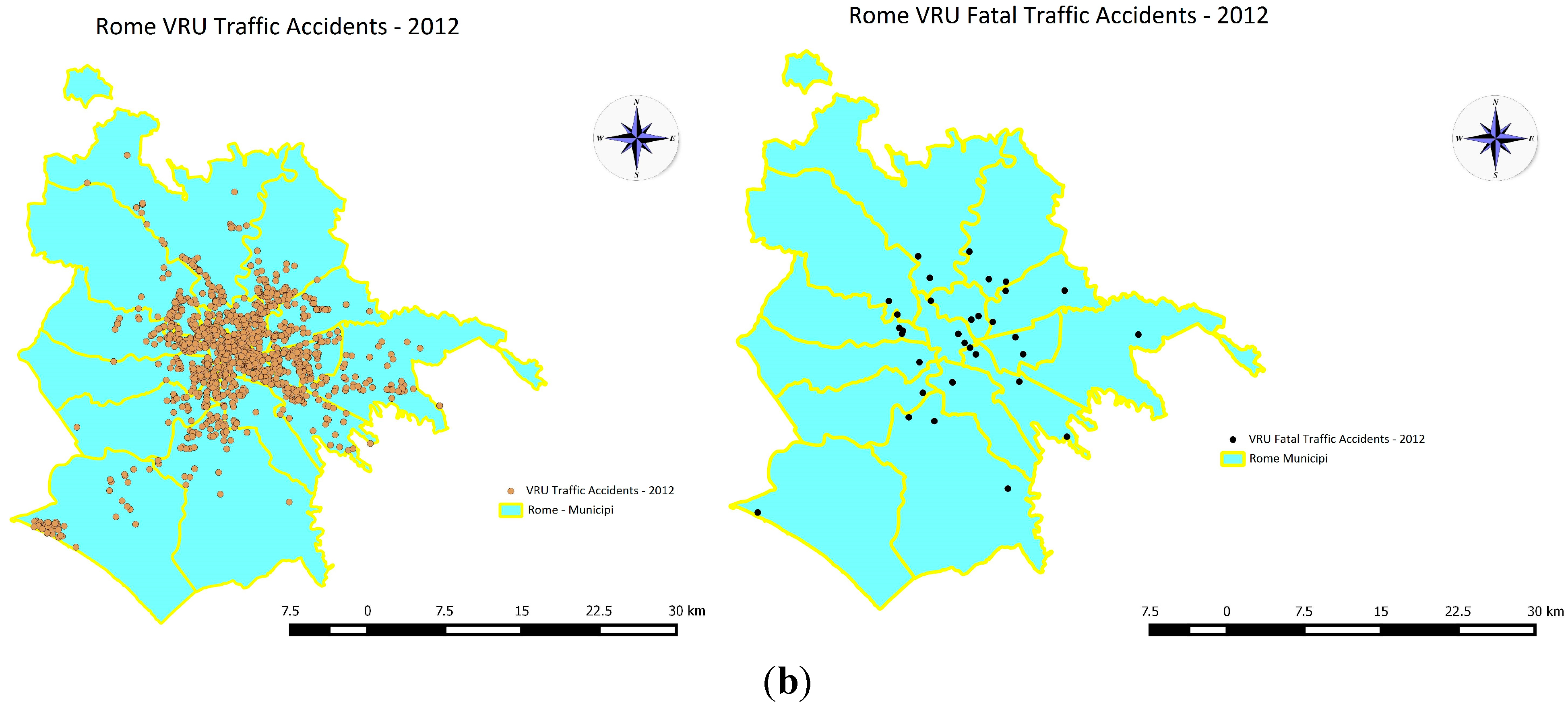
5. Results
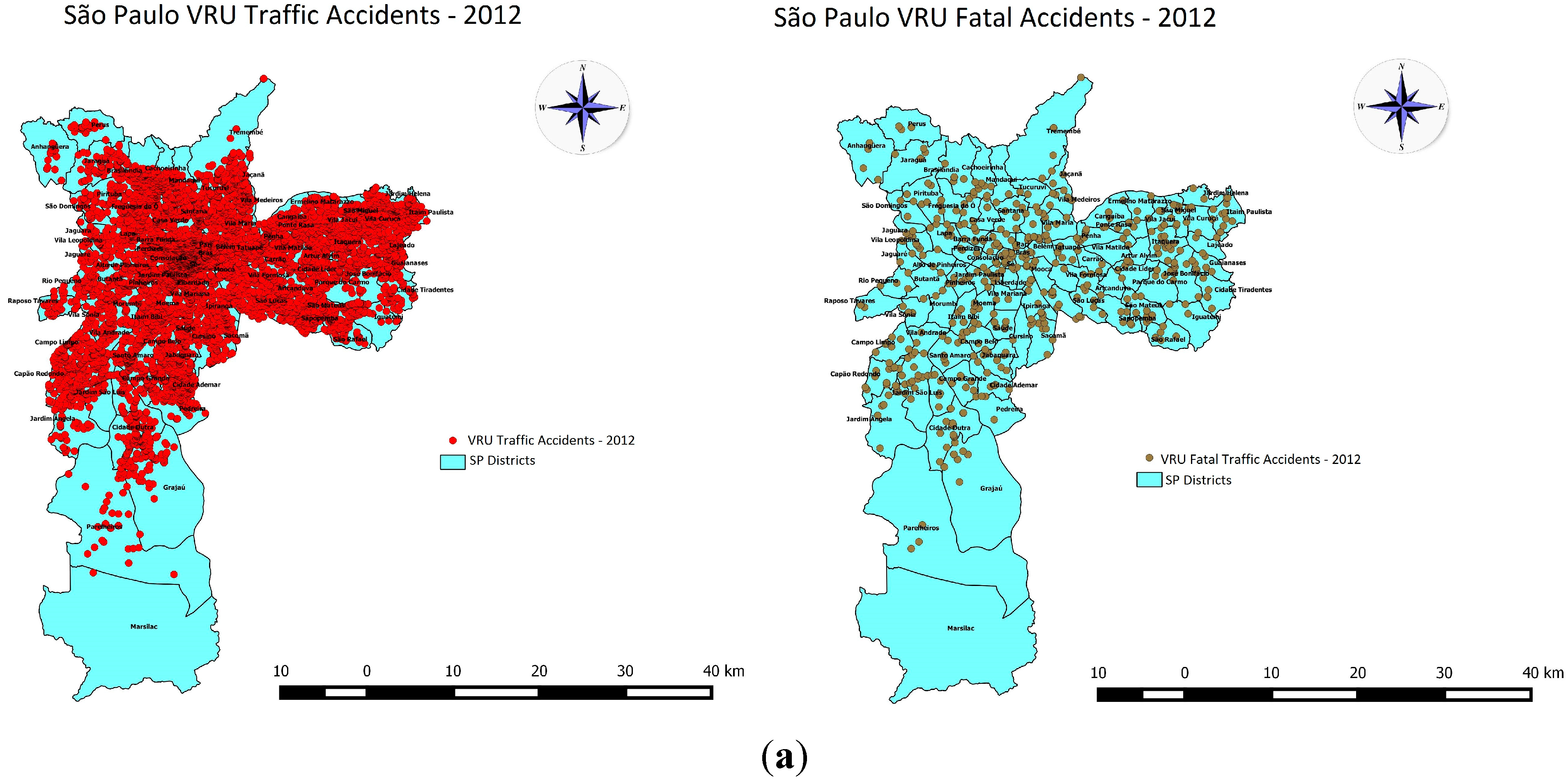
5.1. Kernel Density Estimator
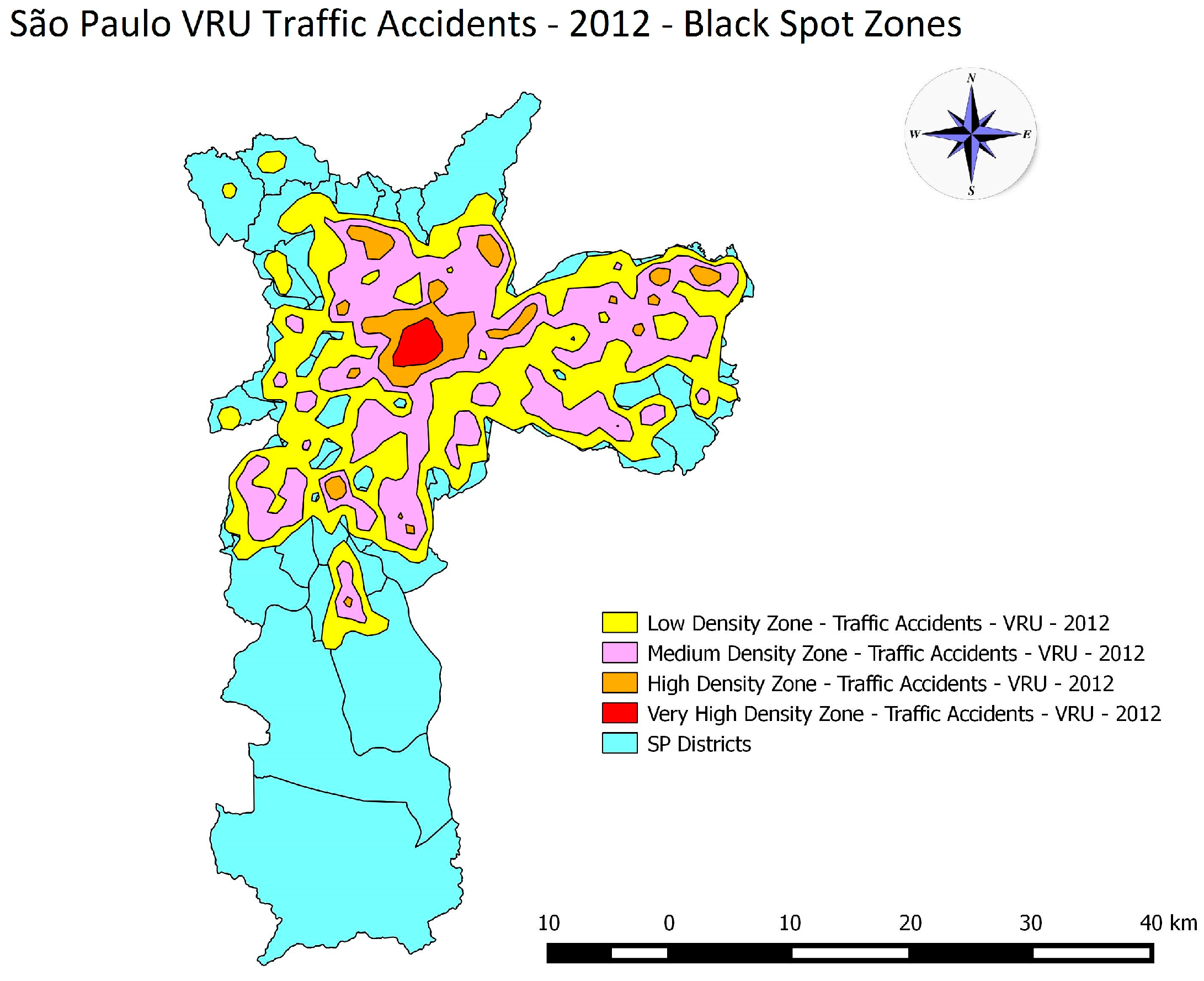
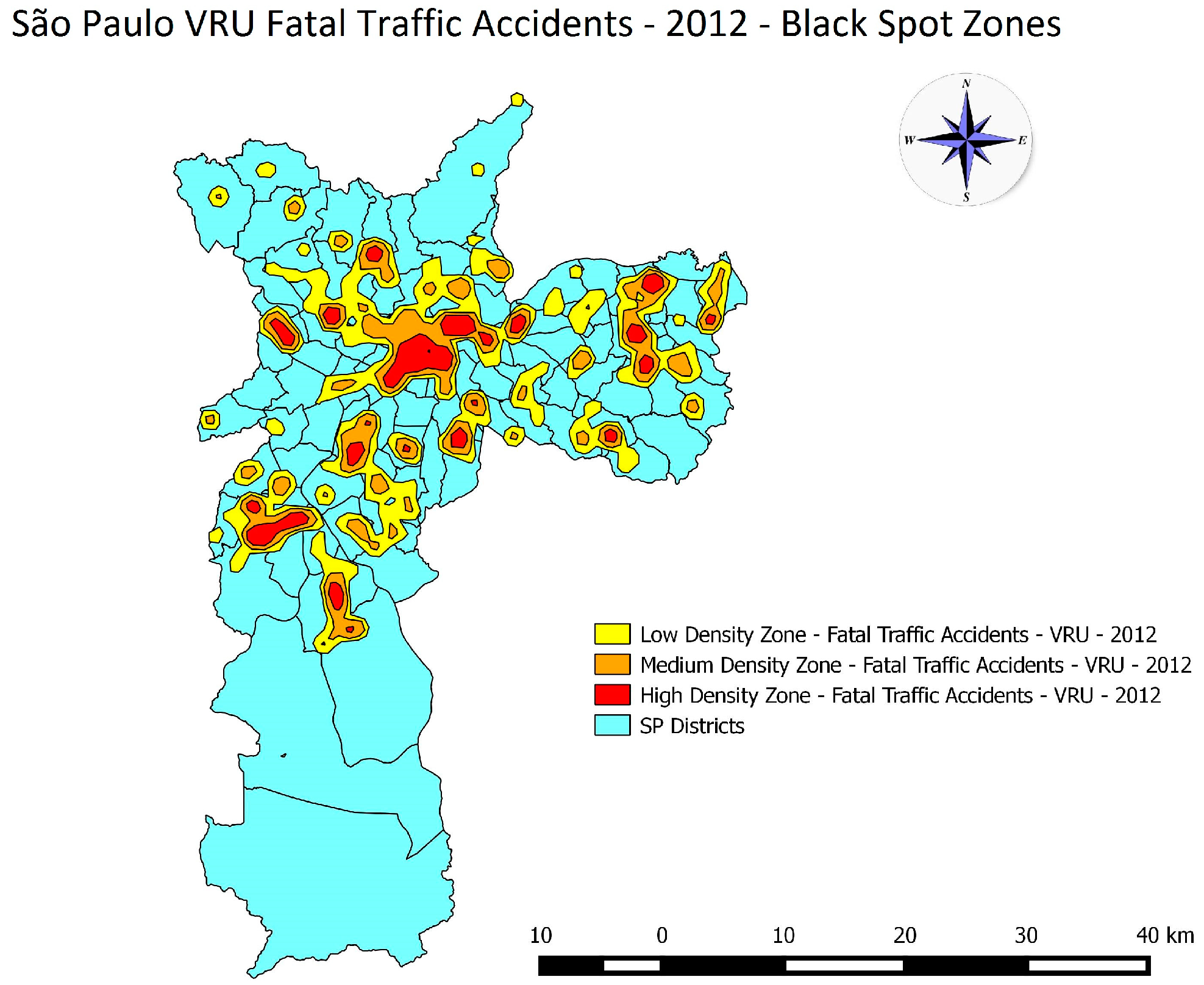
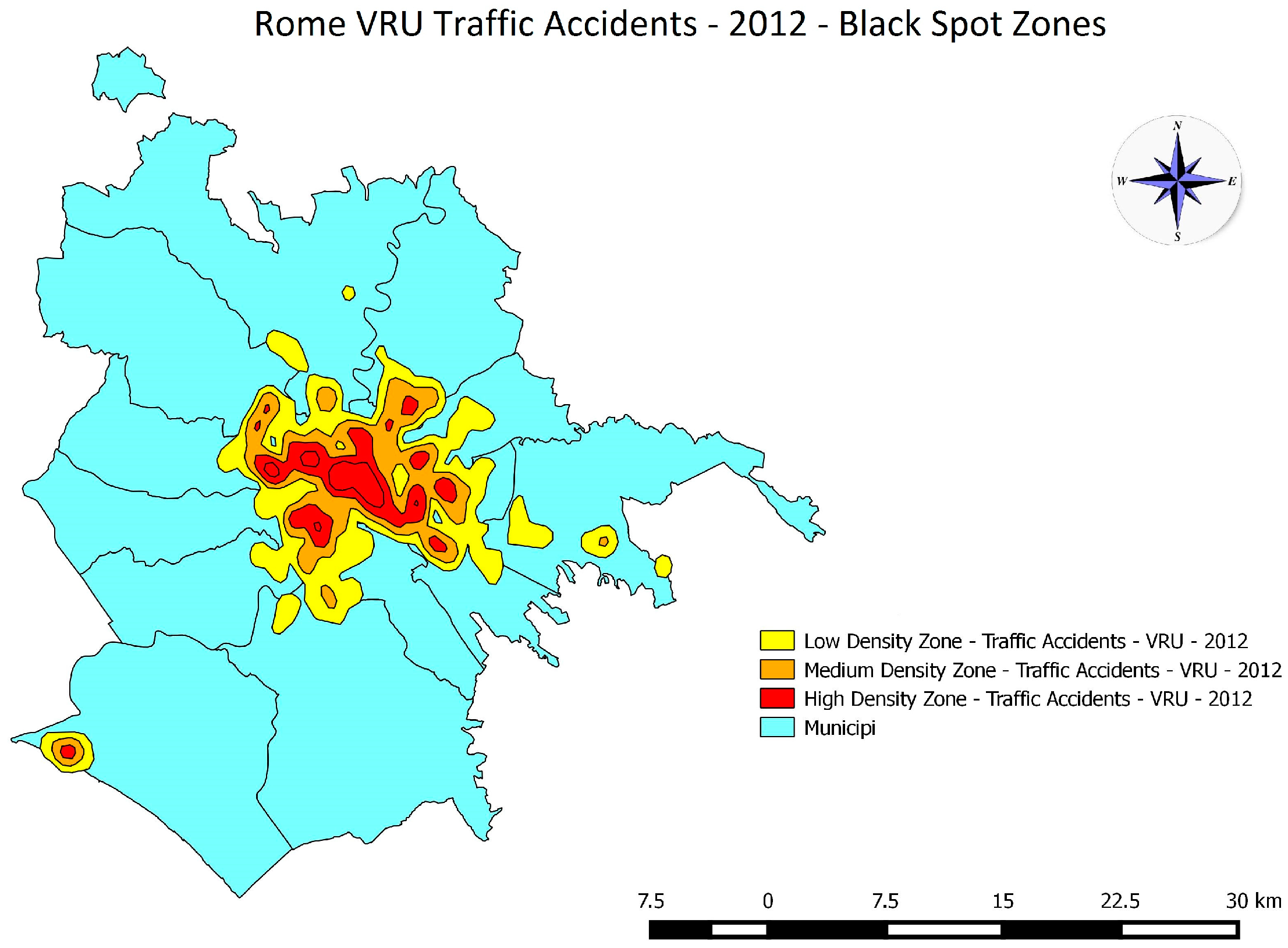
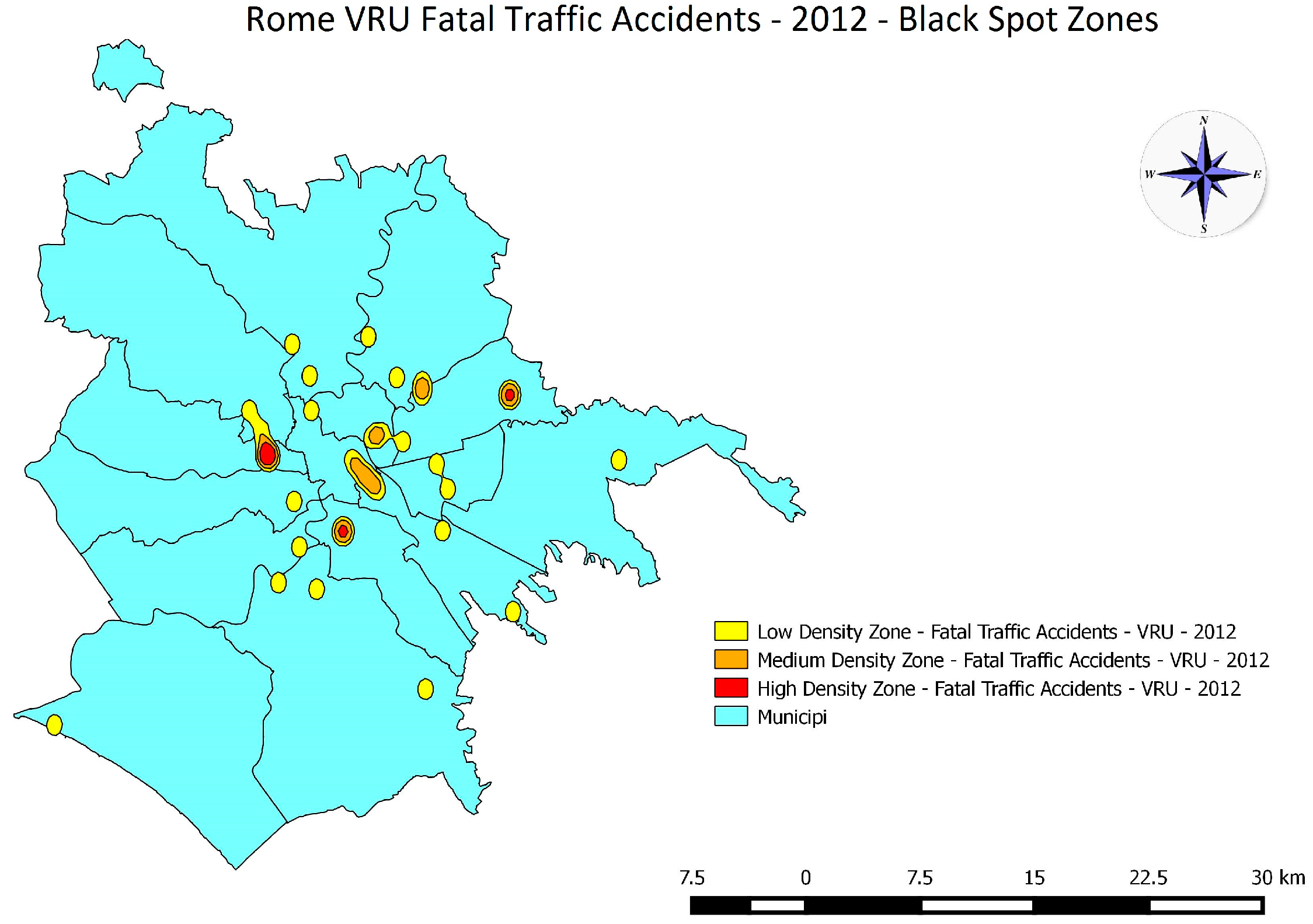
5.2. Statistical Analysis
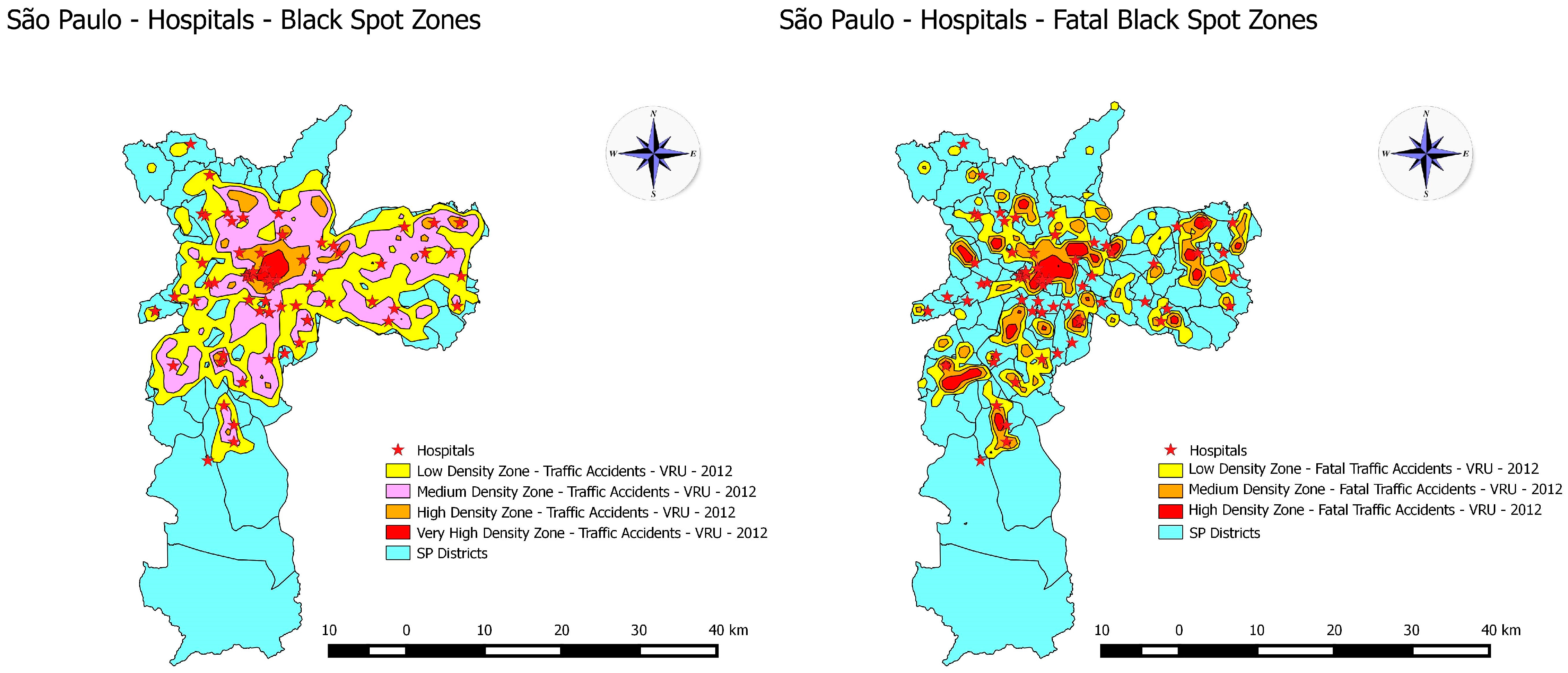
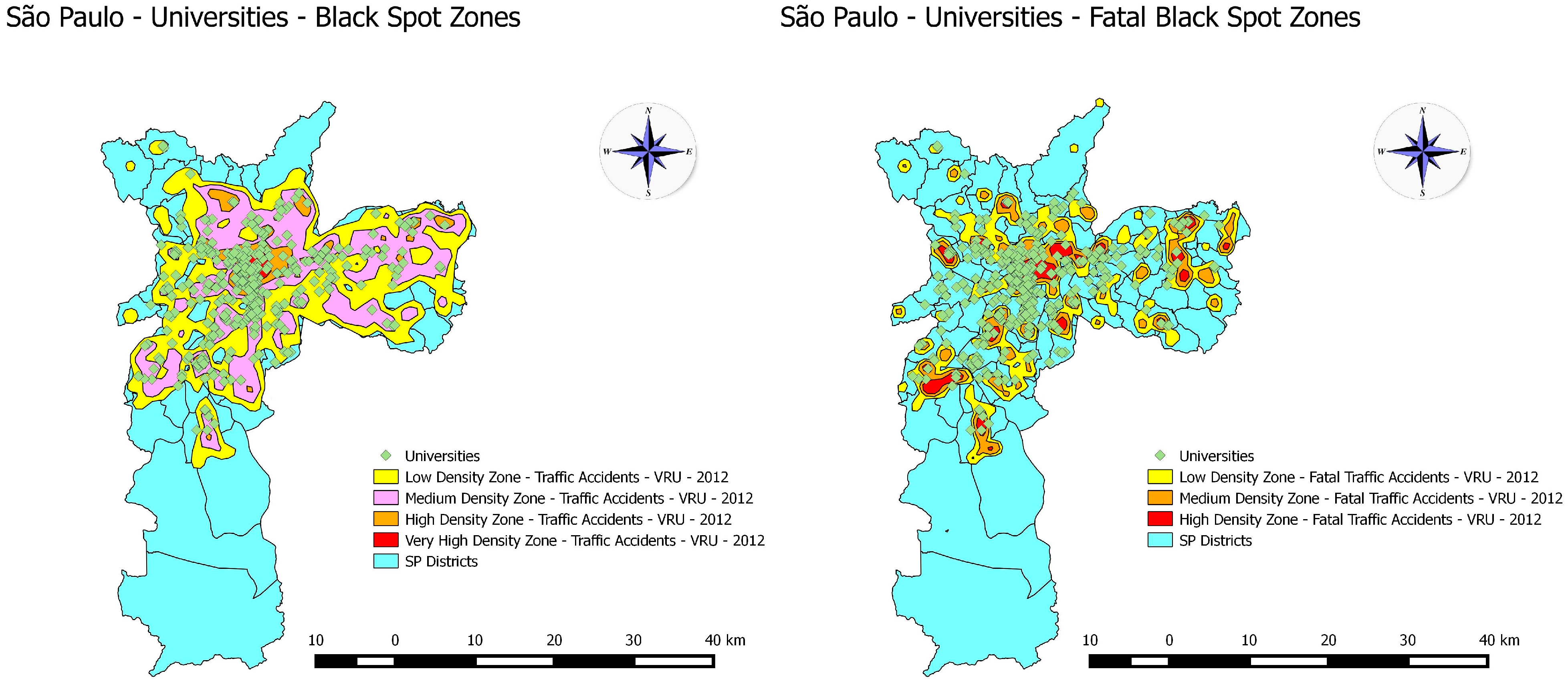
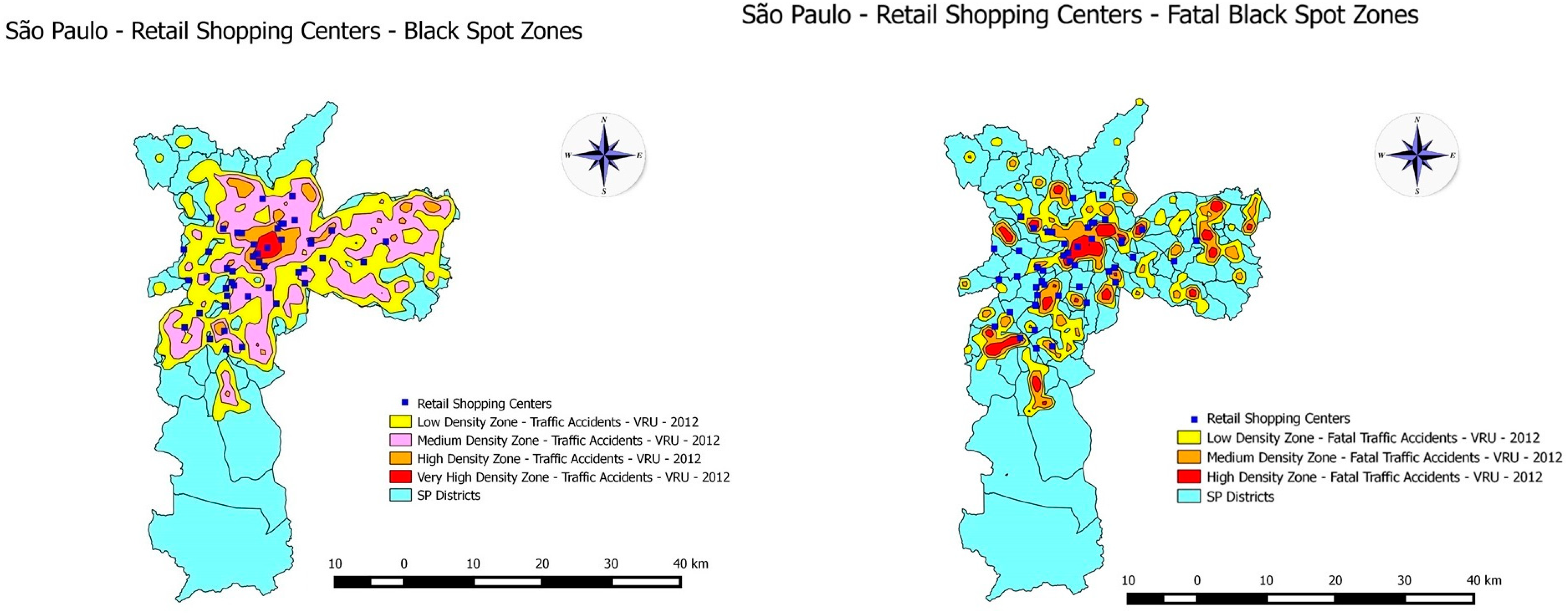
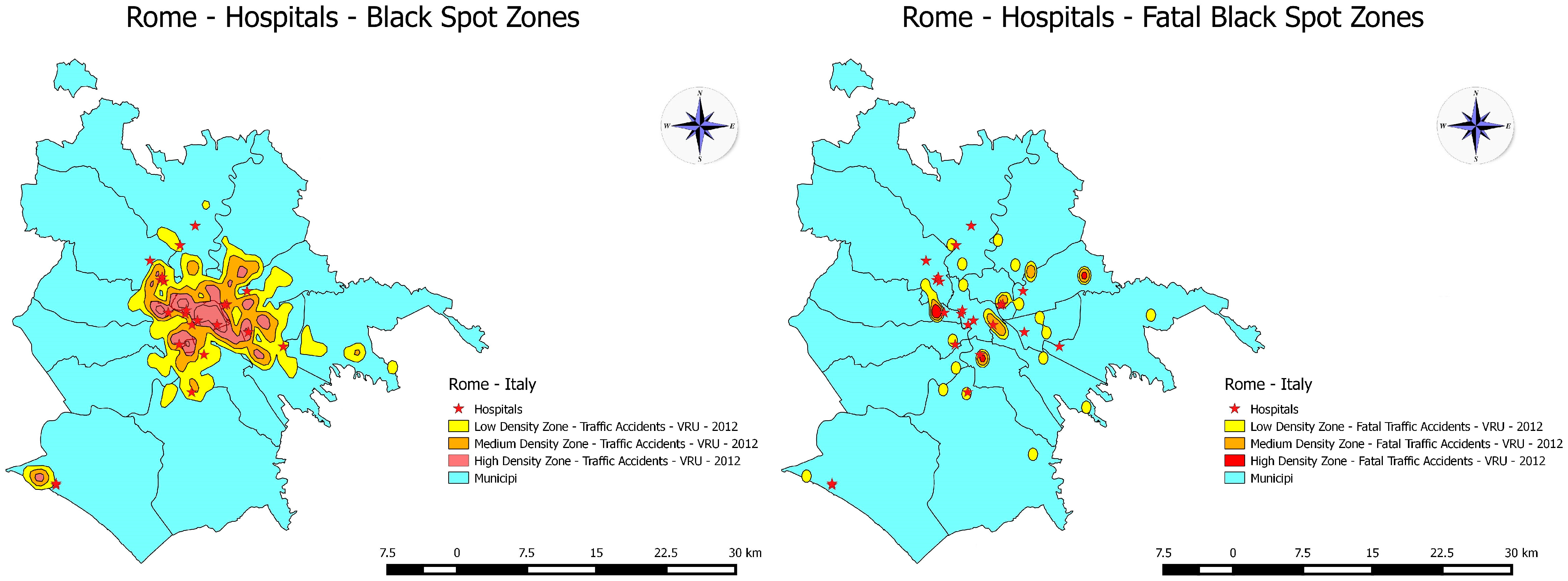
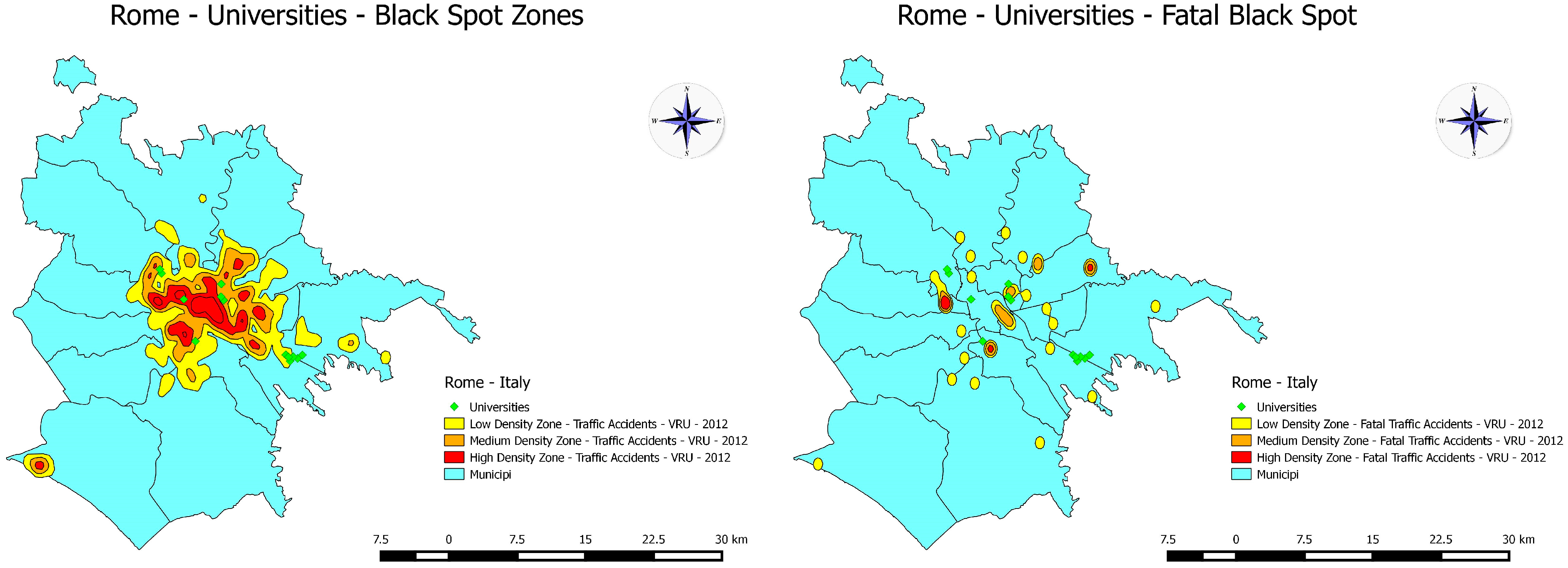
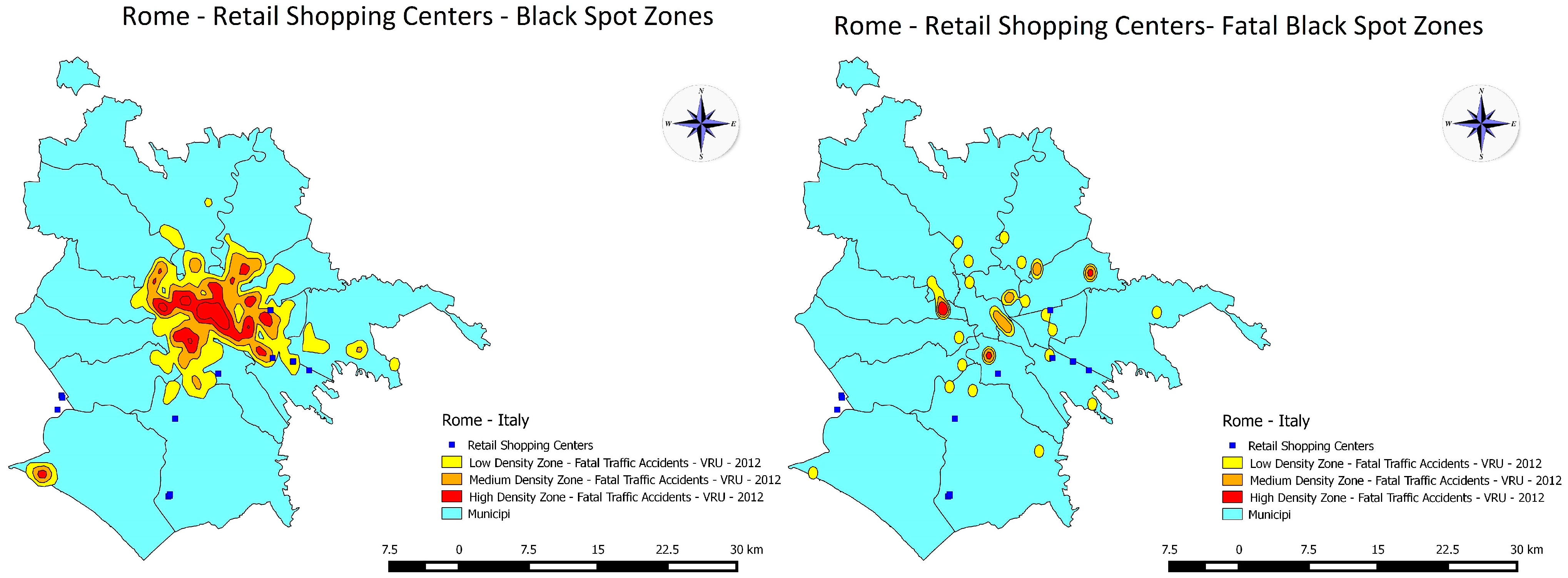
5.2.1. São Paulo: Total VRU Traffic Accidents
| Explanatory Variable | Regression Coefficient | Standard Error | t-Value | p-Value |
|---|---|---|---|---|
| Intercept | 1.3852 | 0.0618 | 22.434 | 0.0000 |
| Trips/inhabitants | 0.0352 | 0.0098 | 3.575 | 0.0006 |
| TGH (Trip Generator Hub) | 0.0140 | 0.0045 | 3.084 | 0.0027 |
| Residual standard error: 0.3611 | ||||
| Multiple R-squared: 0.2906 | ||||
| Adjusted R-squared: 0.2754 | ||||
| F-statistic: 19.05 | ||||
| p-value: 0.0000 | ||||
| Residual analysis: | ||||
| Observed Moran’s Index: −0.0221 | ||||
| p = 0.8609 (Moran test) | ||||
| Expectation: −0.0106 | ||||
| Variance: 0.0043 | ||||
| Kolmogorov–Smirnov test: p = 0.1651 | ||||
5.2.2. São Paulo: Fatal VRU Traffic Accidents
| Explanatory Variable | Regression Coefficient | Standard Error | t-Value | p-Value |
|---|---|---|---|---|
| Intercept | 0.4134 | 0.0513 | 8.051 | 0.0000 |
| Trips/inhabitants | 0.0426 | 0.0076 | 5.601 | 0.0000 |
| Residual standard error: 0.3078 | ||||
| Multiple R-squared: 0.2502 | ||||
| Adjusted R-squared: 0.2423 | ||||
| F-statistic: 31.37 | ||||
| p-value: 0.0000 | ||||
| Residual analysis: | ||||
| Observed Moran’s Index: 0.1051 | ||||
| p = 0.0664 (Moran test) | ||||
| Expectation: −0.0138 | ||||
| Variance: 0.0042 | ||||
| Kolmogorov-Smirnov test: p = 0.6124 | ||||
5.2.3. Rome: Total VRU Traffic Accidents
| Explanatory Variable | Regression Coefficient | Standard Error | t-Value | p-Value |
|---|---|---|---|---|
| Intercept | 0.6570 | 0.1627 | 4.038 | 0.0000 |
| Demographic Density | 0.0002 | 0.000002 | 10.589 | 0.0000 |
| Residual standard error: 1.317 | ||||
| Multiple R-squared: 0.4959 | ||||
| Adjusted R-squared: 0.4915 | ||||
| F-statistic: 112.1 | ||||
| p-value: 0.0000 | ||||
| Residual analysis: | ||||
| Observed Moran’s Index: 0.3758 | ||||
| p = 0.0000 (Moran test) | ||||
| Expectation: −0.0113 | ||||
| Variance: 0.0022 | ||||
| Kolmogorov-Smirnov test: p = 0.7016 | ||||
| Test | Statistic Value | p-Value |
|---|---|---|
| Lagrange Multiplier Error—LMerr | 0.1058 | 0.0000 |
| Lagrange Multiplier Spatially-Lagged—LMlag | 3.1272 | 0.0000 |
| Robust Lagrange Multiplier Error—RLMerr | 5.9186 | 0.2344 |
| Robust Lagrange Multiplier Spatially-Lagged—RLMlag | 8.9401 | 0.0000 |
| Spatial Autoregressive Moving Average—SARMA | 9.0458 | 0.0109 |
| Explanatory Variable | Regression Coefficient | Standard Error | z-Value | p-Value |
|---|---|---|---|---|
| Intercept | −0.1444 | 0.1501 | 0.9616 | 0.3363 |
| Demographic Density | 0.0001 | 0.0000 | 7.9150 | 0.0000 |
| Rho: 0.63342 | ||||
| Likelihood Ratio Test - LR test value: 68.206 | ||||
| p-value: 0.0000 | ||||
| Asymptotic standard error: 0.068453 | ||||
| z-value: 9.2533 | ||||
| Wald statistic: 85.624 | ||||
| Log likelihood: −161.426 for lag model | ||||
| ML residual variance (sigma squared): 0.88966 (sigma: 0.94322) | ||||
| AIC: 330.85 (AIC for linear regression: 397.06) | ||||
| LM test for residual autocorrelation | ||||
| test value: 7.5693 | ||||
| p-value: 0.005937 | ||||
| Residual analysis: | ||||
| Observed Moran’s Index: −0.1040 | ||||
| p = 0.9794 (Moran test) | ||||
| Expectation: −0.0087 | ||||
| Variance: 0.0022 | ||||
| Moran I statistic standard deviation = −2.0413 | ||||
| p-value: 0.9794 | ||||
5.2.4. Rome: Fatal VRU Traffic Accidents
6. Conclusions
7. Final Considerations
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Haque, M.M.; Chin, H.C.; Debnath, A.K. Sustainable, safe, smart—Three key elements of Singapore’s evolving transport policies. Transp. Policy 2013, 27, 20–31. [Google Scholar] [CrossRef]
- Machado, C.A.S.; Giannotti, M.A.; Shinohara, E.J.; Nishisaki, H.; Quintanilha, J.A. Characterization of the sites of traffic accidents involving vulnerable road users (VRU) in São Paulo city. In Proceedings of the Transport Research Arena (TRA 2014)—5th Conference Transport Solutions: From Research to Deployment-Innovative Mobility, Mobilise Innovation, Paris, France, 14–17 April 2014; p. 10.
- Santos, G.; Behrendt, H.; Maconi, L.; Shirvani, T.; Teytelboym, A. Part I: Externalities and economic policies in road transport. Res. Transp. Econ. 2010, 28, 2–45. [Google Scholar] [CrossRef]
- Small, K.; Verhoef, E.T. The Economics of Urban Transportation; Routledge: London, UK, 2007; p. 276. [Google Scholar]
- Suzuki, H.; Cervero, R.; Iuchi, K. Transforming Cities with Transit—Transit and Land-Use Integration for Sustainable Urban Development; Urban Development Series; The World Bank: Washington, DC, USA, 2013; p. 205. [Google Scholar]
- Klassen, J.; El-Basyouny, K.; Islam, M.T. Analyzing the severity of bicycle-motor vehicle collision using spatial mixed logit models: A city of Edmonton case study. Saf. Sci. 2014, 62, 295–304. [Google Scholar] [CrossRef]
- Nabors, D.; Goughnour, E.; Thomas, L.; Desantis, W.; Sawyer, M. Bicycle road safety audit guidelines and prompt lists. In Federal Highway Administration–FHWA, Final Report; FHWA: Washington, DC, USA, 2012; p. 88. [Google Scholar]
- Otte, D.; Jänsch, M.; Haasper, C. Injury protection and accident causation parameters for vulnerable road users based on German In-Depth Accident Study GIDAS. Accid. Anal. Prev. 2012, 44, 149–153. [Google Scholar] [CrossRef] [PubMed]
- Schepers, P.; Hagenzieker, M.; Methorst, R.; van Wee, B.; Wegman, F. A conceptual framework for road safety and mobility applied to cycling safety. Accid. Anal. Prev. 2014, 62, 331–340. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.; Okabe, A. Different ways of thinking about street networks and spatial analysis. Geogr. Anal. 2014, 46, 341–344. [Google Scholar] [CrossRef]
- Theofilatos, A.; Yannis, G. A review of the effect of traffic and weather characteristics on road safety. Accid. Anal. Prev. 2014, 72, 244–256. [Google Scholar] [CrossRef] [PubMed]
- Çela, L.; Shiode, S.; Lipovac, K. Integrating GIS and spatial analytical techniques in an analysis of road traffic accidents in Serbia. Int. J. Traffic Transp. Eng. 2013, 3, 1–15. [Google Scholar] [CrossRef]
- Bíl, M.; Andrášik, R.; Janoška, Z. Identification of hazardous road locations of traffic accidents by means of kernel density estimation and cluster significance evaluation. Accid. Anal. Prev. 2013, 55, 265–273. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Quddus, M.A.; Ison, S.G. The effect of traffic and road characteristics on road safety: A review and future research direction. Saf. Sci. 2013, 57, 264–275. [Google Scholar] [CrossRef]
- World Health Organization (WHO). World Report on Road Traffic Injury Prevention; Peden, M., Scurfield, R., Sleet, D., Mohan, D., Hyder, A.A., Jarawan, E., Mathers, C., Eds.; WHO: Geneva, Switzerland, 2004; p. 217. [Google Scholar]
- Moeinaddini, M.; Asadi-Shekari, Z.; Shah, M.Z. The relationship between urban street networks and the number of transport fatalities at the city level. Saf. Sci. 2014, 62, 114–120. [Google Scholar] [CrossRef]
- World Health Organization (WHO). Global Status Report on Road Safety 2013—Supporting a Decade of Action; WHO: Geneva, Switzerland, 2013; p. 318. [Google Scholar]
- Ministry of Healthy. 2013. Available online: http://www2.datasus.gov.br/DATASUS/index.php?area=0205&VObj=http://tabnet.datasus.gov.br/cgi/deftohtm.exe?sim/cnv/ext10 (accessed on 6 May 2013).
- Koh, P.P.; Wong, Y.D. Comparing pedestrians’ needs and behaviours in different land use environments. J. Transp. Geogr. 2013, 26, 43–50. [Google Scholar] [CrossRef]
- Flahaut, B.; Mouchart, M.; San Martin, E.; Thomas, I. The local spatial autocorrelation and the kernel method for identifying black zones—A comparative approach. Accid. Anal. Prev. 2003, 35, 991–1004. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Aty, M.; Chundi, S.S.; Lee, C. Geo-spatial and log-linear analysis of pedestrian and bicyclist crashes involving school-aged children. J. Saf. Res. 2007, 38, 571–579. [Google Scholar] [CrossRef]
- Blazquez, C.A.; Celis, M.S. A spatial and temporal analysis of child pedestrian crashes in Santiago, Chile. Accid. Anal. Prev. 2013, 50, 304–311. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Kockelman, K.M. A Poisson-lognormal conditional-autoregressive model for multivariate spatial analysis of pedestrian crash counts across neighborhoods. Accid. Anal. Prev. 2013, 60, 71–84. [Google Scholar] [CrossRef] [PubMed]
- Xie, Z.; Yan, J. Detecting traffic accident clusters with network kernel density estimation and local spatial statistics: An integrated approach. J. Transp. Geogr. 2013, 31, 64–71. [Google Scholar] [CrossRef]
- Amin, S.R.; Zareie, A.; Amador-Jiménez, L.E. Climate change modeling and the weather-related road accidents in Canada. Transp. Res. Part D: Transp. Environ. 2014, 32, 171–183. [Google Scholar] [CrossRef]
- Andrade, L.; Vissoci, J.R.N.; Rodrigues, C.G.; Finato, K.; Carvalho, E.; Pietrobon, R.; Souza, E.M.; Nihei, O.K.; Lynch, C.; Carvalho, M.D.B. Brazilian road traffic fatalities: A spatial and environmental analysis. PLoS ONE 2014, 9, 1–10. [Google Scholar]
- Soltani, A.; Askari, S. Analysis of intra-urban traffic accidents using spatiotemporal visualization techniques. Transp. Telecommun. J. 2014, 15, 227–232. [Google Scholar] [CrossRef]
- Vandenbulcke, G.; Thomas, I.; Panis, L.I. Predicting cycling accident risk in Brussels: A spatial case-control approach. Accid. Anal. Prev. 2014, 62, 341–357. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Liu, P.; Chen, J.; Wang, H. Comparative analysis of the spatial analysis methods for hotspot identification. Accid. Anal. Prev. 2014, 66, 80–88. [Google Scholar] [CrossRef] [PubMed]
- Habibovic, A.; Davidsson, J. Causation mechanisms in car-to-vulnerable road user crashes: Implications for active safety systems. Accid. Anal. Prev. 2012, 49, 493–500. [Google Scholar] [CrossRef] [PubMed]
- Habibovic, A.; Davidsson, J. Requirements of a system to reduce car-to-vulnerable road user crashes in urban intersections. Accid. Anal. Prev. 2011, 43, 1570–1580. [Google Scholar] [CrossRef] [PubMed]
- Anderson, T.K. Kernel density estimation and K-means clustering to profile road accident hotspots. Accid. Anal. Prev. 2009, 41, 359–364. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.M.; Abdel-Aty, M. Evaluation and spatial analysis of automated red-light running enforcement cameras. Transp. Res. Part C: Emerg. Technol. 2015, 50, 130–140. [Google Scholar] [CrossRef]
- Durduran, S.S. A decision making system to automatic recognize of traffic accidents on the basis of a GIS platform. Expert Syst. Appl. 2010, 37, 7729–7736. [Google Scholar] [CrossRef]
- Erdogan, S.; Yilmaz, I.; Baybura, T.; Gullu, M. Geographical information systems aided traffic accident analysis system case study: City of Afyonkarahisar. Accid. Anal. Prev. 2008, 40, 174–181. [Google Scholar] [CrossRef] [PubMed]
- Kingham, S.; Sabel, C.E.; Bartie, P. The impact of the “school run” on road traffic accidents: A spatio-temporal analysis. J. Transp. Geogr. 2011, 19, 705–711. [Google Scholar] [CrossRef]
- Steenberghen, T.; Aerts, K.; Thomas, I. Spatial clustering of events on a network. J. Transp. Geogr. 2010, 18, 411–418. [Google Scholar] [CrossRef]
- Xiao, J.; Liu, Y. Traffic incident detection using multiple-kernel support vector machine. J. Transp. Res. Board 2012, 2324, 44–52. [Google Scholar] [CrossRef]
- Xie, Z.; Yan, J. Kernel density estimation of traffic accidents in a network space. Comput. Environ. Urban Syst. 2008, 32, 396–406. [Google Scholar] [CrossRef]
- Yalcin, G.; Duzgun, H.S. Spatial analysis of two-wheeled vehicles traffic crashes: Osmaniye in Turkey. KSCE J. Civ. Eng. 2015. [CrossRef]
- Brunsdon, C. Estimating probability surfaces for geographical point data: An adaptive kernel algorithm. Comput. Geosci. 1995, 21, 877–894. [Google Scholar] [CrossRef]
- Xie, X.; Wu, J. Some improvement on convergence rates of kernel density estimator. Appl. Math. 2014, 5, 1684–1696. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis—Monographs on Statistics and Applied Probability, 1st ed.; Chapman and Hall: London, UK, 1986; p. 200. [Google Scholar]
- Wand, M.P.; Jones, M.C. Kernel Smoothing—Monographs on Statistics and Applied Probability, 1st ed.; Chapman and Hall: London, UK, 1995; p. 212. [Google Scholar]
- Steenberghen, T.; Dufays, T.; Thomas, I.; Flahaut, B. Intra-urban location and clustering of road accidents using GIS: A Belgian example. Int. J. Geogr. Int. Sci. 2004, 18, 169–181. [Google Scholar] [CrossRef]
- Ahmed, A.; Khan, B.A.; Khurshid, M.B.; Khan, M.B.; Waheed, A. Estimating national road crash fatalities using aggregate data. Int. J. Inj. Control Saf. Promot. 2015. [CrossRef]
- Bjørnskau, T.; Nævestad, T.-O.; Akhtar, J. Traffic safety among motorcyclists in Norway: A study of subgroups and risk factors. Accid. Anal. Prev. 2012, 49, 50–57. [Google Scholar] [CrossRef] [PubMed]
- Chiou, Y.-C.; Fu, C. Modeling crash frequency and severity using multinomial-generalized Poisson model with error components. Accid. Anal. Prev. 2013, 50, 73–82. [Google Scholar] [CrossRef] [PubMed]
- Kaplan, S.; Prato, C.G. Risk factors associated with bus accident severity in the United States: A generalized ordered logit model. J. Saf. Res. 2012, 43, 171–180. [Google Scholar] [CrossRef]
- Nazif-Munoz, J.I.; Quesnel-Vallée, A.; van den Berg, A. Did Chile’s traffic law reform push police enforcement?—Understanding Chile’s traffic fatalities and injuries reduction. Inj. Prev. 2014. [CrossRef]
- Nóbrega, L.M.; Cavalcante, G.M.S.; Lima, M.M.S.M.; Madruga, R.C.R.; Jorge, M.L.R.; d’avila, S. Prevalence of facial trauma and associated factors in victims of road traffic accidents. Am. J. Emerg. Med. 2014, 32, 1382–1386. [Google Scholar] [CrossRef] [PubMed]
- Philip, P.; Chaufton, C.; Orriols, L.; Lagarde, E.; Amoros, E.; Laumon, B.; Akerstedt, T.; Taillard, J.; Sagaspe, P. Complaints of poor sleep and risk of traffic accidents: A population-based case-control study. PLoS ONE 2014, 9, e114102. [Google Scholar] [CrossRef] [PubMed]
- Pirdavani, A.; Bellemans, T.; Brijs, T.; Kochan, B.; Wets, G. Assessing the road safety impacts of a teleworking policy by means of geographically weighted regression method. J. Transp. Geogr. 2014, 39, 96–110. [Google Scholar] [CrossRef]
- Pirdavani, A.; Bellemans, T.; Brijs, T.; Wets, G. Application of geographically weighted regression technique in spatial analysis of fatal and injury crashes. J. Transp. Eng. 2014. [CrossRef]
- Rangel, T.; Vassallo, J.M.; Arenas, B. Effectiveness of safety-based incentives in public private partnerships: Evidence from the case of Spain. Transp. Res. Part A: Policy Pract. 2012, 46, 1166–1176. [Google Scholar] [CrossRef]
- Yao, S.; Loo, B.P.Y.; Lam, W.W.Y. Measures of activity-based pedestrian exposure to the risk of vehicle-pedestrian collisions: Space-time path vs. potential path tree methods. Accid. Anal. Prev. 2015, 75, 320–332. [Google Scholar] [CrossRef] [PubMed]
- Agbelie, B.R.D.K. An empirical analysis of three econometric frameworks for evaluating economic impacts of transportation infrastructure expenditures across countries. Transp. Policy 2014, 35, 304–310. [Google Scholar] [CrossRef]
- Qian, X.; Ukkusuri, S.V. Spatial variation of the urban taxi ridership using GPS data. Appl. Geogr. 2015, 59, 31–42. [Google Scholar] [CrossRef]
- Wang, Y.; Potoglou, D.; Orford, S.; Gong, Y. Bus stop, property price and land value tax: A multilevel hedonic analysis with quantile calibration. Land Use Policy 2015, 42, 381–391. [Google Scholar] [CrossRef]
- Chakrabortya, A.; Mishra, S. Land use and transit ridership connections: Implications for state-level planning agencies. Land Use Policy 2013, 30, 458–469. [Google Scholar] [CrossRef]
- Lambert, D.M.; Brown, J.P.; Florax, R.J.G.M. A two-step estimator for a spatial lag model of counts: Theory, small sample performance and an application. Reg. Sci. Urban Econ. 2010, 40, 241–252. [Google Scholar] [CrossRef]
- Frondoni, R.; Mollo, B.; Capotorti, G. A landscape analysis of land cover change in the Municipality of Rome (Italy): Spatio-temporal characteristics and ecological implications of land cover transitions from 1954 to 2001. Landsc. Urban Plan. 2011, 100, 117–128. [Google Scholar] [CrossRef]
- Zuur, A.F.; Ieno, E.N.; Smith, G.M. Analysing Ecological Data, 26th ed.; Springer: New York, NY, USA, 2007; p. 672. [Google Scholar]
- Zhang, L.; Gove, J.H.; Heath, L.S. Spatial residual analysis of six modeling techniques. Ecol. Model. 2005, 186, 154–177. [Google Scholar] [CrossRef]
- Razali, N.M.; Wah, Y.B. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Lilliefors, H.W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Duncan, D.T.; Kawachi, I.; Kum, S.; Aldstadt, J.; Piras, G.; Matthews, S.A.; Arbia, G.; Castro, M.C.; White, K.; Williams, D.R. A spatially explicit approach to the study of socio-demographic inequality in the spatial distribution of trees across boston neighborhoods. Spat. Demogr. 2014, 2, 1–29. [Google Scholar]
- Boots, B.; Tiefelsdorf, M. Global and local spatial autocorrelation in bounded regular tessellations. J. Geogr. Syst. 2000, 2, 319–348. [Google Scholar] [CrossRef]
- Lauridsen, J.; Kosfeld, R. A test strategy for spurious spatial regression, spatial nonstationarity, and spatial cointegration. Pap. Reg. Sci. 2006, 85, 363–377. [Google Scholar] [CrossRef]
- Anselin, L. Lagrange multiplier test diagnostics for spatial dependence and spatial heterogeneity. Geogr. Anal. 1988, 20, 1–17. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the Second International Symposium on Information Theory; Petrov, B., Csáki, F., Eds.; Akadémiai Kiadó: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Dirick, L.; Claeskens, G.; Baesens, B. An Akaike information criterion for multiple event mixture cure models. Eur. J. Oper. Res. 2015, 241, 449–457. [Google Scholar] [CrossRef]
- Symonds, M.R.E.; Moussalli, A. A brief guide to model selection, multimodel inference and model averaging in behavioural ecology using Akaike’s information criterion. Behav. Ecol. Sociobiol. 2011, 65, 13–21. [Google Scholar] [CrossRef]
- Cheung, Y.B. Zero-inflated models for regression analysis of count data: A study of growth and development. Stat. Med. 2002, 21, 1461–1469. [Google Scholar] [CrossRef] [PubMed]
- Min, Y.; Agresti, A. Random effect models for repeated measures of zero-inflated count data. Stat. Model. 2005, 5, 1–19. [Google Scholar] [CrossRef]
- European Commission. Towards Low Carbon Transport in Europe-Communicating Transporet Research an Innovation; European Union, Directorate General for Mobility and Transport: Brussels, Belgium, 2012; p. 24. [Google Scholar]
- Passafaro, P.; Rimano, A.; Piccini, M.P.; Metastasio, R.; Gambardella, V.; Gullace, G.; Lettieri, C. The bicycle and the city: Desires and emotions versus attitudes, habits and norms. J. Environ. Psychol. 2014, 38, 76–83. [Google Scholar] [CrossRef]
- Camilloni, L.; Farchi, S.; Chini, F.; Rossi, P.G.; Borgia, P.; Guasticchi, G. How socioeconomic status influences road traffic injuries and home injuries in Rome. Int. J. Inj. Control Saf. Promot. 2013, 20, 134–143. [Google Scholar] [CrossRef]
- European Transport Safety Council (ETSC). A Challenging Start towards the E.U. 2020 Road Safety Target; 6th Road Safety PIN Report; ETSC: Brussels, Belgium, 2012; p. 96. [Google Scholar]
- Gorios, C.; Souza, R.M.; Gerolla, V.; Maso, B.; Rodrigues, C.L.; Armond, J.E. Acidentes de transporte de crianças e adolescentes em serviço de emergência de hospital de ensino, Zona Sul da cidade de São Paulo. Rev. Bras. Ortop. 2014, 49, 391–395. [Google Scholar] [CrossRef]
- Vasconcellos, E.A. Reassessing traffic accidents in developing countries. Transp. Policy 1995, 2, 263–269. [Google Scholar] [CrossRef]
- Vasconcellos, E.A. Urban development and traffic accidents in Brazil. Accid. Anal. Prev. 1999, 31, 319–328. [Google Scholar] [CrossRef] [PubMed]
- Bassani, M.; Dalmazzo, D.; Marinelli, G.; Cirillo, C. The effects of road geometrics and traffic regulations on driver-preferred speeds in northern Italy. An exploratory analysis. Transp. Res. Part F: Traffic Psychol. Behav. 2014, 25, 10–26. [Google Scholar] [CrossRef]
- Wegman, F.; Zhang, F.; Dijkstra, A. How to make more cycling good for road safety? Accid. Anal. Prev. 2012, 44, 19–29. [Google Scholar] [CrossRef] [PubMed]
- Ghafghazi, G.; Hatzopoulou, M. Simulating the environmental effects of isolated and area-wide traffic calming schemes using traffic simulation and microscopic emission modeling. Transportation 2014, 41, 633–649. [Google Scholar] [CrossRef]
- Ariën, C.; Brijs, K.; Brijs, T.; Ceulemans, W.; Vanroelen, G.; Jongen, E.M.M.; Daniels, S.; Wets, G. Does the effect of traffic calming measures endure over time?—A simulator study on the influence of gates. Transp. Res. Part F: Traffic Psychol. Behav. 2014, 22, 63–75. [Google Scholar] [CrossRef]
- Alemany, R.; Ayuso, M.; Guillén, M. Impact of road traffic injuries on disability rates and long-term care costs in Spain. Accid. Anal. Prev. 2013, 60, 95–102. [Google Scholar] [CrossRef] [PubMed]
- Salvarani, C.P.; Colli, B.O.; Carlotti Júnior, C.G. Impact of a program for the prevention of traffic accidents in a southern Brazilian city: A model for implementation in a developing country. Surg. Neurol. 2009, 72, 6–14. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machado, C.A.S.; Giannotti, M.A.; Neto, F.C.; Tripodi, A.; Persia, L.; Quintanilha, J.A. Characterization of Black Spot Zones for Vulnerable Road Users in São Paulo (Brazil) and Rome (Italy). ISPRS Int. J. Geo-Inf. 2015, 4, 858-882. https://doi.org/10.3390/ijgi4020858
Machado CAS, Giannotti MA, Neto FC, Tripodi A, Persia L, Quintanilha JA. Characterization of Black Spot Zones for Vulnerable Road Users in São Paulo (Brazil) and Rome (Italy). ISPRS International Journal of Geo-Information. 2015; 4(2):858-882. https://doi.org/10.3390/ijgi4020858
Chicago/Turabian StyleMachado, Cláudia A. Soares, Mariana Abrantes Giannotti, Francisco Chiaravalloti Neto, Antonino Tripodi, Luca Persia, and José Alberto Quintanilha. 2015. "Characterization of Black Spot Zones for Vulnerable Road Users in São Paulo (Brazil) and Rome (Italy)" ISPRS International Journal of Geo-Information 4, no. 2: 858-882. https://doi.org/10.3390/ijgi4020858
APA StyleMachado, C. A. S., Giannotti, M. A., Neto, F. C., Tripodi, A., Persia, L., & Quintanilha, J. A. (2015). Characterization of Black Spot Zones for Vulnerable Road Users in São Paulo (Brazil) and Rome (Italy). ISPRS International Journal of Geo-Information, 4(2), 858-882. https://doi.org/10.3390/ijgi4020858






