Discriminating Irrigated and Rainfed Maize with Diurnal Fluorescence and Canopy Temperature Airborne Maps
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Area and Field Campaigns

2.2. Canopy Temperature
2.3. Field Data
2.4. Airborne Hyperspectral Imagery Acquisition and Processing Techniques
| Sensor | Spectral Range (nm) | N° of Bands | FWHM (nm) | IFOV (mrad) |
|---|---|---|---|---|
| CASI 1500 | 380–1050 | 72 | 2.4–14.4 | 0.5 |
| AHS | 430–1030 | 20 | 28 | 2.5 |
| 1550–1750 | 1 | 200 | ||
| 2000–2560 | 42 | 13 | ||
| 3300–5400 | 7 | 300 | ||
| 8200–12,700 | 10 | 400 |
| RUN | Time (UTC) | θs (°) |
|---|---|---|
| CASI #1 | 08:40 | 42 |
| CASI #4 | 11:24 | 24 |
| CASI #5 | 14:20 | 43 |
| AHS #1 | 08:26 | 45 |
| AHS #2 | 11:04 | 25 |
| AHS#3 | 14:01 | 40 |
| Index | Formula | Reference |
|---|---|---|
| NDVI | (R800 − R680)/(R800 + R680) | [29] |
| OSAVI | (R800 − R680)/(R800 + R680 + 0.16) | [30] |
| TCARI | 3 × [(R700 − R670) − 0.2 × (R700 − R550) × (R700/R670)] | [31] |
| TCARI/OSAVI | TCARI/OSAVI | [31] |
| VARI | (R560− R670)/(R560 + R670− R473) | [32] |
| PRI | (R531 − R570)/(R531 + R570) | [10] |
2.5. Data Analysis
3. Results and Discussion
3.1. Field Data
| Parameter | Irr2 | Irr1 | Irr0 | η2 | ||
|---|---|---|---|---|---|---|
| Mean ± SD | % Decrease Compared to Irr2 | Mean ± SD | % Decrease Compared to Irr2 | |||
| ΔF/Fm' | 0.39 ± 0.01 | 0.36 ± 0.03 | −7.7 | 0.33 ± 0.03 | −15 | 0.52 |
| Gi | 254 ± 60 | 207 ± 20 | −18.5 | 200 ± 30 | −21.3 | n. a. |
| Ai | 42.43 ± 3.42 | 36.87 ± 3.42 | −13.1 | 32 ± 1.65 | −24.6 | n. a. |
| Chl | 52.8 ± 4.0 | 49.8 ± 4.9 | −5.7 | 49.9 ± 2.9 | −5.5 | 0.12 |
| EWT | 0.0135 ± 0.0006 | 0.0130 ± 0.0004 | −3.7 | 0.0127 ± 0.0005 | −5.9 | 0.33 |
| RWC | 95.4 ± 0.5 | 92.5 ± 0.9 | −3 | 93.1 ± 1.9 | −2.4 | 0.57 |
3.2. Thermal Data
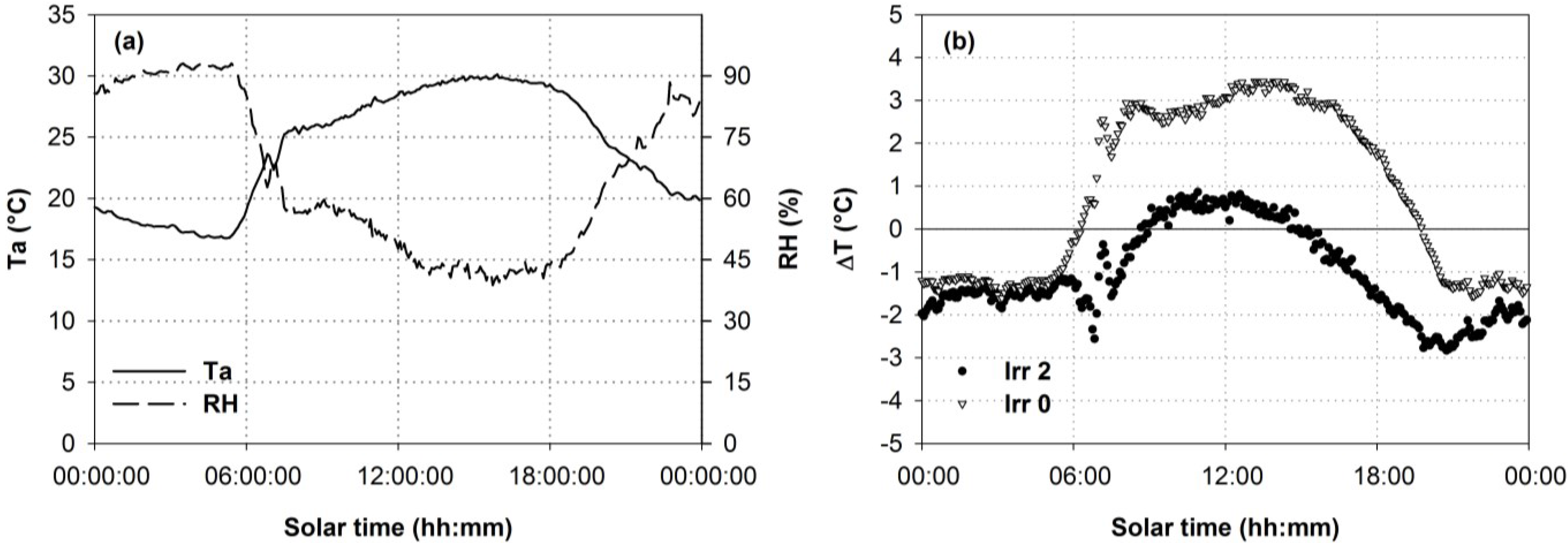
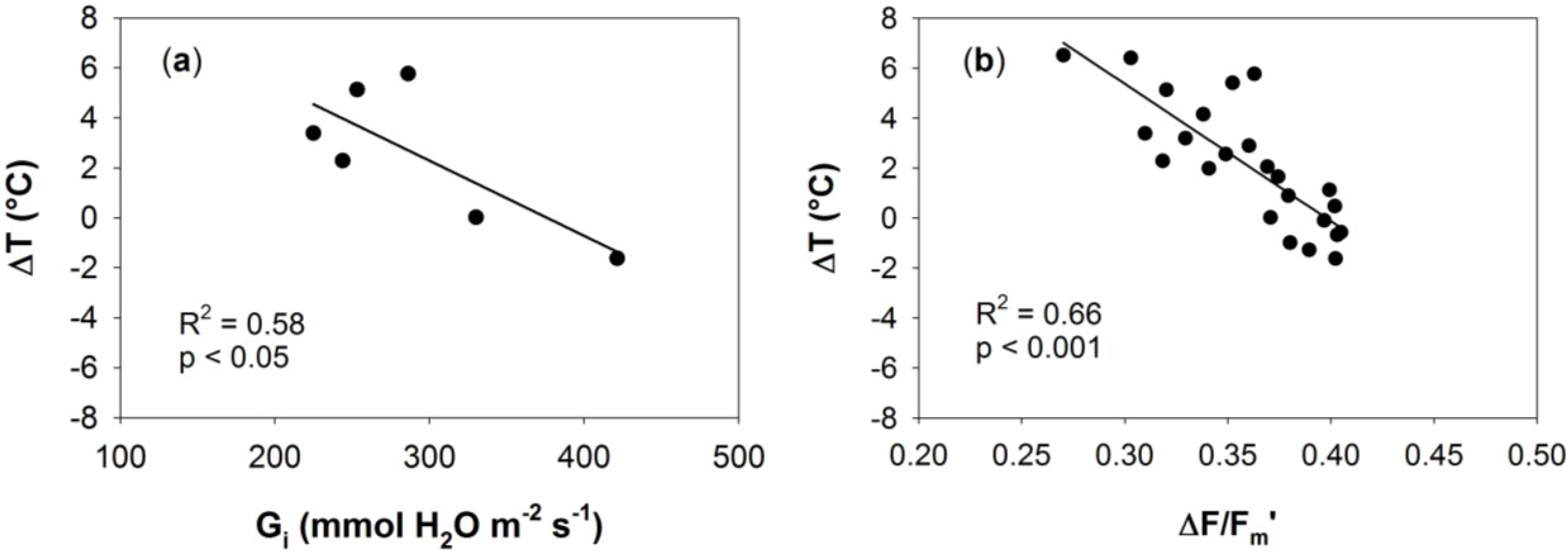

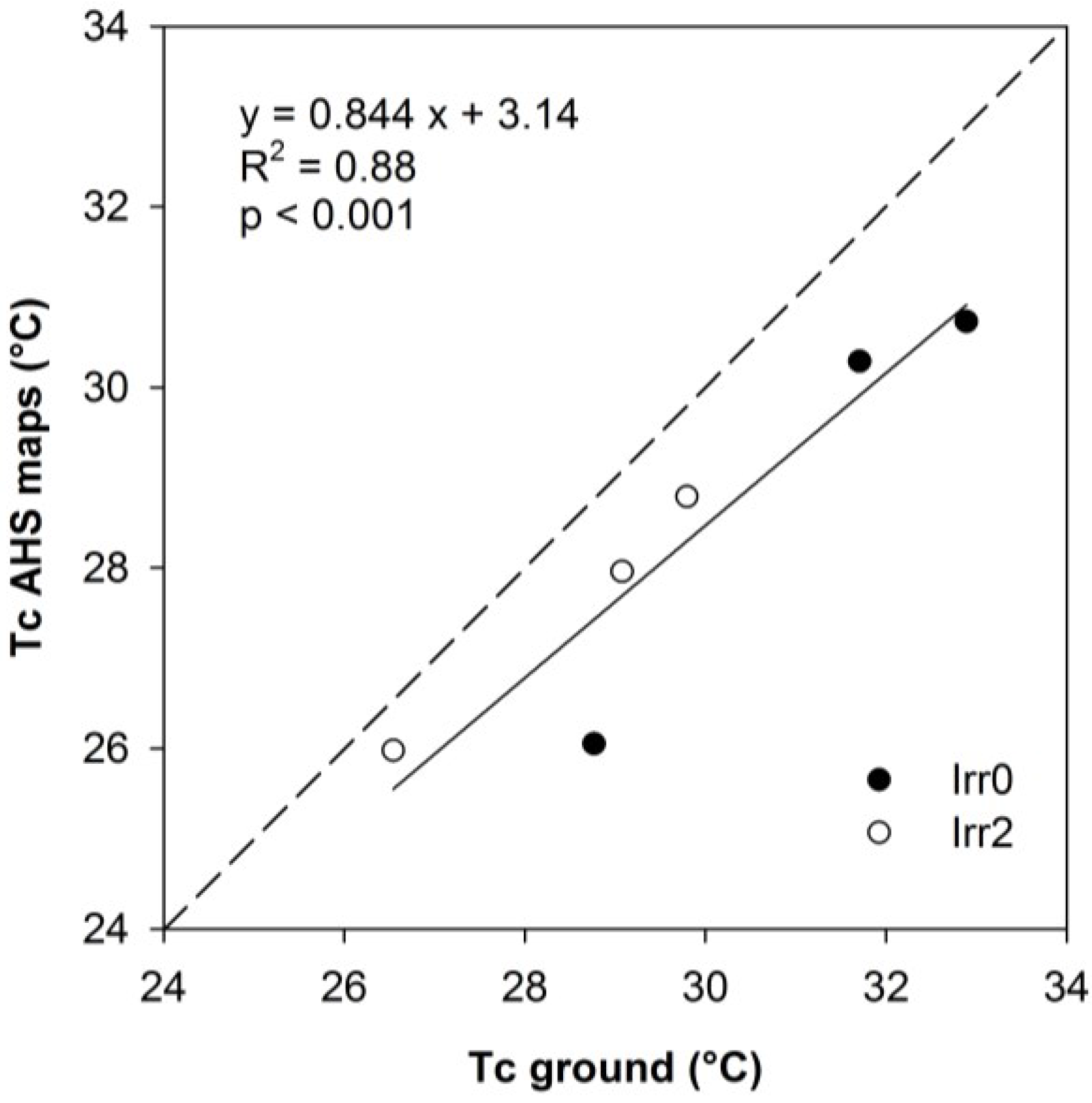

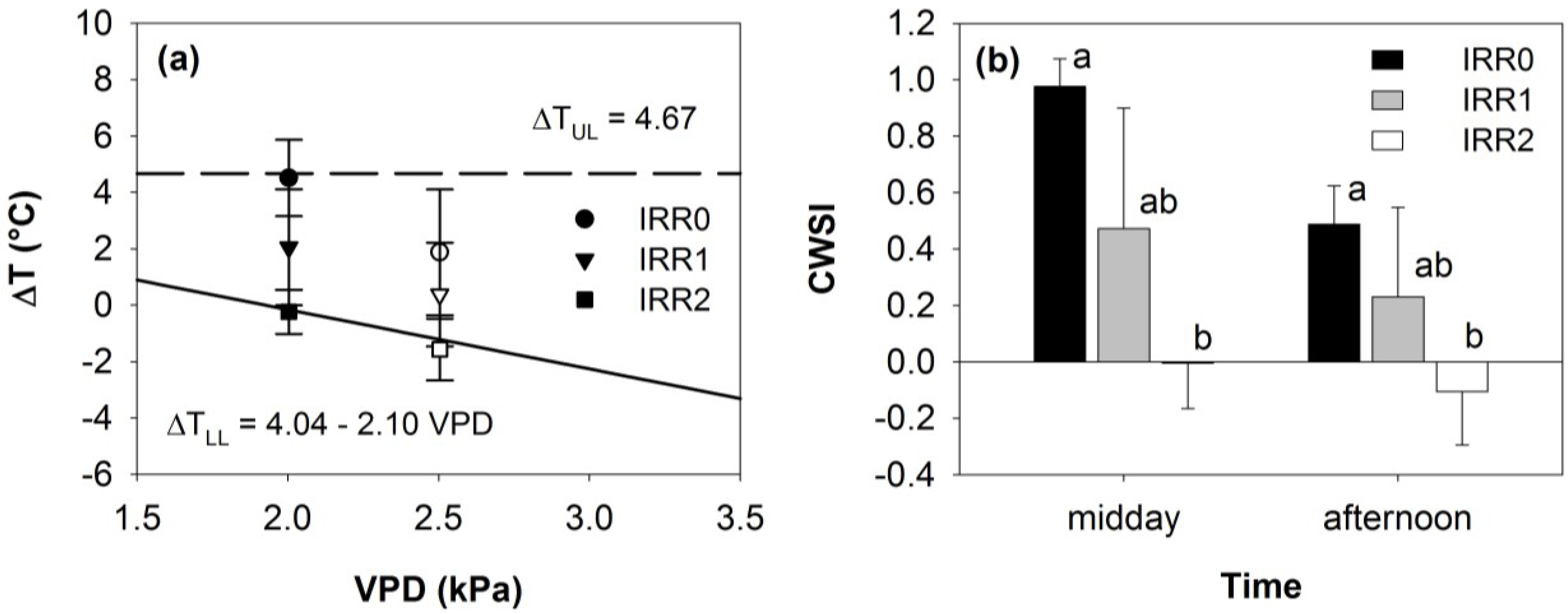
3.3. Relationships between Optical Indices and Fluorescence and Field Parameters Measured at Midday
3.4. Diurnal Variations of Optical Indices and Fluorescence
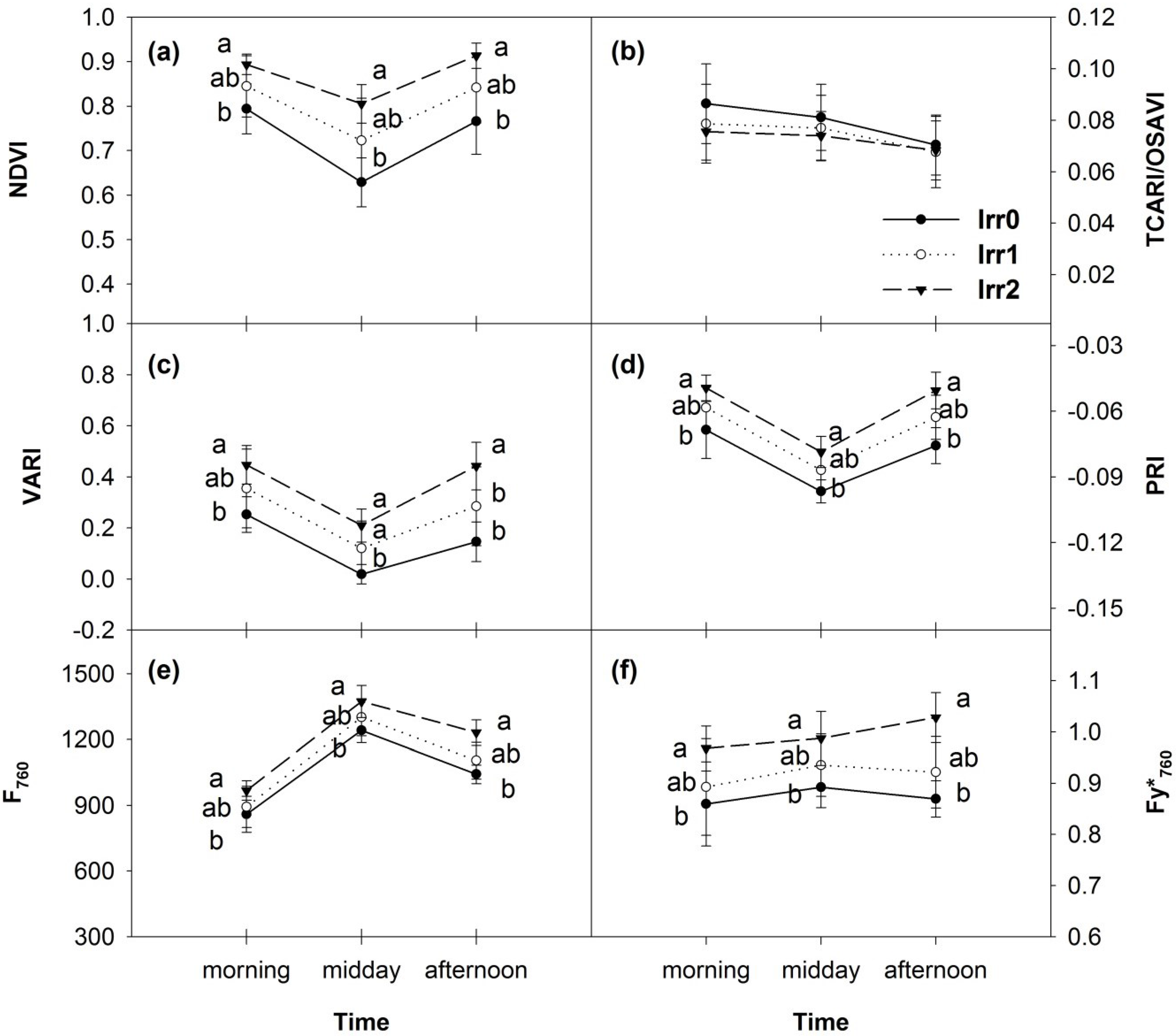
3.5. Synthesis of Thermal and Optical Data
| Morning | Midday | Afternoon |
|---|---|---|
| NDVI (11.045) | Tc and ΔT (14.060) | PRI (13.815) |
| PRI (10.085) | NDVI (13.265) | F760 and Fy*760 (13.715) |
| Tc and ΔT (9.465) | VARI (12.285) | VARI (12.635) |
| VARI (9.26) | PRI (11.535) | NDVI (12.065) |
| F760 and Fy*760 (7.22) | F760 and Fy*760 (9.465) | Tc and ΔT (10.205) |
| TCARI/OSAVI (2.195) | TCARI/OSAVI (1.34) | TCARI/OSAVI (0.32) |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fereres, E.; Orgaz, F.; Gonzalez-Dugo, V. Reflections on food security under water scarcity. J. Exp. Bot. 2011. [Google Scholar] [CrossRef]
- Jury, W.A.; Vaux, H.J., Jr. The emerging global water crisis: Managing scarcity and conflict between water users. In Advances in Agronomy; Donald, L.S., Ed.; Academic Press: Waltham, MA, USA, 2007; Volume 95, pp. 1–76. [Google Scholar]
- Yordanov, I.; Velikova, V.; Tsonev, T. Plant responses to drought, acclimation, and stress tolerance. Photosynthetica 2000, 38, 171–186. [Google Scholar] [CrossRef]
- Chaves, M.M.; Flexas, J.; Pinheiro, C. Photosynthesis under drought and salt stress: Regulation mechanisms from whole plant to cell. Ann. Bot. 2009, 103, 551–560. [Google Scholar] [CrossRef] [PubMed]
- Taghvaeian, S.; Chávez, J.; Hansen, N. Infrared thermometry to estimate crop water stress index and water use of irrigated maize in Northeastern Colorado. Remote Sens. 2012, 4, 3619–3637. [Google Scholar] [CrossRef]
- Torrion, J.; Maas, S.; Guo, W.; Bordovsky, J.; Cranmer, A. A three-dimensional index for characterizing crop water stress. Remote Sens. 2014, 6, 4025–4042. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D.; Pinter, P.J., Jr.; Reginato, R.J.; Hatfield, J.L. Normalizing the stress-degree-day parameter for environmental variability. Agric. Meteorol. 1981, 24, 45–55. [Google Scholar] [CrossRef]
- Maes, W.H.; Steppe, K. Estimating evapotranspiration and drought stress with ground-based thermal remote sensing in agriculture: A review. J. Exp. Bot. 2012, 63, 4671–4712. [Google Scholar] [CrossRef] [PubMed]
- Flexas, J.; Bota, J.; Cifre, J.; Escalona, J.M.; Galmes, J.; Gulias, J.; Lefi, E.K.; Martinez-Canellas, S.F.; Moreno, M.T.; Ribas-Carbo, M.; et al. Understanding down-regulation of photosynthesis under water stress: Future prospects and searching for physiological tools for irrigation management. Ann. Appl. Biol. 2004, 144, 273–283. [Google Scholar] [CrossRef]
- Gamon, J.A.; Peñuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Panigada, C.; Rossini, M.; Meroni, M.; Cilia, C.; Busetto, L.; Amaducci, S.; Boschetti, M.; Cogliati, S.; Picchi, V.; Pinto, F.; et al. Fluorescence, pri and canopy temperature for water stress detection in cereal crops. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 167–178. [Google Scholar] [CrossRef]
- Rossini, M.; Fava, F.; Cogliati, S.; Meroni, M.; Marchesi, A.; Panigada, C.; Giardino, C.; Busetto, L.; Migliavacca, M.; Amaducci, S.; et al. Assessing canopy pri from airborne imagery to map water stress in maize. ISPRS J. Photogramm. Remote Sens. 2013, 86, 168–177. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Williams, L.E.; Suárez, L.; Berni, J.A.J.; Goldhamer, D.; Fereres, E. A pri-based water stress index combining structural and chlorophyll effects: Assessment using diurnal narrow-band airborne imagery and the CWSI thermal index. Remote Sens. Environ. 2013, 138, 38–50. [Google Scholar] [CrossRef]
- Römer, C.; Wahabzada, M.; Ballvora, A.; Pinto, F.; Rossini, M.; Panigada, C.; Behmann, J.; Léon, J.; Thurau, C.; Bauckhage, C.; et al. Early drought stress detection in cereals: Simplex volume maximisation for hyperspectral image analysis. Funct. Plant Biol. 2012, 39, 878–890. [Google Scholar] [CrossRef]
- Meroni, M.; Rossini, M.; Guanter, L.; Alonso, L.; Rascher, U.; Colombo, R.; Moreno, J. Remote sensing of solar-induced chlorophyll fluorescence: Review of methods and applications. Remote Sens. Environ. 2009, 113, 2037–2051. [Google Scholar] [CrossRef]
- Cheng, Y.-B.; Middleton, E.; Zhang, Q.; Huemmrich, K.; Campbell, P.; Corp, L.; Cook, B.; Kustas, W.; Daughtry, C. Integrating solar induced fluorescence and the photochemical reflectance index for estimating gross primary production in a cornfield. Remote Sens. 2013, 5, 6857–6879. [Google Scholar] [CrossRef]
- Lancashire, P.D.; Bleiholder, H.; Langeluddecke, P.; Stauss, R.; van den Boom, T.; Weber, E.; Witzenberger, A. A uniform decimal code for growth stages of crops and weeds. Ann. Appl. Biol. 1991, 119, 561–601. [Google Scholar] [CrossRef]
- Prasad, P.V.V.; Staggenborg, S.A.; Ristic, Z. Impacts of drought and/or heat stress on physiological, developmental, growth, and yield processes of crop plants. In Response of Crops to Limited Water: Understanding and Modeling Water Stress Effects on Plant Growth Processes. Advances in Agricultural Systems Modeling Series 1; Ahuja, L.H., Saseendran, S.A., Eds.; ASA-CSSA: Madison, WI, USA, 2008. [Google Scholar]
- Cilia, C.; Panigada, C.; Rossini, M.; Meroni, M.; Busetto, L.; Amaducci, S.; Boschetti, M.; Picchi, V.; Colombo, R. Nitrogen status assessment for variable rate fertilization in maize through hyperspectral imagery. Remote Sens. 2014, 6, 6549–6565. [Google Scholar] [CrossRef]
- Sumayao, C.R.; Kanemasu, E.T.; Brakke, T.W. Using leaf temperature to assess evapotranspiration and advection. Agric. Meteorol. 1980, 22, 153–166. [Google Scholar] [CrossRef]
- Bilger, W.; Schreiber, U.; Bock, M. Determination of the quantum efficiency of photosystem-ii and of nonphotochemical quenching of chlorophyll fluorescence in the field. Oecologia 1995, 102, 425–432. [Google Scholar] [CrossRef]
- Webb, N.; Nichol, C.; Wood, J. User Manual for the Sunscan Canopy Analysis System (2.0 Version); Potter: Cambridge, UK, 2008; p. 83. [Google Scholar]
- Van Evert, F.K.; Campbell, G.S. Cropsyst: A collection of object-oriented simulation models of agricultural systems. Agron. J. 1994, 86, 325–331. [Google Scholar]
- Gillespie, A.R. Spectral mixture analysis of multispectral thermal infrared images. Remote Sens. Environ. 1992, 42, 137–145. [Google Scholar] [CrossRef]
- Jackson, R.D. Canopy temperature and crop water stress. Adv. Irrig. 1982, 1, 43–85. [Google Scholar]
- Idso, S.B. Non-water-stressed baselines: A key to measuring and interpreting plant water stress. Agric. Meteorol. 1982, 27, 59–70. [Google Scholar] [CrossRef]
- Irmak, S.; Haman, D.Z.; Bastug, R. Determination of crop water stress index for irrigation timing and yield estimation of corn. Agron. J. 2000, 92, 1221–1227. [Google Scholar] [CrossRef]
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Advancements and Retro Gradation of Natural Vegetation; Texas A & M University, Remote Sensing Center: Greenbelt, MD, USA, 1974; p. 371. [Google Scholar]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Maier, S.W.; Günther, K.P.; Stellmes, M. Remote Sensing and Modelling of Solar Induced Fluorescence. In Proceedings of the 1st Workshop on Remote Sensing of Solar Induced Vegetation Fluorescence, Noodwijk, The Netherlands, 19–20 June 2002; ESTEC: Noordwijk, The Netherlands, 2002. [Google Scholar]
- Zarco-Tejada, P.J.; Berni, J.A.J.; Suárez, L.; Sepulcre-Cantó, G.; Morales, F.; Miller, J.R. Imaging chlorophyll fluorescence with an airborne narrow-band multispectral camera for vegetation stress detection. Remote Sens. Environ. 2009, 113, 1262–1275. [Google Scholar] [CrossRef]
- Rossini, M.; Meroni, M.; Migliavacca, M.; Manca, G.; Cogliati, S.; Busetto, L.; Picchi, V.; Cescatti, A.; Seufert, G.; Colombo, R. High resolution field spectroscopy measurements for estimating gross ecosystem production in a rice field. Agric. For. Meteorol. 2010, 150, 1283–1296. [Google Scholar] [CrossRef]
- Pearson, K. On the coefficient of racial likeness. Biometrika 1926, 18, 105–117. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, J.; Kinzelbach, W.; Cheng, G.; Li, X.; Zhao, W. Coupling a svat heat and water flow model, a stomatal-photosynthesis model and a crop growth model to simulate energy, water and carbon fluxes in an irrigated maize ecosystem. Agric. For. Meteorol. 2013, 176, 10–24. [Google Scholar] [CrossRef]
- Gonzalez-Dugo, V.; Zarco-Tejada, P.; Nicolás, E.; Nortes, P.A.; Alarcón, J.J.; Intrigliolo, D.S.; Fereres, E. Using high resolution uav thermal imagery to assess the variability in the water status of five fruit tree species within a commercial orchard. Precis. Agric. 2013, 14, 660–678. [Google Scholar] [CrossRef]
- Perry, E.M.; Roberts, D.A. Sensitivity of narrow-band and broad-band indices for assessing nitrogen availability and water stress in an annual crop all rights reserved. No part of this periodical may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording, or any information storage and retrieval system, without permission in writing from the publisher. Agron. J. 2008, 100, 1211–1219. [Google Scholar] [CrossRef]
- Roberts, D.A.; Dennison, P.E.; Peterson, S.; Sweeney, S.; Rechel, J. Evaluation of airborne visible/infrared imaging spectrometer (aviris) and moderate resolution imaging spectrometer (modis) measures of live fuel moisture and fuel condition in a shrubland ecosystem in southern california. J. Geophys. Res. Biogeosci. 2006, 111, G04S02. [Google Scholar]
- Çakir, R. Effect of water stress at different development stages on vegetative and reproductive growth of corn. Field Crop. Res. 2004, 89, 1–16. [Google Scholar] [CrossRef]
- Suárez, L.; Zarco-Tejada, P.J.; Berni, J.A.J.; Gonzalez-Dugo, V.; Fereres, E. Modelling pri for water stress detection using radiative transfer models. Remote Sens. Environ. 2009, 113, 730–744. [Google Scholar] [CrossRef]
- Suárez, L.; Zarco-Tejada, P.J.; Gonzalez-Dugo, V.; Berni, J.A.J.; Sagardoy, R.; Morales, F.; Fereres, E. Detecting water stress effects on fruit quality in orchards with time-series pri airborne imagery. Remote Sens. Environ. 2010, 114, 286–298. [Google Scholar] [CrossRef]
- Rossini, M.; Nedbal, L.; Guanter, L.; Ač, A.; Alonso, L.; Burkart, A.; Cogliati, S.; Colombo, R.; Damm, A.; Drusch, M.; et al. Red and far-red sun-induced chlorophyll fluorescence as a measure of plant photosynthesis. Geophys. Res. Lett. 2015, 42, 2014GL062943. [Google Scholar]
- Bellvert, J.; Zarco-Tejada, P.J.; Girona, J.; Fereres, E. Mapping crop water stress index in a ‘pinot-noir’ vineyard: Comparing ground measurements with thermal remote sensing imagery from an unmanned aerial vehicle. Precis. Agric. 2014, 15, 361–376. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossini, M.; Panigada, C.; Cilia, C.; Meroni, M.; Busetto, L.; Cogliati, S.; Amaducci, S.; Colombo, R. Discriminating Irrigated and Rainfed Maize with Diurnal Fluorescence and Canopy Temperature Airborne Maps. ISPRS Int. J. Geo-Inf. 2015, 4, 626-646. https://doi.org/10.3390/ijgi4020626
Rossini M, Panigada C, Cilia C, Meroni M, Busetto L, Cogliati S, Amaducci S, Colombo R. Discriminating Irrigated and Rainfed Maize with Diurnal Fluorescence and Canopy Temperature Airborne Maps. ISPRS International Journal of Geo-Information. 2015; 4(2):626-646. https://doi.org/10.3390/ijgi4020626
Chicago/Turabian StyleRossini, Micol, Cinzia Panigada, Chiara Cilia, Michele Meroni, Lorenzo Busetto, Sergio Cogliati, Stefano Amaducci, and Roberto Colombo. 2015. "Discriminating Irrigated and Rainfed Maize with Diurnal Fluorescence and Canopy Temperature Airborne Maps" ISPRS International Journal of Geo-Information 4, no. 2: 626-646. https://doi.org/10.3390/ijgi4020626
APA StyleRossini, M., Panigada, C., Cilia, C., Meroni, M., Busetto, L., Cogliati, S., Amaducci, S., & Colombo, R. (2015). Discriminating Irrigated and Rainfed Maize with Diurnal Fluorescence and Canopy Temperature Airborne Maps. ISPRS International Journal of Geo-Information, 4(2), 626-646. https://doi.org/10.3390/ijgi4020626










