Simulating Urban Growth Using a Random Forest-Cellular Automata (RF-CA) Model
Abstract
:1. Introduction
2. Implementation of the RF-CA Model
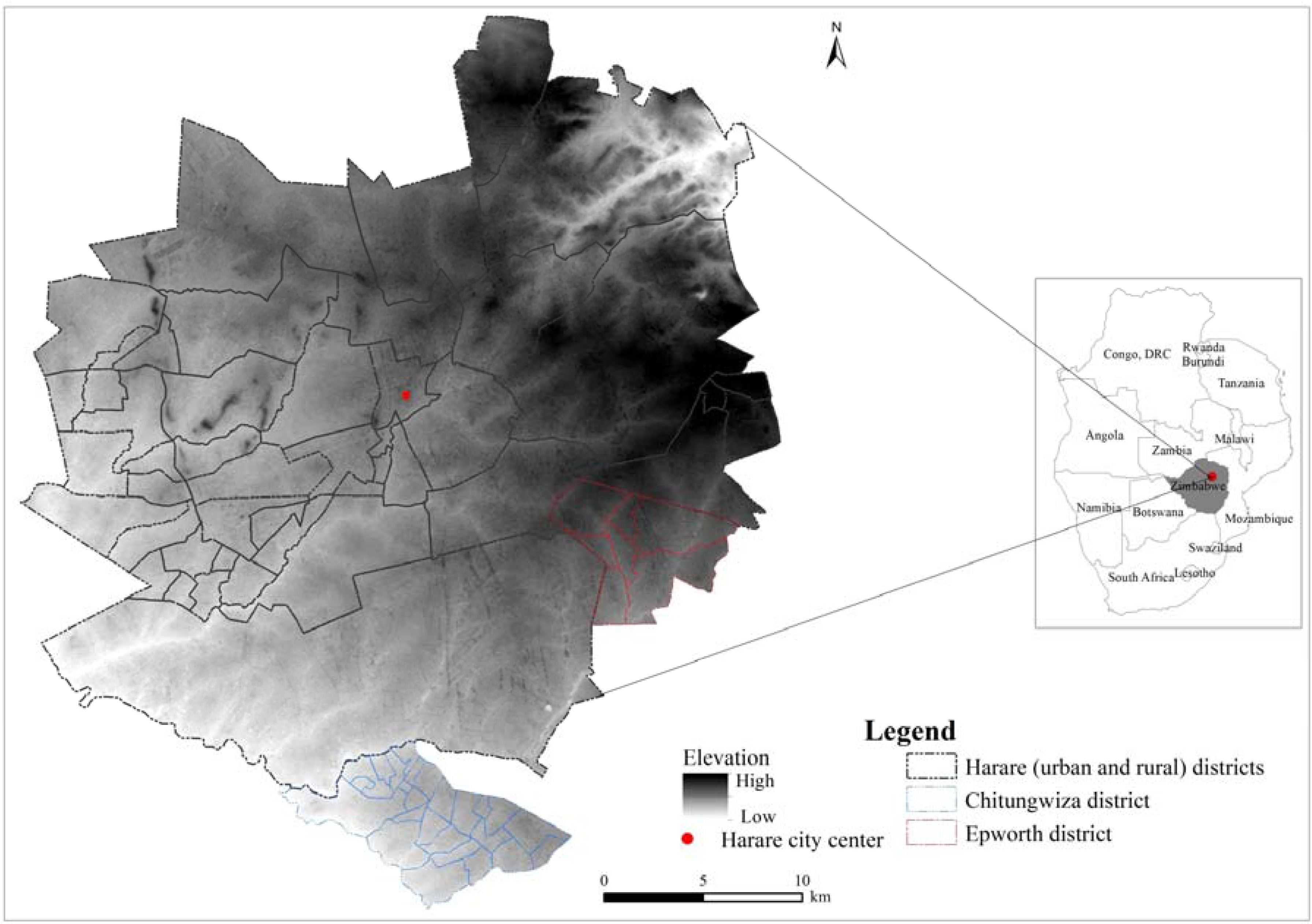
2.1. Study Area and Data
| Variable | Source |
|---|---|
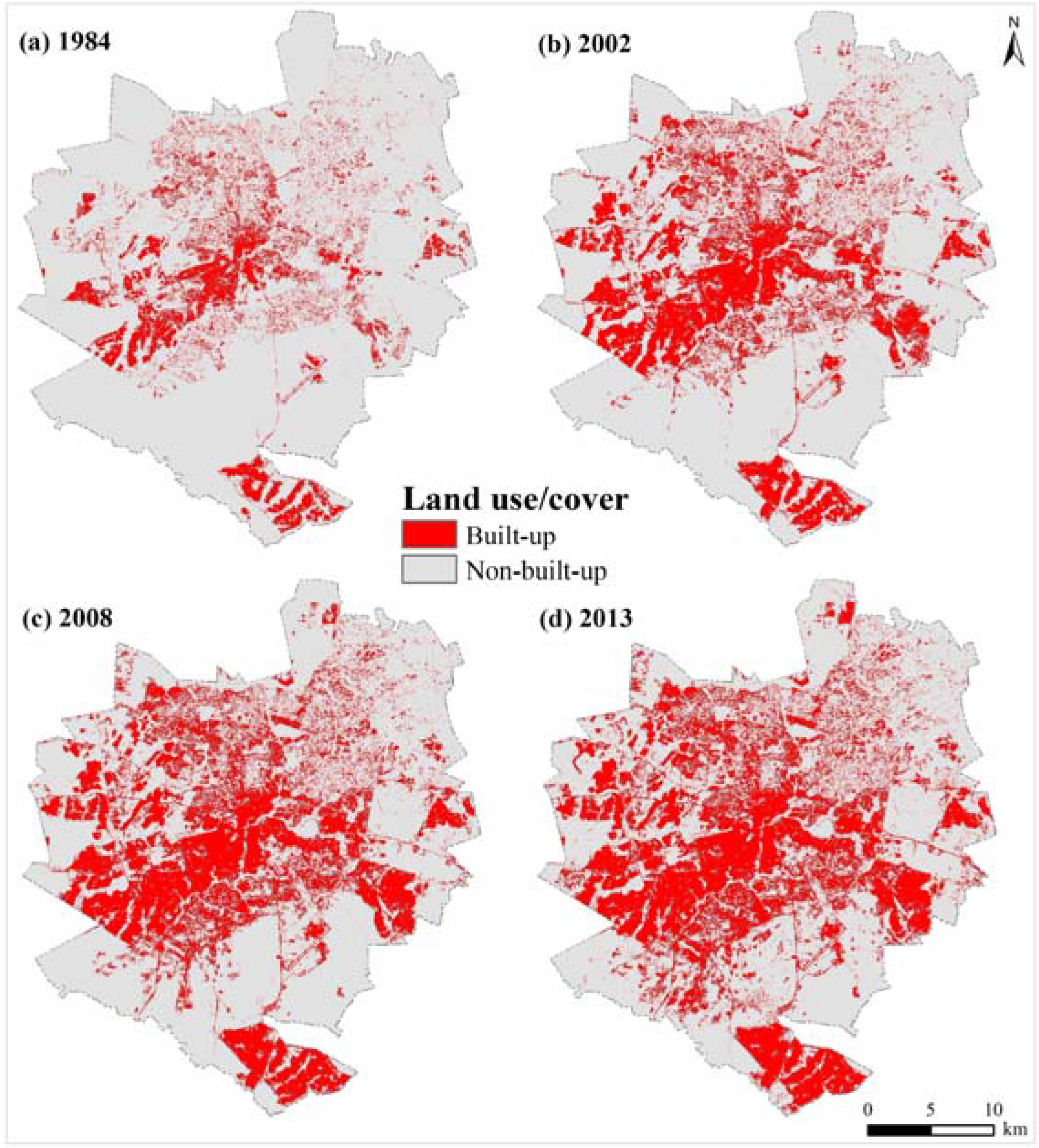
| Land use/cover maps (1984, 2002, 2008 and 2013)
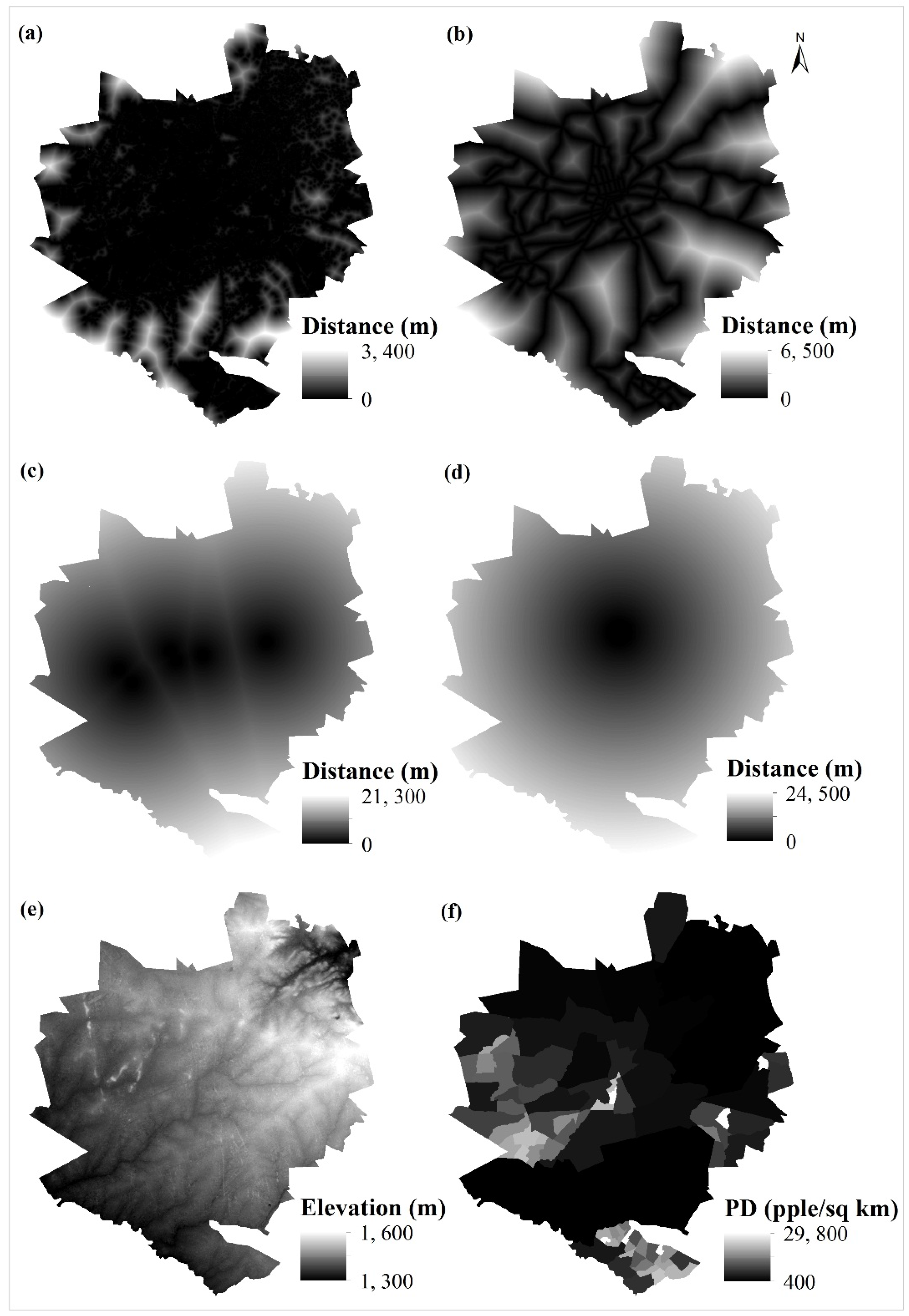
Distance to built-up areas (1984, 2002) Distance to major roads (1984–2002, 2002–2008) Distance to major industrial centers Distance to city center Elevation Population density (2002) | Classified from Landsat data Derived from land use/cover maps Digitised from 1:30,000 scale Harare Street maps Digitised from 1:30,000 scale Harare Street maps Digitised from 1:30,000 scale Harare Street maps Derived from ASTERGDEM Derived from Zimbabwe Statistical Office |
| Land Use/Cover Class | Description |
|---|---|
| Built-up | Residential, commercial and services, industrial, transportation, communication and utilities, construction sites, and landfills. |
| Non-built-up | All wooded areas, riverine vegetation, shrubs and bushes, grass cover, golf courses, parks, cultivated land, fallow land, land under irrigation, bare exposed areas, transitional areas and water. |
2.2. Model Calibration and Simulation
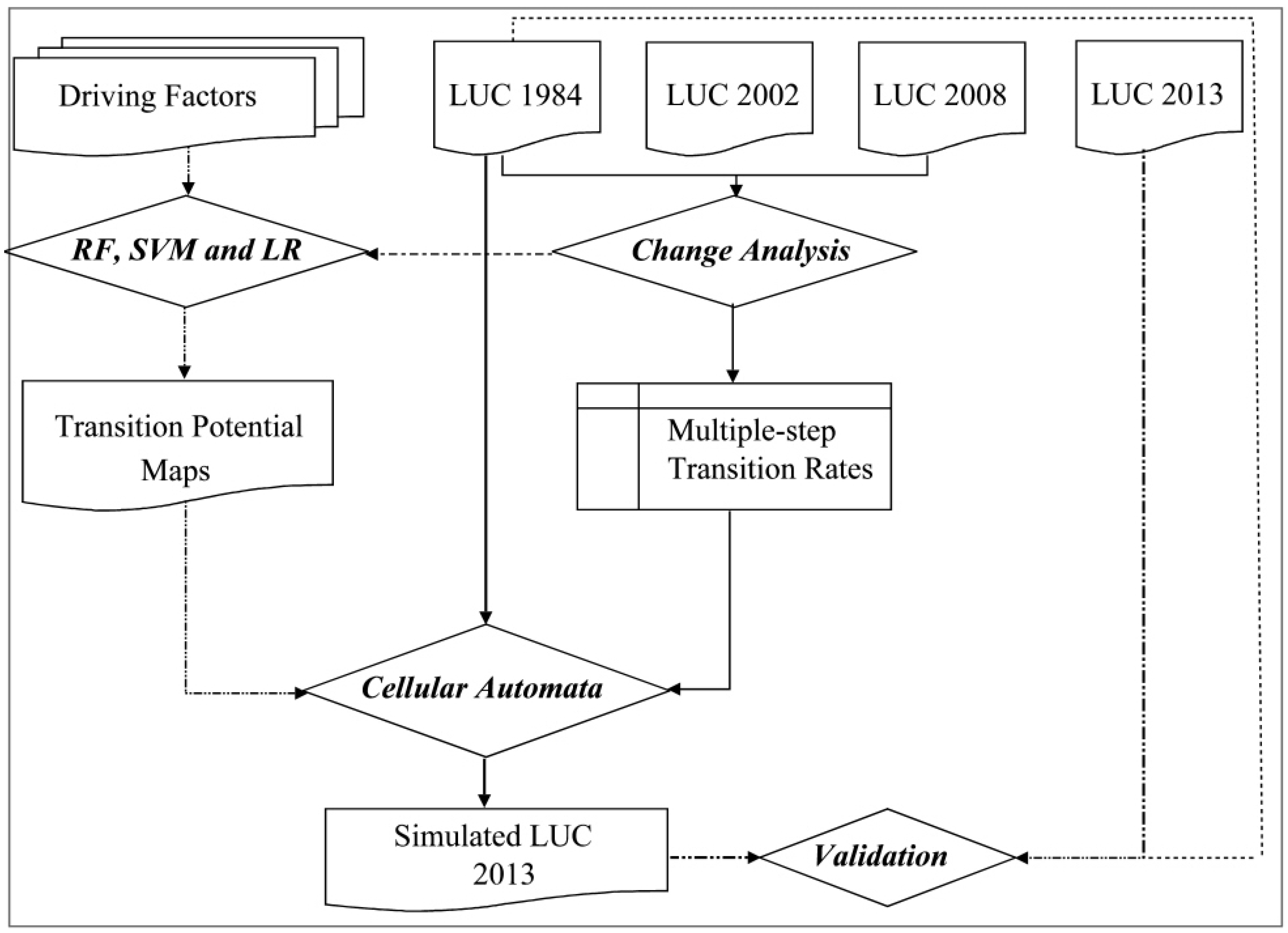
2.2.1. Computation of Transition Rates
| Period | Single-Step Transition Rates | Multiple-Step Transition Rates |
|---|---|---|
| 1984–2002 | 14 | 1 |
| 2002–2008 | 10 | 2 |
| 1984–2008 | 22 | 1 |
| 2008–2013 | 11 | 2 |
| (b) | ||
| Period | Single-Step Simulation Accuracy | Multiple-Step Simulation Accuracy |
| 1984–2002 | 6 | 50 |
| 1984–2008; 2002–2008 | 6 | 44 |
| 1984–2002; 2002–2008 and 1984–2008 | 6 | 50 |
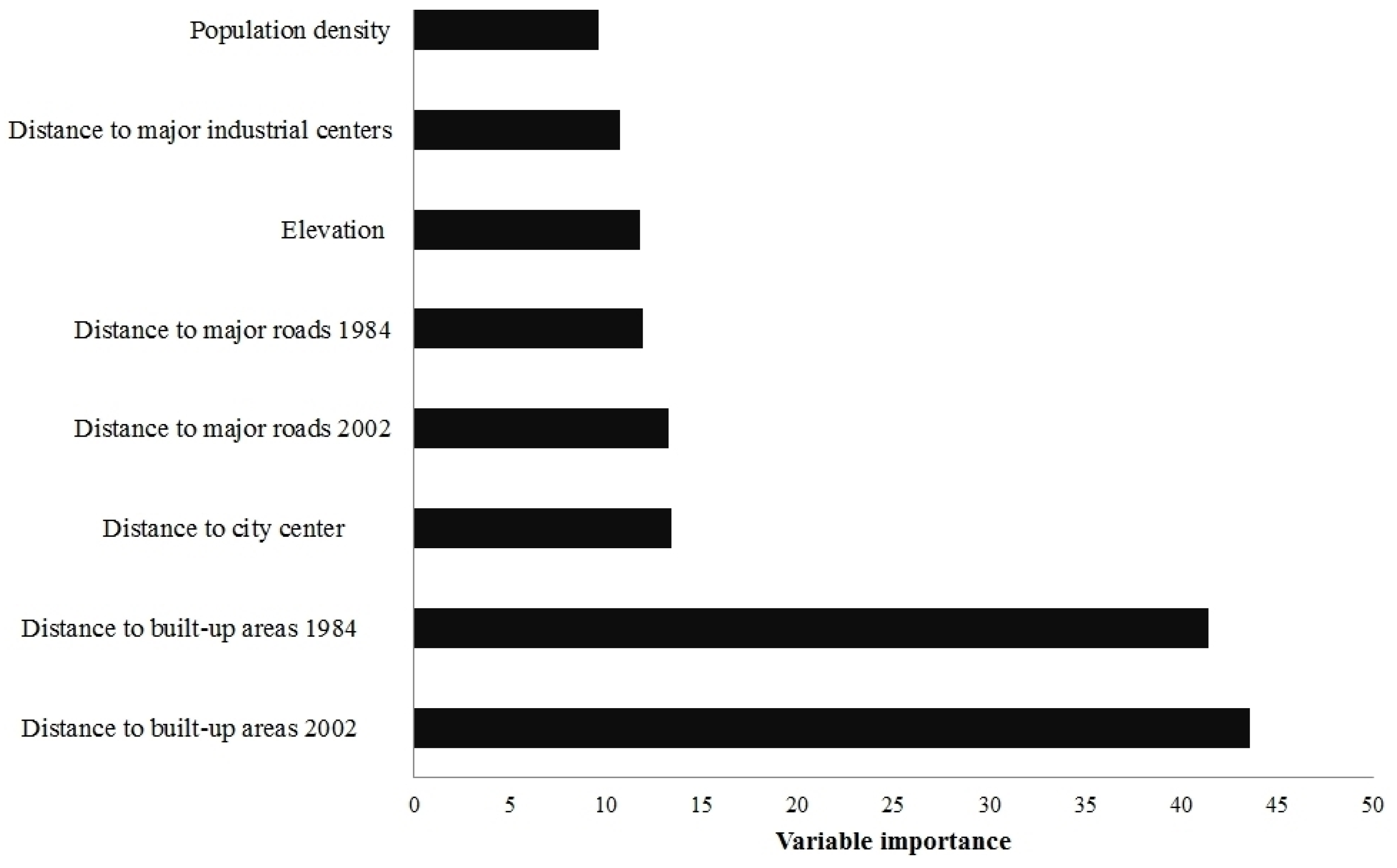
2.2.2. Transition Potential Modelling
2.2.3. Simulation based On the CA Model
3. Results and Discussion
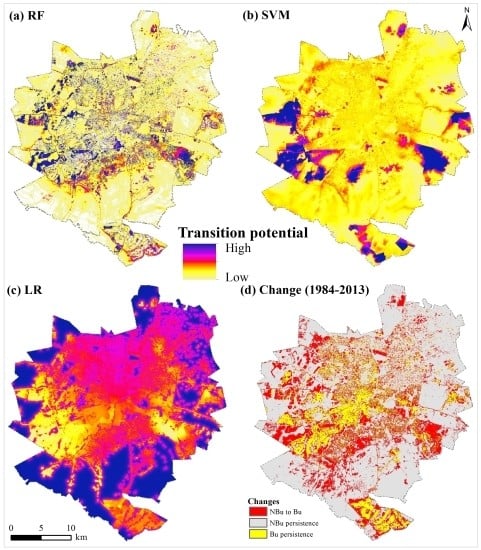
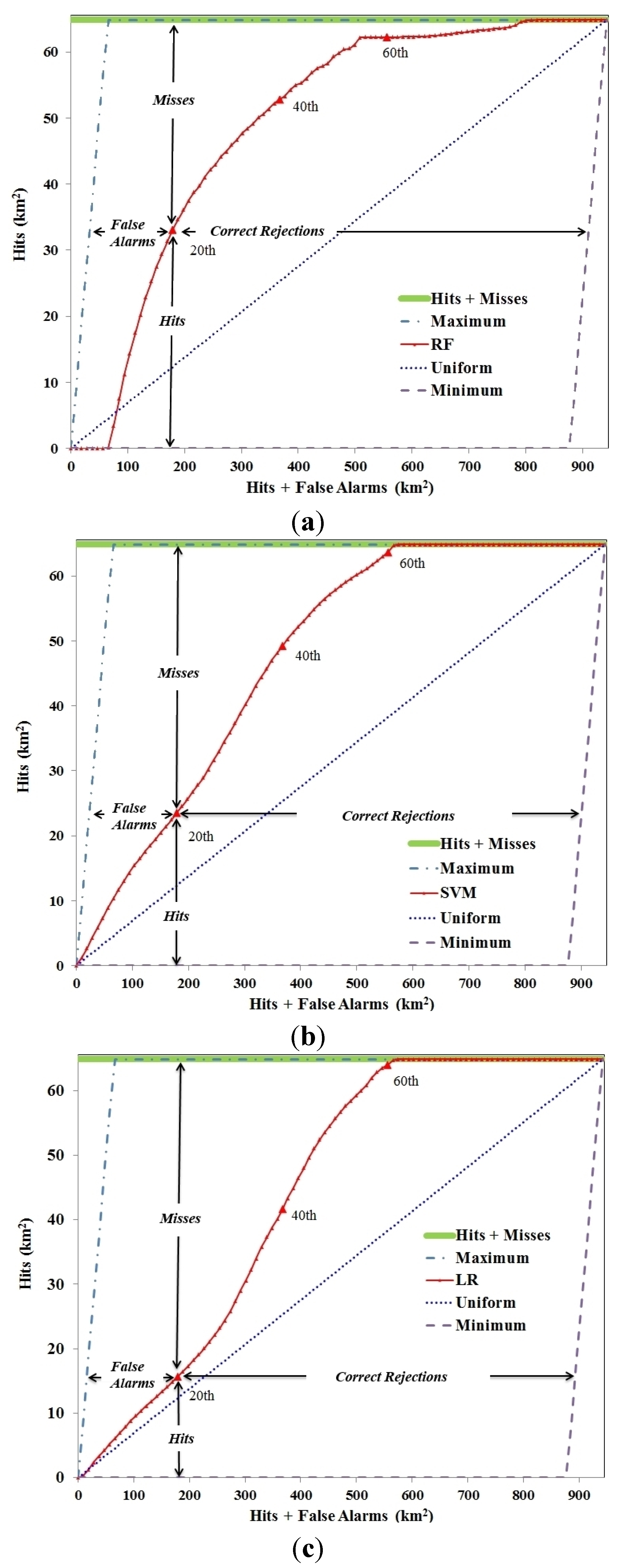
3.1. Evaluating the Goodness-of-Fit of Transition Potential Maps
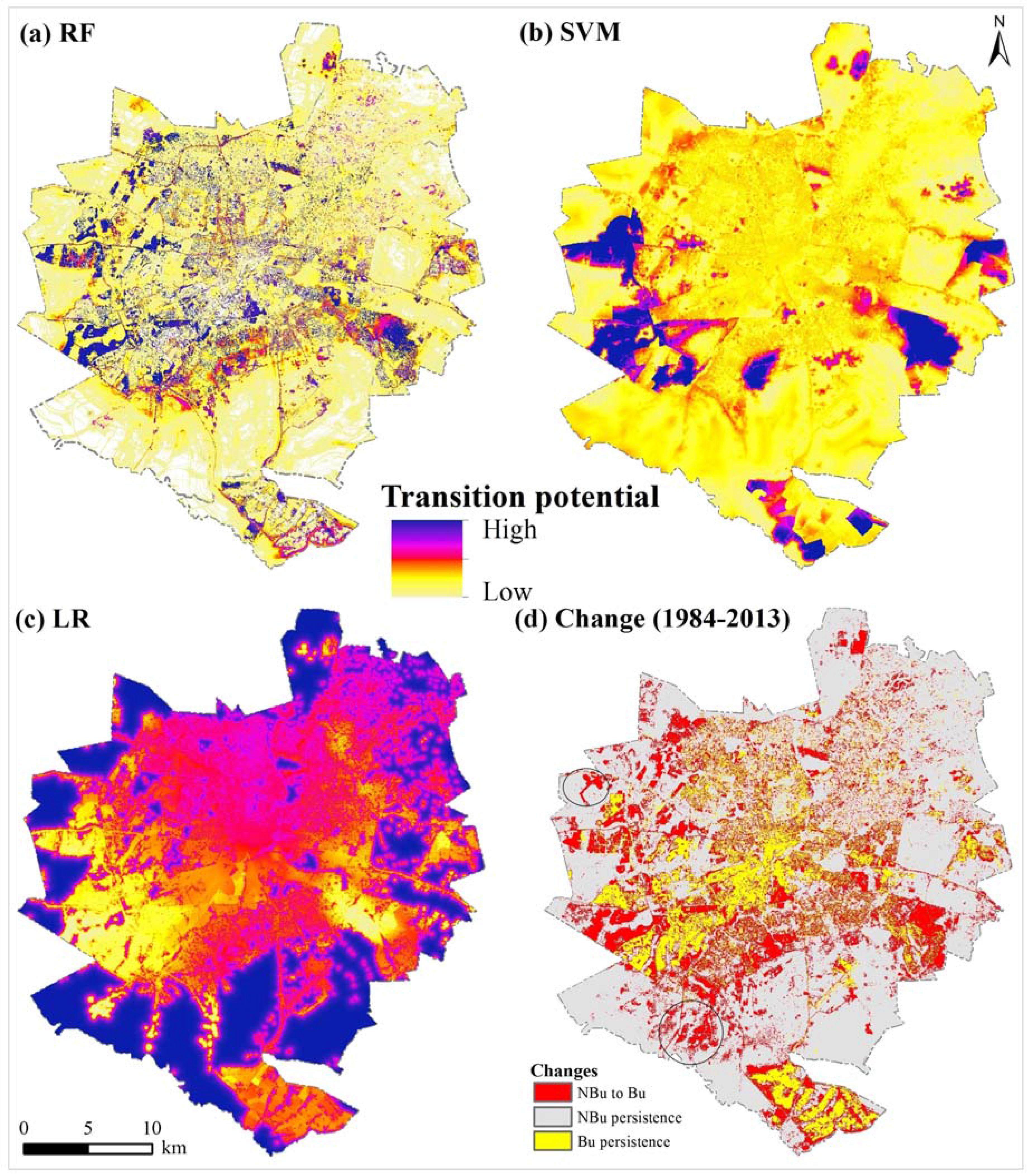
3.2. RF-CA Model Validation
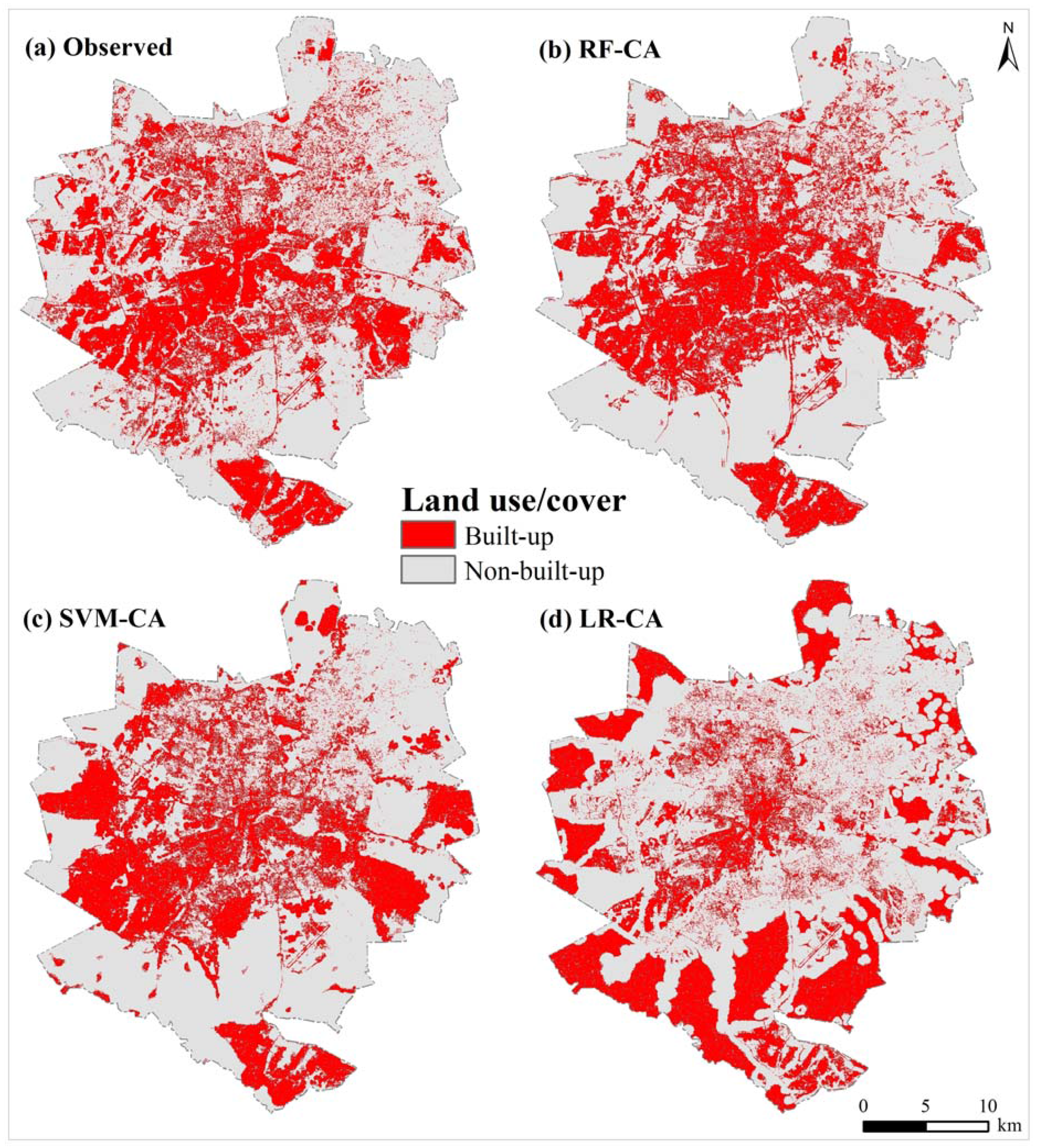
| Model | KSimulation | KTranslocation | KTransition | Figure of Merit (%) |
|---|---|---|---|---|
| RF-CA | 0.51 | 0.51 | 0.99 | 47 |
| SVM-CA | 0.39 | 0.4 | 0.98 | 39 |
| LR-CA | −0.22 | −0.22 | 0.99 | 6 |
3.3. Analysis of Components of Agreement and Disagreement
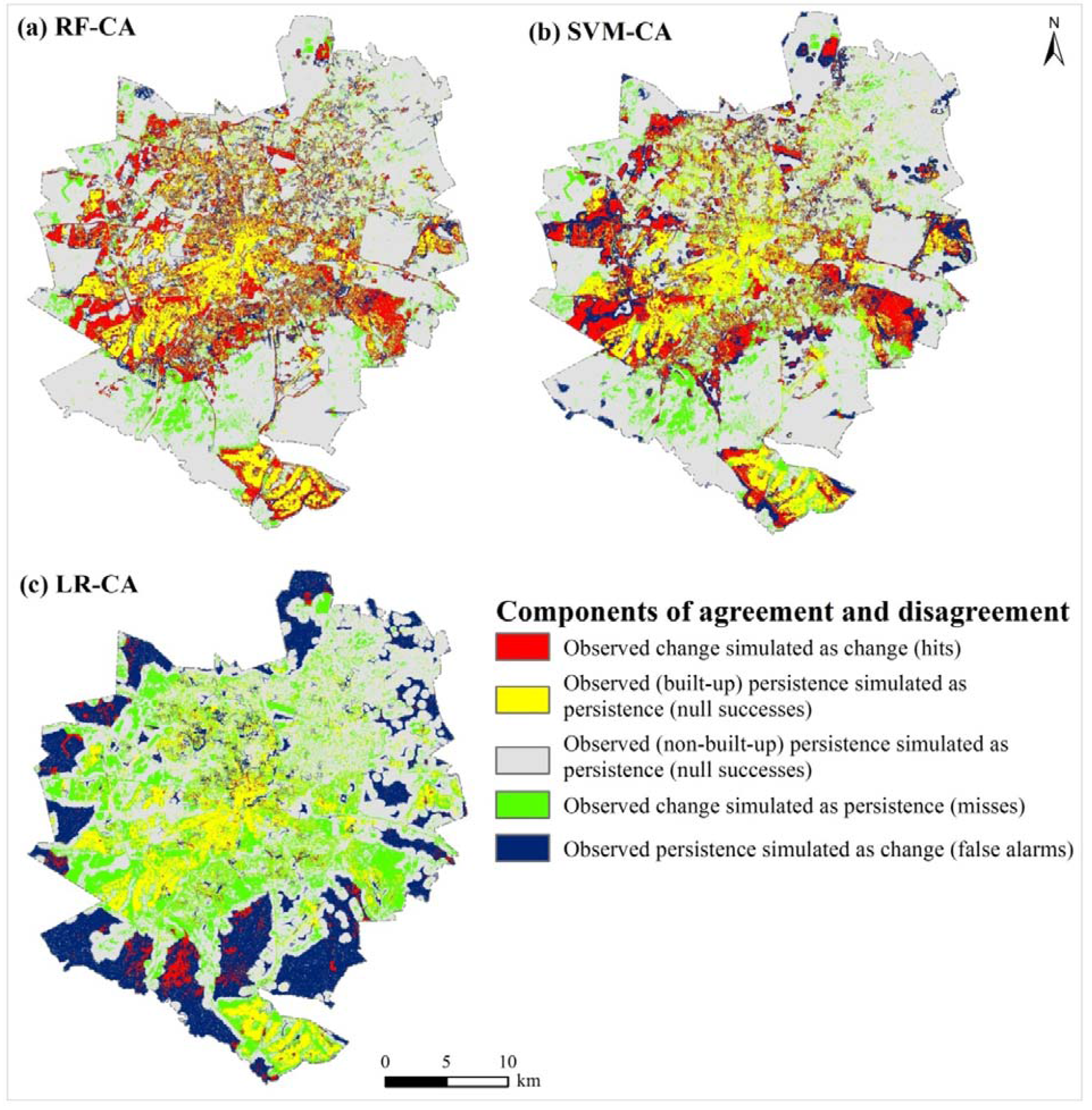
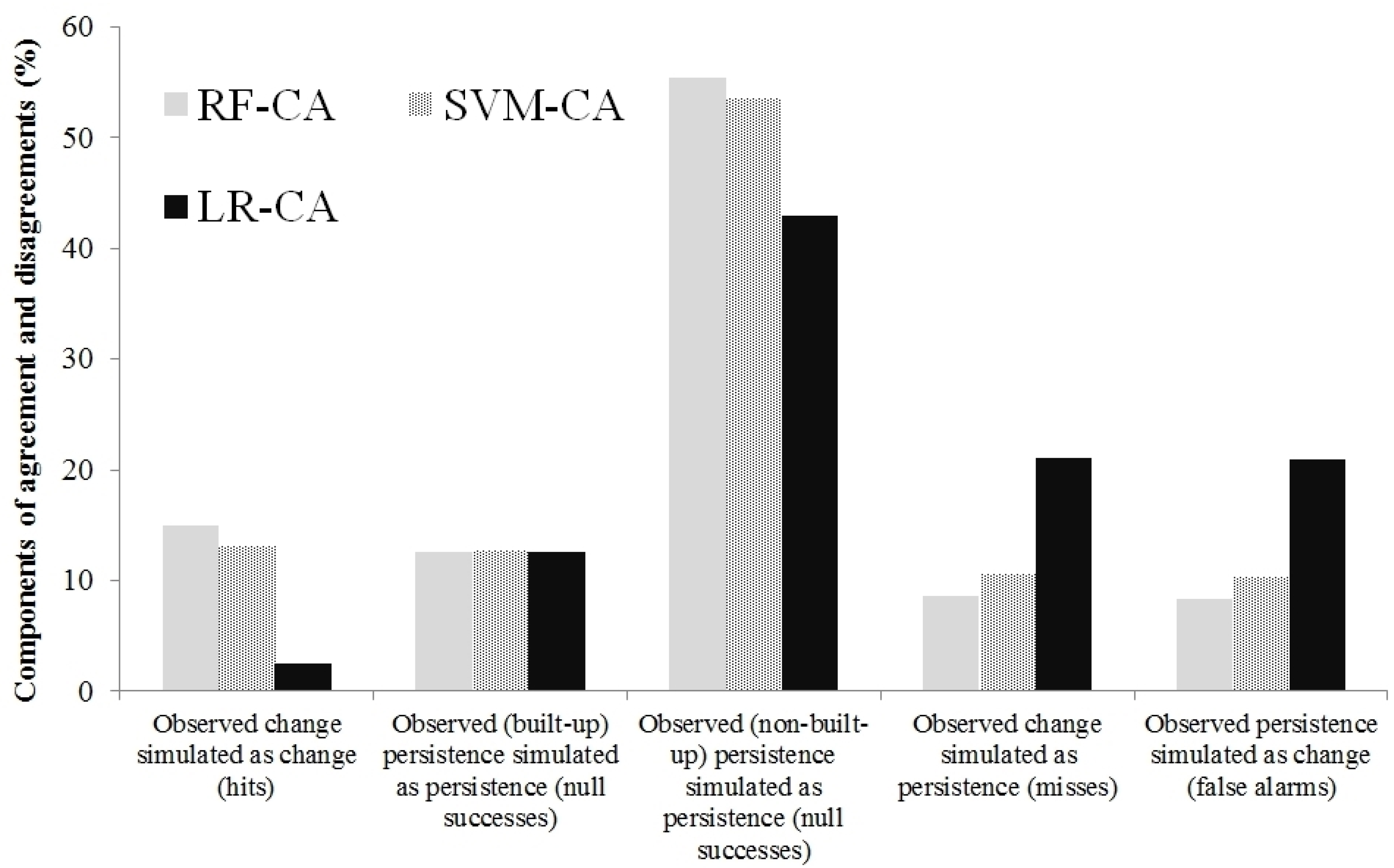
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Eastman, J.R.; Solorzano, L.A.; van Fossen, M.E. Transition potential modeling for land-cover change. In GIS, Spatial Analysis, and Modeling; Maguire, D.J., Batty, M., Goodchild, M.F., Eds.; ESRI Press: California, UK, 2005; pp. 357–385. [Google Scholar]
- Torrens, P.M. Simulating sprawl. Ann. Assoc. Am. Geogr. 2008, 96, 248–275. [Google Scholar]
- Cheng, J.; Masser, I. Understanding spatial and temporal processes of urban growth: Cellular automata modelling. Environ. Plann. B 2004, 31, 167–194. [Google Scholar]
- Griffiths, P.; Hostert, P.; Gruebner, O.; van der Linden, S. Mapping megacity growth with multisensory data. Remote Sens. Environ. 2010, 114, 426–439. [Google Scholar]
- Pacione, M. Sustainable urban development in the UK: Rhetoric or reality? Geography 2007, 92, 246–263. [Google Scholar]
- Lopez, E.; Bocco, G.; Mendoza, M.; Duhau, E. Predicting land-cover and land-use in the urban fringe—A case study in Morelia city, Mexico. Landsc. Urban Plan. 2001, 55, 271–285. [Google Scholar]
- United Nations. World Urbanization Prospects: The 2011 Revision. 2012. Available online: http://esa.un.org/unpd/wup/index.htm (accessed on 25 July 2012).
- Masser, I. Managing our urban future: The role of remote sensing and geographic information systems. Habitat Int. 2001, 25, 503–512. [Google Scholar]
- Brown, A. Cities for the urban poor in Zimbabwe: urban space as a resource for sustainable development. Dev. Pract. 2001, 11, 263–281. [Google Scholar]
- Rakodi, C. Harare—Inheriting a Settler-Colonial City: Change or Continuity? John Wiley & Sons.: Chichester, UK, 1995. [Google Scholar]
- Linard, C.; Tatem, A.J.; Gilbert, M. Modelling spatial patterns of urban growth in Africa. Appl. Geogr. 2013, 44, 23–32. [Google Scholar]
- Clarke, K.C.; Hoppen, S.; Gaydos, L. A self-modifying cellular automaton model of historical urbanization in the San Fransisco Bay Area. Environ. Plann. B 1997, 24, 247–261. [Google Scholar]
- Batty, M. Urban evolution on the desktop: Simulation with the use of extended cellular automata. Environ. Plann. B 1998, 30, 1943–1967. [Google Scholar]
- Li, X.; Yeh, A.G. Calibration of cellular automata by using neural networks for the simulation of complex urban systems. Environ. Plann. A 2001, 33, 1445–1462. [Google Scholar]
- Pijanowski, B.C.; Pithadia, S.; Shellito, B.A.; Alexandridis, K. Calibrating a neural network-based change model for two metropolitan areas of the Upper Midwest of the United States. Int. J. Geogr. Inf. Sci. 2005, 19, 197–215. [Google Scholar]
- Chunyang, H.; Okada., N.; Zhang, O.; Shia, P.; Zhang, J. Modeling urban expansion scenarios by coupling cellular automata model and system dynamic model in Beijing, China. Appl. Geogr. 2006, 26, 323–345. [Google Scholar]
- Mundia, C.N.; Aniya, M. Modeling urban growth of Nairobi city using cellular automata and geographical information systems. Geogr. Rev. Jpn. 2007, 80, 777–788. [Google Scholar]
- Shan, J.; Alkheder, S.; Wang, J. Genetic algorithm for the calibration of cellular automata urban growth modeling. Photogramm. Eng. Remote Sens. 2008, 74, 1267–1277. [Google Scholar]
- Yeh, A.G.O.; Li, X. Cellular automata and GIS for urban planning. In Manual of Geographic Information Systems; Madden, M., Ed.; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2009; pp. 591–619. [Google Scholar]
- Al-Ahmadi, K.; See, L.; Heppenstall, A.; Hogg, J. Calibration of a fuzzy cellular automata model of urban dynamics in Saudi Arabia. Ecol. Complex. 2009, 6, 80–101. [Google Scholar]
- Moreno, N.; Wang, F.; Marceau, D.J. A geographic object-based approach in cellular automata modeling. Photogramm. Eng. Remote Sens. 2010, 76, 183–191. [Google Scholar]
- White, R.; Engelen, G. Cellular automata as the basis of integrated dynamic regional modeling. Environ. Plann. B 1997, 24, 235–246. [Google Scholar]
- Tobler, W. Cellular geography. In Philosophy in Geography; Gale, S., Olsson, G., Eds.; Dordrecht Reidel: Dordrecht, The Netherlands, 1979; pp. 379–386. [Google Scholar]
- Couclelis, H. Cellular worlds: A framework for modeling micro-macro dynamics. Environ. Plann. A 1985, 17, 585–596. [Google Scholar]
- Engelen, G.; White, R.; Uljee, I.; Drazan, P. Using cellular automata for integrated modeling of socio-environmental systems. Environ. Monit. Assess. 1995, 34, 203–214. [Google Scholar]
- Liu, Y. Modelling Urban Development with Geographical Information Systems and Cellular Automata; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2009; p. 188. [Google Scholar]
- Soares-Filho, B.S.; Cerqueira, G.C.; Pennachin, C.L. Modeling the spatial transition probabilities of landscape dynamics in an Amazonian colonization frontier. BioScience 2002, 51, 1059–1067. [Google Scholar]
- Batty, M.; Xie, Y. Urban growth using cellular automata models. In GIS, Spatial Analysis, and Modeling; Maguire, D.J., Batty, M., Goodchild, M.F., Eds.; ESRI Press: Redlands, CA, USA, 2005; pp. 151–172. [Google Scholar]
- Wu, F.; Webster, C.J. Simulation of land development through the integration of cellular automata and multicriteria evaluation. Environ. Plann. B 1998, 25, 103–126. [Google Scholar]
- Verburg, P.; de Nijs, T.; Ritsema van Eck, J.; Visser, H.; de Jong, K. A method to analyse neighbourhood characteristics of land use patterns. Comput. Environ. Urban Syst. 2004, 28, 667–690. [Google Scholar]
- Liu, X.; Li, X.; Shi, X.; Wu, S.; Liu, T. Simulating complex urban development using kernel-based non-linear cellular automata. Ecol. Model. 2008, 211, 169–181. [Google Scholar]
- Liu, Y.; Feng, Y.; Pontius, R. Spatially-explicit simulation of urban growth through self-adaptive genetic algorithm and cellular automata modelling. Land 2014, 3, 719–738. [Google Scholar]
- Yang, Q.; Li, X.; Shi, X. Cellular automata for simulating land use changes based on support vector machines. Comput. Geosci. 2008, 34, 592–602. [Google Scholar]
- Torrens, P.M. How Cellular Models of Urban Systems Work (1. Theory); CASA Working Paper Series (28); Centre for Advanced Spatial Analysis (UCL): London, UK, 2000. Available online: http://www.casa.ucl.ac.uk/working_papers/paper28.pdf (accessed on 17 August 2009).
- Li, X.; Yeh, A. Neural-network-based cellular automata for simulating multiple land use changes using GIS. Int. J. Geogr. Inf. Sci. 2002, 16, 323–343. [Google Scholar]
- Resler, L.; Shao, Y.; Tomback, D.; Malanson, G. Predicting functional role and occurrence of Whitebark Pine (Pinus albicaulis) at Alpine Treelines: Model accuracy and variable importance. Ann. Assoc. Am. Geogr. 2014, 104, 1–20. [Google Scholar]
- Kocabas, V.; Dragicevic, S. Assessing cellular automata model behaviour using sensitivity analysis approach. Comput. Environ. Urban 2006, 30, 921–953. [Google Scholar]
- Lin, Y.P.; Chu, H.J.; Wu, C F.; Verburg, P.H. Predictive ability of logistic regression, auto-logistic regression and neural network models in empirical land-use change modeling—A case study. Int. J. Geogr. Inf. Sci. 2011, 25, 65–87. [Google Scholar]
- Tayyebi, A.; Pijanowski, B.C.; Linderman, M.; Gratton, C. Comparing three global parametric and local non-parametric models to simulate land use change in diverse areas of the world. Environ. Modell. Softw. 2014, 59, 202–221. [Google Scholar]
- Tayyebi, A.; Pijanowski, B.C. Modeling multiple land use changes using ANN, CART and MARS: Comparing tradeoffs in goodness of fit and explanatory power of data mining tools. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 102–116. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar]
- Mellor, A.; Haywood, A.; Stone, C.; Jones, S. The performance of random forests in an operational setting for large area Sclerophyll forest classification. Remote Sens. 2013, 5, 2838–2856. [Google Scholar]
- Rodriguez-Galiano, V.F.; Chica-Olmo, M.; Abarca-Hernandez, F.; Atkinson, P.M.; Jeganathan, C. Random forest classification of Mediterranean land cover using multi-seasonal imagery and multi-seasonal texture. Remote Sens. Environ. 2012, 121, 93–107. [Google Scholar]
- Gamanya, R.; de Maeyer, P.; de Dapper, M. Object-oriented change detection for the city of Harare, Zimbabwe. Expert Syst. Appl. 2009, 36, 571–588. [Google Scholar]
- Zinyama, L.; Tevera, D.; Cumming, S. Harare: The Growth and Problems of the City; Zinyama, L., Tevera, D., Cumming, S., Eds.; University of Zimbabwe Publications: Harare, Zimbabwe, 1993. [Google Scholar]
- Colquhoun, S. Present problems facing the harare city council. In Harare: The Growth and Problems of the City; Zinyama, L., Tevera, D., Cumming, S., Eds.; University of Zimbabwe Publications: Harare, Zimbabwe, 1993; pp. 33–41. [Google Scholar]
- Mutizwa-Mangiza, N.D. Urban centres in Zimbabwe: Inter-censal changes, 1962–1982. Geography 1986, 71, 148–151. [Google Scholar]
- ZimStats (Zimbabwe National Statistics Agency). Census 2012: Preliminary Report; ZimStats (Zimbabwe National Statistics Agency): Harare, Zimbabwe, 2012. [Google Scholar]
- Kamusoko, C.; Gamba, J.; Murakami, H. Monitoring urban spatial growth in Harare Metropolitan Province, Zimbabwe. ARS 2013, 2, 322–331. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. 2005. Available online: http://r-project.kr/sites/default/files/2%EA%B0%95%EA%B0%95%EC%A2%8C%EC%86%8C%EA%B0%9C_%EC%8B%A0%EC%A2%85%ED%99%94.pdf (accessed on 3 April 2014).
- Soares-Filho, B.S.; Rodrigues, H.O.; Costa, W.L.S. Modeling Environmental Dynamics with Dinamica EGO. 2009. Available online: http://www.csr.ufmg.br/dinamica/ (accessed on 3 August 2009).
- Soares-Filho, B.; Alencar, A.; Nepstad, D.; Cerqueira, G.; Vera Diaz, M.; Rivero, S.; Solorzano, L.; Voll, E. Simulating the response of land-cover changes to road paving and governance along a major Amazon highway: The Santarem-Cuiaba corridor. Glob. Chang. Biol. 2004, 10, 745–764. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. Proceedings of the Fifth Annual Workshop on Computational Learning Theory; ACM, 1992; pp. 144–152. Available online: http://dl.acm.org/citation.cfm?id=130401 (accessed on 22 February 2014).
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 2000. [Google Scholar]
- Watanachaturaporn, P.; Arora, M.K.; Varshney, P.K. Multisource classification using support vector machines: An empirical comparison with decision tree and neural network classifiers. Photogramm. Eng. Remote Sens. 2008, 74, 239–246. [Google Scholar]
- Hornik, K.; Meyer, D.; Karatzoglou, A. Support vector machines in R. J. Stat. Softw. 2006, 15, 1–28. [Google Scholar]
- Soares-Filho, B.; Coutinho Cerqueira, G.; Lopes Pennachin, C. DINAMICA: A stochastic cellular automata model designed to simulate the landscape dynamics in an Amazonian colonization frontier. Ecol. Model. 2002, 154, 217–235. [Google Scholar]
- Yue, W.; Liu, Y.; Fan, P. Measuring urban sprawl and its drivers in large Chinese cities: The case of Hangzhou. Land Use Policy 2013, 31, 358–370. [Google Scholar]
- Meentemeyer, R.; Tang, W.; Dorning, M.; Vogler, J.; Cunniffe, N.; Shoemaker, D. FUTURES: Multilevel simulations of emerging urban-rural landscape structure using a stochastic patch-growing algorithm. Ann. Assoc. Am. Geogr. 2013, 103, 785–807. [Google Scholar]
- Pontius, R.G., Jr.; Malanson, J. Comparison of the structure and accuracy of two land change models. Int. J. Geogr. Inf. Sci. 2005, 19, 243–265. [Google Scholar]
- The State of Land Change Modeling. In Advancing Land Change Modeling: Opportunities and Research Requirements; The National Academies Press: Washington, DC, USA, 2014.
- Pontius, R.G., Jr.; Schneider, L. Land-use change model validation by an ROC method. Agric. Ecosyst. Environ. 2001, 85, 239–248. [Google Scholar]
- Mas, J.; Soares Filho, B.; Pontius, R.; Farf’an Guti’errez, M.; Rodrigues, H. A suite of tools for ROC analysis of spatial models. ISPRS Int. J. Geo-Inf. 2013, 2, 869–887. [Google Scholar]
- Pontius, R., Jr.; Parmentier, B. Recommendations for using the relative operating characteristic (ROC). Landsc. Ecol. 2014, 29, 367–382. [Google Scholar]
- Pontius, R., Jr.; Si, K. The total operating characteristic to measure diagnostic ability for multiple thresholds. Int. J. Geogr. Inf. Sci. 2014, 28, 570–583. [Google Scholar]
- Wang, N.; Brown, D.G.; An, L.; Yang, S.; Ligmsnn-Zielinsak, A. Comparative performance of logistic regression and survival analysis for detecting spatial predictors of land-use change. Int. J. Geogr. Inf. Sci. 2013, 27, 1960–1982. [Google Scholar]
- Rodriguez-Galiano, V.F.; Chica-Olmo, M.; Chica-Rivas, M. Predictive modelling of gold potential with the integration of multisource information based on random forest: A case study on the Rodalquilar area, Southern Spain. Int. J. Geogr. Inf. Sci. 2014, 28, 1336–1354. [Google Scholar]
- Visser, H.; de Nijs, T. The map comparison kit. Environ. Modell. Softw. 2006, 21, 346–358. [Google Scholar]
- Vliet, J.; Bregt, A.K.; Hagen-Zanker, A. Revisiting Kappa to account for change in the accuracy assessment of land-use change models. Ecol. Model. 2011, 222, 1367–1375. [Google Scholar]
- Pontius, R.G., Jr.; Walker, R.; Yao-Kumah, R.; Arima, E.; Aldrich, S.; Caldas, M.; Vergara, D. Accuracy assessment for a simulation model of Amazonian deforestation. Ann. Assoc. Am. Geogr. 2007, 97, 677–695. [Google Scholar]
- Pontius, R.G., Jr.; Boersma, W.; Castella, J.C.; Clarke, K.; de Nijs, T.; Dietzel, C.; Duan, Z.; Fotsing, E.; Goldstein, N.; Kok, K.; et al. Comparing the input, output, and validation maps for several models of land change. Ann. Regional Sci. 2008, 42, 11–37. [Google Scholar]
- Mertens, B.; Lambin, E. Land-cover-change trajectories in Southern Cameroon. Ann. Assoc. Am. Geogr. 2000, 90, 467–494. [Google Scholar]
- Braimoh, A.; Vlek, P. Land-cover change trajectories in Northern Ghana. Environ. Manag. 2005, 36, 356–373. [Google Scholar]
- Dietzel, C.; Clarke, K. The effect of disaggregating land use categories in cellular automata during model calibration and forecasting. Comput. Environ. Urban Syst. 2006, 30, 78–101. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamusoko, C.; Gamba, J. Simulating Urban Growth Using a Random Forest-Cellular Automata (RF-CA) Model. ISPRS Int. J. Geo-Inf. 2015, 4, 447-470. https://doi.org/10.3390/ijgi4020447
Kamusoko C, Gamba J. Simulating Urban Growth Using a Random Forest-Cellular Automata (RF-CA) Model. ISPRS International Journal of Geo-Information. 2015; 4(2):447-470. https://doi.org/10.3390/ijgi4020447
Chicago/Turabian StyleKamusoko, Courage, and Jonah Gamba. 2015. "Simulating Urban Growth Using a Random Forest-Cellular Automata (RF-CA) Model" ISPRS International Journal of Geo-Information 4, no. 2: 447-470. https://doi.org/10.3390/ijgi4020447
APA StyleKamusoko, C., & Gamba, J. (2015). Simulating Urban Growth Using a Random Forest-Cellular Automata (RF-CA) Model. ISPRS International Journal of Geo-Information, 4(2), 447-470. https://doi.org/10.3390/ijgi4020447