The Relationship between an Invasive Shrub and Soil Moisture: Seasonal Interactions and Spatially Covarying Relations
Abstract
:1. Introduction
2. Methodology
2.1. Study Area and Data Collection
2.2. Data Analysis
3. Results and Discussion
3.1. Descriptive Analysis of LAI and VWC Sequences
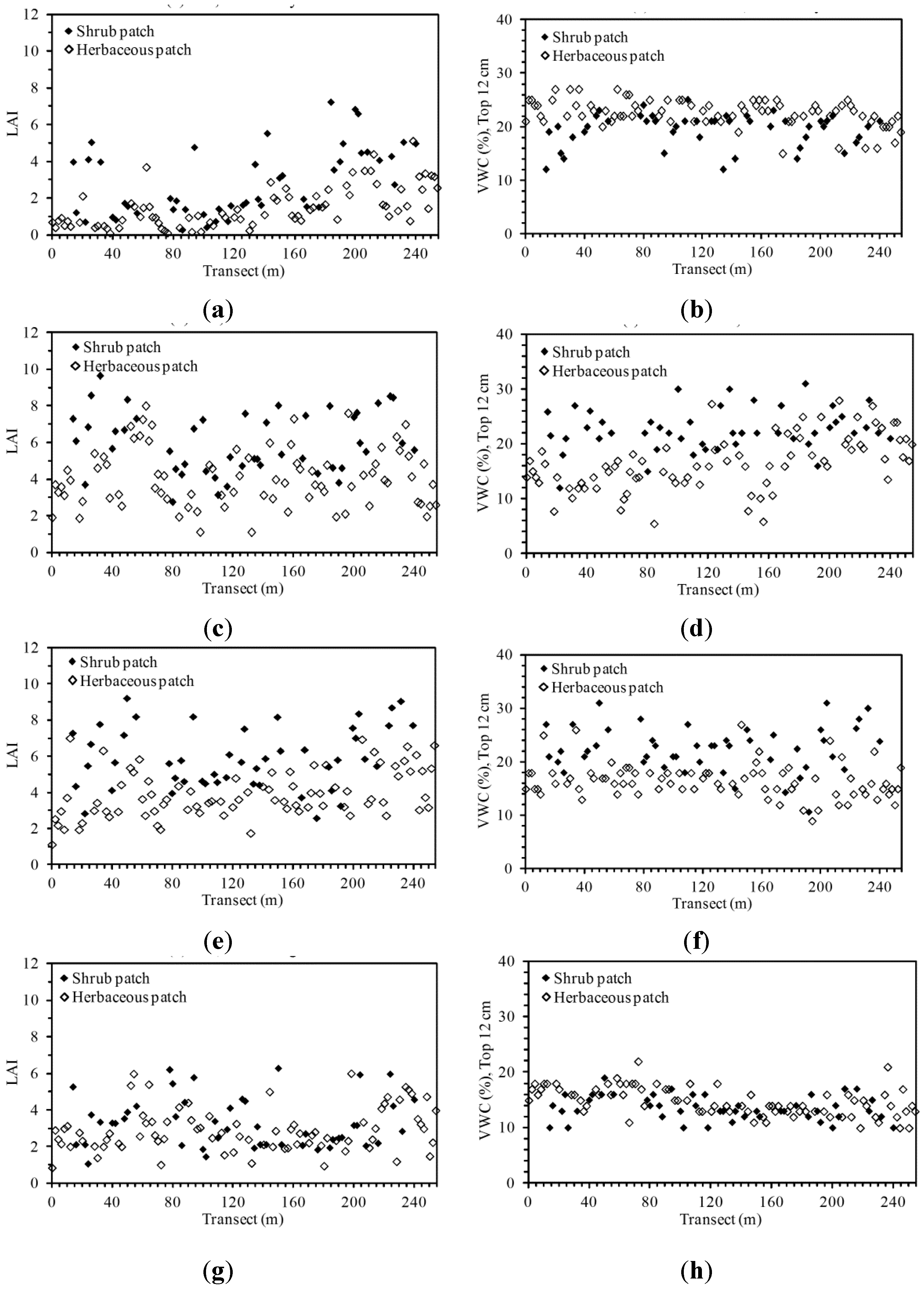
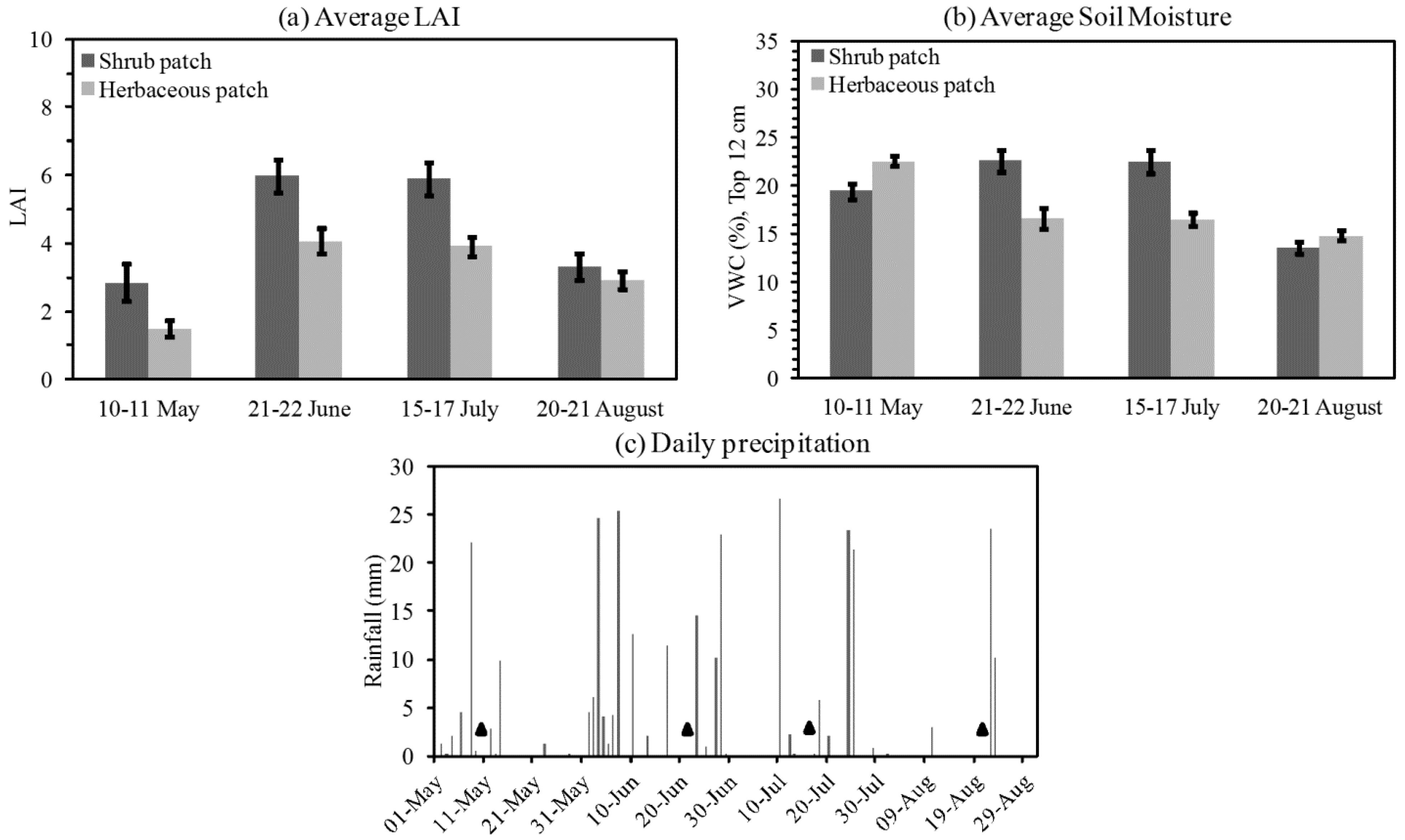
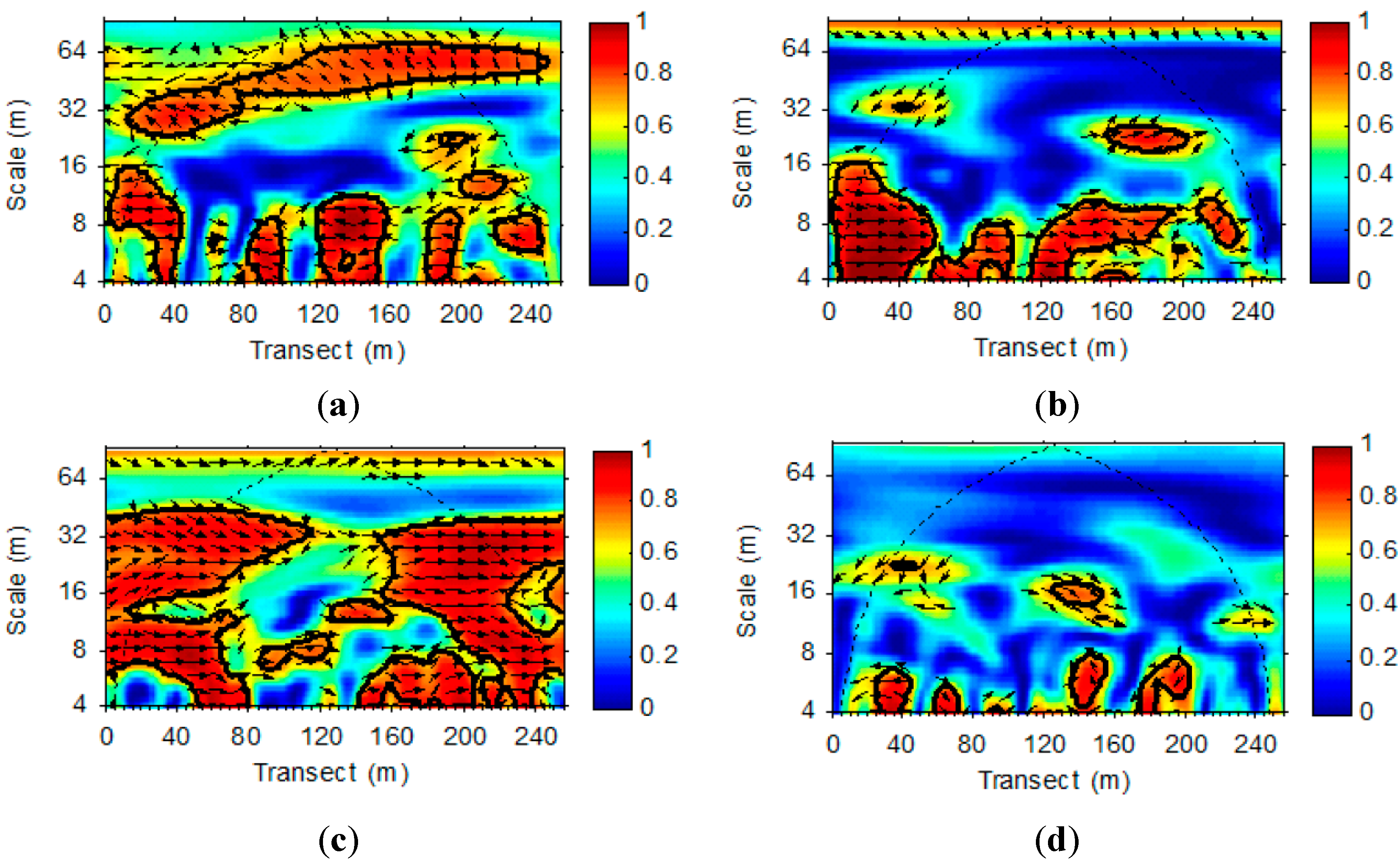
3.2. Wavelet Analysis of LAI and VWC Sequences
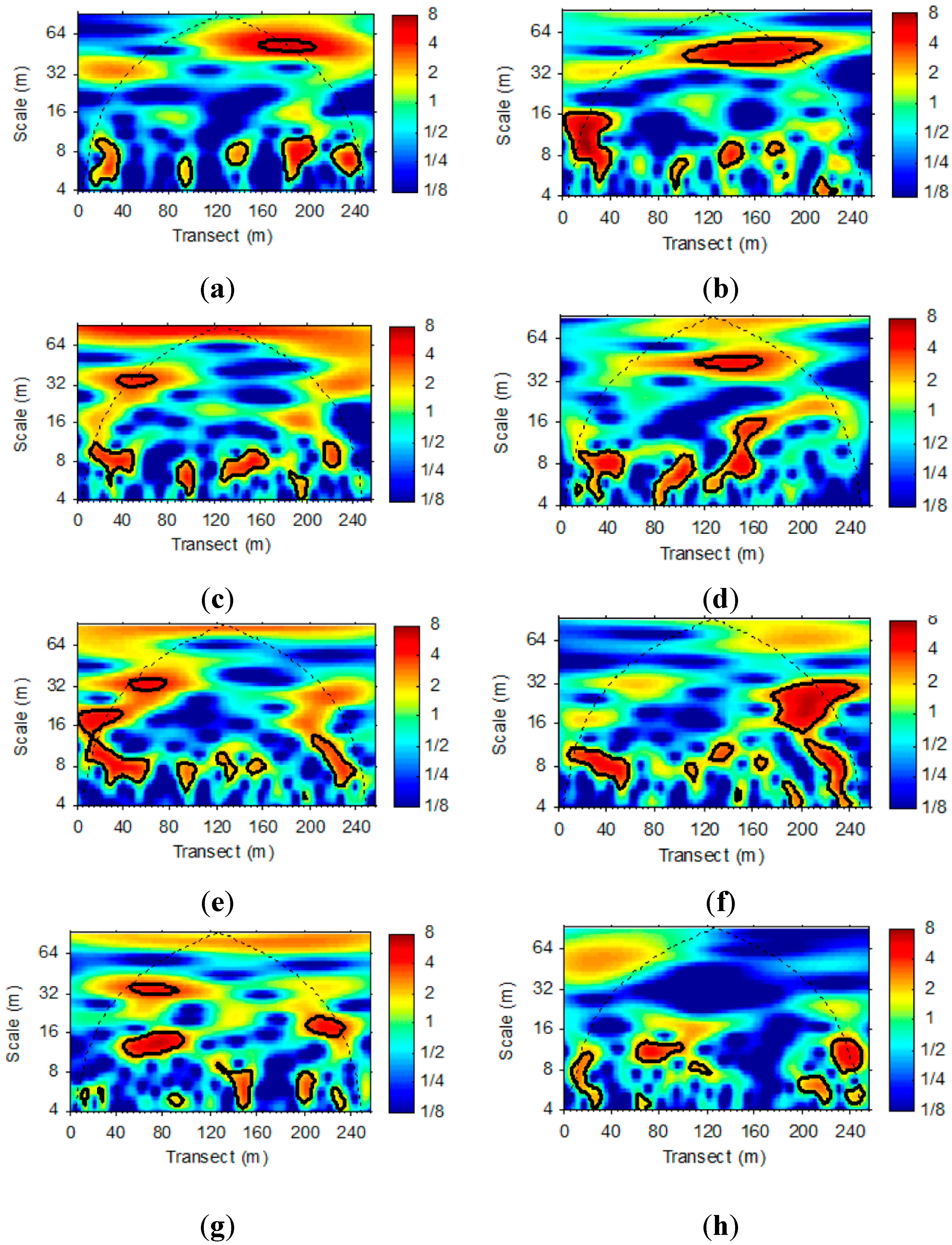
4. Conclusions and Future Studies
Acknowledgments
Conflicts of Interest
References
- Archer, S.; Schimel, D.S.; Holland, E.A. Mechanisms of shrubland expansion: Land use, climate or CO2? Clim. Chang. 1995, 29, 91–99. [Google Scholar]
- D’Odorico, P.; Okin, G.S.; Bestelmeyer, B.T. A synthetic review of feedbacks and drivers of shrub encroachment in arid grasslands. Ecohydrology 2011, 5, 520–530. [Google Scholar] [CrossRef]
- Eldridge, D.J.; Bowker, M.A.; Maestre, F.T.; Roger, E.; Reynolds, J.F.; Whitford, W.G. Impacts of shrub encroachment on ecosystem structure and functioning: Towards a global synthesis. Ecol. Lett. 2011, 14, 709–722. [Google Scholar] [CrossRef] [PubMed]
- Frazier, A.; Wang, L. Characterizing spatial patterns of invasive species using sub-pixel classifications. Remote Sens. Environ. 2011, 115, 1997–2007. [Google Scholar] [CrossRef]
- He, Y.; de Wekker, S.F.J.; D’Odorico, P.; Fuentes, J. On the impact of shrub encroachment on microclimate conditions in the northern Chihuahuan desert. J. Geophys. Res. 2010, 115, D21120. [Google Scholar] [CrossRef]
- Van Auken, O.W. Shrub invasions of North American semiarid grasslands. Annu. Rev. Ecol. Evol. Syst. 2000, 31, 197–215. [Google Scholar]
- Borgmann, K.L.; Rodewald, A.D. Forest restoration in urbanizing landscapes: Interactions between land uses and an exotic shrub. Restor. Ecol. 2005, 13, 334–340. [Google Scholar] [CrossRef]
- Webster, C.R.; Jenkins, M.A.; Jose, S. Woody invaders and the challenges they pose to forest ecosystems in the eastern United States. J. For. 2006, 104, 366–374. [Google Scholar]
- Tassie, D.; Sherman, K. Invasive Honeysuckles (Lonicera spp.) Best Management Practices in Ontario. Available online: http://www.ontarioinvasiveplants.ca/index.php/managecontrol (accessed on 4 September 2014).
- Bever, J.D.; Westover, K.M.; Antonovics, J. Incorporating the soil community into plant population dynamics: The utility of the feedback approach. J. Ecol. 1997, 85, 561–573. [Google Scholar] [CrossRef]
- Reynolds, H.L.; Packer, A.; Bever, J.D.; Clay, K. Grassroots ecology: Plant-microbe-soil interactions as drivers of plant community structure and dynamics. Ecology 2003, 84, 2281–2291. [Google Scholar] [CrossRef]
- Van der Stoel, C.D.; van der Putten, W.H.; Duyts, H. Development of a negative plant-soil feedback in the expansion zone of the clonal grass Ammophila arenaria following root formation and nematode colonization. J. Ecol. 2002, 90, 978–988. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; D’Odorico, P.; Porporato, A.; Ridolfi, L. On the spatial and temporal links between vegetation, climate and soil moisture. Water Resour. Res. 1999, 35, 3709–3722. [Google Scholar] [CrossRef]
- D’Odorico, P.; Caylor, K.; Okin, G.S.; Scanlon, T.M. On soil moisture-vegetation feedbacks and their possible effects on the dynamics of dryland ecosystems. J. Geophys. Res. 2007, 112, G04010. [Google Scholar]
- Li, X.Y.; Zhang, S.-Y.; Peng, H.-Y.; Hu, X.; Ma, Y.-J. Soil water and temperature dynamics in shrub-encroached grasslands and climatic implications: Results from Inner Mongolia steppe ecosystem of north China. Agric. For. Meteorol. 2013. [Google Scholar] [CrossRef]
- Potts, D.L.; Scott, R.L.; Bayram, S.; Carbonara, J. Woody plants modulate the temporal dynamics of soil moisture in a semi-arid mesquite savanna. Ecohydrology 2010, 3, 20–27. [Google Scholar]
- Wang, L.; D’Odorico, P.; Manzoni, S.; Proporato, A.; Macko, S. Soil carbon and nitrogen dynamics in southern African savannas: The effect of vegetation-induced patch-scale heterogeneities and large scale rainfall gradients. Clim. Chang. 2009, 94, 63–76. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.J.; Gao, G.Y.; Yao, X.L.; Zhou, J. Soil moisture and evapotranspiration of different land cover types in the Loess Plateau, China. Earth Syst. Sci. 2012, 16, 2883–2892. [Google Scholar] [CrossRef]
- Vinnikov, K.Y.; Robock, A.; Speranskaya, N.; Schlosser, C.A. Scales of temporal and spatial variability of midlatitude soil moisture. J. Geophys. Res. 1996, 101, 7163–7174. [Google Scholar] [CrossRef]
- Jacobs, J.; Mohanty, B.P.; Hsu, E.-C.; Miller, D. SMEX02: Field scale variability, time stability and similarity of soil moisture. Remote Sens. Environ. 2004, 92, 436–446. [Google Scholar] [CrossRef]
- Zeng, X.; Shen, S.S.P.; Zeng, X.; Dickinson, R.E. Multiple equilibrium states and the abrupt transitions in a dynamical system of soil water interacting with vegetation. Geophys. Res. Lett. 2004, 31, L05501. [Google Scholar]
- Grime, J.P. Plant Strategies, Vegetation Processes, and Ecosystem Properties, 2nd ed.; John Wiley and Sons Ltd.: Chichester, UK, 2006; p. 456. [Google Scholar]
- Bhark, E.W.; Small, E.E. Association between plant canopies and the spatial patterns infiltration in shrubland and grassland of the Chihuahuan desert, New Mexico. Ecosystems 2003, 6, 185–196. [Google Scholar] [CrossRef]
- CAN-EYE Web Seit. Available online: http://www6.paca.inra.fr/can-eye (accessed on 4 September 2014).
- Weather Data. Available online: http://www.utm.utoronto.ca/geography/resources/meteorological-station/weather-data (assessed on 4 September 2014).
- Dale, M.R.T.; Dixon, P.M.; Fortin, M.-J.; Legendre, P.; Myers, D.E.; Rosenberg, M.S. Conceptual and mathematical relationships among methods for spatial analysis. Ecography 2002, 25, 558–577. [Google Scholar] [CrossRef]
- Rosenberg, M. Wavelet analysis for detecting anisotropy in point patters. J. Veg. Sci. 2004, 15, 277–284. [Google Scholar] [CrossRef]
- Daubechies, I.; Grossman, A.; Meyer, Y.J. Painless non-orthogonal expansions. J. Math. Phys. 1986, 27, 1271–1283. [Google Scholar] [CrossRef]
- Daubechies, I. Wavelet transforms and orthonormal wavelet bases. In Different Perspectives on Wavelets; Daubechies, I., Ed.; American Mathematical Society: Providence, RI, USA, 1993; pp. 173–205. [Google Scholar]
- Dale, M.R.T.; Mah, M. The use of wavelets for spatial pattern analysis in ecology. J. Veg. Sci. 1998, 9, 805–814. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlin. Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Biswas, A.; Si, B.C. Scale and location specific temporal stability of soil water storage in a hummocky landscape. J. Hydrol. 2011, 408, 100–112. [Google Scholar] [CrossRef]
- He, Y.; Khan, A.; Mui, A. Integrating remote sensing and wavelet analysis for studying fine-scaled vegetation spatial variation among three different ecosystems. Photogramm. Eng. Remote Sens. 2012, 78, 161–168. [Google Scholar] [CrossRef]
- He, Y.; Guo, X.; Si, B.C. Detecting grassland spatial variation by a wavelet approach, International. J. Remote Sens. 2007, 28, 1527–1545. [Google Scholar] [CrossRef]
- Torrence, C.; Webster, P. Interdecadal changes in the ESNO-Monsoon System. J. Clim. 1999, 12, 2679–2690. [Google Scholar] [CrossRef]
- Crosswavelet and Wavelet Coherence Matlab Package. Available online: http://noc.ac.uk/using-science/crosswavelet-wavelet-coherence (assessed on 4 September 2014).
- McGrew, J.C.; Monroe, C.B. An Introduction to Statistical Problem Solving in Geography, 2nd ed.; McGraw-Hill: Boston, MA, USA, 2000; p. 110. [Google Scholar]
- Villegas, J.C.; Breshears, D.D.; Zou, C.B.; Law, D.J. Ecohydrological controls of soil evaporation in deciduous drylands: How the hierarchical effects of litter, patch and vegetation mosaic cover interact with phenology and season. J. Arid Environ. 2010, 74, 595–602. [Google Scholar] [CrossRef]
- Veihmeyer, F.J.; Hendrickson, A.H. Soil moisture in relation to plant growth. Rev. Plant. Physiol. 1950, 1, 285–304. [Google Scholar] [CrossRef]
- Sivandran, G.; Bras, R.L. Identifying the optimal spatially and temporally invariant root distribution for a semiarid environment. Water Resour. Res. 2012, 48, W12525. [Google Scholar]
- Alvarez, L.J.; Epstein, H.E.; Li, J.; Okin, G.S. Spatial patterns of grasses and shrubs in an arid grassland environment. Ecosphere 2011, 2. [Google Scholar] [CrossRef]
- Biswas, A.; Si, B.C. Identifying effects of local and nonlocal factors of soil water storage using cyclical correlation analysis. Hydrol. Process. 2012, 26, 3669–3677. [Google Scholar] [CrossRef]
- Gherboudj, I.; Magagi, R.; Berg, A.A.; Toth, B. Soil moisture retrieval over agricultural fields from multi-polarized and multi-angular RADARSAT-2 SAR data. Remote Sens. Environ. 2011, 115, 33–43. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
He, Y. The Relationship between an Invasive Shrub and Soil Moisture: Seasonal Interactions and Spatially Covarying Relations. ISPRS Int. J. Geo-Inf. 2014, 3, 1139-1153. https://doi.org/10.3390/ijgi3031139
He Y. The Relationship between an Invasive Shrub and Soil Moisture: Seasonal Interactions and Spatially Covarying Relations. ISPRS International Journal of Geo-Information. 2014; 3(3):1139-1153. https://doi.org/10.3390/ijgi3031139
Chicago/Turabian StyleHe, Yuhong. 2014. "The Relationship between an Invasive Shrub and Soil Moisture: Seasonal Interactions and Spatially Covarying Relations" ISPRS International Journal of Geo-Information 3, no. 3: 1139-1153. https://doi.org/10.3390/ijgi3031139
APA StyleHe, Y. (2014). The Relationship between an Invasive Shrub and Soil Moisture: Seasonal Interactions and Spatially Covarying Relations. ISPRS International Journal of Geo-Information, 3(3), 1139-1153. https://doi.org/10.3390/ijgi3031139



