Holistics 3.0 for Health
Abstract
:1. Introduction
1.1. Big Data
1.2. Machine Learning
1.3. Holistics 3.0
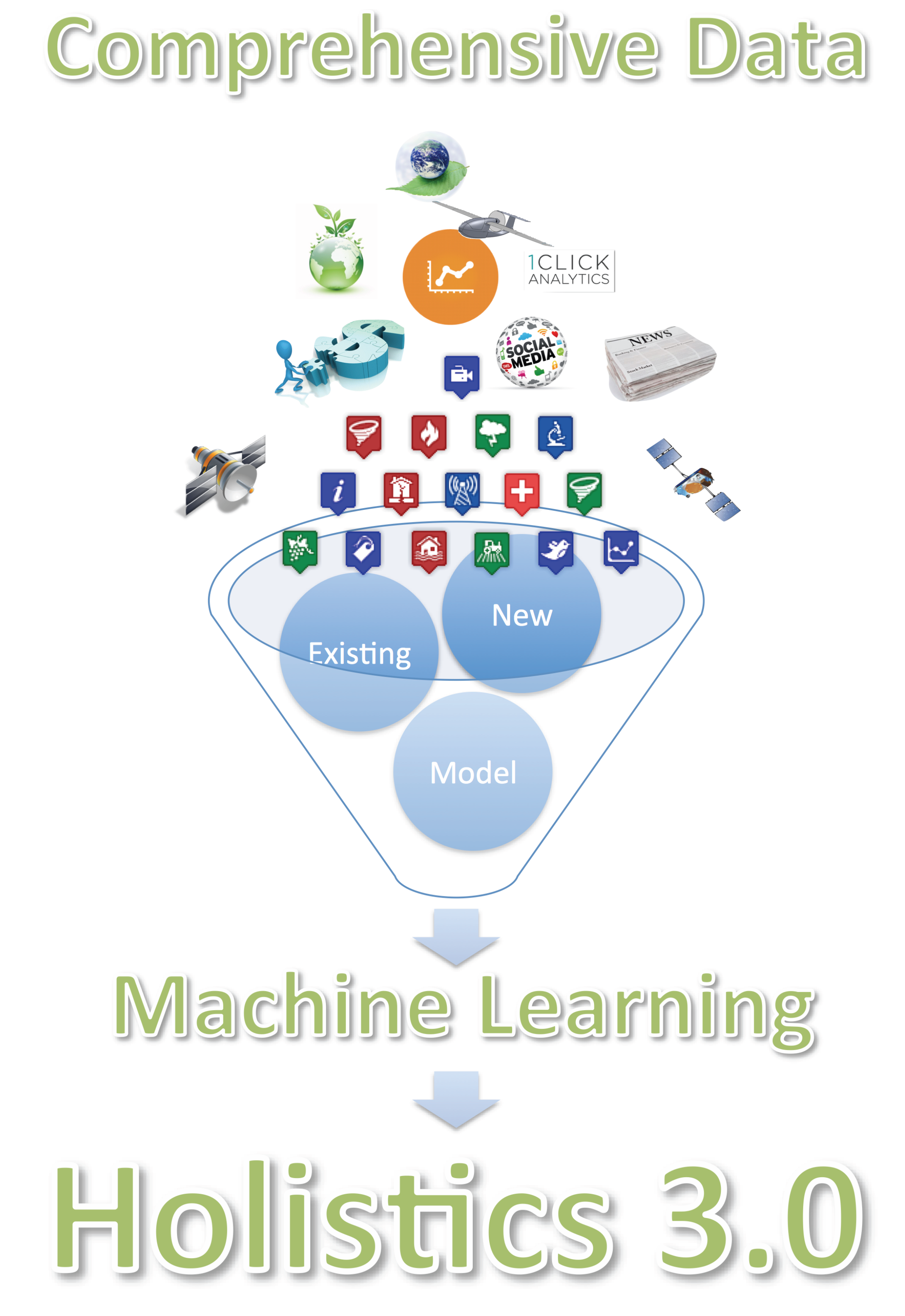
2. Mining Meaning from Data
3. Some Examples
| Health Outcomes | Short-Term Studies | Long-Term Studies | |||||
|---|---|---|---|---|---|---|---|
| PM10 | PM2.5 | UFP | PM10 | PM2.5 | UFP | ||
| Mortality | |||||||
| All causes | xxx | xxx | x | xx | xx | x | |
| Cardiovascular | xxx | xxx | x | xx | xx | x | |
| Pulmonary | xxx | xxx | x | xx | xx | x | |
| Pulmonary effects | |||||||
| Lung function, e.g., PEF | xxx | xxx | xx | xxx | xxx | ||
| Lung function growth | xxx | xxx | |||||
| Asthma and COPD exacerbation | |||||||
| Acute respiratory symptoms | xx | x | xxx | xxx | |||
| Medication use | x | ||||||
| Hospital admission | xx | xxx | x | ||||
| Lung cancer | |||||||
| Cohort | xx | xx | x | ||||
| Hospital admission | xx | xx | x | ||||
| Cardiovascular effects | |||||||
| Hospital admission | xxx | xxx | x | x | |||
| ECG-related endpoints | |||||||
| Autonomic nervous system | xxx | xxx | xx | ||||
| Myocardial substrate and vulnerability | xx | x | |||||
| Vascular function | |||||||
| Blood pressure | xx | xxx | x | ||||
| Endothelial function | x | xx | x | ||||
| Blood markers | |||||||
| Pro inflammatory mediators | xx | xx | xx | ||||
| Coagulation blood markers | xx | xx | xx | ||||
| Diabetes | x | xx | x | ||||
| Endothelial function | x | x | xx | ||||
| Reproduction | |||||||
| Premature birth | x | x | |||||
| Birth weight | xx | x | |||||
| IUR/SGA | x | x | |||||
| Fetal growth | |||||||
| Birth defects | x | ||||||
| Infant mortality | xx | x | |||||
| Sperm quality | x | x | |||||
| Neurotoxic effects | |||||||
| Central nervous system | x | xx | |||||
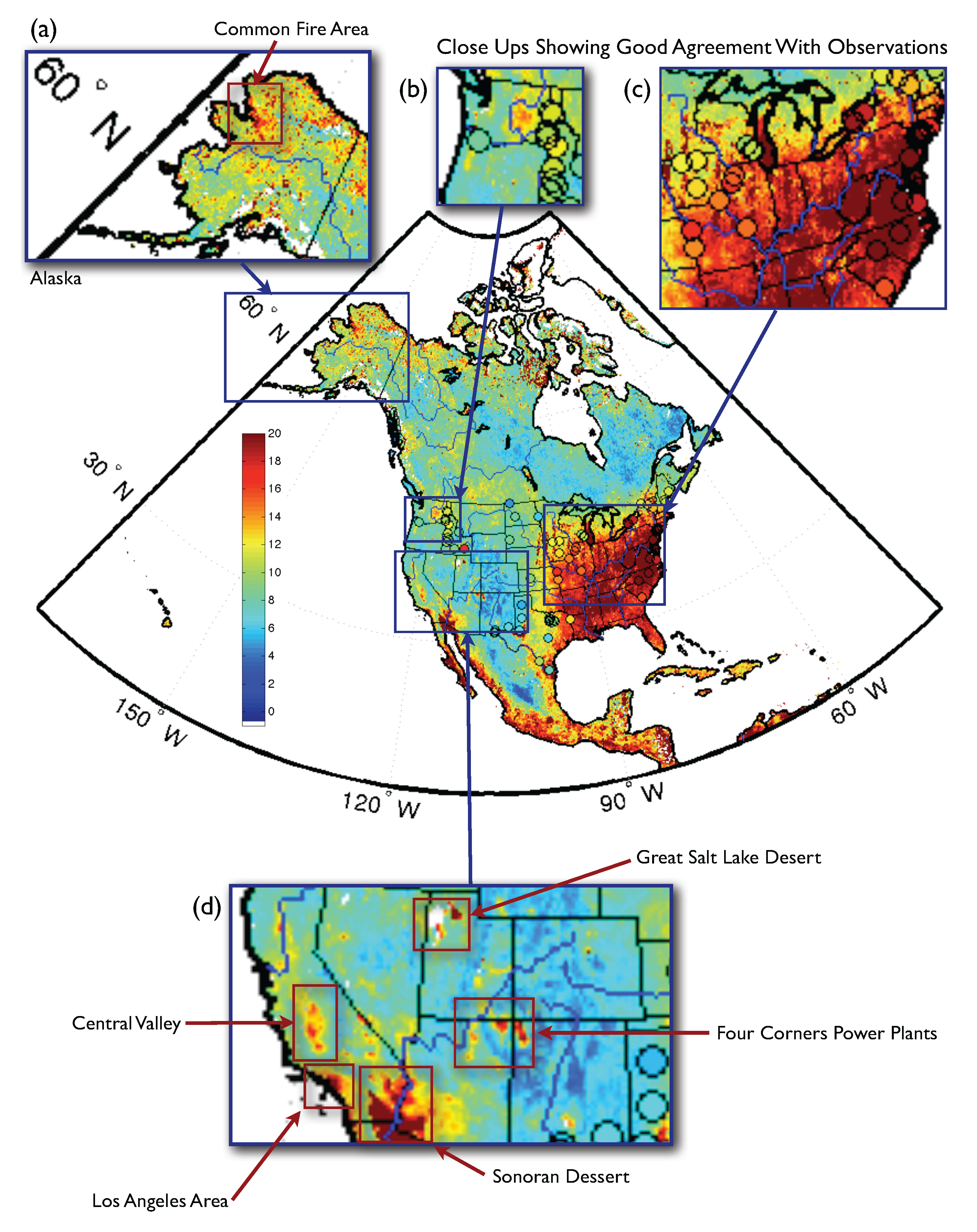
3.1. Airborne Particulate Matter
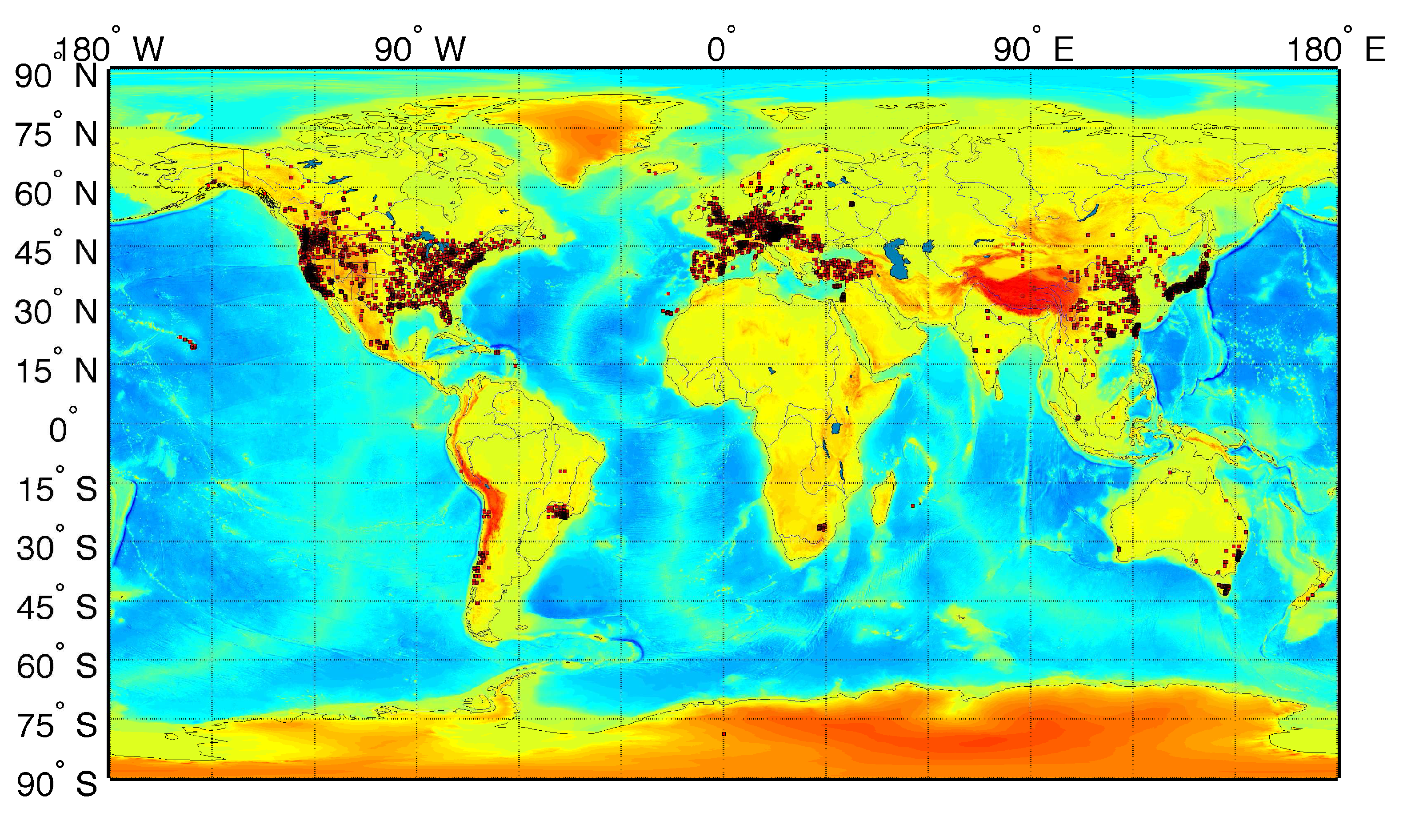
3.2. Life Expectancy and Socioeconomic Data from the U.S. Census
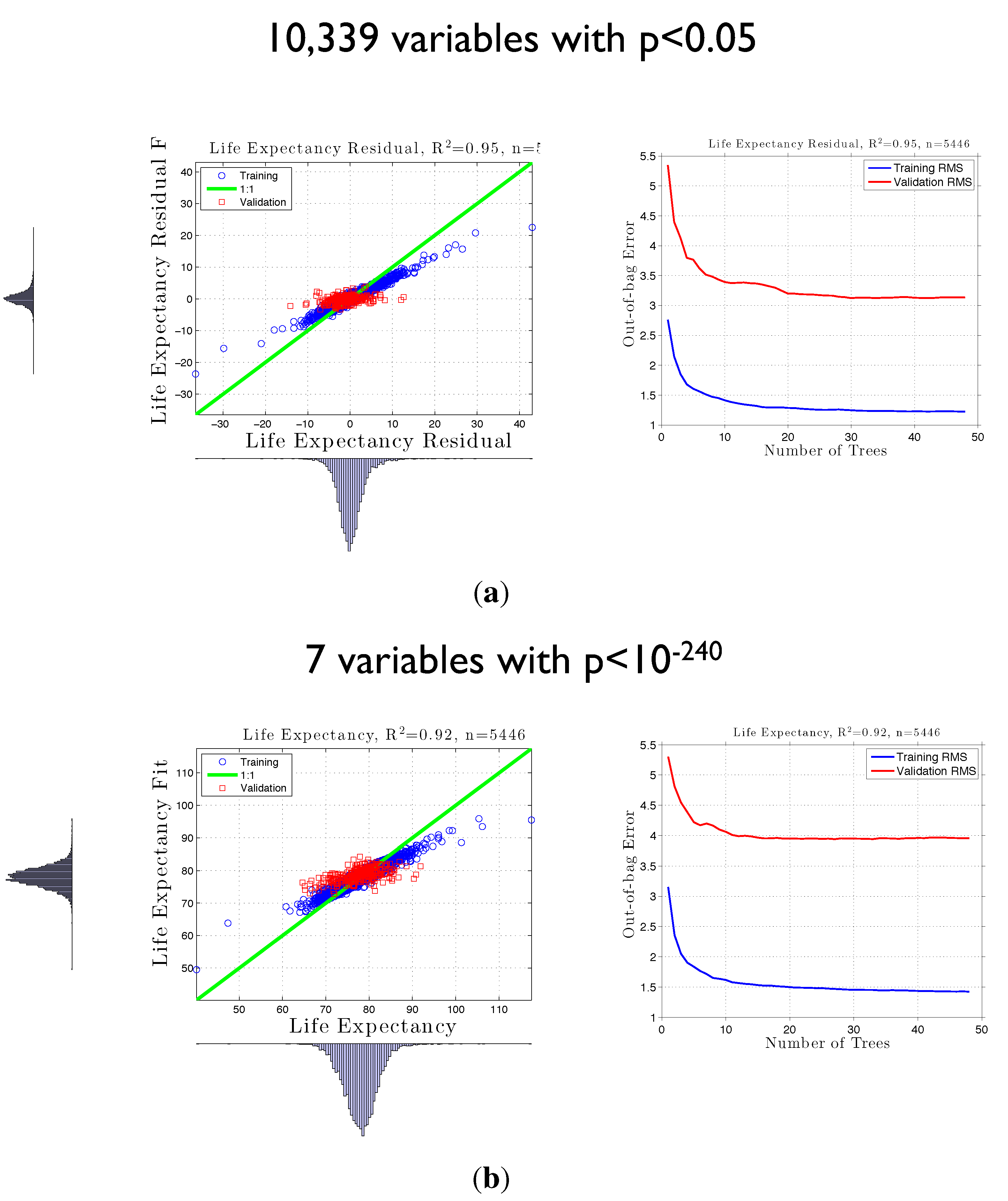
3.3. False Positives
4. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jacobs, A. The pathologies of big data. Commun. ACM 2009, 52, 36–44. [Google Scholar] [CrossRef]
- Guhaniyogi, R.; Finley, A.O.; Banerjee, S.; Gelfand, A.E. Adaptive Gaussian predictive process models for large spatial datasets. Environmetrics 2011, 22, 997–1007. [Google Scholar] [CrossRef] [PubMed]
- Finley, A.O.; Banerjee, S.; Gelfand, A.E. Bayesian dynamic modeling for large space-time datasets using Gaussian predictive processes. J. Geogr. Syst. 2012, 14, 29–47. [Google Scholar] [CrossRef]
- European Space Agency (ESA). Big Data from Space; European Space Agency: Frascati, Italy, 2013. [Google Scholar]
- Hay, S.; George, D.; Moyes, C.; Brownstein, J. Big data opportunities for global infectious disease surveillance. PLoS Med. 2013, 10, e1001413. [Google Scholar] [CrossRef] [PubMed]
- Karimi, H.A. (Ed.) Big Data: Techniques and Technologies in Geoinformatics; CRC Press: Boca Raton, FL, USA, 2014; p. 312.
- Barton, D.; Court, D. Making advanced analytics work for you. Harv. Bus. Rev. 2012, 90, 78–83. [Google Scholar] [PubMed]
- Davenport, T.; Patil, D. Data Scientist: The Sexiest Job of the 21st Century. Harvard Business Review, Ocotber 2012. [Google Scholar]
- McAfee, A.; Brynjolfsson, E. Big Data: The Management Revolution. Harvard Business Review, October 2012. [Google Scholar]
- Murdoch, T.; Detsky, A. The inevitable application of big data to health care. JAMA 2013, 309, 1351–1352. [Google Scholar] [CrossRef] [PubMed]
- Pearl, J. Causality: Models, Reasoning and Inference; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Noble, D.; Casalino, L. Can accountable care organizations improve population health? Should they try? JAMA 2013, 11, 119–120. [Google Scholar]
- Ruckerl, R.; Schneider, A.; Breitner, S.; Cyrys, J.; Peters, A. Health effects of particulate air pollution: A review of epidemiological evidence. Inhalation Toxicol. 2011, 23, 555–592. [Google Scholar] [CrossRef]
- Engel-Cox, J.A.; Hoff, R.M.; Haymet, A.D.J. Recommendations on the use of satellite remote-sensing data for urban air quality. J. Air Waste Manag. Assoc. 2004, 54, 1360–1371. [Google Scholar] [CrossRef] [PubMed]
- Engel-Cox, J.A.; Holloman, C.H.; Coutant, B.W.; Hoff, R.M. Qualitative and quantitative evaluation of MODIS satellite sensor data for regional and urban scale air quality. Atmos. Environ. 2004, 38, 2495–2509. [Google Scholar] [CrossRef]
- Engel-Cox, J.A.; Hoff, R.M.; Rogers, R.; Dimmick, F.; Rush, A.C.; Szykman, J.J.; Al-Saadi, J.; Chu, D.A.; Zell, E.R. Integrating lidar and satellite optical depth with ambient monitoring for 3-dimensional particulate characterization. Atmos. Environ. 2006, 40, 8056–8067. [Google Scholar] [CrossRef]
- Liu, Y.; Sarnat, J.A.; Kilaru, A.; Jacob, D.J.; Koutrakis, P. Estimating ground-level PM2.5 in the Eastern United States using satellite remote sensing. Environ. Sci. Technol. 2005, 39, 3269–3278. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Franklin, M.; Kahn, R.; Koutrakis, P. Using aerosol optical thickness to predict ground-level PM2.5 concentrations in the St. Louis area: A comparison between MISR and MODIS. Remote Sens. Environ. 2007, 107, 33–44. [Google Scholar] [CrossRef]
- Liu, Y.; Paciorek, C.; Koutrakis, P. Estimating daily PM2.5 exposure in Massachusetts with satellite aerosol remote sensing data, meteorological, and land use information. Epidemiology 2008, 19, S116. [Google Scholar]
- Van Donkelaar, A.; Martin, R.V.; Park, R.J. Estimating ground-level PM2.5 using aerosol optical depth determined from satellite remote sensing. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Van Donkelaar, A.; Martin, R.; Verduzco, C.; Brauer, M.; Kahn, R.; Levy, R.; Villeneuve, P. A hybrid approach for predicting PM2.5 exposure response. Environ. Health Perspect. 2010, 118. [Google Scholar] [CrossRef]
- Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Kahn, R.; Levy, R.; Verduzco, C.; Villeneuve, P.J. Global estimates of ambient fine particulate matter concentrations from satellite-based aerosol optical depth: Development and application. Environ. Health Perspect. 2010, 118, 847–855. [Google Scholar] [CrossRef] [PubMed]
- Van Donkelaar, A.; Martin, R.V.; Levy, R.C.; da Silva, A.M.; Krzyzanowski, M.; Chubarova, N.E.; Semutnikova, E.; Cohen, A.J. Satellite-based estimates of ground-level fine particulate matter during extreme events: A case study of the Moscow fires in 2010. Atmos. Environ. 2011, 45, 6225–6232. [Google Scholar] [CrossRef]
- Martin, R.V. Satellite remote sensing of surface air quality. Atmos. Environ. 2008, 42, 7823–7843. [Google Scholar] [CrossRef]
- Hoff, R.M.; Christopher, S.A. Remote sensing of particulate pollution from space: Have we reached the promised land? J. Air Waste Manag. Assoc. 2009, 59, 645–675. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, B.; Moebus, S.; Dragano, N.; Stang, A.; Moehlenkamp, S.; Schmermund, A.; Memmesheimer, M.; Broecker-Preuss, M.; Mann, K.; Erbel, R.; et al. Chronic residential exposure to particulate matter air pollution and systemic inflammatory markers. Environ. Health Perspect. 2009, 117, 1302–1308. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Hoff, R.M.; Engel-Cox, J.A. The relation between Moderate Resolution Imaging Spectroradiometer (MODIS) aerosol optical depth and PM2.5 over the United States: A geographical comparison by US Environmental Protection Agency Regions. J. Air Waste Manag. Assoc. 2009, 59, 1358–1369. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Lyapustin, A.; Wang, Y.; Kondragunta, S.; Laszlo, I.; Ciren, P.; Hoff, R.M. A multi-angle aerosol optical depth retrieval algorithm for geostationary satellite data over the United States. Atmos. Chem. Phys. 2011, 11, 11977–11991. [Google Scholar] [CrossRef]
- Weber, S.A.; Engel-Cox, J.A.; Hoff, R.M.; Prados, A.I.; Zhang, H. An improved method for estimating surface fine particle concentrations using seasonally adjusted satellite aerosol optical depth. J. Air Waste Manag. Assoc. 2010, 60, 574–585. [Google Scholar] [CrossRef] [PubMed]
- Kumar, N.; Chu, A.D.; Foster, A.D.; Peters, T.; Willis, R. Satellite remote sensing for developing time and space resolved estimates of ambient particulate in Cleveland, OH. Aerosol Sci. Technol. 2011, 45, 1090–1108. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.J.; Liu, Y.; Coull, B.; Schwartz, J.; Koutrakis, P. PM2.5 prediction modeling using MODIS AOD and its implications for health effect studies. Epidemiology 2011, 22, S215. [Google Scholar] [CrossRef]
- Lee, H.J.; Liu, Y.; Coull, B.A.; Schwartz, J.; Koutrakis, P. A novel calibration approach of MODIS AOD data to predict PM2.5 concentrations. Atmos. Chem. Phys. 2011, 11, 7991–8002. [Google Scholar] [CrossRef]
- Choi, Y.S.; Ho, C.H.; Chen, D.; Noh, Y.H.; Song, C.K. Spectral analysis of weekly variation in PM10 mass concentration and meteorological conditions over China. Atmos. Environ. 2008, 42, 655–666. [Google Scholar] [CrossRef]
- Liu, Y.; Koutrakis, P.; Kahn, R. Estimating fine particulate matter component concentrations and size distributions using satellite-retrieved fractional aerosol optical depth: Part 1—Method development. J. Air Waste Manag. Assoc. 2007, 57, 1360–1369. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Koutrakis, P.; Kahn, R.; Turquety, S.; Yantosca, R.M. Estimating fine particulate matter component concentrations and size distributions using satellite-retrieved fractional aerosol optical depth: Part 2—A case study. J. Air Waste Manag. Assoc. 2007, 57, 1360–1369. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Paciorek, C.J.; Koutrakis, P. Estimating regional spatial and temporal variability of PM2.5 concentrations using satellite data, meteorology, and land use information. Environ. Health Perspect. 2009, 117, 886–892. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, D.; Kahn, R.A.; He, K. Review of the applications of multiangle imaging spectroradiometer to air quality research. Sci. China Ser. D-Earth Sci. 2009, 52, 132–144. [Google Scholar] [CrossRef]
- Liu, Y.; Kahn, R.A.; Chaloulakou, A.; Koutrakis, P. Analysis of the impact of the forest fires in August 2007 on air quality of Athens using multi-sensor aerosol remote sensing data, meteorology and surface observations. Atmos. Environ. 2009, 43, 3310–3318. [Google Scholar] [CrossRef]
- Liu, Y.J.; Harrison, R.M. Properties of coarse particles in the atmosphere of the United Kingdom. Atmos. Environ. 2011, 45, 3267–3276. [Google Scholar] [CrossRef]
- Liu, Y.; He, K.; Li, S.; Wang, Z.; Christiani, D.C.; Koutrakis, P. A statistical model to evaluate the effectiveness of PM2.5 emissions control during the Beijing 2008 Olympic Games. Environ. Int. 2012, 44, 100–105. [Google Scholar] [CrossRef] [PubMed]
- Lyamani, H.; Olmo, F.J.; Alcantara, A.; Alados-Arboledas, L. Atmospheric aerosols during the 2003 Heat Wave in southeastern Spain I: Spectral optical depth. Atmos. Environ. 2006, 40, 6453–6464. [Google Scholar] [CrossRef]
- Pelletier, B.; Santer, R.; Vidot, J. Retrieving of particulate matter from optical measurements: A semiparametric approach. J. Geophys. Res.-Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Wang, Q.; Shao, M.; Liu, Y.; William, K.; Paul, G.; Li, X.; Liu, Y.; Lu, S. Impact of biomass burning on urban air quality wstimated by organic tracers: Guangzhou and Beijing as cases. Atmos. Environ. 2007, 41, 8380–8390. [Google Scholar] [CrossRef]
- Natunen, A.; Arola, A.; Mielonen, T.; Huttunen, J.; Komppula, M.; Lehtinen, K.E.J. A multi-year comparison of PM2.5 and AOD for the Helsinki region. Boreal Environ. Res. 2010, 15, 544–552. [Google Scholar]
- Paciorek, C.J.; Liu, Y.; Moreno-Macias, H.; Kondragunta, S. Spatiotemporal associations between GOES aerosol optical depth retrievals and ground-level PM2.5. Environ. Sci. Technol. 2008, 42, 5800–5806. [Google Scholar] [CrossRef] [PubMed]
- Paciorek, C.J.; Liu, Y. Limitations of remotely sensed aerosol as a spatial proxy for fine particulate Matter. Environ. Health Perspect. 2009, 117. [Google Scholar] [CrossRef]
- Paciorek, C.J.; Liu, Y. Assessment and Statistical Modeling of the Relationship between Remotely Sensed Aerosol Optical Depth and PM2.5 in the Eastern United States; Research Report; Health Effects Institute: Boston, MA, USA, 2012. [Google Scholar]
- Rajeev, K.; Parameswaran, K.; Nair, S.K.; Meenu, S. Observational evidence for the radiative impact of Indonesian smoke in modulating the sea surface temperature of the equatorial Indian Ocean. J. Geophys. Res.-Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Schaap, M.; Apituley, A.; Timmermans, R.M.A.; Koelemeijer, R.B.A.; de Leeuw, G. Exploring the relation between aerosol optical depth and PM2.5 at Cabauw, The Netherlands. Atmos. Chem. Phys. 2009, 9, 909–925. [Google Scholar] [CrossRef]
- Tian, D.; Wang, Y.; Bergin, M.; Hu, Y.; Liu, Y.; Russell, A.G. Air quality impacts from prescribed forest fires under different management practices. Environ. Sci. Technol. 2008, 42, 2767–2772. [Google Scholar] [CrossRef] [PubMed]
- Van de Kassteele, J.; Koelemeijer, R.B.A.; Dekkers, A.L.M.; Schaap, M.; Homan, C.D.; Stein, A. Statistical mapping of PM10 concentrations over western Europe using secondary information from dispersion modeling and MODIS satellite observations. Stoch. Environ. Res. Risk Assess. 2006, 21, 183–194. [Google Scholar] [CrossRef]
- Zhang, J.; Reid, J.S. An analysis of clear sky and contextual biases using an operational over ocean MODIS aerosol product. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Lary, D.J.; Remer, L.A.; MacNeill, D.; Roscoe, B.; Paradise, S. Machine learning and bias correction of MODIS aerosol optical depth. IEEE Geosci. Remote Sens. Lett. 2009, 6, 694–698. [Google Scholar] [CrossRef]
- Hyer, E.J.; Reid, J.S.; Zhang, J. An over-land aerosol optical depth data set for data assimilation by filtering, correction, and aggregation of MODIS Collection 5 optical depth retrievals. Atmos. Meas. Tech. 2011, 4, 379–408. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, J.; Reid, J.S.; Hyer, E.J.; Hsu, N.C. Critical evaluation of the MODIS Deep Blue aerosol optical depth product for data assimilation over North Africa. Atmos. Meas. Tech. Discuss. 2012, 5, 7815–7865. [Google Scholar] [CrossRef]
- Reid, J.S.; Hyer, E.J.; Johnson, R.S.; Holben, B.N.; Yokelson, R.J.; Zhang, J.; Campbell, J.R.; Christopher, S.A.; Girolamo, L.D.; Giglio, L.; et al. Observing and understanding the Southeast Asian aerosol system by remote sensing: An initial review and analysis for the Seven Southeast Asian Studies (7SEAS) program. Atmos. Res. 2013, 122, 403–468. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lary, D.J.; Woolf, S.; Faruque, F.; LePage, J.P. Holistics 3.0 for Health. ISPRS Int. J. Geo-Inf. 2014, 3, 1023-1038. https://doi.org/10.3390/ijgi3031023
Lary DJ, Woolf S, Faruque F, LePage JP. Holistics 3.0 for Health. ISPRS International Journal of Geo-Information. 2014; 3(3):1023-1038. https://doi.org/10.3390/ijgi3031023
Chicago/Turabian StyleLary, David John, Steven Woolf, Fazlay Faruque, and James P. LePage. 2014. "Holistics 3.0 for Health" ISPRS International Journal of Geo-Information 3, no. 3: 1023-1038. https://doi.org/10.3390/ijgi3031023






