Abstract
Biosurveillance activities focus on acquiring and analyzing epidemiological and biological data to interpret unfolding events and predict outcomes in infectious disease outbreaks. We describe a mathematical modeling framework based on geographically aligned data sources and with appropriate flexibility that partitions the modeling of disease spread into two distinct but coupled levels. A top-level stochastic simulation is defined on a network with nodes representing user-configurable geospatial “patches”. Intra-patch disease spread is treated with differential equations that assume uniform mixing within the patch. We use U.S. county-level aggregated data on animal populations and parameters from the literature to simulate epidemic spread of two strikingly different animal diseases agents: foot-and-mouth disease and highly pathogenic avian influenza. Results demonstrate the capability of this framework to leverage low-fidelity data while producing meaningful output to inform biosurveillance and disease control measures. For example, we show that the possible magnitude of an outbreak is sensitive to the starting location of the outbreak, highlighting the strong geographic dependence of livestock and poultry infectious disease epidemics and the usefulness of effective biosurveillance policy. The ability to compare different diseases and host populations across the geographic landscape is important for decision support applications and for assessing the impact of surveillance, detection, and mitigation protocols.
1. Introduction
Emerging infectious diseases are of critical concern from the perspectives of global economics, security, and public health. Most new infectious diseases important to public health have emerged from animal reservoirs and are considered zoonotic [1]. Other animal epidemics such as the 2001 outbreak of foot-and-mouth disease (FMD) in the UK resulted in the culling of approximately four million animals and a cost of $3.7–6.3 billion [2]. The current epizootic spread of highly pathogenic avian influenza (HPAI) A subtype H5N1 among wild avian and domestic poultry species has resulted in 200 million birds destroyed with an impact of $10 billion dollars [3] and continues to pose a significant zoonotic threat [4]. As of the end of 2012, there have been 610 human H5N1 influenza infections worldwide with a 59% case fatality [5]. The emergence of the 2009 pandemic influenza A (H1N1) strain as a triple re-assortment of swine influenza viruses underscores the need for intensive monitoring in livestock populations for future infectious diseases with great zoonotic potential [6]. Early detection of emergent infectious disease threats, enabled by enhanced surveillance efforts, can mitigate the downstream morbidity, mortality, and economic consequences resulting from large-scale infectious disease outbreaks.
Biosurveillance activities focus on acquiring and analyzing epidemiological and biological data to interpret unfolding events and predict outcomes in infectious disease outbreaks. During the early hours and days of a new biological event, data on crucial parameters such as the number of secondary infections generated by a primary case and the serial generation time are typically crude [7]. Data quality generally improves as the event progresses. The large uncertainty in the estimate of the basic reproductive number during the early days of the 2003 SARS epidemic in Beijing narrowed as the outbreak progressed [8]. Similarly, the case fatality ratio associated with the 2009 influenza A H1N1 pandemic strain was initially estimated with a broad range of 0.8%–1.8% [9]. Garske and co-workers [10] identified shifts in case ascertainment from mild to severe cases as the pandemic progressed and the reporting delay between symptom onset and death in the early days of the event as primary reasons why disease severity was difficult to assess. Thus, models that, with limited information, can provide practical guidance and a range of possible outcomes under various control and surveillance scenarios could be valuable tools for scientists and policy makers.
Progress in information science and technology is giving rise to real-time public health data collection capabilities, mandating the need for “decision-aid models” that can be linked to surveillance data and provide real-time feedback during an epidemic [11]. These models will provide support to policymakers and inform their decisions about when, where, and how intensely to implement control measures such as quarantine, movement restrictions, vaccine strategies, and culling in the case of animal diseases.
Because outbreaks can arise from multiple possible known and unknown pathogen-host systems, models that support biosurveillance activities must be flexible and dynamic in nature, able to incorporate new and better quality data as a situation evolves. Changes in parameters, such as a virus mutation resulting in altered virulence, or changes in host distribution or competence must be easily incorporated into a successful model framework. In some cases, the structure of transmission pathways may need to change to accommodate new qualitative characteristics of a progressing outbreak. For instance, a previously unknown transmission route for pathogen transmission might be discovered and need to be incorporated. At the start of an epidemic, parameters are often highly uncertain, but uncertainty can be reduced as the epidemic progresses and better data become available and a more detailed understanding of etiological mechanisms emerges. An ideal model framework must be able to evolve with the changing state of knowledge.
We describe a mathematical modeling approach that is flexible enough to incorporate diversity of pathogen-host systems and an evolving state of knowledge about the systems. Flexibility is achieved by partitioning the modeling of disease spread and mitigation into two distinct but coupled levels. First is a top-level stochastic simulation with patches (or nodes) interacting via a contact network defined on a lattice [12] consisting of all short- and long-distance interactions relevant for disease transmission. Within each node is a “hidden” second level, internal to a patch, where disease spread follows the standard mean-field SIR-like ordinary differential equations [13]. This framework incorporates mitigation strategies on both the top level and bottom level models, allowing for such varied policies as movement control, surveillance, quarantine, vaccine, and culling. Finally, given the multiple levels of uncertainty in disease outbreaks, we incorporated stochasticity in spatial spread and ran the model multiple times with variation in parameter values and initial location of an outbreak. This quantification of uncertainty provides a plausible range of outcomes for decision makers to consider.
The framework we outline here builds upon and extends existing work to model spatial spread of animal disease [14,15,16,17,18,19,20]. Our work highlights the important and interacting roles of geography, and the spatial aspects of host diversity, host distribution, long and short distance movement, human-livestock interactions, and possible interventions.
The model framework described here has the ability to handle a wide variety of host species and significant drivers of disease spread arising from the host-pathogen biology (e.g., length of no clinical signs period), control measures (e.g., effect of local vs. global movement controls), and geographic dependence (initiation of the outbreak in areas of dense livestock production vs. more rural settings) that might provide windows of opportunity for mitigating an outbreak. Incorporating the spatial structure of the susceptible host contact network has been shown to be important for predicting emergent population-scale epidemiological parameters like the basic reproductive number and attack rates [21,22,23]. The highly detailed models of the 2001 FMD in the UK by Keeling et al. [23] and Ferguson et al. [14] were possible due to the availability of precise geo-location data on livestock holdings. Publicly available agricultural census data on livestock populations in the U.S. exist only in aggregated form at the county level. The model described here can be scaled to the county level to provide information and insight even with a lack of specific, high-quality farm location and livestock movement data.
In this work, we highlight the generality and usefulness of this framework by presenting two applications of our model, simulating epidemics of two economically important animal diseases with different hosts: foot-and-mouth disease (FMD) and highly pathogenic avian influenza (HPAI). FMD and HPAI spread in very different animal host populations (cattle, sheep, and pigs for FMD and poultry for HPAI) and have dichotomous etiological properties (FMD: species-dependent natural history, low mortality, high potential to become endemic and HPAI: homogenous natural history, nearly 100% mortality). We use only publicly available livestock population data, aggregated at the county level and updated every five years, by the National Agricultural Statistics Service [24].
2. Materials and Methods
This model is a spatially-based simulation based geographically at the county level in the United States and similar to the one described previously [25]. The top-level (“inter-patch”) model is a stochastic simulation where each “patch” is a geographic or epidemiological unit within which uniform mixing (i.e., homogenous inter-host contact rates) is assumed to hold. A schematic showing the model construct with states represented as boxes and transitions as arrows is shown in Figure 1. Each susceptible host population within a patch X and species (or livestock type) a follows the disease-specific natural history shown in Figure 1.
We begin with the inter-patch model for geographic spread. At time t during the simulation, if a particular patch X is susceptible (i.e., free of infected hosts), its probability of becoming infected at time t is given by
pX (t) = 1 − exp(−ΓX (t))
The kernel, ΓX(t), describing infection spread, is a function of the distance from nearby infected patches and connection with distant infected patches via livestock movement. The county infection kernel is also dependent on mitigations involving reduction of livestock movement at long-distance or short-distance scales. The “intra-patch” states of the disease model characterize the natural history of the disease in hosts of species or livestock type a in county (or patch) X. Disease compartments include susceptible hosts ( 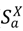 ), asymptomatic infected hosts that will progress to symptoms (
), asymptomatic infected hosts that will progress to symptoms ( 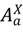 ), aymptomatic infected hosts that will not progress to symptoms (i.e., a carrier state), (
), aymptomatic infected hosts that will not progress to symptoms (i.e., a carrier state), ( 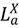 ), symptomatic infected hosts (
), symptomatic infected hosts ( 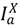 ), recovered hosts who have cleared the infection either naturally or via immunization (
), recovered hosts who have cleared the infection either naturally or via immunization ( 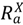 ), and infected hosts that have died from the disease (
), and infected hosts that have died from the disease ( 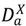 ). As with any compartmental disease model, compartments can easily be added or subtracted depending on the disease system considered.
). As with any compartmental disease model, compartments can easily be added or subtracted depending on the disease system considered.
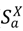 ), asymptomatic infected hosts that will progress to symptoms (
), asymptomatic infected hosts that will progress to symptoms ( 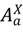 ), aymptomatic infected hosts that will not progress to symptoms (i.e., a carrier state), (
), aymptomatic infected hosts that will not progress to symptoms (i.e., a carrier state), ( 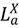 ), symptomatic infected hosts (
), symptomatic infected hosts ( 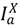 ), recovered hosts who have cleared the infection either naturally or via immunization (
), recovered hosts who have cleared the infection either naturally or via immunization ( 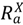 ), and infected hosts that have died from the disease (
), and infected hosts that have died from the disease ( 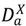 ). As with any compartmental disease model, compartments can easily be added or subtracted depending on the disease system considered.
). As with any compartmental disease model, compartments can easily be added or subtracted depending on the disease system considered.There are states associated with the mitigation/response architecture as well. In addition to the movement controls discussed, we consider quarantine of susceptible hosts, vaccination of both susceptible (prophylactic) and infected (treatment to reduce infectivity) hosts, and culling for animal hosts. The states related to control measures are susceptibles who have been successfully quarantined ( 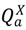 ), susceptibles who have been successfully vaccinated and are still capable of being infected at a lower rate for a short period of time before they are moved to the recovered class (
), susceptibles who have been successfully vaccinated and are still capable of being infected at a lower rate for a short period of time before they are moved to the recovered class ( 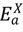 ), infected hosts that have been successfully treated by vaccination (
), infected hosts that have been successfully treated by vaccination ( 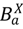 ), and animals who have been culled (
), and animals who have been culled ( 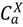 ). The dynamics of disease transmission and progression are described by the coupled system of equations detailed in the appendix.
). The dynamics of disease transmission and progression are described by the coupled system of equations detailed in the appendix.
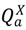 ), susceptibles who have been successfully vaccinated and are still capable of being infected at a lower rate for a short period of time before they are moved to the recovered class (
), susceptibles who have been successfully vaccinated and are still capable of being infected at a lower rate for a short period of time before they are moved to the recovered class ( 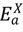 ), infected hosts that have been successfully treated by vaccination (
), infected hosts that have been successfully treated by vaccination ( 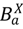 ), and animals who have been culled (
), and animals who have been culled ( 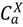 ). The dynamics of disease transmission and progression are described by the coupled system of equations detailed in the appendix.
). The dynamics of disease transmission and progression are described by the coupled system of equations detailed in the appendix.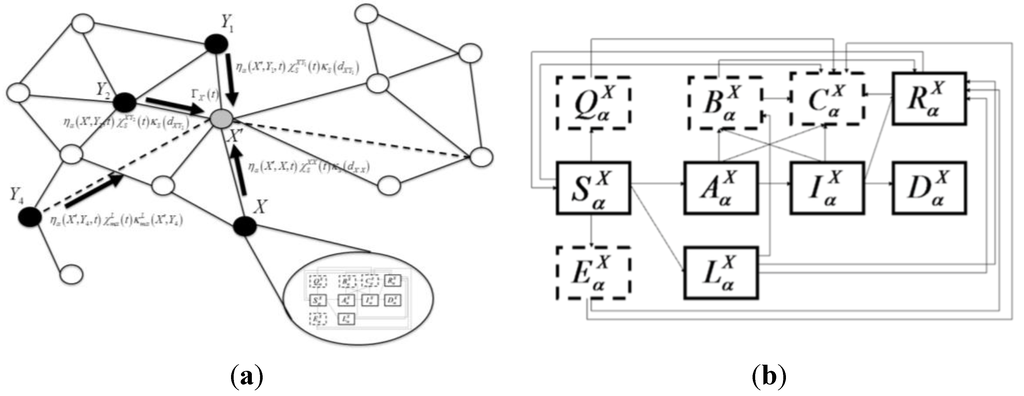
Figure 1.
Schematic for the intra-county disease transmission and progression model. Boxes indicate states for animals of species a in county X. Solid boxes label the natural history disease states: susceptible ( 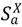 ), no clinical signs infected (
), no clinical signs infected ( 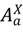 ), infected latent carrier state (
), infected latent carrier state ( 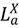 ), symptomatic infected (
), symptomatic infected ( 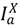 ), recovered (
), recovered ( 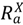 ), and dead (
), and dead ( 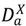 ) (due only to disease mortality). States bordered by dashed lines represent mitigation states: quarantined susceptibles (
) (due only to disease mortality). States bordered by dashed lines represent mitigation states: quarantined susceptibles ( 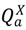 ), prophylactically vaccinated susceptibles (
), prophylactically vaccinated susceptibles ( 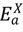 ), vaccinated infected animals(
), vaccinated infected animals( 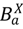 ), and culled animals (
), and culled animals ( 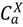 ).
).
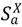 ), no clinical signs infected (
), no clinical signs infected ( 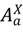 ), infected latent carrier state (
), infected latent carrier state ( 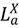 ), symptomatic infected (
), symptomatic infected ( 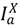 ), recovered (
), recovered ( 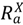 ), and dead (
), and dead ( 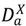 ) (due only to disease mortality). States bordered by dashed lines represent mitigation states: quarantined susceptibles (
) (due only to disease mortality). States bordered by dashed lines represent mitigation states: quarantined susceptibles ( 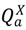 ), prophylactically vaccinated susceptibles (
), prophylactically vaccinated susceptibles ( 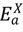 ), vaccinated infected animals(
), vaccinated infected animals( 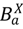 ), and culled animals (
), and culled animals ( 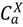 ).
).
The surveillance/control measure architecture on the disease natural history is governed by “gating” functions that take values of zero or one depending on time and determine when mitigation will turn on and off, 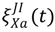 . Mitigation effectiveness is defined as the degree of success that is achieved when implemented. These are given by the parameters
. Mitigation effectiveness is defined as the degree of success that is achieved when implemented. These are given by the parameters 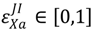 . For example, in Equation S3a (Supplementary), the term
. For example, in Equation S3a (Supplementary), the term 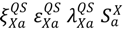 describes the rate at which susceptibles are being quarantined. While the transition rate
describes the rate at which susceptibles are being quarantined. While the transition rate 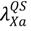 determines the number of susceptible hosts that can possibly be quarantined per unit time, the parameter
determines the number of susceptible hosts that can possibly be quarantined per unit time, the parameter 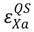 determines the quality of the control measure. The control measure parameters can be a function of both species type and location, so highly specific control measures can be constructed. For vaccination, we assume that the underlying biology is the dominant efficacy factor, so these variables are not location dependent. We assume all animals designated for culling will be culled, so we set the efficacy at 1.
determines the quality of the control measure. The control measure parameters can be a function of both species type and location, so highly specific control measures can be constructed. For vaccination, we assume that the underlying biology is the dominant efficacy factor, so these variables are not location dependent. We assume all animals designated for culling will be culled, so we set the efficacy at 1.
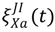 . Mitigation effectiveness is defined as the degree of success that is achieved when implemented. These are given by the parameters
. Mitigation effectiveness is defined as the degree of success that is achieved when implemented. These are given by the parameters 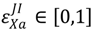 . For example, in Equation S3a (Supplementary), the term
. For example, in Equation S3a (Supplementary), the term 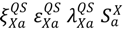 describes the rate at which susceptibles are being quarantined. While the transition rate
describes the rate at which susceptibles are being quarantined. While the transition rate 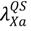 determines the number of susceptible hosts that can possibly be quarantined per unit time, the parameter
determines the number of susceptible hosts that can possibly be quarantined per unit time, the parameter 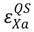 determines the quality of the control measure. The control measure parameters can be a function of both species type and location, so highly specific control measures can be constructed. For vaccination, we assume that the underlying biology is the dominant efficacy factor, so these variables are not location dependent. We assume all animals designated for culling will be culled, so we set the efficacy at 1.
determines the quality of the control measure. The control measure parameters can be a function of both species type and location, so highly specific control measures can be constructed. For vaccination, we assume that the underlying biology is the dominant efficacy factor, so these variables are not location dependent. We assume all animals designated for culling will be culled, so we set the efficacy at 1.2.1. Simulations
Our simulations are structured in the following way: The top-level of the simulation is the inter-county model, which has a time step of ∆t = 1 day. During each time step, all counties are looped over. If a county has infected animals the state variables { 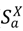 ,
, 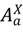 ,
, 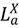 ,
, 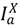 ,
, 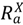 ,
, 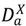 ,
, 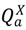 ,
, 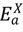 ,
, 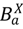 ,
, 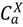 } are updated by integrating Equation (S3a–j) of the intra-county model using a fourth-order Runge-Kutta method. If a county does not have infected animals, Equation (1) is updated and a random number n∈ [0,1] is drawn from a uniform distribution. If n ≤ pX(t) then the county will become infected, if n > pX(t) then the county will remain uninfected. If infected, ~100 infected asymptomatic animals will be introduced and will be allocated to either the carrier state or the no clinical signs but progressing to symptoms state according to the branching ratio
} are updated by integrating Equation (S3a–j) of the intra-county model using a fourth-order Runge-Kutta method. If a county does not have infected animals, Equation (1) is updated and a random number n∈ [0,1] is drawn from a uniform distribution. If n ≤ pX(t) then the county will become infected, if n > pX(t) then the county will remain uninfected. If infected, ~100 infected asymptomatic animals will be introduced and will be allocated to either the carrier state or the no clinical signs but progressing to symptoms state according to the branching ratio 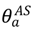 . The number of initially infected animals was chosen to be the same as in Manore et al. [25], an approximation of the number of infected animals present before an outbreak would be detected, but can be changed as necessary. We applied the two-level mathematical model of epidemic disease to simulate disease spread among a multi-species susceptible host population for two pathogens, FMD and HPAI.
. The number of initially infected animals was chosen to be the same as in Manore et al. [25], an approximation of the number of infected animals present before an outbreak would be detected, but can be changed as necessary. We applied the two-level mathematical model of epidemic disease to simulate disease spread among a multi-species susceptible host population for two pathogens, FMD and HPAI.
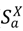 ,
, 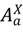 ,
, 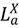 ,
, 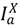 ,
, 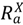 ,
, 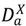 ,
, 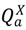 ,
, 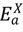 ,
, 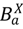 ,
, 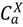 } are updated by integrating Equation (S3a–j) of the intra-county model using a fourth-order Runge-Kutta method. If a county does not have infected animals, Equation (1) is updated and a random number n∈ [0,1] is drawn from a uniform distribution. If n ≤ pX(t) then the county will become infected, if n > pX(t) then the county will remain uninfected. If infected, ~100 infected asymptomatic animals will be introduced and will be allocated to either the carrier state or the no clinical signs but progressing to symptoms state according to the branching ratio
} are updated by integrating Equation (S3a–j) of the intra-county model using a fourth-order Runge-Kutta method. If a county does not have infected animals, Equation (1) is updated and a random number n∈ [0,1] is drawn from a uniform distribution. If n ≤ pX(t) then the county will become infected, if n > pX(t) then the county will remain uninfected. If infected, ~100 infected asymptomatic animals will be introduced and will be allocated to either the carrier state or the no clinical signs but progressing to symptoms state according to the branching ratio 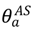 . The number of initially infected animals was chosen to be the same as in Manore et al. [25], an approximation of the number of infected animals present before an outbreak would be detected, but can be changed as necessary. We applied the two-level mathematical model of epidemic disease to simulate disease spread among a multi-species susceptible host population for two pathogens, FMD and HPAI.
. The number of initially infected animals was chosen to be the same as in Manore et al. [25], an approximation of the number of infected animals present before an outbreak would be detected, but can be changed as necessary. We applied the two-level mathematical model of epidemic disease to simulate disease spread among a multi-species susceptible host population for two pathogens, FMD and HPAI. Both sets of simulations were constructed using only county-level aggregated census data [24]. The patches are defined as individual US counties with county seats as the geospatial centroids. For each disease we ran multiple simulations sampling from appropriate parameter distributions for three different initial outbreak start locations in California, Arkansas, and Georgia for HPAI and California, Iowa, and Texas for FMD. For each location we ran 400 realizations, sampling over parameter probability density functions for each initial condition, with a time cutoff of 1000 days.
We then determined the consequence of these two diseases, measured as the total number of animals infected in each realization as a function of biological parameters (e.g., incubation times, symptomatic infectious periods) and control measure parameters (quarantine, movement control, vaccination efficacies). In addition, we examined the effect of geography (i.e., different initial conditions) on the epidemic spread. In the next two subsections, we discuss the specific choices made for the FMD and HPAI model parameters.
2.2. Foot-and-Mouth Disease
FMD virus is a member of the Picornaviridae family of viruses that infects ungulates or “hoof stock” like cattle, swine, sheep, goats, and deer [21]. The clinical disease caused by FMD virus is characterized by fever, anorexia, and the appearance of vesicles on the mucous membranes of the mouth and the feet. Although mortality associated with FMD is usually below 5%, morbidity can reach 100% [26]. The disease reduces the commercial value of an animal by reducing its weight and milk output. FMD is not zoonotic, though humans can carry and spread the virus easily to new locations and animals [22]. FMD greatly decreases livestock productivity, and affected countries cannot participate in international trade of animals and animal products.
Cattle show the clearest clinical signs and, thus, can be considered sentinel animals. Sheep and goats do not show noticeable clinical signs and can easily spread the disease to other domestic animals [27,28,29,30,31]. The primary methods of FMD transmission are aerosols, direct and indirect contacts with infected animal, and ingestion. Movement of infected animals is by far the most important spatial transmission factor, followed by movement of contaminated animal products [32].
We used the 2007 U.S. Department of Agriculture National Agriculture Statistics Service [24] agricultural census spatial data to initialize county-level population distributions of the species of interest, i.e., beef cattle, dairy cattle, cattle on feedlots, pigs, and sheep. Figure 2a,b show the density of hogs and cattle, respectively, in the United States from the 2007 census. In Table 1, we show the model parameters we used in the simulation. We parsimoniously treated all biological and epidemiological parameters as normally distributed. Mean values and standard deviations for the parameter distributions (unless explicitly stated in the reference) were determined from literature sources by taking the mean as the center of the range of values specified and the standard deviation was assumed to be one half of the range. The control measure parameters were assumed to be uniformly distributed over their specified ranges. Starting values for the transmission and susceptibility parameters for symptomatic cattle were taken from previous FMD modeling efforts [23]. We make the assumption that animals in the carrier state with no clinical signs are half as infectious as the symptomatic animal, since infectivity of the carrier state is highly uncertain [33]. When they do not show clinical signs, hogs and pigs have the same infectivity as cattle or sheep, but their infectiousness increases by a factor of two relative to cattle for the symptomatic phase, due to their propensity for generating aerosol droplets containing high concentrations of the virus [34]. We set the transmission parameters for sheep identical to cattle. The short-range length scale of spread is set at five miles, which is somewhat larger than the empirically derived kernel, estimated by DEFRA, during the 2001 UK outbreak (4 km) [23], where the prevalent mechanisms were animal movement and transmission of virus by trucks, equipment, and fomites. For cattle, hogs, and sheep, there are detailed data on the inter-state movements of animals [35]. We converted the monthly data into frequencies for the long-distance animal transport term.
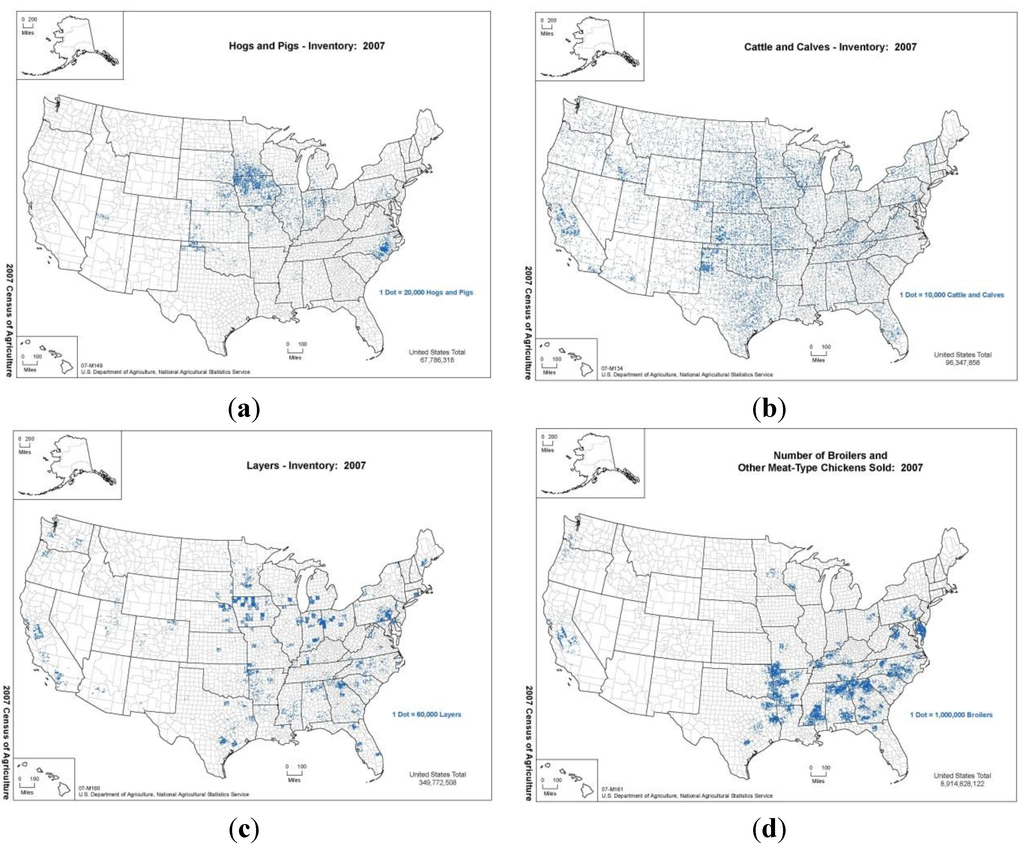
Figure 2.
Plots of density of (a) hogs and pigs, (b) cattle and calves in the United States according to the USDA NASS 2007 census (top row, left to right). Plots of density of (c) layers and (d) broilers in the United States according to the USDA NASS 2007 census (bottom row, left to right). In our simulations, regions with high density of host species result in faster spread with higher consequence.

Table 1.
Biological and control measure model parameters used for the foot-and-mouth disease (FMD) simulations.
| Model Parameter | Cattle | Hogs | Sheep |
|---|---|---|---|
| Transmission Rate/Subclinical Animal | 0.000000115 | 0.000000115 | 0.000000115 |
| Transmission Rate/Clinical Animal | 0.00000023 | 0.00000050 | 0.00000023 |
| Transmission Rate/Seroconverted non-progressing animal | 0.000000115 | 0.000000115 | 0.000000115 |
| Susceptibility per animal | 15.2 | 7.55 | 15.2 |
| Subclinical stage residence time (days) | 4–8 | 7–5 | 10–14 |
| Clinical signs stage residence time (days) | 14–21 | 14–21 | 14–21 |
| Seroconverted stage residence time (days) | 120–1277.5 | 120–1277.5 | 120–1277.5 |
| Infected animals that progress to clinical signs (fraction) | 0.95–1.0 | ||
| Infected animals that dies (fraction) | 0.01 | ||
| Recovery stage residence time (duration of immunity) | 90–180 | ||
| Vaccine protection efficacy for susceptibles (fraction) | 0.60–0.95 | ||
| Vaccine protection efficacy for infected animals (fraction) | 0.60–0.95 | ||
| Culling rate (animals per day) | All animals on infected premises in 48 h | ||
| Vaccination policy | Available in 21 days; ring+supressive tactic | ||
| Quarantine policy (fractional efficacy) | 0.10–0.90 | ||
| Inter-state movement control efficacy (fraction) | 0.10–0.90 | ||
| Short-range movement control efficacy (fraction) | 0.10–0.90 | ||
| Radius of surveillance zone (miles) | 20 | ||
| Time between decision and quarantine (county level-days) | 1–2 | ||
| Time between detection and culling (county level-days) | 1–2 | ||
| Time between detection and vaccination (county level-days) | 17 | ||
| Characteristic length of local speed (miles) | 5 | ||
Disease progression parameters were taken from various literature sources. The incubation time for cattle is typically 4 to 8 days [36,37]. Pigs generally progress faster and can show symptoms 2 to 5 days after infection [27,38]. Sheep typically take longer to progress, at 14 to 21 days [39]. Most of the dispersion in incubation times reflects uncertainty on transmission mode and inoculation dose size. The symptomatic stage for all animal species is fairly uniform and lasts 14 to 21 days [32,40]. Carrier animals can remain infectious in both the clinical and nonclinical signs states for long durations, e.g., 4 months to 3.5 years for cattle. While 95% to 100% of all cattle and hogs will progress to clinical signs [32,41], sheep are particularly susceptible for progression to the nonclinical signs carrier state [30,42]. Up to 25% of infected sheep will fail to develop lesions, so we assign a large range (25% to 50%) for the fraction of infected sheep that will progress to symptoms.
The length of time an animal has immunity after they have cleared the virus is proportional to the decay time of neutralizing antibodies elicited by primary infection. The antigenic variability of FMD is well known, and infection with one FMD serotype will not confer protection against other subtypes [39,43]. Thus, immunity against re-infection with the identical subtype is not permanent and it is approximately 90 to 180 days for cattle, hogs, and sheep according to Carrillo et al. [36] and Orsel et al. [37].
The following assumptions were made for the surveillance and response parameters shown in Table 1. At the county level, we have a time interval of 1–21 days between detection and the initiation of both quarantine and culling responses. A uniformly distributed range of (0.10–0.90) is chosen for the efficacy of both short-range and inter-state movement controls, as well as quarantine, to reflect a high degree of uncertainty in these parameters. Large uncertainty exists in factors like compliance and level of committed resources, in part due to the lack of practical experience with FMD, given that the last U.S. outbreak was in 1929. All animals designated for slaughter/disposal are culled within two days. A strain-matched FMD vaccine for treatment and prophylaxis is not available until 17 days post-detection in our simulations, which reflects time needed to match the genotype and for mass-production. Efficacy will depend on how well the strain is matched, so we assign a wide uniformly distributed range of 0.6–0.95.
2.3. Highly Pathogenic Avian Influenza
Avian influenza is a global infectious disease of birds caused by type A strains of the influenza virus. Many wild bird species carry these viruses with no apparent signs of harm. In poultry, the viruses cause two distinctly different forms of disease–one common and mild (low pathogenecity avian influenza), the other rare and highly lethal (HPAI) with mortality rates that can approach 100%. Clinical signs may include lesions, severe depression, loss of appetite, decline in egg production, facial edema, and hemorrhages on internal membrane surfaces. Infected birds shed the virus in fecal and nasal discharges. Apart from being highly contagious among poultry, avian influenza viruses can be transmitted between farms by the movement of live poultry, people (especially shoes and other clothing), vehicles, equipment, feed, and cages. Additionally, the disease can be spread through improper disposal of infected carcasses, manure, or poultry by-products. Insects and rodents may mechanically carry the virus from infected to susceptible poultry.
We populated the model with 2007 U.S. Department of Agriculture, National Agricultural Statistical Service [24] agricultural census poultry data on layers, pullets, broilers, and turkeys. Figure 2c,d show the density of layers and broilers, respectively, in the United States from the 2007 census. Table 2 shows the model parameters for the HPAI simulations. As in the FMD case, we assume the biological/epidemiological parameters are normally distributed while the control measure parameters are uniformly distributed. The intra-county transmission model parameters were calibrated to reproduce the 60% flock attack rates observed in poultry houses during Asian HPAI epizootic events [43] in separate runs with control measures set to match those outbreaks.
The mechanisms for disease spread include bird-to-bird contact at the individual farm level, movement of infected animals, and human-mediated routes of transmission involving contaminated trucks, equipment, or other fomites. We assume that none of the birds are infective until they manifest symptoms, which is consistent with the fecal-to-oral route where the virus must be shed in diarrhea into places where birds may peck. Only local spread between facilities was simulated, assuming that birds will appear at an average of approximately five miles between where they are hatched from eggs and where they are slaughtered (production), which is consistent with the observation that inter-state transport of poultry is limited [44].

Table 2.
Biological and control measure model parameters used for the highly pathogenic avian influenza (HPAI) simulations.
| Model Parameters | Poultry |
|---|---|
| Transmission Rate/Subclinical Animal | 0 |
| Transmission Rate/Clinical Signs Animal | 0.000000425 |
| Transmission Rate/Serconverted Non-progressing Animal | N/A |
| Susceptibility/Animal | 1.0 |
| Subclinical Stage Residence Time (days) | 1–3 |
| Clinical Signs Stage Residence Time (days) | 1–1.5 |
| Seroconverted Stage Residence Time (days) | N/A |
| Infected Animals that Progress to Clinical Signs (fraction) | 1.0 |
| Infected Animals that die | 0.975 |
| Recovery Stage Residence Time (duration of immunity) | Indefinite |
| Vaccination Protection Efficacy for Susceptibles | N/A |
| Vaccination Protection Efficacy for Infected Animals | N/A |
| Culling Rate (animals per day) | 53,500 |
| Quarantine Policy (fractional efficacy) | 0–1.0 |
| Vaccination Policy | N/A. |
| Interstate Movement Control Efficacy (fraction) | N/A |
| Short Range Movement Control Efficacy | 0–0.5 |
| Radius of Surveillance Zone (miles) | 6.2 |
| Time Between Detection and Quarantine (days) | 2.67 if not in surveillance zone.1 if in surveillance zone. |
| Time Between Detection and Culling (days) | 5.67 if not in surveillance zone.1 if in surveillance zone. |
| Time Between Detection and Vaccination (days) | N/A |
| Characteristic length of local spread (miles) | 5.53 |
Ranges for the disease progression parameters were based on reported literature values for recent HPAI outbreaks. The incubation period in poultry can vary between 1.6–8 days depending on the strain [45]. We chose a range in incubation times given by the work of Shortridge et al. [46]. For the infectious period (and assuming viral shedding in naive poultry will be large) we chose a range of 1–1.5 days [45]. After this period, poultry will recover or die with a clinical mortality rate of 97.5%. We assume immunity of recovered poultry to repeat infections [47,48,49,50].
The mitigation strategies evaluated are quarantine, culling, and movement controls. Vaccination was not chosen because it can lead to viral shedding in vaccinated, uninfected birds, and, also, generation of the nonclinical signs “carrier” states, which could increase the risk of between-flock transmission before outbreaks are detected [51,52,53]. The parameters used in the simulations are shown in Table 2.
The overall efficacy of mitigation and movement controls, both at the regional and national (inter-state) scales during a large HPAI outbreak, is largely uncertain. The past experiences in the U.S. with HPAI (Pennsylvania 1983, Texas 2004) show that rapid response and good biosecurity measures are important. The maximum effectiveness of inter-county movement controls is assigned as relatively low (50%) and quarantine efficacy is given the full range of uncertainty (i.e., 0–1) because of the phenomenon known as area spread [54], which includes unknown biosecurity breaches and other traditional farm and community practices that can result in movement of infectious agents. This is of particular importance for HPAI that is established in the environment [54,55,56].
For each disease, HPAI and FMD, we simulated 400 separate epidemics initiated at each of three locations. For each simulation run, 100 animals were assumed to be infected with disease in a population entirely composed of susceptible animals at the start of day 1 with disease progression parameters and mitigative efficacies selected at random from the ranges provided in Table 1 (for HPAI) and Table 2 (for FMD). The epidemic was stochastically simulated, producing an output file containing the population of each type of animal in every U.S. county for each disease stage (see Figure 1) during every day of the epidemic. Epidemic simulations were ended at 1000 days if they had not already been extinguished, and the total consequence numbers presented here include only the first 1000 days for these epidemics.
For each disease, we examined the distribution of animals across the U.S. and chose locations representing distinct clusters of livestock. For HPAI, we seeded the epidemic in California, Arkansas, and Georgia because of the geographic diversity represented by each of the states and the high density of layers and broilers in these states. For FMD, we chose California, Texas, and Iowa in order to capture diversity in geography while considering states with high density of cattle (CA, TX) and pigs (IA). In considering the impact of geography on epidemic spread, it is important to note that we included an explicit inter-state transportation of animals in the FMD model, based on the USDA’s published interstate livestock movements [57], while assuming no interstate transport of poultry occurred (Figure 2). This partly because of the nature of the industries and partly because of the increased ability to isolate poultry from wildlife, compared to cattle.
We use statistical model selection methods (AIC) to identify the main drivers of the severity or consequences of the epidemic among both the disease and control measure model parameters [58]. The disease parameters that are identified as significant reveal which elements of the host-pathogen biology and the mitigation strategies drive the size of the epidemic. Likewise, we identify the control measures are most critical to controlling disease spread and the dependency on the effectiveness of these mitigation strategies.
3. Results
The two largest drivers for the overall economic cost of livestock epidemics are the magnitude and duration of the epidemic, and we compare the day of the epidemic peak and total animals for HPAI and FMD (Figure 3). Each symbol represents the overall output of a simulated epidemic, with the overall size of the epidemic, measured in total number of animals infected and plotted on a logarithmic y-axis, and the day of the peak of the epidemic on the x-axis. For both diseases, geography was a good predictor of the rapidity and scale of the epidemic. Figure 4 shows a representative run for HPAI with three starting locations. For HPAI, epidemics initiated in California remain small and peak rapidly, while epidemics initiated in Arkansas peak rapidly, but are, in general, the largest epidemics of the three sites. The epidemics started in Georgia, while nearly as large as those started in Arkansas, reach a peak only after 3–6 weeks, instead of the 1 week characteristic of those started in California and the 10 days characteristic of those started in Arkansas.
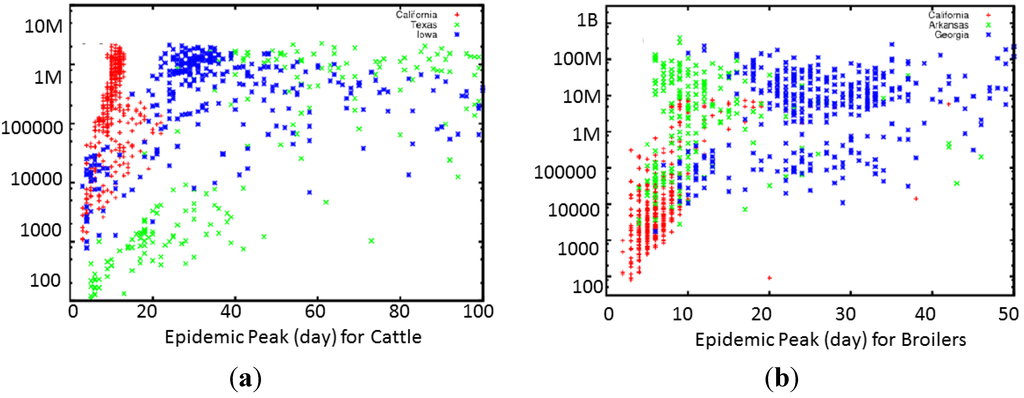
Figure 3.
Scatter plot of the total number of infected animals vs. duration of the epidemic for 1200 realizations of the consequence model for (a) FMD and (b) HPAI. Each dot corresponds to a single run with a randomly sampled set of parameters. Different colors label initial location of epidemic spread. Although both plots show dependence on geography, the HPAI plot shows much tighter clustering of epidemic length and size depending on the starting location of the epidemic. An exception is that for FMD, outbreaks started in California tend to peak high and fast.
Figure 4.
Inter-county level spread of HPAI. Green dots indicate counties where there are susceptible poultry according to the 2007 USDA NASS agricultural census data for layers, pullets, broilers, and turkeys. Blue dots indicate counties where there are at least 10 infected asymptomatic birds, red dots indicate counties with at least 1 symptomatic infected bird. Black crosses indicate counties which either initially have no susceptible poultry or where the susceptibles have been depopulated via quarantine measures, culling, or disease mortality.
For HPAI epidemics, the effect of incubation time on the overall rapidity of the epidemic peaking is large, with short incubation times leading to higher consequences and very rapid epidemic peaks. This reflects our decision to sample incubation times ranging from 1 to 7 days, consistent with the broad variability observed in this parameter, and the relatively isolated nature of California providing the conditions for highly repeatable epidemic simulations.

Table 3.
Model selection (AIC) outputs for highly pathogenic avian influenza.
| Disease Endpoint | Model | Aicc | ΔAICC | Wi |
|---|---|---|---|---|
| Total Infected | Global | 13,906.4 | 0 | 0.4954626 |
| Location + Asym + Infect+ Trigger + Intraquar + Interquar + Duration (Without fatality rate) | 13,914.4 | 8 | 0.0090747 | |
| Location + Asym + Infect + Fatality + Trigger + Duration (Without short- and long-range quarantine effect) | 13,990.4 | 84 | 0.0000000 | |
| Location + Trigger + Intraquar + Interquar + Duration (Without disease characteristics) | 13,947.4 | 41 | 0.0000000 | |
| Asym + Infect + Fatality (Only disease characteristics) | 14,510.4 | 604 | 0.0000000 | |
| Asym + Infect + Fatality+Trigger + Intraquar + Interquar + Duration (Without location effects) | 14,004.6 | 98.2 | 0.0000000 | |
| Dead | Global | 45,178.1 | 0 | 0.4954626 |
| Location + Asym + Infect+ Trigger + Intraquar + Interquar + Duration (Without fatality rate) | 45,235.2 | 57.1 | 0.0000000 | |
| Location + Asym + Infect + Fatality + Trigger + Duration (Without short- and long-range quarantine effect) | 45,502.4 | 324.3 | 0.0000000 | |
| Location + Trigger + Intraquar + Interquar + Duration (Without disease characteristics) | 45,425.1 | 1216.6 | 0.0000000 | |
| Asym + Infect + Fatality (Only disease characteristics) | 45,830.3 | 652.2 | 0.0000000 | |
| Asym + Infect + Fatality + Trigger + Intraquar + Interquar + Duration (Without location effects) | 45,298.6 | 120.5 | 0.0000000 | |
| Peak | Global | 37,007.7 | 0 | 0.500000 |
| Location + Asym + Infect + Trigger + Intraquar + Interquar + Duration (Without fatality rate) | 37,034.2 | 26.5 | 0.000001 | |
| Location + Asym + Infect + Fatality + Trigger + Duration (Without short- and long-range quarantine effect) | 37,414.5 | 406.8 | 0.000000 | |
| Location + Trigger + Intraquar + Interquar + Duration (Without disease characteristics) | 37,469.8 | 462.1 | 0.000000 | |
| Asym + Infect + Fatality (Only disease characteristics) | 37,725.6 | 717.9 | 0.000000 | |
| Asym + Infect + Fatality + Trigger + Intraquar + Interquar + Duration (Without location effects) | 37,348.4 | 340.7 | 0.000000 | |
| PeakT | Global | 36,914.1 | 0 | 1.000000 |
| Location + Asym + Infect + Trigger + Intraquar + Interquar + Duration (Without fatality rate) | 36,942.4 | 36,914.1 | 0.000000 | |
| Location + Asym + Infect + Fatality + Trigger+Duration (Without short- and long-range quarantine effect) | 37,296.5 | 382.4 | 0.000000 | |
| Location + Trigger + Intraquar + Interquar + Duration (Without disease characteristics) | 37,463.3 | 549.2 | 0.000000 | |
| Asym + Infect + Fatality (Only disease characteristics) | 37,725.6 | 811.5 | 0.000000 | |
| Asym + Infect + Fatality + Trigger + Intraquar + Interquar + Duration (Without location effects) | 37,157.5 | 549.2 | 0.000000 |
Location = California, Georgia, or Arkansas. Fatality rate = case fatality rate. Asym = time of asymptomatic period, Trigger = day epidemic is reported. Intraquar = Within state quarantine control. Interquar = Interstate quarantine animal movement control. Duration = duration of the epidemic. Minimum AICC is the lowest AICC score. AICC = (−2 × log-likelihood) + (2 × K); Model—these are the candidate models representing model inputs; ΔAIC is a model’s AIC minus the best model’s AIC; Wi or Akaike weights are calculated as follows: w = exp(−0.5 × ΔAIC). This is the same as taking the inverse natural logarithm of (−0.5 × ΔAIC).Wi (Akaike weights) are the normalized relative model likelihoods and are calculated as follows: Wi = exp(−0.5 × ΔAICi)/∑Rr = 1 exp(−0.5 × Δr), where R is the set of candidate models.
For the epidemic endpoints for HPAI, the peak time of the epidemic or how fast it spread was not impacted by the intrinsic disease fatality rate (ANOVA, F1,1194 = 0.90, P = 0.34) or the day the response was triggered (F1,1194 = 3.20, P = 0.075). The number of total dead animals was not dependent on the day the response was triggered as well (F1,1196 = 1.93, P = 0.165). The total number of infected animals was also not impacted by the intrinsic mortality rate (F1,1194 = 0.24, P = 0.62). All other disease characteristics and mitigation that were varied impacted the severity and duration of the HPAI epidemic (Table 3).
For FMD, by contrast, there is very little correlation between the incubation time and either the scale or duration of the epidemic. This is likely due to the relatively low variability observed in this parameter, and because the inter-state transport aspect of our model introduces significant stochastic noise into the overall consequence of the simulation. Figure 5 illustrates the scale vs. rapidity for a single realization of the FMD simulation for beef cattle, hogs, and dairy cattle for a single realization. As with HPAI, geography is important in the spread of FMD. However, unlike HPAI, with long distance livestock transportation and more subclinical cases, FMD outbreaks often quickly grew to national levels. Figure 6 shows a typical run for FMD started in three counties (top left panel).
Figure 7 and Figure 8 show the sensitivities of consequence magnitude to control measures. In Figure 7, we show how FMD outbreak magnitude (measured in terms of dead beef cattle) varies with the time delay between disease detection and initiation of culling of infected animals. Figure 8 shows how the efficacy of quarantine correlates in reducing HPAI consequence in terms of total dead poultry.
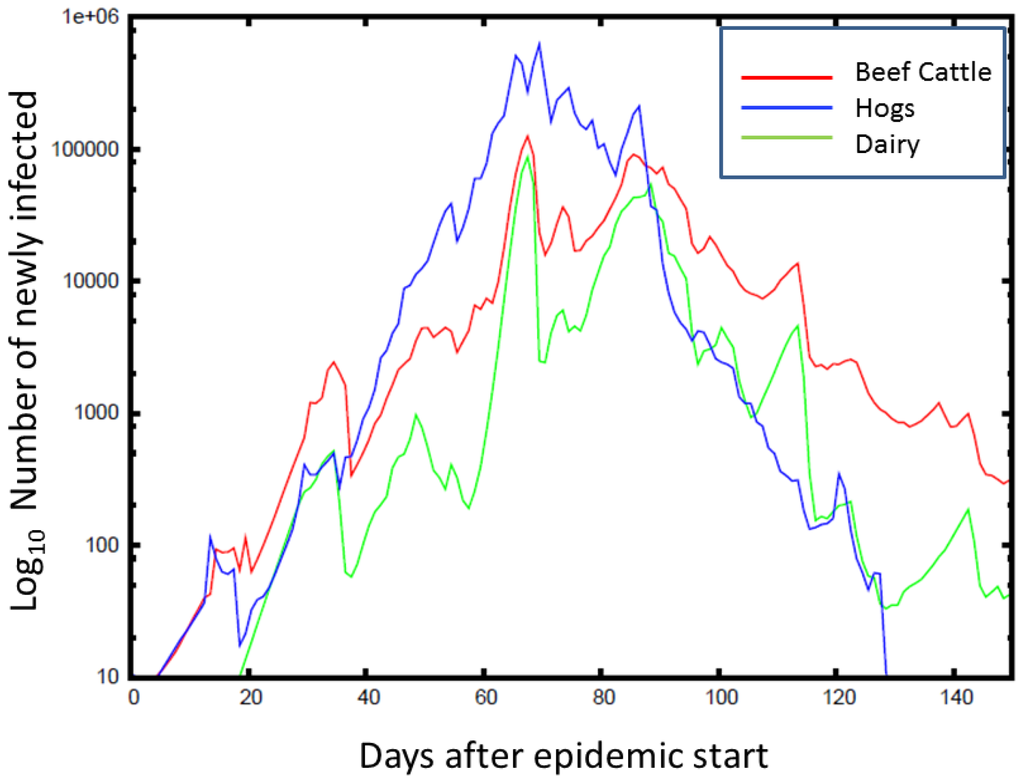
Figure 5.
Time series (averaged over counties and simulations) for the number of newly infected animals from FMD is plotted against the time of the epidemic peak, with the color indicating the animal type. On average, the FMD outbreaks peak at around 80 days, with hogs being the most affected. The epidemic peaks at a lower number for beef cattle, but lasts longer than for hogs.
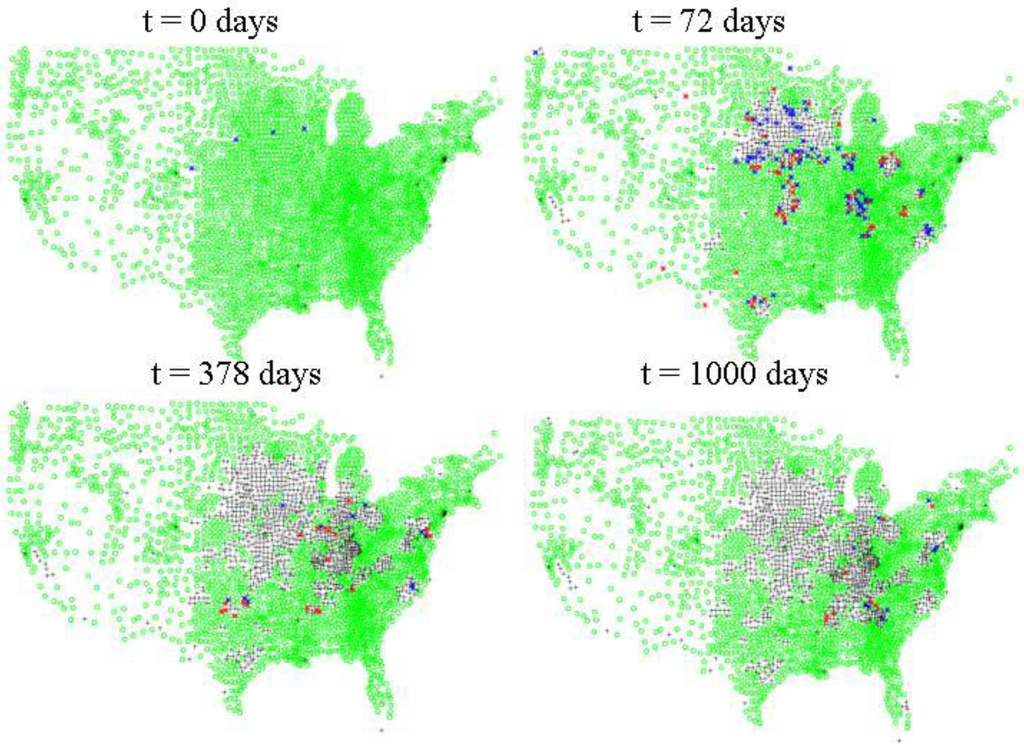
Figure 6.
Inter-county level spread of FMD. Green dots indicate where there are susceptible populations of cattle, hogs and/or sheep according to the 2007 USDA NASS agricultural census data. Blue dots indicate where there are 10 or greater asymptomatic animals, red dots indicate where there are one or more symptomatic animals. Black crosses indicate counties which either had no initial susceptible populations or that are depopulated of susceptibles by mitigative measures, i.e., quarantine, culling and/or vaccination.
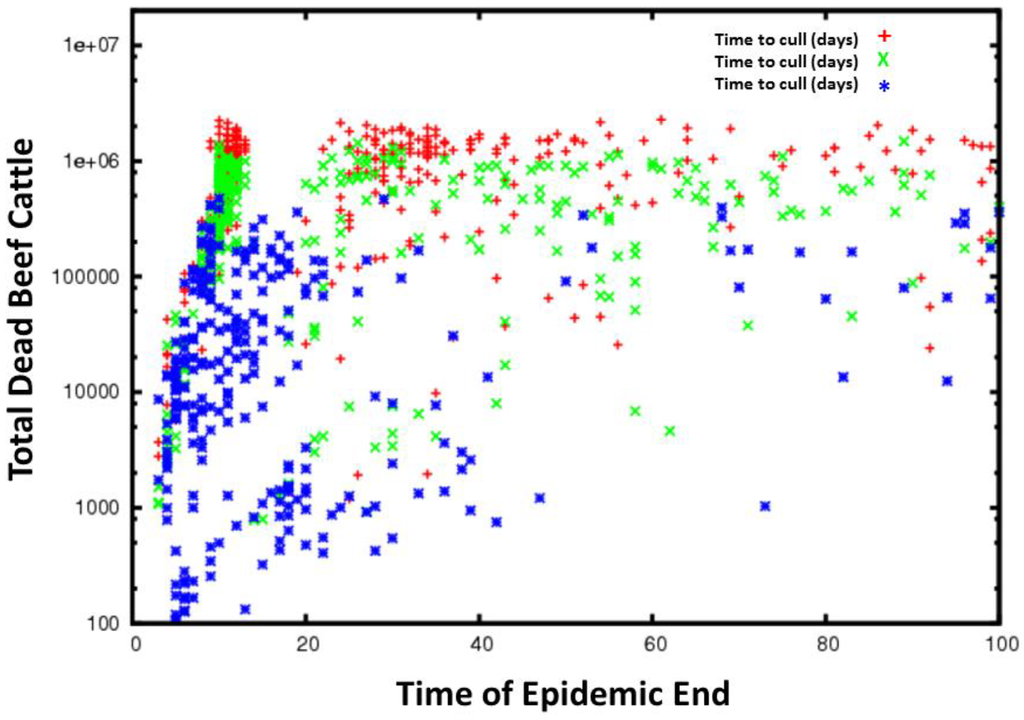
Figure 7.
Time series for all simulations for FMD grouped by the time to cull animals. The red plus signs are cull delay of 14–21 days, the green crosses a cull delay of 7–14 days and the blue stars a cull delay of 1–7 days. Less delay in culling generally results in fewer total dead cattle and in slower epidemic spread.
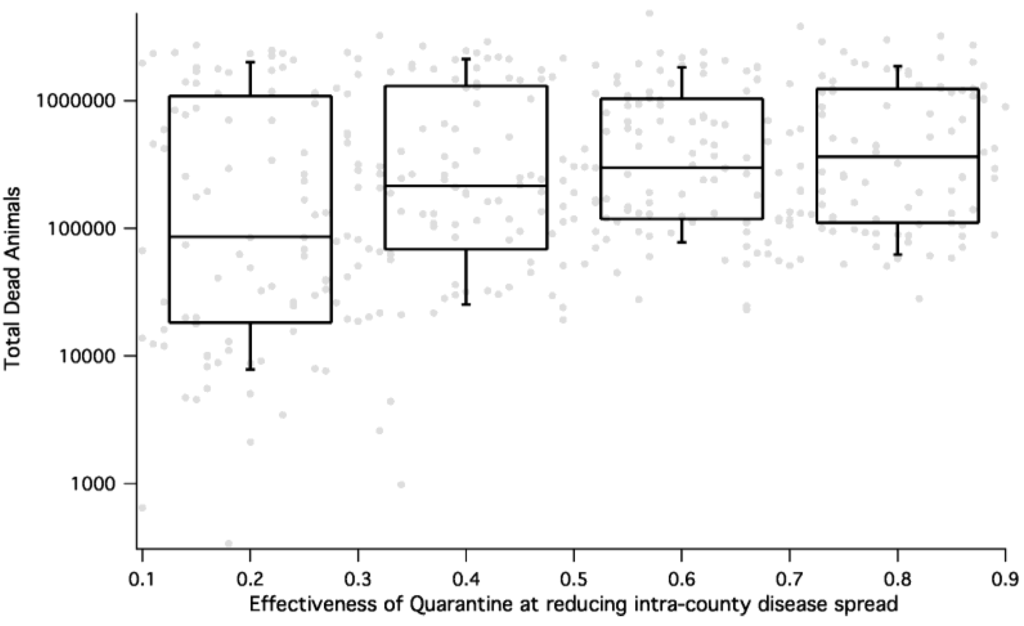
Figure 8.
HPAI consequence (measured as total number dead during a simulation) as a function of efficacy of quarantine for all epidemic simulations. The percent of animals not protected by quarantine is on the x-axis and the total number of dead animals on the y-axis. We see that for HPAI, effective quarantine results in reduction of dead animals by almost an order of magnitude.
4. Discussion
We presented a model framework with appropriate granularity (given limited data on geolocations of livestock holdings and animal movement) and complexity to simulate a variety of infectious diseases with mitigation and illustrated its use in an analysis of outbreaks of HPAI and FMD. The model allows for a realistic characterization of the differences in disease progression and geographic distribution of a variety of different hosts, as well as differences in our ability to mitigate the outbreaks. The model also runs rapidly enough that the sensitivity of the consequence to disease progression parameters, disease mitigation parameters, and geography can all be characterized. It does require, however, that realistic ranges for all parameters be appropriately defined for this sensitivity analysis to work appropriately; we took great care in this respect for the present study.
Geography is a critical aspect of the epidemics that is captured by our model. Indeed, the spread of HPAI exhibits diffusion-like properties within the context of geographical barriers and varying host density among counties. This kind of spatial spread is more easily mitigated by isolation or quarantine as see in Figure 8 and may be more forgiving with regards to time before mitigation begins. As expected, FMD, which spreads rapidly across the nation, appears to have major aspects of its epidemic properties determined by the spatial distribution of host and carrier animals. Although there were no differences in the epidemic outcomes for FMD based on our chosen starting locations, this was not the case for HPAI in poultry. With this said, it is worth reviewing the structure of our distance-dependent spread kernel and long-range transport matrix. Specifically, when comparing outcome vs. geography of initiation, epidemics that begin in California reflect dependence on long-range transport mechanisms. Epidemics started in California usually form a tight band, because it is an isolated, homogenous system. Larger dispersion happens in regions with high host density and high connectivity (e.g., Arkansas and Georgia for HPAI and the Midwest for FMD).
We acknowledge that a weakness of the simulations shown here is that the county is probably not the best epidemiological unit for the spread of animal diseases, and that farm-level resolution is probably required for high accuracy [59]. However, we show that a properly formulated model that contains all of the salient features of disease transmission can give reasonable results and provide the correct sensitivities to geographic host distributions and control measures in the absence of higher resolution data. If farm level data were to become available, this model framework could be adapted so that nodes represent farms rather than counties. We expect that the within-county spread would be slowed in this construct, inferring that the simulations shown here are generally representative of a “worst-case scenario” while providing coarse scale insight for mitigation and surveillance at a county or state level.
There are many things that impact the spread of an infectious disease epidemic in animals that include host genetics [60] and the environment [61]—with potential implications for impacting disease spread associated with climate change [62]. However, using appropriately scaled models to match the data collected from previous epidemics and observed disease characteristics can help alleviate the impacts of these micro impacts on overall simulations. In addition, the use of multiple simulations based on all potential ranges of disease parameters, as done in this study, can help quantify the variation that may be expected in any given future outbreak.
The application of the model to FMD and HPAI scenarios demonstrate the ability of the model to capture the epidemic spread of very different diseases with different hosts. The strengths of the model include the incorporation of the geospatial nature of the host-contact network without any highly specific calibration towards a particular disease, the contribution of multiple species and livestock types to the epidemiology, the range of magnitude of symptoms, etc. (resulting from the host-pathogen interaction), and the variance in the disease parameters themselves, reflecting the uncertainty in the virulence of a particular pathogen. The incorporation of mitigation at multiple scales is also an important contribution in the move toward modeling for policy.
It is important to point out that disease detection is dependent on farmers and stakeholders not only detecting disease but reporting on any sick animals. While official reporting of disease in animals is the right thing to do, it takes courage due to the potential for severe economic costs. It is important to continue to educate the farmers and the public that not only has rapid disease detection been proven to slow and even stop an epidemic from taking it off, the overall economics are substantially less than detecting disease later [63,64].
These aspects make the model framework ideal for the evaluation of emerging infectious disease threats. More than 70% of the most important human infections (AIDS, cholera, dengue fever, SARS, H5N1 influenza) are of zoonotic origin, arising from known and unknown wildlife reservoirs. Large domestic animals herds of agricultural livestock can provide efficient conduits for pathogen transfers from wild animals to humans [1]. Even without spread to humans, pathogens affecting livestock pose threats to food security and can cause significant economic losses. Early genetic, environmental, or epidemiological surveillance of disease “hotspots” or emergent outbreaks can initially yield sparse and/or low-fidelity data. Given that our simulations can sample over this uncertainty, this model can produce early, initial consequence estimates that can be gradually refined iteratively e.g., through Bayesian estimation techniques as described in [65] as more data become available. Human populations, with the appropriate couplings to animal populations, can be added to also assess the zoonotic risk. This knowledge gives more effective decision support to activities such as resource allocation prioritization and policy generation or modification than simple extrapolation of known diseases.
This model framework can be adapted to multiple outbreak stages. The patches, or network nodes, in the model can change scope and definition as an outbreak progresses. At the start of an outbreak, nodes could be defined as individual hosts. Disease parameters for transmission and progression could be sampled from probability densities estimated from initial data. During this phase, no use would be made of the of the within-patch ordinary differential equation model since statistical fluctuations dominate and the uniform mixing approximation is not valid for this phase of the event. Eventually, if the outbreak increases in scope, patches or nodes would change to represent different epidemiological units at different scales (e.g., family groups, herds, farms, cities, counties, etc.). Patch configuration changes would depend primarily on the fidelity of data available, but also on either qualitative assessments of where uniform mixing is expected to hold or on which choice of epidemiological unit patch representation gives best fits for model parameter estimation. We would expect this process to not only generate better models, but to increase computational efficiency as the patch size increases, since more hosts can be simulated with fewer patches.
5. Conclusions
Computational decision support models for biosurveillance activities require a great deal of flexibility in the quality and types of data that they must incorporate to give actionable results for controlling infectious disease outbreaks. We have presented a mathematical modeling framework that describes the spread of infectious diseases among multiple species of hosts while incorporating spatial heterogeneity in the host-contact network, the roles that different species play in the epidemiology, and the effects of human intervention. We have shown that by using low-fidelity, publicly available county-level population aggregations and parameters extracted from the biological and epidemiological literature, it was possible to simulate two pathogens of high interest, FMD and HPAI, and equitably describe their consequences.
We also see that each of the different details incorporated in the model structure matter—different dependence on disease properties, different mitigation strategies, different host species, geographic heterogeneity in host population distributions—all impact the outcome of the epidemic. Highly detailed models which are difficult to adapt to different diseases and hosts may give different answers on the propagation of the epidemics due to the uncertainties in each of the above factors that can each impact the outcome. More detailed models may give better predictions on a local scale in particular. However, knowing critical regions for more rapid and extensive propagation of the disease will assist in knowing where to apply mitigation and animal movement control strategies and where to expend effort on more detailed models. Geography and the spatial clustering of animals even at a regional level are key to consider for developing mitigation strategies and applying available resources.
In conclusion, the model framework presented here can be thought of as providing a “first line of defense” for managing and preventing emerging infectious disease outbreaks in livestock and poultry in the United States. The general nature of the model architecture can be adapted to multiple host species and multiple pathogens while incorporating important aspects of spatial heterogeneity and long-distance transport. It is parameterized and initialized with publicly available data and incorporates common mitigation strategies. Additionally, the model is computationally efficient, so can easily be run multiple times for many different scenarios to offer real-time feedback to policy makers and scientists. Model frameworks such as this can be used to inform mitigation and surveillance measures, especially in the face of high uncertainty.
The current model structure applies only to directly-transmitted diseases. We plan to adapt the model to incorporate vector-borne diseases spread by ticks, mosquitoes, midges, etc. The high diversity in vector species and distributions along with their very close, but not often straightforward, dependence on local weather and climate will provide added challenges to adapting this model framework. Incorporating seasonality and its effect on pathogen transmission and animal or human behavior would also be interesting.
Conflicts of Interest
The authors have no conflicts of interests.
Author Contributions
Montiago X. LaBute conceived of the study and wrote the original code for the model. Benjamin H. McMahon conceived of the study, participated in its design, debugged the adapted code, and made the figures. Mac Brown conceived of the study, participated in its design, and calibrated the model to USDA data. Carrie Manore conceived of the study, participated in its design, adapted the original code of the model, ran the code for the designed scenarios, and drafted the manuscript. Jeanne M. Fair conceived of the study, participated in its design, and helped parameterize the model. All authors read, amended and approved the final manuscript.
Acknowledgments
This work was performed in part by Defense Threat Reduction Agency (DTRA) under CBT-09-IST-05-1-0092. CM was supported in part by NSF Grant CHE-1314019. We thank Hector Hinojosa for comments on an early manuscript draft. We have benefited from discussions with A. Deshpande, T. Doerr, and S. White. Los Alamos National Security, LLC, is operator of the Los Alamos National Laboratory (LANL) under Contract No. DE-AC52-06NA25396 with the U.S. Department of Energy.
References
- Wolfe, N.D.; Dunavan, C.P.; Diamond, J. Origins of major human infectious diseases. Nature 2007, 447, 279–283. [Google Scholar] [CrossRef]
- Kao, R.R. The role of mathematical modelling in the control of the 2001 FMD epidemic in the UK. Trends Microbiol. 2002, 10, 279–286. [Google Scholar] [CrossRef]
- Fasina, F.O.; Sirdar, M.M.; Bisschop, S.P.R. The financial cost implications of the highly pathogenic notifiable avian influenza H5N1 in Nigeria. Onderstepoort J. Vet. Res. 2008, 75, 39–46. [Google Scholar]
- Globig, A.; Staubach, C.; Beer, M.; Koppen, U.; Fiedler, W.; Nieburg, M.; Wilking, H.; Starick, E.; Teifke, J.P.; Werner, O.; et al. Epidemiological and ornithological aspects of outbreaks of highly pathogenic Avian influenza virus H5N1 of Asian lineage in wild birds in Germany, 2006 and 2007. Transbound. Emerg. Dis. 2009, 56, 57–72. [Google Scholar] [CrossRef]
- WHO World Health Organization Epidemic and Pandemic Alert and Response. Available online: http://www.who.int/influenza/human_animal_interface/H5N1_cumulative_table_archives/en/index.html (accessed on 30 December 2012).
- Shinde, V.; Bridges, C.B.; Uyeki, T.M.; Shu, B.; Balish, A.; Xu, X.; Lindstrom, S.; Gubareva, L.V.; Deyde, V.; Garten, R.J.; et al. Triple-reassortant swine influenza a (H1) in humans in the United States, 2005–2009. N. Engl. J. Med. 2009. [Google Scholar] [CrossRef]
- Lipsitch, M.; Bergstrom, C.T. Invited commentary: Real-time tracking of control measures for emerging infections. Am. J. Epidemiol. 2004, 160, 517–519. [Google Scholar] [CrossRef]
- Cowling, B.J.; Ho, L.M.; Leung, G.M. Effectiveness of control measures during the SARS epidemic in Beijing: A comparison of the Rt curve and the epidemic curve. Epidemiol. Infect. 2008, 136, 562–566. [Google Scholar]
- Fraser, C.; Donnelly, C.A.; Cauchemez, S.; Hanage, W.P.; van Kerkhove, M.D.; Hollingsworth, T.D.; Griffin, J.; Baggaley, R.F.; Jenkins, H.E.; Lyons, E.J.; et al. Pandemic potential of a strain of influenza a (H1N1): Early findings. Science 2009, 324, 1557–1561. [Google Scholar] [CrossRef]
- Garske, T.; Legrand, J.; Donnelly, C.A.; Ward, H.; Cauchemez, S.; Fraser, C.; Ferguson, N.M.; Ghani, A.C. Assessing the severity of the novel influenza a/H1N1 pandemic. Br. Med. J. 2009, 339. [Google Scholar] [CrossRef]
- Bettencourt, L.M.A.; Ribeiro, R.M.; Chowell, G.; Lant, T.; Castillo-Chavez, C. Towards Real Time Epidemiology: Data Assimilation, Modeling and Anomaly Detection of Health Surveillance Data Streams. In Proceedings of the 2007 Intelligence and Security Informatics: Biosurveillance. Second NSF Workshop, New Brunswick, NJ, USA, 22 May 2007; pp. 79–90.
- Watts, D.J.; Strogatz, S.H. Collective dynamics of “small world” networks. Nature 1998, 394, 440–442. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. I. Proc. R. Soc. Lond. A 1927. [Google Scholar] [CrossRef]
- Ferguson, N.M.; Donnelly, C.A.; Anderson, R.M. The foot-and-mouth epidemic in Great Britain: Pattern of spread and impact of interventions. Science 2001, 292, 1155–1160. [Google Scholar] [CrossRef]
- Gao, D.; Cosner, C.; Cantrell, R.S.; Beier, J.C.; Ruan, S. Modeling the spatial spread of rift valley fever in Egypt. Bull. Math. Biol. 2013, 75, 523–542. [Google Scholar] [CrossRef]
- Gilbert, M.; Aktas, S.; Mohammed, H.; Roeder, P.; Sumption, K.; Tufan, M.; Slingenbergh, J. Patterns of spread and persistence of foot-and-mouth disease types A, O and Asia-1 in turkey: A meta-population approach. Epidemiol. Infect. 2005, 133, 537–545. [Google Scholar] [CrossRef]
- Tran, C.; Yost, R.; Yanagida, J.; Saksena, S.; Fox, J.; Sultana, N. Spatio-temporal occurrence modeling of highly pathogenic avian influenza subtype H5N1: A case study in the Red River Delta, Vietnam. ISPRS Int. J. Geo-Inf. 2013, 2, 1106–1121. [Google Scholar] [CrossRef]
- Arino, J.; Jordan, R.; van den Driessche, P. Quarantine in a multi-species epidemic model with spatial dynamics. Math. Biosci. 2007, 206, 46–60. [Google Scholar] [CrossRef]
- Niu, T.; Gaff, H.D.; Papelis, Y.E.; Hartley, D.M. An epidemiological model of rift valley fever with spatial dynamics. Comput. Math. Methods Med. 2012. [Google Scholar] [CrossRef]
- Xue, L.; Scott, H.M.; Cohnstaedt, L.W.; Scoglio, C. A network-based meta-population approach to model rift valley fever epidemics. J. Theor. Biol. 2012, 306, 129–144. [Google Scholar]
- Belsham, G.J. Distinctive features of foot-and-mouth disease virus, a member of the picornavirus family; aspects of virus protein synthesis, protein processing and structure. Progr. Biophys. Mol. Biol. 1993, 60, 241–260. [Google Scholar]
- Rivas, A.L.; Kunsberg, B.; Chowell, G.; Smith, S.D.; Hyman, J.M.; Schwager, S.J. Human-mediated foot-and-mouth disease epidemic dispersal: Disease and vector clusters. J. Vet. Med. Series B 2006, 53, 1–10. [Google Scholar]
- Keeling, M.; Woolhouse, M.E.J.; Shaw, D.J.; Matthews, L.; Chase-Topping, M.; Haydon, D.T.; Cornell, S.J.; Kappey, J.; Wilesmith, J.; Grenfell, B.T. Dynamics of the 2001 UK foot and mouth epidemic: Stochastic dispersal in a heterogeneous landscape. Science 2001, 294, 813–817. [Google Scholar] [CrossRef]
- NASS National Agriculture Statistics Service. Available online: http://www.nass.usda.gov/Census (accessed on 2 September 2009).
- Manore, C.; McMahon, B.; Fair, J.; Hyman, J.; Brown, M.; LaBute, M. Disease properties, geography, and mitigation strategies in a simulation spread of rinderpest across the United States. Vet. Res. 2011, 42. [Google Scholar] [CrossRef]
- Meyer, R.F.; Knudsen, R.C. Foot-and-mouth disease: A review of the virus and the symptoms. J. Environ. Health 2001, 64, 21–23. [Google Scholar]
- Alexandersen, S.; Donaldson, A.I. Further studies to quantify the dose of natural aerosols of foot-and-mouth disease virus for pigs. Epidemiol. Infect. 2002, 128, 313–323. [Google Scholar]
- Callens, M.; de Clercq, K.; Gruia, M.; Danes, M. Detection of foot-and-mouth disease by reverse transcription polymerase chain reaction and virus isolation in contact sheep without clinical signs of foot-and-mouth disease. Vet. Q. 1998, 20, S37–S40. [Google Scholar] [CrossRef]
- Barnett, P.V.; Cox, S.J. The role of small ruminants in the epidemiology and transmission of foot-and-mouth disease. Vet. J. 1999, 158, 6–13. [Google Scholar] [CrossRef]
- Hughes, G.J.; Mioulet, V.; Haydon, D.T.; Kitching, R.P.; Donaldson, A.I.; Woolhouse, M.E. Serial passage of foot-and-mouth disease virus in sheep reveals declining levels of viraemia over time. J. Gen. Virol. 2002, 83, 1907–1914. [Google Scholar]
- Knowles, N.J.; Samuel, A.R. Molecular epidemiology of foot-and-mouth disease virus. Virus Res. 2003, 91, 65–80. [Google Scholar] [CrossRef]
- Donaldson, A.I.; Alexandersen, S. Predicting the spread of foot and mouth disease by airborne virus. Revue Sci. Tech. Off. Int. Epizoot. 2002, 21, 569–575. [Google Scholar]
- Alexandersen, S.; Quan, M.; Murphy, C.; Knight, J.; Zhang, Z. Studies of quantitative parameters of virus excretion and transmission in pigs and cattle experimentally infected with foot-and-mouth disease virus. J. Comp. Pathol. 2003, 129, 268–282. [Google Scholar] [CrossRef]
- Sellers, R.F.; Parker, J. Airborne excretion of foot-and-mouth disease virus. J. Hyg. 1969, 67, 671. [Google Scholar] [CrossRef]
- Shields, M.E. Agro-terrorism, biotechnology, and biosis. J. Agric. Food Inf. 2003, 5, 19–23. [Google Scholar] [CrossRef]
- Carrillo, C.; Lu, Z.; Borca, M.V.; Vagnozzi, A.; Kutish, G.F.; Rock, D.L. Genetic and phenotypic variation of foot-and-mouth disease virus during serial passages in a natural host. J. Virol. 2007, 81, 11341–11351. [Google Scholar] [CrossRef]
- Orsel, K.; Bouma, A.; Dekker, A.; Stegeman, J.A.; de Jong, M.C.M. Foot and mouth disease virus transmission during the incubation period of the disease in piglets, lambs, calves, and dairy cows. Prev. Vet. Med. 2009, 88, 158–163. [Google Scholar] [CrossRef]
- Golde, W.T.; Nfon, C.K.; Toka, F.N. Immune evasion during foot-and-mouth disease virus infection of swine. Immunol. Rev. 2008, 225, 85–95. [Google Scholar] [CrossRef]
- Kitching, R.P.; Hughes, G.J. Clinical variation in foot and mouth disease: Sheep and goats. Revue Sci. Tech. Off. Int. Epizoot. 2002, 21, 505–512. [Google Scholar]
- Donnelly, C.A.; Anderson, R.M. Transmission intensity and impact of control policies on the foot and mouth epidemic in Great Britain. Nature 2001, 413, 542–548. [Google Scholar] [CrossRef]
- Quan, M.; Murphy, C.M.; Zhang, Z.; Alexandersen, S. Determinants of early foot-and-mouth disease virus dynamics in pigs. J. Comp. Pathol. 2004, 131, 294–307. [Google Scholar]
- Alexandersen, S.; Zhang, Z.; Donaldson, A.I. Aspects of the persistence of foot-and-mouth disease virus in animals: The carrier problem. Microbes Infect. 2002, 4, 1099–1110. [Google Scholar] [CrossRef]
- Vong, S.; Coghlan, B.; Mardy, S.; Holl, D.; Seng, H.; Ly, S.; Miller, M.J.; Buchy, P.; Froehlich, Y.; Dufourcq, J.B.; et al. Low frequency of poultry-to-human H5Ni virus transmission, Southern Cambodia, 2005. Emerg. Infect. Dis. 2006, 12, 1542–1547. [Google Scholar] [CrossRef]
- Marin, C.; Lainez, M. Salmonella detection in feces during broiler rearing and after live transport to the slaughterhouse. Poult. Sci. 2009, 88, 1999–2005. [Google Scholar] [CrossRef]
- Mase, M.; Imada, T.; Nakamura, K.; Tanimura, N.; Imai, K.; Tsukamoto, K.; Yamaguchi, S. Experimental assessment of the pathogenicity of H5N1 influenza a viruses isolated in Japan. Avian Dis. 2005, 49, 582–584. [Google Scholar] [CrossRef]
- Shortridge, K.F.; Zhou, N.N.; Guan, Y.; Gao, P.; Ito, T.; Kawaoka, Y.; Kodihalli, S.; Krauss, S.; Markwell, D.; Murti, K.G.; et al. Characterization of avian H5N1 influenza viruses from poultry in Hong Kong. Virology 1998, 252, 331–342. [Google Scholar] [CrossRef]
- Osterhaus, A.; Poland, G.A. Vaccines against seasonal and avian influenza: Recent advances. Vaccine 2008, 26, D1–D2. [Google Scholar]
- Bouma, A.; Claassen, I.; Natih, K.; Klinkenberg, D.; Donnelly, C.A.; Koch, G.; van Boven, M. Estimation of transmission parameters of H5N1 avian influenza virus in chickens. PLoS Pathog. 2009. [Google Scholar] [CrossRef]
- Latorre-Margalef, N.; Gunnarsson, G.; Munster, V.J.; Fouchier, R.A.M.; Osterhaus, A.; Elmberg, J.; Olsen, B.; Wallensten, A.; Haemig, P.D.; Fransson, T.; et al. Effects of influenza a virus infection on migrating mallard ducks. Proc. R. Soc. B-Biol. Sci. 2009, 276, 1029–1036. [Google Scholar] [CrossRef]
- Sasaki, T.; Kokumai, N.; Ohgitani, T.; Sakamoto, R.; Takikawa, N.; Lin, Z.F.; Okamatsu, M.; Sakoda, Y.; Kida, H. Long lasting immunity in chickens induced by a single shot of influenza vaccine prepared from inactivated non-pathogenic H5N1 virus particles against challenge with a highly pathogenic avian influenza virus. Vaccine 2009, 27, 5174–5177. [Google Scholar] [CrossRef]
- Cagle, C.; Wasilenko, J.; Adams, S.C.; Cardona, C.J.; Thanh Long, T.; Tung, N.; Spackman, E.; Suarez, D.L.; Smith, D.; Shepherd, E.; et al. Differences in pathogenicity, response to vaccination, and innate immune responses in different types of ducks infected with a virulent H5N1 highly pathogenic avian influenza virus from Vietnam. Avian Dis. 2012, 56, 479–487. [Google Scholar]
- Couch, R.B.; Patel, S.M.; Wade-Bowers, C.L.; Nino, D. A randomized clinical trial of an inactivated avian influenza a (H7N7) vaccine. PLoS One 2012. [Google Scholar] [CrossRef]
- Leung, Y.H.C.; Luk, G.; Sia, S.-F.; Wu, Y.-O.; Ho, C.-K.; Chow, K.-C.; Tang, S.-C.; Guan, Y.; Peiris, J.S.M. Experimental challenge of chicken vaccinated with commercially available H5 vaccines reveals loss of protection to some highly pathogenic avian influenza H5N1 strains circulating in Hong Kong/China. Vaccine 2013, 31, 3536–3542. [Google Scholar] [CrossRef]
- Iwami, S.; Takeuchi, Y.; Liu, X.N.; Nakaoka, S. A geographical spread of vaccine-resistance in avian influenza epidemics. J. Theor. Biol. 2009, 259, 219–228. [Google Scholar] [CrossRef]
- Lebarbenchon, C.; Albespy, F.; Brochet, A.-L.; Grandhomme, V.; Renaud, F.; Fritz, H.; Green, A.J.; Thomas, F.; van der Werf, S.; Aubry, P.; et al. Spread of avian influenza viruses by common teal (anas crecca) in Europe. PLoS One 2009, 4. [Google Scholar] [CrossRef]
- Rivas, A.L.; Chowell, G.; Schwager, S.J.; Fasina, F.O.; Hoogesteijn, A.L.; Smith, S.D.; Bisschop, S.P.R.; Anderson, K.L.; Hyman, J.M. Lessons from Nigeria: The role of roads in the geo-temporal progression of avian influenza (H5N1) virus. Epidemiol. Infect. 2010, 138, 192–198. [Google Scholar] [CrossRef]
- USDA Interstate Livestock Movements. Available online: http://www.ers.usda.gov/Data/InterstateLivestockMovements/ (accessed on 4 March 2009).
- Burnham, M.R.; Peebles, E.D.; Branton, S.L.; Jones, M.S.; P.D., G. Effects of f-strain mycoplasma gallisepticum inoculation at twelve weeks of age on the blood characteristics of commercial egg laying hens. Poult. Sci. 2003, 82, 1397–1402. [Google Scholar] [CrossRef]
- Bates, T.W.; Carpenter, T.E.; Thurmond, M.C. Benefit-cost analysis of vaccination and preemptive slaughter as a means of eradicating foot-and-mouth disease. Am. J. Vet. Res. 2003, 64, 805–812. [Google Scholar] [CrossRef]
- Doeschl-Wilson, A.B.; Davidson, R.; Conington, J.; Roughsedge, T.; Hutchings, M.R.; Villanueva, B. Implications of host genetic variation on the risk and prevalence of infectious diseases transmitted through the environment. Genetics 2011, 188, 683–693. [Google Scholar] [CrossRef]
- Rasmussen, S. Modelling of discrete spatial variation in epidemiology with SAS using Glimmix. Comput. Methods Progr. Biomed. 2004, 76, 83–89. [Google Scholar] [CrossRef]
- Martin, V.; Chevalier, V.; Ceccato, P.; Anyamba, A.; De Simone, L.; Lubroth, J.; de la Rocque, S.; Domenech, J. The impact of climate change on the epidemiology and control of rift valley fever. Revue Sci. Tech.-Off. Int. Epizoot. 2008, 27, 413–426. [Google Scholar]
- Hagerman, A.D.; Ward, M.P.; Anderson, D.P.; Looney, J.C.; McCarl, B.A. Rapid effective trace-back capability value: A case study of foot-and-mouth in the Texas High Plains. Prev. Vet. Med. 2013, 110, 323–328. [Google Scholar] [CrossRef]
- Elbakidze, L.; Highfield, L.; Ward, M.; McCarl, B.A.; Norby, B. Economics analysis of mitigation strategies for FMD introduction in highly concentrated animal feeding regions. Rev. Agric. Econ. 2009, 31, 931–950. [Google Scholar] [CrossRef]
- Bettencourt, L.M.A.; Ribeiro, R.M. Real time bayesian estimation of the epidemic potential of emerging infectious diseases. PLoS One 2008, 3. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).