Abstract
Public transit plays a key role in shaping the transportation structure of large and fast growing cities. To cope with high population and employment density, such cities usually resort to multi-modal transit services, such as rail, BRT and bus. These modes are strategically connected to form an effective transit network. Among the transit modes, bus stops need to be properly deployed to maintain an acceptable walking accessibility. This paper presents a hierarchical process for optimizing bus stop locations in the context of fast growing multi-modal transit services. Three types of bus stops are identified hierarchically, which includes connection stops, key stops and ordinary stops. Connection stops are generated manually to connect with other transit facilities. Key stops and ordinary stops are optimized with coverage models that are respectively weighted by network centrality measure and potential demand. A case study in a Chinese city suggests the hierarchical approach may generate more effective stop distribution.
1. Introduction
Public transit has been advocated for facilitating mobility and mitigating environmental impacts of transport in large cities. Transit stop spacing is an important indicator in deploying public transit services. Large cities typically have a more complicated land use structure and development density, and in many cases they provide multi-modal transit service, such as for rail, BRT and bus. In fast growing cities, the public transit system needs to be structured dynamically to serve changing transit demands. On the one hand, in newly developed areas, the transit service has to be planned to connect with the current system. On the other hand, economic growth generates new and increasing travel demand within cities, which requires the provision of more, and more efficient, integrated rapid transit systems.
However, irrational distribution of bus stops leads to a low public bus service quality. For example, redundant distribution of bus stops within short distances in most central areas increase unnecessary bus stopping and passenger waiting time [1]. Furthermore, bus stop inadequacy often exists in urban outskirts. Such a dispersed pattern results in a low walking accessibility, satisfying less public transport demands and also causing social inequity. The performance of a transit system can be significantly improved if the spacing of bus stops is optimized [2].
Typically, coverage models and their variants have been applied to optimize the distribution of transit stops. However, these methods put most emphasis on spatial distribution, and less attention is given to network structures and actual transit demand in prioritizing distribution of transit stops. More importantly, the study of stop optimization in a multi-modal transit environment is seriously inadequate.
This paper presents a hierarchical process for optimizing the distribution of bus stops in the context of multi-modal transit development in large cities. Firstly, reviews are made on stop spacing, stop location optimization, and measurement of node importance in a road network. Secondly, the hierarchical process for bus stop optimization is introduced. Then the process is evaluated with a case study of Wuhan city in China. Finally, we discuss factors related to the optimizing process, and give conclusions.
2. Stop Spacing and Coverage Models
2.1. Stop Spacing
Stop spacing is important for single bus routes. As each time a bus stops consumes time, for a bus route with a given length, more stops implicate a longer stopping time during a bus run. On the other hand, fewer stops along a route implies longer walking distance for passengers, which might lead to lower bus patronage. In order to maintain operational efficiency, there should be a balance between bus speed and stop spacing. In addition, spacing of bus stops has close linkage with transit trip demand distribution. Through mathematical models, stop spacing along a given bus route may be optimized based on varying transit demand along the route [3]. A case study of a route from Portland, Oregon, indicated that the theoretical optimized bus stop spacing averaged 250 ft longer than that of the current system [4]. Based on optimized spacing, transit operating cost savings could be achieved.
Potential demand is a key factor in stop placement. In addition to the socio-economic status of residents, transit usage is also influenced by so-called street side factors, such as the spacing between stops, distance to the nearest intersections, presence of sidewalks, adjacent land use, pedestrian access, and safety concerns [5]. A spatial interaction coverage model has been developed to account for the attractiveness of a stop, as well as importance of distance decay.
2.2. Coverage Model for Optimizing Stop Locations
Apart from spacing stops along single routes, it is also important to evaluate stop coverage for the whole urban transit system. A simple and effective measurement of stop coverage is to make buffer areas around bus stops, and count the proportion of area or population in the buffer areas. The buffer distance is the service extent of a stop. For multimodal transit system, transit stops may have different service extent. A case study in Sydney, Australia, has shown travelers are willing to walk a longer distance to the train than to the bus [6]. Redundancy exists in stop coverage when two stops are too close to each other. The standard of service distance in a central area might be different from other areas of a city. The number of bus stops might be optimized using a computer simulation method [7].
The set covering problem model (SCP) was applied for optimizing stop locations [8]. The objective was set to minimize the number of stops while all network nodes are covered within a predefined distance. Candidate stops were created at road network nodes and edges that are longer than a predefined distance. This approach mainly relies on road networks, where demand location and volume are not considered. Later, models with more factors have been developed. Location set covering problem (LSCP) provides an integer mathematical model for optimizing locations of facilities, such as emergency service facilities [9]. Owing to its ability to measure coverage efficiency, LSCP is typically adapted to optimize location of bus stops [1]. A hybrid set cover problem (HSCP) has been proposed for supporting the analysis of both transit access and accessibility in existing and expanded areas [10,11].
In addition to the LSCP model, Murray et al. [12] have summarized another two basic types of deterministic coverage location models: the model of maximal covering location problem (MCLP) that allows covering as much demand as possible using a limited number of facilities, and those that increase the likelihood of facility availability through the provision of backup coverage by lower-level facilities. There is also multi-level location set covering problem (ML-LSCP), in which facilities need to cover demand points a number of times while demand is also changing [13].
3. Methodology
3.1. General Framework
A road network of arcs and nodes are created. The nodes serve as candidate stops, from which bus stops are selected with optimizing models. Three types of bus stops are hierarchically identified, the connection stops, the key stops and the ordinary stops. The connection stops link bus transit to other transport mode, such as passenger stations of rail and road intercity transport, subway stations, and major activity sites. The key stops are topologically important stops that may serve as transfer centers of bus trips. The ordinary stops at the lowest level ensure appropriate spatial coverage of bus stops.
A hierarchical process is proposed for optimizing distribution of bus stops in the context of multi-modal transit in large cities (Figure 1). Firstly, connection stops are identified with reference to inter-city transport hubs, subway stations and other important activity places. Connection stops serve as input to coverage models at the second and third level. Secondly, based on road network, topological importance of each candidate stop is evaluated with degree centrality. The topological values are applied as weight in coverage model for distributing key stops. Thirdly, potential demand of each candidate stop is estimated by imposing a service area on raster-based population distribution. The demand values are input to the coverage model for ordinary stop optimization.
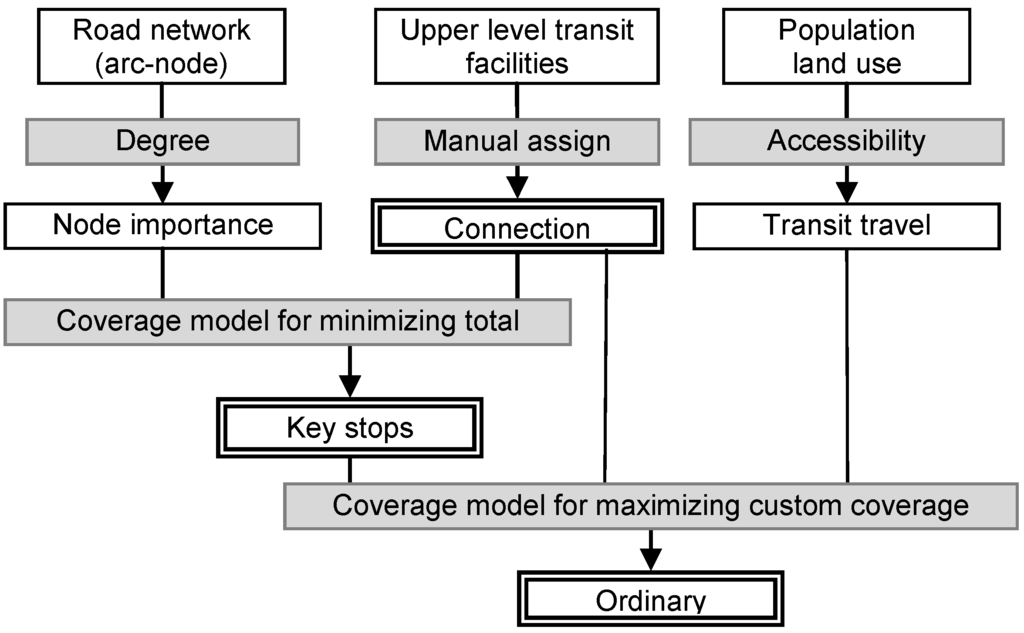
Figure 1.
Framework for hierarchical bus stop optimization.
In coverage models, upper-level stops serve as the constraint to the lower-level stops. Connection stops are usually designated in conjunction with inter-city transport hubs. Therefore, there is no need to optimize the locations of connection stops.
3.2. Coverage Model for Optimizing Key Stops
Locations of key stops are optimized with coverage model that respects the existence of connection stops and relies on topological importance of candidates. The objective of the coverage model for key stop generation is set as a p-media problem, i.e., to identify a given number of stops, while minimizing total weighted distance from all nodes to the stops. This option requires setting the number of key stops to be generated in advance. The weight for the model is the node topological value, i.e., the degree centrality value in this case. Also, based on the hierarchical process, connection stops have been checked, and need to be put as criteria into the model.
The form of the coverage model is:
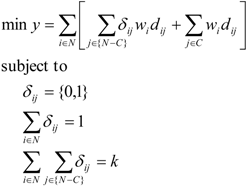 where N is the whole node set in the network, C is the set of connection stops that has been identified in advance, wi is the topological value (degree centrality) of node i, dij is the distance between node i and candidate j, k is the number of key stops to be optimized.
where N is the whole node set in the network, C is the set of connection stops that has been identified in advance, wi is the topological value (degree centrality) of node i, dij is the distance between node i and candidate j, k is the number of key stops to be optimized.
Node importance in a network can be described by centrality in graph theory. Four widely used measures of centrality are degree centrality, betweenness, closeness, and eigenvector centrality. The degree centrality counts the number of arcs incident upon a node. For road network, crossroads is the most common type of intersection, which means a degree centrality of 4. The betweenness of a vertex indicates the number of times that a vertex appears in the shortest path of any pair of other vertexes [14]. There are also other methods to measure node importance in a network, such as space syntax [15] and random walk [16]. This study takes the simplest degree centrality as weight for the coverage model.
3.3. Coverage Model for Optimizing Ordinary Stops
3.3.1. Coverage Model
The objective of the optimizing model is to maximize the customer coverage, weighted by node-based transit travel demand. Such objective requires setting a maximum distance for each candidate stop. The coverage model for ordinary stop optimization requires potential transit travel demand data. Upper level stops, i.e., the connection stops and key stops, are necessary input to the coverage model.
The coverage model is composed of three components. The first part is the demands covered by connection stops, the second part is the demands covered by key stops, and the third part is the demands covered by the ordinary stop that are to be optimized. During optimization, when the maximal covering distance of stops is set, the first two components become constants.
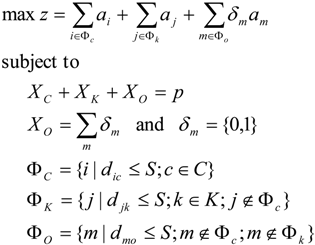 where ɑ is the transit demand at nodes, XC is the number of connection stops in set C, XK is the number of key stops in set K, XO is the number of ordinary stops, p is the total number of stops to be optimized, ΦC is the set of nodes allocated to connection stops, ΦK is the set of nodes allocated to the key stops, ΦO is the set of nodes allocated to ordinary stops, S is the maximal distance served by stops.
where ɑ is the transit demand at nodes, XC is the number of connection stops in set C, XK is the number of key stops in set K, XO is the number of ordinary stops, p is the total number of stops to be optimized, ΦC is the set of nodes allocated to connection stops, ΦK is the set of nodes allocated to the key stops, ΦO is the set of nodes allocated to ordinary stops, S is the maximal distance served by stops.
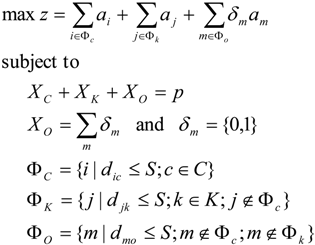
As connection stops are multi-modal transit stops, and key stops are key locations in network, both these two types of stops may have large service S. In addition to hierarchical processing, a zone-based optimizing approach may be applied. As the central area of a city usually has higher density, the service distance of stop can be smaller than that for outside area. From this perspective, a city may be partitioned into several zones, where each zone may have its own serving distance.
3.3.2. Transit Travel Demand
Transit travel demand is an input factor into the coverage model. The potential transit travel demand of a node in road network is composed of two parts, i.e., production and attraction. These values are referred to as potential values because the nodes are potential bus stops. The production values are calculated using the accessibility model in which inhabitants living nearer to bus stops have higher probability to travel by bus. The accessibility model is a negative logistic function based on distance decay concept [17]. The negative logistic function takes the form of p = ea−bd/(1 + ea−bd), where p is probability, a and b are calibrated parameters, d is distance. To resemble a real bus stop, the maximum distance around each node is set to 500 m in the accessibility model. When the production values are calculated for all the nodes, a total potential trip production for the whole city is derived.
The attraction part of transit demand is related to locations for jobs and other types of urban activities. In urban land use classification, institutional, commercial, industrial and transport station areas create job opportunities. The magnitude of attraction depends very much on activity location, type, density and usage time. Spatial interaction models are utilized for quantifying the attractiveness of these locations, usually incorporating accessibility measurement [18]. The spatial components of accessibility model, such as distance decay, competitions and job diversity, may generate different images of job attractiveness in urban areas [19]. In estimating transit attractiveness, if it is difficult to acquire number of jobs on land use units, accessibility measure may be utilized as potential demand for the coverage model.
To facilitate demand estimation, population and land use data are disaggregated as raster datasets in GIS. Usually population data is available from large statistical units, such as the case in Chinese statistical system. In order to acquire detailed spatial distribution of population, census statistical data are disaggregated using Monte Carlo simulation method, based on land use structure [20]. The raster-based population data is an effective input into the accessibility model for transit demand estimation.
The transit travel demand for each candidate stop (i.e., node) is the sum of its estimated production and attraction. When adjacent nodes are closer than the service coverage distance, they will generate overlapped service areas. Usually transit demand in the overlapped areas need to be assigned to nearby stops, in which each stop will receive part of the demand based on distance. In this stage, as the nodes are only candidate stops with potential demand, this overlap-area issue is ignored. Each node has its own complete service area, even if the area is overlapped with that of the surrounding nodes.
4. Case Study
4.1. The Case of Wuhan
Wuhan is a metropolitan city located in central China. Yangtze River, the largest river of China, meets the smaller Han River in the middle of the city. East Lake, the largest urban lake of China, occupies 33 km2. While the big rivers and lakes endow the city with a distinctive morphology, they also impede travels across the city. Till 2013, five bridges and one tunnel crossing the Yangtze River have been built. However, only two bridges serve as the major corridors of bus transport. More than 50 bus routes are concentrated on each of the two bridges. The public transit system in Wuhan comprises of bus, taxi, ferry and rail transport. Bus transit is the major transit mode, for example, buses covered 73% of all transit trips and over 4 million passenger trips per day in 2011 [21]. The city has been constructing rail routes since 2010. By 2020, eight routes will form the rail network in central area of the city, which brings the problem of adjusting bus routes and stops.
The study area covers the main urban area, which is circumscribed by the third ring road of Wuhan (Figure 2). The original data sets for the case of Wuhan city include road network, population, land use, candidate stop, railway station, planned subway station, ferry port and so on. Candidate stops are road network nodes, and there are 1335 nodes in total. Currently there are 733 bus stops and 238 lines in the study area. The population is disaggregated into raster cells of 30 m by 30 m.
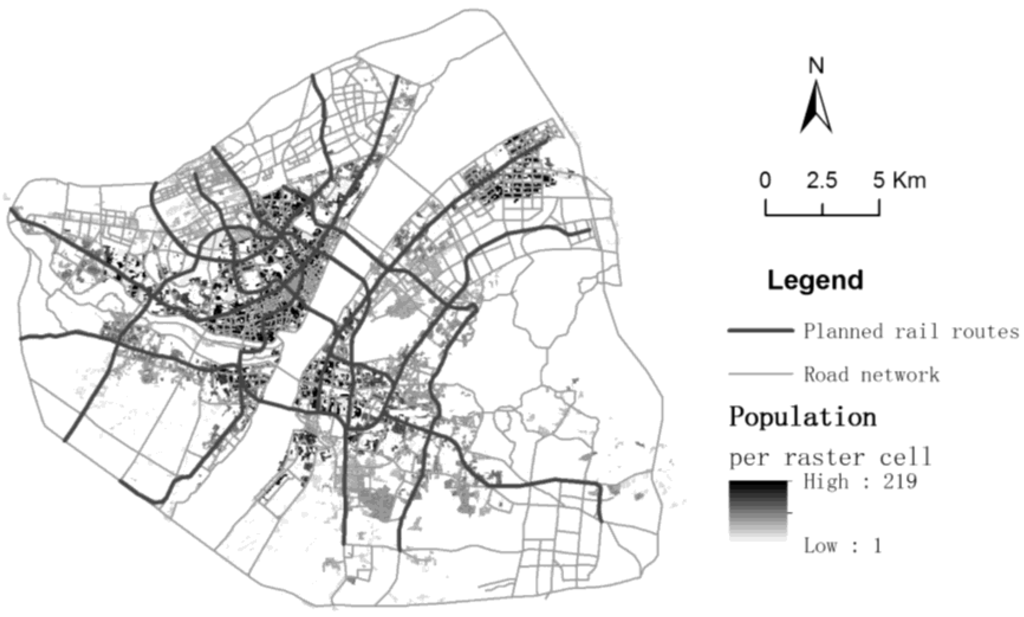
Figure 2.
The main urban area of Wuhan, China.
4.2. Implementation of the Three Stages
In the first stage, connection stops are identified based on the distribution of transport facilities, i.e., railway station, planned subway station and ferry port. Nodes that are closest to these facilities are designated manually as connection stops. In total there are 160 connection stops created.
In the second stage, the node degree centrality is firstly computed in ArcGIS, and input as weight into the coverage model for key stops. This stage generates 40 key stops, making a total of 200 stops available before optimizing in the next stage.
Ordinary stops are optimized in the third stage, based on demand weighted coverage model. This model also requires setting the service distance of stops. The objective is to find a location set in which the total demand is maximized. In this case study 450 ordinary stops will be optimized, and totally 650 stops will be achieved when taking the connection stops and key stops into account. The coverage distance for the model is set to 400 m. All nodes within the distance of a candidate stop are allocated to the stop, and demands from these nodes are summed up.
The weight for the coverage model is the potential transit travel demand at candidate stops. The demand value is composed of production value and attraction value, all of which are derived from a negative logistic accessibility model.
4.3. Results and Analysis
These scenarios are implemented using the Location-Allocation module in ArcGIS, which provides both the p-median and weighted demand coverage models. The distribution of existing and optimized stops is depicted in Figure 3.
The optimized 650 stops is a much smaller figure than the existing 733 stops. There is a drop of stops in the central area, and an increase of stops in the outer area. Comparing to the existing situation, although the total number of stops is reduced, the optimized stops spread more evenly in the study area. This indicates the redundant bus stops in the central areas are reduced and the service coverage of the outer areas is enlarged.
Using spatial analysis functions in GIS, we create buffer areas of stops with different distances, and compute the population and land area coverage (Figure 4). The coverage values are normalized with percentage. Concerning population coverage, the existing stop set has higher coverage within 300 m, and has lower coverage above 400 m than that of the optimized stop set. The growth curves of population coverage by distance are remarkably different, which suggests the optimization result is advantageous only if we consider service distance above 400 m. For the land area coverage, the optimized stop set prevails over the existing stop set from 300 m buffer, which also implies a reduction of redundant stops through optimization.
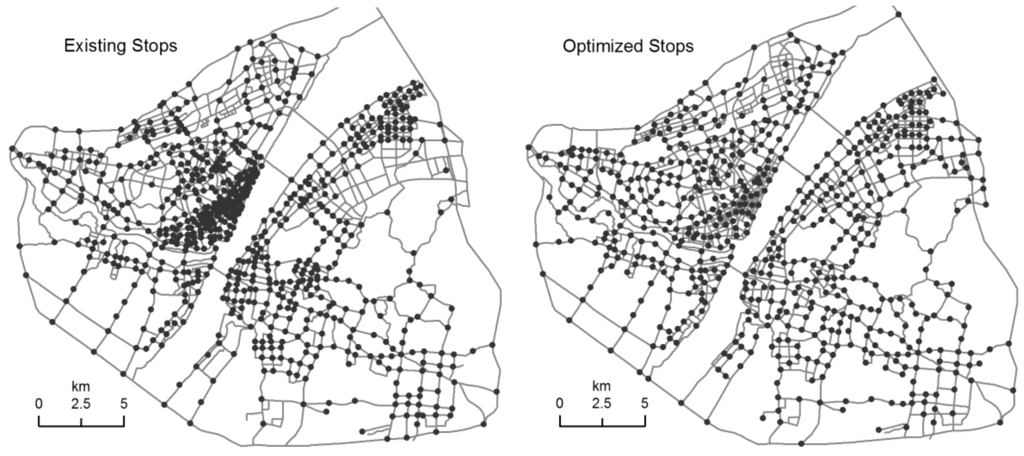
Figure 3.
Distribution of existing and optimized bus stops.
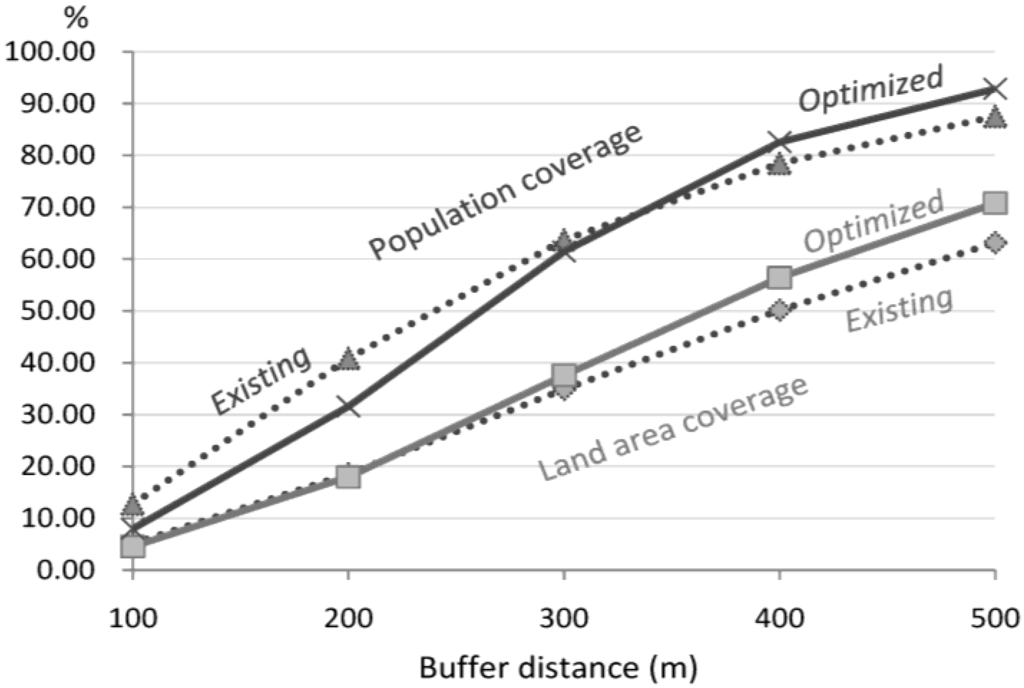
Figure 4.
Coverage by different buffer distance around stops.
Although both the land area coverage and population coverage have increased after optimization, the growing of area coverage is more remarkable. Transit stops serve residing locations as well as job locations, therefore, in addition to population coverage, job coverage deserves to be explored to achieve a more comprehensive evaluation.
Spacing between stops may also indicate the effect of optimization. The closeness between adjacent stops is measured with the distance along road network in GIS. Stop distance is classified by an interval of 100 m, and the frequency at each interval is counted for both existing and optimized stop set. To make sense, the first 1000 distance values in both stop sets are included for comparison. Figure 5 clearly describes the difference between the two stop sets. While the existing stop distances concentrate between 300 and 800 m, most optimized distances fall between 500 and 900 m.
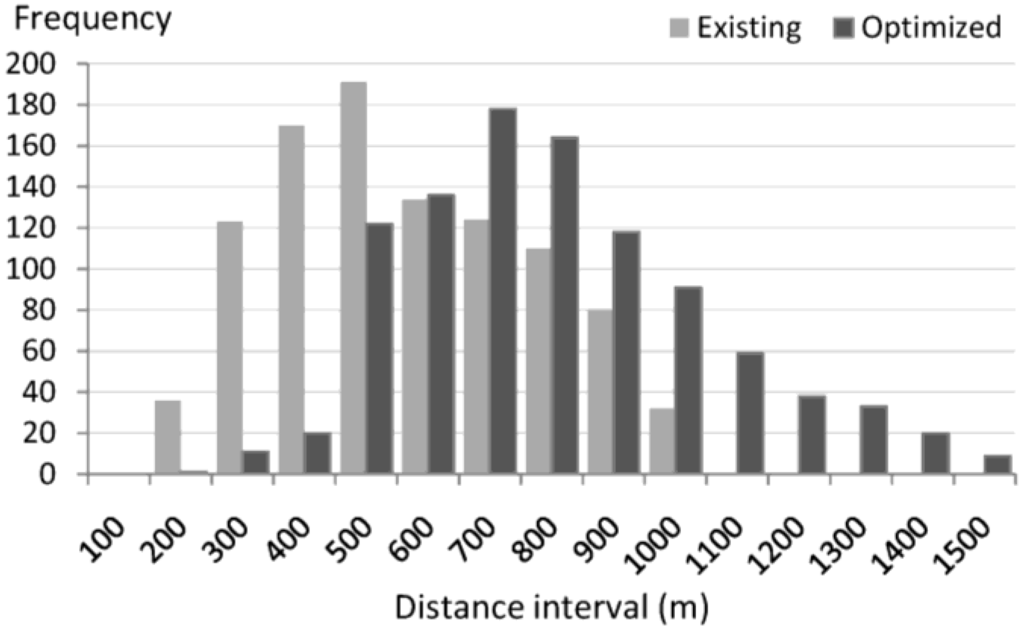
Figure 5.
Distribution of distance between stops.
5. Conclusions
This paper has presented a hierarchical process for optimizing distribution of bus stops in the city of Wuhan in China, where a multi-modal transit system is planned and under development. Three levels of bus stops have been defined for the optimizing process. The first level is for bus stops connecting important transit facilities of other modes. The second level is for key bus stops that have both location and topological importance in the road network. The third level is for ordinary bus stops that are optimized for the purpose of maximizing transit coverage. Among the three levels, higher level stops serve as pre-requisites for the optimization of stops at the lower levels.
The optimized result has been compared with the existing situation, and has shown a good improvement on service coverage and necessary total number of stops. In general, redundant stops in the central area of the city are reduced, while in the outer area, more stops can be deployed. A better service coverage is achieved by deploying fewer bus stops, which indicates the effectiveness of the approach. The hierarchical approach is based on a combination of raster and vector data models in GIS, which allows the most flexible computing and more effective evaluations during the analyses. For example, a different numbers of key stops and ordinary stops may be assigned in the second and third stage respectively. Also, the maximal allowable distance in the maximizing coverage model may be tested with different values. This enables exploring the best number of stops while maintaining an acceptable service level.
The proposed hierarchical framework has demonstrated great potential for optimizing locations of bus stops. A distinguishing feature is that the coverage models generate stops on an area basis, rather than along an individual route; optimized stops spread evenly across the study area, which ensures maximal demand coverage. However, such optimization would not be practical unless transit routes are properly deployed to connect the stops. Therefore, while the coverage model could be further improved by incorporating other demand factors, a broader framework for integrating routes and stop optimization is necessary.
Acknowledgments
The research is supported by the National Natural Science Foundation of China (41271396; 41231171).
Author Contributions
Both authors contributed to the study design and analysis. Zhengdong Huang conducted evaluation and manuscript writing. Xuejun Liu conducted data collection and database construction.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Murray, A.T. Strategic analysis of public transport coverage. Socio. Econ. Plan. Sci. 2001, 35, 175–188. [Google Scholar] [CrossRef]
- Chien, S.I.; Qin, Z. Optimitation of bus stop locations for improving transit accessibility. Transp. Plan. Technol. 2004, 27, 211–227. [Google Scholar] [CrossRef]
- Wirasinghe, S.C.; Ghoneim, N.S. Spacing of bus-stops for many to many travel demand. Transp. Sci. 1981, 15, 210–221. [Google Scholar] [CrossRef]
- Li, H.; Bertini, R.L. Assessing a model for optimal bus stop spacing with high-resolution archived stop-level data. Transp. Res. Record 2009, 2, 24–32. [Google Scholar]
- Delmelle, E.M.; Li, S.; Murray, A.T. Identifying bus stop redundancy: A GIS-based spatial optimization approach. Comput. Environ. Urban Syst. 2012, 36, 445–455. [Google Scholar] [CrossRef]
- Daniels, R.; Mulley, C. Explaining walking distance to public transport: The dominance of public transport supply. J. Transp. Land Use 2013, 6, 5–20. [Google Scholar] [CrossRef]
- Alterkawi, M.M. A computer simulation analysis for optimizing bus stops spacing: The case of Riyadh, Saudi Arabia. Habitat. Int. 2006, 30, 500–508. [Google Scholar] [CrossRef]
- Ceder, A.; Prashker, J.; Stern, H.I. An algorithm to evaluate public transportation stops for minimizing passenger walking distance. Appl. Math. Model. 1983, 7, 19–24. [Google Scholar] [CrossRef]
- Toregas, C.; Swain, R.; ReVelle, C.; Bergman, L. The location of emergency service facilities. Oper. Res. 1971, 19, 1363–1373. [Google Scholar] [CrossRef]
- Murray, A.T. A coverage model for improving public transit system accessibility and expanding access. Ann. Oper. Res. 2003, 123, 143–156. [Google Scholar] [CrossRef]
- Matisziw, T.C.; Murray, A.T.; Kim, C. Strategic route extension in transit networks. Eur. J. Oper. Res. 2006, 171, 661–673. [Google Scholar] [CrossRef]
- Murray, A.T.; Tong, D.; Kim, K. Enhancing classic coverage location models. Int. Reg. Sci. Rev. 2010, 33, 115–133. [Google Scholar] [CrossRef]
- Church, R.L.; Gerrard, R.A. The multi-level location set covering model. Geogr. Anal. 2003, 35, 277–289. [Google Scholar] [CrossRef]
- Freeman, L.C. Centrality in social networks conceptual clarification. Soc. Netw. 1978, 1, 215–239. [Google Scholar] [CrossRef]
- Jiang, B.; Claramunt, C. Integration of space syntax into GIS: New perspectives for urban morphology. Trans. GIS 2002, 6, 295–309. [Google Scholar]
- Pearson, K. The problem of the random walk. Nature 1905, 72. [Google Scholar] [CrossRef]
- Kimpel, T.J.; Dueker, K.J.; El-Geneidy, A.M. Using GIS to measure the effect of overlapping service areas on passenger boardings at bus stops. URISA J. 2007, 19, 5–11. [Google Scholar]
- Sanchez, T.W.; Shen, Q.; Peng, Z.-R. Transit mobility, jobs access and low-income labour participation in US metropolitan areas. Urban Stud. 2004, 41, 1313–1331. [Google Scholar] [CrossRef]
- Cheng, J.; Bertolini, L. Measuring urban job accessibility with distance decay, competition and diversity. J. Transp. Geogr. 2013, 30, 100–109. [Google Scholar] [CrossRef]
- Huang, Z.; Ottens, H.F.L.; Masser, I. A doubly weighted approach to urban data disaggregation in GIS—A case study of Wuhan, China. Trans. GIS 2007, 11, 197–211. [Google Scholar] [CrossRef]
- Wuhan Transport Planning Institute. Wuhan Transportation Annual Report 2012 (Blue Book); Wuhan Transport Planning Institute: Wuhan, China, 2012. (In Chinese) [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).