1. Introduction
The rapid development of geospatial data collection techniques, and the growth of the World Wide Web (web) for a wide range of “geo”-applications, has resulted in recent increases in the availability of geospatial data. The number and variety of sources of geospatial data, exemplified by sites such as the OpenStreetMap project, the (British) Ordnance Survey (OS) OpenSpace service, and the US Census Bureau, show that it is possible to create, revise, download, distribute, embed and add value to, an enormous range of data. Progress in web services has resulted in thousands of Web Map Servers (WMS) providing hundreds of thousands of readily usable map layers, and Web Feature Servers (WFS) supplying raw data of enormous variety and provenance.
The “democratising” nature of the web means that such data can result from efforts of both professional geospatial scientists or engineers, providing authoritative, official, “formal” data, and enthusiastic amateurs with no formal training in collection, processing and analysis, who can contribute “informal” information. The collaboration of such distinct groups in contributing, integrating, archiving and disseminating “geo”-data is not currently undertaken in a regular and systematic way. However, it is clear that, in order for extensive and ambitious strategies such as multi-national spatial data infrastructures to succeed, input from a range of mapping projects and data sources is required, and mechanisms for handling geospatial data of varying sources need to be developed. For example, the INSPIRE (Infrastructure for Spatial Information in Europe) initiative, which initially aimed to create a Europe-wide spatial data infrastructure (SDI) exclusively from governmental and official geospatial datasets [
1], could potentially benefit from additionally considering cheaper and more timely contributions from citizen-based sources [
2].
Such integration of informal and formal datasets must also be considered, and indeed is increasingly implemented, in other contemporary projects such as development of databases for in-car navigation systems, and rapid mapping solutions in emergency response situations. Further examples of the integration of formal and informal datasets include the use of informal volunteered geographic information (VGI) in site-engineering projects, in developing city-centre pedestrian databases [
3] and in utilities projects, notably in developing countries [
4]. As critical decision-making may rely on effective integration, it is important to consider its feasibility, notably by assessing the properties and characteristics of the varying contributing types of data, such as its quality [
5]. Variability in accuracy of location, attribute coding, time-stamp, geographic scale, and other components of data quality, can be measured and judged and the evaluation of relative geospatial data quality is an important and necessary pre-requisite to successful data integration and effective collaborative mapping.
The development of such mechanisms requires a coordinated approach to data collection, and also a valid method for data integration. This paper presents a customised tool which is intended to help users judge the viability of data integration, and thus improve the frequency and quality of multiple data source conflation for mapping and SDI database creation.
It can be difficult to effectively make such an assessment of the varying value and relevance of a range of data sourced from differing communities. There is a distinct contrast between those who capture and collate geospatial data as members of the public, contributing User Generated Content (UGC) (which is not limited to spatial data, although specifically geospatial UGC is usually called Volunteered Geographic Information, or VGI) and those state-sponsored or commercial organisations which provide official or Formal Data (FD). Differences between the resultant datasets, in terms of measurement source, quality, coverage and purpose, are evident: for example, low cost GNSS receivers and the availability of GNSS signals make it possible for the public to acquire positional information about different locations using standard mobile phone handsets and upload it to local or personal databases; whilst access to virtual reference stations (VRS) and networks of high accuracy correction facilities used as standard by national mapping agencies give significantly different results even for basic point positioning. The mapping based on volunteered efforts, personal computers and the Internet [
6] is different in many respects to traditional large-scale topographic mapping projects, long the hallmark of official governmental agencies.
The variable quality (including variation in inherent accuracy) of Volunteered Geographic Information can result from a combination of an untrained data collector, unsystematic approaches to data collection over extensive spatial extents, and low-accuracy capture technology. However, its ready availability, often at no financial cost, can make its use for supplementing, enhancing or updating Formal Data appealing: the result may be the type of collaborative mapping and geospatial database development which can be applied to the types of activities mentioned above.
Geospatial data integration involves the bringing together of discrete items and sets of data which often reveal inconsistency and incompleteness. Such data integration is not just a matter of overlaying a set of layers in a geographic information system, but also assessing how well the positional, geometric and other properties of features in one dataset can be converged with the other [
7]. In order for such convergence, and ultimate data integration to assist in the development of SDIs and other projects, both positional and geometric correspondences of datasets, amongst other properties, have to be established. It is these properties of geospatial datasets which are considered in this paper, and in particular, a comparison of their relative positional and geometric accuracies—an area of significant long-standing interest in the fields of surveying and geomatics [
8]—has been effected in a tool which can be used to summarise the integration possibilities for informal and formal datasets.
The results of the research described here include a system which can allow those who are attempting to integrate datasets to determine whether they can be completely or partially combined, or not at all. The eventual judgement of this depends on the user, but the tools provided will assist in such judgement being informed by a quantitative assessment and a visual representation of the comparison between sample geospatial datasets. The datasets consist of point, line and polygon features which are examined, using established standards for spatial data accuracy to consider point positions; buffering and overlay methods for comparing linear data; and the calculation of “moments invariant” for comparing areal objects. Further discussion considers the utility of such a system, and its contribution to collaborative mapping projects.
2. User Generated Content and Formal Data
A major example of an extensive informal geospatial data archive is the OpenStreetMap (OSM) project [
9]. Anybody can access and contribute data to the geospatial datasets in OSM without any restrictions or limitations. The OSM information, and its underlying map data, can be viewed freely, uploaded by creating a user account, and edited online through a wiki-like interface. The free accessibility of OSM data (licence, cost, sharing) and opening up of a new paradigm of “peoples’ geo-data” can be considered the main profit of this project. “Mapping parties” and systematic data collection efforts involve thousands of amateur geospatial data collectors. Many more web users are able to access current OSM data without any charge. The OSM sources allow visitors to search anywhere on a world map and download different portions remotely. However, the level of detail can vary widely, and in addition, the problem of heterogeneous data quality is evident when handling such highly variable geospatial data.
Several studies have subjected the OSM data to tests of quality, addressing issues such as completeness, topicality, and accuracy. For example, Zielstra and Zipf [
10] studied the quality of the route network in OSM data in Germany, comparing it with the commercial Tele Atlas dataset. The comparisons revealed that the positional accuracy of the road lines was sufficient to allow OSM data to be used for many routing applications, but that there was a shortcoming in the completeness of the regional OSM datasets. Haklay [
11] used similar techniques of completeness testing to conclude that a comparison of OSM data with smaller-scale OS data is favourable. Girres and Touya [
12] considered both the positional accuracy of OSM data compared to French national mapping agency data (the average displacement of point locations was 6.65 m) and the classification of features (which showed consistency for major roads, but less agreement on classification of minor routes).
These studies have tended to address the quality of VGI data at small scales (typically map scales of 1:50,000 and smaller). By contrast, Al-Bakri and Fairbairn [
13] assessed geospatial data quality at much larger scales, reporting on positional accuracy testing at scales equivalent to 1:2,500, and also considering the semantic classification accuracy of the feature coding and attribute designation of the objects in the OSM data [
14]. The geometrical accuracy testing is a fundamental component of the tool demonstrated here, and is quantitatively reported to the user on-screen. The relative matching of the informal OSM data with the formal data produced by an official topographic mapping agency, the Ordnance Survey of Great Britain (OS) is examined. Another comparison was undertaken of OSM data with official mapping agency data from the Iraqi General Directorate of Survey (GDS). In addition, further datasets have been gathered by trained surveyors using higher-order field survey (FS) to determine whether the introduction of a more rigorous data collection regime can yield positional data which matches the formal, systematic, official data, and which could be integrated with it for the purposes of collaborative mapping.
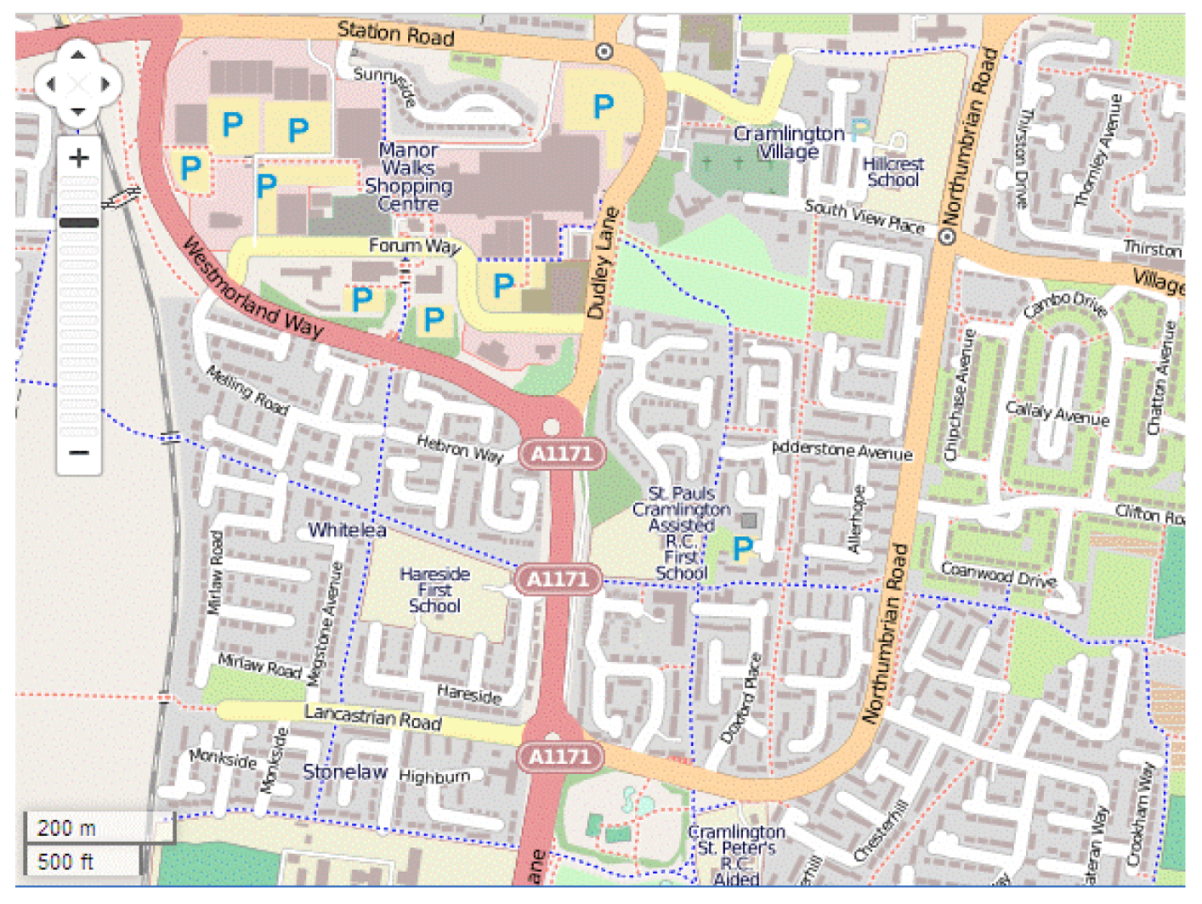
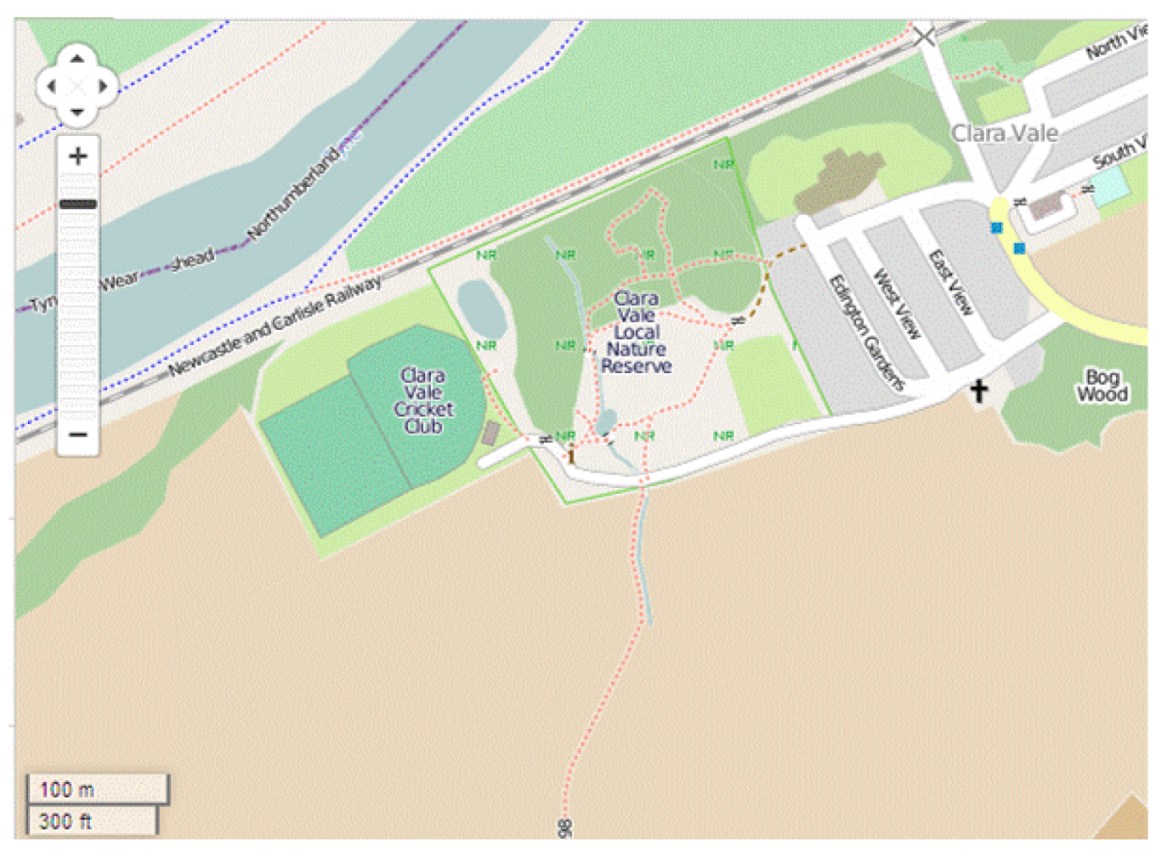
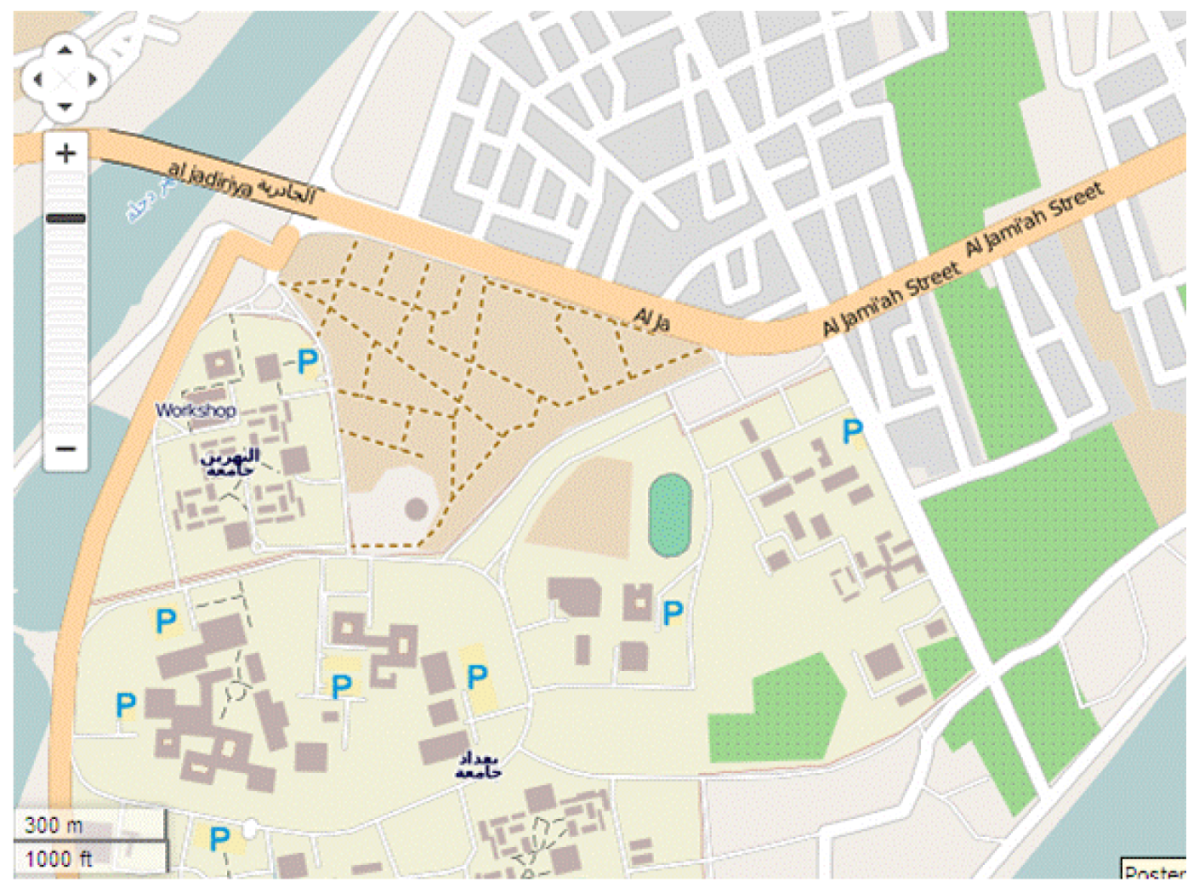
It was shown in Al-Bakri and Fairbairn [
13] that matching of OS and OSM data is more accurate in areas of cultural (anthropogenic) detail, whilst the “fuzzy” nature of some natural topographic features means that geometric discrepancies between OS and OSM data in rural areas are likely to be larger. Two OS datasets were sampled, one of an urban area where “hard” detail (buildings, kerb lines, and street furniture) predominates, another of a more rural area where “soft” detail (vegetation boundaries, water edges, terrain features) is the more common type of object. The former was situated in the town of Cramlington, UK, whilst the “soft” detail was characterised by the environment around the village of Clara Vale, UK. The Iraqi dataset selected was for an urban area, close to the centre of Baghdad, but also covering a more extensive university campus estate. For each area, the formal, accurate, traditionally-derived Ordnance Survey MasterMap data or GDS dataset was tested against the open access data from web-based VGI (
i.e., OpenStreetMap), and also against the field survey undertaken by experienced surveyors (
Figure 1,
Figure 2,
Figure 3).
Figure 1.
OpenStreetMap representation of the study area at Cramlington.
Figure 1.
OpenStreetMap representation of the study area at Cramlington.
Figure 2.
OpenStreetMap representation of the study area at Clara Vale.
Figure 2.
OpenStreetMap representation of the study area at Clara Vale.
Figure 3.
OpenStreetMap representation of the study area at Baghdad.
Figure 3.
OpenStreetMap representation of the study area at Baghdad.
The large scale MasterMap data has been created over many years of successive Ordnance Survey (OS) revision, using a mixture of control survey, photogrammetric plotting, and field and GPS survey updates. The General Directorate for Survey (GDS) dataset is sourced from photogrammetric plotting using rectified and geo-referenced air-survey imagery. By contrast, most of the OpenStreetMap (OSM) data in the UK study areas has been collected by “lower order” data collection, primarily GPS tracking, whilst for the Iraq case study it has been manually traced from Yahoo satellite imagery, not registered by accurate ground control and therefore “geo-referenced” visually. The regulation field survey (FS) was captured by establishing a reference framework using Leica and Topcon GPS receivers, then picking up detail using total stations, or GPS in RTK mode in some open areas. It is suggested that positional variability between these User Generated Content datasets and Formal Data is dependent on associated influences such as the experience of the surveyor, and the type of instrument used to capture data.
This project, therefore, addressed a range of factors including type of detail mapped (“hard”; “soft”), agency undertaking data collection (official suppliers of formal data in Great Britain and in Iraq), data collection method (field survey; handheld GPS unit; tracing from aerial imagery), and experience of the individual surveyor (professional mapper; interested citizen) expecting each factor to have some effect on the results obtained. Tests were undertaken addressing comparative positional accuracy of points (including corner points of polygons, intersections of line features, and individual point features), directional measures of discrepancies between datasets, relative variation in paths of linear features (employing buffering techniques), and a comparison of geometric properties (including moments) of polygons. In each case, standard quantitative testing methodologies have been applied such that the reporting of results, both numerically and visually, shows valid and useful summaries of relative accuracy and allows for an assessment of possible integration.
3. Evaluation of Positional Discrepancy
3.1. Statistical Methods for Error Characterization
The assessment of matching of position was undertaken by adapting established methods for spatial data accuracy measurement used by mapping agencies to establish absolute accuracy standards for map products. Such statistical methods have long been used by formal mapping agencies for characterising maps and include the National Map Accuracy Standard (NMAS) [
15], the Engineering Map Accuracy Standard (EMAS) [
16], and Accuracy Standards for Large Scale Maps [
17]. The major drawback of such standards is their reliance on measuring the errors at map scale rather than ground scale: this can be considered problematic when changing traditional mapping systems into digital formats which can be output at varying scales. More recent spatial data accuracy standards such as the National Standard for Spatial Data Accuracy (NSSDA) have enabled effective testing of digital datasets [
8,
18]. All testing methods show similarities in approach: the comparison of one dataset with a reference data source, assumed to be of a higher accuracy, the analysis of actual distances between common points in each dataset, and further tests of geometric characteristics.
Here, the comparison is between the informal OSM data and the formal governmental datasets, and also between the rigorous FS dataset and the formal data. No assumption is made as to which is the more accurate—the comparisons are undertaken to assess the discrepancies among the datasets.
The NSSDA provides a formal approach to how tested points should be identified, measured and distributed across the map. For positional accuracy testing, for example, it suggests that twenty or more test points are required, well defined, easy to measure and identifiable in each dataset. The ideal distribution of tested points is even, with at least 20% in each quadrant when the dataset covers a rectangular area. The intervals between points should be at least 10% of the diagonal distance of extent of the dataset [
19]. The NSSDA index of relative horizontal matching is stated at the 95% confidence interval, and is calculated using root mean standard error (RMSE):
where:
n: The number of check points
Er, Nr: The coordinates in one dataset
Ec, Nc: The coordinates in a compared dataset
![Ijgi 02 00349 i001]()
,
![Ijgi 02 00349 i002]()
: The direct linear distance discrepancies for the i
th checked point
The NSSDA measure of accuracy can be computed for two cases:
If RMSEE = RMSEN then the overall dataset-to-dataset discrepancy = 1.7308 RMSE
If
RMSEE ≠
RMSEN then it equals = 2.4477 × 0.5 × (
RMSEE +
RMSEN) [
20].
Tests were undertaken using the NSSDA methodology to examine the relative positional discrepancies of locations in the UK case study areas, for the formal and informal datasets, in the “hard” detail areas, and in the “soft” detail areas, with a further comparison for the Iraqi datasets among those captured from remote sensing imagery (informal), from field survey, and from formal topographic data captured by GDS. The distribution and number of the tested points matched the NSSDA approach and the results indicated the magnitude and direction of positional discrepancies (all in meters).
Table 1 shows some initial results of the testing undertaken, indicating that the discrepancy between the OpenStreetMap, informal data (OSM) and the formal, Ordnance Survey (OS) dataset is relatively large. This mismatch is higher than the limits for standard accuracy measures of data used by the Ordnance Survey (RMSE of position 1.0 m for urban areas, 2.5 m for rural areas), indicating that the OSM data cannot meet the threshold of relative accuracy to allow it to be integrated successfully with the OS data. The check field surveys (FS) were more closely aligned to the OS data, than to the OSM dataset.
Table 1.
Comparisons of Root Mean Standard Error (RMSE) and National Standard for Spatial Data Accuracy (NSSDA) positional discrepancies for compared datasets.
Table 1.
Comparisons of Root Mean Standard Error (RMSE) and National Standard for Spatial Data Accuracy (NSSDA) positional discrepancies for compared datasets.
| | RMSE (m) | NSSDA Accuracy (m) |
|---|
Urban area,
UK | FS/OS | 0.492 | 0.846 |
| FS/OSM | 5.429 | 9.143 |
| OS/OSM | 5.331 | 8.989 |
Rural area,
UK | FS/OS | 1.843 | 3.190 |
| FS/OSM | 11.650 | 20.162 |
| OS/OSM | 10.887 | 18.832 |
Baghdad,
Iraq | FS/GDS | 1.246 | 2.149 |
| FS/OSM | 5.903 | 10.190 |
| GDS/OSM | 5.806 | 10.012 |
The matching of datasets is closer in the urban areas (including in Baghdad), where features can be more precisely distinguished, but the range of discrepancies between the compared datasets is still too large to suggest that integrating such varying geospatial datasets may be possible.
3.2. Assessing Directional Variability of Discrepancies
Further descriptive statistics were applied to determine whether there was any directional bias in the discrepancies, by separating the easting and northing values for each coordinate. Initial results showed that, for each comparison (
Table 2), the eastings variability was larger than the northings. However,
Figure 4 shows graphically that the plotted mismatches reveal an isotropic and non-systematic nature.
Circular statistics, a type of directional statistics where the single response is angular or directional, but not scalar, were used to confirm and quantify the direction of positional discrepancies. Such an approach is encountered in a number of disciplines including computer science [
21], geosciences [
22], geology [
23], agricultural sciences [
24], geography [
25], and environmental science [
26]. Fisher [
27] and Jammalamadaka and Sengupta [
28] provide useful descriptions of the development of directional statistics and how to calculate them by employing vector addition. For a resultant vector which sums the unit vectors of each discrepancy, its “mean directional angle”,
![Ijgi 02 00349 i003]()
, and the length of combined vectors (resultant),
![Ijgi 02 00349 i004]()
, can be computed, the latter being a scaled measure of isotropy (zero) or anisotropy (one): “circular variance”,
V, is its complement. The initial exploration of the datasets involved these summary statistics and revealed (
Table 3) that the discrepancies between formal and informal data in the rural area were slightly more uniform in terms of direction than for the urban zones, but in each case the variance was high enough to conclude that there was no systematic explanation for the differences.
Table 2.
Summary of positional discrepancies statistics of compared datasets.
Table 2.
Summary of positional discrepancies statistics of compared datasets.
| | | Mean (m) | Standard Deviation (m) |
|---|
Urban area,
UK | FS/OS-Easting | 0.191 | 0.341 |
| FS/OS-Northing | 0.075 | 0.301 |
| FS/OSM-Easting | 1.433 | 4.464 |
| FS/OSM-Northing | 0.068 | 2.894 |
| OS/OSM-Easting | 1.242 | 4.417 |
| OS/OSM-Northing | 0.143 | 2.865 |
Rural area,
UK | FS/OS-Easting | 0.709 | 1.154 |
| FS/OS-Northing | 0.259 | 1.282 |
| FS/OSM-Easting | 3.600 | 7.720 |
| FS/OSM-Northing | 1.870 | 8.110 |
| OS/OSM-Easting | 2.900 | 7.590 |
| OS/OSM-Northing | 1.610 | 7.450 |
Baghdad,
Iraq | FS/GDS-Easting | 0.277 | 0.766 |
| FS/GDS-Northing | 0.137 | 0.957 |
| FS/OSM-Easting | 1.972 | 4.066 |
| FS/OSM-Northing | 0.354 | 3.910 |
| GDS/OSM-Easting | 1.695 | 4.167 |
| GDS/OSM-Northing | 0.217 | 3.797 |
Figure 4.
Magnitude and direction of mismatches between Ordnance Survey (OS) and OpenStreetMap (OSM) data, Cramlington, UK.
Figure 4.
Magnitude and direction of mismatches between Ordnance Survey (OS) and OpenStreetMap (OSM) data, Cramlington, UK.
Table 3.
Circular statistics for comparisons of geospatial datasets.
Table 3.
Circular statistics for comparisons of geospatial datasets.
| | Mean Direction of Positional Discrepancy ( ![Ijgi 02 00349 i003]() ) ) | Mean ResultantLength ( ![Ijgi 02 00349 i004]() ) ) | Circular Var. (V) |
|---|
Urban area,
UK | OS/OSM | 313.743° | 0.133 | 0.867 |
Rural area,
UK | OS/OSM | 43.395° | 0.277 | 0.723 |
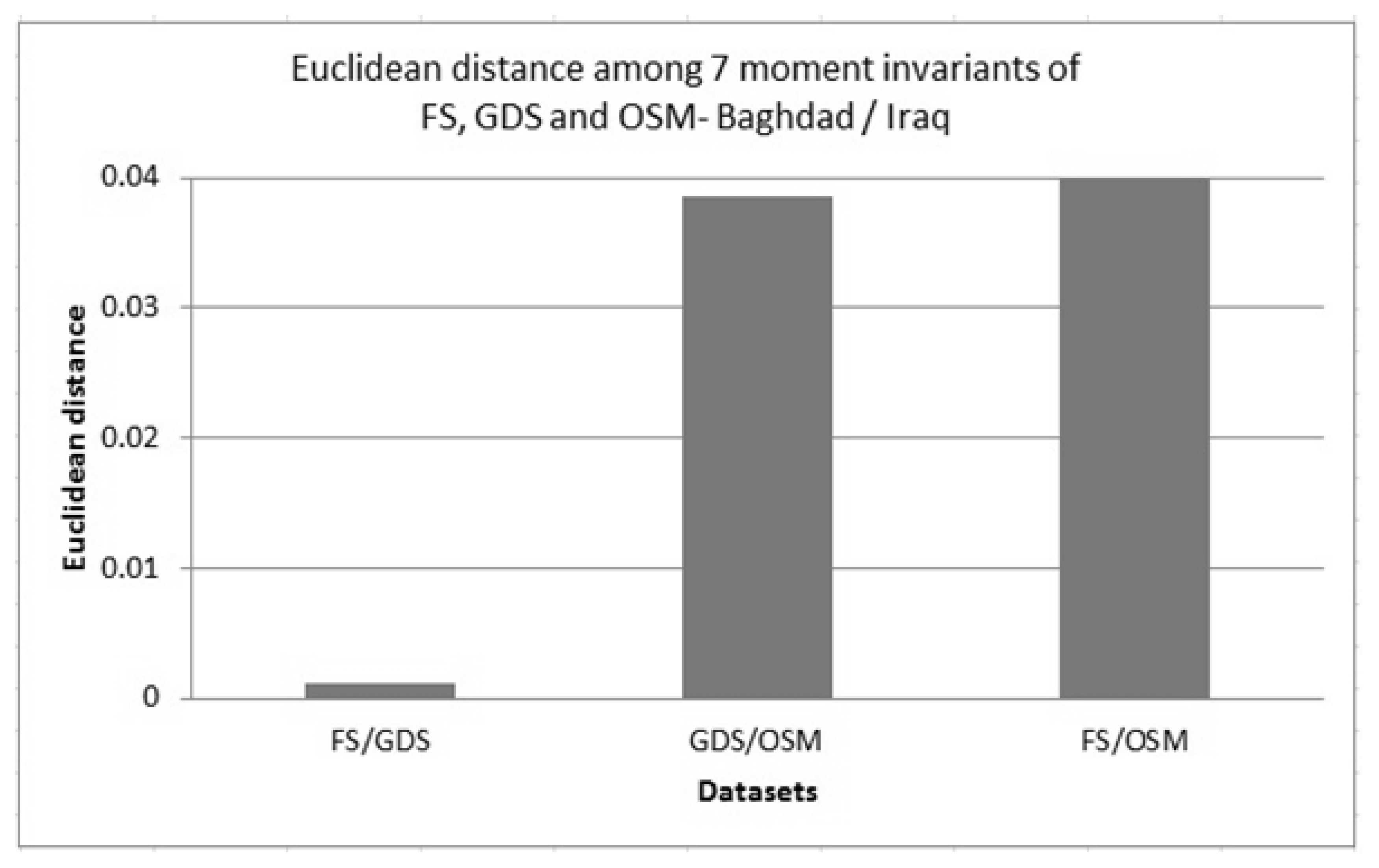
Baghdad,
Iraq | GDS/OSM | 282.595° | 0.236 | 0.764 |
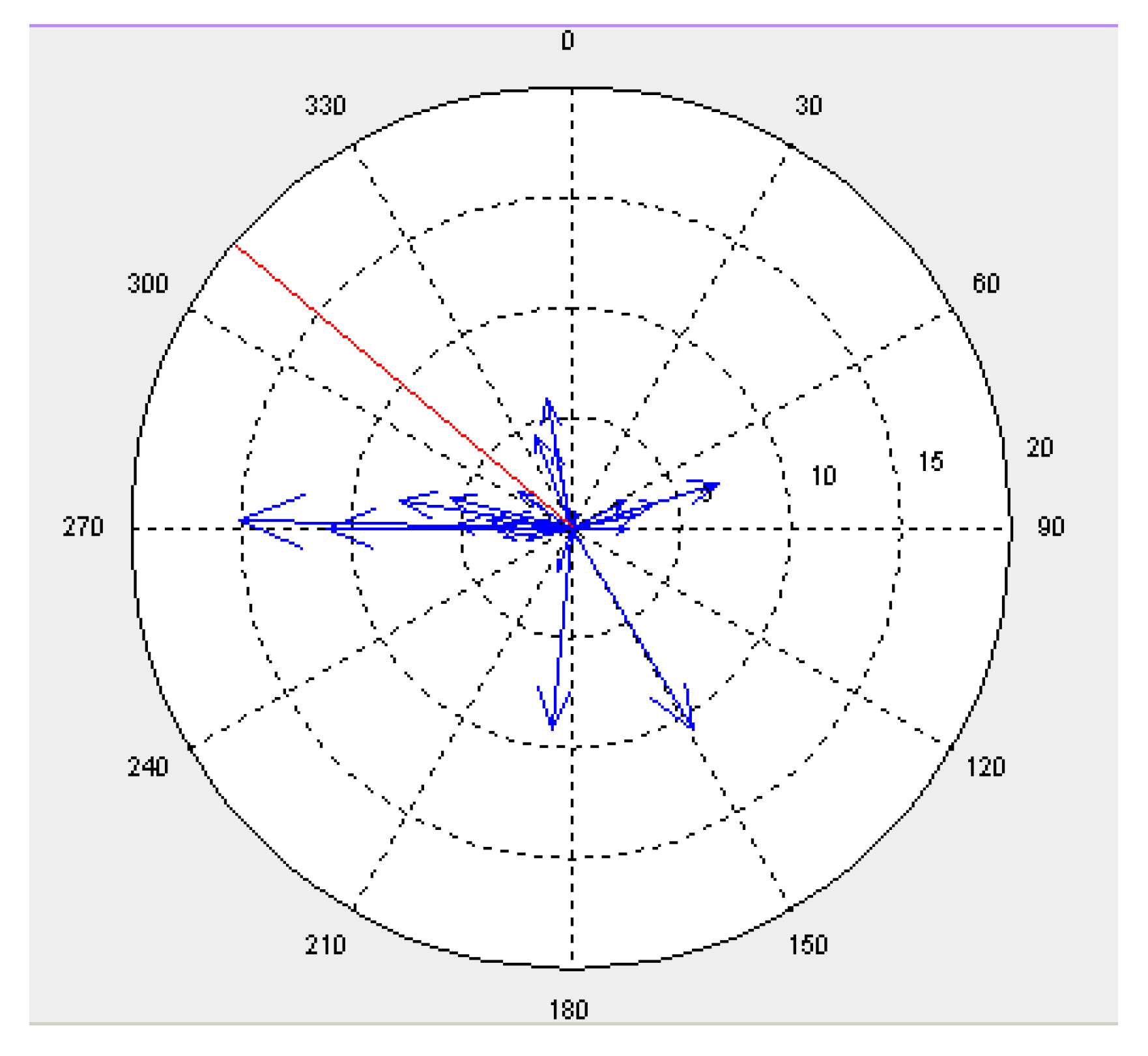
For visual analysis, a circular data distribution of the discrepancies was displayed as a vector diagram plot arrow data plot, providing information on significant characteristics of the data, such as the size and direction of positional differences between sampled points in two different datasets and the mean direction of the discrepancies (
Figure 5). A circular histogram could also be used to summarise the number of discrepancies observed in each direction. Visual inspection confirmed the isotropic distribution, with both the magnitude and the direction of mismatches unpredictable. The variability of the directional divergences is less apparent than the positional discrepancies between formal and informal (OSM) data, which can be summarised as being higher than standard thresholds leading to a conclusion that integrating such datasets at large geospatial scales would be ill-advised.
Figure 5.
Example of vector diagram plotting of each discrepancy by size (blue) and mean direction (red) (concentric circles are at 5 m interval).
Figure 5.
Example of vector diagram plotting of each discrepancy by size (blue) and mean direction (red) (concentric circles are at 5 m interval).
4. Measuring Linear Geometric Accuracy
When topographic line features such as complex rivers and boundaries, or even simple roads or railways, are considered, comparison using point accuracy may be insufficient to capture the spatial complexity and variability of the dataset objects. Point measures may be straightforward to understand and calculate, but they cannot capture all aspects of linear matching. Thus, in addition to considering positional discrepancies of points along the compared lines, linear matching procedures can be usefully examined to assist in developing an integration assessment tool, using techniques of determining shape or curvature similarity between two compared lines. Buffering methods, and assessment of buffer overlay, have been popular techniques [
29,
30]. Buffers of variable size can be constructed around lines in each dataset (e.g., line X buffer XB, line Q buffer QB), within which statistical calculations can be carried out. The following measurements are taken:
These measures can be used to give the deviation of a line in one dataset from the line of another, or to compare two lines together. The average displacement between the two lines, for example, can be calculated as:
where: 2
bsi: The total buffering width that has been generated around the centre of the line.
Iteratively increasing the buffer size will yield differing results when measuring displacement of lines or overlap of buffer areas, but these will stabilise at some appropriate buffer size. Once again, the OS, GDS, FS and OSM datasets were examined, with a comparison carried out primarily for some road centre-lines in the urban Cramlington, UK and Baghdad, Iraq study areas. Buffer sizes have been incremented from 0.5 m to 12.5 m, in 0.5 m intervals for comparisons involving informal OSM data.
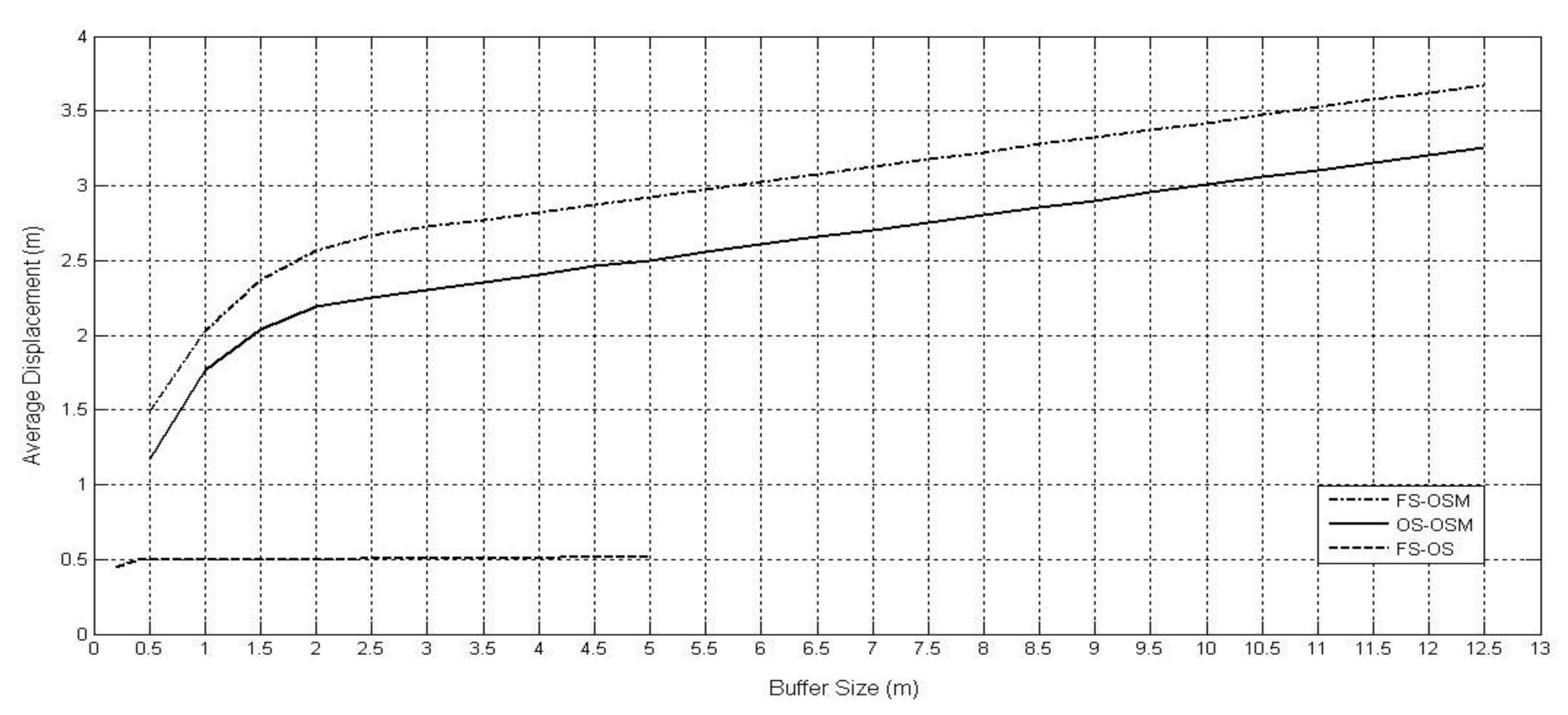
Graphs reveal that the average displacement of comparative pairs of lines reaches a sill as buffer size increases. The significant differences between the OSM data and the formal dataset in the same area are considerably larger than any comparison of the more rigorous field survey (FS) with formal data: the average displacement for the comparison of OS- OSM (solid line in
Figure 6, Cramlington) is approaching 3.5 m when the buffer size is 12.5 m.
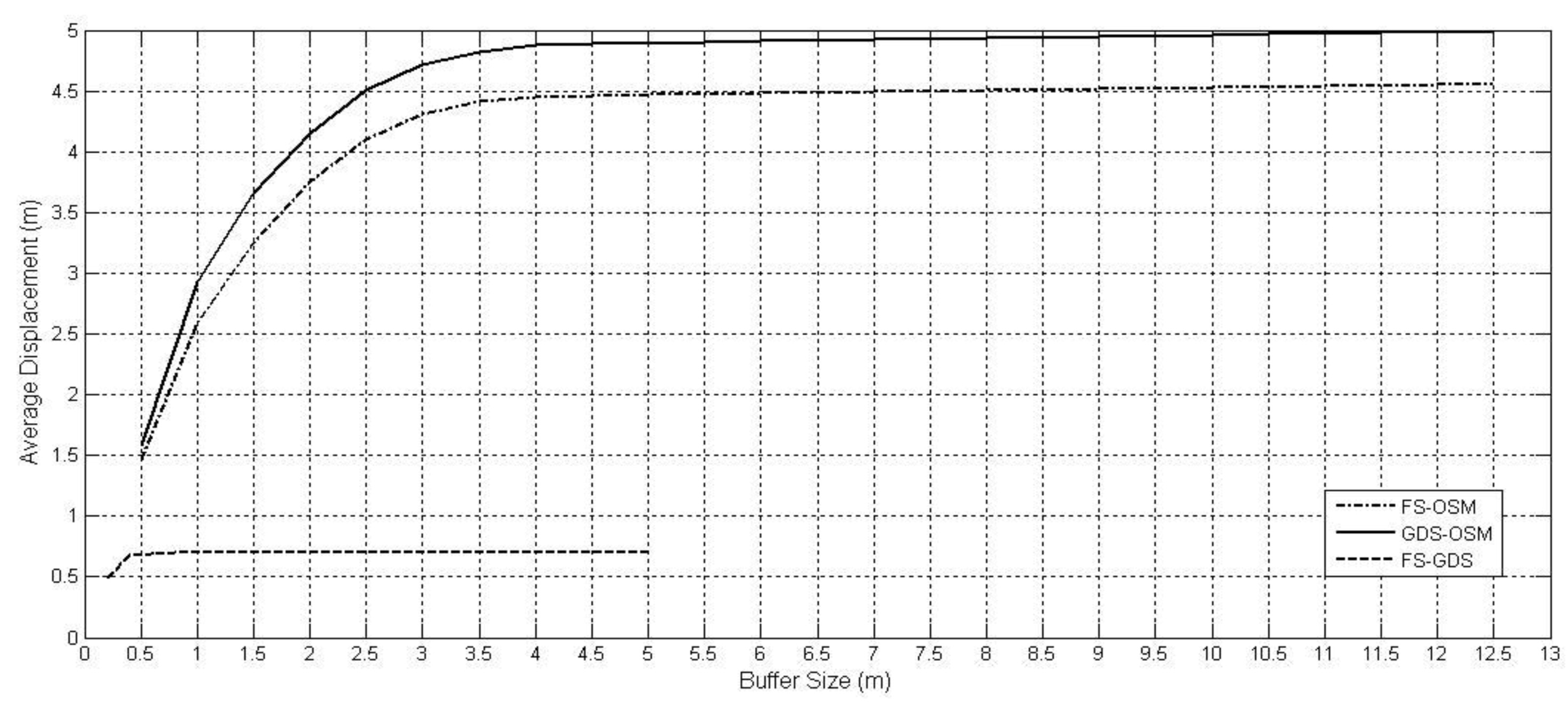
Figure 7 (Baghdad) similarly shows that the FS data is very close to GDS datasets (average displacement about 0.7m for buffer size of 0.5 m beyond which the graph remains constant) but comparing the OSM data to GDS shows a displacement of about 5 m for a buffer size of 5 m.
It is possible to also interpret the slope of the graphs, with steeper gradients indicating greater variability and confirming the lower levels of matching. Further investigation of displacement information can be undertaken with reference to the buffer measures already taken. For example, the areas outside the buffers of line features in one dataset can be compared to the areas inside the buffers of the second dataset. The characteristic curve for such graphs is downward towards the x-axis.
The conclusion with reference to the linear data is similar to that obtained from the point position comparison. The path of major line features in the OSM dataset can diverge significantly from the official dataset. Although the displacement statistics and the overlap percentages might favour the possible integration of the formal data with the informal, but rigorously collected field survey data, they would caution against integration of the OSM data with the formal data.
Figure 6.
Average displacement information of roads in an urban area, UK.
Figure 6.
Average displacement information of roads in an urban area, UK.
Figure 7.
Average displacement information of roads in Baghdad, Iraq.
Figure 7.
Average displacement information of roads in Baghdad, Iraq.
5. Area Shape Similarity
5.1. Moments Invariant
Shape analysis is the final approach introduced here for assessing geometric form similarity. Methods of shape analysis play an important role in image processing systems for shape comparison, matching, and recognition. The use of shape analysis can give a further indication of the errors in geospatial datasets, again by comparing datasets sourced from VGI and those sourced from formal, official sources. Metrics which characterise the planar shape of polygon features within a dataset include compactness, convexity and dispersion, and derivatives, such as the Hausdorff distance, used when comparing polygons.
In this study, use is made of “moments invariant”, unit-free metrics which characterise a range of shape properties, invariant to changes in size, rotation or location of the shape, which thus give an opportunity to compare corresponding area features within geospatial datasets. Initially developed by Hu [
31] and relying on calculations using the array of regular pixels completely occupying a shape (
i.e., raster computation), further development by Chen [
32] has shown that moments invariant can be calculated using the coordinates of the boundary line of an area or polygon feature, structured in a vector format.
A basic one dimensional “moment” of order
(p + q) over a general line, such as a closed boundary line, is defined by the equation:
For
p,
q = 0,1,2,3,...
where:
![Ijgi 02 00349 i005]()
is a line integral along a curve C.
The “central moment” can be defined as:
where:
![Ijgi 02 00349 i006]()
, and
![Ijgi 02 00349 i007]()
, x
0, y
0 being the coordinates of the polygon centroid.
The integral must be evaluated along the outer-edge of the object. The central moment, characterising the centre of gravity of the shape, is invariant to translation, and when normalised is also invariant to change of scales. Thus Chen’s scale-normalised central moments are given by:
where:
a = p + q + 1, for p + q= 2, 3, 4,...
From these normalised central moments, a set of seven compound spatial moments is developed. These unit-less metrics are calculated as follows:
An interpretation of these moments has been attempted by Noh and Rhee [
33]: for example, they suggest that moment 2 (Ω
2) reflects the covariance value of vertical and horizontal axes when the variance intensity of vertical axis and horizontal axis are similar, whilst moments 5, 6 and 7 (Ω
5, Ω
6, Ω
7) are values reflecting properties of shapes which are invariant against size, rotation and location respectively. For this study, moments invariant have been calculated for comparative shapes in each of the datasets investigated.
5.2. Using Moments Invariant Computations
Each of the seven moments calculated has value in describing some characteristic of the shapes considered, and therefore a method was sought to combine the moments invariant into one summary measurement. This was done by plotting, for each equivalent feature considered, the values for each of its moments (in this case, moments Ω
i,
i = 1, 2, 3,…,7) in a seven-dimensional space. Each polygon to be compared occupies one position in that space, summarising its moments’ values, and the alignment of positions of corresponding features gives an indication of the match between such polygon features. Closely comparable area symbols will exhibit small inter-moments Euclidian distance in seven-dimensional space, whilst those polygons which do not match well will reveal a much larger distance. The actual distance adopted, therefore, as a metric for matching is defined as:
where:
ds: a descriptor value showing difference (zero if (
![Ijgi 02 00349 i008]()
) and (
![Ijgi 02 00349 i009]()
) are identical in all areal respects); the magnitude of
ds will give a reasonable measure of differences between shapes;
M and N: the same feature in two separate datasets;
![Ijgi 02 00349 i008]()
and
![Ijgi 02 00349 i009]()
: the sets of moments invariant for the features in each dataset [
34].
The E, N coordinates of outlines of each polygon in the UK urban and rural datasets, and the Iraqi dataset were used to calculate moments invariant values. Each dataset covers a different area, but the polygon features within each area do exhibit some uniformity: block houses in the UK urban area, irregular natural area features in the UK rural area, large institutional block buildings in the Iraqi example. The resultant moments values calculated for individual polygon features in each dataset showed similarity, with the simpler, more regular polygon shapes for the urban datasets differing significantly from the moments invariant calculated for the irregular, complex shapes characterised in the rural areas (
Table 4). The averaging of the moments invariant values of all polygons in each dataset was felt to be justified, therefore, and a single characterising moments value was obtained for each moment invariant, one to seven. These were plotted as indicated above and a single descriptor value was derived to indicate “distance” between two complete datasets.
Figure 8 shows an example of the plotted results of such “distances”. The magnitude of the differences between the informal OSM datasets and formal GDS datasets is clear: once again there appears to be a significant mismatch between OpenStreetMap data and the official government dataset.
Table 4.
Examples of moments invariant calculations from one polygon feature in each dataset.
Table 4.
Examples of moments invariant calculations from one polygon feature in each dataset.
| | | Formal Data | OpenStreetMap | Field Survey |
|---|
| Urban area, UK | Moments 1 to 7 | 1.890 | 1.569 | 1.851 |
| 0.730 | 0.336 | 0.677 |
| 0.268 | 0.061 | 0.233 |
| 0.822 | 0.334 | 0.750 |
| 0.189 | 0.022 | 0.154 |
| 0.493 | 0.132 | 0.433 |
| 7.437e−008 | 7.109e−007 | 1.831e−008 |
| Rural area, UK | Moments 1 to 7 | 75,443.993 | 48,225,499,296.0 | 20,495.184 |
| 1,073,970,995.775 | 9.070e+020 | 58,999,866.027 |
| 19,370,141,980,978.6 | 2.095e+031 | 230,717,651,378.386 |
| 19,370,660,096,412.9 | 2.095e+031 | 230,747,917,719.997 |
| 1.610e+026 | 3.445e+062 | 2.418e+022 |
| 3.801e+017 | 5.190e+041 | 1.028e+015 |
| −8,238,135,246,848 | 3.714e+027 | −1,834,908,876,800 |
| Baghdad, Iraq | Moments 1 to 7 | 1.384 | 1.360 | 1.385 |
| 0.155 | 0.134 | 0.155 |
| 0.008 | 0.004 | 0.008 |
| 0.151 | 0.131 | 0.151 |
| 0.002 | 0.001 | 0.002 |
| 0.035 | 0.027 | 0.035 |
| 1.337e−006 | −1.796e−006 | 7.211e−006 |
Figure 8.
An example of the comparison of Euclidean distance of 7 moment invariants for three datasets (field survey (FS), General Directorate for Survey (GDS) and OSM) in Baghdad, Iraq.
Figure 8.
An example of the comparison of Euclidean distance of 7 moment invariants for three datasets (field survey (FS), General Directorate for Survey (GDS) and OSM) in Baghdad, Iraq.
6. A Tool for Assessing Geospatial Dataset Matching
The measures of matching of datasets detailed above were incorporated into a visual tool which can be used to assist in judging the potential for data integration. The intention was to create a user-friendly interface incorporating quantitative and visual analysis of dataset comparison that could be used to assess geometrical similarity of tested datasets. The processing steps in point, line and area matching were developed in the MATLAB software package, and a graphical user interface (GUI) was created also to report on the results of calculations and visualization of the comparisons [
35]. With this user-controlled interface, data can be input as text-based files of planimetric coordinates from the datasets, computations are applied using the formulae and methodology indicated above, and the graphical representation of the input data and the analysis can also be exported in a report. Each dataset, formal (FM), official data (consisting of OS and GDS data), rigorously collected field survey data (FS), and the informal OpenStreetMap (OSM) data, has been examined using this interface, examples of which are shown below. Point, linear and areal comparisons are made for each combination of datasets, although the most important is the direct comparison of the formal and the informal data.
Although these user-friendly interfaces are shown to be effective in reporting the input, computation, mapping and output of data, there is no specific decision-making function attached to the system. No thresholds of acceptability are presented to guide the user, as it is felt that considered judgment should be the main determinant of whether integration of data should be recommended. The major factor, in any data integration exercise, is, of course, the eventual application of any combined dataset. As has been indicated at the start of this paper, the range of potential application areas for the integration of formal and informal data is enormous, and each will make demands on the datasets used in their execution. What is appropriate for one task may not be so for another. This is particularly true of a core characteristic of a geospatial dataset, its scale. The focus of this work has been on large scale data and it is suggested here that significant attention be paid to this aspect before any dataset integration is considered.
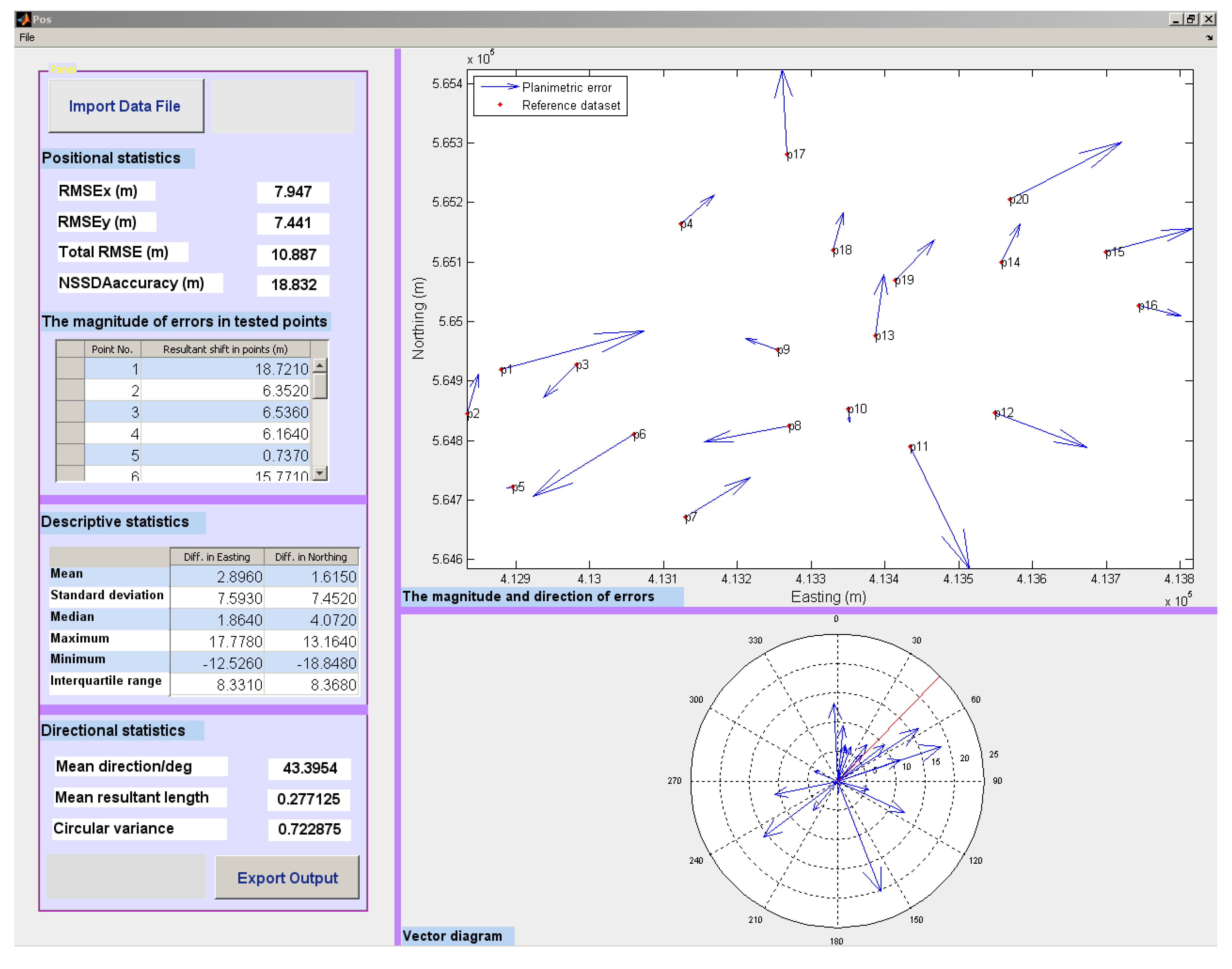
Figure 9 shows an example MATLAB GUI reporting the comparison between the point positions, in the formal Ordnance Survey data (here taken as the “reference data”), compared to the OpenStreetMap data for the rural study area, in Clara Vale, UK. The positional, descriptive and directional statistics are reported numerically, along with graphical rendering of the magnitude of discrepancies, plotted on a scaled map and a summary vector diagram.
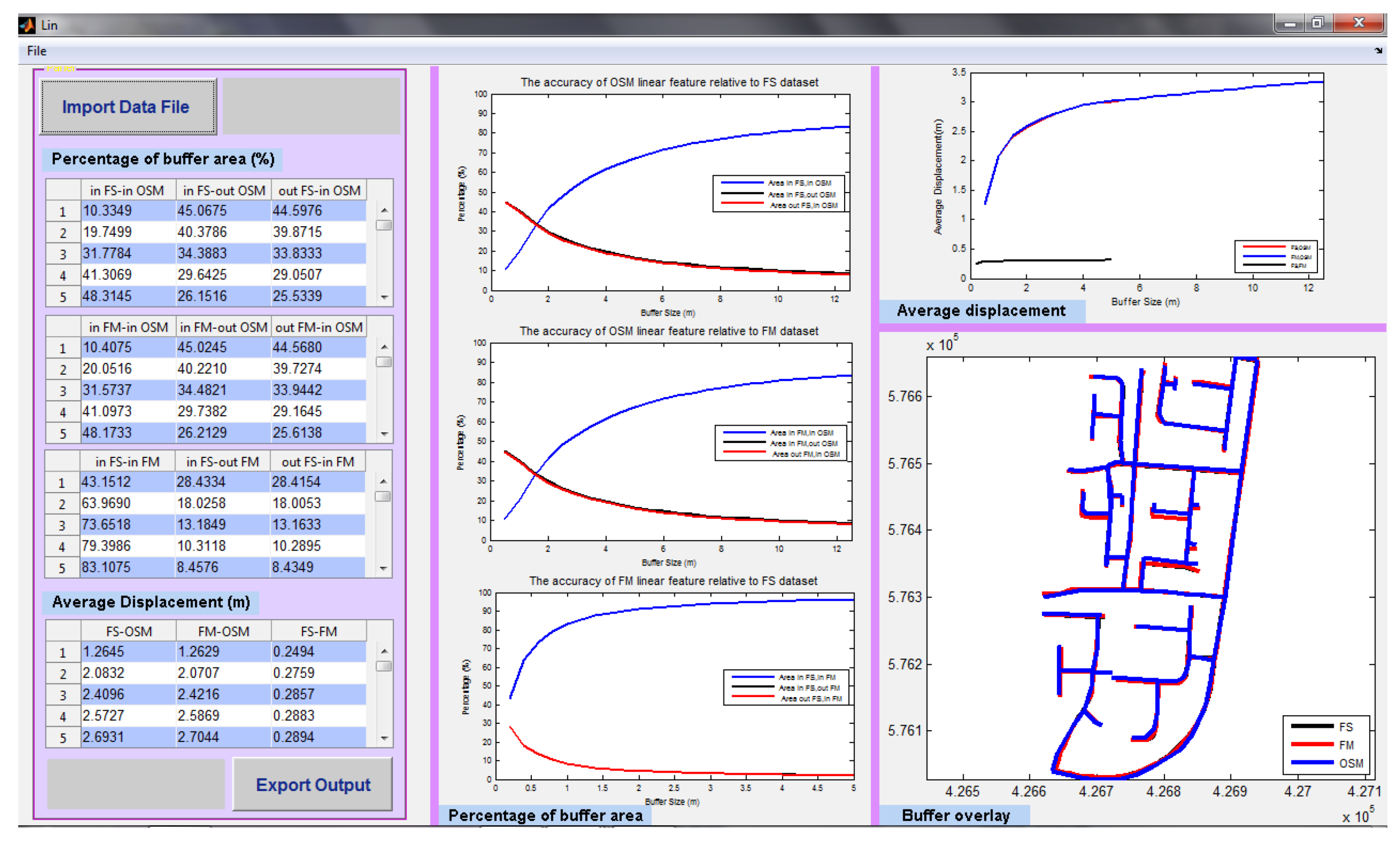
Similarly,
Figure 10 shows the GUI which was designed for assessing linear matching, in this case comparing the formal data (FM), with the rigorous field survey (FS), and the informal OSM data, in the urban study area (Cramlington, UK). Here, calculations of the percentage buffer overlap are presented in numerical and graphical form, along with an overlay of the linear features (in this case, road centre-lines). The calculated average displacement graph shows all three datasets simultaneously, whilst the linear features are accurately mapped in the final window in this interface.
Figure 9.
The positional similarity measurement results for the comparison of OS-OSM datasets in Clara Vale-UK.
Figure 9.
The positional similarity measurement results for the comparison of OS-OSM datasets in Clara Vale-UK.
Figure 10.
The linear similarity measurement results for the comparison of FS, OS—noted as FM, formal data, and OSM in Cramlington, UK.
Figure 10.
The linear similarity measurement results for the comparison of FS, OS—noted as FM, formal data, and OSM in Cramlington, UK.
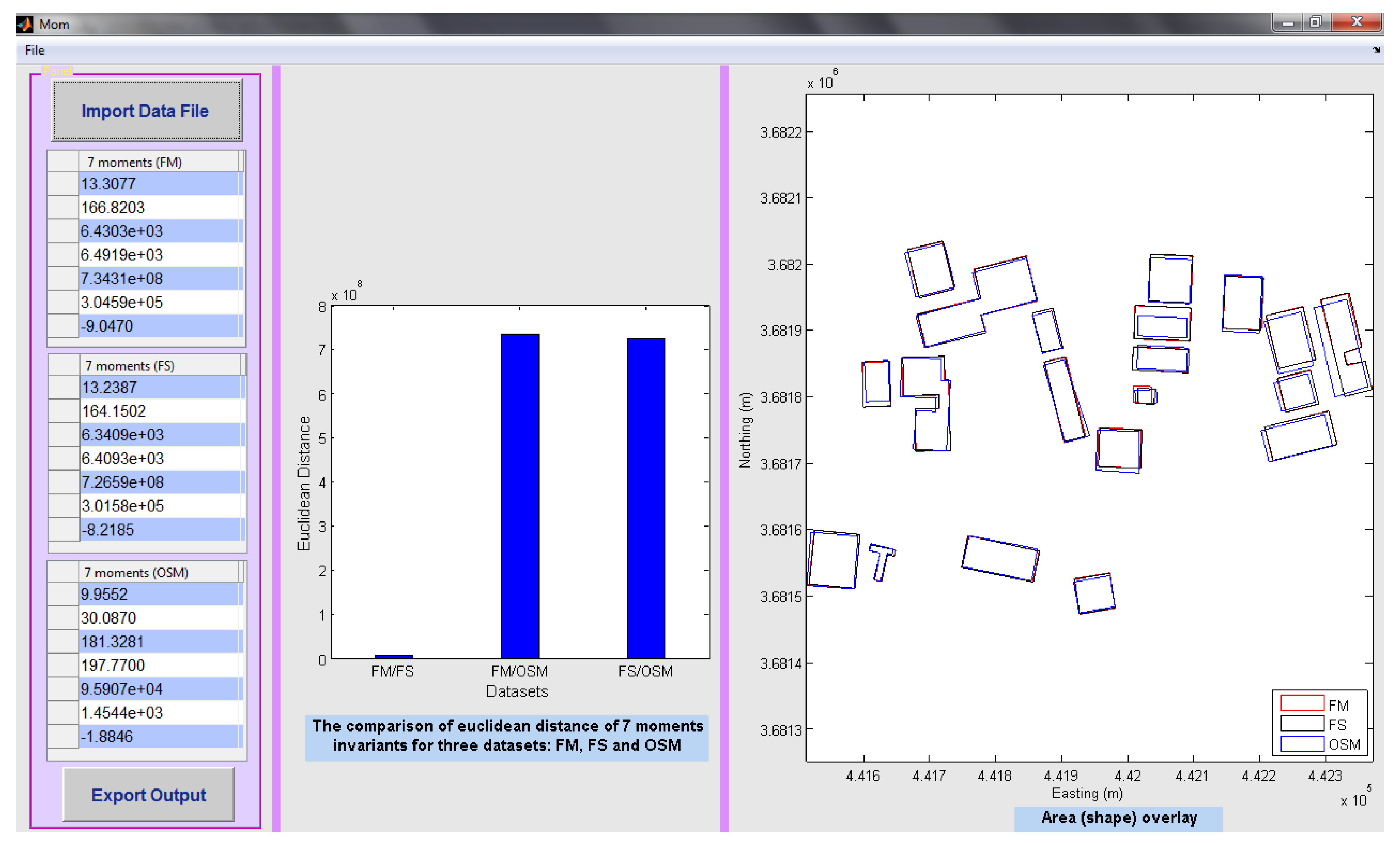
Finally,
Figure 11 demonstrates the polygon-based interface, summarizing the moments calculations, and again providing a mapped overlay, for visual judgment of discrepancies. Here, the seven moments invariant are calculated for each dataset: FM, the formal data, is part of the GDS dataset for metropolitan Baghdad, Iraq, whilst the field survey (FS) and OSM data are compared alongside. The overall position of the summary moments value for each dataset is plotted in seven-dimensional space, and the bar chart in the GUI shows the distance from one dataset to another. The simple datasets considered here are shown in map form, also.
Figure 11.
The interface of the output results of area shape similarity measurement for three datasets (FS, GDS—noted as FM, formal data, and OSM) in Baghdad, Iraq.
Figure 11.
The interface of the output results of area shape similarity measurement for three datasets (FS, GDS—noted as FM, formal data, and OSM) in Baghdad, Iraq.
7. Conclusion and Discussion
A methodology and system has been developed to derive measures for assessing shape and positional quality among datasets for integration purposes. Different methods have been used for obtaining valuable descriptions of geometric matching (based on positional accuracy and shape fidelity). The NSSDA has been chosen to select and analyse tested points, then calculate the RMSE values, yielding comparative measures of positional discrepancy. For error direction analysis, circular statistics have been adopted. Linear geometric similarity has been tested by establishing buffers around the lines in the relevant datasets, with analysis of the relative uniformity of such buffer zones (union, intersection, etc.). Shape metrics, including moments invariant, have been applied to evaluate polygon matching.
The results of this analysis show that comparing official datasets (the OS and GDS data) with rigorous FS datasets gives good matching, especially for areas of “hard” detail. However, the positional and shape measurements of the informal OSM data do not match the formal data in any of the case study areas examined. The conclusion is that, when examined from a geometrical matching perspective, there would be significant problems in trying to integrate the OSM data with official data, at the large scales considered here. The major intention of this paper has not been to assess the accuracy of OSM against a perceived “truth”, rather to undertake some comparison. The measured discrepancies which have resulted from the work described here clearly militate against integration. A major reason for the discrepancies noted is obviously the varying data collection procedures: the VGI presented in the OSM dataset can be sourced from GPS devices of significantly varying precision, from satellite images or aerial photographs, or simply from local knowledge. The “source” tag attached to each feature in the OSM dataset is commonly used to specify the origin of the data [
36]. This can be used to gain a preliminary view of the accuracy of the geometry: an OSM feature, tagged with source “landsat”, will usually be less accurately captured than one obtained by “GPS tracking”. Even for those features captured in the field using GPS, the majority have been sampled using low-accuracy GPS receivers such as Garmin, Holux GPSlim236 and iPhone GPS. Occasionally, features in OSM will be averaged by eye from many GPS positions and tracks recorded by several individuals over time, and often detail is inferred rather than actually measured, due to access problems or lack of experience in field survey. For those OSM features digitized from Yahoo aerial or satellite imagery (the standard data source for those contributors remote from the mapped area), lack of familiarity may further degrade quality. The recognition of features such as one way streets or dual carriageways can be difficult from small-scale imagery. A local contributor is likely to have better knowledge about an area of interest, as well as having access to the locality, but much OSM data is remotely mapped (for example, some of the OSM data in Baghdad has been created by an OSM contributor living in UK). In addition to local knowledge, it may be that further independent datasets and expert opinion can assist in enhancing the OSM dataset’s quality: the addition of a field survey dataset in the studies reported in this paper could be equated to an extra moderating input into the comparison process. Comber
et al. [
37] have shown how such expert knowledge can enhance the accuracy of VGI data captured for land use survey. There are further personal attributes, such as experience and abilities of the VGI collector, which will affect the OSM dataset’s integrity and value.
The nature of the feature type is also a determinant of the observed discrepancies. Al-Bakri and Fairbairn [
13] have shown that rural and natural VGI data (soft detail) has a lower positional accuracy and completeness compared to the “hard”, built environment, data collected in urban sites. Integrating formal and informal datasets in urban areas could therefore be done with greater confidence than in rural locations.
The measurement of accuracy of geospatial datasets and the assessment of possible integration goes beyond positional and geometric issues. The meaning of symbols and the categorisation of objects in the real world are addressed by the semantic data added to, or derived from, the measured coordinated dataset. A further study of the semantics of each dataset has been undertaken [
14], and a measure of “closeness” of attribute information was attempted, measuring the semantic similarity of XML schema elements in order to additionally assess the possibilities of data integration from a range of “crowdsourced” and official sources. The measurement of semantic similarity between OSM and official datasets in this study yielded mismatching similar to the tests on geometric properties. Further extensions to this methodology could address temporal accuracy, completeness and lineage, all comparable characteristics.
It should also be recognised that VGI can consist not only of measured data from the field or from remotely-sensed imagery, but also user created photographs (e.g., Flickr), textual descriptions and user updating of geospatial datasets (e.g., TomTom MapShare, Google MapMaker): these can also contribute to “crowdsourced” UGC and their accuracy can be examined using techniques outlined here.
As the potential use of VGI is given increasing prominence, and “crowdsourced” data is presented as both an initial dataset, for example in areas where large-scale mapping does not exist (such as in remote areas hit by disasters), and as a contributor to integrated spatial data infrastructures (including updating of official datasets), it is important to urge caution. A valid implication of this study is that OSM data could be described as being of lower accuracy that the formal datasets. The positional and geometric accuracy of VGI can, therefore, give cause for concern: its presentation as a panacea for the improvement of out-dated, large-scale, official datasets should be viewed with scepticism in most cases, and with rejection in many. In some of the applications suggested at the start of this paper, including in-car navigation systems, on site-engineering and utilities projects, and any systems based on accurate land-parcel delineation, it is probably better to have no mapping at all, rather than some inaccurate, possibly incomplete, user generated content. Although the involvement of local communities and enthusiastic individuals and projects in extending the range of geospatial datasets is to be welcome, it is clear that such involvement must be considered as part of a wider and systematic programme of mapping activity, exhibiting consistency, care and checking.
The MATLAB GUI code which was developed to produce the interface used in undertaking the assessment is presented in Al-Bakri [
38].
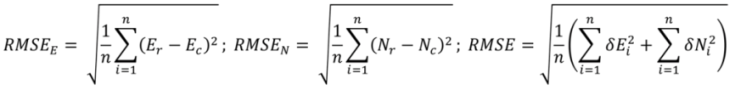
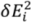 ,
, 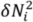 : The direct linear distance discrepancies for the ith checked point
: The direct linear distance discrepancies for the ith checked point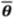 , and the length of combined vectors (resultant),
, and the length of combined vectors (resultant), 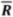 , can be computed, the latter being a scaled measure of isotropy (zero) or anisotropy (one): “circular variance”, V, is its complement. The initial exploration of the datasets involved these summary statistics and revealed (Table 3) that the discrepancies between formal and informal data in the rural area were slightly more uniform in terms of direction than for the urban zones, but in each case the variance was high enough to conclude that there was no systematic explanation for the differences.
, can be computed, the latter being a scaled measure of isotropy (zero) or anisotropy (one): “circular variance”, V, is its complement. The initial exploration of the datasets involved these summary statistics and revealed (Table 3) that the discrepancies between formal and informal data in the rural area were slightly more uniform in terms of direction than for the urban zones, but in each case the variance was high enough to conclude that there was no systematic explanation for the differences.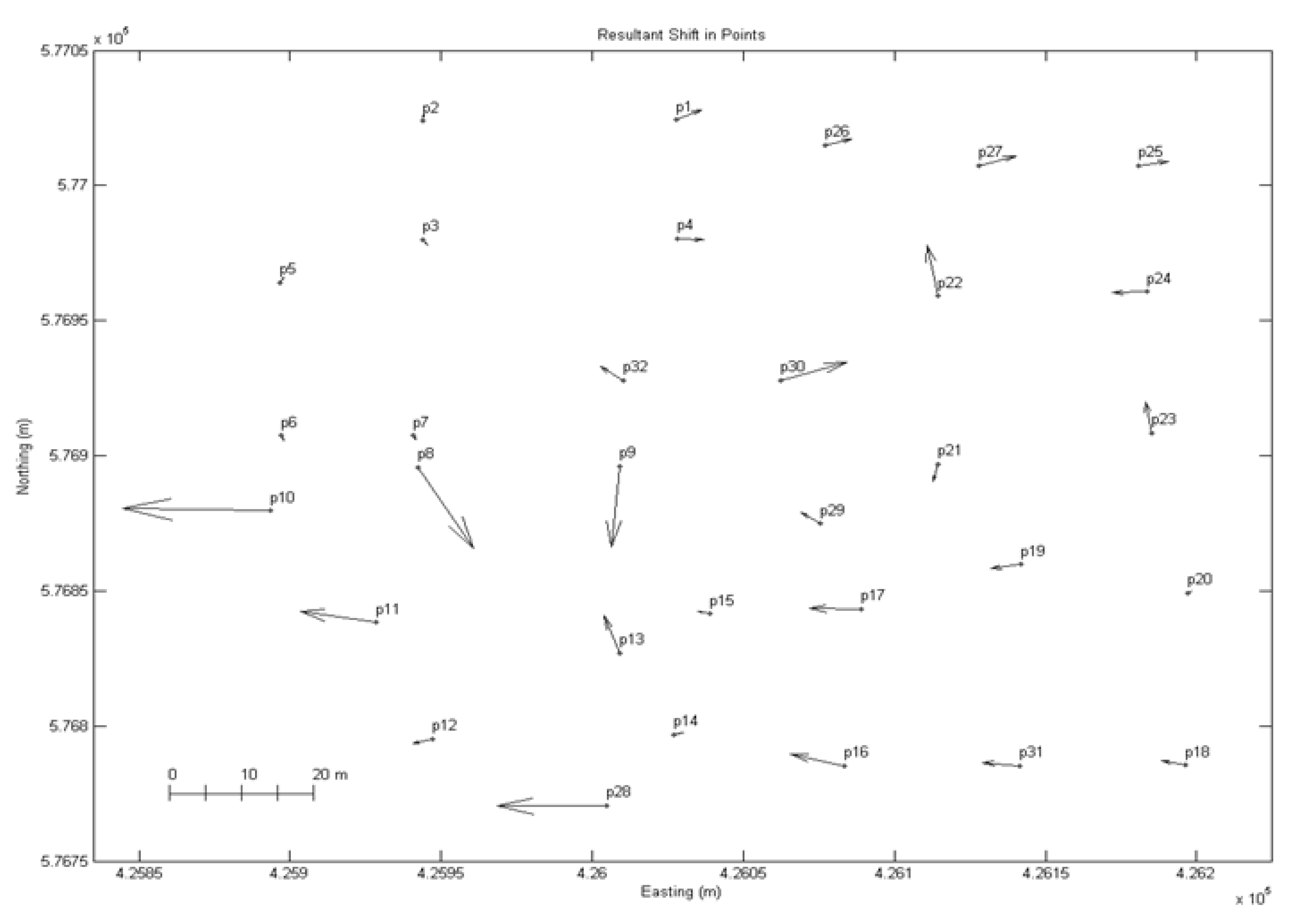
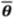 )
)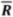 )
)
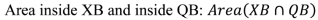
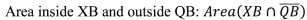
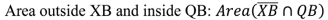
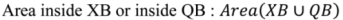
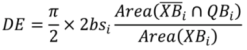
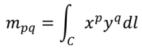
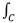 is a line integral along a curve C.
is a line integral along a curve C.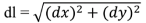
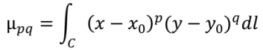
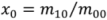 , and
, and 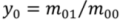 , x0, y0 being the coordinates of the polygon centroid.
, x0, y0 being the coordinates of the polygon centroid.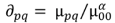
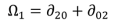
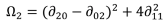
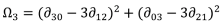
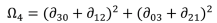
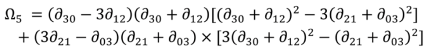
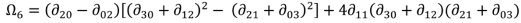
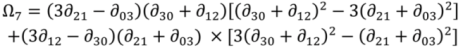
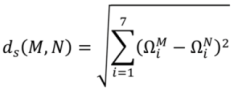
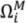 ) and (
) and ( 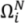 ) are identical in all areal respects); the magnitude of ds will give a reasonable measure of differences between shapes;
) are identical in all areal respects); the magnitude of ds will give a reasonable measure of differences between shapes;