A Novel Method for Estimating Building Height from Baidu Panoramic Street View Images
Abstract
1. Introduction
2. Materials and Methods
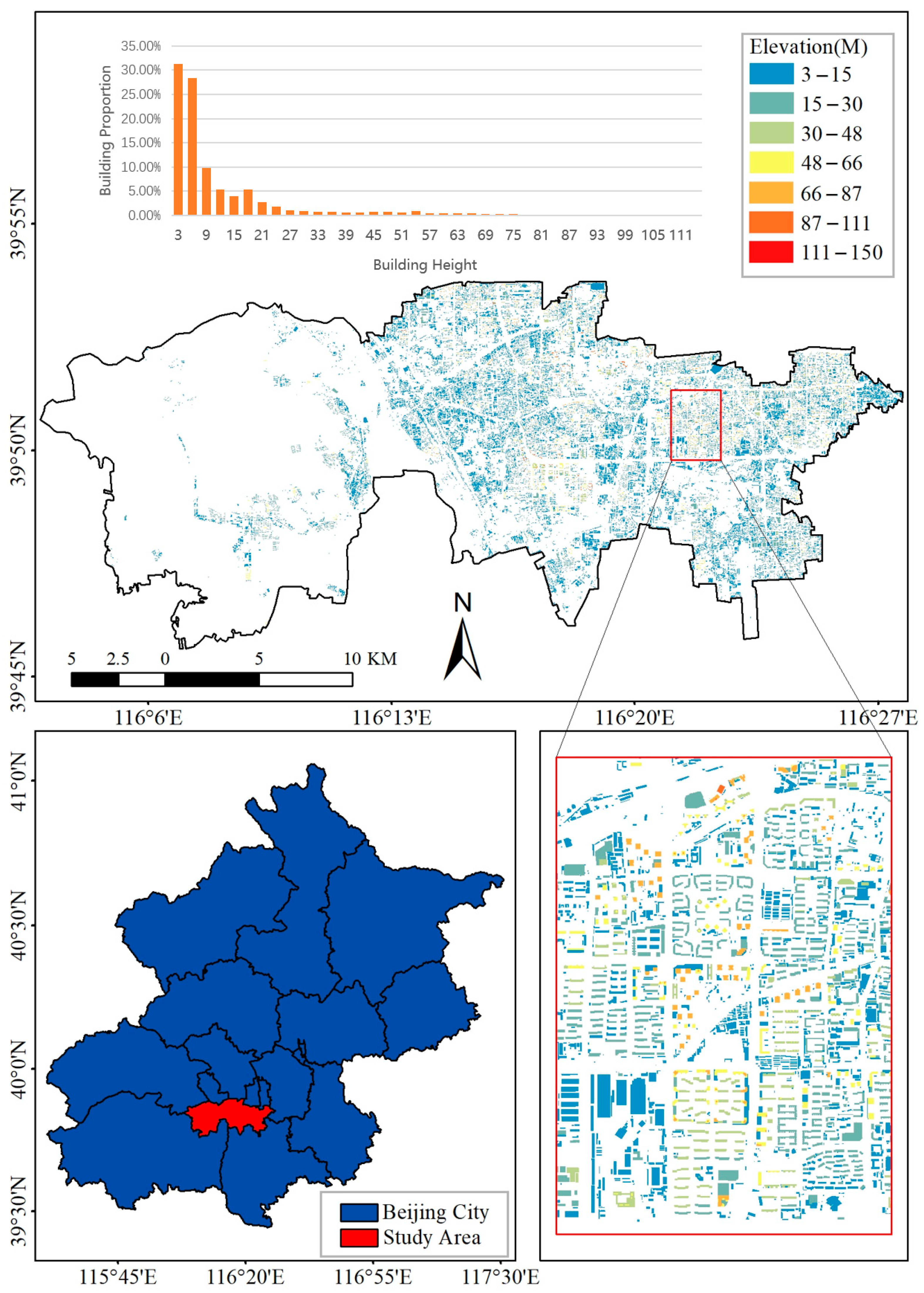
2.1. Study Area
2.2. Data Collection
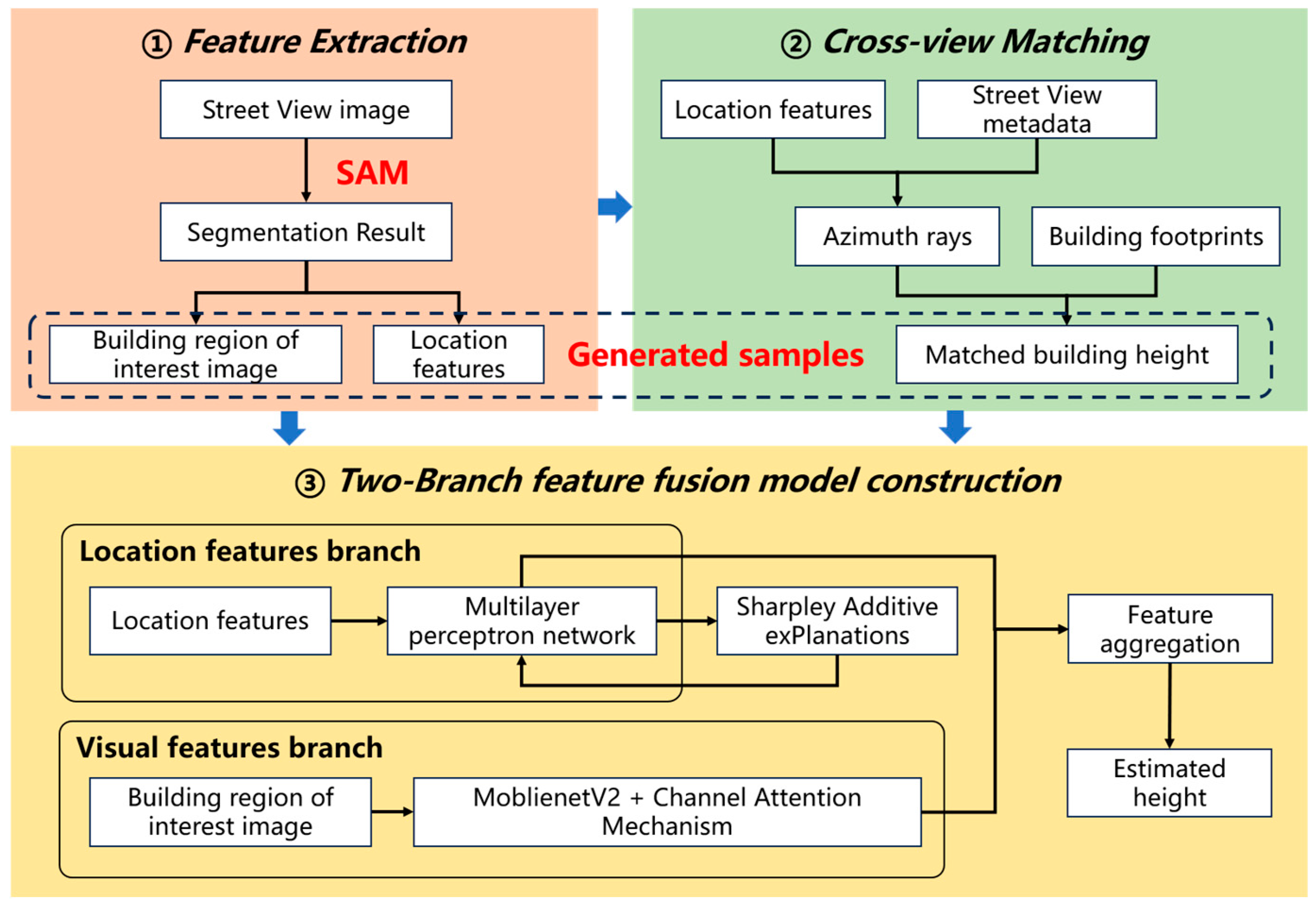
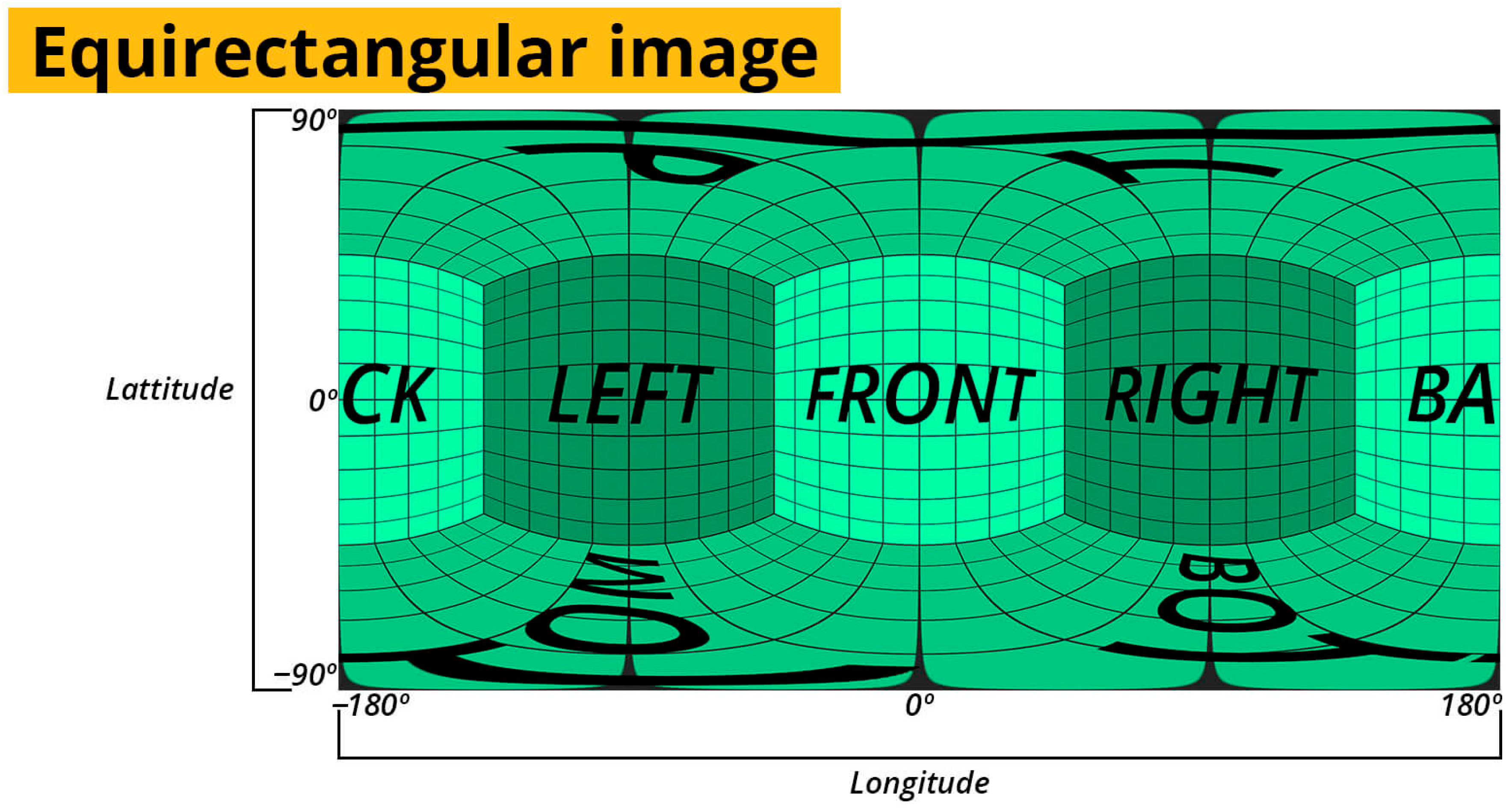
2.3. Methods
2.3.1. Building Region of Interest and Location Features Extraction
2.3.2. Cross-View Matching Between Street View Images and Building Footprints
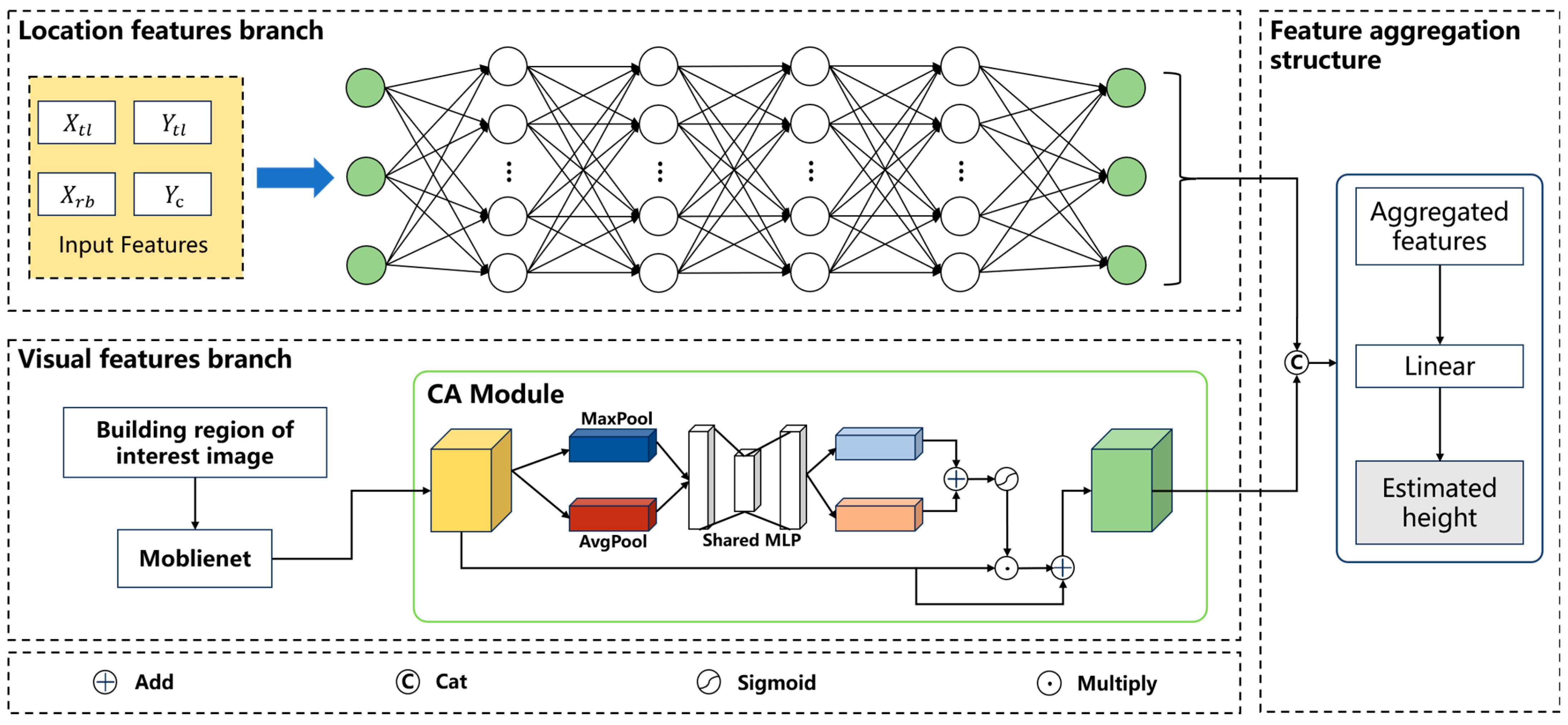
2.3.3. Two-Branch Feature Fusion Model (TBFF) Construction for Height Estimation
2.3.4. Model Training and Evaluation
3. Results
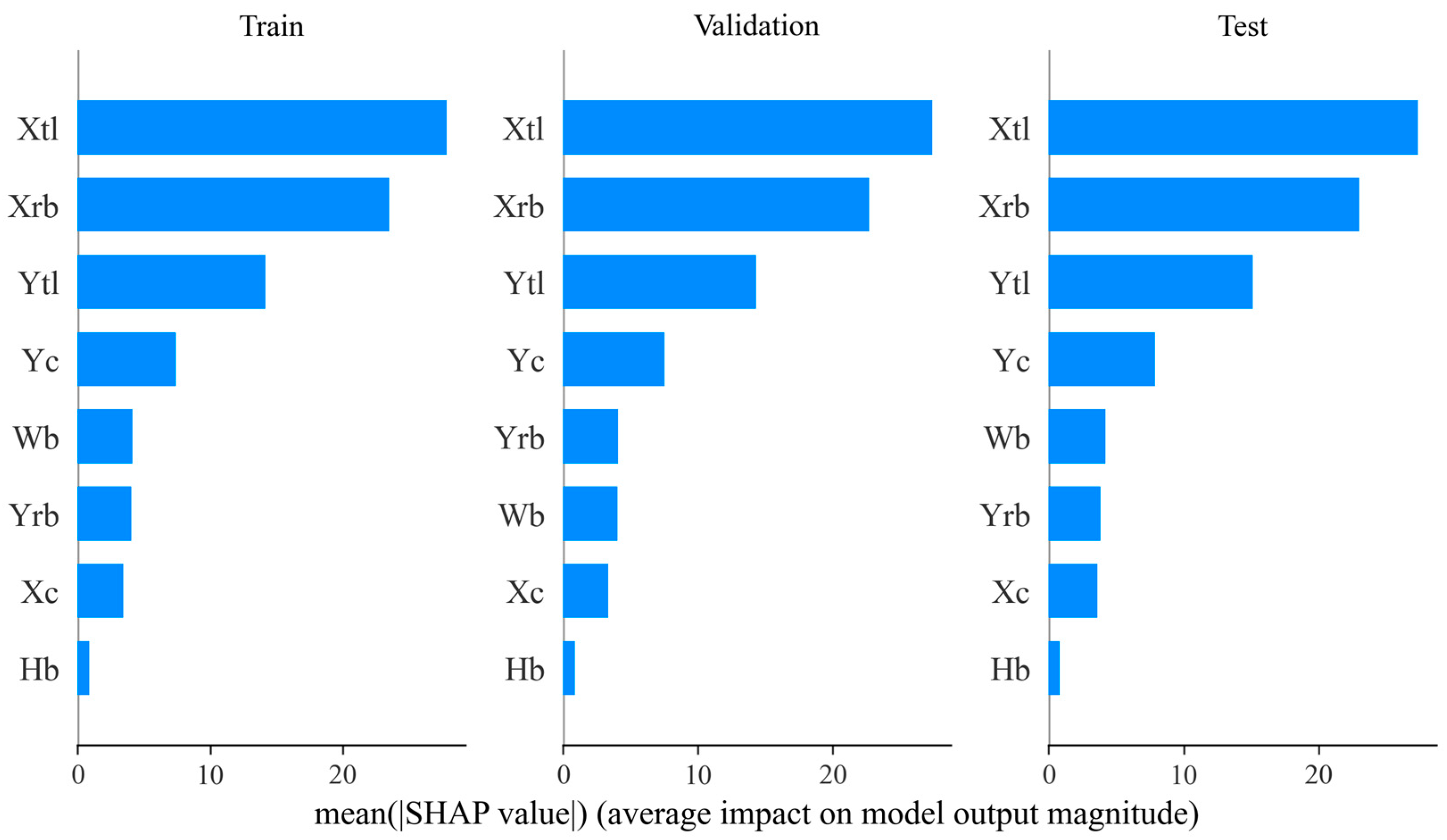
3.1. Location Features Selection Results
3.2. Ablation Study
4. Discussion
4.1. Location Features Importance Analysis
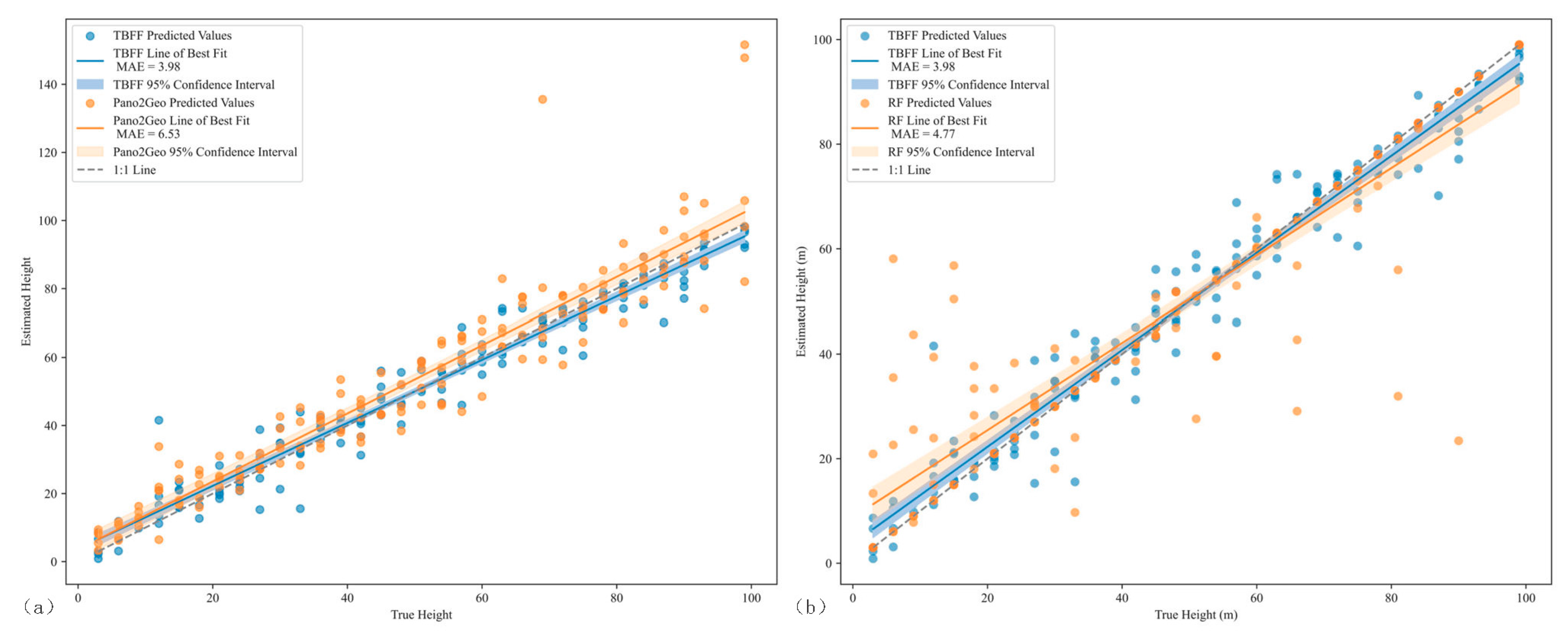
4.2. Comparison with Other Models
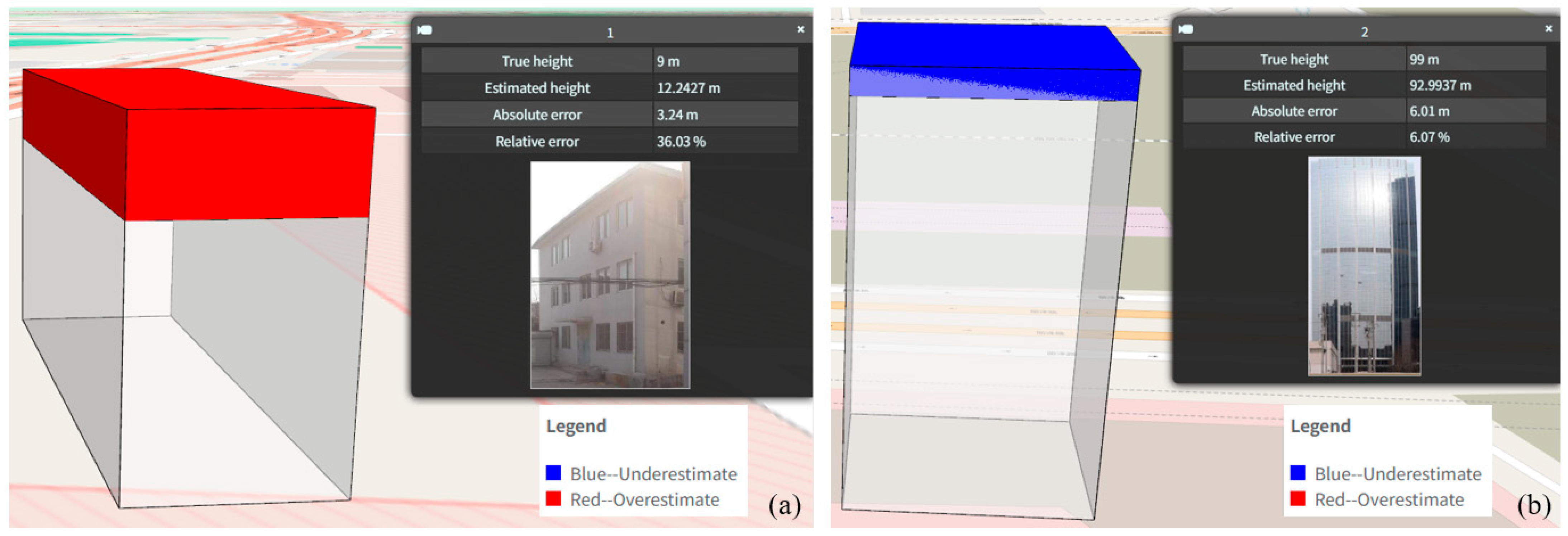
4.3. Features Uncertainty Analysis
4.4. Practical Implications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TBFF | Two-Branch feature fusion |
| SAM | Segment Anything Model |
| MLP | Multi-Layer Perceptron |
| FOV | Field of view |
| SAR | Synthetic aperture radar |
| ROI | Region of interest |
| LOD | Level of Detail |
References
- Biljecki, F.; Ledoux, H.; Stoter, J. Generating 3D city models without elevation data. Comput. Environ. Urban. Syst. 2017, 64, 1–18. [Google Scholar] [CrossRef]
- Chau, K.-W.; Wong, S.K.; Yau, Y.; Yeung, A. Determining optimal building height. Urban. Stud. 2007, 44, 591–607. [Google Scholar] [CrossRef]
- Khorshidi, S.; Carter, J.; Mohler, G.; Tita, G. Explaining crime diversity with google street view. J. Quant. Criminol. 2021, 37, 361–391. [Google Scholar] [CrossRef]
- Schug, F.; Frantz, D.; van der Linden, S.; Hostert, P. Gridded population mapping for Germany based on building density, height and type from Earth Observation data using census disaggregation and bottom-up estimates. PLoS ONE 2021, 16, e0249044. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.; Kim, T. Automatic building height extraction by volumetric shadow analysis of monoscopic imagery. Int. J. Remote Sens. 2013, 34, 5834–5850. [Google Scholar] [CrossRef]
- Xu, W.; Feng, Z.; Wan, Q.; Xie, Y.; Feng, D.; Zhu, J.; Liu, Y. Building Height Extraction From High-Resolution Single-View Remote Sensing Images Using Shadow and Side Information. J. Sel. Top. Appl. Earth Observ. Remote Sens. 2024, 17, 6514–6528. [Google Scholar] [CrossRef]
- Zhang, C.; Cui, Y.; Zhu, Z.; Jiang, S.; Jiang, W. Building height extraction from GF-7 satellite images based on roof contour constrained stereo matching. Remote Sens. 2022, 14, 1566. [Google Scholar] [CrossRef]
- Guida, R.; Iodice, A.; Riccio, D. Height retrieval of isolated buildings from single high-resolution SAR images. Trans. Geosci. Remote Sens. 2010, 48, 2967–2979. [Google Scholar] [CrossRef]
- Lao, J.; Wang, C.; Zhu, X.; Xi, X.; Nie, S.; Wang, J.; Cheng, F.; Zhou, G. Retrieving building height in urban areas using ICESat-2 photon-counting LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102596. [Google Scholar] [CrossRef]
- Shao, Y.; Taff, G.N.; Walsh, S.J. Shadow detection and building-height estimation using IKONOS data. Int. J. Remote Sens. 2011, 32, 6929–6944. [Google Scholar] [CrossRef]
- Sun, Y.; Shahzad, M.; Zhu, X.X. Building height estimation in single SAR image using OSM building footprints. In Proceedings of the 2017 Joint Urban Remote Sensing Event (JURSE), Dubai, United Arab Emirates, 6–8 March 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Kim, H.; Han, S. Interactive 3D building modeling method using panoramic image sequences and digital map. Multimed. Tools Appl. 2018, 77, 27387–27404. [Google Scholar] [CrossRef]
- Biljecki, F.; Ito, K. Street view imagery in urban analytics and GIS: A review. Landsc. Urban. Plan. 2021, 215, 104217. [Google Scholar] [CrossRef]
- Long, Y.; Liu, L. How green are the streets? An analysis for central areas of Chinese cities using Tencent Street View. PLoS ONE 2017, 12, e0171110. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Chen, L.; He, X. Sky View Factor Calculation based on Baidu Street View Images and Its Application in Urban Heat Island Study. J. Geo-Inf. Sci. 2021, 23, 1998–2012. [Google Scholar]
- Zhao, Y.; Qi, J.; Zhang, R. Cbhe: Corner-based building height estimation for complex street scene images. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 2436–2447. [Google Scholar] [CrossRef]
- Al-Habashna, A.a. Building height estimation using street-view images, deep-learning, contour processing, and geospatial data. In Proceedings of the 2021 18th Conference on Robots and Vision (CRV), Burnaby, BC, Canada, 26–28 May 2021; pp. 103–110. [Google Scholar] [CrossRef]
- Díaz, E.; Arguello, H. An algorithm to estimate building heights from Google street-view imagery using single view metrology across a representational state transfer system. In Proceedings of the Dimensional Optical Metrology and Inspection for Practical Applications V, Baltimore, MD, USA, 16–17 April 2016; pp. 58–65. [Google Scholar] [CrossRef]
- Ureña-Pliego, M.; Martínez-Marín, R.; González-Rodrigo, B.; Marchamalo-Sacristán, M. Automatic building height estimation: Machine learning models for urban image analysis. Appl. Sci. 2023, 13, 5037. [Google Scholar] [CrossRef]
- Li, H.; Yuan, Z.; Dax, G.; Kong, G.; Fan, H.; Zipf, A.; Werner, M. Semi-Supervised Learning from Street-View Images and OpenStreetMap for Automatic Building Height Estimation. arXiv 2023, arXiv:2307.02574. [Google Scholar] [CrossRef]
- Fan, K.; Lin, A.; Wu, H.; Xu, Z. Pano2Geo: An efficient and robust building height estimation model using street-view panoramas. ISPRS-J. Photogramm. Remote Sens. 2024, 215, 177–191. [Google Scholar] [CrossRef]
- Ning, H.; Li, Z.; Ye, X.; Wang, S.; Wang, W.; Huang, X. Exploring the vertical dimension of street view image based on deep learning: A case study on lowest floor elevation estimation. Int. J. Geogr. Inf. Sci. 2022, 36, 1317–1342. [Google Scholar] [CrossRef]
- Ho, Y.-H.; Lee, C.-C.; Diaz, N.; Brody, S.; Mostafavi, A. Elev-vision: Automated lowest floor elevation estimation from segmenting street view images. ACM J. Comput. Sustain. Soc. 2024, 2, 1–18. [Google Scholar] [CrossRef]
- Ho, Y.-H.; Li, L.; Mostafavi, A. ELEV-VISION-SAM: Integrated Vision Language and Foundation Model for Automated Estimation of Building Lowest Floor Elevation. arXiv 2024, arXiv:2404.12606. [Google Scholar] [CrossRef]
- Available online: https://map.baidu.com/ (accessed on 22 October 2024).
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Yue, H.; Xie, H.; Liu, L.; Chen, J. Detecting people on the street and the streetscape physical environment from Baidu street view images and their effects on community-level street crime in a Chinese city. ISPRS Int. J. Geo-Inf. 2022, 11, 151. [Google Scholar] [CrossRef]
- Available online: https://en.wikipedia.org/wiki/List_of_street_view_services (accessed on 22 October 2024).
- Zhang, C.; Liu, L.; Cui, Y.; Huang, G.; Lin, W.; Yang, Y.; Hu, Y. A comprehensive survey on segment anything model for vision and beyond. arXiv 2023, arXiv:2305.08196. [Google Scholar] [CrossRef]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.-Y. Segment anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 4015–4026. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar] [CrossRef][Green Version]
- Marcilio, W.E.; Eler, D.M. From explanations to feature selection: Assessing SHAP values as feature selection mechanism. In Proceedings of the 33rd SIBGRAPI Conference on Graphics, Patterns and Images (SIBGRAPI), Porto de Galinhas, Brazil, 7–10 November 2020. [Google Scholar] [CrossRef]
- Lundberg, S. A unified approach to interpreting model predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, X.; Zhang, J.; Sun, D.; Zhou, X.; Mi, C.; Wen, H. Insights into geospatial heterogeneity of landslide susceptibility based on the SHAP-XGBoost model. J. Environ. Manag. 2023, 332, 117357. [Google Scholar] [CrossRef]
- Ekanayake, I.; Meddage, D.; Rathnayake, U. A novel approach to explain the black-box nature of machine learning in compressive strength predictions of concrete using Shapley additive explanations (SHAP). Case Stud. Constr. Mater. 2022, 16, e01059. [Google Scholar] [CrossRef]
- Nohara, Y.; Matsumoto, K.; Soejima, H.; Nakashima, N. Explanation of machine learning models using shapley additive explanation and application for real data in hospital. Comput. Meth. Programs Biomed. 2022, 214, 106584. [Google Scholar] [CrossRef]
- Ogawa, Y.; Oki, T.; Chen, S.; Sekimoto, Y. Joining street-view images and building footprint gis data. In Proceedings of the 1st ACM SIGSPATIAL International Workshop on Searching and Mining Large Collections of Geospatial Data, Beijing, China, 2 November 2021; pp. 18–24. [Google Scholar] [CrossRef]
- Kothuri, R.K.V.; Ravada, S.; Abugov, D. Quadtree and R-tree indexes in oracle spatial: A comparison using GIS data. In Proceedings of the 2002 ACM SIGMOD International Conference on Management of Data, Madison, WI, USA, 3–6 June 2002; pp. 546–557. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar] [CrossRef]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.-C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V. Searching for mobilenetv3. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27–28 October 2019; pp. 1314–1324. [Google Scholar] [CrossRef]
- Guo, M.-H.; Xu, T.-X.; Liu, J.-J.; Liu, Z.-N.; Jiang, P.-T.; Mu, T.-J.; Zhang, S.-H.; Martin, R.R.; Cheng, M.-M.; Hu, S.-M. Attention mechanisms in computer vision: A survey. Comput. Vis. Media. 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar] [CrossRef]
- Xiao, X.; Yan, M.; Basodi, S.; Ji, C.; Pan, Y. Efficient hyperparameter optimization in deep learning using a variable length genetic algorithm. arXiv 2020, arXiv:2006.12703. [Google Scholar] [CrossRef]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Yang, B. A mathematical investigation on the distance-preserving property of an equidistant cylindrical projection. arXiv 2021, arXiv:2101.03972. [Google Scholar] [CrossRef]
- Available online: https://stateofvr.com/1_the-basics.html (accessed on 7 May 2025).
- Che, Y.; Li, X.; Liu, X.; Wang, Y.; Liao, W.; Zheng, X.; Zhang, X.; Xu, X.; Shi, Q.; Zhu, J. 3D-GloBFP: The first global three-dimensional building footprint dataset. Earth Syst. Sci. Data Discuss. 2024, 16, 5357–5374. [Google Scholar] [CrossRef]
- Available online: https://portal.ogc.org/files/?artifact_id=33758 (accessed on 11 July 2025).









| Image Type | Medthod | References |
|---|---|---|
| Perspective | Single view geometry | Zhao et al. [16] |
| Al-Habashna [17] | ||
| Díaz & Arguello [18] | ||
| Proportional relationship | Ureña-Pliego [19] | |
| Multimodal feature fusion | Li et al. [20] | |
| Panoramic | Single view geometry | Fan et al. [21] |
| Ning et al. [22] | ||
| Ho et al. [23] | ||
| Ho et al. [24] |
| Hyperparameters | Description | Initial Value | Optimal Value |
|---|---|---|---|
| Batch size | The number of samples input into the model each time | 8, 16, 32, 64, 128 | 64 |
| Learning rate | The step size for parameter updates based on gradients during each iteration | 0.00001, 0.0001, 0.001 | 0.0008 |
| Epoch | The number of training iterations | 100, 150, 200, 250 | 200 |
| Hidden unit number | The number of neurons in the hidden layer of the location features branch | 16, 32, 64 | 64 |
| No | Location Features | RMSE (95% CI) | MAE (95% CI) | MAPE |
|---|---|---|---|---|
| 1 | all features | 15.82 [13.98, 17.70] | 12.10 [10.60, 13.60] | 0.41 |
| 2 | Xtl, Xrb, Ytl, Yc | 16.83 [14.88, 18.71] | 13.23 [11.68, 14.88] | 0.52 |
| No | Fusion Type | RMSE (95% CI) | MAE (95% CI) | MAPE |
|---|---|---|---|---|
| 1 | Location features branch (Xtl, Xrb, Ytl, Yc) | 16.83 [14.88, 18.71] | 13.23 [11.68, 14.88] | 0.52 |
| 2 | Visual features branch (MoblienetV2 + Channel Attention) | 6.77 [5.48, 8.27] | 4.67 [3.98, 5.48] | 0.17 |
| 3 | TBFF (all location features) | 6.41 [5.23, 7.73] | 4.51 [3.87, 5.28] | 0.16 |
| 4 | TBFF (Xtl, Xrb, Ytl, Yc) | 5.69 [4.69, 6.88] | 3.97 [3.40, 4.65] | 0.15 |
| No | Model | RMSE (95% CI) | MAE (95% CI) | MAPE |
|---|---|---|---|---|
| 1 | Pano2Geo | 10.51 [7.04, 13.79] | 6.52 [5.33, 7.97] | 0.22 |
| 2 | RF | 11.83 [8.52, 15.09] | 4.76 [3.28, 6.54] | 0.32 |
| 3 | TBFF | 5.69 [4.69, 6.88] | 3.97 [3.40, 4.65] | 0.15 |
| Dimensions | Street View Imagery | Oblique UAV Photogrammetry | Airborne LiDAR |
|---|---|---|---|
| Spatial accuracy | Meter level | Centimeter level | Centimeter level |
| Coverage | Along streets | Local (task planning) | Local (cost-limited) |
| Update frequency | High (depends on map vendor updates) | Medium (active collection required) | Low (cost-limited) |
| Data costs | Low (public API) | Medium (equipment + manpower) | High |
| Applicable scenarios | Height quick estimate | Fine-scale modeling of target objects | High precision requirements |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, S.; Liu, J.; Che, X.; Wang, Y.; Huang, H. A Novel Method for Estimating Building Height from Baidu Panoramic Street View Images. ISPRS Int. J. Geo-Inf. 2025, 14, 297. https://doi.org/10.3390/ijgi14080297
Ge S, Liu J, Che X, Wang Y, Huang H. A Novel Method for Estimating Building Height from Baidu Panoramic Street View Images. ISPRS International Journal of Geo-Information. 2025; 14(8):297. https://doi.org/10.3390/ijgi14080297
Chicago/Turabian StyleGe, Shibo, Jiping Liu, Xianghong Che, Yong Wang, and Haosheng Huang. 2025. "A Novel Method for Estimating Building Height from Baidu Panoramic Street View Images" ISPRS International Journal of Geo-Information 14, no. 8: 297. https://doi.org/10.3390/ijgi14080297
APA StyleGe, S., Liu, J., Che, X., Wang, Y., & Huang, H. (2025). A Novel Method for Estimating Building Height from Baidu Panoramic Street View Images. ISPRS International Journal of Geo-Information, 14(8), 297. https://doi.org/10.3390/ijgi14080297







