A Reversible Compression Coding Method for 3D Property Volumes
Abstract
1. Introduction
2. Related Works
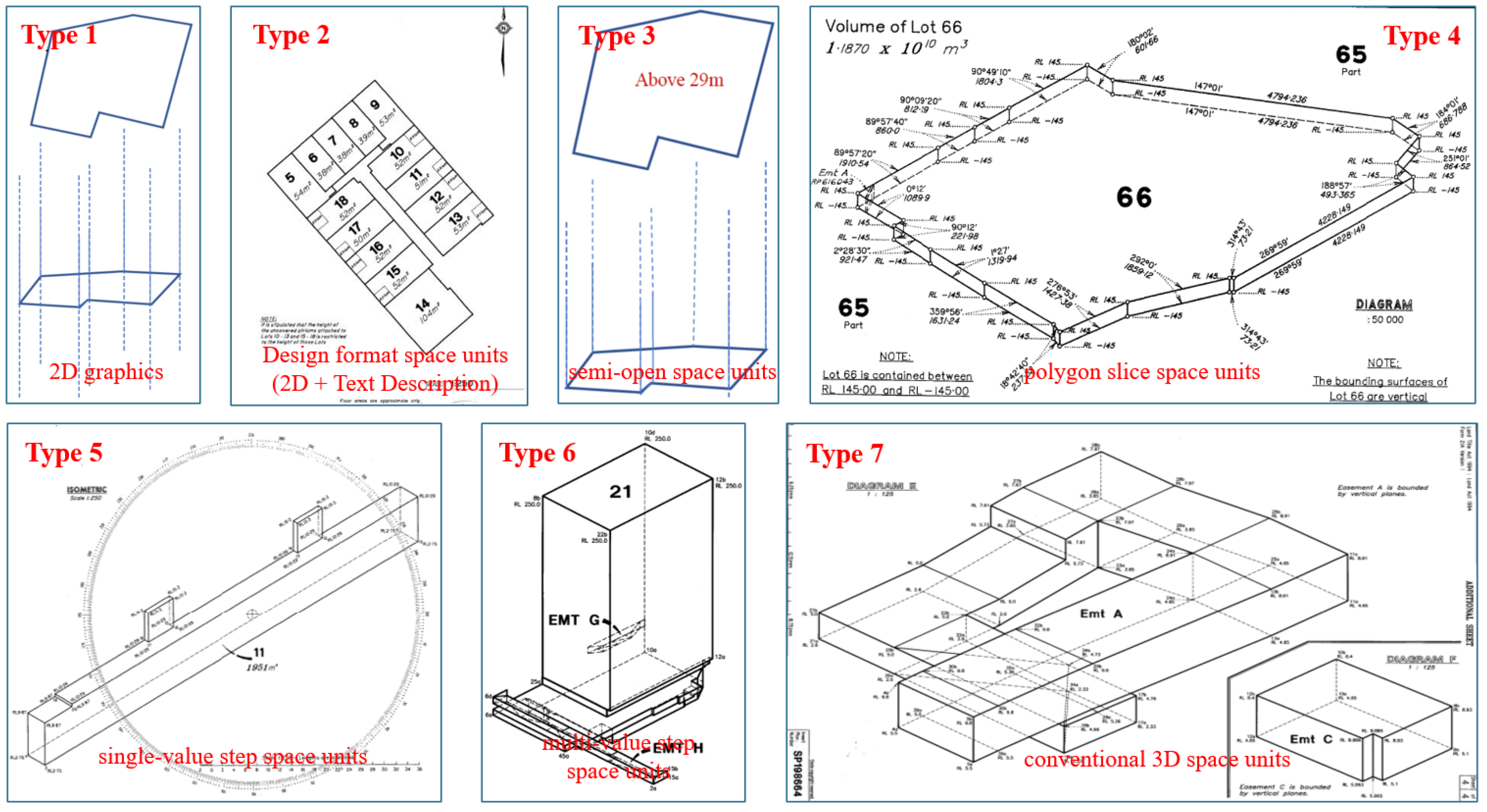
2.1. 3D Property Volume
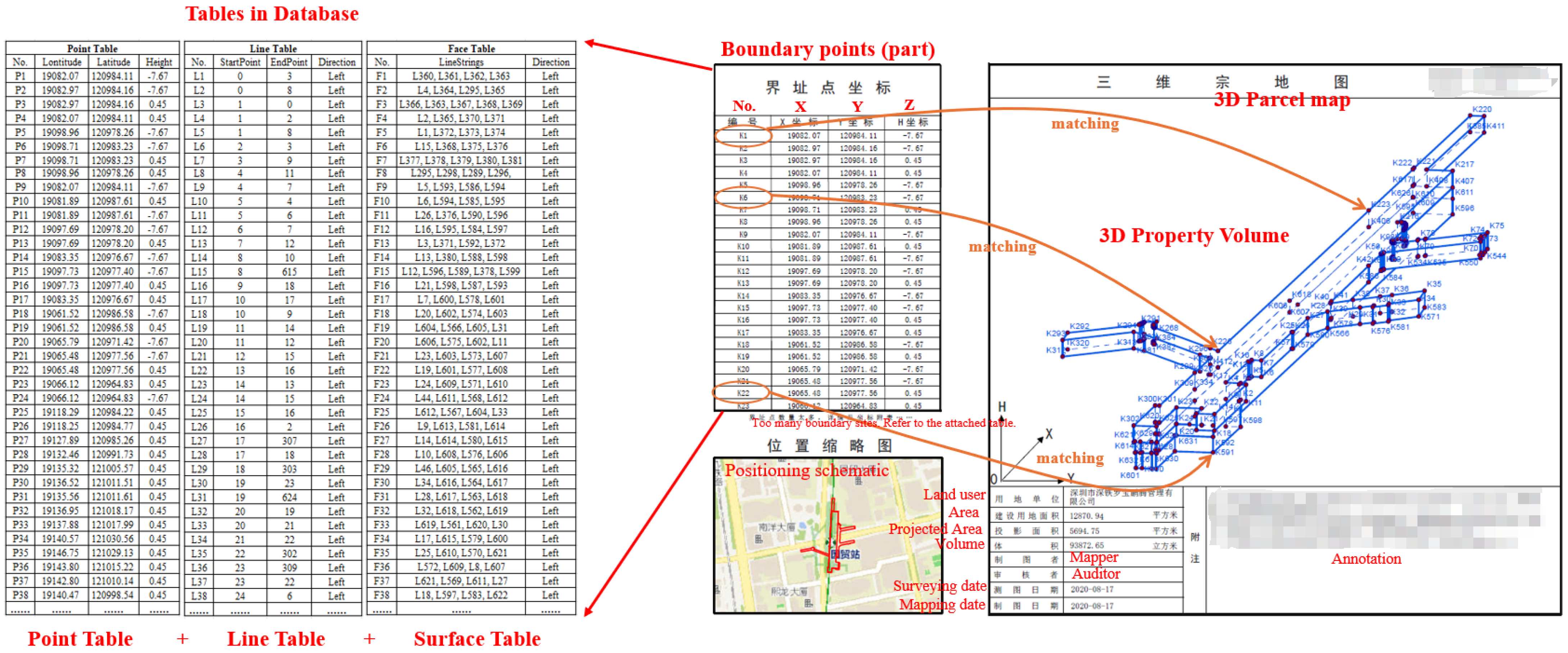
2.2. Compressing a 3D Property Volume
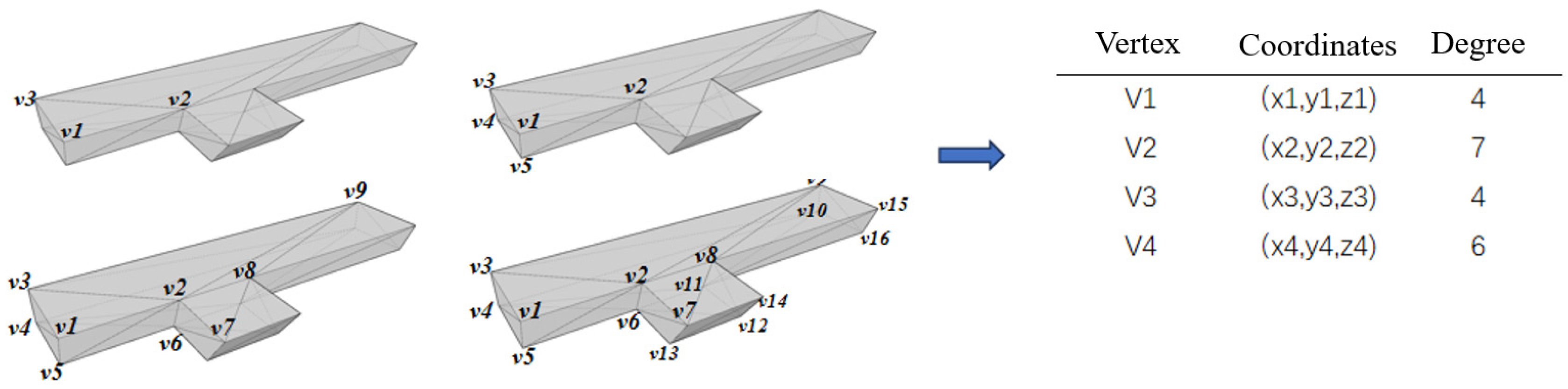
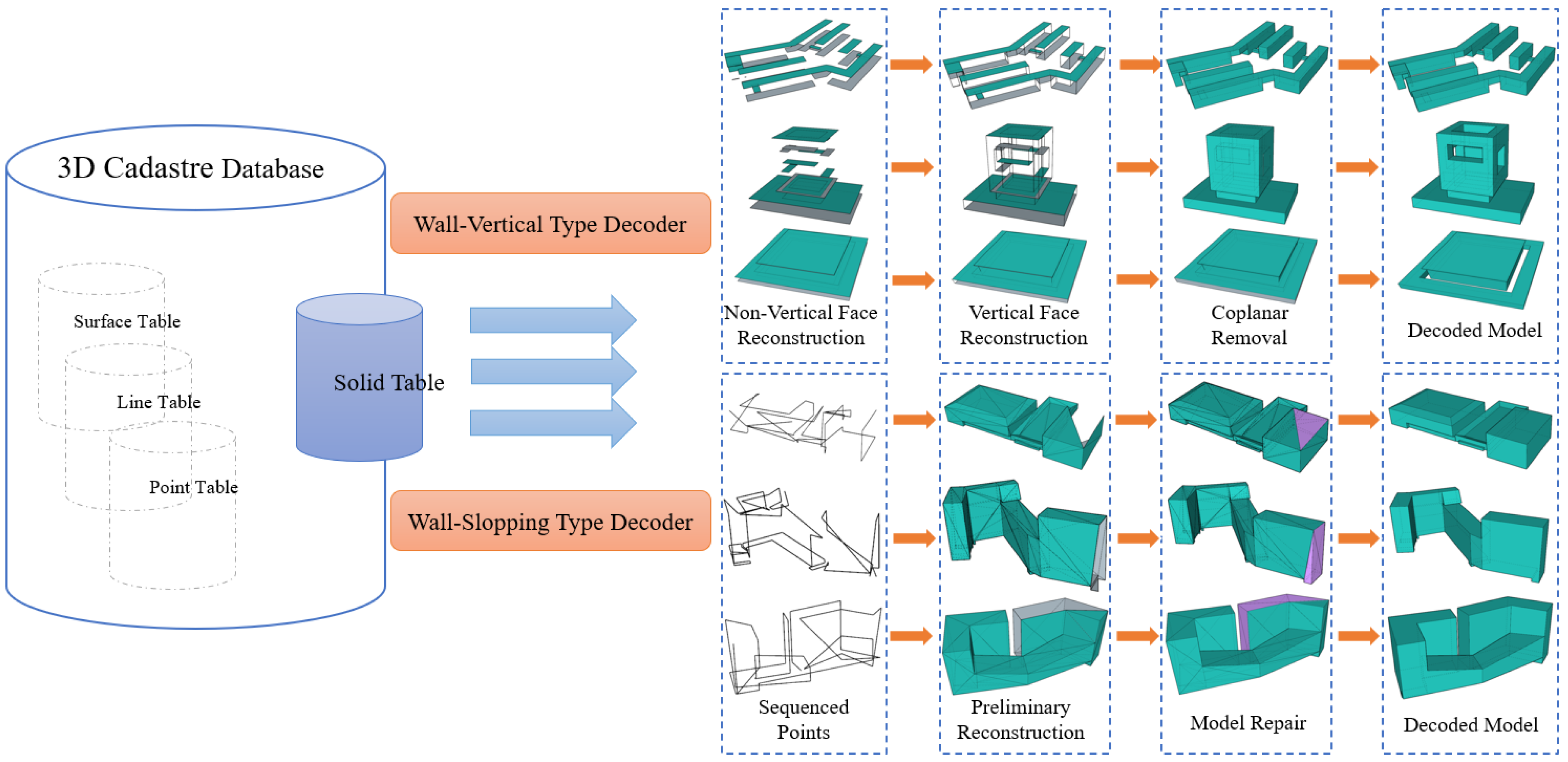
3. Methodology
3.1. The Context of the 3DPV-CC Solution
3.2. Classifier
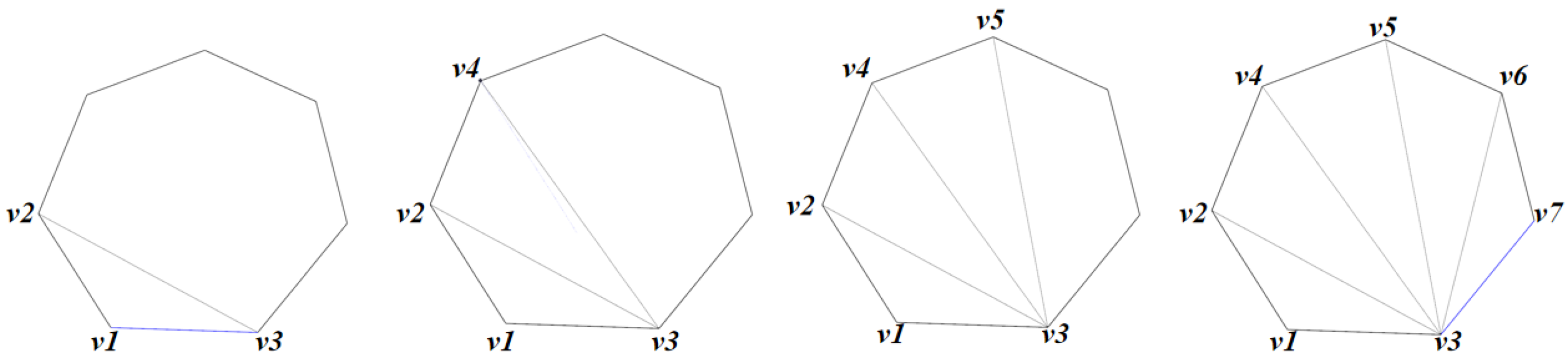
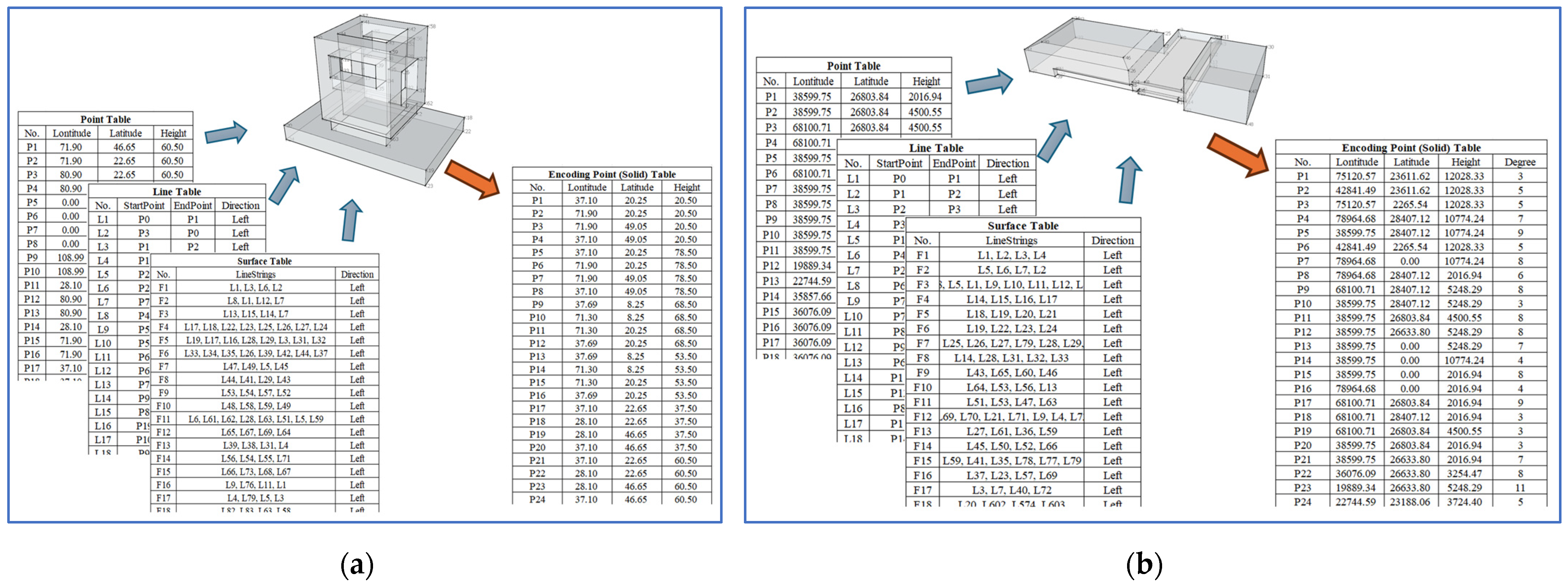
3.3. Encoder
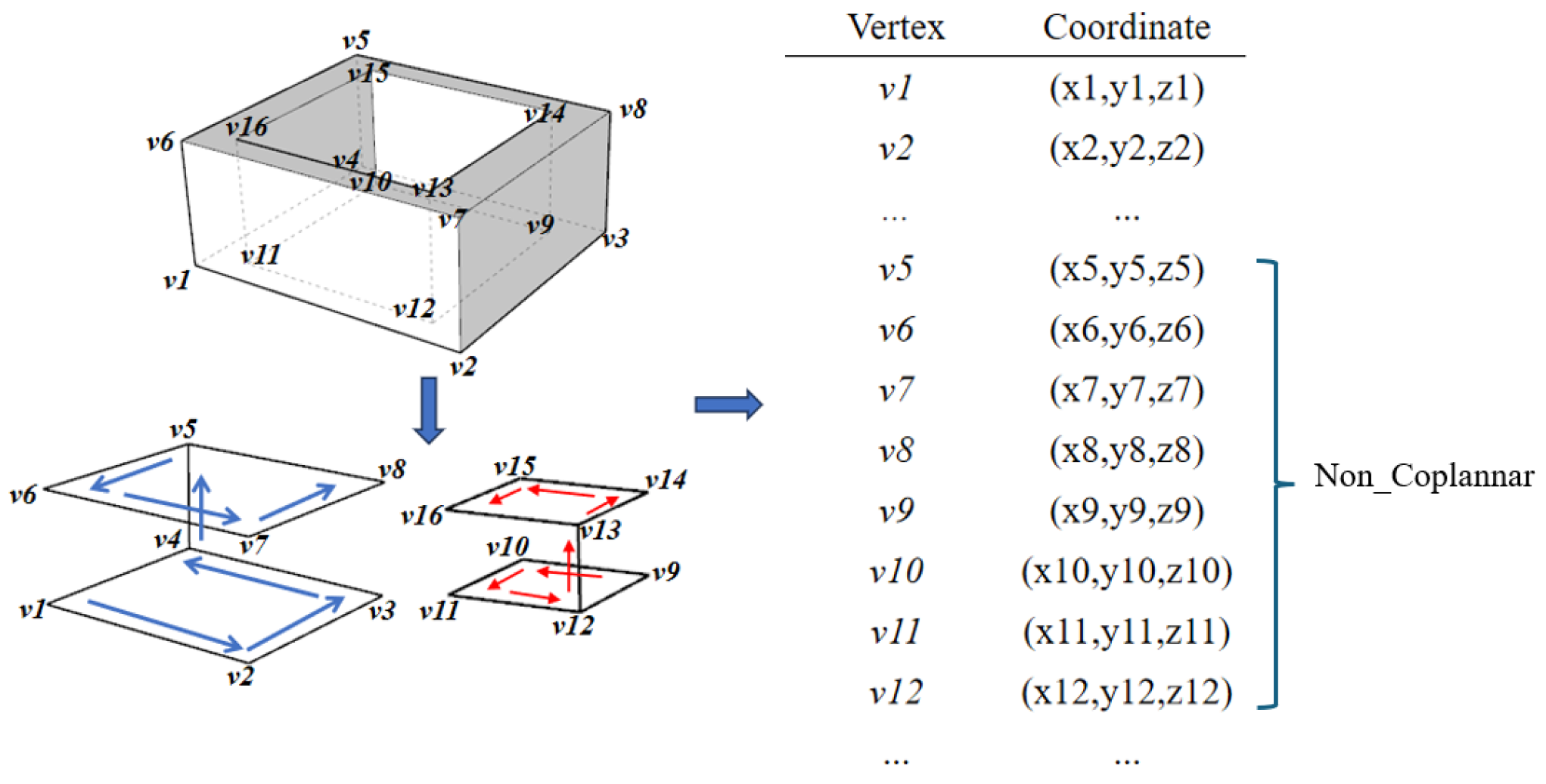
3.3.1. Vertical Type Encoder
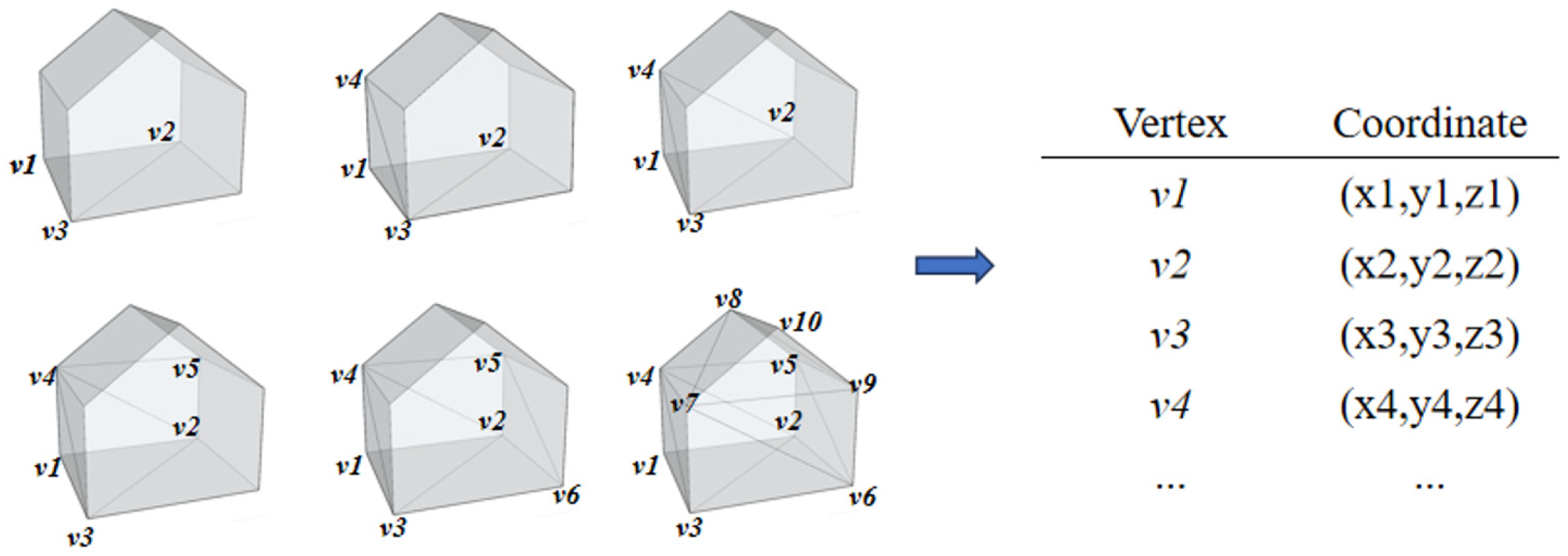
3.3.2. Slopping Type Encoder
3.4. Decoder
3.4.1. Decoding Process for the Vertical Type
3.4.2. Decoding Process for the Slope Model
3.5. Repair Process
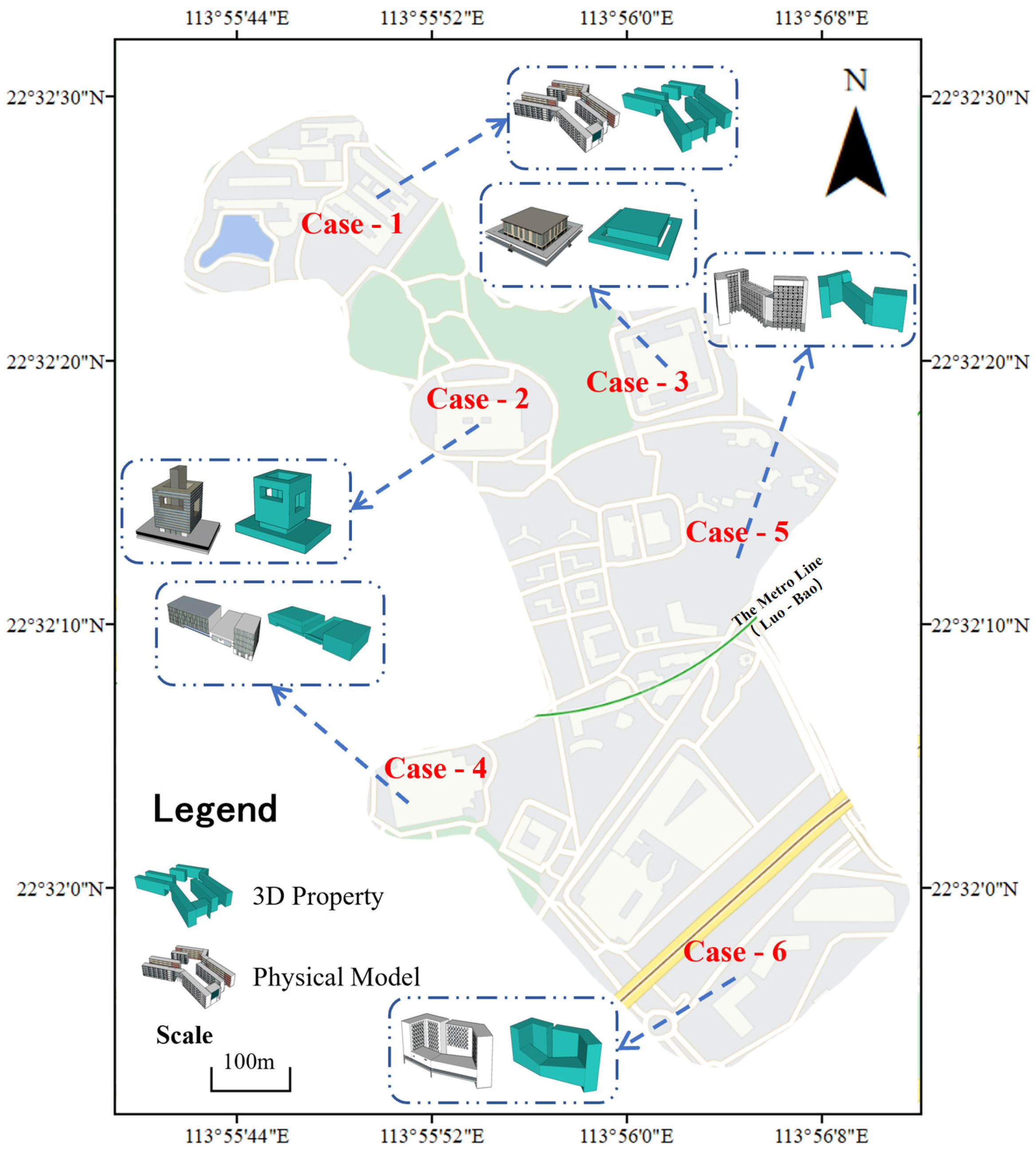
4. Case Study
4.1. Data and the Experimental Environment
4.2. Encoding and Decoding Experiments of 3DPV-CC
4.3. The Effect Analysis
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kalogianni, E.; van Oosterom, P.; Dimopoulou, E.; Lemmen, C. 3D Land Administration: A Review and a Future Vision in the Context of the Spatial Development Lifecycle. ISPRS Int. J. Geo-Inf. 2020, 9, 107. [Google Scholar] [CrossRef]
- Li, C.; Zhao, Z.; Chen, Y.; Zhu, W.; Qiu, J.; Jiang, S.; Guo, R. Modeling the Urban Low-Altitude Traffic Space Based on the Land Administration Domain Model—Case Studies in Shenzhen, China. Land 2024, 13, 2062. [Google Scholar] [CrossRef]
- Kalogianni, E.; Dimopoulou, E.; Thompson, R.; Lemmen, C.; Ying, S.; van Oosterom, P. Development of 3D spatial profiles to support the full lifecycle of 3D objects. Land Use Policy 2020, 98, 104–177. [Google Scholar] [CrossRef]
- Zhang, J.-Y.; Yin, P.-C.; Li, G.; Gu, H.-H.; Zhao, H.; Fu, J.-C. 3D Cadastral Data Model Based on Conformal Geometry Algebra. ISPRS Int. J. Geo-Inf. 2016, 5, 20. [Google Scholar] [CrossRef]
- Ying, S.; Chen, N.; Li, W.; Li, C.; Guo, R. Distortion visualization techniques for 3D coherent sets: A case study of 3D building property units. Comput. Environ. Urban Syst. 2019, 78, 101382. [Google Scholar] [CrossRef]
- Salleh, S.; Ujang, U.; Azri, S. Topological Relationships in R3 for 3d Cadastre. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 48, 165–170. [Google Scholar] [CrossRef]
- Emamgholian, S.; Taleai, M.; Shojaei, D. Exploring the applications of 3D proximity analysis in a 3D digital cadastre. Geo-Spat. Inf. Sci. 2021, 24, 201–214. [Google Scholar] [CrossRef]
- Jaljolie, R.; Riekkinen, K.; Dalyot, S. A topological-based approach for determining spatial relationships of complex volumetric parcels in land administration systems. Land Use Policy 2021, 109, 105637. [Google Scholar] [CrossRef]
- Sun, J.; Mi, S.; Olsson, P.-O.; Paulsson, J.; Harrie, L. Utilizing BIM and GIS for Representation and Visualization of 3D Cadastre. ISPRS Int. J. Geo-Inf. 2019, 8, 503. [Google Scholar] [CrossRef]
- Ying, S.; Guo, R.; Li, L.; Van Oosterom, P.; Stoter, J. Construction of 3D volumetric objects for a 3D cadastral system. Trans. GIS 2015, 19, 758–779. [Google Scholar] [CrossRef]
- Guo, R.; Li, L.; Ying, S.; Luo, P.; He, B.; Jiang, R. Developing a 3D cadastre for the administration of urban land use: A case study of Shenzhen, China. Comput. Environ. Urban Syst. 2013, 40, 46–55. [Google Scholar] [CrossRef]
- Asghari, A.; Kalantari, M.; Rajabifard, A. Advances in techniques to formulate the watertight concept for cadastre. Trans. GIS 2021, 25, 213–237. [Google Scholar] [CrossRef]
- Knoth, L.; Atazadeh, B.; Rajabifard, A. Developing a new framework based on solid models for 3D cadastres. Land Use Policy 2020, 92, 104480. [Google Scholar] [CrossRef]
- Asghari, A.; Kalantari, M.; Rajabifard, A. A structured framework for 3D cadastral data validation− a case study for Victoria, Australia. Land Use Policy 2020, 98, 104359. [Google Scholar] [CrossRef]
- Thompson, R.; van Oosterom, P.; Soon, K.H. A Conceptual Model supporting a range of 3D parcel representations through all stages: Data Capture, Transfer and Storage. In FIG Working Week; International Federation of Surveyors: Copenhagen, Denmark, 2016; Volume 2. [Google Scholar]
- Kalogianni, E.; Dimopoulou, E.; Greece, R. Investigating 3D spatial units’ types as basis for refined 3d spatial profiles in the context of LADM revision. In Proceedings of the 6th International FIG Workshop on 3D Cadastres, Delft, The Netherlands, 2 October 2018. [Google Scholar]
- Ying, S.; Li, C.; Chen, N.; Jia, Y.; Guo, R.; Li, L. Object Analysis and 3D Spatial Modelling for Uniform Natural Resources in China. Land 2021, 10, 1154. [Google Scholar] [CrossRef]
- Deering, M. Geometry compression. In Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 6–11 August 1995; pp. 13–20. [Google Scholar]
- Bajaj, C.L.; Pascucci, V.; Zhuang, G. Single resolution compression of arbitrary triangular meshes with properties. Comput. Geom. 1999, 14, 167–186. [Google Scholar] [CrossRef]
- Janečka, K.; Váša, L. Compression of 3D geographical objects at various level of detail. In The Rise of Big Spatial Data; Springer International Publishing: Cham, Switzerland, 2016; pp. 359–372. [Google Scholar]
- Gurung, T.; Luffel, M.; Lindstrom, P.; Rossignac, J. Zipper: A compact connectivity data structure for triangle meshes. Comput. Aided Des. 2013, 45, 262–269. [Google Scholar] [CrossRef]
- Siddeq, M.M.; Rodrigues, M.A. Novel 3D compression methods for geometry. connectivity and texture. 3D Res. 2016, 7, 1–18. [Google Scholar] [CrossRef]
- Nguyen, V.P.; Ung, E.M.; Krishna, A.; Tham, S. Lossless compression of topology of 3D triangulated irregular networks. In Proceedings of the 10th International Conference on Information, Communications and Signal Processing (ICICS), Singapore, 2–4 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Wei, W.; Liu, Y.; Duan, X.; Guo, C. Representation method of 3D model mesh chain code. J. Comput. Aided Des. Comput. Graph. 2017, 29, 537–548. [Google Scholar]
- Li, M.; Nan, L. Feature-preserving 3D mesh simplification for urban buildings. ISPRS J. Photogramm. Remote Sens. 2021, 173, 135–150. [Google Scholar] [CrossRef]
- Lin, D.; Zhao, C.; Tian, Q.; Xu, Y.; Wang, R.; Qu, Z. GMM-ICQ: A GMM vertex-optimization-based implicitly-connected quadrilateral format for 3D mesh storage. Comput. Graph. 2024, 118, 34–47. [Google Scholar] [CrossRef]
- Zhao, X.; Zeng, X.; Gao, L.; Xu, Y.; Wang, Y. DMGC: Deep Triangle Mesh Geometry Compression via Connectivity Prediction. In Proceedings of the 33rd Workshop on Network and Operating System Support for Digital Audio and Video, Vancouver, BC, Canada, 7–10 June 2023; pp. 15–21. [Google Scholar]
- Wang, Z.; Zhou, S.; Park, J.J.; Paschalidou, D.; You, S.; Wetzstein, G.; Guibas, L.; Kadambi, A. Alto: Alternating latent topologies for implicit 3d reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 259–270. [Google Scholar]
- Balreira, D.G.; da Silveira, T.L.T. Triangular matrix-based lossless compression algorithm for 3D mesh connectivity. Vis. Comput. 2024, 40, 3961–3970. [Google Scholar] [CrossRef]
- Li, L.; Guo, R.; Ying, S.; Zhu, H.; Wu, J.; Liu, C. 3D Modeling of the Cadastre and the Spatial Representation of Property. In Urban Informatics; Springer: Berlin/Heidelberg, Germany, 2021; pp. 589–607. [Google Scholar]
- Li, C.; Kuai, X.; He, B.; Zhao, Z.; Lin, H.; Zhu, W.; Liu, Y.; Guo, R. Visibility-Based R-Tree Spatial Index for Consistent Visualization in Indoor and Outdoor Scenes. ISPRS Int. J. Geo-Inf. 2023, 12, 498. [Google Scholar] [CrossRef]
- Li, C.; Guo, R.; Zhao, Z.; He, B.; Kuai, X.; Wang, W.; Chen, X. Conceptual Modeling Method for Urban Low-Altitude Passage Easement. J. Geo-Inf. Sci. 2024, 26, 1811–1826. [Google Scholar]
- Cho, S.; Kim, D.; Pearlman, W.A. Lossless Compression of Volumetric Medical Images with Improved Three-Dimensional SPIHT Algorithm. J. Digit. Imaging 2004, 17, 57–63. [Google Scholar] [CrossRef]
- Xiong, Z.; Wu, X.; Cheng, S.; Hua, J. Lossy-to-lossless compression of medical volumetric data using three-dimensional integer wavelet transforms. IEEE Trans. Med. Imaging 2003, 22, 459–470. [Google Scholar] [CrossRef]













| No. | The Original State | 3DPV-CC | |||||
|---|---|---|---|---|---|---|---|
| Point | Line | Surface | Size (KB) | Compressed Size (KB) | Compression Rate | Recovery Rate | |
| Case 1 | 123 | 190 | 78 | 20.3 | 12.5 | 38.42% | 100% |
| Case 2 | 64 | 96 | 37 | 14.7 | 10.0 | 31.97% | 100% |
| Case 3 | 32 | 48 | 21 | 12.6 | 9.48 | 24.76% | 100% |
| Case 4 | 49 | 79 | 32 | 14 | 10.1 | 27.86% | 93.62% |
| Case 5 | 69 | 110 | 43 | 15.9 | 11.5 | 27.67% | 96.27% |
| Case 6 | 38 | 60 | 24 | 13.1 | 10.0 | 23.66% | 93.15% |
| No. | Original Size (KB) | 3DPV-CC | ZIP | 7Z | RAR | ||||
|---|---|---|---|---|---|---|---|---|---|
| Size | Ratio | Size | Ratio | Size | Ratio | Size | Ratio | ||
| Case 1 | 20.3 | 12.5 | 38.42% | 18.6 | 8.37% | 18.4 | 9.36% | 18.5 | 8.87% |
| Case 2 | 14.7 | 10 | 31.97% | 13.3 | 9.52% | 13.3 | 9.52% | 13.3 | 9.52% |
| Case 3 | 12.6 | 9.48 | 24.76% | 11.4 | 9.52% | 11.3 | 10.32% | 11.3 | 10.32% |
| Case 4 | 14 | 10.1 | 27.86% | 12.7 | 9.29% | 12.6 | 10.0% | 12.6 | 10.0% |
| Case 5 | 15.9 | 11.5 | 27.67% | 14.5 | 8.81% | 14.5 | 8.81% | 14.5 | 8.81% |
| Case 6 | 13.1 | 10 | 23.66% | 11.9 | 9.16% | 11.8 | 9.92% | 11.8 | 9.92% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Qiu, J.; Guo, H.; Zhu, W.; Li, C. A Reversible Compression Coding Method for 3D Property Volumes. ISPRS Int. J. Geo-Inf. 2025, 14, 263. https://doi.org/10.3390/ijgi14070263
Zhao Z, Qiu J, Guo H, Zhu W, Li C. A Reversible Compression Coding Method for 3D Property Volumes. ISPRS International Journal of Geo-Information. 2025; 14(7):263. https://doi.org/10.3390/ijgi14070263
Chicago/Turabian StyleZhao, Zhigang, Jiahao Qiu, Han Guo, Wei Zhu, and Chengpeng Li. 2025. "A Reversible Compression Coding Method for 3D Property Volumes" ISPRS International Journal of Geo-Information 14, no. 7: 263. https://doi.org/10.3390/ijgi14070263
APA StyleZhao, Z., Qiu, J., Guo, H., Zhu, W., & Li, C. (2025). A Reversible Compression Coding Method for 3D Property Volumes. ISPRS International Journal of Geo-Information, 14(7), 263. https://doi.org/10.3390/ijgi14070263