Abstract
Origin–destination (OD) flows are essential for urban studies, yet their acquisition is often hampered by high costs and privacy constraints. Prevailing inference methodologies inadequately address latent spatial dependencies between non-contiguous and distant areas, which are useful for understanding modern transportation systems with expanding regional interactions. To address these challenges, this paper propose a hybrid learning model with the Global–Local Graph Attention Network and XGBoost (GLGAT-XG) to infer OD flows from both global and local geographic contextual information. First, we represent the study area as an undirected weighted graph. Second, we design the GLGAT to encode spatial correlation and urban feature information into the embeddings within a multitask setup. Specifically, the GLGAT employs a graph transformer to capture global spatial correlations and a graph attention network to extract local spatial correlations followed by weighted fusion to ensure validity. Finally, OD flow inference is performed by XGBoost based on the GLGAT-generated embeddings. The experimental results of multiple real-world datasets demonstrate an 8% improvement in RMSE, 7% in MAE, and 10% in CPC over baselines. Additionally, we produce a multi-scale OD dataset in Xian, China, to further reveal spatial-scale effects. This research builds on existing OD flow inference methodologies and offers significant practical implications for urban planning and sustainable development.
1. Introduction
Origin–destination (OD) flow data record the number of trips between origins and destination zones, reflecting the spatial interactions between geographical units [1]. It is essential for advancing sustainable urban mobility and optimizing transportation management and has broad applications in epidemic control [2], urban planning [3], traffic engineering [4], and emergency management [5]. For example, OD flow data play an important role in the travel demand modeling stage of traffic planning, which allows researchers to analyze how infrastructure and land use affect the trip distribution of residents, thus supporting infrastructure design, travel forecasting and policy evaluation [6]. Despite advancements in data collection methods, the availability of high-quality OD flow data remains limited due to the significant costs of large-scale sampling and as privacy and data security concerns [7]. Therefore, constructing OD flow inference models to generate statistically similar synthetic data offers an effective solution for addressing above limitations and replacing real data in practical applications. Notably, a recent publication in Nature emphasizes the potential of machine-generated datasets for protecting privacy and mitigating data biases, encouraging researchers and practitioners to adopt data generation techniques [8].
OD flow inference usually refers to generating the number of human flows between zones using fitted or trained models based on the socio-economic characteristics of geospatial units (e.g., population, land use) and their interacting characteristics (e.g., distances, spatial correlations) [9]. Existing methods for inferring OD flows can be divided into three categories. The first category is the classical spatial interactive models, which rely on various assumptions and theoretical frameworks. Representative models include the gravity model [10], the radiation model [11], and the intervening opportunities model [12]. However, these models exhibit simple structures, rely on fixed inputs, and primarily focus on opportunities and costs, limiting their capability to capture the complexities of human mobility patterns. The second category is based on machine learning (ML) models [13,14,15]. These ML-based models incorporate richer urban features such as land use, points of interests (POIs), road networks, and other interacting features between zones than traditional models. Then, artificial neural network (ANN) or tree-based models automatically learn high-dimensional feature representations and explore the non-linear relationship between these features and OD traffic between zones. The third category involves deep learning models based on GNNs. In addition to incorporating urban features of origin and destination zones, several studies conceptualize cities as graphs, where zones are represented as nodes and interactions between zones as edges, using a GNN to implement OD flow inference [16]. Compared to ML-based methods mentioned above, GNNs are not only able to fit complex non-linear relationships but also capture spatial correlations among geographic units and thus have been widely used in the current stage of OD flow inference. Recently, efforts on OD flow inference have been made by combining GNNs with tree-based algorithms, such as GMEL [17], ConvGCN-RF [18], and TGAT-ML [19].
Despite numerous studies on OD flow inference, current methodologies have the following limitations:
- Limited ability to capture complex geographic relationships. While many existing GNN-based models account for spatial neighborhood correlations and outperform ML-based models, their spatial modeling components (e.g., GCN and GAT) may fail to adequately capture complex geographic relationships [20]. GCNs and GATs rely on a message passing mechanism, which updates a central node’s information by aggregating data from adjacent nodes within a local range. Although stacking multiple layers can expand the receptive field, this mechanism is generally confined to 2–3 hop neighbors [21]. These limitations in local graph attention hinder the ability to account for non-geographically neighboring regions, particularly the spatial dependencies of distant nodes in large-scale graphs. Figure 1 illustrates the modeling differences between the local graph attention layer and the global graph attention layer.
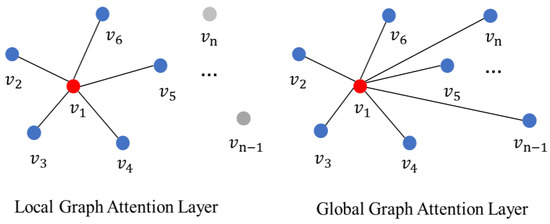 Figure 1. Local graph attention layer vs. global graph attention layer.
Figure 1. Local graph attention layer vs. global graph attention layer. - Sensitivity to fixed spatial scales. Most existing studies focus on a fixed spatial scale, such as census tracts, traffic analysis zones (TAZs), and fixed-size grids. However, researchers have found that the performance of human mobility inference is highly sensitive to the spatial scale of analysis units [22,23]. Identifying a model-friendly scale of spatial analysis unit can further enhance the inference performance of models.
To address the aforementioned limitations, we propose a hybrid learning model that combines a novel global–local graph attention network and XGBoost (3.0.0) regression model (GLGAT-XG), leveraging an efficient three-component architecture: encoder, decoder, and flow inference. Before the encoder, we take urban geographical units as nodes, build node urban features according to the key factors in the classical theory and the built environment 5D principle, and use the distances between the units as the weights of the edges to construct an undirected weighted graph network. In the encoder, we propose a global–local graph attention network (GLGAT) to learn node embeddings. It uses simplified graph transformer (SGFormer [24]) to capture the global (i.e., all zones) and GAT to emphasize local (i.e., geographic neighborhoods) spatial correlations of the nodes, followed by weighted fusion. We then use a multitask objective function in the decoder to impose more constraints on the training of the GLGAT, ensuring a valid representation of the node embeddings. Finally, we feed the learned origin and destination embeddings—concatenated with the distance between each origin–destination pair—into an XGBoost regression model for OD flow inference. Additionally, to examine the impact of spatial scale on OD flow inference accuracy, we construct OD flow datasets at varying spatial scales. In addition, we employ the Shapley additive explanations (SHAP) framework to quantitatively reveal the impact of different features on the model inference results.
Specifically, the main contributions of this study are as follows:
- We develop a novel node embedding model based on the global–local graph attention. The model combines simplified graph transformer and GAT to capture the spatial connectivity of both neighboring and non-neighboring nodes, overcoming the limitations of OD flow inference models based only on a GCN and GAT in understanding large-scale complex spatial relationships.
- We construct a multi-scale OD flow dataset using large-scale taxi trajectory data in Xi’an, China. This dataset enables an exploration of how different spatial scales affect OD inference accuracy, offering insights for further performance improvement.
- We conduct extensive experiments on real-world datasets from multiple cities. The empirical results show that our model has superior OD inference accuracy and robustness compared to the baseline models.
The rest of the paper is organized as follows: Section 2 reviews the existing literature related to OD flow inference methods; Section 3 outlines the fundamental concepts used throughout this work; Section 4 introduces the architecture of our proposed model and the underlying techniques; Section 5 describes the data preprocessing and experimental setups; Section 6 presents and discusses the experimental results; and Section 7 concludes the paper and suggests potential directions for future research.
2. Related Works
OD flow inference can be divided into three main categories according to modeling methodology: traditional models, machine learning-based models, and graph neural network-based models. These types of models are known as ‘trip distribution’ in the four-step model in transport, ‘spatial interaction models’ in geography, and human mobility models in computer science.
2.1. Traditional Models
Traditional models primarily consist of the gravity model and the intervention opportunity class models. The most representative is the gravity model proposed by K. Zipf [10], which suggests that the movement of people between two places is driven by mutual attraction, with spatial distance acting as a source of friction. Unlike gravity model, the intervening opportunity class models, such as the radiation model [11], population-weighted opportunity (PWO) model [22], and opportunity priority selection (OPS) model [25], are micro-mechanism models. These models assume individuals compare opportunities at origin, intervention, and destination when choosing a trip. The difference is the criteria used to compare opportunities across locations, which are usually expressed in terms of population. However, these models usually rely on population and distance characteristics of the modeled area, leading to limitations in capturing non-linear and irregular distributions, such as the interaction between urban indicators and human mobility.
2.2. Machine Learning Based Models
ML-based models can incorporate a wider range of urban features, such as land use types, POIs, transport networks and other inter-zone interaction features. They can also effectively establish non-linear relationships between these features and mobility patterns. For instance, Pourebrahim et al. employed an ANN and RF models to infer movement between census tracts in New York City, finding that the RF outperformed both traditional models and the ANN [13]. They identified population, distance, the number of Twitter users and employment as significant inferences. Simini et al. extended the single-constraint gravity model to a multi-layer feed-forward neural network (FFNN) named Deep Gravity, which significantly improves the inference accuracy by incorporating more urban metrics of origins and destinations, such as land use and POIs [14]. Robinson et al. leveraged ANNs and XGBoost models to infer group movements across 3106 counties in the United States and 207 countries globally, yielding superior outcomes relative to the above traditional models [15]. However, these ML-based models are unable to take into account the topological properties (i.e., the structure of relationships between geographical units) of an urban spatial interaction network and spatial proximity effects. According to Tobler’s First Law of Geography, the correlation between neighboring things in a geographic space is more significant [26]. At the same time, their effectiveness has been demonstrated in existing studies [18,27].
2.3. Graph Neural Network-Based Models
In recent years, GNNs have provided a new perspective for spatial inference modeling [28]. GNNs can handle various data structures of arbitrary shapes except sequences and grids, and they capture spatial dependencies by establishing distances or topological relationships between geographical units. Many studies have demonstrated that GNNs can overcome the limitations of the above ML-based models and improve inference accuracy [29,30]. Existing studies on GNNs in the field of OD research focus on spatio-temporal traffic forecasting [31,32,33]. As described in Section 1, it requires the support of historical data, whereas OD flow inference does not. Therefore, some studies have tried to apply a GNN and geosemantic information to extract features of OD networks without knowing any historical information. Based on the model structure, existing GNN-based models can be classified into two-component models (i.e., encoder and decoder) and three-component models (i.e., encoder, decoder and flow inference). As an example, Yao et al. proposed a spatial interaction graph convolutional network (SI-GCN), which uses the GCNs as an encoder and a bilinear function as a decoder for missing OD flow interpolation [16]. In the two-component model, the encoder is used to generate all node embeddings, and the decoder uses bilinear functions, multi-layer perceptrons (MLPs), or tree models to generate OD flows directly. In the three-component model, the decoder is mainly used to train the encoder, which calculates the error by combining the true OD flows and feeding back the error to the encoder to update its parameters. Following this, an independent flow inference is used to infer the final OD flow based on the learned embeddings. Examples include the geographically contextualized multitask embedded learner (GMEL) model proposed by Liu et al. and the hybrid learning models proposed by Yin et al. and Shi et al. [17,18,19]. Among them, Shi et al. [19] compared the two-component model with the three-component model on Guangzhou City commuting data. The results showed that the flow inference in the three-component model can improve accuracy efficiently. A summary of all the above models is shown in Table 1.

Table 1.
A systematic summary on methods for OD flow inference.
Regardless of the type of OD flow inference model, the encoder usually employs a GCN or GAT to capture the spatial interdependencies between regions to generate node embeddings. However, these GNNs are prone to over-smoothing and over-compression issues [34,35]. These issues impede the stacking of multiple layers in message passing-based GNNs, confining their receptive field to a mere 2–3 hops from neighboring nodes. As a result, this significantly hampers the capacity of these methods to address the challenge of long-range dependency resolution; in other words, it is difficult to fully consider spatial relationships between non-geographic adjacent distant regions. Nejadshamsi found that considering the relational characteristics of these non-geographical zones further improves model performance as in cities where the metro network plays a key role in transport, the areas connected by the metro network have similar travel patterns [36]. Therefore, it is necessary to employ a network component that can model global relational capabilities. Graph transformers (GTs) leverage global attention mechanisms to adaptively compute node importance, effectively mitigating over-smoothing and over-compression issues [37]. The fully connected architecture of GTs eliminates structural biases, enabling them to effectively learn graph structures that are essential for downstream tasks, such as node embedding. However, to the best of our knowledge, there are currently no studies that have employed the effectiveness of GTs in the area of OD inference. This highlights an open issue as to whether the global graph attention mechanism can facilitate urban spatial correlation modeling and improve OD inference accuracy.
In addition, from the definition of OD flow data mentioned in Section 1, it is clear that they are typically aggregated based on spatial analysis units. As can be seen in Table 1, most of the existing OD flow inference studies are based on predefined spatial analysis units, whereas the size and shape of the spatial analysis unit can significantly affect the results, i.e., the modified area unit problem (MAUP). Several empirical results show that the effectiveness of crowd flow inference models significantly depends on the spatial scale of analysis [22,23]. This indicates that many studies ignore the scale sensitivity of spatial data distribution, i.e., the relationships between different attributes vary with scale. Therefore, Wang et al. explored the effects of different spatial scales on cross-city human flow inference based on 500 m × 500 m and 1000 m × 1000 m spatial units [38]. Guo et al. checked the generalization ability of their model on OD datasets at different spatial scales in several cities [39]. However, the above studies did not further investigate the impact of using different scales of spatial analysis units in the same city on the performance of the model.
3. Problem Formulation
This section mainly introduces the important definitions and problem of this study.
- Definition 1 (Urban Geographic Units).We partition the city into N non-overlapping urban geographic units , ,…, . The geographic units can be irregularly shaped, such as census tracts, postcodes, TAZs, etc., or regularly shaped, such as grids.
- Definition 2 (OD Graph Network).The OD graph network is an undirected weighted graph , where is the set of urban geographic units that serves as the nodes of the graph, is set of edge features describing correlation strengths (i.e., travel distance), where are geographically adjacent and is the set of urban features that serves as the node attributes.
- Definition 3 (Geographical Adjacent Matrix).The geographic adjacency matrix is an N × M matrix, where = 1 if node and node are geographically adjacency connected; = 0 otherwise.
- Definition 4 (Urban Features).Each urban geographic unit contains a variety of characteristics, such as land use, transport facilities, population, etc. We use vector to denote the attributes of unit i as the urban features.
- Definition 5 (OD Flows).OD flows are a set of triplets , where and denote the origin and destination units, respectively, and represents the number of trips from to . We also define two types of node-level flows: inflow and outflow. The outflow, denoted as , represents the total number of trips departing from . The inflow, denoted as , represents the total number of trips arriving at .
- Problem (OD Flow Inference).Given an undirected weighted graph , we develop model M to infer the OD flow ∈ ; that is, . In this paper, is the GLGAT-XG.
4. Methodology
This section describes the overall framework of the proposed hybrid model GLGAT-XG for the spatial inference of OD flows. As shown in Figure 2, our model consists of four components: preprocesssing, encoder, decoder and flow inference.
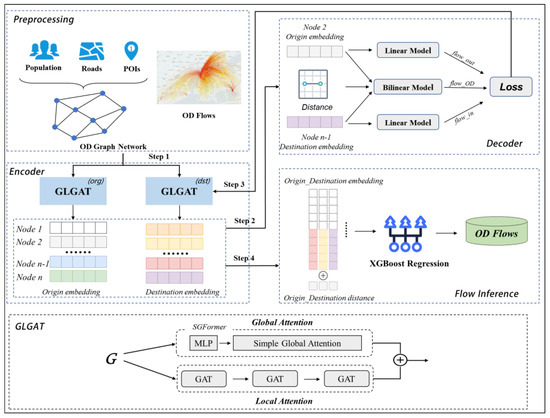
Figure 2.
The framework of the GLGAT-XG model for OD flow inference.
Firstly, in the preprocessing module, each urban geographic unit is used as a node, multi-source data are employed as node urban features, and distances between urban geographic units are applied as edges to construct an undirected weighted OD graph network, which will be presented in Section 5.1. The OD graph network and OD flows are the input data for the remaining components of the model. Secondly, in the encoder module, in order to learn the characteristics of the supply and demand attributes corresponding to the origin and destination, respectively, the encoder extracts the node embeddings for the origin and the destination using two independent and identical GLGATs, respectively. Thirdly, in the decoder module, multitask learning is chosen to train GLGAT by back-propagating the fitting error to improve the validity of the node embedding representation. Finally, in the flow inference module, based on the node embeddings generated by the trained GLGAT and distances between nodes, the advanced multiple regression model XGBoost is employed to infer the OD flow between two zones. The detailed illustrations of the encoder, decoder and flow inference are as follows.
4.1. Encoder Using GLGAT for Node Embedding
After preprocessing (i.e., Step 1), the next step is to learn node embedding (i.e., Step 2). As mentioned in Definition 5, the process is to map the urban features and spatial correlations of the nodes into a low-dimensional representation. In the encoder, we develop the GLGAT for node embedding, and its architecture is shown in Figure 2. GLGAT is composed of one SGFormer and three paralleled GATs, which can overcome the limitation that the GAT model only captures the spatial correlation of a finite number of nodes in the neighborhood. Specifically, we use SGFormer to focus on the spatial relationships among all the nodes in the OD graph network to achieve a global spatial semantic feature representation. Also, to avoid the model focusing too much on the distant non-geographical neighborhood nodes and relatively ignoring the proximal geographical neighborhood nodes, which may contain a great deal of useful information, GLGAT uses GAT to synchronously capture the spatial feature relationships of local neighborhood nodes to ensure accurate spatial perception and then sums them by a simple weighted fusion, as shown in Equation (1).
where is the fusion weights.
In addition, OD flows can be seen as a spatial interaction between supply and demand [22]; thus, we employ two independent and identical GLGATs to encode this information so as to learn the supply and demand characteristics of each urban geographic unit separately.
4.1.1. SGFormer for Global Relationship Learning
GTs have proven effective in mitigating the impact of noisy, collapsed, or redundant connecting edges by leveraging a global attention mechanism, which aggregates information from all other nodes in the graph during each layer update [21]. However, most current GTs are primarily designed for smaller-scale graphs, such as molecular graphs [40]. When applied to larger-scale graph data, such as the thousands of nodes in this study, the quadratic complexity of global attention can become a notable bottleneck. This complexity hinders its further use. To address this challenge, we employ SGFormer, which enables the efficient modeling of a large-scale graph while preserving the effectiveness of global attention. It simplifies the global attention network by reducing it from a multi-layer structure to a single-layer design.
The key component of SGFormer is a simple global attention model, which is proven to capture implicit dependencies between nodes with linear complexity. Before inputting the simple global attention layer, a shallow MLP is needed to map the node features to the node embeddings in the potential space for subsequent attention calculation and dissemination. The simple global attention layer is a single-layer attention network with formulas defined as Equations (2) and (3):
where , , and are the linear feed-forward layers, denotes the Frobenius norm, is the hyper-parameter for link, and 1 is an N-dimensional all-one column vector; the diagonal operation changes the N-dimensional column vector into an N × N diagonal matrix. Z integrates both all-pair attentive propagation over N nodes and the self-loop propagation. The all-pair attentive propagation allows the model to capture the influence from other nodes, while the self-loop propagation preserves the information of the centered nodes.
Because SGFormer does not require positional encoding, feature or graph preprocessing, or additional loss, it is easy to integrate and use in other models. Also, since only one layer of global attention is used, the model is very lightweight, facilitating efficient training and inference.
4.1.2. GAT for Local Relationship Learning
To effectively consider the importance of neighboring nodes in spatial dependency learning, the GAT integrates the attention mechanism into the node aggregation operation. This process can be divided into two main stage: firstly, attention scores are computed for neighboring nodes based on the features of the connecting nodes and the edge feature, and second, node features are updated by aggregating information from these weighted neighboring nodes.
Assuming that the features of the l-th layer node Vi are , its neighbor node is Vj, and the feature of the edge between them is . GAT at this point performs a linear transformation on the node features and edge features, as shown in Equation (4).
where and are trainable parameter matrices. is the message vector passed to neighboring nodes. is the transformed edge feature.
Before aggregating these message vectors, an attention score for each edge is calculated. Then, the attention scores are normalized by softmax. The process is shown in Equations (5) and (6), respectively.
where is the non-linear activation function, is a trainable parameter vector that maps the concatenation of messages into a scalar value, T denotes transpose, | denotes the concatenation operation, denotes the attention score of the neighboring node j to the central node i, is the normalized attention score, and is the set of neighboring nodes for node i.
Then, the nodes are aggregated to update the features of the central node, and the aggregation process consists of two parts representing the neighborhood impact and self-impact, respectively:
where is a trainable parameter matrix.
4.2. Decoder Using Multitask Learning for GLGAT Training
Aiming to ensure the effectiveness of the GLGAT learned embeddings, we adopt a more restrictive multitask learning framework in the decoder, as shown in Figure 2. Given the strong correlation between OD flows and supply–demand characteristics, Liu found that adding the sub-task of inflow–outflow inference significantly improved OD inference as the main task [9]. Following their approach, we combine origin–destination embeddings and the distance between them to infer OD flows using a bilinear layer, and use single layer linear to infer outflows and inflows based on the origin embeddings and the destination embeddings, respectively, as described below.
where , , and are the generated OD flow, origin outflow, and destination inflow, respectively; , , and are trainable parameters; is the origin embedding; is the destination embedding; and dij is the distance between the origin and destination.
The inferred values are then combined with the true values to calculate the loss values using the MSE function. The loss functions for each task are as follows:
where is the total number of OD pairs, and is the number of geographic units. Finally, the total loss function in the GLGAT training process is formulated as a linearly weighted combination of the estimation errors from all three tasks, as shown in Equation (14).
where and denote the weights assigned to the main task and the subtasks, respectively. represents the error in the OD flow estimation for the main task, Lossin is the error in the inflow estimation for the destination in the subtask, and Lossout is the error in the outflow estimation.
After calculating the overall loss, it is back-propagated to train the parameters of the GLGAT and update the node embeddings in order to minimize the total error. The model parameters that yield the best performance on the validation dataset are then used to generate the final embeddings.
4.3. Flow Inference Using XGBoost for OD Flow Inference
With embedding learning, there is no longer a need to perform labor-intensive feature computation as the model automatically learns the feature distribution, reducing the need for feature engineering [41]. Therefore, we directly use the learnt node embeddings as inputs to the XGBoost regression model to infer OD flows. As an efficient implementation of GBDT, XGBoost not only inherits the advantages of GBDT but also makes a lot of optimizations at the algorithmic level. By iteratively evaluating the maximum information gain of the features, XGBoost is able to automatically select and combine useful numerical features to fit the target, with an excellent ability to fit non-linear relationships between input and output, which is well suited to processing structured data.
Specifically, we connect the node embedding vectors of the origin and destination (generated by the trained GLGAT) with their distance features as inputs to XGBoost to obtain the final OD flow estimation. This process is formulated in Equation (15).
5. Experiment Description
This section describes the details of the experiment, including data description and preprocessing, experimental environment, evaluation metrics, and baseline models.
5.1. Data Description and Preprocessing
In this study, we use three publicly available datasets and one self-constructed dataset. Each dataset consists of OD flow data and relevant urban indicator data. The three open datasets are from New York City, Los Angeles, and Seattle and are cited from Rong et al. [42]. For these U.S. cities, OD flow data are obtained from the LODES (Longitudinal Employer–Household Dynamics Origin–Destination Employment Statistics) project, maintained by the U.S. Census Bureau. This dataset provides stable commuting flows between home and work locations in 2015, aggregated to the census tract level. Urban indicator data include demographic attributes (e.g., population, income), POIs, and road network characteristics. Demographic data are sourced from the ACS (American Community Survey), while POIs and road network data are derived from the OpenStreetMap (OSM). These datasets collectively reflect the built environment and urban functions relevant to human mobility and transportation behavior.
However, as the U.S. datasets are limited to fixed-size spatial units (i.e., census tracts), they are unsuitable for evaluating model performance under different spatial division schemes. To address this, we construct a multi-scale dataset based on taxi trajectory data collected from the central area of Xi’an, China—a major urban center in Northwest China. The Xi’an dataset provides greater flexibility in spatial zoning, allowing us to analyze the effect of scale variation on OD flow inference.
The Xi’an taxi dataset was collected on 4 November 2019. Each record includes the vehicle ID, timestamp, latitude and longitude, passenger status (1 = occupied and 0 = vacant), and a GPS sampling interval of 10 s. To extract reliable OD pairs, we first performed data cleaning (e.g., removing duplicates, handling missing or invalid values) using the Pandas library in Python (3.10.6). Next, geographic coordinates were converted to the WGS84 reference system, and trajectories were matched to the road network using a geometric map-matching algorithm. The final OD flows were then aggregated based on various spatial zoning schemes (e.g., grid, TAZ, street). Finally, we obtained about 350,000 OD pair sequences by Algorithm 1. Figure 3 illustrates the extent of the study area and the kernel density analysis maps for the pick-up and drop-off points.
| Algorithm 1. Origin and Destination Extraction Algorithm |
| Input: T: Taxi trajectory dataset, where each ti represents a trip with a sequence of ordered points. Output: O: Set of origin points from T D: Set of destination points from T Procedure: Initialize: O = [], D = [] For each trip ti in T: Sorting: Sort data by “Vehicle Num” and then by “Time”. Shift: Use Shift() to move “Status” down by one row, storing the result in “Status_next”. Compute: Calculate Status Change = Status—Status_next: If Status Change == 1: Add to O ElseIf Status Change == −1: Add to D Return O, D |
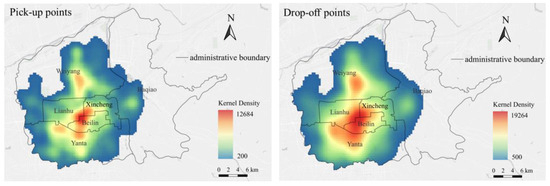
Figure 3.
Kernel density analysis of taxi pick-up and drop-off points in study area.
For the urban features, we select population, POIs, and road network indicators after referring to the impact guided by the impact factors considered in classical gravity and radiation models and the built environment’s 5D principle. These features are summarized in Table 2. The population data are sourced from a high-resolution (100 m) gridded dataset shared by Chen et al. on the Figshare platform [43]. This dataset was generated using a population downscaling method based on stacked ensemble learning and geospatial big data, calibrated against China’s Seventh National Population Census. The POI data are collected from the Gaode Map Open Platform (https://lbs.amap.com/, accessed on 20 August 2024). For this study, we select eight major categories of POIs that are closely related to human mobility. These categories include food and beverage services, shopping services, living services, company and enterprise locations, business and residential areas, science, education and cultural services, sports and leisure services, and transportation facilities, totaling 703,724 entries. The road network data were sourced from OpenStreetMap (OSM) and included attributes such as the road type, name, and number of lanes. For this study, we focused on key road types such as motorways, primary roads, secondary roads, and feeder roads, resulting in a total of 17,243 road entries. Finally, all data were spatially aligned with geographical analysis units through the GeoPandas and Shapely libraries.

Table 2.
Summary of urban indicators.
All the aforementioned data processing tasks are accomplished using widely available tools. This makes it easy to adapt to other cities with similar data sources. Moreover, the processed dataset can not only support OD flow inference but also be utilized for downstream tasks such as transportation planning and spatial accessibility assessment, providing practical value for the urban decision-making process.
In order to verify the influence of the spatial scale on the OD flow inference modeling, we adopt the three methods of using streets, TAZs, and regular grids as the zoning configurations. The specific shapes and statistics are shown in Figure 4 and Table 3, respectively. It should be noted that streets refer to administrative divisions at the street level, not road sections. Among them, four different sizes of grids, 500 m, 1000 m, 1500 m and 2000 m, are used as urban geographic units, covering the range from a fine scale to a coarse scale. These spatial scales are chosen because of their representativeness and comparability under current experimental conditions. However, we acknowledge that this choice does not fully capture the diversity of global urban forms, which will be further explored in future work. To evaluate the proposed model, we randomly divide the OD flow data into a training set (60%), validation set (20%), and test set (20%). The final results are re-scaled to the normal values to calculate the inference accuracy.
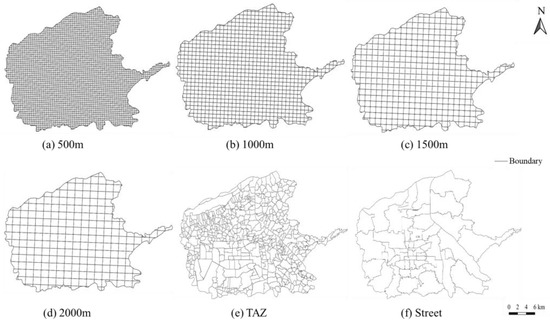
Figure 4.
The results of the different spatial scales in the study area.

Table 3.
Statistics of multi-scale spatial analysis units.
5.2. Baseline Models
To show the effectiveness of our model, we compare it to the following baselines:
- Gravity Model [10]. This is a classical model that proposes that OD flow between two zones is directly proportional to population and inversely proportional to distance.
- RF. This is a decision tree ensemble learning approach to circumvent overfitting and enhance performance. In this study, urban features and distance are directly concatenated as input to infer OD flows.
- GBRT. This is an iterative decision tree generation algorithm consisting of multiple decision trees as weak learners.
- XGBoost. This is a gradient boosting tree model that can be considered state of the art in many classification and regression tasks.
- Deep Gravity [14]. This is an enhanced version of the gravity model that takes more factors into account when modeling by using an FCNN.
- GCN [16]. This uses GCNs to embed information about urban features in geographically neighboring regions and uses a bilinear function to infer OD flows.
- GCN-RF [18]. This is similar to the abovementioned GCN model; however, the OD flows are inferred by using the RF.
- GMEL [17]. This uses two separate GATs to learn and generate embeddings for origin and destination, respectively. The GBRT is used to infer OD flows.
In this study, all the above models are retrained. Similar inputs are used in all models except the gravity model.
5.3. Experiment Setting
The proposed model is trained using pytorch, DGL and Sk-learn libraries. The training parameters are set as follows: we trained the model for 2000 epochs using the Adam Optimizer, using early stopping with 100 epochs to avoid overfitting, with a momentum of 0.9, a learning rate of 0.0001, and a batchsize of 64 to process. Unless otherwise stated, the parameters are selected using gridsearch with the searching space.
The model building parameters are set as follows: Having many GCN layers may lead to an oversmoothing problem [21]. Therefore, GAT in the GLGAT module uses a three-layer network with 256 layers of hidden layers. The global–local fusion weight is 0.7, which will be validated by subsequent experiments in the parameter sensitivity analysis section. Referring to the optimal settings given in the original work [17], the task weights in the decoder, and , are set to 0.5 and 0.25, respectively.
5.4. Evaluation Metrics
To quantitatively evaluate the performance of the models, we selected three metrics: the mean absolute error (MAE), root mean squared error (RMSE), and common part of commuters (CPC), based on both error and similarity. The CPC is an improved version of the Sørensen similarity index (SSI), which is widely used in spatial interaction modeling to assess the strengths and weaknesses of models. And its value ranges from [0,1], which can intuitively reflect the model inference accuracy, and the higher the model accuracy, the closer the value is to 1. The calculation of each indicator is as follows:
6. Results and Discussion
In this section, we conduct systematic experiments to analyze and discuss the proposed model. We summarize these experiments and discussions to answer the following research questions (RQs):
RQ 1: How does the overall performance of the proposed GLGAT-XG compare to the baseline model?
RQ 2: How does the fusion parameter in GLGAT affect the model performance, and is the overall model design effective?
RQ 3: What are the differences when GLGAT-XG processes OD flow datasets of different spatial scales?
RQ 4: How do the input features of the GLGAT-XG affect the inference results?
RQ 5: What application scenarios can the GLGAT-XG further support?
6.1. Performance Comparison with Baselines (RQ 1)
To validate the effectiveness of the proposed model, this subsection tests it against baseline models in three U.S. city datasets. Table 4 shows the experimental results. Based on the three evaluation metrics used in Section 5.4. Evaluation Metrics, our model exhibits the best performance in all respects. The RMSE, MAE, and CPC in NYC, LA, and Seattle are on average 8%, 7%, and 10% higher than the GMEL, respectively. We further analyze and explain the possible causes of each model’s performance, as shown below. The results of the experiments in the New York city show that the traditional model based on physical knowledge (i.e., gravity) performs the worst of all models. This is mainly explained by the fact that its validation relies on pre-defined theoretical frameworks and parameters and its simple formulae, which can severely limit its ability to understand complex non-linear relationships between inputs and outputs. ML-based models (i.e., RF, GBRT, XGBoost and Deep Gravity) perform better than gravity models. The data-driven modeling mechanism allows these models to handle non-linear relationships better. However, these models can only consider the node characteristics of the origin and the destination, the network topology characteristics and spatial proximity effects cannot be taken into account. The GNN-based model overcomes these drawbacks. This indicates its potential as a promising approach to solving the OD flow inference problem. Comparing the GCN and GCN-RF, the results also demonstrate the superiority of the three-component model over the two-component model. Among the baselines, the GMEL benefits from using the graph attention mechanism, the multitask learning strategy, and the three-component form; its performance is quite encouraging. In contrast to the GMEL, the proposed model takes into account a more comprehensive array of spatial semantic information. It is capable of capturing potential relationships between distant, non-geographic neighborhoods, thereby providing more effective insights for OD flow inference.

Table 4.
Performance of all models on three urban test datasets.
Figure 5 shows the distribution of the inferred and true results of the proposed model on the three city test sets. Looking further at the city subplots, it can be found that most of the scattered data of our model in NYC are distributed near the diagonal line, and the data in LA and Seattle are more scattered compared to NYC. In Seattle, it is easier to overestimate the inference value, and the effect becomes worse compared to the former cities. This may be due to differences in urban structure and OD flow data collection methods between cities. Notwithstanding, the performance of the proposed method on all metrics remains superior among all methods and exhibits effective generalization.
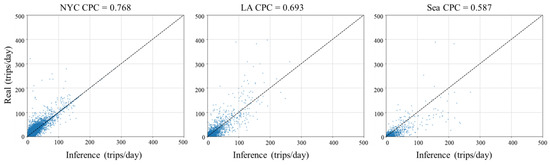
Figure 5.
Comparison of the inference effect of GLGAT-XG in different cities.
These findings not only verify the effectiveness of our model in various urban environments but also demonstrate its potential to replace existing commonly used OD flow inference models, thereby supporting practical applications in traffic demand modeling.
6.2. Performance Comparison with Model Variants (RQ 2)
To verify the rationality of the model design and parameter settings, this subsection conducts ablation experiments and sensitivity analysis experiments on the proposed model.
Ablation experiments of different functional modules. This part focuses on verifying the impact of using different node embedders (i.e., encoders) and flow inferences on the overall model. As demonstrated in Table 5, a comparison is made between the GLGAT-RF, GLGAT-GBRT, and GLGAT-XGBoost models, which use different tree models as the flow inference. It can be found that the performance of the tree model itself is positively correlated with the overall performance of the OD inference model, given the same node embedder. Therefore, we select the XGBoost that performed the best in this study. Then, comparing methods GCN-XGBoost, GAT-XGBoost, GLGAT-XGBoost, which use the same flow inference with different node embedders, it can be similarly found that the node embedder performance is positively correlated with the overall performance of the OD inference model. For this reason, we propose GLGAT to improve the performance of the encoder to achieve better inference results.

Table 5.
The performance of different model variants on the NYC test dataset.
Sensitivity analysis of fusion weighting . This part aims to explore the effect of different fusion weight parameters on the performance of the proposed model. Figure 6 shows the variation in the RMSE and CPC obtained by GLGAT-XG on the NYC test set using different weights . The results show that the performance of it shows an overall trend of increasing and then decreasing with the increase in . The x-axis is the different combinations of weights, and we experiment with the value from 0 to 1, increasing it by 0.1 each time, and the y-axis is the evaluation metric of the model performance. Combined with Equation (1), it can be seen that GLGAT does not use the global graph attention mechanism when is 0, at which time GLGAT is equal to GAT; when is 1, GLGAT does not use the local graph attention, at which time GLGAT is equal to SGFormer. Therefore, it can be shown that the use of the global attention mechanism improves the inference accuracy of the model, but it also follows the law of diminishing marginal utility, i.e., over-reliance also leads to a degradation of model performance. Finally, we set to 0.7 to ensure the validity of GLGAT.
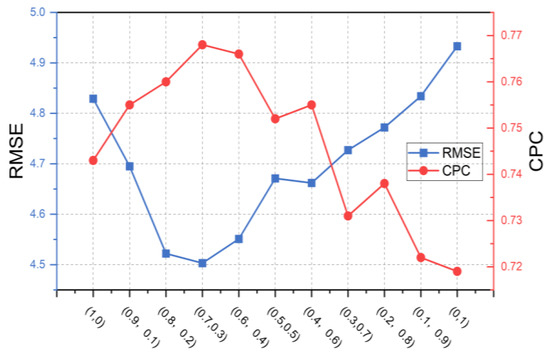
Figure 6.
Performance comparison of GLGAT-XG with different fusion weights.
6.3. Performance Comparison with Multi-Scale Units of Analysis (RQ 3)
To reveal the impact of the spatial scale on OD flow inference, this subsection conducts a quantitative comparison on datasets of different scales within the same city. As shown in Figure 7, the model’s inference accuracy follows a rise-then-fall trend as the spatial scale increases. At the 500 m scale, data detail is much greater and the model can capture acceptable spatial variability. However, it can be affected by noise and local variations, resulting in poor inference accuracy. Local details are properly aggregated at the 1000 m scale, noise is suppressed, and the model extracts functional spatial patterns more effectively, improving accuracy. Beyond 1000 m, the spatial aggregation causes much of the detail information to be lost, leading to the model’s inability to effectively differentiate feature differences between different zones. This overly broad aggregation reduces the model’s ability to capture details, decreasing inference accuracy. Furthermore, we find that the model inferred better when using grids as the analysis units compared to irregularly shaped units such as streets or TAZs. Regular shapes are simpler and more explicit in terms of boundary effects and adjacencies and may help the model to extract spatial features more consistently. These findings are crucial for urban planning as they provide guidance for selecting an appropriate spatial scale for OD flow analysis. This helps to mitigate policy ineffectiveness caused by scale mismatch and provides a basis for subsequent planning decisions.
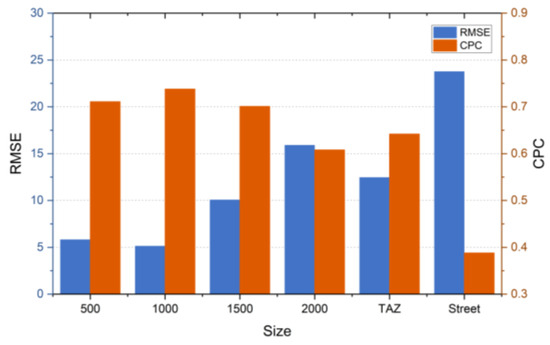
Figure 7.
Performance comparison of GLGAT-XG on multi-scale OD test dataset in Xi’an.
Figure 8 shows the visualization of the real and inferred OD flows in Xi’an, where the edge values denote the total flow between the two zones. The GLGAT-XG model successfully captures the overall structure and key features of the OD flow network in Xi’an, performing particularly well under grid units. Although the inferred results in some high-flow areas are slightly lower than the actual values, the model accurately reflects the “center-to-periphery” flow distribution pattern, showcasing its strong capability in reproducing spatial flow networks.
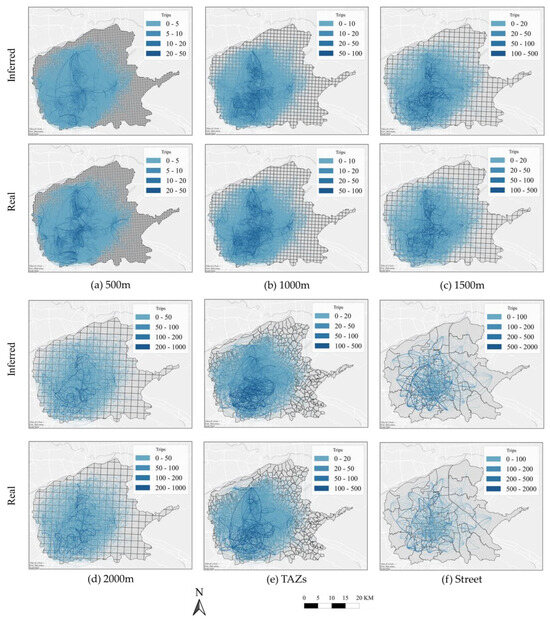
Figure 8.
Visualization of distribution of real and inferred OD flows on multi-scale OD test dataset in Xi’an.
6.4. An Interpretation of the Impact of Urban Features (RQ 4)
To explore the impact of different input features on the model output results, this subsection conducts an interpretable analysis of urban indicators that affect the model’s inference performance in order to determine which features play a key role. Specifically, we utilize Shapley additive explanations (SHAP) to assess the magnitude and direction of each input feature’s impact on the model’s results. Figure 9 illustrates the contribution of various urban indicator characteristics to the model inference at the 1000 m grid scale. From the SHAP value distribution of the top 20 most influential features shown in Figure 9, it is evident that distance is the most significant factor influencing the model, with a negative impact. This aligns with the travel cost factor in the gravity model, where higher travel costs typically reduce the willingness of individuals to choose to travel. In addition to distance, the top five influential features include the following: transport facilities at the origin, catering facilities at the destination, catering facilities at the origin, and the length of the primary road at the origin. These features show a positive contribution to the OD flow, as reflected in their higher SHAP values.
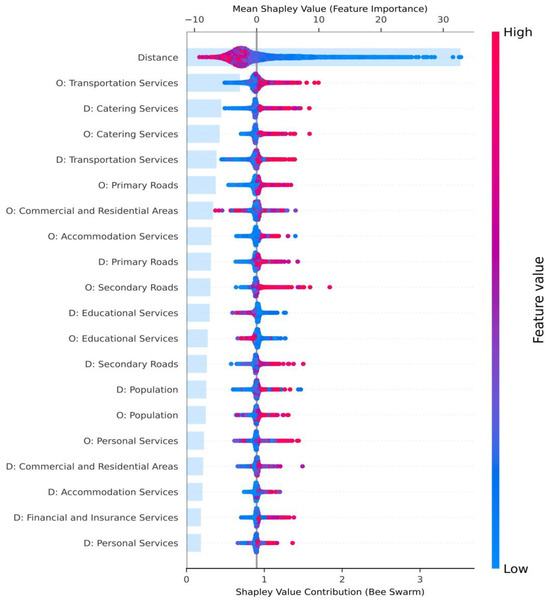
Figure 9.
The distribution of Shapley values for the top 20 features in GLGAT-XG.
The explanation for the above findings is as follows: Transport services are often hubs where large numbers of people congregate and move frequently. Public transport and taxis are complementary modes of transportation, and many people opt for taxis for the “first mile” or “last mile” after reaching transport facilities. For instance, at major transport hubs such as bus terminals, railway stations, or airports, passengers often use taxis to reach their next destination, especially if public transport options do not provide a direct connection. Secondly, Xi’an, a culinary capital, has many restaurant facilities (e.g., bars, night markets, and snack streets) that attract both residents and tourists. Areas with a high concentration of restaurant facilities tend to be busy commercial districts with limited parking resources. In such areas, people are more likely to choose taxis to avoid parking difficulties, particularly in famous dining neighborhoods where parking is a common issue. Lastly, primary roads connect major urban areas, such as business districts, residential areas, and transport hubs. High-density primary road areas are more accessible, allowing passengers to reach their destinations directly via taxi. This is especially true for longer journeys or when traveling across districts, as areas with a high density of primary roads serve as convenient starting points for taxi travel. Interestingly, population characteristics, which are often central to traditional models, did not have a significant impact on our model. This may be because taxi demand is more closely related to the income levels of residents rather than the sheer population size of an area. Population density alone does not account for income disparities; areas with high population density but relatively low incomes may see residents opting for more affordable public transport rather than taxis.
These findings demonstrate the compatibility of our model with traditional models and strengthen the credibility of our interpretation of the results. Additionally, from a planning perspective, the results also highlight key intervention points: increasing the density of transportation facilities and improving the accessibility of main roads in high-demand areas can effectively meet travel demands. These insights are valuable for demand-responsive public transit planning and transit-oriented development (TOD) site selection.
6.5. The Application of the GLGAT-XG Model (RQ 5)
Based on the modeling of the non-linear relationship between flow distribution and urban geographic features, the GLGAT-XG offers several practical applications: (1) Future OD Flows Distribution Prediction: It can support long-term traffic planning by helping to understand future high-demand areas, rationalizing resource allocation to meet expected growth. By integrating predictive urban indicators (e.g., future land use, population growth, or infrastructure projects) as the inputs, GLGAT-XG can predict future OD flow. (2) Spatial Missing OD Flow Imputation: Missing data in certain zones are a common issue due to device failures or data storage limitations. By training GLGAT-XG with OD flow data from known regions, the model can generate highly reliable data for regions with missing data, supporting robust modeling in cities with limited sensing infrastructure. (3) OD flow inference for unmonitored or unsurveyed areas: Comprehensive surveys across different zones can be costly and time-consuming. Through transfer learning adaptation to local geographic contexts, the model generates plausible OD flow distributions to support mobility assessment and planning decisions in data-scarce cities or new developments.
7. Conclusions
OD flow data can effectively reveal the complex linkages between urban transport, land use, and economic development. In this paper, we propose a three-component OD flow inference model—encoder, decoder, and flow inference—that combines global and local graph attention networks. We then examine the model’s performance across multiple spatial scales and quantitatively evaluate how each urban indicator influences OD flow inference at the optimal scale.
The main findings of this study are summarized as follows: (1) The global graph attention network enhances the model’s ability to capture spatial correlations, thus improving the accuracy of inferring OD flows. (2) The three-component OD flow inference model outperforms the two-component model in accuracy and stability. Next, the performance improvement of the encoder and flow inference also helps to further enhance the accuracy of external flow inference. (3) A suitable spatial scale can further improve the accuracy of OD flow inference. Experiments on the multi-scale OD dataset indicate that the model performs better at the 1000 m grid scale compared to other scales. (4) At the 1000 m grid scale, distance emerges as the most influential urban characteristic indicator, followed by transport services and catering services at both origin and destination points. In summary, our model advances current inference methodology and provides a feasible substitute in situations where direct survey data are scarce.
There are still some limitations in this paper. Firstly, the data sources used in this study have inherent limitations in terms of both spatial and temporal coverage, which may result in analytical conclusions that do not fully represent the actual situation in the city. In the future, the OD flows can be obtained through mobile phone data, which can be used to further calibrate the model to better understand crowd movement. Secondly, we empirically identified six scales of analysis and explored the impact of spatial scale effects on the accuracy of OD flow inferences, which are not conducive to a comprehensive understanding of model performance variation and optimal scale selection. In the future, we intend to use a multitask learning approach to combine scale segmentation with OD flow inference to determine the optimal analysis scale in a data-driven manner. Moreover, we will integrate urban trajectory datasets from multiple cities for cross-city experiments and improve the model’s adaptability to different urban morphologies and functional structures by transfer learning. We will extract richer semantic information (e.g., land use, traffic accessibility, etc.) from OSM to further improve the model’s context-awareness and inference accuracy.
Author Contributions
Conceptualization, Zhenyu Shan and Fei Yang; methodology, Zhenyu Shan and Yaping Cui; funding acquisition, Fei Yang; software, Zhenyu Shan, Xingzi Shi; validation, Yaping Cui; formal analysis, Fei Yang; resources, Zhenyu Shan and Fei Yang; writing—original draft, Zhenyu Shan; writing—review and editing, Yaping Cui, and Fei Yang; visualization, Zhenyu Shan and Xingzi Shi; project administration, Fei Yang. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 52072313; the China Ministry of Transport Planning and Research Institute Open Project, grant number KYL202312-0160; and Shanxi Provincial Department of Transportation 2024 Annual Transportation Science and Technology Research Projects, grant number 24-12R.
Data Availability Statement
The multi-scale OD dataset in Xi’an supporting the conclusions of this article will be made available by the authors on request. The New York City-, Los Angeles-, and Seattle-related datasets are available in GitHub at https://github.com/tsinghua-fib-lab/OD_benckmark, accessed date 15 July 2024.
Acknowledgments
The authors would like to sincerely thank the anonymous reviewers for their constructive comments and valuable suggestions to improve the quality of this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhao, Y.; Cheng, S.; Gao, S.; Wang, P.; Lu, F. Predicting origin-destination flows by considering heterogeneous mobility patterns. Sustain. Cities Soc. 2025, 118, 106015. [Google Scholar] [CrossRef]
- Hu, T.; Wang, S.; She, B.; Zhang, M.; Huang, X.; Cui, Y.; Khuri, J.; Hu, Y.; Fu, X.; Wang, X.; et al. Human Mobility Data in the COVID-19 Pandemic: Characteristics, Applications, and Challenges. Int. J. Digit. Earth 2021, 14, 1126–1147. [Google Scholar] [CrossRef]
- Casali, Y.; Aydin, N.Y.; Comes, T. Machine Learning for Spatial Analyses in Urban Areas: A Scoping Review. Sustain. Cities Soc. 2022, 85, 104050. [Google Scholar] [CrossRef]
- Fadlullah, Z.M.; Tang, F.; Mao, B.; Kato, N.; Akashi, O.; Inoue, T.; Mizutani, K. State-of-the-Art Deep Learning: Evolving Machine Intelligence toward Tomorrow’s Intelligent Network Traffic Control Systems. IEEE Commun. Surv. Tutor. 2017, 19, 2432–2455. [Google Scholar] [CrossRef]
- Bassolas, A.; Barbosa-Filho, H.; Dickinson, B.; Dotiwalla, X.; Eastham, P.; Gallotti, R.; Ghoshal, G.; Gipson, B.; Hazarie, S.A.; Kautz, H.; et al. Hierarchical Organization of Urban Mobility and Its Connection with City Livability. Nat. Commun. 2019, 10, 4817. [Google Scholar] [CrossRef]
- Wang, J.; Song, J.; Zhao, C.; Ban, X.J. Distributionally robust origin–destination demand estimation. Transp. Res. Part C Emerg. Technol. 2024, 165, 104716. [Google Scholar] [CrossRef]
- Kamel Boulos, M.N.; Kwan, M.-P.; El Emam, K.; Chung, A.L.-L.; Gao, S.; Richardson, D.B. Reconciling Public Health Common Good and Individual Privacy: New Methods and Issues in Geoprivacy. Int. J. Health Geogr. 2022, 21, 1. [Google Scholar] [CrossRef]
- Savage, N. Synthetic Data Could Be Better than Real Data. Nature 2023. [Google Scholar] [CrossRef]
- Liu, K. Approaches for Human Mobility Data Generation: Research Progress and Trends. J. Geo-Inf. Sci. 2024, 26, 1–12. [Google Scholar] [CrossRef]
- Zipf, G.K. The P 1 p 2 D Hypothesis: On the Intercity Movement of Persons. Am. Sociol. Rev. 1946, 11, 677. [Google Scholar] [CrossRef]
- Simini, F.; González, M.C.; Maritan, A.; Barabási, A.-L. A Universal Model for Mobility and Migration Patterns. Nature 2012, 484, 96–100. [Google Scholar] [CrossRef] [PubMed]
- Stouffer, S.A. Intervening Opportunities: A Theory Relating Mobility and Distance. Am. Sociol. Rev. 1940, 5, 845. [Google Scholar] [CrossRef]
- Pourebrahim, N.; Sultana, S.; Niakanlahiji, A.; Thill, J.-C. Trip Distribution Modeling with Twitter Data. Comput. Environ. Urban Syst. 2019, 77, 101354. [Google Scholar] [CrossRef]
- Simini, F.; Barlacchi, G.; Luca, M.; Pappalardo, L. A Deep Gravity Model for Mobility Flows Generation. Nat. Commun. 2021, 12, 6576. [Google Scholar] [CrossRef]
- Robinson, C.; Dilkina, B. A Machine Learning Approach to Modeling Human Migration. In Proceedings of the 1st ACM SIGCAS Conference on Computing and Sustainable Societies, Menlo Park, CA, USA, 20–21 June 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Yao, X.; Gao, Y.; Zhu, D.; Manley, E.; Wang, J.; Liu, Y. Spatial Origin-Destination Flow Imputation Using Graph Convolutional Networks. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7474–7484. [Google Scholar] [CrossRef]
- Liu, Z.; Miranda, F.; Xiong, W.; Yang, J.; Wang, Q.; Silva, C. Learning Geo-Contextual Embeddings for Commuting Flow Prediction. Proc. AAAI Conf. Artif. Intell. 2020, 34, 808–816. [Google Scholar] [CrossRef]
- Yin, G.; Huang, Z.; Bao, Y.; Wang, H.; Li, L.; Ma, X.; Zhang, Y. CONVGCN-RF: A Hybrid Learning Model for Commuting Flow Prediction Considering Geographical Semantics and Neighborhood Effects. GeoInformatica 2022, 27, 137–157. [Google Scholar] [CrossRef]
- Shi, Q.; Zhuo, L.; Tao, H.; Yang, J. A Fusion Model of Temporal Graph Attention Network and Machine Learning for Inferring Commuting Flow from Human Activity Intensity Dynamics. Int. J. Appl. Earth Obs. Geoinf. 2024, 126, 103610. [Google Scholar] [CrossRef]
- Klemmer, K.; Safir, N.S.; Neill, D.B. Positional Encoder Graph Neural Networks for Geographic Data. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Virtual Conference, 25–27 April 2023; pp. 1379–1389. [Google Scholar] [CrossRef]
- Wu, Q.; Zhao, W.; Li, Z.; Wipf, D.; Yan, J. Nodeformer: A Scalable Graph Structure Learning Transformer for Node Classification. In Proceedings of the 36th Conference on Neural Information Processing Systems (NeurIPS), New Orleans, LA, USA, 10–16 December 2022. [Google Scholar] [CrossRef]
- Yan, X.-Y.; Zhao, C.; Fan, Y.; Di, Z.; Wang, W.-X. Universal Predictability of Mobility Patterns in Cities. J. R. Soc. Interface 2014, 11, 20140834. [Google Scholar] [CrossRef]
- Pei, T.; Liu, Y.X.; Guo, S.H.; Shu, H.; Du, Y.; Ma, T.; Zhou, C. Principle of Big Geodata Mining. Acta Geogr. Sin. 2019, 74, 586–598. [Google Scholar] [CrossRef]
- Lv, C.; Qi, M.; Li, X.; Yang, Z.; Ma, H. Sgformer: Semantic Graph Transformer for Point Cloud-Based 3D Scene Graph Generation. Proc. AAAI Conf. Artif. Intell. 2024, 38, 4035–4043. [Google Scholar] [CrossRef]
- Liu, E.; Yan, X. New Parameter-Free Mobility Model: Opportunity Priority Selection Model. Phys. A 2019, 526, 121023. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46 (Suppl. 1), 234. [Google Scholar] [CrossRef]
- Xing, X.; Huang, Z.; Cheng, X.; Zhu, D.; Kang, C.; Zhang, F.; Liu, Y. Mapping human activity volumes through remote sensing imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5652–5668. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar] [CrossRef]
- Pan, Z.; Liang, Y.; Wang, W.; Yu, Y.; Zheng, Y.; Zhang, J. Urban Traffic Prediction from Spatio-Temporal Data Using Deep Meta Learning. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, H.; Chen, H.; Wo, T.; Xu, J.; Zheng, K. Origin-Destination Matrix Prediction via Graph Convolution. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar] [CrossRef]
- Cheng, Z.; Trépanier, M.; Sun, L. Real-Time Forecasting of Metro Origin-Destination Matrices with High-Order Weighted Dynamic Mode Decomposition. Transp. Sci. 2022, 56, 904–918. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, K.; Wen, D.; Chen, D.; Lv, H.; Zhang, Q. Deep Learning for Metro Short-Term Origin-Destination Passenger Flow Forecasting Considering Section Capacity Utilization Ratio. IEEE Trans. Intell. Transp. Syst. 2023, 24, 7943–7960. [Google Scholar] [CrossRef]
- Lv, S.; Wang, K.; Yang, H.; Wang, P. An Origin–Destination Passenger Flow Prediction System Based on Convolutional Neural Network and Passenger Source-Based Attention Mechanism. Expert Syst. Appl. 2024, 238, 121989. [Google Scholar] [CrossRef]
- Li, Q.; Han, Z.; Wu, X.-M. Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar] [CrossRef]
- Alon, U.; Yahav, E. On the Bottleneck of Graph Neural Networks and Its Practical Implications. In Proceedings of the International Conference on Learning Representations, Virtual Conference, 3–7 May 2021. [Google Scholar] [CrossRef]
- Nejadshamsi, S.; Bentahar, J.; Eicker, U.; Wang, C.; Jamshidi, F. A Geographic-Semantic Context-Aware Urban Commuting Flow Prediction Model Using Graph Neural Network. Expert Syst. Appl. 2025, 261, 125534. [Google Scholar] [CrossRef]
- Zhang, B.; Fan, C.; Liu, S.; Huang, K.; Zhao, X.; Huang, J.; Liu, Z. The Expressive Power of Graph Neural Networks: A Survey. IEEE Trans. Knowl. Data Eng. 2025, 37, 1455–1474. [Google Scholar] [CrossRef]
- Wang, L.; Geng, X.; Ma, X.; Liu, F.; Yang, Q. Cross-City Transfer Learning for Deep Spatio-Temporal Prediction. In Proceedings of the 28th International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 1893–1899. [Google Scholar] [CrossRef]
- Guo, J.; Bai, S.; Li, X.; Xian, K.; Liu, E.; Ding, W.; Ma, X. A Universal Geography Neural Network for Mobility Flow Prediction in Planning Scenarios. Comput.-Aided Civ. Infrastruct. Eng. 2025; in press. [Google Scholar] [CrossRef]
- Wu, Z.H.; Jain, P.; Wright, M.A.; Mirhoseini, A.; Gonzalez, J.E.; Stoica, I. Representing Long-Range Context for Graph Neural Networks with Global Attention. In Proceedings of the 35th Conference on Neural Information Processing Systems (NeurIPS), Virtual Conference, 6–14 December 2021. [Google Scholar] [CrossRef]
- Cai, M.; Pang, Y.; Sekimoto, Y. Spatial Attention Based Grid Representation Learning for Predicting Origin–Destination Flow. In Proceedings of the 2022 IEEE International Conference on Big Data (Big Data), Osaka, Japan, 13–16 December 2022; pp. 485–494. [Google Scholar] [CrossRef]
- Rong, C.; Ding, J.; Li, Y. An Interdisciplinary Survey on Origin-Destination Flows Modeling: Theory and Techniques. ACM Comput. Surv. 2024, 57, 1–49. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, C.; Ge, Y.; Zhang, X.; Zhou, Y. A 100-M Gridded Population Dataset of China’s Seventh Census Using Ensemble Learning and Geospatial Big Data. Earth Syst. Sci. Data, 2024; Submitted. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).