The Machine Learning-Based Mapping of Urban Pluvial Flood Susceptibility in Seoul Integrating Flood Conditioning Factors and Drainage-Related Data †
Abstract
1. Introduction
2. Literature Review
2.1. Urban Flooding
2.2. Modeling Flood Susceptibility
3. Materials and Methods
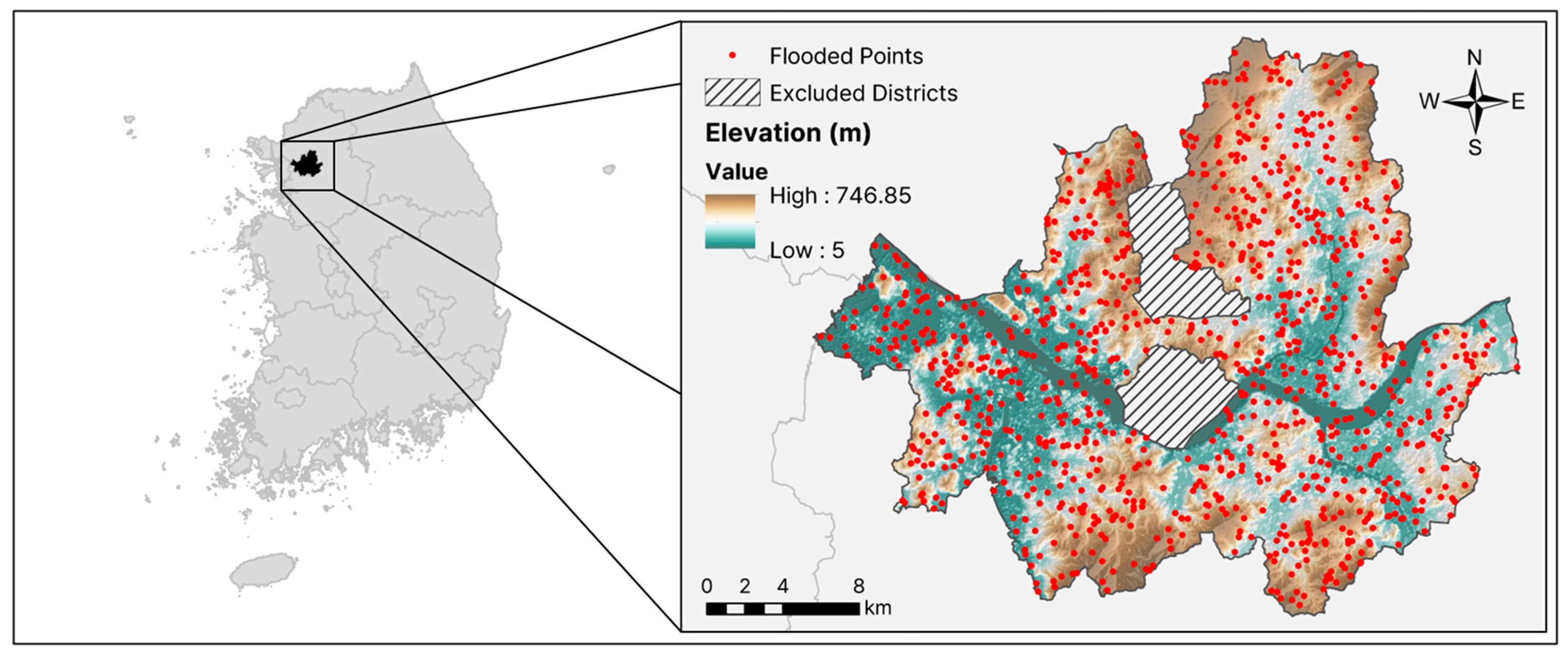
3.1. Spatial Datasets
3.2. Factor Selection
3.3. Machine Learning Methods
3.3.1. Logistic Regression
3.3.2. Random Forest
3.3.3. Support Vector Machines
3.4. Model Building
3.5. Model Evaluation Criteria
4. Results
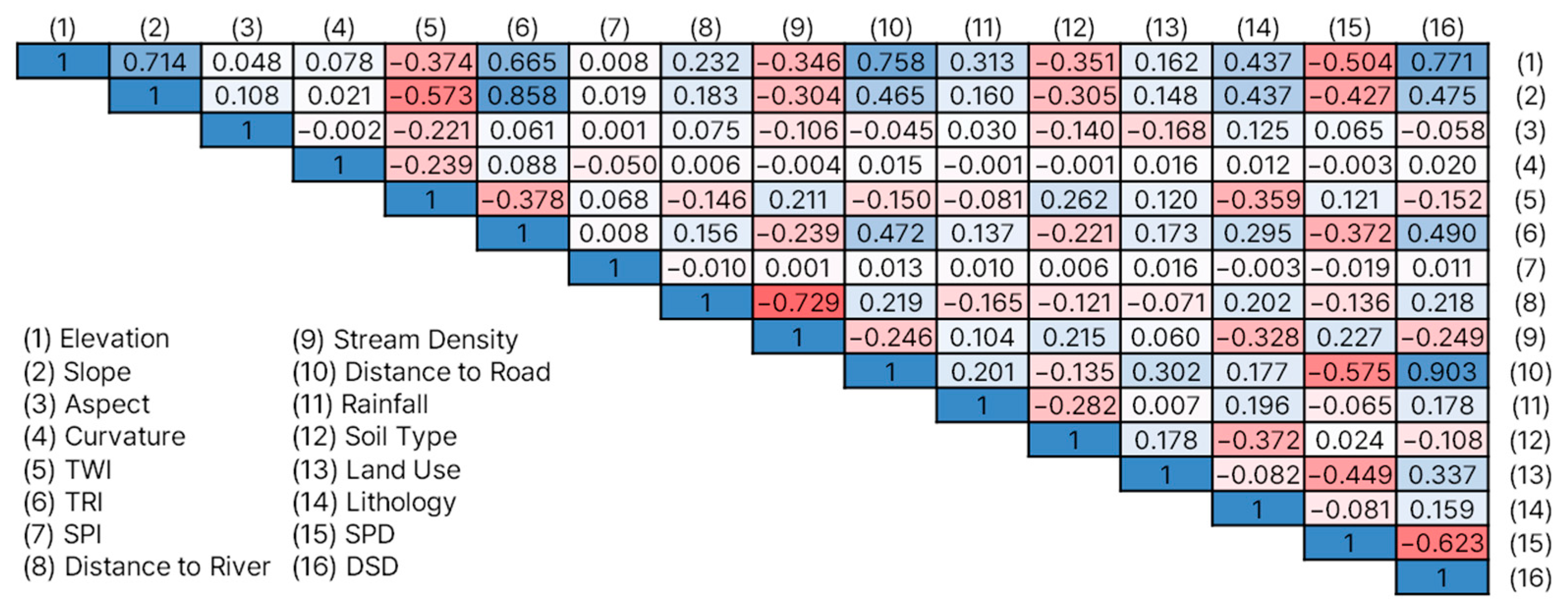
4.1. Correlation and Multi-Collinearity Analysis
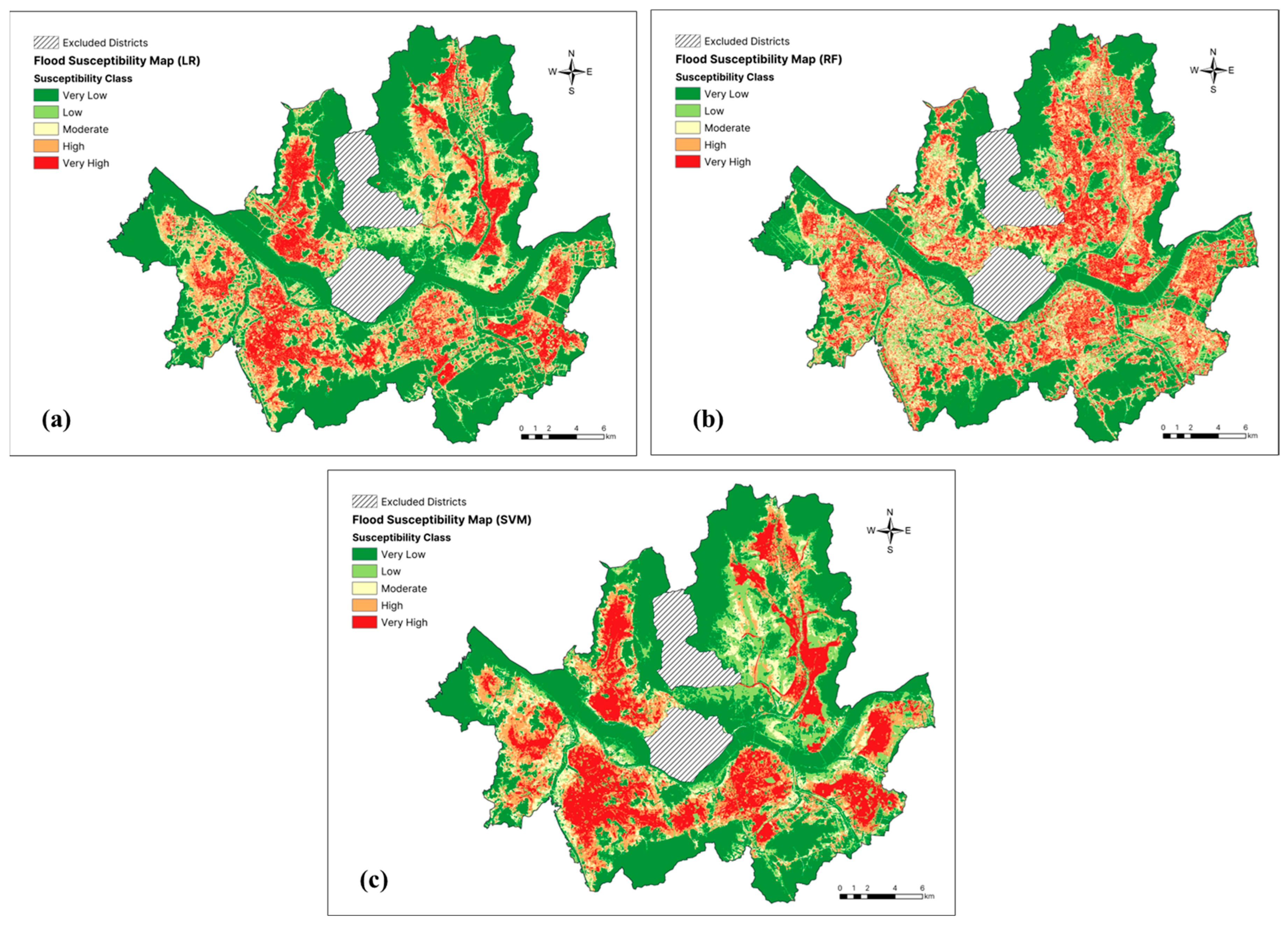
4.2. Generation of Flood Susceptibility Maps
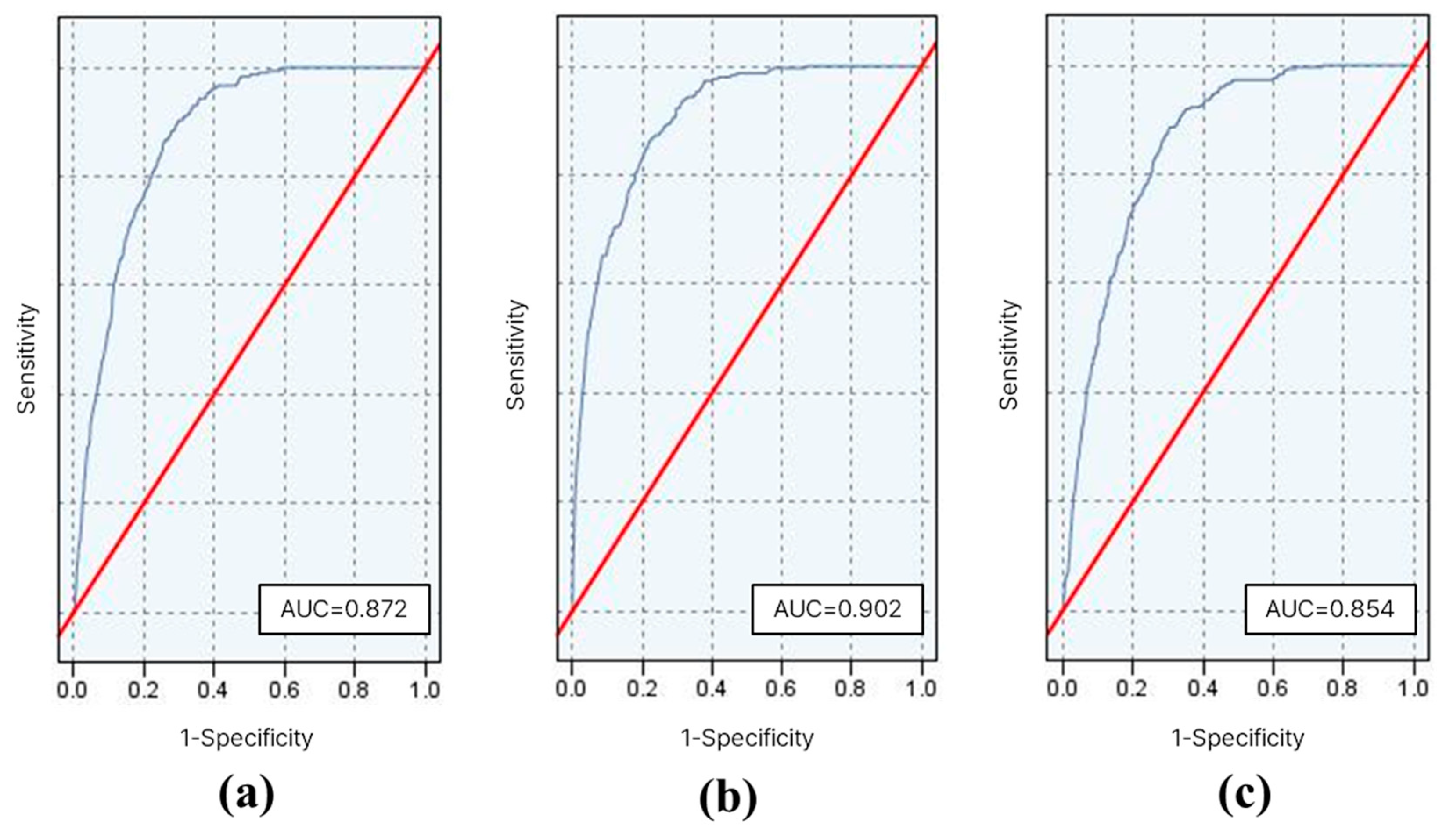
4.3. Validating the Models
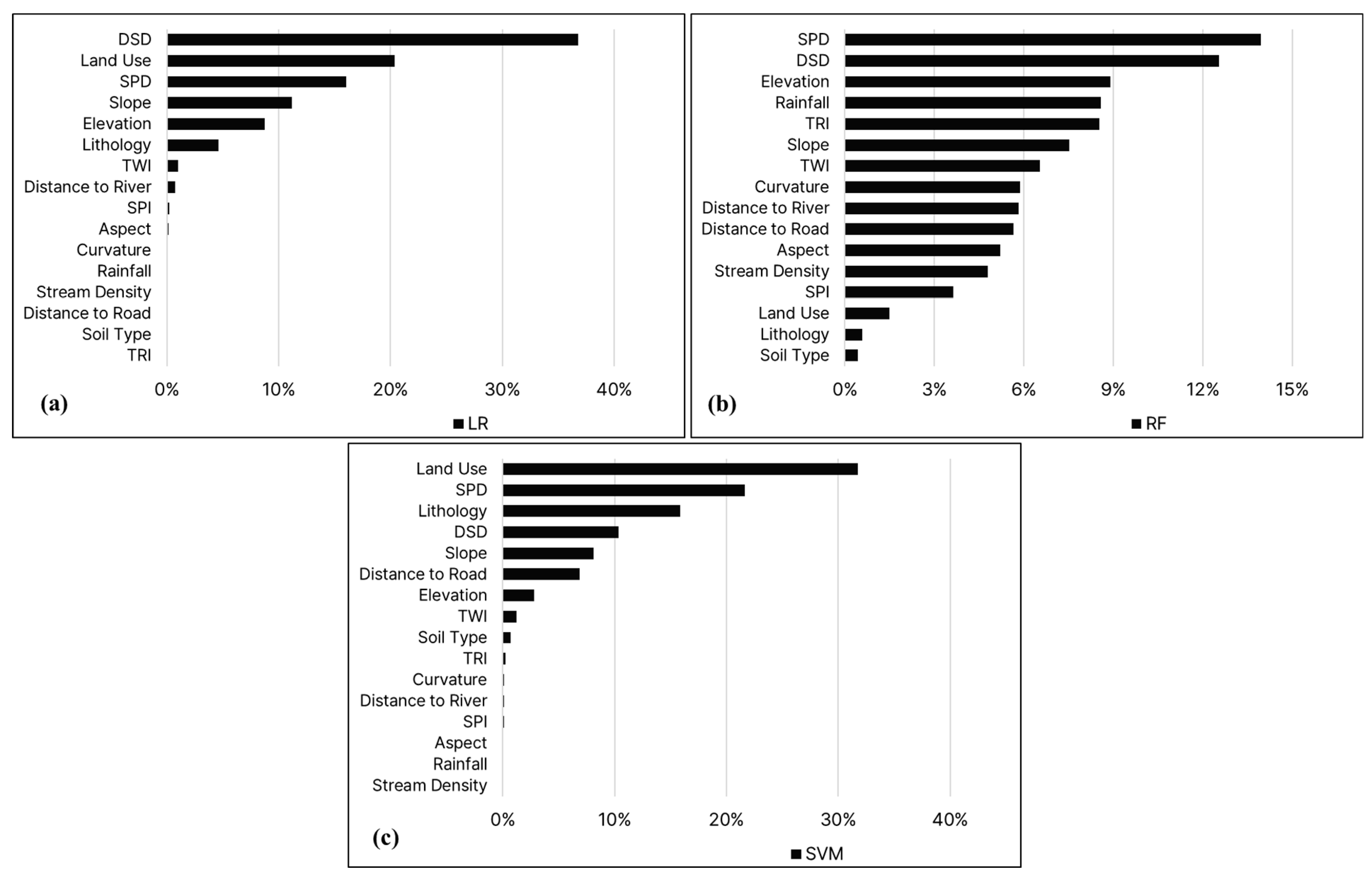
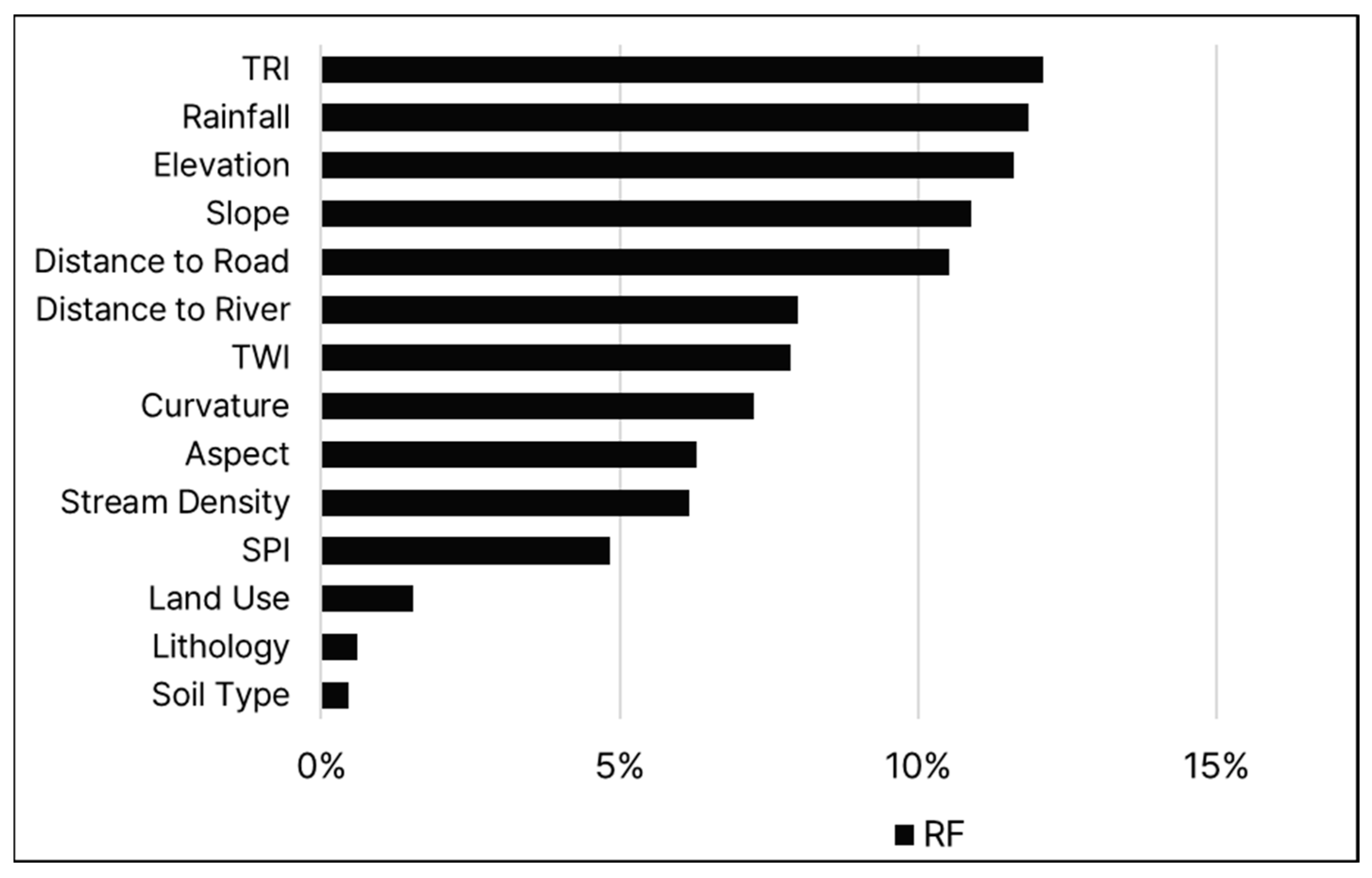
4.4. Relative Importance and Partial Dependence of Flood Conditioning Factors
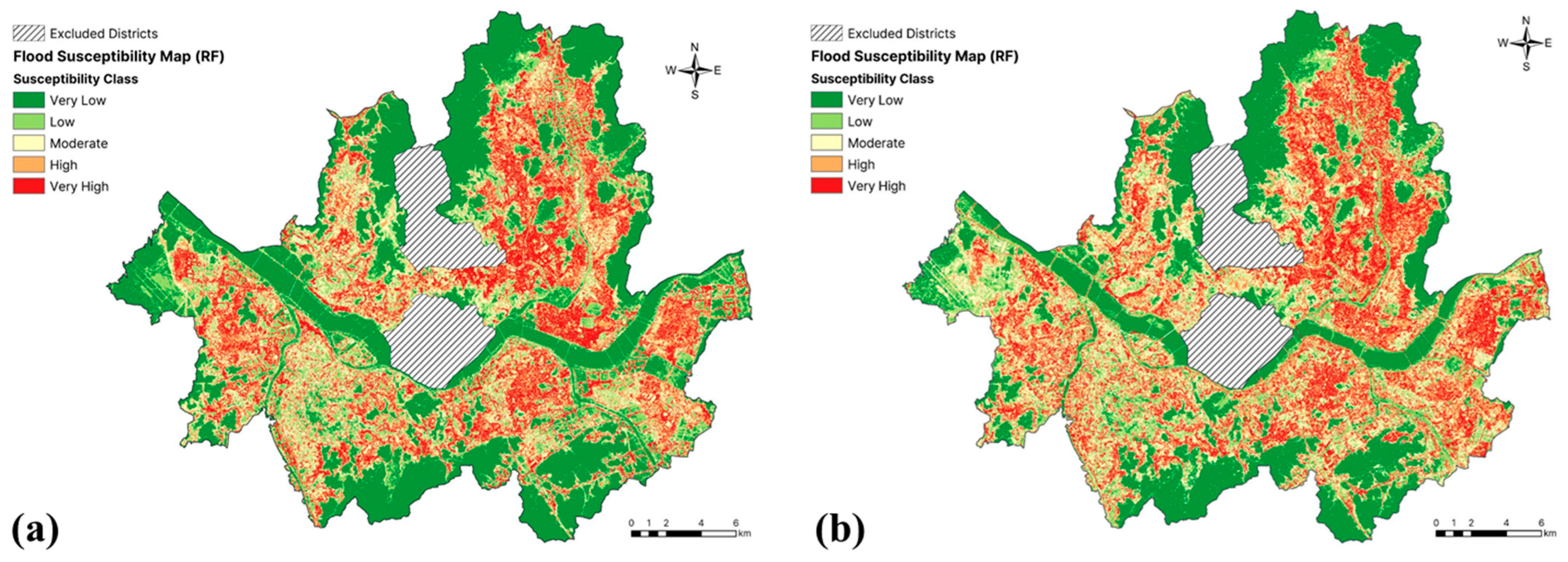
4.5. Impact of Drainage-Related Variables
5. Discussion
5.1. Flood Susceptibility Maps
5.2. Impact of Flood Conditioning Factors
5.3. Model Performance Comparison
5.4. Study Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bloch, R.; Jha, A.K.; Lamond, J. Cities and flooding: A guide to integrated urban flood risk management for the 21st century; World Bank: Washington DC, USA, 2012; ISBN 978-0-8213-9477-9. [Google Scholar]
- Ha, G.; Jung, J. The Impact of Urbanization and Precipitation on Flood Damages. J. Korea Plan. Assoc. 2017, 52, 237–252. [Google Scholar] [CrossRef]
- Korea Research Institute for Human Settlements. KRIHS Issue Report No. 67; Korea Research Institute for Human Settlements: Sejong, Republic of Korea, 2022. [Google Scholar]
- Park, S.; Kim, J.; Kang, J. Exploring Optimal Deep Tunnel Sewer Systems to Enhance Urban Pluvial Flood Resilience in the Gangnam Region, South Korea. J. Environ. Manag. 2024, 357, 120762. [Google Scholar] [CrossRef]
- Flores, A.B.; Collins, T.W.; Grineski, S.E.; Amodeo, M.; Porter, J.R.; Sampson, C.C.; Wing, O. Federally Overlooked Flood Risk Inequities in Houston, Texas: Novel Insights Based on Dasymetric Mapping and State-of-the-Art Flood Modeling. Ann. Am. Assoc. Geogr. 2023, 113, 240–260. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.C.; Jung, H.S.; Lee, M.J.; Lee, S. Spatial Prediction of Flood Susceptibility Using Random-Forest and Boosted-Tree Models in Seoul Metropolitan City, Korea. Geomat. Nat. Hazards Risk 2017, 8, 1185–1203. [Google Scholar] [CrossRef]
- Lee, S.; Lee, S.; Lee, M.J.; Jung, H.S. Spatial Assessment of Urban Flood Susceptibility Using Data Mining and Geographic Information System (GIS) Tools. Sustainability 2018, 10, 648. [Google Scholar] [CrossRef]
- Lee, J.Y.; Kim, J.S. Detecting Areas Vulnerable to Flooding Using Hydrological-Topographic Factors and Logistic Regression. Appl. Sci. 2021, 11, 5652. [Google Scholar] [CrossRef]
- Narimani, R.; Jun, C.; Shahzad, S.; Oh, J.; Park, K. Application of a Novel Hybrid Method for Flood Susceptibility Mapping with Satellite Images: A Case Study of Seoul, Korea. Remote Sens. 2021, 13, 2786. [Google Scholar] [CrossRef]
- Lei, X.; Chen, W.; Panahi, M.; Falah, F.; Rahmati, O.; Uuemaa, E.; Kalantari, Z.; Ferreira, C.S.S.; Rezaie, F.; Tiefenbacher, J.P.; et al. Urban Flood Modeling Using Deep-Learning Approaches in Seoul, South Korea. J. Hydrol. 2021, 601, 126684. [Google Scholar] [CrossRef]
- Palla, A.; Colli, M.; Candela, A.; Aronica, G.T.; Lanza, L.G. Pluvial Flooding in Urban Areas: The Role of Surface Drainage Efficiency. J. Flood Risk Manag. 2018, 11, S663–S676. [Google Scholar] [CrossRef]
- Carmin, J.; Dodman, D.; Chu, E.; Carmin, J.; Dodman, D.; Chu, E. Urban Climate Adaptation and Leadership: From Conceptual Understanding to Practical Action Green Growth and Poverty Reduction: Policy Coherence for Pro-Poor Growth; OECD Regional Development Working Papers; OECD Publishing: Paris, France, 2013. [Google Scholar]
- Atta-ur-Rahman; Parvin, G.A.; Shaw, R.; Surjan, A. Cities, Vulnerability, and Climate Change. In Urban Disasters and Resilience in Asia; Butterworth-Heinemann: Oxford, UK, 2016. [Google Scholar]
- Lee, S.; Kim, B.; Choi, H.; Noh, S.J. A Review on Urban Inundation Modeling Research in South Korea: 2001-2022. J. Korea Water Resour. Assoc. 2022, 55, 707–721. [Google Scholar]
- Ha, J.; Kang, J.E. Assessment of Flood-Risk Areas Using Random Forest Techniques: Busan Metropolitan City. Nat. Hazards 2022, 111, 2407–2429. [Google Scholar] [CrossRef]
- Agonafir, C.; Lakhankar, T.; Khanbilvardi, R.; Krakauer, N.; Radell, D.; Devineni, N. A Review of Recent Advances in Urban Flood Research. Water Secur. 2023, 19, 100141. [Google Scholar] [CrossRef]
- Chang, H.; Franczyk, J. Climate Change, Land-Use Change, and Floods: Toward an Integrated Assessment. Geogr. Compass 2008, 2, 1549–1579. [Google Scholar] [CrossRef]
- Seydi, S.T.; Kanani-Sadat, Y.; Hasanlou, M.; Sahraei, R.; Chanussot, J.; Amani, M. Comparison of Machine Learning Algorithms for Flood Susceptibility Mapping. Remote Sens. 2023, 15, 192. [Google Scholar] [CrossRef]
- Wubalem, A.; Tesfaw, G.; Dawit, Z.; Getahun, B.; Mekuria, T.; Jothimani, M. Comparison of Statistical and Analytical Hierarchy Process Methods on Flood Susceptibility Mapping: In a Case Study of the Lake Tana Sub-Basin in Northwestern Ethiopia. Open Geosci. 2021, 13, 1668–1688. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Ostfeld, A. Data-Driven Modelling: Some Past Experiences and New Approaches. J. Hydroinform. 2008, 10, 3–22. [Google Scholar] [CrossRef]
- Fernández, D.S.; Lutz, M.A. Urban Flood Hazard Zoning in Tucumán Province, Argentina, Using GIS and Multicriteria Decision Analysis. Eng. Geol. 2010, 111, 90–98. [Google Scholar] [CrossRef]
- Rahman, M.; Ningsheng, C.; Islam, M.M.; Dewan, A.; Iqbal, J.; Washakh, R.M.A.; Shufeng, T. Flood Susceptibility Assessment in Bangladesh Using Machine Learning and Multi-Criteria Decision Analysis. Earth Syst. Environ. 2019, 3, 585–601. [Google Scholar] [CrossRef]
- Hammami, S.; Zouhri, L.; Souissi, D.; Souei, A.; Zghibi, A.; Marzougui, A.; Dlala, M. Application of the GIS Based Multi-Criteria Decision Analysis and Analytical Hierarchy Process (AHP) in the Flood Susceptibility Mapping (Tunisia). Arab. J. Geosci. 2019, 12, 653. [Google Scholar] [CrossRef]
- Das, S. Flood Susceptibility Mapping of the Western Ghat Coastal Belt Using Multi-Source Geospatial Data and Analytical Hierarchy Process (AHP). Remote Sens. Appl. 2020, 20, 100379. [Google Scholar] [CrossRef]
- Vojtek, M.; Vojteková, J. Flood Susceptibility Mapping on a National Scale in Slovakia Using the Analytical Hierarchy Process. Water 2019, 11, 364. [Google Scholar] [CrossRef]
- Prasad, P.; Loveson, V.J.; Das, B.; Kotha, M. Novel Ensemble Machine Learning Models in Flood Susceptibility Mapping. Geocarto Int. 2022, 37, 1892209. [Google Scholar] [CrossRef]
- Al-Juaidi, A.E.M.; Nassar, A.M.; Al-Juaidi, O.E.M. Evaluation of Flood Susceptibility Mapping Using Logistic Regression and GIS Conditioning Factors. Arab. J. Geosci. 2018, 11, 765. [Google Scholar] [CrossRef]
- Kim, H.I.; Han, K.Y.; Lee, J.Y. Prediction of Urban Flood Extent by LSTM Model and Logistic Regression. KSCE J. Civ. Environ. Eng. Res. 2020, 40, 273–283. [Google Scholar]
- Jung, M.; Kim, J.G.; Uranchimeg, S.; Kwon, H.H. The Probabilistic Estimation of Inundation Region Using a Multiple Logistic Regression Analysis. J. Korea Water Resour. Assoc. 2020, 53, 121–129. [Google Scholar] [CrossRef]
- Abedi, R.; Costache, R.; Shafizadeh-Moghadam, H.; Pham, Q.B. Flash-Flood Susceptibility Mapping Based on XGBoost, Random Forest and Boosted Regression Trees. Geocarto Int. 2022, 37, 5479–5496. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Xue, W.; Shahabi, H.; Li, S.; Hong, H.; Wang, X.; Bian, H.; Zhang, S.; Pradhan, B.; et al. Modeling Flood Susceptibility Using Data-Driven Approaches of Naïve Bayes Tree, Alternating Decision Tree, and Random Forest Methods. Sci. Total Environ. 2020, 701, 134979. [Google Scholar] [CrossRef] [PubMed]
- Mahdizadeh Gharakhanlou, N.; Perez, L. Flood Susceptible Prediction through the Use of Geospatial Variables and Machine Learning Methods. J. Hydrol. 2023, 617, 129121. [Google Scholar] [CrossRef]
- Zhao, G.; Pang, B.; Xu, Z.; Yue, J.; Tu, T. Mapping Flood Susceptibility in Mountainous Areas on a National Scale in China. Sci. Total Environ. 2018, 615, 1133–1142. [Google Scholar] [CrossRef] [PubMed]
- Sahana, M.; Rehman, S.; Sajjad, H.; Hong, H. Exploring Effectiveness of Frequency Ratio and Support Vector Machine Models in Storm Surge Flood Susceptibility Assessment: A Study of Sundarban Biosphere Reserve, India. Catena 2020, 189, 104450. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebur, M.N. Flood Susceptibility Mapping Using a Novel Ensemble Weights-of-Evidence and Support Vector Machine Models in GIS. J. Hydrol. 2014, 512, 332–343. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood Susceptibility Assessment Using GIS-Based Support Vector Machine Model with Different Kernel Types. Catena 2015, 125, 91–101. [Google Scholar] [CrossRef]
- Shafapour Tehrany, M.; Shabani, F.; Neamah Jebur, M.; Hong, H.; Chen, W.; Xie, X. GIS-Based Spatial Prediction of Flood Prone Areas Using Standalone Frequency Ratio, Logistic Regression, Weight of Evidence and Their Ensemble Techniques. Geomat. Nat. Hazards Risk 2017, 8, 1538–1561. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, X.; Yang, K.; Zeng, S.; Hong, A. Modeling Rules of Regional Flash Flood Susceptibility Prediction Using Different Machine Learning Models. Front. Earth Sci. 2023, 11, 1117004. [Google Scholar] [CrossRef]
- Korea Meteorological Association. Changma White Paper; Korea Meteorological Association: Seoul, Republic of Korea, 2022.
- Khojeh, S.; Ataie-Ashtiani, B.; Hosseini, S.M. Effect of DEM Resolution in Flood Modeling: A Case Study of Gorganrood River, Northeastern Iran. Nat. Hazards 2022, 112, 2673–2693. [Google Scholar] [CrossRef]
- Gangani, P.; Mangukiya, N.K.; Mehta, D.J.; Muttil, N.; Rathnayake, U. Evaluating the Efficacy of Different DEMs for Application in Flood Frequency and Risk Mapping of the Indian Coastal River Basin. Climate 2023, 11, 114. [Google Scholar] [CrossRef]
- Seleem, O.; Heistermann, M.; Bronstert, A. Efficient Hazard Assessment for Pluvial Floods in Urban Environments: A Benchmarking Case Study for the City of Berlin, Germany. Water 2021, 13, 2476. [Google Scholar] [CrossRef]
- Seleem, O.; Ayzel, G.; de Souza, A.C.T.; Bronstert, A.; Heistermann, M. Towards Urban Flood Susceptibility Mapping Using Data-Driven Models in Berlin, Germany. Geomat. Nat. Hazards Risk 2022, 13, 1640–1662. [Google Scholar] [CrossRef]
- Sørensen, R.; Zinko, U.; Seibert, J. On the Calculation of the Topographic Wetness Index: Evaluation of Different Methods Based on Field Observations. Hydrol. Earth Syst. Sci. 2006, 10, 101–112. [Google Scholar] [CrossRef]
- Riadi, B.; Barus, B.; Widiatmaka; Yanuar, M.J.P.; Pramudya, B. Identification and Delineation of Areas Flood Hazard Using High Accuracy of DEM Data. IOP Conf. Ser. Earth Environ. Sci. 2018, 149, 012035. [Google Scholar] [CrossRef]
- Grohmann, C.H.; Smith, M.J.; Riccomini, C. Multiscale Analysis of Topographic Surface Roughness in the Midland Valley, Scotland. IEEE Trans. Geosci. Remote 2011, 49, 1200–1213. [Google Scholar] [CrossRef]
- Das, S.; Pardeshi, S.D. Integration of Different Influencing Factors in GIS to Delineate Groundwater Potential Areas Using IF and FR Techniques: A Study of Pravara Basin, Maharashtra, India. Appl. Water Sci. 2018, 8, 197. [Google Scholar] [CrossRef]
- Liu, W.; Song, X.; Huang, F.; Hu, L. Experimental Study on the Disintegration of Granite Residual Soil under the Combined Influence of Wetting–Drying Cycles and Acid Rain. Geomat. Nat. Hazards Risk 2019, 10, 1912–1927. [Google Scholar] [CrossRef]
- Tariq, A.; Yan, J.; Ghaffar, B.; Qin, S.; Mousa, B.G.; Sharifi, A.; Huq, M.E.; Aslam, M. Flash Flood Susceptibility Assessment and Zonation by Integrating Analytic Hierarchy Process and Frequency Ratio Model with Diverse Spatial Data. Water 2022, 14, 3069. [Google Scholar] [CrossRef]
- Pandey, M.; Arora, A.; Arabameri, A.; Costache, R.; Kumar, N.; Mishra, V.N.; Nguyen, H.; Mishra, J.; Siddiqui, M.A.; Ray, Y.; et al. Flood Susceptibility Modeling in a Subtropical Humid Low-Relief Alluvial Plain Environment: Application of Novel Ensemble Machine Learning Approach. Front. Earth Sci. 2021, 9, 659296. [Google Scholar] [CrossRef]
- Edet, A.E.; Okereke, C.S.; Teme, S.C.; Esu, E.O. Application of Remote-Sensing Data to Groundwater Exploration: A Case Study of the Cross River State, Southeastern Nigeria. Hydrogeol. J. 1998, 6, 394–404. [Google Scholar] [CrossRef]
- Falah, F.; Rahmati, O.; Rostami, M.; Ahmadisharaf, E.; Daliakopoulos, I.N.; Pourghasemi, H.R. Artificial Neural Networks for Flood Susceptibility Mapping in Data-Scarce Urban Areas. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J. Applied Linear Regression Models, 4th ed.; McGraw-Hill/Irvin: New York, NY, USA, 2004; ISBN 978-0-0723-8691-2. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- He, Q.; Wang, M.; Liu, K. Rapidly Assessing Earthquake-Induced Landslide Susceptibility on a Global Scale Using Random Forest. Geomorphology 2021, 391, 107889. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Tien Bui, D.; Pradhan, B.; Lofman, O.; Revhaug, I. Landslide Susceptibility Assessment in Vietnam Using Support Vector Machines, Decision Tree, and Nave Bayes Models. Math. Probl. Eng. 2012, 2012, 974638. [Google Scholar] [CrossRef]
- Hong, H.; Tsangaratos, P.; Ilia, I.; Liu, J.; Zhu, A.X.; Chen, W. Application of Fuzzy Weight of Evidence and Data Mining Techniques in Construction of Flood Susceptibility Map of Poyang County, China. Sci. Total Environ. 2018, 625, 575–588. [Google Scholar] [CrossRef] [PubMed]
- Tharwat, A. Classification Assessment Methods. Appl. Comput. Inform. 2018, 17, 168–192. [Google Scholar] [CrossRef]
- Ferri, C.; Hernández-Orallo, J.; Modroiu, R. An Experimental Comparison of Performance Measures for Classification. Pattern Recognit. Lett. 2009, 30, 27–38. [Google Scholar] [CrossRef]
- Sung, J.H.; Kang, D.H.; Seo, Y.H.; Kim, B.S. Analysis of Extreme Rainfall Characteristics in 2022 and Projection of Extreme Rainfall Based on Climate Change Scenarios. Water 2023, 15, 3986. [Google Scholar] [CrossRef]
- Collins, T.W.; Grineski, S.E.; Chakraborty, J.; Flores, A.B. Environmental Injustice and Hurricane Harvey: A Household-Level Study of Socially Disparate Flood Exposures in Greater Houston, Texas, USA. Environ. Res. 2019, 179, 108772. [Google Scholar] [CrossRef]
- Mahdizadeh Gharakhanlou, N.; Perez, L. Spatial Prediction of Current and Future Flood Susceptibility: Examining the Implications of Changing Climates on Flood Susceptibility Using Machine Learning Models. Entropy 2022, 24, 1630. [Google Scholar] [CrossRef] [PubMed]
- Salazar, J.J.; Garland, L.; Ochoa, J.; Pyrcz, M.J. Fair Train-Test Split in Machine Learning: Mitigating Spatial Autocorrelation for Improved Prediction Accuracy. J. Pet. Sci. Eng. 2022, 209, 109885. [Google Scholar] [CrossRef]


| Primary Input Data | Data Type (Resolution) | Source (Year) | Derived Variables |
|---|---|---|---|
| SRTM DEM | Grid (30 m) | NASA JPL (2013) | Elevation |
| Slope | |||
| Aspect | |||
| Curvature | |||
| TWI | |||
| TRI | |||
| SPI | |||
| Automatic Weather Station (AWS) Automated Synoptic Observing System (ASOS) stations | Point | Korea Meteorological Administration (2010–2022) | Rainfall |
| Stream network data | Polylines | National Geographic Information Institute (2023) | Stream density |
| Distance to river | |||
| Geological map | Polygon (1:50,000) | Korea Institute of Geoscience and Mineral Resources (2021) | Lithology |
| Land use and land cover map | Polygon (1:25,000) | Ministry of Environment (2022) | LULC |
| Soil map | Polygon (1:25,000) | National Institute of Agricultural Sciences (1999) | Soil type |
| Road network data | Polylines | Ministry of Land, Infrastructure, and Transport (2023) | Distance to road |
| Sewage network data | Points | Seoul Metropolitan Government (2023) | Distance to storm drains |
| Polylines | Sewer pipe density |
| Flood Conditioning Factor | Tolerance | VIF |
|---|---|---|
| Elevation | 0.169 | 5.905 |
| Slope | 0.171 | 5.848 |
| Aspect | 0.930 | 1.075 |
| Curvature | 0.842 | 1.187 |
| TWI | 0.513 | 1.948 |
| TRI | 0.286 | 3.496 |
| SPI | 0.847 | 1.181 |
| Distance to a River | 0.471 | 2.123 |
| Stream Density | 0.422 | 2.369 |
| Distance to a Road | 0.146 | 6.835 |
| Rainfall | 0.820 | 1.220 |
| Soil Type | 0.793 | 1.260 |
| Land Use | 0.646 | 1.548 |
| Lithology | 0.725 | 1.379 |
| SPD | 0.463 | 2.159 |
| DSD | 0.131 | 7.632 |
| Susceptibility Class | LR | RF | SVM |
|---|---|---|---|
| Very High | 13.75 | 17.23 | 18.08 |
| High | 12.91 | 15.42 | 12.73 |
| Moderate | 12.43 | 15.50 | 9.11 |
| Low | 12.23 | 17.46 | 16.84 |
| Very Low | 48.68 | 34.38 | 43.24 |
| Evaluation Metric | LR | RF | SVM |
|---|---|---|---|
| ROC-AUC | 0.872 | 0.902 | 0.854 |
| Accuracy | 0.795 | 0.837 | 0.802 |
| F1-score | 0.812 | 0.842 | 0.817 |
| Kappa | 0.593 | 0.673 | 0.603 |
| Evaluation Metric | RF Including Drainage-Related Variables | RF Excluding Drainage-Related Variables |
|---|---|---|
| ROC-AUC | 0.902 | 0.869 |
| Accuracy | 0.837 | 0.778 |
| F1-score | 0.842 | 0.788 |
| Kappa | 0.673 | 0.557 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bersabe, J.T.; Jun, B.-W. The Machine Learning-Based Mapping of Urban Pluvial Flood Susceptibility in Seoul Integrating Flood Conditioning Factors and Drainage-Related Data. ISPRS Int. J. Geo-Inf. 2025, 14, 57. https://doi.org/10.3390/ijgi14020057
Bersabe JT, Jun B-W. The Machine Learning-Based Mapping of Urban Pluvial Flood Susceptibility in Seoul Integrating Flood Conditioning Factors and Drainage-Related Data. ISPRS International Journal of Geo-Information. 2025; 14(2):57. https://doi.org/10.3390/ijgi14020057
Chicago/Turabian StyleBersabe, Julieber T., and Byong-Woon Jun. 2025. "The Machine Learning-Based Mapping of Urban Pluvial Flood Susceptibility in Seoul Integrating Flood Conditioning Factors and Drainage-Related Data" ISPRS International Journal of Geo-Information 14, no. 2: 57. https://doi.org/10.3390/ijgi14020057
APA StyleBersabe, J. T., & Jun, B.-W. (2025). The Machine Learning-Based Mapping of Urban Pluvial Flood Susceptibility in Seoul Integrating Flood Conditioning Factors and Drainage-Related Data. ISPRS International Journal of Geo-Information, 14(2), 57. https://doi.org/10.3390/ijgi14020057







