Benford’s Law and Transport Infrastructure: The Analysis of the Main Road Network’s Higher-Level Segments in the EU

Abstract

Benford’s Law, also known as the First-Digit Law, describes the non-uniform distribution of leading digits in many naturally occurring datasets. This phenomenon can be observed in data such as financial transactions, tax records, or demographic indicators, but the application of Benford’s Law to data from the field of transport infrastructure remains largely underexplored. As interest in using statistical distributions to identify spatial and regional patterns grows, this paper explores the applicability of Benford’s Law to anthropogenic geographic data, particularly whether the lengths of higher-level segments of the main road network across European Union member states follow Benford’s Law. To evaluate the conformity of the data from all European Union countries with Benford’s distribution, Pearson’s ${\chi }^2$ test of association, the p-value, and the Kolmogorov–Smirnov test were used. The results consistently show low ${\chi }^2$ values and high p-values, indicating a strong agreement between observed and expected distributions. The relationship between the distribution of higher-level segment lengths and the leading digits of these lengths was studied as well. The findings suggest that the length distribution of the main road networks’ higher-level segments closely follows Benford’s Law, emphasizing its potential as a simple yet effective tool for assessing the reliability and consistency of geographic and infrastructure datasets within the European context.

1. Introduction

Benford’s Law is a mathematical phenomenon that describes the counterintuitive distribution of leading digits in many naturally occurring datasets. According to this law, not all digits from 1 to 9 are equally likely to appear as the leading digit. The digit 1 appears as the leading digit in about 30% of cases, with the probability decreasing as the leading digit increases.

Although it might initially seem like a purely mathematical curiosity, Benford’s Law surprisingly often occurs in nature. Joannes-Boyau et al. [1] showed that travelled distances of hurricanes since the 1840s satisfy Benford’s Law. Sambridge et al. [2] demonstrated that leading-digit distributions of earthquake depths adhere closely to Benford’s Law. More recent studies confirmed compliance for earthquake magnitudes [3] and recurrence times of seismic events [4]. Benford’s Law is capable of identifying quantum phase transitions in a manner similar to its application in detecting earthquakes [5]. Consequently, despite their fundamentally different physical origins, both seismic activity and quantum cooperative phenomena can be analysed using comparable techniques. This law is evident across a wide range of astronomical datasets as well. The intensity of gamma rays detected on Earth by the Fermi space telescope and the rotational frequencies of spinning stellar remnants known as pulsars both satisfy Benford’s Law [6]. The distances of galaxies and stars satisfy Benford’s Law too [7], as well as the masses of exoplanets [2]. The law does not apply universally, yet it recurs in a remarkably wide range of datasets. Seismic signals produced by debris flows satisfy Benford’s Law, whereas those caused by ambient noise (e.g., seismic data from rockfalls) do not [8]. It is already well established that Benford’s Law also applies to many datasets created by humans, such as financial, economic, bank transactions [9], accounting records [10], tax data [11], gross domestic product figures [12], etc. Also, socio-geographical distances between cities [13] follow this statistical distribution. For an overview of applications and exercises, see, e.g., ref. [14] and the references therein.

The fact that Benford’s distribution appears in data from many different natural areas relates to the fact that nature constantly produces processes that span several orders of magnitude and exhibit multiplicative or exponential tendencies.

Recent studies have shown that Benford’s Law can reveal spatial and regional patterns in geographic datasets [15], but its application within the field of geographical information remains relatively underexplored [16]. In the context of spatial analysis, the significance of complying with Benford’s Law can be seen in its role as an indicator of the naturalness, quality, and integrity of spatial data. Compliance with Benford’s Law may indicate that the data in question were generated naturally rather than through artificial partitioning. The law helps in detecting spatial anomalies or inconsistencies in data processing. Benford’s Law can also serve as a diagnostic tool during data preprocessing prior to spatial modeling, machine learning, or geostatistical analyses. In contrast to well-established geographic principles such as Tobler’s laws [17,18,19], Benford’s Law has received limited attention regarding spatial data, particularly in the context of infrastructure and transport networks.

A notable exception demonstrating the applicability of Benford’s Law in a spatial context is the study by Kopczewska and Kopczewski [13], which examines the geographical distribution of cities and their populations. In work [13], the authors explore the detection of a hidden order that drives the observed spatial heterogeneity. They view the geographical system of cities as a complex, nonlinear, three-dimensional network that is neither random nor independent, but instead exhibits strong spatial heterogeneity. They explain this hidden order through the lens of Benford’s Law. Since Benford’s Law holds for natural datasets, they argue that spatial phenomena such as natural urbanization tend to conform to Benford’s distribution, whereas spatial processes governed by artificial organizational rules (e.g., political boundaries) deviate from it. By comparing the level of conformity to Benford’s distribution, the authors show that the mutual 3D socio-geographical distances between populations and cities in most countries follow Benford’s Law, indicating that city geolocations exhibit a natural spatial distribution. Based on an analysis of historical settlement patterns, they conclude that the geolocation of cities and inhabitants worldwide has followed an evolutionary process leading to a natural spatial arrangement consistent with Benford’s Law.

A comparison of the distribution of several numerical properties of geographic objects with Benford’s distribution is presented in the study by [16]. The author investigates whether the numerical attributes of geographic entities conform to Benford’s Law. The results show that the examined numerical properties correspond to Benford’s Law to a certain extent, with only small differences observed between different types of geographic objects. The spatial patterns of deviations from Benford’s Law are similar for some aspects, but differ considerably for others. This finding suggests that there is no general rule determining which numerical properties, geographic objects, or spatial regions comply with Benford’s Law. In this sense, a more detailed examination of Benford’s Law in the context of geographic information and across various datasets represents a logical step toward its future application.

A new line of research on Benford’s Law in the spatial context is also outlined by Fernandes, Ciardhuáin, and Antunes [20], who investigated whether network traffic data, such as packet sizes and connection counts, conform to Benford’s and Zipf’s laws. They found that integrating Benford’s test with several different metrics can effectively identify anomalies in data flow (e.g., cyberattacks). Although this does not concern road traffic infrastructure, the underlying principle is analogous to traffic flow.

In the broader context of spatial analysis, data applicability, and validation related to the use of Benford’s Law, several open questions (research gaps) remain that should be addressed in studies. Most existing works analyse the distribution of digits, but only rarely investigate whether deviations from Benford’s Law exhibit spatial autocorrelation. Such an approach could reveal spatial “hotspots” of unreliable data within a territory [1,16].

Kopczewska and Kopczewski [13] and Szabó et al. [21] have pointed out that the literature lacks reference values or “baseline” for Benfords’ distributions for different types of geographic data (e.g., road distances, parcel areas, traffic intensities). Without such benchmarks, it is difficult to interpret what constitutes a significant deviation.

Studies by Yang et al. [22] and Fernandes et al. [20] have shown that Benford’s distribution has been tested in time series data (e.g., sediment motion), but no research has yet examined the spatio-temporal behavior of Benford’s conformity.

Mansouri et al. [23] and Joannes-Boyau et al. [1] emphasised that Benfords’ tests are currently applied only to a single dataset at a time. In practice, however, traffic data originate from multiple sensors, GPS devices, and systems. There is also a lack of research applying Benford’s analysis to assess consistency between different sources of traffic data. Moreover, various studies employ different metrics, thresholds, and sample sizes.

In the context of spatial data, there is still no unified methodological framework defining when a dataset is sufficiently large and suitable for Benford’s analysis [23,24].

Despite the considerable number of research gaps that have emerged in recent years, we focused on addressing at least one of them–specifically, the gap highlighted by Kopczewska and Kopczewski [13]: the lack of studies examining the spatial application of Benford’s Law in the context of infrastructure and transportation networks. This research gap motivated us to investigate whether anthropogenic activities also generate datasets that follow this law. Our work was partly inspired by Mocnik’s study [16], in which the author argues for the relevance of research that analyses subsets of OpenStreetMap data to determine which parts conform to Benford’s Law and which do not.

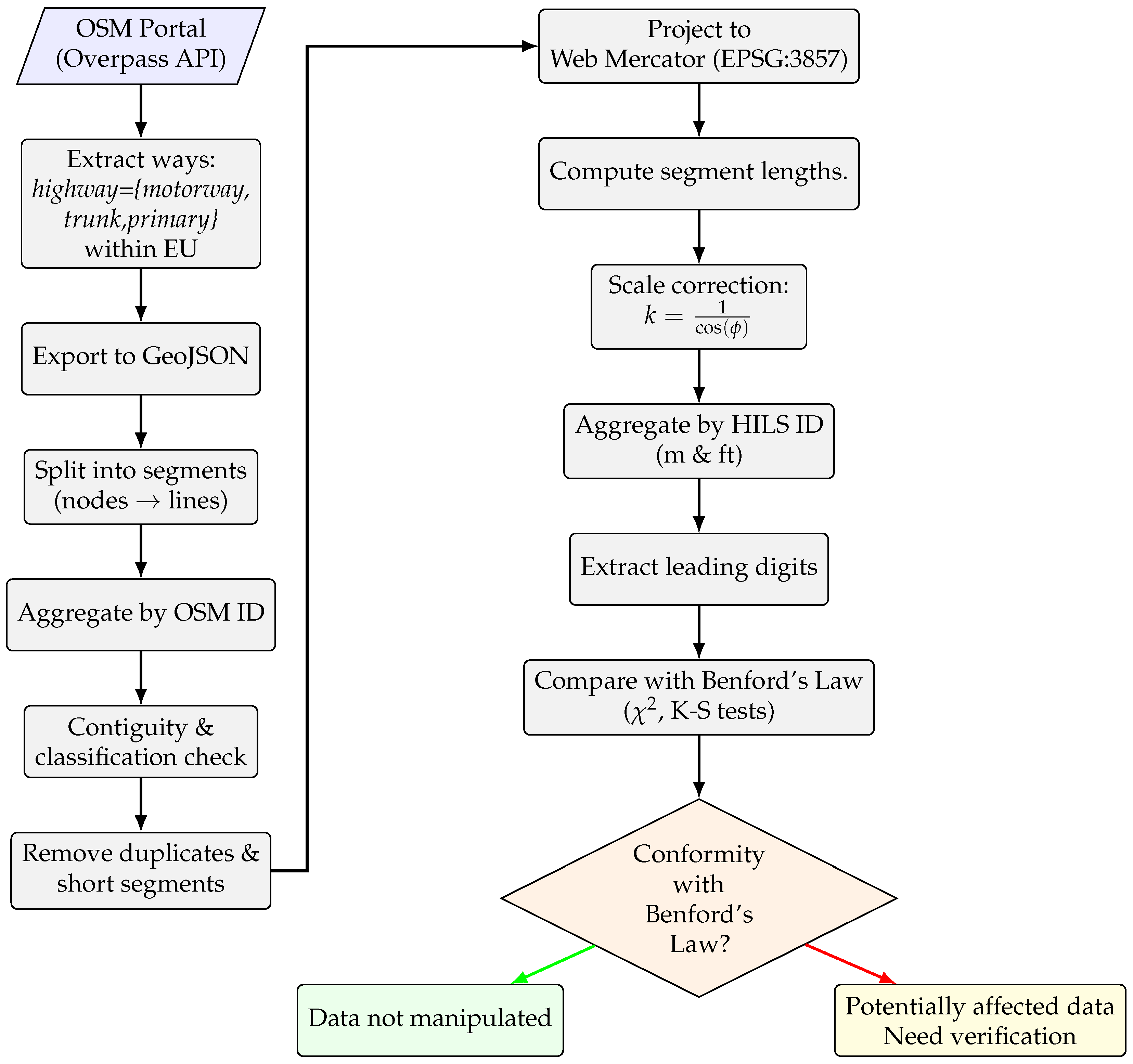
In this paper, we examine whether the outcomes of anthropogenic geographic activities, specifically transport infrastructure, conform to Benford’s Law. The lengths of higher-level segments of the main road network of 27 European Union member states were used in the analysis. To assess whether the higher-level segment length data from all European Union countries conform to Benford’s distribution, the Pearson’s ${\chi }^2$ test of association and p-value were employed. The findings reliably indicate low ${\chi }^2$ values and high p-values, suggesting a strong alignment between observed and expected distributions. The Kolmogorov–Smirnov test was used to verify the observation. Moreover, the relationship between the higher-level segment lengths and the leading digits of these lengths was analysed.

2. Methodology

2.1. Benford’s Law

Benford’s Law describes the counterintuitive observation that in many naturally occurring datasets, the leading digit $d\in \{1,2,\dots ,9\}$ is not uniformly distributed. Instead, smaller digits appear more frequently, with their occurrence probabilities decreasing logarithmically. Although Simon Newcomb was the first to observe this phenomenon in the 19th century [25], the law is named after physicist Frank Benford, who systematically studied this distribution across a wide range of datasets [26]. Consequently, it is also known as the Newcomb-Benford Law [27], or the First-Digit Law [28].

This phenomenon is quantified by the probability distribution formula [29]:

$$P_d={log}_{10}\left(1+{\displaystyle \frac{1}{d}}\right),$$

(1)

where $P_d$ is the probability of occurrence of a number with the leading digit d as shown in

Table 1. Benford’s distribution.

Digit	Expected Frequency (%)	Magnitude
1	30.1
2	17.6
3	12.5
4	9.7
5	7.9
6	6.7
7	5.8
8	5.1
9	4.6

.

Benford’s Law usually appears in datasets that span several orders of magnitude and are not constrained by artificially imposed boundaries or uniform scales. Although it is seemingly simple, it reveals a hidden order within the numerical chaos of the real world, even in areas where one might not expect it. A remarkable feature of Benford’s Law is that it is scale-invariant, which means that it holds regardless of the units in which the data are expressed. For example, whether financial transactions are recorded in dollars, euros, or yen, or distances are measured in meters or miles, the distribution of the leading digits remains consistent with Benford’s pattern [14]. This unit independence makes the law extremely powerful for cross-domain and cross-context analyses, as it ensures that the observed phenomenon reflects essential properties of the data rather than arbitrary choices of measurement. Its possible applications therefore offer a new perspective on the quality and consistency of available data, enabling robust detection of irregularities and hidden structures across diverse fields.

2.2. Data Extraction and Processing

The input dataset was obtained from the OpenStreetMap (OSM) portal [30], a collaborative project that provides freely accessible geographic information, using the Overpass API, which allows querying and extracting geospatial data according to specific attributes. In this study, all ways tagged as highway = motorway, highway = trunk, or highway = primary within the geographic boundaries of the European Union (EU) were selected. The query included all nodes determining each way, thereby capturing the full geometry of each road segment, including bridges and tunnels associated with these road types. The resulting data were exported in GeoJSON format [31], a widely supported structure that maintains both spatial and attribute information in a lightweight format, for subsequent processing.

2.2.1. Creation and Aggregation of Higher-Level Segments

Each way from OSM is divided into individual segments, defined as the straight lines between two consecutive nodes. A node is one of the core elements of OSM. It consists of a single point in space defined by its latitude, longitude, node identifier (ID), and optionally altitude.

To address the complexity and dynamic nature of OSM data, where single physical routes may be represented by multiple ways or where ways may have been split/merged over time a rigorous aggregation and cleaning process was implemented to form higher-level segments (HILSs):

1.

Initial HILS Aggregation (Based on OSM ID).

Raw OSM segments sharing the same OSM way ID were initially aggregated into pre-final HILS. This simplified aggregation served as the base segment unit.

2.

Contiguity and Classification Check.

The pre-final HILSs were subjected to a subsequent topological and functional validation. Pre-final HILSs were only further aggregated into the final HILS unit if they were geometrically contiguous and maintained a consistent functional classification (i.e., the same way tag) at their junction nodes. This step effectively filtered out segments that were incorrectly tagged or where the road type changed. This approach mitigated the issue of unstable OSM IDs by enforcing that each final HILS represents one logical, uninterrupted path of a specific functional road class.

3.

Noise and Edge Cases.

Minor segments or those forming topological noise (e.g., duplicated segments or segments with erroneous tagging) were identified through a spatial filtering routine and removed to ensure that the analysis focused only on the coherent main road network.

For the purposes of this study, all motorway, trunk, and primary road HILSs are collectively referred to as HILSs of the main road network. This terminology provided a clear and unambiguous definition of the set of roads under consideration, encompassing the highest-level road categories in OSM across the EU.

2.2.2. Length Computation and Projection Distortion

To compute the lengths of HILSs, the GeoJSON data were imported into MATLAB 2024b environment [32] using geotable structures, and filenames were sanitised for structured storage. The road segments’ geometries were processed using the Mapping Toolbox [33]. All geometries were projected into the Web Mercator coordinate reference system (EPSG:3857) to ensure that distance computations were performed in meters. Multi-part geometries were identified using NaN delimiters to separate coordinate sequences. For each contiguous segment, latitude and longitude coordinates were transformed into projected coordinates $(x,y)$, and the Euclidean distance between consecutive points was calculated as:

$$E_i=\sqrt{{(x_{i+1}-x_i)}^2+{(y_{i+1}-y_i)}^2}.$$

(2)

The total length of each segment was then obtained by summing these distances:

$$L=\sum _i{E}_i,$$

(3)

and recorded both in meters and in converted units (feet). The lengths of all segments of the same IDs were subsequently summed to obtain the total length of each HILS, and the results were stored in structured variables for subsequent statistical analysis. The same analysis was provided with data in meters and converted units.

Because the Web Mercator projection (EPSG:3857) was used to compute the lengths, a correction that introduces significant scale distortion at latitudes ($\varphi$) typical for the European continent (${35}^{\circ }$ N to ${70}^{\circ }$ N). The scale factor (k) that inflates lengths in Web Mercator is given by the secant of the latitude:

$$k={\displaystyle \frac{1}{cos\left(\varphi \right)}}$$

(4)

Using the extracted HILS length data corrected by scale factor k, the leading digits of individual HILSs of the main road network for each EU member state were identified, and their frequency distribution was determined and converted into percentage values to enable a comparative analysis. The data processing workflow chart is depicted at Figure 1.

2.3. Metrics

In order to test the conformity of the road-length data from all EU countries with Benford’s distribution, the Pearson’s ${\chi }^2$ test of association, the p-value, and the Kolmogorov–Smirnov test were used. More concretely, we test whether the observed frequency distribution ($O_d$) of the leading digits of HILS lengths deviates significantly from the expected distribution ($E_d$) derived from Benford’s Law.

The Pearson’s ${\chi }^2$ test of association is a standard statistical method used to assess the goodness-of-fit between observed and expected distributions; thus, it is suitable for hypothesis testing [34]. To calculate the ${\chi }^2$ statistic, the following relation can be used [34]:

$${\chi }^2=\sum _{d=1}^c{\displaystyle \frac{{(O_d-E_d)}^2}{E_d}},$$

(5)

where $O_d$ stands for frequencies in the observed distribution, $E_d$ represents frequencies in the expected distribution, to which ones compares, and c denotes the number of categories (frequencies). Lower ${\chi }^2$ values indicate better adherence to the expected distribution.

The p-value is a statistical measure used in hypothesis testing to determine the strength of evidence against a null hypothesis. It represents the probability that the observed results, or more extreme ones, could occur purely by chance, assuming the null hypothesis is true. The p-value, which indicates the difference between observed and expected frequencies, can be calculated using the relation [35]:

$$p\text{-}\mathrm{value}=1-F_{{\chi }^2}\left({\chi }^2;f\right),$$

(6)

where $F_{{\chi }^2}$ is the cumulative distribution function of the ${\chi }^2$ distribution and f represents the number of degrees of freedom. This function determines the probability that a ${\chi }^2$ distributed random variable is less than or equal to ${\chi }^2$. The cumulative distribution function of the ${\chi }^2$ distribution [36] is incorporated in most statistical software.

The Kolmogorov–Smirnov test (K-S test) is a nonparametric statistical procedure commonly employed for comparing distributions [37]. The one-sample K-S test was applied to assess whether the data deviate from a specified theoretical distribution by comparing the empirical distribution function of the sample with the expected distribution function of that theoretical model.

3. Experiments and Discussion on the Results

The ${\chi }^2$ statistic, supported by the p-value, and K-S test were evaluated in this study. Furthermore, to gain a more comprehensive understanding of the relationship between the distribution of the leading digits of HILS lengths of the main road network and the actual lengths of these HILSs, a graphical comparison and assessment were conducted.

3.1. ${\chi }^2$ Statistic, Kolmogorov-Smirnov Test, and p-Value

To perform hypothesis testing, the following null hypothesis was formulated:

“The leading digits of the HILSs of the main road network of EU member states follow Benford’s Law.”

In order to evaluate the hypothesis, a ${\chi }^2$ statistic, K-S test, and p-value were calculated at a $0.05$ significance level. Any deviations from the expected distribution were analysed and interpreted.

Calculating the p-value in relation to the ${\chi }^2$ statistic is essential for deciding whether to accept or reject the null hypothesis; if $p\text{-}\mathrm{value}\ge 0.05$, the data are consistent with Benford’s Law, and the null hypothesis is not rejected, while if $p\text{-}\mathrm{value}<0.05$, the data are not consistent with Benford’s Law, and the null hypothesis is rejected.

One could argue that the ${\chi }^2$ test performs well mainly with small to medium sample sizes, as it becomes very sensitive with extremely large datasets (as is the case here). In such cases, even minor deviations can lead to the rejection of the null hypothesis, even if they are practically insignificant. Therefore, for large datasets, alternative measures such as the Euclidean distance [38], Mean Absolute Deviation [39], or Kolmogorov-Smirnov test [37] are often recommended. These metrics assess the magnitude of deviation between the empirical and theoretical distributions [40]. However, they do not provide a formal statistical test (such as the one that produces a p-value), and it is not always clear what constitutes an acceptable small deviation from Benford’s Law. This lack of clarity was a decisive factor in choosing the ${\chi }^2$ test with the p-value in this study. However, in an effort to obtain additional validation of the reliability of the proposed claims, to verify results, the one-sample Kolmogorov–Smirnov test was used as well.

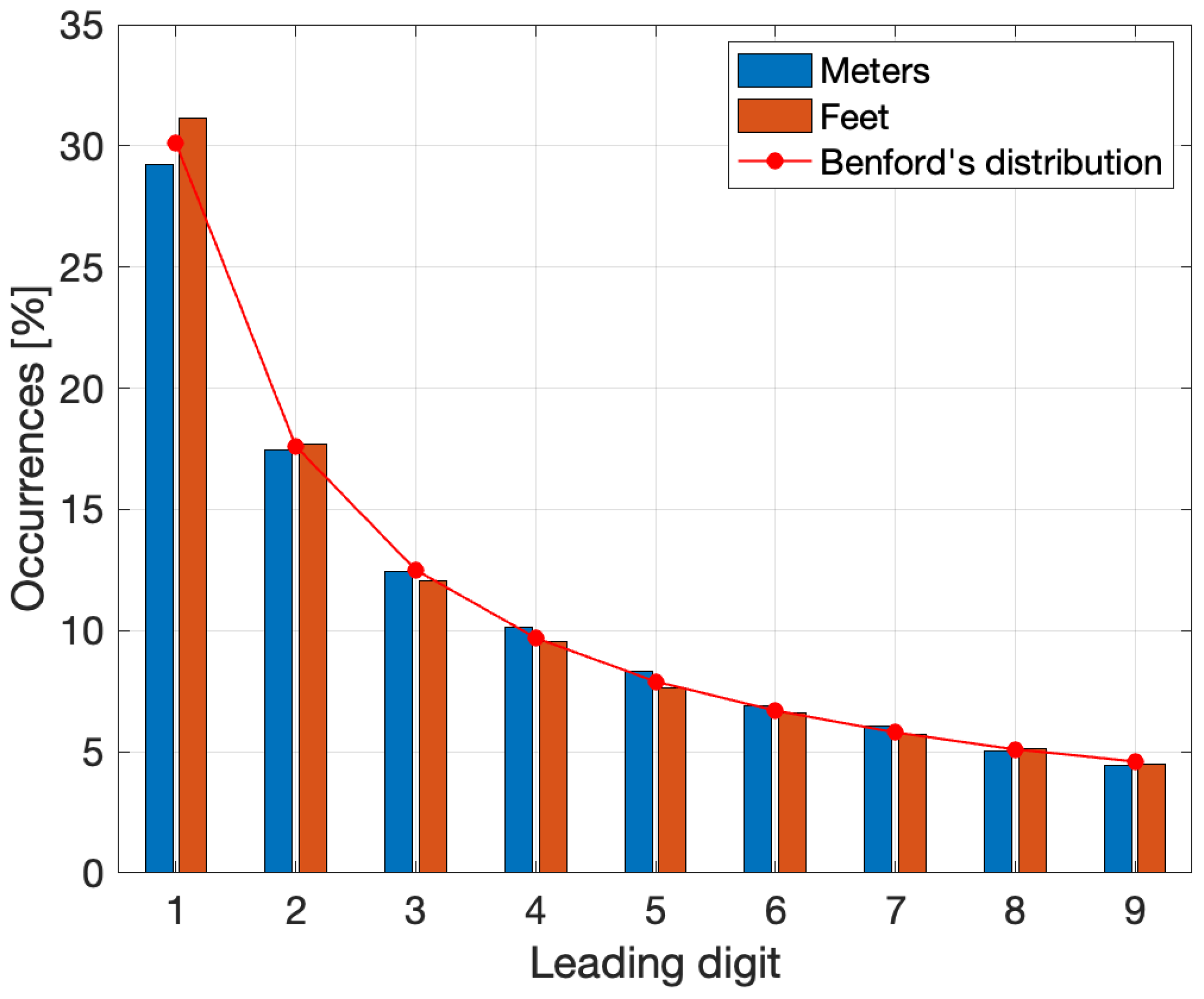
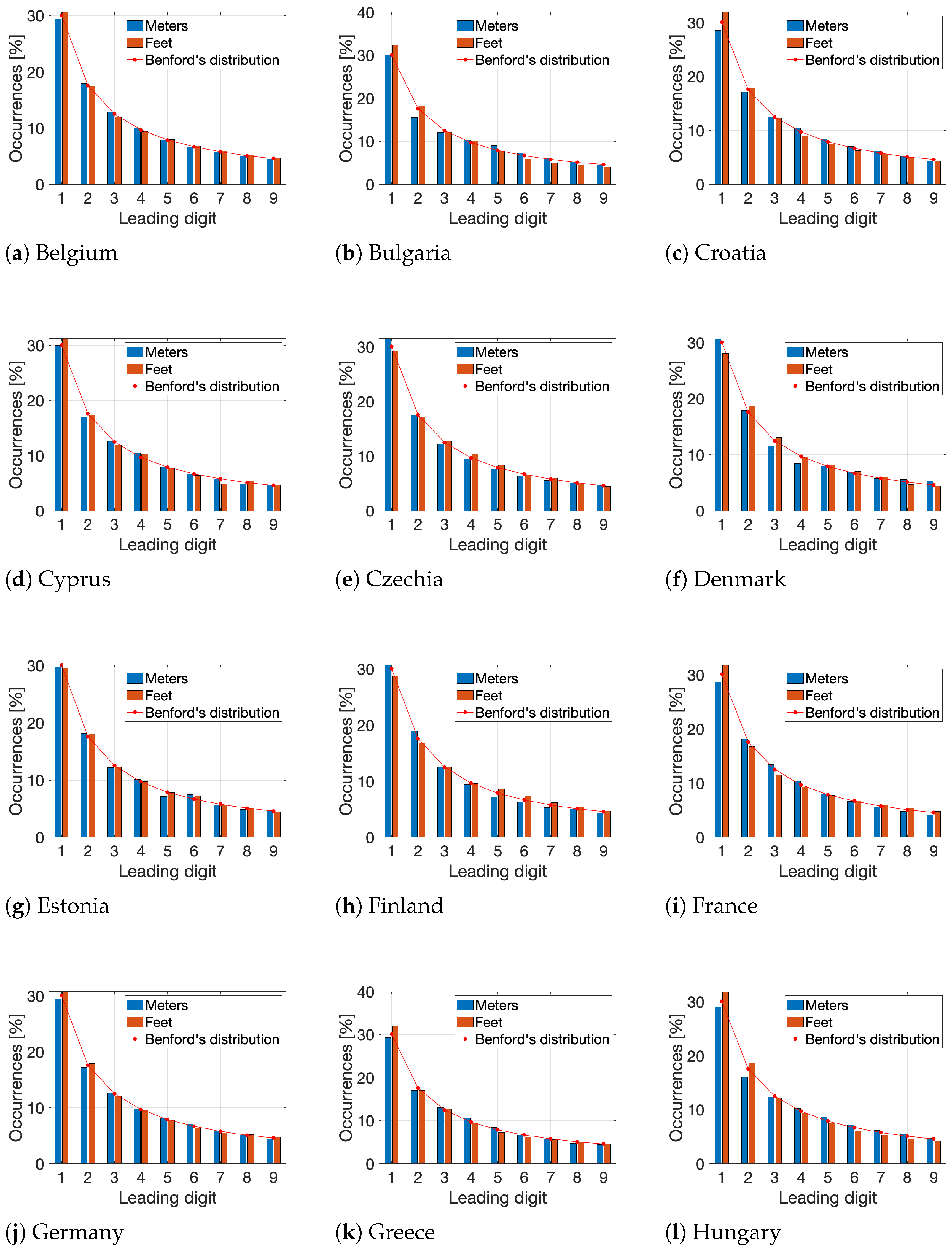
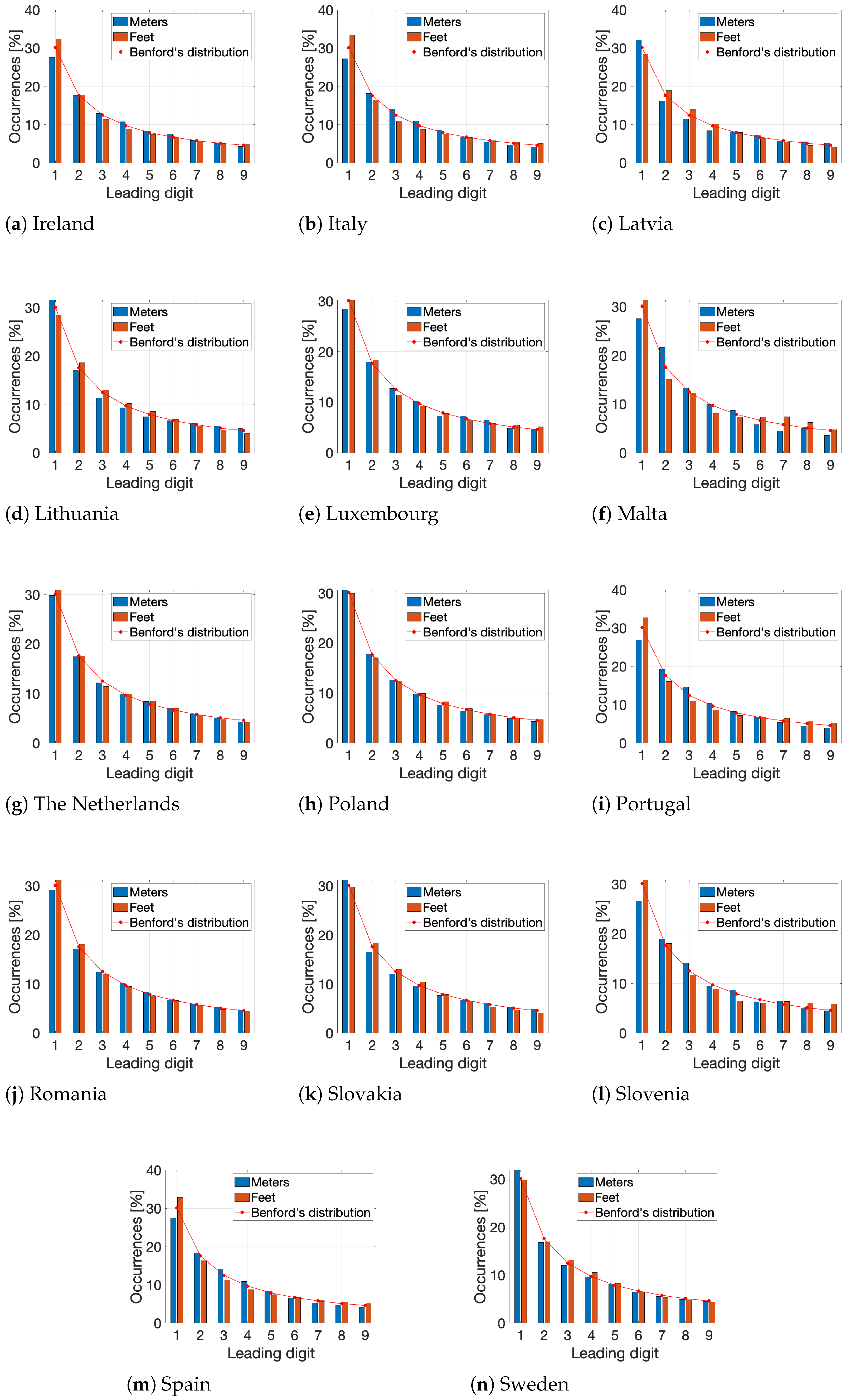
In the initial stage of the experiment, the subset data_distrib, which contained information on the frequency distributions of the HILSs of the main road networks for all 27 EU member states, was visualised using bar charts (see Figure 2, Figure 3 and Figure 4), offering a clear overview of the observed frequencies.

Subsequently, the ${\chi }^2$ values were calculated using the data_distrib subset. For 8 degrees of freedom (since there are 9 possible leading digits, 1–9, minus 1 degree of freedom) and a significance level of $0.05$, the critical ${\chi }^2$ value is approximately 15.507 [41], with lower ${\chi }^2$ values indicating better conformity to the expected distribution, in this case Benford’s distribution.

The ${\chi }^2$ statistic results listed in

Table 2. Values of ${\chi }^2$, p-value and K-S test.

Country	${\mathit{\chi }}^2$	p-Value	K-S Value
Austria	0.0918	1.0000	0.0112
Belgium	0.0449	1.0000	0.0074
Bulgaria	0.5166	0.9998	0.0255
Croatia	0.2522	1.0000	0.0201
Cyprus	0.0927	1.0000	0.0071
Czechia	0.1171	1.0000	0.0142
Denmark	0.3931	0.9999	0.0132
Estonia	0.2238	1.0000	0.0052
Finland	0.2705	1.0000	0.0206
France	0.2876	1.0000	0.0147
Germany	0.0685	1.0000	0.0103
Greece	0.2104	1.0000	0.0137
Hungary	0.3910	0.9999	0.0279
Ireland	0.4676	0.9999	0.0250
Italy	0.8212	0.9991	0.0284
Latvia	0.6841	0.9996	0.0203
Lithuania	0.3346	1.0000	0.0152
Luxembourg	0.3327	1.0000	0.0166
Malta	1.5100	0.9829	0.0333
The Netherlands	0.0952	1.0000	0.0082
Poland	0.0511	1.0000	0.0097
Portugal	1.1101	0.9975	0.0319
Romania	0.1175	1.0000	0.0152
Slovakia	0.1783	1.0000	0.0107
Slovenia	0.9058	0.9988	0.0349
Spain	0.7868	0.9993	0.0266
Sweden	0.1865	1.0000	0.0180

confirmed a high level of conformity with Benford’s distribution across all 27 EU countries, as indicated by the ${\chi }^2$ values ranging from 0.0449 to 1.5100. The lowest values were recorded for Belgium (0.0449), Poland (0.0511), Germany (0.0685), Austria (0.0918), Cyprus (0.0927), and the Netherlands (0.0952), representing a shift of two orders of magnitude compared to Malta (1.5100) and Portugal (1.1101), and a shift of one order of magnitude compared to 19 countries. Malta and Portugal were the only two countries with a ${\chi }^2$ value greater than 1.

The p-value in the experiment ranged from 0.9829 to 1.0000, with 17 countries (Austria, Belgium, Croatia, Cyprus, Czechia, Estonia, Finland, France, Germany, Greece, Lithuania, Luxembourg, the Netherlands, Poland, Romania, Slovakia, Sweden) demonstrating such high conformity with Benford’s Law that the p-value did not differ from 1 (see Table 2).

The K-S test values ranged from 0.0071 to 0.0349. The lowest values were recorded for Cyprus (0.0071), Belgium (0.0074), the Netherlands (0.0082), and Poland (0.0097), while the values for the remaining states were considerably higher. The highest values were observed for Slovenia (0.0349), Malta (0.0333), and Portugal (0.0319). At the $0.05$ significance level, the K-S test did not reveal a statistically significant difference between the empirical distribution of the leading digits in data_distrib and the Benford distribution, as indicated by the K-S test values listed in Table 2 and supported by the ${\chi }^2$ statistics and corresponding p-values. These results demonstrate conformity with Benford’s Law.

The scale invariance of Benford’s Law has been tested as well. Because Benford’s Law is scale-invariant, the ideal expectation is that the empirical leading digit distribution remains effectively unchanged after unit conversion. Therefore we computed the leading digit histogram for both representations and quantify agreement with Benford’s distribution, which in both cases pass successfully this condition–see Figure 2, Figure 3 and Figure 4.

3.2. The Higher-Level Segments’ Length Distribution

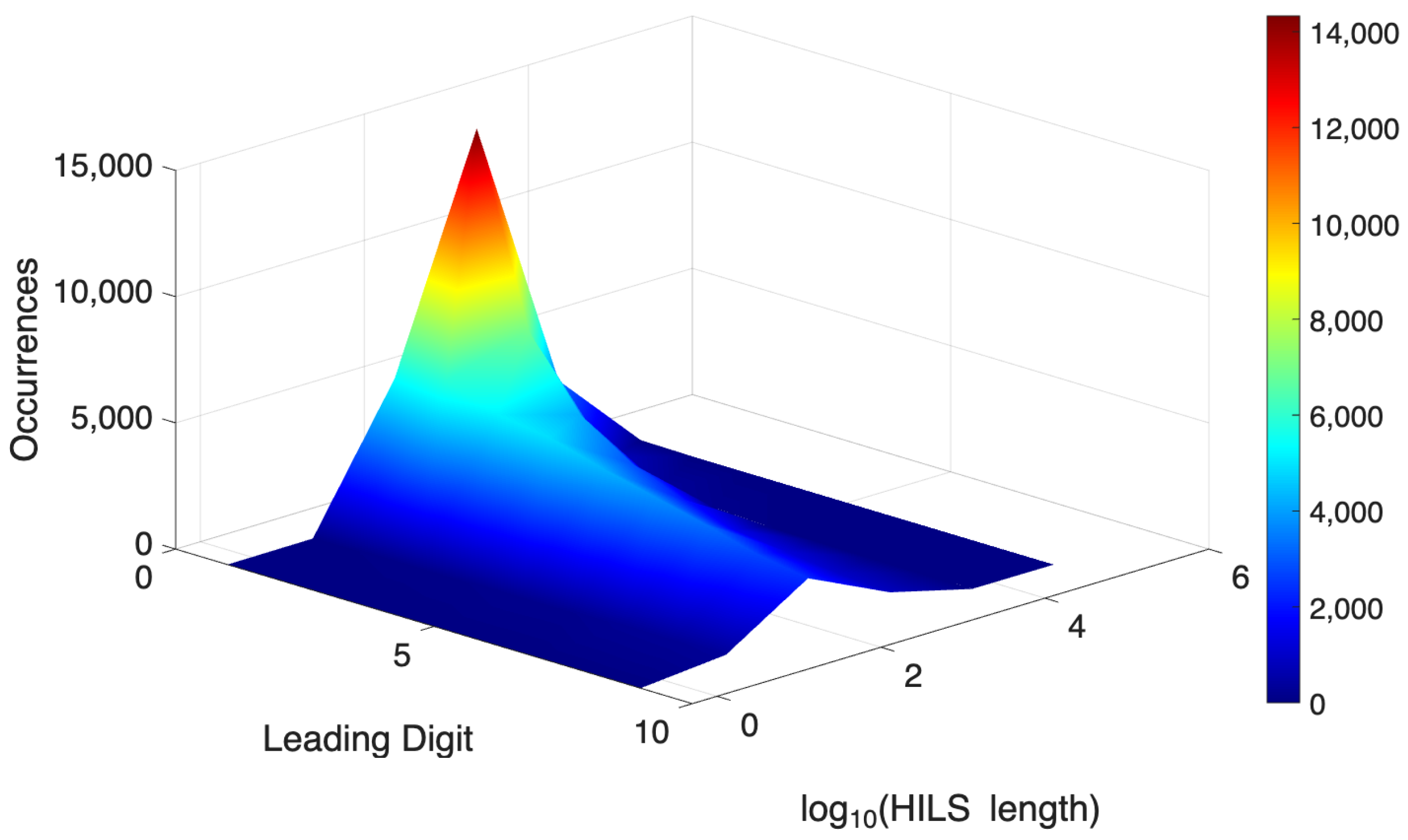
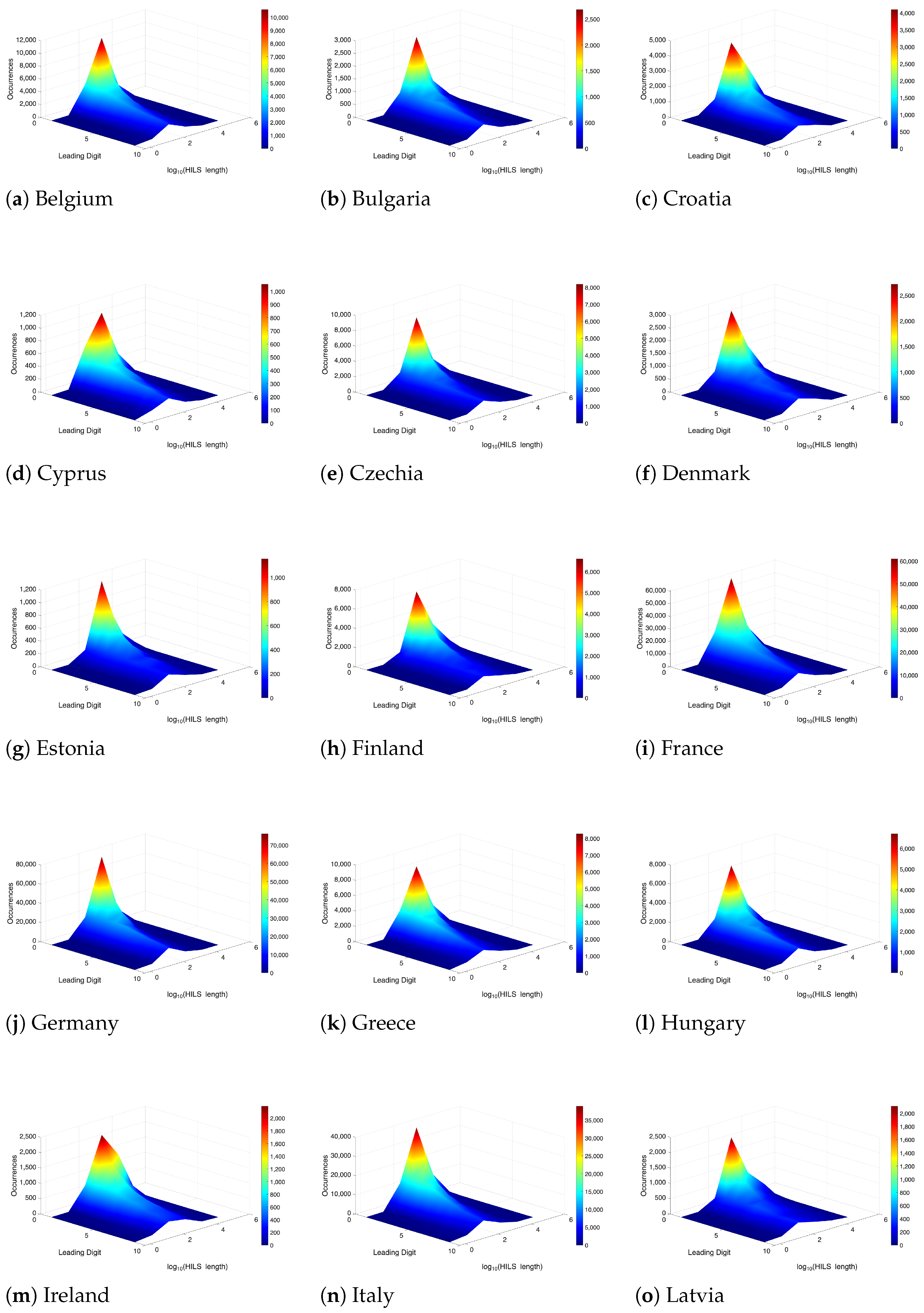
The relationship between the distribution of the lengths of HILSs and the leading digits of these lengths was examined country by country. The situation in each country is illustrated in Figure 5, Figure 6 and Figure 7. The x-axis represents leading digits of the lengths of the main road networks’ HILSs, the y-axis shows the decimal logarithms of these lengths, and the z-axis indicates the frequencies of HILSs of a given length associated with a given leading digit.

From these figures, it is evident that in all observed countries, HILSs of the main road network with lengths of the order of tens of meters predominate in most, if not all, of the 9 categories defined by leading digits. The highest frequencies on the logarithmic scale occur between the values of 1 and 2, which corresponds to the order of tens of meters. This interpretation follows from the nature of the logarithmic axis, where a value of 1 represents ${10}^1=10$ meters and a value of 2 represents ${10}^2=100$ meters. The peaks of the curves, obtained as cross-sections of the 3D plots parallel to the $R_{yz}$ plane, therefore fall within the range of approximately 10 to 100 m, indicating that most of the observed HILS lengths in the respective category are of this magnitude. In Ireland (see Figure 6), however, there is a relatively high number of HILSs with lengths in the range of hundreds of meters, considering the total number of HILSs analysed in that country. This phenomenon, although to a lesser extent, can also be observed in Croatia (see Figure 6). Conversely, relatively few HILSs of the main road network with lengths in the hundreds of meters, relative to the total number of analysed HILSs, are particularly notable in Germany, Cyprus, and Luxembourg. This trend is also partially evident in Hungary, the Netherlands, Bulgaria, and Portugal. In countries where very short HILSs prevail and longer ones are rare, this may indicate a high density of the road network but also the risk of traffic being “transferred” across sections where longer direct routes are missing. Conversely, countries such as Ireland may have a higher proportion of long HILSs, which suggests faster interregional accessibility but weaker fine-grained connectivity at the local level.

Depending on the size of each country and the development of its transport infrastructure, the number of HILSs of the most frequent length typically ranges from several thousand to tens of thousands. The only exceptions are the island states Cyprus and Malta. The similarity between the shapes of charts corresponding to individual countries depicted in Figure 5, Figure 6 and Figure 7 is remarkably high, although the shape of the chart associated with Malta, Ireland, and Latvia slightly differs from the other profiles. Cross-sections of the 3D plots taken parallel to the $R_{xz}$ plane mimic Benford’s distribution, while those parallel to the $R_{yz}$ plane resemble a normal distribution. The fact that the lengths of HILSs of the main road network in the analysed countries follow Benford’s distribution suggests that the formation of main road networks gives rise to patterns typically observed in naturally occurring datasets, indicating a certain universal character of these processes across different geographical and institutional contexts.

3.3. Practical Applications of the Findings

While this paper observes that the lengths of HILSs in EU countries follow Benford’s Law, the underlying causal mechanism merits deeper discussion. Previous works have shown that Benford-like distributions commonly arise in datasets governed by multiplicative processes, scale invariance, and combination of heterogeneous influences [42,43]. In the case of road infrastructure, although segment lengths are affected by diverse factors (terrain, funding availability, urbanisation patterns, political decisions), these factors do not act additively, but rather interact multiplicatively over time. This aligns with HILSs demonstration that the product of independent random variables, even with arbitrary distribution, tends to converge in Benford’s distribution. Moreover, the planning and growth of road networks often occur across multiple spatial and temporal scales, without a natural unit of measurement, creating a scale-invariant context where Benford’s Law is statistically favored [44]. Thus, while no single deterministic model dictates road lengths, their emergence from a multi-factorial, multiplicative, and scale-free development process helps explain the convergence in Benford’s distribution.

According to above statements, HILSs demonstrate an inherent conformity with Benford’s Law, mainly because they meet the key requirement of multiplicative growth across various scales. This arises from the statistical regularity created by the interaction of multiple independent factors (policy-making, planning, investment, terrain) over time, which leads the HILSs’ length distribution towards a logarithmic, Benford-like pattern.

However, this natural conformity is often disrupted by external, human-influenced factors such as political decisions, intentional rounding practices, or legislative cutoffs. Therefore, the measurable deviation from Benford’s Law should not be seen as definitive proof of data fraud but rather as a helpful supplementary tool for identifying anomalies and maintaining quality. A high or consistent pattern of deviation in a specific nation often indicates the influence of systematic, human-imposed constraints that compromise the data’s inherent integrity. This deviation may point to a highly centralised, rigid planning regime, manifested through political decisions or legislative cutoffs, that introduces non-multiplicative limits on infrastructure development. Alternatively, these subtle national differences could signal nation-specific methodological issues in data collection or reporting, such as intentional rounding or specific cutoffs mandated by national agencies. In any case, the measurable deviation acts as a clear indicator of external human factors requiring further investigation into the specific causes, whether fraudulent manipulation, methodological issues, or specific national planning policies.

The discovery that the examined infrastructure elements of the transportation network conform to Benford’s Law is significant from several perspectives. If new or updated data on HILS lengths deviate from the expected distribution, this may indicate possible typographical errors during data entry, inconsistencies between different data sources (e.g., national vs. European registries), or potential data alterations (in project reports, official records, public procurement, planning documents, or for budgetary or project-related purposes). In this context, internal database consistency checks based on Benford’s Law offer a cost-effective way to flag potentially problematic data and help auditors focus their attention where it is most needed, without requiring manual inspection of all records.

Furthermore, Benford’s Law can serve as a quick quality control test. For instance, inaccurate length calculations may stem from the use of inappropriate algorithms, such as applying Euclidean distance instead of geodetic distance, or from incorrectly projected GPS coordinates without proper metric conversion. Road segment lengths can also be distorted due to sparse GPS point sampling, excessive filtering, or snapping processes. Since Benford’s Law allows data quality assessment, it thus reduces costs associated with later corrections.

Finally, in times when roads are extended, shortened, or reorganized, Benford’s Law can serve as a basis for detecting infrastructure change. A deviation from Benford’s Law conformity can signal structural changes in the network, allowing automatic identification of modifications or real-time monitoring of how construction activities impact the structure of the road network.

The analysis of length distribution can serve as a tool for identifying peripheral or insufficiently serviced regions. In regional strategies, it can then be determined whether it is more appropriate to supplement the network with shorter connecting segments, which improve accessibility for smaller settlements, or with longer routes, which provide more efficient long-distance connections.

4. Conclusions

Tobler’s laws of geography represent fundamental principles of spatial relationships. In contrast to these spatial principles, Benford’s Law focuses on the statistical distribution of numerical data and provides a novel perspective for analysing patterns within datasets, such as those related to transport infrastructure.

This research aims to bridge the gap between spatial theory and statistical data analysis by applying Benford’s Law to transport infrastructure data. It offers a new tool for validating data quality, identifying anomalies, and revealing underlying structural patterns in transport networks, which can ultimately support improved planning and decision-making processes.

The lengths of higher-level segments of the main road network in the 27 European Union member states were used in the analysis. To assess whether the higher-level segment length data of the main road network of all EU countries conform to Benford’s distribution, a ${\chi }^2$ test was performed, and the resulting p-value was used to evaluate the significance of the results. The additional validation of the reliability of our results came from the Kolmogorov-Smirnov test.

Overall, it can be concluded that EU member states have relatively well-developed main road networks, although we recognise that their quality may vary between countries. The higher-level segments of the main road network in each EU state adhere very well to Benford’s Law.

Although the ${\chi }^2$ test is known to be very sensitive, often leading to the rejection of the null hypothesis due to minor discrepancies, this was not the case in this study. In all examined instances, the test yielded low ${\chi }^2$ values and p-values above the standard significance level (0.05). These results were supported by the Kolmogorov-Smirnov test, which indicates minimal differences between observed and expected frequencies, showing strong conformity with Benford’s Law. Therefore, there is no reason to reject the null hypothesis: “The leading digits of the HILSs of the main road network of EU member states follow Benford’s Law.” On the contrary, the results support its acceptance, as the empirical data align closely with the theoretical distribution predicted by Benford’s Law. This strong conformity holds even in the context of a large dataset, further reinforcing the robustness of the results and the reliability of the applied statistical methods.

In summary, the analysis reveals that despite national differences in the distribution of higher-level segment lengths, the overall structure of the main road networks across the observed countries exhibits a striking degree of similarity.

The findings of this study offer several practically applicable insights in the fields of transport policy, spatial planning, and geospatial data management. For policymakers and regional planners, the identification of universal, self-organizing patterns in the development of road infrastructure provides a valuable foundation for more efficient and targeted investment in transport networks. The observed convergence in the length characteristics of main road segments across EU member states, including strong conformity with Benford’s Law, indicates the presence of naturally occurring organizational principles that transcend national planning decisions. This supports the case for enhanced regional cooperation and the development of common transport policies within the EU framework, such as through funding mechanisms like the Connecting Europe Facility (CEF).

The combination of spatial theory and statistical analysis enables the modelling of infrastructure development and the forecasting of the consequences of various investment strategies. In cases of divergence between countries, planners may investigate the underlying causes of such anomalies, whether rooted in historical, geographic, or institutional differences.

If road segments across different countries follow similar statistical distributions, it suggests that infrastructure development occurs in a relatively balanced manner. This insight may serve as an argument for or against further intervention by EU-level institutions. At the same time, it provides a reference framework for evaluating planned infrastructure projects, where significant deviations from the expected distribution may point to systemic imbalances, planning deficiencies, or specific contextual factors that require further investigation.

Beyond planning implications, this study also has important relevance for the field of data quality assessment and validation. In this context, Benford’s Law emerges as an effective tool for automated auditing of large geospatial datasets, particularly where manual validation is impractical. The ability to detect suspicious anomalies, inconsistencies, or artificial manipulations in data is critical, especially in environments that rely on open data and transparency in public administration, where data quality directly affects the reliability of analytical outputs and policy decisions.

Finally, the integration of spatial theories, such as Tobler’s laws, with data-driven statistical approaches like Benford’s Law opens new possibilities for interdisciplinary research into complex geographic systems. This approach not only deepens our understanding of the spatial structure and evolution of transport networks but also supports more transparent, adaptive, and evidence-based decision-making in spatial development and public investment.

Future studies could build on this approach by incorporating additional datasets or exploring similar applications across other fields.