Context-Aware Anomaly Detection of Pedestrian Trajectories in Urban Back Streets Using a Variational Autoencoder
Abstract
1. Introduction
2. Related Works
2.1. Definition of Anomalies
2.2. Anomaly Detection
2.3. Generative Model-Based Approaches
3. Methodology
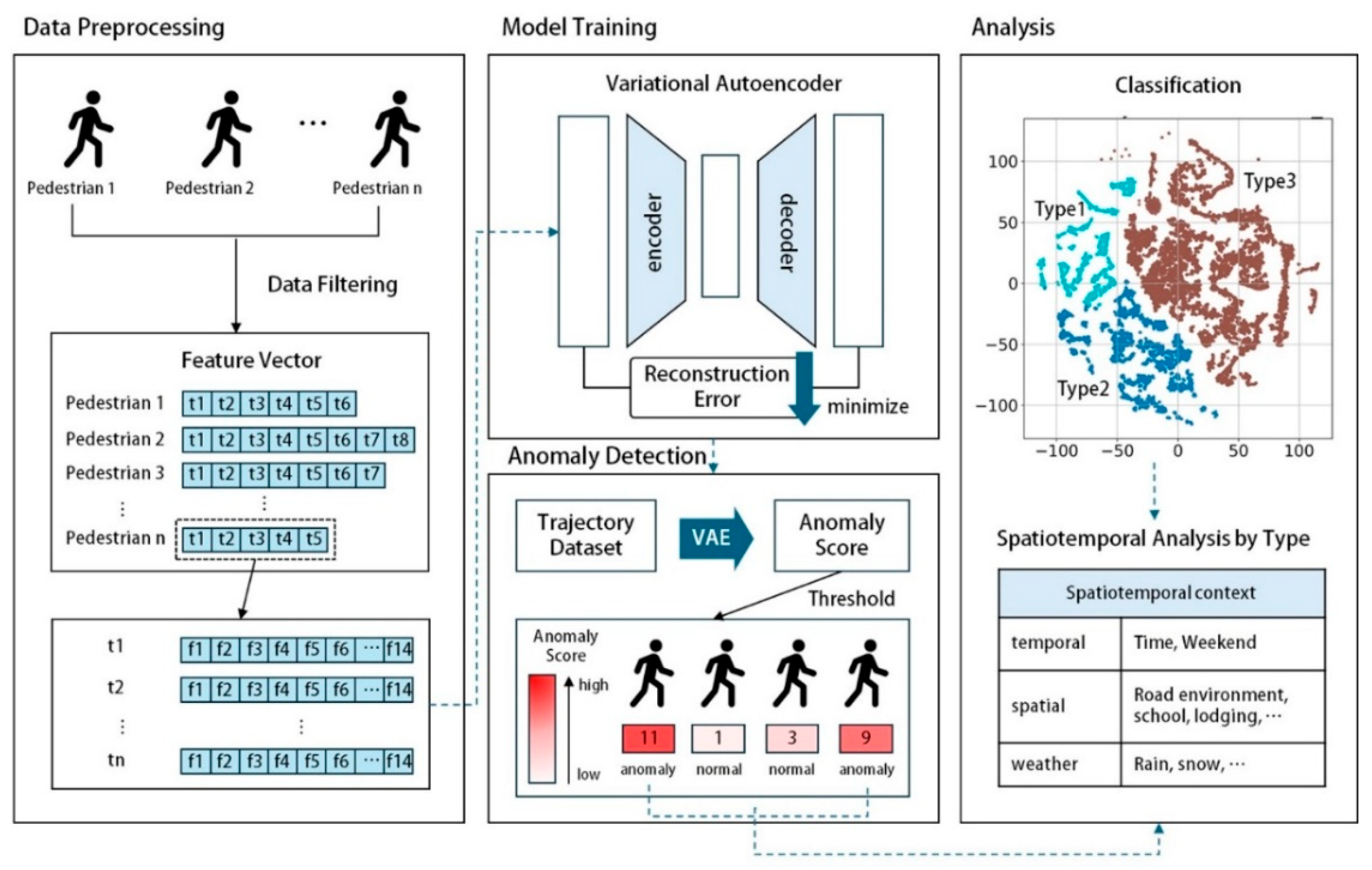
3.1. Framework Overview
- Data Preprocessing: Short trajectories are filtered out, and 14 movement features are extracted across three levels: point-level, trajectory-level, and grid-based.
- Model Training: Training and validation datasets are constructed. Each trajectory is represented as a feature vector composed of the number of points multiplied by the number of features. Experiments are conducted by modifying training conditions using the validation set, and model parameters are selected based on the best-performing configuration.
- Anomaly Detection: The trained model reconstructs the input trajectories, and anomalies are identified based on reconstruction errors. Trajectories with high reconstruction errors or poor reconstruction performance are classified as anomalous.
- Analysis: Anomalous trajectories are clustered into distinct types, and their spatiotemporal characteristics are analyzed.
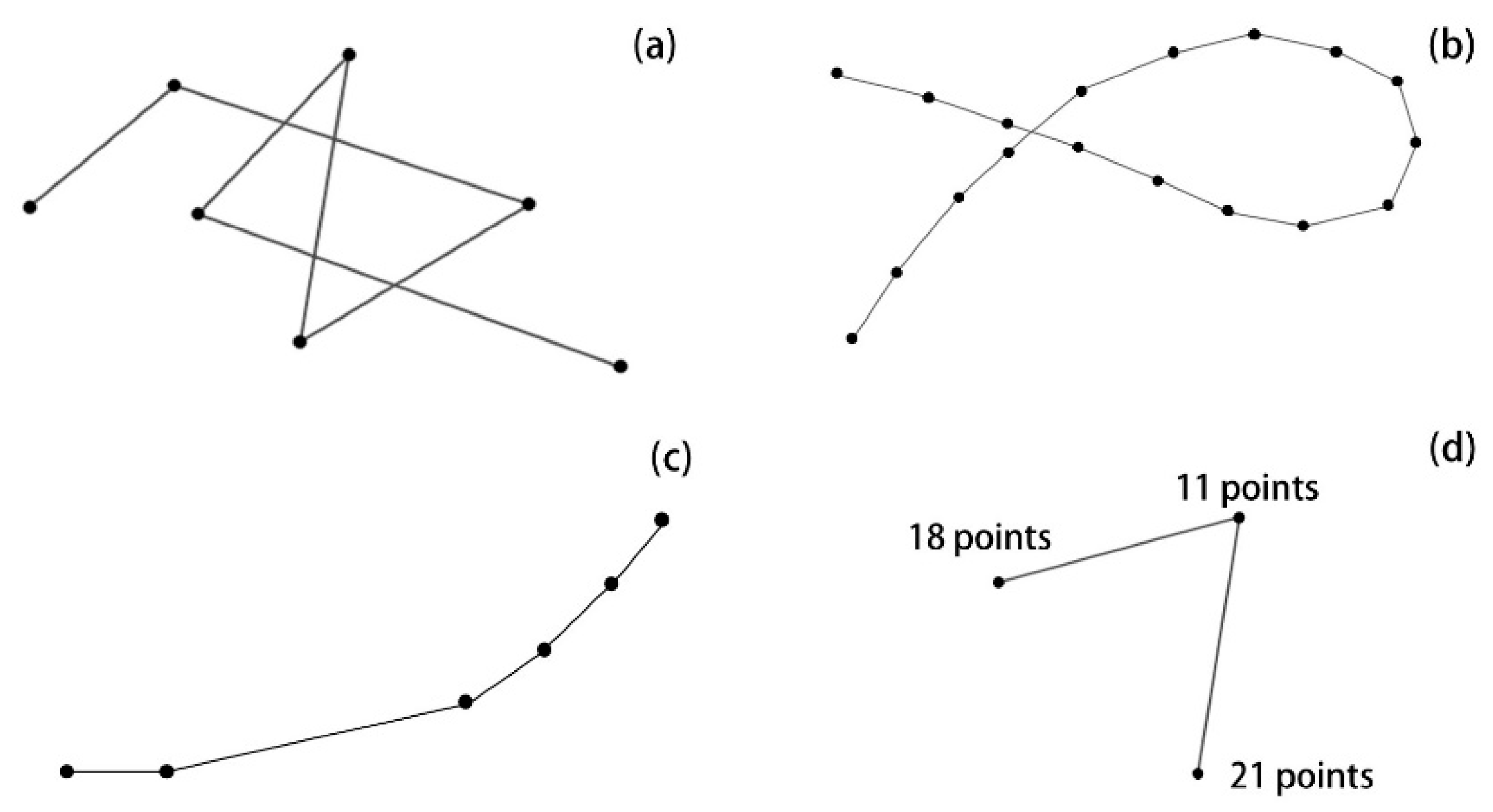
3.2. Data Preprocessing
3.3. Model Training
3.3.1. Training Data Construction
3.3.2. Model Architecture and Training Workflow
- (1)
- Data Transformation Module
- (2)
- Reconstruction Module
- : Input trajectory segment
- : Mean of latent variable
- : Standard deviation of latent variable
- : Sampled latent variable
- : Noise sampled from standard normal distribution
- : Reconstructed segment
- : Prior distribution
- : Posterior distribution inferred by encoder
- (3)
- Anomaly Detection Module
3.4. Anomaly Detection and Analysis
4. Experiments
4.1. Experimental Setup
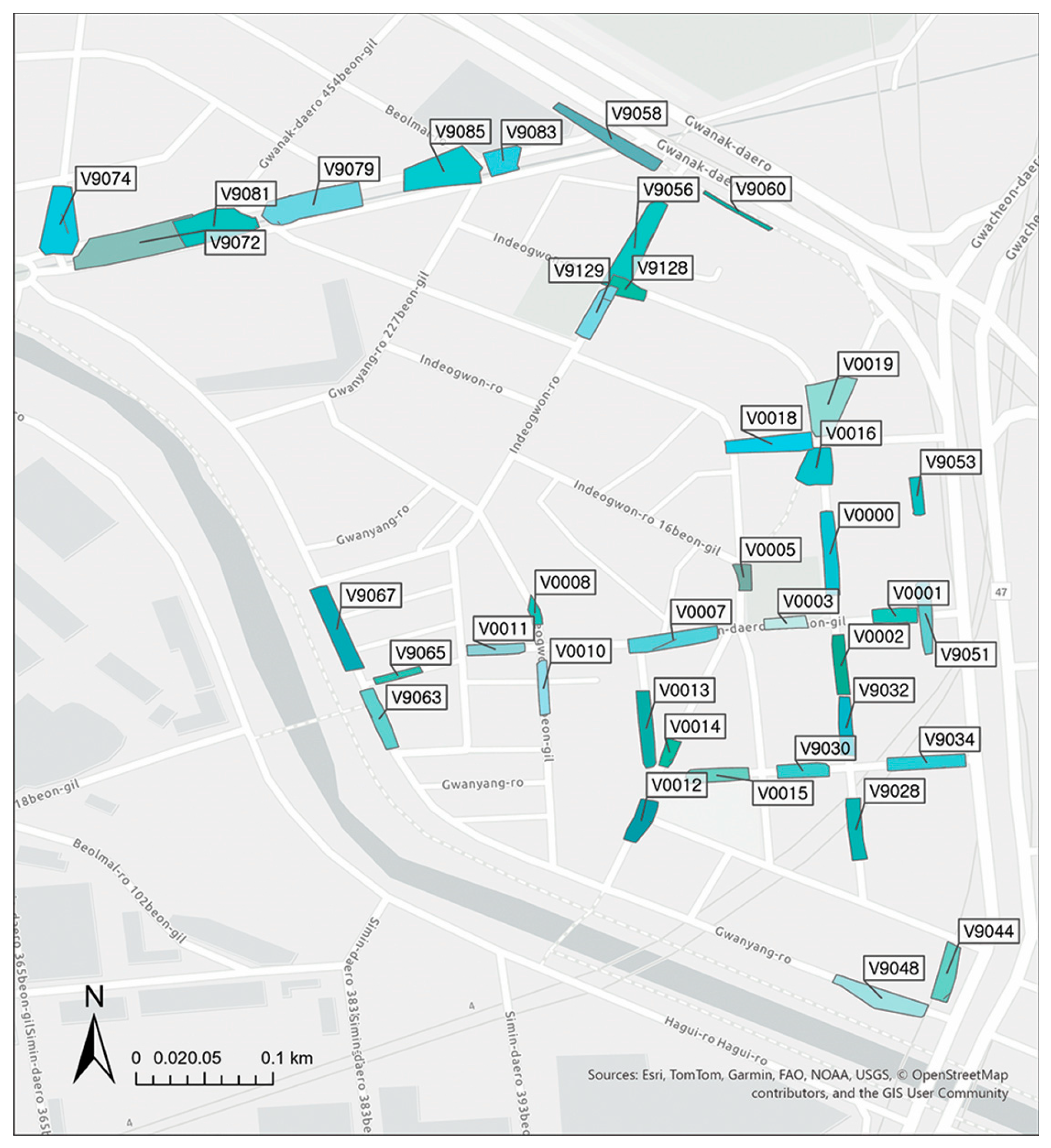
4.1.1. Data
4.1.2. Evaluation Metrics
- True Positive (TP): Correctly predicted as positive.
- True Negative (TN): Correctly predicted as negative.
- False Positive (FP): Incorrectly predicted as positive.
- False Negative (FN): Incorrectly predicted as negative.
4.2. Model Optimization and Performance Evaluation
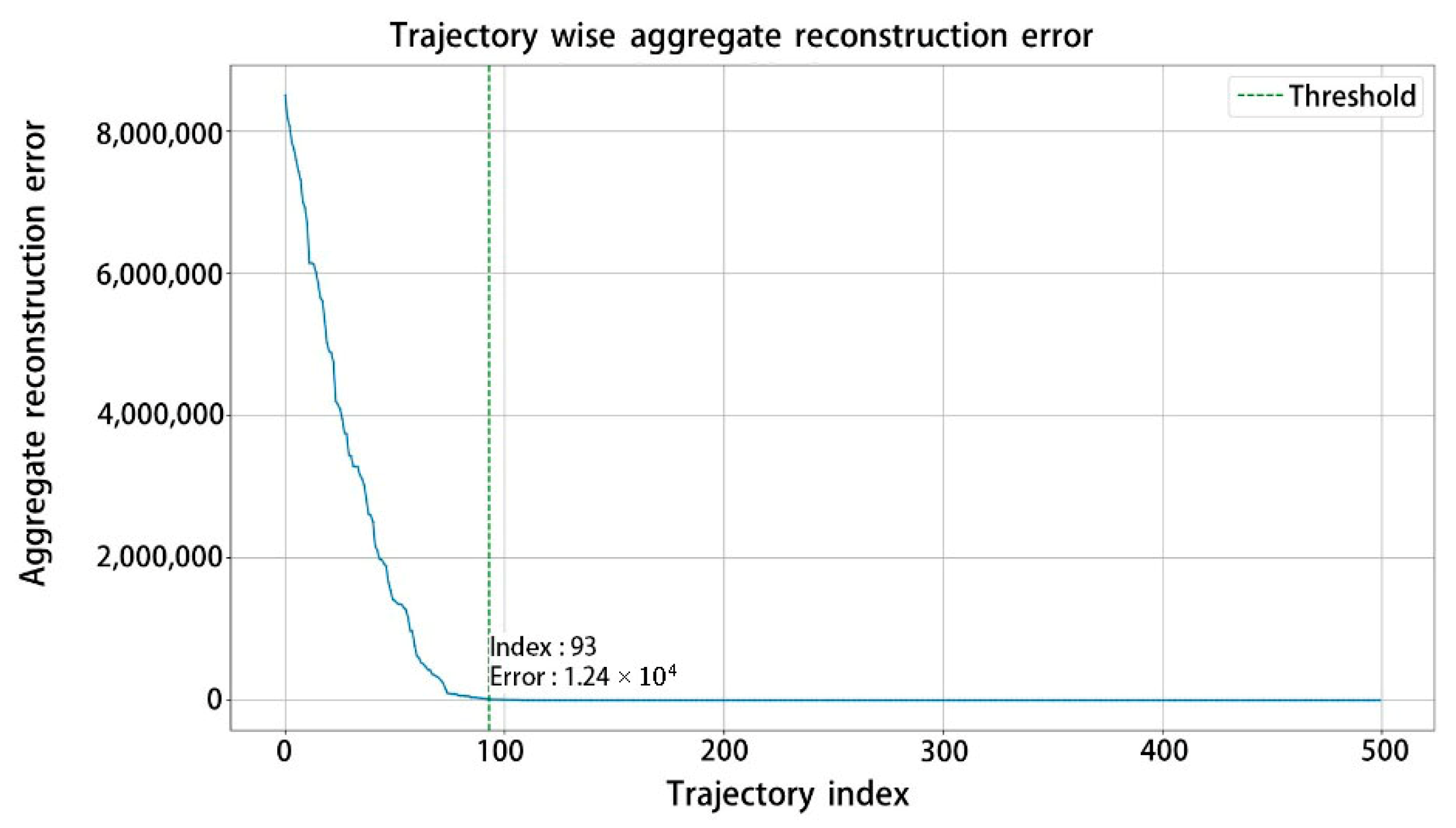
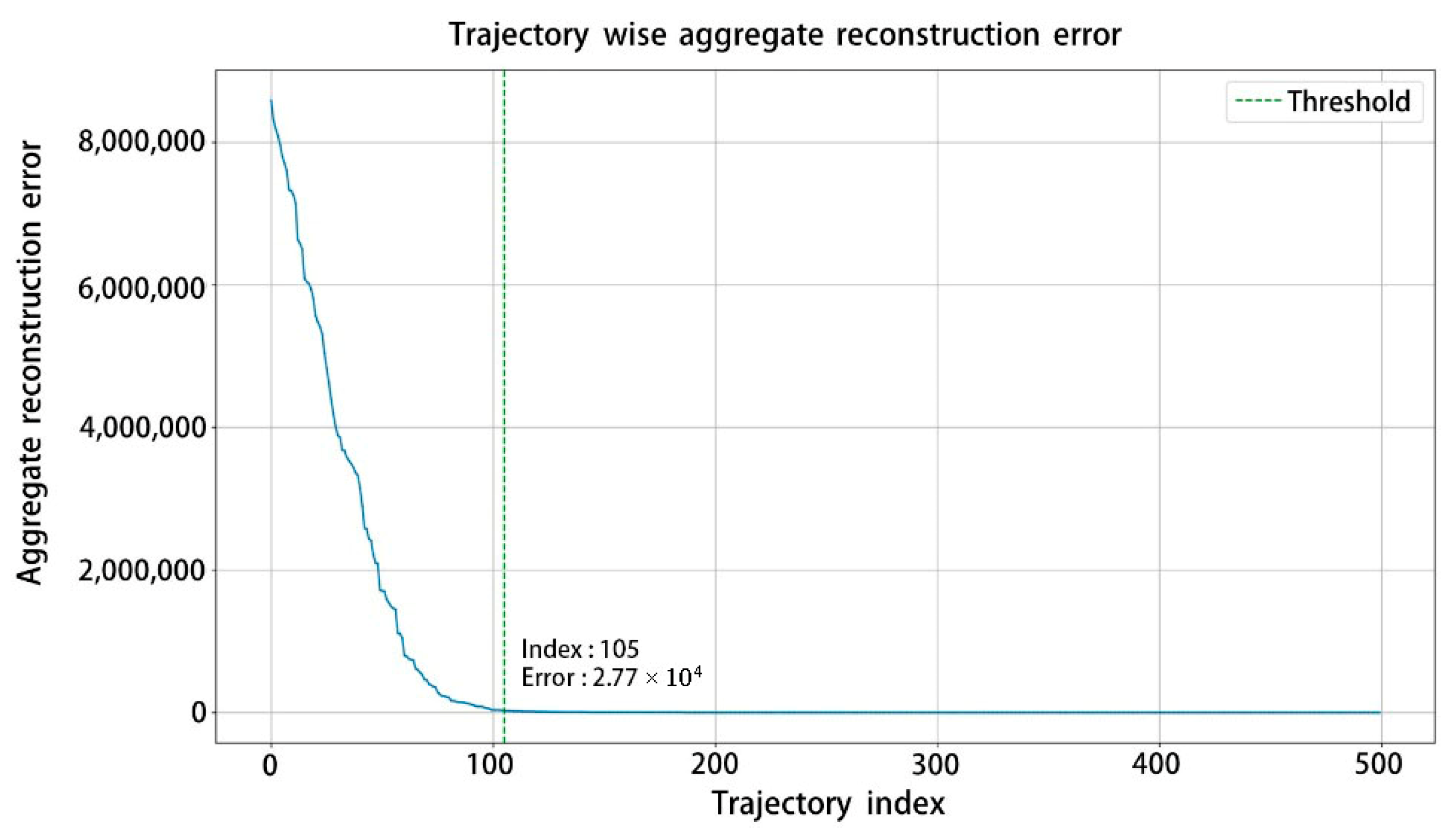
4.3. Anomaly Detection Results
4.4. Analysis of Detection Results
4.4.1. Anomaly Type Classification
4.4.2. Spatiotemporal Context Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, H.; Xu, X.; Fan, Y.; Zhang, C.; Peng, Y. An auto encoder network based method for abnormal behavior detection. In Proceedings of the 2021 4th International Conference on Software Engineering and Information Management, Yokohama, Japan, 16–18 January 2021; pp. 243–251. [Google Scholar]
- Wang, C.; Li, K.; Chen, L. Deep unified attention-based sequence modeling for online anomalous trajectory detection. Future Gener. Comput. Syst. 2023, 144, 1–11. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, W.; Xue, F.; Chang, Y. A trajectory outlier detection method based on variational auto-encoder. Math. Biosci. Eng. 2023, 20, 15075–15093. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Ting, K.M.; Shang, Y. A Principled Distributional Approach to Trajectory Similarity Measurement and its Application to Anomaly Detection. J. Artif. Intell. Res. 2024, 79, 865–893. [Google Scholar] [CrossRef]
- Xie, Z.; Bai, X.; Xu, X.; Xiao, Y. An anomaly detection method based on ship behavior trajectory. Ocean Eng. 2024, 293, 116640. [Google Scholar] [CrossRef]
- Kim, K.Y.; Kim, H.C.; Oh, S.H. Characteristic analysis of pedestrian behavior on local street in residential area. Korean Soc. Civ. Eng. D 2002, 22, 197–205. [Google Scholar]
- Berroukham, A.; Housni, K.; Lahraichi, M.; Boulfrifi, I. Deep learning-based methods for anomaly detection in video surveillance: A review. Bull. Electr. Eng. Inform. 2023, 12, 314–327. [Google Scholar] [CrossRef]
- Huang, H.; Zhao, B.; Gao, F.; Chen, P.; Wang, J.; Hussain, A. A novel unsupervised video anomaly detection framework based on optical flow reconstruction and erased frame prediction. Sensors 2023, 23, 4828. [Google Scholar] [CrossRef]
- D’amicantonio, G.; Bondarau, E. uTRAND: Unsupervised Anomaly Detection in Traffic Trajectories. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 7638–7645. [Google Scholar]
- Lee, J.; Cho, J.; Kim, J.; Lee, D.; Kang, Y. Research trends analysis of vision-based trajectory prediction using deep learning. J. Korean Soc. Geospat. Inf. Sci. 2022, 30, 113–128. [Google Scholar]
- Zhang, D.; Li, N.; Zhou, Z.H.; Chen, C.; Sun, L.; Li, S. iBAT: Detecting anomalous taxi trajectories from GPS traces. In Proceedings of the 13th International Conference on Ubiquitous Computing, Beijing, China, 17–21 September 2011; pp. 99–108. [Google Scholar]
- Lin, Q.; Zhang, D.; Connelly, K.; Ni, H.; Yu, Z.; Zhou, X. Disorientation detection by mining GPS trajectories for cognitively-impaired elders. Pervasive Mob. Comput. 2015, 19, 71–85. [Google Scholar] [CrossRef]
- Liu, M.; Yang, K.; Fu, Y.; Wu, D.; Du, W. Driving maneuver anomaly detection based on deep auto-encoder and geographical partitioning. ACM Trans. Sens. Netw. 2023, 19, 37. [Google Scholar] [CrossRef]
- Kang, Y. GeoAI application areas and research trends. J. Korean Geogr. Assoc. 2023, 58, 395–418. [Google Scholar]
- Li, X.; Kiringa, I.; Yeap, T.; Zhu, X.; Li, Y. Anomaly detection based on unsupervised disentangled representation learning in combination with manifold learning. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN) 2020, Glasgow, UK, 19–24 July 2020; pp. 1–10. [Google Scholar]
- Yu, W.; Huang, Q. A deep encoder-decoder network for anomaly detection in driving trajectory behavior under spatio-temporal context. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103115. [Google Scholar] [CrossRef]
- Guzman, E.; Howe, R.D. Sidewalk Hazard Detection Using Variational Autoencoder and One-Class SVM. arXiv 2024, arXiv:2501.00585. [Google Scholar] [CrossRef]
- Kolluri, J.; Das, R. Intelligent multimodal pedestrian detection using hybrid metaheuristic optimization with deep learning model. Image Vis. Comput. 2023, 131, 104628. [Google Scholar] [CrossRef]
- Hu, H.; Kim, J.; Zhou, J.; Kirsanova, S.; Lee, J.; Chiang, Y. Context-Aware Trajectory Anomaly Detection. In Proceedings of the 1st ACM SIGSPATIAL International Workshop on Geospatial Anomaly Detection, Atlanta, GA, USA, 29 October 2024; pp. 12–15. [Google Scholar]
- Suzuki, N.; Hirasawa, K.; Tanaka, K.; Kobayashi, Y.; Sato, Y.; Fujino, Y. Learning motion patterns and anomaly detection by human trajectory analysis. In Proceedings of the 2007 IEEE International Conference on Systems, Man and Cybernetics, Montreal, QC, Canada, 7–10 October 2007; pp. 498–503. [Google Scholar]
- Lan, D.T.; Yoon, S. Trajectory Clustering-Based Anomaly Detection in Indoor Human Movement. Sensors 2023, 23, 3318. [Google Scholar] [CrossRef]
- Yoon, S. Anomalous Indoor Human Trajectory Detection Based on the Transformer Encoder and Self-Organizing Map. IEEE Access 2023, 11, 131848–131865. [Google Scholar] [CrossRef]
- Doan, T.N.; Kim, S.; Vo, L.C.; Lee, H.J. Anomalous trajectory detection in surveillance systems using pedestrian and surrounding information. IEIE Trans. Smart Process. Comput. 2016, 5, 256–266. [Google Scholar] [CrossRef]
- Bera, A.; Kim, S.; Manocha, D. Realtime anomaly detection using trajectory-level crowd behavior learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Las Vegas, NV, USA, 20–26 June 2016; pp. 50–57. [Google Scholar]
- Fuse, T.; Kamiya, K. Statistical anomaly detection in human dynamics monitoring using a hierarchical dirichlet process hidden markov model. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3083–3092. [Google Scholar] [CrossRef]
- Liu, H.; Wu, C.; Li, B.; Zong, Z.; Shu, Y. Research on Ship Anomaly Detection Algorithm Based on Transformer-GSA Encoder. IEEE Trans. Intell. Transp. Syst. 2025, 26, 8752–8763. [Google Scholar] [CrossRef]
- Qiu, M.; Mao, S.; Zhu, J.; Yang, Y. Spatiotemporal multi-feature fusion vehicle trajectory anomaly detection for intelligent transportation: An improved method combining autoencoders and dynamic Bayesian networks. Accid. Anal. Prev. 2025, 211, 107911. [Google Scholar] [CrossRef]
- Shi, H.; Dong, S.; Wu, Y.; Nie, Q.; Zhou, Y.; Ran, B. Generative adversarial network for car following trajectory generation and anomaly detection. J. Intell. Transp. Syst. 2024, 29, 53–66. [Google Scholar] [CrossRef]
- Rezaee, K.; Rezakhani, S.M.; Khosravi, M.R.; Moghimi, M.K. A survey on deep learning-based real-time crowd anomaly detection for secure distributed video surveillance. Pers. Ubiquitous Comput. 2024, 28, 135–151. [Google Scholar] [CrossRef]
- Xia, D.; Li, Y.; Ao, Y.; Wei, X.; Chen, Y.; Hu, Y.; Li, Y.; Li, H. Parallel recurrent neural network with transformer for anomalous trajectory detection. Appl. Intell. 2025, 55, 519. [Google Scholar] [CrossRef]
- Olive, X.; Basora, L.; Viry, B.; Alligier, R. Deep trajectory clustering with autoencoders. In Proceedings of the ICRAT 2020, 9th International Conference for Research in Air Transportation, Tampa, FL, USA, 23–26 June 2020. [Google Scholar]
- Zissis, D.; Chatzikokolakis, K.; Vodas, M.; Spiliopoulos, G.; Bereta, K. A data driven approach to maritime anomaly detection. In Proceedings of the 1st Maritime Situational Awareness Workshop MSAW, Singapore, 24 January 2019. [Google Scholar]
- Jiao, R.; Bai, J.; Liu, X.; Sato, T.; Yuan, X.; Chen, Q.A.; Zhu, Q. Learning representation for anomaly detection of vehicle trajectories. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 9699–9706. [Google Scholar]
- Anik, B.T.H.; Islam, Z.; Abdel-Aty, M. A time-embedded attention-based transformer for crash likelihood prediction at intersections using connected vehicle data. Transp. Res. Part C Emerg. Technol. 2024, 169, 104831. [Google Scholar] [CrossRef]
- Chang, Y.J. Anomaly detection for travelling individuals with cognitive impairments. ACM SIGACCESS Access. Comput. 2010, 97, 25–32. [Google Scholar] [CrossRef]
- Zhao, Q.; Shi, Y.; Liu, Q.; Franti, P. A grid-growing clustering algorithm for geo-spatial data. Pattern Recognit. Lett. 2015, 53, 77–84. [Google Scholar] [CrossRef]
- Shi, L.; Wang, L.; Zhou, S.; Hua, G. Trajectory unified transformer for pedestrian trajectory prediction. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 9675–9684. [Google Scholar]
- Westny, T.; Olofsson, B.; Frisk, E. Diffusion-based environment-aware trajectory prediction. arXiv 2024, arXiv:2403.11643. [Google Scholar]
- Wahyono Harjoko, A.; Dharmawan, A.; Adhinata, F.D.; Kosala, G.; Jo, K.H. Loitering Detection Using Spatial-Temporal Information for Intelligent Surveillance Systems on a Vision Sensor. J. Sens. Actuator Netw. 2023, 12, 9. [Google Scholar]
- Nunez, J.; Li, Z.; Escalera, S.; Nasrollahi, K. Identifying Loitering Behavior with Trajectory Analysis. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2024; pp. 251–259. [Google Scholar]



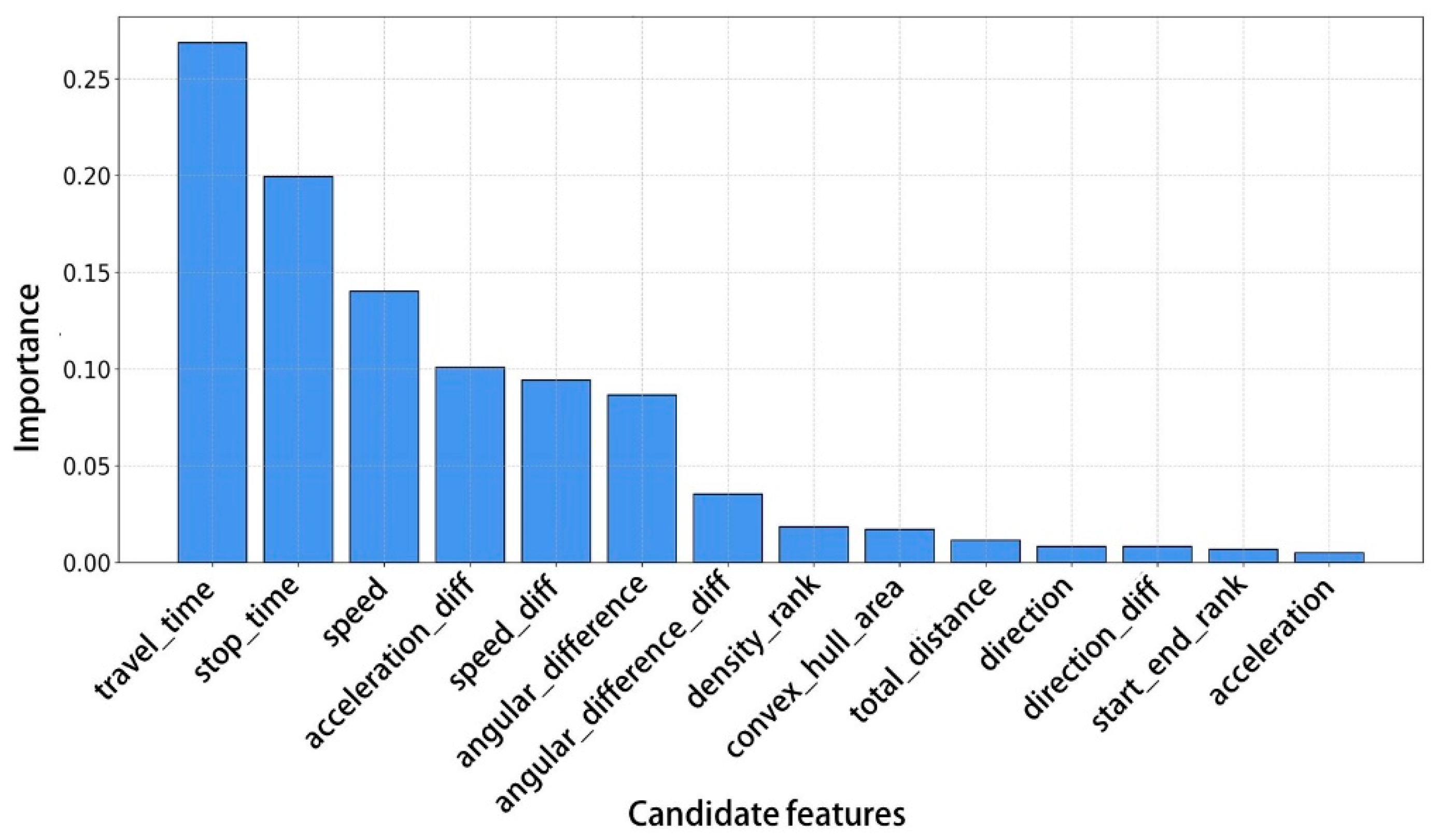

| Category | Feature | Description |
|---|---|---|
| Point-wise Movement Features | Speed | Distance between two points divided by time interval; indicates pedestrian speed. |
| Acceleration | Change in speed between two points divided by time; indicates acceleration or deceleration. | |
| Direction | Angle between two points relative to north; ranges from 0° to 360°. | |
| Angular Difference | Absolute difference between consecutive directions; indicates direction change. | |
| Global Trajectory-level Features | Travel Distance | The total length of the path traveled by the object. |
| Travel Time | Total duration of the movement. | |
| Stop Time | Total time during which speed is zero. | |
| Convex Hull Area | The area of the smallest convex polygon enclosing all points. | |
| Grid-based Features | Density Rank | Points counted per grid; ranks grids from lowest to highest density (1 to 4). |
| Start-End Rank | Counts start/end points per grid; ranks grids from lowest to highest (1 to 4). | |
| Speed Difference | Difference between average grid speed and individual point speed. | |
| Acceleration Difference | Difference between average grid acceleration and individual point acceleration. | |
| Direction Difference | Difference between average grid direction and individual point direction. | |
| Angular Difference Change | Difference between average grid angular difference and individual point angular difference. |
| Round | Collection Period | Number of CCTVs | Number of Trajectories | Number of Points |
|---|---|---|---|---|
| 1 | 2023.09.20. 00:00:00 –09.26. 11:59:59 | 16 | 616,246 | 27,520,631 |
| 2 | 2023.12.06. 12:00:00 –12.20. 16:59:59 | 12 | 2,011,105 | 25,435,082 |
| 3 | 2024.05.20. 18:00:00 –05.27. 12:59:59 | 38 | 1,225,023 | 17,426,458 |
| Experimental Condition | Description |
|---|---|
| Input Features | Set of features used by the model for anomaly detection |
| Window Size | Length of the temporal segment |
| Scaler | Min-Max scaler, Standard scaler |
| Number of Latent Dimensions | Number of dimensions in the low-dimensional latent space |
| Number of Input Features | Window Size | Scaler | Number of Latent Dimensions | Accuracy | F1-Score |
|---|---|---|---|---|---|
| 4 | - | - | - | 92.00 | 75.00 |
| 6 | 2 | Min-Max | 3 | 97.80 | 94.63 |
| 6 | |||||
| 9 | |||||
| 12 | |||||
| Standard | - | 96.00 | 90.91 | ||
| 3 | - | - | 97.60 | 93.34 | |
| 4 | - | - | 97.00 | 92.23 | |
| 5 | - | - | 97.00 | 92.23 | |
| 14 | - | - | - | 96.80 | 91.67 |
| Feature Combination & K | Silhouette Score | DBI |
|---|---|---|
| Set A, K = 3 | 0.63 | 0.69 |
| Set A, K = 4 | 0.59 | 0.98 |
| Set A, K = 5 | 0.39 | 1.13 |
| Set A, K = 6 | 0.37 | 1.12 |
| Set B, K = 3 | 0.60 | 0.71 |
| Set B, K = 4 | 0.51 | 0.74 |
| Set B, K = 5 | 0.51 | 0.92 |
| Set B, K = 6 | 0.52 | 0.84 |
| Cluster | Label | Characteristics | Number of Trajectories |
|---|---|---|---|
| 0 | Wandering | Frequent changes in direction and moderate stop duration | 4644 |
| 1 | Slow-linear | Short travel and stop durations Angular difference similar to normal trajectories Slower speed than normal trajectories | 12,514 |
| 2 | Stationary | Prolonged stopping and very slow movement Minimal directional changes | 2606 |
| Context Type | Variable | Description |
|---|---|---|
| Temporal Context | Time | Categorical variable indicating the hour of the day (in hourly intervals) |
| Weekend | Binary variable indicating whether it is a weekend (Sat/Sun: 0, Weekday: 1) | |
| Spatial Context | CCTV ID | Categorical variable representing the unique identifier of the CCTV camera |
| Road Type | Categorical variable classifying road types into four categories: alleyway–Commercial: 0, alleyway–Residential: 1, arterial road: 2, narrow road with sidewalk: 3 | |
| School | Binary variable indicating the presence of a nearby school (Yes: 0, No: 1) | |
| Lodging | Binary variable indicating the presence of accommodation facilities (Yes: 0, No: 1) | |
| Park | Binary variable indicating the presence of a nearby park (Yes: 0, No: 1) | |
| Environmental Context | Weather | Categorical variable representing daily weather conditions (Clear: 0, Rain: 1, Snow: 2, Cloudy/Foggy: 3) |
| CCTV ID | Wandering (Cluster 0) | Slow-Linear (Cluster 1) | Stationary (Cluster 2) | Road Type | School | Lodging | Park |
|---|---|---|---|---|---|---|---|
| 0000 | 18.34 | 78.38 | 3.26 | 0 | X | X | O |
| 0001 | 8.62 | 90.31 | 1.05 | 0 | X | X | X |
| 0002 | 9.76 | 88.38 | 1.84 | 0 | X | X | X |
| 0003 | 16.11 | 82.54 | 1.34 | 0 | X | X | O |
| 0005 | 8.91 | 86.83 | 4.24 | 0 | X | X | O |
| 0007 | 11.93 | 83.31 | 4.75 | 0 | X | X | X |
| 0008 | 7.55 | 92.44 | 0.00 | 1 | X | X | X |
| 0010 | 6.98 | 91.91 | 1.10 | 1 | X | X | X |
| 0011 | 7.63 | 91.60 | 0.76 | 1 | X | X | X |
| 0012 | 33.33 | 37.03 | 29.62 | 1 | X | X | X |
| 0013 | 10.84 | 79.51 | 9.63 | 1 | X | X | X |
| 0014 | 14.34 | 76.37 | 9.28 | 1 | X | X | X |
| 0015 | 28.57 | 60.71 | 10.71 | 1 | X | X | X |
| 0016 | 21.34 | 73.07 | 5.57 | 0 | X | X | X |
| 0018 | 21.56 | 64.43 | 14.00 | 0 | X | X | X |
| 0019 | 10.25 | 86.97 | 2.76 | 0 | X | X | X |
| 9028 | 75.00 | 0.00 | 25.00 | 1 | X | O | X |
| 9030 | 55.75 | 0.00 | 44.24 | 1 | X | O | X |
| 9032 | 95.65 | 0.00 | 4.34 | 1 | X | O | X |
| 9034 | 92.85 | 0.00 | 7.14 | 1 | X | O | X |
| 9044 | 38.18 | 0.00 | 61.81 | 2 | X | X | X |
| 9048 | 12.76 | 0.00 | 87.23 | 3 | X | X | X |
| 9051 | 73.14 | 0.00 | 26.85 | 2 | X | X | X |
| 9053 | 74.06 | 0.00 | 25.93 | 2 | X | X | X |
| 9056 | 67.72 | 0.00 | 32.27 | 0 | X | X | X |
| 9058 | 75.32 | 0.00 | 24.67 | 2 | X | X | X |
| 9060 | 71.42 | 0.00 | 28.57 | 2 | X | X | X |
| 9063 | 60.00 | 0.00 | 40.00 | 3 | X | X | X |
| 9065 | 73.91 | 0.00 | 26.08 | 1 | X | X | X |
| 9067 | 13.33 | 0.00 | 86.66 | 3 | X | X | X |
| 9072 | 27.27 | 0.00 | 72.72 | 3 | O | X | X |
| 9074 | 38.46 | 0.00 | 61.53 | 3 | O | X | X |
| 9079 | 22.75 | 0.00 | 77.24 | 3 | O | X | X |
| 9081 | 32.00 | 0.00 | 68.00 | 3 | O | X | X |
| 9083 | 17.64 | 0.00 | 82.35 | 3 | X | X | X |
| 9085 | 26.52 | 0.00 | 73.47 | 3 | X | X | X |
| 9128 | 18.73 | 69.41 | 11.84 | 0 | X | X | X |
| 9129 | 51.48 | 0.00 | 48.51 | 0 | X | X | O |
| Type | Clear | Rain | Snow | Cloudy/Foggy |
|---|---|---|---|---|
| Wandering (Cluster 0) | 12.5 | 17 | 9 | 34.2 |
| Slow-linear (Cluster 1) | 83.7 | 71.3 | 97.7 | 45.1 |
| Stationary (Cluster 2) | 3.8 | 11.7 | 3.3 | 20.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, J.; Kang, Y. Context-Aware Anomaly Detection of Pedestrian Trajectories in Urban Back Streets Using a Variational Autoencoder. ISPRS Int. J. Geo-Inf. 2025, 14, 438. https://doi.org/10.3390/ijgi14110438
Cho J, Kang Y. Context-Aware Anomaly Detection of Pedestrian Trajectories in Urban Back Streets Using a Variational Autoencoder. ISPRS International Journal of Geo-Information. 2025; 14(11):438. https://doi.org/10.3390/ijgi14110438
Chicago/Turabian StyleCho, Juyeon, and Youngok Kang. 2025. "Context-Aware Anomaly Detection of Pedestrian Trajectories in Urban Back Streets Using a Variational Autoencoder" ISPRS International Journal of Geo-Information 14, no. 11: 438. https://doi.org/10.3390/ijgi14110438
APA StyleCho, J., & Kang, Y. (2025). Context-Aware Anomaly Detection of Pedestrian Trajectories in Urban Back Streets Using a Variational Autoencoder. ISPRS International Journal of Geo-Information, 14(11), 438. https://doi.org/10.3390/ijgi14110438








