How Does Built Environment Influence Housing Prices in Large-Scale Areas? An Interpretable Machine Learning Method by Considering Multi-Dimensional Accessibility
Abstract
1. Introduction
2. Related Works
2.1. Influencing Mechanism of Housing Prices
2.2. Hedonic Price Model
2.3. Machine Learning in Street View Images Studies
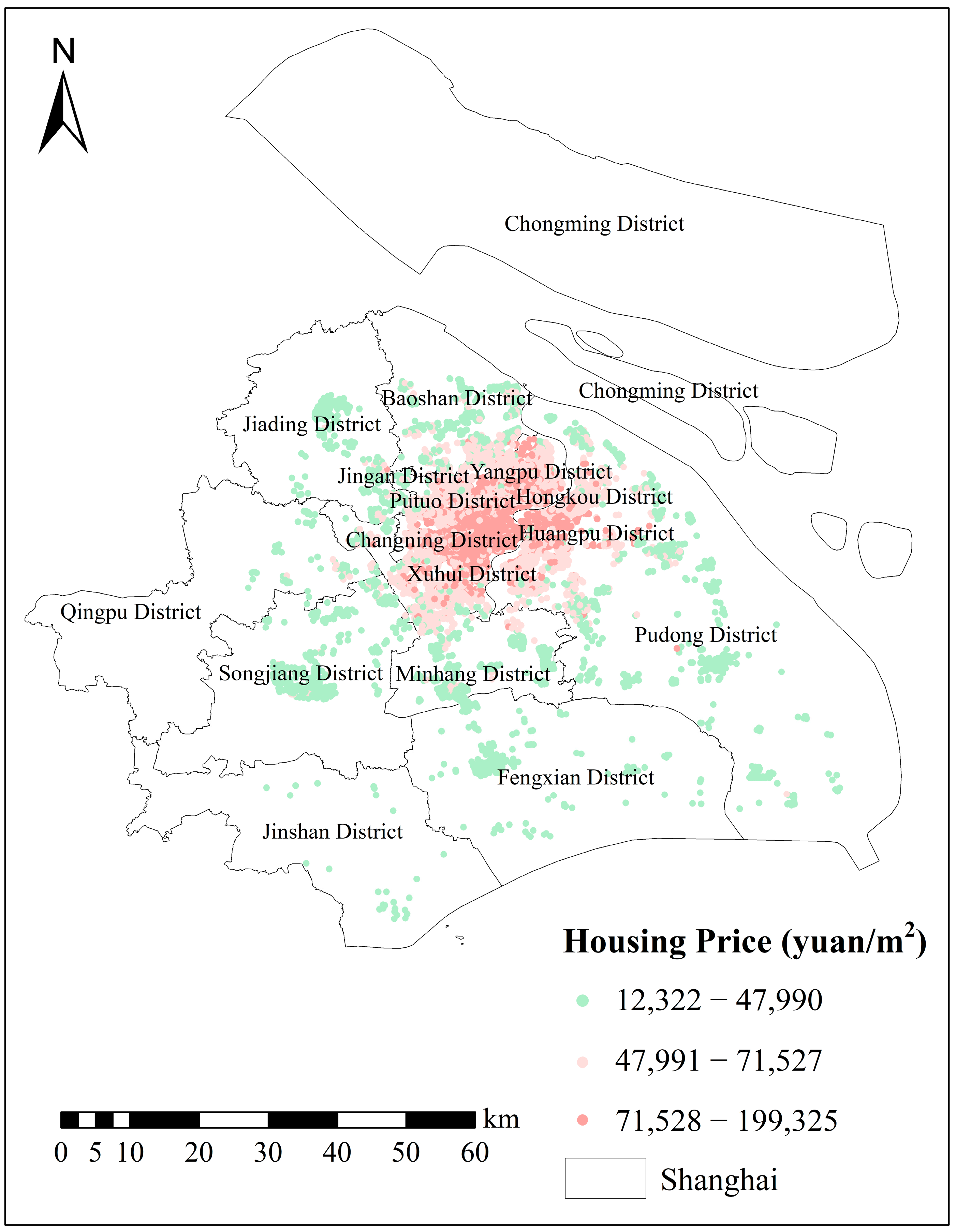
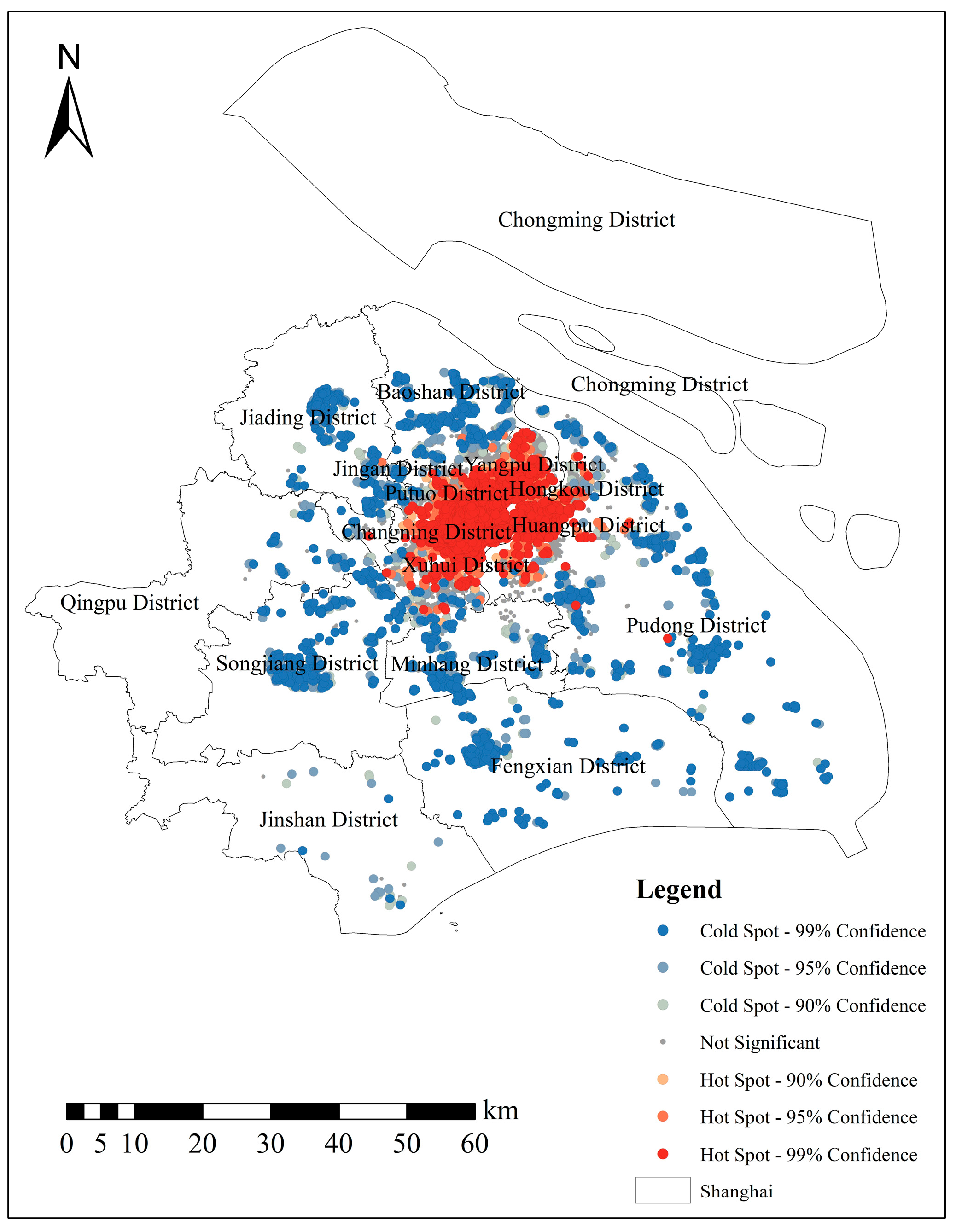
3. Study Area
4. Data Collection
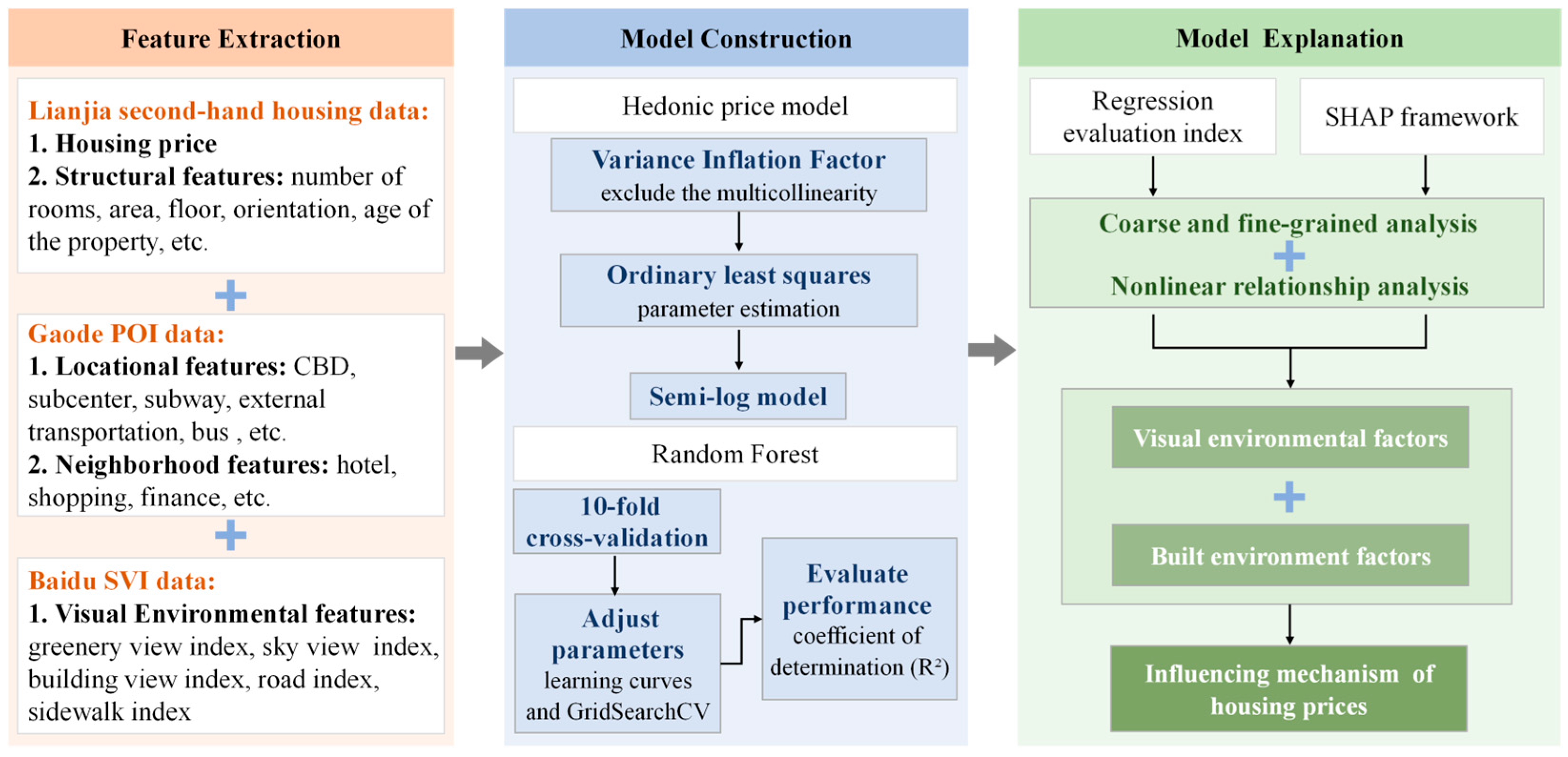
5. Method
5.1. Influencing Factor Extraction
5.2. Model Construction
5.3. Shapley Additive Explanations
6. Results and Analysis
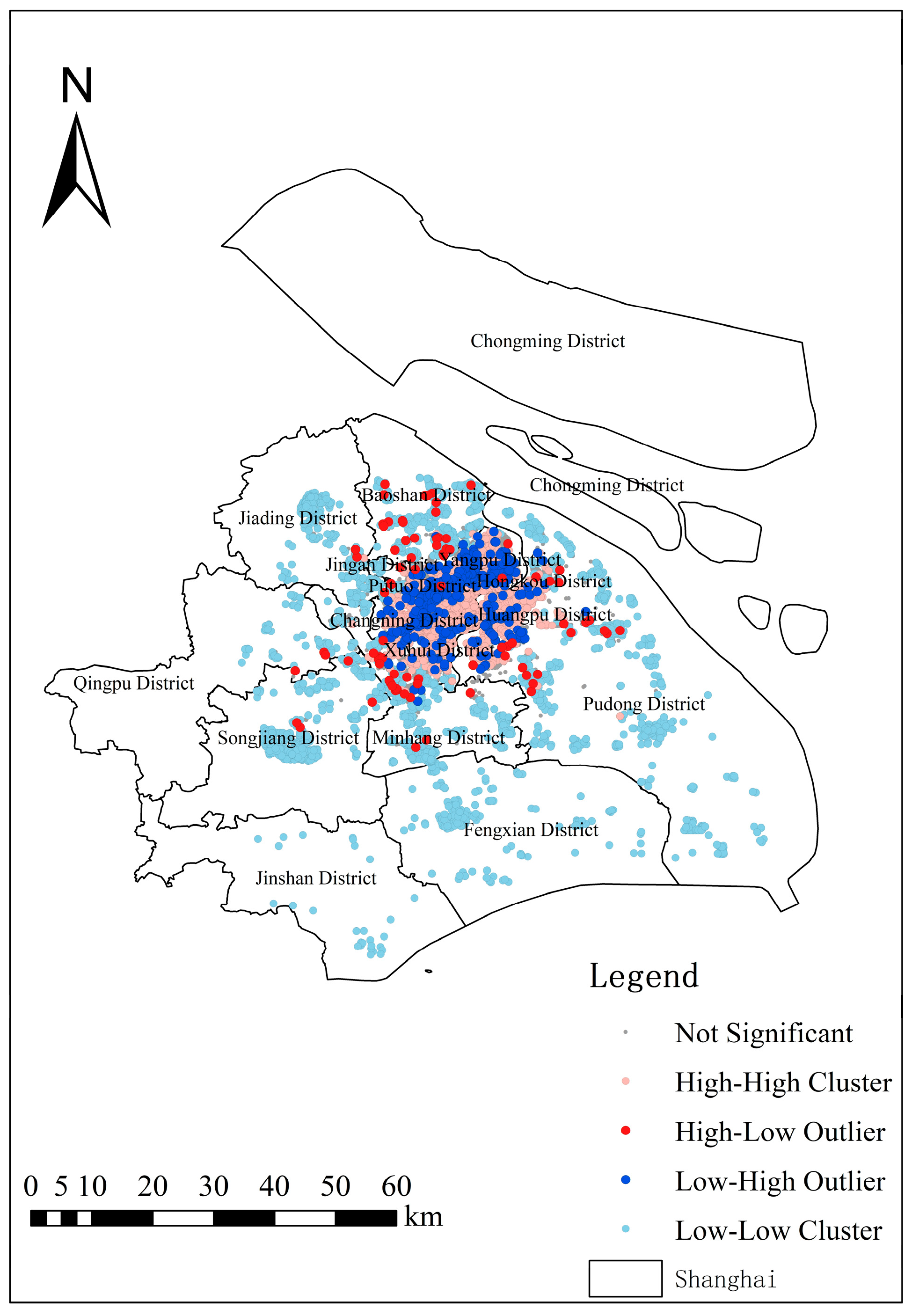
6.1. Spatial Autocorrelation Results Analysis
6.2. Hedonic Price Model Results Analysis
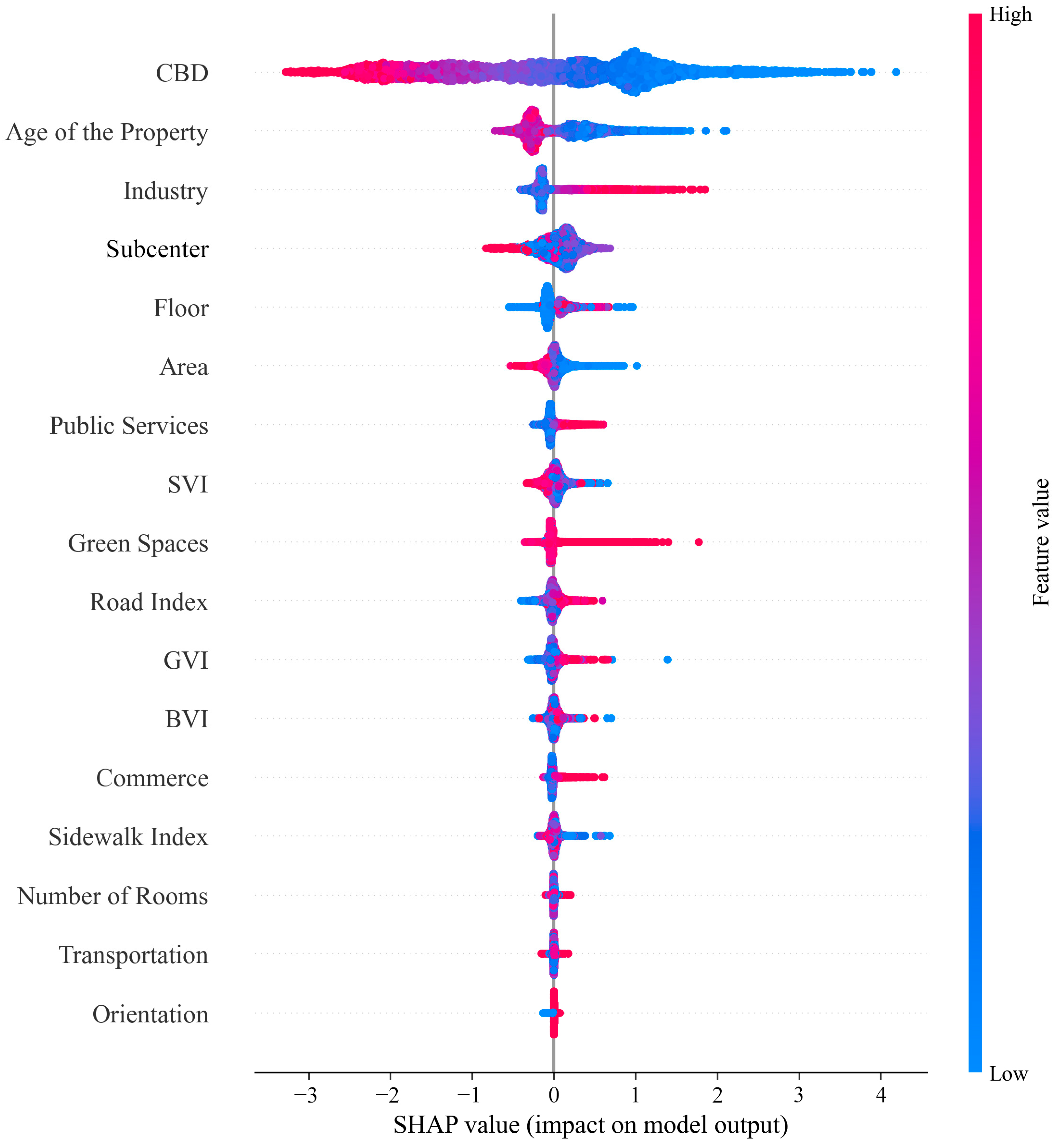
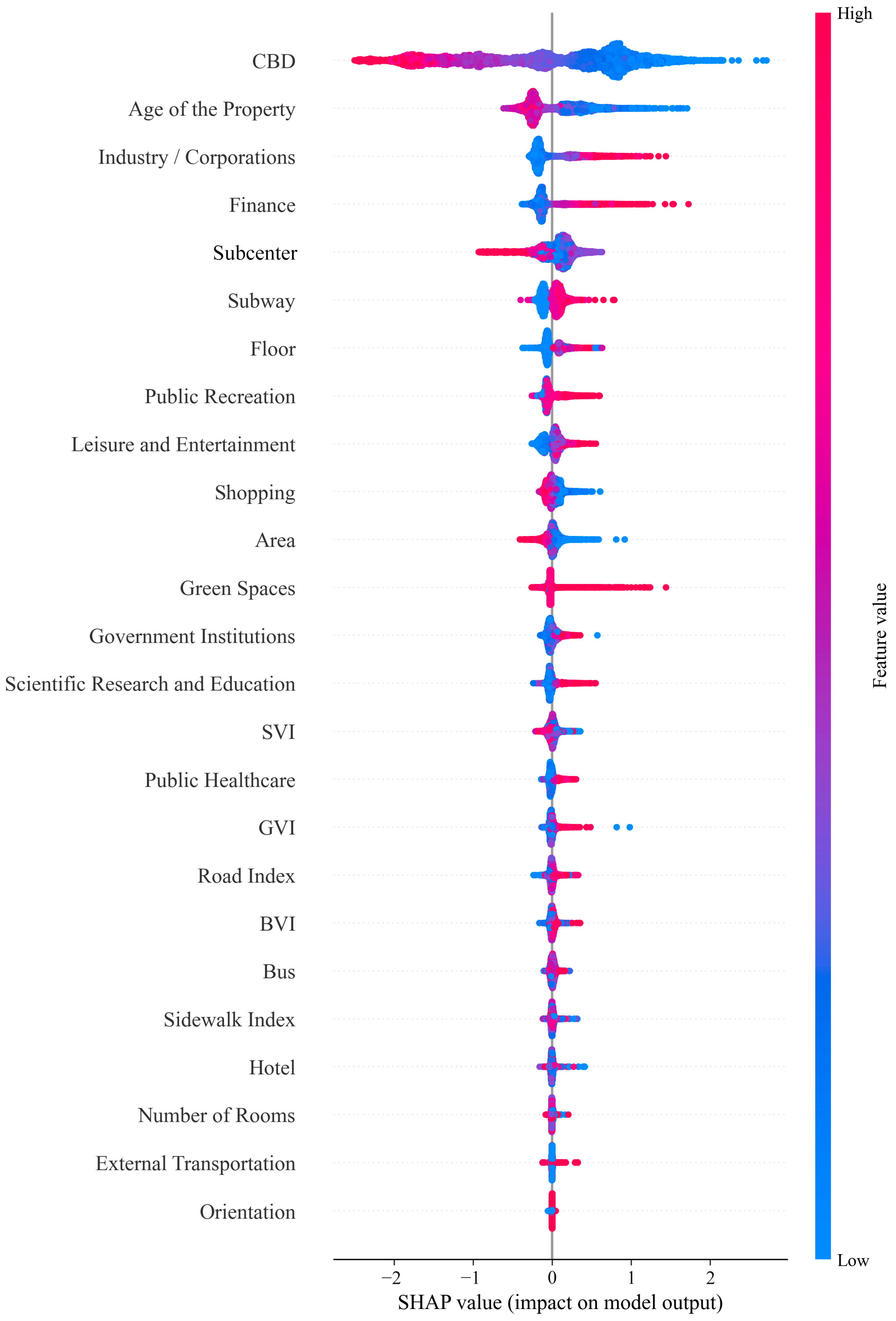
6.3. Machine Learning Model Interpretation
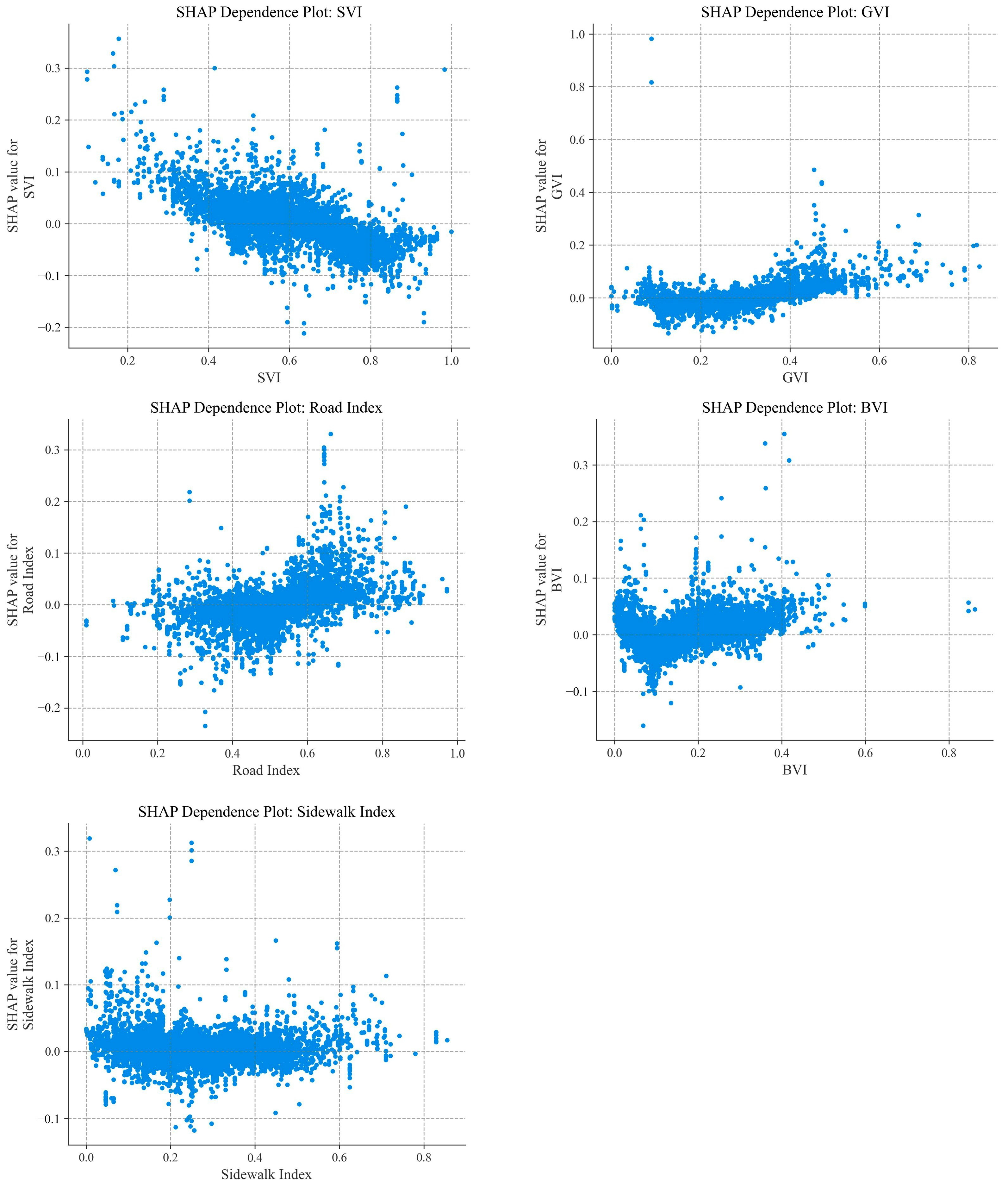
6.4. Nonlinear Relationship Analysis
7. Discussion
7.1. Results Discussion
7.2. Limitations and Potential Improvements
- ①
- This study only selects Shanghai as the research area. Due to the differences in built environments across cities, the results of this study may vary when applied to other cities. Future research could consider conducting empirical analyses in cities such as Beijing and Shenzhen. The feasibility of the framework is further verified by changing the size of the buffer zone and the number of RF trees according to the specific local conditions.
- ②
- This study acknowledges potential endogeneity due to household self-selection in residential locations. Unobserved neighborhood characteristics may correlate with key predictors such as distance to CBD or GVI. High-income households may prefer homes near the CBD due to unobserved advantages like school quality and social prestige, possibly underestimating the negative correlation between housing prices and distance from the CBD. In the future, we will supplement the omitted variables into the model to control the endogeneity problem to the greatest extent. In the future, questionnaire data will be incorporated to obtain the variables such as residents’ subjective perceptions and motivations for their housing choices. Furthermore, we will actively seek an effective instrumental variable and use spatial econometric models to more rigorously identify the impact of the built environment on housing prices.
- ③
- This study overlooked the analysis of spatial heterogeneity and spatial dependence, which could potentially bias our findings, especially concerning key variables such as “distance to CBD”. According to previous studies [80], the distance to the CBD is indeed the most important factor. In our future research, more in-depth insights will be provided, and potential biases will be reduced through spatial econometric models or the Geographically Weighted Regression (GWR) method.
- ④
- The spatial weight matrices used in this experiment were all spatial adjacency matrices, and no economic distance matrices or technical correlation matrices were employed. In future experiments, we will further utilize nighttime light remote sensing data to construct matrices such as economic distance matrices for spatial analysis.
7.3. Implications for Urban Planning
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Factors (Coarse-Grained) | 800-m Buffer Zone | 1000-m Buffer Zone | 1200-m Buffer Zone | Factors (Fine-Grained) | 800-m Buffer Zone | 1000-m Buffer Zone | 1200-m Buffer Zone |
|---|---|---|---|---|---|---|---|
| CBD | −1.0032 *** | −0.9249 *** | −0.9985 *** | CBD | −0.9642 *** | −0.8895 *** | −0.9770 *** |
| Subcenter | 0.2794 *** | 0.2396 *** | 0.2765 *** | Subcenter | 0.2675 *** | 0.2411 *** | 0.2879 *** |
| Commerce | 0.0398 *** | 0.0320 *** | 0.0374 *** | Finance | 0.0014 *** | 0.0092 *** | 0.0061 *** |
| Public Services | 0.0291 *** | 0.0997 *** | 0.0457 *** | Subway | 0.0811 *** | 0.1016 *** | 0.0678 *** |
| Model performance | |||||||
| R2 | 0.7513 | 0.7680 | 0.7526 | R2 | 0.7611 | 0.7918 | 0.7591 |
| RMSE | 0.1753 | 0.1693 | 0.1748 | RMSE | 0.1718 | 0.1604 | 0.1725 |
| MAE | 0.1347 | 0.1287 | 0.1342 | MAE | 0.1309 | 0.1208 | 0.1318 |
References
- Liangjin, Z.; Enjun, X. Research Review on Infliencing Factor of House Price Abroad. J. Technol. Econ. 2018, 37, 111–119. [Google Scholar]
- Chen, M.; Liu, Y.; Arribas-Bel, D.; Singleton, A. Assessing the value of user-generated images of urban surroundings for house price estimation. Landsc. Urban Plan. 2022, 226, 104486. [Google Scholar] [CrossRef]
- Bailey, J.R.; Lindquist, W.B.; Rachev, S.T. Hedonic Models Incorporating Environmental, Social, and Governance Factors for Time Series of Average Annual Home Prices. J. Risk Financ. Manag. 2024, 17, 375. [Google Scholar] [CrossRef]
- Xu, X.; Qiu, W.; Li, W.; Liu, X.; Zhang, Z.; Li, X.; Luo, D. Associations between Street-View Perceptions and Housing Prices: Subjective vs. Objective Measures Using Computer Vision and Machine Learning Techniques. Remote Sens. 2022, 14, 891. [Google Scholar] [CrossRef]
- Li, H.; Chen, P.; Grant, R. Built environment, special economic zone, and housing prices in Shenzhen, China. Applied Geography 2021, 129, 102429. [Google Scholar] [CrossRef]
- Kaklauskas, A.; Gudauskas, R. 17—Intelligent decision-support systems and the Internet of Things for the smart built environment. In Start-Up Creation; Pacheco-Torgal, F., Rasmussen, E., Granqvist, C.-G., Ivanov, V., Kaklauskas, A., Makonin, S., Eds.; Woodhead Publishing: Cambridge, UK, 2016; pp. 413–449. [Google Scholar] [CrossRef]
- Xiao, Y. Urban Morphology and Housing Market; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Yang, L.; Wang, B.; Zhou, J.; Wang, X. Walking accessibility and property prices. Transp. Res. Part D Transp. Environ. 2018, 62, 551–562. [Google Scholar] [CrossRef]
- Gu, Z.; Tang, M.; Luo, X.; Feng, J. Examination of the impacts of hospital accessibility on housing prices: Heterogeneity across attributes, space and price quantiles. J. Hous. Built Environ. 2023, 39, 179–200. [Google Scholar] [CrossRef]
- Wen, H.; Xiao, Y.; Hui, E.C.M. Quantile effect of educational facilities on housing price: Do homebuyers of higher-priced housing pay more for educational resources? Cities 2019, 90, 100–112. [Google Scholar] [CrossRef]
- Chen, K.; Lin, H.; Cao, F.; Han, Y.; You, S.; Shyr, O.; Lu, Y.; Huang, X. Do hospital and rail accessibility have a consistent influence on housing prices? Empirical evidence from China. Front. Environ. Sci. 2022, 10, 1044600. [Google Scholar] [CrossRef]
- Chiesura, A. The role of urban parks for the sustainable city. Landsc. Urban Plan. 2004, 68, 129–138. [Google Scholar] [CrossRef]
- Jim, C.Y.; Chen, W.Y. Impacts of urban environmental elements on residential housing prices in Guangzhou (China). Landsc. Urban Plan. 2006, 78, 422–434. [Google Scholar] [CrossRef]
- van den Berg, M.; van Poppel, M.; van Kamp, I.; Andrusaityte, S.; Balseviciene, B.; Cirach, M.; Danileviciute, A.; Ellis, N.; Hurst, G.; Masterson, D.; et al. Visiting green space is associated with mental health and vitality: A cross-sectional study in four european cities. Health Place 2016, 38, 8–15. [Google Scholar] [CrossRef]
- Gubbels, J.S.; Kremers, S.P.J.; Droomers, M.; Hoefnagels, C.; Stronks, K.; Hosman, C.; de Vries, S. The impact of greenery on physical activity and mental health of adolescent and adult residents of deprived neighborhoods: A longitudinal study. Health Place 2016, 40, 153–160. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Jia, T.; Zhang, X.; Li, S.; Zhang, Y. Do street-level scene perceptions affect housing prices in Chinese megacities? An analysis using open access datasets and deep learning. PLoS ONE 2019, 14, e0217505. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Yao, X.; Liu, Y.; Zhu, Y.; Chen, W.; Zhao, X.; Chi, T. Measuring Impacts of Urban Environmental Elements on Housing Prices Based on Multisource Data—A Case Study of Shanghai, China. ISPRS Int. J. Geo Inf. 2020, 9, 106. [Google Scholar] [CrossRef]
- Fan, Z.; Yu, L. Street view imagery: Methods and applications based on artificial intelligence. Natl. Remote Sens. Bull. 2021, 25, 1043–1054. [Google Scholar] [CrossRef]
- Lee, C.L. An examination of the risk-return relation in the Australian housing market. Int. J. Hous. Mark. Anal. 2017, 10, 431–449. [Google Scholar] [CrossRef]
- Al-Masum, M.A.; Lee, C.L. Modelling housing prices and market fundamentals: Evidence from the Sydney housing market. Int. J. Hous. Mark. Anal. 2020, 12, 746–762. [Google Scholar] [CrossRef]
- Trojanek, R.; Gluszak, M. Spatial and time effect of subway on property prices. J. Hous. Built Environ. 2018, 33, 359–384. [Google Scholar] [CrossRef]
- Yamagata, Y.; Murakami, D.; Yoshida, T.; Seya, H.; Kuroda, S. Value of urban views in a bay city: Hedonic analysis with the spatial multilevel additive regression (SMAR) model. Landsc. Urban Plan. 2016, 151, 89–102. [Google Scholar] [CrossRef]
- Malpezzi, S. Hedonic Pricing Models: A Selective and Applied Review. Hous. Econ. Public Policy 2002, 1, 67–89. [Google Scholar] [CrossRef]
- Rosen, S. Hedonic Prices and Implicit Markets: Product Differentiation in Pure Competition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Efthymiou, D.; Antoniou, C. How do transport infrastructure and policies affect house prices and rents? Evidence from Athens, Greece. Transp. Res. Part A Policy Pract. 2013, 52, 1–22. [Google Scholar] [CrossRef]
- Huang, H.; Yin, L. Creating sustainable urban built environments: An application of hedonic house price models in Wuhan, China. J. Hous. Built Environ. 2015, 30, 219–235. [Google Scholar] [CrossRef]
- Bolitzer, B.; Netusil, N.R. The impact of open spaces on property values in Portland, Oregon. J. Environ. Manag. 2000, 59, 185–193. [Google Scholar] [CrossRef]
- Glaeser, E.L.; Kominers, S.D.; Luca, M.; Naik, N. Big Data and Big Cities: The Promises and Limitations of Improved Measures of Urban Life. Econ. Inq. 2018, 56, 114–137. [Google Scholar] [CrossRef]
- Li, H. Institutions, Economic Transition and Urban Land Expansion in China. Ph.D. Thesis, Universiteit Utrecht, Utrecht, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Han, R.; Wu, S.; He, F.; Sun, Q. Natural Attraction and Driving Forces: Analyzing the Impact of Parkland on Residential Prices and Typological Difference*. J. Sustain. For. 2025, 44, 50–70. [Google Scholar] [CrossRef]
- Hu, L.; He, S. How does the second-hand housing price regulatory policy differentiate the housing price premiums for multi-dimensional school qualities? Evidence from a quasi-natural experiment in urban China. Int. J. Hous. Policy 2024, 1–22. [Google Scholar] [CrossRef]
- Wen, H.; Zhang, Y.; Zhang, L. Do educational facilities affect housing price? An empirical study in Hangzhou, China. Habitat Int. 2014, 42, 155–163. [Google Scholar] [CrossRef]
- Yi, W.; Ruiping, R.; Deng, G. Neighborhood Quality and Housing Value: Evidence from Urban Micro Data. J. Manag. Sustain. 2024, 2, 128. [Google Scholar] [CrossRef]
- Fletcher, M.; Gallimore, P.; Mangan, J. Heteroscedasticity in hedonic house price models. J. Prop. Res. 2000, 17, 93–108. [Google Scholar] [CrossRef]
- Linneman, P. Some empirical results on the nature of the hedonic price function for the urban housing market. J. Urban Econ. 1980, 8, 47–68. [Google Scholar] [CrossRef]
- Carroll, T.M.; Clauretie, T.M.; Jensen, J. Living next to godliness: Residential property values and churches. J. Real Estate Financ. Econ. 1996, 12, 319–330. [Google Scholar] [CrossRef]
- Dai, J.; Lv, P.; Ma, Z.; Bi, J.; Wen, T. Environmental risk and housing price: An empirical study of Nanjing, China. J. Clean. Prod. 2020, 252, 119828. [Google Scholar] [CrossRef]
- Strohbach, M.W.; Arnold, E.; Haase, D. The carbon footprint of urban green space—A life cycle approach. Landsc. Urban Plan. 2012, 104, 220–229. [Google Scholar] [CrossRef]
- Haaland, C.; van den Bosch, C.K. Challenges and strategies for urban green-space planning in cities undergoing densification: A review. Urban For. Urban Green. 2015, 14, 760–771. [Google Scholar] [CrossRef]
- Belcher, R.N.; Chisholm, R.A. Tropical Vegetation and Residential Property Value: A Hedonic Pricing Analysis in Singapore. Ecol. Econ. 2018, 149, 149–159. [Google Scholar] [CrossRef]
- Donovan, G.H.; Butry, D.T. The effect of urban trees on the rental price of single-family homes in Portland, Oregon. Urban For. Urban Green. 2011, 10, 163–168. [Google Scholar] [CrossRef]
- Asgarzadeh, M.; Koga, T.; Hirate, K.; Farvid, M.; Lusk, A. Investigating oppressiveness and spaciousness in relation to building, trees, sky and ground surface: A study in Tokyo. Landsc. Urban Plan. 2014, 131, 36–41. [Google Scholar] [CrossRef]
- Nutsford, D.; Pearson, A.L.; Kingham, S.; Reitsma, F. Residential exposure to visible blue space (but not green space) associated with lower psychological distress in a capital city. Health Place 2016, 39, 70–78. [Google Scholar] [CrossRef]
- Luttik, J. The value of trees, water and open space as reflected by house prices in the Netherlands. Landsc. Urban Plan. 2000, 48, 161–167. [Google Scholar] [CrossRef]
- Jim, C.Y.; Chen, W.Y. Value of scenic views: Hedonic assessment of private housing in Hong Kong. Landsc. Urban Plan. 2009, 91, 226–234. [Google Scholar] [CrossRef]
- Karato, K.; Movshuk, O.; Shimizu, C. Semiparametric Model of Hedonic Housing Prices in Japan. Asian Econ. J. 2015, 29, 325–345. [Google Scholar] [CrossRef]
- Lancaster, K.J.J.J.o.p.e. A new approach to consumer theory. J. Political Econ. 1966, 74, 132–157. [Google Scholar] [CrossRef]
- Sakia, R. The Box-Cox Transformation Technique: A Review. J. R. Stat. Soc. Ser. D Stat. 1992, 41, 169–178. [Google Scholar] [CrossRef]
- Tam, V.W.Y.; Fung, I.W.H.; Wang, J.; Ma, M. Effects of locations, structures and neighbourhoods to housing price: An empirical study in Shanghai, China. Int. J. Constr. Manag. 2022, 22, 1288–1307. [Google Scholar] [CrossRef]
- Yu, P.; Changcheng, K.; Anrong, D. Street Greenspace Justice Assessment Study of Dongcheng District in Beijing Based on Street View Data. Chin. Landsc. Archit. 2020, 36, 51–56. [Google Scholar] [CrossRef]
- Naik, N.; Kominers, S.D.; Raskar, R.; Glaeser, E.L.; Hidalgo, C.A. Computer vision uncovers predictors of physical urban change. Proc. Natl. Acad. Sci. USA 2017, 114, 7571–7576. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar] [CrossRef]
- Song, L.; Liu, D.; Kwan, M.-P.; Liu, Y.; Zhang, Y. Machine-based understanding of noise perception in urban environments using mobility-based sensing data. Comput. Environ. Urban Syst. 2024, 114, 102204. [Google Scholar] [CrossRef]
- Zhou, B.; Lapedriza, A.; Khosla, A.; Oliva, A.; Torralba, A. Places: A 10 Million Image Database for Scene Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1452–1464. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Zhou, B.; Liu, L.; Liu, Y.; Fung, H.H.; Lin, H.; Ratti, C. Measuring human perceptions of a large-scale urban region using machine learning. Landsc. Urban Plan. 2018, 180, 148–160. [Google Scholar] [CrossRef]
- Ramírez, T.; Hurtubia, R.; Lobel, H.; Rossetti, T. Measuring heterogeneous perception of urban space with massive data and machine learning: An application to safety. Landsc. Urban Plan. 2021, 208, 104002. [Google Scholar] [CrossRef]
- Yin, L.; Wang, Z. Measuring visual enclosure for street walkability: Using machine learning algorithms and Google Street View imagery. Appl. Geogr. 2016, 76, 147–153. [Google Scholar] [CrossRef]
- Wang, L.; Hou, C.; Zhang, Y.; He, J. Measuring solar radiation and spatio-temporal distribution in different street network direction through solar trajectories and street view images. Int. J. Appl. Earth Obs. Geoinf. 2024, 132, 104058. [Google Scholar] [CrossRef]
- Jiang, S.; Alves, A.; Rodrigues, F.; Ferreira, J.; Pereira, F.C. Mining point-of-interest data from social networks for urban land use classification and disaggregation. Comput. Environ. Urban Syst. 2015, 53, 36–46. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, X.; Wang, G.; Bi, X. A New Point-of-Interest Classification Model with an Extreme Learning Machine. Cogn. Comput. 2018, 10, 951–964. [Google Scholar] [CrossRef]
- Li, H.; Miao, L. A Study of the Non-Linear Relationship Between Urban Morphology and Vitality in Heritage Areas Based on Multi-Source Data and Machine Learning: A Case Study of Dalian. ISPRS Int. J. Geo Inf. 2025, 14, 177. [Google Scholar] [CrossRef]
- Xu, J.; Liu, Y.; Liu, Y.; An, R.; Tong, Z. Integrating street view images and deep learning to explore the association between human perceptions of the built environment and cardiovascular disease in older adults. Soc. Sci. Med. 2023, 338, 116304. [Google Scholar] [CrossRef]
- Sirmans, G.S.; Macpherson, D.A.; Zietz, E.N. The Composition of Hedonic Pricing Models. J. Real Estate Lit. 2005, 13, 3–43. [Google Scholar] [CrossRef]
- Hu, L.; He, S.; Han, Z.; Xiao, H.; Su, S.; Weng, M.; Cai, Z. Monitoring housing rental prices based on social media: An integrated approach of machine-learning algorithms and hedonic modeling to inform equitable housing policies. Land Use Policy 2019, 82, 657–673. [Google Scholar] [CrossRef]
- Li, H.; Wei, Y.D.; Wu, Y.; Tian, G. Analyzing housing prices in Shanghai with open data: Amenity, accessibility and urban structure. Cities 2019, 91, 165–179. [Google Scholar] [CrossRef]
- Dou, M.; Gu, Y.; Fan, H. Incorporating neighborhoods with explainable artificial intelligence for modeling fine-scale housing prices. Appl. Geogr. 2023, 158, 103032. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar] [CrossRef]
- Li, Z. Extracting spatial effects from machine learning model using local interpretation method: An example of SHAP and XGBoost. Comput. Environ. Urban Syst. 2022, 96, 101845. [Google Scholar] [CrossRef]
- Salih, A.M.; Raisi-Estabragh, Z.; Galazzo, I.B.; Radeva, P.; Petersen, S.E.; Lekadir, K.; Menegaz, G. A Perspective on Explainable Artificial Intelligence Methods: SHAP and LIME. Adv. Intell. Syst. 2025, 7, 2400304. [Google Scholar] [CrossRef]
- Lipovetsky, S.; Conklin, M. Analysis of regression in game theory approach. Appl. Stoch. Models Bus. Ind. 2001, 17, 319–330. [Google Scholar] [CrossRef]
- Ribeiro, M.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier; Association for Computational Linguistics: Stroudsburg, PA, USA, 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
- Štrumbelj, E.; Kononenko, I. Explaining prediction models and individual predictions with feature contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Datta, A.; Sen, S.; Zick, Y. Algorithmic Transparency via Quantitative Input Influence: Theory and Experiments with Learning Systems. In Proceedings of the 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2016; pp. 598–617. [Google Scholar] [CrossRef]
- Liao, X.; Deng, M.; Huang, H. Analyzing Multiscale Spatial Relationships between the House Price and Visual Environment Factors. Appl. Sci. 2021, 12, 213. [Google Scholar] [CrossRef]
- Luo, H.; Zhao, S.; Yao, R. Determinants of Housing Prices in Dalian City, China: Empirical Study Based on Hedonic Price Model. J. Urban Plan. Dev. 2021, 147, 05021017. [Google Scholar] [CrossRef]
- Potrawa, T.; Tetereva, A. How much is the view from the window worth? Machine learning-driven hedonic pricing model of the real estate market. J. Bus. Res. 2022, 144, 50–65. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, R. Impacts of Street-Visible Greenery on Housing Prices: Evidence from a Hedonic Price Model and a Massive Street View Image Dataset in Beijing. ISPRS Int. J. Geo Inf. 2018, 7, 104. [Google Scholar] [CrossRef]
- Zhu, J.; Gong, Y.; Liu, C.; Du, J.; Song, C.; Chen, J.; Pei, T. Assessing the Effects of Subjective and Objective Measures on Housing Prices with Street View Imagery: A Case Study of Suzhou. Land 2023, 12, 2095. [Google Scholar] [CrossRef]
- Chen, J.; Hao, Q. The impacts of distance to CBD on housing prices in Shanghai: A hedonic analysis. J. Chin. Econ. Bus. Stud. 2008, 6, 291–302. [Google Scholar] [CrossRef]
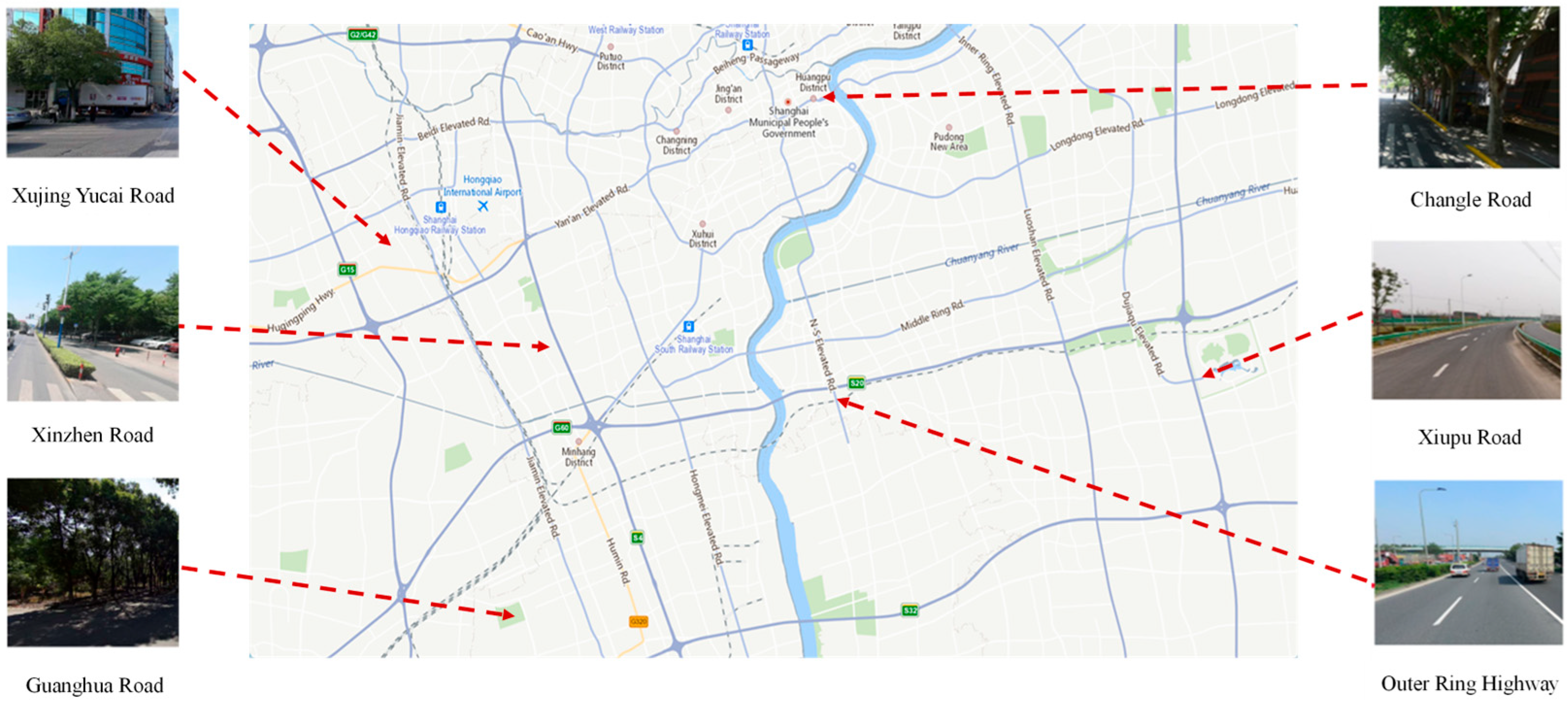


| Field Name | Field Attributes | Example |
|---|---|---|
| District and street | The house’s district and street | Tianshan Road Subdistrict, Changning District |
| Neighborhood name | The name of neighborhood | Xinfeng Community |
| Property type | The type of property | one room, one living room, one kitchen, one bathroom |
| Floor level | Number of floors | 6 |
| Building area | Floor area (m2) | 50.4 |
| Orientation | Binary value: 1 for south-facing and north-south-facing, 0 otherwise | 1 |
| Listing price | The second-hand home’s listed sale price (10,000 yuan/m2) | 5.72 |
| Unit price | Housing unit price (10,000 yuan/m2) | 6.68 |
| Field Name | Field Attributes | Example |
|---|---|---|
| ID | Unique Identifier for POI | B0FFI6407I |
| Name | Name of POI | Super Life Plaza (Xincun Branch) |
| X | Longitude of POI | 31.266869 |
| Y | Latitude of POI | 121.435744 |
| District | Administrative Region of POI | Putuo District |
| Type | POI Type (Major Category; Intermediate Category; Minor Category) | Shopping Services; Supermarket; Grocery Store |
| Address | Specific Location of POI | 50 m north of the intersection of Yichuan Road and Xincun Road |
| Coarse-Grained POI | Fine-Grained POI | Gaode POI Subcategories |
|---|---|---|
| Commerce | Hotel | Hotels, Inns, and Guesthouses |
| Shopping | Convenience Store, Supermarket, Shopping Mall, Specialty Shopping Streets, Integrated Markets | |
| Finance | Banks, ATMs, Securities Firms, Insurance Companies, Financial Companies, Financial and Insurance Service Institutions | |
| Entertainment and Leisure | Leisure Venues, Cinemas and Theaters, Entertainment Venues, Golf-related, Sports and Leisure Service Venues | |
| Transportation | External Transportation | Airport, Train Station, Long-Distance Bus Station, Port Terminal, Ferry Station |
| Public Transportation | Bus Station | |
| Subway | Subway Station | |
| Industry | Companies and Enterprises | Industrial Parks, Companies, Agriculture, Forestry, Animal Husbandry, and Fishery Bases, Factories |
| Public Services | Public Tourism | Museums, Libraries, Archives, Science Museums, Art Museums, Exhibition Halls, Planetariums |
| Research and Education | Universities, High Schools, Primary Schools, Kindergartens, Vocational and Technical Schools, Research Institutions | |
| Government Agencies | Government Agencies, Social Organizations, Public Security and Judicial Institutions, Foreign Organizations, Democratic Parties, Industry and Taxation Agencies, Traffic Vehicle Management | |
| Public Healthcare | General Hospitals, Specialized Hospitals, Emergency Centers, Disease Prevention Institutions | |
| Green Spaces | Green Spaces | Parks, Zoos, Botanical Gardens, Aquariums, Urban Squares, Scenic Spots |
| Variable | Mean | Standard Deviation | Minimum Value | Maximum Value | Description | |
|---|---|---|---|---|---|---|
| Dependent Variable | Housing Price | 5.827 | 2.04 | 1.148 | 19.988 | Housing unit price (10,000 yuan/m2) |
| Structural Features | Number of Rooms | 3.594 | 1.311 | 1 | 18 | Number of rooms |
| Area | 87.123 | 43.805 | 21 | 1042.17 | Floor area (m2) | |
| Floor | 10.624 | 7.547 | 1 | 80 | Number of floors | |
| Orientation | 0.833 | 0.373 | 0 | 1 | Binary value: 1 for south-facing and north-south-facing, 0 otherwise | |
| Property Age | 19.149 | 9.814 | 1 | 107 | Calculated as 2018 minus construction year | |
| Locational Features | CBD | 13.387 | 9.047 | 0.35 | 58.545 | Distance to People’s Square of Shanghai (km) |
| Subcenter | 14.371 | 9.717 | 0.34 | 63.156 | Distance to the nearest subcenter(km) | |
| Transportation | 0.496 | 0.050 | 0 | 0.8 | Average distance to transportation POIs within 1000 m (km) | |
| External Transportation | 0.098 | 0.148 | 0 | 0.7 | Average distance to external transportation POIs within 1000 m | |
| Subway | 0.229 | 0.183 | 0 | 0.7 | Average distance to subway station POIs within 1000 m (km) | |
| Bus | 0.422 | 0.058 | 0 | 0.7 | Average distance to public bus station POIs within 1000 m (km) | |
| Neighborhood Features | Commerce | 0.510 | 0.074 | 0 | 0.8 | Average distance to commerce POIs within 1000 m (km) |
| Hotel | 0.348 | 0.049 | 0 | 0.7 | Average distance to hotel POIs within 1000 m (km) | |
| Shopping | 0.397 | 0.061 | 0 | 0.7 | Average distance to shopping POIs within 1000 m (km) | |
| Finance | 0.327 | 0.046 | 0 | 0.7 | Average distance to finance POIs within 1000 m (km) | |
| Leisure and Entertainment | 0.388 | 0.069 | 0 | 0.7 | Average distance to leisure and entertainment POIs within 1000 m (km) | |
| Industry | 0.479 | 0.075 | 0.4 | 0.8 | Average distance to industry POIs within 1000 m (km) | |
| Industry/Corporations | 0.359 | 0.067 | 0.3 | 0.8 | Average distance to industry/corporations POIs within 1000 m (km) | |
| Public Services | 0.515 | 0.091 | 0 | 0.8 | Average distance to public services POIs within 1000 m (km) | |
| Public Recreation | 0.264 | 0.154 | 0 | 0.7 | Average distance to public recreation POIs within 1000 m (km) | |
| Scientific Research and Education | 0.337 | 0.053 | 0 | 0.7 | Average distance to scientific research and education POIs within 1000 m (km) | |
| Public Healthcare | 0.336 | 0.091 | 0 | 0.7 | Average distance to public healthcare POIs within 1000 m (km) | |
| Government Institutions | 0.390 | 0.079 | 0 | 0.7 | Average distance to government institutions POIs within 1000 m (km) | |
| Green Spaces | 0.314 | 0.092 | 0 | 0.7 | Average distance to green spaces POIs within 1000 m (km) | |
| Visual Environmental Features | GVI | 0.205 | 0.084 | 0.001 | 0.75 | Average GVI within 400 m |
| SVI | 0.466 | 0.103 | 0.018 | 0.75 | Average SVI within 400 m | |
| BVI | 0.125 | 0.069 | 0.001 | 0.729 | Average BVI within 400 m | |
| Road Index | 0.087 | 0.015 | 0.021 | 0.148 | Average road index within 400 m | |
| Sidewalk Index | 0.013 | 0.006 | 0 | 0.049 | Average sidewalk index within 400 m |
| Hyperparameter | Coarse-Grained | Fine-Grained | Description |
|---|---|---|---|
| n_estimators | 180 | 180 | The number of decision trees in the ensemble |
| random_state | 42 | 42 | A seed value to ensure reproducibility by controlling the stochasticity in forest generation |
| max_depth | 22 | 49 | The maximum depth of each tree. Limiting the tree depth can help prevent overfitting |
| min_samples_leaf | 1 | 1 | The minimum number of samples required to be at a leaf node. This parameter can also help control overfitting |
| min_samples_split | 2 | 2 | The minimum number of samples for node splitting. Increasing this value can prevent the model from learning too much from the noise in the data |
| max_features | 10 | 16 | The number of features to consider when looking for the best split. The default value is “sqrt(n_features)” for classification and “n_features” for regression |
| I | p | Z |
|---|---|---|
| 0.7993 | p < 0.001 | 690.7280 |
| Category | Factors (Coarse-Grained) | Standardized Coefficients | VIF | Factors (Fine-Grained) | Standardized Coefficients | VIF |
|---|---|---|---|---|---|---|
| Structural features | Number of Rooms | −0.0148 *** | 3.62 | Number of Rooms | −0.0069 *** | 3.63 |
| Area | 0.0078 *** | 3.64 | Area | −0.0136 *** | 3.67 | |
| Floor | 0.0529 *** | 1.64 | Floor | 0.0430 *** | 1.67 | |
| Orientation | 0.0274 *** | 1.04 | Orientation | 0.0276 *** | 1.05 | |
| Age of the Property | −0.1475 *** | 2.17 | Age of the Property | −0.1669 *** | 2.28 | |
| Locational features | CBD | −0.9249 *** | 7.22 | CBD | −0.8895 *** | 8.62 |
| Subcenter | 0.2396 *** | 6.13 | Subcenter | 0.2411 *** | 7.13 | |
| Transportation | 0.0101 *** | 1.35 | External Transportation | 0.0069 *** | 1.08 | |
| Subway | 0.1016 *** | 1.80 | ||||
| Bus | 0.0007 *** | 1.93 | ||||
| Neighborhood features | Commerce | 0.0320 *** | 3.10 | Hotel | −0.0586 *** | 2.82 |
| Shopping | −0.1590 *** | 4.38 | ||||
| Finance | 0.0092 *** | 2.23 | ||||
| Leisure and Entertainment | 0.1560 *** | 5,91 | ||||
| Industry | 0.0923 *** | 2.45 | Industry/Corporations | −0.0340 *** | 4.92 | |
| Public Services | 0.0997 *** | 3.72 | Public Recreation | 0.0520 *** | 1.76 | |
| Scientific Research and Education | 0.0460 *** | 1.54 | ||||
| Government Institutions | 0.0987 *** | 6.32 | ||||
| Public Healthcare | 0.0353 *** | 2.06 | ||||
| Green Spaces | 0.0379 *** | 1.37 | Green Spaces | 0.0240 *** | 1.50 | |
| Visual Environmental features | GVI | 0.0463 *** | 3.22 | GVI | 0.0240 *** | 3.29 |
| SVI | −0.0725 *** | 5.53 | SVI | −0.0553 *** | 5.63 | |
| BVI | 0.0182 *** | 3.90 | BVI | 0.0213 *** | 4.07 | |
| Road Index | 0.0730 *** | 1.70 | Road Index | 0.0514 *** | 1.74 | |
| Sidewalk Index | −0.0303 *** | 1.41 | Sidewalk Index | −0.0018 *** | 1.50 |
| Model | Level | R2 | RMSE | MAE |
|---|---|---|---|---|
| Hedonic price model | coarse-grained | 0.7680 | 0.1693 | 0.1287 |
| fine-grained | 0.7918 | 0.1604 | 0.1208 |
| Variable (Fine-Grained) | Semi-Log | Liner | Variable (Coarse-Grained) | Semi-Log | Liner | ||||
|---|---|---|---|---|---|---|---|---|---|
| t-Value | Coefficient | t-Value | Coefficient | t-Value | Coefficient | t-Value | Coefficient | ||
| CBD | −168.4 | −0.89 | −128.7 | −1.601 | CBD | −181.2 | −0.925 | −137.4 | −0.804 |
| Subcenter | 50.193 | 0.2411 | 57.789 | 0.6532 | Subcenter | 50.972 | 0.2398 | 56.381 | 0.3043 |
| Age of the Property | −61.43 | −0.167 | −53.5 | −0.342 | Age of the Property | −52.68 | −0.148 | −46.64 | −0.15 |
| Shopping | −42.36 | −0.159 | −38.45 | −0.34 | Public Services | 31.811 | 0.0997 | 41.044 | 0.1475 |
| Leisure and Entertainment | 35.661 | 0.156 | 35.121 | 0.3615 | Industry | 31.035 | 0.0923 | 45.21 | 0.1543 |
| Subway | 42.12 | 0.1016 | 32.941 | 0.187 | Road Index | 29.547 | 0.0731 | 24.963 | 0.0708 |
| Government Institutions | 21.815 | 0.0987 | 30.822 | 0.3281 | SVI | −16.25 | −0.073 | −13.15 | −0.067 |
| Hotel | −19.39 | −0.059 | −22.5 | −0.16 | Floor | 21.778 | 0.0529 | 25.772 | 0.0719 |
| SVI | −12.96 | −0.055 | −9.547 | −0.096 | GVI | 13.588 | 0.0463 | 15.065 | 0.0589 |
| Public Recreation | 21.784 | 0.052 | 19.167 | 0.1076 | Green Spaces | 17.028 | 0.0379 | 19.406 | 0.0495 |
| Road Index | 21.624 | 0.0514 | 17.707 | 0.099 | Commerce | 9.5865 | 0.032 | 17.096 | 0.0656 |
| Scientific Research and Education | 20.6 | 0.046 | 18.397 | 0.0967 | Sidewalk Index | −13.45 | −0.03 | −13.23 | −0.034 |
| Floor | 18.509 | 0.043 | 21.744 | 0.1188 | Orientation | 14.144 | 0.0274 | 12.419 | 0.0277 |
| Public Healthcare | 13.674 | 0.0353 | 11.634 | 0.0706 | BVI | 4.8485 | 0.0182 | 6.7184 | 0.0289 |
| Industry/Corporations | 8.5153 | 0.034 | 25.167 | 0.2365 | Number of Rooms | −4.105 | −0.015 | −9.613 | −0.04 |
| Orientation | 15.024 | 0.0276 | 13.331 | 0.0577 | Transportation | 4.5688 | 0.0101 | 1.4984 | 0.0038 |
| GVI | 7.3474 | 0.024 | 9.4387 | 0.0725 | Area | 2.1656 | 0.0078 | 15.416 | 0.0641 |
| Green Spaces | 10.884 | 0.024 | 15.003 | 0.0777 | |||||
| BVI | 5.862 | 0.0213 | 7.1894 | 0.0614 | |||||
| Area | −3.939 | −0.014 | 10.542 | 0.0855 | |||||
| Finance | 3.4156 | 0.0092 | 6.3549 | 0.0402 | |||||
| Number of Rooms | −2.019 | −0.007 | −8.077 | −0.065 | |||||
| External Transportation | 3.7026 | 0.0069 | 4.623 | 0.0203 | |||||
| Sidewalk Index | −0.821 | −0.002 | −0.526 | −0.003 | |||||
| Bus | 0.2746 | 0.0007 | −6.797 | −0.04 | |||||
| Model | Level | R2 | RMSE | MAE |
|---|---|---|---|---|
| Random Forest | Coarse-grained | 0.8236 | 0.8243 | 0.5334 |
| Fine-grained | 0.8389 | 0.7887 | 0.5014 |
| Variable (Fine-Grained) | Hedonic Price Model | RF | Variable (Coarse-Grained) | Hedonic Price Model | RF |
|---|---|---|---|---|---|
| CBD | 1 | 1 | CBD | 1 | 1 |
| Subcenter | 2 | 5 | Subcenter | 2 | 4 |
| Age of the Property | 3 | 2 | Age of the Property | 3 | 2 |
| Shopping | 4 | 10 | Public Services | 4 | 7 |
| Leisure and Entertainment | 5 | 9 | Industry | 5 | 3 |
| Subway | 6 | 6 | Road Index | 6 | 10 |
| Government Institutions | 7 | 13 | SVI | 7 | 8 |
| Hotel | 8 | 22 | Floor | 8 | 5 |
| SVI | 9 | 15 | GVI | 9 | 11 |
| Public Recreation | 10 | 8 | Green Spaces | 10 | 9 |
| Road Index | 11 | 18 | Commerce | 11 | 13 |
| Scientific Research and Education | 12 | 14 | Sidewalk Index | 12 | 14 |
| Floor | 13 | 7 | Orientation | 13 | 17 |
| Public Healthcare | 14 | 16 | BVI | 14 | 12 |
| Industry/Corporations | 15 | 3 | Number of Rooms | 15 | 15 |
| Orientation | 16 | 25 | Transportation | 16 | 16 |
| GVI | 17 | 17 | Area | 17 | 6 |
| Green Spaces | 18 | 12 | |||
| BVI | 19 | 19 | |||
| Area | 20 | 11 | |||
| Finance | 21 | 4 | |||
| Number of Rooms | 22 | 23 | |||
| External Transportation | 23 | 24 | |||
| Sidewalk Index | 24 | 21 | |||
| Bus | 25 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wang, Y.; Xia, X.; Chen, S.; Jiang, W. How Does Built Environment Influence Housing Prices in Large-Scale Areas? An Interpretable Machine Learning Method by Considering Multi-Dimensional Accessibility. ISPRS Int. J. Geo-Inf. 2025, 14, 436. https://doi.org/10.3390/ijgi14110436
Wang Z, Wang Y, Xia X, Chen S, Jiang W. How Does Built Environment Influence Housing Prices in Large-Scale Areas? An Interpretable Machine Learning Method by Considering Multi-Dimensional Accessibility. ISPRS International Journal of Geo-Information. 2025; 14(11):436. https://doi.org/10.3390/ijgi14110436
Chicago/Turabian StyleWang, Ziyi, Yu Wang, Xinyu Xia, Shaozhu Chen, and Wei Jiang. 2025. "How Does Built Environment Influence Housing Prices in Large-Scale Areas? An Interpretable Machine Learning Method by Considering Multi-Dimensional Accessibility" ISPRS International Journal of Geo-Information 14, no. 11: 436. https://doi.org/10.3390/ijgi14110436
APA StyleWang, Z., Wang, Y., Xia, X., Chen, S., & Jiang, W. (2025). How Does Built Environment Influence Housing Prices in Large-Scale Areas? An Interpretable Machine Learning Method by Considering Multi-Dimensional Accessibility. ISPRS International Journal of Geo-Information, 14(11), 436. https://doi.org/10.3390/ijgi14110436





