STAE-BiSSSM: A Traffic Flow Forecasting Model with High Parameter Effectiveness
Abstract
1. Introduction
- 1.
- Currently, mainstream traffic forecasting models are Transformer-based models. Quadratic computational complexity of attention mechanism results in a large number of parameters for this class of models, leading to high hardware requirements and high training cost, making model difficult deployment. Therefore, finding models with fewer parameters and excellent performance to replace Transformer has become a trend, such as RetNet [55], RWKV [56] and Mamba [57].
- 2.
- There exists a disconnect in the optimization dimensions of current research efforts—some studies focus solely on improving the model’s network structure to enhance its fitting capability, while others concentrate exclusively on mining the features of traffic flow data. These two aspects fail to achieve organic integration, making it difficult to fully exert the synergistic effect of “structure adapting to data and data feeding back to structure”.
- We designed a novel bidirectional selective state space model (BiSSSM) which is able to capture the bidirectional dependency of the traffic flow from both forward and backward direction of time series and better learn the dynamic change patterns of traffic flow.
- We combined spatio-temporal adaptive embedding (STAE) and BiSSSM as a new model, STAE-BiSSSM, where STAE enriches the representation of traffic flow feature, thus enhancing the learning outcomes of BiSSSM.
- STAE-BiSSSM shows the outstanding long- and short-term forecasting ability across five authoritative real-world datasets. In particular, on datasets METRLA and PeMSBAY, STAE-BiSSSM outperforms the SOTA model STAEformer.
- Compared with STAEformer, STAE-BiSSSM has higher parameter effectiveness. While possessing superior performance, the number of trainable parameters of STAE-BiSSSM is much less than STAEformer.
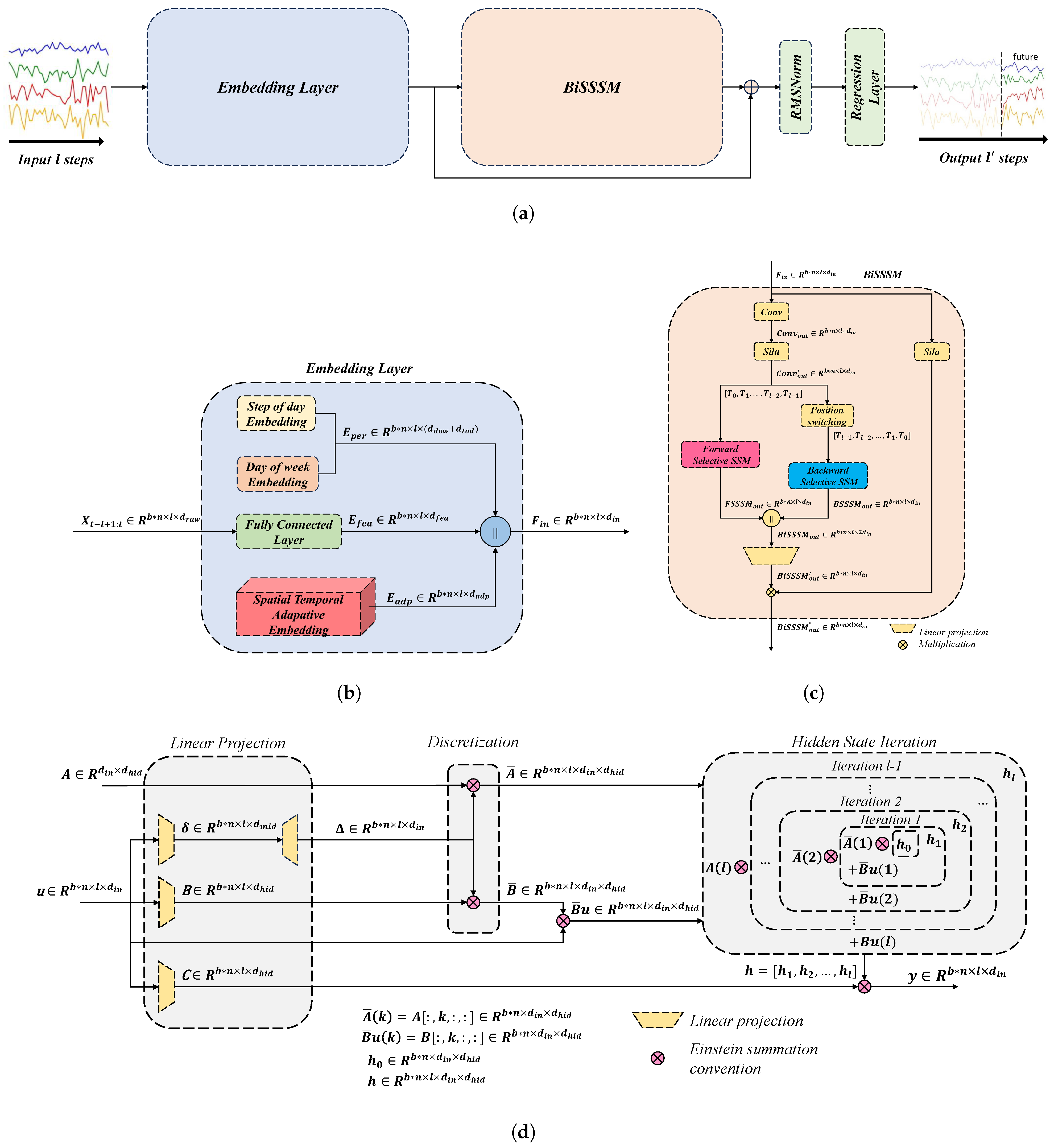
2. Methodology
2.1. Problem Definition
2.2. Embedding Layer
2.3. Selective State Space Model (SSSM)
| Algorithm 1 Inference Process of SSM for time series modeling. |
|
| Algorithm 2 Inference Process of Selective SSM (SSSM) for time series modeling. |
|
2.4. STAE-Bidirectional SSSM (STAE-BiSSSM)
| Algorithm 3 Inference Process of STAE-Bidirectional SSSM (STAE-BiSSSM) for traffic flow forecasting (Ours). |
|
3. Experimental Study
3.1. Description of Experimental Datasets and Baseline Models
3.1.1. Experimental Datasets
3.1.2. Baseline Models
- 1.
- Historical Inertia (HI) [60]: HI serves as the conventional benchmark, reflecting standard industry practices.
- 2.
- STGCN [34]: STGCN proposes a spatio-temporal convolution block (ST-Conv Block) that consists of a spatial graph convolutional layer (GCN) and a temporally gated convolutional layer (Gated CNN) to realize the joint extraction of spatio-temporal features.
- 3.
- DCRNN [40]: DCRNN proposes diffusion convolution to model the spatial dependence of directed graphs by bidirectional stochastic wandering (forward diffusion and backward diffusion).
- 4.
- AGCRN [42]: AGCRN dynamically generates the adjacency matrix through learnable node embedding.
- 5.
- GWNet [43]: GWNet introduces an adaptive graph modeling approach to discover the implicit path dependence in traffic flow, and dilated causal convolution (DCC) is used to extract the long time series dependency.
- 6.
- GTS [44]: GTS develops a forecasting approach for multiple interrelated time series, learning a graph structure in conjunction with a GNN, which addresses the shortcomings of earlier methods.
- 7.
- MTGNN [45]: MTGNN generates an asymmetric neighborhood matrix by learning the node embedding matrix to capture unidirectional causality in multidimensional time series.
- 8.
- STNorm [61]: STNorm achieves multimodal feature fusion through temporal embedding, spatial embedding and feature embedding, which enhances model learning.
- 9.
- GMAN [48]: GMAN enhances the model’s ability to resolve complex spatio-temporal patterns by parallelizing multiple attention modules (spatial attention, temporal attention and transformational attention) to capture different dimensional dependencies in traffic data separately.
- 10.
- PDFormer [49]: PDFormer introduces a Delayed Feature Transformation (DFT) module based on attention mechanism. The DFT Module can better model information delay in real traffic situations, thus improving the forecasting accuracy of the model.
- 11.
- STID [53]: STID proposes a spatio-temporal unique heat coding method, which enriches the feature representation and makes features discriminative. Thanks to spatio-temporal unique heat coding, it greatly improves the performance of fully connected networks on traffic flow forecasting.
- 12.
- STAEformer [54]: STAEformer proposes a spatio-temporal adaptive embedding to enhance feature representation and distinguishability and thus makes the vanilla Transformer SOTA for traffic flow forecasting.
3.2. Metrics of Model Evaluation
- 1.
- Mean Average Error (MAE):
- 2.
- Root Mean Square Error (RMSE):
- 3.
- Mean Absolute Percentage Error (MAPE):
3.3. Experiments Implementation
3.4. Experiment Results
3.4.1. Metrics Analysis
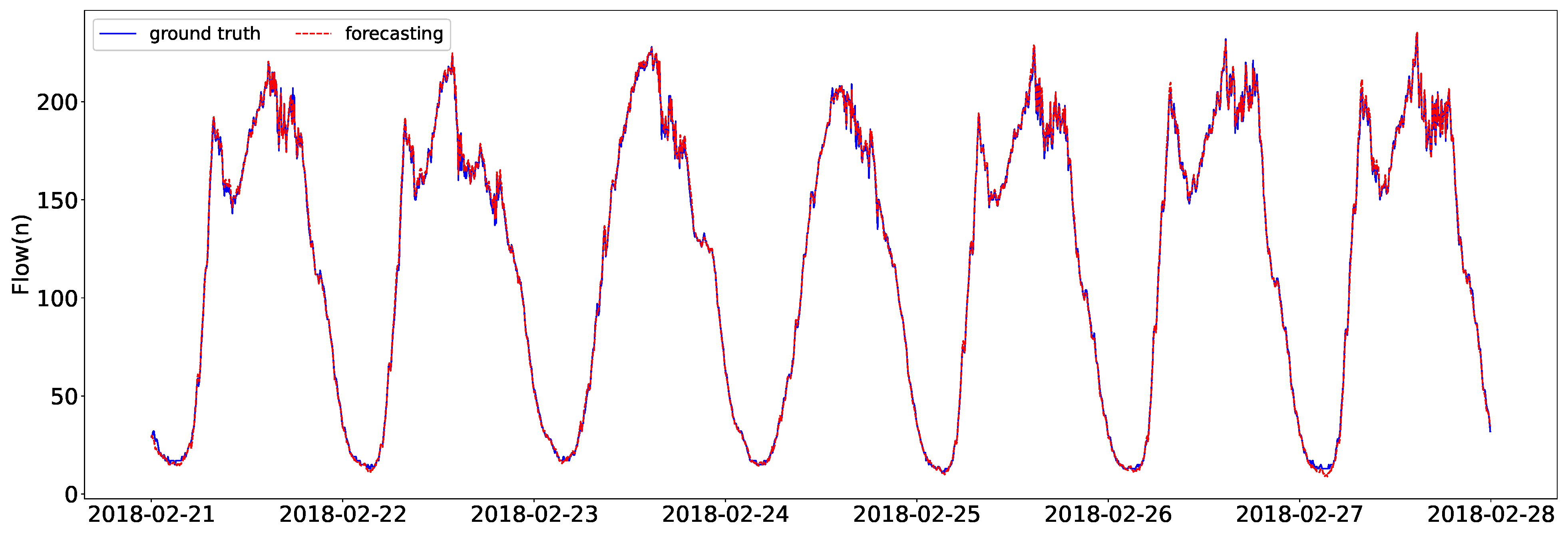
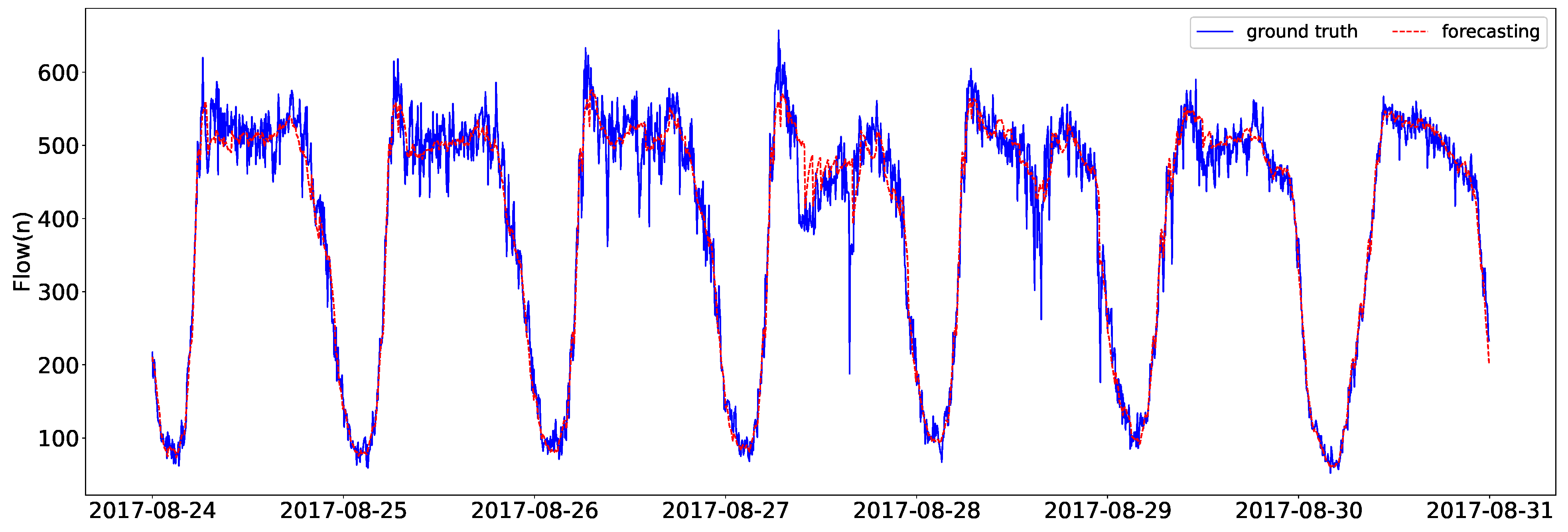
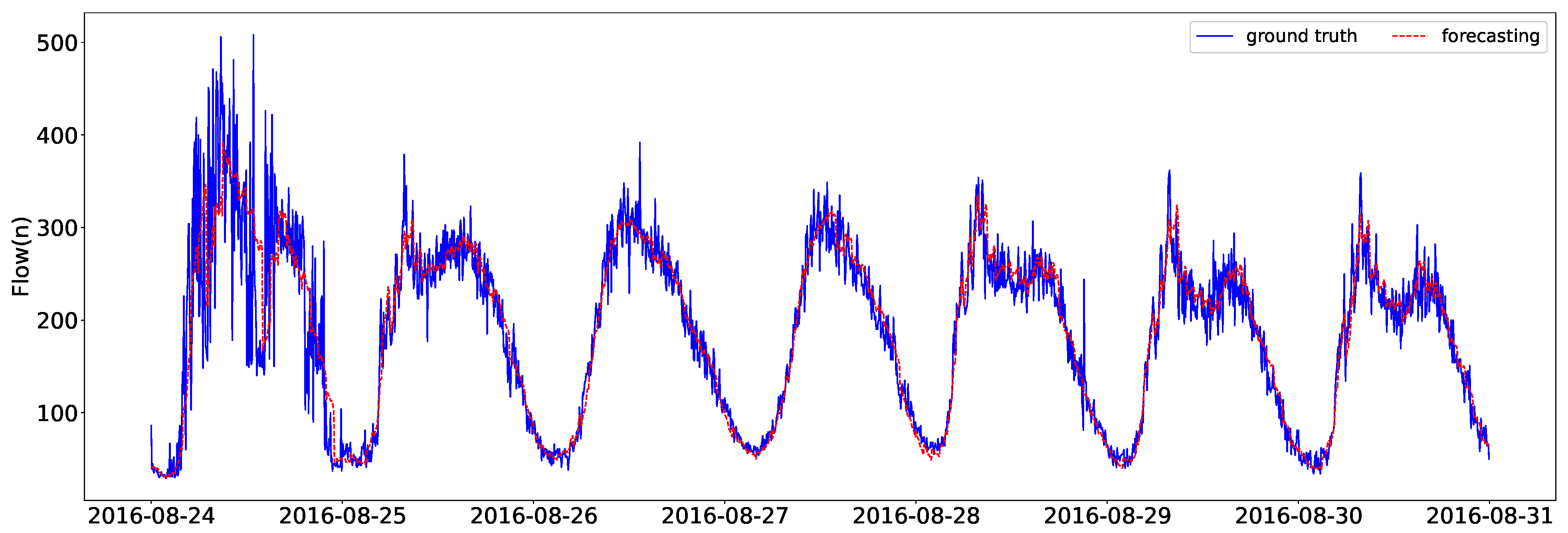
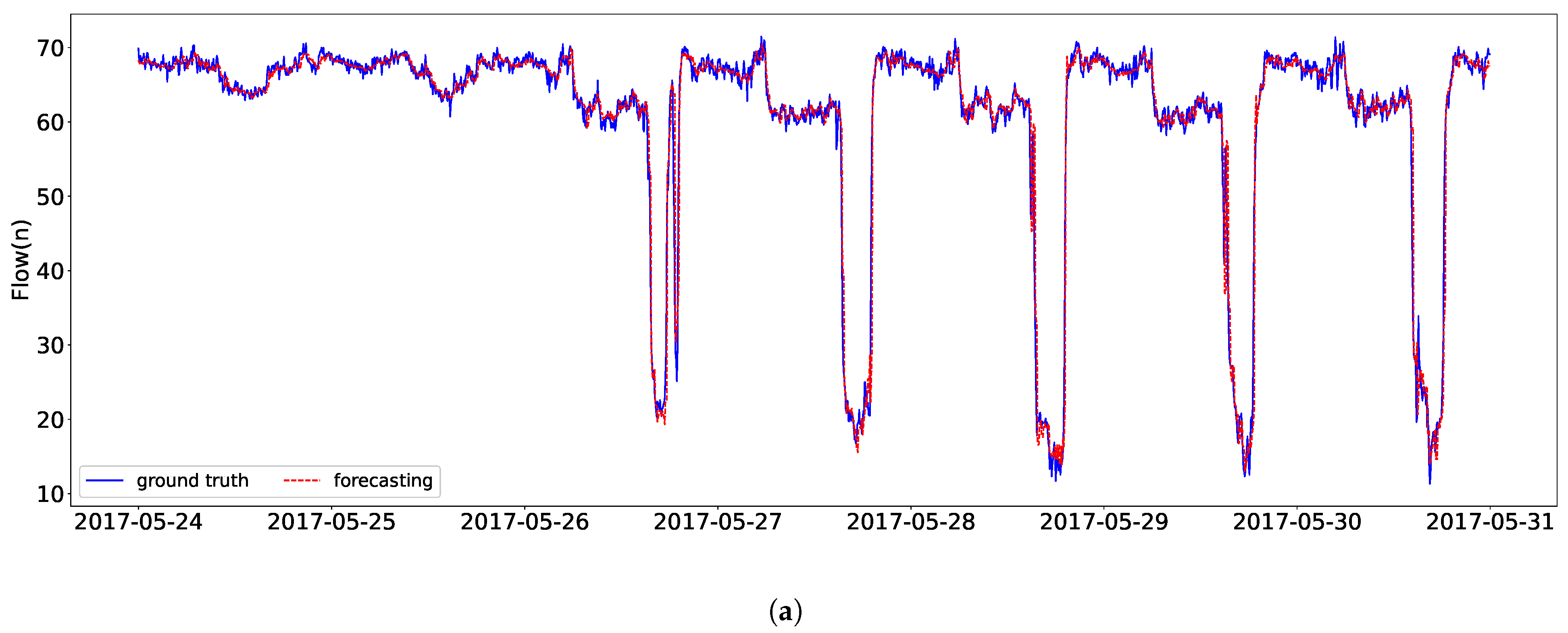
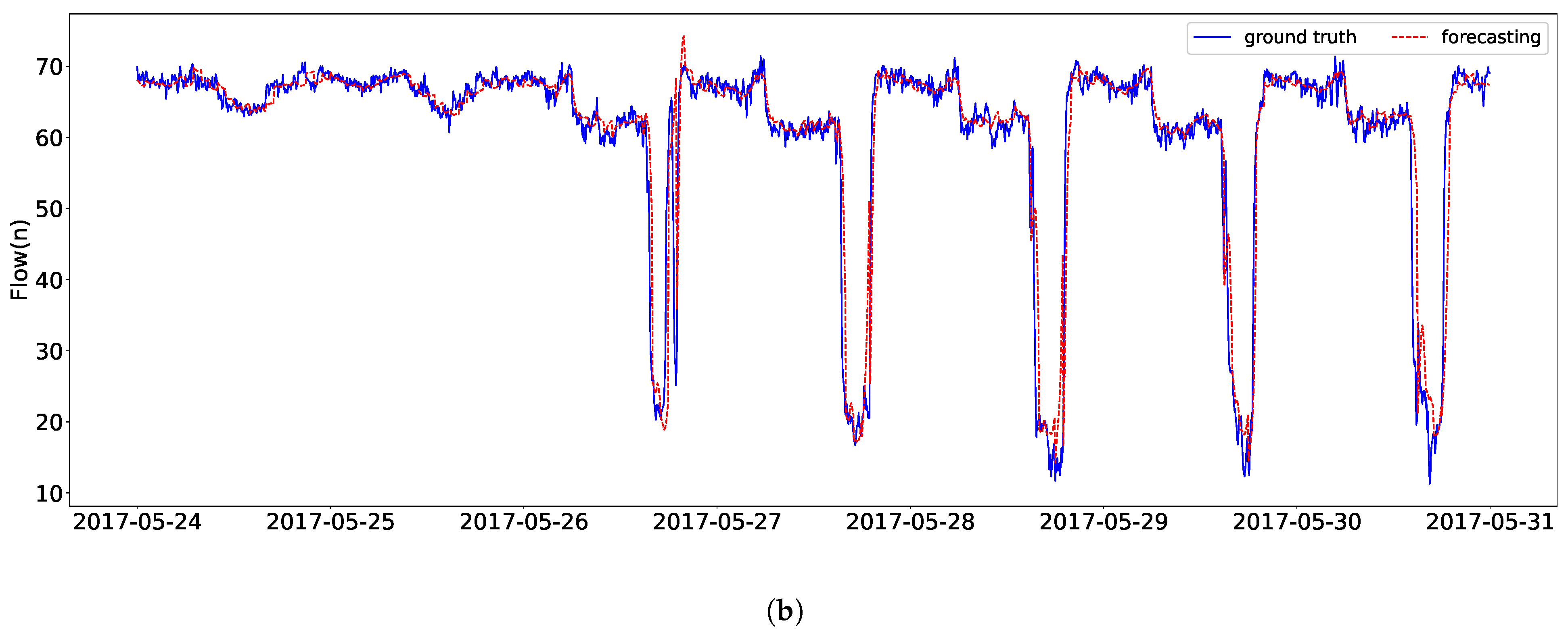
3.4.2. Real Case Analysis
3.5. Ablation Study
- FSSSM: It removes the spatio-temporal adaptive embedding and backward SSSM in STAE-BiSSSM.
- STAE-FSSSM: It removes the backward SSSM in STAE-BiSSSM.
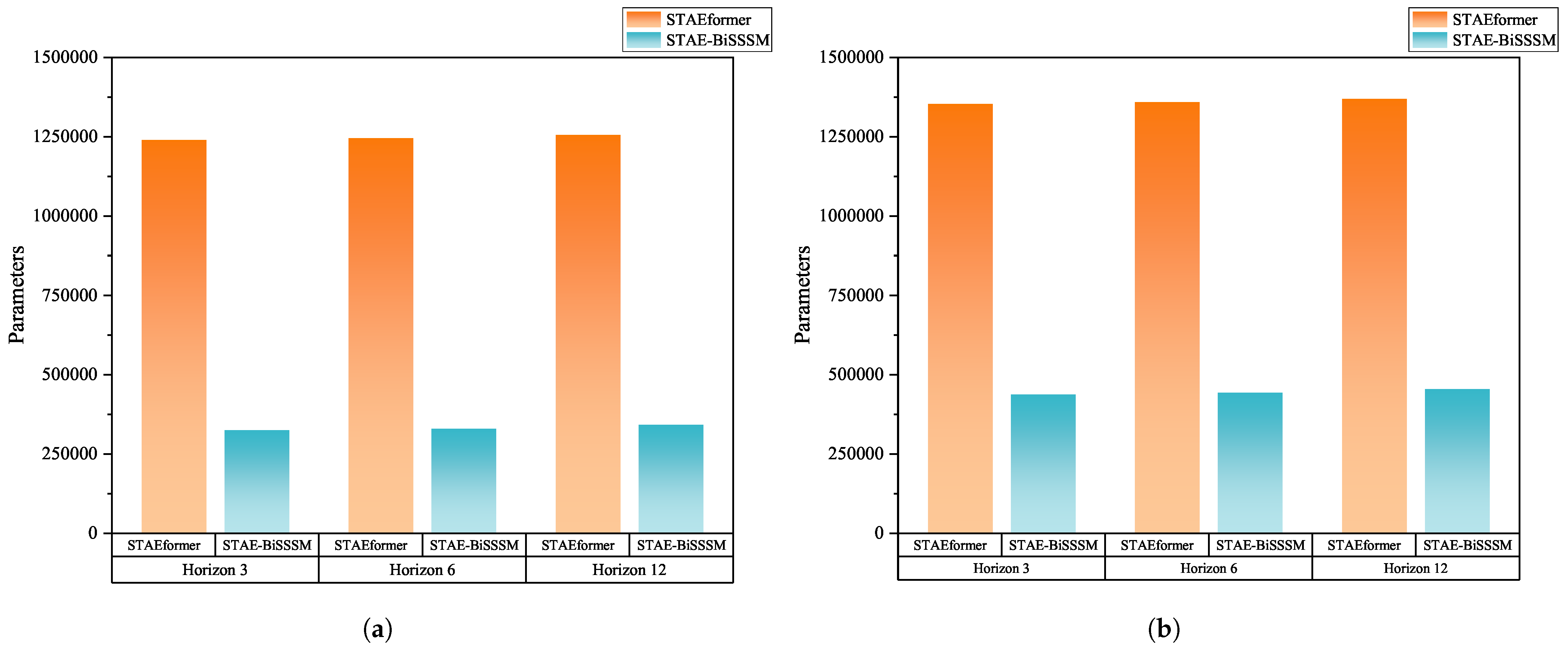
3.6. Parameter Effectiveness Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SSM | State space models |
| SSSM | Selective state space model |
| BiSSSM | Bidirectional selective state space model |
| STAE | Spatial–temporal adaptive embedding |
| STAE-BiSSSM | Spatial–temporal adaptive embedding–Bidirectional selective state space model |
| SOTA | State-of-the-art |
References
- Chen, S.; Cheng, K.; Yang, J.; Zang, X.; Luo, Q.; Li, J. Driving Behavior Risk Measurement and Cluster Analysis Driven by Vehicle Trajectory Data. Appl. Sci. 2023, 13, 5675. [Google Scholar] [CrossRef]
- Huang, S.; Zhu, G.; Tang, J.; Li, W.; Fan, Z. Multi-Perspective Semantic Segmentation of Ground Penetrating Radar Images for Pavement Subsurface Objects. IEEE Trans. Intell. Transp. Syst. 2025, 26, 14339–14352. [Google Scholar] [CrossRef]
- Boukerche, A.; Wang, J. Machine Learning-based traffic prediction models for Intelligent Transportation Systems. Comput. Netw. 2020, 181, 107530. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, Z.; Zhang, Y.; Huang, Y.; Chen, H.; Yu, Z. A comprehensive study of speed prediction in transportation system: From vehicle to traffic. iScience 2022, 25, 103909. [Google Scholar] [CrossRef]
- Medina-Salgado, B.; Sánchez-DelaCruz, E.; Pozos-Parra, P.; Sierra, J.E. Urban traffic flow prediction techniques: A review. Sustain. Comput. Inform. Syst. 2022, 35, 100739. [Google Scholar] [CrossRef]
- Williams, B.M.; Hoel, L.A. Modeling and Forecasting Vehicular Traffic Flow as a Seasonal ARIMA Process: Theoretical Basis and Empirical Results. J. Transp. Eng. 2003, 129, 664–672. [Google Scholar] [CrossRef]
- Min, W.; Wynter, L. Real-time road traffic prediction with spatio-temporal correlations. Transp. Res. Part Emerg. Technol. 2011, 19, 606–616. [Google Scholar] [CrossRef]
- Hou, Q.; Leng, J.; Ma, G.; Liu, W.; Cheng, Y. An adaptive hybrid model for short-term urban traffic flow prediction. Phys. Stat. Mech. Its Appl. 2019, 527, 121065. [Google Scholar] [CrossRef]
- Emami, A.; Sarvi, M.; Bagloee, S.A. Short-term traffic flow prediction based on faded memory Kalman Filter fusing data from connected vehicles and Bluetooth sensors. Simul. Model. Pract. Theory 2020, 102, 102025. [Google Scholar] [CrossRef]
- Bakibillah, A.; Tan, Y.H.; Loo, J.Y.; Tan, C.P.; Kamal, M.; Pu, Z. Robust estimation of traffic density with missing data using an adaptive-R extended Kalman filter. Appl. Math. Comput. 2022, 421, 126915. [Google Scholar] [CrossRef]
- Chang, S.Y.; Wu, H.C.; Kao, Y.C. Tensor Extended Kalman Filter and its Application to Traffic Prediction. Trans. Intell. Transport. Syst. 2023, 24, 13813–13829. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B.S. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Wu, C.H.; Ho, J.M.; Lee, D. Travel-time prediction with support vector regression. IEEE Trans. Intell. Transp. Syst. 2004, 5, 276–281. [Google Scholar] [CrossRef]
- Yao, Z.; Shao, C.F.; Gao, Y.L. Research on methods of short-term traffic forecasting based on support vector regression. J. Beijing Jiaotong Univ. 2006, 30, 19–22. [Google Scholar]
- Cheng, S.; Lu, F.; Peng, P.; Wu, S. Short-term traffic forecasting: An adaptive ST-KNN model that considers spatial heterogeneity. Comput. Environ. Urban Syst. 2018, 71, 186–198. [Google Scholar] [CrossRef]
- Sun, Y.; Shi, Y.; Jia, K.; Zhang, Z.; Qin, L. A Dual-Stream Cross AGFormer-GPT Network for Traffic Flow Prediction Based on Large-Scale Road Sensor Data. Sensors 2024, 24, 3905. [Google Scholar] [CrossRef]
- Carianni, A.; Gemma, A. Overview of Traffic Flow Forecasting Techniques. IEEE Open J. Intell. Transp. Syst. 2025, 6, 848–882. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Shi, C.; Huang, Y.; Yang, Y.; Ke, R.; Zhao, J. Sensing Data Supported Traffic Flow Prediction via Denoising Schemes and ANN: A Comparison. IEEE Sens. J. 2020, 20, 14317–14328. [Google Scholar] [CrossRef]
- Huang, W.; Song, G.; Hong, H.; Xie, K. Deep Architecture for Traffic Flow Prediction: Deep Belief Networks With Multitask Learning. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2191–2201. [Google Scholar] [CrossRef]
- Yasdi, R. Prediction of Road Traffic using a Neural Network Approach. Neural Comput. Appl. 1999, 8, 135–142. [Google Scholar] [CrossRef]
- More, R.; Mugal, A.; Rajgure, S.; Adhao, R.B.; Pachghare, V.K. Road traffic prediction and congestion control using Artificial Neural Networks. In Proceedings of the 2016 International Conference on Computing, Analytics and Security Trends (CAST), Pune, India, 19–21 December 2016; pp. 52–57. [Google Scholar] [CrossRef]
- Tian, Y.; Pan, L. Predicting Short-Term Traffic Flow by Long Short-Term Memory Recurrent Neural Network. In Proceedings of the 2015 IEEE International Conference on Smart City/SocialCom/SustainCom (SmartCity), Chengdu, China, 19–21 December 2015; pp. 153–158. [Google Scholar] [CrossRef]
- Fu, R.; Zhang, Z.; Li, L. Using LSTM and GRU neural network methods for traffic flow prediction. In Proceedings of the 2016 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 11–13 November 2016; pp. 324–328. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, K.; Li, J.; Lin, X.; Yang, B. LSTM-based traffic flow prediction with missing data. Neurocomputing 2018, 318, 297–305. [Google Scholar] [CrossRef]
- Yang, B.; Sun, S.; Li, J.; Lin, X.; Tian, Y. Traffic flow prediction using LSTM with feature enhancement. Neurocomputing 2019, 332, 320–327. [Google Scholar] [CrossRef]
- Du, S.; Li, T.; Gong, X.; Yang, Y.; Horng, S.J. Traffic flow forecasting based on hybrid deep learning framework. In Proceedings of the 2017 12th International Conference on Intelligent Systems and Knowledge Engineering (ISKE), Nanjing, China, 24–26 November 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, H.; Feng, X.; Chen, Z. Short-term traffic flow prediction with Conv-LSTM. In Proceedings of the 2017 9th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 11–13 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Duan, Z.; Yang, Y.; Zhang, K.; Ni, Y.; Bajgain, S. Improved Deep Hybrid Networks for Urban Traffic Flow Prediction Using Trajectory Data. IEEE Access 2018, 6, 31820–31827. [Google Scholar] [CrossRef]
- Ma, D.; Sheng, B.; Jin, S.; Ma, X.; Gao, P. Short-Term Traffic Flow Forecasting by Selecting Appropriate Predictions Based on Pattern Matching. IEEE Access 2018, 6, 75629–75638. [Google Scholar] [CrossRef]
- Yao, H.; Tang, X.; Wei, H.; Zheng, G.; Li, Z. Revisiting Spatial-Temporal Similarity: A Deep Learning Framework for Traffic Prediction. arXiv 2018, arXiv:1803.01254. [Google Scholar] [CrossRef]
- Narmadha, S.; Vijayakumar, V. Spatio-Temporal vehicle traffic flow prediction using multivariate CNN and LSTM model. Mater. Today Proc. 2023, 81, 826–833. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, K.; Liu, C.; Xu, X. Urban Short - Term Traffic Flow Prediction Algorithm Based on CNN-LSTM Model. In Proceedings of the 2023 3rd International Conference on Consumer Electronics and Computer Engineering (ICCECE), Guangzhou, China, 6–8 January 2023; pp. 214–217. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.Y.; Liu, J. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting. In Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence. International Joint Conferences on Artificial Intelligence Organization, Stockholm, Sweden, 13–19 July 2018; pp. 3634–3640. [Google Scholar] [CrossRef]
- Cao, D.; Wang, Y.; Duan, J.; Zhang, C.; Zhu, X.; Huang, C.; Tong, Y.; Xu, B.; Bai, J.; Tong, J.; et al. Spectral Temporal Graph Neural Network for Multivariate Time-series Forecasting. arXiv 2021, arXiv:2103.07719. [Google Scholar] [CrossRef]
- Chen, Y.; Segovia-Dominguez, I.; Gel, Y.R. Z-GCNETs: Time Zigzags at Graph Convolutional Networks for Time Series Forecasting. arXiv 2021, arXiv:2105.04100. [Google Scholar] [CrossRef]
- Diao, Z.; Wang, X.; Zhang, D.; Liu, Y.; Xie, K.; He, S. Dynamic spatial-temporal graph convolutional neural networks for traffic forecasting. In Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence and Thirty-First Innovative Applications of Artificial Intelligence Conference and Ninth AAAI Symposium on Educational Advances in Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar] [CrossRef]
- Fang, Z.; Long, Q.; Song, G.; Xie, K. Spatial-Temporal Graph ODE Networks for Traffic Flow Forecasting. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, New York, NY, USA, 14–18 August 2021; pp. 364–373. [Google Scholar] [CrossRef]
- Guo, K.; Hu, Y.; Sun, Y.; Qian, S.; Gao, J.; Yin, B. Hierarchical Graph Convolution Network for Traffic Forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 151–159. [Google Scholar] [CrossRef]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting. arXiv 2018, arXiv:1707.01926. [Google Scholar] [CrossRef]
- Zhao, L.; Song, Y.; Zhang, C.; Liu, Y.; Wang, P.; Lin, T.; Deng, M.; Li, H. T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3848–3858. [Google Scholar] [CrossRef]
- Bai, L.; Yao, L.; Li, C.; Wang, X.; Wang, C. Adaptive Graph Convolutional Recurrent Network for Traffic Forecasting. arXiv 2020, arXiv:2007.02842. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Graph WaveNet for Deep Spatial-Temporal Graph Modeling. arXiv 2019, arXiv:1906.00121. [Google Scholar]
- Shang, C.; Chen, J.; Bi, J. Discrete Graph Structure Learning for Forecasting Multiple Time Series. arXiv 2021, arXiv:2101.06861. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks. arXiv 2020, arXiv:2005.11650. [Google Scholar] [CrossRef]
- Jiang, R.; Wang, Z.; Yong, J.; Jeph, P.; Chen, Q.; Kobayashi, Y.; Song, X.; Fukushima, S.; Suzumura, T. Spatio-Temporal Meta-Graph Learning for Traffic Forecasting. arXiv 2023, arXiv:2211.14701. [Google Scholar] [CrossRef]
- Zhang, Q.; Chang, J.; Meng, G.; Xiang, S.; Pan, C. Spatio-Temporal Graph Structure Learning for Traffic Forecasting. Proc. AAAI Conf. Artif. Intell. 2020, 34, 1177–1185. [Google Scholar] [CrossRef]
- Zheng, C.; Fan, X.; Wang, C.; Qi, J. GMAN: A Graph Multi-Attention Network for Traffic Prediction. arXiv 2019, arXiv:1911.08415. [Google Scholar] [CrossRef]
- Jiang, J.; Han, C.; Zhao, W.X.; Wang, J. PDFormer: Propagation Delay-Aware Dynamic Long-Range Transformer for Traffic Flow Prediction. Proc. AAAI Conf. Artif. Intell. 2023, 37, 4365–4373. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. arXiv 2022, arXiv:2106.13008. [Google Scholar]
- Zhou, G.; Guo, X.; Liu, Z.; Li, T.; Li, Q.; Xu, K. TrafficFormer: An Efficient Pre-trained Model for Traffic Data. In Proceedings of the 2025 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 12–15 May 2025; pp. 1844–1860. [Google Scholar] [CrossRef]
- Pu, B.; Liu, J.; Kang, Y.; Chen, J.; Yu, P.S. MVSTT: A Multiview Spatial-Temporal Transformer Network for Traffic-Flow Forecasting. IEEE Trans. Cybern. 2024, 54, 1582–1595. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, Z.; Wang, F.; Wei, W.; Xu, Y. Spatial-Temporal Identity: A Simple yet Effective Baseline for Multivariate Time Series Forecasting. arXiv 2022, arXiv:2208.05233. [Google Scholar] [CrossRef]
- Liu, H.; Dong, Z.; Jiang, R.; Deng, J.; Deng, J.; Chen, Q.; Song, X. Spatio-Temporal Adaptive Embedding Makes Vanilla Transformer SOTA for Traffic Forecasting. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, New York, NY, USA, 21–25 October 2023; pp. 4125–4129. [Google Scholar] [CrossRef]
- Sun, Y.; Dong, L.; Huang, S.; Ma, S.; Xia, Y.; Xue, J.; Wang, J.; Wei, F. Retentive Network: A Successor to Transformer for Large Language Models. arXiv 2023, arXiv:2307.08621. [Google Scholar] [CrossRef]
- Peng, B.; Alcaide, E.; Anthony, Q.; Albalak, A.; Arcadinho, S.; Biderman, S.; Cao, H.; Cheng, X.; Chung, M.; Grella, M.; et al. RWKV: Reinventing RNNs for the Transformer Era. arXiv 2023, arXiv:2305.13048. [Google Scholar] [CrossRef]
- Gu, A.; Dao, T. Mamba: Linear-Time Sequence Modeling with Selective State Spaces. arXiv 2024, arXiv:2312.00752. [Google Scholar]
- Gu, A.; Goel, K.; Ré, C. Efficiently Modeling Long Sequences with Structured State Spaces. arXiv 2022, arXiv:2111.00396. [Google Scholar] [CrossRef]
- Zhang, B.; Sennrich, R. Root Mean Square Layer Normalization. arXiv 2019, arXiv:1910.07467. [Google Scholar] [CrossRef]
- Cui, Y.; Xie, J.; Zheng, K. Historical Inertia: An Ignored but Powerful Baseline for Long Sequence Time-series Forecasting. CoRR 2021, arXiv:2103.16349. [Google Scholar]
- Deng, J.; Chen, X.; Jiang, R.; Song, X.; Tsang, I.W. ST-Norm: Spatial and Temporal Normalization for Multi-variate Time Series Forecasting. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, New York, NY, USA, 14–18 August 2021; pp. 269–278. [Google Scholar] [CrossRef]



| Dataset | Number of Sensors | Time Steps | Sample Interval | Time Range | Location |
|---|---|---|---|---|---|
| PeMSD4 | 307 | 16,992 | 5 min | 01/2018–02/2018 | California District 4 |
| PeMSD7 | 883 | 28,224 | 5 min | 05/2017–08/2017 | California District 7 |
| PeMSD8 | 170 | 17,856 | 5 min | 07/2016–08/2016 | California District 8 |
| METRLA | 207 | 34,272 | 5 min | 03/2012–06/2012 | Los Angeles |
| PeMSBAY | 325 | 52,116 | 5 min | 01/2017–05/2017 | San Francisco Bay Area |
| Hyperparameter | Description | Dimension Size |
|---|---|---|
| Embedding dimension of feature embedding | 24 | |
| Embedding dimension of time of day embedding | 24 | |
| Embedding dimension of day-of-week embedding | 24 | |
| Embedding dimension of spatial–temporal adaptive embedding | 80 | |
| Size of convolution kernel | 5 | |
| Dimension of hidden state | 64 | |
| Dimension of middle-rank state | 16 |
| Dataset | PeMSD4 | PeMSD7 | PeMSD8 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Metric | MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | |
| Model | ||||||||||
| HI | 42.35 | 61.66 | 29.92% | 49.03 | 71.18 | 22.75% | 36.66 | 50.45 | 21.63% | |
| GWNet | 18.53 | 29.92 | 12.89% | 20.47 | 33.47 | 8.61% | 14.40 | 23.39 | 9.21% | |
| DCRNN | 19.63 | 31.26 | 13.59% | 21.16 | 34.14 | 9.02% | 15.22 | 24.17 | 10.21% | |
| AGCRN | 19.38 | 31.25 | 13.40% | 20.57 | 34.40 | 8.74% | 15.32 | 24.41 | 10.03% | |
| STGCN | 19.57 | 31.38 | 13.44% | 21.74 | 35.27 | 9.24% | 16.08 | 25.39 | 10.60% | |
| GTS | 20.96 | 32.95 | 14.66% | 22.15 | 35.10 | 9.38% | 16.49 | 26.08 | 10.54% | |
| MTGNN | 19.17 | 31.70 | 13.37% | 20.89 | 34.06 | 9.00% | 15.18 | 24.24 | 10.20% | |
| STNorm | 18.96 | 30.98 | 12.69% | 20.50 | 34.66 | 8.75% | 15.41 | 24.77 | 9.76% | |
| GMAN | 19.14 | 31.60 | 13.19% | 20.97 | 34.10 | 9.05% | 15.31 | 24.92 | 10.13% | |
| STAE-BiSSSM (Ours) | 18.46 | 30.16 | 12.24% | 19.91 | 33.16 | 8.43% | 13.84 | 23.23 | 9.24% | |
| Dataset | METRLA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Horizon | 15 min | 30 min | 60 min | |||||||
| Metric | MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | |
| Model | ||||||||||
| HI | 6.80 | 14.21 | 16.72% | 6.80 | 14.21 | 16.72% | 6.80 | 14.20 | 10.15% | |
| GWNet | 2.69 | 5.15 | 6.99% | 3.08 | 6.20 | 8.47% | 3.51 | 7.28 | 9.96% | |
| DCRNN | 2.67 | 5.16 | 6.86% | 3.12 | 6.27 | 8.42% | 3.54 | 7.47 | 10.32% | |
| AGCRN | 2.85 | 5.53 | 7.63% | 3.20 | 6.52 | 9.00% | 3.59 | 7.45 | 10.47% | |
| STGCN | 2.75 | 5.29 | 7.10% | 3.15 | 6.35 | 8.62% | 3.60 | 7.43 | 10.35% | |
| GTS | 2.75 | 5.27 | 7.12% | 3.14 | 6.33 | 8.62% | 3.59 | 7.44 | 10.25% | |
| MTGNN | 2.69 | 5.16 | 6.89% | 3.05 | 6.13 | 8.16% | 3.47 | 7.21 | 9.70% | |
| STNorm | 2.81 | 5.57 | 7.40% | 3.18 | 6.59 | 8.47% | 3.57 | 7.51 | 10.24% | |
| GMAN | 2.80 | 5.55 | 7.41% | 3.12 | 6.49 | 8.73% | 3.44 | 7.35 | 10.07% | |
| PDFormer | 2.83 | 5.45 | 7.77% | 3.20 | 6.46 | 9.19% | 3.62 | 7.47 | 10.91% | |
| STID | 2.82 | 5.53 | 7.75% | 3.19 | 6.57 | 9.39% | 3.55 | 7.55 | 10.95% | |
| STAEformer | 2.65 | 5.11 | 6.85% | 2.97 | 6.00 | 8.13% | 3.34 | 7.02 | 9.70% | |
| STAE-BiSSSM (Ours) | 2.60 | 4.92 | 6.75% | 2.86 | 5.59 | 7.88% | 3.22 | 6.51 | 9.49% | |
| Dataset | PeMSBAY | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Horizon | 15 min | 30 min | 60 min | |||||||
| Metric | MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | |
| Model | ||||||||||
| HI | 3.06 | 7.05 | 6.85% | 3.06 | 7.04 | 6.84% | 3.05 | 7.03 | 6.83% | |
| GWNet | 1.30 | 2.73 | 2.71% | 1.63 | 3.73 | 3.73% | 1.99 | 4.60 | 4.71% | |
| DCRNN | 1.31 | 2.76 | 2.73% | 1.65 | 3.75 | 3.71% | 1.97 | 4.60 | 4.68% | |
| AGCRN | 1.35 | 2.88 | 2.91% | 1.67 | 3.82 | 3.81% | 1.94 | 4.50 | 4.55% | |
| STGCN | 1.36 | 2.88 | 2.86% | 1.70 | 3.84 | 3.79% | 2.02 | 4.63 | 4.72% | |
| GTS | 1.37 | 2.92 | 2.85% | 1.72 | 3.86 | 3.88% | 2.06 | 4.60 | 4.88% | |
| MTGNN | 1.33 | 2.80 | 2.81% | 1.66 | 3.77 | 3.75% | 1.95 | 4.50 | 4.62% | |
| STNorm | 1.33 | 2.82 | 2.76% | 1.65 | 3.77 | 3.66% | 1.92 | 4.45 | 4.46% | |
| GMAN | 1.35 | 2.90 | 2.87% | 1.65 | 3.82 | 3.74% | 1.92 | 4.49 | 4.52% | |
| PDFormer | 1.32 | 2.83 | 2.78% | 1.64 | 3.79 | 3.71% | 1.91 | 4.43 | 4.51% | |
| STID | 1.31 | 2.79 | 2.78% | 1.64 | 3.73 | 3.73% | 1.91 | 4.42 | 4.55% | |
| STAEformer | 1.31 | 2.78 | 2.76% | 1.62 | 3.68 | 3.62% | 1.88 | 4.34 | 4.41% | |
| STAE-BiSSSM (Ours) | 1.13 | 2.33 | 2.28% | 1.36 | 2.96 | 2.93% | 1.62 | 3.63 | 3.72% | |
| Dataset | Model | FSSSM | STAE-FSSSM | STAE-BiSSSM | |
|---|---|---|---|---|---|
| Metric | |||||
| PeMSD4 | MAE | 21.85 | 18.54 | 18.46 | |
| RMSE | 35.11 | 30.20 | 30.16 | ||
| MAPE | 14.82% | 12.51% | 12.24% | ||
| METRLA | MAE | 3.92 | 3.24 | 3.22 | |
| RMSE | 7.84 | 6.53 | 6.51 | ||
| MAPE | 11.94% | 9.82% | 9.49% | ||
| PeMSBAY | MAE | 2.03 | 1.64 | 1.62 | |
| RMSE | 4.43 | 3.65 | 3.63 | ||
| MAPE | 4.82% | 3.88% | 3.72% | ||
| Datasets | Models | STAEformer | STAE-BiSSSM | |
|---|---|---|---|---|
| Horizon | ||||
| METRLA | 3 (15 min) | 1,242,555 | 327,195 | |
| 6 (30 min) | 1,248,030 | 332,670 | ||
| 9 (60 min) | 1,258,980 | 343,620 | ||
| PeMSBAY | 3 (15 min) | 1,355,835 | 440,475 | |
| 6 (30 min) | 1,361,310 | 445,950 | ||
| 9 (60 min) | 1,372,260 | 456,900 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Qu, Q.; Chen, X. STAE-BiSSSM: A Traffic Flow Forecasting Model with High Parameter Effectiveness. ISPRS Int. J. Geo-Inf. 2025, 14, 388. https://doi.org/10.3390/ijgi14100388
Liu D, Qu Q, Chen X. STAE-BiSSSM: A Traffic Flow Forecasting Model with High Parameter Effectiveness. ISPRS International Journal of Geo-Information. 2025; 14(10):388. https://doi.org/10.3390/ijgi14100388
Chicago/Turabian StyleLiu, Duoliang, Qiang Qu, and Xuebo Chen. 2025. "STAE-BiSSSM: A Traffic Flow Forecasting Model with High Parameter Effectiveness" ISPRS International Journal of Geo-Information 14, no. 10: 388. https://doi.org/10.3390/ijgi14100388
APA StyleLiu, D., Qu, Q., & Chen, X. (2025). STAE-BiSSSM: A Traffic Flow Forecasting Model with High Parameter Effectiveness. ISPRS International Journal of Geo-Information, 14(10), 388. https://doi.org/10.3390/ijgi14100388





