Adversarial Obstacle Placement with Spatial Point Processes for Optimal Path Disruption

Abstract

We investigate the Optimal Obstacle Placement (OOP) problem under uncertainty, framed as the dual of the Optimal Traversal Path problem in the Stochastic Obstacle Scene paradigm. We consider both continuous domains, discretized for analysis, and already discrete spatial grids that form weighted geospatial networks using 8-adjacency lattices. Our unified framework integrates OOP with stochastic geometry, modeling obstacle placement via Strauss (regular) and Matérn (clustered) processes, and evaluates traversal using the Reset Disambiguation algorithm. Through extensive Monte Carlo experiments, we show that traversal cost increases by up to 40% under strongly regular placements, while clustered configurations can decrease traversal costs by as much as 25% by leaving navigable corridors compared to uniform random layouts. In mixed (with both true and false obstacles) scenarios, increasing the proportion of true obstacles from 30% to 70% nearly doubles the traversal cost. These findings are further supported by statistical analysis and stochastic ordering, providing rigorous insights into how spatial patterns and obstacle compositions influence navigation under uncertainty.

1. Introduction

Efficient pathfinding in uncertain or dynamic spatial environments is a central problem in geographic information science (GIScience), having broad applications in autonomous navigation, urban mobility planning, defense logistics, and environmental monitoring. Real-world scenarios—such as maritime navigation in mine-infested zones, cities with dynamic construction, or landscapes fragmented by environmental hazards—require agents to make routing decisions under uncertainty. The Stochastic Obstacle Scene (SOS) problem and its discrete analogue, the Canadian Traveler’s Problem (CTP), capture this challenge by modeling settings where agents must traverse from a source to a destination through regions containing uncertain obstacles [1,2].

In addition to work on the CTP, our study connects with several broader strands of research:

(i) Spatial point process modeling of obstacles. The use of stochastic geometry to model spatial uncertainty is well established in ecological and environmental planning. Classical references such as [3,4,5] provide comprehensive treatments of point process models including the Strauss, Matérn, and hardcore processes. These approaches have been applied to urban growth, forestry, and habitat modeling, and here we adapt them to adversarial obstacle placement in navigation domains.

(ii) Navigation and path planning under uncertainty. Beyond CTP, the robotics and motion-planning literature has long addressed navigation in partially known or dynamic environments. Ref. [6] surveys motion planning algorithms such as probabilistic roadmaps and RRTs, which account for uncertainty in obstacle fields. Ref. [7] introduces risk-aware planning for mobile robots operating with incomplete information, highlighting themes similar to our disambiguation-based traversal.

(iii) Empirical studies in GIS-based routing. In applied GIS, several studies examine how spatial patterning of hazards influences routing outcomes without invoking the CTP framework. For example, recent work on flood evacuation [8] and off-road path planning [9] demonstrates the importance of integrating spatial randomness and hazard clustering into path evaluation. Our framework contributes to this line of work by explicitly modeling the influence of obstacle pattern on traversal cost.

While much of the literature focuses on developing effective traversal strategies for a navigating agent (NAVA), the inverse problem—how an adversary might strategically place obstacles to hinder movement—has received relatively little attention. This dual formulation, known as the Optimal Obstacle Placement (OOP) problem, introduces a second agent, the obstacle-placing agent (OPA), who aims to maximize the expected traversal cost of the NAVA. The OOP problem, introduced by [10] as the Optimal Placement with Disambiguations (OPD) problem, generalizes the SOS framework. Prior work examined specific layouts or background clutter but did not systematically study how spatial pattern (regularity, uniformity, clustering) shapes traversal cost. Our contribution lies in addressing this gap by systematically evaluating the impact of obstacle pattern geometry and obstacle composition on navigability.

The importance of OOP is not limited to theoretical curiosity; it varies with the geospatial use case. In maritime defense, adversaries may deploy mines in spatially regular patterns to maximize disruption of naval logistics. In urban environments, construction zones and artificial blockages may act as strategically placed obstacles that reroute traffic. In environmental settings, clustered hazards such as flood debris or landslides may mimic Matérn-type patterns, creating narrow corridors for evacuation. These prospective applications illustrate why understanding obstacle placement under uncertainty is useful across multiple domains, from defense to urban planning to disaster response. A recent flood-evacuation routing study underscores the practical importance of path planning under spatial risk [8].

In this work, we develop a unified framework for the OOP problem that incorporates both continuous and discretized spatial representations. The continuous setting models obstacles as disks having uncertain status; the discrete setting uses an 8-adjacency spatial grid to convert the environment into a weighted geospatial network. We assume two types of obstacles exist in the navigation domain: true obstacles (which are non-traversable or block the traversal), such as mines, and false obstacles (which are traversable) such as mine-like objects (i.e., objects resembling mines). This duality supports GIS-compatible analysis alongside tractable computational methods. A NAVA uses a greedy strategy—called the Reset Disambiguation (RD) algorithm [11]—that re-evaluates the shortest path whenever a true obstacle is encountered, incurring a disambiguation cost based on sensor uncertainty. Sensors provide probability marks (modeled with a Beta distribution), prompting disambiguation actions that influence final traversal costs. In this setting, the NAVA can only disambiguate (but not neutralize) the obstacle and thus can determine the actual status of the obstacle as true or false at an additional cost to traversal cost. Recent work on grid-based and off-road path planning demonstrates continued interest in coupling advanced algorithms with geospatial data [9,12]. While motivated by SOS/CTP, our focus lies in understanding how spatial obstacle patterns influence traversal cost across a broader class of stochastic environments. We do not propose new CTP algorithms but instead explore how underlying spatial processes affect algorithmic performance.

Our obstacle placement strategies leverage spatial point processes to model different spatial patterns. In particular, we use the Strauss process to represent spatial regularity and the Matérn process to represent spatial aggregation/clustering. This design enables controlled comparisons of obstacle layout and composition. Through extensive Monte Carlo (MC) experiments, we examine how traversal cost varies under different spatial configurations and ratios of true to false obstacles. To analyze outcomes, we employ robust regression, random forest [13], and zero-inflated negative binomial models [14], offering both statistical rigor and flexibility.

Theoretical analysis complements these empirical findings by establishing a stochastic ordering among the path-weight distributions. Configurations consisting solely of false obstacles are stochastically dominated by mixed-obstacle configurations, which are in turn dominated by true-only arrangements in terms of induced traversal cost. Specifically, it shows that when obstacles are all false (i.e., not truly blocking), the resulting paths tend to be shorter and less costly to traverse. When some of the obstacles are true (i.e., actual obstructions), the paths become more uncertain and typically longer. In the most obstructive case—when all obstacles are true—the traversal cost is highest. This establishes a clear ordering: false-only configurations lead to the lowest expected traversal cost, followed by mixed obstacles, with true-only configurations resulting in the highest cost. These findings demonstrate how spatial structure and obstacle composition jointly influence navigability in adversarial settings.

The OOP problem also bears conceptual similarity to the well-known network interdiction problem [15,16], which models a leader–follower game where an interdictor disables parts of a network to increase traversal costs for an adversary. However, our framework differs significantly: it emphasizes partial information, spatially extended obstacles (e.g., disk regions), and dynamic learning (via disambiguation). These elements are rarely addressed in the classical interdiction literature, although recent extensions (e.g., [17,18,19]) begin to incorporate such dynamics. We illustrate the model with a naval logistics scenario and note its relevance for urban mobility, ecology, and flood evacuation.

The main contributions of this paper are as follows:

• We propose a unified OOP framework that couples obstacle placement with stochastic geometry via Strauss and Matérn point processes, capturing both regular and clustered obstacle layouts.
• We extend OOP analysis to compositional settings that include false-only, true-only, and mixed obstacle fields, thus accounting for both physical blockage and deceptive clutter.
• We conduct extensive Monte Carlo experiments across a wide range of parameter settings and analyze outcomes using robust regression, random forests, and zero-inflated models to quantify the effects of obstacle pattern and composition.
• We introduce stochastic ordering as a rigorous tool to compare traversal cost distributions under alternative obstacle placement strategies.
• We present an illustrative geospatial case study to demonstrate the real-world applicability of the proposed framework.

The remainder of this paper is organized as follows. Section 2 formalizes the OOP problem and our assumptions. Section 3 discusses the GIS-based implications of our findings, highlighting applications in urban mobility, environmental modeling, and maritime navigation. Section 4 outlines the experimental design and statistical modeling approach. Results and insights are presented in Section 5 and an illustrative geospatial case study is provided in Section 6. Section 7 explores theoretical comparisons using stochastic ordering. Finally, Section 8 offers conclusions and future research directions. Proofs of theoretical results and details of the extensive Monte Carlo experiments are deferred to the Supplementary File.

2. The Optimal Obstacle Placement Problem

The SOS problem, introduced by Papadimitriou and Yannakakis [1], originally focused on computing the Optimal Traversal Path (OTP) for a NAVA in a stochastic environment with obstacles. Its discrete analogue, the CTP, has received substantial attention in both theory and applications [2,20,21]. A complementary and less-explored formulation considers an OPA whose objective is to strategically insert obstacles to hinder the NAVA’s movement by maximizing traversal cost. This formulation defines the OOP problem, introduced by [10], which identifies worst-case obstacle configurations (for the NAVA) within a designated insertion window. Both the OTP and OOP problems can be studied in continuous and discrete domains, and their interplay underpins a broader class of adversarial path planning problems.

2.1. The Continuous OOP Problem

Consider a bounded region $\Omega \subset {\mathbb{R}}^2$, where an OPA inserts obstacles modeled as disks $D_x$ centered at $x\in \mathcal{X}$ with fixed radius $r>0$. Let ${\mathcal{X}}_{\mathcal{F}}$ and ${\mathcal{X}}_{\mathcal{T}}$ denote the centers of false and true obstacles, generated from spatial point processes ${\mathcal{P}}_{\mathcal{F}}$ and ${\mathcal{P}}_{\mathcal{T}}$, respectively.

A NAVA traverses from s to $t\in \Omega$, relying on a sensor that assigns probabilities $p:\mathcal{X}\to [0,1]$, where $p\left(x\right)$ indicates the probability that obstacle x is true. Sensor outputs are modeled with Beta distributions: $p\left(x\right)\equiv \mathrm{Beta}(a,b)$, with $a<b$ for false and $a>b$ for true obstacles—ensuring that true obstacles are, on average, assigned higher probabilities. Increasing the gap $|a-b|$ models higher sensor discrimination.

The sensor marks are drawn independently as $p_F$ for $x\in {\mathcal{X}}_{\mathcal{F}}$ and $p_T$ for $x\in {\mathcal{X}}_{\mathcal{T}}$, according to the following:

$$p\left(x\right)=\left\{\begin{array}{cc}{p}_F,\hfill & \mathrm{if}x\in {\mathcal{X}}_{\mathcal{F}}\hfill \\ p_T,\hfill & \mathrm{if}x\in {\mathcal{X}}_{\mathcal{T}}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

Although the NAVA observes the obstacle locations $\mathcal{X}={\mathcal{X}}_{\mathcal{T}}\cup {\mathcal{X}}_{\mathcal{F}}$, their true status remains unknown unless disambiguated. Each disambiguation incurs a fixed cost $c>0$, typically interpreted as time, which is added to the overall traversal cost.

The continuous OTP problem then seeks the minimum-cost $(s,t)$ path avoiding true obstacles, while the continuous OOP problem seeks to maximize this cost through strategic obstacle placement. To navigate the uncertain environment, the NAVA evaluates paths by balancing Euclidean distance and the risk based on $p\left(x\right)$. Heuristic strategies such as the Risk-Aware Greedy Algorithm [22,23] select paths based on a composite measure of length and estimated risk. These methods may be enhanced through probabilistic planners like Rapidly-exploring Random Trees (RRTs) or risk-weighted A* variants, enabling adaptive traversal in uncertain and spatially complex environments [24,25].

2.2. The Discretized OOP Problem

To facilitate computation, the continuous domain $\Omega$ is discretized into an $n\times m$ grid, forming an 8-adjacency integer lattice [10]. Obstacles are modeled as disks of fixed radius [26], and grid resolution is chosen to closely approximate continuous traversal. The resulting graph $G=(V,E)$ contains vertices at grid points and edges connecting adjacent vertices, including diagonals. Each interior vertex links to eight neighbors: four unit-length and four diagonal ($\sqrt{2}$-length) edges. Additionally, edge connections are added along the grid boundary to preserve connectivity. A start vertex s and target vertex t are designated. The NAVA seeks a path from s to t while minimizing a traversal cost that incorporates both Euclidean distance and the risk associated with uncertain obstacles, disambiguated at cost $c>0$ when necessary. This discrete setup corresponds to the CTP with spatially dependent stochastic costs [20,21,27].

Obstacles are placed within a designated window between source and target, representing the adversarial region of influence. This window is sized to cover the main traversal corridor while leaving peripheral areas open, ensuring that placement decisions are consequential but do not trivially block all routes.

The OPA’s objective in the discretized OOP problem is to place obstacles within an insertion window ${\Omega }_{\mathcal{O}}\subset \Omega$—typically a homothetic subregion—to maximize expected traversal cost. A coastal defense analogy illustrates the setting: an OPA delays an intruding vessel (NAVA) navigating through a mined nearshore zone (Figure 1). The annular (i.e., ring-shaped) obstacle-free window ensures that traversal remains feasible but strategically costly. The grid is aligned such that $\partial \left({\Omega }_{\mathcal{O}}\right)$ coincides with grid cell boundaries.

Obstacle radius is set to $r=4.5$ [26]. This value is chosen to ensure that each obstacle intersects several grid edges (roughly spanning 9–10 units on a $101\times 101$ grid), thereby exerting a nontrivial effect on traversal. At the same time, the radius is small enough that feasible corridors between the source and the target remain available. This scaling follows prior studies on the SOS framework [11], where obstacle radii were selected relative to grid resolution to balance obstruction with navigability.

In the discrete setting, traversal is modeled on a weighted graph where each edge e has a baseline length $\ell \left(e\right)$, equal to the Euclidean distance between its endpoints ($\ell \left(e\right)=1$ for horizontal/vertical, $\ell \left(e\right)=\sqrt{2}$ for diagonals). Obstacle disks intersecting an edge add uncertainty to its cost, with disambiguation determining whether the edge is blocked or available.

The NAVA follows the RD algorithm, which adaptively recomputes shortest paths based on perceived risk. For a path $\pi (s,t)$ from s to t, the weight of edge e is defined as

$$w\left(e\right)=\ell \left(e\right)+\frac{1}{2}F\left(e\right),\mathrm{where}F\left(e\right)=\sum _{x\in \mathcal{X}}{\mathbf{1}}_{D_r\left(x\right)\cap e\ne \varnothing }\left({\displaystyle \frac{c\left(x\right)}{1-p\left(x\right)}}\right),$$

(1)

with $p\left(x\right)$ the sensor-assigned probability that obstacle x is true, $c\left(x\right)$ the disambiguation cost, and ${\mathbf{1}}_{\{·\}}$ the indicator function. The term $F\left(e\right)$ captures the cumulative risk from all uncertain obstacles intersecting edge e.

The total path weight is then

$$W(\pi ,\mathcal{X})=\sum _{e\in \pi (s,t)}w\left(e\right),$$

(2)

used to approximate the expected traversal cost perceived by the NAVA before disambiguation. When no obstacles are present, $W(\pi ,\mathcal{X})=L_{\pi }={\sum }_{e\in \pi (s,t)}\ell \left(e\right)$, and the NAVA simply follows the shortest path. With uncertain obstacles, $W(\pi ,\mathcal{X})$ becomes stochastic (i.e., random) due to Beta-distributed $p\left(x\right)$ and also the stochastic nature of obstacle locations. The RD algorithm adaptively recomputes paths upon disambiguating true obstacles, resetting traversal from the current location. It extends Dijkstra’s algorithm to accommodate dynamic edge weights derived from spatial uncertainty [28].

2.3. The Distinction Between Continuous vs. Discrete Traversal

Two formulations of the OOP problem can be distinguished. In the continuous formulation, the agent’s trajectory is modeled as an arbitrary curve in the plane that avoids true obstacles. This description is natural in open domains such as maritime navigation or off-road mobility, where paths are not confined to predefined routes.

In the discrete formulation, movement is represented as a walk on a graph. This graph may arise either from discretizing the continuous domain (e.g., an $n\times m$ lattice) or from a naturally occurring network such as streets, corridors, or utility grids. Although the underlying space may be physically continuous and traversable along edges, the model treats traversal as node-to-node steps: the agent moves only between adjacent vertices and never halts at intermediate points on an edge. Thus, the discreteness stems from the representation of movement, not from the geometry of the environment itself. In our study we employ an 8-adjacency lattice, which permits orthogonal and diagonal moves; restricting to 4-adjacency is possible but typically lengthens paths by removing diagonal shortcuts.

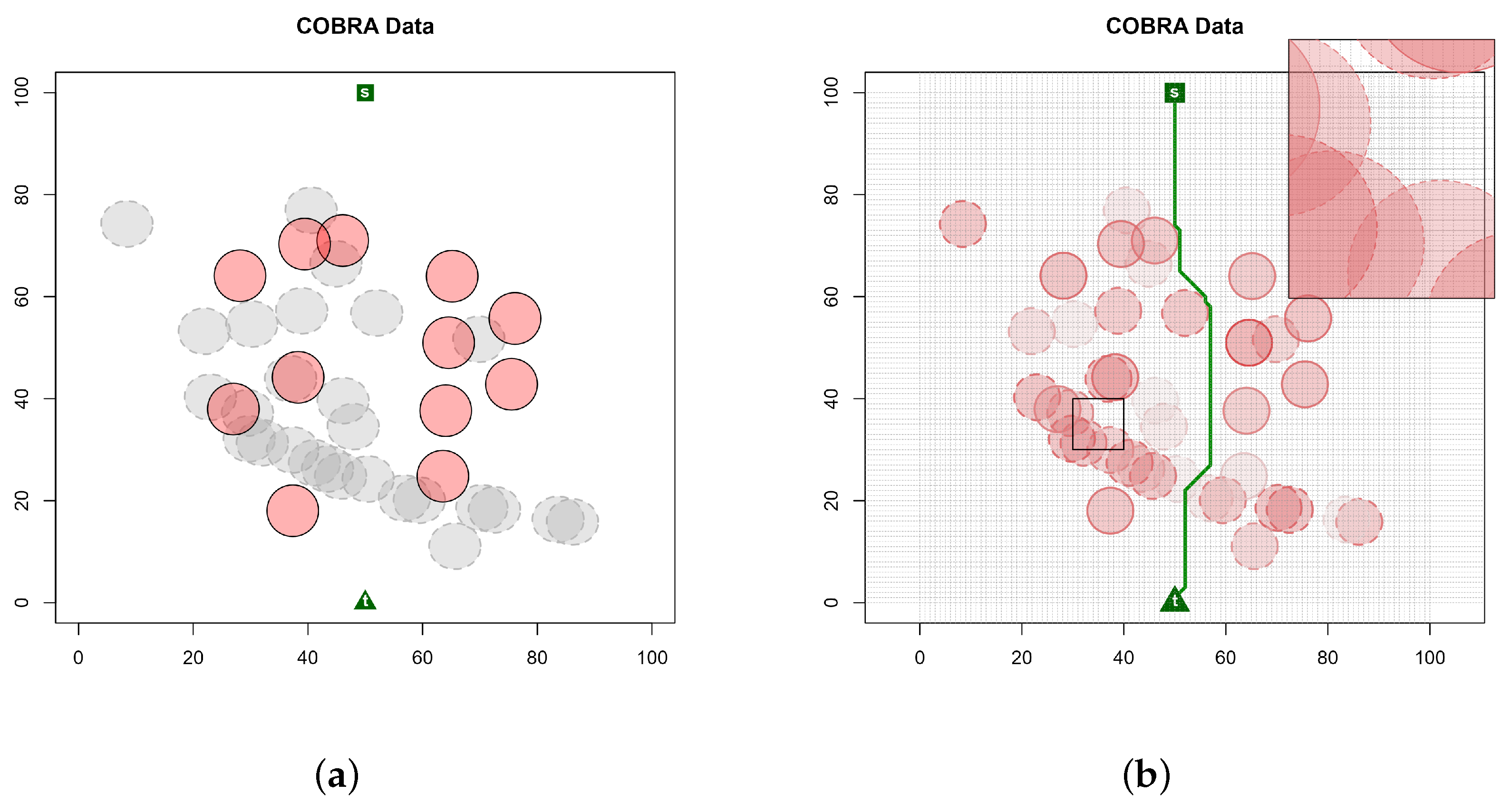
Application domains align naturally with these formulations: road networks, building layouts, and infrastructure grids lend themselves to the discrete model, while navigation in open terrain or sea is better captured by the continuous one. Figure 1 illustrates this distinction using Coastal Battlefield Reconnaissance and Analysis (COBRA) data with 12 mines and 27 false obstacles (mine-like objects) [26]. The left panel shows the original mine and clutter field, while the right panel overlays an 8-adjacency spatial grid on the same region and depicts a sample NAVA traversal path using the RD algorithm computed on the corresponding graph representation. To better illustrate the spatial grid, we zoom in on a rectangular region at the top right of the right-panel plot.

2.4. OOP as an Optimization Problem

Let $C(\pi ,\mathcal{X})$ denote the realized traversal cost from s to t on G, and recall $W(\pi ,\mathcal{X})$ as the perceived (pre-traversal) path weight based on sensor marks. Before traversal, $C(\pi ,\mathcal{X})$ and $W(\pi ,\mathcal{X})$ are distinct random variables: W anticipates cost under uncertainty, whereas C includes the actual disambiguation outcomes and their costs.

The OTP problem—continuous or discrete—can be written as

$$\begin{array}{c}\hfill \underset{\mathcal{X}}{min}\mathbf{E}\left[C(\pi ,\mathcal{X})\right]\mathrm{s}.\mathrm{t}.\mathcal{X}\subseteq {\Omega }_{\mathcal{O}},{\mathcal{X}}_{\mathcal{T}}\cap \pi =\varnothing ,\left|\mathcal{X}\right|=n,\end{array}$$

(3)

where $\mathbf{E}\left[C(\pi ,\mathcal{X})\right]$ is the expected traversal cost, ${\Omega }_{\mathcal{O}}\subset \Omega$ is the insertion window, and n the number of obstacles placed by the OPA. The OOP problem replaces min with max in (3). The weight $W(\pi ,\mathcal{X})$ depends on the spatial configuration $\mathcal{X}={\mathcal{X}}_{\mathcal{T}}\cup {\mathcal{X}}_{\mathcal{F}}$ and the associated probability marks.

Remark 1.

(Traversal Route: Path or Walk?) In the discretized setting, the NAVA may revisit vertices/edges due to re-planning after disambiguation, so the route is a walk in the graph-theoretic sense [29]. For readability and consistency with routing terminology, we still use “path” to refer to the traversed sequence, which approximates a continuous trajectory in space.

3. GIS-Based Implications and Applications

The proposed OOP framework integrates naturally with GIS-enabled spatial decision-support systems (SDSS) by linking stochastic obstacle layouts, sensor-informed uncertainty, and re-planning into standard geospatial workflows (raster surfaces, vector networks, and live sensor layers).

3.1. Urban Mobility and Traffic Resilience

Transportation agencies regularly face temporary blockages (construction, events, incidents) that disrupt routing. RD-based re-planning provides a principled way to stress-test adaptive detour strategies on partially observable street networks. Our finding that moderately regular obstacle patterns raise traversal costs complements vulnerability studies showing how dispersed link failures degrade performance [30]. The setup is directly compatible with mainstream GIS network datasets for worst-case delay analysis.

3.2. Landscape Ecology and Wildlife Corridors

In fragmented habitats, uncertain permeability (roads, fences, land-use transitions) can be modeled as probabilistic obstacles. Sensor-driven disambiguation mirrors perceptual uncertainty and pairs well with resistance surfaces and circuit-theory connectivity [31], enabling the evaluation of corridor designs under varying obstacle densities and sensing quality.

3.3. Maritime and Defense Logistics

Mine-suspected or cluttered waters mirror our coastal navigation setting. Coupling RD with acoustic/optical sensor feeds supports the estimation of worst-case transit times and the assessment of sensor placement strategies, extending risk-aware routing for autonomous surface vessels [32]. The representation aligns with standard electronic navigational charts.

3.4. Integration with GIS Platforms

The discretized domain corresponds to raster-cell adjacency, while the graph abstraction maps to polyline networks. Sensor probabilities can be stored as raster values or edge attributes, enabling what-if analyses in SDSS tools (e.g., ArcGIS ModelBuilder, QGIS Processing). Recent work on off-road routing, flood evacuation, and hex-grid navigation [8,9,12] illustrates the utility of spatially aware, risk-based routing.

By linking stochastic obstacle modeling with GIS analytics, our framework bridges theory and practice for adaptive, risk-aware routing across transportation, ecology, and defense.

In GIS, the obstacle window ${\Omega }_{\mathcal{O}}$ has direct geographical meaning (e.g., road segments subject to closure; minefields constraining shipping lanes). RD operates on the corresponding network or grid.

Dynamic settings can be handled by updating ${\Omega }_{\mathcal{O}}$ over time (e.g., shifting flood debris, time-varying closures). While full temporal modeling is beyond the scope here, our design accommodates such updates. The urban evacuation case study (Section 3) exemplifies how ${\Omega }_{\mathcal{O}}$ and RD map to an operational GIS context.

4. Methodology and Experimental Setting

4.1. Literature on Traversal Algorithms and Prior Work on Optimal Obstacle Placement

Prior work on stochastic obstacle navigation proposes several heuristic algorithms for the NAVA, including BAO [33], Simulated Risk Disambiguation (SRA) [34], Distance to Termination (DT) [35], and Reset Disambiguation (RD) [34]. Each has advantages and limitations: BAO is exhaustive but computationally demanding, DT underuses disambiguation, and SRA requires parameter tuning. RD offers a practical balance in grid-based SOS settings. These studies largely focus on traversal rather than obstacle placement.

The OOP problem has been studied in settings where an adversary seeks to maximize the traversal cost of a NAVA. Early work used grid-based formulations with random clutter and evaluated heuristic traversal under different placement strategies [11]. Subsequent research explored variants combining placement with traversal heuristics, such as RD, DT, SRA, and BAO [33,34,35], but generally relied on fixed or simplified configurations and did not systematically assess how spatial point processes shape navigability.

Our framework couples OOP with Strauss and Matérn spatial point process models to analyze how obstacle regularity, clustering, and composition affect traversal outcomes, and it pairs this with statistical modeling for rigorous inference. For the traversal baseline, RD has complexity $O\left(k·\left(\right|E|+|V|log|V\left|\right)\right)$ with Dijkstra’s algorithm, where k is the number of disambiguations. In our $101\times 101$ grids, $\left|V\right|\approx {10}^4$, $\left|E\right|\approx 8\left|V\right|$, and typical runs have $k<20$; empirically, RD completes in under one second per realization on a standard desktop.

4.2. Proposed Framework

We propose a unified framework for the OOP problem that couples (i) spatial point processes (Strauss and Matérn) for obstacle layout, (ii) stochastic sensor marks (Beta distributions), and (iii) traversal evaluation using RD. This enables systematic analysis of how spatial structure and composition of obstacles influence traversal cost. Figure 2 illustrates our empirical evaluation approach, from obstacle generation to statistical modeling of outcomes.

While prior work mainly examined specific layouts or validation scenarios, our methodological contribution is threefold. First, we integrate OOP with stochastic geometry (Strauss, Matérn) to evaluate regularity, clustering, and density effects. Second, we extend OOP to compositional settings—false-only, true-only, and mixed—capturing both deceptive clutter and physical blockage. Finally, we analyze traversal cost distributions using robust regression, random forests, and stochastic ordering to rigorously quantify and compare obstacle impacts.

4.3. Spatial Point Patterns for Obstacle Insertion

Obstacle placement is modeled using spatial point processes to assess how spatial structure affects traversal cost. We analyze two deviations from complete spatial randomness: regularity via the Strauss process and clustering via the Matérn cluster process [3,5].

For regular placement, we use $\mathrm{Strauss}(n,d,\gamma )$, where n is the number of obstacles, d the interaction distance, and $\gamma$ the inhibition parameter. A Strauss point process is a simple way to generate regular (inhibitory) layouts. It adds a soft “do-not-come-too-close” rule between points within an interaction distance d: the inhibition parameter $\gamma \in [0, 1]$ controls how strong that repulsion is ($\gamma =1$ approximately yielding complete spatial randomness—CSR; $\gamma \to 0$ approximately yielding near–hard-core spacing). In obstacle terms, Strauss produces evenly spaced mines/roadblocks that blanket a corridor with few large gaps. Greater regularity is expected to increase traversal cost through more effective corridor coverage.

For clustered placement, we use Matérn$(\kappa ,r_0,\mu )$ with parent intensity $\kappa$, cluster radius $r_0$, and mean offspring $\mu$. A Matérn cluster process produces aggregated layouts. Parent points occur sparsely (sampled from a Poisson process with intensity $\kappa$); each parent generates a Poisson number (with mean $\mu$) of offspring obstacles within a cluster radius $r_0$ (parents then discarded). The Matérn cluster process generates aggregated patterns having pockets of dense obstacles separated by relatively open areas—i.e., realistic “debris fields” or localized blockages. Clustering can leave larger obstacle-free gaps, often decreasing traversal cost.

Our experiments vary d, $\gamma$, $r_0$, and $\kappa$, as well as the true–false composition ratio $\rho$, to jointly evaluate spatial arrangement and composition.

4.4. Experimental Setting

We consider $\Omega =[0, 100]\times [0, 100]$ discretized to a $101 \times 101$ grid, yielding an 8-adjacency graph $G=(V,E)$ with unit and diagonal ($\sqrt{2}$) edges. The NAVA starts at $s=(50, 100)$ and targets $t=(50, 1)$. Obstacles are disks of radius $r=4.5$ with centers sampled from the insertion window ${\Omega }_O=[10, 90]\times [10, 90]$. This radius ensures each disk intersects multiple edges without fully blocking the corridor. To isolate spatial configuration effects, all the disks have equal size (heterogeneous radii are a natural extension).

Sensor marks follow Beta distributions: $p_F\sim \mathrm{Beta}(2, 6)$ for false obstacles and $p_T\sim \mathrm{Beta}(6, 2)$ for true obstacles. Disambiguation incurs a fixed cost $c=5$ [10,36]. Stronger discrimination can be modeled by $p_F\sim \mathrm{Beta}(a,b)$ and $p_T\sim \mathrm{Beta}(b,a)$ with $a<2$ and $b>6$.

4.5. Key Parameters in the OOP Framework

Regularity (Strauss $\gamma$) models deliberate spacing (e.g., minefields); clustering (Matérn $r_0,\kappa$) captures natural aggregation (e.g., debris); and the counts of true/false obstacles drive blockage and disambiguation burdens.

Parameter ranges span realistic regimes while maintaining feasible traversal. For Strauss: d scales with $r=4.5$ from near overlap ($d\approx r$) to wide separation ($d\gtrsim 2r$), with $\gamma$ from 0 (strong inhibition) to 1 (CSR). For Matérn: $r_0\in \{5,\dots , 50\}$ and $\kappa \in \{2,\dots , 15\}$. Sensor-accuracy effects generalize beyond the baseline Beta choices and are analyzed via stochastic ordering in Section 7.

Obstacle Placement Strategies:

• Regularity (Strauss): $\gamma \in \{0.0,0.1,\dots , 1.0\}$; $d\in \{0.5,1.0,\dots , 15.0\}$.
• Clustering (Matérn): $\mu =10$ offspring per parent; $\kappa \in \{2, 4,\dots , 12\}$; $r_0\in \{2.5, 5, 7.5, 10, 15, 25, 50\}$ (larger $r_0$ approaches uniformity).

Obstacle Composition: We simulate (i) false-only with $n_F\in \{10, 20,\dots , 100\}$, (ii) true-only with $n_T\in \{10, 20,\dots , 100\}$, and (iii) mixed with $n=n_F+n_T\in \{20,30,\dots ,100\}$ across varying ratios. In mixed settings, true obstacles drive mean cost by blocking edges; false obstacles primarily inflate variability via added disambiguations. The Supplementary File contains further experiments (30/70, 50/50, 70/30; Strauss and Matérn) that corroborate these patterns. Section 7 formalizes these trends via stochastic ordering.

Analysis Methods: Traversal cost $C(\pi ,\mathcal{X})$ and disambiguation behavior are analyzed via (i) robust linear regression to quantify spatial effects, (ii) random forest regression to identify key predictors, and (iii) zero-inflated negative binomial regression for modeling disambiguation counts. Unlike prior studies that incorporated fixed background clutter [10], our setting removes such clutter and allows both true and false obstacle placement by the OPA. This design enables a systematic exploration of how spatial structure and obstacle composition jointly impact traversal outcomes.

5. Monte Carlo Experiments and Results

We evaluated how obstacle patterns affect traversal cost via MC simulations using the RD algorithm [11]. Obstacle placement follows Strauss (regular) and Matérn (clustered) processes, with uniform placement as a baseline [37]. This tripartite division is rigorous because it captures the full spectrum of real-world scenarios, from pure decoy placement to pure obstruction to realistic mixtures of both. Additional variations for the mixed case, including different ratios of true to false obstacles and varied clustering strengths, are included in the Supplementary File. Figure 3 illustrates typical RD traversals under Strauss and Matérn obstacle placements, highlighting differences in route detours, disambiguation costs, and overall traversal length.

5.1. Obstacle Pattern: Uniformity to Regularity (Strauss) — False-Obstacle-Only Case

We evaluated the effect of increasing spatial regularity on traversal outcomes by varying the Strauss $(n,d,\gamma )$ process parameters: $\gamma$ (repulsion strength) and d (interaction distance).

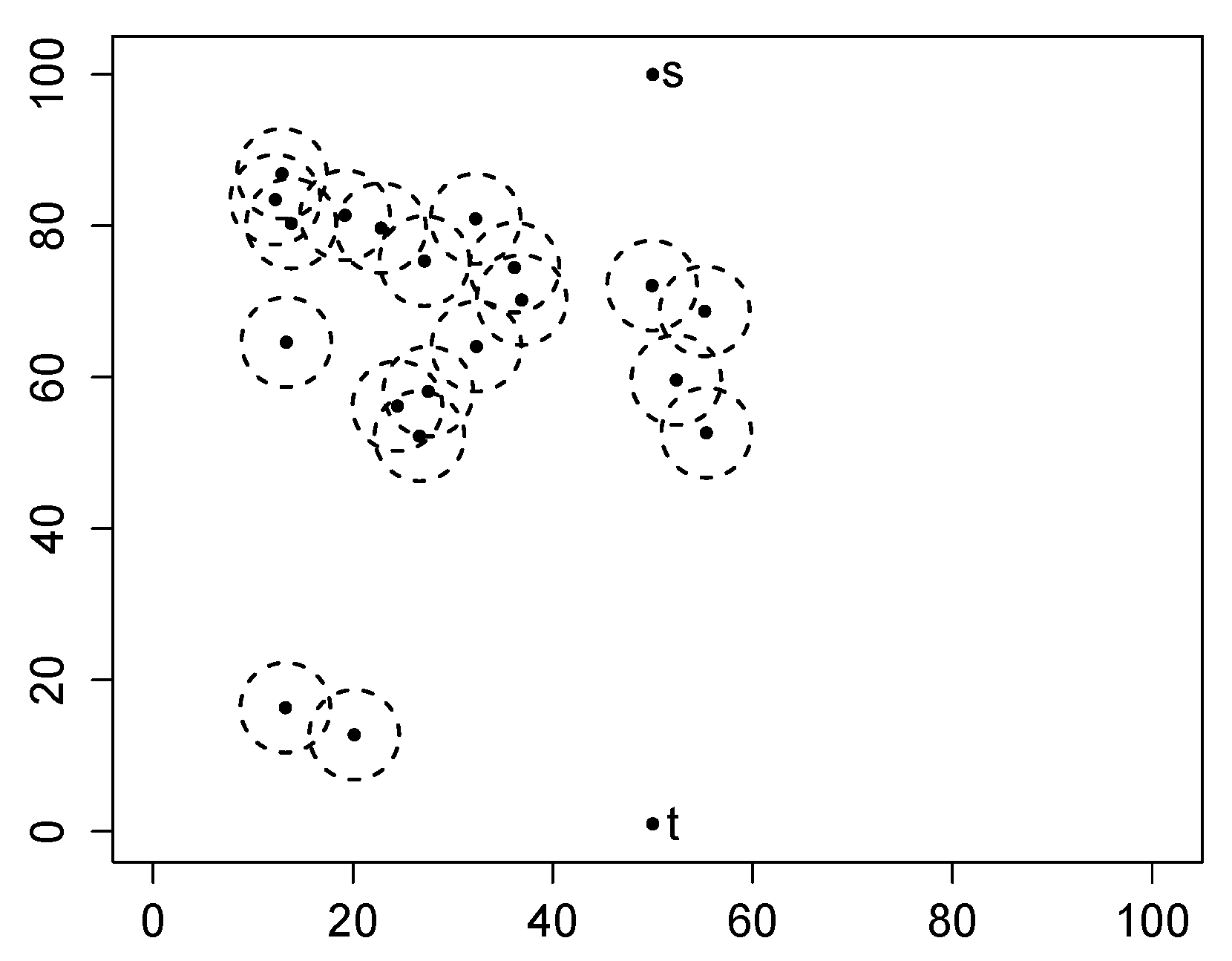
To ensure comprehensive coverage, we simulated 30 values of $\gamma$ and 22 values of d for each selected number of false obstacles $n_F\in \{10,20,\dots ,100\}$, with 100 MC replications per parameter setting. This results in $11\times 30\times 22\times 100=726,000$ total trials. For each realization, we recorded the total traversal cost C and the number of disambiguations incurred. The RD algorithm adaptively recomputes the path after each disambiguation based on updated obstacle information. A representative simulation outcome is displayed in Figure 4a.

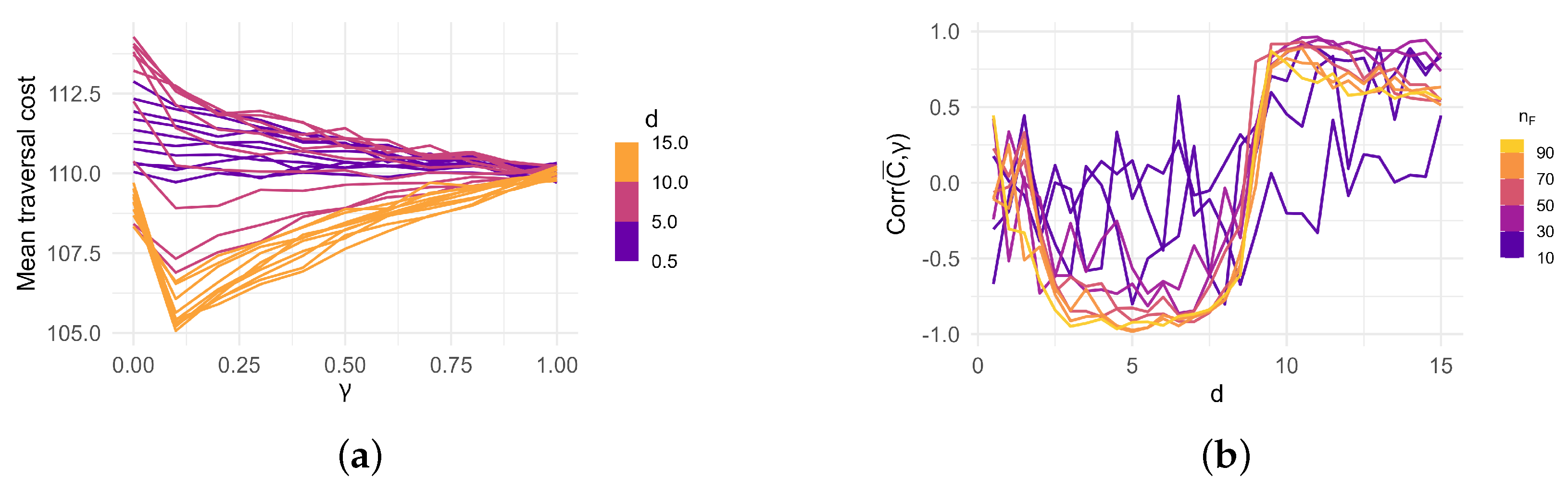
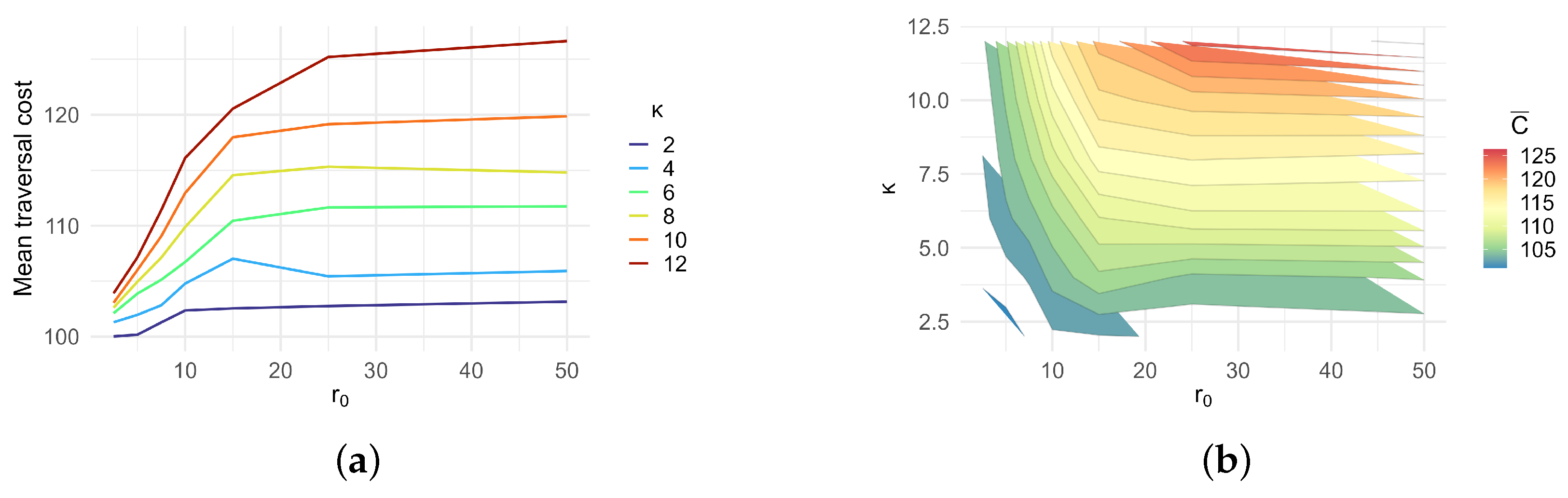
Figure 5a illustrates the mean traversal cost $\overline{C}$ as a function of the Strauss inhibition parameter $\gamma$, across various interaction distances d. The correlation between $\overline{C}$ and $\gamma$ for each d value is shown in Figure 5b.

For small d, increased regularity (i.e., decreasing $\gamma$) has little impact, as obstacles remain closely spaced and overlapping. Consequently, traversal paths do not change significantly. In contrast, for intermediate d (around $1.5r$), regularity promotes even spacing, which effectively blocks direct traversal routes and increases cost. When d exceeds $2r$, obstacles are spaced too widely to obstruct paths effectively, leading to lower traversal cost.

Figure 6 displays the mean traversal cost $\overline{C}$ as a function of d across various $\gamma$ values. A unimodal (concave-down) pattern emerges: traversal cost peaks around $d\approx 1.5r$, where obstacle spacing is most disruptive. For small d, overlapping obstacles act as a single obstruction zone, and for large d, the configuration becomes too sparse to significantly hinder navigation.

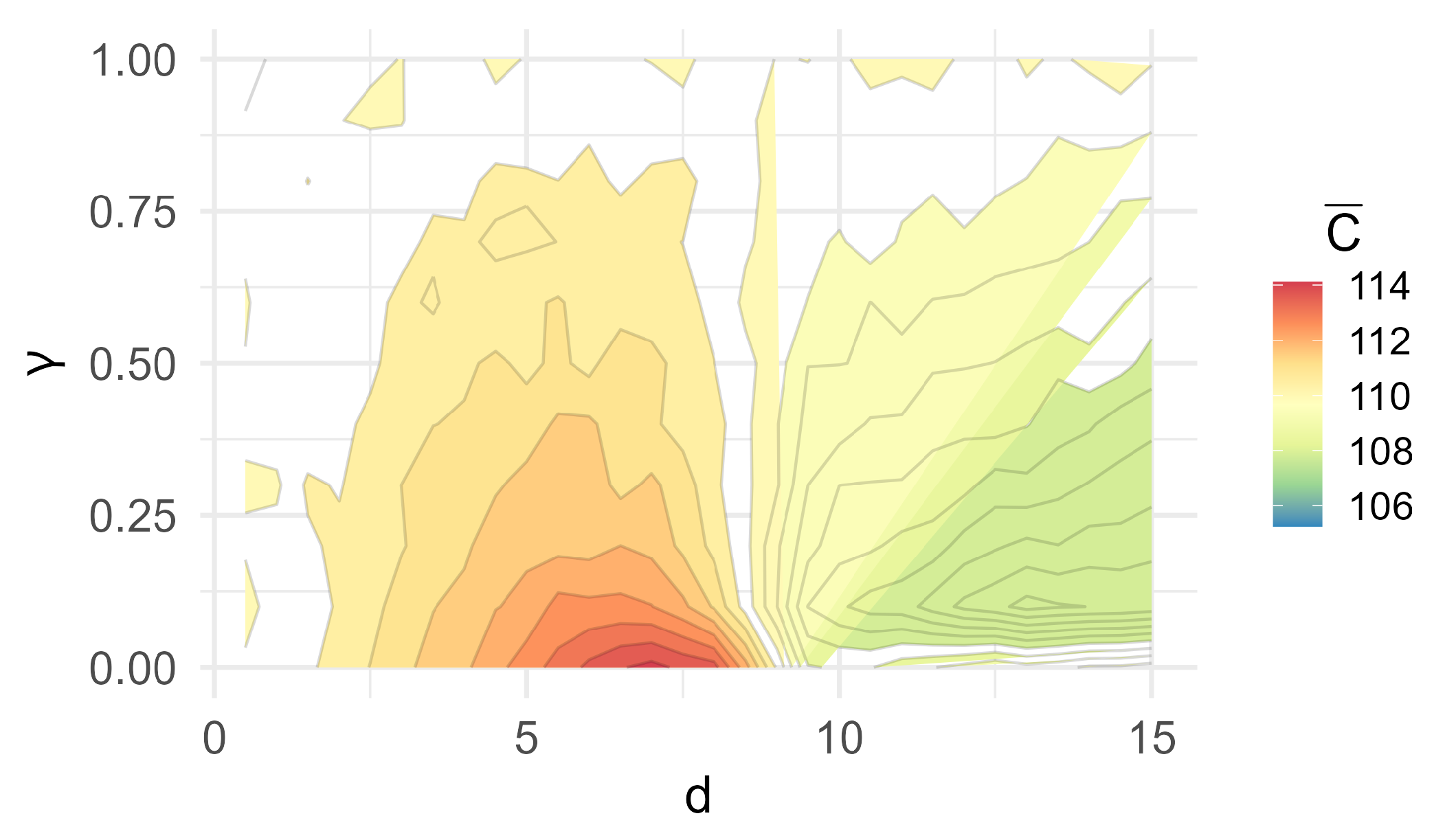
Figure 7 shows a filled contour plot of mean traversal cost $\overline{C}$ over the $\gamma$–d space. The plot confirms earlier trends: traversal cost peaks when regularity is high (small $\gamma$) and spacing is moderate ($d\approx 1.5r$). For larger d values ($\gtrsim 2r$), $\overline{C}$ becomes nearly insensitive to $\gamma$, effectively corresponding to uniform placement.

Below are our key findings for the false-obstacle-only case. To maximize traversal cost when placing false obstacles, the OPA should do the following:

• Select moderate interaction distances ($1.3r\le d\le 1.8r$).
• Use low inhibition values ($\gamma <0.1$) to induce strong regularity.
• Increase obstacle count $n_F$ to saturate the corridor.

Remark 2

(True-Obstacle-Only and Mixed-Obstacle Cases Under Regularity). We performed similar MC experiments under true-obstacle-only and mixed-obstacle cases, and below we summarize our findings. See the Supplementary File for more details.

Summary of Findings for All Obstacle Compositions Under Regularity

Below we summarize the findings for all obstacle compositions under regularity cases:

• False Obstacles: Traversal cost peaks for $d\in (6,8)$ and $\gamma <0.1$. For large d, regularity matters less, and $\gamma \approx 1$ (uniformity) can be more effective.
• True Obstacles: Higher density saturates the environment; regularity has limited added effect, but moderate d and low $\gamma$ still maximize cost.
• Mixed Obstacles: Increasing $n_T$ raises disambiguation frequency and causes more resets, significantly raising traversal cost.

5.2. Obstacle Pattern: Uniformity to Clustering (Matérn) — False-Obstacle-Only Case

In the false-obstacle-only case, we examined how clustering affects traversal cost using the Matérn process with varying parameters $\kappa$ (number of clusters), $r_0$ (cluster radius), and $\mu$ (mean obstacles per cluster). We varied $\kappa \in \{1,\dots ,10\}$, $r_0\in \{2.5,5,\dots ,25\}$, and $n_F\in \{10,20,\dots ,100\}$. Each configuration was simulated with 100 MC replications, resulting in $11\times 30\times 100=33,000$ measurements per $n_F$. A sample realization is shown in Figure 8.

Figure 9a shows how mean traversal cost $\overline{C}$ varies with $r_0$ for different $\kappa$ values. For $r_0\gtrsim 15$, $\overline{C}$ levels off, as clustering no longer meaningfully alters the path. However, for tighter clusters ($r_0\lesssim 15$), cost drops due to larger obstacle-free gaps. This effect intensifies with larger $n_F$. For fixed $r_0$, increasing $\kappa$ disperses obstacles, raising traversal cost by increasing obstruction in the navigation region.

Figure 9b indicates that traversal cost is highest at $\kappa \approx 12$ and $r_0\approx 50$, where obstacles are most spatially dispersed. To maximize traversal difficulty in the clustered setting, the OPA should do the following:

• Use a high number of clusters ($\kappa$) to spread obstacles widely.
• Select $r_0\gtrsim 15$ to avoid tight clustering and minimize wide open gaps.
• Employ a sufficiently large number of obstacles ($n_F$) to fill the region effectively.

Remark 3

(True-Obstacle-Only and Mixed-Obstacle Cases Under Clustering). We performed similar MC experiments under true-obstacle-only and mixed-obstacle cases, and below we summarize our findings. See the Supplementary File for more details.

Summary of Findings for All Obstacle Compositions Under Clustering

• False Obstacles: Widely spaced clusters with large $\kappa$ and $r_0$ hinder traversal more effectively than tight clusters.
• True Obstacles: Increased spread heightens cost further due to unavoidable disambiguation events.
• Mixed Obstacles: A greater proportion of true obstacles increases resets, compounding the traversal burden.

Table 1. Optimal Obstacle Placement strategies for increasing the traversal cost. Scenarios “False Only” and “True Only” refer to environments having only false or only true obstacles, respectively; “Mixed” includes both types.

Scenario	Regularity (Strauss Process)	Clustering (Matérn Process)
False Only	Moderate $d\in (6,8)$, Low $\gamma <0.1$	Larger $r_0$, High $\kappa$
True Only	Moderate $d\in (6,8)$, Low $\gamma <0.4$	Larger $r_0$, High $\kappa$
Mixed	Same as false obs., prefer $n_T>n_F$	Same as true obs., prefer $n_T>n_F$

summarizes optimal placement strategies (to maximize the traversal cost of the NAVA) under both Strauss and Matérn settings, across all obstacle types.

5.3. Dependence of Traversal on Obstacle Size

We conducted a traversal comparison between obstacles of fixed size and heterogeneous radii. Using the same Strauss process parameters ($\gamma =0.1, d=7$) and obstacle count (n = 50 with 30 false obstacles), we compared fixed radius, $r=4.5$, for all obstacles, against varying radii, $r\in \{3,4.5,6,7.5\}$, randomly assigned with corresponding disambiguation costs of $\{3,5,7,9\}$. The disambiguation cost is set in such a way that disambiguation is encouraged when the probability of an obstacle being true is moderate or small. As shown in Figure 10, the setting with obstacles of different radii resulted in a total traversal cost of 114.63, while the fixed-radius case led to a cost of 109.77. Although using the same number of obstacles with similar placement patterns, the radius-varying obstacles created more complex edge intersection patterns, particularly where larger obstacles blocked critical path segments. As demonstrated in previous analysis, the Strauss process proves effective at creating traversal disruption. The additional impact observed with heterogeneous obstacle sizes suggests that real-world environments having varying obstacle sizes may further increase the disruptive effects of spatial point process, which presents as a future research direction.

Remark 4.

We did not include variable obstacle size as a systematic factor in the main set of experiments or in the regression analysis. In operational obstacle placement applications, inserted obstacles are usually of uniform size, so focusing on equal-radius settings better reflects the intended deployment scenario. Moreover, keeping obstacle size fixed avoids confounding interactions with other variables of interest such as clustering, regularity, and the ratio of true to false obstacles, thereby isolating the effects of these primary drivers on traversal cost.

5.4. Regression Models and Predictor Importance

To quantify how spatial regularity parameters $(d,\gamma )$ and obstacle count $n_F$ influence traversal cost, we fit robust linear regression models to log-transformed cost data using M-estimation with Huber weights [38], implemented via rlm in the MASS package in R. We chose this modeling approach due to the right-skewness and existence of outliers in the traversal costs.

5.4.1. Robust Regression Model

We modeled the log-transformed traversal cost (C) as a second-order polynomial with interaction terms:

$$\widehat{C}={\beta }_0+{\beta }_i\mathrm{linear}\mathrm{terms}+{\beta }_j\mathrm{quadratic}\mathrm{terms}+{\beta }_k\mathrm{two}\text{-}\mathrm{way}\mathrm{interactions}.$$

(4)

In the false-obstacle-only case with Strauss regularity, the final model (after dropping the non-significant $\gamma n_F$ interaction) is

$$\widehat{C}=99.270-4.21\gamma +0.33d+0.1897n_F+1.68{\gamma }^2-0.025d^2+0.0006n_F^2+0.365\gamma d-0.0064d{n}_F.$$

(5)

The coefficients indicate the following: (i) $\gamma$ effect: decreases cost for small d, increases it for larger d; a stronger interaction parameter lowers traversal cost when obstacles are moderately spaced but raises it when they are farther apart. (ii) d effect: concave-down (unimodal); the influence of obstacle spacing on traversal cost follows a concave-down pattern, with costs peaking at an intermediate distance. (iii) $n_F$ effect: concave-up growth; increasing the number of false obstacles raises traversal cost in a concave-up manner, with the effect becoming stronger as more obstacles are added. The residual standard error improves from 4.48 to 3.78 with robust regression, confirming its effectiveness. Here are one-sentence interpretations for each case:

Similar models were fitted for the true-only and mixed-obstacle cases under both Strauss and Matérn patterns. See the Supplementary File for detailed coefficients. A summary of selected models appears in

Table 2. Summary of robust linear models for traversal cost (only significant terms are retained).

Setting	Main Effects	Quadratic Terms	Interactions
False Obstacles (Regular)	$\gamma ,d,n_F$	${\gamma }^2,d^2,n_F^2$	$\gamma d,d{n}_F$
True Obstacles (Regular)	$\gamma ,d,n_T$	${\gamma }^2,d^2,n_T^2$	$\gamma d,d{n}_T$
Mixed Obstacles (Regular)	$\gamma ,d,n_F,n_o$	${\gamma }^2,d^2,n_F^2,n_o^2$	$\gamma d,d{n}_o,\gamma n_F$
False Obstacles (Clustered)	$\kappa ,r_0$	$r_0^2$	$\kappa r_0$
True Obstacles (Clustered)	$\kappa ,r_0$	$r_0^2$	$\kappa r_0$
Mixed Obstacles (Clustered)	$\kappa ,r_0,n_F$	${\kappa }^2,r_0^2,n_F^2$	$\kappa r_0,\kappa n_F,r_0{n}_F$

.

5.4.2. Random Forest Regression

To assess the relative importance of predictors influencing traversal cost, we applied random forest (RF) regression [13] with 100 trees, implemented using the randomForest package in R. This nonparametric method complements the robust regression models by identifying nonlinear interactions and ranking predictors by their contribution to variance reduction.

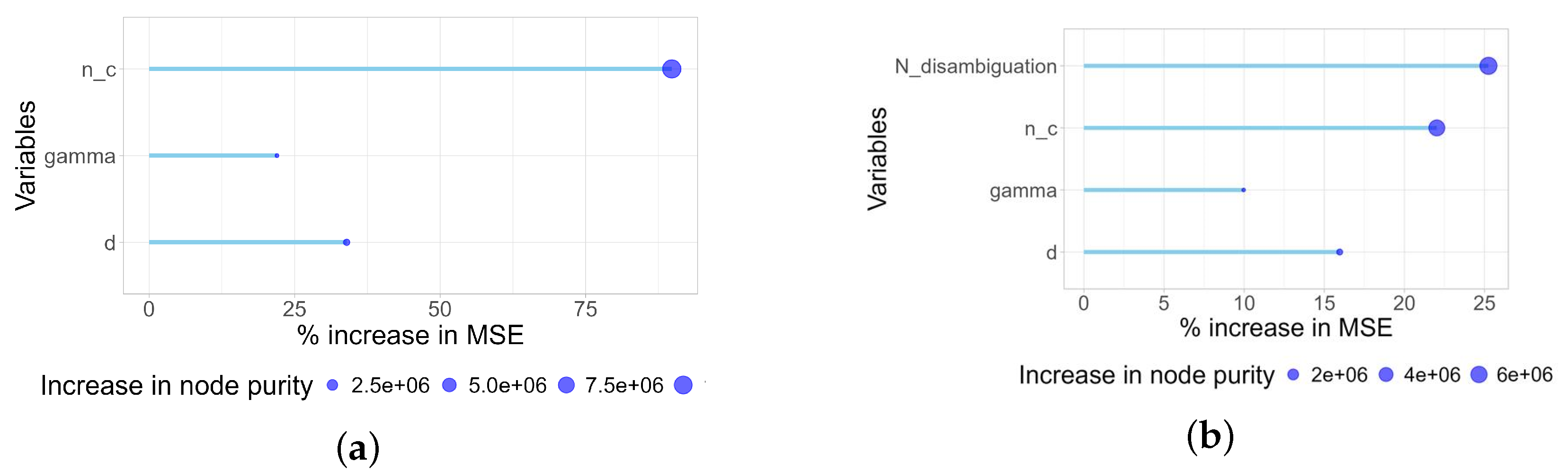
In the false-obstacle-only case with Matérn clustering, the most influential variables are $n_F$ (highest impact), $r_0$, and $\kappa$ (lowest impact). While the RF model explains 66.86% of the variance, its mean squared residual is 19.04, indicating limited predictive accuracy for exact cost values. However, it provides valuable insight into predictor influence. Figure 11a visualizes the variable importance rankings.

RF-based variable importance results for other obstacle compositions (true-only and mixed) under both Strauss and Matérn settings are qualitatively consistent. See the Supplementary File for detailed plots and model diagnostics.

Table 3. Most significant predictors ranked by RF variable importance (with decreasing importance from left to right).

Scenario	Key Predictors
False Obstacles (Regular)	$n_F,d,\gamma$
True Obstacles (Regular)	$n_T,d,\gamma$
Mixed Obstacles (Regular)	$n_o,n_F,d$
False Obstacles (Clustered)	$r_0,\kappa$
True Obstacles (Clustered)	$r_0,\kappa$
Mixed Obstacles (Clustered)	$n_F,r_0,\kappa$

summarizes the top-ranked predictors for each setting.

5.4.3. Modeling Number of Disambiguations

Disambiguations ($N_{dis}$) play a central role in traversal cost, particularly in settings with true or mixed obstacles. To better understand the factors influencing $N_{dis}$, we fit zero-inflated negative binomial (ZINB) models [14] using the zeroinfl function in R. Here, the ZINB specification is appropriate because disambiguation counts are discrete, highly overdispersed relative to a Poisson model, and include an excess of zeros corresponding to obstacle-free traversals.

In the false-obstacle-only scenario under Strauss regularity, we include $\gamma$ and d as predictors in the count model and $n_F$ in the zero-inflation model. The fitted model yields (i) $\gamma$ coefficient: $-0.062$ (higher regularity increases disambiguations), (ii) d coefficient: $-0.054$ (greater spacing reduces disambiguations), and (iii) $n_F$ in the logit model: negative effect on probability of zero disambiguations.

This indicates that regular spacing of obstacles increases disambiguation frequency, while increasing obstacle count makes disambiguation events more likely.

Similar patterns hold across other obstacle types:

• In both true-only and mixed scenarios, $N_{dis}$ decreases with $\gamma$ and d, and it increases with $n_T$ or $n_F$.
• In Matérn-clustered layouts, $r_0$ significantly affects disambiguations (larger $r_0$ reduces $N_{dis}$), while $\kappa$ shows limited influence.

See the Supplementary File for full model summaries.

5.5. Summary of Recommendations from Monte Carlo Analysis

5.5.1. Recommendations for OPA (Adversarial Obstacle Placement Perspective)

This work is written from the angle of the OPA to maximize traversal cost for the NAVA. Based on our finding, we recommend the OPA to do the following.

• Strauss Regularity: Place obstacles with high regularity (low $\gamma$) and moderate spacing ($d\in (6,8)$) to create evenly distributed barriers that blanket the corridor.
• Matérn Clustering: Favor dispersed configurations with large $r_0$ and high $\kappa$ to cover more area and reduce the chance of long, unobstructed corridors.
• Mixed Obstacles: Prioritize true obstacles over false ($n_T>n_F$) since they force resets and disambiguations, amplifying traversal cost.

5.5.2. Recommendations for NAVA (Defensive/Traversal Perspective)

Our suggestions would be different for the NAVA (to minimize its traversal cost), not necessarily the opposite of the recommendations for the OPA. The main reason is that their capabilities are different, with the NAVA having no obstacle insertion capability, while the OPA is lacking a sensor to guide its insertion schemes (or to better predict the NAVA’s traversal). Based on our findings, we recommend the NAVA to do the following.

• Strauss Regularity: When obstacle spacing is conspicuously uniform, interpret it as adversarial placement. Counter by routing toward the periphery of the insertion window, probing selectively at high-leverage obstacles, and avoiding blanket central zones.
• Matérn Clustering: Clusters often leave navigable inter-cluster corridors. Counter by scouting for these low-density seams, delaying disambiguations until bottlenecks are reached, and aligning paths along the sparse axis of elongated clusters.
• Mixed Obstacles: Early probes help infer the $n_T/n_F$ ratio. If false obstacles dominate, thread the corridor with minimal probing; if true obstacles dominate, pre-commit to wider detours with fewer but strategically placed disambiguations.

From the OPA’s side, deliberate regularity or dense clustering maximizes cost. From the NAVA’s side, diagnosing these patterns is critical: regularity ⇒ treat as adversarial and route wide; clustering ⇒ exploit inter-cluster corridors for lower-cost traversal. In practice, adversarial recognition (regular layouts) signals the need for caution and probing economy, while clustered layouts indicate exploitable corridors consistent with natural or incidental blockage.

Remark 5.

Although linear and count models are primarily used for analyzing covariate influence on traversal cost and disambiguations, they also support prediction when obstacle configurations and spatial parameters are known or estimated. For instance, the spatstat.model package in R [37] provides ppm for Strauss and clusterfit for Matérn processes. These tools allow practitioners to calibrate models from real spatial data and forecast traversal cost under plausible obstacle arrangements. These aspects are deferred for future work.

6. Illustrative Geospatial Case Study

To illustrate the real-world relevance of our framework, we constructed a street network for downtown Auburn, Alabama, centered at Toomer’s Corner—the symbolic intersection of College Street and Magnolia Avenue and one of the busiest pedestrian and vehicle corridors in the city. This setting provides a natural testbed: disruptions along the main streets of Auburn can immediately affect both everyday traffic and emergency evacuation.

Obstacles were modeled as disk-shaped disruption zones positioned directly on the street network. These zones represent realistic short-term blockages such as construction sites, accident scenes, or barricades during football game weekends. Two spatial patterns were imposed: (i) a regular pattern approximating a Strauss process, mimicking evenly spaced work sites or coordinated closures, and (ii) a clustered pattern generated by a Matérn process, reflecting incidents concentrated in a few downtown blocks. Each disruption was designated either as a true obstacle (completely blocking traffic) or a false obstacle (appearing disruptive but passable), with sensor readings providing uncertain information on their status.

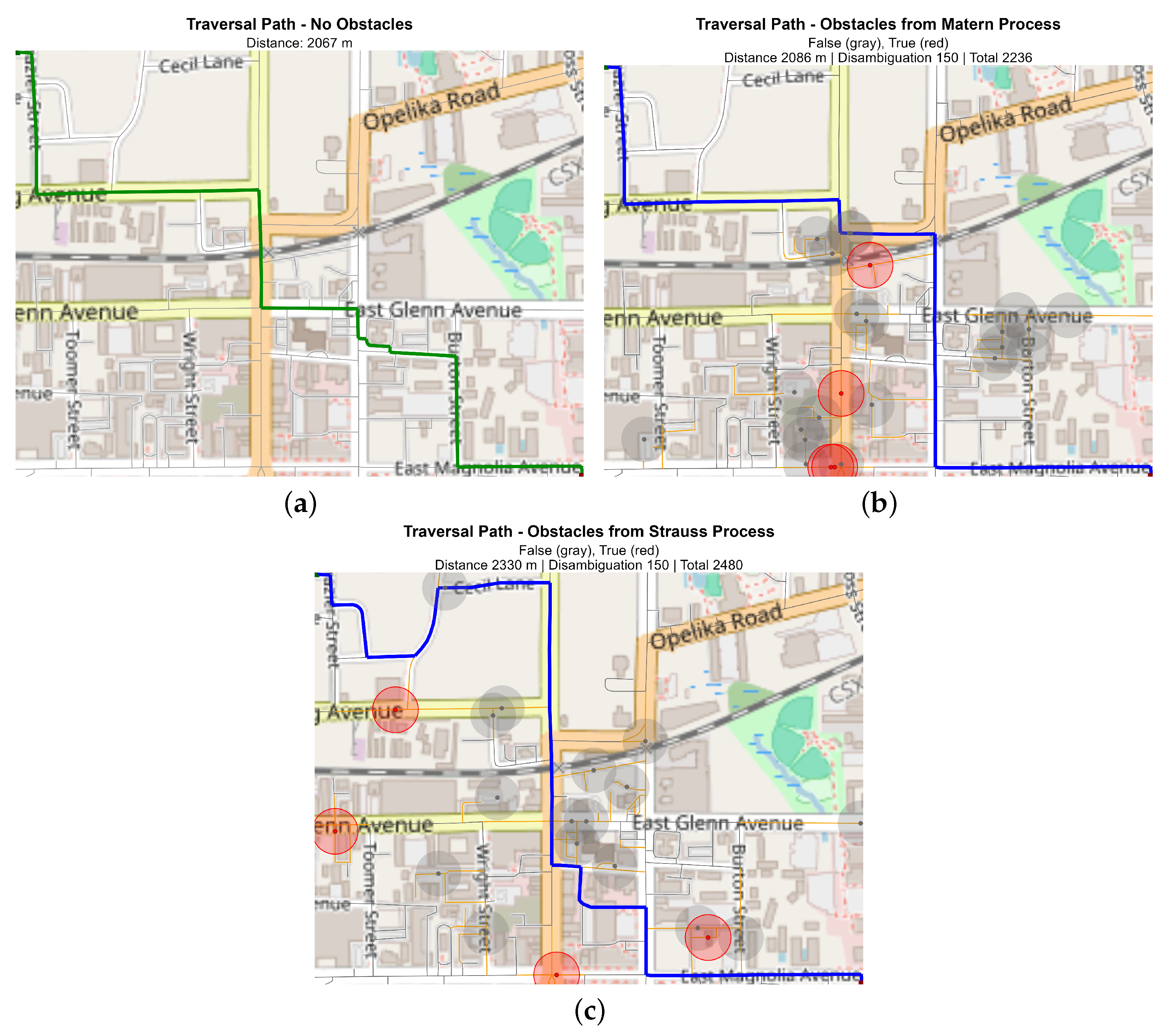
Figure 12 compares RD-based traversal paths from the northwestern corner of downtown Auburn to the southeastern side along the main street network. In the baseline case (no disruptions), the optimal route measures 2067 m. When clustered obstacles are introduced, traversal length increases to 2236 m, as detours occur only near localized blockages but unobstructed corridors remain open. By contrast, regular spacing of obstacles forces repeated detours and resets, raising the total cost to 2480 m.

This case demonstrates the practical implications of obstacle spatial patterns: for Auburn drivers or emergency responders, recognizing whether blockages are scattered in a regular sequence (as might occur with coordinated construction projects) or concentrated in clusters (as in storm debris or localized accidents) fundamentally changes the best routing strategy. From a planning perspective, this insight highlights how adversarial or coordinated disruptions can be more damaging than naturally clustered ones, even when the total number of obstacles is the same.

7. Stochastic Ordering of Traversal Costs

Beyond average outcomes, it is often important to compare entire distributions of traversal cost across different obstacle settings. Stochastic ordering provides a rigorous way to formalize such comparisons.

The main findings can be summarized as follows (see the Supplementary File for the technical details and proofs of these results):

• Effect of Obstacle Composition: Traversal costs are stochastically smallest when only false obstacles are present, largest when only true obstacles are present, and intermediate in mixed settings. This ordering holds not just in expectation but also for medians and other quantiles. This means that routes are systematically easier to find in environments filled only with false obstacles, while environments dominated by true obstacles are the most restrictive. Mixed settings fall in between, reflecting the balance between passable clutter and impassable barriers.
• Effect of Obstacle Ratio: As the proportion of true obstacles increases while holding the total number of obstacles fixed, the distribution of traversal costs systematically shifts upward. As the share of true obstacles increases, the likelihood of longer or more costly routes rises. In practice, this highlights how even small increases in hazardous objects can shift the overall navigation risk profile.
• Effect of Sensor Quality: Higher-fidelity sensors, which more reliably distinguish true from false obstacles, lead to stochastically smaller traversal costs than lower-fidelity sensors. Better sensors that more reliably separate false from true obstacles reduce the burden of unnecessary detours. In applied navigation systems, this underscores the value of investing in high-fidelity sensing technologies.
• Effect of Spatial Structure: Obstacle arrangement strongly shapes both the magnitude and variability of costs. Clustered patterns often allow wider unobstructed corridors and hence lower average cost but higher variability; regular patterns create consistent blocking and yield higher mean costs with lower variability; uniform patterns fall in between. The way obstacles are arranged influences both the average cost and the variability of travel. Clustering can sometimes leave wide corridors open, regular spacing tends to block paths more uniformly, and random arrangements fall in between these extremes.
• Implications for the NAVA: Although exact dominance results for realized traversal costs remain conjectural under the RD algorithm, both theoretical and empirical evidence consistently support the ordering: false-only configurations yield the lowest traversal costs, followed by mixed, and true-only with the highest. This clearly indicates that navigation is easiest in false-only fields, harder in mixed settings, and hardest in true-obstacle environments. This provides a clear risk ranking of environments for practical planning.

Overall, these results provide a rigorous foundation for understanding how obstacle type, composition, sensor fidelity, and spatial arrangement jointly determine the distribution of navigation outcomes.

8. Discussion and Conclusions

This study develops a unified geospatial framework to analyze how different obstacle patterns influence navigation efficiency under uncertainty. By simulating adversarially placed obstacles using spatial point processes and evaluating pathfinding outcomes, we demonstrate that the spatial arrangement of obstacles systematically influences traversal costs.

Monte Carlo experiments across false-only, true-only, and mixed environments show that regular placements generally create the greatest obstruction, while clustered arrangements often leave wider corridors and lower average costs. These effects are modulated by spatial parameters such as the strength of repulsion in Strauss models or the cluster radius in Matérn processes. Regression and machine learning models highlight the number of obstacles, spacing, and repulsion strength as dominant predictors of cost, while the number of disambiguations emerges as a reliable proxy for traversal burden. Stochastic ordering results further confirm that traversal is consistently easier in false-only environments, hardest in true-only settings, and intermediate in mixed fields.

From an applied perspective, the results highlight that obstacle placement patterns strongly influence real-world disruption. Regularly spaced true obstacles tend to force repeated detours and thus yield higher traversal costs, whereas clustered obstacles may leave broader unobstructed corridors and be less damaging, even when the total number of disruptions is the same. Such insights can inform planning for urban evacuation, flood response, maritime minefields, and off-road mobility under debris or landslides.

Future research should investigate deterministic or semi-deterministic placement strategies, adaptive learning agents, and extensions to continuous or three-dimensional spaces, and there should be a more systematic investigation of obstacle size and its interaction with other factors. These directions would enhance the framework’s relevance for geospatial intelligence, autonomous navigation, and environmental planning.