Automatic Vehicle Trajectory Behavior Classification Based on Unmanned Aerial Vehicle-Derived Trajectories Using Machine Learning Techniques
Abstract
1. Introduction
1.1. Motivation
1.2. Related Works
1.3. Need for Further Study and Research Purpose
1.4. Objectives
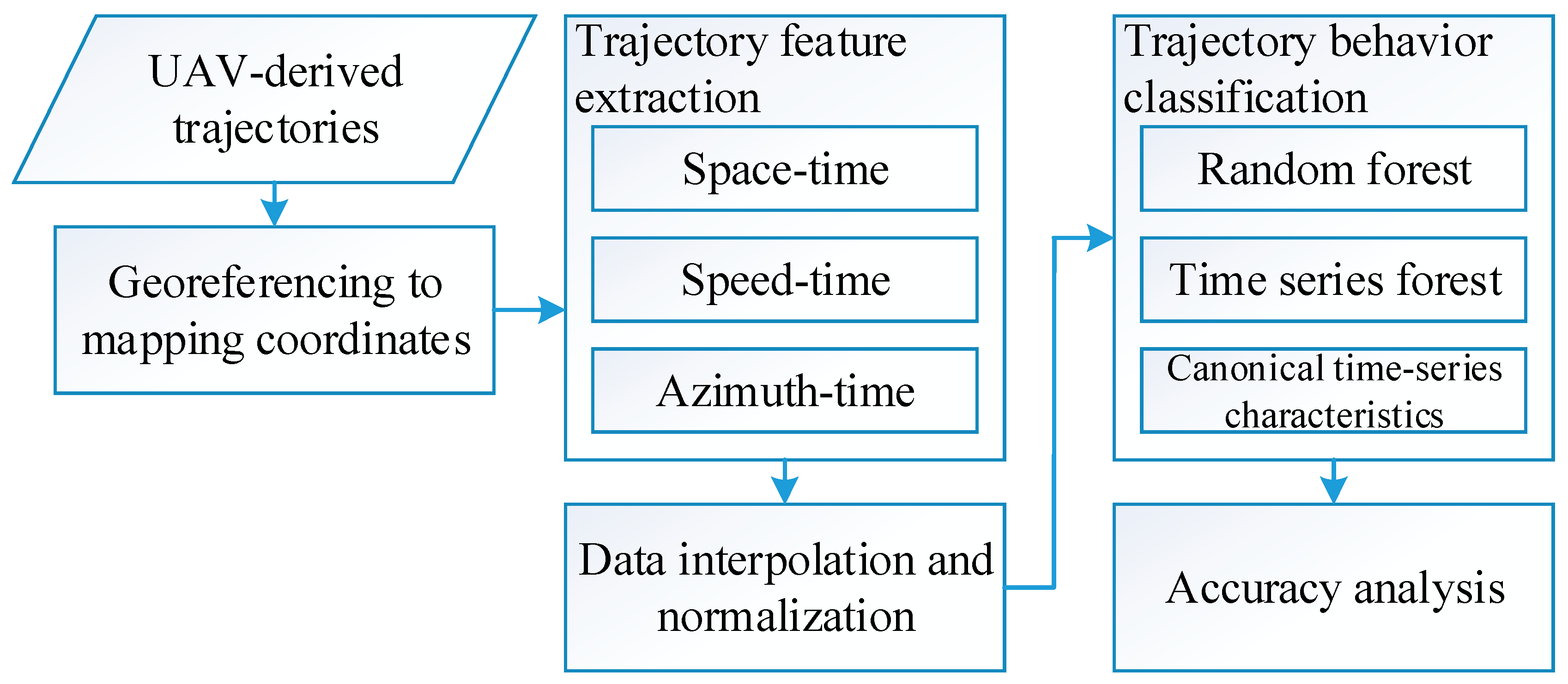
2. Methodology
2.1. Trajectory Georeferencing
2.2. Trajectory Feature Extraction
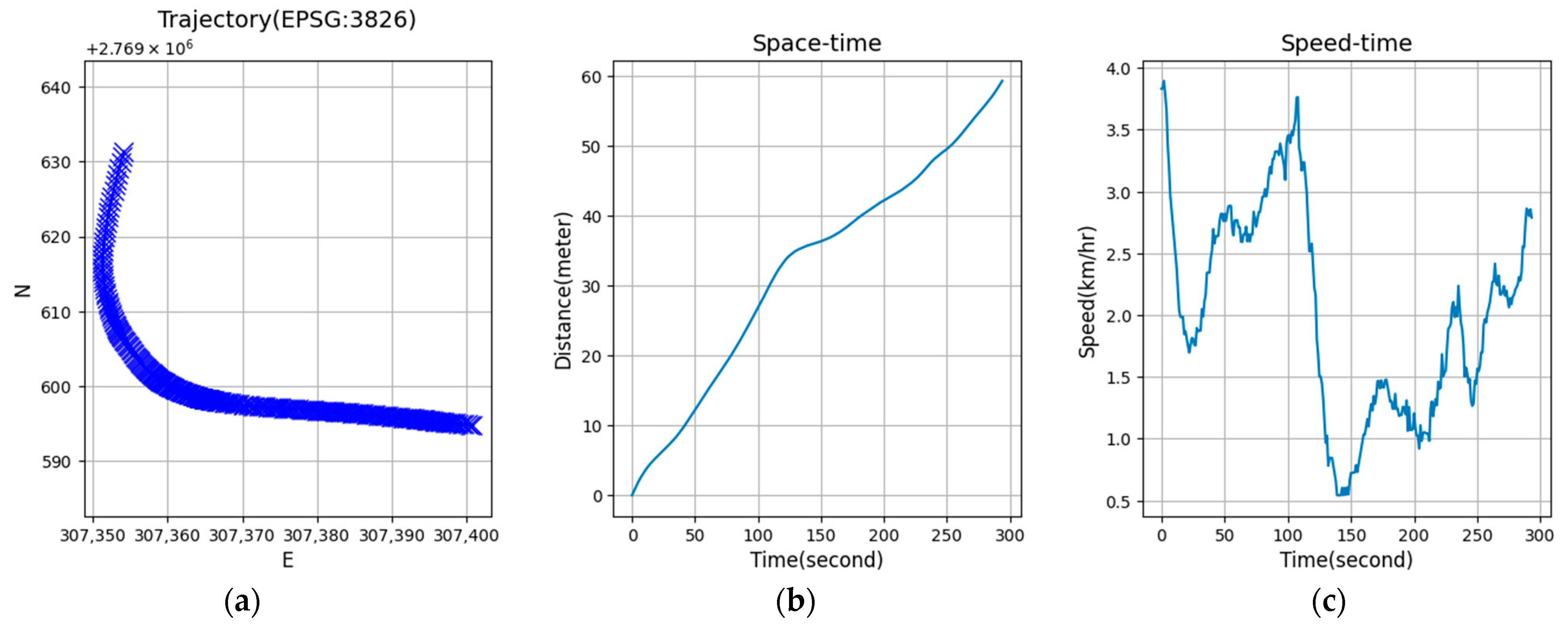
2.2.1. Generation of Space–Time Sequences
2.2.2. Generation of Speed–Time Sequences
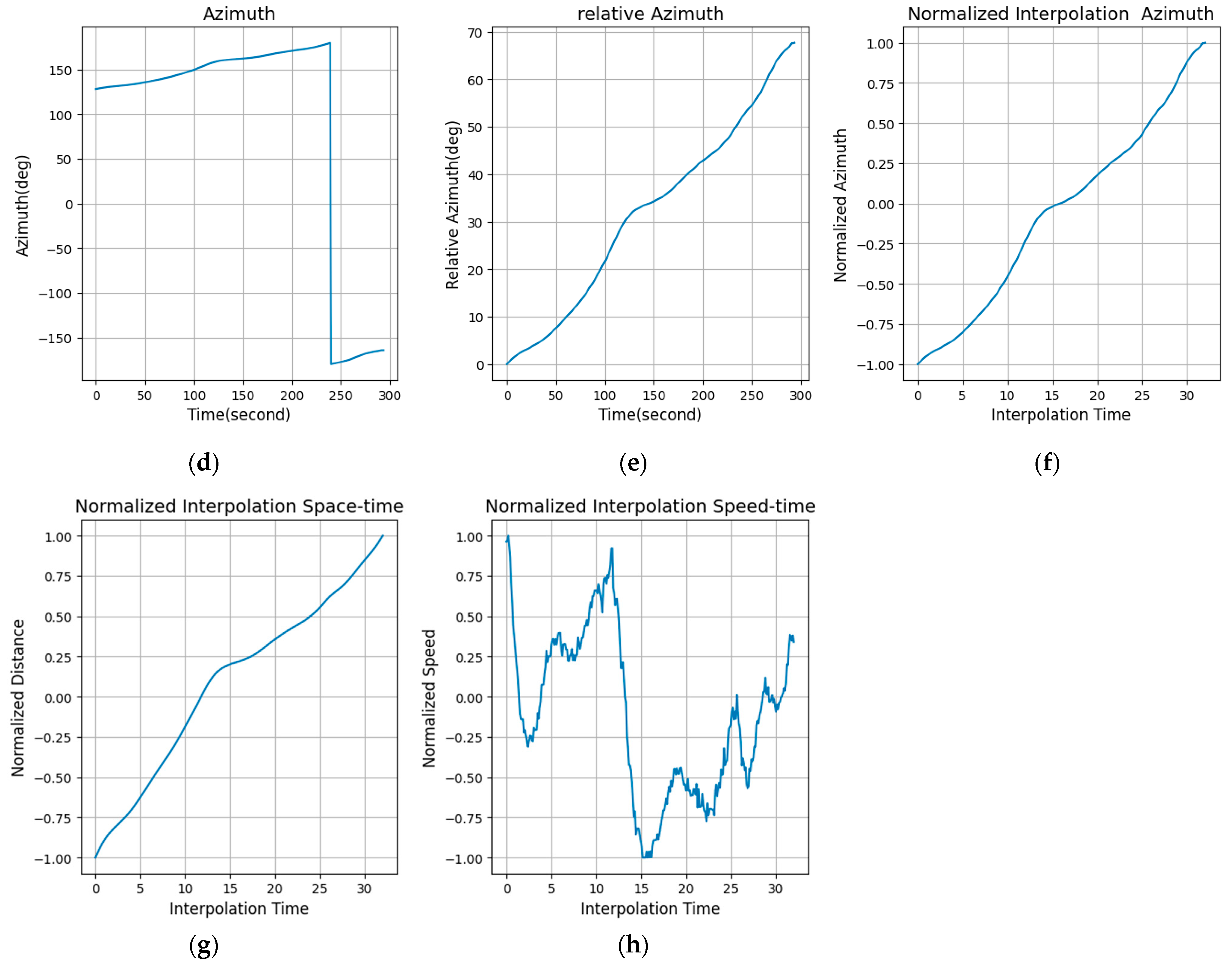
2.2.3. Generation of Azimuth–Time Sequences
2.3. Interpolation and Normalization
2.4. Trajectory Behavior Classification
2.4.1. Types of Trajectory Behaviors
2.4.2. Classifier for Trajectory Behaviors
2.4.3. Accuracy Indices
3. Experimental Results
3.1. Dataset
3.2. Georeferencing
3.3. Trajectory Behavior Datasets and Model Training
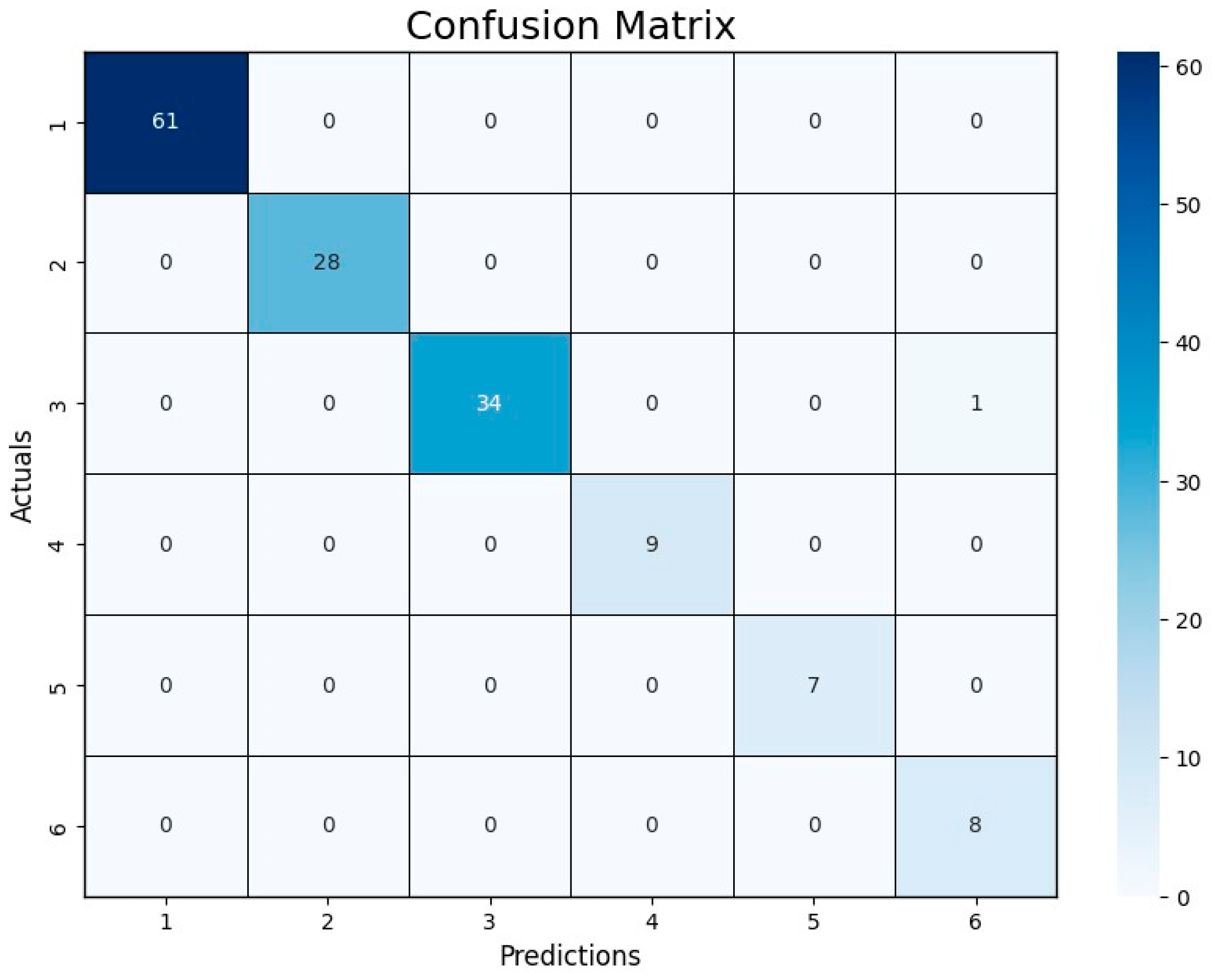
3.3.1. Evaluation of Test Data
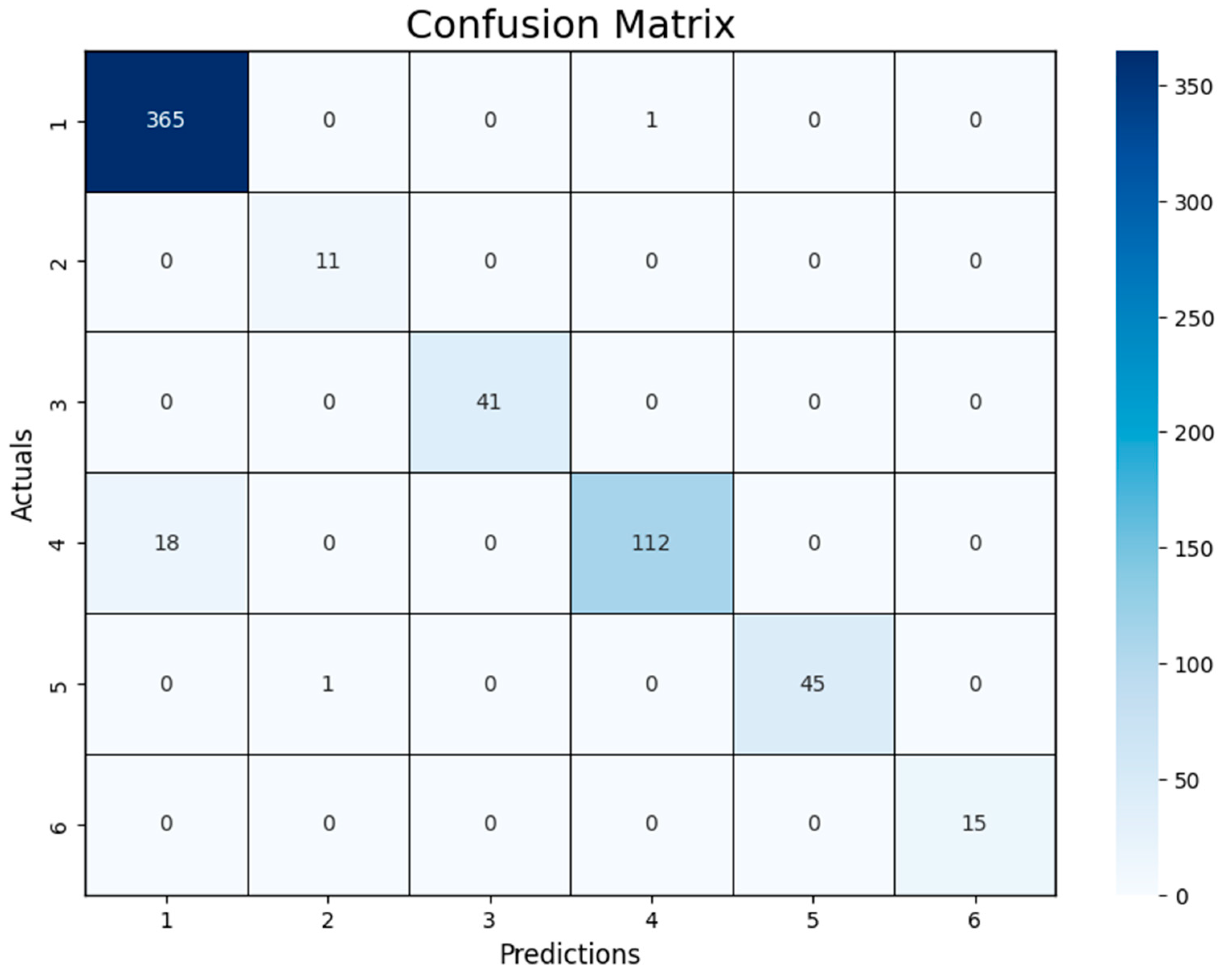
3.3.2. Evaluation of Similar Intersections
3.3.3. Evaluation of Dissimilar Intersections
3.3.4. Comparison of Different Sequences
3.3.5. Summary
4. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, H.; Chen, X.; Yu, M.; Uradziński, M.; Cheng, L. The usefulness of sensor fusion for unmanned aerial vehicle indoor positioning. Int. J. Intell. Unmanned Syst. 2024, 12, 1–18. [Google Scholar] [CrossRef]
- Yang, X. Unmanned visual localization based on satellite and image fusion. J. Phys. Conf. Ser. 2019, 1187, 042026. [Google Scholar] [CrossRef]
- Battiston, A.; Sharf, I.; Nahon, M. Attitude estimation for collision recovery of a quadcopter unmanned aerial vehicle. Int. J. Robot. Res. 2019, 38, 1286–1306. [Google Scholar] [CrossRef]
- Lee, H.; Yoon, J.; Jang, M.S.; Park, K.J. A robot operating system framework for secure UAV communications. Sensors 2021, 21, 1369. [Google Scholar] [CrossRef] [PubMed]
- Li, Y. Short-term prediction of motorway travel time using ANPR and loop data. J. Forecast. 2008, 27, 507–517. [Google Scholar] [CrossRef]
- Kong, Q.J.; Li, Z.; Chen, Y.; Liu, Y. An approach to urban traffic state estimation by fusing multisource information. IEEE Trans. Intell. Transp. Syst. 2009, 10, 499–511. [Google Scholar] [CrossRef]
- Kurniawan, J.; Syahra, S.G.; Dewa, C.K. Traffic congestion detection: Learning from CCTV monitoring images using convolutional neural network. Procedia Comput. Sci. 2018, 144, 291–297. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, C.; Du, B.; Zhang, L. Density Map-based vehicle counting in remote sensing images with limited resolution. ISPRS J. Photogramm. Remote Sens. 2022, 189, 201–217. [Google Scholar] [CrossRef]
- Barmpounakis, E.; Geroliminis, N. On the new era of urban traffic monitoring with massive drone data: The pNEUMA large-scale field experiment. Transp. Res. Part C Emerg. Technol. 2020, 111, 50–71. [Google Scholar] [CrossRef]
- Guido, G.; Gallelli, V.; Rogano, D.; Vitale, A. Evaluating the accuracy of vehicle tracking data obtained from Unmanned Aerial Vehicles. Int. J. Transp. Sci. Technol. 2016, 5, 136–151. [Google Scholar] [CrossRef]
- Rajagede, R.A.; Dewa, C.K. Recognizing Arabic letter utterance using convolutional neural network. In Proceedings of the 2017 18th IEEE/ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD), Kanazawa, Japan, 26–28 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 181–186. [Google Scholar]
- Berghaus, M.; Lamberty, S.; Ehlers, J.; Kalló, E.; Oeser, M. Vehicle trajectory dataset from drone videos including off-ramp and congested traffic–Analysis of data quality, traffic flow, and accident risk. Commun. Transp. Res. 2024, 4, 100133. [Google Scholar] [CrossRef]
- Xu, Z.; Yuan, J.; Yu, L.; Wang, G.; Zhu, M. Machine Learning-Based Traffic Flow Prediction and Intelligent Traffic Management. Int. J. Comput. Sci. Inf. Technol. 2024, 2, 18–27. [Google Scholar] [CrossRef]
- Ke, R.; Li, Z.; Tang, J.; Pan, Z.; Wang, Y. Real-time traffic flow parameter estimation from UAV video based on ensemble classifier and optical flow. IEEE Trans. Intell. Transp. Syst. 2018, 20, 54–64. [Google Scholar] [CrossRef]
- Biswas, D.; Su, H.; Wang, C.; Stevanovic, A. Speed estimation of multiple moving objects from a moving UAV platform. ISPRS Int. J. Geo-Inf. 2019, 8, 259. [Google Scholar] [CrossRef]
- Ke, R.; Feng, S.; Cui, Z.; Wang, Y. Advanced framework for microscopic and lane-level macroscopic traffic parameters estimation from UAV video. IET Intell. Transp. Syst. 2020, 14, 724–734. [Google Scholar] [CrossRef]
- Khan, M.A.; Ectors, W.; Bellemans, T.; Janssens, D.; Wets, G. Unmanned aerial vehicle-based traffic analysis: A case study for shockwave identification and flow parameters estimation at signalized intersections. Remote Sens. 2018, 10, 458. [Google Scholar] [CrossRef]
- Kaufmann, S.; Kerner, B.S.; Rehborn, H.; Koller, M.; Klenov, S.L. Aerial observations of moving synchronized flow patterns in over-saturated city traffic. Transp. Res. Part C Emerg. Technol. 2018, 86, 393–406. [Google Scholar] [CrossRef]
- Liu, P.; Kurt, A.; Özgüner, Ü. Trajectory prediction of a lane changing vehicle based on driver behavior estimation and classification. In Proceedings of the 17th international IEEE conference on intelligent transportation systems (ITSC), Qingdao, China, 8–11 October 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 942–947. [Google Scholar]
- Zhang, M.; Fu, R.; Morris, D.D.; Wang, C. A framework for turning behavior classification at intersections using 3D LIDAR. IEEE Trans. Veh. Technol. 2019, 68, 7431–7442. [Google Scholar] [CrossRef]
- Chen, S.; Xue, Q.; Zhao, X.; Xing, Y.; Lu, J.J. Risky driving behavior recognition based on vehicle trajectory. Int. J. Environ. Res. Public Health 2021, 18, 12373. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, C.; Li, Z.; Wang, R.; Bo, C.; Sotelo, M.A.; Xu, Y. UB-LSTM: A trajectory prediction method combined with vehicle behavior recognition. J. Adv. Transp. 2020, 2020, 8859689. [Google Scholar] [CrossRef]
- Zhang, H.; Fu, R. An Ensemble Learning–Online Semi-Supervised Approach for Vehicle Behavior Recognition. IEEE Trans. Intell. Transp. Syst. 2021, 23, 10610–10626. [Google Scholar] [CrossRef]
- Saeed, W.; Saleh, M.S.; Gull, M.N.; Raza, H.; Saeed, R.; Shehzadi, T. Geometric features and traffic dynamic analysis on 4-leg intersections. Int. Rev. Appl. Sci. Eng. 2024, 15, 171–188. [Google Scholar] [CrossRef]
- Razali, H.; Mordan, T.; Alahi, A. Pedestrian intention prediction: A convolutional bottom-up multi-task approach. Transp. Res. Part C Emerg. Technol. 2021, 130, 103259. [Google Scholar] [CrossRef]
- Zhou, Y.; Tan, G.; Zhong, R.; Li, Y.; Gou, C. PIT: Progressive interaction transformer for pedestrian crossing intention prediction. IEEE Trans. Intell. Transp. Syst. 2023, 24, 14213–14225. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Deng, H.; Runger, G.; Tuv, E.; Vladimir, M. A time series forest for classification and feature extraction. Inf. Sci. 2013, 239, 142–153. [Google Scholar] [CrossRef]
- Lubba, C.H.; Sethi, S.S.; Knaute, P.; Schultz, S.R.; Fulcher, B.D.; Jones, N.S. CATCH22: CAnonical Time-series CHaracteristics: Selected through highly comparative time-series analysis. Data Min. Knowl. Discov. 2019, 33, 1821–1852. [Google Scholar] [CrossRef]
- Su, C.W.; Wong, W.K.I.; Chang, K.K.; Yeh, T.H.; Kung, C.C.; Huang, M.C.; Wen, C.S. Pedestrian And Vehicle Trajectory Extraction Based on Aerial Images. Transp. Plan. J. 2020, 49, 235–258. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Zhang, T.; Song, W.; Fu, M.; Yang, Y.; Wang, M. Vehicle motion prediction at intersections based on the turning intention and prior trajectories model. IEEE/CAA J. Autom. Sin. 2021, 8, 1657–1666. [Google Scholar] [CrossRef]
- Huang, R.; Zhuo, G.; Xiong, L.; Lu, S.; Tian, W. A Review of Deep Learning-Based Vehicle Motion Prediction for Autonomous Driving. Sustainability 2023, 15, 14716. [Google Scholar] [CrossRef]




| Intersection A | Intersection B | Intersection C | |
|---|---|---|---|
| Test area | Songren and Xinyi roads intersection | Civic Boulevard and Xiangyang roads intersection | Guangfu North and Jiankang roads intersection |
| Duration (min:sec) | 17:17 | 11:46 | 13:01 |
| Number of extracted trajectories | 738 | 609 | 446 |
| Number of Control Points | RMSE E (m) | RMSE N (m) | |
|---|---|---|---|
| Intersection A | 7 | 0.110 | 0.151 |
| Intersection B | 7 | 0.641 | 0.344 |
| Intersection C | 7 | 0.092 | 0.094 |
| Training and Test Data (Intersection A) | |||||||
| Categories | 1 Go Straight | 2 Turn Left | 3 Turn Right | 4 Stop and Go Straight | 5 Stop and Turn Left | 6 Stop and Turn Right | Total |
| Training (80%) | 256 | 107 | 128 | 32 | 33 | 34 | 590 |
| Testing (20%) | 61 | 28 | 35 | 9 | 7 | 8 | 148 |
| Total | 317 | 135 | 163 | 41 | 40 | 42 | 738 |
| Independent test data (Intersections B and C) | |||||||
| Intersection B | 366 | 11 | 41 | 130 | 46 | 15 | 609 |
| Intersection C | 235 | 42 | 61 | 53 | 36 | 19 | 446 |
| Total | 601 | 53 | 102 | 183 | 82 | 39 | 1061 |
| Classifier | Dimensions for Space–Time | Dimensions for Azimuth–Time | Dimensions for Azimuth–Time and Speed–Time |
|---|---|---|---|
| RF | 32 × 590 | 32 × 590 | 64 × 590 |
| TSF | (6 × 3) × 590 | (6 × 3) × 590 | (8 × 3) × 590 |
| Catch22 | 22 × 590 | 22 × 590 | 22 × 590 |
| RF | TSF | Catch22 | ||
|---|---|---|---|---|
| Space–Time | Accuracy | 70.95 | 70.27 | 70.27 |
| Precision | 71.36 | 64.55 | 64.31 | |
| Recall | 68.92 | 62.83 | 65.56 | |
| F1 score | 68.37 | 62.32 | 64.15 | |
| Azimuth–Time | Accuracy | 97.30 | 97.79 | 99.32 |
| Precision | 97.37 | 96.40 | 98.15 | |
| Recall | 93.97 | 97.20 | 99.52 | |
| F1 score | 95.04 | 96.54 | 98.78 | |
| Integrated sequences (azimuth– and speed–time) | Accuracy | 99.32 | 98.65 | 97.97 |
| Precision | 98.14 | 96.67 | 96.18 | |
| Recall | 99.52 | 99.05 | 97.20 | |
| F1 score | 98.78 | 97.66 | 96.44 |
| Class | Accuracy | Precision | Recall | F1 Score | |
|---|---|---|---|---|---|
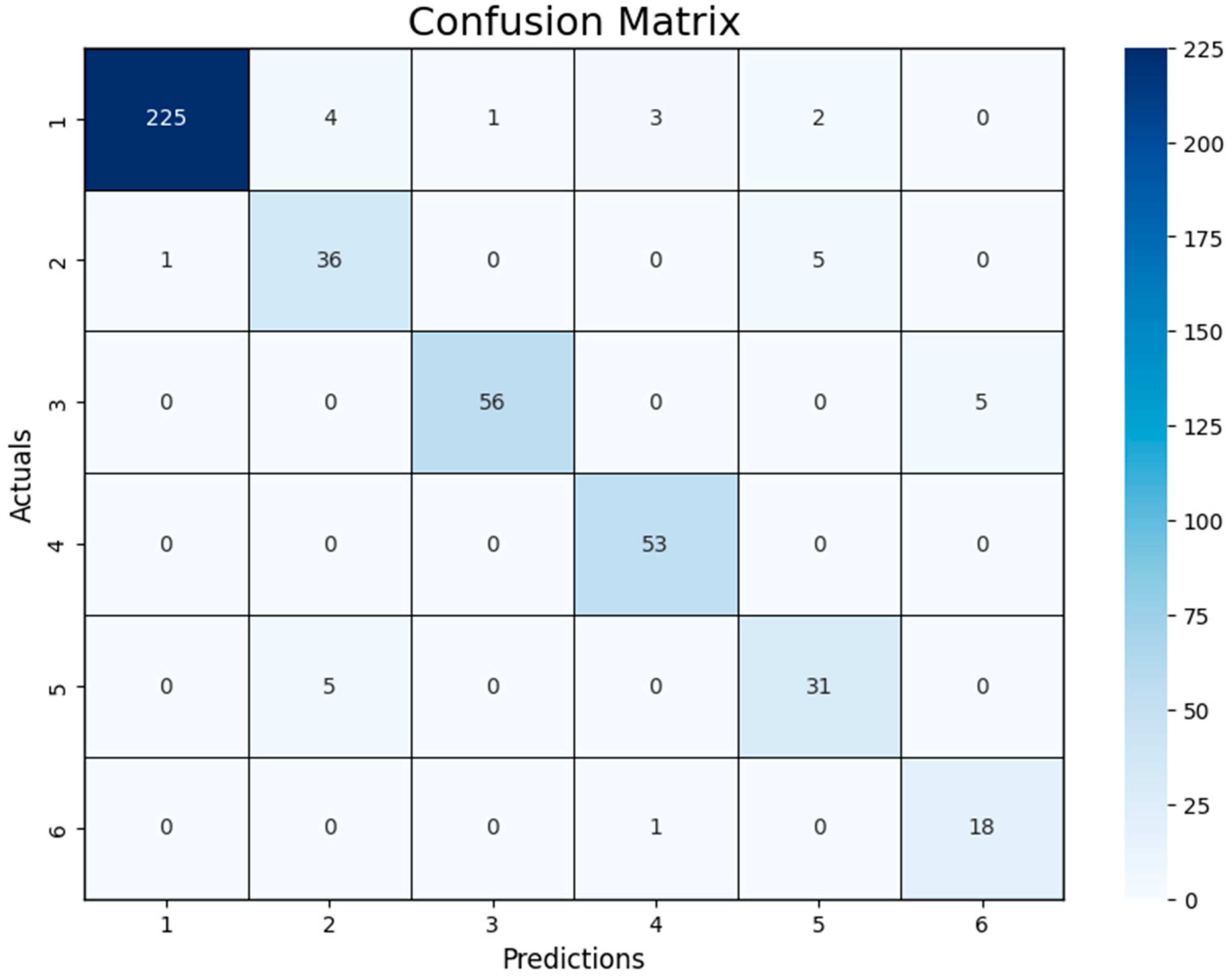
| 1 | Go Straight | 100.00 | 100.00 | 100.00 | 100.00 |
| 2 | Turn Left | 100.00 | 100.00 | 100.00 | 100.00 |
| 3 | Turn Right | 99.32 | 100.00 | 97.14 | 98.55 |
| 4 | Stop and Go Straight | 100.00 | 100.00 | 100.00 | 100.00 |
| 5 | Stop and Turn Left | 100.00 | 100.00 | 100.00 | 100.00 |
| 6 | Stop and Turn Right | 99.32 | 88.89 | 100.00 | 94.12 |
| RF | TSF | Catch22 | ||
|---|---|---|---|---|
| Space–Time | Accuracy | 52.71 | 55.99 | 51.56 |
| Precision | 37.50 | 38.05 | 34.68 | |
| Recall | 40.58 | 37.13 | 37.61 | |
| F1 score | 30.31 | 31.08 | 28.21 | |
| Azimuth–Time | Accuracy | 79.97 | 89.00 | 91.30 |
| Precision | 73.07 | 87.78 | 92.30 | |
| Recall | 74.71 | 89.31 | 92.42 | |
| F1 score | 68.26 | 87.15 | 91.90 | |
| Integrated sequences (azimuth– and speed–time) | Accuracy | 92.61 | 96.72 | 90.15 |
| Precision | 83.97 | 97.68 | 82.60 | |
| Recall | 86.93 | 97.28 | 88.36 | |
| F1 score | 83.83 | 97.37 | 82.85 |
| Class | Accuracy | Precision | Recall | F1 Score | |
|---|---|---|---|---|---|
| 1 | Go Straight | 96.88 | 95.30 | 99.73 | 97.46 |
| 2 | Turn Left | 99.83 | 91.67 | 100.00 | 95.65 |
| 3 | Turn Right | 100.00 | 100.00 | 100.00 | 100.00 |
| 4 | Stop and Go Straight | 96.88 | 99.12 | 86.15 | 92.18 |
| 5 | Stop and Turn Left | 99.84 | 100.00 | 97.83 | 98.90 |
| 6 | Stop and Turn Right | 100.00 | 100.00 | 100.00 | 100.00 |
| RF | TSF | Catch22 | ||
|---|---|---|---|---|
| Space–Time | Accuracy | 57.40 | 56.28 | 52.91 |
| Precision | 39.00 | 39.00 | 37.30 | |
| Recall | 38.75 | 36.78 | 34.84 | |
| F1 score | 37.89 | 37.19 | 35.02 | |
| Azimuth–Time | Accuracy | 55.16 | 56.95 | 85.87 |
| Precision | 63.11 | 68.73 | 79.50 | |
| Recall | 65.40 | 68.56 | 85.54 | |
| F1 score | 56.00 | 58.03 | 81.13 | |
| Integrated sequences (azimuth– and speed–time) | Accuracy | 88.12 | 93.95 | 87.22 |
| Precision | 80.21 | 88.44 | 80.57 | |
| Recall | 81.68 | 92.35 | 84.88 | |
| F1 score | 79.78 | 90.19 | 82.30 |
| Class | Accuracy | Precision | Recall | F1 Score | |
|---|---|---|---|---|---|
| 1 | Go Straight | 97.53 | 99.56 | 95.74 | 97.61 |
| 2 | Turn Left | 96.64 | 80.00 | 85.71 | 82.76 |
| 3 | Turn Right | 98.65 | 98.25 | 91.80 | 94.92 |
| 4 | Stop and Go Straight | 99.10 | 92.98 | 100.00 | 96.36 |
| 5 | Stop and Turn Left | 97.31 | 81.58 | 86.11 | 83.78 |
| 6 | Stop and Turn Right | 98.65 | 78.26 | 94.74 | 85.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teo, T.-A.; Chang, M.-J.; Wen, T.-H. Automatic Vehicle Trajectory Behavior Classification Based on Unmanned Aerial Vehicle-Derived Trajectories Using Machine Learning Techniques. ISPRS Int. J. Geo-Inf. 2024, 13, 264. https://doi.org/10.3390/ijgi13080264
Teo T-A, Chang M-J, Wen T-H. Automatic Vehicle Trajectory Behavior Classification Based on Unmanned Aerial Vehicle-Derived Trajectories Using Machine Learning Techniques. ISPRS International Journal of Geo-Information. 2024; 13(8):264. https://doi.org/10.3390/ijgi13080264
Chicago/Turabian StyleTeo, Tee-Ann, Min-Jhen Chang, and Tsung-Han Wen. 2024. "Automatic Vehicle Trajectory Behavior Classification Based on Unmanned Aerial Vehicle-Derived Trajectories Using Machine Learning Techniques" ISPRS International Journal of Geo-Information 13, no. 8: 264. https://doi.org/10.3390/ijgi13080264
APA StyleTeo, T.-A., Chang, M.-J., & Wen, T.-H. (2024). Automatic Vehicle Trajectory Behavior Classification Based on Unmanned Aerial Vehicle-Derived Trajectories Using Machine Learning Techniques. ISPRS International Journal of Geo-Information, 13(8), 264. https://doi.org/10.3390/ijgi13080264





