Abstract
Geographically weighted regression (GWR) is a classical method for estimating nonstationary relationships. Notwithstanding the great potential of the model for processing geographic data, its large-scale application still faces the challenge of high computational costs. To solve this problem, we proposed a computationally efficient GWR method, called K-Nearest Neighbors Geographically weighted regression (KNN-GWR). First, it utilizes a k-dimensional tree (KD tree) strategy to improve the speed of finding observations around the regression points, and, to optimize the memory complexity, the submatrices of neighbors are extracted from the matrix of the sample dataset. Next, the optimal bandwidth is found by referring to the spatial clustering relationship explained by K-means. Finally, the performance and accuracy of the proposed KNN-GWR method was evaluated using a simulated dataset and a Chinese house price dataset. The results demonstrated that the KNN-GWR method achieved computational efficiency thousands of times faster than existing GWR algorithms, while ensuring accuracy and significantly improving memory optimization. To the best of our knowledge, this method was able to run hundreds of thousands or millions of data on a standard computer, which can inform improvement in the efficiency of local regression models.
1. Introduction
Owing to the influence of geographical location, changes in the relationship or structure between variables is an important issue in spatial data analysis. The geographically weighted regression (GWR) model, originally developed by Fotheringham and Brunsdon [1,2], is a common tool for exploring spatial non-smoothness. Currently, GWR is widely used in a variety of fields, such as geology [3,4,5], ecology [6,7], house price modeling [8,9,10,11], epidemiology [12,13,14], and environmental science [7,15]. The popular GWR packages are Spgwr [16], MGWR (PySAL) [17], GWmodel [18], and FastGWR [19]. With the expansion of demand for geographic information technology and resources in various industries [20,21], geographic data with high spatial and temporal resolution have seen explosive growth while promoting innovation in GIS methods [22,23,24,25,26]. Many studies have explicitly reported the computational limitations of GWR when oriented to large-scale geographic data [19,27] in order to fully utilize the geographical information.
Each regression point in GWR is regressed individually based on the distance matrix, and the optimal bandwidth selection is performed before that, which makes it computationally intensive and requires a large amount of memory usage. However, the application of GWR to extract information from large-scale geographic data is difficult. Harris estimated that it would take two or more weeks to complete the experiment using the Spgwr package for a dataset of one hundred thousand points (and five predictor variables) [28]. Li pointed out that the maximum number of records that can be handled by the current open-source GWR software is approximately fifteen thousand observations on a standard desktop [19]. In Yu’s experiment [29], random sampling of a house price dataset was forced to reduce the calculation cost owing to the computational demand of building a GWR model for the 68,906 house price dataset; therefore, 3437 data were selected for the GWR calculation. Although this method addresses the problem of computational volume, it can lead to incomplete exploitation of data information. Feuillet provided a method to deal with a large sample dataset by building GWR sub-models [30]. Wang proposed an improved method based on a computational unified device architecture (CUDA) parallel architecture that can handle GWR corrections for millions of data points [31]. Tasyurek reverse-nearest-neighbor geographically weighted regression (RNN-GWR) only calculates updated data points when dealing with frequently updated datasets, which can result in a higher computational efficiency with guaranteed calculation results [32]. Although many efforts have been made, there is still a lack of an effective GWR algorithm that can analyze large numbers of geographic data in a limited timeframe. Currently, data sets with millions of observations are becoming increasingly common. During the analysis of the GWR regression process, we found that for each regression point, a certain distance (bandwidth) radius range of observation points is analyzed, and therefore observations outside of this range are not considered in the calculation. Additionally, the current optimal bandwidth search range is typically global, and reducing unnecessary calculations can alleviate the computational burden of GWR. Thus, implementing new improvements to the GWR algorithm are necessary to address computational bottlenecks, enable its application in extremely large datasets, and fully exploit data information.
Currently, the nearest-neighbor indexing method demonstrates better performance in the computational optimization of some models, with the k-dimensional tree (KD tree) being the most commonly used. Meenakshi suggested a new index structure KD tree with a linked list (k-dLst tree) for retrieving spatial records with duplicate keys [33]. To improve the computationally expensive state of performing repeated distance evaluations in the search space, a special tree-based structure (called a KD tree) was used to speed up the nearest-neighbor search [34]. Chi-Ren Shyu developed a web server (named ProteinDBS) for the life science community to search for similar protein tertiary structures in real time, which returned search results in hierarchical order from a database of over 46,000 chains in a few seconds and showed considerable accuracy [35]. Böhm performed a range search by indexing K-Nearest-Neighbor join queries [36]. Muja proposed the Fast Library for Approximate Nearest Neighbors (FLANN) library, which reduced the time for nearest-neighbor search by an order of magnitude [37,38]. The FLANN library has been applied in many studies to improve computational efficiency [37,39]. The advantages of nearest-neighbor indexing for optimal computation have been demonstrated in these studies.
When dealing with large amounts of data, clustering methods can help to better understand the distribution patterns and structure of the data, thus revealing hidden information in the data [40,41]. K-means, a widely-used clustering algorithm, partitions a dataset into K clusters and assigns each data point to the nearest cluster. This method has been extensively implemented to analyze data in various domains [40,42]. Macqueen argued that spatial clustering uses spatial location and relationships as feature terms to discover spatial clustering relationships [43,44]. Li used K-means clustering to analyze the impact of building environmental factors on the variation of rail ridership in the study area and proposed differentiated planning guidance for different regions [45]. Hernández employed the K-means clustering algorithm to identify distinct clusters of tourism types within large geographic areas [46]. Deng applied a combination approach of geographically weighted regression and K-means clustering to partition the study area into distinct regions and devise regional policies to mitigate PM2.5 concentrations [47]. The aforementioned studies all indicate that K-means clustering has significant advantages in discovering the spatial distribution of geographic data.
The main objective of this study is to develop a method that can quickly calibrate GWR to overcome the challenges of processing large-scale geographic data. This paper contributes to the previous literature as follows. (1) Using a K-D tree to accelerate the speed of searching for observation points around the regression point. In the GWR model, searching for neighboring points usually requires traversing the entire dataset, leading to significant time consumption as the dataset size increases. Therefore, this paper attempts to incorporate the KD tree into the GWR model to take advantage of its fast search capabilities to quickly identification of surrounding observation points in each local regression process. (2) Transforming the large matrix into a small matrix in the regression process. When using the Bi-square kernel function to calculate the weight matrix, the full sample matrix can cause significant memory and time consumption. Therefore, the matrices of independent variables, dependent variables, and weight matrices involved in the regression are transformed into corresponding small matrices according to the bandwidth. (3) Optimizing the search range of optimal bandwidth. The optimal bandwidth in GWR is extracted in the process of global traversal, which is time-consuming. This may be caused by considering only the local scale of operation of the model represented by the bandwidth and ignoring the spatial relationships implied by the bandwidth at local spatial locations. Therefore, this paper attempts to use K-means to cluster the geographic location data and refer to the obtained clustering results to limit the search range of the optimal bandwidth. Finally, this paper incorporates the KD tree index and K-means clustering into the GWR model, restructuring the matrices of independent variables, dependent variables and weight matrices involved in the calculation, and proposes a new model called KNN-GWR. The potential of using KNN-GWR models for geographically weighted regression on large-scale geographic data was explored in this paper, using simulated data and a dataset of house prices in selected regions of China.
2. Method
2.1. Geographically Weighted Regression
GWR is used as a local fitting technique, and its regression coefficient varies with the geographical location. The mathematical expression is as follows:
where represent the coordinates of the point in space, denotes the intercept value, and is the spatial variation coefficient of the independent variable. , is the response variable at location , is the predictor variable, and is the error term. is the size of the sample dataset and is the number of independent variables. The GWR calibration in matrix form is given by:
where is a ) matrix of the independent variables, is a matrix of the response variable, and the matrix of and can be calculated, respectively, by:
And
where is a space weight matrix and is expressed as:
where is an n × n diagonal matrix. It is calculated using a specified kernel function and bandwidth (). For example, the adaptive bi-square weighting function is as follows:
where represents the spatial distance between points i and j. represents the adaptive bandwidth, and means that the number of neighbors around regression point i is constant, but the distance is variable.
Where the coefficients of the model can be expressed in matrix form:
To calibrate the GWR model, a cross-validation (CV) approach is typically used to iterate the bandwidth. In other words, the optimal bandwidth is selected by minimizing the following CV scores:
In general, the traversal of ranges from one to n. Because each regression point in the GWR does not participate in its own local regression calculation, . When , the operation scale of the GWR model is global, so .
2.2. Geographically Weighted Regression with K-Nearest Neighbors
To speed up the computation and optimize the storage of the weight matrix in the GWR, the KD tree was adopted to find the observation points around the regression point. In this manner, hundreds of thousands or even millions of calculations are filtered. Thus, the large-scale regression problem can be transformed into an acceptable calc value. This method allows GWR to run hundreds of thousands or even millions of data records on an ordinary computer. The flow of the algorithm is illustrated in Figure 1.
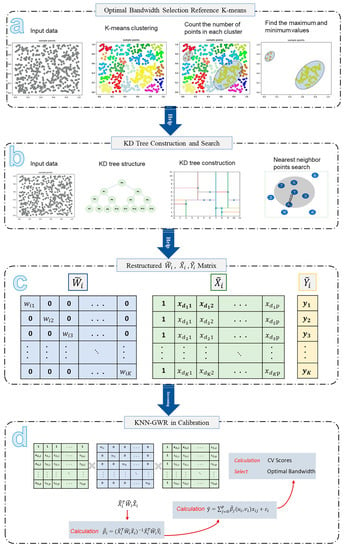
Figure 1.
Flow chart of K-nearest neighbor geographically weighted regression. (a) Optimal bandwidth selection reference k-means. (b) KD Tree construction and search. (c) Restructured , , . (d) KNN-GWR in calibration.
The algorithm can be divided into four parts. Part a: Optimal bandwidth selection reference K-means. K-means clustering is performed on the incoming data to explain the spatial relationships in the dataset. Part b: KD tree construction and search. Establishing the KD tree for the incoming data and searching the observation points around the regression point according to the GWR bandwidth optimization rule based on the results obtained in Part a. Part c: Restructured , , . The weight matrix , the independent variable matrix and the dependent variable matrix of the GWR regression process are reconstructed according to the requirements of each regression point based on the findings in Part b. The reconstructed results are , , and , respectively. Part d: KNN-GWR in calibration. Running the model based on the results of Part c and outputting the results of the optimal bandwidth run to complete the model diagnosis.
2.2.1. Optimal Bandwidth Selection Reference K-Means
We counted the optimal bandwidth in some studies, which was usually within a smaller range [19,48,49]; the specific range of values depended on the research field, specific dataset, the researcher’s experience and judgment, and in general was usually ≤200. However, GWR usually searches for the optimal bandwidth on a global scale, which is less necessary in local regression. Murakami pointed out the use of rank reduction and pre-compression to eliminate the effect of data size in the regression of large datasets [49]. Geographically adjacent observation points were considered to have highly similar characteristics; therefore, in the KNN-GWR, they should be grouped into the same category or group as much as possible when performing geographic analysis. In this study, K-means clustering was utilized to analyze the latitude and longitude coordinates of geographic data, thereby facilitating a more comprehensive examination of the distribution patterns and spatial relationships of the data. For K-means clustering of big datasets, a set of values is defined and referred to as KC values, where the optimal number of clusters will be generated from this set of KC values, with . Using the heuristic approach, the square root value of half the data size is [50,51,52], where is obtained by the following formula:
where n denotes the number of observation points. and are the results of moving up or down by one number. and are the results of moving up or down by two different numbers.
The sum of squared errors was used to calculate the clustering error of the sample to select the optimal KC value [53,54].
The formula is as follows.
where is the g-th cluster, s is a sample point in , and is the center of .
The pseudocode of the Determine Optimal Bandwidth Range algorithm is given in Algorithm 1. The clusters obtained by the K-means clustering method are labeled as , respectively. The number of observation points in each cluster was counted using the Num() function to represent the cluster size. For example, Num() represents the number of observation points in Cluster . The Num() function helps find the largest and smallest clusters, denoted as and . and represent the upper and lower limits of the spatial distribution of all observation points based on spatial location features. The cross-validation (CV) method was chosen to determine the optimal bandwidth. The formula is as follows.
| Algorithm 1: Optimal Bandwidth Selection Reference K-means |
|
2.2.2. KD Tree Construction and Search
Using the bi-square kernel function in GWR, the surrounding observations need to be found to participate in the calculation during the local regression of regression point i. For two-dimensional geographic data, traditional linear search methods involve brute-force computation of the distances between all pairs of points in the dataset. Assuming a sample size of n, the time complexity of this method is . Since there is no adjacency between point i and point (5, 6, 7, 8, 9) in the limit range of R, as shown in Figure 2. Therefore, the distance calculation between point i and point (5, 6, 7, 8, 9) is not necessary. Further, by reducing the number of visited nodes and the corresponding distance calculation, the speed of finding surrounding points can be improved. In this study, a KD tree was created for all regression points based on spatial coordinates in order to effectively filter invalid calculations when searching for observations around regression points.
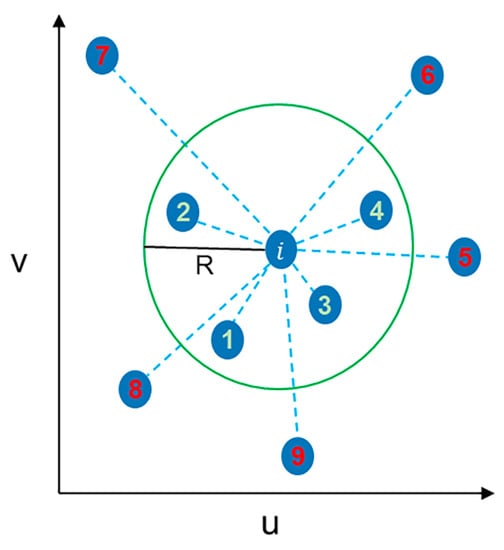
Figure 2.
An example of finding observations within a certain range around the regression point. 1, 2, 3, and 4 are points within the bandwidth distance from point i, and 5, 6, 7, 8, and 9 are points outside the bandwidth distance from point i.
A K-dimensional tree (KD tree) built based on distance is an extended version of a binary tree for speeding up the dataset search. If the points include the dimension, they are first sorted according to the value of a dimension, such as u. Then, the middle point is selected as the split (parent) node, and all points are divided into two parts according to the coordinates on the u axis. The u value of the left subspace is smaller than that of the parent node, and the u value of the right subspace must be greater than or equal to the u value of the parent node. This process continues repeatedly until both subregions have no sample points (the terminating node is a leaf node), and finally, the region division of the KD tree is formed. Using this approach, sample points are saved on the appropriate nodes. In this case, the time complexity for performing a perimeter point lookup is . After the tree structure is established, this algorithm starts from the root node and recursively searches the left and right child nodes to find all points within the radial range of the regression point. The lookup of the observation points around the regression point was completed quickly after the KD tree was constructed, which accelerated the process of reconstructing the matrix in the KNN-GWR method.
2.2.3. Geographically Weighted Regression with K-Nearest Neighbors and Model Evaluation
Press stated that the desirable characteristics of an algorithm are to be fast, computationally inexpensive, and to use as little memory as possible with high computational accuracy [55]. When the bi-square kernel function is selected as the kernel function for GWR, only the observation points within the bandwidth participate in the regression calculation. Here, the zero rows and columns of the weight matrix were removed to minimize the computational cost. In the local regression calculation of regression point i, the construction of the KD tree speeds up the search for the points surrounding regression point i. Considering the above, the KNN-GWR algorithm was set up in this study. The expression of the KNN-GWR algorithm is expressed as follows:
The formula for calculating is shown below.
The corresponding and matrices are determined based on the bandwidth of the regression point and KD tree data structure. The matrices of and can be calculated by
And
where is composed of independent variables from the observation points within the bandwidth around the regression point i ( is a matrix). is composed of the dependent variable of the observation points within the bandwidth around the regression point i ( is a matrix). K is a constant equal to the number of observation points around the regression point. [1, 2, …, K] is the point number in the bandwidth range after sorting by distance. is a space weight matrix and is expressed as:
The equation for the weight matrix is expressed as
where represents the spatial distance between points i and j and represents the spatial distance between points i and K.
The hat matrix is the projection matrix from the observed to the fitted , where each row of the hat matrix is:
where
where is the fitted value of using a bandwidth. The residual vector is then
and the residual sum of squares is
The estimation accuracy of the GWR model was evaluated by comparing the fitted dependent variable values with the dependent variable values of the sample data, as .
The calculated runtime ratio of the KNN-GWR algorithm to other GWR packages is described by the runtime increase rate (RIR).
The pseudo-code of KNN-GWR algorithm is given in Algorithm 2.
| Algorithm 2: KNN-GWR Algorithm |
| I Optimizing bandwidth search by minimizing CV scores |
| 1. Given the initial data , , , and |
| 2. Start the loop : |
| 3. Build KD tree spatial index |
| 4. Starting loop with : |
| 5. Take the data from the result of 3 steps: |
| 6. Reconfiguration , , and |
| 7. Calculate , |
| 8. End of loop |
| 9. Calculate |
| 10. End of loop |
| II Optimal bandwidth selection based on minimum CV criterion |
| 11. Start the loop : |
| 12. Reconfiguration , , and |
| 13. Calculate , |
| 14. End of loop |
| 15. Return , |
| 16. Spatial analysis and model diagnosis using , |
2.2.4. Computational Complexity of GWR and KNN-GWR in Calibration
Time Complexity
In the GWR regression calculation, the time complexity of matrix is and the big is an asymptotic notation used to describe the upper bound of an algorithm’s efficiency. Calculating its inverse, , requires [19,30,56] ( is the number of independent variables, (p + 1) ≤ 10 in common). Therefore, the time complexity of computing is [19,31]. The calculation of is repeated at each regression point location n times; therefore, the total time complexity of the GWR calibration for a known bandwidth is . If the golden partition is used to find the optimal bandwidth, the time complexity is close to , and the total time complexity of the bandwidth selection and model calibration is [19]. The time complexity of KNN-GWR is explained in the same manner as above. In the KNN-GWR model, is a matrix and is a matrix. The time complexity of the matrix is , and the time complexity of the matrix is . Calculating its inverse, , takes , which can be neglected. is computed at each regression point n times; therefore, the total time complexity of the KNN-GWR calibration for a known bandwidth is . If the golden partition is used to find the optimal bandwidth, the time complexity is close to , and the total time complexity of the bandwidth selection and model calibration is . Therefore, in theory, the time complexity of KNN-GWR is much lower than that of GWR. The time complexity of each algorithm is listed in Table 1.

Table 1.
Comparison of time complexity among KNN-GWR, FastGWR, MGWR (PySAL), GWmodel, and Spgwr.
Memory Complexity
The KNN-GWR algorithm improves the matrix and dataset storage model of the GWR operation by adopting distance sorting and a data structure. The weight matrix of the GWR method is stored as an diagonal matrix, which requires storage spaces during the operation, and the memory complexity is . In the process of GWR regression calculation, , , and inherit the memory complexity of the weight matrix . The KNN-GWR algorithm avoids this situation during the calculation. The weight matrix is calculated by selecting only the points within the GWR bandwidth ( is a matrix), and the and matrices are reconstructed accordingly ( is a matrix; is a matrix). The memory complexity of the KNN-GWR algorithm is affected by K, and the memory complexity is . (typically, ). The memory complexity of each algorithm is presented in Table 2.

Table 2.
Comparison of memory complexity between KNN-GWR and other GWR packages.
3. Experiment
3.1. Data Source
To explore the actual performance of KNN-GWR, two datasets were used in the experiment—the simulated dataset [31] and the house price dataset in China from the Anjuke.com website (accessed on 25 March 2022). A simulated dataset was used to verify the viability of the model. The Chinese house price dataset was used to test the scalability of the KNN-GWR model.
3.1.1. Simulated Dataset
The test data were distributed in a square area with a side length of units and the data sample points were evenly distributed in this area. The sample size of each line was m, the total number of samples was , and the distance between adjacent sample points was . Considering the lower left corner of the square area as the origin of the coordinate system, the calculation formula for the sample point position is as follows:
where and are the remainder and integer part of divided by [57]. The experimental data samples were generated using a predefined GWR model with the following equation:
To standardize the regression coefficient , all regression coefficients were limited to the interval ( was a fixed constant) [31]. The regression coefficient beta of the model follows the following five functions.
This paper prepared 8 sets of simulated datasets with different numbers: 1000, 5000, 10,000, 15,000, 20,000, 50,000, 100,000, and 1,000,000.
3.1.2. House Price Dataset in China
The study area ranged from 108°21′ to 122°42′ E and 23°33′ to 42°40′ N. Fourteen provinces or municipalities were mainly involved (Anhui, Jiangxi, Henan, Hubei, Hunan, Shanxi, Hebei, Jiangsu, Zhejiang, Fujian, Beijing, Tianjin, and Shanghai). The total area was approximately 17,454,000 square kilometers comprising two world-class urban agglomerations, Beijing–Tianjin–Hebei and Yangtze River Delta, as shown in Figure 3.
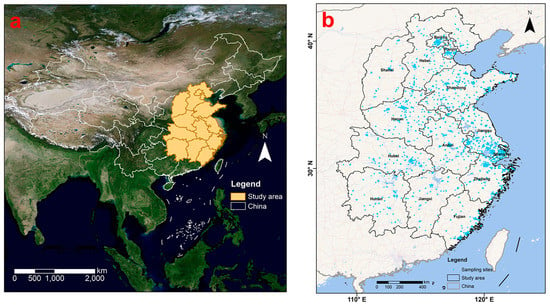
Figure 3.
Study area. (a) Geographical location of each province of the study area in China. (b) Distribution of house price dataset in the study area.
The house price dataset used in this study was collected from www.anjuke.com (accessed on 25 March 2022). The experimental dataset was selected from residential land price statistics with geographic location, including the number of bedrooms (NBeds), bathrooms (NBaths), floor area (Area), and age of the house (Age). Detailed information on the experimental dataset is shown in Figure 4. In this study, 123,691 research data were sequentially divided into 7 different datasets by random sampling: 1000, 5000, 10,000, 15,000, 20,000, 50,000, and 100,000. Seven sets of datasets were applied to MGWR (PySAL), GWmodel, Spgwr, and KNN-GWR, which satisfy the following expression.
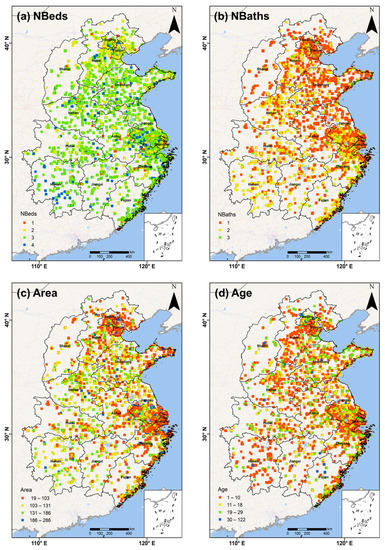
Figure 4.
Details of each independent variable (a) Map of NBeds parameter estimates for the predictor variables. (b) Map of NBaths parameter estimation for predictor variables. (c) Map of Area parameter estimates for the predictor variables. (d) Map of Age parameter estimation for the predictor variables.
3.2. Testing Specifications and Environment
The differences in runtime between the KNN-GWR and other GWR packages (MGWR(PySAL), GWmodel, and Spgwr) were compared. Details of the equipment used in the experiments are listed in Table 3.

Table 3.
Device parameters for running study GWR models.
3.3. Results
3.3.1. Case One: Simulated Dataset
In Figure 5, the coefficients and the respective dependent variable values for the simulated data are presented, along with the coefficients and predicted values of the dependent variable obtained by applying the KNN-GWR method. As shown in Figure 5, the five coefficients β selected by the model are closely related to the locations of the sample points and exhibit spatial non-stationarity. The spatial distribution of the coefficients obtained by the KNN-GWR method is quite similar to the distribution of the simulated data, indicating that it addresses the spatial non-stationarity.
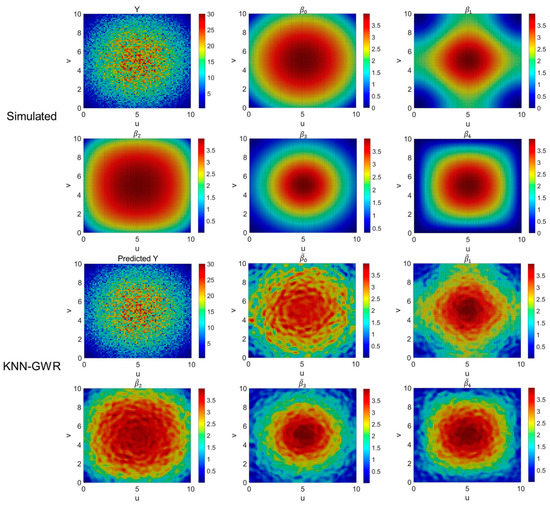
Figure 5.
Estimated regression coefficients of KNN-GWR method on simulated dataset.
Due to the transformation of a large matrix into a small matrix, the regression efficiency of KNN-GWR is significantly improved compared with that of GWR. As shown in Figure 6 and Table 4, the average running times of KNN-GWR at 1000, 5000, and 50,000 points are 0.34, 3.59, and 31.77 s, respectively. However, the average running time of MGWR(PySAL) increased from 3.71 s at 1000 points to 178.52 s at 10,000 points, and then reached 6327.91 s at 50,000 points. Figure 7 showed the comparison of KNN-GWR with other GWR packages in terms of runtime increase ratio. The results indicated that for 10,000 observations, KNN-GWR was approximately 49.7 times faster than MGWR(PySAL), approximately 58.9 times faster than GWmodel, and approximately 3224.2 times faster than Spgwr. Spgwr cannot obtain the results because the data are larger than 10,000 observations. In addition, when the data increased to 50,000 observations, KNN-GWR was approximately 199.2 times faster than MGWR(PySAL) and approximately 260.7 times faster than GWmodel. KNN-GWR implements calibration operations at amounts of data greater than 50,000, whereas in other GWR packages memory bottlenecks are caused by storing redundant computations.
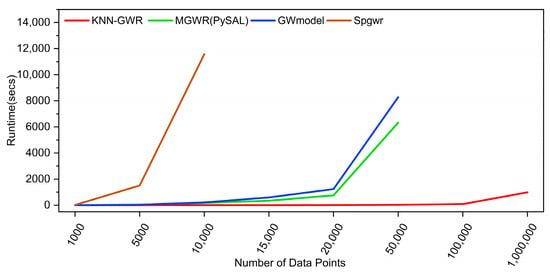
Figure 6.
Comparison of the computational speeds of four software packages(KNN-GWR, MGWR (PySAL), GWmodel, and Spgwr) in simulated dataset experiments.

Table 4.
Information on the runtime and of four software packages (KNN-GWR, MGWR(PySAL), GWmodel, and Spgwr) in simulated dataset experiments.
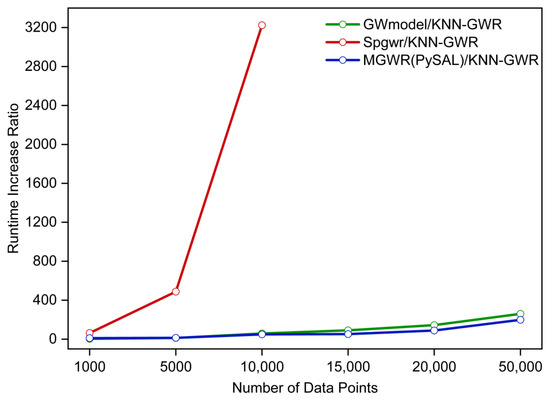
Figure 7.
Comparison of KNN-GWR with other GWR packages in terms of runtime increase ratio (tested using simulated dataset).
The advantage of geographically weighted regression methods for analyzing geographic data was retained in the KNN-GWR method, and the storage of the full sample matrix by other GWR software models was changed in the KNN-GWR method to store only the matrix consisting of the observations involved in the regression.
3.3.2. Case Two: House Price Dataset in China
The local model can discover the rich information in geographic data and we performed KNN-GWR modeling on the house price data collected from www.anjuke.com. KNN-GWR generated local parameter estimates that reflect information on the spatial heterogeneity affecting house prices. The performance of KNN-GWR and its spatial non-smoothness are explored visually through local coefficient estimation of mapped variables. Figure 8a–d show the spatial patterns of the KNN-GWR model estimated coefficients.
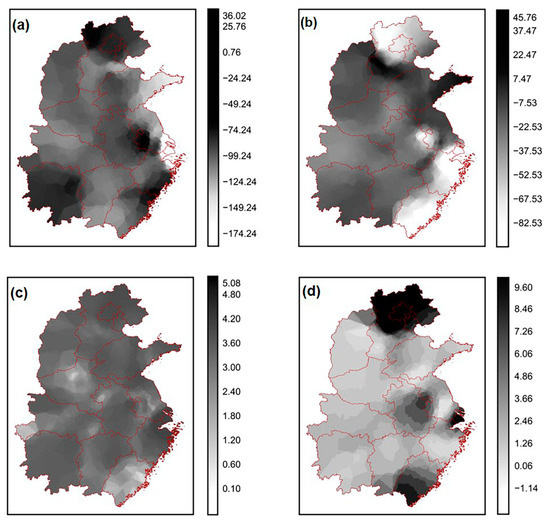
Figure 8.
Space mapping for: (a) number of bedrooms in the house, (b) number of bathrooms, (c) area of the house, and (d) age of the house, by KNN-GWR modeling.
The results indicate that Area is positively correlated with residential land price, and the larger the residential area, the higher the residential land price (Figure 8c). And it seems reasonable that the effects of age are greater in Beijing–Tianjin–Hebei and the Yangtze River Delta. As these cities are better developed, housing construction has slowed down in recent years, resulting in higher house prices in some areas. In addition, the number of bathrooms is negatively correlated with house prices in some coastal cities, possibly because higher housing prices have dampened the greater demand for the number of bathrooms.
Compared with other GWR packages, the KNN-GWR method demonstrated high efficiency in processing housing price datasets in the study area. As shown in Figure 9 and Table 5, as the number of data increases, the running time of KNN-GWR remains relatively stable, while the running time of all the other GWR packages increases rapidly. For instance, with 50,000 observations, the KNN-GWR method requires 51.21 s, while MGWR (PySAl) and GWmodel require 4116.12 and 7445.82 s, respectively. This indicates that KNN-GWR is capable of processing large-scale geographic datasets relatively quickly, while other GWR packages struggled to achieve the same level of efficiency. In addition, as shown in Figure 10, KNN-GWR has an efficiency improvement of a thousand times compared to other GWR software packages. This indicates that KNN-GWR overcomes the memory limitations and process larger datasets more efficiently than other GWR packages. Overall, these findings demonstrate the usefulness of the KNN-GWR method in analyzing large-scale geographic data and its potential to outperform in computational efficiency and memory optimization compared to existing GWR algorithms.
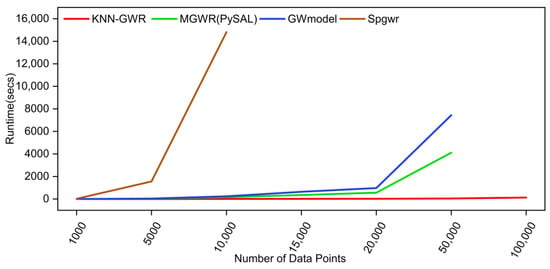
Figure 9.
Comparison of the computational speeds of four software packages (KNN-GWR, MGWR(PySAL), GWmodel, and Spgwr) in the house price dataset in China.

Table 5.
Information on the runtime of four software packages (KNN-GWR, MGWR(PySAL), GWmodel, and Spgwr) in the house price dataset in China.
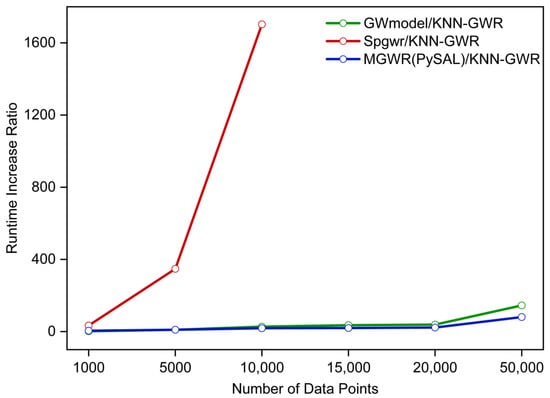
Figure 10.
Comparison of KNN-GWR with other GWR packages in terms of runtime increase ratio (tested using house price dataset in China).
4. Discussion
The KNN-GWR proposed in this paper is an optimized version of GWR. Specifically, it optimized the computational efficiency and memory of GWR by strategies such as constructing KD tree, referencing geographical clustering and reconstructing regression matrices. In essence, there is no difference between KNN-GWR and GWR in exploring spatial non-stationarity. However, KNN-GWR is better suited for processing geographical big data applications and address the changes associated with it.
Therefore, in our experimental results, KNN-GWR has a good fitting degree, just like GWR. Compared with GWR, the advantages of KNN-GWR in computational optimization are as follows. First, the KD tree is used to establish a spatial data index structure that can quickly identification the observation points around the regression point. Second, KNN-GWR reconstructed the weight matrix , independent variable matrix (n ), and dependent variable matrix in the local regression calculation for each regression point (the reconstructed matrices are ; ; ). In this process, observation points that are not within the bandwidth in the local regression of each regression point are directly removed according to the spatial data index structure established by the KD tree. Memory complexity is reduced from to , where n is the number of observation points. Third, KNN-GWR references the spatial clustering relationship obtained by K-means, which in turn helps to find the optimal bandwidth. To optimize GWR performance, increasing the hardware configuration is one approach; however, it is often necessary to optimize performance of GWR without relying on hardware enhancements.
To demonstrate the practicability of KNN-GWR, simulated data and the Chinese house price dataset were used for the experiments. The results show that GWR cannot handle regression tasks of large amount of data; in contrast, KNN-GWR has great potential to handle a large amount of geographic data, which can largely alleviate the dilemma of GWR in terms of data size. In this paper, we collected house price data from 14 provinces and municipalities and applied it to verify the practical significance of the model in a real geographical environment. When analyzing the house price data of 14 provinces and municipalities, it was found that the factors affecting the house price in coastal cities, more developed areas and slow-developing areas differed. For example, the Age variable has strong effects on house prices in Beijing and Shanghai, but relatively weak effects in other provinces. In terms of runtime, taking simulated data as an example, for 50,000 observations, KNN-GWR is several hundred times faster than MGWR(PySAL), and the GWmodel. In terms of the memory required for calculation, the memory requirement of KNN-GWR is affected by the number K of the nearest neighbors. Generally speaking, the required memory is very small. The memory assignment of KNN-GWR was compared with that of FastGWR , MGWR(PySAL) , GWmodel , and Spgwr (the number of independent variables of the database is four, and the adjusted bandwidth is 93). For 50,000 observations, KNN-GWR required 33.8 KB of memory, FastGWR required 976.6 KB, and MGWR(PySAL), GWmodel, and Spgwr required 9.31 GB of memory. KNN-GWR has the same ability as GWR to explore spatial non-stationarity. However, in terms of memory usage, KNN-GWR stores a small matrix consisting of observations involved in the regression rather than a full sample matrix.
5. Conclusions
Geographically weighted regression has become a classical method for exploring the spatial non-stationarity in geographic data. However, it faces computational challenges when applied to geographical big data. Previous studies have adopted strategies such as parallelism to optimize GWR, which can handle applications with millions of geographical spatial data, but still encounter problems of memory and computational efficiency. This paper aims to address this limitation, and the main research results are summarized as follows:
(1) The KD tree is proposed to organize geographical spatial data, which can quickly identify the observation points around the regression points in local regression calculations. This greatly optimizes the time-consuming search process in the geographically weighted regression model and significantly improves the computational efficiency.
(2) This paper reconstructed the weight matrix, the independent variable matrix, and the dependent variable matrix based on the characteristics of the kernel function in GWR. This achieves the transformation from a large matrix to a small matrix , avoiding the large memory consumption caused by the large matrix during regression calculation in classical geographically weighted regression.
(3) The spatial clustering relationships of the geographic data obtained by the K-means clustering method are referenced to help narrow the search for the optimal bandwidth. This reduces the computational waste in the process of determining the optimal bandwidth in GWR.
Author Contributions
Conceptualization, Xiaoyue Yang; methodology, Xiaoyue Yang, Yi Yang and Shenghua Xu; software, Xiaoyue Yang and Yi Yang; formal analysis, Xiaoyue Yang; data curation, Xiaoyue Yang, Zhengyuan Chai and Gang Yang; writing—original draft, Xiaoyue Yang; writing—review and editing, Yi Yang, Shenghua Xu and Jiakuan Han; visualization, Xiaoyue Yang and Jiakuan Han; supervision, Shenghua Xu, Jiakuan Han, Zhengyuan Chai and Gang Yang; funding acquisition, Yi Yang. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 42001343; and the National Natural Science Foundation of China, grant number 42071384.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M.E. Geographically Weighted Regression; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Shi, T.; Hu, X.; Guo, L.; Su, F.; Tu, W.; Hu, Z.; Liu, H.; Yang, C.; Wang, J.; Zhang, J.; et al. Digital mapping of zinc in urban topsoil using multisource geospatial data and random forest. Sci. Total Environ. 2021, 792, 148455. [Google Scholar] [CrossRef]
- Jiang, W.; Rao, P.; Cao, R.; Tang, Z.; Chen, K. Comparative evaluation of geological disaster susceptibility using multi-regression methods and spatial accuracy validation. J. Geogr. Sci. 2017, 27, 439–462. [Google Scholar] [CrossRef]
- Kumar, S.; Lal, R.; Liu, D. A geographically weighted regression kriging approach for mapping soil organic carbon stock. Geoderma 2012, 189–190, 627–634. [Google Scholar] [CrossRef]
- Davies, T.J.; Regetz, J.; Wolkovich, E.M.; McGill, B.J.; Kerkhoff, A. Phylogenetically weighted regression: A method for modelling non-stationarity on evolutionary trees. Glob. Ecol. Biogeogr. 2018, 28, 275–285. [Google Scholar] [CrossRef]
- Mellin, C.; Mengersen, K.; Bradshaw, C.J.A.; Caley, M.J. Generalizing the use of geographical weights in biodiversity modelling. Glob. Ecol. Biogeogr. 2014, 23, 1314–1323. [Google Scholar] [CrossRef]
- Yang, L.; Chau, K.W.; Szeto, W.Y.; Cui, X.; Wang, X. Accessibility to transit, by transit, and property prices: Spatially varying relationships. Transp. Res. Part D Transp. Environ. 2020, 85, 102387. [Google Scholar] [CrossRef]
- Wu, C.; Ren, F.; Hu, W.; Du, Q. Multiscale geographically and temporally weighted regression: Exploring the spatiotemporal determinants of housing prices. Int. J. Geogr. Inf. Sci. 2018, 33, 489–511. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Crespo, R.; Yao, J. Geographical and Temporal Weighted Regression (GTWR). Geogr. Anal. 2015, 47, 431–452. [Google Scholar] [CrossRef]
- Huang, B.; Wu, B.; Barry, M. Geographically and temporally weighted regression for modeling spatio-temporal variation in house prices. Int. J. Geogr. Inf. Sci. 2010, 24, 383–401. [Google Scholar] [CrossRef]
- Hong, Z.; Mei, C.; Wang, H.; Du, W. Spatiotemporal effects of climate factors on childhood hand, foot, and mouth disease: A case study using mixed geographically and temporally weighted regression models. Int. J. Geogr. Inf. Sci. 2021, 35, 1611–1633. [Google Scholar] [CrossRef]
- Hong, Z.; Hao, H.; Li, C.; Du, W.; Wei, L.; Wang, H. Exploration of potential risks of Hand, Foot, and Mouth Disease in Inner Mongolia Autonomous Region, China Using Geographically Weighted Regression Model. Sci. Rep. 2018, 8, 17707. [Google Scholar] [CrossRef]
- Mainardi, S. Modelling spatial heterogeneity and anisotropy: Child anaemia, sanitation and basic infrastructure in sub-Saharan Africa. Int. J. Geogr. Inf. Sci. 2012, 26, 387–411. [Google Scholar] [CrossRef]
- Lu, X.Y.; Chen, X.; Zhao, X.L.; Lv, D.J.; Zhang, Y. Assessing the impact of land surface temperature on urban net primary productivity increment based on geographically weighted regression model. Sci. Rep. 2021, 11, 22282. [Google Scholar] [CrossRef]
- Bivand, R.; Yu, D.; Nakaya, T.; Garcia-Lopez, M.-A. Package SPGWR; R Software Package; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Oshan, T.; Li, Z.; Kang, W.; Wolf, L.; Fotheringham, A. mgwr: A Python Implementation of Multiscale Geographically Weighted Regression for Investigating Process Spatial Heterogeneity and Scale. ISPRS Int. J. Geo-Inf. 2019, 8, 269. [Google Scholar] [CrossRef]
- Gollini, I.; Lu, B.; Charlton, M.; Brunsdon, C.; Harris, P. GWmodel: An R Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models. J. Stat. Softw. 2015, 63, 1–50. [Google Scholar] [CrossRef]
- Li, Z.; Fotheringham, A.S.; Li, W.; Oshan, T. Fast Geographically Weighted Regression (FastGWR): A scalable algorithm to investigate spatial process heterogeneity in millions of observations. Int. J. Geogr. Inf. Sci. 2019, 33, 155–175. [Google Scholar] [CrossRef]
- Sudmanns, M.; Tiede, D.; Lang, S.; Bergstedt, H.; Trost, G.; Augustin, H.; Baraldi, A.; Blaschke, T. Big Earth data: Disruptive changes in Earth observation data management and analysis? Int. J. Digit. Earth 2019, 13, 832–850. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, H.; Wang, L.; Huang, B.; Ranjan, R.; Zomaya, A.; Jie, W. Remote sensing big data computing: Challenges and opportunities. Future Gener. Comput. Syst. 2015, 51, 47–60. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Lü, G.; Batty, M.; Strobl, J.; Lin, H.; Zhu, A.X.; Chen, M. Reflections and speculations on the progress in Geographic Information Systems (GIS): A geographic perspective. Int. J. Geogr. Inf. Sci. 2018, 33, 346–367. [Google Scholar] [CrossRef]
- Apte, J.S.; Messier, K.P.; Gani, S.; Brauer, M.; Kirchstetter, T.W.; Lunden, M.M.; Marshall, J.D.; Portier, C.J.; Vermeulen, R.C.H.; Hamburg, S.P. High-Resolution Air Pollution Mapping with Google Street View Cars: Exploiting Big Data. Environ. Sci. Technol. 2017, 51, 6999–7008. [Google Scholar] [CrossRef]
- Lee, J.-G.; Kang, M. Geospatial Big Data: Challenges and Opportunities. Big Data Res. 2015, 2, 74–81. [Google Scholar] [CrossRef]
- Mendi, A.F.; Demir, Ö.; Sakaklı, K.K.; Çabuk, A. A New Approach to Land Registry System in Turkey: Blockchain-Based System Proposal. Photogramm. Eng. Remote Sens. 2020, 86, 701–709. [Google Scholar] [CrossRef]
- Finley, A.O. Comparing spatially-varying coefficients models for analysis of ecological data with non-stationary and anisotropic residual dependence. Methods Ecol. Evol. 2011, 2, 143–154. [Google Scholar] [CrossRef]
- Harris, R. Grid-enabling Geographically Weighted Regression: A Case Study of Participation in Higher Education in England. Trans. GIS 2010, 14, 43–61. [Google Scholar] [CrossRef]
- Yu, D. Modeling Owner-Occupied Single-Family House Values in the City of Milwaukee: A Geographically Weighted Regression Approach. GISci. Remote Sens. 2007, 44, 267–282. [Google Scholar] [CrossRef]
- Feuillet, T.; Commenges, H.; Menai, M.; Salze, P.; Perchoux, C.; Reuillon, R.; Kesse-Guyot, E.; Enaux, C.; Nazare, J.A.; Hercberg, S.; et al. A massive geographically weighted regression model of walking-environment relationships. J. Transp. Geogr. 2018, 68, 118–129. [Google Scholar] [CrossRef]
- Wang, D.; Yang, Y.; Qiu, A.; Kang, X.; Han, J.; Chai, Z. A CUDA-Based Parallel Geographically Weighted Regression for Large-Scale Geographic Data. ISPRS Int. J. Geo-Inf. 2020, 9, 653. [Google Scholar] [CrossRef]
- Tasyurek, M.; Celik, M. RNN-GWR: A geographically weighted regression approach for frequently updated data. Neurocomputing 2020, 399, 258–270. [Google Scholar] [CrossRef]
- Meenakshi; Gill, S. k-dLst Tree: K-d Tree with Linked List to Handle Duplicate Keys. In Proceedings of the Emerging Trends in Expert Applications and Security, Singapore, 17–18 February 2018; pp. 167–175. [Google Scholar]
- Chen, Z.Y.; Liao, I.Y.; Ahmed, A. KDT-SPSO: A multimodal particle swarm optimisation algorithm based on k-d trees for palm tree detection. Appl. Soft Comput. 2021, 103, 107156. [Google Scholar] [CrossRef]
- Shyu, C.R.; Chi, P.H.; Scott, G.; Xu, D. ProteinDBS: A real-time retrieval system for protein structure comparison. Nucleic Acids Res. 2004, 32, W572–W575. [Google Scholar] [CrossRef] [PubMed]
- Böhm, C.; Krebs, F. The k-Nearest Neighbour Join: Turbo Charging the KDD Process. Knowl. Inf. Syst. 2004, 6, 728–749. [Google Scholar] [CrossRef]
- Muja, M.; Lowe, D.G. Scalable Nearest Neighbor Algorithms for High Dimensional Data. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2227–2240. [Google Scholar] [CrossRef]
- Muja, M. Fast approximate nearest neighbors with automatic algorithm configuration. Proc. Viss. 2009, 1, 331–340. [Google Scholar]
- Boukerche, A.; Zheng, L.; Alfandi, O. Outlier detection: Methods, models, and classification. ACM Comput. Surv. (CSUR) 2020, 53, 1–37. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Fahad, A.; Alshatri, N.; Tari, Z.; Alamri, A.; Khalil, I.; Zomaya, A.Y.; Foufou, S.; Bouras, A. A Survey of Clustering Algorithms for Big Data: Taxonomy and Empirical Analysis. IEEE Trans. Emerg. Top. Comput. 2014, 2, 267–279. [Google Scholar] [CrossRef]
- Zhao, W.-L.; Deng, C.-H.; Ngo, C.-W. k-means: A revisit. Neurocomputing 2018, 291, 195–206. [Google Scholar] [CrossRef]
- Macqueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1967; Volume 1. [Google Scholar]
- Selim, S.Z.; Ismail, M.A. K-Means-Type Algorithms: A Generalized Convergence Theorem and Characterization of Local Optimality. IEEE Trans. Pattern Anal. Mach. Intell. 1984, PAMI-6, 81–87. [Google Scholar] [CrossRef]
- Li, S.; Lyu, D.; Huang, G.; Zhang, X.; Gao, F.; Chen, Y.; Liu, X. Spatially varying impacts of built environment factors on rail transit ridership at station level: A case study in Guangzhou, China. J. Transp. Geogr. 2020, 82, 102631. [Google Scholar] [CrossRef]
- Hernández, J.M.; Bulchand-Gidumal, J.; Suárez-Vega, R. Using accommodation price determinants to segment tourist areas. J. Destin. Mark. Manag. 2021, 21, 100622. [Google Scholar] [CrossRef]
- Deng, X.; Gao, F.; Liao, S.; Li, S. Unraveling the association between the built environment and air pollution from a geospatial perspective. J. Clean. Prod. 2023, 386, 135768. [Google Scholar] [CrossRef]
- Murakami, D.; Tsutsumida, N.; Yoshida, T.; Nakaya, T.; Lu, B. Scalable GWR: A Linear-Time Algorithm for Large-Scale Geographically Weighted Regression with Polynomial Kernels. Ann. Am. Assoc. Geogr. 2020, 111, 459–480. [Google Scholar] [CrossRef]
- Murakami, D.; Griffith, D.A. Spatially varying coefficient modeling for large datasets: Eliminating N from spatial regressions. Spat. Stat. 2019, 30, 39–64. [Google Scholar] [CrossRef]
- Mardia, K.V.; Kent, J.T.; Bibby, J.M. Multivariate Analysis; Academic Press: London, UK, 1979. [Google Scholar]
- Carlis, J.; Bruso, K. Rsqrt: An Heuristic for Estimating the Number of Clusters to Report. Electron. Commer. Res. Appl. 2012, 11, 152–158. [Google Scholar] [CrossRef]
- Hassanat, A.B.; Abbadi, M.A.; Altarawneh, G.A.; Alhasanat, A.A. Solving the Problem of the K Parameter in the KNN Classifier Using an Ensemble Learning Approach. Comput. Sci. 2014, 12, 33–39. [Google Scholar]
- Sugar, C.A.; James, G.M. Finding the Number of Clusters in a Dataset. J. Am. Stat. Assoc. 2003, 98, 750–763. [Google Scholar] [CrossRef]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Harris, P.; Fotheringham, A.S.; Crespo, R.; Charlton, M. The Use of Geographically Weighted Regression for Spatial Prediction: An Evaluation of Models Using Simulated Data Sets. Math. Geosci. 2010, 42, 657–680. [Google Scholar] [CrossRef]
- Chen, F.; Mei, C.-L. Scale-adaptive estimation of mixed geographically weighted regression models. Econ. Model. 2021, 94, 737–747. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).