Multiuser Incomplete Preference K-Nearest Neighbor Query Method Based on Differential Privacy in Road Network
Abstract
1. Introduction
- (1)
- Aiming at the problem of the incompleteness of query users’ preference, this paper proposes a completion algorithm for multiuser incomplete preference, which proposes the concept of frequent pattern tree HUFP-tree and mines frequent itemsets and strong association rules based on this. Then it completes the incomplete data of multiple users according to the association rules, which reduces the complexity of the query and improves the accuracy of query results.
- (2)
- Aiming at the difference in the user’s preference for multiple queries, this paper proposes a clustering and grouping algorithm based on multiuser preference. According to the proposed concept of multiuser preference weight coefficient, the algorithm classifies the attributes of data objects by multi-query users and then groups them within the cluster for the road network distance between query users, which improves the accuracy and efficiency of query results.
- (3)
- In order to improve the efficiency of the multiuser incomplete preference k neighbor query algorithm in the road network environment, this paper proposes a reduction and refining algorithm for data objects, which first prunes the data objects according to the distance of the road network, then deletes the data points with weak dominance, which can filter out a large number of unqualified data objects, and finally performs a k neighbor query on the data objects after refining them to obtain the query results. This method effectively reduces the query time and improves the query efficiency.
- (4)
- In order to protect the privacy of the query result data in the k-nearest neighbor query with an incomplete preference of multiple users under the road network environment, this paper proposes a privacy budget allocation algorithm. This uses differential privacy technology to add Laplace noise to the query results according to the weight ratio of the results, effectively protecting the privacy of the data.
2. Related Work
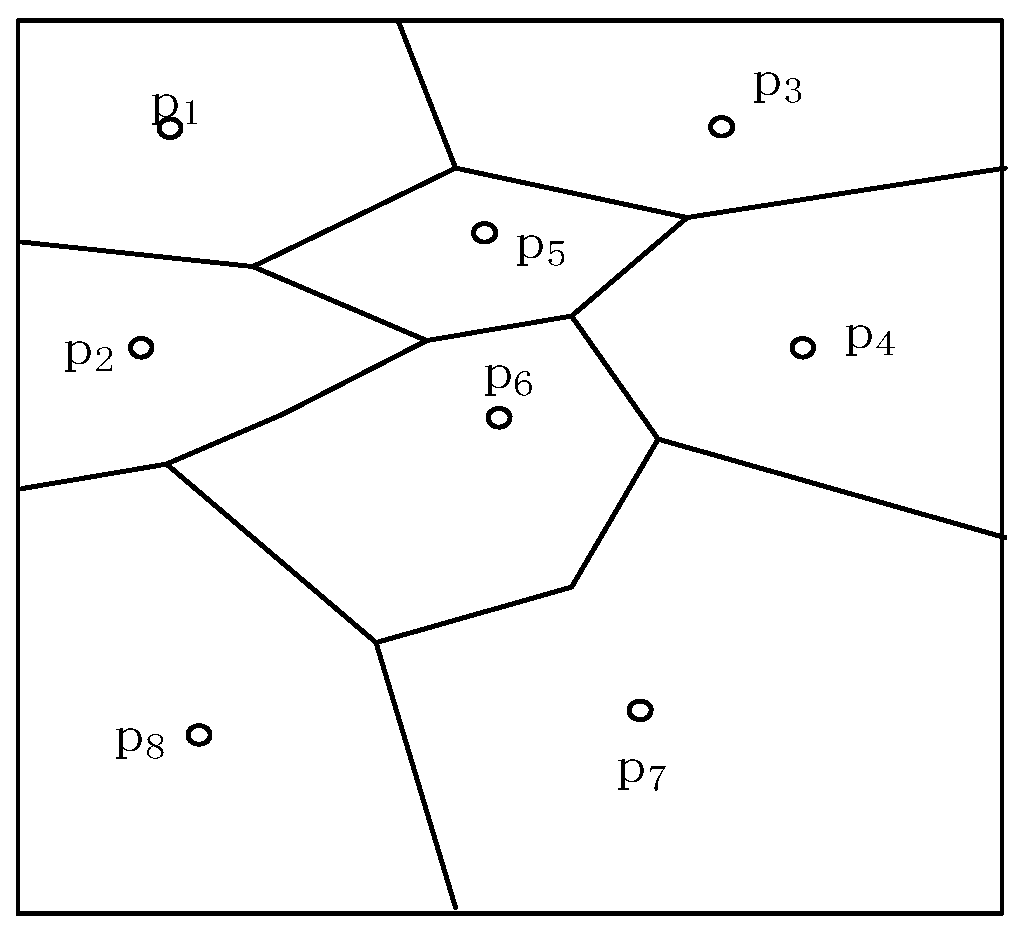
3. Definitions and Symbol Descriptions
- (1)
- Each NVP corresponds to only one data point.
- (2)
- The edge of the Voronoi network graph is formed by the vertical bisector of two adjacent data points. The distance between the data points at both ends of the vertical bisector and the road network of the vertical bisector is equal.
- (3)
- The network Voronoi diagram divides the space into non-overlapping NVPS and the road network distance from any point in each NVP to the NVP generation point is smaller than the distance to the other NVP generation points.
4. Multiuser Incomplete Preference Clustering Method Based on Association Rules
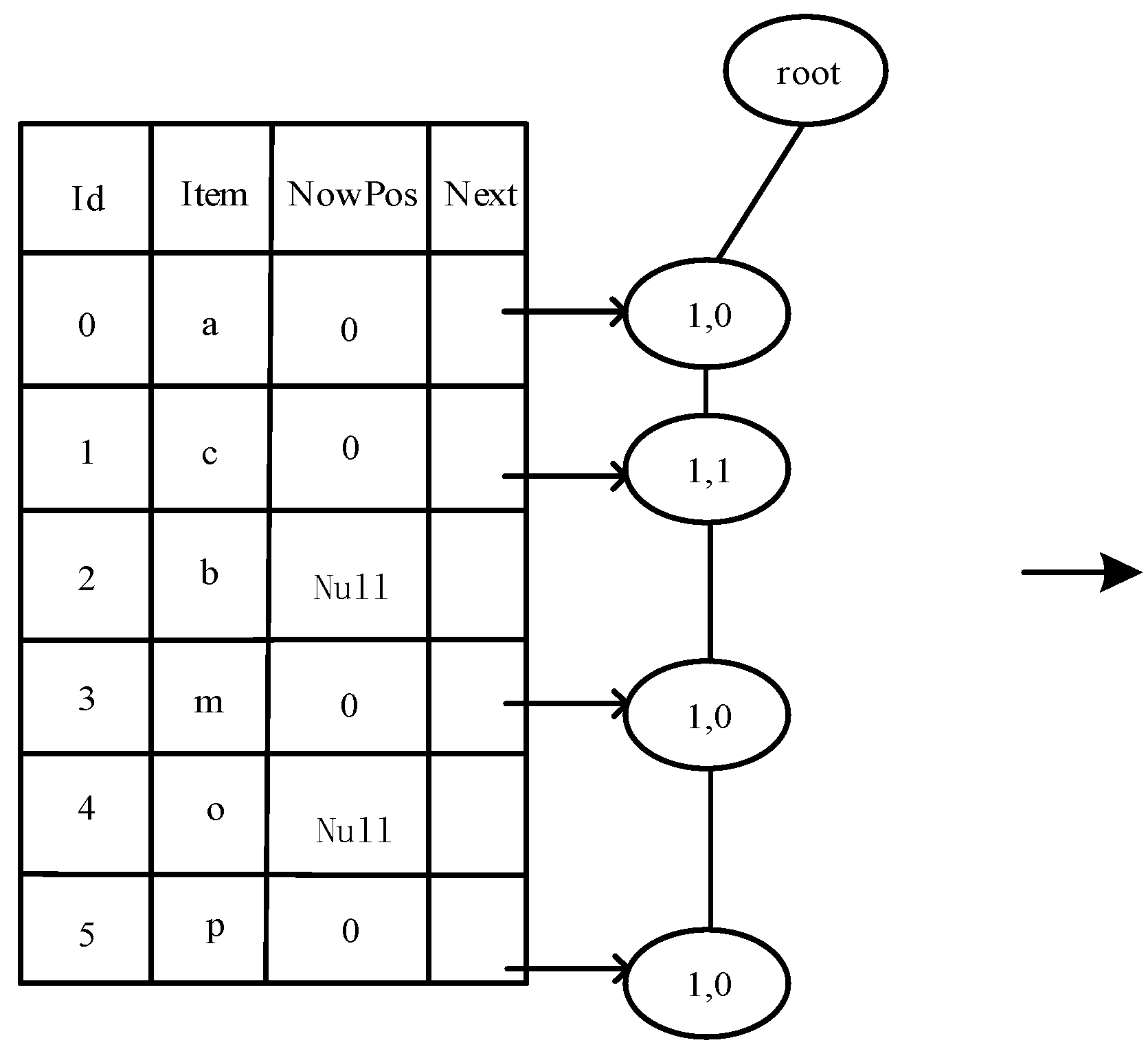
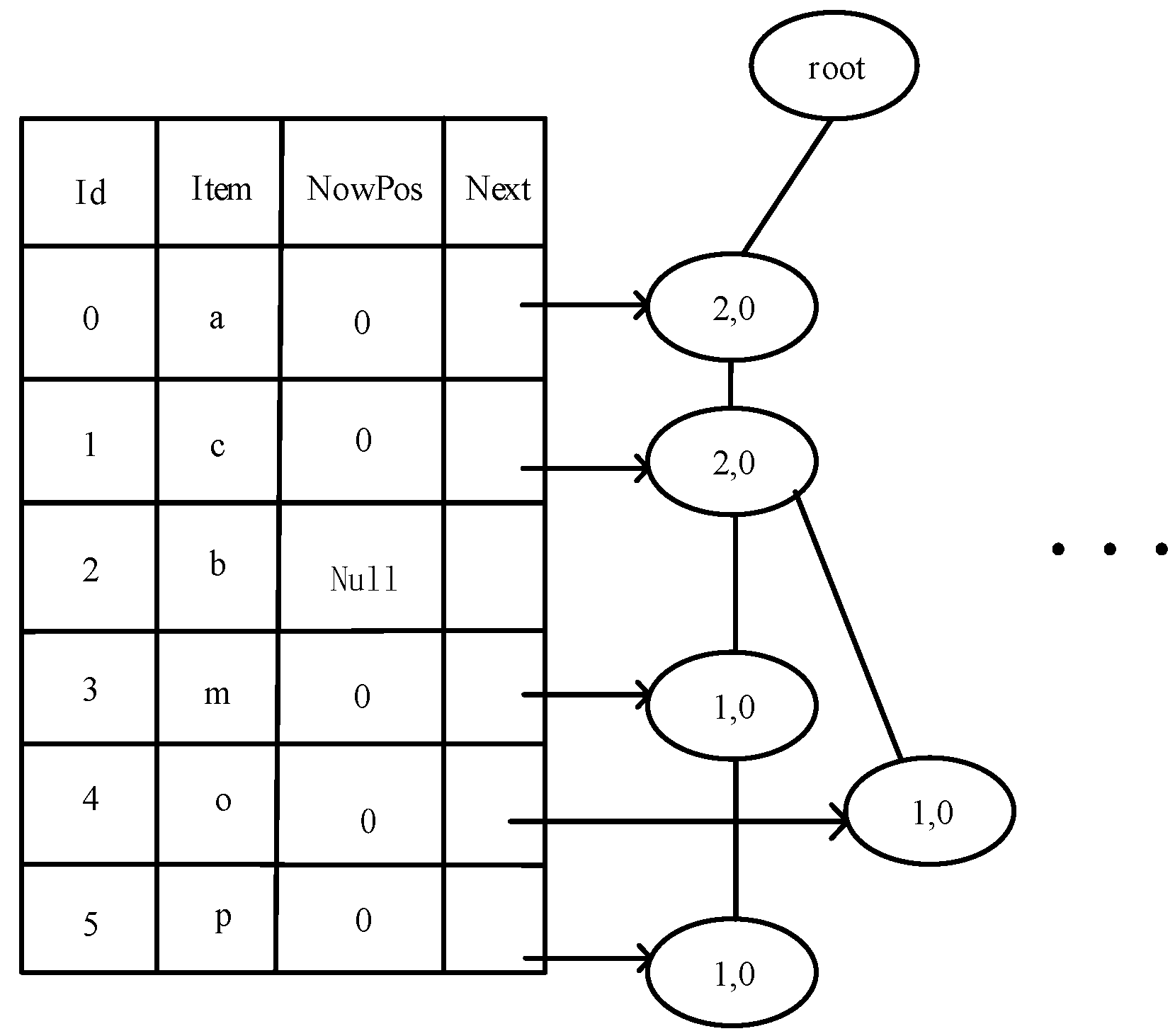
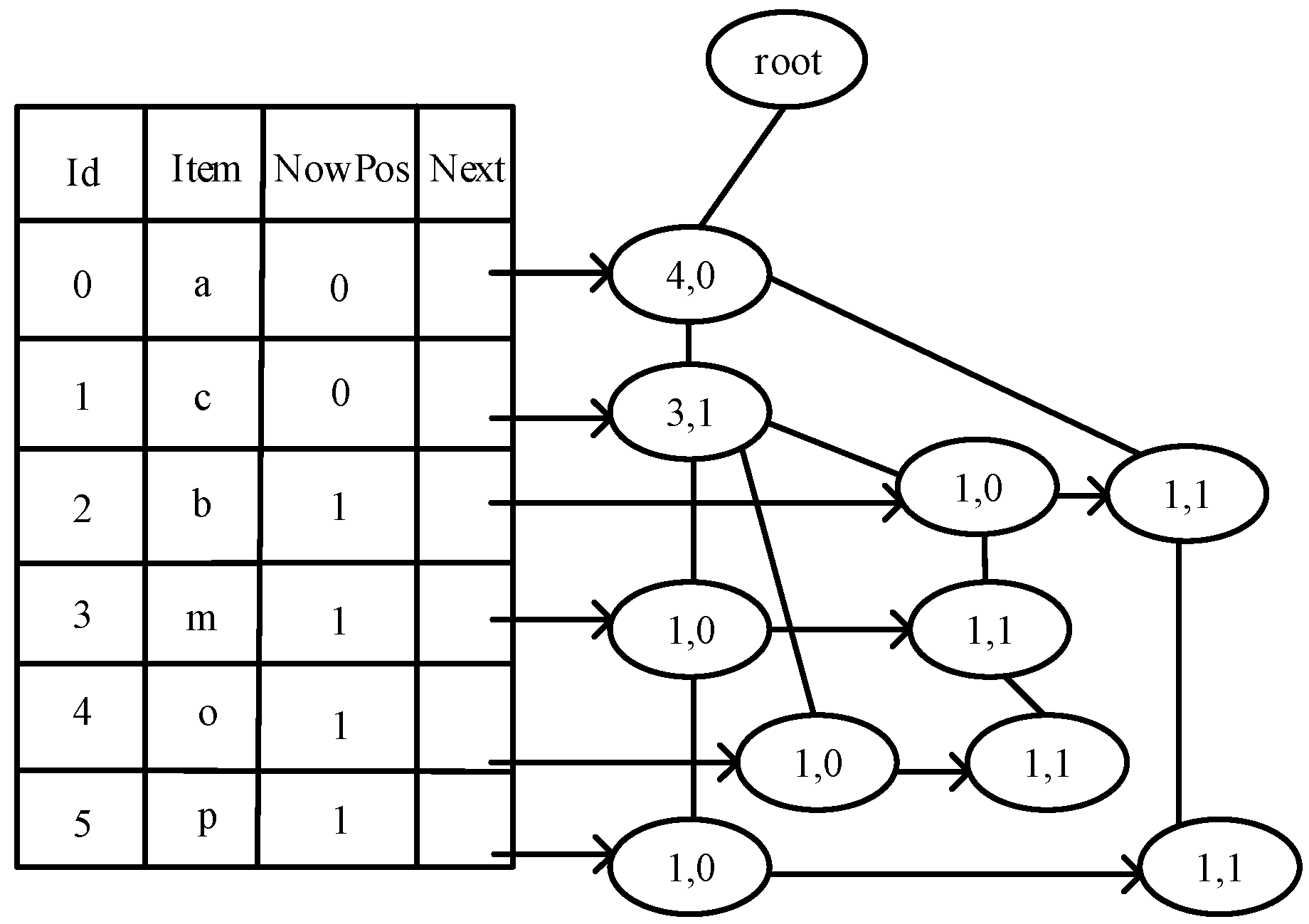
4.1. Multiuser Incomplete Preference Completion Method
| Algorithm 1: Multiuser incomplete preference completion algorithm (PCAR) |
| Input: Transaction set D = {D1, D2, …, Dn}, di is the item set in Dn, and the minimum support threshold supmin. Output: Preference after multiuser completion. begin 1: candi , candiRes ; 2: for each di Di, calculate sup(Di); 3: if sup(di) > supmin; 4: candi di; 5: end if; 6: else 6: delete di 7: end else; 8: end for; 9: Sort the items in Candi in descending order of frequency count and get the corresponding ordinal number; 10: creating a root Noderoot = null; 11: create a frequent item header table; 12: for di in candi; 13: if the item header table ordinal number is equal to the node di ordinal number; &&Itemfirst==null; 14: count(Itemcou) + 1, Itemnow saves the di location, Itemnowptr and Itemfirst point to di, Itemparent point to di’s parent; 15: end if 16: if the ordinal number of the header table is equal to the ordinal number of the node di &&Itemfirs!==null 17: count(Itemcou) + 1, Itemnow saves the di location, Itemparent point to di’s parent, Itemnowptr and Itembro point to di; 18: end if; 19: end for 20: for di in candi; 21: sets the count of nodes in the di to root path as an item, the count value of the serial number corresponding to di in the header table; 22: if count value < supmin; 23: delete the corresponding node to get the frequent itemset; 24: end if 25: end for 26: candi_f Merging all frequent itemsets results in extremely frequent itemsets; 27: for Di in D; 28: if Di has missing dimensions 29: for X in candiRes 30: completion Di; 31: end for 32: end if 33: end for end |
4.2. Multiuser Clustering Algorithm Based on Association Rules
| Algorithm 2: Multiuser clustering algorithm based on association rules (MCR) |
| Input: Query user Q = {q1, q2, …, qi}, frequent itemsets candiRes Output: multiuser clustering C. begin 1: , , ; 2: for X in candiRes 3: if then 4: 5: end if 6: end for 7: for F in ASSR 8: find the subset of itemset B 9: if then 10: 11: end if 12: end for 13: ; 14: for j in Q 15: Get the key preference of each query user based on the preference of each query user and the corresponding item header table Ai, Bj; 16: Calculating positive correlation coefficient according to association rules ; 17: Calculate the similarity measure between every two query users compare(Ai,Bj); 18: end for 19: if 20: 21: end if 22: else Cj Bj 23: i i + 1 24: return C; end |
5. Multiuser Preference K-Nearest Neighbor Query Algorithm Based on Differential Privacy in Road Network
5.1. Reduced Data Object
5.2. Refining Data Objects
| Algorithm 3: Reduction and refinement algorithm of data objects in road network (RAR) |
| Input: Data object set P, road segment set R, cluster set C = {c1, c2, …, cm}, ci = {p1, p2, k, pi}; Output: Candidate result set CondiResSet; begin 1: Construct a Voronoi diagram of the road network from road segments and data objects as generated points; 2: ResSet ; 3: for ci in C then 4: Determining the minimum circumcircle of ci to form the query region CH(ci); 5: if p in CH(ci) then 6: AR circle(p,);/*gets the minimum circumscribed circle of the query center and data objects*/ 7: end if 8: if p in AR then 9: ConSet += p;/*theorem 6*/ 10: end if 11: if CH(ci) and VNVP(p)intersect then 12: ConSet ConSet + p;/*theorem 7*/ 13: end if 14: else 15: r CH(ci) sections intersecting R 16: if p in r then 17: ConSet ConSet + p;/*theorem 8*/ 18: end if 19: end else 20: for pi && pj in ConSet then 21: δ-SNS dominance comparison of pi and pj; 22: if pi dominates pj then 23: PreSet pj;/*theorem 9*/ 24: end if 25: end for 26: CondiResSet ConSet-PreSet; 27: return CondiResSet; end for end |
| Algorithm 4: Multiuser preference k-nearest neighbor query algorithm based on differential privacy in road network (PIPKQ) |
| Input: Candidate result set CondiResSet, cluster set C = {c1, c2, …, cm}, privacy budget ε; Output: Noisy result set ResSet; begin 1: for each CondiResSet then/*traverse the candidate result set of each cluster*/ 2: for p in CondiResSet then 3: candidate d(,p) 4: sort(d(,p)); 5: ResSet the first k shortest distance data objects; 6: end for 7: Assign privacy budget parameters to each cluster ; 8: Calculate the noise added in each cluster ; 9: end for; 10: return noisy result set ResSet; end |
5.3. Privacy Analysis
5.4. Usability Analysis
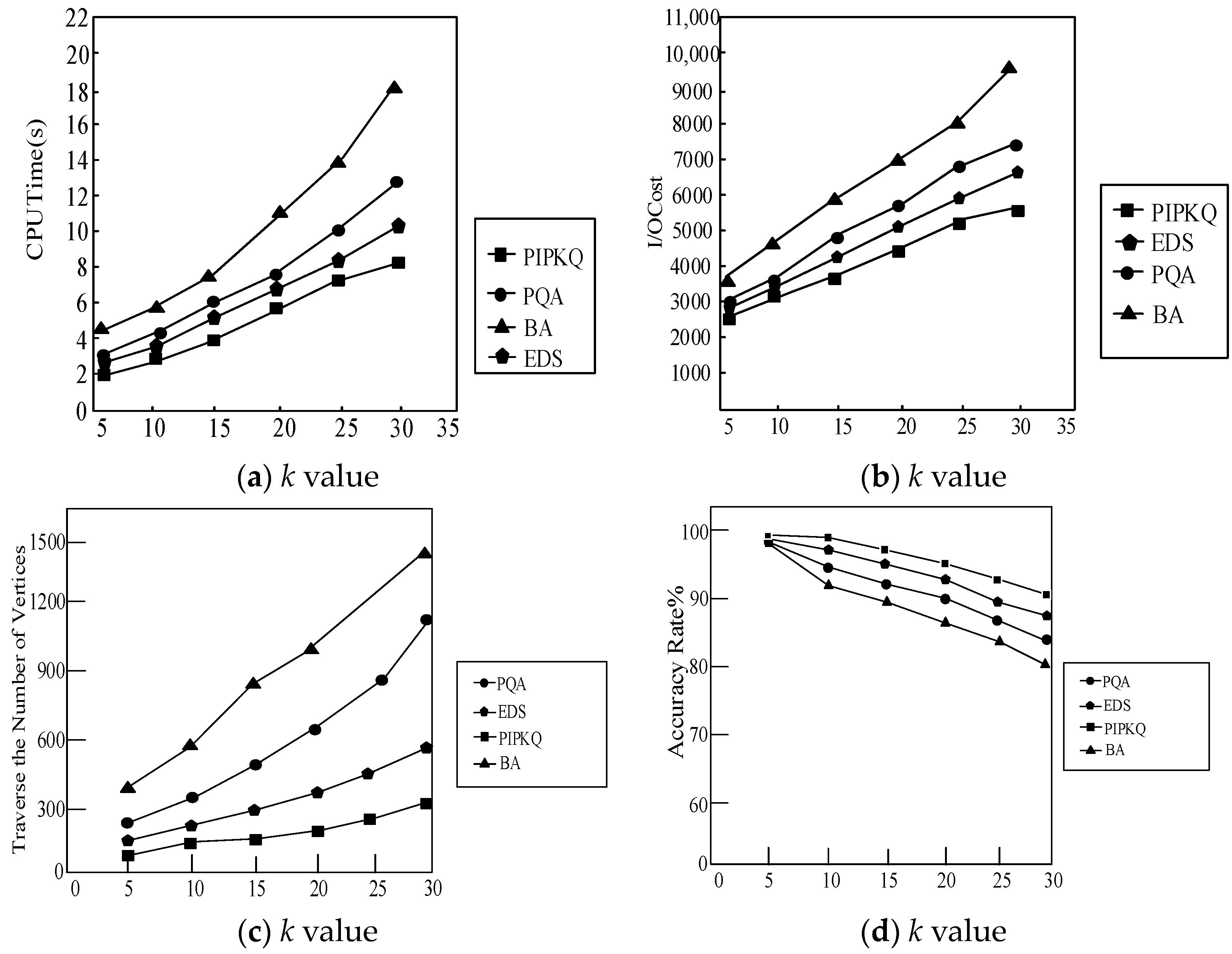
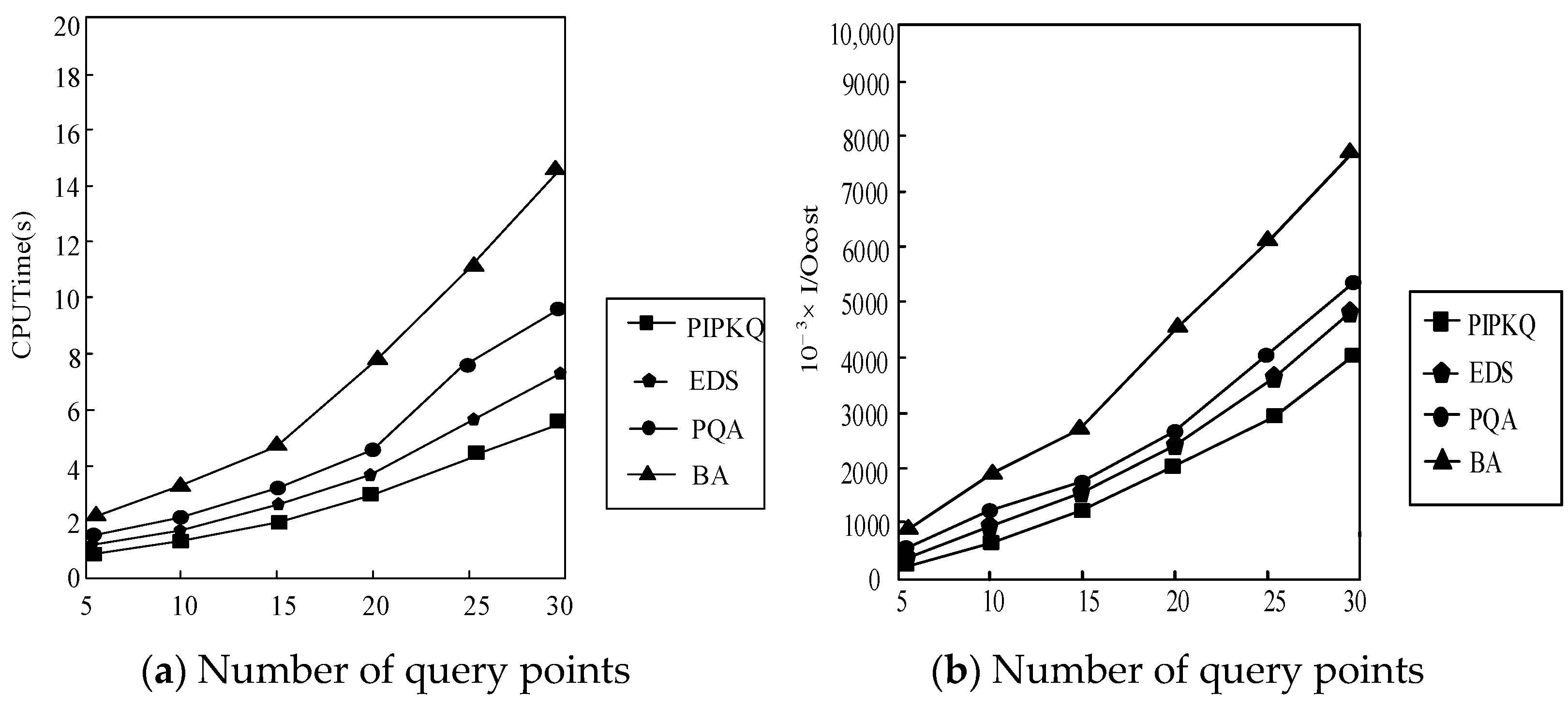
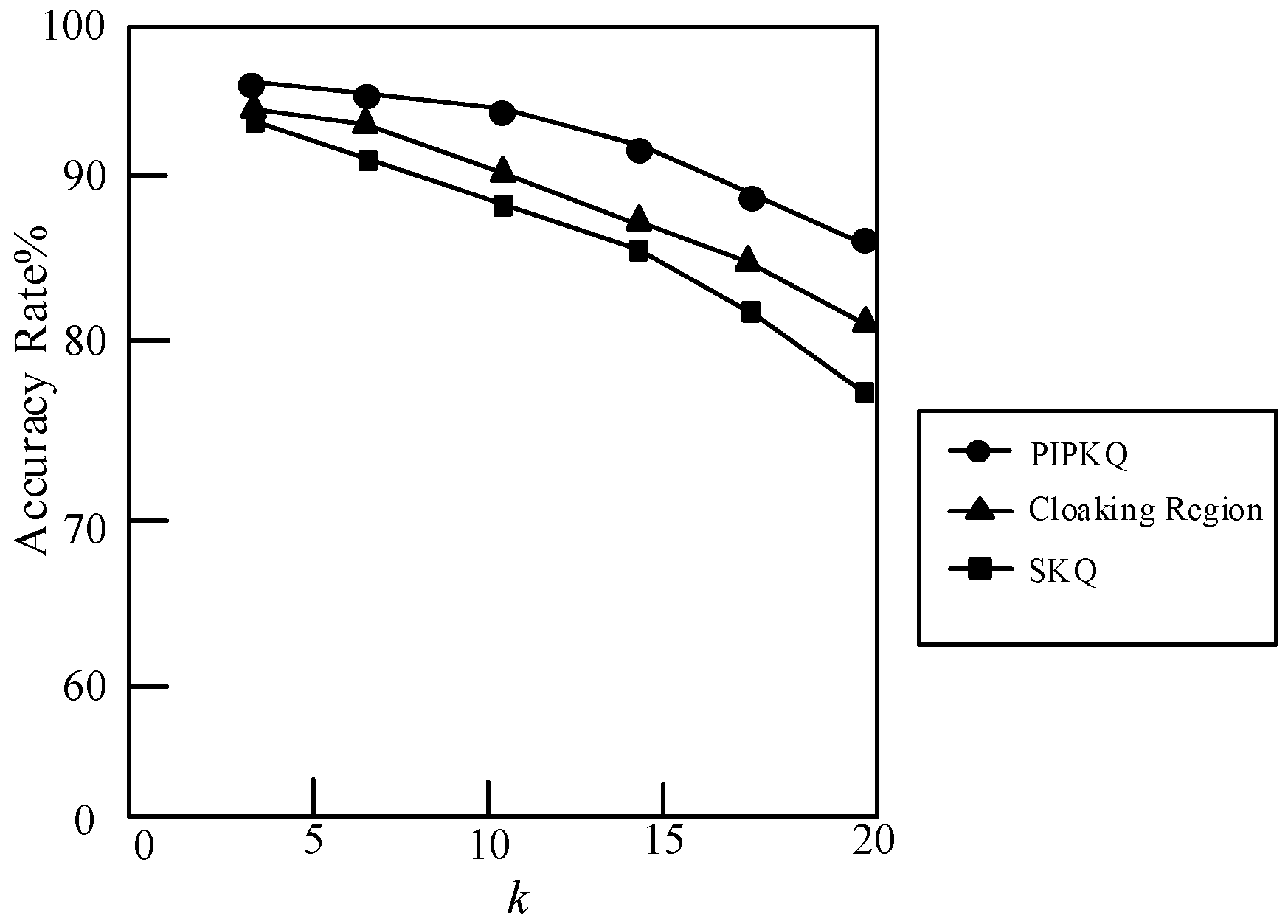
6. Experiment Analysis
6.1. Algorithm Comparative Analysis
6.2. Privacy Analysis
7. Conclusions
- Multiuser incomplete preference continuous k-nearest neighbor query based on privacy-preserving in road networks.
- Multiuser incomplete preference k-nearest neighbor query based on privacy protection in an edge computing environment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Hu, Y.; Hao, X.; Zhang, L.; Hao, Z. High-dimensional data approximate k-nearest neighbor query based on dimension grouping dimensionality reduction. Comput. Res. Dev. 2021, 58, 609–623. [Google Scholar]
- Yang, R.; Niu, B. OIQ-tree: An Index Supporting Continuous k-Nearest Neighbor Query over Large Scale Spatial Text Data Streams. Chin. J. Comput. 2021, 44, 1732–1750. [Google Scholar]
- Zhang, L.; Li, S.; Guo, Y.; Hao, X. A method for k nearest neighbor query of line segment in obstructed spaces. J. Inf. Process. Syst. 2020, 16, 406–420. [Google Scholar]
- Ding, X.; Sheng, S.; Liu, J.; Zhou, P. Efficient Probabilistic K-NN Computation in Uncertain Sensor Networks. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2575–2587. [Google Scholar] [CrossRef]
- You, M.L.; Lu, H.; Mamoulis, N.; Vaitis, M. Ranking spatial data by quality preferences. IEEE Trans. Knowl. Data Eng. 2010, 23, 433–446. [Google Scholar] [CrossRef]
- Rocha-Junior, J.B.; Vlachou, A.; Doulkeridis, C.; Nørvag, K. Efficient processing of top-k spatial preference queries. Proc. VLDB Endow. 2010, 4, 93–104. [Google Scholar] [CrossRef]
- Wang, Y.; Hassan, A.; Duan, X.; Zhang, X. An efficient multiple-user location-based query authentication approach for social networking. J. Inf. Secur. Appl. 2019, 47, 284–294. [Google Scholar] [CrossRef]
- Wang, W.; Xia, F.; Nie, H.; Chen, Z.; Gong, Z.; Kong, X.; Wei, W. Vehicle Trajectory Clustering Based on Dynamic Representation Learning of Internet of Vehicles. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3567–3576. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H.; Wang, J.; Hu, Q.; Wang, X.; Leng, M. A Novel Index Method for K Nearest Object Query over Time-Dependent Road Networks. Complexity 2019, 1–18. [Google Scholar] [CrossRef]
- Li, F.; Yao, B.; Kumar, P. Group enclosing queries. IEEE Trans. Knowl. Data Eng. 2010, 23, 1526–1540. [Google Scholar] [CrossRef]
- Cai, T.; Li, J.; Mian, A.; Li, R.-H.; Sellis, T.; Yu, J.X. Target-aware holistic influence maximization in spatial social networks. IEEE Trans. Knowl. Data Eng. 2020, 13, 1993–2007. [Google Scholar] [CrossRef]
- Chen, Z.; Yao, B.; Wang, Z.J.; Gao, X.; Shang, S.; Ma, S.; Guo, M. Flexible aggregate nearest neighbor queries and its keyword-aware variant on road networks. IEEE Trans. Knowl. Data Eng. 2020, 33, 3701–3715. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, L.; Ma, J.; Hu, G.; Liu, J.; Qiao, Y. Knowledge graph-based spatial-aware user community preference query algorithm for lbsns. Big Data Res. 2021, 23, 100169. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, X.; Yang, X.; Zhang, Y.; Zhang, X. Processing Multiple-user Location-based Keyword Queries. IEICE Trans. Inf. Syst. 2018, 101, 1552–1561. [Google Scholar] [CrossRef]
- Saad, N.H.M.; Ibrahim, H.; Sidi, F.; Yaakob, R.; Alwan, A. Efficient Skyline Computation on Uncertain Dimensions. IEEE Access 2021, 9, 96975–96994. [Google Scholar] [CrossRef]
- O’connor, M.; Cosley, D.; Konstan, J.A.; Riedl, J. PolyLens: A Recommender System for Groups of Users. In Proceedings of the Seventh European Conference on Computer Supported Cooperative Work, Bonn, Germany, 16–20 September 2001; Springer: Dordrecht, The Netherlands, 2001; pp. 199–218. [Google Scholar]
- Amer-Yahia, S.; Roy, S.B.; Chawlat, A.; Das, G.; Yu, C. Group recommendation: Semantics and efficiency. Proc. VLDB Endow. 2009, 2, 754–765. [Google Scholar] [CrossRef]
- Yu, Z.; Yu, Z.; Zhou, X.; Nakamura, Y. Handling conditional preferences in recommender systems. In Proceedings of the 14th International Conference on Intelligent User Interfaces, Sanibel Island, FL, USA, 8–11 February 2009; pp. 407–412. [Google Scholar]
- Zheng, K.; Su, H.; Zheng, B.; Shang, S.; Xu, J.; Liu, J.; Zhou, X. Interactive top-k spatial keyword queries. In Proceedings of the 2015 IEEE 31st International Conference on Data Engineering, Seoul, Republic of Korea, 13–17 April 2015; IEEE: Piscataway, HJ, USA, 2015; pp. 423–434. [Google Scholar]
- Dritsas, E.; Maria, T.; Panagiotis, G.; Spyros, S. Trajectory Clustering and k-NN for Robust Privacy Preserving Spatiotemporal Databases. Algorithms 2018, 11, 207. [Google Scholar] [CrossRef]
- Dritsas, E.; Kanavos, A.; Trigka, M.; Sioutas, S.; Tsakalidis, A. Storage Efficient Trajectory Clustering and k-NN for Robust Privacy Preserving Spatio-Temporal Databases. Algorithms 2019, 12, 266. [Google Scholar] [CrossRef]
- Guan, Y.; Lu, R.; Zheng, Y.; Zhang, S.; Shao, J.; Wei, G. EPGQ:Efficient and Private Feature-based Group Nearest Neighbor Query over Road Networks. IEEE Internet Things J. 2022, 9, 20492–20502. [Google Scholar] [CrossRef]
- Zhou, C.; Chen, Y.; Tian, H. K-nearest neighbor Query method for protecting location privacy and query content privacy in road network. J. Softw. 2020, 31, 471–492. [Google Scholar]
- Dwork, C.; Roth, A. The algorithmic foundations of differential privacy. Found. Trends Theor. Comput.Sci. 2014, 9, 211–407. [Google Scholar] [CrossRef]
- Sankar, L.; Rajagopalan, S.R.; Poor, H.V. Utility-privacy tradeoffs in databases:An information-theoretic approach. IEEE Trans. Inf. Forensics Secur. 2013, 8, 838–852. [Google Scholar] [CrossRef]
- Kaaniche, N.; Masmoudi, S.; Znina, S.; Laurent, M. Privacy preserving cooperative computation for personalized web search applications. In Proceedings of the 35th Annual ACM Symposium on Applied Computing, Brno, Czech Republic, 30 March–3 April 2020; pp. 250–258. [Google Scholar]
- Rahali, S.; Laurent, M.; Masmoudi, S.; Roux, C.; Mazeau, B. A Validated Privacy-Utility Preserving Recommendation System with Local Differential Privacy. In Proceedings of the 2021 IEEE 15th International Conference on Big Data Science and Engineering (BigDataSE), Shenyang, China, 20–22 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 118–127. [Google Scholar]
- Zhang, X.; Xu, Y.; Meng, X. Spatial Data Approximate k-Nearest Neighbor Query Based on Localized Differential Privacy. Comput. Res. Dev. 2022, 59, 1610–1624. [Google Scholar]
- Fan, Z.; Xu, X. APDPk-means: A new differential privacy clustering algorithm based on arithmetic progression privacy budget allocation. In Proceedings of the 2019 IEEE 21st International Conference on High Performance Computing and Communications; IEEE 17th International Conference on Smart City; IEEE 5th International Conference on Data Science and Systems(HPCC/SmartCity/DSS), Zhangjiajie, China, 10–12 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1737–1742. [Google Scholar]
- Zhou, P.; Wang, K.; Guo, L.; Gong, S.; Zheng, B. A privacy-preserving distributed contextual federated online learning framework with big data support in social recommender systems. IEEE Trans. Knowl. Data Eng. 2019, 33, 824–838. [Google Scholar] [CrossRef]
- Viappiani, P.; Boutilier, C. On the equivalence of optimal recommendation sets and myopically optimal query sets. Artif. Intell. 2020, 286, 103328. [Google Scholar] [CrossRef]
- Okabe, A.; Satoh, T.; Furuta, T.; Suzuki, A.; Okano, K. Generalized Network Voronoi Diagrams: Concepts, Computational Methods, and Applications. Int. J. Geogr. Inf. Sci. 2008, 22, 965–994. [Google Scholar] [CrossRef]
- Lukasiewicz, T.; Martinez, M.V.; Simari, G.I. Probabilistic preference logic networks. In ECAI 2014; IOS Press: Amsterdam, The Netherlands, 2014; pp. 561–566. [Google Scholar]
- Blum, A.; Ligett, K.; Roth, A. A learning theory approach to noninteractive database privacy. J. ACM(JACM) 2013, 60, 1–25. [Google Scholar] [CrossRef]
- Li, S.; Dou, Y.; Hao, X. K-dominant spatial Skyline query method in road network environment. Comput. Res. Dev. 2020, 57, 227–239. [Google Scholar]
- John, A.; Singh, S.K.; Adimoolam, M.; Ananth Kumar, T. Dynamic Sorting and Average Skyline Method for Query Processing in Spatial-temporal Data. Int. J. Data Sci. 2021, 6, 1–18. [Google Scholar] [CrossRef]
- Xun, Y.; Paulet, R.; Bertino, E.; Varadharajan, V. Practical Approximate K Nearest Neighbor Queries with Location and Query Privacy. IEEE Trans. Knowl. Data Eng. 2016, 28, 1. [Google Scholar]
- Yang, S.; Tang, S.; Zhang, X. Privacy-preserving K Nearest Neighbor Query with Authentication on Road Networks. J. Parallel Distrib. Comput. 2019, 134, 25–36. [Google Scholar] [CrossRef]

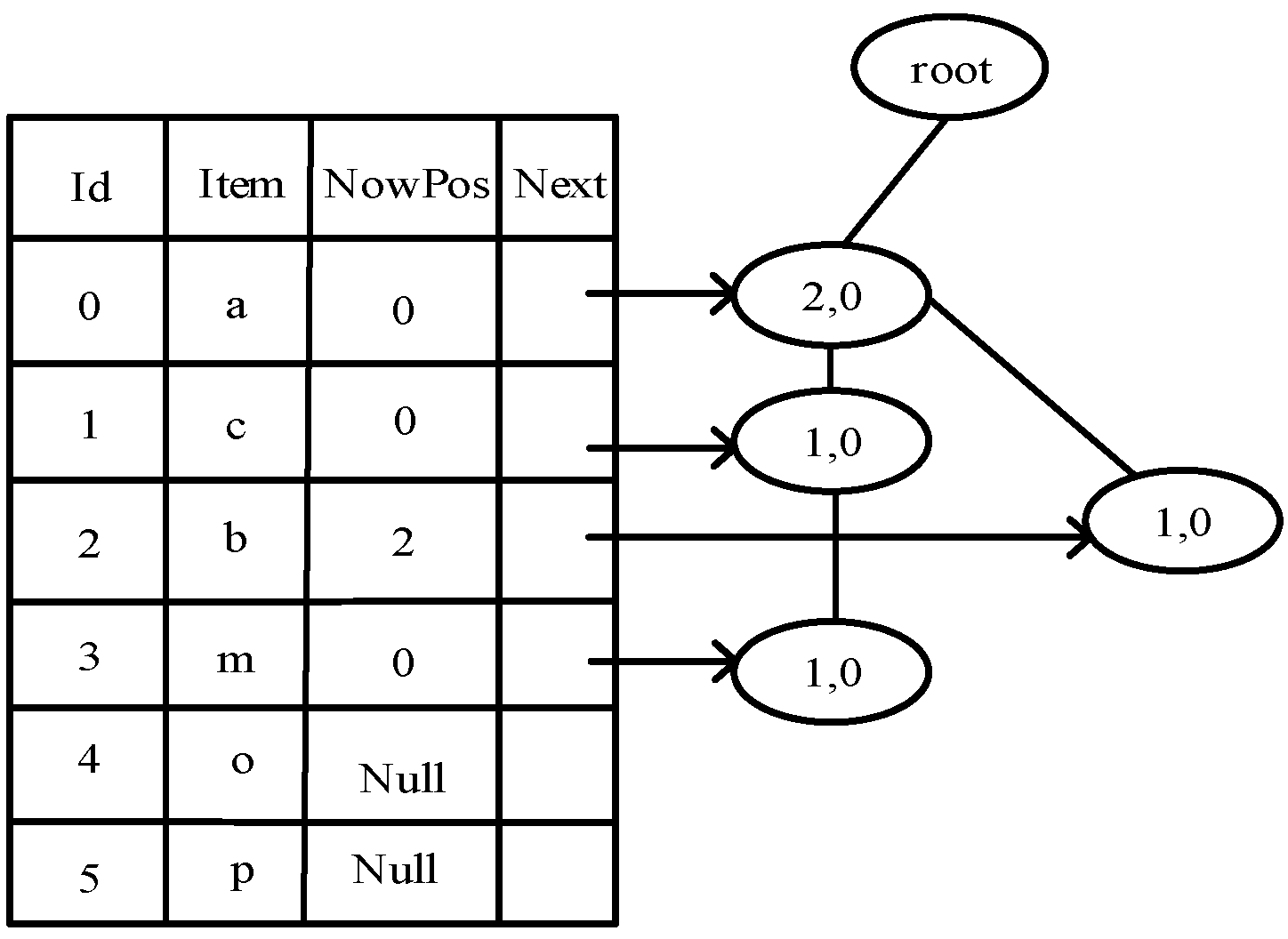
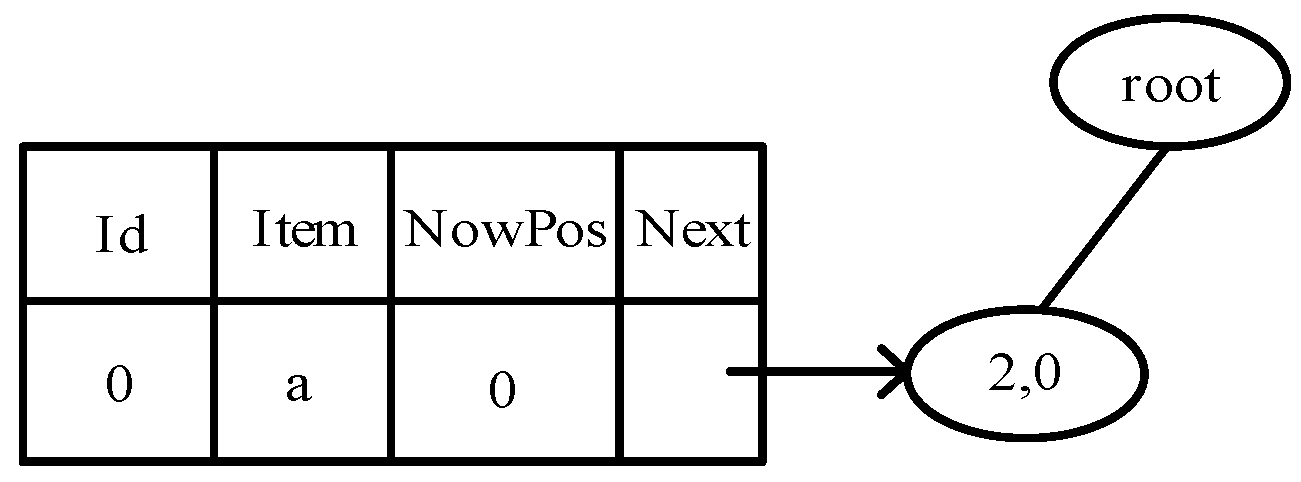
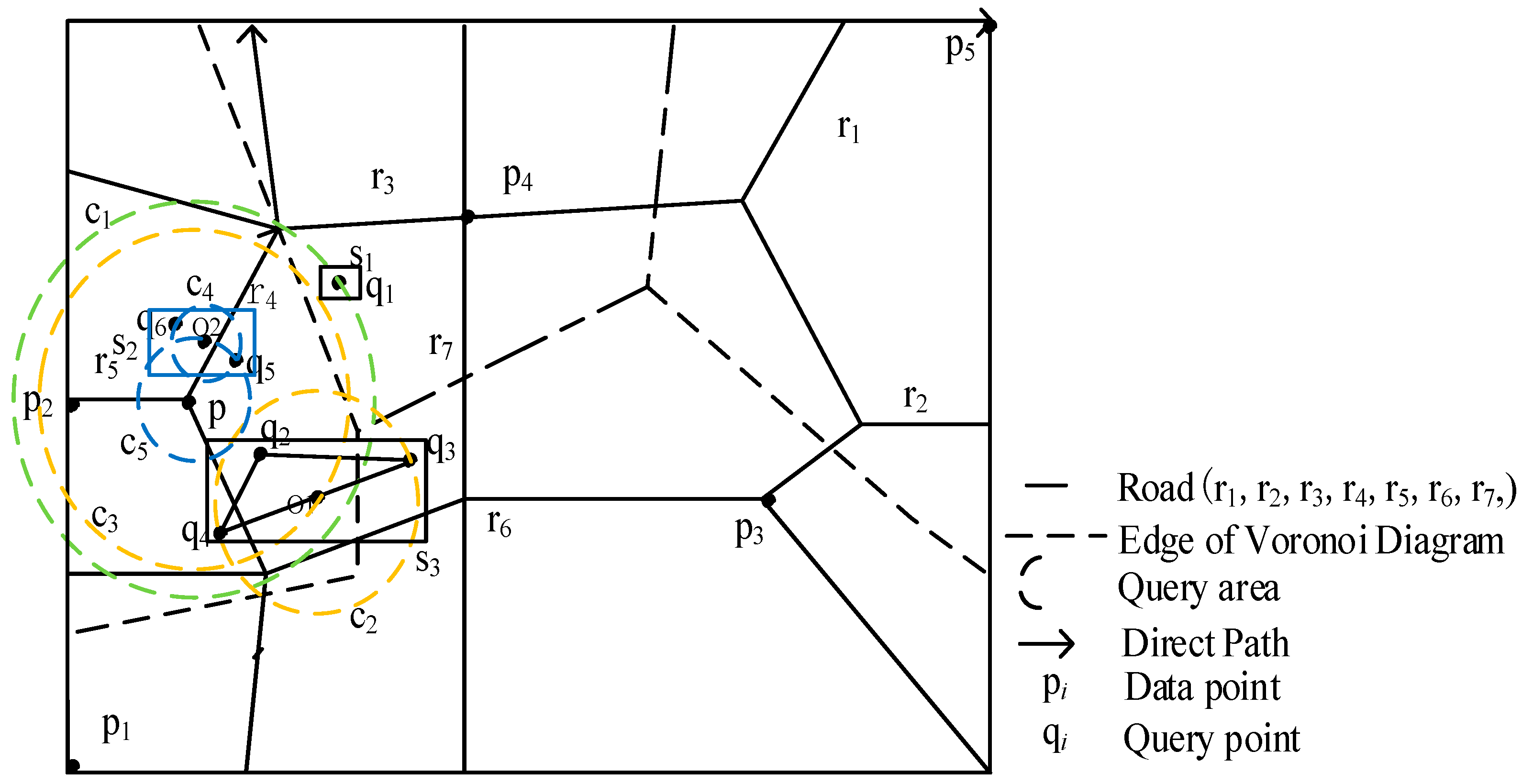
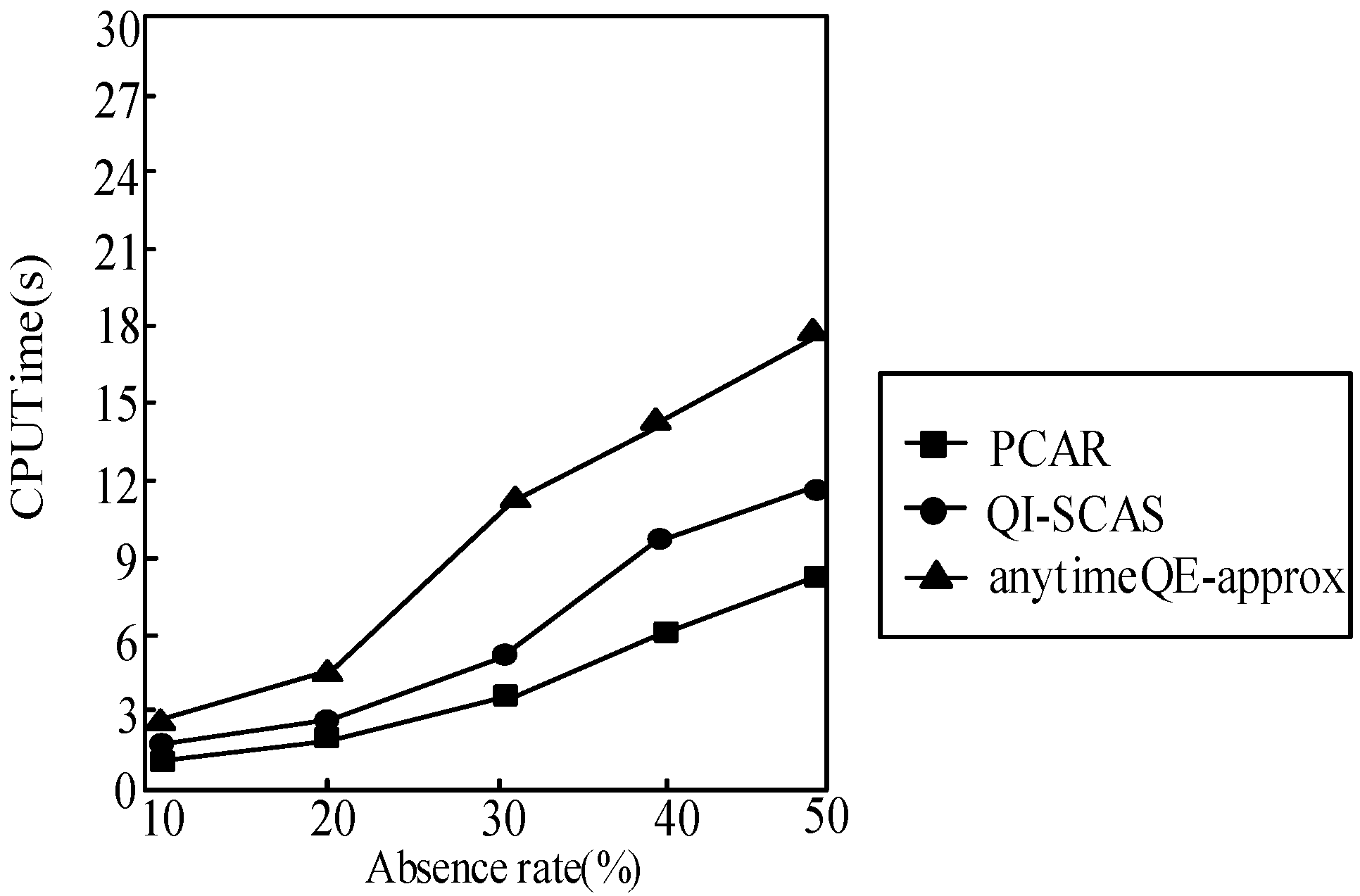


| TID | Itemsets |
|---|---|
| 01 | {a, c, d, g, m, p} |
| 02 | {a, c, l, o} |
| 03 | {a, b, c, m, o} |
| 04 | {a, b, f, p, s} |
| a | b | c | d | f | g | l | m | o | p | s |
| 4 | 2 | 3 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 1 |
| a | b | c | m | o | p |
| 4 | 2 | 3 | 2 | 2 | 2 |
| TID | Itemsets |
|---|---|
| 01 | {a, c, m, p} |
| 02 | {a, c, o} |
| 03 | {a, c, b, m, o} |
| 04 | {a, b, p} |
| Cafe | Taste | Environment | Service | Per Capita Price | Road Network Distance/m |
|---|---|---|---|---|---|
| p1 | 1 | 2 | 2 | 70 | 20 |
| p2 | 1 | 1 | 2 | 70 | 50 |
| p3 | 3 | 3 | 1 | 80 | 5 |
| p4 | 4 | 2 | 2 | 50 | 10 |
| p5 | 1 | 1 | 4 | 65 | 30 |
| Cafe | Taste | Environment | Service | Per Capita Price | Road Network Distance/m |
|---|---|---|---|---|---|
| A |   | - |  | - |  |
| B |   |  |  |  |  |
| C |  |   |  | - | - |
| D |  | - | - | - | - |
| E |  | - |  |  |   |
| Parameters | Default | Range |
|---|---|---|
| k | 10 | 5, 10, 15, 20, 25, 30, 35 |
| The data point number | 500 k | 50 k, 100 k, 500 k, 1 M, 1.5 M, 2 M |
| The query object number | 10 | 5, 10, 15, 20, 25, 30, 35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhang, X.; Li, S. Multiuser Incomplete Preference K-Nearest Neighbor Query Method Based on Differential Privacy in Road Network. ISPRS Int. J. Geo-Inf. 2023, 12, 282. https://doi.org/10.3390/ijgi12070282
Zhang L, Zhang X, Li S. Multiuser Incomplete Preference K-Nearest Neighbor Query Method Based on Differential Privacy in Road Network. ISPRS International Journal of Geo-Information. 2023; 12(7):282. https://doi.org/10.3390/ijgi12070282
Chicago/Turabian StyleZhang, Liping, Xiaojing Zhang, and Song Li. 2023. "Multiuser Incomplete Preference K-Nearest Neighbor Query Method Based on Differential Privacy in Road Network" ISPRS International Journal of Geo-Information 12, no. 7: 282. https://doi.org/10.3390/ijgi12070282
APA StyleZhang, L., Zhang, X., & Li, S. (2023). Multiuser Incomplete Preference K-Nearest Neighbor Query Method Based on Differential Privacy in Road Network. ISPRS International Journal of Geo-Information, 12(7), 282. https://doi.org/10.3390/ijgi12070282





