Quantitative Relations between Morphostructural Similarity Degree and Map Scale Change in Contour Clusters in Multi-Scale Map Space
Abstract
1. Introduction
2. Datasets and Their Pre-Processing
2.1. Experimental Datasets
2.2. Pre-Processing of the Dataset
3. Methodology
3.1. Extraction of Terrain Line
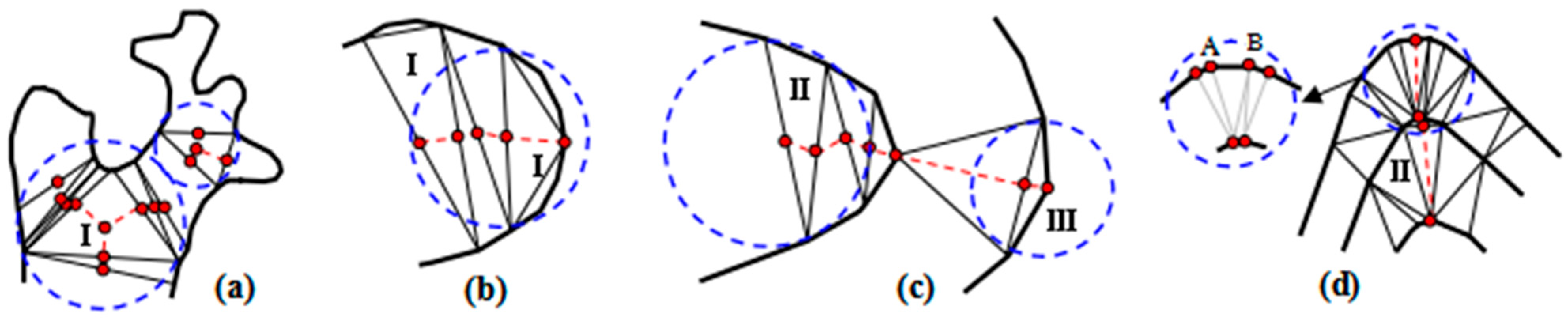
3.1.1. Recognition of Contour Curve Cluster
3.1.2. Detection of Terrain Feature Points
3.1.3. Tracking and Connection of Terrain Line
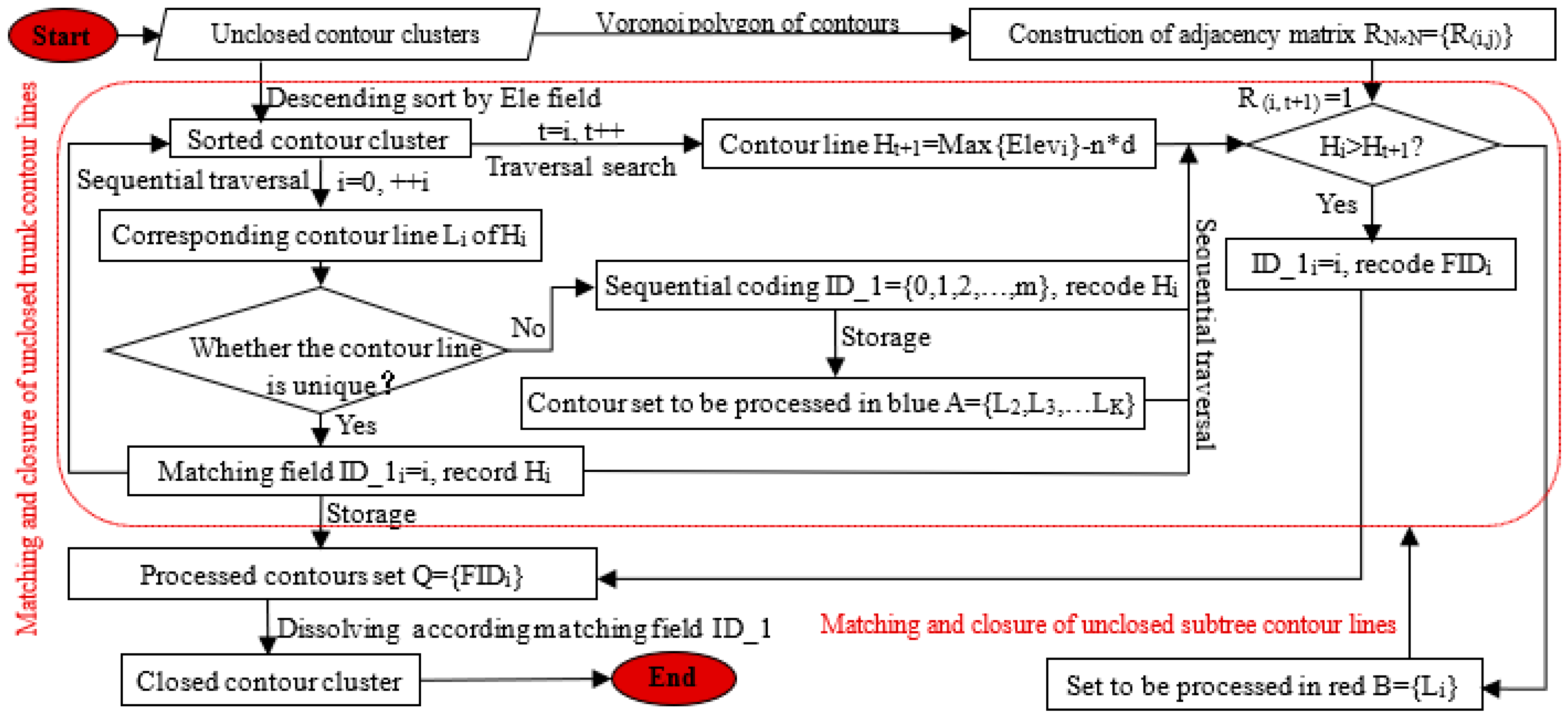
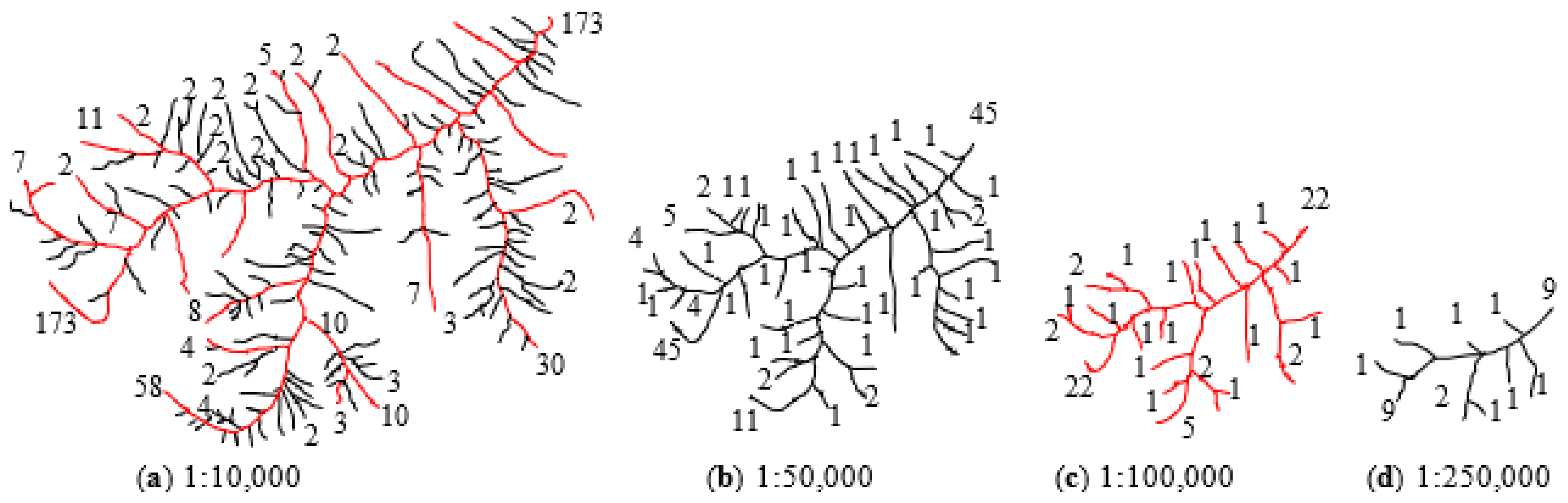
3.2. Construction of Hierarchical Tree of Terrain Lines
3.3. Quantitative Expression Method of Multi-Scale Contour Cluster Morphostructural Similarity
3.3.1. Topological Similarity
3.3.2. Directional Similarity
3.3.3. Distance Similarity
3.3.4. Attribute Similarity
3.3.5. Multi-Scale Morphostructural Similarity Degree
4. Experiments and Results
4.1. Results Analysis of Pre-Processing
4.2. Extraction Results Accuracy Evaluation of Terrain Lines
4.3. Quantitative Trends of Multi-Scale Morphostructural Indices
4.3.1. Neighbor Scale Morphostructural Indices
- (1)
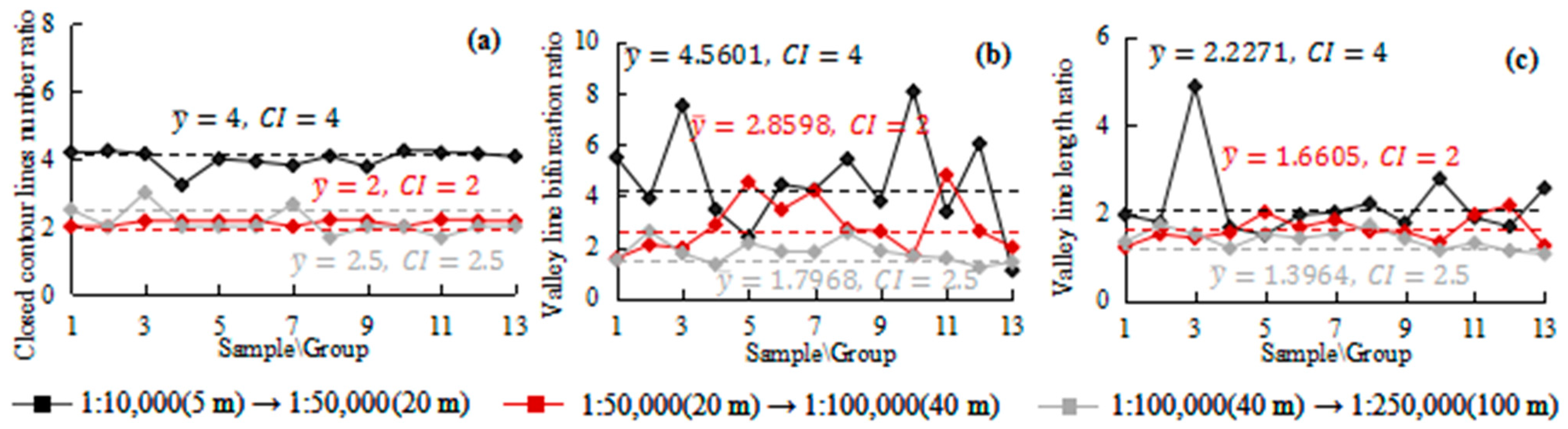
- In contrast to the bifurcation ratio and length ratio of neighbor scale valley lines, the average of closed contour lines number ratio is equal to the contour interval ratio (CI) of neighbor scale contour clusters. However, the number ratio of neighbor scale closed contour lines is not a constant; therefore, it fluctuates around the average of neighbor scale contour interval ratio due to differences in surface relief, steep slope, and surface fragmentation [7]. For instance, as the contour cluster is generalized from 1:100,000 to 1:250,000, the neighbor scale closed contour lines number ratio fluctuates around 2.5 (Figure 8a).
- (2)
- Although the length ratio and bifurcation ratio of neighbor scale valley lines both fluctuate around their average, the fluctuation degree of the latter among different samples is greater than the former (Figure 8c). The maximum fluctuation range of the latter is [1.1, 8.0588] with a difference of 6.9588 (Figure 8b). There is no specific proportional relationship between the neighbor scale morphostructural indices and the corresponding contour interval ratio or contour interval distance ratio of neighbor scale contour clusters. Consequently, the following sections further investigate the changing trends of multi-scale morphostructural similarity indices with map scale.
4.3.2. Multi-Scale Morphostructural Indices
- (1)
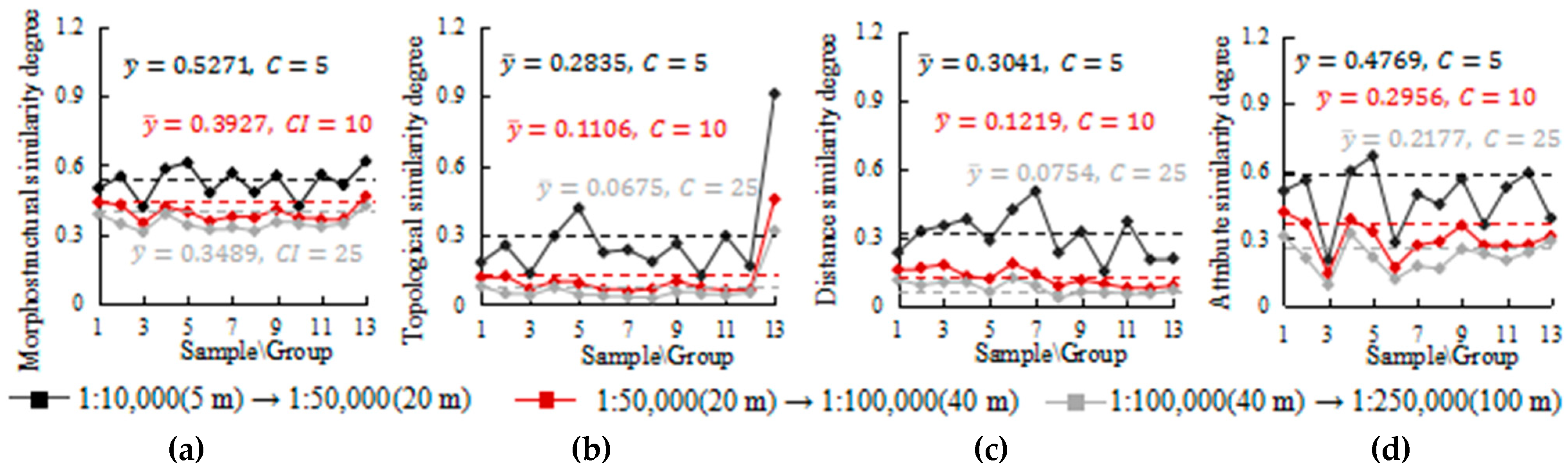
- Multi-scale morphostructural similarity indices of contour cluster gradually decrease with the increasing map scale change, regardless of multi-scale morphostructural similarity degree or other measures, such as distance similarity degree. For example, the average of multi-scale morphostructural similarity degree decreases from 0.5271 to 0.3849 as the map scale change increases from 5 to 25 (Figure 9a).
- (2)
- Compared with the same index of different map scale changes, the standard deviation of multi-scale morphostructural similarity indices decreases with the increasing map scale change. For example, the multi-scale morphostructural similarity degree decreases from 0.0666 to 0.0321 as the map scale change increases from 5 to 25. However, the variation coefficients of other indices decrease at first and then increase, except for topological similarity degree (Table 6). This indicates that the dispersion degree between multi-scale morphostructural similarity degree and its average gradually decreases with the increase in map scale change (black line > red > gray) (Figure 9). However, the degree of relative fluctuation among different samples decreases from 0.1265 to 0.0884 at first, and then increases from 0.0884 to 0.0923 (Table 6). Therefore, when the map scale change (C) is 10, the fluctuation degree of morphostructural similarity degree is the gentlest, which is confirmed by Figure 9.
- (3)
- Compared with different indices of the same map scale change, the standard deviation and variation coefficient of multi-scale morphostructural similarity degree are both minimum (Table 6). This indicates that the agglomeration degree of multi-scale morphostructural similarity degree is the largest, and all fluctuate around its average. For example, when the map scale change is 10, all of the multi-scale morphostructural similarity degree fluctuates around 0.3927 (Figure 9a). This conclusion further indicates that the relations between morphostructural similarity degree and map scale change between multi-scale contour clusters can be expressed quantitatively by the same function. Therefore, the following contents further formulate the quantitative relations between morphostructural similarity degree and map scale change in multi-scale contour clusters.
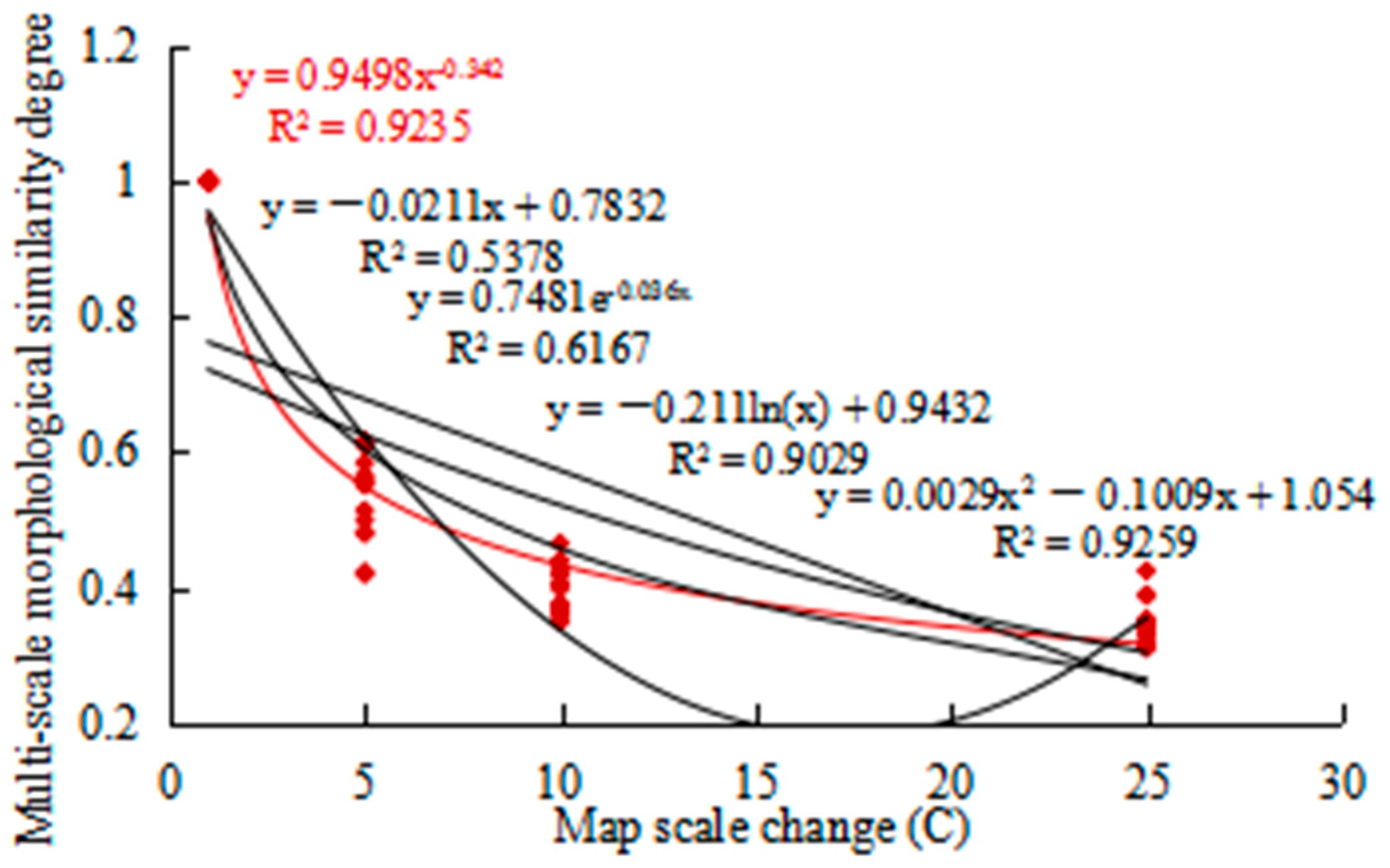
4.4. Quantitative Relations between Multi-Scale Morphostructural Similarity Degree and Map Scale Change
4.4.1. Quantitative Relations
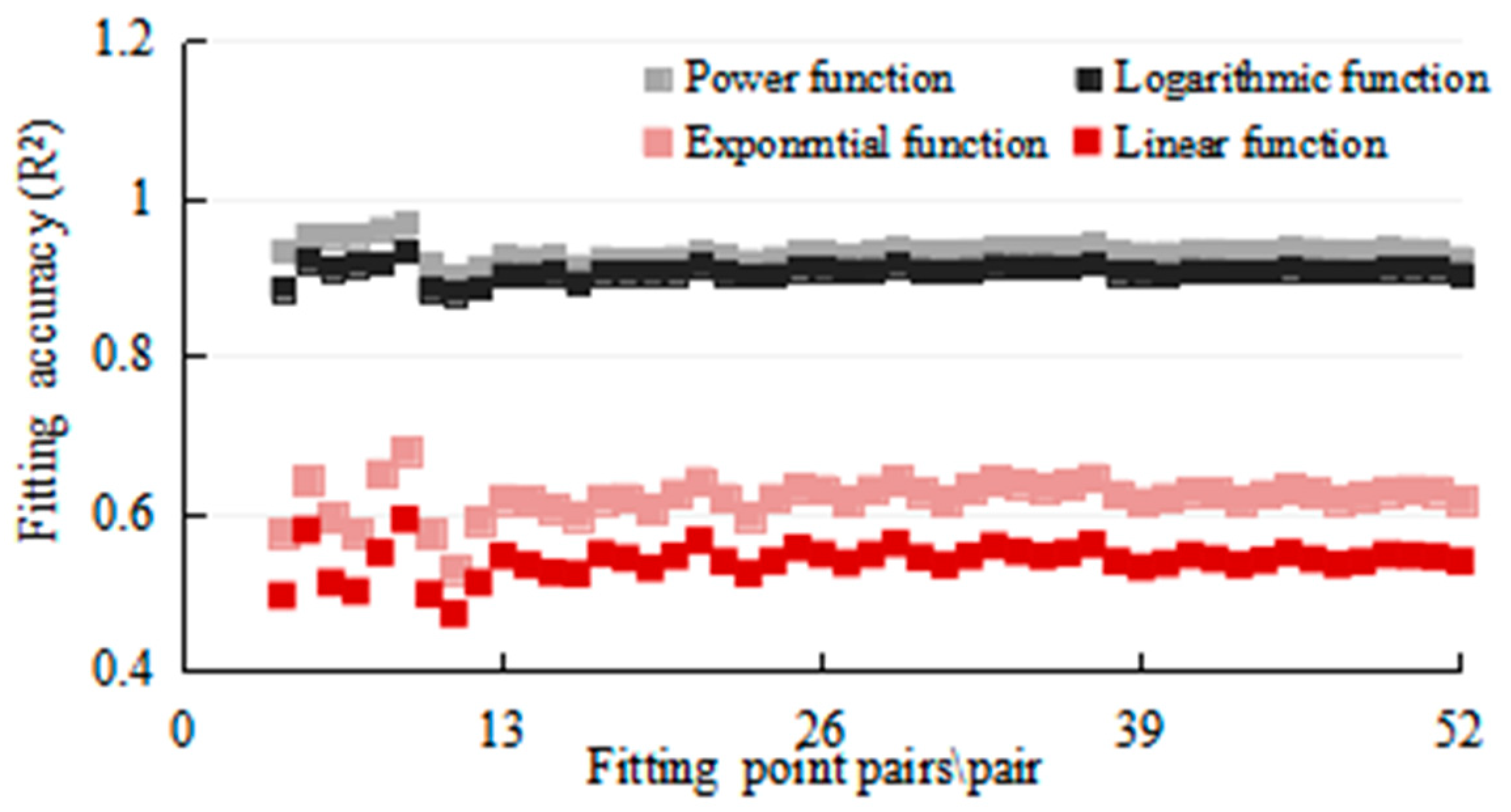
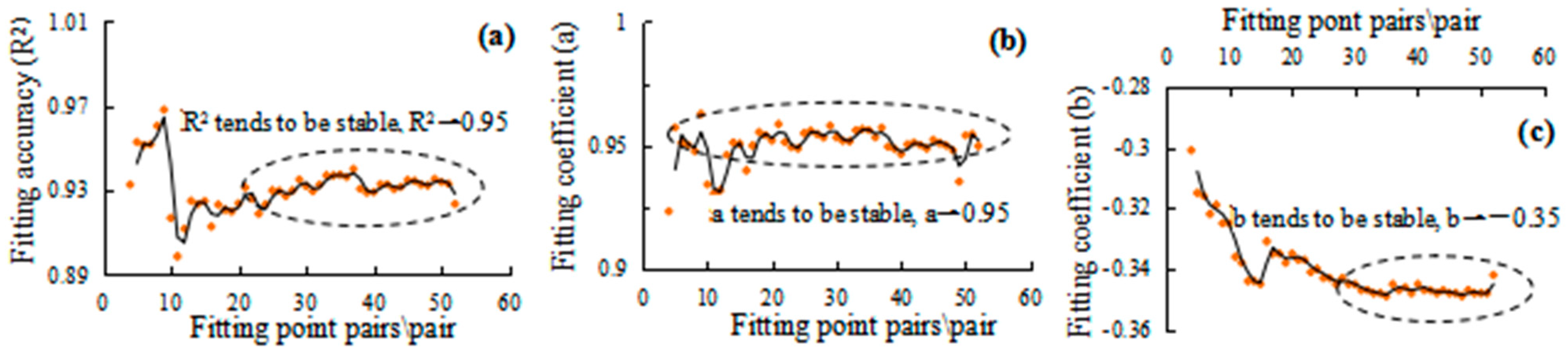
4.4.2. Influence of Sample Size on the Types and Precisions of Fitting Function
5. Discussion
6. Conclusions and Future Works
6.1. Conclusions
6.2. Future Works
- (1)
- Conducting more experiments to improve the accuracy and adaptability of the proposed models and formulas. Scale changes are an inductive behavior of spatial thinking, and it is necessary to obtain universal, unified, and high-level spatial knowledge from a large number of specific, individual, and underlying data through granularity filtering, hierarchical merging, and linguistic generalization [51]. Therefore, it would be more useful to perform the analysis on more map samples. Additionally, it is essential to explore the extent to which the preservation of geomorphological characteristics at smaller scales is possible, as the nature of maps is changing from topographic to general geographic.
- (2)
- Is it possible to design one model that can calculate the spatial similarity degree of individual point objects, and/or object groups, such as point clouds, parallel line clusters, intersected line networks, tree-like networks discrete polygon groups, by taking map scale change as an independent variable? Previous studies on models for spatial similarity relations in multi-scale map spaces indicated that there is a quantitative relationship between map scale change and spatial similarity degree. However, this quantitative relationship has not been determined, and some studies consider it to be a power function, while others consider it to be an exponential function.
- (3)
- It is worth exploring approaches for automatically obtaining the parameters used in the algorithms and operators that are not parameter free with the help of the models and formulae of multi-scale spatial similarity relations. Progress in this area will lay a good foundation for full automation of map generalization.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, R.Z. Spatial Analysis; Higher Education Press: Beijing, China, 2001. [Google Scholar]
- Yan, H.W. Fundamental theories of spatial similarity relations in multi-scale map spaces. Chin. Geogr. Sci. 2010, 20, 18–22. [Google Scholar] [CrossRef]
- Rodríguez, A.; Egenhofer, M. Determining semantic similarity among entity classes from different ontologies. IEEE Trans. Knowl. Data Eng. 2003, 15, 442–456. [Google Scholar] [CrossRef]
- Rodríguez, A.; Egenhofer, M. Comparing geospatial entity classes: An asymmetric and context-dependent similarity measure. Int. J. Geogr. Inf. Sci. 2004, 18, 229–256. [Google Scholar] [CrossRef]
- Yan, H.W.; Li, J. Spatial Similarity Relations in Multi-Scale Map Spaces; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Chehreghan, A.; Abbaspour, R.A. A geometric-based approach for road matching on multi-scale datasets using a genetic algorithm. Cartogr. Geogr. Inf. Sci. 2018, 45, 255–269. [Google Scholar] [CrossRef]
- Wang, R.; Yan, H.W.; Lu, X.M. Topological relations quantitative expression method of multi-scale contour cluster. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 579–588. [Google Scholar]
- Li, W.W.; Raskin, R.; Goodchil, M.F. Semantic similarity measurement based on knowledge mining: An artificial neural net approach. Int. J. Geogr. Inf. Sci. 2012, 26, 1415–1435. [Google Scholar] [CrossRef]
- Li, B.; Fonseca, F. TDD: A comprehensive model for qualitative spatial similarity assessment. Spat. Cogn. Comput. 2006, 6, 31–62. [Google Scholar] [CrossRef]
- Yuan, M.; Nara, A.; Bothwell, J. Space-time representation and analytics. Ann. GIS 2014, 20, 1–9. [Google Scholar] [CrossRef]
- Yan, X.F.; Ai, T.H.; Yang, M.; Yin, H.M. A graph convolution neural network for classification of building patterns using spatial vector data. ISPRS J. Photogamm. Remote Sens. 2019, 150, 259–273. [Google Scholar] [CrossRef]
- Fan, H.C.; Yang, B.S.; Zipf, A.; Rousell, A. A polygon-based approach for matching openstreetmap road network with regional transit authority data. Int. J. Geogr. Inf. Sci. 2016, 30, 748–764. [Google Scholar] [CrossRef]
- Zhang, M. Methods and Implementations of Road-Network Matching; Technical University of Munich: Munich, Germany, 2009. [Google Scholar]
- Guo, W.Y.; Liu, H.Y.; Sun, Q.; Yu, A.Z.; Ding, Z.Y. A multisource contour matching method considering the similarity of geometric features. Acta Geod. Cartogr. Sin. 2019, 48, 643–653. [Google Scholar]
- Yan, H.W.; Wang, J.Y. Description Approaches and Automates Generalization Algorithms for Groups of Map Objects; The Science Press: Beijing, China, 2009. [Google Scholar]
- Wang, J.Y.; Wu, F. Principle and Method of Digital Map Automatic Cartography Generalization; PLA Piblishing House: Beijing, China, 1998. [Google Scholar]
- Wang, J.Y.; Li, Z.L.; Wu, F. Progress in Digital Map Generalization; The Science Press: Beijing, China, 2011. [Google Scholar]
- Li, Z.L.; Sui, H.G. An integrated technique for automated generalization of contour maps. Cartogr. J. 2000, 37, 29–37. [Google Scholar] [CrossRef]
- Guo, Q.S.; Wu, H.H.; Li, P.C. Spatial relation rules and progressive graphic simplification of contours. Geomat. Inf. Sci. Wuhan Univ. 2000, 25, 31–34. [Google Scholar]
- Wu, H.H. Research on Basic Theory and Technique of Map Generalization; Surveying and Mapping Publishing House: Beijing, China, 2004. [Google Scholar]
- Ai, T.H. The drainage network extraction from contour lines for contour line generalization. ISPRS J. Photogramm. Remote Sens. 2007, 62, 93–103. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, Q.K.; Lan, M. Study on the algorithm of contour curvature in topographic map. Res. Soil Water Conserv. 2014, 21, 125–129. [Google Scholar]
- Ai, T.H.; Li, J.Z. A DEM generalization by minor valley branch detection and grid filling. ISPRS J. Photogramm. Remote Sens. 2010, 65, 198–207. [Google Scholar] [CrossRef]
- Chen, Y.M.; Zhou, Q.M. A scale-adaptive DEM for multi-scale terrain analysis. Int. J. Geogr. Inf. Sci. 2013, 27, 1329–1348. [Google Scholar] [CrossRef]
- Guo, W.Y.; Liu, H.Y.; Sun, Q.; Yu, A.Z.; Chen, H.X. A Contour Group Mixed Similarity Measurement Model for Region Incremental Updating. J. Geo Inf. Sci. 2019, 21, 147–156. [Google Scholar]
- Shu, F.G.; Long, Y.; Zhou, T.; Cao, Y. An extraction method of catchment basin based on cooperation of contour cluster and river network in river generalization. Acta Geod. Cartogr. Sin. 2013, 42, 774–781. [Google Scholar]
- Wu, H.H. GIS and Basic Model and Algorithm of Map Information Generalization; Wuhan University Press: Wuhan, China, 2012. [Google Scholar]
- Gao, J. Cartographic Tracing: Collection of Academician Gaojun; Survey and Mapping Publishing House: Beijing, China, 2012. [Google Scholar]
- Fei, L.F. Experiments of group-generalization of contour lines on topographic maps. J. Wuhan Tech. Univ. Surv. Mapp. 1993, 18, 6–22. [Google Scholar]
- Yan, H.W.; Shen, Y.Z.; Li, J. Approach to calculating spatial similarity degrees of the same river basin networks on multi-scale maps. Geocarto Int. 2016, 31, 765–782. [Google Scholar] [CrossRef]
- Gao, X.R.; Yan, H.W.; Lu, X.M. Semantic similarity measurement for building polygon aggregation in multi-scale map space. Acta Geod. Cartogr. Sin. 2022, 51, 95–103. [Google Scholar]
- Fan, H.C.; Zipf, A.; Fu, Q.; Neis, P. Quality assessment for building footprints data on OpenStreetMap. Int. J. Geogr. Inf. Sci. 2014, 28, 700–719. [Google Scholar] [CrossRef]
- Wu, Z. Introduction Theory to Modern Geomorphology; The Science Press: Beijing, China, 2009. [Google Scholar]
- Chen, C.Y. The physiognomy types and characteristics of loess in middle-east Gansu province. J. Ningde Teach. Coll. Nat. Sci. 2004, 3, 380–382. [Google Scholar]
- Qiao, C.F.; Zhao, R.L.; Chen, J.; Chen, Y.H. A voronoi interior adjacency-based approach for generating a contour tree. Geomat. Inf. Sci. Wuhan Univ. 2005, 30, 801–804. [Google Scholar]
- McMaster, R.B.; Shea, K.S. Generalization in Digital Cartography; Association of American Geographers: Washington, DC, USA, 1992. [Google Scholar]
- Li, W.J.; Qiu, J.; Lin, Z.Y.; Long, Y. Approach of curve bends recognition and contour cluster structuralization. Acta Geod. Cartogr. Sin. 2013, 42, 295–303. [Google Scholar]
- Wu, F.; Li, W.M. Representation of topological spatial relations between contour lines based on terrain features. Eng. J. Wuhan Univ. 2006, 39, 140–144. [Google Scholar]
- Tang, L. Automatic extraction of specific geomorphologic elements from contours. In Proceedings of the 5th SDH Conference, Charleston, SC, USA, 3–7 August 1992; Volume 2, pp. 554–566. [Google Scholar]
- Yuan, K.S. Modern Cartography Course; The Science Press: Beijing, China, 2007. [Google Scholar]
- Zhang, Q.N.; Quan, H. Construction and application of river-tree. Acta Sci. Nat. Univ. Sunyatseni 2005, 44, 101–104. [Google Scholar]
- Horton, H.R. Erosional development of streams and their drainage basins-hydrophysical approach to quantitative morphology. GSA Bull 1945, 56, 275–370. [Google Scholar] [CrossRef]
- Serres, B.D.; Roy, A. Flow direction and branching geometry at junctions in Dendritic river network. Prof. Geogr. 1990, 42, 149–201. [Google Scholar] [CrossRef]
- Thomson, R.; Brooks, R. Exploiting perceptual grouping for map analysis, understanding and generalization: The case of road and river networks. In Graphics Recognition: Algorithms and Applications; Volume 2390 of Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2002; pp. 141–150. [Google Scholar]
- Zhang, Q.N. Generalization of drainage network with density differences. Acta Geod. Cartogr. Sin. 2006, 35, 191–196. [Google Scholar]
- Huang, X.Q. Hydrology; Higher Education Press: Beijing, China, 1985. [Google Scholar]
- Liao, R. Hydrologic Principle; China Waterpower Press: Beijing, China, 2007. [Google Scholar]
- Wu, F.; Zhu, K.P. Geometric accuracy assessment of linear features’ simplification algorithms. Geomat. Inf. Sci. Wuhan Univ. 2008, 33, 600–603. [Google Scholar]
- Joao, E.M. Causes and Consequences of Map Generalization; Taylor and Francis: London, UK, 1998. [Google Scholar]
- Nigel, W. Geographical Data Analysis; Wiley & Sons Ltd.: Hoboken, NJ, USA, 1995. [Google Scholar]
- Ai, T.H.; Huang, Y.L.; Huang, Y.F. The hierarchical watershed partitioning and generalization of river network. Acta Geod. Cartogr. Sin. 2007, 36, 231–243. [Google Scholar]




| Research Fields | Data Structure (Specific Research Orientation) | Key Issues |
|---|---|---|
| Contour generalization | DEM or contours (mainly focuses on raster datasets, including automation of generalization algorithm [19,20,21,22,23,24,26], semi-automatic control of generalization algorithm and process [23,27,28], curve bends recognition [22,29], and line simplification [18,29]. | Research in this field has reached a mature stage. (1) However, most existing algorithms rely on the Töpfer rule, which is based on cartographic experience to determine the selection quantity. (2) The reliability of the generalization results is heavily dependent on the individual experience of the cartographer. (3) Previous research has mainly focused on DEM and lacks exploration based on vector contours. The semi-automatic generalization algorithm falls short in terms of automation, intelligence, and generalization efficiency of the software. |
| Spatial similarity relation and its application of other individual objects or object groups | Raster or vector (basic theories [1,2,5], mixed similarity [5,30], semantic similarity [8,31], topological similarity [7], geometric similarity [6,11], spatial similarity assessment [9], human spatial cognition [10], pattern recognition [11,12], and spatial data matching [6,12,13,14,32]. | Some achievements have been reached. (1) However, researchers have mainly focused on the quantitative measurement of spatial similarity relations using geometric indices of objects, such as length, area, sinuosity, curvature, etc.; (2) In the process of map generalization, the different geographical features of different objects have been ignored. |
| Spatial similarity relation between contours and its application | Raster or contours (mixed similarity [5,25], topological similarity [7], geometric feature similarity of multi-source contours, and contour matching [14]. | Relevant researches are rare. (1) Additionally, previous research has primarily concentrated on the multi-source spatial similarity relations of contours generated from raster datasets, such as ASTER GDEM and SRTM. (2) Only traditional geometric indices of contour line, such as length, sinuosity, and longest common subsequence, etc., were considered, whereas the “clustering nature” and “bending nesting relations” between contour lines were ignored. |
| Sample | Map Scale | A (km2) | NU | NC | Sample | A (km2) | NU | NC | Sample | A (km2) | NU | NC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1:10,000 | 1.2105 | 162 | 42 | 6 | 1.8084 | 107 | 51 | 11 | 2.3252 | 258 | 46 |
| 1:50,000 | 34 | 10 | 26 | 13 | 21 | 11 | ||||||
| 1:100,000 | 16 | 5 | 10 | 6 | 8 | 5 | ||||||
| 1:250,000 | 4 | 2 | 4 | 3 | 7 | 3 | ||||||
| 2 | 1:10,000 | 3.4408 | 103 | 51 | 7 | 3.9368 | 263 | 61 | 12 | 2.8006 | 199 | 54 |
| 1:50,000 | 23 | 12 | 35 | 16 | 22 | 13 | ||||||
| 1:100,000 | 7 | 6 | 13 | 8 | 10 | 6 | ||||||
| 1:250,000 | 3 | 3 | 5 | 3 | 3 | 3 | ||||||
| 3 | 1:10,000 | 5.3838 | 124 | 54 | 8 | 2.5028 | 103 | 45 | 13 | 2.3345 | 185 | 53 |
| 1:50,000 | 27 | 13 | 30 | 11 | 22 | 13 | ||||||
| 1:100,000 | 13 | 6 | 10 | 5 | 8 | 6 | ||||||
| 1:250,000 | 3 | 2 | 3 | 3 | 5 | 3 | ||||||
| 4 | 1:10,000 | 2.4095 | 99 | 42 | 9 | 2.0133 | 259 | 49 | ||||
| 1:50,000 | 28 | 13 | 31 | 13 | ||||||||
| 1:100,000 | 9 | 6 | 12 | 6 | ||||||||
| 1:250,000 | 5 | 3 | 6 | 3 | ||||||||
| 5 | 1:10,000 | 3.0428 | 99 | 52 | 10 | 1.7728 | 94 | 51 | ||||
| 1:50,000 | 28 | 13 | 18 | 12 | ||||||||
| 1:100,000 | 9 | 6 | 8 | 6 | ||||||||
| 1:250,000 | 5 | 3 | 5 | 3 |
| FID | ID_1 | Elev | FID | ID_1 | Elev | FID | ID_1 | Elev |
|---|---|---|---|---|---|---|---|---|
| 110 | 0 | 4460 | 127 | 10 | 4280 | 154 | 14 | 4200 |
| 108 | 1 | 4440 | 137 | 11 | 4260 | 159 | 14 | 4200 |
| 7 | 2 | 4420 | 134 | 11 | 4260 | 171 | 15 | 4180 |
| 20 | 3 | 4400 | 135 | 11 | 4260 | 178 | 15 | 4180 |
| 8 | 4 | 4380 | 145 | 12 | 4240 | 175 | 15 | 4180 |
| 11 | 5 | 4360 | 148 | 12 | 4240 | 173 | 15 | 4180 |
| 107 | 6 | 4340 | 147 | 12 | 4240 | 172 | 15 | 4180 |
| 23 | 7 | 4320 | 146 | 12 | 4240 | 170 | 15 | 4180 |
| 113 | 8 | 4320 | 185 | 13 | 4220 | 167 | 16 | 4160 |
| 116 | 9 | 4300 | 188 | 13 | 4220 | 168 | 16 | 4160 |
| 115 | 9 | 4300 | 187 | 13 | 4220 | 166 | 16 | 4160 |
| 124 | 9 | 4300 | 189 | 13 | 4220 | 112 | 17 | 4140 |
| 125 | 10 | 4280 | 155 | 14 | 4200 | 99 | 18 | 4120 |
| 128 | 10 | 4280 | 158 | 14 | 4200 | 105 | 19 | 4100 |
| FID | ID_1 | Elev |
|---|---|---|
| 14 | 21 | 4360 |
| 15 | 20 | 4340 |
| 113 | 8 | 4320 |
| Samples | 1:10,000 | 1:50,000 | ||||||
|---|---|---|---|---|---|---|---|---|
| LR | SD | PE\km | SMD | LR | SD | PE\km | SMD | |
| Sample 1 | 1.0150 | 0.9852 | 0.0024 | 0.6532 | 0.9727 | 1.0279 | 0.0102 | 0.4028 |
| Sample 5 | 0.9686 | 0.9987 | 0.0026 | 0.8945 | 0.9195 | 1.1130 | 0.0098 | 0.7207 |
| Sample 9 | 0.9691 | 1.1363 | 0.0100 | 0.4785 | 0.9327 | 1.2007 | 0.0027 | 0.4564 |
| Indices | C | Indices | C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 0.2835 | 0.3041 | 0.4769 | 0.5271 | 5 | 0.7421 | 0.3334 | 0.2922 | 0.1265 | ||
| 10 | 0.1106 | 0.1219 | 0.2956 | 0.3927 | 10 | 0.9973 | 0.3202 | 0.2481 | 0.0884 | ||
| 25 | 0.0675 | 0.0754 | 0.2177 | 0.3489 | 25 | 1.1865 | 0.3529 | 0.3002 | 0.0923 | ||
| 5 | 2.2103 | 0.1014 | 0.1393 | 0.0666 | |||||||
| 10 | 0.1103 | 0.0391 | 0.0733 | 0.0347 | |||||||
| 25 | 0.0801 | 0.0266 | 0.0653 | 0.0321 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Yan, H.; Lu, X. Quantitative Relations between Morphostructural Similarity Degree and Map Scale Change in Contour Clusters in Multi-Scale Map Space. ISPRS Int. J. Geo-Inf. 2023, 12, 256. https://doi.org/10.3390/ijgi12070256
Wang R, Yan H, Lu X. Quantitative Relations between Morphostructural Similarity Degree and Map Scale Change in Contour Clusters in Multi-Scale Map Space. ISPRS International Journal of Geo-Information. 2023; 12(7):256. https://doi.org/10.3390/ijgi12070256
Chicago/Turabian StyleWang, Rong, Haowen Yan, and Xiaomin Lu. 2023. "Quantitative Relations between Morphostructural Similarity Degree and Map Scale Change in Contour Clusters in Multi-Scale Map Space" ISPRS International Journal of Geo-Information 12, no. 7: 256. https://doi.org/10.3390/ijgi12070256
APA StyleWang, R., Yan, H., & Lu, X. (2023). Quantitative Relations between Morphostructural Similarity Degree and Map Scale Change in Contour Clusters in Multi-Scale Map Space. ISPRS International Journal of Geo-Information, 12(7), 256. https://doi.org/10.3390/ijgi12070256






