1. Introduction
The Voronoi diagram (VD) is one of the fundamental geographical constructions for partitioning a geographical space through a competitive means [
1,
2,
3,
4]. Specifically, the VD partitions the geographic space into a set of Voronoi regions based on a given set of points of interest, also known as generators. Each Voronoi region contains all the locations that share the same nearest generator, allowing for space tessellation and providing an adjacency structure for topology generation [
5]. In addition, a Voronoi region can be used as container for geographical entities, making it an effective indexing structure for organizing spatial data. Due to these unique characteristics, the VD has been widely used in various geographical applications, such as mobile phone data analysis [
6], facility service area delimitations [
7], spatial data mining [
8,
9], and etc.
The order
k Voronoi diagram (OkVD) is a generalization of the VD that has also received significant attention in the literature [
1,
10,
11]. Given a set of generators, the OkVD is meant to partition the geographical space into a set of order
k Voronoi regions (OkVR), where all locations within an OkVR share the same
k nearest generators. These generators are determined by their order of proximity to the location, i.e., the first nearest generator, the second nearest generator, and so on until the
kth nearest generator. This OkVD provides an effective tool to determine
k nearest generators for any location, which is a critical step for numerous spatial analysis tasks, such as spatial interpolations [
12], accessibility evaluations [
13], and
k nearest neighbor queries [
14,
15,
16]. Given the broad applications of the OkVD in the geographical analysis, it is therefore necessary to develop efficient algorithms for constructing OkVDs in real-world geographical spaces.
In the literature, efficient algorithms for constructing Voronoi diagrams (VDs) have been the subject of much research. Early studies focused on the construction of VDs in homogeneous and isotropic planar spaces, where the distance between any two locations is measured by Euclidean distance [
3,
17]. However, recognizing that movements in urban areas is generally constrained by road networks, Erwig [
18] first proposed a network Voronoi diagram (NVD) model for partitioning the urban geographical space. The NVD model quantifies distances between any two locations in the road network explicitly by using shortest path algorithms to compute the network distance [
19]. Building on this work, Okabe et al. [
1] developed an efficient algorithm for constructing NVDs by modifying conventional shortest path algorithms. Ohsawa [
20] applied the concept of Order
k Voronoi region for solving the problem of
k nearest neighbor queries. As an alternative approach, Ai et al. [
2] proposed an NVD construction algorithm by discretizing each road link into a set of linear units of equal length and using the stream flowing approach to construct NVDs. Chen et al. [
21] proposed several new NVD models for partitioning the urban geographic space constrained by multi-mode public transport networks and developed effective algorithms for constructing NVDs in public transport networks.
To the best of our knowledge, there are few algorithms in the literature have been developed to construct order
k NVD (OkNVD) in real road networks, with the notable exception of Okabe et al. [
1]. For convenience, this algorithm is hereafter referred to as Okabe’s algorithm. This algorithm consists of two stages. In the first stage, the
k nearest generators for each node are determined by performing the one-to-all shortest path algorithm (e.g., Dijkstra’s algorithm)
times to construct completed one-to-all shortest path trees rooted at all generators, where |F| is the number of generators. The
k nearest generators for each node can be determined by sorting
shortest paths from all generators to the node. In the second stage, the OkNVD is constructed by determining all nodes and links belonging to each order
k network Voronoi region (OkNVR). The idea of a lower-bound envelope is introduced to divide boundary links that belongs to at least two OkNVRs. Although Okabe’s algorithm is straightforward and easy to implement, the first stage of Okabe’s algorithm tends to have computational overheads, because it calculates too many unnecessary shortest paths, given that
is generally much larger than the
k value. Furthermore, no detailed procedure was provided for implementing the idea of a lower-bound envelope method in the second stage.
Along the line of previous work [
1], this study proposes an effective and efficient algorithm for constructing OkNVD in road networks. The proposed algorithm also consists of two stages, which extends the previous algorithm in the following aspects.
A new one-to-all
k shortest path procedure is proposed in the first stage to efficiently determine the
k nearest generators at each node. As an extension of Okabe’s algorithm, the proposed procedure simultaneously constructs |F| shortest path trees in a single path searching process, sharing the same priority queue to coordinate the construction of shortest path trees from different generators. Unlike Dijkstra’s algorithm [
22], the proposed procedure closes a node after it has been selected from the priority queue
k times from different generators, allowing it to exactly determine the shortest paths from the
k nearest generators. This results in partial shortest path trees being constructed, improving Okabe’s algorithm. Furthermore, the proposed procedure can directly determine the order of k nearest generators according to their order of selection from the priority queue without the need for shortest path sorting at each node.
A new recursive procedure is introduced in the second stage to effectively divide boundary links into different OkNVRs. This study rigidly proves the hierarchical tessellation property of OkNVD. Specifically, each order j NVR is covered by a set of order j + 1 NVRs, and these order j + 1 NVRs are mutually exclusive except at the boundary points (j = 0, 1, …, k − 1). Using this hierarchical tessellation property, the introduced procedure, therefore, can recursively divide every boundary link into the order first, second, …, until the kth NVRs.
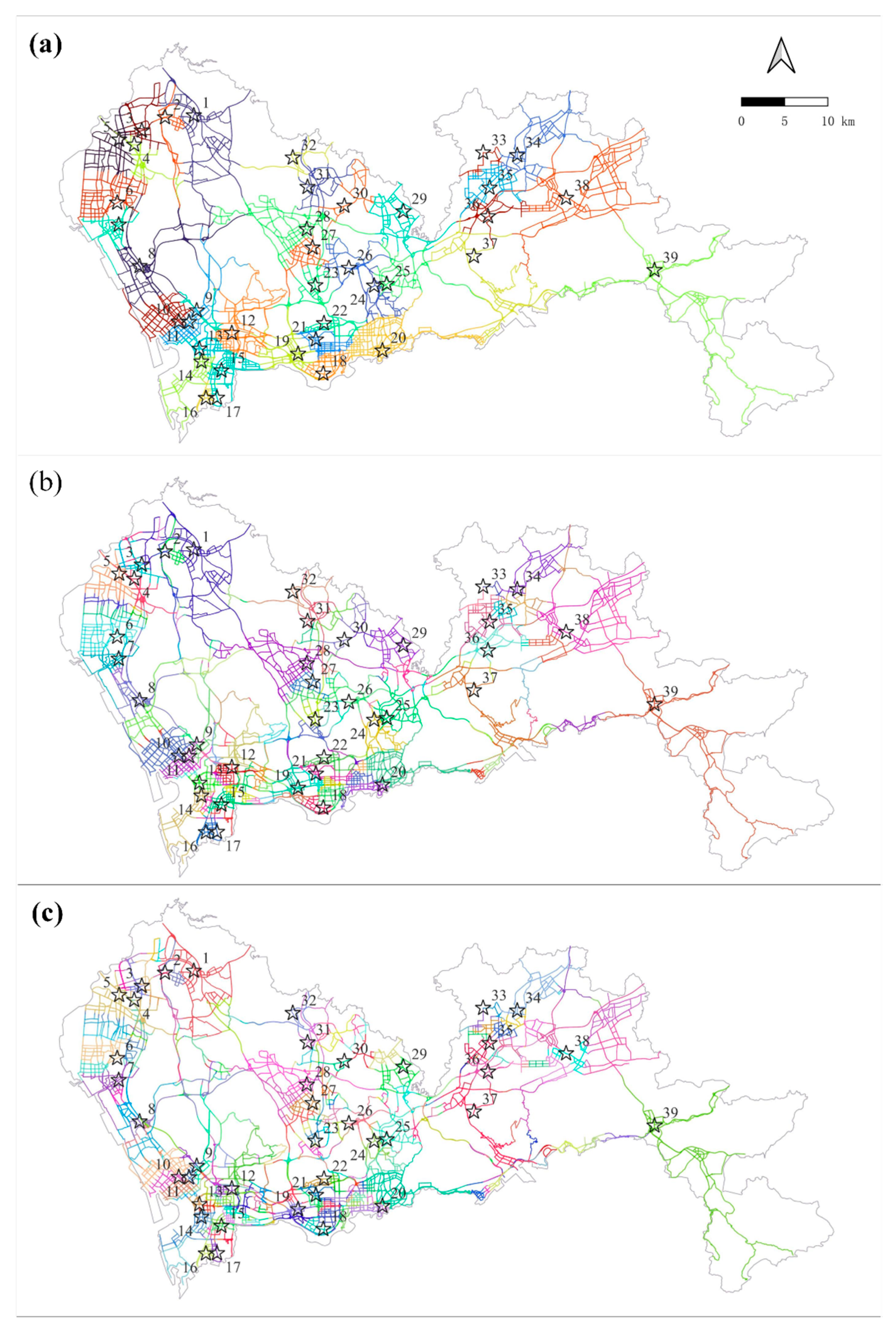
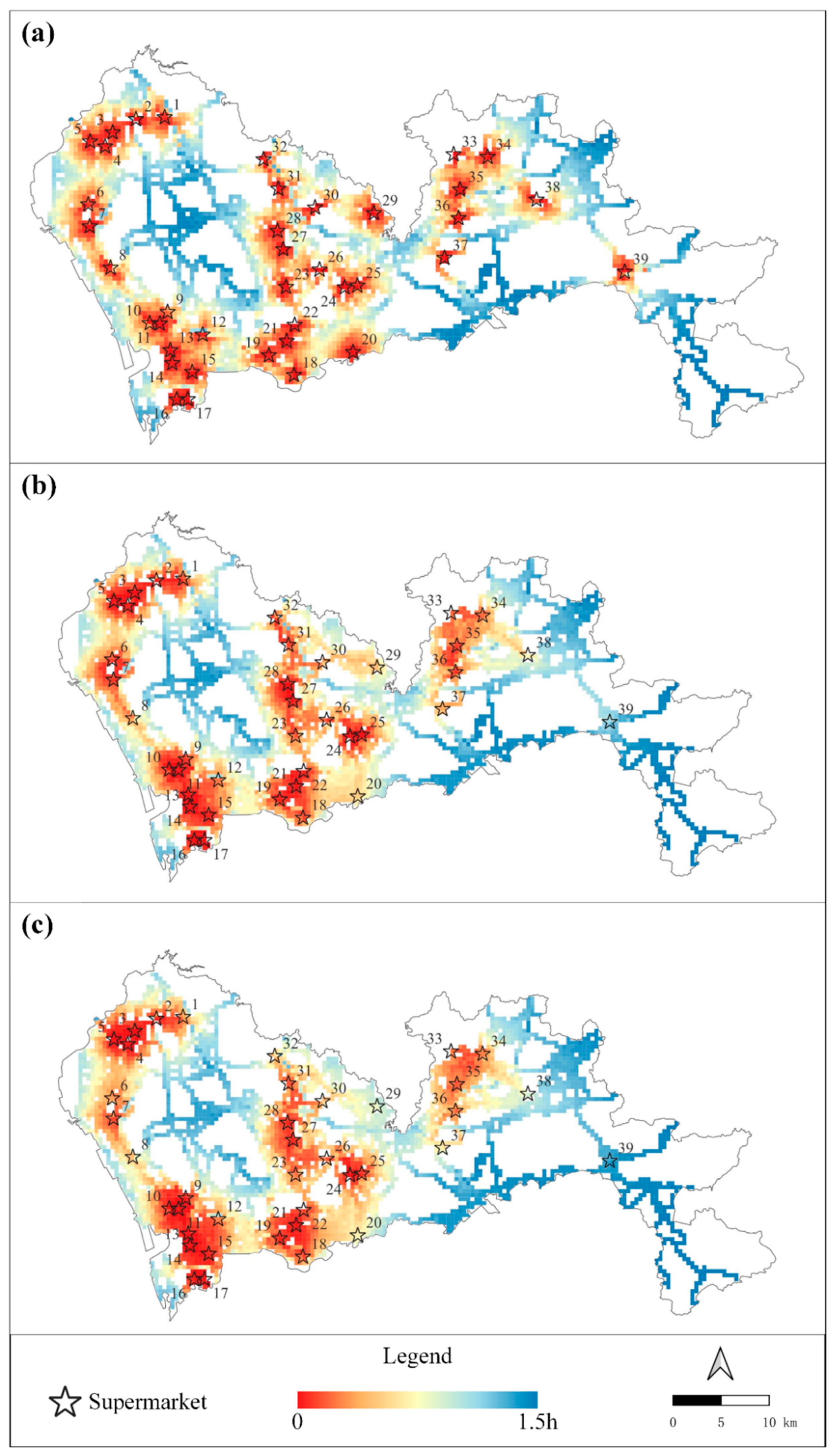
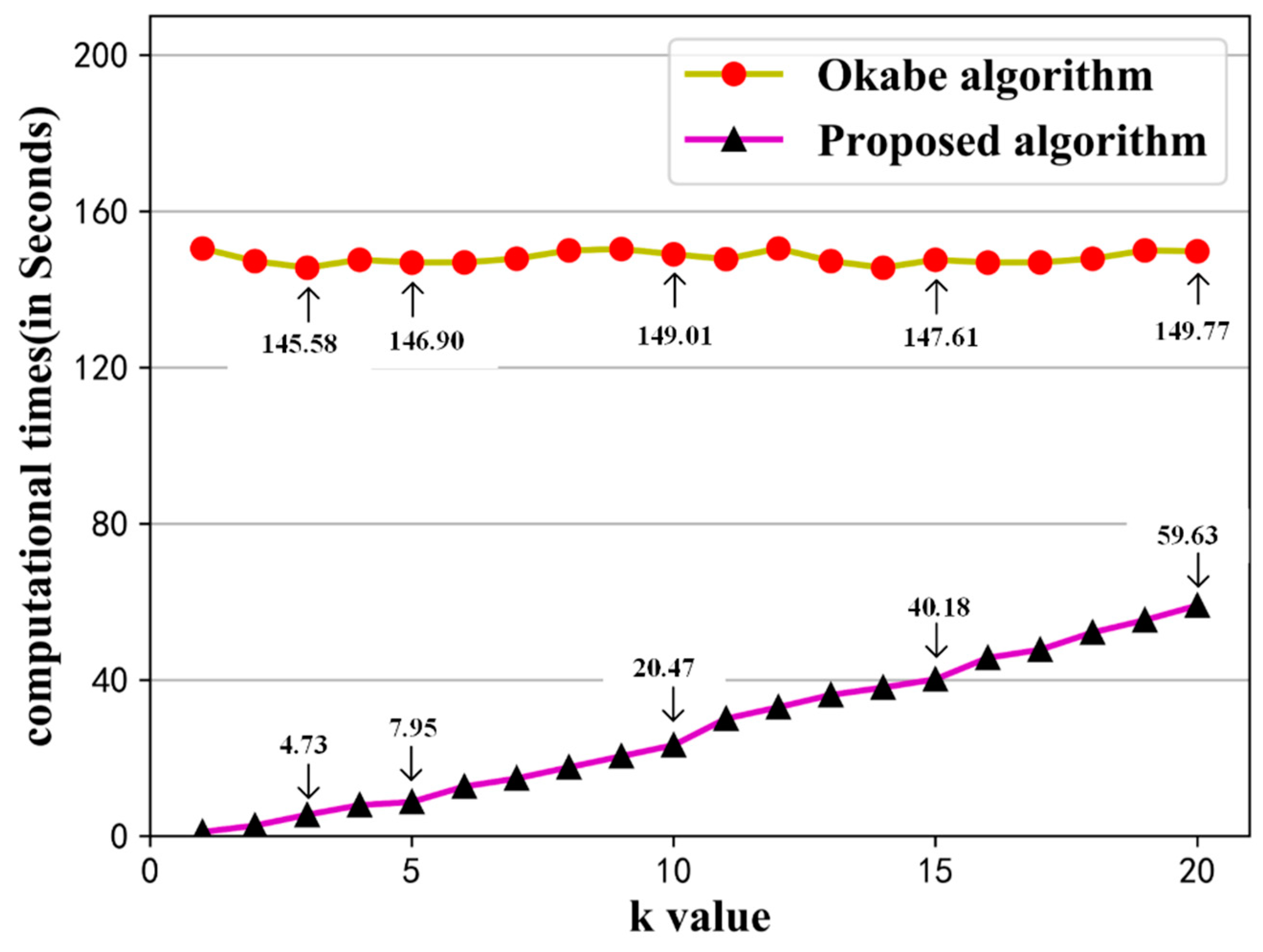
To demonstrate the applicability of the proposed OkNVD construction algorithm, a comprehensive case study of evaluating place-based accessibility is carried out in Shenzhen, a mega-city in China. Computational experiments are also conducted using five real road networks with various settings of k and values. Results show that the proposed OkVD algorithm performed significantly better than state-of-the-art algorithms.
The remainder of this article is organized as follows.
Section 2 gives the model formulation of OkNVD and proves its hierarchical tessellation property.
Section 3 describes the proposed OkNVD construction algorithm.
Section 4 reports the numerical example of OkNVD application in place-based accessibility, and computational experiments using five real road networks.
Section 5 presents the conclusions together with recommendations for future research in the area.
2. Model Formulation of Order k Network Voronoi Diagrams
The list of notations used in this article is summarized in Abbrevations. A road network can be represented by a directed graph,
, consisting of a set of nodes
, and a set of links
. Each link
has a tail node
and a head node
, and a positive link cost
(length or travel time). Each node
has a set of successor nodes
and a set of predecessor nodes
. Any location
in the road network can be represented as
using the linear reference technique [
23], where
is the relative position on the link
. The values of
and
refer to the tail and head nodes of the link respectively. With location
, the link
can be divided into two partial links
and
, and their link costs are assumed to be proportional to relative positions as:
Let
be the shortest path from origin
to destination
. The path cost, denoted by
, can be calculated by the summation of corresponding link costs along the path:
where
is the binary variable of link-path incidence relationship,
indicates link
on the path
and otherwise
.
Let
be a set of generators located in the road network, where
is the number of generators in
. Generators are typically a certain type of service facility. Given any location
in the network, its first outward nearest generator, denoted by
, satisfies:
where
is the cost of the shortest path from generator
to location
and
is the cost of the shortest path from any other generator
(i.e.,
) to location
. Subsequently, its
th outward nearest generator, denoted by
, can be identified as that satisfying:
Then, the set of
outward nearest generators can be determined and denoted by
. Therefore, the outward OkNVD (order
k network Voronoi diagram), denoted by
, is to partition the road network into a set of sub-networks, called outward OkNVRs (order
network Voronoi regions), denoted by
, such that all locations within any
share the same set of
nearest generators,
. The outward OkNVR,
, can be expressed as
where ∧ represents that all conditions are satisfied simultaneously.
Because the road network is directed, the inward OkNVD can also be defined by using the shortest path in a reverse direction from location
to the corresponding generator. Let
be the set of
inward nearest generators. The
th inward nearest generator satisfies following condition:
where
is the cost of the shortest path from location
to the
th inward nearest generator
. Then, the inward OkNVD, denoted by
, consists of a set of inward OkNVRs,
. Each inward OkNVR,
, delimits all locations sharing the same set of
inward nearest generators,
, and it can be mathematically expressed as
The outward and inward OkNVDs are applicable for different types of generators and different applications. The outward OkNVDs are commonly for emergency facilities (e.g., fire stations) and applications whose outward travel cost is critical; while the inward OkNVDs are usually for service facilities (e.g., supermarkets and shopping malls) and applications whose inward travel cost is critical.
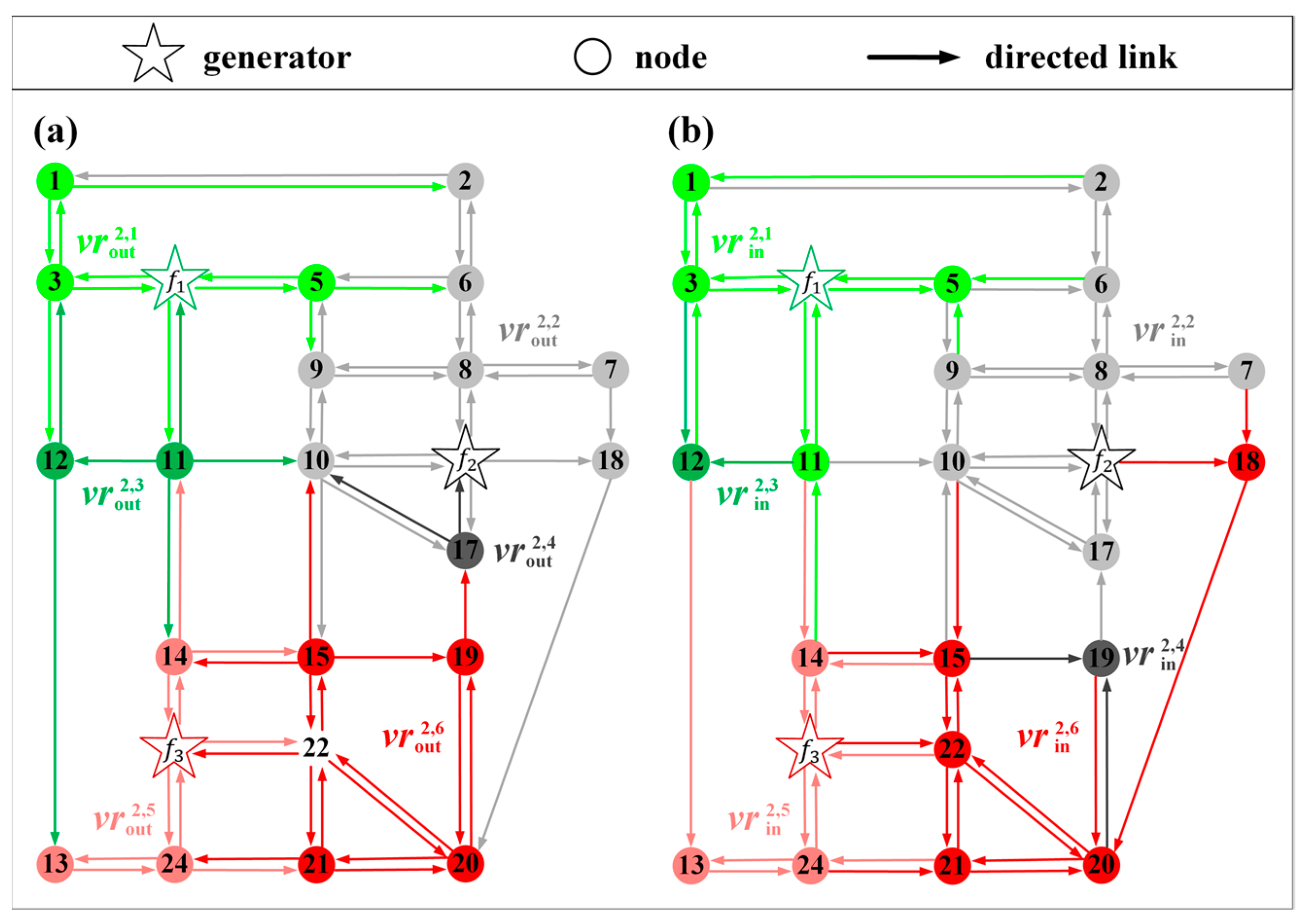
Figure 1 and
Figure 2 illustrate the outward and inward OkNVDs in a well-known small road network, namely the Sioux Falls network.
Figure 1a,b respectively give the outward and inward OkNVDs when
, in which OkNVDs degrade to the classical outward and inward NVDs. In both two figures, generators are given in star shapes, and their Voronoi regions are shown in the same color. As can be seen, the outward NVDs are not identical to the inward counterparts, since the road network is directed. It can also be seen that both outward and inward NVDs form a tessellation on the road network with two observations: (1) All NVDs cover the whole network (i.e., collectively exhaustive); and (2) Voronoi regions are mutually exclusive except at the boundary points. This is because the Sioux Falls network (as most real road networks) is fully connected, i.e., there exists at least one path between any two locations in the road network.
Figure 2a,b respectively shows the outward and inward OkNVDs when
in the same Sioux Falls network. In these two OkNVDs, six OkNVRs are given in different colors. Each OkNVR delimits all locations sharing the same
nearest generators. For example, all locations within in
have the same first and second nearest generators,
and
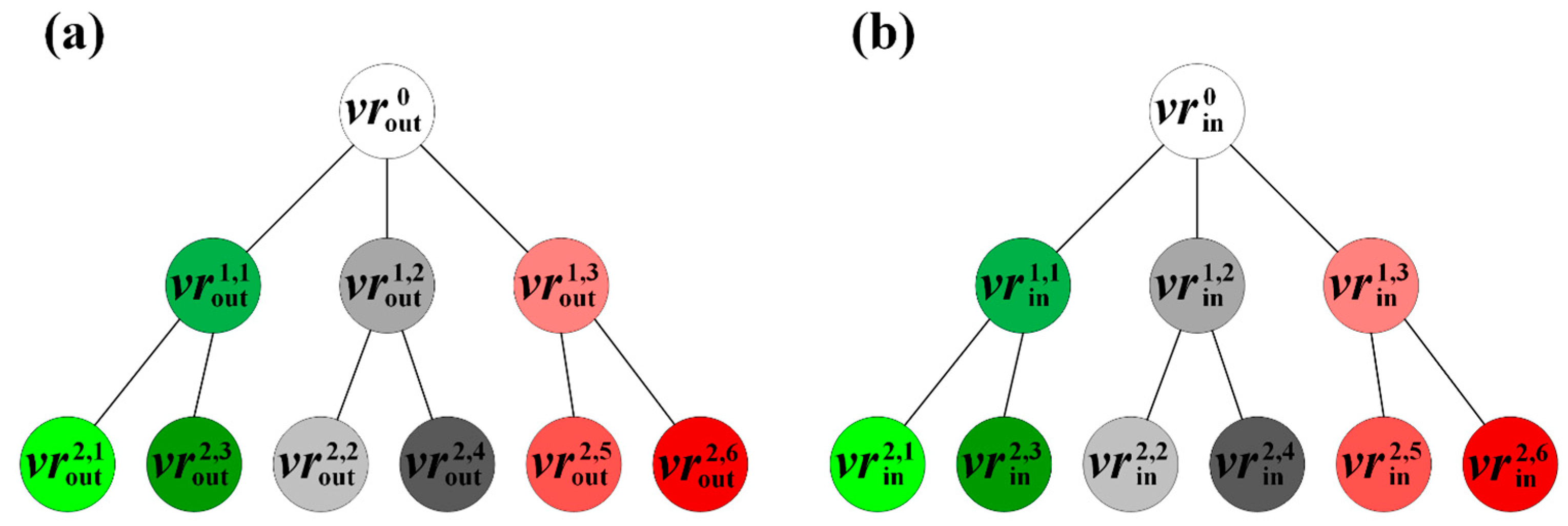
. As can be seen, the outward (or inward) order second NVDs not only form a tessellation on the whole network but also on each outward (or inward) order first NVR. Thereby, the order-second NVD together with the order first NVD form a hierarchical tessellation on the road network. This hierarchical tessellation can also be represented by the tree structure shown in
Figure 3a,b, in which the Voronoi regions were kept the same color as
Figure 2a,b. The original road network is represented as a single root node at level 0 of the tree. The order first NVD is to partition the original network into a set of order first NVRs, which are represented as child nodes of nodes at level 1. Each order first NVR is further divided into a set of order second NVRs representing as its child nodes, i.e., nodes at level 2.
Since both outward and inward OkNVDs have an identical tessellation property, we only present the outward case for simplicity. Given a OkNVR, , it is said to be a child region of order NVR, , if holds. All child NVRs of form the child region set, denoted by . Conversely, this is said to be the parent region of any. The tessellation property of OkNVD can be proved rigidly as below.
Proposition 1. If the road network is fully connected, the outward order first NVD forms a tessellation on the road network.
Proposition 2. If the road network is fully connected,forms a tessellation on.
According to Propositions 1 and 2, OkNVRs are stacked under their parent NVRs (i.e., order NVRs, …, until the order first NVRs), forming a level hierarchical tessellation on the road network. This hierarchical tessellation property of OkNVDs can be useful for many applications to organize spatial data. Such a property is fully utilized in the next section to construct OkNVDs.
3. Proposed Algorithm for Constructing OkNVDs
This section presents the proposed algorithms for constructing outward and inward OkNVDs in the road network. We first describe the algorithm for constructing outward OkNVD, called
ConstructOutwardOkNVD. As shown in Algorithm 1, this
ConstructOutwardOkNVD algorithm consists of two stages. The first stage is to efficiently determine the shortest paths to
at each node
. To this end, a new one-to-all k shortest path finding procedure, called
FindKNearestPOIs, is proposed. The second stage is to construct the outward OkNVD. Each node
only belongs to a OkNVR and can be easily determined using the calculated
. However, a link
may belong to multiple OkNVRs. In the second stage, a recursive procedure, called
AddLinkToOkNVRs, is introduced to effectively divide the link into corresponding OkNVRs using the above hierarchical tessellation property. The detailed steps of
FindKNearestPOIs and
AddLinkToOkNVRs procedures are described in the following sections.
| Algorithm 1: Detailed steps of the proposed algorithm. |
| Procedure: ConstructOutwardOkNVD |
Inputs: Road network , Generator set , and k value
Returns: Outward OkNVD
Stage 1. K nearest generators search:
01: Call procedure FindKNearestPOIs to calculate for each node .
Stage 2. The OkNVD construction:
02: For each node
03: Retrieve the node’s using , and add into .
04: End For
05: For each link pair of and
06: Call procedure AddLinkToOkNVRs(, ) to divide the link into corresponding OkNVRs.
07: End For
06: Return OkNVD. |
3.1. The FindKNearestPOIs Procedure
To calculate shortest paths from
at each node
, a straightforward approach [
1] consists of two steps. The first step is to perform the classical one-to-all Dijkstra’s algorithm by
times to construct the completed one-to-all shortest path trees rooted at all generators. Accordingly,
shortest paths from all generators at each node
are calculated. The second step is to sort the calculated
shortest paths at each node to determine
. Using the F-Heap data structure [
24], Dijkstra’s algorithm runs in the worst-case complexity of
, where
is the number of nodes and
is the number of links. Therefore, the step requires
. Since the second step requires
, this approach runs in the worst-case complexity of
. Such an approach is easy for implementation. However, its computational performance significantly degrades with
, i.e., the number of generators. It tends to have computational overheads by calculating too many unnecessary shortest paths, given that
is generally much larger than the
value in practice.
In this study, a new one-to-all k shortest path procedure, i.e., FindKNearestPOIs, is proposed to efficiently determine only shortest paths from rather than shortest paths from all generators. The proposed procedure modifies the Dijkstra’s algorithm in three aspects. Firstly, the proposed procedure simultaneously constructs shortest path trees in a single path searching process. The Dijkstra’s algorithm maintains only one label at each node. The proposed procedure, however, maintains a label list with size at each node to record the shortest paths from different generators. Secondly, the proposed procedure makes use of only one priority queue for constructing all shortest path trees. By sharing a single priority queue, shortest path trees from all generators can be coordinated during the path-searching process. Thirdly, the proposed procedure closes a node when it was selected from the priority queue by times instead of a single selection used in Dijkstra’s algorithm. After the node was closed, shortest paths from were exactly determined at the node according to the monotonic increasing property of the priority queue. In addition, the ascending order of shortest paths from different generators can be directly obtained according to their selection order from the priority queue. Therefore, the proposed procedure can efficiently determine shortest paths from without the requirement of constructing completed shortest path trees from all generators and sorting the shortest paths at each node.
Algorithm 2 gives the detailed steps of the proposed FindKNearestPOIs procedure. Unlike Dijkstra’s algorithm, each node in the proposed procedure maintains three objects, including a label set , a selected generator set and an open status . The label set employs an array list structure with the size of . The ith location of the label set, denoted by , records the shortest path from the ith generator . This way efficiently retrieves the shortest path from a specific generator. Note that it is not necessary to generate labels at each node; and a null object is used if the shortest path from a certain generator has not been generated. The selected generator set, , employs a linked list structure for recording the order of generators whose shortest paths to node were selected from the priority queue. Finally, the open status is a binary indicator, and indicates that is open.
In the initialization step, and of all nodes are set to be empty, and of all nodes are set to be true. A path (or called label) from each generator to itself, denoted by , is created and set its path cost as zero. An additional property, denoted by , is introduced at the label to store the generator order . This created path is added into the priority queue, denoted by .
At each iteration, a path
at the top of the priority queue
is selected. Its generator order,
, is then added into the selected generator set
. Once the number of generators in
reached the
value, the node
is closed by setting the
attribute to be false. In this case,
shortest paths from
have been determined at node
, and thus all paths of
still in the priority queue are eliminated without considerations. Subsequently, the selected path
is extended to its successor nodes, which are not closed. Through an open successor node
, a temporal path
is created by
, where
is a path concatenation operator. The newly created path
compares to the existing path
as
from the same generator. If the existing path
or
holds, the newly created path is kept and inserted into the priority queue; and it is discarded otherwise. The procedure continues the path selection and extension process until
is empty. When the procedure terminates, it can determine the
nearest generators of each node
(i.e.,
) at the selected generator set
and k shortest paths from
of each node
at the label set
.
| Algorithm 2: Detailed steps of the FindKNearestPOIs procedure. |
| Procedure: FindKNearestPOIs |
Inputs: Road network , Generator set , and k value
Step 1. Initialization:
01: For each node
02: Set label set as an empty array list with size.
03: Set selected generator set , and Set open status .
04: End For
05: Initialize the priority queue .
06: For each generator
07: Create path from to itself, and Set cost as and generator as .
08: Set and add the path into .
09: End For
Step 2. Path selection:
10: If , Then Stop.
11: Select the path at the top of and remove it from .
12: Add the path’s generator into .
13: If the size of equals to K Then
14: Set .
15: For each in
16: If , Then remove it from .
17: End For
18: End If
Step 3. Path extension:
19: For each successor node
20: If Then
21: Create path and Set and
22: Retrieve existing path .
23: If or Then
24: If , Then remove it from .
25: Set , , and .
26: Add into .
27: End If
28: End If
29: End For
30: Go back to Step 2. |
We can prove the optimality of the proposed FindKNearestPOIs procedure as below.
Proposition 3. When the proposed FindKNearestPOIs procedure terminates, it can determine shortest paths from K nearest generatorsfor all nodes.
The worst-case complexity of the proposed
FindKNearestPOIs procedure is analyzed. Using the F-Heap data structure [
24], the selection of the minimum cost path from the priority queue requires
, and both remove and add path into the priority queue requires
, where
is the maximum paths in the priority queue. Since
is the maximum number of path selection from the priority queue, the proposed procedure thus runs in the worst-case complexity of
. This complexity is significantly better than the previous Okabe’s algorithm, i.e.,
.
3.2. The AddLinkToOkNVRs Procedure
In Okabe’s algorithm [
1], a complicated idea of a lower-bound envelope was introduced to divide boundary links which belong to at least two distinctive OkNVRs. However, no detailed procedure was given to implement such an idea.
In this study, a new recursive procedure,
AddLinkToOkNVRs, is introduced to effectively divide boundary links into different OkNVRs using the hierarchical tessellation property, i.e., Propositions 1 and 2. The detailed steps of the introduced procedure is given in Algorithm 3.
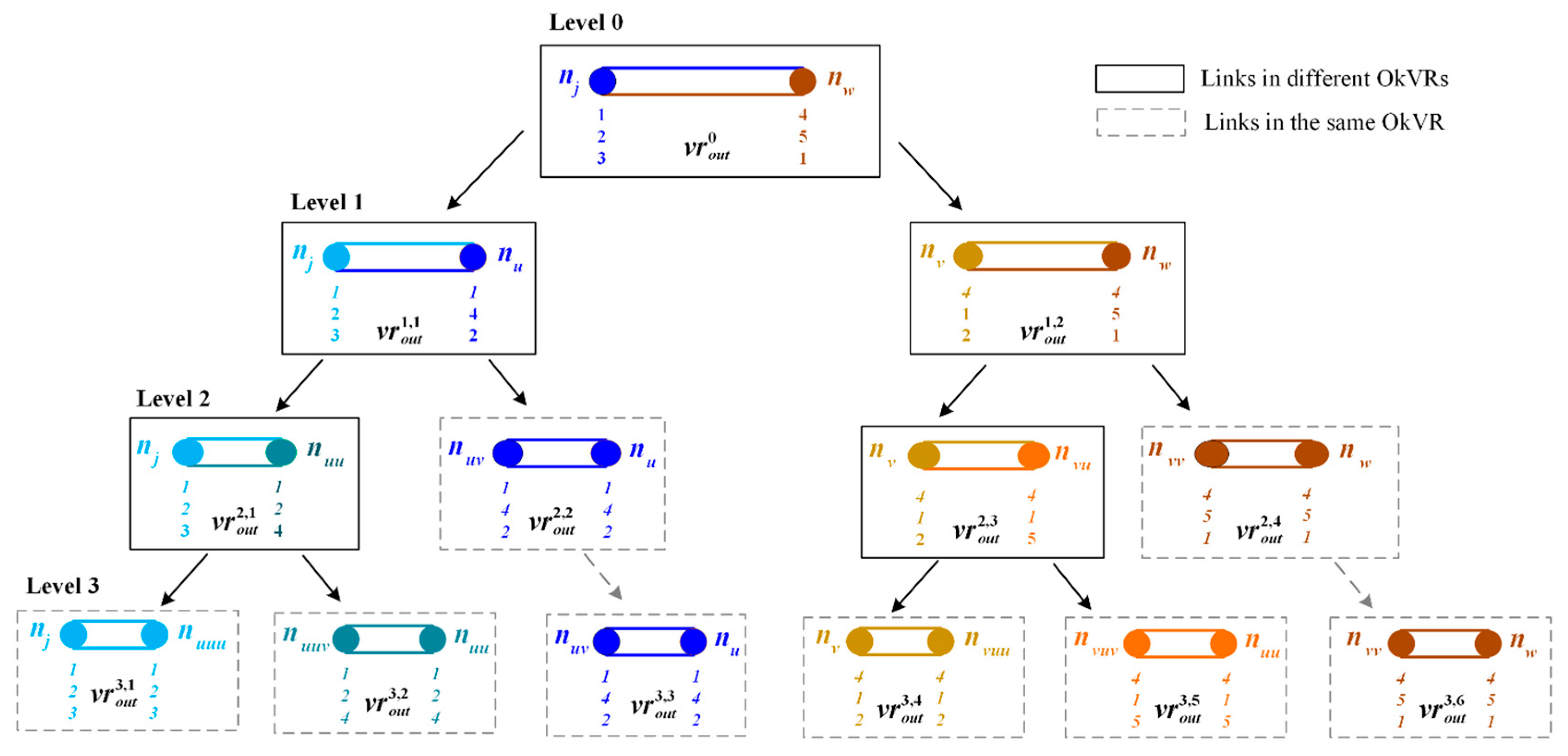
Figure 4 illustrates this procedure using a simple example of two directed links
and
. Two end nodes,
and
, are given in the figure with the selected generator sets,
and
. Because
holds, these two links are not in the same OkNVR, so called boundary links (their end nodes are shown in different colors). This
AddLinkToOkNVRs procedure divides boundary links into a set of partial links through the hierarchical tessellation from the first level until the
kth level. When dividing links at the first level, we focus on only
(i.e., Generator 1) and
(i.e., Generator 4) and their shortest paths,
and
.
The procedure consists of three steps. The first step (i.e., Step 2.1) is to divide links
and
into four partial links. Using the equal travel times between left-bound route
and right-bound route
, we can determine break point
on link
(or
on link
) as
Then, the path cost for is calculated as and its generator is set as . Similar, the path cost for is determined as and . On the same break point, we create two new nodes, namely a left-bound node and right-bound node . Then, we divide two links and into four newly partial links, including two left-bound partial links, and , and two right-bound partial links, and . For example, partial link represents part of link from 0 to using the linear reference.
The second step (i.e., Step 2.2) is to determine the selected generator sets ( and ) and label sets ( and ) for newly created nodes and . It is easy to determine (e.g., Generator 1) and (e.g., Generator 4) as the first and second generators of the left-bound node , e.g., . A reverse order is used for the right-bound node , i.e., . Since and have identical path sets, we use to represent them, i.e., and . Subsequently, we construct candidate paths to determine other nearest generators in addition to and . Because candidate paths should pass through two end nodes, and , we construct and for any path and maintained at and respectively. All constructed candidate paths are inserted into the priority queue, denoted by . Then, the top paths from are identified and stored at , and their generators are inserted into and , e.g., and . After this step was performed, we divided two input links into four partial links within two NVRs, e.g., and , at the first level.
The last step (i.e., Step 2.3) is to recursively call the AddLinkToOkNVRs procedure for the link division at the next level by using the newly created left-bound links ( and ) and right-bound links ( and ) as two input links respectively.
For the link division at the
ith level, this procedure focuses on only Scenario 2 of
. This is because we have Scenario 1 of
for
, in which
and
are kept for the setting (
and
) and label sets (
and
) at the
ith level. The link division of the
ith level has the similar three steps as that of the first level. This procedure recursively performed until Scenario 3 of
for
holds. After the procedure terminated, input links were divided into a set of partial links belonging to different OkNVRs, e.g.,
,…,
in the illustrative example.
| Algorithm 3: Detailed steps of the AddLinkToOkNVRs procedure. |
| Procedure: AddLinkToOkNVRs |
Inputs: Links and
01: Set and Set as empty array lists with size.
02: For to
03: If Then (Scenario 1)
04: Set and .
05: Else (Scenario 2)
Step 2.1. Divide two links into four partial links:
06: Retrieve and .
07: Calculate and .
08: Create left-bound path and Set and .
09: Create right-bound path and Set and .
10: Create left-bound node and partial links and .
11: Create right-bound node and partial links and .
Step 2.2. Set the selected generator set and the label set for two newly created nodes:
12: Set and .
13: Set and .
14: If Then
15: Set and .
16: Set priority queue .
17: For to
18: Retrieve and .
19: Create candidate path and Set and .
20: Create candidate path and Set and .
21: Add them into .
22: End For
23: For to
24: Select the path at the top of and remove it from .
25: Set and .
26: Set .
27: End For
28: End If
29: Set and .
Step 2.3. Recursively divide four newly created partial links:
30: Call AddLinkToOkNVRs and AddLinkToOkNVRs.
31: Return.
32: End If
33: End For
34: Add and into using as the k nearest generators. (Scenario 3) |
We can prove the optimality of the introduced AddLinkToOkNVRs procedure below.
Proposition 4. When the introduced AddLinkToOkNVRs procedure terminates, it can correctly divide two input links into a set of OkNVRs.
The worst-case complexity of the introduced AddLinkToOkNVRs procedure is also analyzed. In the procedure, Step 2.1 runs in ; and Step 2.2 runs in using the F-heap data structure. Because the procedure recursively divides input links from the first level until the k level, it runs in the complexity of .
3.3. Complexity Analysis of the Proposed OkNVD Construction Algorithms
With Propositions 3 and 4, we can easily prove the optimality of the proposed ConstructOutwardOkNVD algorithm as follows.
Proposition 5. When the ConstructOutwardOkNVD algorithm terminates, it can correctly construct outward OkNVDs in the road network.
Proof. It can be easily followed by Propositions 3 and 4. □
Based on the worst-case complexity of
AddLinkToOkNVRs procedure (see
Section 3.2), we can determine that the second stage of the
ConstructOutwardOkNVD algorithm runs in
. Since its first stage runs in
(see
Section 3.1), the
ConstructOutwardOkNVD algorithm therefore runs in
.
The proposed ConstructOutwardOkNVD algorithm can be modified easily to construct inward OkNVDs, namely the ConstructInwardOkNVD algorithm. Both FindKNearestPOIs and AddLinkToOkNVRs procedures should be modified by using the backward search (i.e., path extension to predecessor nodes) instead of the forward search (i.e., path extension to successor nodes). For example, the modified FindKNearestPOIs procedure should create a new path from each predecessor node (see Lines 19 and 22). The ConstructInwardOkNVD algorithm has the same worst-case complexity as the ConstructOutwardOkNVD algorithm.
5. Conclusions
The order
k network Voronoi diagram (OkNVD) is an effective geometric construction to partition the network space into a set of order
k network Voronoi regions (OkNVRs) such that all locations within an OkNVR share the same
k nearest generators. Despite the broad applications of OkNVD, few effective and efficient algorithms had been developed to construct OkNVD in real road networks. This study proposed a novel OkNVD construction algorithm consisting of two stages. In the first stage, a new one-to-all
k shortest path procedure was proposed to efficiently determine the
k nearest generators for each network node in a single shortest path search process. This proposed procedure improves the worst-case complexity from previous
[
1] to
. In the second stage, a new recursive procedure was introduced to effectively divide boundary links into different OkNVRs using the hierarchical tessellation property. The introduced procedure can effectively solve the link division issue that had not been addressed by the previous study [
1].
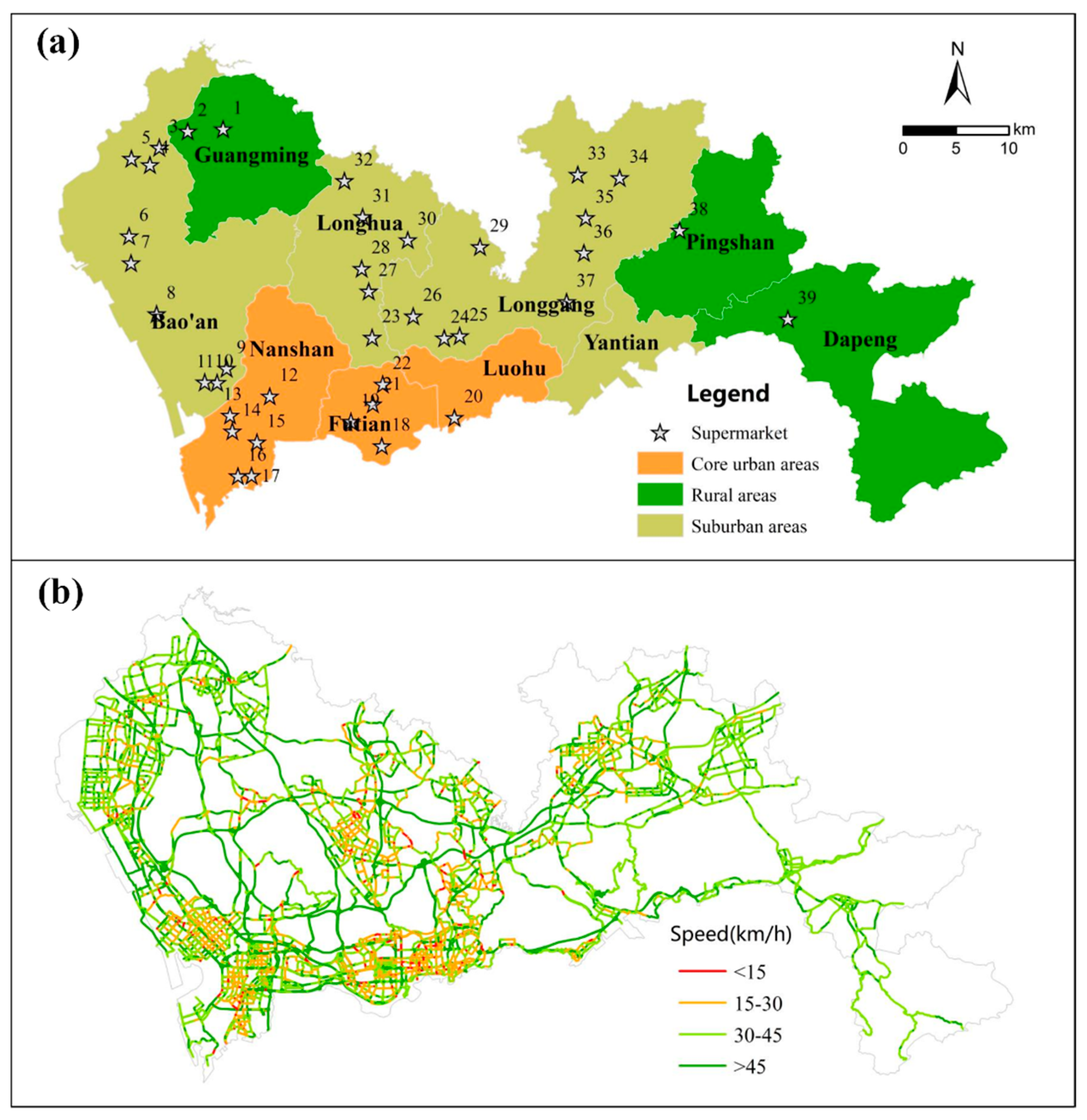
To demonstrate the applicability of the proposed OkNVD construction algorithm, a comprehensive case study in Shenzhen city was carried out. Results of the case study demonstrated that the proposed OkNVD construction algorithm can well quantify place-based accessibility in a fine-gained spatial resolution. Results of computational experiments showed that the proposed algorithm was significantly faster than previous Okabe’s algorithm for all five testing networks under different k and settings. For example, it performed about 65 times faster than Okabe’s algorithm in the Shenzhen network when k = 3 and . This computational advantage would be more obvious in real large-scale applications, in which the number of generators are large and the k value is small.
Several directions for future research are worth pursuing. Firstly, this study assumed that link costs are static and deterministic. Traffic conditions in real road networks are dynamic and stochastic [
29]. How to incorporate such dynamic and stochastic travel times into the proposed algorithm needs further investigation. Secondly, the proposed algorithm considers only the road transport mode. The extension of this proposed algorithm into the multi-mode transport networks, such as metro and bus, is warranted for further study. Last but not least, finding
k nearest generators is a critical step for many network analyses, such as spatial interpolation, spatial clustering, outlier detection, and
k nearest neighbor query, etc. [
12,
14,
28]. Subsequent studies should investigate how to incorporate the proposed algorithm in these network analysis methods.