Abstract
The Belt and Road has developed rapidly in recent years. Constructing a comprehensive traffic network is conducive to promoting the development of the the Belt and Road. To optimize the layout of the Belt and Road comprehensive traffic network, this paper identifies important cities. First, a weighted super adjacency matrix is defined, which includes sea, air, railway transportation and trans-shipment transportation between these transportation modes. With this matrix, the Belt and Road comprehensive traffic network (B&RCTN) is constructed. To identify important node cities, this paper proposes a method to calculate multi-layer centrality which considers inter-layer relationships. With the results of the above four centrality indexes, the Entropy Weight TOPSIS is used to synthesize the evaluation of the four indexes. Finally, the multi-layer comprehensive centrality rank of node cities is obtained. Result shows that there are 72 important cities in B&RCTN. These important cities are mainly distributed in the east and west of Eurasia. Eastern cities are located in East Asia and Southeast Asia, including 36 cities such as Singapore, Shanghai, Guangzhou, Shenzhen and Hong Kong. Western cities are concentrated in West Asia, Western Europe and North Africa along the Mediterranean coast, including 31 cities such as Istanbul, Dubai, Vienna, Trieste and Koper. There are few important cities in central Eurasia, except Almaty in Central Asia and Colombo in South Asia. In addition, important cities also include Moscow in Eastern Europe, Lagos and Lome in West Africa. Finally, based on the distribution of important cities, this paper puts forward some suggestions on the development of the Belt and Road comprehensive transportation.
1. Introduction
In recent years, the Belt and Road initiative has become a great endeavor to build a community with a shared future for mankind. In the process of the Belt and Road con-struction, the construction of the Belt and Road comprehensive traffic network con-necting land, sea, and air is a practical demand to support its development [1]. The cities along the line, as the node elements of transportation connection construction, are the basis of the construction of the Belt and Road comprehensive traffic network [2]. Ex-ploring the importance of node cities in the network is of great significance to the overall planning and layout optimization of the Belt and Road comprehensive traffic network [3].
Currently, scholars have paid attention to countries in the Belt and Road, mainly focused on studying their trade cooperation [4,5], economic situation [6], cultural exchanges [7], etc. With the in-depth promotion of the Belt and Road initiative, cities develop in concert, and urban agglomeration patterns form. Some studies have focused on the Belt and Road cities and urban agglomerations, studying their green development [8], logistics capabilities [9], industrialization [10], industrial structure [11] and resilience [12]. Although the above studies promote exchanges and cooperation between cities along the Belt and Road, there is little research on the comprehensive traffic system between cities. All city interactions are based on their traffic connectivity, providing practical support for cooperation between cities. Studying cities in the Belt and Road comprehensive traffic system is of great significance to the development of the Belt and Road. Therefore, some scholars have studied the node cities on the Belt and Road sea transportation. Some studies qualitatively evaluate cities’ importance from policy and hardware facilities [13], etc. Some references study the position of nodes in the traffic topology network based on complex network theory and quantitatively evaluate the node significance of sea transport networks by measuring the centrality of nodes [14].
The Belt and Road comprehensive traffic system involves sea transportation, air transportation and railway transportation. Different transportation modes have different traffic networks, and there are connections among them [15]. Therefore, the Belt and Road comprehensive traffic network shows the characteristics of a multi-layer heterogeneous network, that is, there are not only intra-layer relations but also inter-layer relations in different transport network layers [16]. At present, scholars have explored the identification of essential nodes in multi-layer heterogeneous networks, including the multi-layer urban traffic network, a multi-layer social network, and a multi-layer neural network [17,18,19,20,21]. From the perspective of research methods, some researchers combine nodes and edges with weight in each layer, and the multi-layer heterogeneous network turns into a single-layer aggregate network. Then, the significance of nodes is analyzed for network cascading failure by removing nodes [22,23]. Others evaluate the significance of nodes by summing the centralities calculated in each layer. The commonly used centrality indexes for network analysis are strength centrality [24,25], eigenvector centrality [26,27], closeness centrality [28], and betweenness centrality [29].
The above studies have some common features, they only focus on intra-layer relationships of multi-layer heterogeneous networks in node importance evaluation, the evaluation systems of centrality indexes they adopted are not comprehensive, and they directly follow the traditional centrality indexes. Different from previous studies, this study not only focuses on the heterogeneity of multi-layer heterogeneous networks, but also fully considers the information contained in the inter-layer relationship, which depicts the actual traffic system more accurately. Meanwhile, this paper constructs the evaluation system that includes multiple centrality indexes and improves each centrality index innovatively according to the feature of the network, which can evaluate the traffic capacity of nodes more comprehensively in a multi-dimensional way. In addition, cost is a crucial factor in transportation activities [30,31], related studies mainly focus on the cost of a single transportation mode, with little research on the cost of multiple transportation modes in multi-layer heterogeneous traffic networks. This study considers cost as a critical consideration, eliminating the differences between different modes to integrate multiple modes better.
The following sections are arranged as follows. In Section 2.1, we explain the study area and data source required for this paper in detail, and describe the overall situation of the data. In Section 2.4, we show the technical route. In Section 2.3, based on traffic data and traffic costs within cities in different transportation modes, this paper constructs the Belt and Road comprehensive traffic network(B&RCTN), including three layers, representing sea transportation, air transportation, and railway transportation respectively. Section 2.4, research samples are selected. Section 2.5 introduces inter-layer relations to improve the four centrality indexes, and uses the entropy weight TOPSIS method to synthesize the four centrality indexes to obtain the multi-layer comprehensive centrality. In Section 3, we show the results and analyze the status of important node cities. In Section 4, we analyze this paper’s results and results in the previous studies and provide suggestions for the Belt and Road comprehensive traffic network layout planning.
2. Materials and Methods
2.1. Study Area and Data Source
More and more countries have signed cooperation agreements with China. According to the Belt and Road Portal, until September 2021, 144 countries have signed cooperation agreements. This paper takes cities along the Belt and Road of sea, air, and railway transportation in the 144 signatories as the study region.
Some cities in the signatories are not included in the study area because of the unpublished and incomplete traffic data. Finally, this paper takes 470 cities as the study area. The regional distribution of 470 cities is shown in Figure 1. The number and proportion of cities in each region are shown in Table 1.
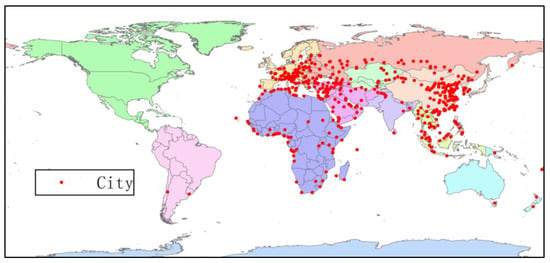
Figure 1.
City distribution.

Table 1.
Distribution of cities within the study area.
Traffic data among cities in the study area can be obtained in the following ways:
- Sea transportation data is obtained from the top 10 liner companies in 2020 published by The International Container Yearbook, and the specific data are from the companies’ websites;
- Air transportation data is selected from the top 10 global air cargo companies in 2020 published on the official website of IATA and got the specific lines through the flight schedules released by the companies;
- Railway transportation data is based on the China-Europe trains published on the website of China Railway Supply Chain Logistics in 2021, and specific lines are obtained according to the official websites of different trains.
2.2. Technical Route
In this paper, the technical route for identifying important node cities in the B&RCTN is shown in Figure 2:
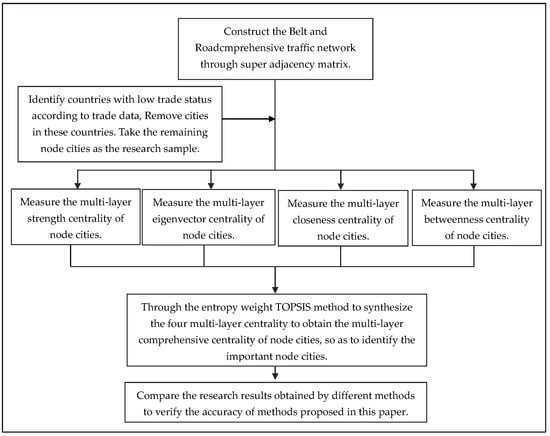
Figure 2.
Technical routes.
The first step is “Network Construction”. Based on the collected data, we adopted python to establish a weighted super-adjacency matrix to construct the Belt and Road comprehensive traffic network.
The second step is “Selection of Study Samples”. According to the trade data collected in the UN Comtrade database, calculate the total volumes and growth rate of trade between the Belt and Road countries in the past three years, then cities in some countries with low trade status can be excluded, the remaining cities in the B&RCTN are taken as research samples, and identify the importance of these cities in the next step.
The third step is “Identification of Important Node Cities”. Based on the super-adjacency matrix, four centrality indexes are selected to measure the traffic capacity of node cities in different aspects. The four centrality indexes are multi-layer strength centrality, multi-layer eigenvector centrality, multi-layer closeness centrality, and multi-layer betweenness centrality. The entropy weight TOPSIS method synthesizes the four indexes to obtain the multi-layer comprehensive centrality of node cities to identify important node cities.
The fourth step is “Verification of identification results”. Comparing the research results obtained by different methods, the accuracy of the methods proposed in this paper is verified.
2.3. Construction of B&RCTN
This paper adopts the idea of constructing a multi-layer network with the super-adjacency matrix [15], through intra-layer traffic section efficiency and inter-layer traffic section efficiency , the matrix removes the difference of various transportation modes, then the Belt and Road sea, air and railway transportation are linked to form the description of the Belt and Road comprehensive traffic network (B&RCTN). The super-adjacency matrix is shown in matrix .
The weighted super-adjacency matrix is composed of the intra-layer relation matrix and the inter-layer relation matrix (). The value of , ranges from 1 to 3 corresponding to sea transportation, air transportation, and railway transportation. represents the intra-layer relation matrix of layer . represents the inter-layer relation matrix between layer and layer . For example, represents the inter-layer relation matrix between the sea transportation layer and air transportation layer.
2.3.1. Construction of Intra-Layer Weighted Relation Matrix ()
is constructed of nodes and edges. The nodes represent cities along the Belt and Road’s lines and the edges represent traffic road sections between neighboring cities in layer .
In layer , the edge weight between node cities is defined as the reciprocal of the cost of the traffic section between cities . The higher the traffic cost, the smaller the edge weight, and the lower the traffic efficiency. The traffic cost of comprises the transportation cost and time cost , as shown in Formula (1):
where transportation cost is the product of transportation distance and rate , i.e., . The unit of is km. the distance of sea transportation is obtained by Port Distance software, and the distance of air transportation and railway transportation is obtained by substituting the longitude and latitude of corresponding cities into the Euclidean Distance formula. The unit of rate is USD/(FTU·km). In sea transportation, the rate is 0.15 according to the China Maritime Service Network. The rate of air transportation is 5.6 according to reference [32], and the rate of railway transportation is 1.2 according to Uniform Transit Tariff Regulations.
Time cost is the product of the cargo value , the interest rate , and the transportation time , i.e., . Among them, the cargo value is selected as the average value of container goods along the Belt and Road in 2021, which is about USD. The interest rate is selected as , which consults the general benchmark interest rate of the bank [33]. The unit of transportation time is the day, which is obtained by dividing the transportation distance from the transportation speed. The sea transportation speed and air transportation speed are km/day and km/day, respectively. For railway transportation, the domestic speed is km/day and the overseas speed is km/day [32,33].
Weighted intra-layer relation matrix , if , then there is a traffic section between cities under the transportation mode , and its weight is ; If , there is no traffic section between node cities in the transportation mode .
2.3.2. Construction of Intra-Layer Weighted Relation Matrix ()
If a city exists in two layers simultaneously, it shows that this city has two transportation modes. It is necessary to establish an inter-layer relationship of this city between two layers, which means that there are two transportation modes for transit in this city. For instance, Xi’an has air and railway transportation, so it appears in the layers of air and railway transportation. Therefore, there is an edge between these two layers, indicating that there are traffic sections in Xi’an that can support both air and rail transit activities. Additionally, road transportation is the main transit operation. Some seaports have realized railway arrival. That is, some railway stations through special railway lines can be directly connected with seaports, and the list of cities that realize railway arrival can be obtained according to the literature [34,35].
is the edge weight of node city connecting layer and layer , and is defined as the reciprocal of the cost of the traffic section between the stations of transportation mode and transportation mode . The cost of the traffic section comprises transportation cost , the time cost and loading & uploading cost , as shown in Formula (2):
where transportation cost is the product of transportation distance and rate , i.e., . The unit of transportation distance is km, which is extracted from the Google distance matrix. The unit of rate is USD/(FTU·km), and the value of ranges from 1 to 2 corresponding to road transportation and railway special line transportation. The rate of railway special line transportation and road transportation are 1 and 1.5 respectively [36].
Time cost is the product of cargo value , interest rate , and traffic time , i.e., . The unit of traffic time is day, which is obtained by dividing the transportation distance from the transportation speed. The transportation speed of the railway special line is km/day, and the road transportation speed is km/day [37].
Loading & uploading cost comprises cargo damage cost, loading & unloading time cost, and loading & unloading operation cost. The cargo damage cost is the product of the cargo damage rate and cargo value , and the cargo damage rate is 0.01% [38]. The loading & unloading cost is the product of loading & unloading time, interest rate , and the cargo value . The time cost and operation cost of loading & unloading between different transportation modes are different according to the literature [37], shown in Table 2.

Table 2.
Loading & unloading time and cost between different transportation modes.
According to the above definition, if the is not equal to 0, it means that in node city there exists a traffic section to transit between transportation modes and . Other elements except diagonal are set to 0, which has no economic meaning.
2.4. Research Sample Selection
This paper aims to identify important node cities, and puts forward policy recommendations based on the distribution of important node cities to promote the Belt and Road cooperation. That is to say, important cities should have good trade conditions to support policy recommendations. Therefore, it is necessary to remove cities with low trade from 470 cities in the B&RCTN, and the remaining cities should be used as research samples to identify their importance.
According to the Belt and Road trade data published in the UN Comtrade database, this paper finds 13 countries with low trade status through the volumes and growth rate of trade in recent three years, such as Niue, Lesotho, Cook Islands, Rwanda, Zimbabwe, Moldova, Equatorial Guinea, Solomon Islands, Bosnia and Herzegovina, Montenegro, Antigua and Barbuda, Venezuela, Cape Verde, and there are 18 node cities belong to these countries in the B&RCTN, such as Kigali, Chisinau, Sarajevo and Podgorica, etc. Excluding these 18 node cities, the remaining 452 node cities are used as the research samples to study their importance.
2.5. Multi-Layer Comprehensive Centrality Measurement of Node Cities in the B&RCTN
Based on the super-adjacency matrix created by integrating multi-dimensional data, such as geographic information and transportation cost, this section measures the status of node cities in the network topology to identify important node cities from the theoretical perspective of complex networks.
According to traditional centrality indexes in complex networks, this paper proposes methods to calculate multi-layer centrality indexes suitable for the comprehensive traffic network. These multi-layer centrality indexes consider inter-layer relationships, measuring the city’s traffic connectivity, accessibility, transit connectivity, and other transportation capabilities. With the results of different multi-layer centrality indexes, the Entropy Weight TOPSIS is used to obtain the multi-layer comprehensive centrality in the B&RCTN. The importance of cities is measured by multi-layer comprehensive centrality. The greater the multi-layer comprehensive centrality, the better the traffic capacity displayed by the city in the transportation system, and the more important the city is in the transportation network.
The cities with the top 15% of the multi-layer comprehensive centrality are important cities with strong transportation capacity. These important cities are transfer points with good transportation accessibility, the ability to maintain the stable operation of the overall transportation network, and are the main window for transportation links between geographical regions.
2.5.1. Multi-Layer Strength Centrality
Strength centrality mainly describes the connectivity of nodes [38]. In single-layer networks, strength centrality represents the number of other nodes associated with a node. In multi-layer networks, strength centrality is typically quantified by overlap strength, which is the accumulation of a node’s strength centrality in each layer.
The B&RCTN not only has intra-layer relationships of sea, air and railway transportation, but also has inter-layer relationships. The overlap strength cannot reflect inter-layer relationships. In addition, the connectivity of nodes is associated with network scale. The larger the network scale is, the greater the strength centrality value of the nodes is. And the network scale in each layer of B&RCTN is apparently different. As the overlap strength only focuses on the direct connections between nodes in each layer, ignoring network scale differences in each layer, it is difficult to accurately describe the connectivity of nodes in the B&RCTN. Therefore, this paper proposes multi-layer strength centrality , and the formula is as follows:
Among them, is the strength centrality of node city in the layer , that is, , describes the traffic efficiency between node city and its neighbors under transportation mode ; describes the total traffic efficiency between all node cities under transportation mode , namely ; represents the total traffic efficiency between station and station in the node city under road transportation or railway special line transportation; represents the total traffic efficiency between stations and stations in all node cities under road transportation or railway special line transportation, namely .
2.5.2. Multi-Layer Eigenvector Centrality
Eigenvector centrality is a valuable complement to strength centrality [39]. Based on the idea that a node’s connectivity depends on both its connections and those of its neighbors, a connection to a more interconnected node contributes to eigenvector centrality greater than a connection to a less interconnected one. According to the literature [37], in multi-layer networks, the differences in different layers’ connectivity will have an impact on the eigenvector centrality of cross-layer nodes Based on it, this paper introduces the traffic efficiency and to evaluate multi-layer eigenvector centrality , as shown in Equation (4):
where refers to the traffic efficiency of node city ’s neighbors in transportation mode ; denotes the traffic efficiency from node city to node city in transportation mode ; denotes the traffic efficiency of node city in transportation mode ; represents the traffic efficiency of node city in transportation mode , when node city in layer is connected to node city in layer ; represents the impact of transportation mode on the traffic efficiency of some node cities under transportation mode , and these affected node cities can switch between transportation modes and , the formula is expressed as ; represents the traffic efficiency of node city from station to station in in road transportation or railway special line transportation.
2.5.3. Multi-Layer Closeness Centrality
The closeness centrality mainly describes the reachability of nodes in the whole network. In unweighted single-layer networks, closeness centrality is usually measured by the average shortest path length between nodes [40]. The smaller the average shortest path is, the better the node’s reachability is, then the greater the closeness centrality is. In the B&RCTN, the reachability of a node city can be measured by the average highest traffic efficiency between node cities. In light of this, this paper proposes multi-layer closeness centrality , which thinks that a node’s reachability and multi-layer closeness centrality can be improved with increasing average highest traffic efficiency, the formula is shown in Equation (5):
where is the total number of cities represented by nodes in the network; is the highest traffic efficiency from node city to node city , which is the reciprocal of the lowest traffic path cost from node city to , i.e.,
A traffic path is composed of multiple traffic sections connected in pairs. The traffic path cost includes not only the transportation cost of each traffic section or , but also the stay time cost. Then, the traffic path cost can be calculated as follow:
where, represents the total transportation cost of all traffic sections in the traffic path; is the stay time cost of a node city in transportation mode , and the stay time cost of a node city for sea, air and railway transportation is $11.3, $4.3 and $6.72, respectively; refers to the number of node cities whose connected traffic sections are all of transportation mode in the traffic path; denotes the number of node cities that stay due to switching transportation modes in the traffic path, and the average stay time cost of these node cities is $4.48.
2.5.4. Multi-Layer Betweenness Centrality
Betweenness centrality is a common method to describe transit capacity of nodes, which is based on shortest paths counting. The betweenness centrality increases as the number of shortest paths via a node increases [41]. In the B&RCTN, the transit capacity of a node is determined by the number of paths with the highest traffic efficiency traveling through a node city. In light of this, this research proposes multi-layer betweenness centrality . That is, the more the number of paths with the highest traffic efficiency is, the transit capacity of the node is, then the greater the multi-layer betweenness centrality is. The formula of multi-layer betweenness centrality is as shown in Equation (8):
where is the number of highest traffic efficiency paths from node city to node city , and is the number of highest traffic efficiency paths from node city to node city that pass through node city in layer . The highest traffic path efficiency can be calculated according to the Formula (6).
2.5.5. Multi-Layer Comprehensive Centrality
The entropy weight TOPSIS is a comprehensive evaluation method, it can reflect the actual data distribution for each index, while also eliminating subjective factors when setting weights. Based on the entropy weight method, the weight of each index is assigned, then the new data can be obtained by multiplying the value and index’s weight. Since the TOPSIS method can reduce the impact of various index dimensions and fully utilize the information of each index to ensure the rationality of the results [42], TOPSIS can be used to synthesize new data of each index, then the multi-layer comprehensive centrality of the evaluation object can be obtained.
3. Results
3.1. Network Topology
Based on the constructed weighted super-adjacency matrix, ArcGIS software is used to describe the B&RCTN topologies, as shown in Figure 3. In the sea transportation layer, there are 204 cities and 1604 routes. In the air transportation layer, there are 224 cities and 974 routes, and in the railway transportation layer, there are 190 cities and 416 routes.
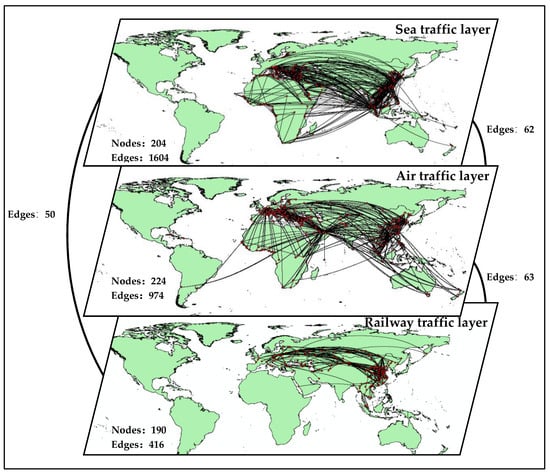
Figure 3.
The Belt and Road comprehensive traffic network.
In addition, according to the number of inter-layer edges of the three-layer network, the number of transit cities between the sea and the air transportation layer is 62. The number of transit cities between the air and the railway transportation layer is 63, and there are 50 transit cities between the sea and the railway transportation layer. From the distribution of node cities, node cities in East Asia, the Mediterranean coast, and Western Europe are more densely distributed. Cities in Central Asia, South Asia, and Southeast Asia are mostly transit points in many routes. There are few node cities in South America, North America and Oceania, which connect with other node cities sparsely.
3.2. Evaluation of Multi-Layer Comprehensive Centrality
Based on the methods proposed in Section 2, the multi-layer strength centrality, the multi-layer eigenvector centrality, the multi-layer closeness centrality, the multi-layer betweenness centrality rank of 452 node cities are shown in Figure 4a–d, respectively, and their geographical distribution are shown in Figure 5a–d.
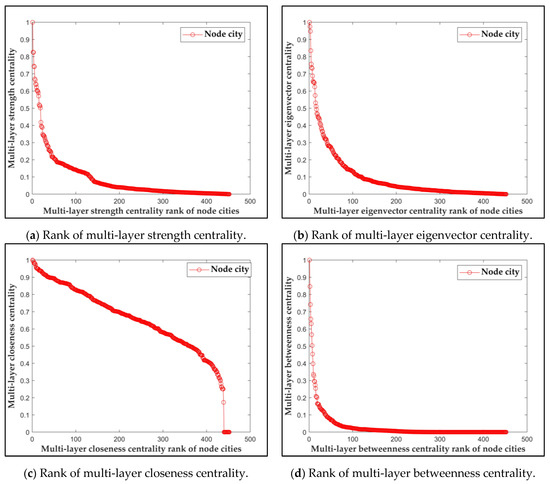
Figure 4.
Rank of different multi-layer centrality of node cities.
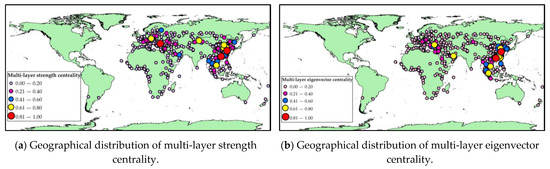
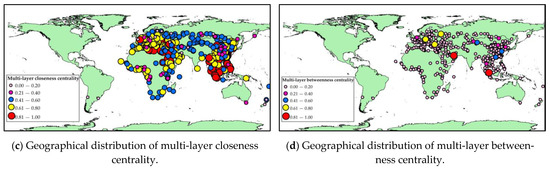
Figure 5.
Geographical distribution of different multi-layer centrality of node cities.
Based on the measurement results of the four centrality indexes mentioned above, the multi-layer comprehensive centrality of node cities is obtained by using the entropy weight TOPSIS. The multi-layer comprehensive centrality rank of node cities is shown in Figure 6a, and the distribution is shown in Figure 6b, and the specific list of node cities is shown in Table 3.
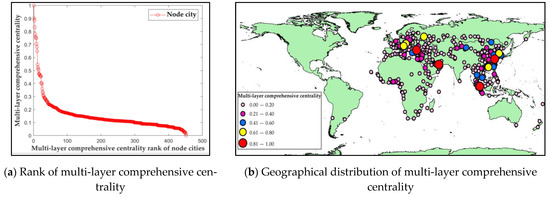
Figure 6.
Multi-layer comprehensive centrality rank of node cities and its distribution.

Table 3.
Node cities in different regions of multi-layer comprehensive centrality.
This paper selects the top 15% of cities as important cities, that is, cities with multi-layer comprehensive centrality greater than 0.2. In order to further analyze the distribution of important cities in different geographical regions, different colours are used to represent East Asia, Southeast Asia, Central Asia, South Asia, West Asia, Eastern Europe, Central and Western Europe, Africa, Oceania, South America and North America in the map. Important cities are drawn on the map, as shown in the Figure 7.
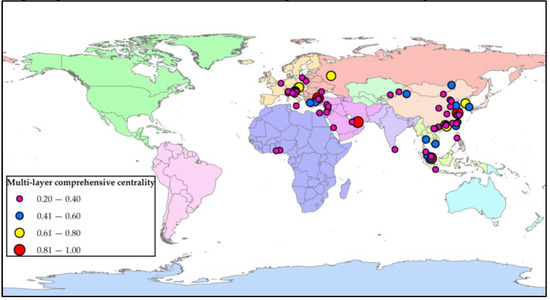
Figure 7.
Geographical distribution of important node cities.
From Figure 7 and Table 3, Node cities with multi-layer comprehensive centrality greater than 0.2 are concentrated, and more than 90% are distributed in the east and west of Eurasia. The eastern cities are mainly concentrated in East and Southeast Asia, including Singapore, Shanghai, Guangzhou, Shenzhen, Hong Kong, Incheon, Ningbo, Urumqi, Qingdao, Kaohsiung, Manchurian, Busan, Bangkok, Ho Chi Minh, Klang, Johor Bahru, etc. And the western cities are concentrated on the Mediterranean coast connecting Asia, Africa and Europe, including Istanbul, Dubai, Vienna, Moscow, Trieste, Izmir, Piraeus, etc.
Second, among the node cities in the middle of Eurasia, only Almaty in Central Asia and Colombo in South Asia have multi-layer comprehensive centrality greater than 0.2, while the multi-layer comprehensive centrality of the rest node cities is between 0 and 0.1. Almaty has developed railway transportation and is a central hub of the east-west Silk Road; with its unique maritime geographical advantages, Colombo is the only place for shipping in Europe, Asia, Africa and the Pacific region.
Third, among the node cities in Eastern Europe, the multi-layer comprehensive cen-trality of Moscow is 0.7, while that of the rest node cities is lower than 0.2. Moscow is located on the trunk line of Eastern European railways, and has developed air transport with solid connectivity.
Finally, the multi-layer comprehensive centrality of node cities in Africa is between 0 and 0.1, while that of Damietta, Said, Lome and Lagos are more than 0.2. Among them, Said and Damietta are located on the Mediterranean Sea, which is the only way for West Asia to enter Africa; Lome and Lagos are located in the center of the coastal urban agglomeration in West Africa.
4. Discussion
4.1. Verification of Identification Results
Network attack is a commonly used method to verify the accuracy of evaluation results [43,44]. With the ranks of nodes, the attack order can be obtained. And by analyzing the decline of network performance, then the accuracy of rank is judged. The size of the largest connected subgraph is used as an index to measure the network performance, the formula is expressed as , Where is the total number of nodes in the B&RCTN; is the number of nodes in the largest connected subgraph of B&RCTN.
4.1.1. Verification Analysis with Previous Results
To verify the accuracy of the proposed methods, analyzing the results of this paper and those of well-established studies is necessary. Since the previous studies did not study the Belt and Road comprehensive traffic system including sea, air and railway transportation, this paper uses the methods proposed in the previous studies to identify important node cities in the B&RCTN [15,38,39], analyzes the results obtained by the previous methods and the results of this paper.
First, through network attack, we analyze the results of multi-layer strength centrality, multi-layer eigenvector centrality, multi-layer closeness centrality, multi-layer betweenness centrality and the result of the traditional strength centrality [38], eigenvector centrality [39], closeness centrality [15], betweenness centrality [15]. The results are shown in Figure 8.
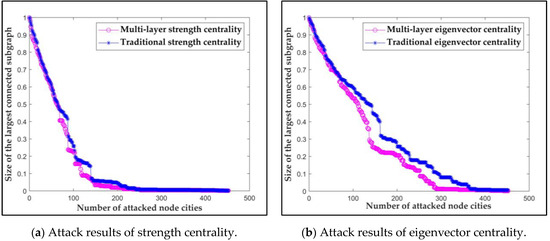
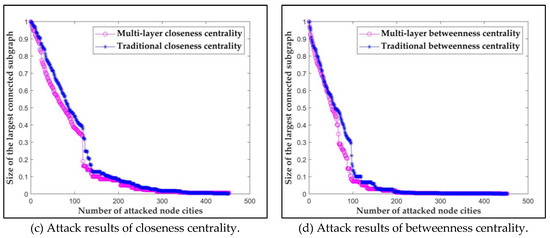
Figure 8.
Attack results of multi-layer centrality and traditional centrality.
In Figure 8, the blue star line declines faster than the purple circle line, indicating that based on the multi-layer centrality attack declines faster. In Figure 8a, with the multi-layer strength centrality attack is always lower than with the traditional strength centrality attack. When the number of attacked nodes reaches 75 to 120, the difference is more obvious. In Figure 8b, when the number of attacked nodes approaches 60, the gap between the two lines increases. When the number of attacked nodes is 141, with the traditional eigenvector centrality attack is 0.5, while with the multi-layer eigenvector centrality attack is only 0.28. In Figure 8c, when the number of attacked nodes is about 120, both lines are noticeably reduced, and the with the multi-layer closeness centrality attack is even lower. In Figure 8d, when the number of attacked nodes is 92, the difference between the two lines is the largest. with the traditional betweenness centrality attack is 0.32, whereas with the multi-layer betweenness centrality attack is only 0.14. The above results show that, the result of multi-layer centrality indexes are more accurate.
Second, analyze attack result of traditional comprehensive centrality and the attack result of multi-layer comprehensive centrality. with the multi-layer comprehensive centrality attack is shown in the blue star line in Figure 9. The traditional comprehensive centrality is obtained by using the entropy weight TOPSIS to combine the four traditional centrality in the previous studies. with the traditional comprehensive centrality attack is shown in the purple circle line. From the general trend, the two lines show a downward trend of first urgent and then gradual, but their rates of decline deviate. When the number of attacked nodes is 82, with the multi-layer comprehensive centrality attack is only 0.1, and with the traditional comprehensive centrality attack is 0.43. Besides, when the number of attacked nodes is 120, with the multi-layer comprehensive centrality attack is 0.01, indicating that the B&RCTN is almost completely failure, however, when the number of attacked nodes reaches 170, with the traditional comprehensive centrality attack is 0.01, and the B&RCTN reaches the same failure result. The results show that, with the multi-layer comprehensive centrality attack decreases faster, which reaching the effect that network performance can be severely damaged only by attacking a small number of nodes.
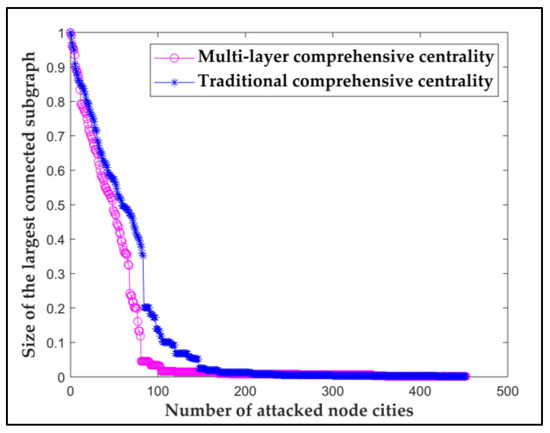
Figure 9.
Attacks results of different comprehensive centrality.
The regional distribution of important node cities identified by the traditional comprehensive centrality and those identified by multi-layer comprehensive centrality are shown Figure 10:
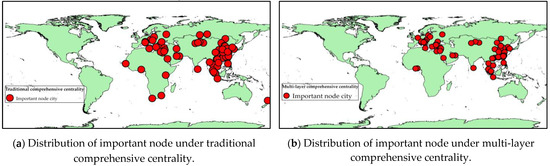
Figure 10.
Distribution of important node cities with different comprehensive centrality.
As seen from Figure 10, The important node cities in Figure 10a,b show a centralized distribution, and the important node cities in the coastal regions of the Mediterranean Sea, East Asia and Southeast Asia are relatively dense. However, some important node cities identified in this paper are not included in those identified by traditional comprehensive centrality, such as Trieste, Koper, Gdansk, Gdynia, Venice, etc. The main reason is that the previous methods homogenize each traffic network layer, which weakens the characteristics of cities at different transportation layers. In addition, compared with the previous methods, this paper fully considers the information contained in inter-layer relationships to describe the transfer cost in traffic activities, which significantly affects the measurement results of closeness and betweenness centrality in this paper.
4.1.2. Verification Analysis with Different Multi-Layer Centrality Results
Through network attack, verify the accuracy of multi-layer comprehensive centrality, by analyzing multi-layer strength centrality, multi-layer eigenvector centrality, multi-layer closeness centrality, multi-layer betweenness centrality, and multi-layer comprehensive centrality, and the results are shown in Figure 11.
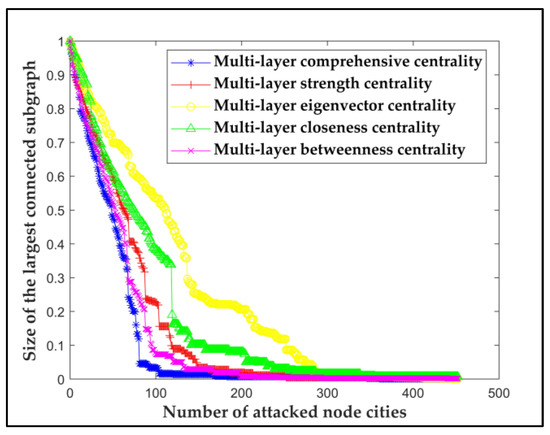
Figure 11.
Attack results of different multi-layer centrality.
In Figure 11, the blue star line depicts based on the multi-layer comprehensive centrality attack, which drops fastest. When the number of attacked nodes is 80, with the multi-layer comprehensive centrality attack is 0.04, but with the multi-layer strength centrality attack, multi-layer eigenvector centrality attack, multi-layer closeness centrality attack and multi-layer betweenness centrality attack is 0.32, 0.59, 0.47 and 0.24, respectively. The results show that, the node ranking in multi-layer comprehensive centrality has more impact on network performance, which verifies the accuracy of multi-layer comprehensive centrality.
4.2. Comparative Analysis Results Based on Geo-Information
According to the comparative analysis, the accuracy of identification methods is verified. This section analyzes identification results from the geographical distribution perspective.
The World Bank evaluated the international logistics performance index (Lpi) of various countries, and the evaluation results are shown in the Figure 12a. In addition to considering the freight volume of different transportation modes, Lpi also considered the geographical location of various countries, the geographical layout of transportation stations, geographical economy and other factors. In this paper, the country of the identified important cities is counted and mapped on the figure by Arcgis based Natural Break, as shown in Figure 12b.
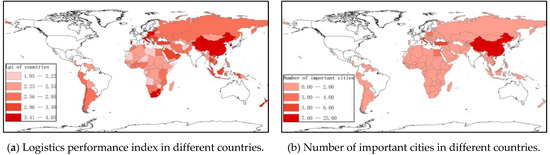
Figure 12.
Logistics performance indexes and number of important cities in different countries.
From the perspective of geographical distribution, there is a significant overlap between countries with higher Lpi and countries with important cities. From Figure 12a,b, it can be seen that most countries in East Asia, Southeast Asia, North Africa, West Asia and Western Europe are dark in colour. Among these countries, the Lpi of Belgium, Singapore, Austria, United Arab Emirates, Luxembourg, Italy, New Zealand, China, Korea, Czech Republic, Portugal, South Africa, Poland, Qatar, Hungary, Israel, Thailand, Malaysia, Estonia, Turkey are all greater than 3.3, ranking in the top 15% of the world and more than 70% of important cities are located in these countries, indicating that many important cities in these countries have good Lpi. These countries have good geographical advantages and form regional urban agglomerations with nearby cities. The Lpi of countries in Central Asia and South Asia is relatively lower, and there are fewer important cities in these regions. The Lpi of African countries varies greatly, with important cities mainly concentrated in North Africa along the Mediterranean coast and West Africa. South America has excellent transportation capabilities but has no important cities due to its remote location from the Belt and Road trading nations.
4.3. Suggestions for Policy Based on the Research Result
This study identified important node cities and briefly analyzed the distribution of these important node cities in Section 3.2. Based on the analysis results, this section provides some policy recommendations for the overall planning and layout optimization of the Belt and Road transportation to promote traffic connectivity between the “Belt and Road” cities.
Important node cities are mainly distributed in the east and west of Eurasia. These important cities have a good transportation cooperation environment and developed transportation capacity. Therefore, for China, South Korea, Malaysia, and Singapore in the east of the Eurasian continent and Turkey, Saudi Arabia, the United Arab Emirates, Italy, Greece, and other countries in the west, it is necessary to introduce policies to build a regional transportation economic belt, reduce customs clearance costs and increase cross-border transport subsidies between countries to promote resource allocation and trade facilitation.
The transportation capacity of node cities in Central and South Asia are generally poor. Central Asia is the core region of the Silk Road Economic Belt. South Asia is one of the important transit points of the Maritime Silk Road, which connects Southeast Asia, East Asia, and Central Asia, showing that the transportation capacity of node cities in this region likely leads to traffic congestion along the Belt and Road. Therefore, from a policy perspective, countries in Central Asia and South Asia, especially Kazakhstan and Sri Lanka, should fully utilize the regional advantages, increase trade policy support with East Asia, Southeast Asia, and West Asia countries, and strengthen transportation links.
Eastern Europe has a vast territory, making connecting all cities in this region more challenging. In the total trade between Eastern Europe and China in 2021, Russia and Belarus account for 41% and 34%, respectively, but their transportation capacity cannot support further trade activities. Therefore, targeted policies to promote transportation development need to be formulated. Based on Moscow’s traffic radiation function, policy support by Russia for establishing cross-border cooperation zones between Vladivostok, St. Petersburg, and neighboring countries should be increased, and the construction of cross-border regional transportation corridors should be accelerated. In Belarus, Brest and Minsk are located on the transportation trunk line. It is beneficial for Belarus to introduce policies to develop the railway branch lines between Brest, Minsk, and nearby cities.
Transportation in African cities is generally undeveloped. 52 African countries have signed cooperation documents, and the Belt and Road, cooperation coverage rate has reached 96%. Among the total trade between these 52 countries, Sierra Leone and Tunisia account for the highest proportion, 28% and 14%, respectively, and their transportation capacity can no longer meet their trade requirements. Regarding policy, Sierra Leone should increase air links between its western city of Freetown and global gateway cities and improve its sea connection with the western urban agglomeration to form an efficient traffic artery. Compared to the node cities in Africa, the northern port cities in Tunisia have development potential, such as Tunisia, Binzit, and Sfax, which can be made into the traffic window of the Mediterranean Free Trade zone. In addition, when formulating the Belt and Road transport policy, North African countries can prioritize reducing the customs clearance process between Mediterranean coastal cities and increasing cross-border transport preferential policies.
5. Conclusions
From the perspective of complex network theory, this paper identifies the important cities in the Belt and Road comprehensive traffic system. First, this paper adopts the weighted super-adjacency matrix to construct the Belt and Road comprehensive traffic network for the first time. This matrix contains sea, air, railway transportation, and transshipment among these traffic modes. Based on the matrix, this paper considers the inter-layer relationships and the heterogeneity of multi-layer networks, innovatively proposes the multi-layer centrality indexes, which evaluate the transport accessibility, transit connectivity, and other transport capabilities of node cities in multiple dimensions. With the results of the multi-layer centrality indexes, entropy weight TOPSIS is used to obtain multi-layer comprehensive centrality, then important node cities with strong comprehensive traffic capacity are identified. The identification result shows that there are 72 important cities in B&RCTN. Finally, based on the distribution of important cities, this paper analyzes the areas with weak traffic connectivity in the current B&RCTN layout, proposes cities that need to prioritize transportation development, and gives suggestions for the policy design of the Belt and Road transportation development.
The research methods and results proposed in this paper have specific theoretical significance and practical value. From a theoretical perspective, this paper provides a new idea for scholars to construct a multi-layer network including multiple traffic modes, which can accurately depict complex traffic systems. Meanwhile, this paper provides methods for identifying important nodes in multi-layer heterogeneous networks, considering the heterogeneity of different network layers and fully paying attention to the information in the inter-layer relationships. From a practical standpoint, this paper identifies important cities that are beneficial to the overall “Belt and Road” traffic connectivity, helps to maintain smooth traffic along the Belt and Road, makes recommendations for the layout planning and optimization of the Belt and Road comprehensive traffic network, and serves as an important reference for the Belt and Road signatories’ future transportation development.
However, admittedly, this paper has the following limitations: (1) The edge weight in the B&RCTN is set based on the traffic section cost, which involves multiple coefficients, such as the loading & unloading cost and loading & unloading time, and this paper takes these coefficients as fixed values. In future research, we will discuss the influence of these coefficients on the research results through sensitivity analysis. (2) This paper mainly uses the traffic relationship between cities to identify important cities. However, trade and traffic affect each other to some extent, and future studies can combine trade relations with traffic relations to study the status of cities.
Author Contributions
Conceptualization, Fengjie Xie; Data curation, Fengjie Xie and Xiao Wang; Formal analysis, Xiao Wang, Fengjie Xie; Funding acquisition, Fengjie Xie, Cuiping Ren; Investigation, Fengjie Xie; Methodology, Fengjie Xie and Xiao Wang; Software, Xiao Wang; Supervision, Fengjie Xie and Cuiping Ren; Writing—original draft, Fengjie Xie, Xiao Wang, Cuiping Ren; Writing—review & editing, Fengjie Xie, Cuiping Ren and Xiao Wang. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Chinese National Funding of Social Sciences (20BGL282), and the National Natural Science Foundation of China (52102418).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, Q. Build a modern comprehensive transportation system of the “the Belt and Road”. Guangming Daily 2018, 4–18, 11. [Google Scholar]
- Guan, X.; Li, Z.; Li, W. Research on status of Chinese container ports based on node importance. J. Shanghai Marit. Univ. 2020, 41, 78–86. [Google Scholar]
- Zhang, L.; Du, H.; Zhao, Y. Correction: Urban networks among Chinese cities along “the Belt and Road”: A case of web search activity in cyberspace. PLoS ONE 2018, 13, e0196141. [Google Scholar] [CrossRef]
- Kohl, T. The Belt and Road Initiative’s effect on supply-chain trade: Evidence from structural gravity equations. Camb. J. Reg. Econ. Soc. 2019, 12, 77–104. [Google Scholar] [CrossRef]
- Chong, Z.H.; Qin, C.L.; Pan, S. The Evolution of the Belt and Road Trade Network and Its Determinant Factors. Emerg. Mark. Financ. Trade 2019, 55, 3166–3177. [Google Scholar] [CrossRef]
- Wang, L.P.; Zou, Z.H.; Liang, S.; Xu, M. Virtual scarce water flows and economic benefits of the Belt and Road Initiative. J. Clean. Prod. 2020, 253, 119936. [Google Scholar] [CrossRef]
- Liaqat, I.; Gao, Y.; Rehman, F.U. National Culture and Financial Inclusion: Evidence from Belt and Road Economies. Sustainability 2022, 14, 3405. [Google Scholar] [CrossRef]
- Huang, M.X.; Li, S.Y. The analysis of the impact of the Belt and Road initiative on the green development of participating countries. Sci. Total Environ. 2020, 722, 137869. [Google Scholar] [CrossRef]
- Sun, Z.C.; Wang, T.; Xiao, X.N.; Zhang, Q.; Guo, H.W. Research on the Measurement of Logistics Capability of Core Cities along “the Belt and Road” in China. Adv. Math. Phys. 2022, 2022, 2223212. [Google Scholar] [CrossRef]
- Zhao, S.D.; Yan, Y.R.; Han, J. Industrial Land Change in Chinese Silk Road Cities and Its Influence on Environments. Land 2021, 10, 806. [Google Scholar] [CrossRef]
- Wu, Q.; Madni, G.R. Environmental protection in selected one belt one road economies through institutional quality: Prospering transportation and industrialization. PLoS ONE 2021, 16, 16. [Google Scholar] [CrossRef]
- Yang, L.J.; Yang, H.N.; Zhao, X.Y.; Yang, Y.C. Study on Urban Resilience from the Perspective of the Complex Adaptive System Theory: A Case Study of the Lanzhou-Xining Urban Agglomeration. Int. J. Environ. Res. Public Health 2022, 19, 13667. [Google Scholar] [CrossRef]
- Yang, G.J.; Huang, X.H.; Huang, J.H.; Chen, H.Y. Assessment of the effects of infrastructure investment under the belt and road initiative. China Econ. Rev. 2020, 60, 101418. [Google Scholar] [CrossRef]
- Wan, C.; Zhao, Y.; Zhang, D. Identifying important ports in maritime container shipping networks along the Maritime Silk Road. Ocean. Coast. Manag. 2021, 211, 105738. [Google Scholar] [CrossRef]
- Boccaletti, S.; Bianconi, G.; Criado, R.; Del Genio, C.I.; Gómez-Gardenes, J.; Romance, M.; Sendina-Nadal, I.; Wang, Z.; Zanin, M. The structure and dynamics of multilayer networks. Phys. Rep. 2014, 544, 1–122. [Google Scholar] [CrossRef] [PubMed]
- Iacovacci, J.; Rahmede, C.; Arenas, A.; Bianconi, G. Functional Multiplex PageRank. Europhys. Lett. 2016, 116, 28004. [Google Scholar] [CrossRef]
- Rui, D.; Ujang, N.; Hamid, H.B. Detecting the urban traffic network structure dynamics through the growth and analysis of multi-layer networks. Phys. A Stat. Mech. Its Appl. 2018, 503, 800–817. [Google Scholar]
- Basaras, P.; Iosifidis, G.; Katsaros, D.; Tassiulas, L. Identifying influential spreaders in complex multilayer networks: A centrality perspective. IEEE Trans. Netw. Sci. Eng. 2017, 6, 31–45. [Google Scholar] [CrossRef]
- Valdeolivas, A.; Tichit, L.; Navarro, C.; Perrin, S.; Odelin, G.; Levy, N.; Cau, P.; Remy, E.; Baudot, A. Random walk with restart on multiplex and heterogeneous biological networks. Bioinformatics 2018, 35, 497–505. [Google Scholar] [CrossRef]
- Al-Garadi, M.A.; Varathan, K.D.; Ravana, S.D. Identifying the influential spreaders in multilayer interactions of online social networks. J. Intell. Fuzzy Syst. 2016, 31, 2721–2735. [Google Scholar] [CrossRef]
- Szell, M.; Lambiotte, R.; Thurner, S. Multirelational organization of large-scale social networks in an online world. Proc. Natl. Acad. Sci. USA 2010, 107, 13636–13641. [Google Scholar] [CrossRef]
- Cardillo, A.; Zanin, M.; Gómez-Gardeñes, J.; Romance, M.; del Amo, A.J.G.; Boccaletti, S. Modeling the multi-layer nature of the European Air Transport Network: Resilience and passengers re-scheduling under random failures. Eur. Phys. J. 2013, 215, 23–33. [Google Scholar] [CrossRef]
- Gao, J.X.; Buldyrev, S.V.; Havlin, S.; Stanley, H.E. Robustness of a network of networks. Phys. Rev. Lett. 2011, 6, 91–98. [Google Scholar] [CrossRef]
- Morris, R.G.; Barthelemy, M. Transport on Coupled Spatial Networks. Phys. Rev. Lett. 2012, 109, 128703. [Google Scholar] [CrossRef]
- Visheratin, A.A.; Trofimenko, T.B.; Mukhina, K.D.; Nasonov, D.; Boukhanovsky, A.V. A multilayer model for diffusion of urgent information in mobile networks. J. Comput. Sci. 2017, 20, 129–142. [Google Scholar] [CrossRef]
- Li, Z.; Shi, Y.; Xu, M.; Zhang, X.; Jiang, S. Hierarchical structure in the global liner shipping network. Syst. Eng.-Theory Pract. 2016, 36, 981–988. [Google Scholar]
- Lohmann, G.; Margulies, D.S.; Horstmann, A. Eigenvector Centrality Mapping for Analyzing Connectivity Patterns in fMRI Data of the Human Brain. PLoS ONE 2010, 5, e10232. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Zhou, M.; Li, F.; Sun, C. Robustness assessment of urban rail transit based on complex network theory: A case study of the Beijing Subway. Saf. Sci. 2015, 79, 149–162. [Google Scholar] [CrossRef]
- Bian, T.; Deng, Y. A new evidential methodology of identifying influential nodes in complex networks. Chaos Solitons Fractals 2017, 103, 101–110. [Google Scholar] [CrossRef]
- Amiripour, S.; Ceder, A.; Mohaymany, A.S. Designing large-scale bus network with seasonal variations of demand. Transp. Res. Part C Emerg. Technol. 2014, 48, 322–338. [Google Scholar] [CrossRef]
- Xue, Y.H.; Wang, J.; Li, L.; He, D.; Hu, B. Optimizing transport efficiency on scale-free networks through assortative or disassortative topology. Phys. Rev. E 2010, 81, 037101. [Google Scholar] [CrossRef]
- Chu, Y.L.; Yang, Z.Z.; Feng, R.M. The Optimal Distribution of Air Cargo Transportation Network Based on Accessibility Index. J. Transp. Syst. Eng. Inf. Technol. 2017, 17, 214–220. [Google Scholar]
- Lu, M.Q.; Chen, Y.; Morphet, R.; Lu, Y.Q.; Li, E.K. The spatial competition between containerised rail and sea transport in Eurasia. Palgrave Commun. 2019, 5, 122. [Google Scholar] [CrossRef]
- General Office of the State Council. Notice of the General Office of the State Council on Printing and Distributing the Three Year Action Plan for Promoting Transportation Structure Adjustment (2018–2020). Gaz. State Counc. People’s Repub. China 2018, 30, 61–66. [Google Scholar]
- Dai, D.S. Policy and Experience of Container Intermodal Transportation Abroad. Commun. Shipp. 2018, 5, 27–30. [Google Scholar]
- Wang, M.; Chen, Y.; Tian, L.; Jiang, S.; Tian, Z.; Du, R. Fluctuation behavior analysis of international crude oil and gasoline price based on complex network perspective. Appl. Energ. 2016, 175, 109–127. [Google Scholar] [CrossRef]
- Burdzik, R.; Ciela, M.; Sadkowski, A. Cargo loading and unloading efficiency analysis in multimodal transport. PROMET-Traffic Transp. 2014, 26, 323–331. [Google Scholar] [CrossRef]
- Battiston, F.; Nicosia, V.; Latora, V. Metrics for the analysis of multiplex networks. Phys. Rev. E 2014, 89, 032804. [Google Scholar] [CrossRef]
- Mincheng, W.; Shibo, H.; Yongtao, Z. A tensor-based framework for studying eigenvector multicentrality in multilayer networks. Proc. Natl. Acad. Sci. USA 2019, 116, 15407–15413. [Google Scholar]
- Wehmuth, K.; Ziviani, A. DACCER: Distributed Assessment of the Closeness CEntrality Ranking in complex networks. Comput. Netw. 2013, 57, 2536–2548. [Google Scholar] [CrossRef]
- Meghanathan, N. Centrality-Based Connected Dominating Sets for Complex Network Graphs. Int. J. Interdiscip. Telecommun. Netw. 2014, 6, 24. [Google Scholar] [CrossRef]
- Boran, F.E. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method. Expert Syst. Appl. 2009, 36, 11363–11368. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.F.; Shi, B.Y.; Lu, X.L.; Jia, J.M. Exploring significant edges of public transport network under targeted attacks. Mod. Phys. Lett. B 2019, 33, 1950114. [Google Scholar] [CrossRef]
- Lai, Q.; Zhang, H.H. Analysis of identification methods of key nodes in transportation network. Chin. Phys. B 2022, 31, 068905. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).