Vertical vs. Horizontal Fractal Dimensions of Roads in Relation to Relief Characteristics
Abstract
:1. Introduction
1.1. Motivation
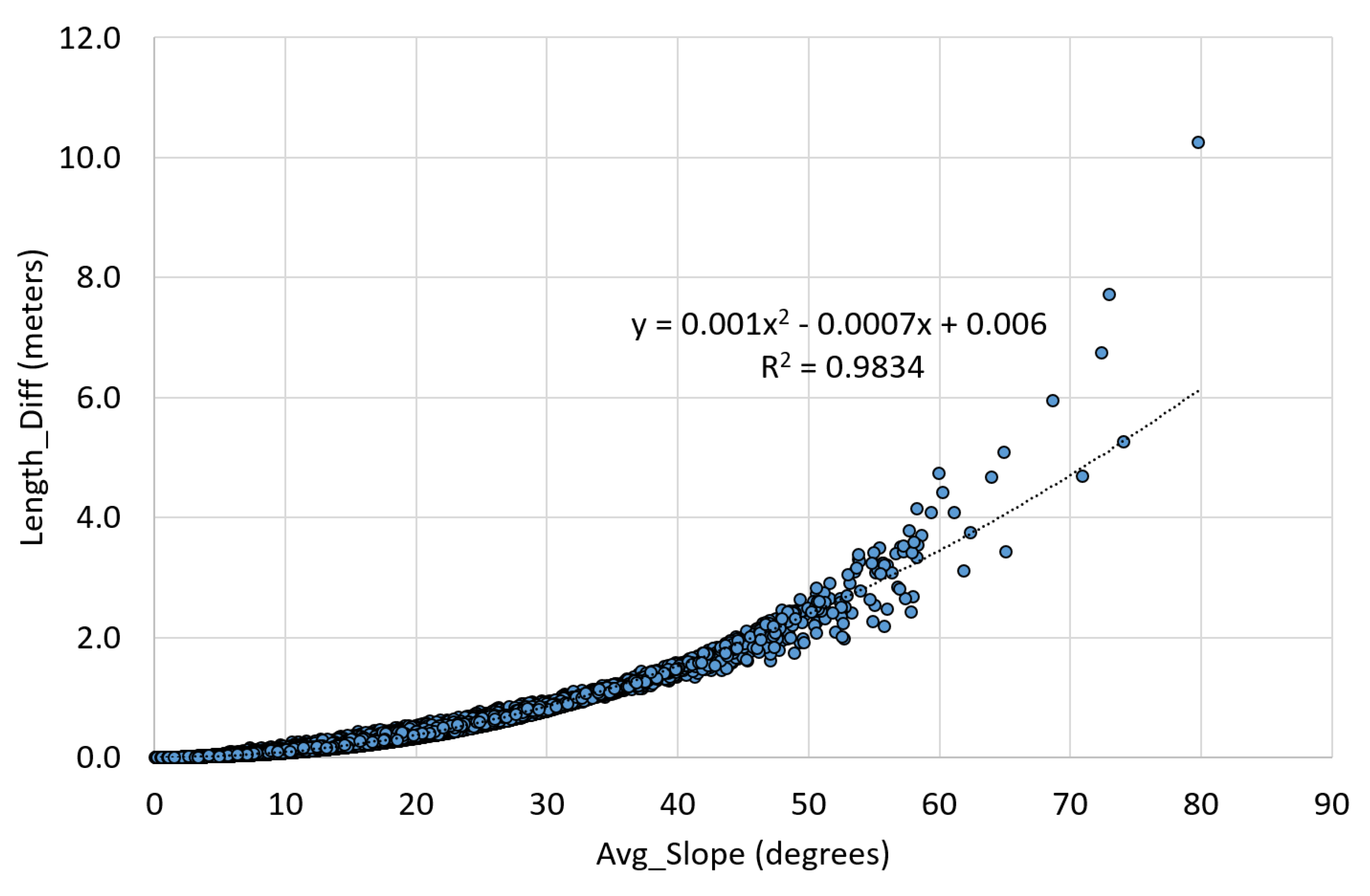
- First, to explicitly demonstrate the magnitude of the length difference between the planar road length and the surface road length derived from a DTM, in correlation with the road slope calculated from the DTM.
- Second, to study road distance complexity using the fractal dimension in the planar and vertical dimensions.
- Third, to investigate the vertical and horizontal fractal dimensions of roads in different geographical regions with distinct topographic characteristics.
1.2. Research Originality and Contributions
1.3. Organization of the Paper
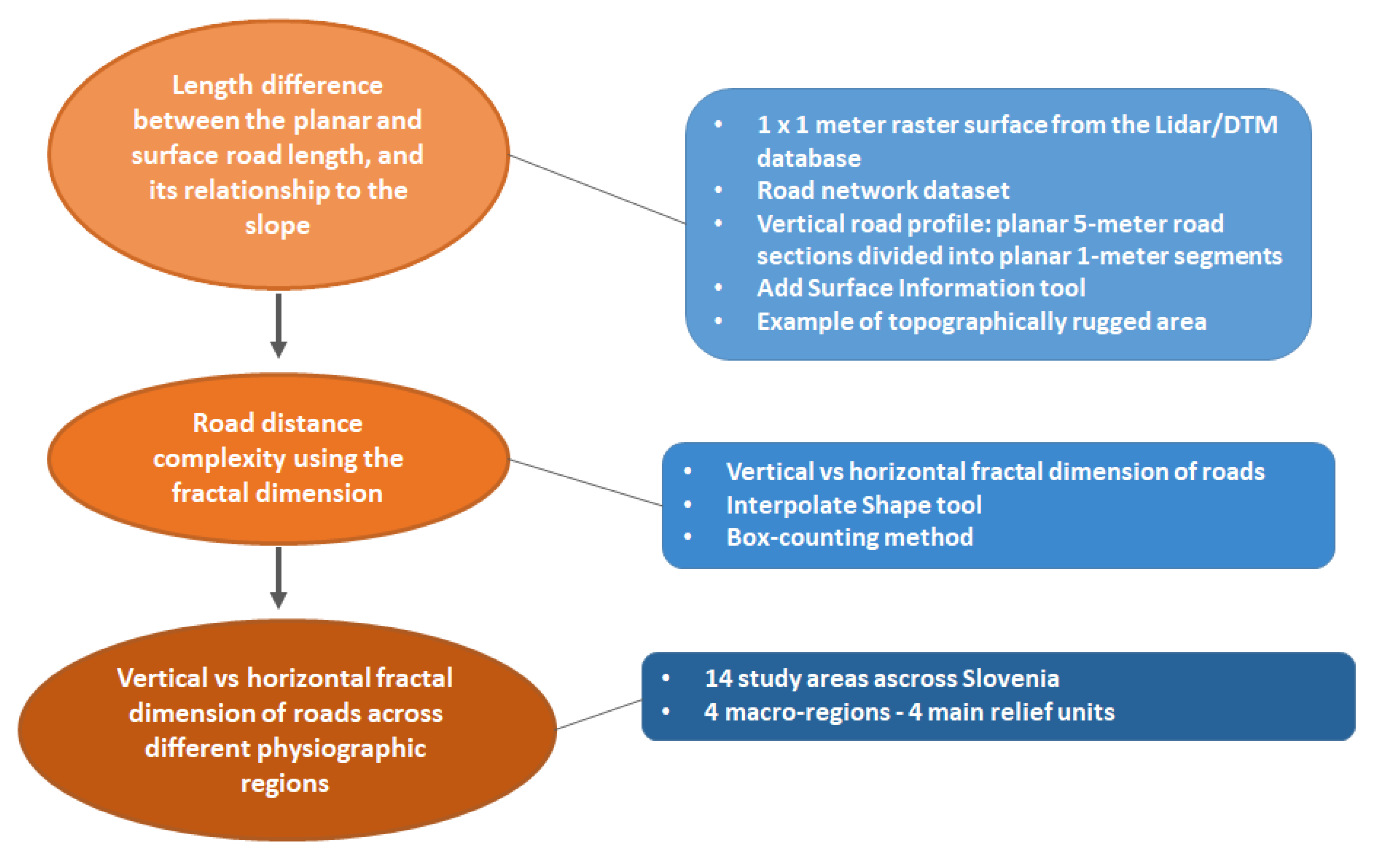
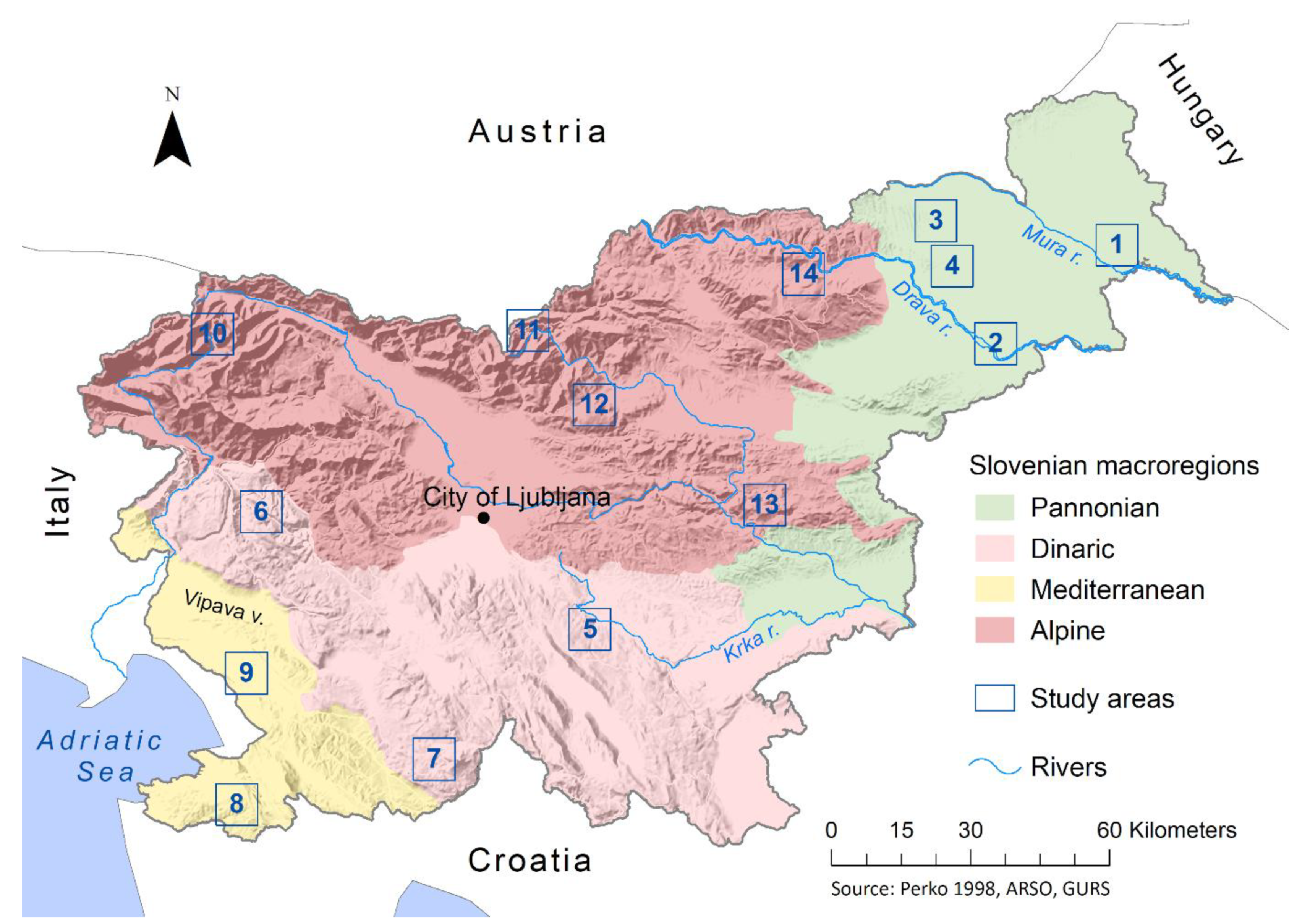
2. Data and Core Method
3. Experiments
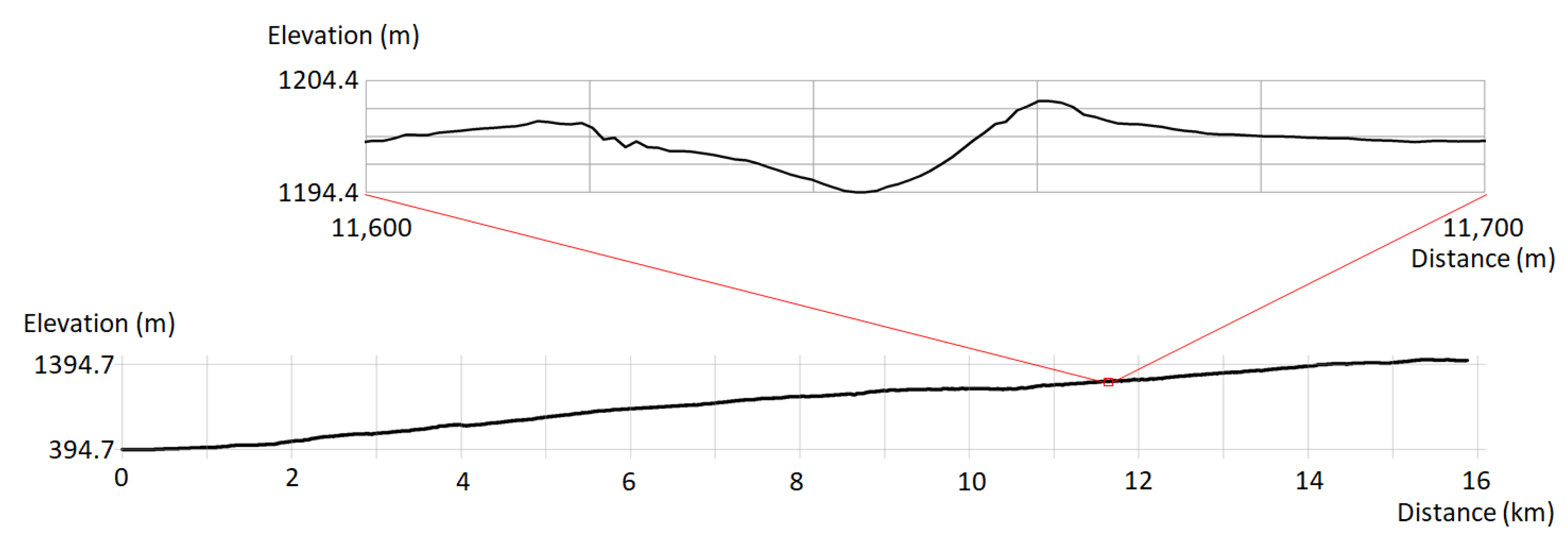
3.1. Experiment 1: Length Difference between the Planar and Surface Road Lengths, and Their Relationship with the Slope
3.2. Experiment 2: Road Distance Complexity Using the Fractal Dimension
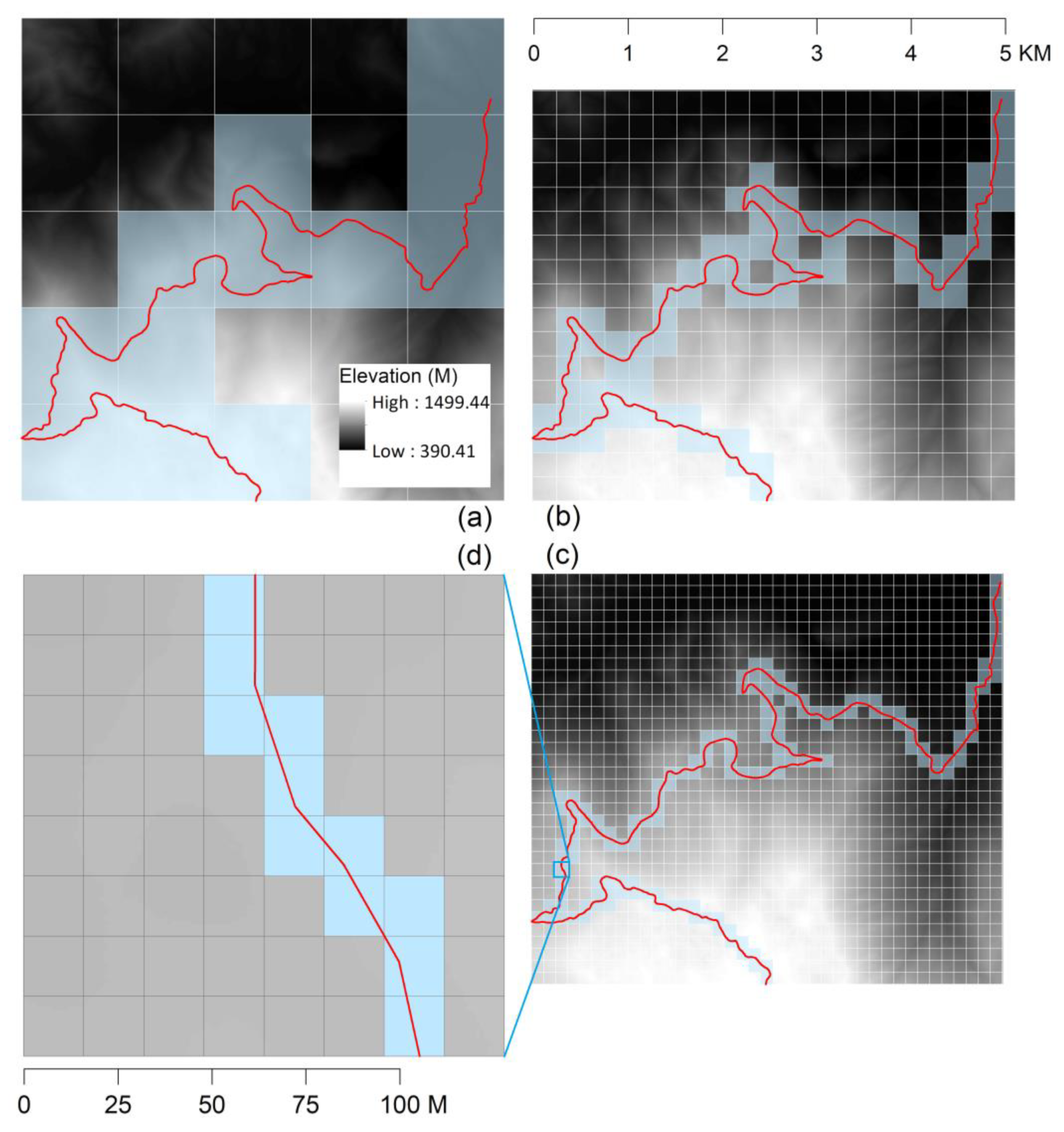
- The ArcGIS Interpolate Shape tool [38] was used to convert a 2D road line into a 3D road line by interpolating the Z-values from a raster surface of a one-meter cell size. Similar to the previous experiment, the interpolation method was bilinear, and the sample distance was equal to the size of the raster cell.
- A vertical profile of the road section was created using the tool Create Profile Graph [38], where the horizontal axis (distance) and vertical axis (elevation) had the same scale, 1:1, in meters. The profile was exported as a table. This table was re-imported as X–Y data into ArcGIS ArcMap, resulting in a planar vector representation of the road section profile. This meant that the x-axis was the distance along the road section, while the y-axis was the elevation of the section.
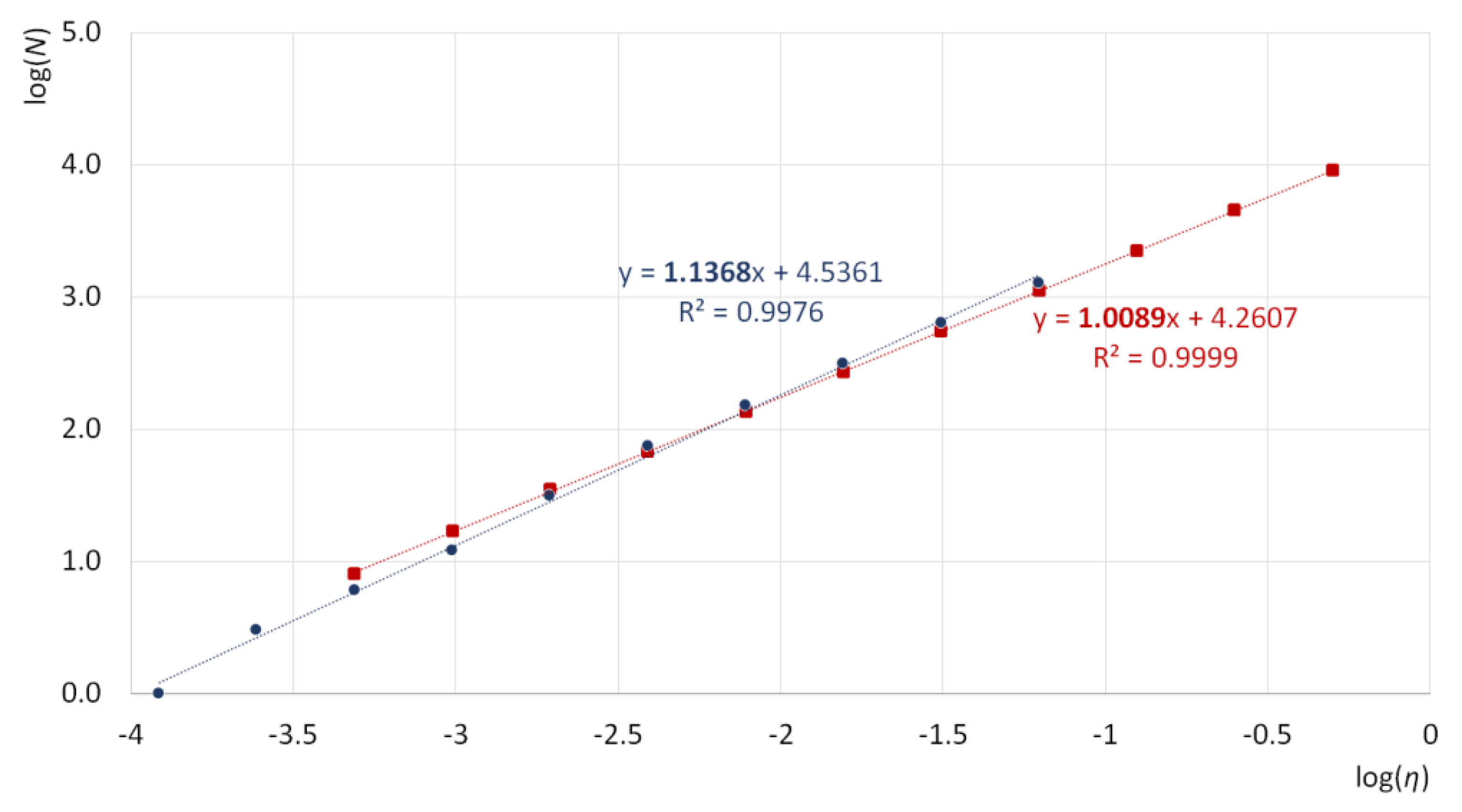
- Box counting, a common approach for calculating the fractal dimension [40,41], was applied to the profile as follows. A sequence of M square vector meshes was created, each covering a profile. The initial mesh had a square side length of ƞ1, while each subsequent mesh had a finer side length ƞi. For each mesh, the number of squares Ni that included part of the profile was counted.
3.3. Experiment 3: Vertical vs. Horizontal Fractal Dimension of Roads
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Statzner, B.; Bonada, N.; Resh, V.H. Why Roads and Rivers Can Be Straight or Winding: How Physical and Sociohistorical Factors Produce Contemporary Regional Landscape Patterns. Freshw. Sci. 2016, 35, 1088–1102. [Google Scholar] [CrossRef]
- Belloc, H. The Road; The British Reinforced Concrete Engineering Co., Ltd.: Manchester, UK, 1923. [Google Scholar]
- Hosseini, S.; Baziyad, H.; Norouzi, R.; Jabbedari Khiabani, S.; Gidófalvi, G.; Albadvi, A.; Alimohammadi, A.; Seyedabrishami, S. Mapping the Intellectual Structure of GIS-T Field (2008–2019): A Dynamic Co-Word Analysis. Scientometrics 2021, 126, 2667–2688. [Google Scholar] [CrossRef]
- Miller, H.J.; Shaw, S.-L. Geographic Information Systems for Transportation: Principles and Applications; Spatial Information Systems; Oxford University Press: Oxford, NY, USA, 2001. [Google Scholar]
- de Smith, M.J. GIS, Distance, Paths and Anisotropy. In Advanced Spatial Analysis: The CASA Book of GIS; Longley, P.A., Batty, M., Eds.; ESRI Press: Redlands, CA, USA, 2003; pp. 309–326. [Google Scholar]
- Zhang, Q.; Giovannini, L.; Simantov, M.; Vries, J.; Vuong, M.; Griffiths, S.; Mercer, B.; Li, X. Extraction of 3D Road Geometry from Airborne IFSAR Data. In Proceedings of the ISPRS Technical Commission III Symposium: Photogrammetry Computer Vision and Image Analysis, Saint Mandé, France, 1–3 September 2010; International Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2010; Volume 38, pp. 24–28. [Google Scholar]
- Kaul, M.; Yang, B.; Jensen, C.S. Building Accurate 3D Spatial Networks to Enable Next Generation Intelligent Transportation Systems. In Proceedings of the 2013 IEEE 14th International Conference on Mobile Data Management, Milan, Italy, 3–6 June 2013; Volume 1, pp. 137–146. [Google Scholar]
- Dubuc, S. GIS-Based Accessibility Analysis for Network Optimal Location Model. An Application for Bio-Energy Projects of the Mineral Industry in the UK. Cybergeo Eur. J. Geogr. 2007. [Google Scholar] [CrossRef]
- Tavares, G.; Zsigraiova, Z.; Semiao, V.; Carvalho, M.G. Optimisation of MSW Collection Routes for Minimum Fuel Consumption Using 3D GIS Modelling. Waste Manag. 2009, 29, 1176–1185. [Google Scholar] [CrossRef]
- Prah, K.; Kramberger, T.; Dragan, D. Primerjava 2D in 3D GIS Modela Pri Načrtovanju Šolskih Prevozov. Dela 2018, 49, 61–74. [Google Scholar] [CrossRef]
- Schröder, M.; Cabral, P. Eco-Friendly 3D-Routing: A GIS Based 3D-Routing-Model to Estimate and Reduce CO2-Emissions of Distribution Transports. Comput. Environ. Urban Syst. 2019, 73, 40–55. [Google Scholar] [CrossRef]
- Goodchild, M.F. Fractals and the Accuracy of Geographical Measures. Math. Geol. 1980, 12, 85–98. [Google Scholar] [CrossRef]
- Richardson, L.F. The Problem of Contiguity: An Appendix to Statistics of Deadly Quarrels. Gen. Syst. Yearb. 1961, 6, 139–187. [Google Scholar]
- Mandelbrot, B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance and Dimension, 1st ed.; W.H.Freeman & Company: San Francisco, CA, USA, 1977; ISBN 978-0-7167-0473-7. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Company: San Francisco, CA, USA, 1982; ISBN 978-0-7167-1186-5. [Google Scholar]
- Lam, N.S.N.; De Cola, L. (Eds.) Fractals in Geography; PTR Prentice Hall: Englewood Cliffs, NJ, USA, 1993; ISBN 0-13-105867-3. [Google Scholar]
- Goodchild, M.F. The Fractional Brownian Process as a Terrain Simulation Model. Simulation 1982, 13, 1133–1137. [Google Scholar]
- Mark, D.M.; Aronson, P.B. Scale-Dependent Fractal Dimensions of Topographic Surfaces: An Empirical Investigation, with Applications in Geomorphology and Computer Mapping. Math. Geol. 1984, 16, 671–683. [Google Scholar] [CrossRef]
- Clarke, K.; Schweizer, D. Measuring the Fractal Dimension of Natural Surfaces Using a Robust Fractal Estimator. Cartogr. Geogr. Inf. Sci. 1991, 18, 37–47. [Google Scholar] [CrossRef]
- Batty, M.; Longley, P.A. The Fractal Simulation of Urban Structure. Environ. Plan. A Econ. Space 1986, 18, 1143–1179. [Google Scholar] [CrossRef]
- Afrianto, F. Fractal Dimensions Analysis of Urban Agglomeration at Road Intersections in Metropolitan Malang Raya. IOP Conf. Ser. Earth Environ. Sci. 2023, 1186, 012010. [Google Scholar] [CrossRef]
- Liu, S.; Chen, Y. A Three-Dimensional Box-Counting Method to Study the Fractal Characteristics of Urban Areas in Shenyang, Northeast China. Buildings 2022, 12, 299. [Google Scholar] [CrossRef]
- De Cola, L. Fractal Analysis of Multiscale Spatial Autocorrelation among Point Data. Environ. Plan. A Econ. Space 1991, 23, 545–556. [Google Scholar] [CrossRef]
- Bai, C.; Cai, X.; Zhang, C.; Sun, Y. Fractal Characteristics of the Road Network in Jiangsu Province. In Proceedings of the 6th Advanced Forum on Transportation of China (AFTC 2010), Beijing, China, 16 October 2010; pp. 241–244. [Google Scholar]
- Mo, Y.; Liu, J.; Lv, S. GIS-Based Analysis of Fractal Features of the Urban Road Network. In Proceedings of the 2015 6th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 23–25 September 2015. [Google Scholar] [CrossRef]
- Wang, H.; Luo, S.; Luo, T. Fractal Characteristics of Urban Surface Transit and Road Networks: Case Study of Strasbourg, France. Adv. Mech. Eng. 2017, 9, 1687814017692289. [Google Scholar] [CrossRef]
- Lu, Y.; Tang, J. Fractal Dimension of a Transportation Network and Its Relationship with Urban Growth: A Study of the Dallas-Fort Worth Area. Environ. Plan. B Plan. Des. 2004, 31, 895–911. [Google Scholar] [CrossRef]
- Lu, Z.; Zhang, H.; Southworth, F.; Crittenden, J. Fractal Dimensions of Metropolitan Area Road Networks and the Impacts on the Urban Built Environment. Ecol. Indic. 2016, 70, 285–296. [Google Scholar] [CrossRef]
- Abid, R.I.; Tortum, A.; Atalay, A. Fractal Dimensions of Road Networks in Amman Metropolitan Districts. Alex. Eng. J. 2021, 60, 4203–4212. [Google Scholar] [CrossRef]
- Daniel, C.B.; Mathew, S.; Saravanan, S. Spatial Interdependence of Fractal Dimension and Topological Parameters of Road Network: A Geographically Weighted Regression Approach. Spat. Inf. Res. 2021, 29, 737–747. [Google Scholar] [CrossRef]
- Deng, H.; Wen, W.; Zhang, W. Analysis of Road Networks Features of Urban Municipal District Based on Fractal Dimension. ISPRS Int. J. Geo-Inf. 2023, 12, 188. [Google Scholar] [CrossRef]
- Clark, J.; Holton, D.A. A First Look at Graph Theory; World Scientific Publishing Company: Singapore, 1991; ISBN 978-981-310-355-9. [Google Scholar]
- NAVTEQ. NAVTEQ’s NAVSTREETS Street Data; Distributed by GISDATA, Ljubljana, Slovenia; NAVTEQ: Chicago, IL, USA, 2008. [Google Scholar]
- Ministry of the Environment of the Republic of Slovenia. Laser Scanning of Slovenia; Distributed by Slovenian Environment Agency, Ljubljana, Slovenia; Geodetic Institute of Slovenia: Ljubljana, Slovenia, 2015.
- Mongus, D.; Zalik, B. Parameter-Free Ground Filtering of LiDAR Data for Automatic DTM Generation. ISPRS J. Photogramm. Remote Sens. 2012, 67, 1–12. [Google Scholar] [CrossRef]
- Mongus, D.; Triglav Čekada, M.; Žalik, B. The analysis of an automatic method for digital terrain model generation from lidar data on Slovenian test cases. Geod. Vestn. 2013, 57, 045–259. [Google Scholar] [CrossRef]
- ArcGIS ArcMap, version 2020. Esri: Redlands, CA, USA, 2020.
- Perko, D. (Ed.) The regionalization of Slovenia; Regionalizacija Slovenije. Geogr. Zb.—Acta Geogr. 1998, 38, 11–57. [Google Scholar]
- Gonzato, G. A Practical Implementation of the Box Counting Algorithm. Comput. Geosci. 1998, 24, 95–100. [Google Scholar] [CrossRef]
- Grassberger, P. On Efficient Box Counting Algorithms. Int. J. Mod. Phys. C 1993, 04, 515–523. [Google Scholar] [CrossRef]
- Gonzato, G.; Mulargia, F.; Ciccotti, M. Measuring the Fractal Dimensions of Ideal and Actual Objects: Implications for Application in Geology and Geophysics. Geophys. J. Int. 2000, 142, 108–116. [Google Scholar] [CrossRef]
- Perko, D.; Hrvatin, M.; Ciglič, R. A Methodology for Natural Landscape Typification of Slovenia. Acta Geogr. Slov. 2015, 55, 235–270. [Google Scholar] [CrossRef]
- Perko, D.; Orožen Adamič, M. (Eds.) Slovenija: Pokrajine in Ljudje; Mladinska Knjiga: Ljubljana, Slovenia, 2001; ISBN 978-86-11-15033-8. [Google Scholar]
- Perko, D. Analiza Površja Slovenije s Stometrskim Digitalnim Modelom Reliefa; Geografija Slovenije; Založba ZRC: Ljubljana, Slovenia, 2001; ISBN 978-961-6182-94-2. [Google Scholar]
| Author(s) | Approach |
|---|---|
| de Smith, 2003 [5] | Algorithm for path finding that takes into account topographic obstacles to find a route between two points in a two-dimensional continuous space with topographic variations. |
| Dubuc, 2007 [8] | Approach to estimate and incorporate the impact of slope on travel time and on transport cost calculations. |
| Tavares et al., 2009 [9] | GIS 3D route modeling for waste collection using fuel consumption as a core criterion and considering local road gradients. |
| Zhang et al., 2010 [6] | Semi-automated approach for 2D road extraction from orthorectified radar imagery and automated elevation assignment from road segments based on an interferometric synthetic aperture radar (IFSAR)-derived digital elevation model (DEM). |
| Kaul et al., 2013 [7] | A filtering and lifting framework that augments a 2D spatial network model with the elevation information extracted from massive aerial laser scan data to produce an accurate 3D model. |
| Prah et al., 2018 [10] | Comparison of 2D and 3D GIS models for school vehicle routing with the travel distance and travel time as core criteria. |
| Schröder and Cabral, 2019 [11] | GIS 3D route modeling to illustrate the effects of road inclination on fuel consumption and carbon dioxide (CO2) emissions, and to optimize routes in the domain of road freight transportation. |
| Author(s) | Application |
|---|---|
| Lu and Tang, 2004 [28] | Study of the relationship between the mass size of cities in the Dallas-Fort Worth, U.S. area and the complexity of their road systems using a modified box-counting method. |
| Bai et al., 2010 [25] | Research on the spatial structures and patterns of road networks in northern and southern Jiangsu Province, China. The methods of the Hausdorff dimension and the covering depth were used. |
| Mo et al., 2015 [26] | Analysis of Shenzhen, China’s municipal road network based on the fractal theory and GIS. The Hausdorff method was used to calculate the road network coverage index, leading to suggestions for road network optimization. |
| Lu at al., 2016 [29] | Research on the fractal dimensions of major road networks in large U.S. metro areas and the associations of these values on the urban built environment. |
| Wang et al., 2017 [27] | Study of the fractal characteristics of urban surface transit and road networks in Strasbourg, using length dimension and branch dimension methods. |
| Abid et al., 2021 [30] | Calculation of five types of fractal dimensions for road networks in 22 districts in the Greater Amman metropolitan area. Each calculated fractal dimension was regressed to the district’s area urban form parameters. |
| Daniel at al., 2021 [31] | Study of the topological parameters of the road network in Tiruchirappalli, India based on the graph theory. Relationships between the fractal dimension and other topological parameters were explored using geographically weighted regression. |
| Deng et al., 2023 [32] | Analysis of the road network features in nine urban municipal districts in Harbin, China based on five fractal dimension methods, including box counting. Each fractal dimension result was linearly regressed with district pattern indicators. |
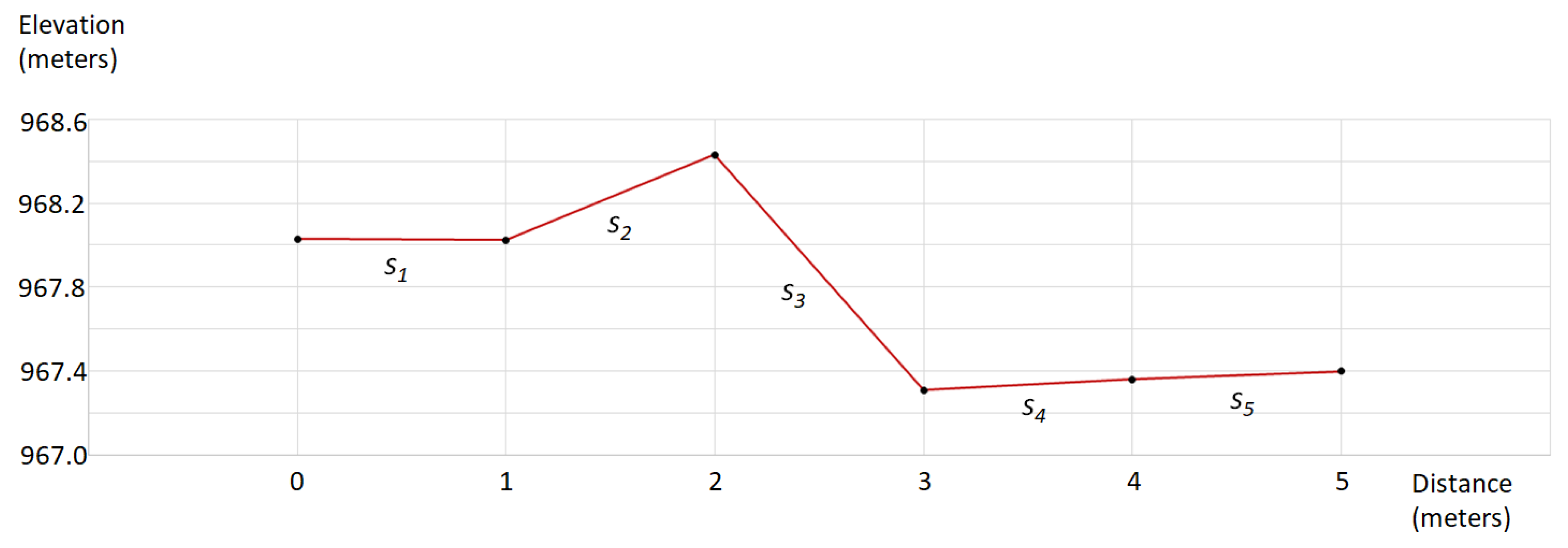
| Segment | Slope (Degrees) | Surface Length (Meters) | Weighted Slope (Degrees) |
|---|---|---|---|
| s1 | 0.29 | 1.00 | 0.29 |
| s2 | 22.05 | 1.08 | 23.81 |
| s3 | 48.24 | 1.50 | 72.36 |
| s4 | 2.86 | 1.00 | 2.86 |
| s5 | 2.30 | 1.00 | 2.30 |
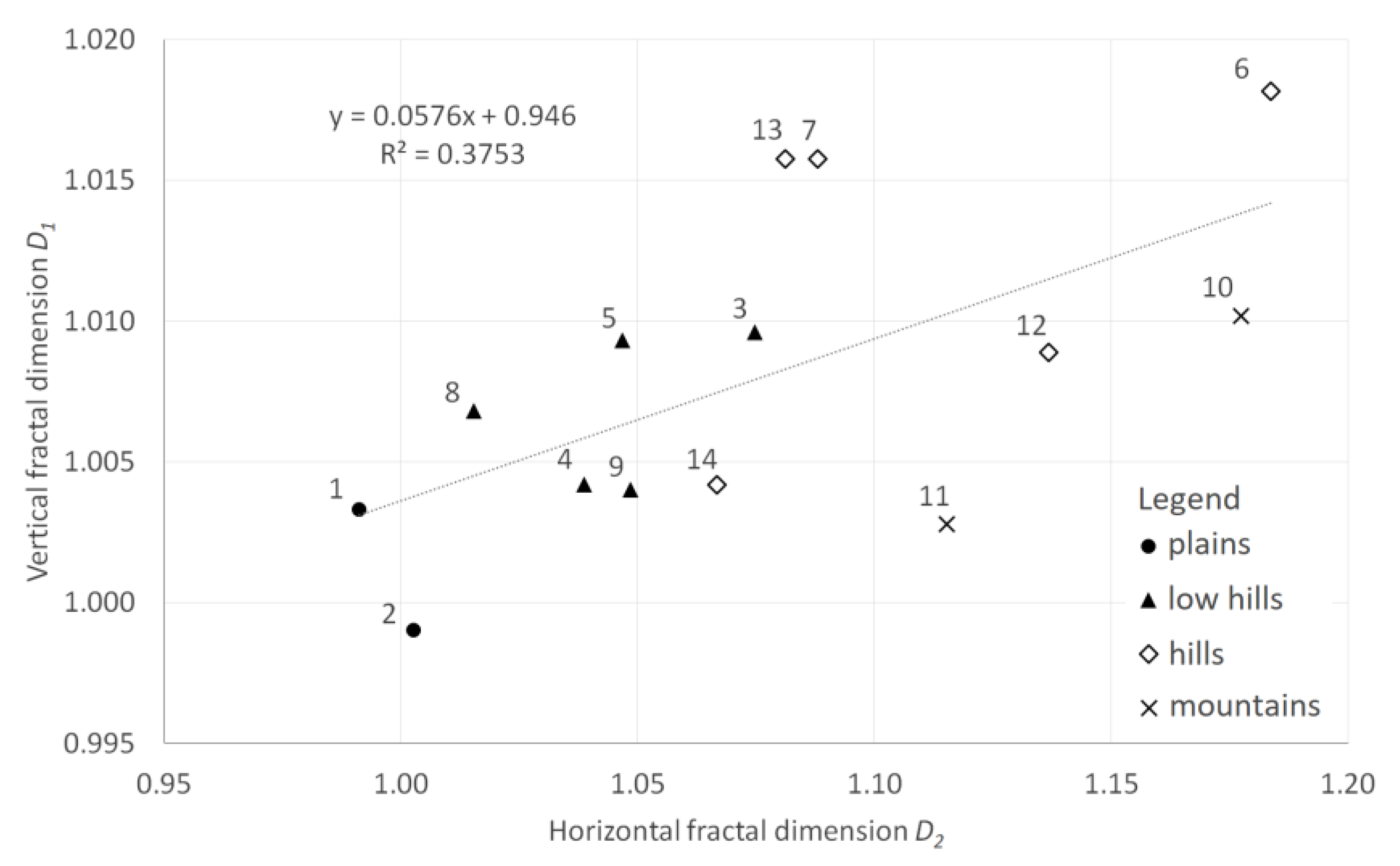
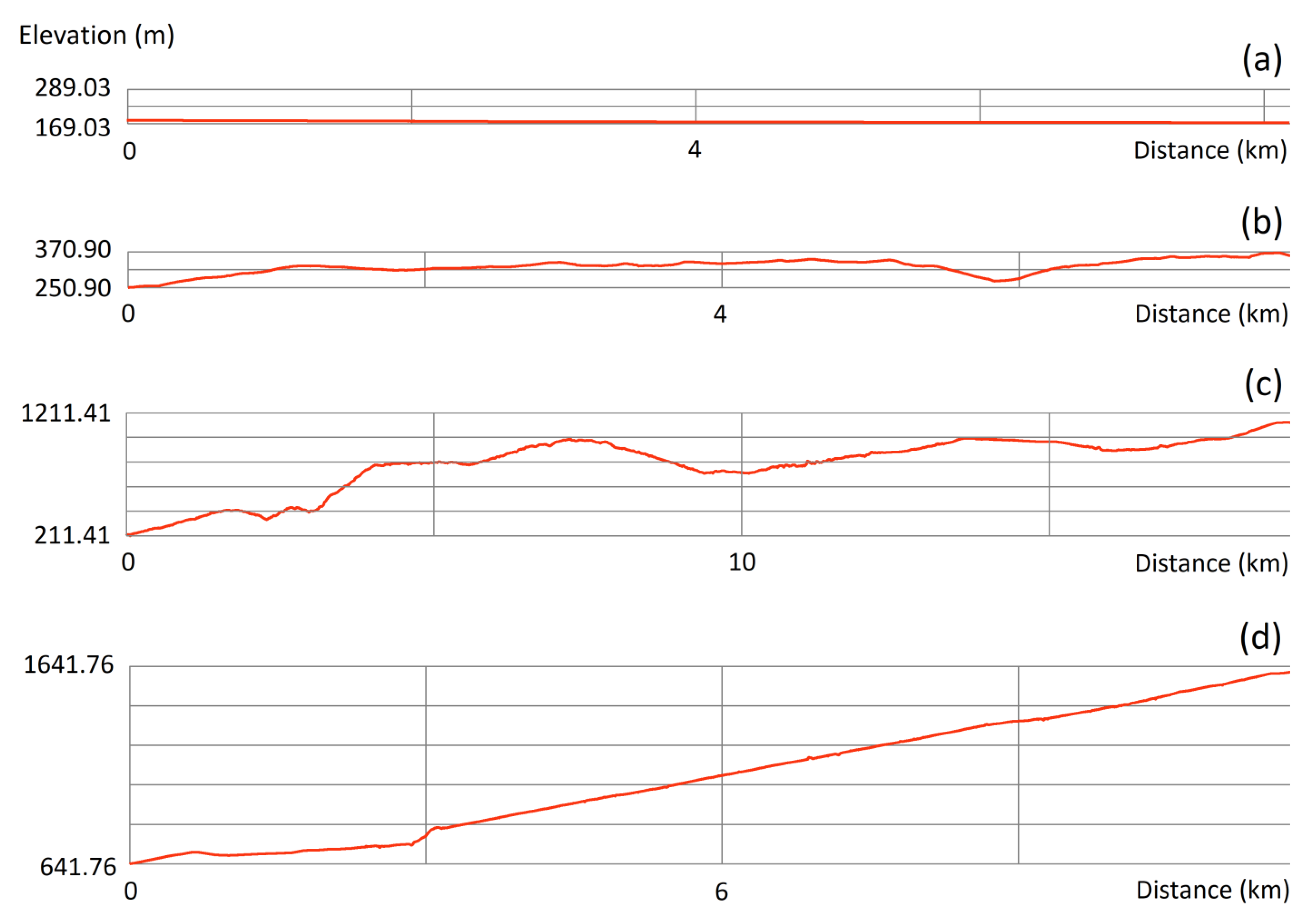
| Site # | Relief Unit | Elevation Range of the Road Section (Meters) | Average Slope of the Road Section (Degrees) | Vertical Fractal Dimension of the Road Section | Horizontal Fractal Dimension of the Road Section | ||
|---|---|---|---|---|---|---|---|
| D1 | R2 | D2 | R2 | ||||
| 1 | Plains | 11.02 | 0.58 | 1.0033 | 1.0000 | 0.9913 | 0.9995 |
| 2 | Plains | 17.19 | 1.25 | 0.9990 | 0.9999 | 1.0027 | 0.9999 |
| 3 | Low hills | 140.30 | 3.77 | 1.0096 | 1.0000 | 1.0748 | 0.9979 |
| 4 | Low hills | 149.54 | 3.68 | 1.0042 | 1.0000 | 1.0387 | 0.9997 |
| 5 | Low hills | 446.14 | 4.61 | 1.0093 | 1.0000 | 1.0468 | 0.9993 |
| 6 | Hills | 922.91 | 12.98 | 1.0182 | 0.9999 | 1.1837 | 0.9978 |
| 7 | Hills | 178.82 | 7.62 | 1.0158 | 1.0000 | 1.0880 | 0.9978 |
| 8 | Low hills | 319.26 | 3.23 | 1.0068 | 1.0000 | 1.0155 | 0.9992 |
| 9 | Low hills | 93.93 | 2.14 | 1.0040 | 1.0000 | 1.0486 | 0.9974 |
| 10 | Mountains | 970.55 | 7.38 | 1.0102 | 1.0000 | 1.1774 | 0.9986 |
| 11 | Mountains | 694.84 | 5.51 | 1.0028 | 1.0000 | 1.1152 | 0.9977 |
| 12 | Hills | 1063.39 | 9.08 | 1.0089 | 0.9999 | 1.1368 | 0.9976 |
| 13 | Hills | 598.38 | 9.60 | 1.0158 | 0.9999 | 1.0812 | 0.9994 |
| 14 | Hills | 1038.71 | 8.39 | 1.0042 | 1.0000 | 1.0667 | 0.9991 |
| Our Research | Existing Research from Table 2 | |
|---|---|---|
| Applying GIS | GIS | GIS [25,26,29,30,31,32] |
| Fractal dimension method | Novel concept of the vertical fractal dimension of roads (vector-based approach for box-counting method implemented in ArcGIS software) | |
| Definition of network | Non-urban roads |
|
| Software | ArcGIS software with the Add Surface Information tool and Interpolate Shape tool |
|
| Spatial data coverage |
|
|
| Time situation | Current | Ten-year span [25] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prah, K.; Shortridge, A.M. Vertical vs. Horizontal Fractal Dimensions of Roads in Relation to Relief Characteristics. ISPRS Int. J. Geo-Inf. 2023, 12, 487. https://doi.org/10.3390/ijgi12120487
Prah K, Shortridge AM. Vertical vs. Horizontal Fractal Dimensions of Roads in Relation to Relief Characteristics. ISPRS International Journal of Geo-Information. 2023; 12(12):487. https://doi.org/10.3390/ijgi12120487
Chicago/Turabian StylePrah, Klemen, and Ashton M. Shortridge. 2023. "Vertical vs. Horizontal Fractal Dimensions of Roads in Relation to Relief Characteristics" ISPRS International Journal of Geo-Information 12, no. 12: 487. https://doi.org/10.3390/ijgi12120487
APA StylePrah, K., & Shortridge, A. M. (2023). Vertical vs. Horizontal Fractal Dimensions of Roads in Relation to Relief Characteristics. ISPRS International Journal of Geo-Information, 12(12), 487. https://doi.org/10.3390/ijgi12120487







