Extraction of Urban Road Boundary Points from Mobile Laser Scanning Data Based on Cuboid Voxel
Abstract
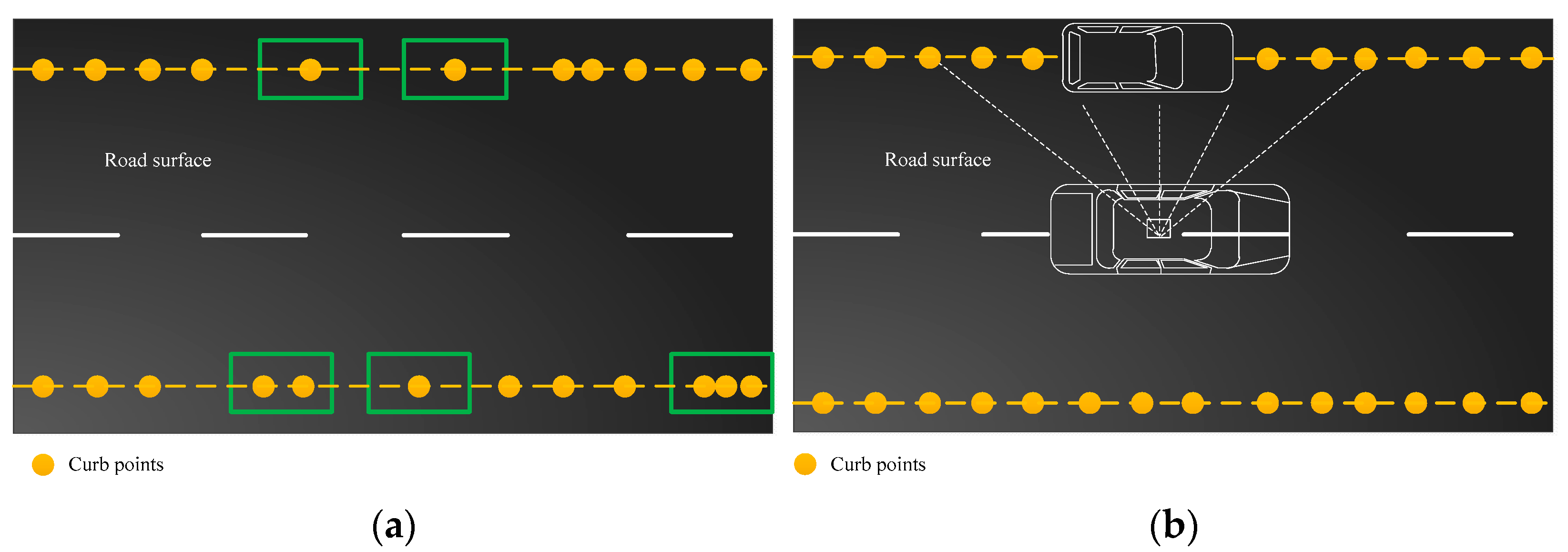
1. Introduction
2. Relevant Works
3. Methodology
3.1. Point Cloud Voxelization
3.2. Extracting Candidate Road Curb Points
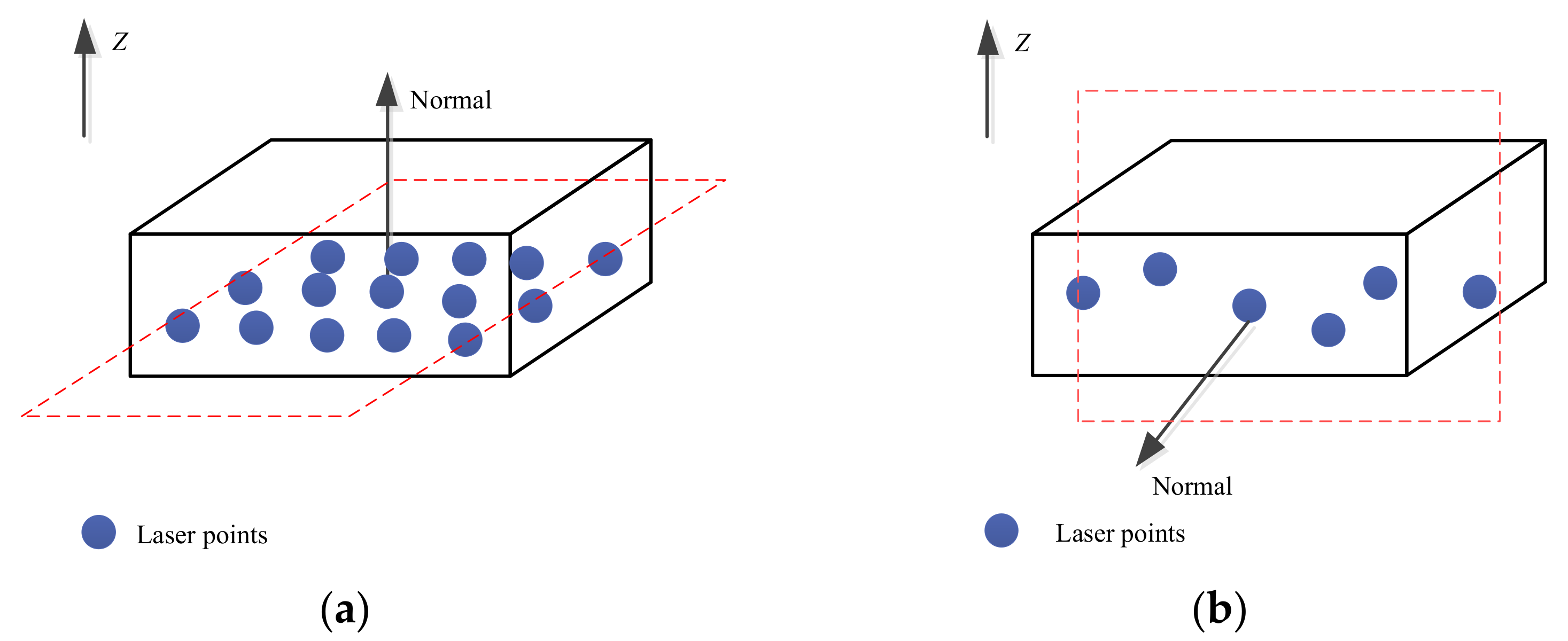
3.2.1. Normal Vector of Voxels
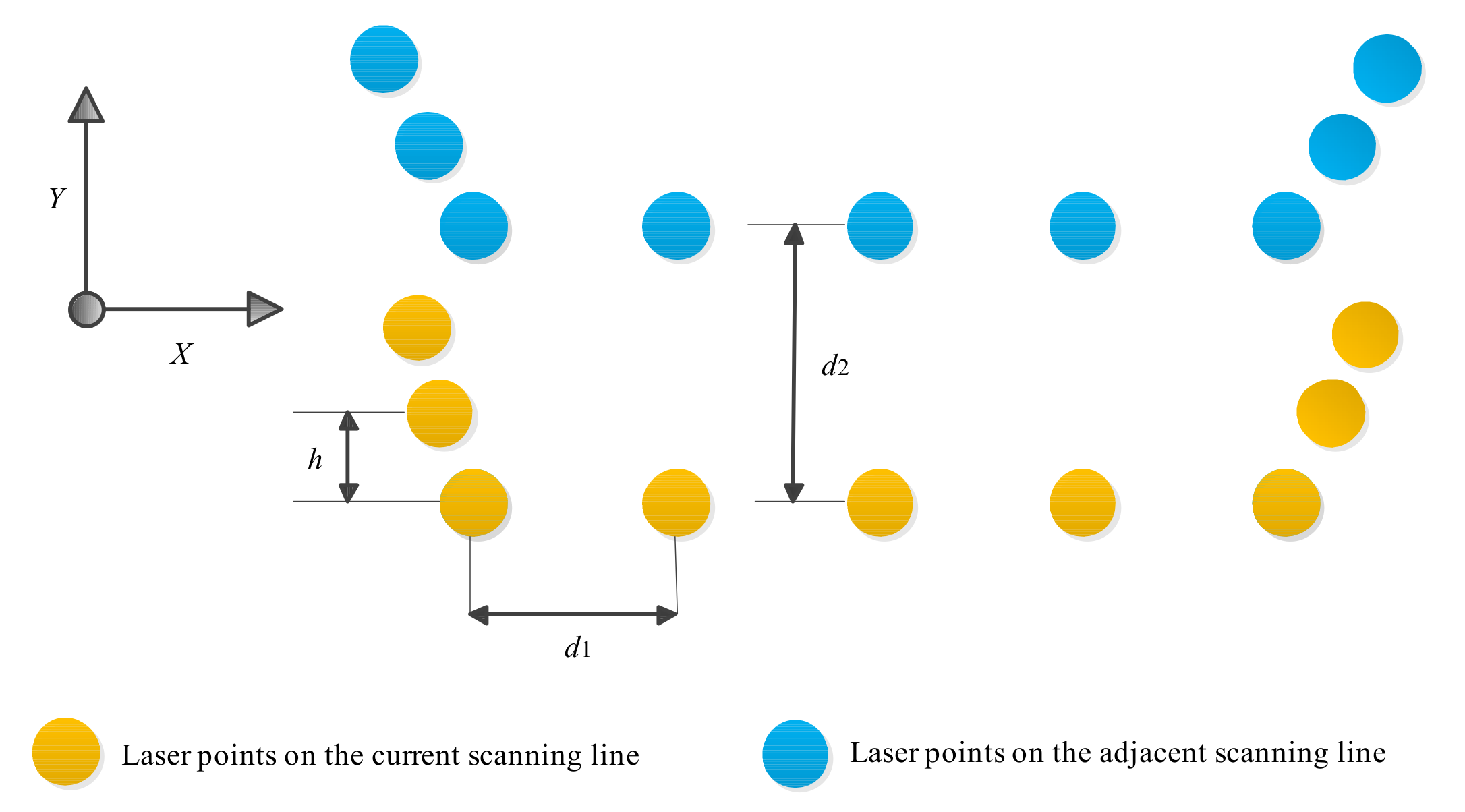
3.2.2. Linear Dimension of Voxels
3.3. Determining the Final Curb Point
3.3.1. Reflection Intensity Constraint of Surface Features
3.3.2. Noise Point Elimination
4. Experimental Results and Analysis
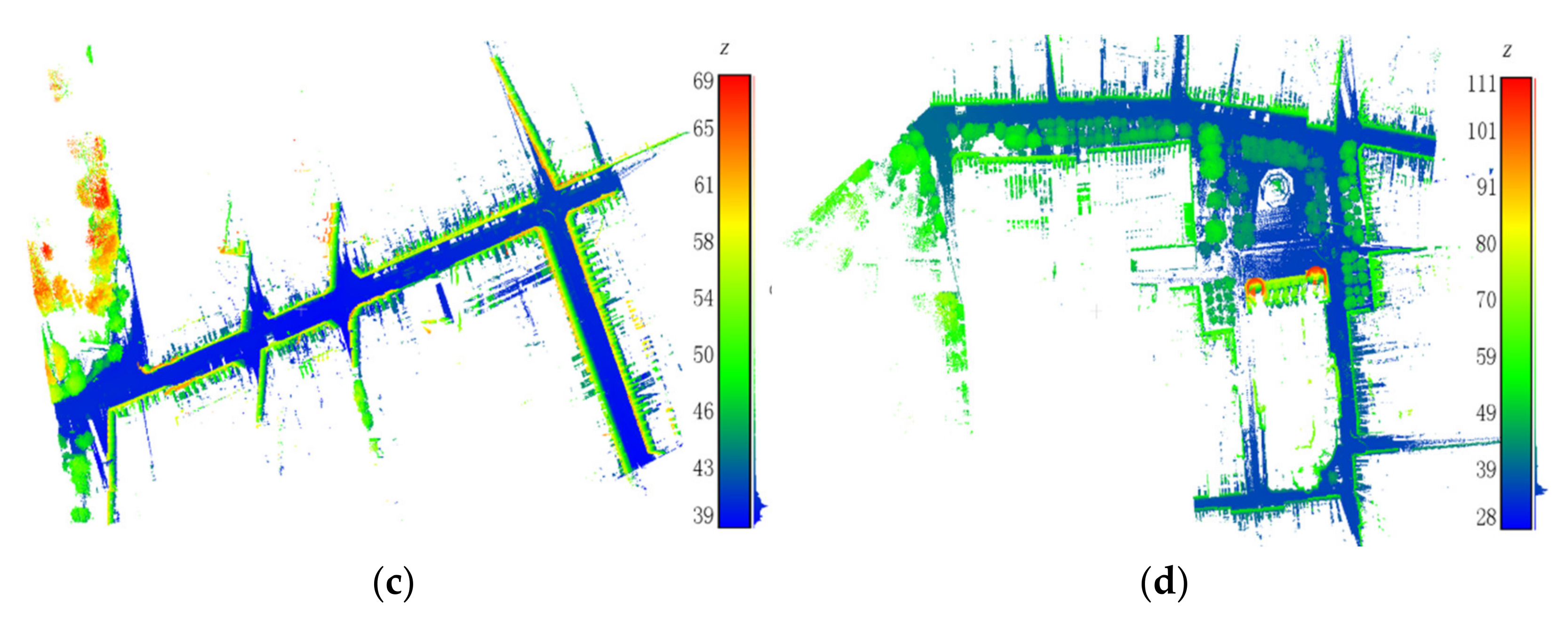
4.1. Experimental Data
4.2. Parameter Setting
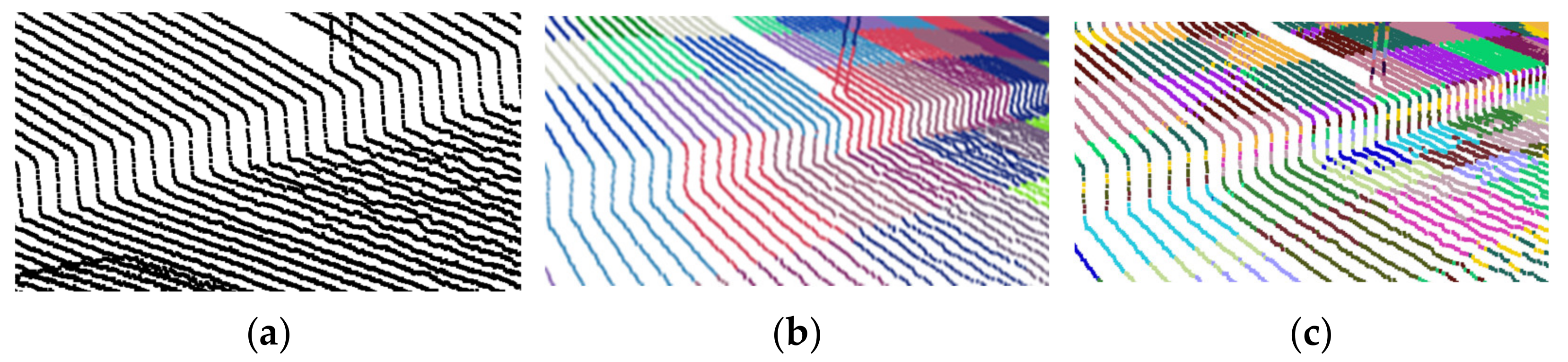
4.3. Experimental Results
4.4. Quantitative Results
4.5. Comparative Analysis of Different Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shirowzhan, S.; Tan, W.; Sepasgozar, S.M.E. Digital Twin and CyberGIS for Improving Connectivity and Measuring the Impact of Infrastructure Construction Planning in Smart Cities. ISPRS Int. J. Geo Inf. 2020, 9, 240. [Google Scholar] [CrossRef]
- Xiao, W.; Cao, H.; Tang, M.; Zhang, Z.; Chen, N.C. 3D Urban Object Change Detection from Aerial and Terrestrial Point Clouds: A Review. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103258. [Google Scholar] [CrossRef]
- Yang, B.; Liu, Y.; Dong, Z.; Liang, F.; Li, B.; Peng, X. 3D Local Feature BKD to Extract Road Information from Mobile Laser Scanning Point Clouds. ISPRS J. Photogramm. Remote Sens. 2017, 130, 329–343. [Google Scholar] [CrossRef]
- Yang, T.; Zhang, L.; Wang, H.; Zhang, Y. Road Vector Map Change Monitoring Based on High Resolution Remote Sensing Images. Remote Sens. 2014, 3, 272–279. [Google Scholar] [CrossRef][Green Version]
- Bastani, F.; He, S.; Abbar, S.; Alizadeh, M.; Balakrishnan, H.; Chawla, S.; Madden, S.; DeWitt, D. RoadTracer: Automatic Extraction of Road Networks from Aerial Images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Xu, Z.; Liu, Y.; Sun, Y.; Liu, M.; Wang, L. RNGDet++: Road Network Graph Detection by Transformer with Instance Segmentation and Multi-Scale Features Enhancement. IEEE Robot. Auto. Let. 2020, 8, 2991–2998. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J.; Guan, H.; Jia, F.; Wang, C. Learning Hierarchical Features for Automated Extraction of Road Markings From 3-D Mobile LiDAR Point Clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 709–726. [Google Scholar] [CrossRef]
- Ma, L.; Li, Y.; Li, J.; Wang, C.; Wang, R.; Chapman, M. Mobile Laser Scanned Point-Clouds for Road Object Detection and Extraction: A Review. Remote Sens. 2018, 10, 1531. [Google Scholar] [CrossRef]
- Wang, C.; Wen, C.; Dai, Y.; Yu, S.; Liu, M. Urban 3D Modeling with Mobile Laser Scanning: A Review. Virtual Real. Intell. Hardw. 2020, 2, 175–212. [Google Scholar] [CrossRef]
- Sisco, E.; Moorthy, A.S.; Watt, L.M. Creation and Release of an Updated NIST DART-MS Forensics Database. J. Am. Soc. Mass Spectrom. 2021, 32, 685–689. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yang, L.; Sheng, Y.; Shen, M. Pole-Like Objects Segmentation and Multiscale Classification-Based Fusion from Mobile Point Clouds in Road Scenes. Remote Sens. 2021, 13, 4382. [Google Scholar] [CrossRef]
- Wang, R.; Peethambaran, J.; Chen, D. LiDAR Point Clouds to 3-D Urban Models: A Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 606–627. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Cao, S.; Yu, Y. Use of Mobile LiDAR in Road Information Inventory: A Review. Int. J. Image Data Fusion 2016, 7, 219–242. [Google Scholar] [CrossRef]
- Huang, R.; Chen, J.; Liu, J.; Liu, L.; Yu, B.; Wu, Y. A Practical Point Cloud Based Road Curb Detection Method for Autonomous Vehicle. Information 2017, 8, 93. [Google Scholar] [CrossRef]
- Hata, A.Y.; Wolf, D.F. Feature Detection for Vehicle Localization in Urban Environments Using a Multilayer LIDAR. IEEE Trans. Intell. Transp. Syst. 2016, 17, 420–429. [Google Scholar] [CrossRef]
- Yang, B.; Fang, L.; Li, J. Semi-Automated Extraction and Delineation of 3D Roads of Street Scene from Mobile Laser Scanning Point Clouds. ISPRS J. Photogramm. Remote Sens. 2013, 79, 80–93. [Google Scholar] [CrossRef]
- Huang, J.; Choudhury, P.K.; Yin, S.; Zhu, L. Real-Time Road Curb and Lane Detection for Autonomous Driving Using LiDAR Point Clouds. IEEE Access. 2021, 9, 144940–144951. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Yu, Y.; Chapman, M.; Wang, C. Automated Road Information Extraction from Mobile Laser Scanning Data. IEEE Trans. Intell. Transp. Syst. 2015, 16, 194–205. [Google Scholar] [CrossRef]
- Viola, P.; Jones, M. Rapid Object Detection Using a Boosted Cascade of Simple Features. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Kauai, HI, USA, 8–14 December 2001. [Google Scholar]
- Von, G.R.G.; Jakubowicz, J.; Morel, J.M.; Randall, G. LSD: A Fast Line Segment Detector with a False Detection Control. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 722–732. [Google Scholar]
- Kumar, P.; Lewis, P.; McCarthy, T. The Potential of Active Contour Models in Extracting Roads from Mobile Laser Scanning Data. Infrastructures 2017, 2, 9. [Google Scholar] [CrossRef]
- Rodríguez, C.B.; García, C.S.; Ordóñez, C.; Alonso, M.C. An Approach to Detect and Delineate Street Curbs from MLS 3D Point Cloud Data. Autom. Constr. 2015, 51, 103–112. [Google Scholar] [CrossRef]
- Varney, N.M.; Asari, V.K. Volumetric Features for Object Region Classification in 3D LiDAR Point Clouds. In Proceedings of the 2014 IEEE Applied Imagery Pattern Recognition Workshop (AIPR), Washington, DC, USA, 14–16 October 2014. [Google Scholar]
- Dong, X.; Ze, L.Y.; Jian, L.; Zheng, M.G.; Yuan, H.F.; Ling, Y.Y. Road Extraction from Point Clouds of Open-Pit Mine Using LPFE-Net. IEEE Geosci. Remote Sens. Lett. 2023, 20, 6501005. [Google Scholar]
- Wen, C.; You, C.; Wu, H.; Wang, C.; Fan, X.; Li, J. Recovery of Urban 3D Road Boundary via Multi-Source Data. ISPRS J. Photogramm. Remote Sens. 2019, 156, 184–201. [Google Scholar] [CrossRef]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Balado, J.; Martínez, S.J.; Arias, P. Novo Road Environment Semantic Segmentation with Deep Learning from MLS Point Cloud Data. Sensors 2019, 19, 3466. [Google Scholar] [CrossRef]
- Rachmadi, F.R.; Uchimura, K.; Koutaki, G.; Ogata, K. Road Edge Detection on 3D Point Cloud Data Using Encoder-Decoder Convolutional Network. In Proceedings of the 2017 International Electronics Symposium on Knowledge Creation and Intelligent Computing (IES-KCIC), Surabaya, Indonesia, 26–27 September 2017. [Google Scholar]
- Harith, A.; Debra, F.; Laefer, D.C. Point cloud voxel classification of aerial urban LiDAR using voxel attributes and random forest approach. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 1569–8432. [Google Scholar]
- Xu, S.; Wang, R.; Zheng, H. Road Curb Extraction from Mobile LiDAR Point Clouds. IEEE Trans. Geosci. Remote Sens. 2017, 55, 996–1009. [Google Scholar] [CrossRef]
- Tran, T.H.; Chaisomphob, T. Automated Extraction of Expressway Road Surface from Mobile Laser Scanning Data. J. Cent. S. Univ. 2020, 27, 1917–1938. [Google Scholar] [CrossRef]
- Papon, J.; Abramov, A.; Schoeler, M.; Worgotter, F. Voxel Cloud Connectivity Segmentation—Supervoxels for Point Clouds. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Zai, D.; Li, J.; Guo, Y.; Cheng, M.; Lin, Y.; Luo, H.; Wang, C. 3-D Road Boundary Extraction from Mobile Laser Scanning Data via Supervoxels and Graph Cuts. IEEE Trans. Intell. Transp. Syst. 2018, 19, 802–813. [Google Scholar] [CrossRef]
- Mi, X.; Yang, B.; Dong, Z.; Chen, C.; Gu, J. Automated 3D Road Boundary Extraction and Vectorization Using MLS Point Clouds. IEEE Trans. Intell. Transp. Syst. 2022, 23, 5287–5297. [Google Scholar] [CrossRef]
- Xu, Y.; Tong, X.; Stilla, U. Voxel-Based Representation of 3D Point Clouds: Methods, Applications, and Its Potential Use in the Construction Industry. Autom. Constr. 2021, 126, 103675. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Cordone, L.; Miramond, B.; Thierion, P. Object Detection with Spiking Neural Networks on Automotive Event Data. In Proceedings of the 2022 International Joint Conference on Neural Networks, Padua, Italy, 18–23 July 2022. [Google Scholar]
- Vo, A.V.; Truong, H.L.; Laefer, D.F.; Bertolotto, M. Octree-Based Region Growing for Point Cloud Segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Unnikrishnan, R.; Lalonde, J.; Vandapel, N.; Hebert, M. Scale selection for geometric fitting in noisy point clouds. Int J. Comput. Geom. Appl. 2010, 20, 543–575. [Google Scholar] [CrossRef]
- Yang, B.; Dong, Z.; Liu, Y.; Liang, F.; Wang, Y. Computing Multiple Aggregation Levels and Contextual Features for Road Facilities Recognition Using Mobile Laser Scanning Data. ISPRS J. Photogramm. Remote Sens. 2017, 126, 180–194. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise; AAAI Press: Washington, DC, USA, 1996; Volume 06, pp. 226–231. [Google Scholar]
- Gao, J.; Chen, Y.; Junior, J.M.; Wang, C.; Li, J. Rapid Extraction of Urban Road Guardrails from Mobile LiDAR Point Clouds. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1572–1577. [Google Scholar] [CrossRef]
- Honma, R.; Date, H.; Kanai, S. MLS Point Cloud Segmentation Based on Feature Points of scanlines. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 1007–1013. [Google Scholar] [CrossRef]
- Ye, C.; Zhao, H.; Ma, L.; Jiang, H.; Li, H.; Wang, R.; Chapman, M.A.; Junior, J.M.; Li, J. Robust Lane Extraction from MLS Point Clouds Towards HD Maps Especially in Curve Road. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1505–1518. [Google Scholar] [CrossRef]
- El-Halawany, S.; Moussa, A.; Lichti, D.D.; El-Sheimy, N. Detection of Road Curb from Mobile Terrestrial Laser Scanner Point Cloud. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 38, 109–114. [Google Scholar] [CrossRef]







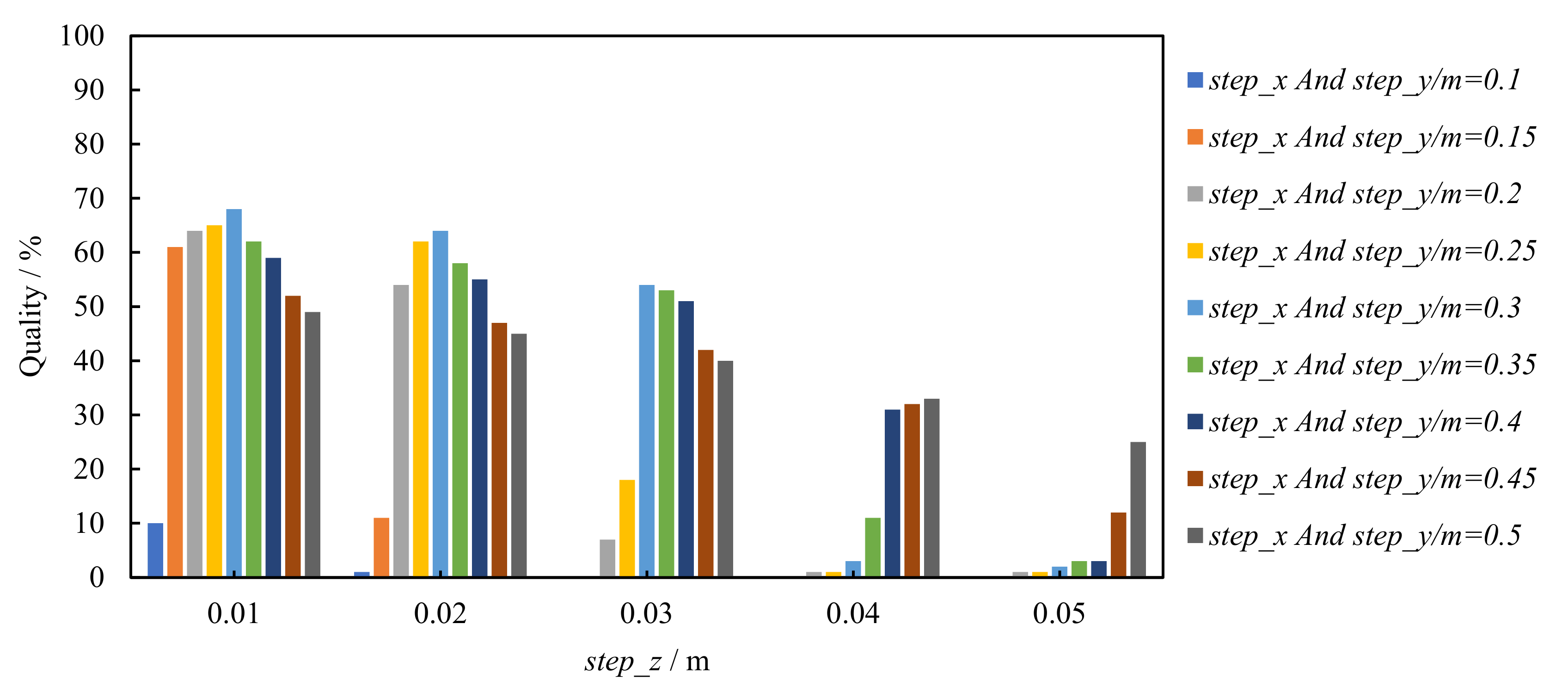
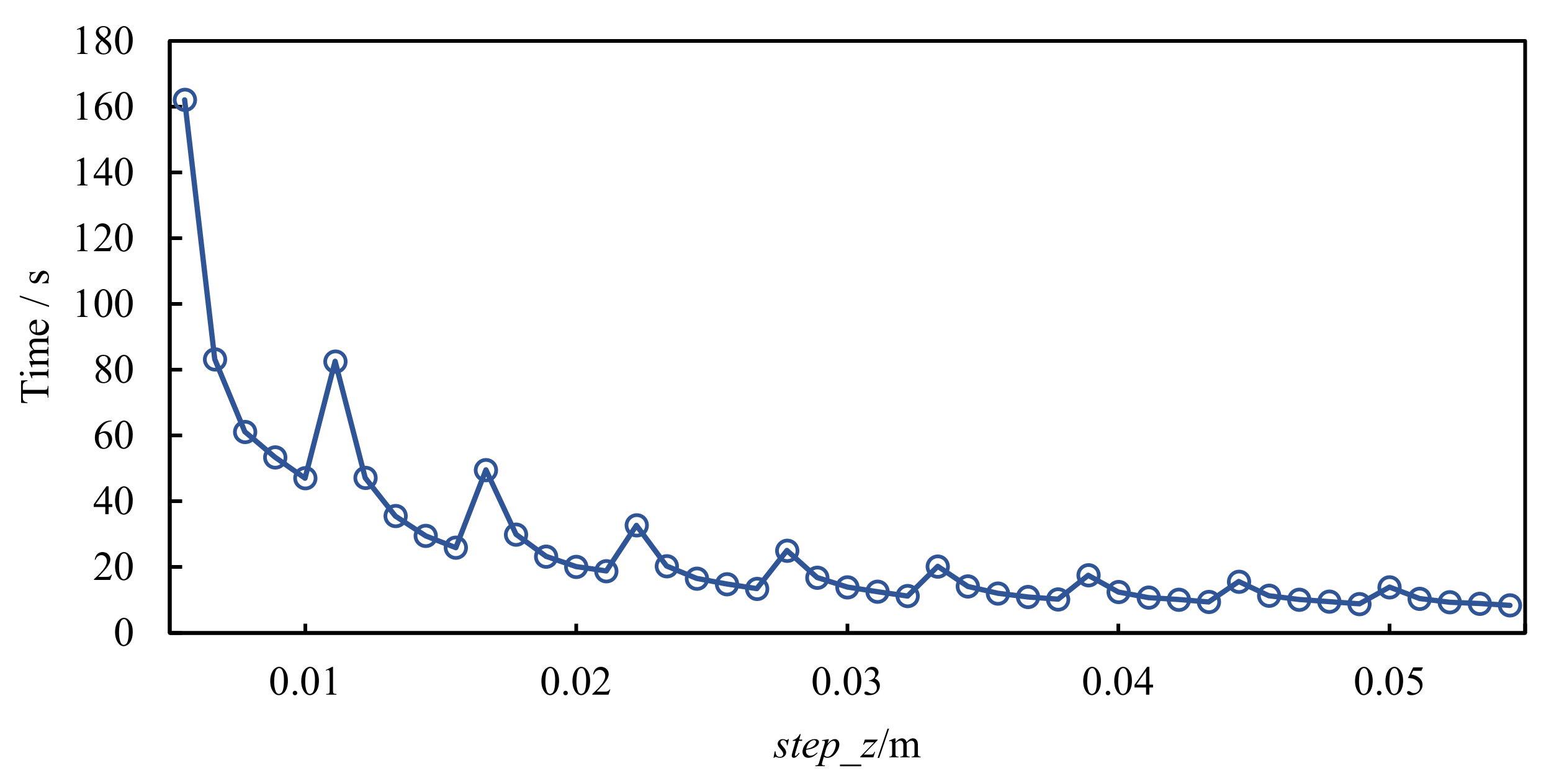
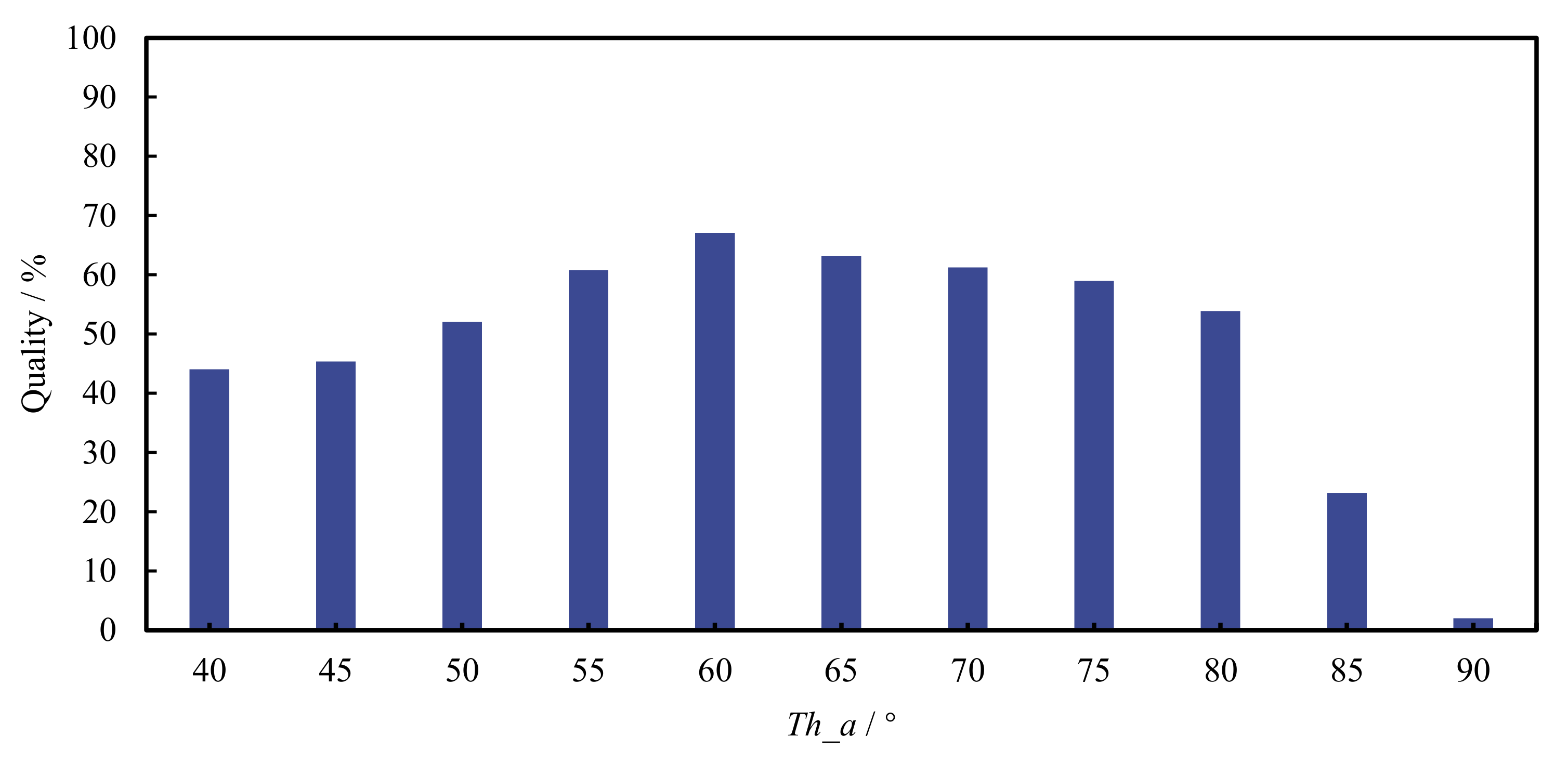
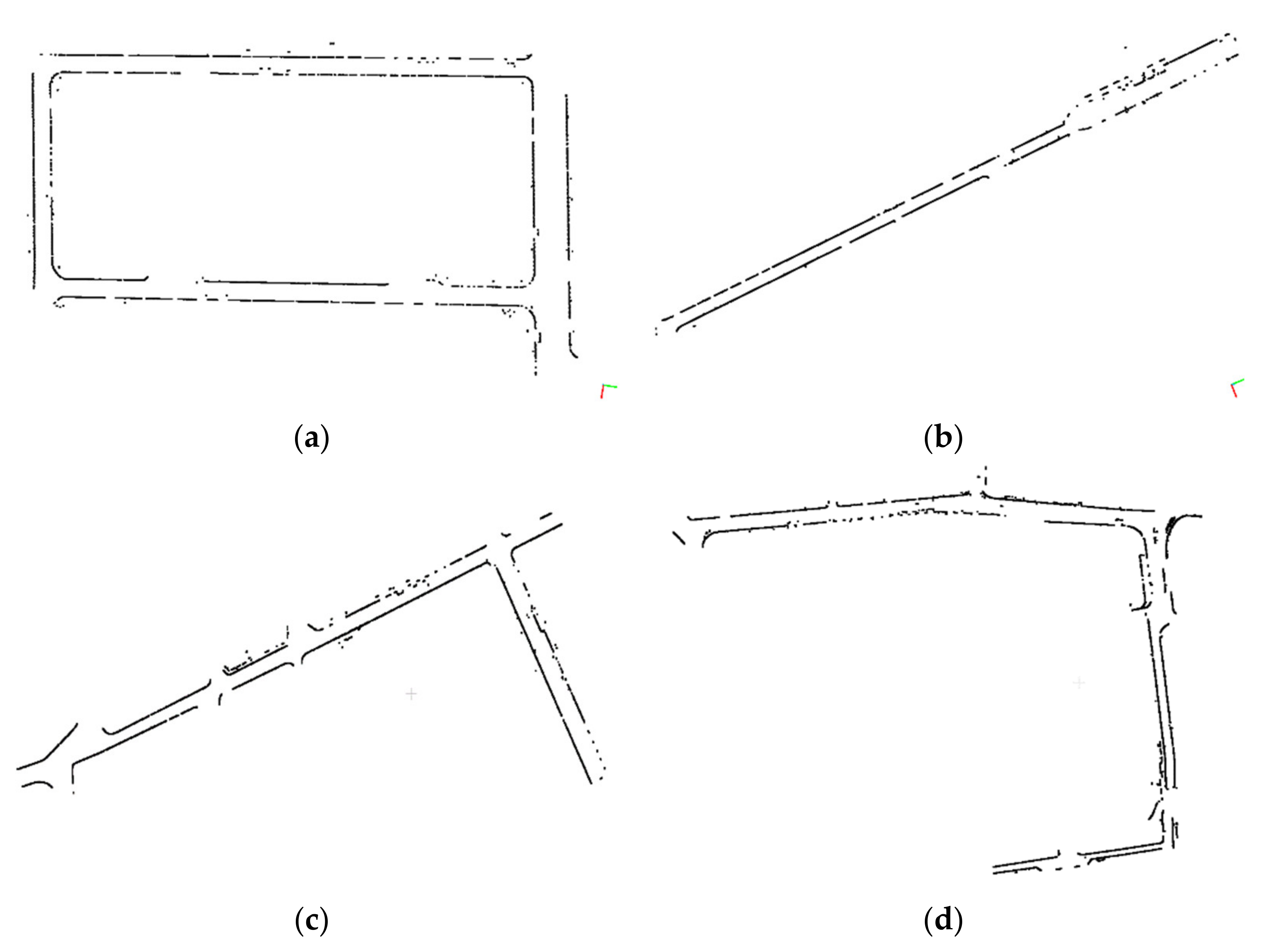
| Parameter | Parameter Value |
|---|---|
| Voxel sizes step_x, step_y, and step_z/m | 0.3, 0.3, 0.02 |
| Included angle threshold Th_a/° | 60 |
| Linear dimension threshold Th_e | 0.1 |
| Intensity range Th_ i | [−12, −10] |
| Searching radius Th_epx | 0.3 |
| Point number threshold in the cluster Th_Minpts | 6 |
| Dataset | Left | Right | Total | |||
|---|---|---|---|---|---|---|
| LS/m | LD/m | RS/m | RD/m | TS/m | TD/m | |
| Data 1 | 674.2 | 534.7 | 580.5 | 469.4 | 1254.7 | 1004.1 |
| Data 2 | 204.9 | 162.5 | 216.8 | 177.3 | 421.7 | 339.8 |
| Data 3 | 433.3 | 304.9 | 391.9 | 370.3 | 825.2 | 675.2 |
| Data 4 | 661.6 | 524.7 | 581.2 | 478.9 | 1242.8 | 1003.6 |
| Dataset | TP/m | FP/m | FN/m | Precision/% | Recall/% | Quality/% |
|---|---|---|---|---|---|---|
| Data 1 | 1004.1 | 27.8 | 250.6 | 97.3 | 80.0 | 78.3 |
| Data 2 | 339.8 | 24.3 | 81.9 | 93.3 | 80.6 | 76.2 |
| Data 3 | 675.2 | 34.4 | 150.0 | 95.2 | 81.8 | 78.5 |
| Data 4 | 1003.6 | 94.6 | 239.2 | 91.4 | 80.8 | 75.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Dong, X.; Liu, G. Extraction of Urban Road Boundary Points from Mobile Laser Scanning Data Based on Cuboid Voxel. ISPRS Int. J. Geo-Inf. 2023, 12, 426. https://doi.org/10.3390/ijgi12100426
Wang J, Dong X, Liu G. Extraction of Urban Road Boundary Points from Mobile Laser Scanning Data Based on Cuboid Voxel. ISPRS International Journal of Geo-Information. 2023; 12(10):426. https://doi.org/10.3390/ijgi12100426
Chicago/Turabian StyleWang, Jingxue, Xiao Dong, and Guangwei Liu. 2023. "Extraction of Urban Road Boundary Points from Mobile Laser Scanning Data Based on Cuboid Voxel" ISPRS International Journal of Geo-Information 12, no. 10: 426. https://doi.org/10.3390/ijgi12100426
APA StyleWang, J., Dong, X., & Liu, G. (2023). Extraction of Urban Road Boundary Points from Mobile Laser Scanning Data Based on Cuboid Voxel. ISPRS International Journal of Geo-Information, 12(10), 426. https://doi.org/10.3390/ijgi12100426







