Abstract
GPS trajectories collected from automotive telematics for insurance purposes go beyond being a collection of points on the map. They are in fact a powerful data source that we can use to extract map and road network properties. While the location of road junctions is readily available, the information about the traffic control element regulating the intersection is typically unknown. However, this information would be helpful, e.g., for contextualizing a driver’s behavior. Our focus is to use a map-matched GPS OBD-dongle dataset provided by a Canadian insurance company to classify intersections into three classes according to the type of traffic control element present: traffic light, stop sign, or no sign. We design a convolutional neural network (CNN) for classifying intersections. The network takes as entries, for a defined number of trips, the speed and the acceleration profiles over each segment of one meter on a window around the intersection. Our method outperforms two other competing approaches, achieving 99% overall accuracy. Furthermore, our CNN model can infer the three classes even with as few as 25 trips.
1. Introduction
The usage-based insurance (UBI) market is attracting more policyholders every year. According to [1], there were 4.5 million UBI policies in 2013, mainly from the United Kingdom, Italy and the United States, out of the one billion insured vehicles worldwide. The UBI market reached over 10 million policies in 2019, as reported by [2].
In a usage-based car insurance program, the premiums are directly linked to the risk exposition as measured by driving behavior indicators based on telemetry data collected by either a dongle in the insured vehicle, or by the insured’s smartphone. This pricing framework allows to better reflect the risk in the premiums than when the rates are based on proxy risk factors. Furthermore, drivers are encouraged to adopt safe driving styles.
Through telemetry data, the insurer can identify impulsive behaviors such as hard braking or harsh accelerations. The insurance premium can then be adapted to reflect the driving style. However, speeding in a school zone could be penalized more severely than on a highway; similarly, hard braking on a slippery road due to bad weather conditions is more dangerous than on a sunny day. The context may help interpret these risky events. According to [3], hard breaking events at intersections are significantly positively correlated with the crash risk. Moreover, drivers must not be penalized for hard braking due to a yellow traffic light, because that would incite them not to stop despite the fact that it is the expected behavior. In order to reward good driving habits, it is thus important for the insurer to differentiate hard braking events according to their location (i.e., at traffic lights or stop signs). Therefore, the contextualization of telemetry data is an important aspect for understanding driver behavior.
Road network data, such as Open Street Map data, contain the location of intersections, but the presence of a traffic control element (TCE) at a road junction is not necessarily available. While some studies [4] were able to use deep learning techniques based on speed and acceleration profiles to infer other types of uncontrolled intersections such as roundabouts, a form of road devices often seen in Europe [5], in order to contextualize intersections, we distinguish three main types of crossroads in Canada: stop signs (STs), traffic lights (TLs) and no signs (NSs). Note that the expected vehicle speed profile in the three cases is different. When reaching a stop sign, a driver should immobilize their vehicle completely, whereas at a traffic light, the behavior will depend on the color of the light. Similarly, a driving event that is reasonable in a traffic light might be hazardous at a stop sign: braking suddenly at a stop sign would be dangerous but it could be a correct behavior at a yellow light by trying not to violate the red light. Thus, knowing the type of junction could help assessing the riskiness of a driver, as we would improve the contextualization of a sudden acceleration or braking. Refs. [6,7] used unsupervised clustering techniques on vehicular communication data to identify driving profile patterns at 22 points of interest. The information about the intersection type was an important aspect in their experimentation as they chose the points of interest at meaningful places [7] such as traffic lights and stop signs in order to characterize driver behavior.
The locations of traffic control elements may be purchased from on-demand geospatial database providers, but this solution is costly, and the information is often outdated. Actually, ref. [8] estimated that the road network was changing by around five to ten percent per year, which means that the information on the type of intersection in these databases could be inaccurate and hence unreliable for decision-making in a UBI context. Fortunately, the large quantity of telematic data collected for UBI contain valuable information that can be exploited by insurers to contextualize driving events.
In this paper, we design an approach to classify intersections according to their traffic control element based on telematic data provided by Intact Financial Corporation, a large Canadian insurance company. First, we give a quick overview of the literature on TCE classification from telemetry data, and we describe a few methods applied in traffic sign detection in Section 2. Then, in Section 3, we propose a methodology to infer traffic regulators at road junctions. The results of our method are compared to two other approaches based on their performance in Section 4. Finally, we conclude with perspectives and challenges after a brief summary of our work in Section 6.
2. Literature Review
Recently, many researchers proposed to exploit GPS traces either to add spatial features on, update [9], or even create [10] maps. Telemetry trip data obtained for UBI or from ride-sharing companies not only help to infer an accurate map at much lower cost than using images collected by a fleet of cars or satellites, but also ensure up-to-date information given the frequent changes of the road network.
TCEs are located at road ends, in the proximity of a pedestrian crossing or a road junction. In a recent meta-analysis of 11 relevant studies, ref. [11] found that TCE detection methods based on crowdsourced data, such as GPS traces, were highly predictive as most traffic regulators could be identified with over 80% accuracy. The analyzed studies acquired ground truth map on site (81%), through information from the transportation official agencies, or from satellite images. However, the authors noted that only 27% of the studies examined different cities in their methods rather than relying solely on publicly available datasets. Furthermore, none of the studies considered more than three different types of TCEs. Additionally, ref. [11] mentioned the need for ground truth open datasets of diversified TCEs and for new vision-based assisted approaches (using imagery data captured by camera) for a better clarification of the junction regulation context, especially when “junctions are sparsely sampled by GPS tracks”, according to [11].
GPS devices usually involve data discontinuities as well as inaccuracies which induce unique challenges. Ref. [9] used GPS traces for identification of new special patterns (slowdowns, standstills and turning choices) on every intersection and segment of the street, which best described the possible location and timing of TCEs, thus overcoming the discontinuities and inaccuracies in the data. STs and TLs were predicted using a set of specified parameters: a stop-sign threshold and a traffic-light threshold defined based on extracted slowdown and standstill patterns, respectively. The method was tested on two datasets of traces, one extracted from Open Street Map (OSM) and the second from vehicle telemetry data collected in Los Angeles. Although that approach achieved good results in the latter dataset, the performance was poor on the first one. While [9] justified that missing data were the reason for the lower performance, it is to be noted that the multicity characteristic of the dataset might have also led to a loss in accuracy.
Based on mobile collected trajectory data in Hanover, Germany, ref. [12] proposed a method to infer three types of TCEs: TLs, NSs and priority signs (PSs). After considering only trajectories within a 100 m window around each intersection’s center, ref. [12] adopted two categories of features described in [13]: physical features relating to the behavior of vehicles when approaching the intersection, computed for each trip, and statistical features extracted for all the trajectories in each intersection’s roadway. A decision tree, a random forest, support vector machines and a neural net were trained as classifiers. Speed-related metrics were found to have a higher importance than stops and duration-related features. Moreover, although TLs were almost fully recognized, PSs were often misclassified as TLs or NSs.
As shown in [14,15,16,17], speed profiles are another way to summarize the information required to visualize and identify traffic regulators. In order to detect movement patterns and assess their usefulness to predict TCEs (TLs, NSs and priority/yield signs), ref. [14] analyzed the movement of vehicles at six road junctions in Hanover, Germany. Aiming to find crossing paths, two trajectory clustering methods, agglomerative clustering [18] and affinity propagation [19] were compared using three similarity measures. Ref. [14] stated that time profiles were more informative than speed profiles to detect whether a junction was controlled by a TL, but speed profiles were better to distinguish all regulator types.
In [15], TCEs were classified based on speed profiles using both temporal and spatial intervals before the junction center. Their data comprised vehicle traces sampled in 25 priority/yield and six TL-controlled intersections in a German city. Overall, ref. [15] obtained a high recall (most TLs were correctly classified) and low precision (most priority/yield signs were misclassified as TLs). The best results were achieved with an interval of eight seconds before the junction center along with a 50 m spatial buffer.
Traffic modeling is an example of transportation system applications where GPS data can be a suitable source of information. Considering the evolution and the complexity of those systems, artificial intelligence helps to enhance traffic prediction abilities [20], for instance, by modeling traffic flow prediction using autoencoders [21] or even by inferring traffic in near real time with pretrained deep learning models over huge traffic data [22].
According to [16], “machine learning should be able to deal with a set of trajectories and infer predictions based both on individual speed profiles and on their mutual variability”. Furthermore, as the choice of features is crucial for the performance of machine learning methods, ref. [16] applied three different approaches (direct, image and functional) to develop speed-profile features coupled with six TCE classifiers. The best combination was a random forest with the functional approach.
Using a similar image approach, ref. [17] proposed a convolutional neural network (CNN) for TCE classification. First, 57 m × 47 m bounding boxes were formed from OSM and then labeled with the true intersection type, according to an open dataset provided by the city of San Francisco. Next, the model was trained on Lyft vehicles’ telemetry data collected via smartphones over 40 days. A kernel density estimator (KDE) with a Gaussian kernel function allowed them to construct diagrams over speed and distance from junction points. These diagrams were preprocessed and then input into the CNN. Although the approach performed well, the large computational costs relating to the KDE and the vision-based method are a major drawback for insurance companies that are seeking to maintain an up-to-date classification process nationwide.
In the literature, numerous TCE classification approaches have been developed, but all of them require thousands of trips. In spite of the gaining popularity of UBI, insurers are not yet able to collect sufficient recent data on all intersections, which harms the process of inferring TCEs. Our aim is to assess the possibility of correctly classifying TCEs while considering only a few trips per intersection. Furthermore, many authors [9,15] highlighted the importance of data quality; preprocessing the data and solving noise and errors represent a key step in our approach. We further enhance our approach by considering both speed and acceleration profiles, so that temporal and spatial parameters are factored in. Additionally, we apply our method in different cities and provinces in Canada.
3. Data and Methods
The insurance company’s UBI dataset studied here comprises over one million car trips taken in Canada by insured drivers between December 2014 and August 2018. Each trip consists of GPS coordinates, speed and bearing measured at one-second intervals by the dongle installed in the vehicle, on top of the date and time of the trip. Trips are map-matched on Open Street Map (OSM) [23] using Open Source Routing Machine (OSRM) [24] and acceleration measurements are computed. This dataset has been studied in [25] for traffic modeling.
In this section, we first describe the collection of ground truth information and the preparation of the data in Section 3.1. Then, in Section 3.2, we explain how our CNN classifier is trained to detect junction type, taking as inputs trips at an intersection and in a direction, more specifically the speed and acceleration profiles over a segment covering the junction. As some intersections in the road network are less busy than others, we are interested in having a method that can perform well even when based on very few trips for the classification phase. We therefore choose to train and test our model with various numbers of trips as inputs. In Section 3.3, we briefly present the two most competitive approaches that were applied for comparison, the first one based on metrics fed in a machine learning model as in [16] and the other relying on a computer vision kernel density estimation inspired by [17].
3.1. Data Collection and Preparation
Here were the steps of the data processing for this study.
- Collecting ground truth intersection locations: From OSM’s road network, we obtained the location of several intersections in nine Canadian cities for which we observed a large number of trips. The intersections were manually labeled with the help of frequently enough updated images from Google Street View according to one of three categories: TL, ST or NS. The distribution of trips in each province was different depending on the number of UBI subscribers present. Moreover, as most TLs and NSs were positioned in arterial or collector roads, whereas STs were more present on local roads, more trips around TLs and NSs were available. Therefore, we balanced the dataset to have a total of 34 junctions of each type (each comprising two directions) for the network’s training. The breakdown of intersections by type and city is shown in Table 1, and the total number of trips in each type of intersections is given in Table 2.
 Table 1. TCEs junction count per city.
Table 1. TCEs junction count per city. Table 2. Trip count per junction type.
Table 2. Trip count per junction type. - Defining a junction window: By exploring the speed variations of vehicles over many intersections, we chose to consider a window, as illustrated in Figure 1, of m before and after the center of the intersection. To set the value of d, we studied some trips individually in order to delimit an interval before and after each intersection, large enough to capture the driving pattern on various road topologies. The idea was to select a sufficiently large window to detect as much as possible any potential pattern in trip characteristics, but not too wide so as to contain points that might involve the characteristics of another intersection close to the one we wanted to classify. As reported by [26], the minimum intersection spacing between four-legged intersections along local roads or between adjacent intersections along collector roads is 60 m while on arterial roads, the minimum is 200 m. Therefore, choosing m prevented most points from the trips of a junction to appear in another. On the other hand, in order to capture the driving pattern, we needed to observe a sufficiently large number of trip points in the window. Note that the maximum speed over a city is around 50 km/h and recall that the average speed may be computed as , where l is the driven distance and is the time interval. In our dataset, GPS observations were sampled each second, so we were able to estimate the minimum number of trip points to be about seven measurements when the window was m wide, which was enough to detect driving patterns. Finally, for each intersection listed in Table 1 in each direction separately, trip points were filtered so that only trips that covered at least 80% of the junction window were kept.
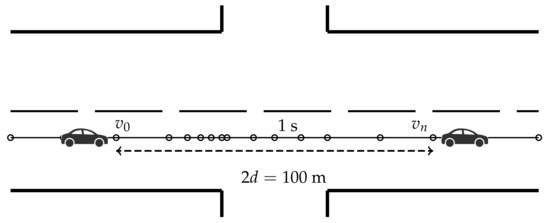 Figure 1. Window of 100 m wide for a driver’s trip in one of the two heading directions of the road segment.
Figure 1. Window of 100 m wide for a driver’s trip in one of the two heading directions of the road segment. - Exploring trips to detect potential patterns in intersections: First, we analyzed the distributions of speeds, accelerations and the duration of trips over the junction window by type of intersection (not shown). From this, it was seen that speeds and accelerations could potentially be useful to differentiate intersection types. In order to discover the possible differences between the three classes of intersections, the local estimates of the joint density of the speeds and accelerations are presented in the form of contour plots. To do this, we considered each heading direction on an intersection separately. As illustrated in Figure 2, these joint densities exhibit specific characteristic depending on the type of TCE at the junction. In the case of TLs (right-hand side of Figure 2), as expected, we observe roughly two modes, one at the speed zero and one around the maximum speed on the road. In the case of STs (left-hand side of Figure 2), nonzero accelerations are observed at low speeds between zero and 30 km/h (possibly reflecting slow transitions or incomplete stops of cars at stop signs). The middle plots in Figure 2 show that speed and accelerations at NS junctions are more similar to TLs than STs.
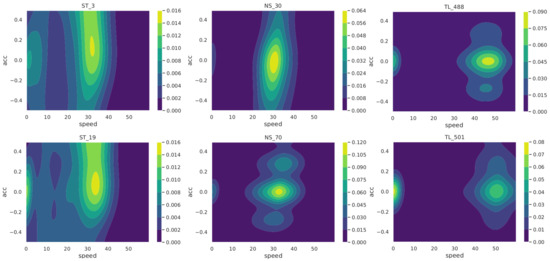 Figure 2. Speed–acceleration density contour plot for a given heading direction at two STs (left), NSs (middle) and TLs (right).Another way to visualize speed change along a given intersection is by plotting several individual driver trip speeds along the junction window. The resulting curves, examples of which are depicted in Figure 3, allowed us to detect similarities between speed profiles of trips at the same intersection type. Unlike NSs, speed curves at STs and TLs show a deflection towards zero as they approach the intersection center, however, the speed curves are closer to each other in the case of STs, creating a characteristic v shape visible in the left-hand side plot of Figure 3.
Figure 2. Speed–acceleration density contour plot for a given heading direction at two STs (left), NSs (middle) and TLs (right).Another way to visualize speed change along a given intersection is by plotting several individual driver trip speeds along the junction window. The resulting curves, examples of which are depicted in Figure 3, allowed us to detect similarities between speed profiles of trips at the same intersection type. Unlike NSs, speed curves at STs and TLs show a deflection towards zero as they approach the intersection center, however, the speed curves are closer to each other in the case of STs, creating a characteristic v shape visible in the left-hand side plot of Figure 3.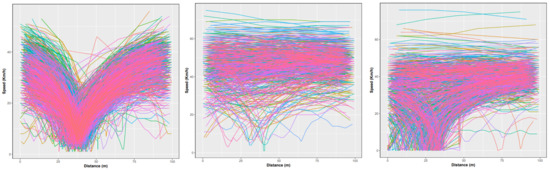 Figure 3. Speed traces of trips over junction window at an ST (left), an NS (middle) and a TL (right).
Figure 3. Speed traces of trips over junction window at an ST (left), an NS (middle) and a TL (right). - Preparing the dataset: Each heading direction was considered separately. Only the trips that covered at least 80% of the bounding box formed by the junction window were selected. We discretized the trips in meters over an interval of length m around the junction center ( m was set in step 2). All paths then had the same dimension and could be represented as one hundred intervals of a distance of one meter each, in which we interpolated speed and acceleration values from the original data measurement. Examples for the speed are depicted in Figure 4.
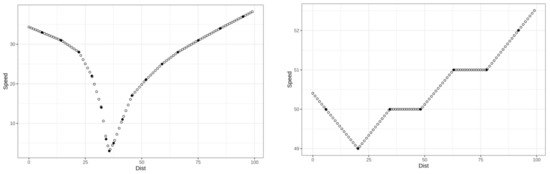 Figure 4. Speed measurements (solid dots) and interpolated values (empty dots) for one trip at an ST (left) or at a TL (right).
Figure 4. Speed measurements (solid dots) and interpolated values (empty dots) for one trip at an ST (left) or at a TL (right). - Solving noise and errors found in our dataset: Telematics trip data collected from dongles are usually more precise than those collected through smartphone applications, but they still are very noisy. Data cleansing is a necessary step to smooth the trajectories (i.e., using speed from GPS location stamp to interpolate positions when they are inaccurate or jumping), and to remove the invalid ones (i.e., missing points in the trips or erroneous speeds). Figure 5 shows the speed profiles of individual trips on a direction before (left) and after (right) this process.
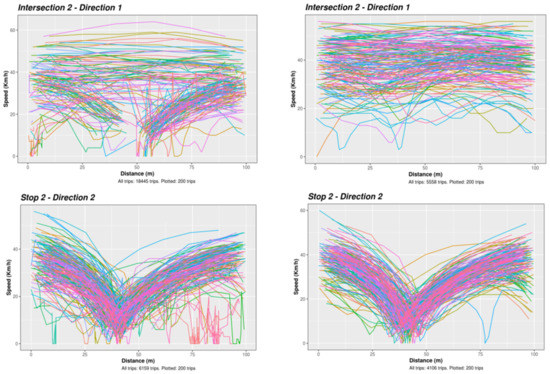 Figure 5. An example of speed profiles of trips on the window at an NS (top) and an ST (bottom), before (left) and after (right) filtering trips and fixing GPS errors.
Figure 5. An example of speed profiles of trips on the window at an NS (top) and an ST (bottom), before (left) and after (right) filtering trips and fixing GPS errors.
3.2. Proposed CNN Classifier for TCE at Junction
Although convolutional neural networks (CNNs) were designed to map image data to an output variable, they work well with time series of equal dimensions, which can be of great use in our classification problem. In fact, one discretized trip may be represented as a matrix, containing the 100 speeds and accelerations over the junction window. A standard CNN classifier can thus take as input D such trips, where is a hyperparameter.
As schematized in Figure 6, our network contained an input layer, three or four convolution blocks and a fully connected layer. Each convolution was followed by a batch normalization, a nonlinear layer and a pooling layer. Details on the layers are as follows:
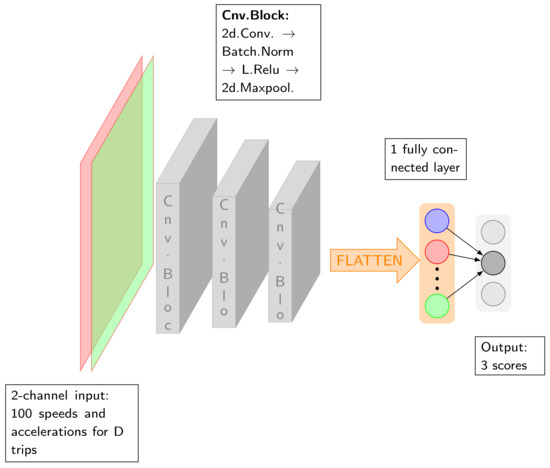
Figure 6.
CNN model architecture for characterizing TCEs at an intersection.
- Input: Our network took as input D trips for an intersection in one direction, and two channels: speed and acceleration. We considered .
- Convolution: A filter of size 3, 5 or 7 was applied to the inputs.
- Batch normalization: A batch norm, as described in [27], helped to accelerate the training of the deep neural net.
- Nonlinear: Leaky-ReLU, introduced by [28], was the activation function and it is defined as
- Pooling: We downsampled the output signals by applying a max-pooling.
- Flattening and fully connected: The last convolution layer was converted to a one-dimensional array, then passed to a fully connected layer. The output was three real numbers, which were the class scores corresponding to the three junction types.
In summary, from a input for one direction at one junction, the CNN output a vector of three scores corresponding to the types ST, NS and TL. The type was predicted as the one with the highest score.
3.3. Other Methods for Classification of TCEs
In this section, we present two competing approaches that we use in Section 4 for evaluating the performance of our proposed CNN: the functional method of [16] and the kernel density estimation CNN model of [17].
The functional method was found by [16] to give better results than two other methods (thE direct and the image approaches) when applied to classify TCEs, and especially when it was combined with a random forest (RF) classifier. We carried out the same description of the data as in [16]. For each D trips in a direction at a junction, we aggregated the speeds into 12 statistics listed in Table 3. These statistics were calculated separately for the 100-meter intervals in the junction window defined in Section 3.1, giving 1200 () speed features. We tested this method with two data descriptions, the first (RF) with all the 1200 metrics and the second (RF_H) where the dimension was reduced to 180 () using a Haar discrete wavelet transform as described and implemented by [16]. The resulting features are fed to an RF classifier with 500 trees. We tested the functional method with an RF, a linear support vector classifier and a logistic regression using the default parameters recommended in the literature and the best performance was obtained by the RF.

Table 3.
Twelve statistics of speed profiles calculated for each distance interval for the functional method.
To apply the method of [17], we first prepared the images as illustrated in Figure 7, for each D trips in a direction at a junction. These images represent the joint distribution of the speed and distance over the junction window created by a kernel density estimator (KDE) with a Gaussian kernel by applying Silverman’s rule of thumb [29]. In [17], such images were fed to a VGG19 classifier, as in [30]. For simplicity, we trained a basic CNN image classifier. The selected architecture had three blocks of convolutions (each comprising a convolution layer, a normalization layer, an activation layer and a pooling layer) and a final block with one convolution and a pooling layer. It used padding and dropout.
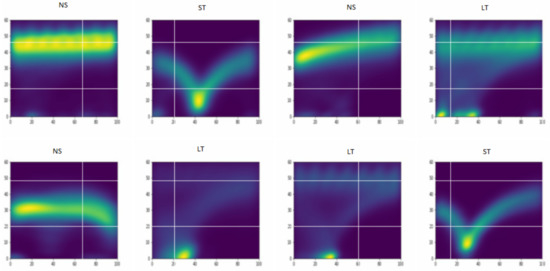
Figure 7.
Examples of kernel density images for the method of [17].
4. Results
We evaluated 12 models: three (CNN_25, CNN_50, and CNN_100) were our proposed CNN classifiers with two channels (speed–acceleration), and D trips per image where over the 100 intervals of distance; six (RF_25, RF_50, RF_100, RF_H_25, RF_H_50 and RF_H_100) were RF classifiers with the functional method tested without or with the dimension reduction; and three (K2D_25, K2D_50 and K2D_100) were CNN classifiers over images resulting from the KDE approach.
4.1. CNN Model Training and Evaluation
We chose to take 60%, 20% and 20% of the junctions for training, validation and test sets, respectively. We noted that the fit was good as the training and the validation losses tended to stay about the same values after about ten epochs, as illustrated in Figure 8.
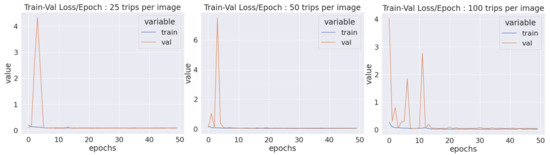
Figure 8.
Training (blue) and validation (orange) losses per epoch for CNN_25 (left), CNN_50 (middle) and CNN_100 (right).
4.2. Metrics
A confusion matrix in the case ST is depicted in Figure 9. For class j, it contains the counts of (true positives), (false positives), (true negatives) and (false negatives). The confusion matrix could be defined similarly for NS, TL}, which allowed us to set and similarly for , and .
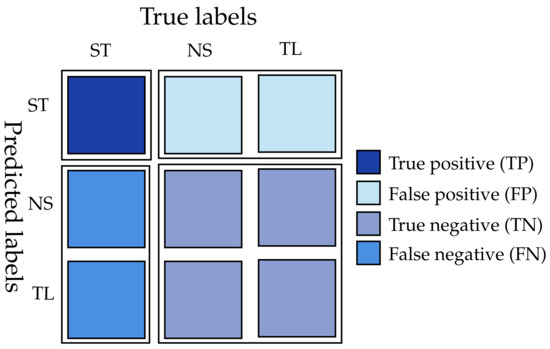
Figure 9.
Confusion matrix for class ST illustrating , , and .
We tuned the hyperparameters of the CNNs in order to maximize overall accuracy on the validation set, defined as:
The performance of the models were compared on the basis of the one-class precision, recall and -score, defined for ST, NS, TL} as:
4.3. Functional Method with RF Training and Evaluation
There was no hyperparameter to tune for the functional method, so we split the junctions in training (80%) and test (20%) sets. Note that the test sets for all methods were identical. From all the statistics in Table 3, F5 (Sarle’s bimodality coefficient), F12 (amplitude) and F6 (median) were found to be the most important predictors of TCE type according to the impurity-based feature importance. This is illustrated in Figure 10.
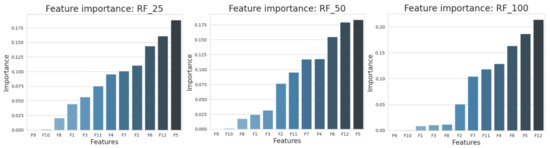
Figure 10.
Feature importance in RF_25 (left), RF_50 (middle) and RF_100 (right).
4.4. K2D Model Training and Evaluation
We considered 60% of the images for the training, 20% for the validation and 20% for the test. As illustrated in Figure 11, the training and validation losses decreased to a point of stability with a small gap in between which depicted a good fit.
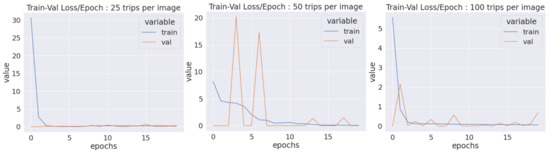
Figure 11.
Training (blue) and validation (orange) losses per epoch for K2D_25 (left), K2D_50 (middle) and K2D_100 (right).
4.5. Testing the Models
The accuracies on the test sets for each of the 12 models are shown in Table 4. While the functional method with RF performed better than the K2D models, our CNN models achieved the highest test accuracies. Our model was capable of inferring the three classes even based on a small number of trips with an excellent overall accuracy.

Table 4.
Test accuracy for the 12 models.
5. Discussion
We were interested in comparing the three methods according to three criteria: the quality of the classification according to the performance metrics, the number of trips required for an accurate prediction and the simplicity and ease of use.
Table 5 shows the performance metrics for the three TCEs and the three approaches, each based on 25, 50 or 100 trips. We can see that for a given number of trips, the ordering of the overall accuracies is always , so the CNN outperforms the other two approaches on this basis. Similarly, for a given number of trips and TCE, the -score of the CNN is always greater than or equal to the -score of the other approaches.Of course, for the three methods, increasing the number of trips available for the classification improves the performance.

Table 5.
Model metrics comparison on the test set.
As seen in the top three rows of Table 5, STs seem to draw less confusion compared to other types in all models. This can be explained by the fact that some TL trips share similar speed–acceleration characteristics with NS trips, for instance when the traffic flow is fluid and the traffic light is green. However, for all , our CNN model as well as the RF model were able to predict all STs without errors, with a precision and recall of 100%.
Although using more trips on each image gives a better overall prediction, among the three models with as input, the CNN_25 had the highest test accuracy score at 97% while maintaining the best -score for all TCE types. Moreover, even with a small number of trips, as both our model’s precision and recall were high, the -score was always above 0.95 indicating that our model performed very well. This is especially interesting when the goal of the model is to contextualize trips with the TCEs in a UBI context, as there are many intersections in which we do not observe a large number of trips. Furthermore, a classifier that is accurate based on only 25 trips is useful as it can be responsive to changes in the road network, for example due to roadworks or even a power outage.
As seen in Table 5, the RF models perform better than the K2D models, and are competitive with our CNNs. However, the CNNs are noticeably better when based on only 25 trips which might be due to the fact that speed profiles are aggregated in RF. Moreover, the wavelet transform involved in the method requires more computation which makes it less scalable. It is also worth mentioning that while using dimension reduction helps [16] overcome the redundancy induced by aggregating speed profiles, the use of these features directly in the models gives better results and requires less computation than when they are transformed by the Haar wavelet transform.
Compared to the K2D approach, our method used a simple data description hence requiring less computation time than the calculation of a KDE over the bounding boxes and the creation of images; it needed as few as 25 trips for classifying junctions and it achieved a higher accuracy, precision, recall and -score on the test set and on all three TCE types.
Note that we also considered combining the predictions from the (two or four) directions in a junction, in order to improve the performance in case of confusion. In fact, the possible scenarios in all the collected junctions were:
- A four-way junction: (ST,ST) and (TL,TL), (ST,ST) and (NS,NS), or (ST,ST) and (ST,ST);
- A two-way junction: (ST,ST), (TL,TL) or (ST,NS).
However, as the labeled data were limited, there was not enough multiroad junctions to demonstrate that this procedure yielded an improvement.
6. Conclusions and Future Work
In this paper, we proposed a new CNN network that allowed us to classify the type of TCE (stop sign, traffic light or no sign) at a given intersection based on UBI telematics trip data. Our method can help to contextualize the behavior of drivers for an insurance company or to add the location and type of TCEs in existing road network databases. The input of our CNN classifier was the speed and acceleration over the junction window for as few as 25 trips. Our method outperformed two other recently proposed approaches in the literature according to accuracy and -score. When using a larger number of trips as inputs, the overall accuracy could reach very high levels; we obtained a 99% accuracy with 100 trips and our CNN method. Our method was applied on intersections from nine different cities located in three provinces of Canada. All stop signs were detected perfectly, but there remained a few cases of traffic lights and no signs that were more difficult to distinguish.
Data quality is crucial to obtain a high accuracy in the classification. While the use of map-matched trajectories limited the noise, several matching problems were observed, e.g., in tunnels, entries and exits to or from highways, curved road segments or parking lots. Those are all forms of noise that should be dealt with before inputting the trips to the CNN. Our careful data preprocessing based on timestamps, speed readings and headings allowed us to correct outliers.
Now that we are able to contextualize the intersection with its TCE, in future work, we will characterize the behavior of a driver given some contextual information, among which the type of intersection. A possible improvement in the CNN classifier for TCEs would be to include turning maneuvers, as the yaw rate provides information on the TCE type. By considering those adjustments, we believe that our method can be adapted for problems involving the detection of other types of junctions, not present in our dataset, such as roundabouts and rotaries. Finally, a real-time approach might be a suitable development to our model should mobile drivers’ data be accessible.
Author Contributions
Conceptualization, Abdelmajid Erramaline, Thierry Badard, Marie-Pier Côté and Olivier Mercier; data curation, Abdelmajid Erramaline; formal analysis, Abdelmajid Erramaline; funding acquisition, Thierry Badard and Marie-Pier Côté; methodology, Abdelmajid Erramaline; project administration, Thierry Badard and Marie-Pier Côté; software, Abdelmajid Erramaline and Olivier Mercier; supervision, Thierry Badard, Marie-Pier Côté and Thierry Duchesne; validation, Thierry Badard, Marie-Pier Côté and Thierry Duchesne; visualization, Abdelmajid Erramaline; writing—original draft, Abdelmajid Erramaline, Thierry Badard and Marie-Pier Côté; writing—review and editing, Abdelmajid Erramaline, Thierry Badard and Marie-Pier Côté. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Intact Financial Corporation and the Natural Sciences and Engineering Research Council of Canada (RDCPJ-515901-17, RGPIN-2019-04190, RGPIN-2019-06788).
Data Availability Statement
Due to the nature of this research, participants of this study did not agree for their data being shared publicly, so supporting data are not available.
Acknowledgments
We thank Yann Méneroux for providing their excellent Haar wavelet transform R codes to implement their method. We are grateful to Etienne Bellemare-Racine and Javier Fernández-Rial Portela for their collaboration during various stages of the project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tselentis, D.; Yannis, G.; Vlahogianni, E. Innovative motor insurance schemes: A review of current practices and emerging challenges. Accid. Anal. Prev. 2017, 98, 139–148. [Google Scholar] [CrossRef] [PubMed]
- Śliwiński, A.; Kuryłowicz, Ł. The Equilibrium on the Motor Insurance Market in Selected CEE Countries. In Economic Development and Financial Markets: Latest Research and Policy Insights from Central and Southeastern Europe; Śliwiński, A., Polychronidou, P., Karasavvoglou, A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 143–164. [Google Scholar] [CrossRef]
- Stipancic, J.; Miranda-Moreno, L.; Saunier, N. Vehicle manoeuvers as surrogate safety measures: Extracting data from the GPS-enabled smartphones of regular drivers. Accid. Anal. Prev. 2018, 115, 160–169. [Google Scholar] [CrossRef] [PubMed]
- Munoz-Organero, M.; Ruiz-Blaquez, R.; Sánchez-Fernández, L. Automatic detection of traffic lights, street crossings and urban roundabouts combining outlier detection and deep learning classification techniques based on GPS traces while driving. Comput. Environ. Urban Syst. 2018, 68, 1–8. [Google Scholar] [CrossRef]
- Poudel, N.; Singleton, P.A. Bicycle safety at roundabouts: A systematic literature review. Transp. Rev. 2021, 41, 617–642. [Google Scholar] [CrossRef]
- Leblanc, B.; Fouchal, H.; de Runz, C. Driver profile detection using points of interest neighbourhood. In Proceedings of the 2019 IEEE 90th Vehicular Technology Conference (VTC2019-Fall), Honolulu, HI, USA, 22–25 September 2019; pp. 1–4. [Google Scholar]
- Leblanc, B.; Ercan, S.; De Runz, C. C-ITS data completion to improve unsupervised driving profile detection. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–5. [Google Scholar]
- Raynal, L. Some elements for modelling updates in topographic databases. In Proceedings of the GIS LIS-International Conference, Denver, CO, USA, 19–21 November 1996; pp. 1223–1232. [Google Scholar]
- Carisi, R.; Giordano, E.; Pau, G.; Gerla, M. Enhancing in vehicle digital maps via GPS crowdsourcing. In Proceedings of the 2011 Eighth International Conference on Wireless On-Demand Network Systems and Services, Bardonecchia, Italy, 26–28 January 2011; pp. 27–34. [Google Scholar]
- Bruntrup, R.; Edelkamp, S.; Jabbar, S.; Scholz, B. Incremental map generation with GPS traces. In Proceedings of the 2005 IEEE Intelligent Transportation Systems, Vienna, Austria, 13–16 September 2005; pp. 574–579. [Google Scholar]
- Zourlidou, S.; Sester, M. Traffic Regulator Detection and Identification from Crowdsourced Data—A Systematic Literature Review. ISPRS Int. J. Geo-Inf. 2019, 8, 491. [Google Scholar] [CrossRef]
- Golze, J.; Zourlidou, S.; Sester, M. Traffic Regulator Detection Using GPS Trajectories. KN J. Cartogr. Geogr. Inf. 2020, 70, 95–105. [Google Scholar] [CrossRef]
- Hu, S.; Su, L.; Liu, H.; Wang, H.; Abdelzaher, T.F. Smartroad: Smartphone-based crowd sensing for traffic regulator detection and identification. ACM Trans. Sens. Netw. (TOSN) 2015, 11, 1–27. [Google Scholar] [CrossRef]
- Wang, C.; Zourlidou, S.; Golze, J.; Sester, M. Trajectory analysis at intersections for traffic rule identification. Geo-Spat. Inf. Sci. 2021, 24, 75–84. [Google Scholar] [CrossRef]
- Zourlidou, S.; Fischer, C.; Sester, M. Classification of street junctions according to traffic regulators. In Proceedings of the Geospatial Technologies for Local and Regional Development: Short Papers, Posters and Poster Abstracts of the 22nd AGILE Conference on Geographic Information Science, Limassol, Cyprus, 17–20 June 2019; Available online: https://agile-online.org/conference/proceedings/proceedings-2019 (accessed on 1 June 2022).
- Méneroux, Y.; Le Guilcher, A.; Saint Pierre, G.; Hamed, M.G.; Mustière, S.; Orfila, O. Traffic signal detection from in-vehicle GPS speed profiles using functional data analysis and machine learning. Int. J. Data Sci. Anal. 2019, 10, 101–119. [Google Scholar] [CrossRef] [Green Version]
- Goyal, D.; Yuen, A.; Kim, H.S.; Murphy, J. Traffic Control Elements Inference using Telemetry Data and Convolutional Neural Networks. In Proceedings of the 8th International Workshop on Urban Computing (UrbComp 2019), SIGKDD Workshop, Anchorage, AK, USA, 5 August 2019. [Google Scholar]
- Müllner, D. Modern hierarchical, agglomerative clustering algorithms. arXiv 2011, arXiv:1109.2378. [Google Scholar]
- Thavikulwat, P. Affinity propagation: A clustering algorithm for computer-assisted business simulations and experiential exercises. In Proceedings of the Conference of the Developments in Business Simulation and Experiential Learning—The Annual ABSEL Conference, Charleston, SC, USA, 5–7 March 2008; Volume 35, pp. 220–224. [Google Scholar]
- Yin, X.; Wu, G.; Wei, J.; Shen, Y.; Qi, H.; Yin, B. Deep learning on traffic prediction: Methods, analysis and future directions. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4927–4943. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar] [CrossRef]
- Aqib, M.; Mehmood, R.; Alzahrani, A.; Katib, I.; Albeshri, A.; Altowaijri, S.M. Smarter traffic prediction using big data, in-memory computing, deep learning and GPUs. Sensors 2019, 19, 2206. [Google Scholar] [CrossRef] [PubMed]
- OpenStreetMap Contributors. Planet Dump. Available online: https://planet.osm.org (accessed on 1 June 2022).
- Luxen, D.; Vetter, C. Real-time routing with OpenStreetMap data. In Proceedings of the 19th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Chicago, IL, USA, 1–4 November 2011; ACM: New York, NY, USA, 2011; pp. 513–516. [Google Scholar] [CrossRef]
- Blais, P.; Badard, T.; Duchesne, T.; Côté, M.P. From Massive Trajectory Data to Traffic Modeling for Better Behavior Prediction in a Usage-Based Insurance Context. ISPRS Int. J. Geo-Inf. 2020, 9, 722. [Google Scholar] [CrossRef]
- Transportation Association of Canada. June 2014 Errata to the Geometric Design Guide for Canadian Roads, 2014. Available online: https://tac-atc.ca/sites/tac-atc.ca/files/site/complete.pdf (accessed on 27 May 2022).
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. In Proceedings of the ICML, Atlanta, GA, USA, 16–21 June 2013; Volume 30, p. 3. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; CRC Press: New York, NY, USA, 1986; Volume 26. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).