Abstract
Understanding organism movement is at the heart of many ecological disciplines. The study of landscape connectivity—the extent to which a landscape facilitates organism movement—has grown to become a central focus of spatial ecology and conservation science. Several computational algorithms have been developed to model connectivity; however, the major models in use today are limited by their lack of flexibility and simplistic assumptions of movement behaviour. In this paper, we introduce a new spatially-explicit, individual- and process-based model called Pathwalker, which simulates organism movement and connectivity through heterogeneous landscapes as a function of landscape resistance, the energetic cost of movement, mortality risk, autocorrelation, and directional bias towards a destination, all at multiple spatial scales. We describe the model’s structure and parameters and present statistical evaluations to demonstrate the influence of these parameters on the resulting movement patterns. Written in Python 3, Pathwalker works for any version of Python 3 and is freely available to download online. Pathwalker models movement and connectivity with greater flexibility compared with the dominant connectivity algorithms currently available in conservation science, thereby, enabling more detailed predictions for conservation practice and management. Moreover, Pathwalker provides a highly capable simulation framework for exploring theoretical and methodological questions that cannot be addressed with empirical data alone.
1. Introduction
- This being human is a guest house.
- Every morning a new arrival.
- A joy, a depression, a meanness,
- some momentary awareness comes
- as an unexpected visitor.
- Welcome and entertain them all!...
- The dark thought, the shame, the malice,
- meet them at the door laughing,
- and invite them in.
- Be grateful for whoever comes,
- because each has been sent
- as a guide from beyond.
Jalaluddin Rumi, translated by Coleman Barks
Organism movement in our beautiful and mysterious world is fundamental to all ecological processes [1,2]. In the context of conservation science, movement is necessary for individuals to utilise resources in their home range and to disperse from natal to adult home ranges; it is central to gene flow, and to expressions of individual behaviour and character. At broader scales in space and time, it plays a key role in population dynamics by enabling populations to shift their geographic ranges in response to disturbances and to changes in climate and land use [3,4].
Commonly studied influences on an animal’s movement behaviour involve biotic and abiotic factors, such as access to resources, the ability to mate, and the avoidance of mortality risks [5]—although the lives and pathways of animals are manifestly richer and more complex than these factors alone [6,7]. Such influences are by no means static or fixed; they are fluid and dynamic through space and time [8] and vary across multiple spatiotemporal scales [9]. These biological processes depend deeply on the interactions and relationships of individual animals with the landscape in which they dwell [10,11].
1.1. Landscape Connectivity
‘Landscape connectivity’, commonly defined to be the extent to which a landscape facilitates the movement of individuals or larger groups of organisms [12], is a dynamic phenomenon based on the cumulative movement choices of individuals across space and time. It provides a helpful methodology for mapping the emergent pathways of animal movement, and has grown to become a central focus of spatial ecology and conservation science [13,14]. Modelling connectivity typically requires two components: (1) a ‘landscape resistance surface’ and (2) an algorithm which uses this resistance surface to predict connectivity [15].
1.1.1. Resistance Surfaces
The dominant connectivity models in use today are based on resistance surfaces, in which the interactions between animal movement and landscape structure are reduced to a cost–benefit relationship of push and pull factors. Specifically, a resistance surface is a pixelated map of the landscape in which each pixel is assigned a numerical value; this value reflects the estimated ‘cost of movement’ through the region of the landscape corresponding to that pixel. It thus provides a measurement of how landscape features affect movement choice. However, despite its widespread usage as the basis for modern connectivity models, the landscape resistance framework does have its limitations as a basis for modelling animal movement—we will revisit this in the discussion section.
Resistance surfaces can be estimated empirically using any of a wide variety of data types, including opportunistic presence-only data, occurrence data, relocation data, genetic data, and GPS telemetry data. The latter two data types are thought to have the strongest performance in estimating resistance [16]; fine-scale telemetry data is often preferred since it is more sensitive to temporal variation than genetic data [17]. Moreover, since dispersal is considered to be the primary process by which organisms move between populations, data (such as telemetry) that reflect dispersal events in a spatially explicit manner are particularly important for understanding the drivers of landscape connectivity [18].
1.1.2. Modelling Connectivity
Once a resistance surface is developed, there are many algorithms one may use to predict connectivity, each with its advantages and limitations. Most applications of connectivity research have recruited one of two types of algorithms: circuit theory or a cost-distance based approach [15]. The most popular of the former type is CircuitScape [19], which models connectivity by simulating the flow of current across a resistance surface, whereby source points are treated as nodes of a circuit and resistance values as the strength of electrical resistors.
This algorithm produces a current density for each pixel on the resistance surface, with areas of high current density representing regions of the landscape predicted to have high connectivity. Thus, animals are modelled as electrons in CircuitScape, and the pathways and complexities of animal movement are reduced to the mechanisms of electrical circuit theory.
Cost-distance algorithms, in contrast, are based upon the predicted cumulative ‘cost of travel’ from source points on a resistance surface, in which the cost of traversing a pixel is given by its resistance value. These algorithms therefore estimate the accessibility of regions in a landscape from a given location. The simplest form of this approach is a least-cost path, which identifies the path (or corridor) of lowest cost between pairs of pixels on the resistance surface [20]. Building on this is the factorial least-cost path algorithm, which computes the least-cost paths between any given collection of source points [21] (implemented in UNICOR [22]).
However, there are severe limitations to the least-cost path approach in practice, centrally that there is little reason to assume that an animal knows (or even thinks in terms of) the cost-ibenefit route of the least-cost path [23]. Moreover, the destination may not be known to the animal prior to and during movement; even if this were so, obtaining the knowledge of their precise destination can be difficult, particularly so with dispersing animals. To remedy the latter issue, the resistant kernels algorithm (also implemented in UNICOR) was developed to predict the density of movement as a function of the source locations, landscape resistance, and dispersal capabilities, without the need for specified destinations [24]. See Figure 1 for an illustration of the connectivity maps output by CircuitScape, factorial least-cost paths and resistant kernels.

Figure 1.
Illustrations of three connectivity models—CircuitScape (b), factorial least-cost paths (c), and resistant kernels (d)—applied to a resistance surface (a). For the resistance surface, the blue, green, and yellow background colours, respectively, represent low, medium, and high resistance values. For the three connectivity maps, the blue, green, and yellow background colours, respectively, represent low, medium, and high connectivity.
1.1.3. Individual-Based Models
Despite their widespread usage and application in diverse ecological contexts, many fundamental drivers of animal movement are absent in the above models. For example, they do not account for the varying mortality risk or patterns of autocorrelation occurring in movement [25,26] (acknowledged as a limitation of CircuitScape in [19]). Nor do they account for the multiple spatial scales at which movement choice occurs [27], among several other factors which play a major role in shaping movement patterns (such as spatiotemporal variability [28,29], differences in age [18], and interspecific interactions [30]).
The algorithms mentioned above predict landscape connectivity using primarily a resistance surface and a collection of specified locations. In contrast, individual- (or agent-) based models simulate movement within a landscape by explicitly simulating the processes that may influence individual movement choice [15], and they can provide a process-based method to predict connectivity. They may be adapted to include parameters that account for the aforementioned aspects of movement which are absent in algorithms such as CircuitScape, meaning that individual-based models typically incorporate much more detail in their predictions of movement and connectivity [31].
Early agent-based models (such as [32,33,34]) were limited in their use for conservation contexts due to the lack of detail afforded to spatial complexity, in which the landscape was treated either as homogeneous or as a binary patch mosaic. Recent and more sophisticated individual-based algorithms, such as HexSim [35] and RangeShifter [36], now use resistance surfaces to provide the same degree of spatial data as used in circuit- or cost-based connectivity models. Although more focused on simulating general population dynamics, they have recently been used in connectivity studies (for example, [37,38]). Though there has been a proliferation of computational algorithms implementing circuit- and cost-based connectivity models, spatially-explicit individual-based models have not yet seen comparatively widespread application in connectivity modelling.
1.2. Pathwalker
In this paper, we introduce and describe a new spatially-explicit, individual- and process-based movement model called Pathwalker, designed to predicted individual movement paths and map connectivity with relatively few parameters. Pathwalker also uses resistance surfaces for its spatial input data. This algorithm combines three basic movement mechanisms, based on: energetic cost of movement, resistance-biased movement choice, and mortality risk. In addition, there are parameters that incorporate two types of directional bias: differing degrees of autocorrelated movement, and movement towards a destination.
Finally, Pathwalker accounts for a multi-scale response to the spatially heterogeneous resistance surface by allowing the movement mechanisms to be functions of landscape resistance at different spatial extents around a focal point. Pathwalker outputs individual movement paths starting from given source points on a resistance surface, together with certain statistics about each path. These paths can be aggregated to produce a movement density surface, which estimates the distribution of movement on the resistance surface and thus gives a process-based prediction of landscape connectivity. There is also the option to produce figures of the individual paths and the density surface (Figure 2).
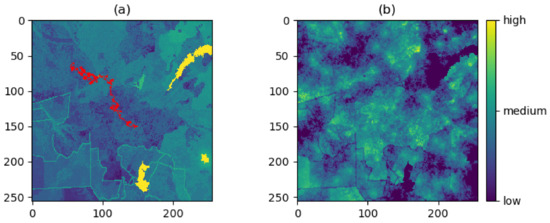
Figure 2.
(a) Displays an example individual path in red on the resistance surface used for the study in [18] and (b) shows a connectivity map produced by aggregating 100 paths from 100 different source locations. Made using Pathwalker.
Within the currently employed framework of landscape resistance and connectivity, the flexibility and detail made available by Pathwalker make it a powerful tool for predicting movement paths in complex landscapes, and for providing predictions of connectivity which may more accurately reflect the multitude of ways an organism moves through their environment [39].
But we have also designed Pathwalker explicitly as a movement and connectivity model with immediate usage in contexts where CircuitScape, resistant kernels or factorial least-cost paths are currently used; it thus has a similar interface and setup to these models, unlike software such as HexSim and RangeShifter. Furthermore, the process-based simulated movement data provided by Pathwalker can be used to test the performance and accuracy of different modelling methods and data sources used in movement and connectivity studies [40], similar to the utility of simulation models like CDPOP [41] used as such in landscape genetics studies [42,43].
This paper illustrates how Pathwalker works. We describe the model structure and parameters, and then perform some elementary computations to show how the different parameters interact and the extent to which they influence the resulting simulated movement. In addition, we provide a Supplementary Materials, which demonstrates a result of theoretical interest using Pathwalker: we derive a movement density function for different levels of autocorrelated movement, which gives valuable information for modelling the effects of dispersal thresholds on connectivity predictions. The Pathwalker software is written in Python 3 and can be obtained freely online at https://github.com/siddharth-unnithankumar/pathwalker (accessed on 26 May 2022), replete with documentation and a test example. To run, it requires Python 3 and the commonly used Python packages numpy and matplotlib.
2. Methods: The Pathwalker Model
The movement simulated by Pathwalker is governed by a set of specified input layers and movement parameters. The model proceeds by tracing a path on a chosen resistance surface from a given set of source points, moving at each step to one of a choice of nine pixels—either staying in the current position or changing to one of the neighbouring eight pixels—according to certain specified probabilistic movement parameters. In this section, we describe the input layers, parameters, and output layers of the model. More technical details and information on file formats can be found in the Pathwalker documentation at https://github.com/siddharth-unnithankumar/pathwalker (accessed on 26 May 2022). The first version of Pathwalker is available to freely download at this link as of November 2021 (file size 1 MB).
2.1. Input Layers
To run Pathwalker, we require two essential input data: (1) a resistance surface and (2) a list of source point coordinates. A third optional input is (3) a list of destination coordinates, which are required if the user wants to simulate movement towards destination locations. A fourth optional input is (4) a risk surface, for use with the risk mechanism (see below).
The resistance surface (and, if used, the risk surface) is to be in ascii format, with the six header rows included. The source coordinates (which typically represent the distribution and density of the studied or simulated population) are to be provided in a .txt file, using the same geospatial projection as the resistance surface layer; this same format applies to the destination coordinates, if used.
2.2. Model Parameters
2.2.1. Movement Mechanisms
The core model parameter is the choice of movement mechanism (Figure 3): energy, attraction, risk, or any combination of these three basic mechanisms, giving a total of seven options. Along with the chosen movement mechanism, the user specifies a second parameter: the maximum total number of steps for the movement path.
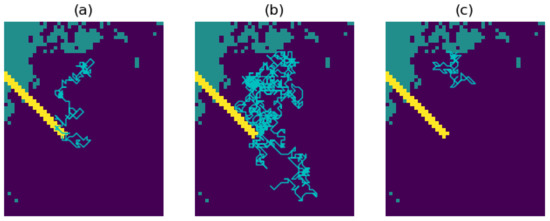
Figure 3.
Paths of maximum length 1000 steps, using the energy (a), attraction (b), and risk (c) mechanisms, simulated on the resistance surface from Figure 1. Notice how the attraction mechanism avoids the areas of higher resistance. The blue, green, and yellow background colours, respectively, represent low (1), medium (50), and high (100) resistance values.
- Energy. We first specify a value for the ‘total energy’ parameter, which represents the maximum allowed cumulative energetic cost of movement. The walker then follows an unbiased random walk on the resistance surface, and thus at each step chooses any one of the nine pixels with equal probability. For the pixels traversed in the walk, a cumulative sum of the resistance values is computed. The walk ends once this sum reaches or exceeds the chosen total energy value, or once the maximum number of steps has been reached.
- Attraction. The walker now follows a resistance-biased random walk. The probability of choosing any one of the nine pixels is given by the inverse of that pixel’s resistance value (where the inverse resistance values are scaled so that the nine inverse values give a probability distribution; in other words, these nine inverse values sum to 1). Thus, the walker will be more likely to move to pixels of lower resistance value and vice versa. The four diagonally adjacent pixels are given a weighting of 1/ to account for the increased distance when moving diagonally. This mechanism does not require any additional parameters to be specified, and the walk ends once the maximum number of steps has been reached.
- Risk. If risk is the only chosen factor in the movement, then we first specify a chosen risk surface; this may be proportional to our resistance surface (the default setting), or a different surface may be chosen but must be scaled so that the values of the risk surface lie between 0 (no risk) and 1 (highest risk). The walker then follows an unbiased random walk on the risk surface. At each step, the probability that the walk ends is given by the value of that pixel in the risk surface. The maximum length of the walk capped at the chosen maximum number of steps.
2.2.2. Spatial Scale of Movement Choice
In addition to the choice of one of the seven movement mechanisms described above, we can choose the spatial scale at which these mechanisms work. This involves two parameters: the scale of the response (the ‘window size’) and the functional form of the response (the ‘scaling function’).
- The window size determines the spatial scale at which the movement responds to resistance values. For example, if the chosen window size is 7-by-7, then the movement will be affected by resistance values in a 7-by-7 pixel neighbourhood of each of the nine pixels. The default scale, a 1-by-1 window, is equivalent to not incorporating spatial scaling.
- The scaling function determines the way in which the walker responds to landscape resistance at a chosen spatial scale n. There are three choices for the scaling function: focal mean, focal maximum, and focal minimum. With the focal mean, the resistance value of a pixel is replaced by the mean average of the resistance values of all pixels in a n-by-n neighbourhood of that pixel. With the focal maximum, the value of a pixel is replaced by the maximum pixel value in that neighbourhood; with the focal minimum, it is replaced by the minimum value. The window size and scaling function also act in this way on the risk surface (if used).
Let us look at an example of this, to see in more detail how this scaling interacts with the movement mechanisms. Suppose we choose a 5-by-5 window with the focal mean scaling function. Define the ‘scaled value’ of a pixel to be the mean average of the resistance values in a 5-by-5 neighbourhood of this pixel. Then, in the case of energy, the cumulative sum is computed from the scaled values of the pixels traversed; for attraction, the probability of choosing one of the nine possible pixels is given by the inverse of the scaled resistance values; with risk, the probability of the walking ending at each pixel traversed is given by the pixel’s scaled value on the risk surface (Figure 4).

Figure 4.
Paths of length 1000 steps with the attraction mechanism. They are parameterised with a 1-by-1 (a), 5-by-5 (b), and 9-by-9 (c) window size, using the focal mean scaling function. The blue, green, and yellow background colours, respectively, represent low (1), medium (50), and high (100) resistance values. Notice how, as the scaling increases, the paths avoid the areas of high resistance with greater distance.
2.2.3. Directionality: Autocorrelation and Destination Bias
Pathwalker provides two parameters for determining the directional bias of the movement: the autocorrelation C parameter, and the degree of bias D towards a destination. They work in tandem with the movement and scaling mechanisms (Figure 5). Both C and D can be simultaneously nonzero; however, the sum is required to equal at most 1.
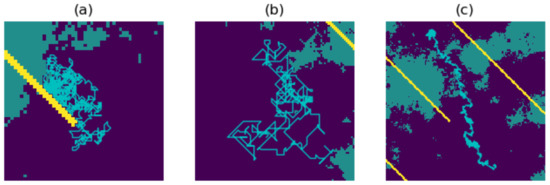
Figure 5.
In (a), no directionality is used, so C and D both equal 0. In (b), we have 0.7 autocorrelation and 0 destination bias; notice how, for many parts of the path, the walker has continued in the same direction of travel. In (c), we have 0 autocorrelation and 0.2 destination bias; notice how the overall direction of the path leads from the source point (near bottom of image) to the specified destination point (near top of image). The blue, green, and yellow background colours, respectively, represent low (1), medium (50), and high (100) resistance values.
- Autocorrelation. This parameter C takes values between 0 and 1, and determines the degree to which the walker is inclined to continue in the present direction of travel. The default value of C is 0, an uncorrelated random walk. If we increase the value of C, then our walk becomes more correlated, with the extreme case resulting in a straight line (in other words, a path in which the walker continues in the same direction with probability 1). For example, if we choose , then the nine movement probabilities are scaled to sum to instead of summing to 1, and there will now be an added probability of 0.3 for continuing in the same direction as the previous step.
- Destination bias. This parameter D takes values between 0 and 1, and determines the degree to which the walk will be biased towards a destination point X on the resistance surface. It works by giving additional preference to moving to the pixel closest to the direction of X. The default value is 0, in which there is no bias towards the destination. As we increase the value of D, the walk becomes more biased towards X, with the extreme case resulting in a path which is a straight line towards X. For example, if , then the nine movement probabilities are scaled to sum to instead of summing to 1, and there will now be an added probability of 0.2 for moving to the pixel closest to the direction of X.
2.2.4. Additional Parameters
Finally, the user specifies four parameters that determine the output of the model: (1) the manner in which the source and destination locations are paired; (2) how many times the model is to run for each source–destination pair; (3) which outputs (individual paths, path statistics, and density surface) are desired; and (4) which figures are desired.
2.3. Output Layers
By default, the algorithm will output one movement path for each source point—in other words, it will return the list of coordinates for the path from each source point. We can also choose for the model to output three statistics for each path: (a) the total number of steps taken, (b) the cumulative energetic cost reached (if energy is involved), and (c) the total accumulated risk (if risk is involved).
In addition to the individual movement paths and their statistics, we can choose to obtain a prediction of landscape connectivity. This is produced by aggregating all of the individual movement paths into a ‘movement density surface’. The density surface has the same format and dimensions as the resistance surface. The value of each pixel is given by the total number of times that pixel was traversed across all movement paths. When producing a density surface to predict connectivity, we recommend running the model several times from each source point (or source–destination point pair), so that the resulting density surface averages the stochastic distribution of possible movement paths. Figures can also be provided for the individual movement paths and density surface (as seen in Figure 2).
2.4. Summary of Pathwalker Setup
To summarise, we first choose a resistance surface on which we would like the paths to run, together with a list of source coordinates. Optionally, we may also provide destination coordinates and/or a risk surface. Then, we choose one of the seven mechanisms for our movement, and the maximum length of the path; if the energy mechanism is used, we also specify a total energy value.
In addition, we can choose to incorporate spatial scaling into the movement by choosing a scaling function and a larger scaling window than the default size of 1-by-1. We can also incorporate autocorrelated movement and destination bias into our walk by choosing a nonzero value for the parameters C and D.
Finally, we choose how to pair the source and destination locations, how many times to run the algorithm from each point, and whether we would like our output to include the coordinates for the individual movement paths, the statistics for each path, the movement density surface, and any figures. See Figure 6 for an illustration of this schematic.
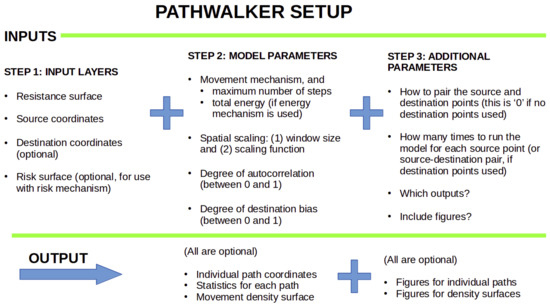
Figure 6.
Schematic for configuring Pathwalker.
3. Case Study
In this section, we provide a study of how the various movement parameters of Pathwalker interact, and the extent to which each component influences Pathwalker’s connectivity predictions. We do this by analysing and comparing the density surfaces resulting from different parameter configurations. All analyses in this paper are performed in Python 3.8.
3.1. Producing the Density Surfaces
We first provide a chosen resistance surface, together with 100 source points distributed uniformly randomly across the resistance surface. For the cases in which we include destination bias, we use the same 100 points as destinations too.
Then, we compute the density surfaces from different configurations of the model. These combinations are comprised of: four movement mechanisms (energy, attraction, risk, or all three combined), two spatial scales (1-by-1 or 7-by-7) with the focal mean scaling function, two degrees of autocorrelation (0 or 0.35), and two degrees of destination bias (0 or 0.35). In producing the density surfaces, we run the model 100 times from each source point, in order to average the stochastic variation in the movement paths.
3.2. Comparison of Density Surfaces
We perform four Mantel tests [44] to compare the influence of each of the four movement parameters (movement mechanism, scale, autocorrelation and destination bias) on the movement simulated by Pathwalker, as follows.
Once the 32 density surfaces are produced, we build a 32-by-32 matrix M whose -entry is given by the root mean squared error between surface i and surface j. The error matrix M provides a measure of similarity between the 32 different density surfaces, where the smaller values of the entries of M correspond to the pairs of surfaces which are more similar.
To then quantify the extent to which the four different parameters influence the movement across the resistance surface (and thus the extent to which they explain the variation of the entries of M) we perform four Mantel tests, each one comparing the error matrix M with the ‘model matrix’ corresponding to one of the four different parameters. We label these model matrices , , , and corresponding to the movement mechanism, scale, autocorrelation, and destination bias, respectively.
We now give an example to see in more detail how one of these model matrices, say (which corresponds to the autocorrelation parameter), is constructed and then compared with M. To construct the 32-by-32 binary matrix , we give the -entry the value 0 if surface i and surface j are produced from differing autocorrelation values—for example, if surface i is produced using autocorrelation and surface j using . We give the -entry the value 1 if surface i and surface j are produced using the same value of the autocorrelation parameter—for example, if both are produced using . Then to compare M and , we perform a Mantel test between M and . This provides a quantification of the similarity of these two matrices, and thus the extent to which changing the autocorrelation parameter accounts for the variation between the density surfaces.
We enact the above procedure twice, first using a simple simulated resistance surface, and secondly using the empirically derived resistance surface from [18] (Figure 7). The first allows us to see clearly how the different parameters influence movement density on a simplistic resistance surface, and the second shows how the model runs with an actual example of a resistance surface used in practice.
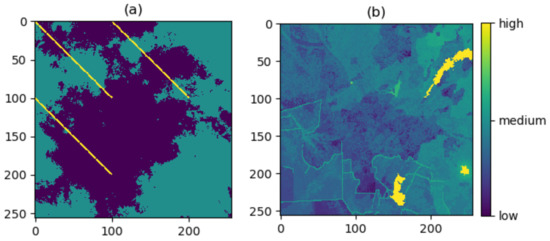
Figure 7.
The two resistance surfaces used in the case study: (a) the simulated resistance surface (taking only the values 1, 50 and 100); and (b), the empirical resistance surface used for the study in [18].
In both cases, the surface consists of 256-by-256 pixels, taking resistance values between 1 and 100, and is surrounded by a barrier of infinite resistance, which ends the walk if touched. When the risk mechanism is involved, we simply take the risk surface to be proportional to the resistance surface (in other words, the risk surface is the resistance surface scaled so that its values lie between 0 and 1). For this analysis, we use the Python 3.8 packages scipy and mantel [45], and for the Supplementary Materials, we use scipy and scikit-learn [46].
4. Results
The Mantel test results comparing the influence of the four movement parameters are similar for the simulated and empirical resistance surfaces (Table 1). Namely, we find in both cases that the two parameters which explain much of the difference between the density surfaces are the movement mechanism (which varied between energy, attraction, risk, and their threeway combination) and the degree of destination bias D (which took the values 0 or 0.35).

Table 1.
Results from the Mantel test between the error matrix M and the four model matrices for both the simulated and empirical resistance surfaces, with Pearson correlation coefficient , two-tailed p-value p, and z-score z. and correspond to the movement mechanism, spatial scale, autocorrelation, and destination bias, respectively.
We can see this from the small p-value (equivalently, high z-score), which indicate that the similarity between M and and also M and make it highly probable that these two factors explain much of the extent to which the density surfaces values differ. In these two cases of movement mechanism and destination bias, the value of the Pearson correlation coefficient , although not close to 1, is typical of Mantel tests in which there is a strong similarity between the two matrices involved.
In comparison, neither the degree of autocorrelation in the movement nor that of spatial scaling produced as much overall difference in the density surfaces. However, when configuring the degree of directionality bias in the model, it is important to note the following: while changing the autocorrelation C from 0 to 0.35 did not have as great an effect on the resulting density surfaces as changing the degree of destination bias D from 0 to 0.35, if we had instead changed the autocorrelation parameter C from 0 to a higher value (say, 0.9), then we could expect more dramatic variation in the resulting density surfaces. The analysis in this paper simply shows that changing the degree of destination bias will have a greater effect on movement density than if we change the autocorrelation parameter by the same amount.
The results of this analysis can be anticipated by looking at Figure 8 and Figure 9. For example, we see that the energy mechanism produces a very different map of density to the attraction mechanism, since the latter causes the movement to often avoid areas of high resistance but does not restrict the extent of movement when in a region of high resistance. Interestingly, in this case study where the risk surface is proportional to the resistance surface, the risk mechanism produces a density of movement similar to that of the energy mechanism, despite the energy and risk mechanisms being theoretically quite different; this similarity would likely be less if the risk surface used is not proportional to the resistance surface.
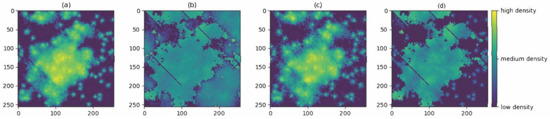
Figure 8.
The four density surfaces produced from the four different movement mechanisms—energy (a), attraction (b), risk (c), and their threeway combination (d)—with the other three parameters kept at their default values.
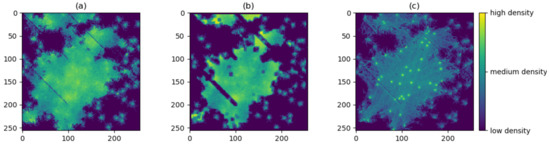
Figure 9.
Three density surfaces produced with the threeway combination movement mechanism, each with one of the other three parameters increased: 0.35 autocorrelation (a), 7-by-7 spatial scaling (b), and 0.35 destination bias (c).
5. Discussion
In this paper, we introduced and described Pathwalker, a new spatially-explicit, individual- and process-based model for simulating organism movement through heterogeneous landscapes. Pathwalker incorporates a variety of movement parameters, which allow greater detail in predicting landscape connectivity than do widely used models such as CircuitScape and resistant kernels. Namely, Pathwalker simulates movement as a function of the landscape resistance, energetic cost, and mortality risk at multiple spatial scales, whilst simultaneously accounting for autocorrelation and destination bias in the movement.
The importance and utility of simulation techniques for addressing fundamental ecological questions has been established in many branches of spatial ecology: for example, the use of CDPOP in landscape genetics [43,47,48], and HexSim in population dynamics [49,50]. In light of this, we designed Pathwalker with a simple and highly flexible framework to explore a wide range of behavioural responses to landscape features, enabling evaluations of theoretical and methodological questions in landscape and movement ecology, conservation science and connectivity modelling (as demonstrated in the Supplementary Materials; see also [40]).
5.1. Relation to Popular Connectivity Models
Popular connectivity models, such as CircuitScape, resistant kernels, and factorial least-cost paths, conspicuously do not account for many key drivers of animal movement, which greatly limits their effective use for handling the complexities and richness of many scenarios in applied ecology and conservation science.
For example, they assume the mortality risk to remain unchanged through different regions of the landscape, and movement choice to occur at a single spatial scale. As noted in [19], CircuitScape further assumes a symmetrical movement probability between two adjacent pixels, even though movement from an area of higher to lower resistance (or energetic cost, or mortality risk) is much more likely than the reverse. Moreover, the simplistic random walk mechanisms in these models assume a ‘memoryless’ walker, despite the influence of autocorrelation on movement patterns [25,26].
In contrast, Pathwalker is able to incorporate these important aspects of movement into its connectivity predictions. Other recent spatially-explicit, individual-based models, such as HexSim and RangeShifter, also include several parameters, which afford greater detail in simulating the factors influencing movement patterns. For example, as with Pathwalker’s risk surface, HexSim allows for the use of multiple resistance-like surfaces which approximate landscape features (such as food and nesting resources), in addition to the spatial input data of landscape resistance.
Though HexSim and RangeShifter have seen some recent application in connectivity studies (such as [37]), these individual-based models are primarily focused on simulating general population dynamics. Pathwalker has instead been designed specifically for simulating individual movement pathways and predicting connectivity, with an interface similar to UNICOR (which implements resistant kernels and factorial least-cost paths) and CircuitScape to allow for its immediate and straightforward usage in connectivity modelling.
5.2. Limitations, Further Developments, and the Wider Context
The process-based mechanisms of Pathwalker attend to some of the important influences on movement patterns, which are absent in models like CircuitScape and many cost-distance approaches, such as resistant kernels. However, other fundamental drivers of movement and connectivity are yet to be accounted for in all resistance-based algorithms discussed above, including individual-based models like Pathwalker. Centrally, within the framework of landscape resistance, we acknowledge that there is little attention given to the enormous effect of spatiotemporal variation in the dynamic relationship between animals and landscape.
Temporally, examples include the dramatic role played by migratory behaviour and various seasonal cycles on movement decisions [28,29,51,52]. Spatially, choices made between landscape features will change depending on the unique composition of each locale traveled through [53,54], with different regions resulting in different estimates of how environmental variables affect movement [55]. Spatiotemporal complexity is at the heart of the relationship between animal and landscape [56], to the extent that movement patterns through space and time cannot be understood through a universally applicable combination of temporally static environmental conditions. We must develop methodologies to reflect this (see recent works, such as [57]).
More generally, resistance-based connectivity models do little to capture the many other ways in which movement patterns are thoroughly affected by key contextual details in which the animal is moving in space and time [23]. The earth’s landscapes are increasingly shaped by anthropogenic presence; for connectivity models to remain relevant and reliable, the dynamic influence of human presence on movement must be given adequate attention [58,59,60]. The rich and interactive relationships between humans and other animals, and the resulting effects on their movement pathways, can rarely be accounted for by the simplistic, temporally static, cost–benefit framework of landscape resistance [61,62,63,64,65]. Resistance-based models also typically assume an unchanging and universal caricature of animal behaviour, despite the established importance of their changing physiological and emotional states on movement decisions [39,66,67].
In order to better understand and evaluate the complex dynamics of animal movement occurring in reality, we must find ways to acknowledge and express in our computational models that animals do not behave as mechanistic automatons, acting and moving in relation to an inert landscape according to economical cost–benefit rules. Their lives are much more creative, loving and charismatic than this [68,69]. If we can develop modelling techniques that are concerned with, for example, the quality as well as the quantity of animal life, then these tools will be of greater value for effective, resilient, and compassionate conservation [70,71,72,73].
From more-than-human geography to conservation physiology, efforts are emerging across ecological disciplines to creatively develop more holistic methodologies and models for understanding and predicting animal movement and connectivity [6,74,75,76]. This provides a tremendous opportunity for interdisciplinary conversation and collaboration to explore and identify new objectives and parameters for connectivity modelling [77]. As discussed in the concluding paragraph of [78], we can better honour the richness and wonder of this living, breathing, more-than-human world by opening to a multiplicity of ways to understand its creative and generative processes [1,79,80,81].
Attending seriously to these manifold complexities of animal movement is thus a central challenge for the future of conservation science and connectivity modelling, and such efforts will take time to be explored and developed. With this in mind, we created Pathwalker within the familiar framework of landscape resistance and random walk theory for its immediate use in simulating movement pathways and modelling landscape connectivity, but as a tool with more detail and flexibility than the popular connectivity models presently used.
5.3. Conclusions
Modelling and predicting organism movement and landscape connectivity is a fundamental part of modern ecological science. However, the dominant connectivity models currently in use are greatly limited by their simplistic and overly reductionist assumptions of movement behaviour. In this paper, we worked to address this by introducing a new spatially-explicit, individual- and process-based model called Pathwalker, which enables the modelling of individual paths and landscape connectivity as a function of resistance-biased movement choice, energetic cost of movement, mortality risk, autocorrelation, and directional bias towards a destination, all at multiple spatial scales.
Moreover, Pathwalker provides a valuable simulation tool for evaluating theoretical and methodological questions in spatial ecology and conservation science. While acknowledging the limitations of resistance-based models to attend to the richness and complexity of animal movement behaviour, we designed Pathwalker with an interface similar to programs such as CircuitScape and UNICOR, for its straightforward and immediate uptake in movement and connectivity modelling.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ijgi11060329/s1, Figure S1: he four density surfaces produced from the four different correlation values; Figure S2: The same four density surfaces, now plotted in three-dimensional space with the same colouring as above; Table S1: Statistics for the four density surfaces produced from the four different correlation values. The first row gives the overall extent of the movement paths on the 500-by-500 resistance surface, and the second row gives the percentage of the total area covered by these paths. The latter two rows give the parameters and value for the fitted power and exponential functions respectively.
Author Contributions
Conceptualisation, Siddharth Unnithan Kumar, Żaneta Kaszta, Samuel A. Cushman; Implementation, Siddharth Unnithan Kumar; Writing, Siddharth Unnithan Kumar, Żaneta Kaszta, Samuel A. Cushman. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Pembroke College, Oxford; and by the Engineering and Physical Sciences Research Council grant number EP/R513295/1.
Data Availability Statement
The data used for the case study in this paper is available on request to the corresponding author. The Pathwalker model, together with documentation and a test example, is available to download online at https://github.com/siddharth-unnithankumar/pathwalker (accessed on 26 May 2022).
Acknowledgments
Siddharth Unnithan Kumar would like to make the following acknowledgments. I deeply thank all my family and friends for their love; Sandhya Patel, Philip Maini, and the cleaners and maintenance staff at Oxford’s mathematical institute for their continuing support; Lila Brustad, Theo Leigh, Josephine Reynell, and Maria Nemtanu for their kindness and generosity (and delicious food); my dear friends from the Nature, Society and Environmental Governance 2021/22 course for their beauty and kinship; Hugo Shakeshaft, Emily Carson, Allegra Wint, and David Abram for their wisdom, wonder, and compassion; and for making my heart sing, I bow to Thich Nhat Hanh, the Buddha, Dhamma and Sangha, Port Meadow, the landscapes of Turtle Island, and the more-than-human earth which is our home.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abram, D. The Spell of the Sensuous: Perception and Language in a More-Than-Human World; Vintage: New York City, NY, USA, 1996. [Google Scholar]
- Ingold, T. Being Alive: Essays on Movement, Knowledge and Description; Routledge: Abingdon-on-Thames, UK, 2011. [Google Scholar] [CrossRef]
- Fahrig, L. Effects of habitat fragmentation on biodiversity. Annu. Rev. Ecol. Evol. Syst. 2003, 34, 487–515. [Google Scholar] [CrossRef]
- Cushman, S.A. Effects of habitat loss and fragmentation on amphibians: A review and prospectus. Biol. Conserv. 2006, 128, 231–240. [Google Scholar] [CrossRef]
- Cushman, S.A.; Elliot, N.B.; Macdonald, D.W.; Loveridge, A.J. A multi-scale assessment of population connectivity in African lions (Panthera leo) in response to landscape change. Landsc. Ecol. 2016, 31, 1337–1353. [Google Scholar] [CrossRef]
- Lorimer, J. Wildlife in the Anthropocene: Conservation after Nature; University of Minnesota Press: Minneapolis, MN, USA, 2015. [Google Scholar]
- Abram, D. Becoming Animal: An Earthly Cosmology; Vintage: New York City, NY, USA, 2010. [Google Scholar]
- Ingold, T. Point, line and counterpoint: From environment to fluid space. In Neurobiology of “Umwelt”; Springer: Berlin/Heidelberg, Germany, 2009; pp. 141–155. [Google Scholar]
- Levin, S.A. The problem of pattern and scale in ecology: The Robert H. MacArthur award lecture. Ecology 1992, 73, 1943–1967. [Google Scholar] [CrossRef]
- Gibbs, J.P. Amphibian movements in response to forest edges, roads, and streambeds in southern New England. J. Wildl. Manag. 1998, 62, 584–589. [Google Scholar] [CrossRef]
- Ingold, T. The Perception of the Environment: Essays on Livelihood, Dwelling and Skill; Routledge: Abingdon-on-Thames, UK, 2000. [Google Scholar]
- Tischendorf, L.; Fahrig, L. On the usage and measurement of landscape connectivity. Oikos 2000, 90, 7–19. [Google Scholar] [CrossRef]
- Rudnick, D.; Ryan, S.J.; Beier, P.; Cushman, S.A.; Dieffenbach, F.; Epps, C.; Gerber, L.R.; Hartter, J.N.; Jenness, J.S.; Kintsch, J.; et al. The role of landscape connectivity in planning and implementing conservation and restoration priorities. Issues Ecol. 2012, 16, 1–23. [Google Scholar]
- Hilty, J.A.; Lidicker, W.Z., Jr.; Merenlender, A.M. Corridor Ecology: The Science and Practice of Linking Landscapes for Biodiversity Conservation; Island Press: Washington, DC, USA, 2012. [Google Scholar]
- Cushman, S.A.; McRae, B.H.; Adriaensen, F.; Beier, P.; Shirley, M.; Zeller, K. Biological corridors and connectivity. In Key Topics in Conservation Biology 2; Macdonald, D.W., Willis, K.J., Eds.; Wiley-Blackwell: Hoboken, NJ, USA, 2013; Chapter 21; pp. 384–404. [Google Scholar]
- Zeller, K.A.; Jennings, M.K.; Vickers, T.W.; Ernest, H.B.; Cushman, S.A.; Boyce, W.M. Are all data types and connectivity models created equal? Validating common connectivity approaches with dispersal data. Divers. Distrib. 2018, 24, 868–879. [Google Scholar] [CrossRef]
- Zeller, K.A.; McGarigal, K.; Whiteley, A.R. Estimating landscape resistance to movement: A review. Landsc. Ecol. 2012, 27, 777–797. [Google Scholar] [CrossRef]
- Elliot, N.B.; Cushman, S.A.; Macdonald, D.W.; Loveridge, A.J. The devil is in the dispersers: Predictions of landscape connectivity change with demography. J. Appl. Ecol. 2014, 51, 1169–1178. [Google Scholar] [CrossRef]
- McRae, B.H.; Dickson, B.G.; Keitt, T.H.; Shah, V.B. Using circuit theory to model connectivity in ecology, evolution, and conservation. Ecology 2008, 89, 2712–2724. [Google Scholar] [CrossRef] [PubMed]
- Adriaensen, F.; Chardon, J.; De Blust, G.; Swinnen, E.; Villalba, S.; Gulinck, H.; Matthysen, E. The application of ‘least-cost’modelling as a functional landscape model. Landsc. Urban Plan. 2003, 64, 233–247. [Google Scholar] [CrossRef]
- Cushman, S.A.; McKelvey, K.S.; Schwartz, M.K. Use of empirically derived source–destination models to map regional conservation corridors. Conserv. Biol. 2009, 23, 368–376. [Google Scholar] [CrossRef]
- Landguth, E.; Hand, B.; Glassy, J.; Cushman, S.; Sawaya, M. UNICOR: A species connectivity and corridor network simulator. Ecography 2012, 35, 9–14. [Google Scholar] [CrossRef]
- Moilanen, A. On the limitations of graph-theoretic connectivity in spatial ecology and conservation. J. Appl. Ecol. 2011, 48, 1543–1547. [Google Scholar] [CrossRef]
- Compton, B.W.; McGarigal, K.; Cushman, S.A.; Gamble, L.R. A resistant-kernel model of connectivity for amphibians that breed in vernal pools. Conserv. Biol. 2007, 21, 788–799. [Google Scholar] [CrossRef] [PubMed]
- Dray, S.; Royer-Carenzi, M.; Calenge, C. The exploratory analysis of autocorrelation in animal-movement studies. Ecol. Res. 2010, 25, 673–681. [Google Scholar] [CrossRef]
- Cushman, S.A.; Chase, M.; Griffin, C. Elephants in space and time. Oikos 2005, 109, 331–341. [Google Scholar] [CrossRef]
- Wiens, J.A. Spatial scaling in ecology. Funct. Ecol. 1989, 3, 385–397. [Google Scholar] [CrossRef]
- Osipova, L.; Okello, M.; Njumbi, S.; Ngene, S.; Western, D.; Hayward, M.; Balkenhol, N. Using step-selection functions to model landscape connectivity for African elephants: Accounting for variability across individuals and seasons. Anim. Conserv. 2019, 22, 35–48. [Google Scholar] [CrossRef]
- Kaszta, Ż.; Cushman, S.A.; Slotow, R. Temporal Non-stationarity of Path-Selection Movement Models and Connectivity: An Example of African Elephants in Kruger National Park. Front. Ecol. Evol. 2021, 9, 207. [Google Scholar] [CrossRef]
- Gorini, L.; Linnell, J.D.; May, R.; Panzacchi, M.; Boitani, L.; Odden, M.; Nilsen, E.B. Habitat heterogeneity and mammalian predator–prey interactions. Mammal Rev. 2012, 42, 55–77. [Google Scholar] [CrossRef]
- DeAngelis, D.L.; Mooij, W.M. Individual-based modeling of ecological and evolutionary processes. Annu. Rev. Ecol. Evol. Syst. 2005, 36, 147–168. [Google Scholar] [CrossRef]
- Kareiva, P.; Shigesada, N. Analyzing insect movement as a correlated random walk. Oecologia 1983, 56, 234–238. [Google Scholar] [CrossRef] [PubMed]
- Schumaker, N.H. Using landscape indices to predict habitat connectivity. Ecology 1996, 77, 1210–1225. [Google Scholar] [CrossRef]
- Hargrove, W.W.; Hoffman, F.M.; Efroymson, R.A. A practical map-analysis tool for detecting potential dispersal corridors. Landsc. Ecol. 2005, 20, 361–373. [Google Scholar] [CrossRef]
- Schumaker, N.H.; Brookes, A. HexSim: A modeling environment for ecology and conservation. Landsc. Ecol. 2018, 33, 197–211. [Google Scholar] [CrossRef]
- Bocedi, G.; Palmer, S.C.; Malchow, A.K.; Zurell, D.; Watts, K.; Travis, J.M. RangeShifter 2.0: An extended and enhanced platform for modelling spatial eco-evolutionary dynamics and species’ responses to environmental changes. Ecography 2021, 44, 1453–1462. [Google Scholar] [CrossRef]
- Schumaker, N.H.; Brookes, A.; Dunk, J.R.; Woodbridge, B.; Heinrichs, J.A.; Lawler, J.J.; Carroll, C.; LaPlante, D. Mapping sources, sinks, and connectivity using a simulation model of northern spotted owls. Landsc. Ecol. 2014, 29, 579–592. [Google Scholar] [CrossRef]
- Henry, R.C.; Palmer, S.C.; Watts, K.; Mitchell, R.J.; Atkinson, N.; Travis, J.M. Tree loss impacts on ecological connectivity: Developing models for assessment. Ecol. Inform. 2017, 42, 90–99. [Google Scholar] [CrossRef]
- Jeltsch, F.; Bonte, D.; Pe’er, G.; Reineking, B.; Leimgruber, P.; Balkenhol, N.; Schröder, B.; Buchmann, C.M.; Mueller, T.; Blaum, N.; et al. Integrating movement ecology with biodiversity research-exploring new avenues to address spatiotemporal biodiversity dynamics. Mov. Ecol. 2013, 1, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Unnithan Kumar, S.; Cushman, S.A. Connectivity modelling in conservation science: A comparative evaluation. 2022; Under review. [Google Scholar]
- Landguth, E.L.; Cushman, S.A. CDPOP: A spatially explicit cost distance population genetics program. Mol. Ecol. Resour. 2010, 10, 156–161. [Google Scholar] [CrossRef] [PubMed]
- Landguth, E.L.; Cushman, S.A.; Schwartz, M.K.; McKelvey, K.S.; Murphy, M.; Luikart, G. Quantifying the lag time to detect barriers in landscape genetics. Mol. Ecol. 2010, 19, 4179–4191. [Google Scholar] [CrossRef] [PubMed]
- Shirk, A.J.; Landguth, E.L.; Cushman, S.A. A comparison of regression methods for model selection in individual-based landscape genetic analysis. Mol. Ecol. Resour. 2018, 18, 55–67. [Google Scholar] [CrossRef] [PubMed]
- Mantel, N. The detection of disease clustering and a generalized regression approach. Cancer Res. 1967, 27, 209–220. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberl, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Cushman, S.A.; Landguth, E.L. Spurious correlations and inference in landscape genetics. Mol. Ecol. 2010, 19, 3592–3602. [Google Scholar] [CrossRef]
- Cushman, S.A.; Shirk, A.J.; Landguth, E.L. Separating the effects of habitat area, fragmentation and matrix resistance on genetic differentiation in complex landscapes. Landsc. Ecol. 2012, 27, 369–380. [Google Scholar] [CrossRef]
- Stronen, A.V.; Schumaker, N.H.; Forbes, G.J.; Paquet, P.C.; Brook, R.K. Landscape resistance to dispersal: Simulating long-term effects of human disturbance on a small and isolated wolf population in southwestern Manitoba, Canada. Environ. Monit. Assess. 2012, 184, 6923–6934. [Google Scholar] [CrossRef][Green Version]
- Heinrichs, J.A.; Lawler, J.J.; Schumaker, N.H. Intrinsic and extrinsic drivers of source–sink dynamics. Ecol. Evol. 2016, 6, 892–904. [Google Scholar] [CrossRef] [PubMed]
- Webster, M.S.; Marra, P.P.; Haig, S.M.; Bensch, S.; Holmes, R.T. The importance of understanding migratory connectivity and seasonal interactions. Trends Ecol. Evol. 2002, 17, 76–83. [Google Scholar] [CrossRef]
- Ingold, T. The temporality of the landscape. World Archaeol. 1993, 25, 152–174. [Google Scholar] [CrossRef]
- Cushman, S.; Raphael, M.; Ruggiero, L.; Shirk, A.; Wasserman, T.; O’Doherty, E. Limiting factors and landscape connectivity: The American marten in the Rocky Mountains. Landsc. Ecol. 2011, 26, 1137–1149. [Google Scholar] [CrossRef]
- Wan, H.Y.; McGarigal, K.; Ganey, J.L.; Lauret, V.; Timm, B.C.; Cushman, S.A. Meta-replication reveals nonstationarity in multi-scale habitat selection of Mexican Spotted Owl. Condor Ornithol. Appl. 2017, 119, 641–658. [Google Scholar] [CrossRef]
- Vergara, M.; Cushman, S.A.; Ruiz-González, A. Ecological differences and limiting factors in different regional contexts: Landscape genetics of the stone marten in the Iberian Peninsula. Landsc. Ecol. 2017, 32, 1269–1283. [Google Scholar] [CrossRef]
- Cushman, S.A. Space and time in ecology: Noise or fundamental driver? In Spatial Complexity, Informatics, and Wildlife Conservation; Springer: Berlin/Heidelberg, Germany, 2010; pp. 19–41. [Google Scholar]
- Zeller, K.A.; Lewsion, R.; Fletcher, R.J.; Tulbure, M.G.; Jennings, M.K. Understanding the importance of dynamic landscape connectivity. Land 2020, 9, 303. [Google Scholar] [CrossRef]
- Bennett, N.J.; Roth, R.; Klain, S.C.; Chan, K.; Christie, P.; Clark, D.A.; Cullman, G.; Curran, D.; Durbin, T.J.; Epstein, G.; et al. Conservation social science: Understanding and integrating human dimensions to improve conservation. Biol. Conserv. 2017, 205, 93–108. [Google Scholar] [CrossRef]
- Kaszta, Ż.; Cushman, S.A.; Hearn, A.J.; Burnham, D.; Macdonald, E.A.; Goossens, B.; Nathan, S.K.; Macdonald, D.W. Integrating Sunda clouded leopard (Neofelis diardi) conservation into development and restoration planning in Sabah (Borneo). Biol. Conserv. 2019, 235, 63–76. [Google Scholar] [CrossRef]
- Benson, E.S. Movement Ecology and the Minimal Animal. LA+ 2016, 30–33. [Google Scholar]
- Pooley, S.; Barua, M.; Beinart, W.; Dickman, A.; Holmes, G.; Lorimer, J.; Loveridge, A.J.; Macdonald, D.W.; Marvin, G.; Redpath, S.; et al. An interdisciplinary review of current and future approaches to improving human–predator relations. Conserv. Biol. 2017, 31, 513–523. [Google Scholar] [CrossRef] [PubMed]
- Peterson, M.N.; Birckhead, J.L.; Leong, K.; Peterson, M.J.; Peterson, T.R. Rearticulating the myth of human–wildlife conflict. Conserv. Lett. 2010, 3, 74–82. [Google Scholar] [CrossRef]
- Benson, E.S. Minimal animal: Surveillance, simulation, and stochasticity in wildlife biology. Antennae 2014, 30, 39–53. [Google Scholar]
- Barua, M. Bio-geo-graphy: Landscape, dwelling, and the political ecology of human-elephant relations. Environ. Plan. D Soc. Space 2014, 32, 915–934. [Google Scholar] [CrossRef]
- Salmón, E. Kincentric ecology: Indigenous perceptions of the human–nature relationship. Ecol. Appl. 2000, 10, 1327–1332. [Google Scholar]
- Nathan, R.; Getz, W.M.; Revilla, E.; Holyoak, M.; Kadmon, R.; Saltz, D.; Smouse, P.E. A movement ecology paradigm for unifying organismal movement research. Proc. Natl. Acad. Sci. USA 2008, 105, 19052–19059. [Google Scholar] [CrossRef]
- Cooke, S.J.; Blumstein, D.T.; Buchholz, R.; Caro, T.; Fernandez-Juricic, E.; Franklin, C.E.; Metcalfe, J.; O’Connor, C.M.; St. Clair, C.C.; Sutherland, W.J.; et al. Physiology, behavior, and conservation. Physiol. Biochem. Zool. 2014, 87, 1–14. [Google Scholar] [CrossRef]
- Lorimer, J. Nonhuman charisma. Environ. Plan. D Soc. Space 2007, 25, 911–932. [Google Scholar] [CrossRef]
- Ingold, T. The optimal forager and economic man. In Nature and Society; Routledge: Abingdon-on-Thames, UK, 2003; pp. 35–54. [Google Scholar]
- Sekar, N.; Shiller, D. Engage with animal welfare in conservation. Science 2020, 369, 629–630. [Google Scholar] [CrossRef]
- Paquet, P.C.; Darimont, C.T. Wildlife conservation and animal welfare: Two sides of the same coin. Anim. Welf. 2010, 19, 177–190. [Google Scholar]
- Wallach, A.D.; Bekoff, M.; Batavia, C.; Nelson, M.P.; Ramp, D. Summoning compassion to address the challenges of conservation. Conserv. Biol. 2018, 32, 1255–1265. [Google Scholar] [CrossRef]
- Parreñas, J.S. Decolonizing Extinction; Duke University Press: Durham, NC, USA, 2018. [Google Scholar]
- Cooke, S.J.; O’Connor, C.M. Making conservation physiology relevant to policy makers and conservation practitioners. Conserv. Lett. 2010, 3, 159–166. [Google Scholar] [CrossRef]
- Hodgetts, T.; Lorimer, J. Methodologies for animals’ geographies: Cultures, communication and genomics. Cult. Geogr. 2015, 22, 285–295. [Google Scholar] [CrossRef]
- Hodgetts, T. Connectivity as a multiple: In, with and as “nature”. Area 2018, 50, 83–90. [Google Scholar] [CrossRef] [PubMed]
- Bunnefeld, N.; Nicholson, E.; Milner-Gulland, E.J. Decision-Making in Conservation and Natural Resource Management: Models for Interdisciplinary Approaches; Cambridge University Press: Cambridge, UK, 2017; Volume 22. [Google Scholar]
- Unnithan Kumar, S.; Maini, P.K.; Chiaverini, L.; Hearn, A.J.; Macdonald, D.W.; Kaszta, Ż.; Cushman, S.A. Smoothing and the environmental manifold. Ecol. Inform. 2021, 66, 101472. [Google Scholar] [CrossRef]
- Kimmerer, R. Braiding Sweetgrass: Indigenous Wisdom, Scientific Knowledge and the Teachings of Plants; Milkweed Editions: Minneapolis, MN, USA, 2013. [Google Scholar]
- Berkes, F. Sacred Ecology; Routledge: Abingdon-on-Thames, UK, 2017. [Google Scholar] [CrossRef]
- Ingold, T. Rethinking the animate, re-animating thought. Ethnos 2006, 71, 9–20. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).