Abstract
This paper seeks to predict the average waiting time, defined as the time spent moving at 1 ms or less, of urban bicyclists during rush hours while performing different maneuvers at intersections. Individual predictive models are built for the three cyclist typologies previously identified on a large database of GPS traces recorded in the city of Bologna, Italy. Individual models are built for the three cyclist typologies and bootstrapping has confirmed the validity and robustness of the results. The results allow the integration of waiting times in route choice models for cyclists, thus improving the rational bases by which cyclists makes their decisions. Moreover, the modeling allows transportation engineers to understand how different cyclist typologies perceive different variables that affect their waiting times. Future work should focus on testing the model transferability to other case studies.
1. Introduction
Recently cycling has received increasing attention in urban planning as it is considered a solution to combat traffic congestion, air pollution, greenhouse gas emission, fossil fuel dependency and physical inactivity [1]. Cyclist route choice models are essential for simulating large-scale traffic scenarios (or digital twins) that include soft mobility. Some articles on cyclist route choice exist, [2,3,4,5,6,7]; however, the influence of cyclist waiting times on route choice models has not yet been studied extensively, despite the fact that it constitutes a significant share of the overall travel time of urban trips (see discussion below). For example, Broach et al. (2012) calibrated a route choice model for cyclists to better understand their preferences for facility typologies without considering waiting times. The authors used GPS units to observe the behavior of 164 cyclists in Portland, Oregon, USA [2]. Ehrgott et al. (2012) proposed a novel model to determine the route-set for the choice of commuter cyclists by formulating a bi-objective routing problem. The two objectives considered are the suitability of a route for cycling and total travel time, without considering that the waiting time is perceived differently with respect to travel time [3]. The lack of studies related to the quantification of cyclist waiting times is mostly due to the lack of waiting time evaluators or estimators for cyclists, as well as the absence of on-site surveys which address this type of problem [8]. However, the impact of stops and delays during bicycle trips has been analyzed in several studies. Börjesson and Eliasson (2012) found that the perception of a 1 minute stop at a traffic light corresponds to 3.1 min of cycling [9]. More recently, Fioreze et al. (2019) have shown that most cyclists considerably overestimate their waiting time: cyclists’ perceived waiting time was approximately five times higher than their actual waiting time [10]. Rupi et al. (2020) have shown that on average waiting time accounts for 15% of total trip duration, based on the analysis of a large data sample of GPS traces [11]. These studies underpin the importance of analyzing a cyclist’s waiting time.
In general, waiting times can be estimated from the cyclist’s speed profile. Different approaches have been taken to calculate the most likely speed profile [12,13,14,15] and to estimate the trend of motion. For example, Strauss and Miranda-Moreno (2017) = approximated the speed profile by averaging over three, four, and seven GPS points before estimating the cyclist’s speed and time-delay at intersections, which is different from waiting time. They consider time loss at intersections as the time difference between the time to cross the intersection while keeping the average speed on the incoming link and the effective time to cross the intersection [12]. For this reason, Rupi et al. (2020) proposed a new tool to estimate the waiting times of cyclists from a large database of GPS traces [11] and confirmed its validity through manual surveys [16,17].
The difference between effective and perceived waiting times is not the same for all the cyclists. Distinct typologies of cyclists show differences in perceiving and value this difference. This is why it is important for route choice models to first identify the typology of cyclists. Poliziani et al. (2021) identified three different typologies of cyclists during rush hour traffic in Bologna, Italy [18]. This was accomplished using a data set constituted by 16,168 GPS traces from 2135 cyclists whose trips were recorded from 7 a.m. to 10 a.m. between April and September 2017. The different typologies of cyclists were identified using a statistical approach called cluster analysis. Given the characteristic of the data, the authors applied a flexible, highly parameterized clustering technique known as a mixture of coalesced generalized hyperbolic distributions (CGHD) proposed by Tortora et al. (2019). In the used model, each typology of cyclists or cluster is assumed to follow a multidimensional coalesced generalized hyperbolic distribution [19], i.e., a more flexible distribution compared to the well-known normal or Student-t distributions. Subsequent analysis of the differences in features between the three clusters revealed three behavioral typologies: RHC (risky and hasty), IIC (inexperienced and inefficient), and SIC (sly and informed) cyclists. Poliziani et al. (2021) revealed key behavioral differences between the aforementioned typologies obtained using cluster analysis. Risky and hasty cyclists tend to choose the shortest path through the use of unsafe roads with vehicle traffic and are hindered by many traffic lights. Sly and informed cyclists prefer longer yet less congested paths with designated cycle-ways to avoid traffic lights. Inexperienced and inefficient cyclists are characterized by low speeds and spend much more time waiting [18]. Having clarified the behavioral differences between the three cyclist typologies, it is likely that cyclists from each typology will exhibit different waiting times while performing the same maneuver.
As such, the goal of the present work is to build individual models for each of these three typologies using the same GPS database to predict a cyclist’s average waiting time while performing a maneuver. These predictions can be part of a cyclist route choice model that includes the impact of waiting times.
2. Methodology and Model
This paper seeks to predict the average waiting times of urban cyclists during rush hours while performing different maneuvers at road intersections. The methodology used allows us to identify individual predictive models for the three cyclist typologies previously identified [18]. The maneuver database is processed in two main steps: (1) a subgroup of 60 high-traveled maneuvers by cyclists are selected, along with 60 maneuver attributes that are thought to predict the average waiting time. The GPS traces are aggregated to obtain the average waiting time for the three cyclist typologies on each selected maneuver, and data cleaning and feature selection are then implemented to progressively reduce model complexity by deleting dependent and irrelevant attributes. (2) The non-parametric kernel regression has been identified as the optimal predictive model among random forest regression and Gaussian kernel SVM and has been implemented to predict average waiting times.
2.1. Data
2.1.1. Cyclists’ GPS Traces
The GPS traces of cyclists were collected during the “Bella Mossa” initiative funded by the EU and the city of Bologna, Italy, which took place from 1 April to 30 September 2017 in the city of Bologna, Italy. The initiative’s objective was to promote sustainable mobility by rewarding people (with coupons for local shops) for recording their GPS traces of sustainable trips (meaning trips made via transit, bike, or walking). The smartphone application “Betterpoints” [20] was used to record and collect the data.
The full data-set contains approximately 270,000 bike GPS traces, composed of more than 62 million points—see Figure 1; the smartphone application records 1 GPS point every 5 s when the bike is in motion. When the bike stops (for example, at intersections), the recording stops, thus saving the smartphone’s battery. The present study focuses only on bike GPS traces recorded during the period of peak travel during the morning on weekdays, from 7 a.m. to 10 a.m., as used by Poliziani et al. (2021), to identify the cyclist typologies [18]. GPS traces are not linked to a specific trip purpose. However, during early morning hours the vast majority are work trips; in this way, it is possible to emphasize the differences in the decisions of cyclists that have to primarily balance security with travel time but are also trying either to arrive punctually or avoid traffic congestion: In fact, daily travel behavior and trip patterns are impacted by travel security [21]. With this analysis, one can also try to eclipse the share of hedonic cyclists, who are less significant from a transportation study point of view.
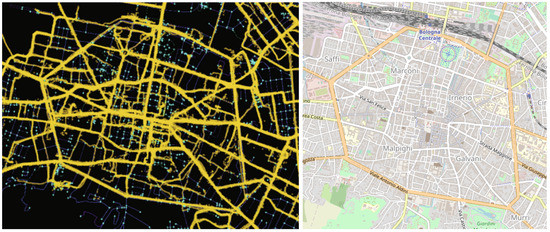
Figure 1.
On the left, a graphical representation of the used GPS traces from Bella Mossa campaign (in yellow) overlapped with the SUMO network of the city of Bologna, Italy (in blue); on the right, the relative open street map of Bologna.
The following data-processing steps have been implemented using the SUMOPy environment [22]. In the first step, the open-street-map (OSM) network covering the urban area of Bologna [23] has been imported into SUMO. This SUMO network is attribute-rich and contains information on road width, road access (e.g., reserved bikeways, shared access, presence of pedestrians, etc.) and speed limits. From these basic attributes, SUMO derives a road priority (1–14), in which low-priority roads are assigned values from 1 to 7. The network has been manually improved over years to both eliminate errors due to an imperfect OSM representation and conversion errors and reproduce the road infrastructure in 2017, the same year of the GPS traces data set.
Next, unrealistic GPS traces, defined as trips outside the study area and traces that were probably not recorded while riding a bike, were deleted. In particular, valid traces must satisfy the following criteria: (1) total trip length lower and higher than the maximum (25,000 m) and the minimum (100 m) distance, respectively; (2) total duration lower and higher than the maximum (7200 s) and the minimum (30 s) duration, respectively; (3) distance between successive points lower and higher than the maximum (1000 m) and the minimum (2 m) distance, respectively; (4) duration between successive points lower than the maximum duration (300 s); (5) average speed lower and higher than the maximum (14 ms) and the minimum (1 ms) average speed, respectively; (6) GPS trace at least partially included in the study area. This trace-filtering step ensures that the GPS traces can be successfully matched to the road network by the map-matching process. During the map-matching, the most likely route (as a sequence of network links) can be identified for each GPS trace [24].
The cyclists’ waiting times have been successively evaluated with a recent algorithm developed on the SUMOPy software [11]. A first check eliminates traces that are not accurate enough to perform this specific analysis.
Successively, the hourly speed profile is extracted for all remaining trips and associated to the matched route. This is conducted in such a way that it is possible not only to estimate travel waiting times, total travel times, and speed but also to associate them to specific network elements: edges (or links), connections (or maneuvers), and nodes (or intersections). In particular, a waiting time is recorded every time the cyclists move slower than the average speed of 1 ms between two successive GPS points, considered as pedestrian speed [11].
2.1.2. Maneuvers Dataset
A maneuver is defined as the unique identifier created by the combination of an incoming and outgoing road lane at a road intersection; a maneuver can be generally classified as heading straight, turning right, turning left, or a u-turn. Generally, turning left is subject to more conflicts with traffic, generating higher waiting times; contrarily, turning right generally does not conflict with traffic. The data used consist of 60 maneuvers selected from the road network of the city of Bologna with 2 main criteria: The first one is to consider only high-traveled maneuvers by cyclists who recorded the GPS traces showed on Section 2.1.1; in this way, the average waiting times evaluated for these maneuvers and for the three cyclist typologies will be more representative of the population. In particular, Rupi et al. (2020) showed that only measuring the waiting time of at least 100 cyclists will accurately reproduce the average of the population, since values are well distributed due to several reasons: cyclists who pass with red at traffic light [25], presence of opposite flow, cyclist physical attributes [26], prudence and dynamic behavior [27], and so on. The second criterion consists of having heterogeneous maneuvers from both the space—spread throughout the study area—and typology—typology of maneuver and presence of traffic light—sides. For each maneuver, 60 attributes have been assigned through different data sources related to the maneuver itself, the crossed maneuvers, and the incoming and outgoing link: maneuver typology, length and rank, presence of cycleway, number of link lanes, link priority, widths and flows, presence of traffic light, traffic light attributes, interaction with pedestrian crossing and other maneuvers, opposite PCE (passenger Car Equivalent) flow, presence of bus lines, and intersection complexity in terms of number of maneuvers allowed. The database is composed by 17 left turns, 24 straight crossings, and 19 right turns; 29 of these had a traffic light, contrary to the other 31. After the GPS trace analysis reported in Section 2.1.1, the following features have been attached to each maneuver for all cyclists and for each of the three cyclist typologies—RHC (risky and hasty), IIC (inexperienced and inefficient), and SIC (sly and informed)—identified by Poliziani et al. (2021) [18]: number of cyclists that used this maneuver, number of occurred waiting times, average waiting time, and list of waiting times. On average, each maneuver has been used by 219 cyclists, and an average of 24 cyclists recorded a waiting time. The average waiting time on the considered maneuvers was 1.94 s considering also the zero waiting times and 17.7 s considering only positive waiting times. The three cyclist typologies, RHG, IIC, and SIC, recorded on average on the considered maneuvers a waiting time every 10, every 7, and every 11 passages, respectively, with average waiting times of 2.59, 4.82, and 3.05 s considering also zero waiting times.
2.1.3. Data Cleaning and Feature Selection
Data cleaning was accomplished by first performing feature aggregation then feature selection using both domain knowledge and mathematical methods. The original data frame contained two columns for several features, one column corresponding to maneuvers with a traffic light and the other to maneuvers without. As such, the two columns for each feature had blank cells where the other column had an entry and were simply merged into a single column for downstream analysis. In addition, only considering filtering significant predictors of average waiting time from a transportation engineering point-of-view generated an initial set of 19 features. Forwards and backwards stepwise linear regression was initially attempted for naive feature selection, the idea being that significant predictors will be left in the final model while insignificant ones will not. However, the attempts indicated a high degree of multicollinearity among the 19 features. To eliminate redundancy, nine variables that had a clear correlation with others were first removed, and then the remaining categorical and continuous features were considered separately. A simple correlation matrix for the three continuous features (see Table 1) did not suggest high correlation, indicating the issue lay among the categorical ones. The three continuous features are: (1) critical volume, which represents the amount of opposite flow at intersection [28]; (2) the average PCE flow at intersection, based on PCE flows measured on all links entering the intersection: these values have been extracted from the city’s digital records [29]; (3) the length of the maneuver in meters.

Table 1.
Continuous features correlation matrix.
Categorical association detection was conducted with the phi-squared effect size test, defined as , where the value is the test statistic from the test of independence—see Table 2.

Table 2.
statistic table.
The threshold value of to conclude that two categorical features are dependent was empirically decided to be . This yielded three pairs of dependent features: features 4 and 5, 4 and 6, and 5 and 6. Features 4 and 6 were chosen to be eliminated based on a transportation significance, leaving 8 final predictors. In particular, the remaining categorical variables are in order: (1) Maneuver typology (left turn, right turn, straight); (2) Lanes edge to (number of lanes on road which maneuver is directed to); (3) Traffic light (true or false); (4) Number maneuvers crossed (number of intermediate maneuver crossed at intersection); (5) Connections node (total number of maneuvers at geographic intersection). The feature called number maneuvers crossed was then modified according to Figure 2. To reduce model complexity, values of 1 and 2 were merged and coded as 1, while values of 3 and higher were merged and coded as 2. Table 3 provides a description of the final 8 features that will be used for model fitting.
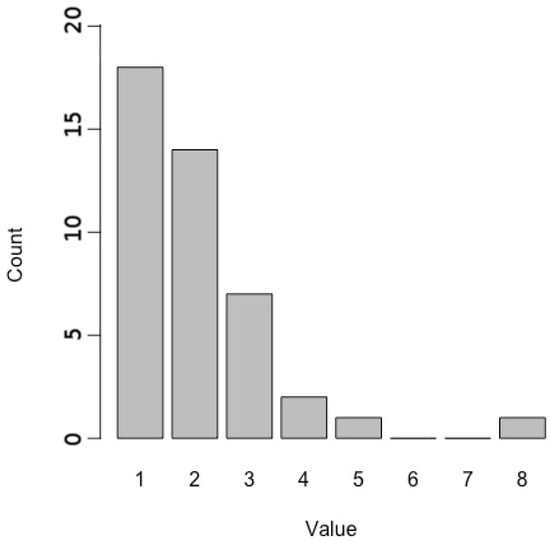
Figure 2.
Histogram of the feature ‘number maneuver crossed’.

Table 3.
Selected feature descriptions.
2.2. Model Selection
Random forest regression and Gaussian kernel support vector machine (SVM) classification methods were initially attempted before settling on nonparametric regression. Model selection was performed only on cyclist typology RHC as all three typologies will use the same model architecture. All computations were performed with the computational software R [30].
2.2.1. Random Forest Regression
Random forest regression [31] is an extension of random forest classification to handle a continuous response which uses an ensemble of regression trees. A single regression tree partitions the feature space through a series of feature binary splits that minimize the residual sum of squares, defined as:
where and are the response averages to the left and right of a binary split. Splits are made until a stopping criterion is satisfied, which, for this implementation, is the minimum number of observations in a group to be designated a terminal node. Random forest improves on a single regression tree by training T individual trees on bootstrap replications of the original data and using a random subset of features to train each tree. Each of the T trees generates a prediction for the ith observation denoted , and the model’s final prediction is the average of all predictions, or . The parameters T and the minimum observations in a terminal node were tuned for optimality with the R package randomForest [32]; models built for T values between 10 and 400 in increments of 10 showed 60 trees minimized mean squared error (MSE) and model complexity, and varying the minimum terminal node value between 1 and 10 identified 1 as MSE-optimal with a value of 1.96. However, by-hand examination of the 60 predicted average waiting times showed large deviations from the actual times, so a more accurate model was desired.
2.2.2. Gaussian Kernel SVM
SVM [33] is a binary classification method that seeks to find the normal vector and offset b of hyperplane that best separates the two classes. This is accomplished with optimization through quadratic programming, which identifies each class’ boundary points, known as support vectors, to establish said plane. Gaussian kernel SVM improves upon the standard SVM by utilizing the Gaussian kernel function to project the data from the original space to the higher-dimensional feature space for better separability. Finding the optimal hyperplane then reduces down to solving the following quadratic program:
subject to and , where C is the regularization parameter and , which codes for the two classes. A new observation can be classified with the decision rule , where b can be determined with the equation , where is any support vector. To implement Gaussian kernel SVM for classification, the continuous response was first discretized into 3 classes according to Table 4.

Table 4.
SVM response discretization.
The goal of the discretization scheme was to preserve balance, which was accomplished. A 48-to-12 train/test split was then selected with a seed and the regularization and gamma parameters tuned for optimality with the R package e1071 [34], which yielded perfect accuracy for that specific train/test split. In order to assess the model’s sensitivity to the split, 100 iterations were run without a seed for the splitting, which yielded accuracy values ranging from 0.75 to a perfect 1.00, indicating a degree of sensitivity likely due to the small number of data points. Furthermore, discretizing the average waiting time to preserve balance lead to a large information loss as the response had values as high as 17.
2.3. Nonparametric Kernel Regression
Nonparametric kernel regression [35] provided a way to preserve the average waiting time’s continuous nature while maintaining the flexibility necessary when dealing with limited observations. The goal of kernel regression is to estimate the empirical relation between and Y, where , with p number of variables, is a random vector of the features, and Y is the average waiting time [36]. This was accomplished through the use of the Nadaraya–Watson estimator, which is implemented in R in the np package [37]. The multivariate estimator of the waiting time about a vector-valued location , , is defined as:
The Nadaraya–Watson estimator can only be used with continuous variables; however, the features are of mixed typology. Therefore, the problem requires a generalization of this estimator. Different kind of kernels can be used for the different typology of variables. The kernel used for the continuous features is the Gaussian kernel with formula for univariate data. The continuous multivariate kernel density estimator is:
The data’s multivariate nature requires a matrix-valued data structure of bandwidths denoted , which has a similar interpretation as the covariance matrix in the multivariate Gaussian distribution when the Gaussian kernel is used. The density estimate can be simplified by substituting the kernel function with the bandwidth-scaled kernel denoted as to yield , with numbers of continuous variables. Each scalar bandwidth denotes the bandwidth of each continuous feature. For computational simplicity, is assumed to be diagonal; that is, each feature is assumed to be independent when calculating bandwidths, so pairwise bandwidths are zero.
The Aitchison and Aitken kernel [38] was used for the nominal variables with levels and is defined as:
where is the bandwidth. The ordinal features were handled with Li and Racine’s kernel [39] are defined as:
where is the bandwidth. With kernel weighing functions defined for continuous, nominal, and ordinal features, the generalized Nadaraya–Watson estimator for mixed data can be expressed as:
based on the mixed product kernel:
2.4. Bandwidth Selection
Bandwidth selection was performed according to the method of leave-one-out least squares cross validation [40], created to address the issues that arise with bandwidth selection through a simple minimization of the residual sum of squares. The least squares cross-validation error is defined as:
where the subscript denotes the ith value is the one being left out, and the optimal bandwidths are values that minimize the error, or . R’s np package implements this method with a brute-force grid search in conjunction with five different initializations, and returns the result with the lowest cross-validation error.
2.5. Bootstrapping
Bootstrapping was used to measure the estimator’s variability, for which closed-form solutions like the Nadaraya–Watson estimator do not exist. Furthermore, bootstrapping can be thought of as cross-validation in the sense that it automatically breaks the data into a training and test set and provides a way to examine a model’s predictive power when certain observations are left out of the training phase.
Formally, bootstrapping is a resampling method in which data points are sampled from the original data set to generate a bootstrap replication [41]; i.e., with original data matrix comprised of p-dimensional vector observations , sample among with replacement n times to obtain a bootstrap replication denoted as , where denotes the ith sample. The statistic of interest is then calculated from , and the whole process is repeated to generate new bootstrap replications and corresponding statistics. Appropriate inference can then be drawn using the statistic’s replications. With this project’s observations, there are possible bootstrap replications, so a complete bootstrap in which all possible replications are considered is computationally infeasible. As such, a random subset of 1000 replications was used, which is known as a Monte Carlo bootstrap. The fact that bootstrap replications are generated through sampling with replacement means that each of the n observations has a chance of being selected at every sampling step, so each sampling step is independent of other steps. This allows the percent of observations left out of each replication to be quantified. Consider a single bootstrap replication which consists of sampling from n observations n times. The probability of an arbitrary observation i being left out is . As such, an average of , or percent, of all observations are left out of any given bootstrap replication, effectively partitioning the original data into training (included observations) and testing (excluded observations) sets. Therefore, bootstrapping the Nadaraya–Watson estimator allows its variation and robustness to be examined.
3. Results
Table 5 summaries the three models, each corresponding to a typology of cyclist.

Table 5.
Feature bandwidths by model typology and feature number.
Table 5 contains the optimal cross-validated bandwidths for each feature previously identified in Table 3. Feature 3, the presence of a traffic light, is nominal with 2 levels, which means its bandwidth range is , where denotes the number of levels. The fact that the models for cyclist typologies 1 and 3 have a bandwidth of means the Aitchison and Aitken kernel for nominal features assigns the same weight of regardless of level. Therefore, the presence of a traffic light does not provide any information when predicting the average waiting time for typologies 1 and 3. The same observation can be made with feature 1, maneuver typology, and the model for IIC. Maneuver typology has three levels and a bandwidth range and consequently does not help predict the average waiting time for IIC. Feature 2, lanes edge to, has a bandwidth equal to 1 for the RHC model, which is the upper bound of an ordinal feature’s bandwidth range of . This means that Li and Racine’s kernel for ordinal features assigns a weight of one regardless of level, which can also be interpreted to mean lanes edge to contain no information that helps predict average waiting time. All other categorical features have a bandwidth somewhere in their respective ranges, the magnitude of which determines the weight an observation carries when predicting the average waiting time at any given point. Features 6, 7, and 8 are continuous in nature and have slightly different bandwidth interpretations. Bandwidths are akin to the parameter in the Gaussian distribution formula because it controls the distribution’s spread and, consequently, the weights assigned to observations; a small bandwidth will assign large weights to observations near the point of estimation and small weights to observations far away, while a large bandwidth will place more emphasis on points far away. It should be noted that the Gaussian kernel will still assign heavier weights to nearby points even with a large bandwidth. The bandwidth for feature 6 (critical volume) in the IIC model is much larger than all the others, which can be interpreted to say that critical volume does not contribute much to predicting average waiting time, as the huge bandwidth assigns similar weights to all observations regardless of distance. Table 6 contains each model’s and . Each model has a high and low , indicating that the nonparametric regression curve fits the data well. The strength of the selected model is further exemplified when compared to random forest regression with 60 trees, which has an of 1.40 and a mean average deviation between predicted and actual values of . Kernel regression is also superior to Gaussian kernel SVM, which demonstrated sensitivity to the the train/test split and caused large information loss through the required discretization of the average waiting time. Furthermore, examining the bootstrapped standard errors reveals that nonparametric regression’s predictive power is robust for the majority of observations even when left out of the fitting phase. Most maneuvers with predicted average waiting times significantly greater than zero have relatively small standard errors, indicating that the models built from the bootstrap replications were reasonably accurate across the board for all 1000 replications.

Table 6.
Model summaries.
The Nadaraya–Watson estimate for each typology and each maneuver is tabulated in the appendix (see Table A1 and Table A2) with bootstrapped standard errors in parentheses.
There are significant differences among the predicted average waiting times for each typology (see Table A1 and Table A2). These results are consistent with Poliziani et al. (2021) [18]: IIC (inexperienced and inefficient) cyclists spend significantly more time waiting, which hints at their inexperience. Waiting times for RHC (risky and hasty) and SIC (sly and informed) are comparable, but the risky behaviors exhibited by RHC may explain the slightly lower values. Feature selection indicated that eight features are necessary and sufficient predictors of average waiting time. Almost all the variables can be easily identified for all maneuvers, apart from the PCE flow and critical volume, which require expensive on-site surveys if not known.
Despite the model’s general robustness, it does struggle with maneuvers whose waiting times are near-zero. The most glaring issue here is with maneuvers such as maneuver 26 (see Table A1), where the bootstrapped standard error is larger than the predicted waiting time, indicating that certain models built with bootstrap replications predicted a negative waiting time. This issue can be addressed by setting a lower bound for the average waiting time at 0, which will reduce variation and improve robustness.
4. Conclusions
A new model has been calibrated which allows us to estimate the waiting times of cyclists on different street maneuvers at intersections for three different cyclist typologies previously identified [18]: The average waiting times of the three cyclist typologies have been found to be consistent with their characterization. Some recent studies have highlighted that the time attribute is dominant for work and study trips of cyclists: Although the trip time of cyclists is not particularly affected by congestion, the waiting times at intersections along the path does significantly impact travel time [1,10]. This research provides a practical contribution to the evaluation of waiting times, concluding that they are essential for the design and management of cycle networks. In fact, the estimated waiting times could be a valid attribute in a route choice model for cyclists, as waiting time accounts for a significant share of trip time in urban settings. In addition, the present study shows how different cyclist typologies differently perceive all significant attributes that affect their waiting time. This information may also contribute to improve path choice models of cyclists.
More work needs to be conducted on extrapolating this model to other cities where cyclists may exhibit different tendencies and to test the predictors with other data. In general, future studies should also design a new route choice model for cyclists including the waiting time influence, as well as the typology of cyclist, for example, using the estimators presented in this paper.
Author Contributions
Conceptualization, Cristian Poliziani, Joerg Schweizer, and Federico Rupi; data curation, Cristian Poliziani and Joerg Schweizer; investigation, Cristian Poliziani; methodology, Jeremy Walker, Cristian Poliziani, Cristina Tortora, Joerg Schweizer, and Federico Rupi; software, Cristian Poliziani and Joerg Schweizer; supervision, Jeremy Walker, Cristian Poliziani, Cristina Tortora, and Joerg Schweizer; validation, Jeremy Walker and Cristina Tortora; writing—original draft, Jeremy Walker, Cristian Poliziani, and Joerg Schweizer; writing—review and editing, Jeremy Walker, Cristian Poliziani, Cristina Tortora, Joerg Schweizer, and Federico Rupi. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
We are grateful to SRM (Società Reti e Mobilità, Bologna) for providing the GPS traces related to the Bella Mossa campaign and to the graduated student Matteo Saracco involved with the manual survey.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Nadaraya–Watson estimates (bootstrapped standard error). From maneuver number 1 to 30.
Table A1.
Nadaraya–Watson estimates (bootstrapped standard error). From maneuver number 1 to 30.
| Maneuver Number | RHC | IIC | SIC |
|---|---|---|---|
| 1 | 0.01 (0.15) | 1.03 (0.11) | 0.15 (0.08) |
| 2 | 0.07 (0.49) | 0.11 (0.52) | 0.08 (0.26) |
| 3 | 0.84 (0.19) | 0.00 (0.10) | 0.00 (0.06) |
| 4 | 0.69 (1.84) | 0.46 (2.21) | 0.00 (2.75) |
| 5 | 0.71 (0.33) | 0.15 (0.15) | 0.00 (0.18) |
| 6 | 2.43 (0.18) | 5.00 (0.13) | 3.23 (0.15) |
| 7 | 2.68 (0.96) | 3.76 (0.98) | 1.29 (0.81) |
| 8 | 0.76 (0.07) | 1.85 (0.06) | 1.02 (0.06) |
| 9 | 1.09 (0.36) | 1.38 (0.34) | 3.28 (0.43) |
| 10 | 1.71 (1.89) | 2.13 (2.30) | 2.00 (2.70) |
| 11 | 0.23 (0.59) | 2.07 (0.62) | 2.23 (0.48) |
| 12 | 0.75 (0.22) | 0.36 (0.10) | 0.09 (0.10) |
| 13 | 1.11 (0.28) | 2.16 (0.28) | 2.82 (0.36) |
| 14 | 2.28 (1.97) | 9.97 (1.93) | 6.16 (1.85) |
| 15 | 2.08 (0.13) | 4.80 (0.17) | 3.30 (0.20) |
| 16 | 6.56 (0.29) | 4.73 (0.09) | 2.75 (0.17) |
| 17 | 0.93 (0.35) | 2.67 (0.31) | 1.77 (0.18) |
| 18 | 2.13 (0.47) | 6.05 (0.48) | 1.74 (0.53) |
| 19 | 1.67 (0.66) | 3.99 (0.65) | 3.73 (0.75) |
| 20 | 0.13 (1.21) | 0.39 (0.93) | 0.13 (0.85) |
| 21 | 1.52 (0.03) | 2.40 (0.03) | 0.34 (0.03) |
| 22 | 7.90 (0.91) | 16.31 (0.89) | 8.19 (0.66) |
| 23 | 2.84 (1.64) | 3.62 (0.80) | 5.11 (0.96) |
| 24 | 8.50 (0.12) | 5.62 (0.06) | 4.00 (0.07) |
| 25 | 0.82 (2.61) | 2.55 (2.94) | 0.77 (2.89) |
| 26 | 0.01 (0.06) | 0.10 (0.07) | 0.04 (0.12) |
| 27 | 2.75 (0.60) | 9.94 (1.24) | 14.99 (1.20) |
| 28 | 3.37 (0.49) | 0.02 (0.47) | 0.28 (0.50) |
| 29 | 0.06 (1.67) | 0.02 (1.38) | 0.30 (1.44) |
| 30 | 0.16 (1.80) | 3.85 (2.28) | 10.81 (2.72) |

Table A2.
Nadaraya–Watson estimates (bootstrapped standard error). From maneuver number 31 to 60.
Table A2.
Nadaraya–Watson estimates (bootstrapped standard error). From maneuver number 31 to 60.
| Maneuver Number | RHC | IIC | SIC |
|---|---|---|---|
| 31 | 0.01 (0.50) | 0.82 (0.43) | 0.02 (0.47) |
| 32 | 5.81 (0.65) | 8.41 (0.24) | 3.63 (0.31) |
| 33 | 3.37 (1.86) | 9.55 (1.92) | 2.14 (2.03) |
| 34 | 0.54 (0.12) | 0.79 (0.10) | 0.91 (0.05) |
| 35 | 6.69 (0.61) | 12.14 (0.55) | 4.80 (0.50) |
| 36 | 5.20 (0.03) | 18.61 (0.06) | 4.50 (0.02) |
| 37 | 0.00 (0.13) | 0.81 (0.07) | 0.40 (0.03) |
| 38 | 1.47 (2.05) | 9.18 (2.28) | 0.15 (2.79) |
| 39 | 1.99 (1.18) | 2.31 (1.32) | 1.85 (2.01) |
| 40 | 9.04 (4.53) | 31.59 (6.18) | 14.21 (5.43) |
| 41 | 1.41 (0.34) | 0.17 (0.45) | 0.12 (0.49) |
| 42 | 0.81 (0.32) | 5.41 (0.16) | 0.51 (0.14) |
| 43 | 1.41 (0.38) | 0.45 (0.19) | 0.00 (0.10) |
| 44 | 0.60 (0.45) | 2.69 (0.15) | 2.09 (0.17) |
| 45 | 15.63 (2.20) | 7.84 (2.56) | 12.75 (2.69) |
| 46 | 3.20 (0.49) | 13.02 (0.16) | 9.23 (0.24) |
| 47 | 2.21 (1.70) | 2.78 (1.86) | 0.47 (1.42) |
| 48 | 0.00 (0.79) | 0.42 (0.69) | 0.22 (0.52) |
| 49 | 6.07 (0.47) | 1.82 (0.34) | 2.08 (0.38) |
| 50 | 0.98 (2.44) | 0.14 (1.66) | 0.54 (1.59) |
| 51 | 1.06 (0.56) | 11.19 (0.61) | 1.78 (0.54) |
| 52 | 0.21 (0.15) | 0.94 (0.06) | 0.00 (0.10) |
| 53 | 0.00 (1.85) | 1.93 (1.64) | 1.12 (1.68) |
| 54 | 0.00 (0.10) | 0.42 (0.17) | 0.00 (0.22) |
| 55 | 3.16 (0.25) | 3.50 (0.24) | 0.94 (0.28) |
| 56 | 4.30 (2.41) | 6.44 (2.17) | 9.45 (2.30) |
| 57 | 1.53 (2.88) | 3.18 (2.54) | 3.00 (2.45) |
| 58 | 4.19 (0.67) | 16.60 (0.34) | 16.40 (0.27) |
| 59 | 16.76 (1.07) | 13.56 (1.18) | 7.75 (0.95) |
| 60 | 0.83 (0.38) | 5.35 (0.17) | 1.66 (0.17) |
References
- Rupi, F.; Schweizer, J. Evaluating cyclist patterns using GPS data from smartphones. ITE Intell. Transp. Syst. 2018, 12, 279–285. [Google Scholar] [CrossRef]
- Broach, J.; Dill, J.; Gliebe, J. Where do cyclists ride? A route choice model developed with revealed preference GPS data. Transp. Res. Part A Policy Pract. 2012, 46, 1730–1740. [Google Scholar] [CrossRef]
- Ehrgott, M.; Wang, J.Y.; Raith, A.; van Houtte, C. A bi-objective cyclist route choice model. Transp. Res. Part A Policy Pract. 2012, 46, 652–663. [Google Scholar] [CrossRef]
- Dill, J. Bicycling for transportation and health: The role of infrastructure. J. Public Health Policy 2009, 30, S95–S110. [Google Scholar] [CrossRef]
- Rupi, F.; Poliziani, C.; Schweizer, J. Data-driven Bicycle Network Analysis Based on Traditional Counting Methods and GPS Traces from Smartphone. ISPRS Int. J. Geo-Inf. 2019, 8, 322. [Google Scholar] [CrossRef] [Green Version]
- Schweizer, J.; Rupi, F.; Poliziani, C. Estimation of link-cost function for cyclists based on stochastic optimisation and GPS traces. IET Intell. Transp. Syst. 2020, 14, 1810–1814. [Google Scholar] [CrossRef]
- Alonso, F.; Faus, M.; Cendales, B.; Useche, S. Citizens’ perceptions in relation to transport systems and infrastructures: Nationwide study in the Dominican Republic. Infrastructures 2021, 6, 153. [Google Scholar] [CrossRef]
- Willberg, E.; Tenkanen, H.; Poom, A.; Salonen, M.; Toivonen, T. Comparing spatial data sources for cycling studies: A review. In Transport in Human Scale Cities; Edward Elgar Publishing: Cheltenham, UK, 2021; pp. 169–187. [Google Scholar]
- Börjesson, M.; Eliasson, J. The value of time and external benefits in bicycle appraisal. Transp. Res. Part A Policy Pract. 2012, 46, 673–683. [Google Scholar] [CrossRef] [Green Version]
- Fioreze, T.; Groenewolt, B.; Koolwaaij, J.; Geurs, K. Perceived versus actual waiting time: A case study among cyclists in Enschede, The Netherlands. Transport Findings, 10 July 2019. [Google Scholar] [CrossRef]
- Rupi, F.; Poliziani, C.; Schweizer, J. Analysing the dynamic performances of a bicycle network with a temporal analysis of GPS traces. Case Stud. Transp. Policy 2020, 8, 770–777. [Google Scholar] [CrossRef]
- Strauss, J.; Miranda-Moreno, L.F. Speed, travel time and delay for intersections and road segments in the Montreal network using cyclist Smartphone GPS data. Transp. Res. Part D Transp. Environ. 2017, 57, 155–171. [Google Scholar] [CrossRef]
- Clarry, A.; Faghih Imani, A.; Miller, E.J. Where we ride faster? Examining cycling speed using smartphone GPS data. Sustain. Cities Soc. 2019, 49, 101594. [Google Scholar] [CrossRef]
- Laranjeiro, P.F.; Merchán, D.; Godoy, L.A.; Giannotti, M.; Yoshizaki, H.T.; Winkenbach, M.; Cunha, C.B. Using GPS data to explore speed patterns and temporal fluctuations in urban logistics: The case of Sao Paulo, Brazil. J. Transp. Geogr. 2019, 76, 114–129. [Google Scholar] [CrossRef]
- Cortés, C.E.; Gibson, J.; Gschwender, A.; Munizaga, M.; Zúñiga, M. Commercial bus speed diagnosis based on GPS-monitored data. Transp. Res. Part C Emerg. Technol. 2011, 19, 695–707. [Google Scholar] [CrossRef]
- Poliziani, C.; Rupi, F.; Schweizer, J. Traffic surveys and GPS traces to explore patterns in cyclist’s in-motion speeds. Transp. Res. Procedia 2021, 60, 410–417. [Google Scholar] [CrossRef]
- Poliziani, C.; Rupi, F.; Schweizer, J.; Saracco, M.; Capuano, D. Cyclist’s waiting time estimation at intersections, a case study with GPS traces from Bologna. Transp. Res. Procedia, 2021; in press. [Google Scholar]
- Poliziani, C.; Rupi, F.; Mbuga, F.; Schweizer, J.; Tortora, C. Categorizing three active cyclist typologies by exploring patterns on a multitude of GPS crowdsourced data attributes. Res. Transp. Bus. Manag. 2021, 40, 100572. [Google Scholar] [CrossRef]
- Tortora, C.; Franczak, B.C.; Browne, R.P.; McNicholas, P.D. A mixture of coalesced generalized hyperbolic distributions. J. Classif. 2019, 36, 26–57. [Google Scholar] [CrossRef] [Green Version]
- Betterpoints. Available online: https://www.betterpoints.ltd/ (accessed on 27 February 2022).
- Alonso, F.; Useche, S.; Faus, M.; Esteban, C. Does Urban Security Modulate Transportation Choices and Travel Behavior of Citizens? A National Study in the Dominican Republic. Front. Sustain. Cities 2020, 2, 42. [Google Scholar] [CrossRef]
- SUMOPy. Available online: https://sumo.dlr.de/docs/Contributed/SUMOPy.html (accessed on 27 February 2022).
- OSM. Available online: https://www.openstreetmap.org/#map=19/44.50163/11.34276 (accessed on 27 February 2022).
- Schweizer, J.; Bernardi, S.; Rupi, F. Map-matching algorithm applied to bicycle global positioning system traces in Bolognaa. ITE Intell. Transp. Syst. 2016, 10, 244–250. [Google Scholar] [CrossRef]
- Fraboni, F.; Marín Puchades, V.; De Angelis, M.; Pietrantoni, L.; Prati, G. Red-light running behavior of cyclists in Italy: An observational study. Accid. Anal. Prev. 2018, 120, 219–232. [Google Scholar] [CrossRef]
- Tengattini, S.; Bigazzi, A.; Rupi, F. Appearance and behaviour: Are cyclist physical attributes reflective of their preferences and habits? Travel Behav. Soc. 2018, 13, 36–43. [Google Scholar] [CrossRef]
- Rossi, R.; Mantuano, A.; Pascucci, F.; Rupi, F. Fitting time headway and speed distributions for bicycles on separate bicycle lanes. Transp. Res. Procedia 2017, 27, 19–26. [Google Scholar] [CrossRef]
- Highway Capacity Manual; Transportation Research Board: Washington, DC, USA, 2000.
- Schweizer, J.; Poliziani, C.; Rupi, F.; Morgano, D.; Magi, M. Building a Large-Scale Micro-Simulation Transport Scenario Using Big Data. ISPRS Int. J. Geo-Inf. 2021, 10, 165. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual ACM Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F.; Chang, C.C.; Lin, C.C.; Meyer, M.D. Package ‘e1071’. The R Journal version 1.7-3. 2019. Available online: https://rdrr.io/rforge/e1071/ (accessed on 27 February 2022).
- Nadaraya, E.A. On estimating regression. Theory Probab. Appl. 1964, 9, 141–142. [Google Scholar] [CrossRef]
- García-Portugués, E. Notes for Nonparametric Statistics, version 6.4.4; Bookdown, 2021; ISBN 978-84-09-29537-1. Available online: https://bookdown.org/egarpor/NP-UC3M/ (accessed on 27 February 2022).
- Hayfield, T.; Racine, J.S. Nonparametric Econometrics: The np Package. J. Stat. Softw. 2008, 27, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Aitchison, J.; Aitken, C.G. Multivariate binary discrimination by the kernel method. Biometrika 1976, 63, 413–420. [Google Scholar] [CrossRef]
- Li, Q.; Racine, J.S. Nonparametric Econometrics: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2007. [Google Scholar]
- Li, Q.; Racine, J. Cross-validated local linear nonparametric regression. Stat. Sin. 2004, 14, 485–512. [Google Scholar]
- Hardle, W.; Marron, J.S. Bootstrap simultaneous error bars for nonparametric regression. Ann. Stat. 1991, 19, 778–796. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).