Assignment of a Synthetic Population for Activity-Based Modeling Employing Publicly Available Data
Abstract
1. Introduction
1.1. Context and Motivation
1.2. Literature Review
1.3. Paper Structure
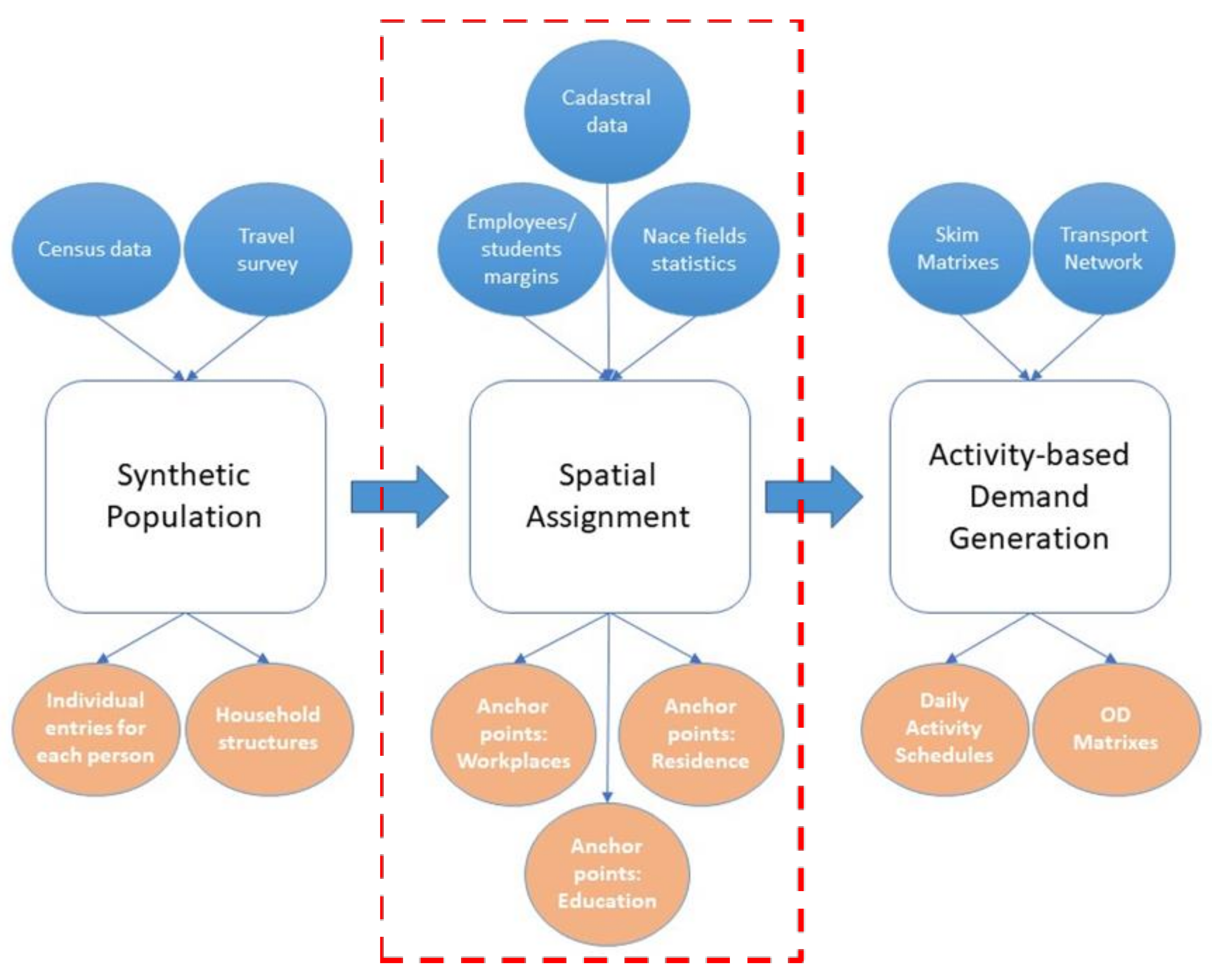
2. Materials and Methods
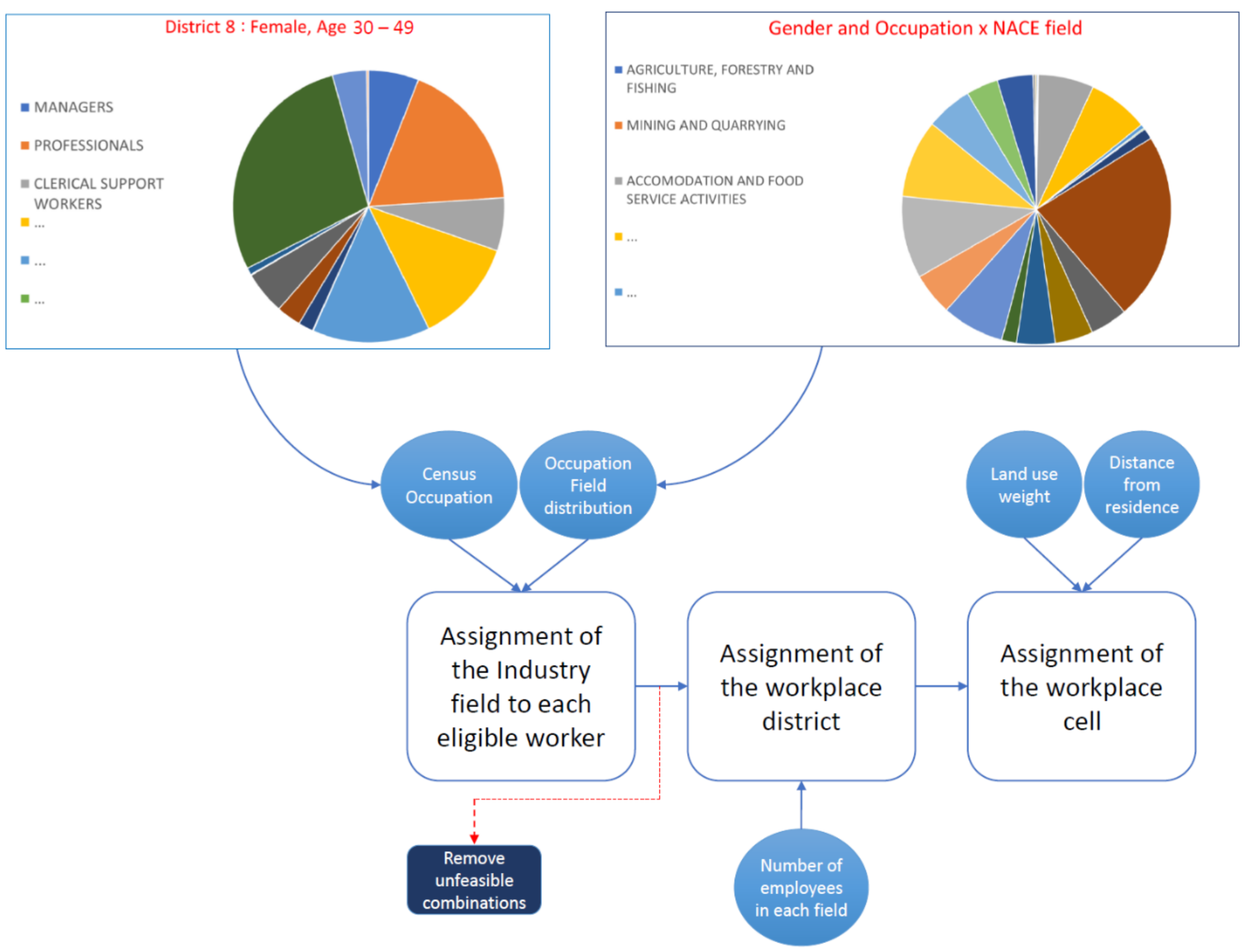
2.1. Assignment of NACE Fields to the Population
2.2. Subzone Assignment
| Algorithm 1 NACE assignment (individual, occupation distribution {A, G, DoR, S}, NACE distribution {G, O}) |
| 1: Loop: Individuali <- Population |
| 2: If ({Ai, Gi, DoRi, Si} == {A, G, DoR, S} and Occupation == NA |
| 3: Occupation<-sample(list of occupations, size = 1, list of probabilities1) |
| 4: NACE<-sample(list of NACE fields, size = 1, list of probabilities2) |
| 5: Else |
| 6: NACE assignment (Individual, occupation distribution {A*, G*, DoR*, S*}, |
| 7: NACE distribution {G*, O*} |
2.3. Last Mile Assignment
3. Spatial Assignment: The Case Study of Tallinn
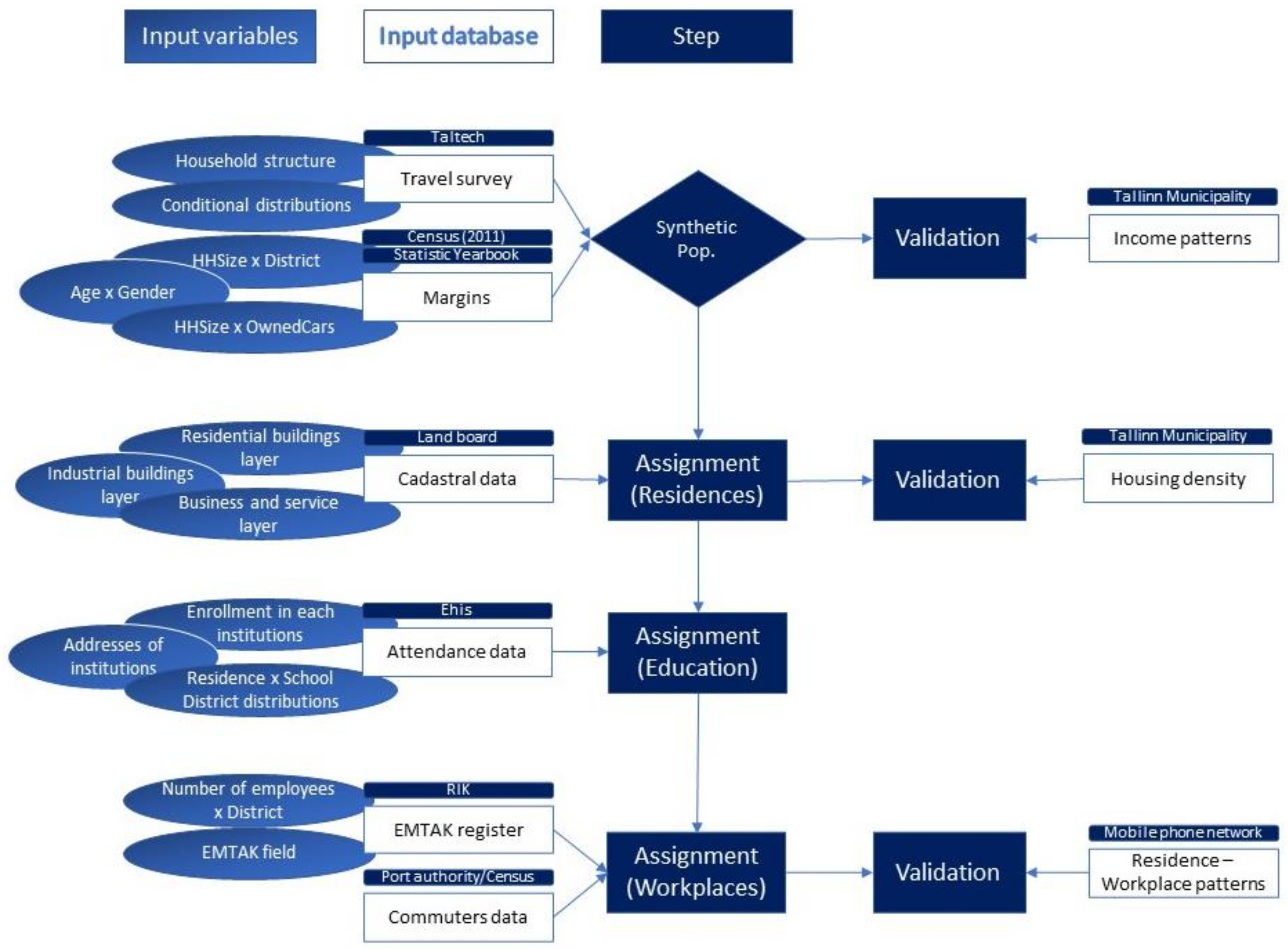
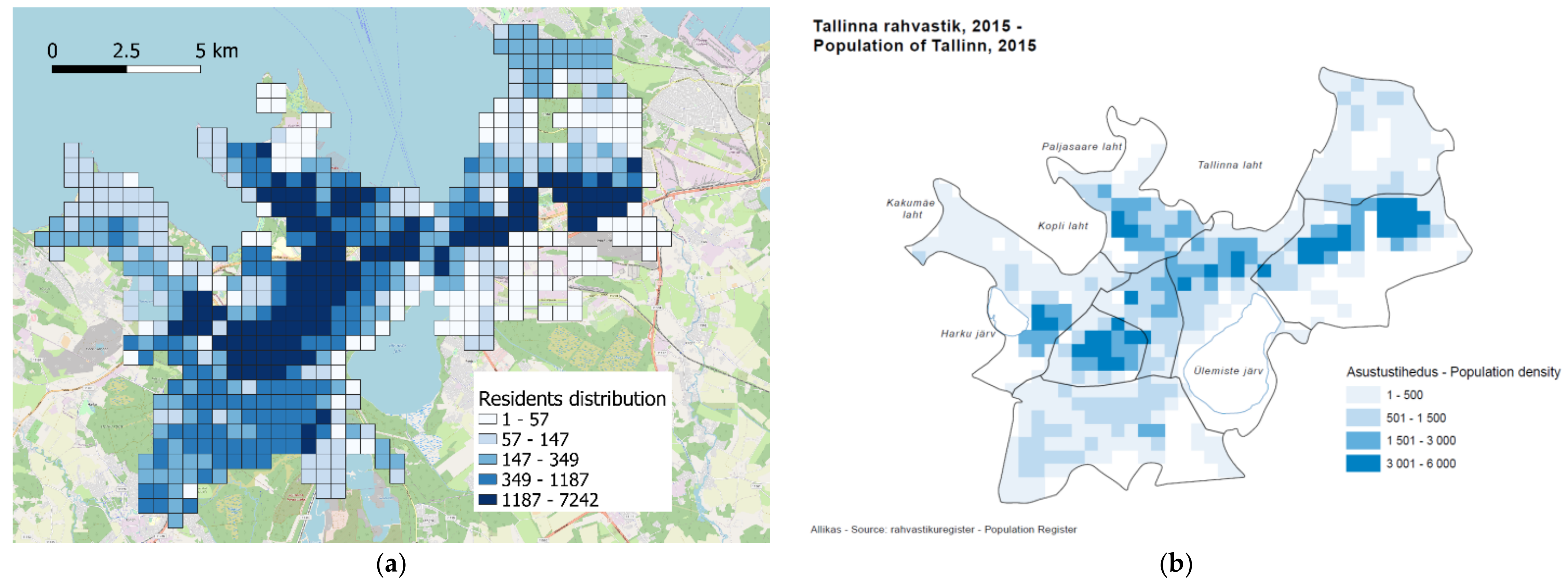
3.1. General Description and Data Availability
3.2. General Description and Data Availability
3.3. Spatial Assignment—Workplaces
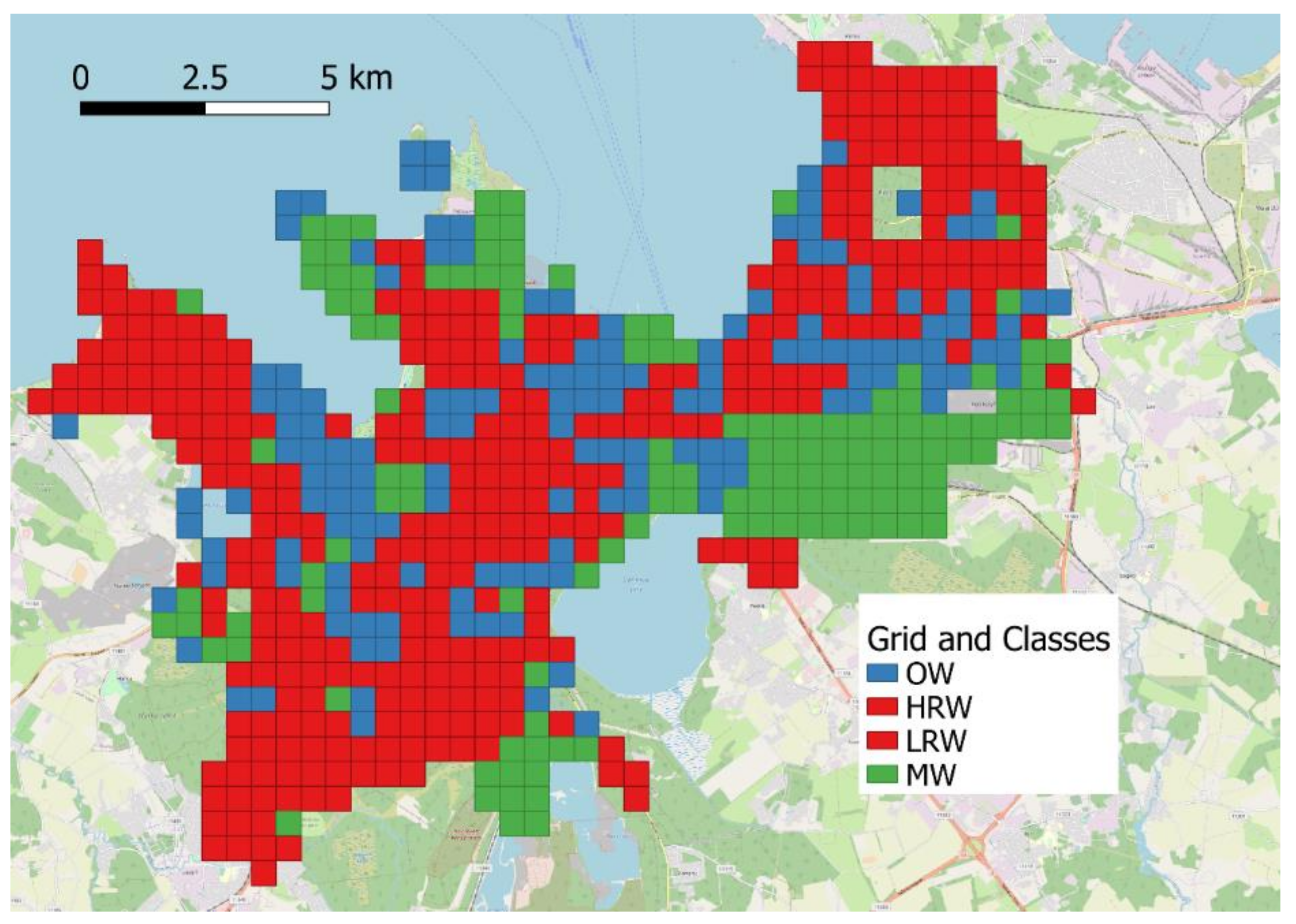
- First, weights based on the class of each cell are assigned, which allow also to calculate the total weight for all the cells in each district;
- Then, the ratio i between each cell weight and total of the weights in the district is calculated according to Equation (2).
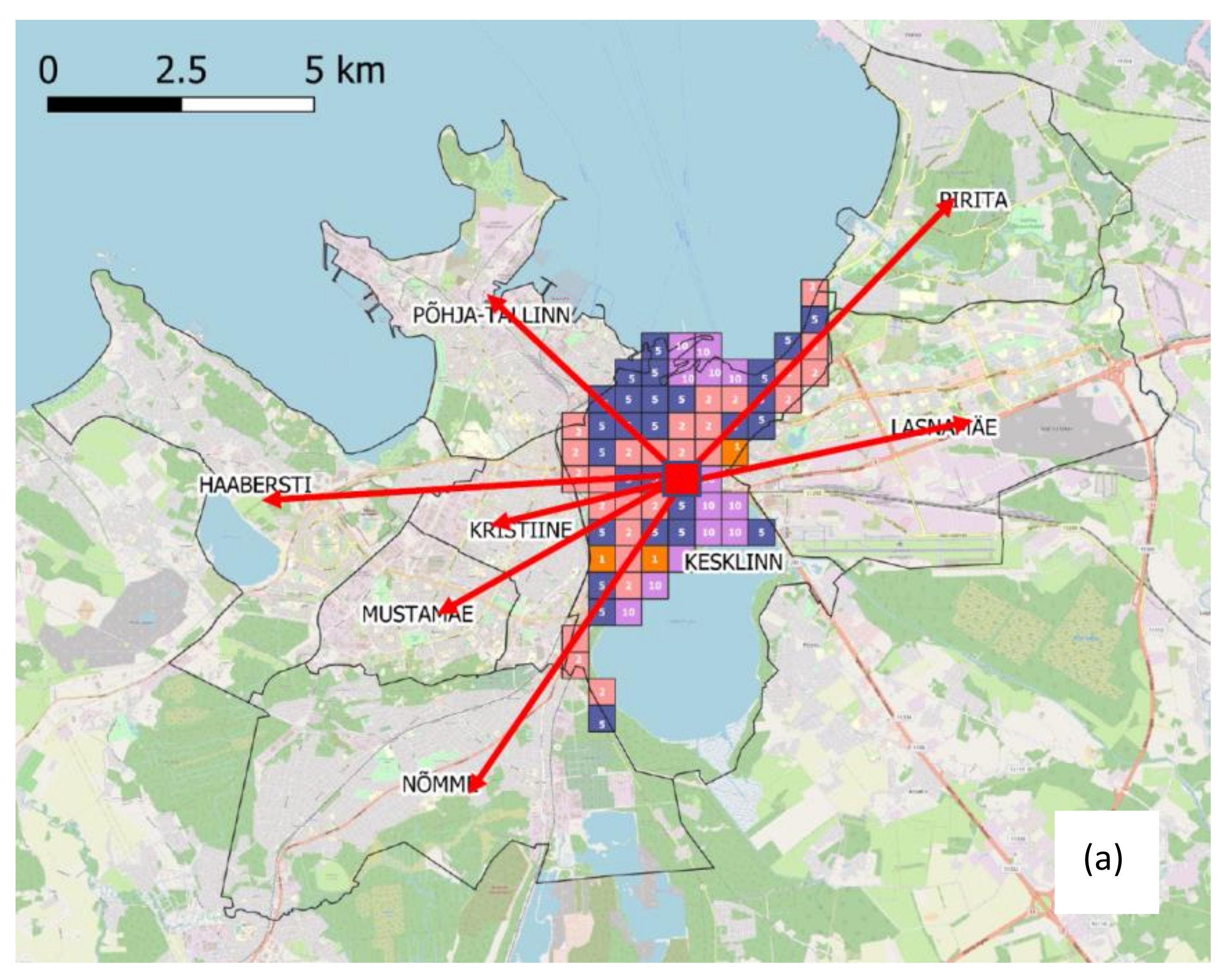
- The distance between each residence cell and each district, calculated as average between all the distances between the cell at hand and the ones included in the district, is computed (see an example in Figure 8a).
- For each cell pair (one being the residence, the other being the eligible workplace), the ratio between their distance and the average distance among the residence cell and all the other cells in the district is calculated.
- Each district has its own gravitational pull calculated based on the number of employees in the remaining fields (“others”). In this case, the probability of working in a district is calculated via Equation (4). Even if a certain noise is added to the total number of jobs in the “other” field, a spatial integrity is kept (distant districts have less chances of being chosen). Besides, it will be showed how the total number of “other” employees in each district remains quite consistent.
- The class of the workplace cell is calculated based on the cell classes distribution within the district via Equation (5).
- Once both the district and the class are assigned for the workplace, the final cell assignment is simply carried out through Equation (6); Figure 8b illustrates how the final cell assignment is carried out within each class.
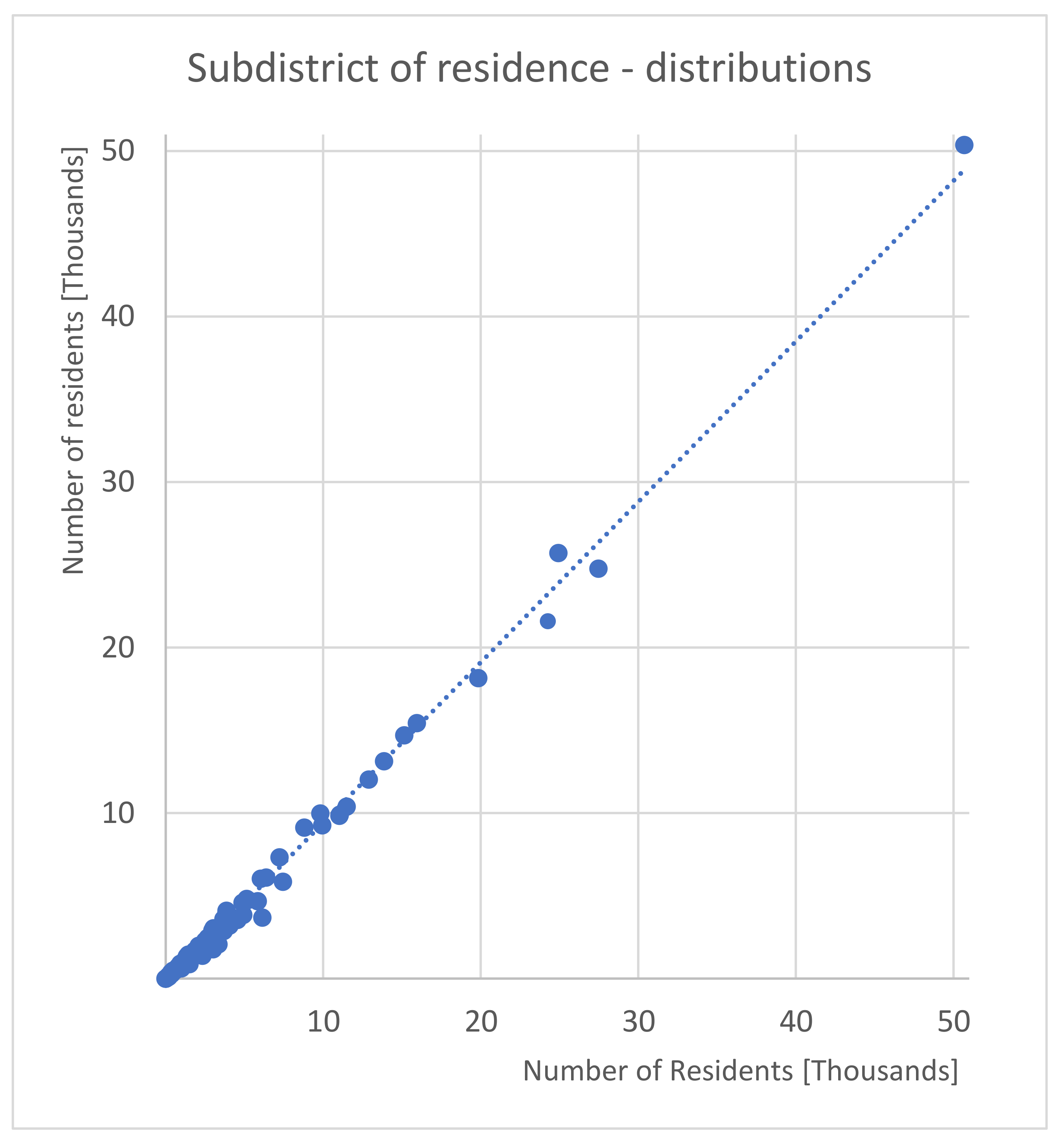
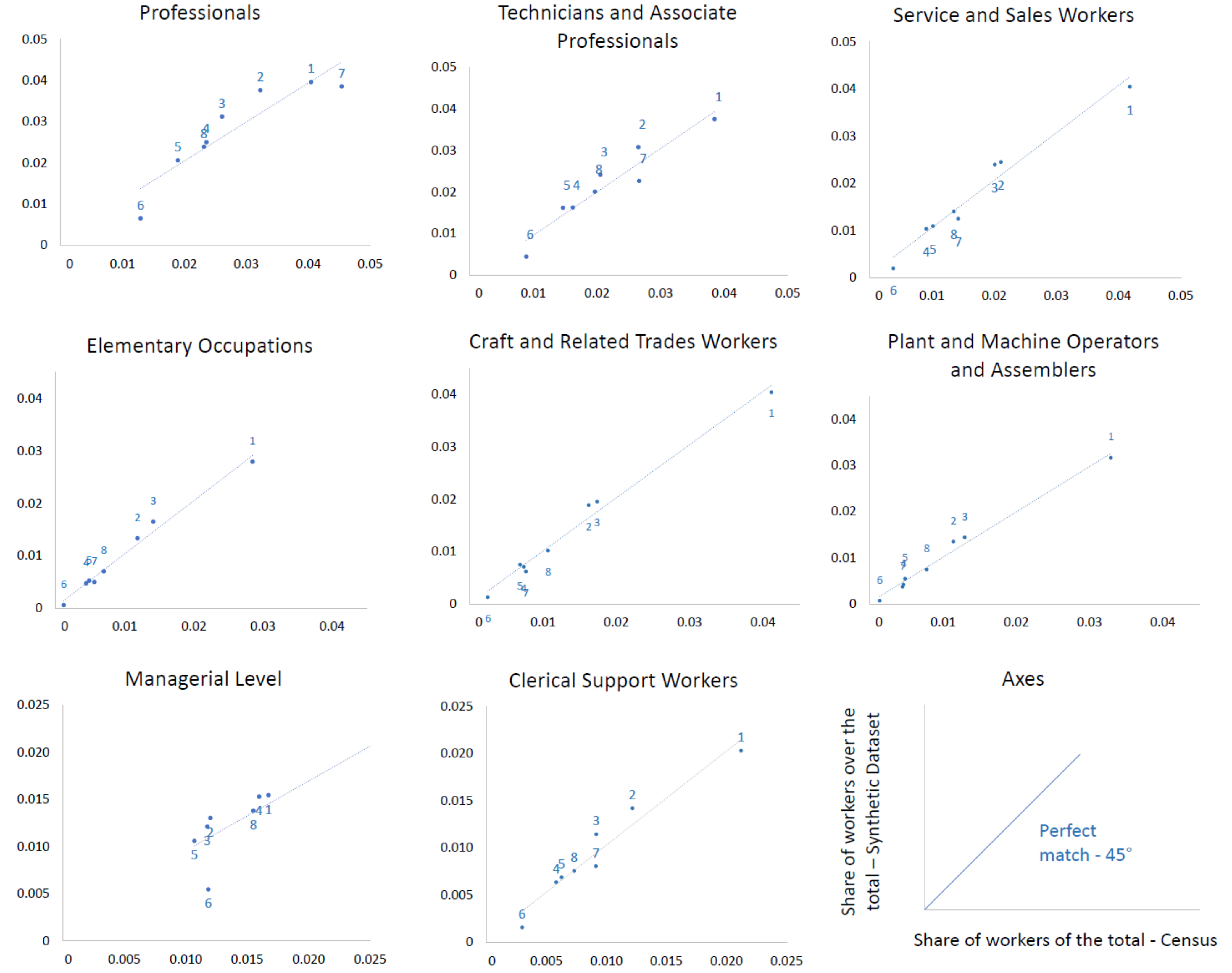
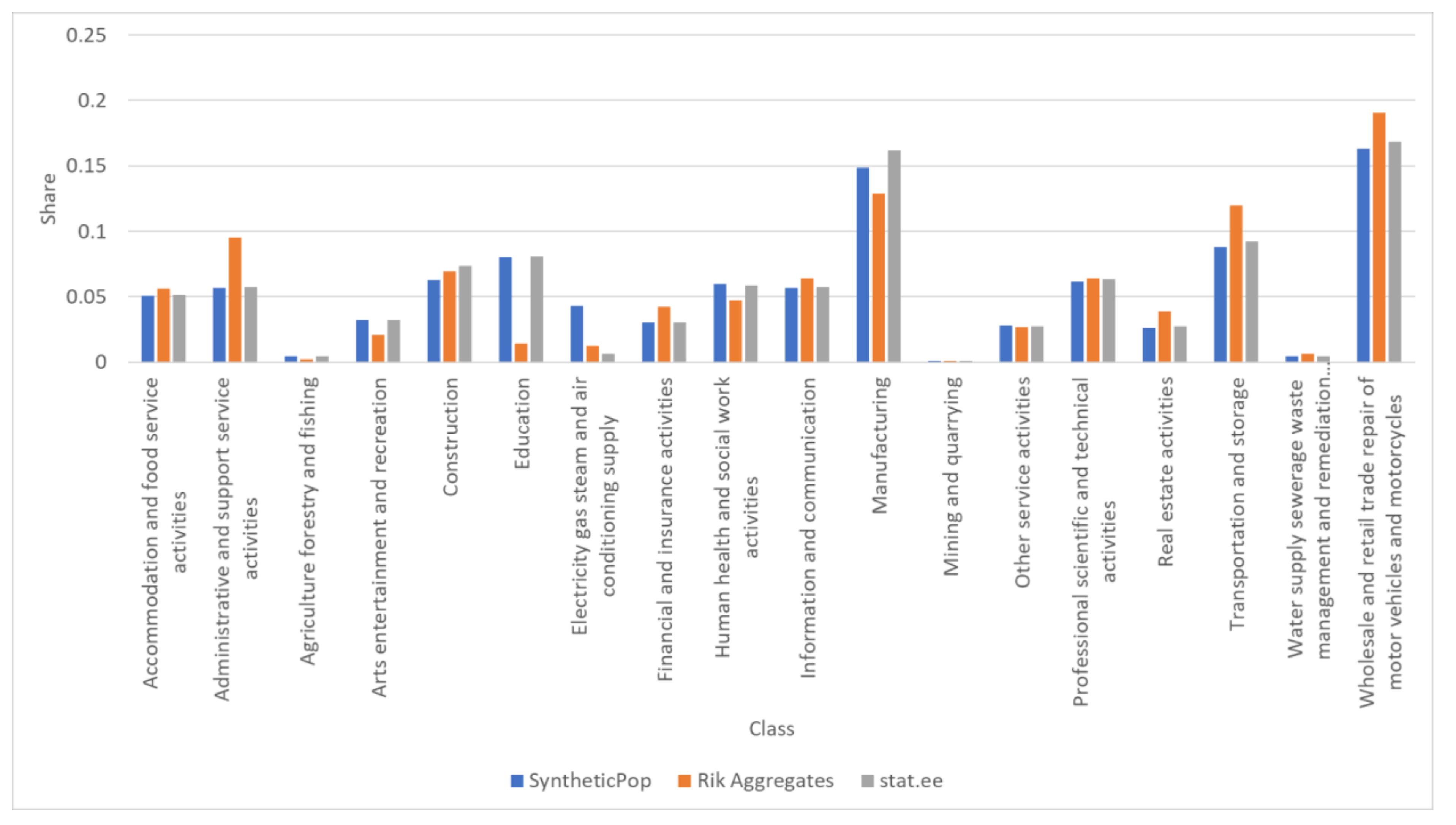
4. Results
- In this study, the weight of distance should be higher for workplaces in the immediate proximity of the habitation. This would reflect a nonlinear pattern in the relevance of distance. The distance would weigh more than the other factors (land use and EMTAK fields) for the cells in the immediate surroundings of the residence location.
- In [37], workplaces are identified as the most frequent cell-ID registered between 11:00 and 16:00 during working days. Cases in which these cell-IDs are the same as the residence ones are excluded. While this filtering probably captures most of homeworkers, retired people, and people with different work schedules (the approach is similar to other studies, such as [38]), it may fail in identifying some outliers (e.g., stay-at-home parents with a gym routine). This would result in an overestimation of the people working and residing in the same district.
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Data | Type of Data | Source | Usage | Public/Private |
| Household structure | Survey data | Survey from TalTech | Synthetic Population | Private |
| Age × gender distribution | Statistical margin | Statistical Yearbook of Tallinn | Synthetic Population | Public |
| Household size × district distribution | Statistical margin | Statistical Yearbook of Tallinn | Synthetic Population | Public |
| Population × subdistrict | Statistical margin | Statistical Yearbook of Tallinn | Synthetic Population | Public |
| Car Ownership × household size | Probability distribution | Survey from TalTech | Synthetic Population | Private |
| Income per family member × subdistrict | Distribution | Municipality of Tallinn | Validation | Upon request |
| Residential buildings × cell (m2) | Land Use | Tallinn Geoportal | Weight assignment | Public |
| Manufacturing and industrial buildings × cell (m2) | Land Use | Tallinn Geoportal | Weight assignment | Public |
| Service and office buildings × cell (m2) | Land Use | Tallinn Geoportal | Weight assignment | Public |
| Enrollment × educational building | Assignment | EHIS database (https://enda.ehis.ee/avalik/avalik/oppeasutus/OppeasutusOtsi.faces: database of educational institutions and enrollment statistics; accessed on 10 December 2020) | Spatial assignment | Public |
| Location of each educational building | Assignment | EHIS database | Spatial assignment | Public |
| Classification of each educational building | Assignment | EHIS database | Spatial assignment | Public |
| District of residence × enrollments in each district | Assignment | EHIS database | Spatial assignment | Upon request |
| Number of employees × district × EMTAK field | Assignment | RIK | Spatial assignment | Publicly available for a fee |
| Gender, age, and district of residence × occupation | Assignment | Census | Spatial assignment | Public |
| Occupation × EMTAK field | Assignment | Census | Spatial assignment | Public |
| Household structure | Survey data | Survey from TalTech | Synthetic population | Private |
| Age × gender distribution | Statistical margin | Statistical Yearbook of Tallinn | Synthetic population | Public |
| Household size × district distribution | Statistical margin | Statistical Yearbook of Tallinn | Synthetic population | Public |
References
- Schrank, D.; Eisele, B.; Lomax, T. 2019 Urban Mobility Report. Available online: https://mobility.tamu.edu/umr/report/#methodology (accessed on 23 July 2021).
- Brannigan, C.; Biedka, M.; Hitchcock, G. Study on Urban Mobility—Assessing and Improving the Accessibility of Urban Areas Final Report and Policy Proposals. Available online: https://ec.europa.eu/transport/themes/urban/news/2017-04-07-study-urban-mobility-%E2%80%93-assessing-and-improving-accessibility-urban_en (accessed on 23 July 2021).
- Lozzi, G.; Marcucci, E.; Gatta, V.; Rodrigues, M.; Teoh, T.; Ramos, C.; Jonkers, E. Sustainable and Smart Urban Transport. Policy Department for Structural and Cohesion Policies Directorate—General for Internal Policies PE. Available online: https://www.europarl.europa.eu/RegData/etudes/STUD/2020/652211/IPOL_STU(2020)652211_EN.pdf (accessed on 23 July 2021).
- United Nations Department of Economic and Social Affairs, Popular Division. The World’s Cities in 2018. Available online: https://digitallibrary.un.org/record/3799524 (accessed on 23 July 2021).
- Benevolo, C.; Dameri, R.P.; D’Auria, B. Smart mobility in smart city: Action taxonomy, ICT intensity and public benefits. In Empowering Organizations; Lecture Notes in Information Systems and Organisation; Springer: Cham, Switzerland, 2016; Volume 11. [Google Scholar]
- Kagho, G.O.; Balac, M.; Axhausen, K.W. Agent-Based Models in Transport Planning: Current State, Issues, and Expectations. Procedia Comput. Sci. 2020, 170, 726–732. [Google Scholar] [CrossRef]
- Nahmias-Biran, B.-H.; Oke, J.B.; Kumar, N.; Lima Azevedo, C.; Ben-Akiva, M. Evaluating the impacts of shared automated mobility on-demand services: An activity-based accessibility approach. Transportation 2020, 48, 1613–1638. [Google Scholar] [CrossRef]
- Moreno, A.T.; Moeckel, R. Population synthesis handling three geographical resolutions. ISPRS Int. J. Geo-Inf. 2018, 7, 174. [Google Scholar] [CrossRef]
- Hafezi, M.H.; Habib, M.A. Synthesizing population for microsimulation-based integrated transport models using atlantic canada micro-data. Procedia Comput. Sci. 2014, 37, 410–415. [Google Scholar] [CrossRef][Green Version]
- Templ, M.; Meindl, B.; Kowarik, A.; Dupriez, O. Simulation of synthetic complex data: The R package simPop. J. Stat. Softw. 2017, 79, 1–38. [Google Scholar] [CrossRef]
- Zhu, Y.; Ferreira, J. Synthetic population generation at disaggregated spatial scales for land use and transportation microsimulation. Transp. Res. Rec. 2014, 2429, 168–177. [Google Scholar] [CrossRef]
- Konduri, K.C.; You, D.; Garikapati, V.M.; Pendyala, R.M. Enhanced Synthetic Population Generator That Accommodates Control Variables at Multiple Geographic Resolutions. Transp. Res. Rec. 2016, 2563, 40–50. [Google Scholar] [CrossRef]
- Yaméogo, B.F.; Gastineau, P.; Hankach, P.; Vandanjon, P. Comparing Methods for Generating a Two-Layered Synthetic Population. Transp. Res. Rec. 2021, 2675, 136–147. [Google Scholar] [CrossRef]
- Lenormand, M.; Deffuant, G. Generating a synthetic population of individuals in households: Sample-free vs sample-based methods. J. Artif. Soc. Soc. Simul. 2013, 16, 12. [Google Scholar] [CrossRef]
- McBride, E.C.; Davis, A.W.; Lee, J.H.; Goulias, K.G. Incorporating land use into methods of synthetic population generation and of transfer of behavioral data. Transp. Res. Rec. 2017, 2668, 11–20. [Google Scholar] [CrossRef]
- Cajka, J.C.; Cooley, P.C.; Wheaton, W.D. Attribute Assignment to a Synthetic Population in Support of Agent-Based Disease Modeling. Methods Rep. RTI Press 2010, 19, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Le, D.T.; Cernicchiaro, G.; Zegras, C.; Ferreira, J. Constructing a Synthetic Population of Establishments for the Simmobility Microsimulation Platform. Transp. Res. Procedia 2016, 19, 81–93. [Google Scholar] [CrossRef]
- Erath, A.L.; Fourie, P.J.; Sun, L.; Vitins, B.J.; Atizaz, A.; van Eggermond, M.A.B.; Ordóñez Medina, S.A. MATSim Singapore Synthetic population and work locations. In Proceedings of the Urban Redevelopment Authority (URA) Planning Analytics Symposium, Singapore, 3 May 2016. [Google Scholar]
- Oke, J.; Akkinepally, A.; Chen, S.; Xie, Y.; Aboutaleb, Y.M.; Lima Azevedo, C.; Zegras, C.; Ferreira, J.; Ben-Akiva, M.; Shaheen, S.; et al. Evaluating the systemic effects of automated on-demand services via large-scale agent-based simulation of auto-dependent prototype cities. Transp. Res. Part A Policy Pract. 2020, 140, 98–126. [Google Scholar] [CrossRef]
- Ortúzar, J.; Willumsen, L.G. Trip Distribution Modelling. In Modeling Transport, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Gallagher, S.; Richardson, L.F.; Ventura, S.L.; Eddy, W. SPEW: Synthetic Populations and Ecosystems of the World. J. Comput. Graph. Stat. 2018, 27, 773–784. [Google Scholar] [CrossRef]
- Ge, Y.; Meng, R.; Cao, Z.; Qiu, X.; Huang, K. Virtual city: An individual-based digital environment for human mobility and interactive behavior. SIMULATION 2014, 90, 917–935. [Google Scholar] [CrossRef]
- Bodenmann, B.R.; Vecchi, I.; Sanchez, B.; Bode, J.; Zeiler, A.; Axhausen, K.W. Implementation of a Synthetic Population for Switzerland. IVT, ETH Zurich. 2017. Available online: https://www.research-collection.ethz.ch/handle/20.500.11850/104334 (accessed on 28 December 2021).
- Wang, L.; Waddell, P.; Outwater, M.L. Incremental Integration of Land Use and Activity-Based Travel Modeling: Workplace Choices and Travel Demand. Transp. Res. Rec. 2011, 2255, 1–10. [Google Scholar] [CrossRef]
- Fournier, N.; Christofa, E.; Akkinepally, A.P.; Azevedo, C.L. Integrated population synthesis and workplace assignment using an efficient optimization-based person-household matching method. Transportation 2021, 48, 1061–1087. [Google Scholar] [CrossRef]
- Balac, M.; Hörl, S. Synthetic population for the state of California based on open-data: Examples of San Francisco Bay area and San Diego County. In Proceedings of the Transportation Research Board 100th Annual Meeting, Washington, DC, USA, 21–29 January 2021. [Google Scholar]
- Wheaton, W.D.; Cajka, J.C.; Chasteen, B.M.; Wagener, D.K.; Cooley, P.C.; Ganapathi, L.; Roberts, D.J.; Allpress, J.L. Synthesized Population Databases: A US Geospatial Database for Agent-Based Models. Methods Rep. RTI Press 2009, 2009, 905. [Google Scholar]
- Wang, H.; Zeng, W.; Cao, R. Simulation of the Urban Jobs—Housing Location Selection and Spatial Relationship Using a Multi-Agent Approach. ISPRS Int. J. Geo-Inf. 2021, 10, 16. [Google Scholar] [CrossRef]
- Hörl, S.; Balac, M. Synthetic Population and travel demand for Paris and Île-de-France based on open and publicly available data. Transp. Res. Part C Emerg. Technol. 2021, 130, 103291. [Google Scholar] [CrossRef]
- Sallard, A.; Balać, M.; Hörl, S. A Synthetic Population for the Greater São Paulo Metropolitan Region.IVT, ETH Zurich. 2020. Available online: https://www.research-collection.ethz.ch/handle/20.500.11850/429951 (accessed on 28 December 2021).
- Ziemke, D.; Kaddoura, I.; Nagel, K. The MATSim open Berlin scenario: A multimodal agent-based transport simulation scenario based on synthetic demand modeling and open data. Procedia Comput. Sci. 2019, 151, 870–877. [Google Scholar] [CrossRef]
- McBride, E.C.; Davis, A.W.; Goulias, K.G. A Spatial Latent Profile Analysis to Classify Land Uses for Population Synthesis Methods in Travel Demand Forecasting. Transp. Res. Rec. 2018, 2672, 158–170. [Google Scholar] [CrossRef]
- Triinu, O. Liikumisviiside Uuring Elektrisõidukite ja Säästva Transpordi Kasutamise Arendamiseks, Tallinn, Estonia. 2015.
- Tallinn City Government Tallinn Arvudes 2015. Statistical Yearbook of Tallinn; Tallinn City Office: Tallinn, Estonia, 2015. [Google Scholar]
- Khachman, M.; Morency, C.; Ciari, F. Impact of the Geographic Resolution on Population Synthesis Quality. ISPRS Int. J. Geo-Inf. 2021, 10, 790. [Google Scholar] [CrossRef]
- Cavoli, C. CREATE—City Report Tallinn, Estonia. Available online: http://www.create-mobility.eu/create/resources/general/download/CITY-REPORT-Tallinn-WSWE-AV3MMA (accessed on 23 July 2021).
- Hadachi, A.; Pourmoradnasseri, M.; Khoshkhah, K. Unveiling large-scale commuting patterns based on mobile phone cellular network data. J. Transp. Geogr. 2020, 89, 102871. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, F.; Liao, S.; Zhou, F.; Cai, G.; Li, S. Portraying Citizens’ Occupations and Assessing Urban Occupation Mixture with Mobile Phone Data: A Novel Spatiotemporal Analytical Framework. ISPRS Int. J. Geo-Inf. 2021, 10, 392. [Google Scholar] [CrossRef]


| Comparison | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Type of data | Used data | PP | [11] | [15] | [16] | [17] | [18] | [22] | [23] | [24] | [25] | [26] | [27] | [29] | [31] |
| Building features | Dwelling type | X | |||||||||||||
| Average transaction price | X | ||||||||||||||
| Firms’ capacities | X | X | |||||||||||||
| Occupied floor area/size | X | X | X | ||||||||||||
| Establishments industry type | X | X | X | ||||||||||||
| Establishments location | X | X | X | X | |||||||||||
| Employment size | X | X | X | X | X | ||||||||||
| Origin–destination data | Workplace destination by industry | X | |||||||||||||
| Workplace origin totals by industry | X | ||||||||||||||
| Workplace origin–destination totals | X | ||||||||||||||
| PT smart card data | X | ||||||||||||||
| Commuting patterns | X | X | X | ||||||||||||
| Commuting OD matrix | X | X | |||||||||||||
| Travel survey (workplaces) | X | X | X | X | X | ||||||||||
| Commuting distance/travel time | X | X | |||||||||||||
| Land use data | Residence–workplace patterns across census tracts | X | X | ||||||||||||
| Cadastral areas | X | X | |||||||||||||
| Margins | NACE/NACS/EMTAK workers total per census tract | X | |||||||||||||
| Job type per education level distribution | X | X | |||||||||||||
| Workers total per census tract | X | ||||||||||||||
| Count of firms per census tract | X | X | |||||||||||||
| Utility function | X | ||||||||||||||
| Random assignment | X | X | X | ||||||||||||
| Synthetic Population | Mustamäe | Lasnamäe | Pohja- Tallinna | Kesklinna | Nomme | Haabersti | Kristiine | Pirita |
|---|---|---|---|---|---|---|---|---|
| Mustamäe | 0.21 | 0.08 | 0.07 | 0.20 | 0.10 | 0.11 | 0.17 | 0.05 |
| Lasnamäe | 0.07 | 0.27 | 0.06 | 0.26 | 0.08 | 0.10 | 0.10 | 0.06 |
| Pohja-Tallinna | 0.10 | 0.10 | 0.14 | 0.26 | 0.08 | 0.12 | 0.14 | 0.06 |
| Kesklinna | 0.08 | 0.11 | 0.09 | 0.34 | 0.08 | 0.09 | 0.14 | 0.06 |
| Nomme | 0.15 | 0.10 | 0.08 | 0.21 | 0.15 | 0.11 | 0.14 | 0.06 |
| Haabersti | 0.16 | 0.09 | 0.09 | 0.20 | 0.10 | 0.16 | 0.14 | 0.05 |
| Kristiine | 0.12 | 0.09 | 0.08 | 0.25 | 0.08 | 0.10 | 0.21 | 0.05 |
| Pirita | 0.07 | 0.22 | 0.08 | 0.25 | 0.08 | 0.10 | 0.11 | 0.08 |
| Results from [37] | Mustamäe | Lasnamäe | Pohja- Tallinna | Kesklinna | Nomme | Haabersti | Kristiine | Pirita |
| Mustamäe | 0.36 | 0.06 | 0.08 | 0.20 | 0.04 | 0.12 | 0.12 | 0.02 |
| Lasnamäe | 0.05 | 0.40 | 0.07 | 0.32 | 0.03 | 0.04 | 0.06 | 0.03 |
| Pohja-Tallinna | 0.05 | 0.08 | 0.33 | 0.28 | 0.03 | 0.08 | 0.12 | 0.02 |
| Kesklinna | 0.06 | 0.09 | 0.10 | 0.54 | 0.03 | 0.06 | 0.09 | 0.02 |
| Nomme | 0.11 | 0.07 | 0.07 | 0.32 | 0.26 | 0.07 | 0.10 | 0.01 |
| Haabersti | 0.16 | 0.07 | 0.08 | 0.20 | 0.04 | 0.35 | 0.10 | 0.01 |
| Kristiine | 0.13 | 0.06 | 0.10 | 0.29 | 0.05 | 0.09 | 0.28 | 0.01 |
| Pirita | 0.02 | 0.22 | 0.08 | 0.31 | 0.04 | 0.04 | 0.10 | 0.20 |
| Delta % | Mustamäe | Lasnamäe | Pohja-Tallinna | Kesklinna | Nomme | Haabersti | Kristiine | Pirita |
|---|---|---|---|---|---|---|---|---|
| Mustamäe | −0.15 | 0.02 | −0.01 | 0.00 | 0.06 | −0.01 | 0.05 | 0.03 |
| Lasnamäe | 0.03 | −0.13 | −0.01 | −0.06 | 0.05 | 0.06 | 0.04 | 0.03 |
| Pohja-Tallinna | 0.05 | 0.02 | −0.19 | −0.02 | 0.05 | 0.04 | 0.02 | 0.04 |
| Kesklinna | 0.02 | 0.02 | −0.01 | −0.20 | 0.05 | 0.03 | 0.05 | 0.04 |
| Nomme | 0.04 | 0.03 | 0.01 | −0.11 | −0.11 | 0.04 | 0.04 | 0.05 |
| Haabersti | 0.00 | 0.02 | 0.01 | 0.00 | 0.06 | −0.19 | 0.04 | 0.04 |
| Kristiine | −0.01 | 0.03 | −0.02 | −0.04 | 0.03 | 0.01 | −0.07 | 0.04 |
| Pirita | 0.05 | 0.00 | 0.00 | −0.06 | 0.04 | 0.06 | 0.01 | −0.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agriesti, S.; Roncoli, C.; Nahmias-Biran, B.-h. Assignment of a Synthetic Population for Activity-Based Modeling Employing Publicly Available Data. ISPRS Int. J. Geo-Inf. 2022, 11, 148. https://doi.org/10.3390/ijgi11020148
Agriesti S, Roncoli C, Nahmias-Biran B-h. Assignment of a Synthetic Population for Activity-Based Modeling Employing Publicly Available Data. ISPRS International Journal of Geo-Information. 2022; 11(2):148. https://doi.org/10.3390/ijgi11020148
Chicago/Turabian StyleAgriesti, Serio, Claudio Roncoli, and Bat-hen Nahmias-Biran. 2022. "Assignment of a Synthetic Population for Activity-Based Modeling Employing Publicly Available Data" ISPRS International Journal of Geo-Information 11, no. 2: 148. https://doi.org/10.3390/ijgi11020148
APA StyleAgriesti, S., Roncoli, C., & Nahmias-Biran, B.-h. (2022). Assignment of a Synthetic Population for Activity-Based Modeling Employing Publicly Available Data. ISPRS International Journal of Geo-Information, 11(2), 148. https://doi.org/10.3390/ijgi11020148






